Enhancing Power Converter Reliability Through a Logistic Regression-Based Non-Invasive Fault Diagnosis Technique
Abstract
1. Introduction
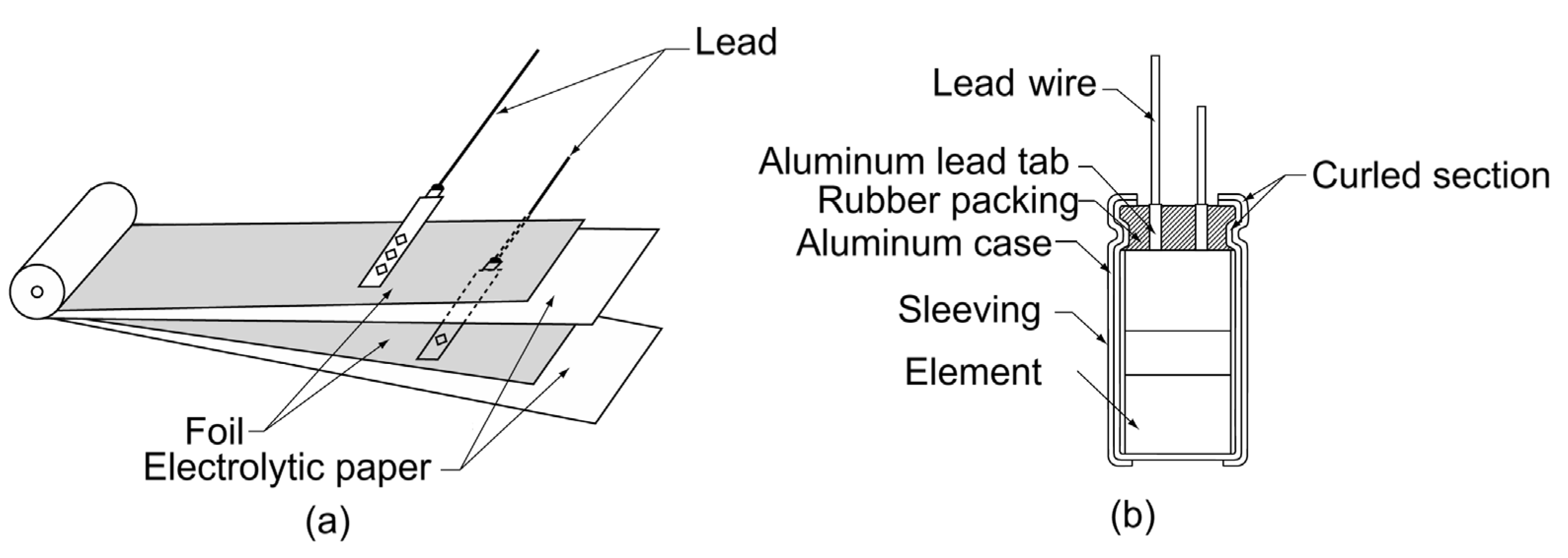
2. Aluminum Electrolytic Capacitors (Al-Caps)
3. Cutting-Edge Online Fault Diagnosis Techniques for Al-Caps
3.1. Signal-Based Online Fault Diagnosis Techniques (SB-ON-FDTs)
3.2. Model-Based Online Fault Diagnosis Techniques (MB-ON-FDTs)
3.3. Data-Based Online Fault Diagnosis Techniques (MB-ON-FDTs)
3.4. Comparing Online Fault Diagnosis Methods
4. Proposed Online Fault Diagnosis Technique for Al-Caps Using Traditional Machine Learning Algorithms
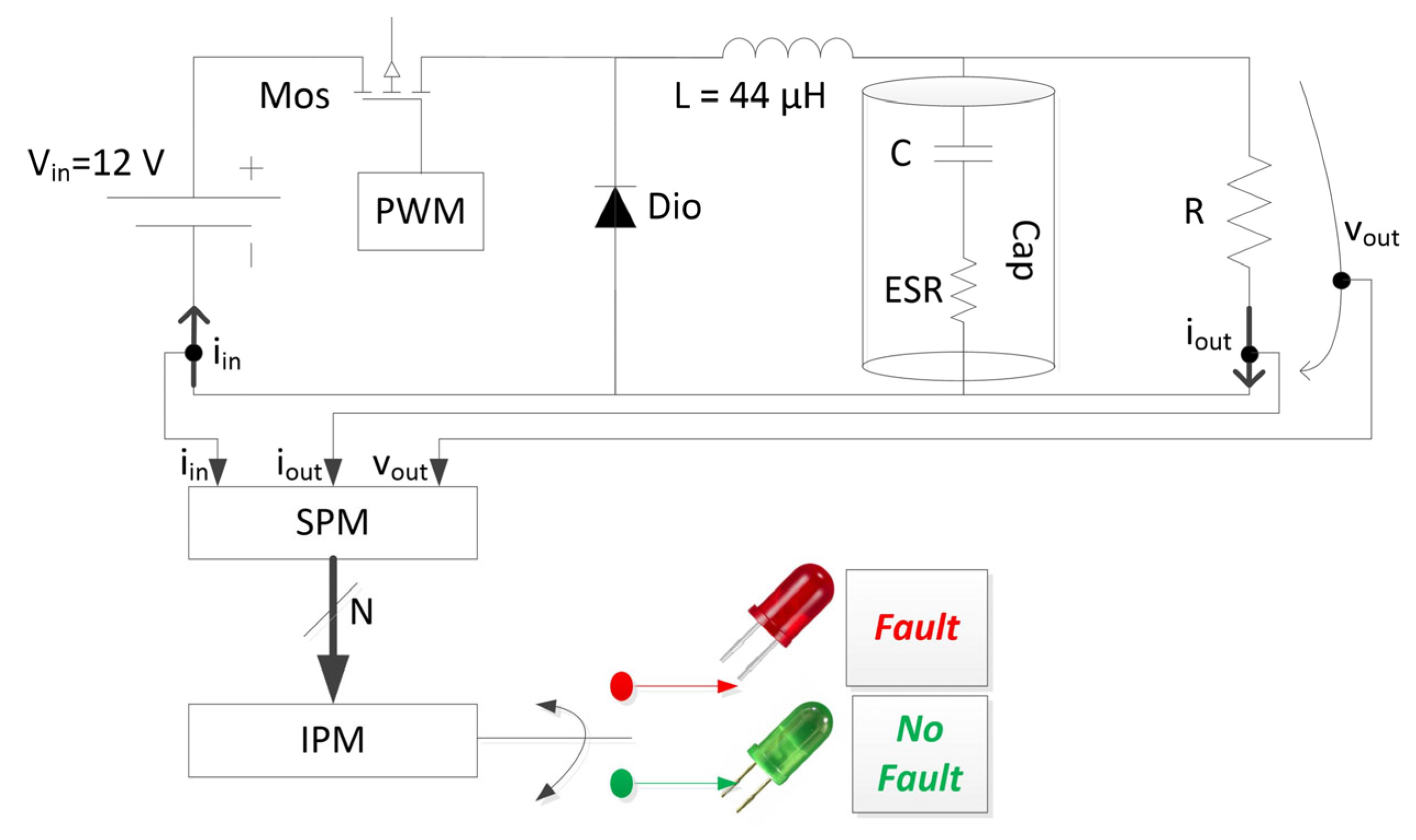
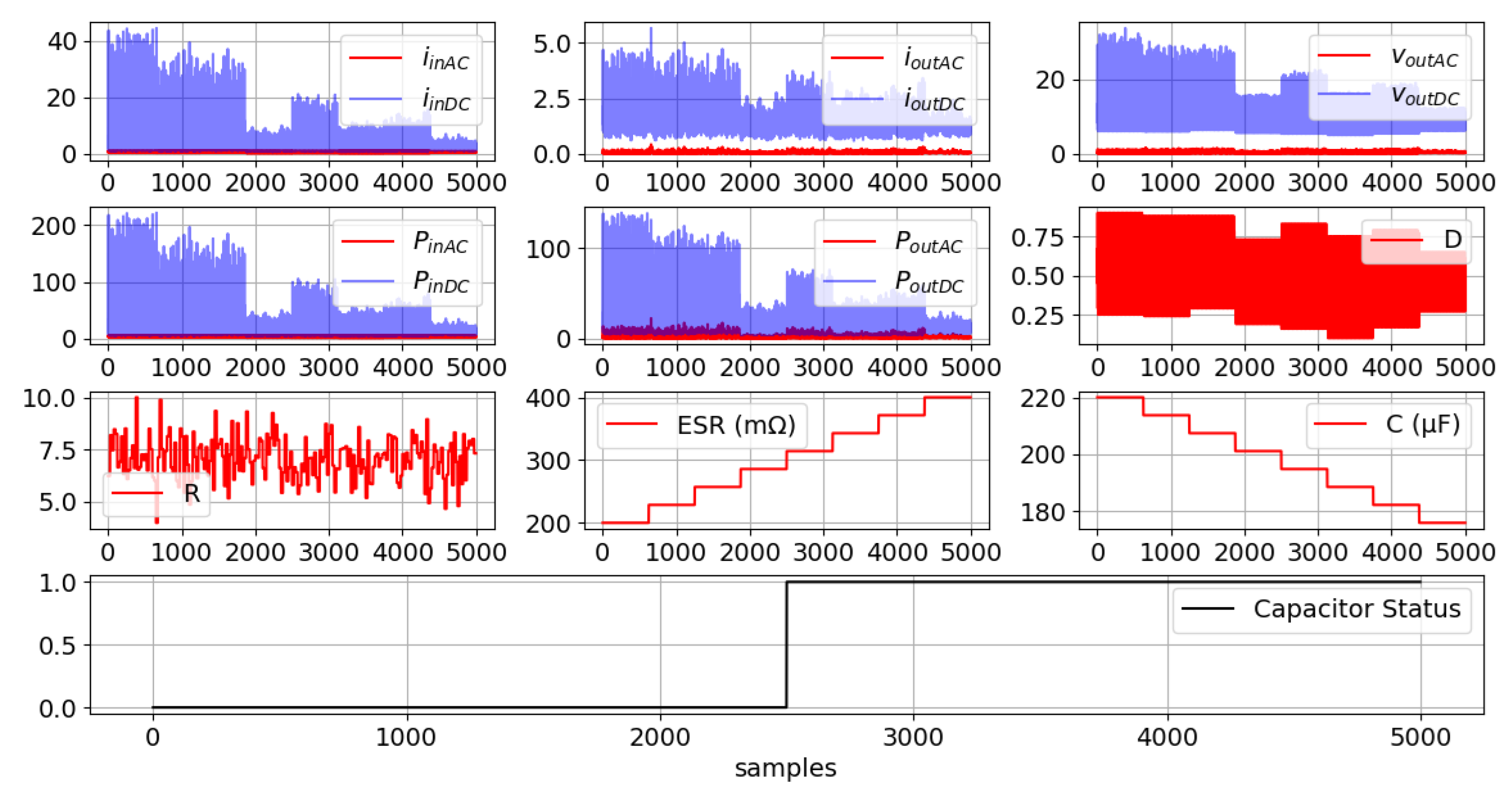
4.1. Buck Converter
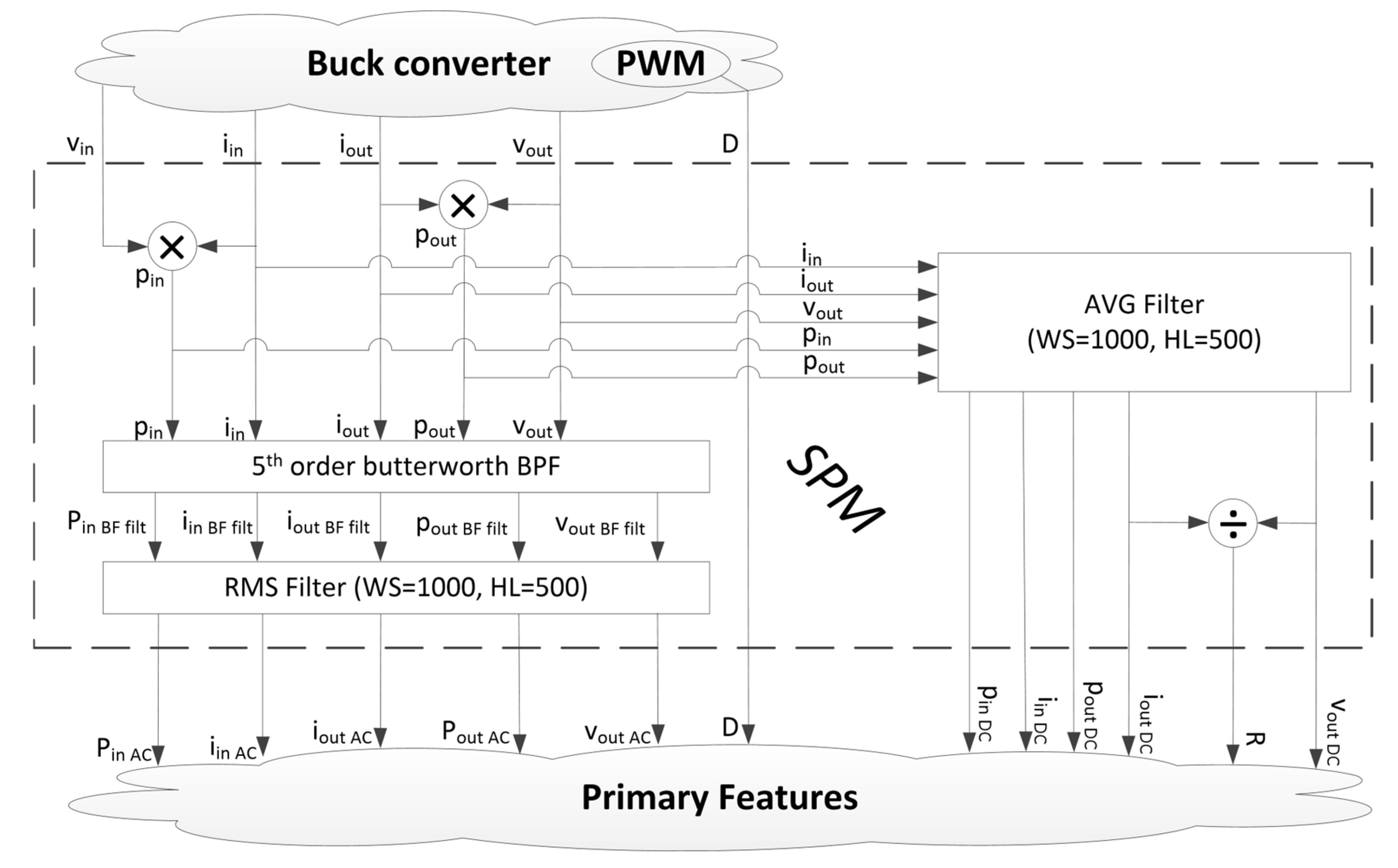
4.2. Signal Processing Module (SPM)
- PinAC—represents the AC component of pin;
- PinDC—represents the DC component of pin;
- PoutAC—represents the AC component of pout;
- PoutDC—represents the DC component of pout;
- iinAC—represents the AC component of iin;
- iinDC—represents the DC component of iin;
- ioutAC—represents the AC component of iout;
- ioutDC—represents the DC component of iout;
- voutAC—represents the AC component of vout;
- voutDC—represents the DC component of vout;
- R—represents the load resistance, calculated as voutDC divided by ioutDC;
- D—represents the duty cycle provided by the PWM.
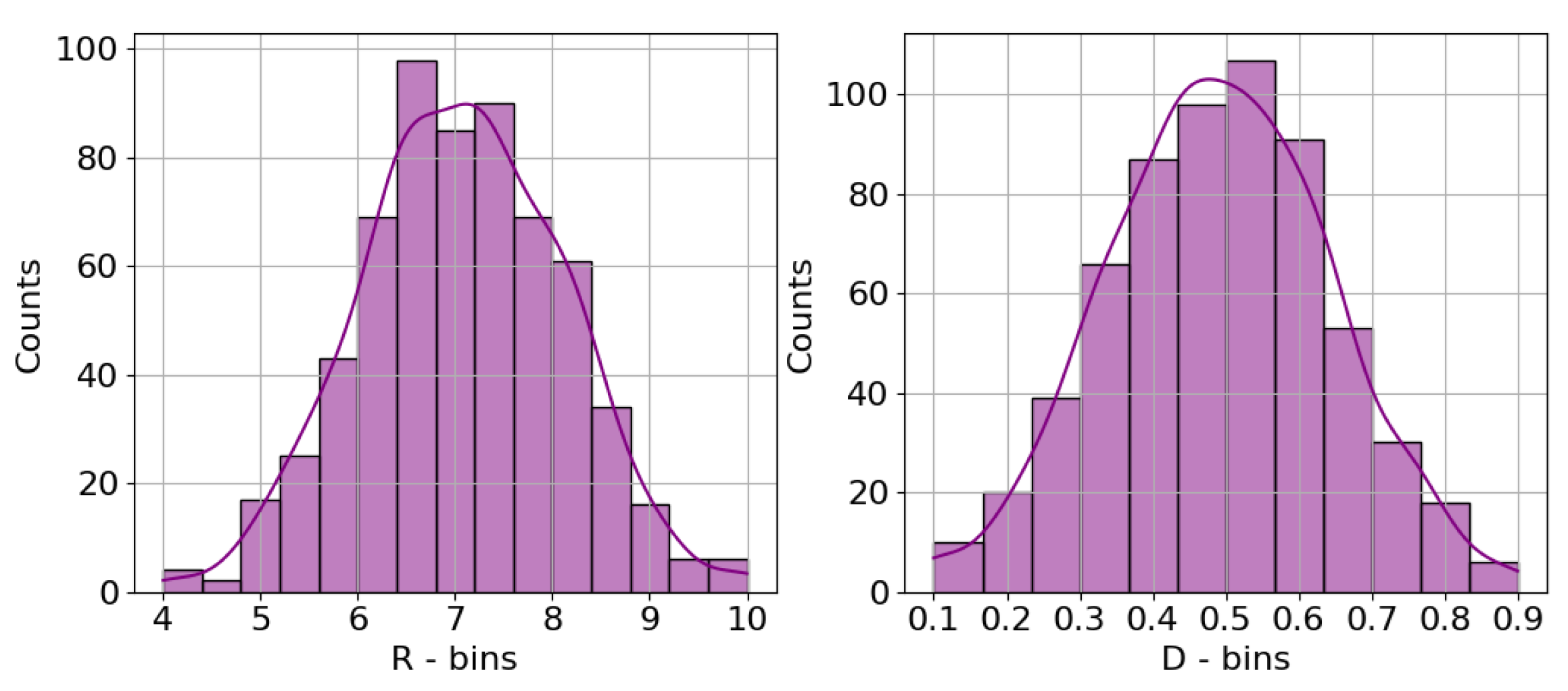
4.3. Dataset Generation Workflow
5. Information Processing Module (IPM) Design
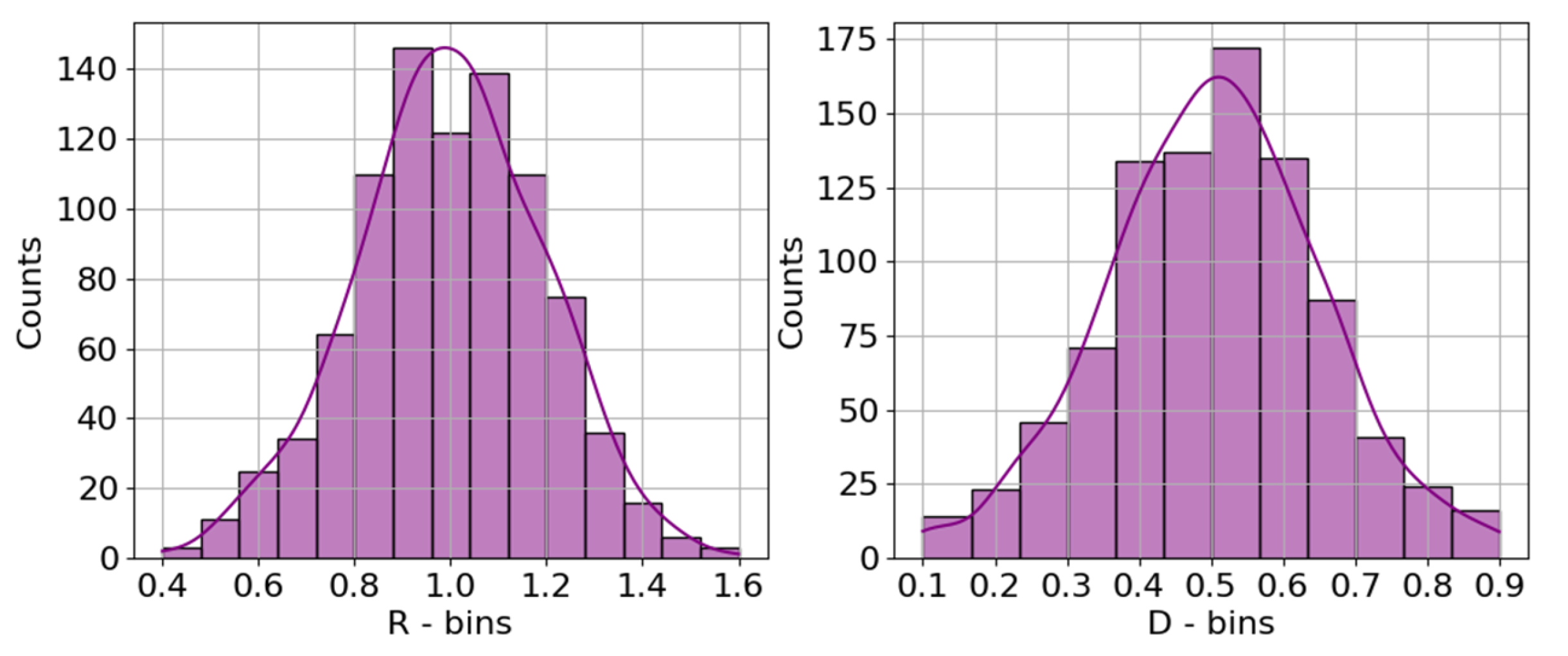
5.1. Exploratory Data Analysis (EDA)
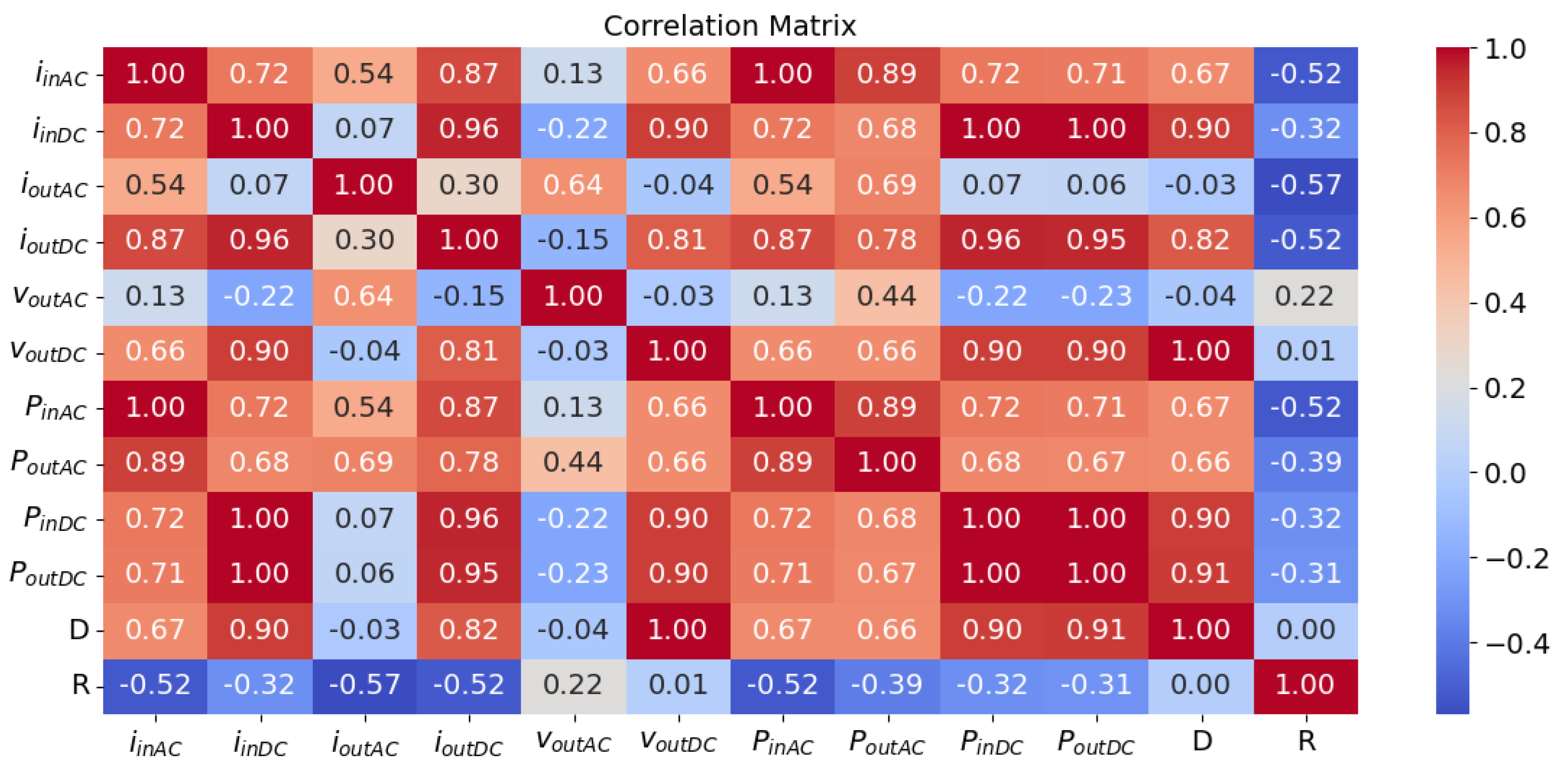
- The features iinAC and PinAC have been identified as redundant due to their high correlation (r ≥ 0.95);
- The features iinDC, ioutDC, PinDC, and PoutDC have been identified as redundant due to their high correlation (r ≥ 0.95);
- The features voutDC and D have been identified as redundant due to their high correlation (r ≥ 0.95);
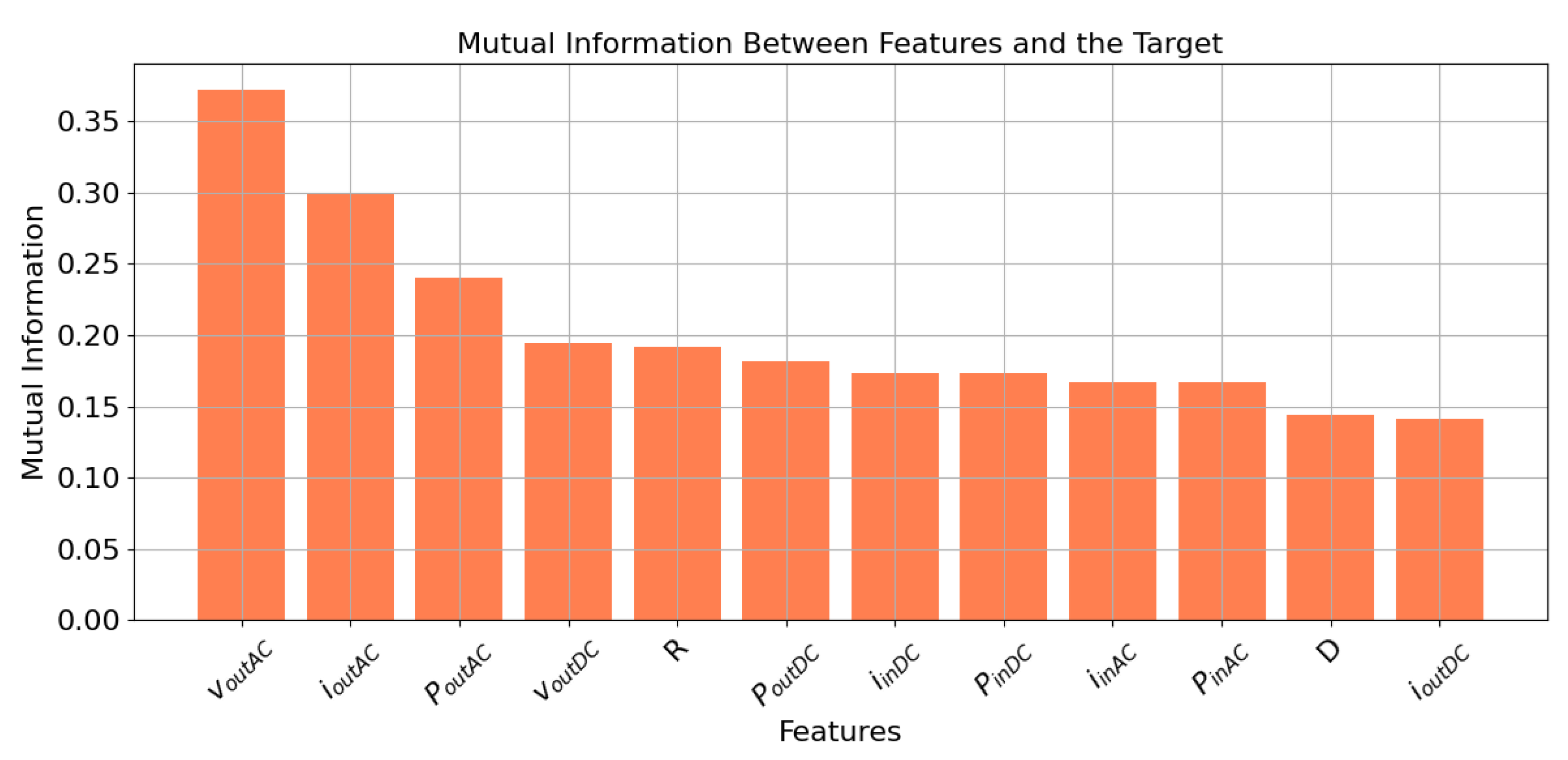
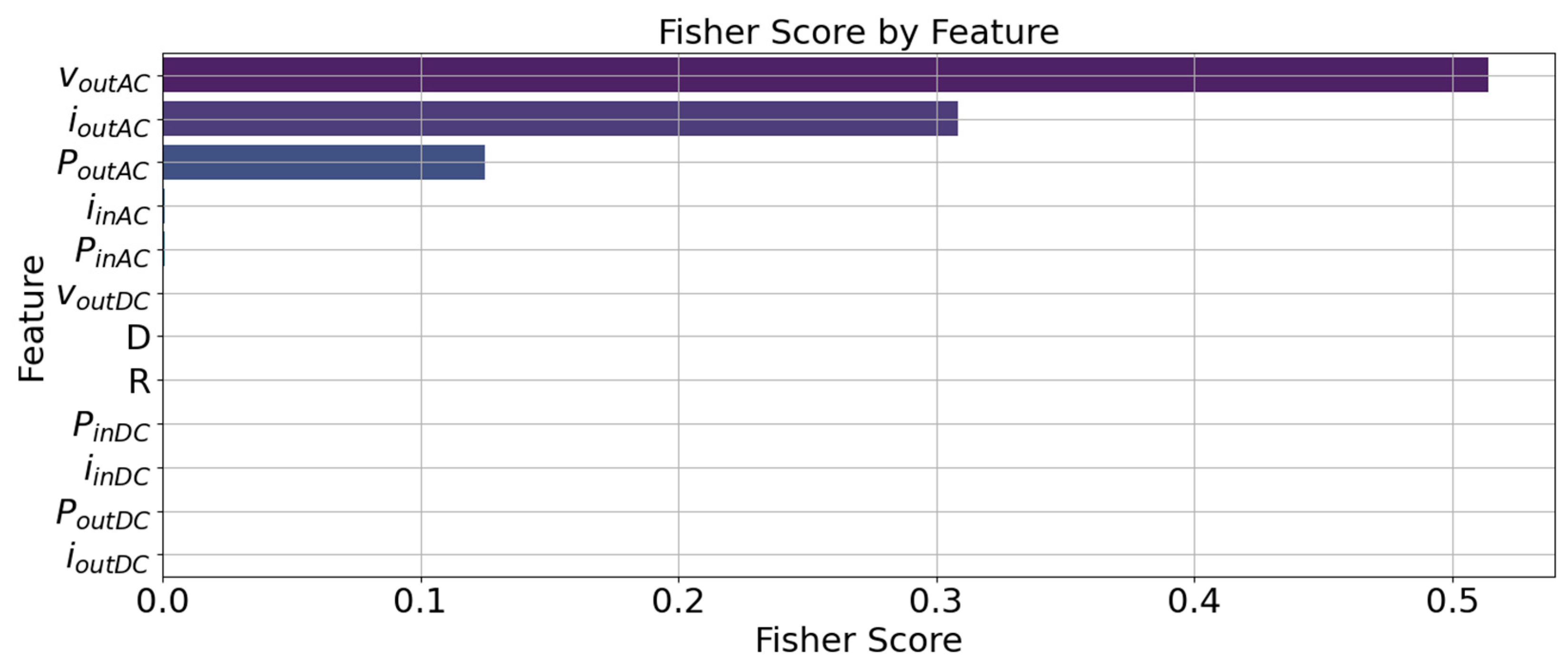
- From the feature set {iinDC, ioutDC, PinDC, and PoutDC}, only PinDC was retained due to having the highest FS value;
- From the feature set {PinAC, iinAC}, iinAC was retained based on its superior MI and FS values;
- From the feature set {voutDC, DC}, voutDC was chosen due to having the highest MI and FS values.
- ioutAC—represents the AC component of iout;
- voutAC—represents the AC component of vout;
- PoutAC—represents the AC component of pout;
- R—represents the load resistance;
- PinDC—represents the DC component of pin;
- iinAC—represents the AC component of iin;
- voutDC—represents the DC component of vout.
5.2. Logistic Regression (LR)
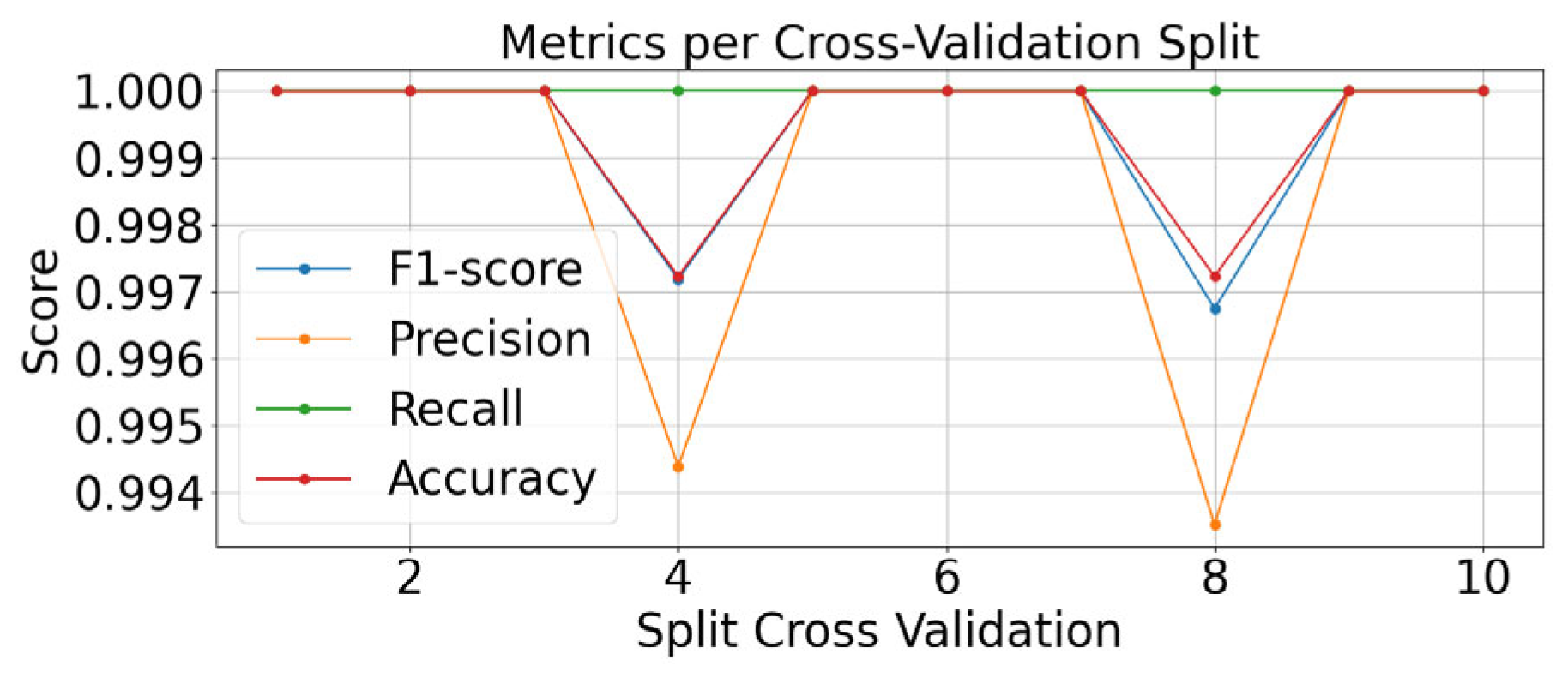
5.3. Cross Validation
- True positive (TP)—represents the number of correct predictions that identify the ”Fault” condition;
- False positive (FP)—represents the number of incorrect predictions that identify the ”Fault” condition;
- True negative (TN)—represents the number of correct predictions that identify the ”No Fault” condition;
- False negative (FN)—represents the number of incorrect predictions that identify the ”No Fault” condition.
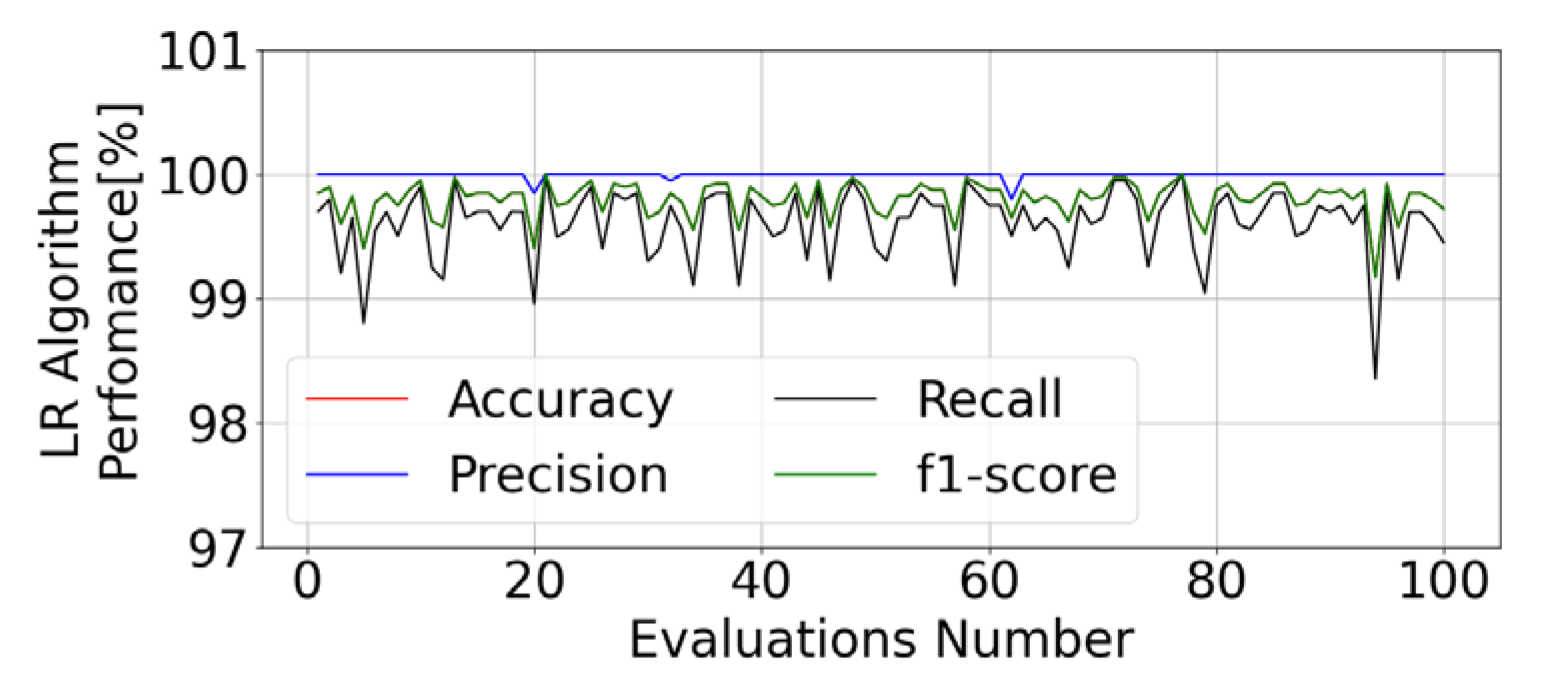
5.4. Model Training and Evaluation
6. Deployment Stage
6.1. FDT Assessment in a Buck Converter Under Progressive Al-Cap Deterioration
- Scenario 1—the electrical specifications of the converter include {vin = 12 V, L = 44 μH, D = 0.888 and R = 0.444 Ω;
- Scenario 2—the electrical specifications of the converter include {vin = 12 V, L = 44 μH, D = 0.444 and R = 0.888 Ω.
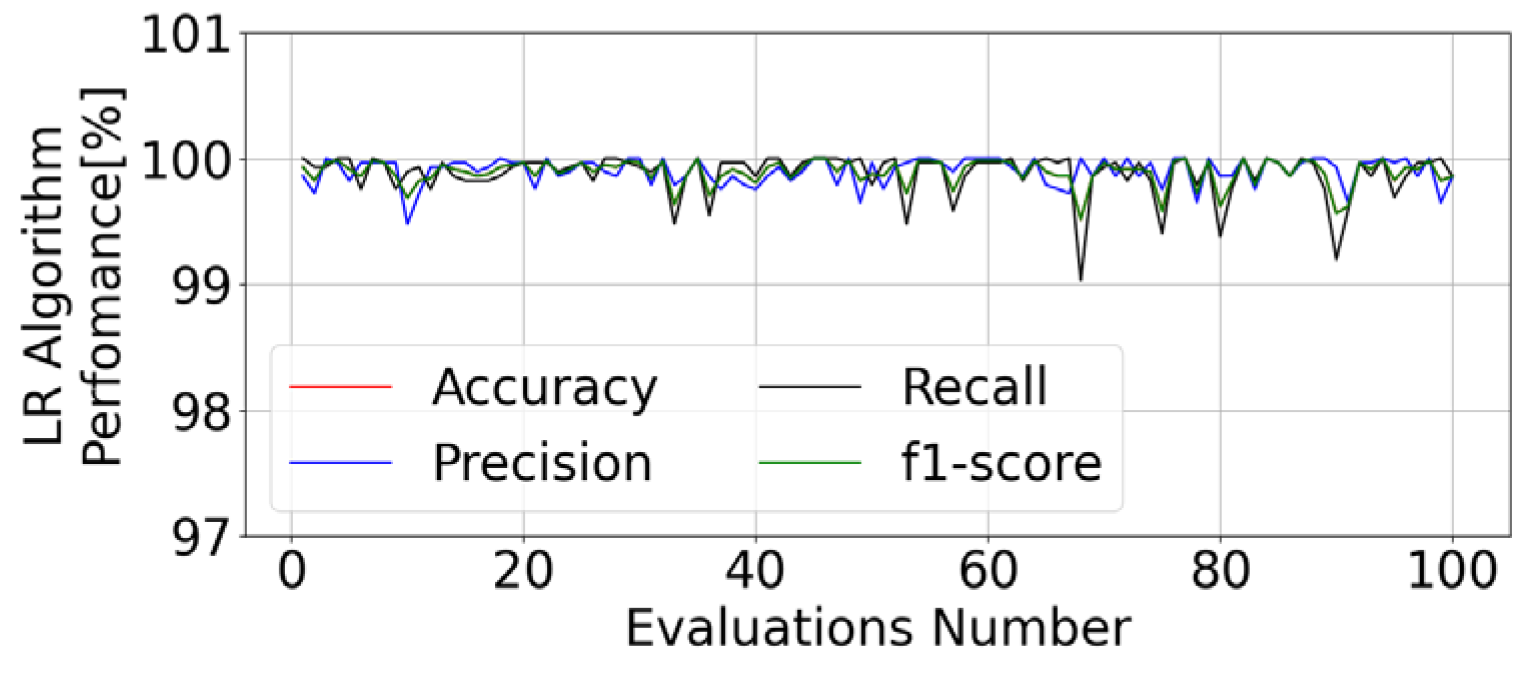
6.2. Robustness Analysis: Model Performance in Noisy Environments
7. Scalability of the Proposed Solution
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3ϕIBC | Three-Phase Interleaved Boost Converter |
| AC | Alternate Current |
| Al-Caps | Aluminum Electrolytic Capacitor |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| ASD | Adjustable Speed Drive |
| BDF | Bandpass Filter |
| BTB | Back-to-Back |
| C | Capacitance |
| CCM | Continuous Conduction Mode |
| CF | Crest Factor |
| CWT | Continuous Wavelet Transform |
| DB | Data Based |
| DC | Direct Current |
| DCM | Discontinuous Conduction Mode |
| DFT | Discrete Fourier Transform |
| DL | Deep Learning |
| DWT | Discrete Wavelet Transform |
| EDA | Exploratory Data Analysis |
| EE | Energy Entropy |
| EMD | Empirical Mode Decomposition |
| EMI | Electromagnetic Interference |
| ESR | Equivalent Series Resistance |
| EV | Electrical Vehicles |
| FS | Fisher Score |
| HCNN | Hybrid Convolutional Neural Network |
| HHT | Hilbert–Huang Transform |
| HS | Hope size |
| IMDs | Implantable Medical Devices |
| IoT | Internet of Things |
| IPM | Information Processing Module |
| KNN | K-Nearest Neighbors |
| LDB | Linear Decision Boundary |
| LinR | Linear Regression |
| LR | Logistic Regression |
| MB | Model Based |
| MI | Mutual Information |
| ML | Machine Learning |
| NB | Naive Bayes |
| NLDB | Non-linear Decision Boundary |
| OFF-FDTs | Offline Fault Diagnosis Techniques |
| ON-FDTs | Online Fault Diagnosis Techniques |
| PCs | Power Converters |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| PWM | Pulse-Width Modulation |
| QON-FDTs | Quasi-Online Fault Diagnosis Techniques |
| RFC | Random Forest Classifier |
| RLMS | Recursive Least Mean Squares |
| RMS | Root mean Square |
| SB | Signal Based |
| SNR | Signal–to-Noise Ratio |
| SPT | Signal Processing Techniques |
| STD | Standard Deviation |
| STLSP | Short-Time Least Squares Prony |
| SVM | Support Vector Machine |
| TML | Traditional Machine Learning |
| TrainDS | Training Dataset |
| UPS | Uninterrupted Power Supply |
| WPT | Wireless Power Transfer |
| WS | Window Size |
| WTD | Wavelet Transform Denoising |
References
- Eurostat. Energy Statistics—An Overview. 2024. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Energy_statistics_-_an_overview (accessed on 2 May 2025).
- Electricity 2024-Analysis and Forecast to 2026; IEA Publications: Paris, France, 2024.
- Scolaro, E.; Beligoj, M.; Estevez, M.; Alberti, L.; Mattetti, M.R.E.M. Electrification of Agricultural Machinery: A Review. IEEE Access 2021, 9, 164520–164541. [Google Scholar] [CrossRef]
- Ahmed, B.; Shabbir, H.; Naqvi, S.R.; Peng, L. Smart Agriculture: Current State, Opportunities, and Challenges. IEEE Access 2024, 12, 144456–144478. [Google Scholar] [CrossRef]
- Meng, L.; Hirayama, T.; Oyanagi, S. Underwater-Drone with Panoramic Camera for Automatic Fish Recognition Based on Deep Learning. IEEE Access 2018, 6, 17880–17886. [Google Scholar] [CrossRef]
- Industrial Electrification. International Institute for Sustainable Development. 2022. Available online: https://www.iisd.org/system/files/2022-05/industrial-electrification-en.pdf (accessed on 2 May 2025).
- Borgosano, S.; Martini, D.; Longo, M.; Foiadelli, F. Electrifying Urban Transportation: A Comparative Study of Battery Swap Stations and Charging Infrastructure for Taxis in Chicago. IEEE Access 2024, 12, 48017–48026. [Google Scholar] [CrossRef]
- Silva, C.; Peres, L. Introducing Electric Bus Fleets in Rio de Janeiro City Methodology and Analysis. IEEE Lat. Am. Trans. 2022, 20, 2087–2095. [Google Scholar] [CrossRef]
- Yang, G.; Ye, Z.; Wu, H.; Li, C.; Wang, R.; Hou, D.; Huang, H.W.X.; Pang, Z.; Dong, N.; Pang, G. A Digital Twin-Based Large-Area Robot Skin System for Safer Human-Centered Healthcare Robots Toward Healthcare 4.0. IEEE Trans. Med. Robot. Bionics 2024, 6, 1104–1115. [Google Scholar] [CrossRef]
- Ma, B.; Kuo, Y.; Jiang, Y.; Huang, G. RubikCell: Toward Robotic Cellular Warehousing Systems for E-Commerce Logistics. IEEE Trans. Eng. Manag. 2024, 71, 9270–9285. [Google Scholar] [CrossRef]
- Costa, L.; Liserre, M. Failure Analysis of the dc-dc Converter: A Comprehensive Survey of Faults and Solutions for Improving Reliability. IEEE Power Electron. Mag. 2018, 5, 42–51. [Google Scholar] [CrossRef]
- Azrul, M.H.S.E.M.; Mashohor, S.; Amran, M.E.; Hafiz, N.F.; Ali, A.M.; Naseri, M.S.; Rasid, M.F.A. Assessment of IoT-Driven Predictive Maintenance Strategies for Computed Tomography Equipment: A Machine Learning Approach. IEEE Access 2024, 12, 195505–195515. [Google Scholar]
- SRahimpour; Husev, O.; Vinnikov, D.; Kurdkandi, N.V.; Tarzamni, H. Fault Management Techniques to Enhance the Reliability of Power Electronic Converters: An Overview. IEEE Access 2023, 11, 13432–13446. [Google Scholar] [CrossRef]
- Cardoso, A.J.M. Diagnosis and Fault Tolerance of Electrical Machines, Power Electronics and Drives; The Institution of Engineering and Technology: Stevenage, UK, 2018. [Google Scholar]
- Amaral, A.M.R.; Cardoso, A.J.M. An Economic Offline Technique for Estimating the Equivalent Circuit of Aluminum Electrolytic Capacitors. IEEE Trans. Instrum. Meas. 2008, 57, 2697–2710. [Google Scholar] [CrossRef]
- Agarwal, N.; Ahmad, M.W.; Anand, S. Quasi-Online Technique for Health Monitoring of Capacitor in Single-Phase Solar Inverter. IEEE Trans. Power Electron. 2018, 33, 5283–5291. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Laadjal, K.; Cardoso, A.J.M. Advancements in Fault Diagnosis Techniques for Aluminum Capacitors Using STLSP and Autoencoder. In Proceedings of the IEEE International Conference on Artificial Intelligence & Green Energy (ICAIGE), Yasmine Hammame, Tunisia, 10–12 October 2024. [Google Scholar]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis with Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Amaral, A.; Laadjal, K.; Cardoso, A.J.M. Optimized Preventive Diagnostic Algorithm for Assessing Aluminum Electrolytic Capacitor Condition Using Discrete Wavelet Transform and Kalman Filter. Electronics 2024, 13, 3265. [Google Scholar] [CrossRef]
- Kumar, G.K.; Elangovan, D. Review on fault-diagnosis and fault-tolerance for DC–DC converters. IET Power Electron. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Cardoso, A.J.M. Simulation Tool to Evaluate Fault Diagnosis Techniques for DC-DC Converters. Symmetry 2022, 14, 1886. [Google Scholar] [CrossRef]
- Nichicon Corporation. General Descriptions of Aluminum Electrolytic Capacitors-Technical Notes CAT.8101E-1. Available online: https://www.nichicon.co.jp/english/products/pdf/aluminum-e.pdf (accessed on 18 April 2025).
- Guide, S. Technical Guide: Aluminum Electrolytic Capacitor, Conductive Polymer Hybrid Aluminum and Electrolytic Capacitor; Panasonic Industry: Osaka, Japan, 2024. [Google Scholar]
- Ho, J.; Jow, T.; Boggs, S. Historical introduction to capacitor technology. IEEE Electr. Insul. Mag. 2010, 26, 20–25. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Laadjal, A.K.; Cardoso, J.M. Assessment of Aluminum Electrolytic Capacitors Health Status Through Signal-Based Techniques. In Proceedings of the IEEE 21st International Power Electronics and Motion Control Conference (PEMC), Pilsen, Czech Republic, 30 September–3 October 2024. [Google Scholar]
- Dubilier, C.C. Aluminum Electrolytic Capacitor Application Guide. Available online: https://www.cde.com/resources/technical-papers/KNO_CD_AEappGuide_R2.pdf (accessed on 1 May 2025).
- Harada, K.; Katsuki, A.; Fujiwara, M. Use of ESR for deterioration diagnosis of electrolytic capacitor. IEEE Trans. Power Electron. 1993, 8, 355–361. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Cardoso, A.J.M. Fault diagnosis on switch-mode power supplies operating in discontinuous mode. In Proceedings of the Second International Conference on Power Electronics, Machines and Drives (PEMD 2004), Edinburgh, UK, 21–23 September 2004. [Google Scholar]
- Amaral, A.M.R.; Cardoso, A.J.M. Using input current and output voltage ripple to estimate the output filter condition of switch mode DC/DC converters. In Proceedings of the IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, Cargese, France, 31 August–3 September 2009. [Google Scholar]
- Aeloiza, E.; Kim, J.-H.; Enjeti, P.; Ruminot, P. A Real Time Method to Estimate Electrolytic Capacitor Condition in PWM Adjustable Speed Drives and Uninterruptible Power Supplies. In Proceedings of the IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 12–16 June 2005. [Google Scholar]
- Venet, P.; Perisse, F.; El-Husseini, M.H.; Rojat, G. Realization of a smart electrolytic capacitor circuit. IEEE Ind. Appl. Mag. 2002, 8, 16–20. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Cardoso, A.J.M. State condition estimation of aluminum electrolytic capacitors used on the primary side of ATX power supplies. In Proceedings of the 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009. [Google Scholar]
- Sundararajan, P.; Sathik, M.; Sasongko, F.; Tan, C.; Pou, J.; Blaabjerg, F. Condition Monitoring of DC-Link Capacitors Using Goertzel Algorithm for Failure Precursor Parameter and Temperature Estimation. IEEE Trans. Power Electron. 2020, 35, 6386–6396. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Laadjal, K.; Cardoso, A.J.M. Enhanced DC-link Capacitors Failure Diagnosis for a Three-Phase Interleaved Converter, Using Hilbert Transform. In Proceedings of the IEEE 21st International Power Electronics and Motion Control Conference (PEMC), Pilsen, Czech Republic, 30 September–3 October 2024. [Google Scholar]
- Wang, G.; Guan, Y.; Zhang, J.; Wu, L.; Zheng, X.; Pan, W. ESR estimation method for DC-DC converters based on improved EMD algorithm. In Proceedings of the IEEE 2012 Prognostics and System Health Management Conference, Beijing, China, 23–25 May 2012. [Google Scholar]
- Chen, Z.; Lin, Q.; Yu, K.; Su, X.; Du, W. A Non-invasive Online ESR Estimating Method for DC-Link Capacitors of UPS. In Proceedings of the 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 27–30 October 2022. [Google Scholar]
- Ren, L.; Gong, C.; Zhao, Y. An Online ESR Estimation Method for Output Capacitor of Boost Converter. IEEE Trans. Power Electron. 2019, 34, 10153–10165. [Google Scholar] [CrossRef]
- Ma, H.; Mao, X.; Zhang, N.; Xu, D. Parameter Identification of Power Electronic Circuits Based on Hybrid Model. In Proceedings of the IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005. [Google Scholar]
- Buiatti, G.M.; Amaral, A.M.R.; Cardoso, A.J.M. ESR Estimation Method for DC/DC Converters Through Simplified Regression Models. In Proceedings of the IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007. [Google Scholar]
- Buiatti, G.M.; Amaral, A.M.R.; Cardoso, A.J.M. Parameter Estimation of a DC/DC Buck converter using a continuous time model. In Proceedings of the European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007. [Google Scholar]
- Buiatti, G.M.; Amaral, A.M.R.; Cardoso, A.J.M. An Online Technique for Estimating the Parameters of Passive Components in Non-Isolated DC/DC Converters. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007. [Google Scholar]
- Buiatti, G.M.; Amaral, A.M.R.; Cardoso, A.J.M. An unified method for estimating the parameters of non-isolated DC/DC converters using continuous time models. In Proceedings of the 29th International Telecommunications Energy Conference, Rome, Italy, 30 September–4 October 2007. [Google Scholar]
- Peng, Y.; Wang, H. Application of Digital Twin Concept in Condition Monitoring for DC-DC Converter. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019. [Google Scholar]
- Soliman, H.; Wang, H.; Gadalla, B.; Blaabjerg, F. Condition monitoring for DC-link capacitors based on artificial neural network algorithm. In Proceedings of the IEEE 5th International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Riga, Latvia, 11–13 May 2015. [Google Scholar]
- Soliman, H.; Abdelsalam, I.; Wang, H.; Blaabjerg, F. Artificial Neural Network based DC-link capacitance estimation in a diode-bridge front-end inverter system. In Proceedings of the IEEE 3rd International Future Energy Electronics Conference and ECCE Asia, Kaohsiung, Taiwan, 3–7 June 2017. [Google Scholar]
- Soliman, H.; Davari, P.; Wang, H.; Blaabjerg, F. Capacitance estimation algorithm based on DC-link voltage harmonics using artificial neural network in three-phase motor drive systems. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Kamel, T.; Biletskiy, Y.; Chang, L. Capacitor aging detection for the DC filters in the power electronic converters using ANFIS algorithm. In Proceedings of the IEEE 28th Canadian Conference on Electrical and Computer Engineering, Halifax, NS, Canada, 3–6 May 2015. [Google Scholar]
- Apsari, D.; Lee, D. Capacitance and ESR Estimation of DC-link Capacitors in AC Machine Drives Based on Hybrid CNN-Attention Model. In Proceedings of the IEEE 10th International Power Electronics and Motion Control Conference, Chengdu, China, 17–20 May 2024. [Google Scholar]
- Rajendran, S.; Jena, D.; Diaz, M.; Devi, V.S.K. Machine learning based condition monitoring of a DC-link capacitor in a Back-to-Back converter. In Proceedings of the IEEE International Conference on Automation/XXV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Curicó, Chile, 24–28 October 2022. [Google Scholar]
- McGrew, T.; Sysoeva, V.; Cheng, C.H.; Miller, C.; Scofield, J.; Scott, M.J. Condition Monitoring of DC-Link Capacitors Using Time–Frequency Analysis and Machine Learning Classification of Conducted EMI. IEEE Trans. Power Electron. 2022, 37, 12606–12618. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Laadjal, K.; ACardoso, J.M. Advanced Fault-Detection Technique for DC-Link Aluminum Electrolytic Capacitors Based on a Random Forest Classifier. Electronics 2023, 12, 2572. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Laadjal, K.; Cardoso, A.J.M. Assessment of the Integrity of Aluminum Electrolytic Capacitors Using a Logistic Regression Model. In Proceedings of the IEEE International Conference on Artificial Intelligence & Green Energy (ICAIGE), Yasmine Hamm, Tunisia, 10–12 October 2024. [Google Scholar]
- Kareem, A.; Basheer, V.; Kumara, V. A Second-Order Sliding Mode Control Scheme with Fuzzy Logic-Based Online Sliding Surface Adjustment for Buck Converters. IEEE Access 2025, 13, 48792–48801. [Google Scholar] [CrossRef]
- Subedi, S.; Gui, Y.; Xue, Y. Applications of Data-Driven Dynamic Modeling of Power Converters in Power Systems: An Overview. IEEE Trans. Ind. Appl. 2025, 61, 2434–2456. [Google Scholar] [CrossRef]
- Venkatramanan, D.; John, V. Dynamic Modeling and Analysis of Buck Converter Based Solar PV Charge Controller for Improved MPPT Performance. IEEE Trans. Ind. Appl. 2019, 55, 6234–6246. [Google Scholar] [CrossRef]
- Mammeri, E.; Santos, O.; Aroudi, A.; Domajnko, J.; Prosen, N.; Salamero, L. Modeling and Control of a Three-Phase Interleaved Buck Converter as a Battery Charger. IEEE Access 2025, 13, 18325–18345. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, J.; Choi, B. A High-Light-Load-Efficiency Low-Ripple-Voltage PFM Buck Converter for IoT Applications. IEEE Trans. Power Electron. 2022, 37, 5763–5772. [Google Scholar] [CrossRef]
- Park, W.; Namgoong, G.; Choi, E.; Lee, B.; Park, H.; Ma, H.; Bien, F. A 94% Peak Efficiency Dual Mode Buck Converter with Fully Integrated On-Time-Based Mode Control for Implantable Medical Devices. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4458–4462. [Google Scholar] [CrossRef]
- Amaral, A.M.R.; Cardoso, A.J.M. Using Python for the Simulation of a Closed-Loop PI Controller for a Buck Converter. Signals 2022, 3, 313–325. [Google Scholar] [CrossRef]
- Giesselmann, M.; Roy, V. Modeling of power supplies for power modulators with LTspice. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 508–514. [Google Scholar] [CrossRef]
- Jović, A.; Brkić, K.; Bogunović, N. A review of feature selection methods with applications, 2015. In Proceedings of the 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015. [Google Scholar]
- Nasir, I.M.; Khan, M.; Yasmin, M.; Shah, J.; Gabryel, M.; Scherer, R.; Damasevicius, R. Pearson Correlation-Based Feature Selection for Document Classification Using Balanced Training. Sensors 2020, 20, 6793. [Google Scholar] [CrossRef] [PubMed]
- Njimbouom, S.; Lee, K.; Lee, H.; Kim, J. Predicting Site Energy Usage Intensity Using Machine Learning Models. Sensors 2023, 23, 82. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Lu, L.; Wei, W. A Novel Supervised Filter Feature Selection Method Based on Gaussian Probability Density for Fault Diagnosis of Permanent Magnet DC Motors. Sensors 2022, 22, 7121. [Google Scholar] [CrossRef]
- Supurtulu, M.; Hatipoglu, A.; Yılmaz, E. An Analytical Benchmark of Feature Selection Techniques for Industrial Fault Classification Leveraging Time-Domain Features. Appl. Sci. 2025, 15, 1457. [Google Scholar] [CrossRef]

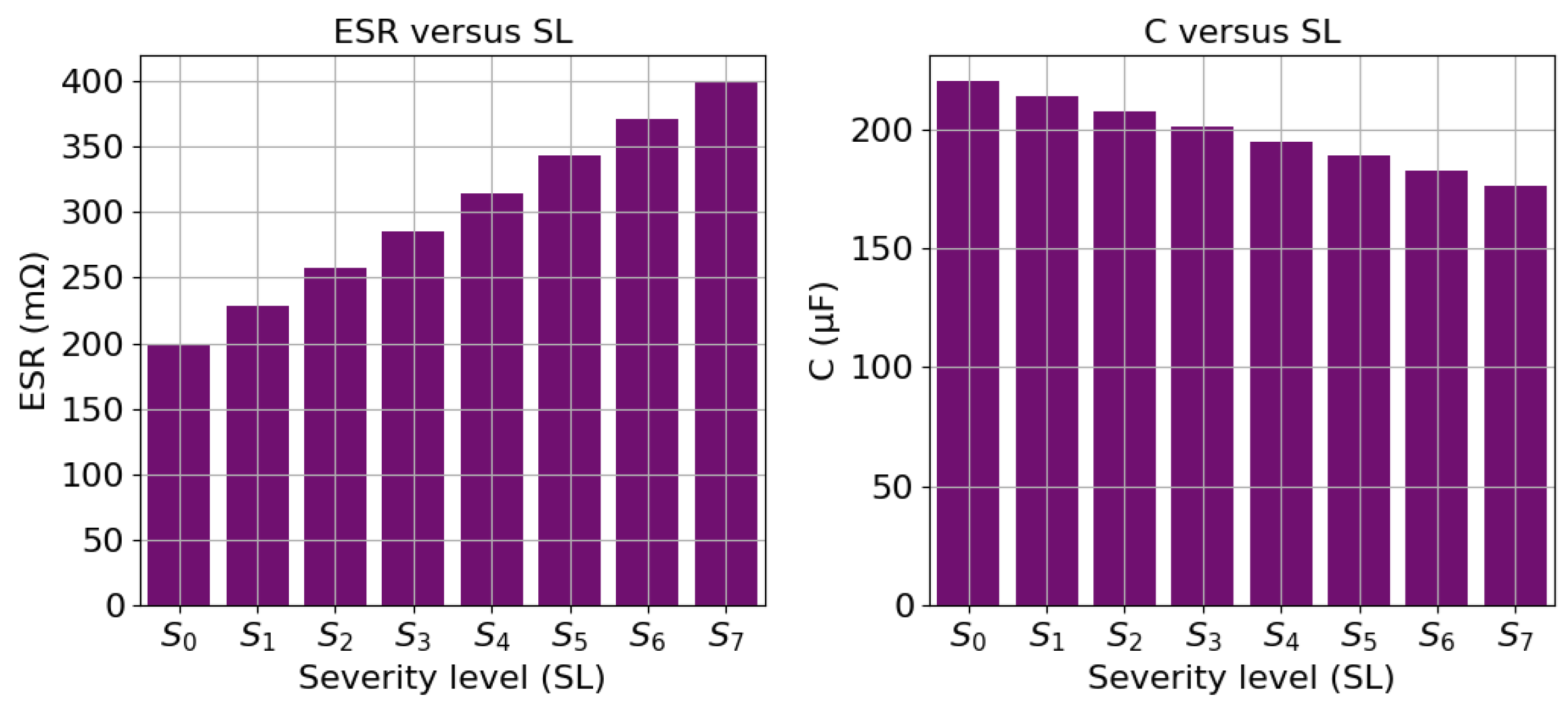


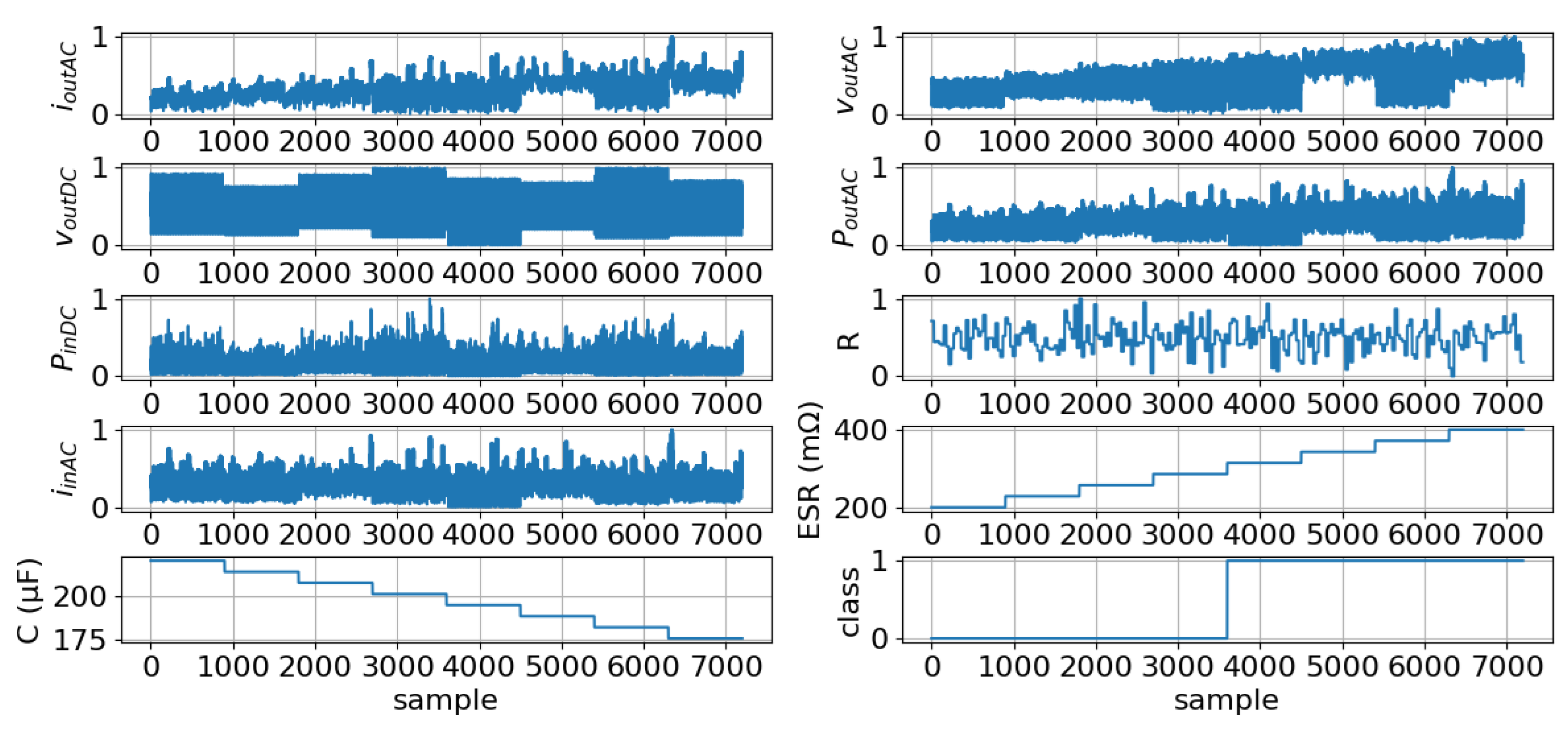
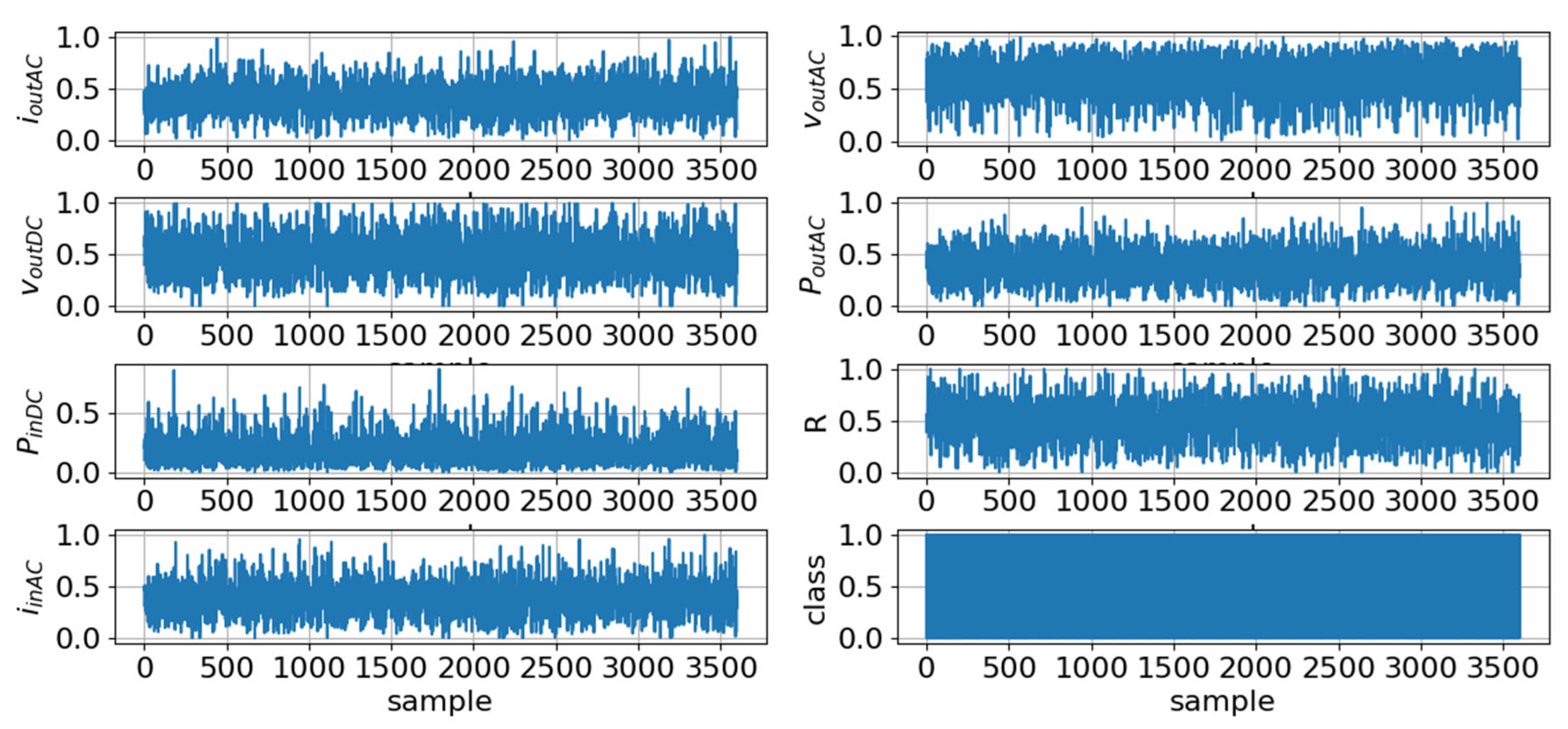
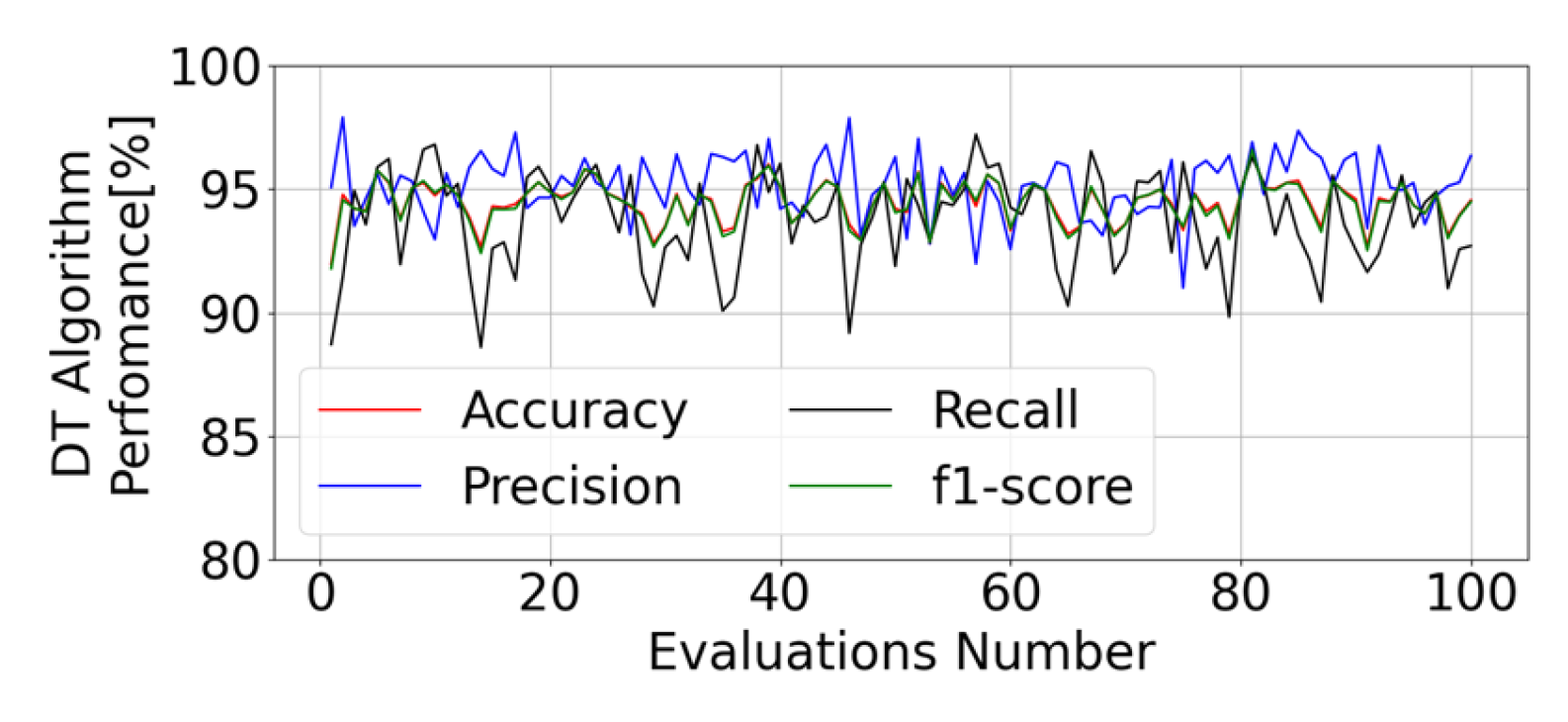
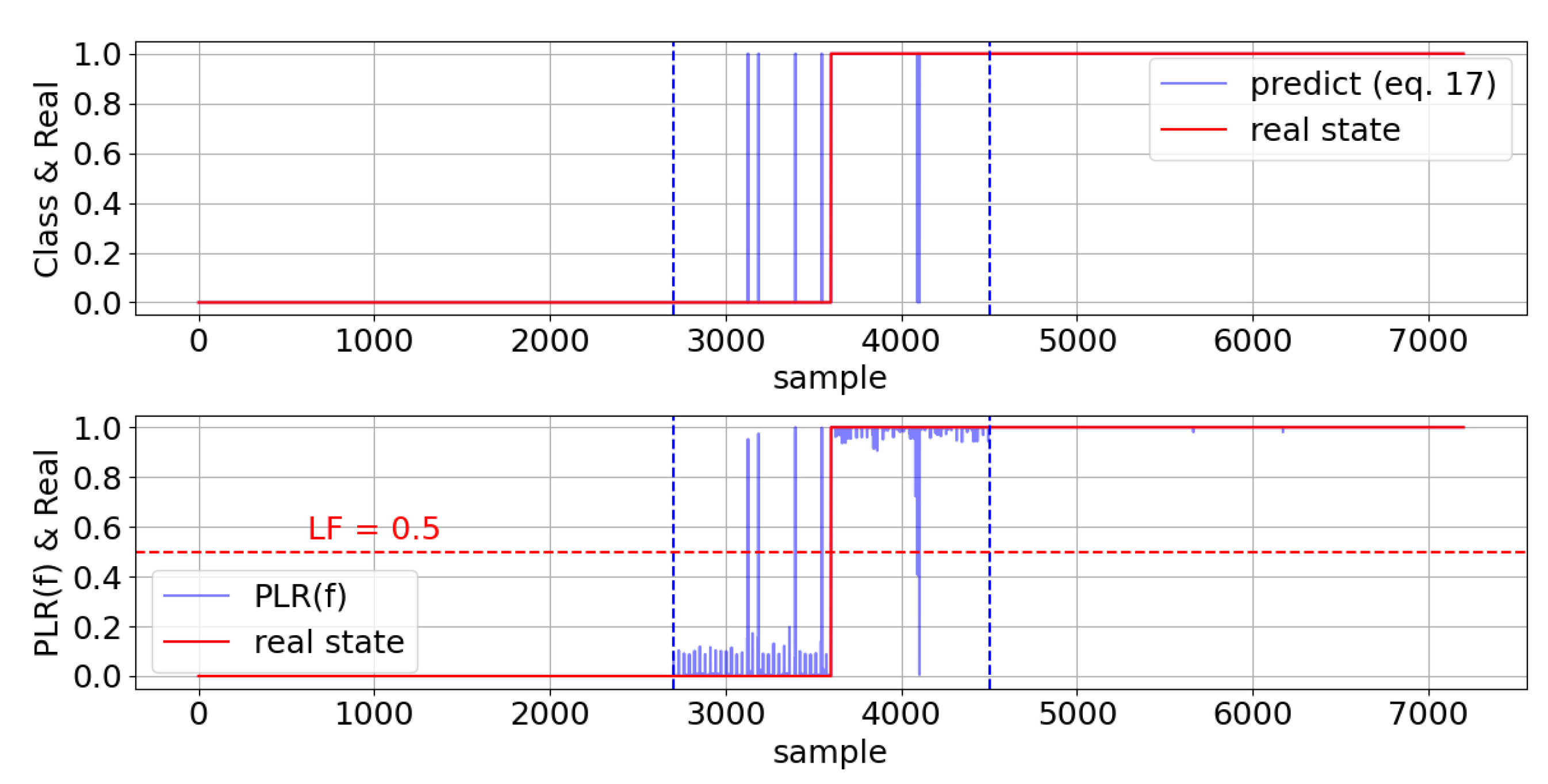
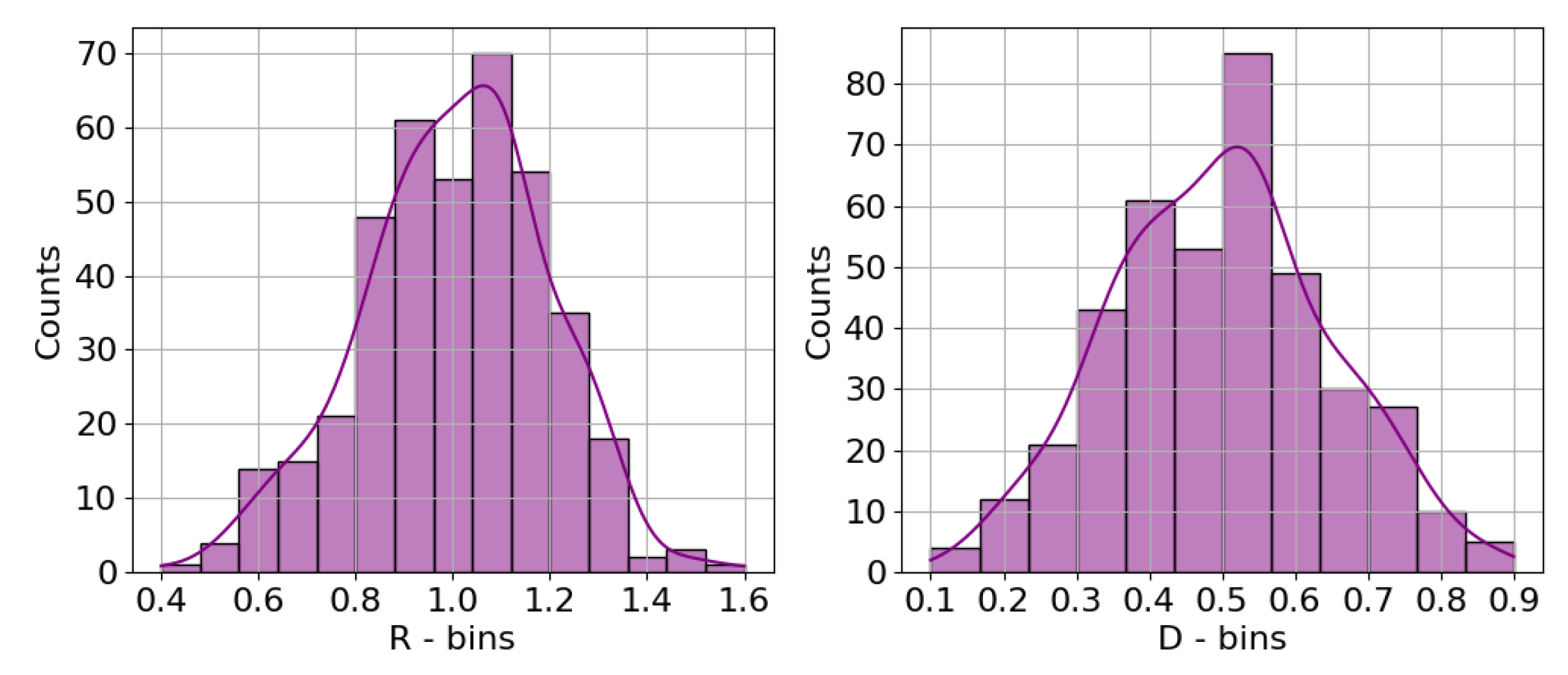
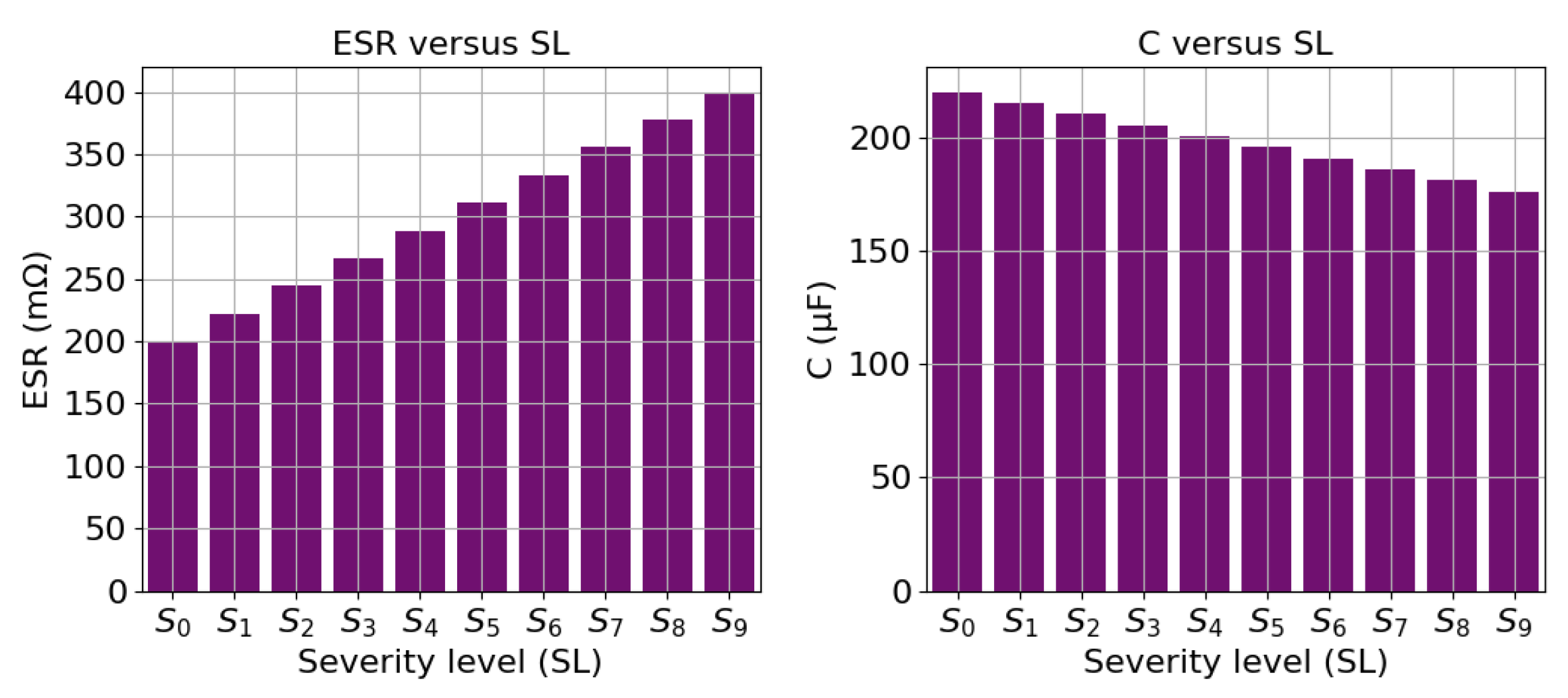
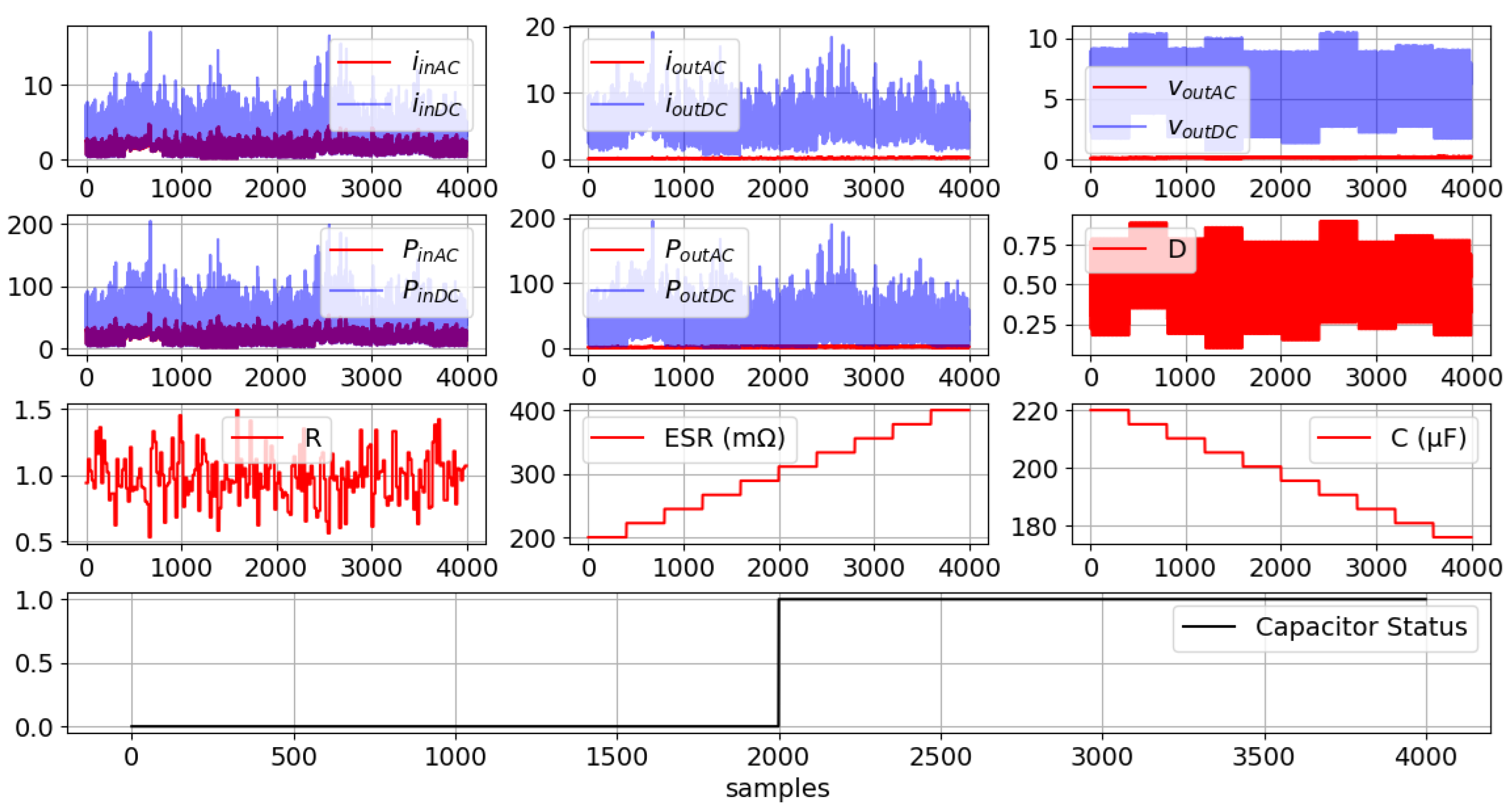

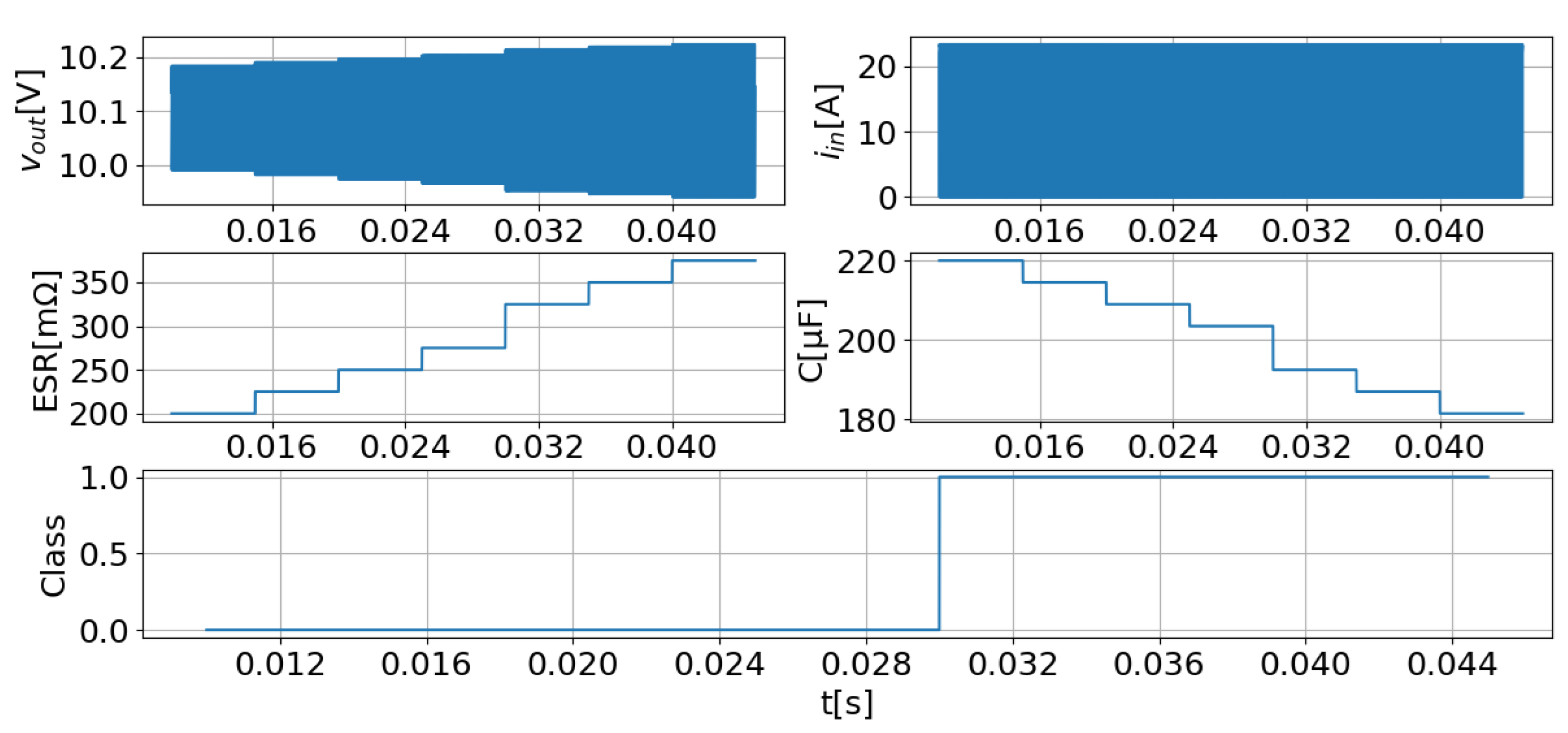

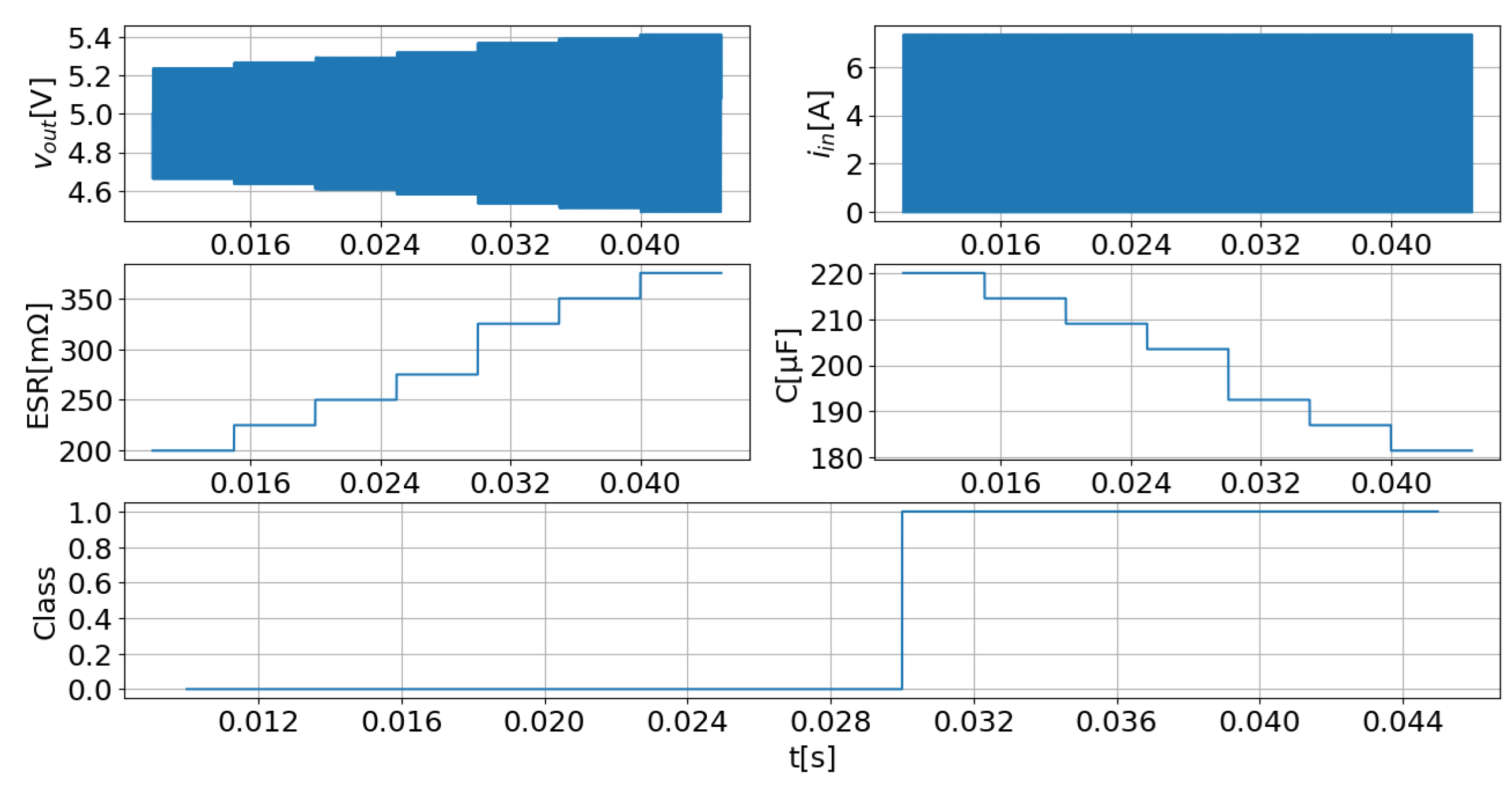
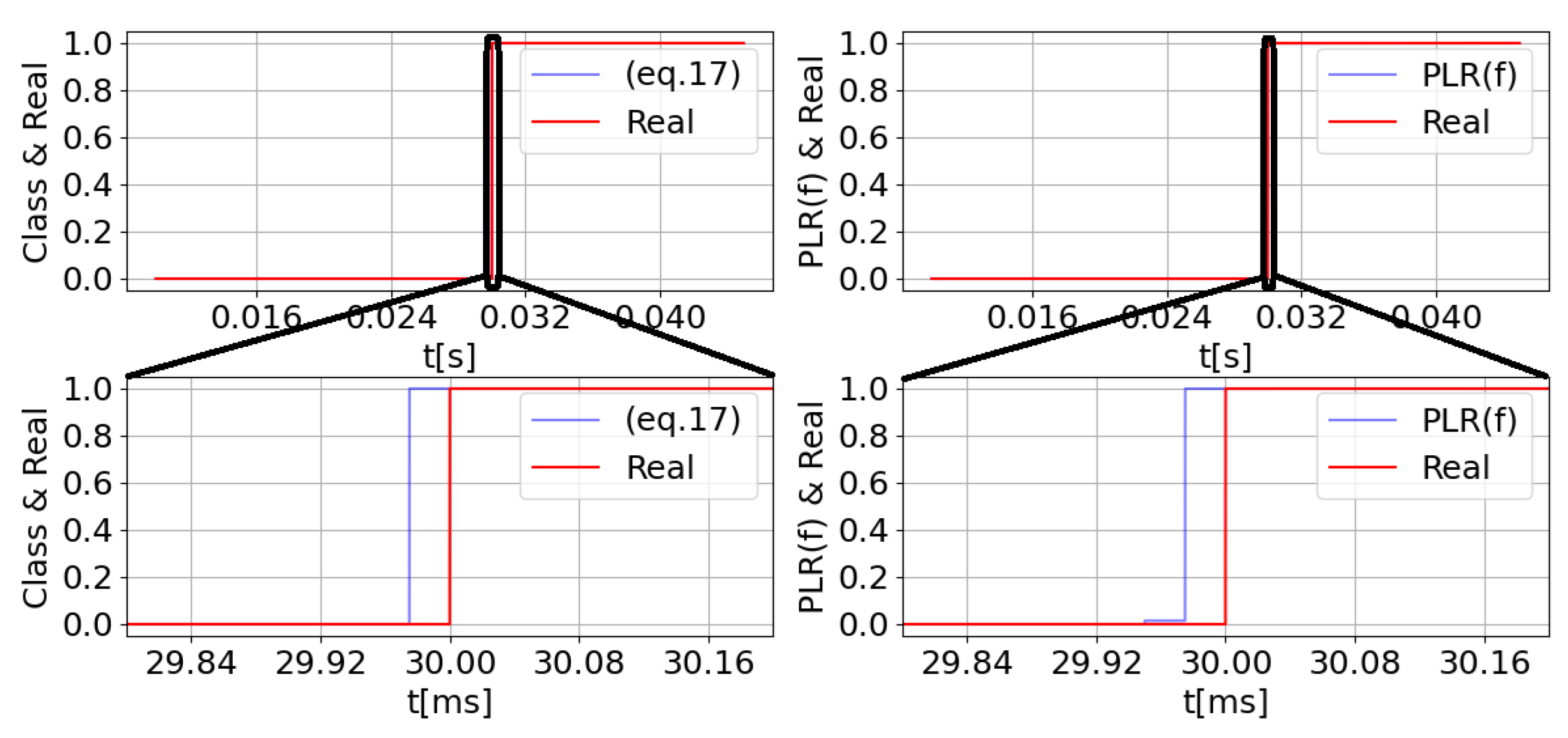
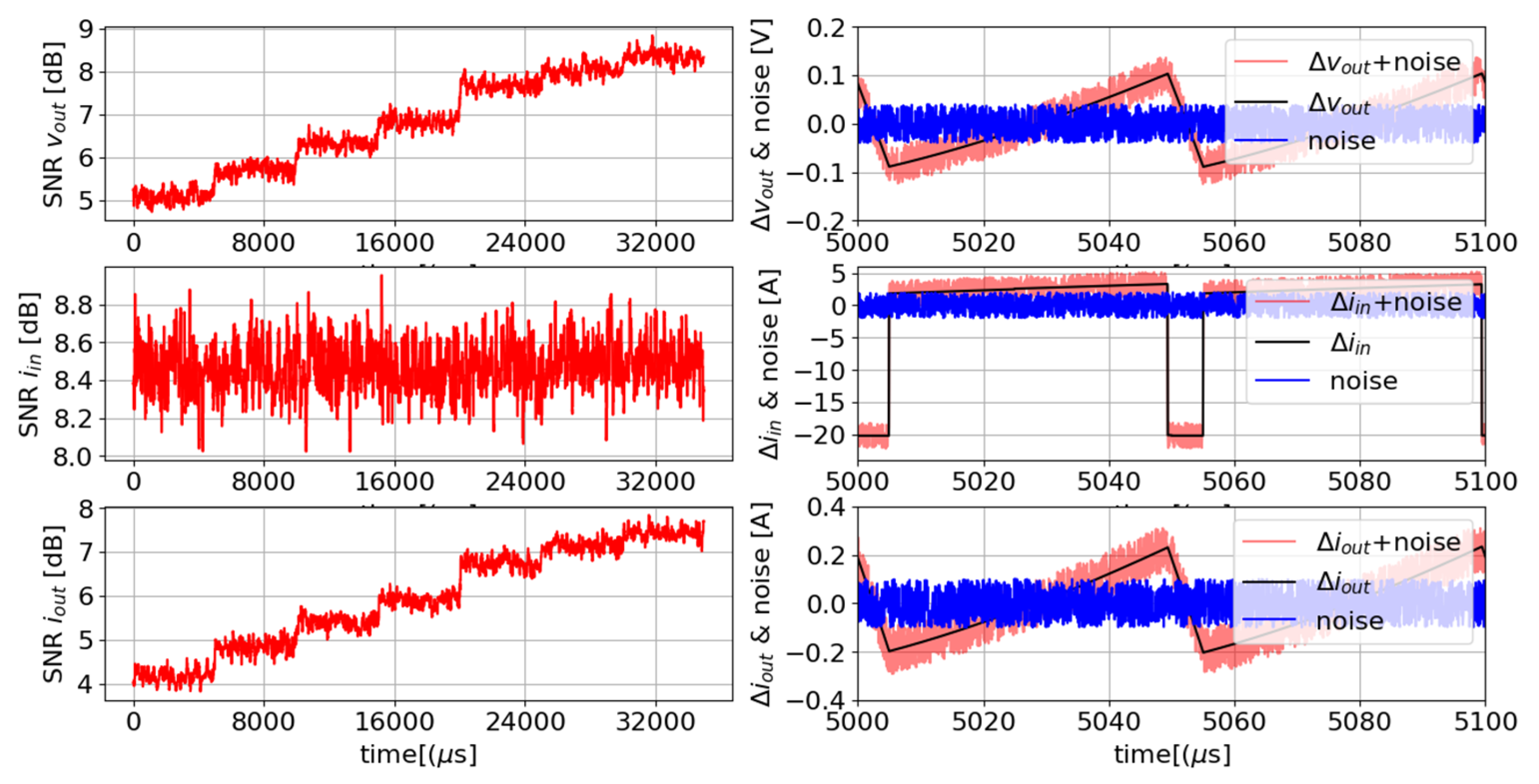
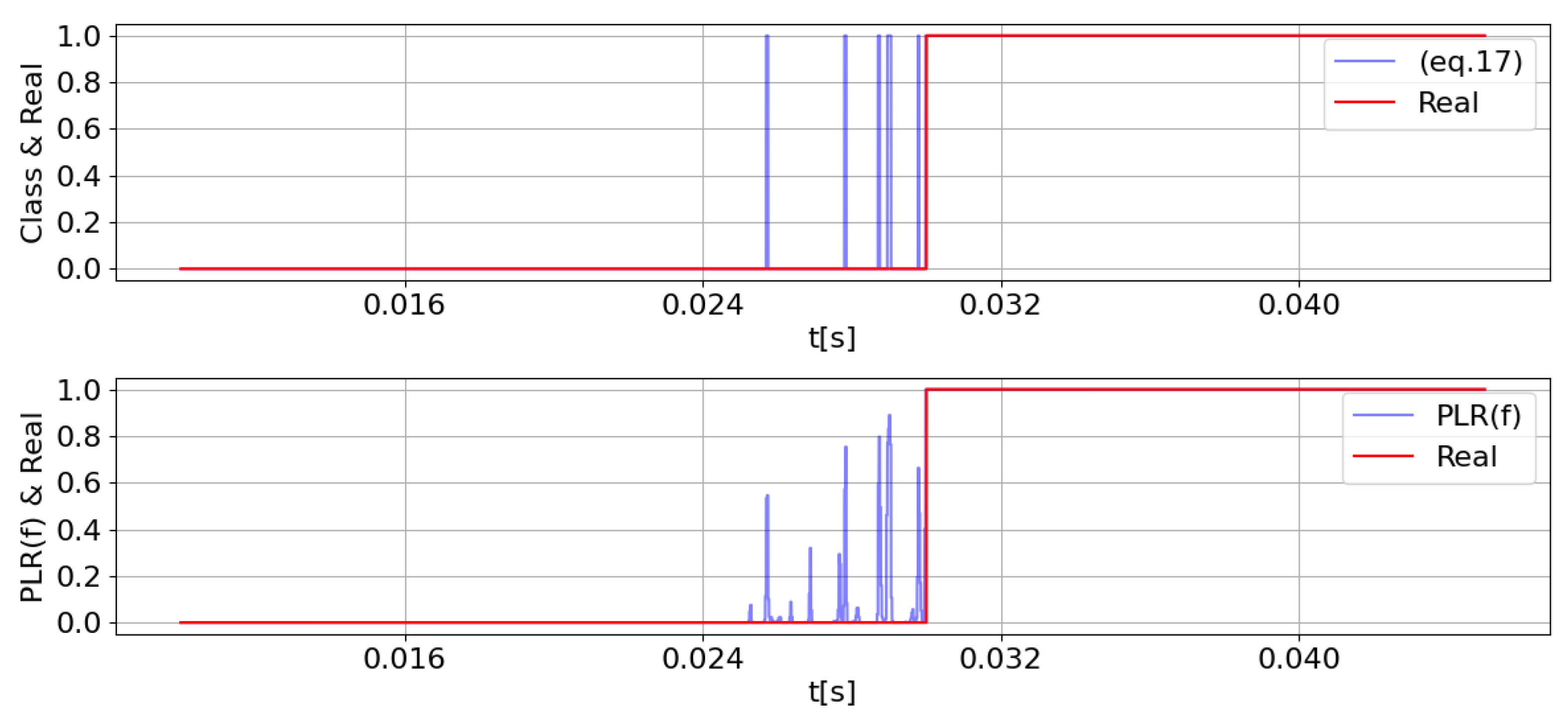
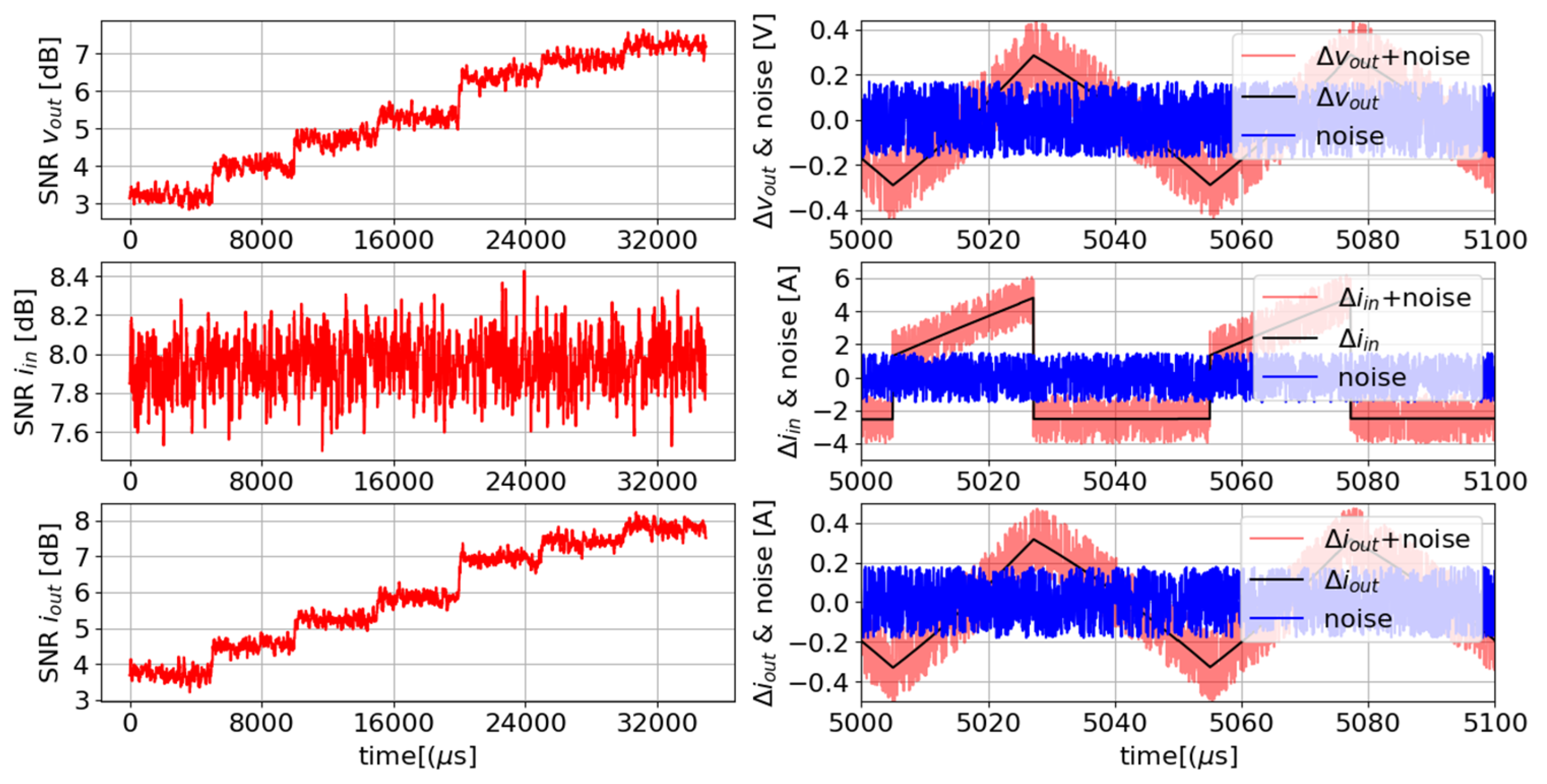
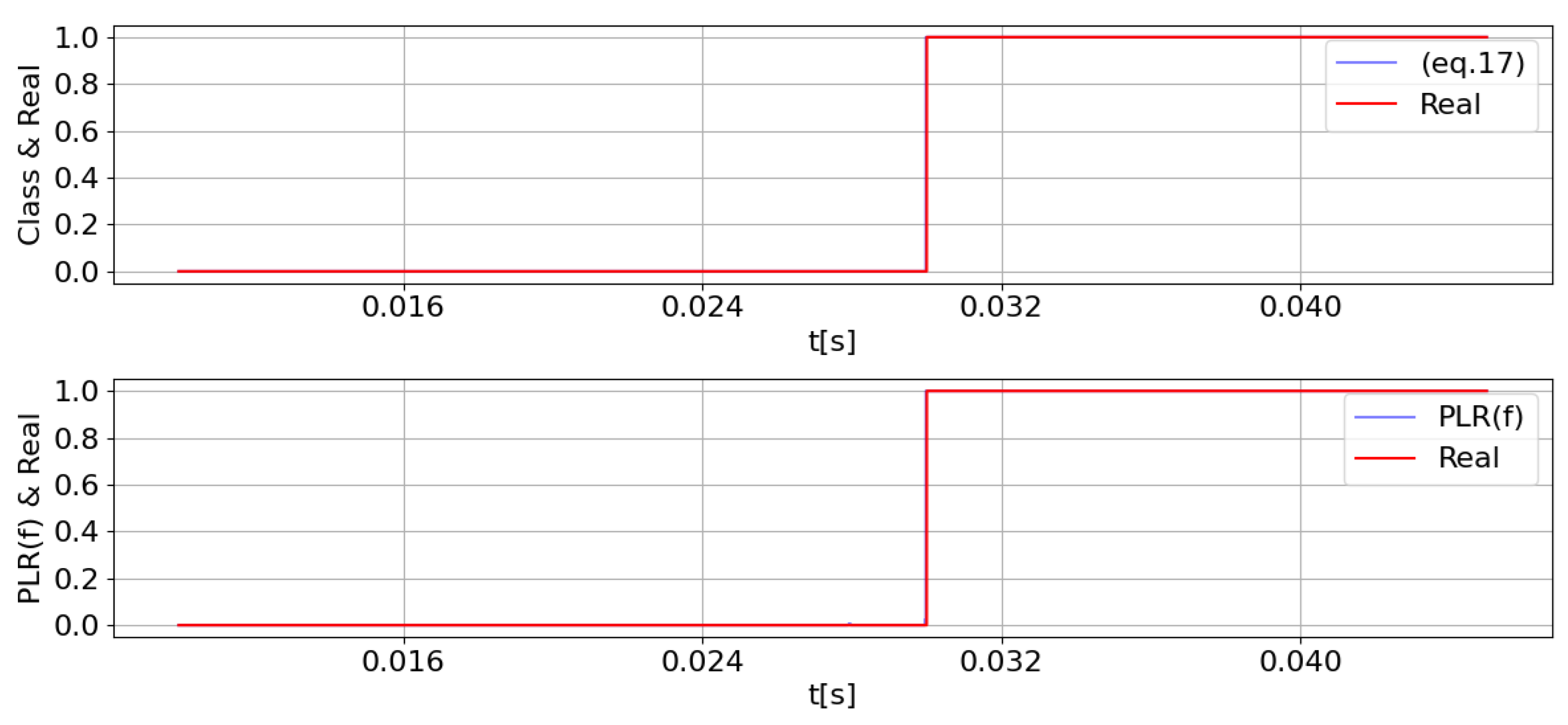
| Scenario | D | R | t = 15 ms | t = 20 ms | t = 25 ms | t = 30 ms | t = 35 ms | t = 40 ms |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.888 | 0.444 | ESR1 | ESR2 | ESR3 | ESR4 | ESR5 | ESR6 |
| C1 | C2 | C3 | C4 | C5 | C6 | |||
| 2 | 0.444 | 0.888 | ESR1 | ESR2 | ESR3 | ESR4 | ESR5 | ESR6 |
| C1 | C2 | C3 | C4 | C5 | C6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaral, A.M.R. Enhancing Power Converter Reliability Through a Logistic Regression-Based Non-Invasive Fault Diagnosis Technique. Appl. Sci. 2025, 15, 6971. https://doi.org/10.3390/app15136971
Amaral AMR. Enhancing Power Converter Reliability Through a Logistic Regression-Based Non-Invasive Fault Diagnosis Technique. Applied Sciences. 2025; 15(13):6971. https://doi.org/10.3390/app15136971
Chicago/Turabian StyleAmaral, Acácio M. R. 2025. "Enhancing Power Converter Reliability Through a Logistic Regression-Based Non-Invasive Fault Diagnosis Technique" Applied Sciences 15, no. 13: 6971. https://doi.org/10.3390/app15136971
APA StyleAmaral, A. M. R. (2025). Enhancing Power Converter Reliability Through a Logistic Regression-Based Non-Invasive Fault Diagnosis Technique. Applied Sciences, 15(13), 6971. https://doi.org/10.3390/app15136971






