Abstract
In microscopic imaging, the key to obtaining a fully clear image lies in effectively extracting and fusing the sharp regions from different focal planes. However, traditional multi-focus image fusion algorithms have high computational complexity, making it difficult to achieve real-time processing on embedded devices. We propose an efficient high-resolution real-time multi-focus image fusion algorithm based on multi-aggregation. we use a difference of Gaussians image and a Laplacian pyramid for focused region detection. Additionally, the image is down-sampled before the focused region detection, and up-sampling is applied at the output end of the decision map, thereby reducing 75% of the computational data volume. The experimental results show that the proposed algorithm excels in both focused region extraction and computational efficiency evaluation. It achieves comparable image fusion quality to other algorithms while significantly improving processing efficiency. The average time for multi-focus image fusion with a 4K resolution image on embedded devices is 0.586 s. Compared with traditional algorithms, the proposed method achieves a 94.09% efficiency improvement on embedded devices and a 21.17% efficiency gain on desktop computing platforms.
1. Introduction
In microscopic observation, ordinary optical microscopes have a very limited depth of field at high magnification, and the imaging system can only capture a sharply focused plane [1]. Multi-focus image fusion extracts the sharp regions from local focused images in video stream data, generating a single image where all regions are in focus. It offers significant advantages in increasing the depth of field in microscopic imaging and enhancing image quality [2]. Due to their high complexity and demanding requirements on computational power and resources, traditional multi-focus image fusion algorithms can only be implemented on terminals such as computers. Benefiting from their low power consumption and portability, embedded microscopic cameras have emerged as one of the most prevalent tools for image acquisition and processing [3]. However, they also face the common challenges of limited computing power and resources inherent in embedded devices. As a result, current real-time high-resolution multi-focus image fusion algorithms are not applicable to embedded microscope systems and can only be used on devices with sufficient computational power and resources [4].
Currently, research on multi-focus image fusion is mainly divided into three categories: spatial domain methods, transform domain methods, and deep learning-based methods [5]. Spatial domain methods operate directly at the pixel level for focus discrimination and fusion operations. Depending on the adopted pixel processing strategies, spatial domain fusion methods can be further classified into block-based and pixel-based approaches. Bai, X. et al. [6] used a gradient-weighted method to evaluate focus regions and generate an initial decision map, which was then refined using morphological opening and closing operations to correct misjudged focused and defocused areas, ultimately achieving multi-focus image fusion. Li et al. [7] proposed a block-based spatial domain multi-focus image fusion method in which the images to be fused are divided into blocks of fixed size. These blocks are then measured and aggregated based on their activity levels to accomplish the fusion. While spatial domain methods are computationally simple, they are affected by the scale of the blocks. A single block may contain both focused and defocused regions, potentially leading to block artifacts in the fusion results [8,9,10]. Transform domain methods first decompose images into sub-band coefficients in the transform domain using specific decomposition rules, such as multi-scale and sparse representations. Then, certain fusion strategies are applied to these sub-band coefficients to produce new coefficients, which are finally reconstructed into the fused image through inverse transformation [11,12]. Wavelet transform, as a multi-scale decomposition tool, provides a rich set of multi-resolution and local detail information, which is beneficial for multi-focus image fusion. Hill et al. [13] proposed using dual-tree complex wavelet transform, which offers shift-invariance and directional selectivity, for image fusion. Sparse representation (SR) can effectively capture image details and minimize information loss, resulting in sharper and more natural fused images, and has thus received wide attention and application. Yang et al. [14] proposed an SR-based multi-focus image fusion scheme, where source images are divided into patches, and sparse coefficients are obtained using an overcomplete dictionary. These coefficients are combined based on a max-selection rule, and the fused image is reconstructed using the combined coefficients and the dictionary. However, transform domain methods suffer from poor parameter adaptability during the transformation process and are prone to boundary artifacts during inverse transformation, along with high computational complexity [15]. Deep learning models, especially convolutional neural networks (CNNs), can learn and extract high-level features from images. Some studies use CNNs and generative adversarial networks (GANs) to directly learn fusion rules for multi-focus images through end-to-end training, achieving remarkable results [16]. Deep learning-based methods convert multi-focus fusion into a classification task that distinguishes focused from defocused regions, and extract and fuse clear regions from source images based on the classification results. Liu et al. [17] introduced deep CNNs into multi-focus image fusion by constructing a training dataset containing sharp image patches and their corresponding blurred versions. A classification model is trained to distinguish between focused and defocused patches. This model accepts a pair of source images as input and generates a fusion decision map through dense block prediction. In addition to CNNs, GANs have also been used in the field of multi-focus image fusion to generate decision maps [18]. However, deep learning-based fusion methods generally rely on large amounts of training data, may suffer from limited generalization ability, and involve complex models with high computational costs [19].
We improve upon spatial domain methods by innovatively combining Gaussian difference images and image pyramids to quickly and comprehensively extract the focused regions of the image. At the same time, considering the characteristics of embedded devices, region-based interpolation down-sampling is applied at the input stage, and nearest-neighbor interpolation up-sampling is applied at the output stage of the decision map to reduce the computational data volume. Ultimately, real-time multi-focus image fusion is achieved on embedded devices for images with a resolution of 3840 × 2160.
2. Methods
Images at different focal planes, captured by adjusting the distance between the sample and the microscope, form a real-time video stream. A new image, formed after multi-focus fusion of two adjacent frames, is then fused with the next frame. The process continues iteratively, ultimately resulting in a fused image with clear details at different focal positions. The workflow of each multi-focus fusion process is illustrated in Figure 1. First, the input source image is down-sampled (DOWN), and then difference of Gaussians image (DOG) and Laplacian pyramids (LPs) are constructed from the down-sampled image to initially extract the sharp regions. Next, the pyramid is reconstructed (LPR) using the difference of Gaussians image to obtain the focused feature map. A decision map is initially constructed based on the maximum value principle (MAX), and morphological operations are applied to filter holes and small target regions in the decision map (FILTER). The decision map is then up-sampled to restore the original resolution (UP). Finally, the image is fused based on the final decision map to obtain the final image.
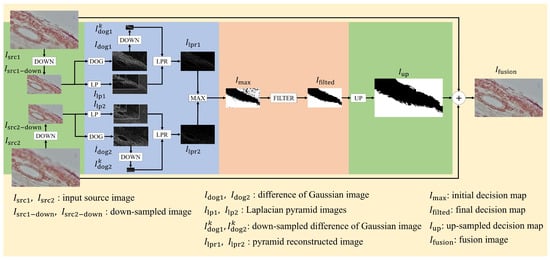
Figure 1.
The framework of the fusion algorithm.
2.1. Focused Region Detection
In microscopic images, the observed objects (such as cells, tissues, circuit boards, etc.) typically have complex three-dimensional structures. These objects exhibit different sharp regions at different focal planes, which are usually composed of edges and texture details. Edges are regions where significant changes in pixel intensity occur, often representing the contours and boundaries of objects, while texture details refer to the fine, intricate structures or patterns on the object’s surface.
In order to reduce the computational complexity of the algorithm in embedded devices, the input image is down-sampled before focus region detection. Regional interpolation down-sampling generates the pixel values of the new image by averaging multiple pixels in the source image, which is represented as
where is the source image, and is the down-sampled image. The coordinates of are mapped to the coordinates of . The value of the target image is the average value of the corresponding region in the original image. By calculating the average value of each 2 × 2 image block from the original image, we obtain the pixel values for the target image. For example, the input source image resolution is 3840 × 2160, and the resolution of the down-sampled image is 1920 × 1080, which reduces the data size compared to the source image.
Difference of Gaussians is commonly used for edge detection and feature extraction. It is obtained by applying Gaussian blur at different scales to the image and calculating the difference between the two blurred images. The difference of Gaussians image allows for the preliminary extraction of edges and contours of the object. The specific calculations are shown in Equations (2) and (3).
where is the Gaussian kernel function, with being the standard deviation of the Gaussian kernel. A larger results in a stronger blurring effect on the image. is the partially focused down-sampled microscopic image, and the Gaussian kernels with different standard deviations are convolved with and then subtracted to obtain the difference of Gaussians image . As shown in Figure 2, when setting σ1 = 1.5 and σ2 = 1.2, extracts most of the edge information and some of the local detail features of the image.
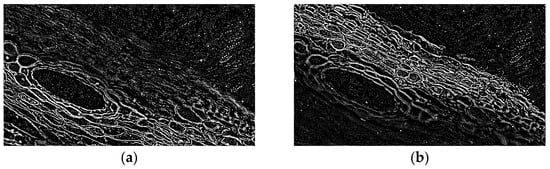
Figure 2.
The difference of Gaussians images derived from the adjacent frames with different focal regions of (a) lower-left part , (b) upper-right part .
Image pyramids are typically divided into two types: Gaussian pyramids and Laplacian pyramids. Through image pyramids, multi-scale image features can be extracted. The Laplacian pyramid is constructed based on the Gaussian pyramid and is used to capture and represent the detailed texture information of the image. First, the Gaussian pyramid is constructed by convolving the image with the Gaussian kernel function and then down-sampling. After the first down-sampling, the image size becomes one-quarter of the original image. This operation is repeated times to obtain levels of the Gaussian pyramid. The image at the -th level can be expressed by Equation (4), “DOWN” represents down-sampling, which removes even rows and even columns.
Next, construct the Laplacian pyramid. Up-sampling the -th level image of the Gaussian pyramid, and make the difference between and the up-sampled image to obtain the layer Laplace image .This process can be expressed by Equation (5), “UP” represents up-sampling, which interpolates with zero padding.
This step is applied to all layers of the Gaussian pyramid to obtain the levels of the Laplacian pyramid. The Laplacian pyramid contains most of the texture information at different scales and some edge information from the image.
The top-level image of the traditional -level Laplacian pyramid is the corresponding top-level image of the Gaussian pyramid. To further obtain more pronounced high-frequency details, the top-level image of the Gaussian pyramid is replaced with the difference of Gaussians image of the same size for reconstruction. The difference of Gaussians image is down-sampled times to obtain , with the sample size matching that of the top-level image of the Gaussian pyramid. is then used as the top-level image of the Laplacian pyramid for image reconstruction. Pyramid reconstruction can be expressed by Equations (6) and (7).
Starting from the top-level image , up-sampling is performed and added to the Laplacian pyramid image at the next lower level to obtain the reconstructed top-level image . This process is repeated by up-sampling layer by layer and adding the corresponding Laplacian difference images. This loop continues until the image reaches the lowest level, resulting in a high-frequency focused information image reconstructed using the difference of Gaussians image as the top-level image.
In the image reconstruction process, the method based on Gaussian image difference enhances the high-frequency components, making texture and edge features more prominent and refined. However, the selection of pyramid levels requires a trade-off between computational efficiency and detail preservation: too many levels can disperse high-frequency information across multiple layers, not only increasing computation time but also reducing fusion quality, while too few levels may lose critical details, resulting in blurred fused images. Through multiple experimental verifications, setting k = 4 for a four-level pyramid decomposition and reconstruction achieves the optimal balance for images with a resolution of 1920 × 1080.
For example, four-layer pyramids are constructed and restored for two different focused regions of the cell slices, resulting in the corresponding focus information maps and , as shown in Figure 3. Compared to the original images, pixels with higher gray values in the focus information maps correspond to clearer pixels in the original image, while pixels with lower gray values correspond to more blurred pixels in the original image.
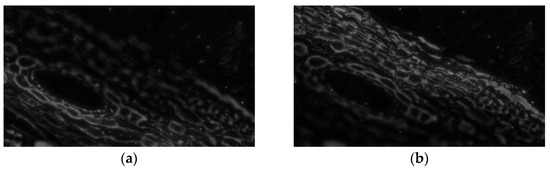
Figure 3.
The focus information maps derived from the adjacent frames with different focal regions of (a) lower-left part , (b) upper-right part ( (for better visualization, histogram equalization was performed on the images).
2.2. Decision Map
The key step in high-quality image fusion is obtaining an accurate decision map for the segmentation of clear and blurred regions. By comparing the corresponding pixels of the focus information maps and based on the maximum value principle, the initial decision map is generated. It is expressed as the following Equation (8).
The plane of microscopic images is irregular, with discontinuous focus areas, and is also influenced by noise and other factors. As shown in Figure 4, the initial decision map contains misjudged focus and defocus areas during detection. This is manifested in the image by tiny black holes in the white pixel regions and tiny white holes in the black pixel regions. To improve the image fusion quality, these small holes in the decision map need to be removed. This can be achieved by applying contour area filtering and morphological methods to eliminate the holes.

Figure 4.
The initial decision map (1920 × 1080 pixels @ 10× magnification).
Morphological operations, such as erosion and dilation, are used to remove small target areas and fill holes. The dilation operation works by convolving the image with a structural element, replacing the center pixel with the maximum value of the area covered by the kernel. This helps to bridge narrow gaps and thin trenches. Erosion, the reverse operation of dilation, is used to eliminate isolated pixel regions or objects.
To effectively eliminate the hole structures in the decision map, morphological closing operations can be employed. The specific procedure involves first performing a dilation operation using a square structuring element to merge the hole regions with the foreground, followed by an erosion operation of the same scale to restore the original contours of the target. The size of the structuring element also influences the image processing results. Experimental results show that, at the current resolution, a structuring element size of 5 × 5 can effectively fill most small holes while preserving image details.
Morphological operations can filter out the majority of hole regions, and the remaining small holes are filtered through area calculations. The area of the hole is approximated as the area of a closed polygon, which is calculated using the shoelace equation [20].
where is the vertex coordinates of the closed polygon, and , . The area is computed by iterating over all the vertices. For example, the area threshold is set as one sixty-fourth of the image area. If the area of the hole is smaller than the threshold , it is considered a small hole and removed from the contour sets. Apply morphological operations and filter out small area contours from to obtain the final decision map . As shown in Figure 5, the final decision map accurately divides the clear and blurred regions while eliminating the interference of misjudged focused and defocused areas.

Figure 5.
The final decision map.
2.3. Image Fusion
For the generated final decision map , up-sampling is performed to restore the image to its original resolution. The decision map is a binary image, so the up-sampled image should also be binary, without introducing pixel values other than 1 and 0. The nearest-neighbor interpolation algorithm is computationally simple and fast and does not introduce any additional pixel values, making it ideal for binary images like the decision map. The basic principle is to find the nearest pixel in the original image to the target image coordinates and assign the value of that pixel to the corresponding position in the target image. The nearest-neighbor interpolation is represented as
where is the up-sampled image, and and are the horizontal and vertical scaling factors, respectively. When the magnification factor is 2, .
Finally, the original image is fused with weighted addition based on the up-sampled decision map, which is represented as
where and are the source images of different focus regions, and is the up-sampled decision map, resulting in the final multi-focus fused image .
3. Experimental Results
The experiments evaluate three aspects of the proposed method: the effectiveness of the focus measure, the quality of image fusion, and the computational efficiency of the algorithm.
For the evaluation of the focus measure method, a comparative experimental approach was adopted. Four representative classical focus evaluation metrics were selected as baseline references: the variance of gray levels [21], gradient energy [22], Laplacian energy [23], and spatial frequency [24]. These methods quantify image sharpness from different perspectives and are widely used and theoretically grounded in focus region extraction.
For image fusion quality and algorithmic efficiency, six types of sample images were selected for the experiments, as shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. To simulate real-time video stream processing, each sample consisted of nine consecutively acquired images at different focal planes, containing both focused and blurred regions. The magnification for the cell slice samples was 10×, and for the circuit board samples, it was 4.2× or 8×. The nine images were fused sequentially as follows: two images were first fused to generate a result, which was then fused with the third image, and the new result was fused with the fourth image, and so on, until all nine images were fused. The proposed algorithm was compared with eight commonly used fusion algorithms in terms of image quality and computational efficiency: dense scale-invariant feature transform (DSIFT) [25], Laplacian pyramid (LP) [26], contourlet transform (CVT) [27], dual-tree complex wavelet transform (DTCWT) [28], nonsubsampled contourlet transform (NSCT) [29], discrete wavelet transform (DWT) [30], guided filtering (GF) [31], and convolutional neural network (CNN) [17] methods. All comparative algorithms were implemented using the parameter settings specified in their respective reference literature.
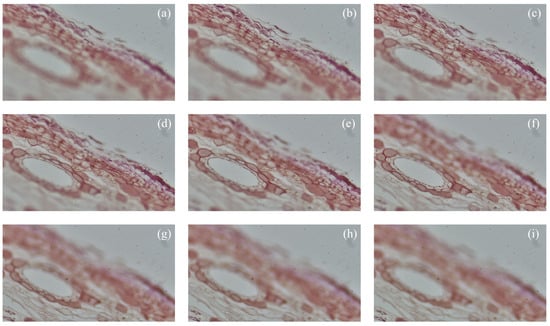
Figure 6.
(a–i) are section images of ten-year pine stem c.s. at different focal planes.
Figure 7.
(a–i) are section images of Capsella older embryo sec. at different focal planes.

Figure 8.
(a–i) are section images of housefly wing w.m. at different focal planes.

Figure 9.
(a–i) are images of circuit board samples at different focal planes.

Figure 10.
(a–i) are images of battery holder circuit samples at different focal planes.

Figure 11.
(a–i) are images of sensor circuit samples at different focal planes.
3.1. Focus Measure
A systematic comparison scheme was designed in this study, focusing on two aspects: extraction performance and computational efficiency. First, the focus region extraction results on the same test samples are compared to generate focus measure maps and assess the accuracy of focus determination. Second, the real-time performance is evaluated by measuring the computation time each algorithm takes to process the same image. During the experiments, variables such as lighting and displacement of samples were strictly controlled to ensure the reliability and repeatability of the comparison results. In Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, the focus measure maps and decision maps generated by the variance, gradient, Laplacian energy, spatial frequency methods, and the proposed algorithm are presented.

Figure 12.
The left and middle images are focus maps based on Gray-Level Variance, while the right one is a corresponding decision map.

Figure 13.
The left and middle images are focus maps based on Energy of Gradient, and the right one is a corresponding decision map.

Figure 14.
The left and middle images are focus maps based on Energy of Laplacian, and the right one is a corresponding decision map.

Figure 15.
The left and middle images are focus maps based on Spatial Frequency, and the right one is a corresponding decision map.

Figure 16.
The left and middle images are focus maps based on Proposed, and the right one is a corresponding decision map.
Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 present the resulting images of different focus measurement algorithms along with their corresponding decision maps. For the gray level variance method, the overall focus measure map appears dim, with insufficient contrast in textures and edges, and the decision map shows blurred boundaries between focused and background regions. As the gray-level variance relies solely on the global variance of pixel intensity distribution, it responds weakly to local detail changes, making it difficult to identify subtle defocus areas. Furthermore, it is susceptible to brightness variations, often misinterpreting them as focus differences under uneven illumination, indicating poor robustness. In the gradient energy method, the focus measure map highlights edge features, but noise interference appears in non-edge regions, leading to local misjudgments in the decision map. First-order gradients are sensitive to high-frequency noise, which can generate false focus signals in low signal-to-noise ratio scenarios like microscopic imaging. In the Laplacian energy method, the decision map contains speckled white noise and irregular patches at the boundaries between bright and dark areas. Since it relies solely on second-order differential features, it responds poorly to low-frequency brightness variations and fails to effectively distinguish between defocus blur and true low-frequency textures. In the spatial frequency method, the focus measure map has a blurred response in the low-frequency region and an uneven energy distribution of high-frequency details, resulting in severe noise in the blank area of the sample in the decision map and low boundary detection accuracy. The focus map generated by the proposed method shows significantly enhanced detail-to-background contrast, and the decision map presents continuous and complete focused regions. Although slight over-extraction occurs at complex edges, it does not affect the subsequent image fusion performance after post-processing.
Table 1 shows the computation time under the same operating environment (Platform: Intel® CoreTM i7-9750H, Santa Clara, CA, USA).

Table 1.
Computation time of gray level variance, gradient energy, Laplacian energy, spatial frequency, and proposed algorithm.
It can be seen from the data in Table 1, the gray-level variance method only needs to calculate the mean and variance of pixel intensity, without complex convolution kernels and Fourier transform, and has the fastest processing speed. The gradient energy method employs convolution operations to compute gradients, leading to a slightly higher computational time compared to the gray level variance method. Similarly, the Laplacian energy method also utilizes convolution operations, resulting in computational times comparable to those of the gradient energy method. The spatial frequency method calculates focus metrics directly in the spatial domain by measuring intensity variations between rows and columns, eliminating the need for frequency-domain transformations. This spatial-domain approach still involves pixel-wise intensity comparisons and multi-step calculations, resulting in higher memory usage and the longest computational time. The proposed algorithm involves two Gaussian filtering operations to construct the difference of Gaussians image, followed by image decomposition and reconstruction. Its computational time is slightly higher than that of the Laplacian energy method but significantly lower than that of the spatial frequency method.
The proposed focus measure algorithm, based on difference of Gaussians and Laplacian pyramid fusion, demonstrates significant advantages in focus information extraction for microscopic images through multi-scale feature fusion and noise suppression strategies. By reconstructing the top layer of the Laplacian pyramid using the high-frequency details enhanced by the difference of Gaussians image, the method retains the traditional Laplacian operator’s sensitivity to cellular edges and textures, while the multi-scale Gaussian kernels effectively suppress noise interference. This approach addresses the shortcomings of traditional methods, such as noise amplification and the loss of low-frequency information, while also balancing computational time consumption.
3.2. Quantitative Evaluation
Quality evaluation is conducted from two aspects: subjective visual comparison and objective quantitative evaluation. Subjective visual comparison analyzes image clarity, artifacts, and depth of field, while objective quantitative evaluation selects commonly used image evaluation indicators for comparison.
3.2.1. Subjective Visual Comparison
The multi-focus image dataset was processed using DSIFT, DWT, GF, CVT, DTCWT, LP, NSCT, CNN, and the proposed algorithm in this paper. The fusion experimental results of the multi-focus image dataset shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 are presented in Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22, respectively.

Figure 17.
Fusion images of the ten-year pine stem c.s. dataset shown in Figure 6 under different algorithms.

Figure 18.
Fusion images of the Capsella older embryo sec. dataset shown in Figure 7 under different algorithms.

Figure 19.
Fusion images of housefly wing w.m. dataset shown in Figure 8 under different algorithms.

Figure 20.
Fusion images of the circuit board sample dataset shown in Figure 9 under different algorithms.

Figure 21.
Fusion images of the battery holder circuit sample dataset shown in Figure 10 under different algorithms.

Figure 22.
Fusion images of the sensor circuit sample dataset shown in Figure 11 under different algorithms.
Figure 17 shows the fusion images of the Ten Year Pine Stem C.s. dataset shown in Figure 6 under different algorithms. Based on the comparison results of the nine algorithms, it can be concluded that DSIFT, DWT, GF, and the proposed method perform relatively well in the fusion of microscopic images of pine stems, effectively preserving the structure of cell walls and the details of pits. Among these, the proposed algorithm demonstrates the best overall performance—it not only clearly presents the continuous texture of the cell wall but also fully retains the key morphological features of the pits, achieving an optimal balance between detail enhancement and structural preservation. In contrast, CVT, DTCWT, LP, NSCT, and CNN exhibit significant deficiencies: CVT introduces blocky, mosaic-like artifacts in the intercellular regions; DTCWT causes wave-like distortions along the cell walls; LP severely blurs the cell textures; NSCT introduces granular noise in the cytoplasmic areas; and CNN results in locally abnormal cell expansion due to overfitting. Although the GF algorithm performs well overall, it still generates artifacts along the cell boundaries. Traditional multi-scale methods and deep learning approaches continue to face challenges in handling complex textures in biological tissues—NSCT tends to over-enhance regions with uneven staining, while CNN struggles to adapt to the multi-scale geometric characteristics of cell walls.
Figure 18 shows the fusion images of the Capsella older embryo Sec. dataset shown in Figure 7 under different algorithms. DSIFT, DWT, GF, CNN, LP, and the proposed method demonstrate relatively effective fusion outcomes, preserving key cellular textures within the red-boxed regions. Notably, the proposed method achieves optimal clarity in vascular bundle structures and stomatal complexes while avoiding artifacts prevalent in other methods: CNN and LP exhibit edge blurring in palisade mesophyll cells, DSIFT introduces grid-like distortions in intercellular spaces, and GF shows faint halo effects around trichome bases. CVT, DTWCT, and NSCT underperform significantly, failing to resolve critical details—CVT produces checkerboard artifacts in spongy mesophyll, DTWCT distorts chloroplast distribution patterns, and NSCT introduces speckle noise in epidermal cell junctions.
Figure 19 shows the fusion images of the housefly wing w.m. dataset shown in Figure 8 under different algorithms. DSIFT, DWT, GF, and the proposed algorithm perform well in overall clarity, effectively fusing the sharp regions of the wing. CVT, DTCWT, and NSCT exhibit poor overall sharpness, with noticeable blurring and artifacts. CNN has an advantage in local contrast but may suffer from over-smoothing or artificial traces. When examining the zoomed-in details of the wing veins, DSIFT and the proposed algorithm demonstrate superior performance, clearly preserving fine textures without obvious artifacts.
Figure 20 shows the fusion images of the circuit board sample dataset shown in Figure 9 under different algorithms. DSIFT and the proposed algorithm demonstrate superior performance in the circuit board fusion results, delivering sharp pin edges, clear solder joints, and well-preserved fine textures with minimal artifacts. GF performs moderately but shows slight halo effects, while DWT and LP suffer from blurring or checkerboard artifacts. CVT, DTCWT, and NSCT exhibit significant blurring and distortions, making them unsuitable for hardware inspection. CNN enhances local contrast but introduces artificial textures. Overall, DSIFT and the proposed method are optimal for circuit board fusion, balancing detail preservation and noise suppression, whereas wavelet-based and pure deep learning approaches need refinement to avoid over-smoothing or artificial enhancements.
Figure 21 shows the fusion images of the battery holder circuit sample dataset shown in Figure 10 under different algorithms. DSIFT and the proposed algorithm demonstrate optimal performance, clearly presenting circuit trace details and solder joint morphology without noticeable artifacts. GF and LP algorithms perform second best, preserving main features but exhibiting slight halo effects or edge aliasing. DWT, CVT, DTCWT, and NSCT algorithms show significant blurring due to limitations in frequency-domain transformation. While the CNN algorithm enhances local contrast, it introduces unrealistic texture details. Overall, the proposed algorithm achieves the best balance between retaining critical circuit features and suppressing artifacts, making it particularly suitable for the inspection requirements of precision electronic components such as battery holders.
Figure 22 shows the fusion images of the sensor circuit dataset shown in Figure 11 under different algorithms. DSIFT and the proposed algorithm demonstrate the best performance, clearly preserving the fine traces and pad details of the golden circuit structures without introducing noticeable artifacts. Although the GF and LP algorithms maintain the overall structural integrity, they suffer from slight blurring and jagged edges, respectively. Other traditional transform-based methods exhibit significant blurring due to the limitations of frequency-domain processing—most notably, DWT introduces checkerboard artifacts, while NSCT excessively smooths component labels. While the CNN method enhances contrast, it also introduces false textures. Overall, the proposed algorithm achieves the optimal balance among detail preservation, artifact suppression, and computational efficiency, significantly outperforming the other methods. It is particularly well-suited for sensor circuit inspection scenarios that require micron-level precision.
3.2.2. Objective Quantitative Evaluation
Different multi-focus image fusion algorithms may exhibit significant differences across various evaluation metrics. To objectively and quantitatively analyze the fusion effect of the fusion algorithms, five evaluation metrics: standard deviation (STD) [32], information entropy (IE) [33], average gradient (AG) [34], structural similarity index (SSIM) [35], and nonlinear correlation information entropy ) [36] are selected for the quantitative analysis of the fusion results. For the calculation of the full-reference metrics SSIM and , the fused image generated from the nine source images was evaluated by computing the structural similarity and nonlinear correlation information entropy between the fused image and each individual source image, followed by averaging all the results.
The fusion results shown in Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 are evaluated using these five criteria, with the results presented in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, respectively. All evaluation criteria follow the principle that the larger the value, the better the fusion effect. The best performance is highlighted in blue, while the second-best performance is marked in orange. To evaluate the data reduction and feature loss during the down-sampling process, we additionally introduced an objective evaluation of the fused images obtained without down-sampling. The fused images without down-sampling are represented by “Proposed *”.

Table 2.
The evaluation results of the fused images shown in Figure 17 for ten-year pine stem c.s.

Table 3.
The evaluation results of the fused images shown in Figure 18 for capsella older embryo sec.

Table 4.
The evaluation results of the fused images shown in Figure 19 for housefly wing w.m. sample.

Table 5.
The evaluation results of the fused images shown in Figure 20 for the circuit board sample.

Table 6.
The evaluation results of the fused images shown in Figure 21 for the battery holder circuit sample.

Table 7.
The evaluation results of the fused images shown in Figure 22 for the sensor circuit sample.
Through quantitative analysis of six different sample groups (ten-year pine stem, Capsella older embryo, housefly wing, circuit board, battery holder circuit, and sensor circuit), the proposed algorithm demonstrates superior performance in most SSIM and metrics, with particularly notable advantages in electronic component samples (e.g., circuit board SSIM reaches 0.929614, sensor circuit reaches 0.828196). Compared to traditional methods, DSIFT preserves details well but is sensitive to noise; frequency-domain approaches such as CVT, DTCWT, and NSCT tend to suffer from high-frequency feature loss; CNNs often produce over-smoothed results in biological samples, though performance improves with electronic samples. Table 8 summarizes the average metric values of each algorithm across the six samples. The results show that the proposed method achieves the highest scores in IE (6.2851), SSIM (0.8940), and (0.82097), and ranks second only to DWT in STD (25.2473 vs. 25.2784). This indicates that the proposed algorithm achieves an effective balance between structural fidelity and detail preservation, demonstrating excellent performance in both biological tissue and electronic component inspection, making it particularly suitable for industrial detection scenarios requiring micron-level precision.

Comparing the experimental results of Proposed and Proposed *, although down-sampling does lead to some loss of image data, the differences between the down-sampled and original resolution images are not significant in terms of quantitative metrics such as AG, STD, IE, and SSIM. This indicates that in most practical applications, the processed down-sampling approach can maintain sufficient feature retention while ensuring computational efficiency.
3.3. Computational Efficiency Evaluation
To effectively evaluate the computational efficiency of the algorithm, processing time tests were conducted on both the Windows platform and the Linux embedded platform. The Windows platform uses an Intel® CoreTM i7-9750H CPU with a clock speed of 2.60 GHz and 8 GB of RAM. The eight algorithms mentioned above were compared with the proposed algorithm. The experimental image resolution was 3840 × 2160, and the average processing time for ten multi-focus image fusion tests was recorded. The comparison algorithms were implemented using the source code provided by the authors, with the programming languages being MATLAB and C++.
In the Windows platform, the average processing time of different algorithms for image fusion is shown in Figure 23. Among them, traditional methods such as CVT, DSIFT, DTCWT, DWT, GF, and NSCT require longer processing time for complex high-resolution images, while the LP and the proposed algorithm in this paper demonstrate superior performance, with fusion times both below 100 ms, enabling real-time fusion. It should be noted that the CNN algorithm is not explicitly included in the figure due to its excessively long inference time.
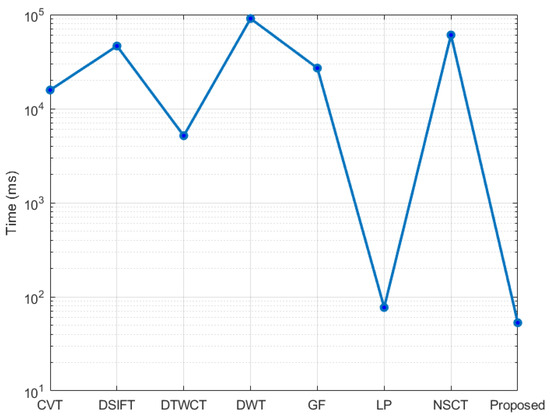
Figure 23.
The average fusion time of CVT, DSIFT, DTCWT, DWT, GF, LP, NSCT, and the proposed algorithm on the Windows platform.
The Linux embedded platform has a CPU of HiSilicon SS928V100 (Shenzhen, China), with a clock speed of 1.2 GHz and 1.4GB of RAM. Since only LP and the proposed algorithm have shorter processing times, and their processing times are in the same order of magnitude in the Windows environment, deployment tests were conducted for LP and the proposed algorithm on the Linux embedded platform. The experimental image resolution was 3840 × 2160, and the average processing time across ten repeated trials was recorded. The comparison algorithms were implemented based on the reference and deployed in the same environment and conditions. The programming language used was C++. The average fusion time of LP and the proposed algorithm on the Linux embedded platform is shown in Table 9.

Table 9.
The average fusion time of LP and the proposed algorithm in the Linux embedded platform.
In the embedded device, the proposed algorithm takes 0.586 s to perform a multi-focus image fusion processing on a 4K image. The processing time of LP is too long and cannot realize real-time processing.
In embedded devices with limited computing resources, LP takes a long time because it requires a large number of floating-point operations to ensure the quality of image fusion. In the proposed algorithm, in the image input stage, the regional interpolation method is used to reduce the image resolution, and in the decision map output stage, the nearest neighbor interpolation method is used to restore the decision map to the original resolution. This effectively reduces the amount of data and improves the computational efficiency of the algorithm. In addition, the pyramid operations used in the focus region detection are all integer operations for 8-bit data, rather than floating-point operations, which is more advantageous on resource-constrained embedded devices and more suitable for deployment in embedded devices
4. Conclusions
The algorithm proposed in this paper utilizes the difference of Gaussians and Laplacian pyramid methods to extract focused regions from microscopic images. To address the limited computational resources of embedded devices, an optimization strategy is introduced to enhance computational efficiency. The innovation lies in down-sampling the input used for focus region detection, thereby reducing the computational load by 75%, while applying up-sampling to the decision map output to ensure the fused image maintains its original resolution quality. Through comparative experiments, the study evaluates the advantages of the focus measure method and the overall algorithm in terms of efficiency and fusion quality. Supplementary Videos 1 and 2 provide dynamic demonstrations of real-time multi-focus image fusion using our proposed algorithm on embedded devices, where the experimental results demonstrate its effectiveness in extracting focused regions from microscopic images while significantly improving computational efficiency and maintaining image quality, enabling real-time performance on low-power embedded platforms. For future improvements, lightweight neural networks (e.g., MobileNet, EfficientNet) will be integrated to enhance the accuracy of focus region detection and improve robustness in complex scenarios such as transparent samples and high-noise environments. Additionally, the algorithm’s generalizability will be validated across various multi-focus imaging applications, including medical endoscopy and industrial inspection, with the aim of establishing more comprehensive evaluation criteria. The core value of this research lies in balancing algorithmic accuracy with deployability on embedded systems, providing a practical solution for real-time image processing in resource-constrained environments. Future work will focus on these directions to facilitate the application of this technology in more complex real-world scenarios.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app15136967/s1.
Author Contributions
Conceptualization, H.C.; Methodology, T.Z.; Software, H.C.; Formal analysis, H.C.; Investigation, X.D.; Data curation, H.H.; Writing—original draft, H.C.; Writing—review & editing, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yuan, T.; Jiang, W.; Ye, Y.Q. Confocal microscopy multi-focus image fusion method based on axial information guidance. Appl. Opt. 2023, 62, 5772–5777. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, L.; Cheng, J. Multi-focus image fusion: A Survey of the state of the art. Inf. Fusion 2020, 64, 71–79. [Google Scholar] [CrossRef]
- Li, X.S.; Zhou, F.Q.; Tan, H.S. Multi-focus image fusion based on nonsubsampled contourlet transform and residual removal. Signal Process. 2021, 184, 108062. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, X.; Peng, X. Shuffle-octave-yolo: A tradeoff object detection method for embedded devices. J. Real-Time Image Process. 2023, 20, 25. [Google Scholar] [CrossRef]
- Hu, Z.H.; Wang, L.; Ding, D.R. An improved multi-focus image fusion algorithm based on multi-scale weighted focus measure. Appl. Intell. 2021, 51, 4453–4469. [Google Scholar] [CrossRef]
- Bai, X.; Liu, M.; Chen, Z.; Wang, P.; Zhang, Y. Multi-focus image fusion through gradient-based decision map construction and mathematical morphology. IEEE Access 2016, 4, 4749–4760. [Google Scholar] [CrossRef]
- Li, S.; Kowk, J.T.; Wang, Y. combination of images with diverse focuses using spatial frequency. Inf. Fusion 2001, 2, 169–176. [Google Scholar] [CrossRef]
- Li, S.T.; Kang, X.D.; Fang, L.Y. Pixel-level image fusion: A survey of the state of the art. Inf. Fusion 2017, 33, 100–112. [Google Scholar] [CrossRef]
- Tian, J.; Liu, G.; Liu, J. Multi-focus image fusion based on edges and focused region extraction. Optik 2018, 171, 611–624. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, X.; Pei, H. Multi-focus image fusion algorithm based on focused region extraction. Neurocomputing 2016, 174, 733–748. [Google Scholar] [CrossRef]
- Yu, M.M.; Zheng, Y.L.; Liao, K.Y. Image quality assessment via spatial-transformed domains multi-feature fusion. IET Image Process. 2022, 14, 648–657. [Google Scholar] [CrossRef]
- Liu, W.; Zheng, Z.; Wang, Z. Robust multi-focus image fusion using lazy random walks with multiscale focus measures. Signal Process. 2021, 179, 107850. [Google Scholar] [CrossRef]
- Hill, P.; Al-Mualla, M.E.; Bull, D. Perceptual Image Fusion Using Wavelets. IEEE Trans. Image Process. 2017, 26, 1076–1088. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Li, S. Multi-focus image fusion and restoration with sparse representation. IEEE Trans. Instrum. Meas. 2009, 59, 884–892. [Google Scholar] [CrossRef]
- Yin, H.; Li, Y.; Chai, Y.; Liu, Z.; Zhu, Z. A novel sparse-representation-based multi-focus image fusion approach. Neurocomputing 2016, 216, 216–229. [Google Scholar] [CrossRef]
- Mustafa, H.T.; Yang, J.; Zareapoor, M. Multi-scale convolutional neural network for multi-focus image fusion. Image Vis. Comput. 2019, 85, 26–35. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Peng, H.; Wang, Z. Multi-focus image fusion with a deep convolutional neural network. Inf. Fusion 2017, 36, 191–207. [Google Scholar] [CrossRef]
- Guo, X.; Nie, R.; Cao, J.; Zhou, D.; Mei, L.; He, K. Fusegan: Learning to fuse multi-focus image via conditional generative adversarial network. IEEE Trans. Multimed. 2019, 21, 1982–1996. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.Y.; Wang, J.Q. Multi-focus image fusion for microscopic depth-of-field extension of waterjet-assisted laser pro-cessing. Int. J. Adv. Manuf. Technol. 2024, 131, 1717–1734. [Google Scholar] [CrossRef]
- Yu, Z.; Bai, X.Z.; Wang, T. Boundary finding based multi-focus image fusion through multi-scale morphological focus-measure. Inf. Fusion 2017, 35, 81–101. [Google Scholar]
- Huang, W.; Jing, Z. Evaluation of focus measures in multi-focus image fusion. Pattern Recognit. Lett. 2007, 28, 493–500. [Google Scholar] [CrossRef]
- Roy, M.; Mukhopadhyay, S. A scheme for edge-based multi-focus Color image fusion. Multimed. Tools Appl. 2020, 79, 24089–24117. [Google Scholar] [CrossRef]
- Pertuz, S.; Puig, D.; Garcia, M.A. Analysis of focus measure operators for shape-from-focus. Pattern Recognit. 2013, 46, 1415–1432. [Google Scholar] [CrossRef]
- Naidu, V.P.S. Multi focus image fusion using the measure of focus. J. Opt. 2012, 41, 117–125. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.P.; Wang, Z.F. Multi-focus image fusion with dense SIFT. Inf. Fusion 2015, 23, 139–155. [Google Scholar] [CrossRef]
- Burt, P.; Adelson, E. The Laplacian pyramid as a compact image code. IEEE Trans. Commun 1983, 31, 532–540. [Google Scholar] [CrossRef]
- Nencini, F.; Garzelli, A.; Baronti, S.; Alparone, L. Remote sensing image fusion using the curvelet transform. Inf. Fusion 2007, 8, 143–156. [Google Scholar] [CrossRef]
- Lewis, J.; O’Callaghan, R.; Nikolov, S.; Bull, D.; Canagarajah, N. Pixel and regionbased image fusion with complex wavelets. Inf. Fusion 2007, 8, 119130. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, B. Multifocus image fusion using the nonsubsampled contourlet transform. Signal Process. 2009, 89, 1334–1346. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.F. Multi-focus image fusion based on wavelet transform and adaptive block. J. Image Graph. 2013, 18, 1435–1444. [Google Scholar]
- Qiu, X.; Li, M.; Zhang, L.; Yuan, X. Guided filter-based multi-focus image fusion through focus region detection. Signal Process. Image Commun. 2019, 72, 35–46. [Google Scholar] [CrossRef]
- Zhang, Q.; Maldague, X. An adaptive fusion approach for infrared and visible images based on NSCT and compressed sensing. Infrared Phys. Technol. 2016, 74, 11–20. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Zhuang, J.J.; Ye, S.C. Image Restoration Quality Assessment Based on Regional Differential Information Entropy. Entropy 2023, 25, 144. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.Q.; Huang, J.C.; Liu, Z. Image quality assessment using natural image statistics in gradient domain. AEU-Int. J. Electron. Commun. 2011, 65, 392–397. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Liu, Z.; Blasch, E.; Xue, Z. Objective Assessment of Multiresolution Image Fusion Algorithms for Context Enhancement in Night Vision: A Comparative Study. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 94–109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).