Smooth Optimised A*-Guided DWA for Mobile Robot Path Planning
Abstract
1. Introduction
2. Global Path Planning
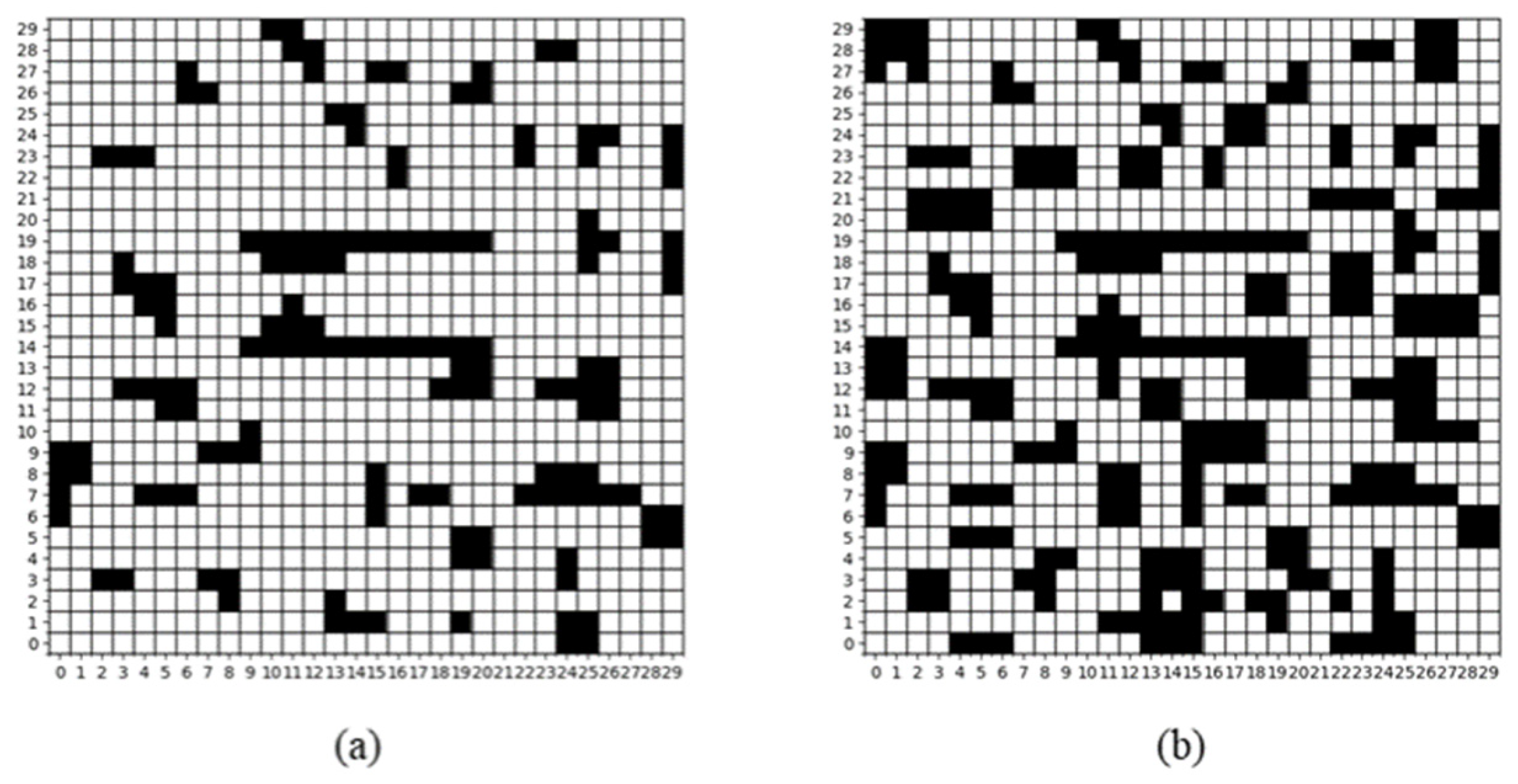
2.1. Environment Building
2.2. Traditional A* Algorithm
2.3. Improved A* Algorithm
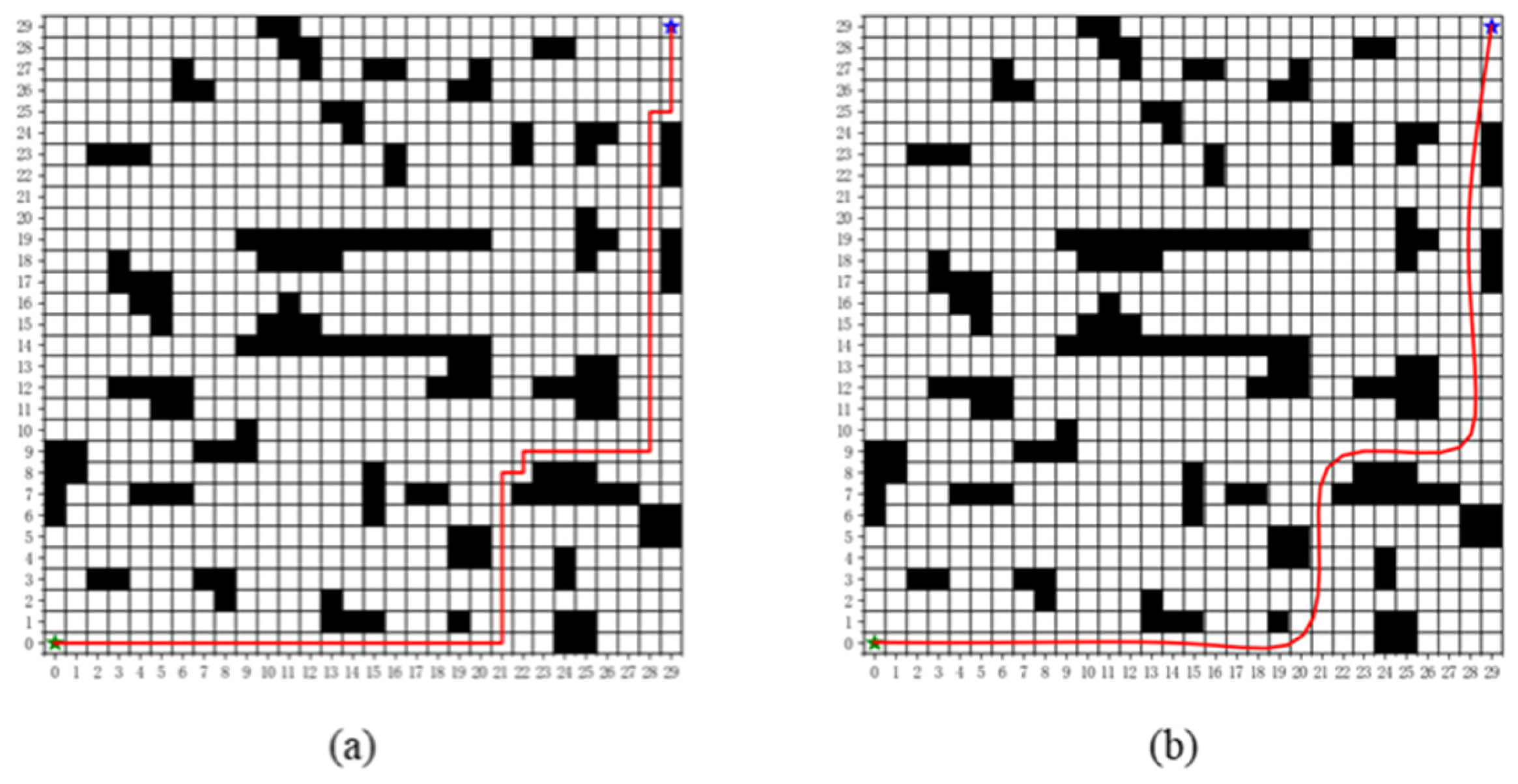
2.3.1. Path Pruning
2.3.2. Path Smoothing
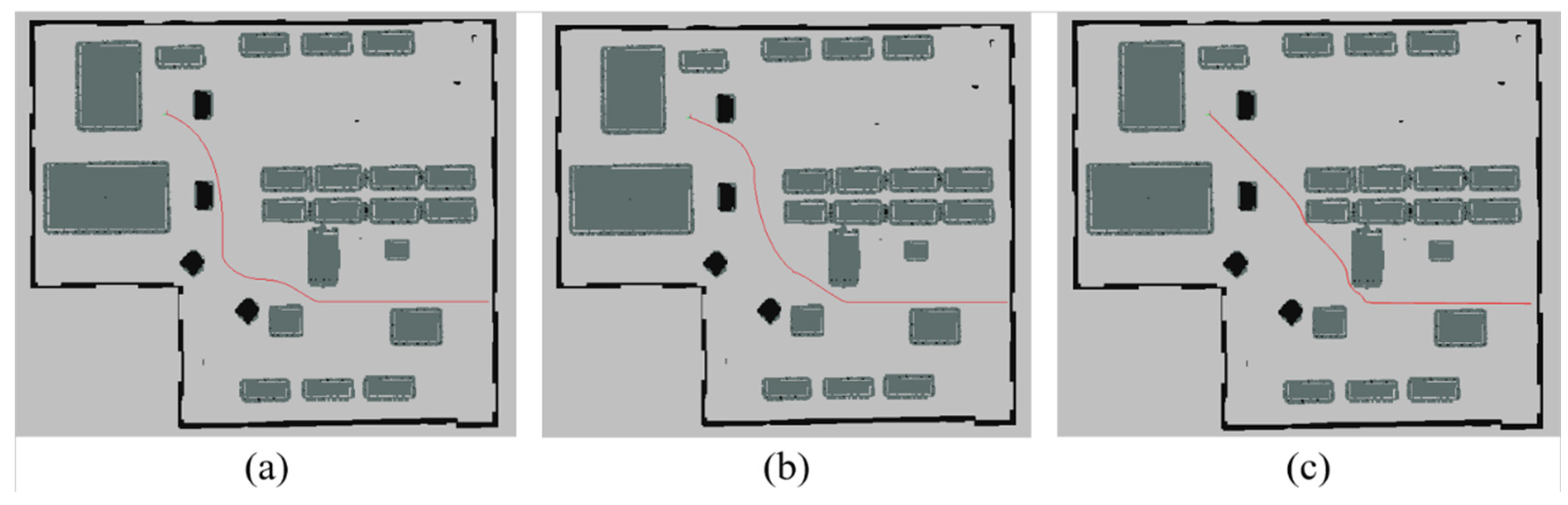
2.4. Comparative Analysis of Improved A* Algorithms
3. Smoothing Optimisation A*-Guided DWA
3.1. DWA Algorithm
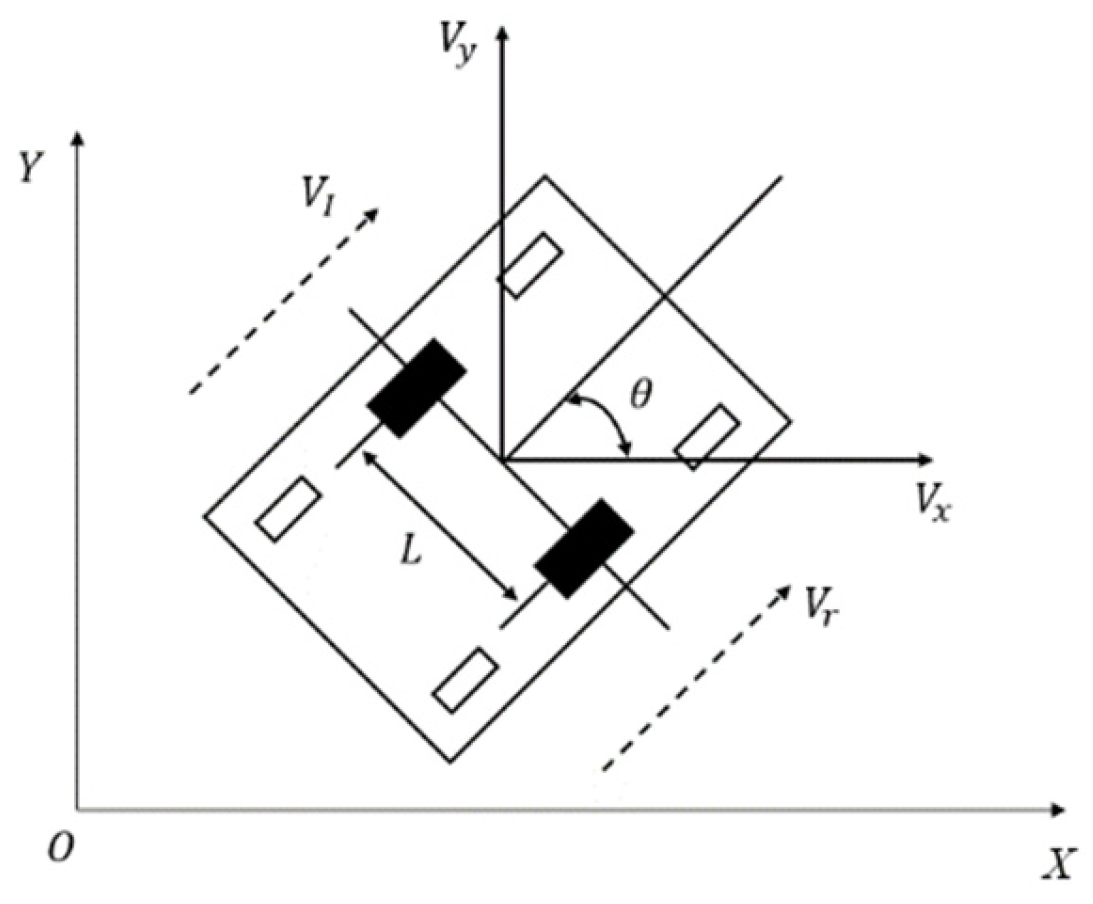
3.1.1. Vehicle Kinematics Modelling
3.1.2. Speed Sampling
- (1)
- Maximum speed and minimum speed
- (2)
- Motor performance
- (3)
- Obstacles
3.1.3. Evaluation Function for DWA
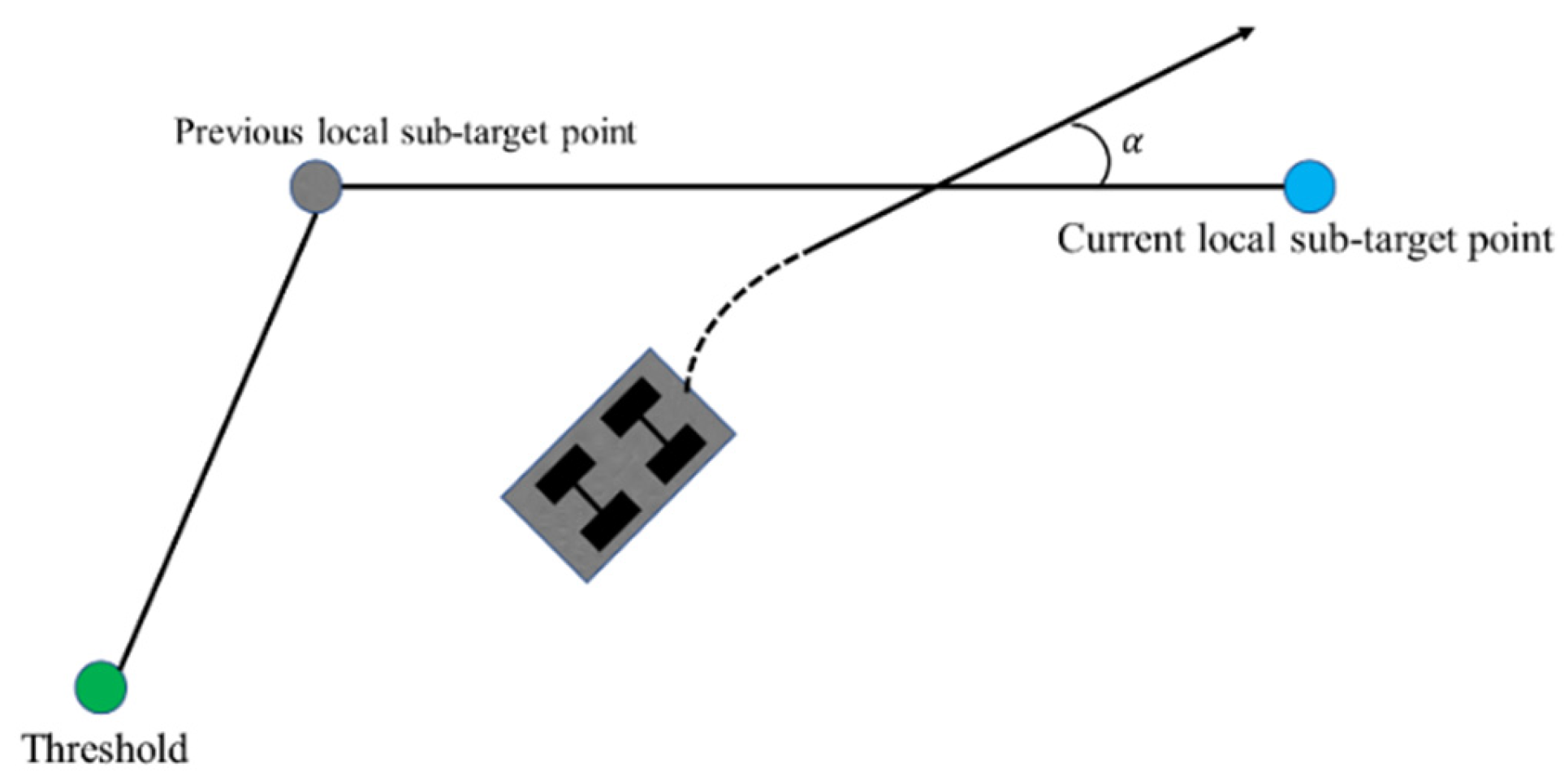
3.2. Enhanced Global Path Constraints
- (1)
- Evaluation subfunction of the distance between the reference trajectory and the global path
- (2)
- Path direction evaluation
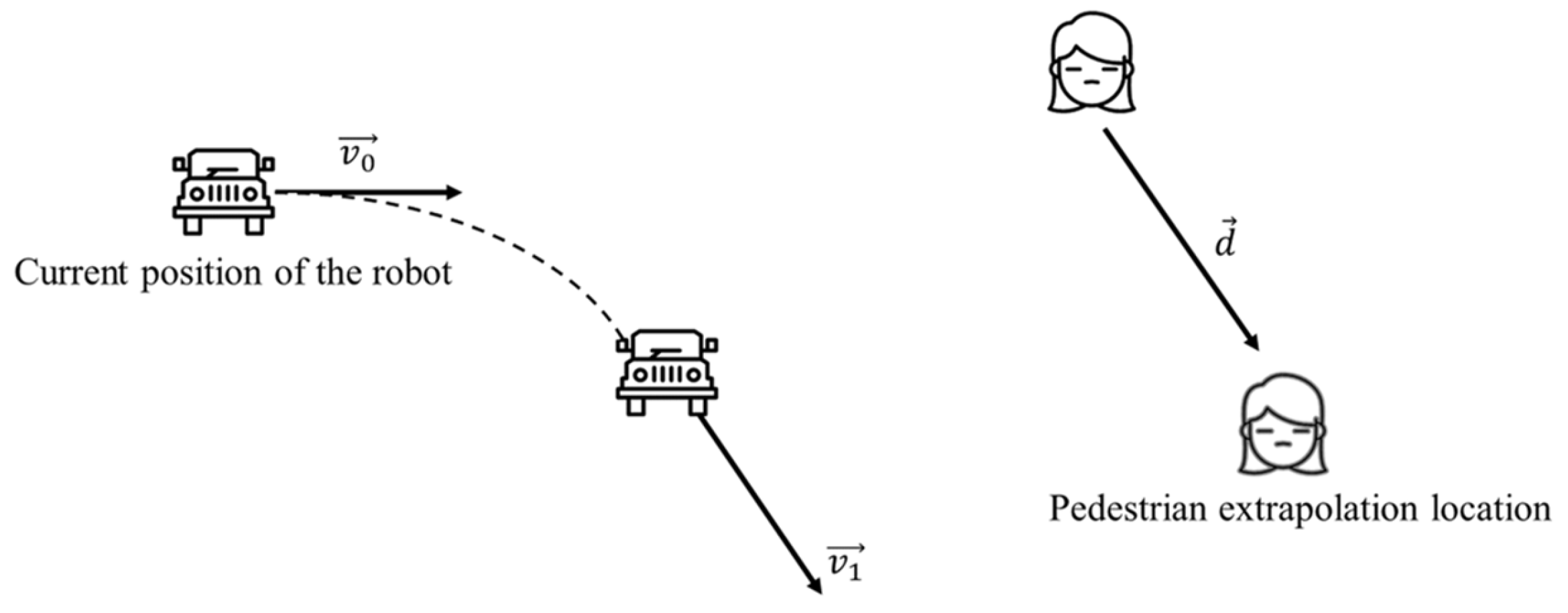
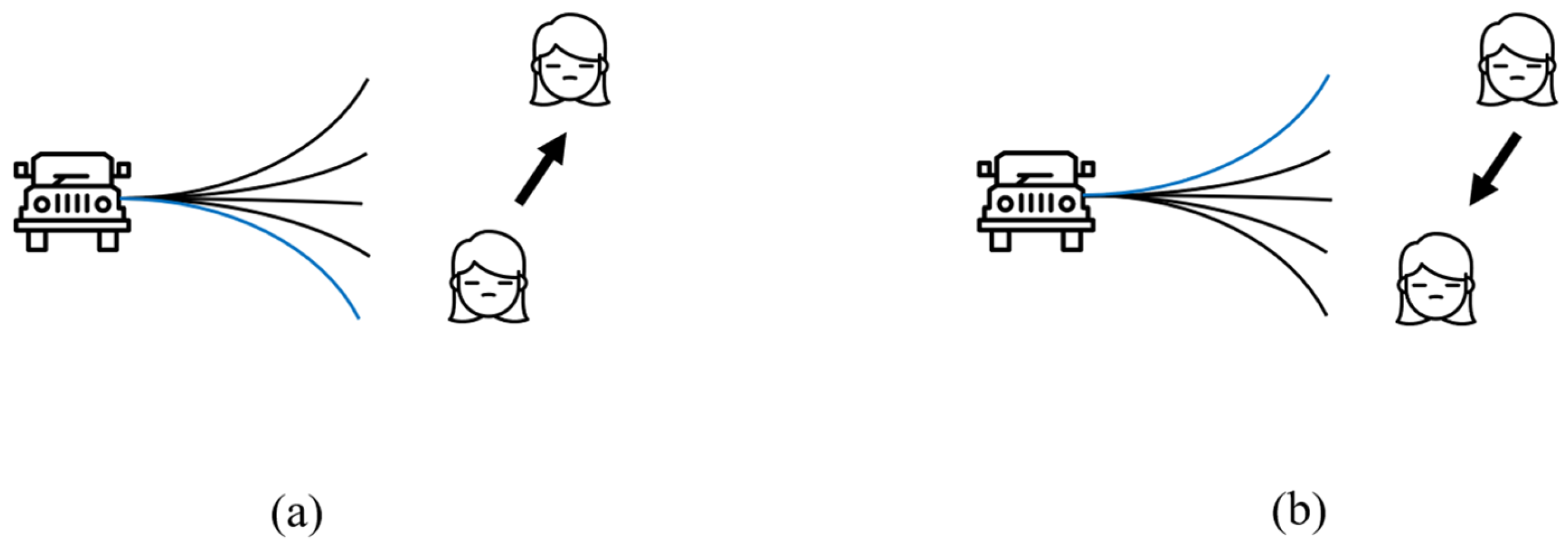
3.3. Optimisation of Obstacle Avoidance Efficiency
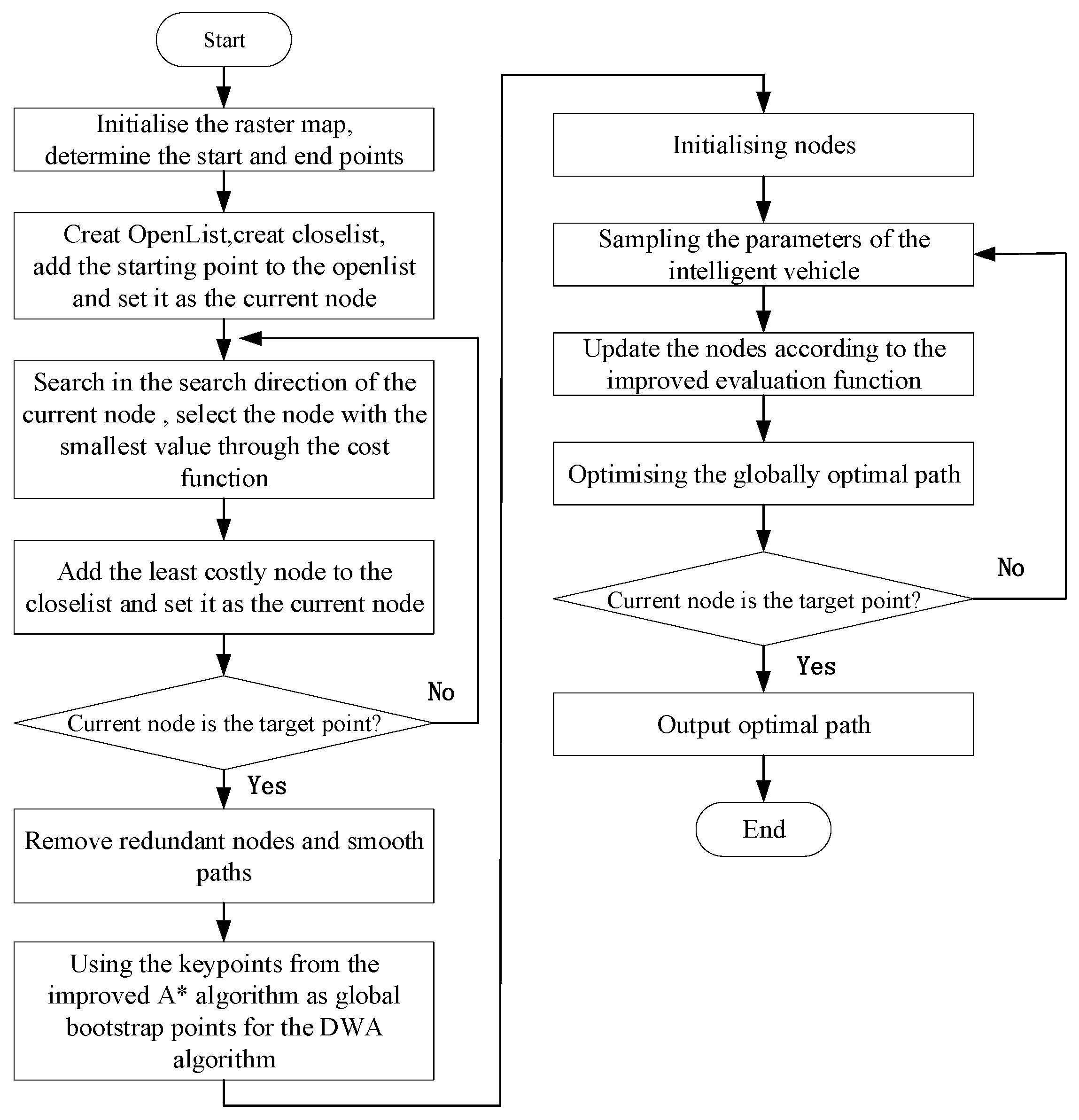
4. Steps and Processes of SOA-DWA Algorithm
5. Simulation Experiments and Analyses
5.1. Ablation Study
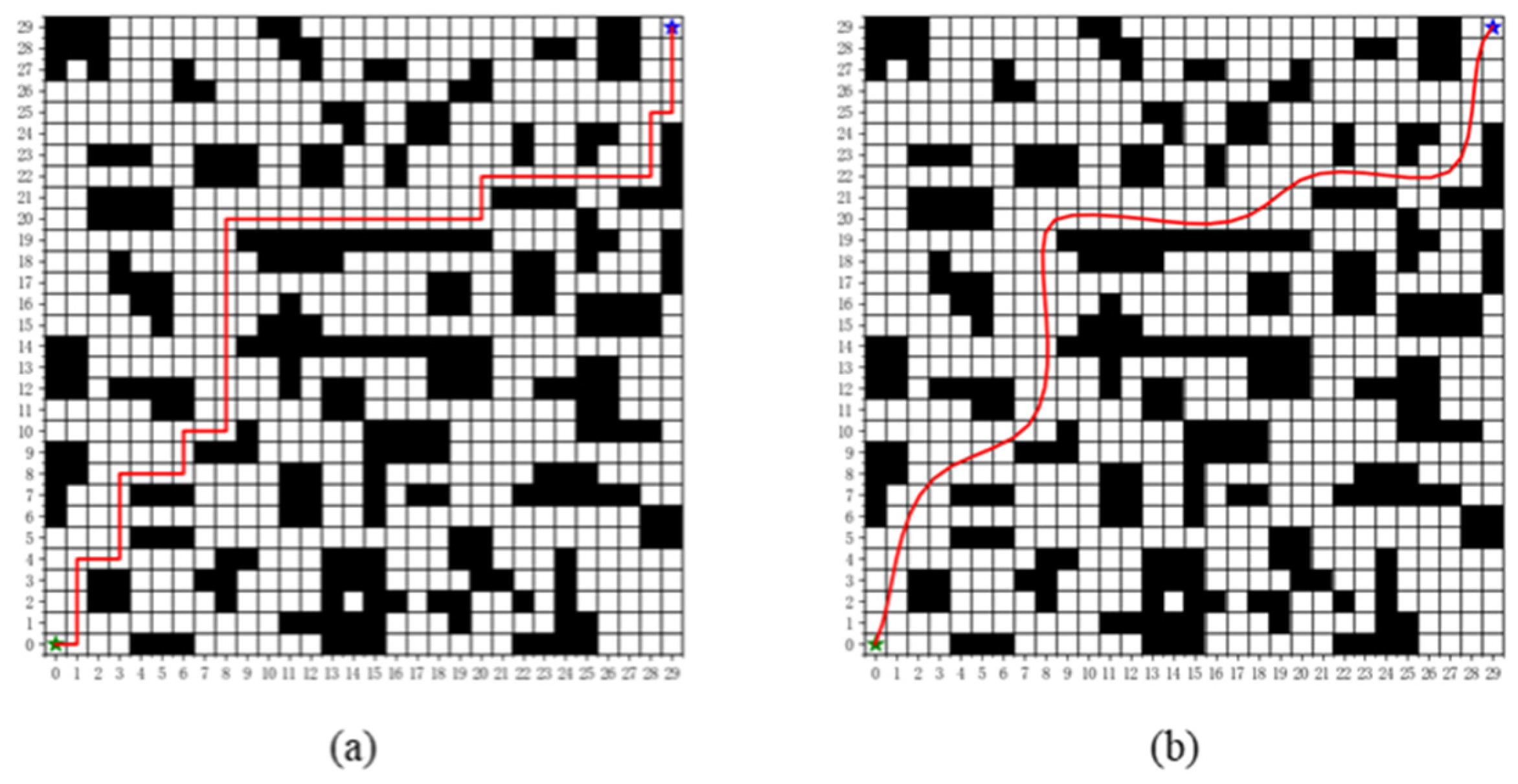
5.2. Validation of Algorithm Effectiveness
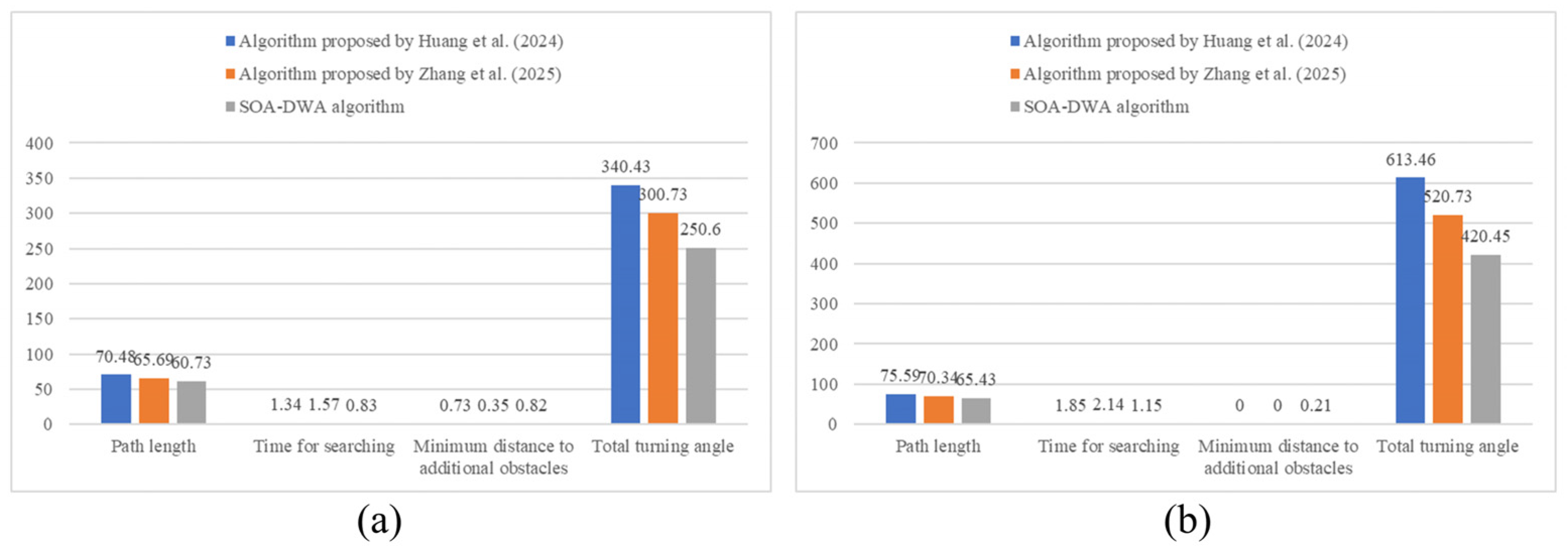
5.3. Comparative Analysis of Algorithm Performance
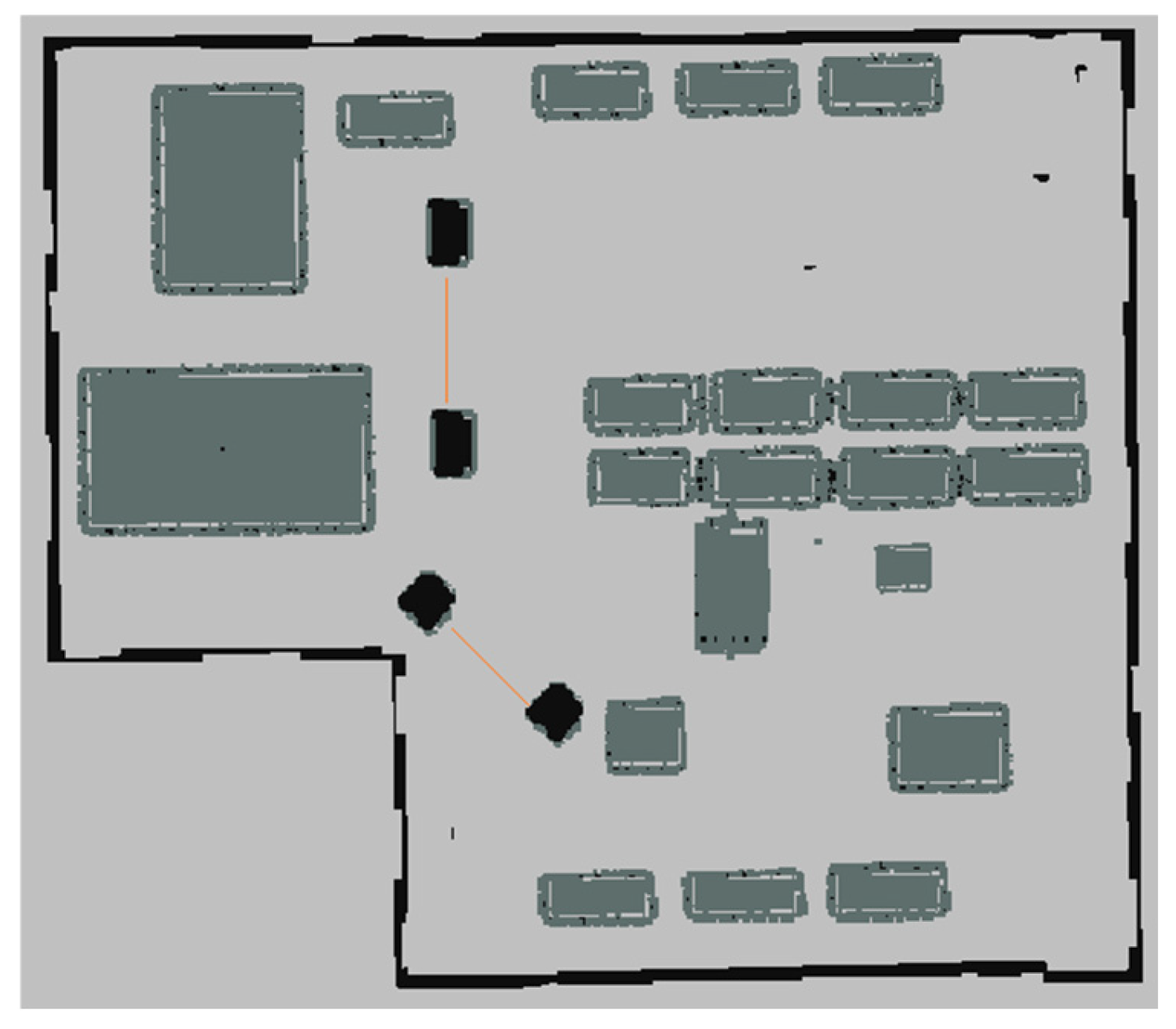
5.4. Mobile Robot Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, T.; Wei, W. Mobile robot path planning based on an improved ACO algorithm and path optimization. Multimed. Tools Appl. 2024, 84, 10899–10922. [Google Scholar] [CrossRef]
- Dang, T.-V.; Tan, P.X. Hybrid Mobile Robot Path Planning Using Safe JBS-A*B Algorithm and Improved DWA Based on Monocular Camera. J. Intell. Robot. Syst. 2024, 110, 151. [Google Scholar] [CrossRef]
- Cao, S.; Sui, G.; Zhou, G. Path tracking control with delay characteristics for unmanned vehicles in aquaculture workshops. J. Fish. China 2024, 48, 133–144. [Google Scholar]
- Katona, K.; Neamah, H.A.; Korondi, P. Obstacle Avoidance and Path Planning Methods for Autonomous Navigation of Mobile Robot. Sensors 2024, 24, 3573. [Google Scholar] [CrossRef] [PubMed]
- Galarza-Falfan, J.; García-Guerrero, E.; Aguirre-Castro, O.; Lopez-Bonilla, O.; Tamayo Pérez, U.; Cárdenas-Valdez, J.; Hernández-Mejía, C.; Borrego-Dominguez, S.; Inzunza Gonzalez, E. Path Planning for Autonomous Mobile Robot Using Intelligent Algorithms. Technologies 2024, 12, 82. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Lun, Q.; Luxin, H.; Boyu, Z.; Shaojie, S.; Fei, G. Survey of UAV motion planning. IET Cyber-Syst. Robot. 2020, 2, 14–21. [Google Scholar]
- Xu, X.; Zeng, J.; Zhao, Y.; Lü, X. Research on global path planning algorithm for mobile robots based on improved A*. Expert Syst. Appl. 2024, 243, 122922. [Google Scholar] [CrossRef]
- Xing, S.; Fan, P.; Ma, X.; Wang, Y. Research on robot path planning by integrating state-based decision-making A* algorithm and inertial dynamic window approach. Intell. Serv. Robot. 2024, 17, 901–914. [Google Scholar] [CrossRef]
- Zhu, D.D.; Sun, J.Q. A New Algorithm Based on Dijkstra for Vehicle Path Planning Considering Intersection Attribute. IEEE Access 2021, 9, 19761–19775. [Google Scholar] [CrossRef]
- Ma, G.; Duan, Y.; Li, M.; Xie, Z.; Zhu, J. A probability smoothing Bi-RRT path planning algorithm for indoor robot. Future Gener. Comput. Syst. 2023, 143, 349–360. [Google Scholar] [CrossRef]
- Ganesan, S.; Ramalingam, B.; Mohan, R.E. A hybrid sampling-based RRT* path planning algorithm for autonomous mobile robot navigation. Expert Syst. Appl. 2024, 258, 125206. [Google Scholar] [CrossRef]
- Orozco-Rosas, U.; Picos, K.; Pantrigo, J.J.; Montemayor, A.S.; Cuesta-Infante, A. Mobile Robot Path Planning Using a QAPF Learning Algorithm for Known and Unknown Environments. IEEE Access 2022, 10, 84648–84663. [Google Scholar] [CrossRef]
- Bonny, T.; Kashkash, M. Highly optimised Q-learning-based bees approach for mobile robot path planning in static and dynamic environments. J. Field Robot. 2021, 39, 317–334. [Google Scholar] [CrossRef]
- Gong, X.; Gao, Y.; Wang, F.; Zhu, D.; Zhao, W.; Wang, F.; Liu, Y. A Local Path Planning Algorithm for Robots Based on Improved DWA. Electronics 2024, 13, 2965. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimisation algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Xiong, N.; Zhou, X.; Yang, X.; Xiang, Y.; Ma, J. Mobile Robot Path Planning Based on Time Taboo Ant Colony Optimisation in Dynamic Environment. Front. Neurorobot. 2021, 15, 642733. [Google Scholar] [CrossRef]
- Hu, M.; Li, X.; Ren, Z.; Zeng, S. Three-dimensional path planning for UAVs based on A* algorithm with improved heuristic function. Acta Armamentarii 2024, 45, 302–307. [Google Scholar]
- Yan, J.; Liu, C.; Sun, H.; Chen, X. Research on path planning algorithm for mobile robots based on improved A* fused with DWA. J. Yuncheng Univ. 2024, 42, 45–51. [Google Scholar]
- Sun, Y.; Wang, R.; Jiang, D. Dynamic path planning for surface vessels based on fusion of A* and DWA algorithms. Chin. J. Sci. Instrum. 2024, 45, 301–310. [Google Scholar]
- Liu, L.; Wang, X.; Wang, X.; Xie, J.; Liu, H.; Li, J.; Wang, P.; Yang, X. Path Planning and Tracking Control of Tracked Agricultural Machinery Based on Improved A* and Fuzzy Control. Electronics 2024, 13, 188. [Google Scholar] [CrossRef]
- Lai, R.; Wu, Z.; Liu, X.; Zeng, N. Fusion Algorithm of the Improved A* Algorithm and Segmented Bézier Curves for the Path Planning of Mobile Robots. Sustainability 2023, 15, 2483. [Google Scholar] [CrossRef]
- He, L.; Ning, Z.; Yuan, L.; Liu, Z. Path planning for service robots using socially constrained adaptive dynamic window approach. J. Xi’an Jiaotong Univ. 2024, 58, 42–51. [Google Scholar]
- Huang, J.; Chen, X. Research on robot fusion algorithm based on improved A* and DWA. Chin. J. Sens. Actuators 2024, 37, 2043–2049. [Google Scholar]
- Zhang, Y.; Li, B.; Huo, T.; Liu, T. Research on robot dynamic obstacle avoidance method combining improved A* algorithm with DWA algorithm. J. Syst. Simul. 2025, 1, 1–10. [Google Scholar]



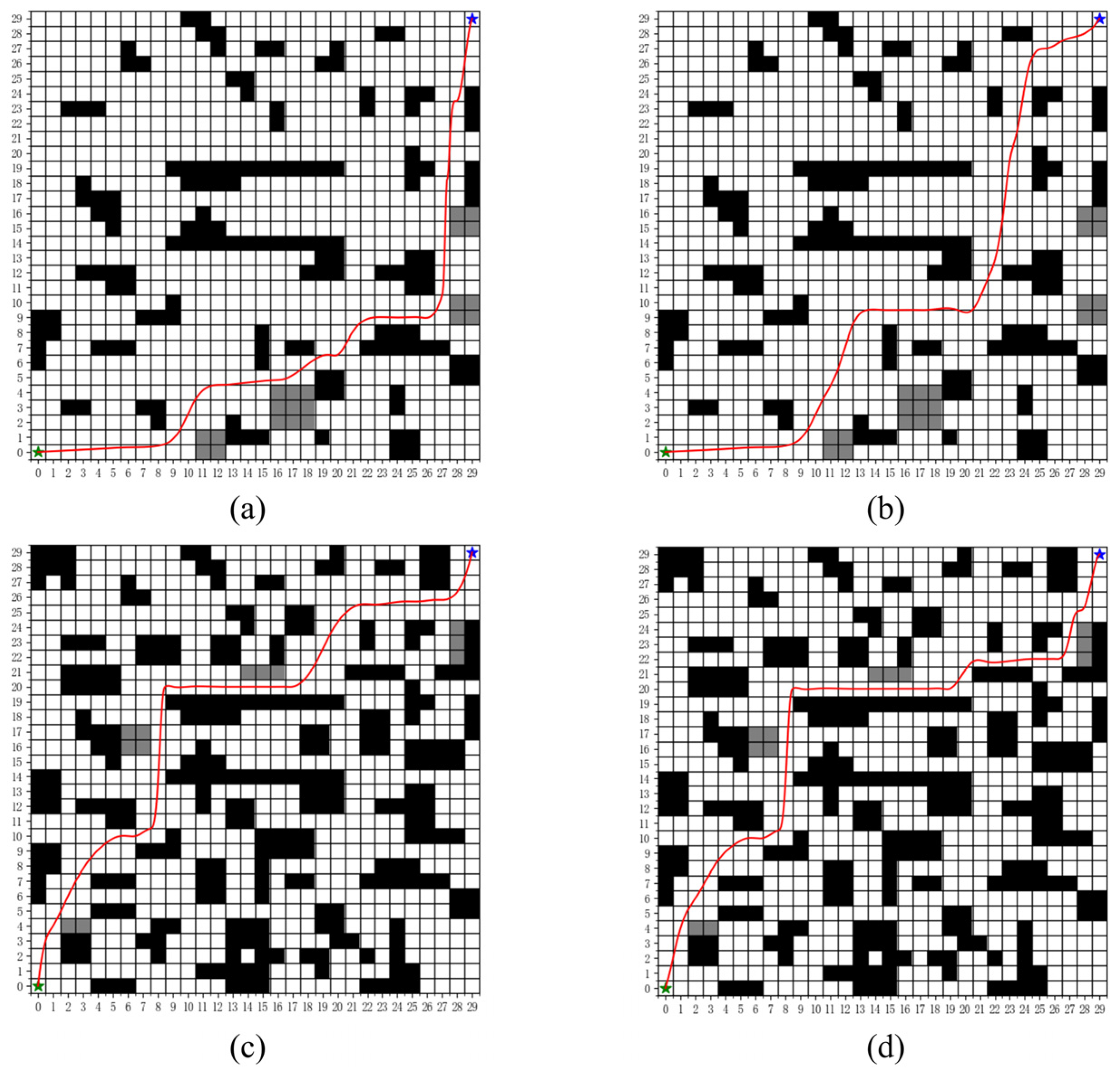
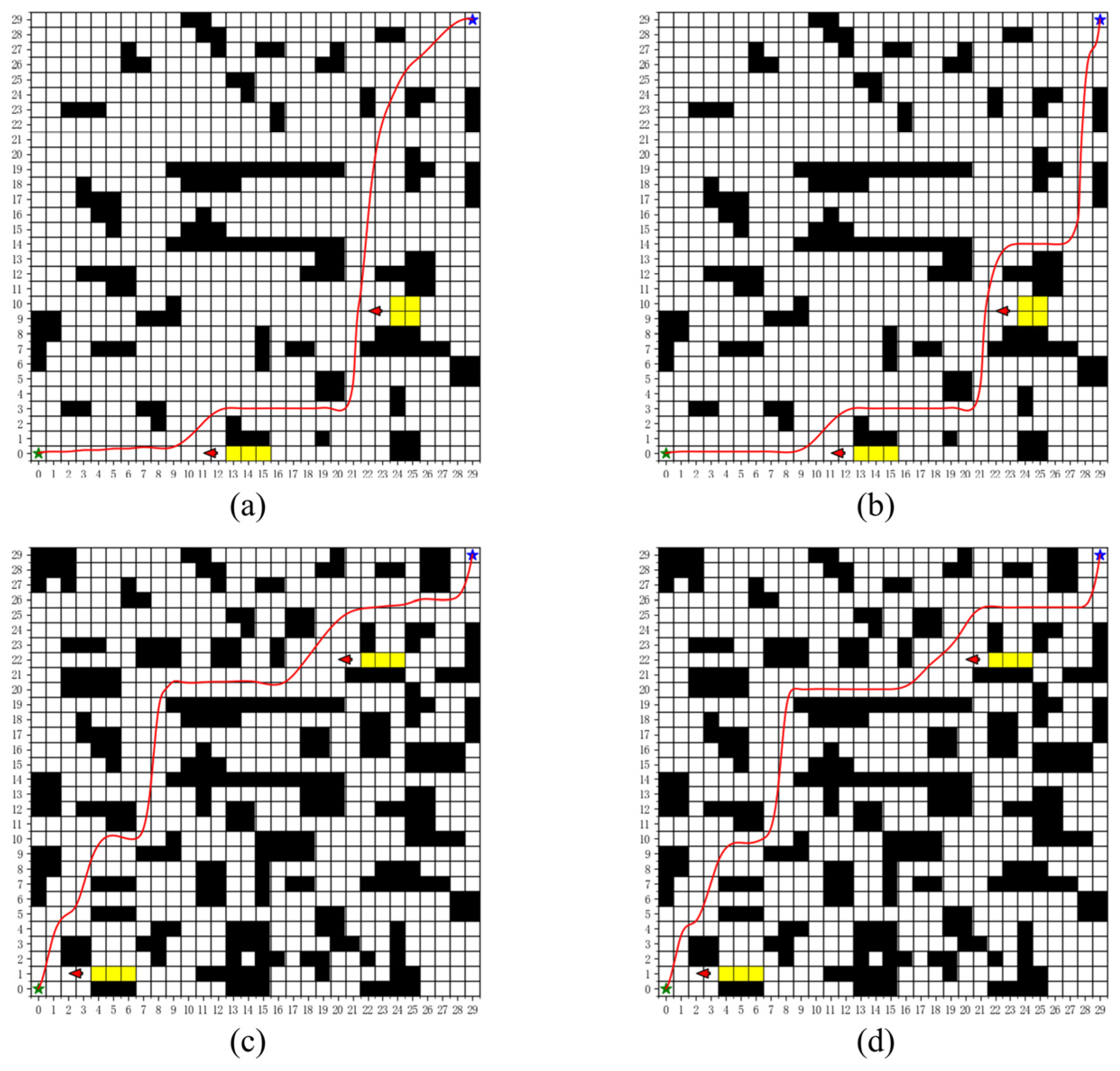



| Environment | Algorithm | Number of Path Points (Mean ± Standard Deviation) | Number of Turning Points (Mean ± Standard Deviation) | Number of Nonsmooth Turning Points (Mean ± Standard Deviation) | Path Length (Mean ± Standard Deviation)/m |
|---|---|---|---|---|---|
| Simple Environment | Traditional A* algorithm | 60.1 ± 1.2 | 7.2 ± 0.4 | 7.0 ± 0.2 | 57.2 ± 0.9 |
| Improved A* algorithm | 8.3 ± 0.3 | 4.1 ± 0.2 | 0 ± 0 | 55.98 ± 0.7 | |
| Complex Environment | Traditional A* algorithm | 60.5 ± 1.5 | 13.2 ± 0.6 | 13.1 ± 0.3 | 58.6 ± 1.0 |
| Improved A* algorithm | 7.2 ± 0.4 | 5.1 ± 0.2 | 0 ± 0 | 49.11 ± 0.8 |
| Parameter | Parameter Meaning |
|---|---|
| Minimum and maximum speed of the current state | |
| Minimum pendulum angular velocity and maximum pendulum angular velocity in the current state | |
| Current velocity, angular velocity | |
| Maximum acceleration and deceleration | |
| Maximum transverse pendulum angular acceleration and deceleration | |
| Sampling period | |
| Distance to the nearest obstacle on the end of the current trajectory | |
| Maximum deceleration | |
| Maximum transverse angular deceleration |
| Environment | Algorithm | Number of Turning Points (Mean ± Standard Deviation) | Number of Nonsmooth Turning Points (Mean ± Standard Deviation) | Total Turning Angle (Mean ± Standard Deviation) | Path Length (Mean ± Standard Deviation)/m | |
|---|---|---|---|---|---|---|
| Static Known Scenario | Scenario 1 | Baseline A* | 7.1 ± 0.94 | 7 ± 0.62 | 643.5 ± 21.1 | 57.2 ± 0.76 |
| A* with pruning | 5.9 ± 0.53 | 6.1 ± 0.48 | 589.6 ± 15.4 | 55.7 ± 0.42 | ||
| A* with smoothing | 5.5 ± 0.46 | 0 ± 0 | 553.7 ± 10.6 | 56.4 ± 0.53 | ||
| Scenario 2 | Baseline A* | 13.4 ± 0.84 | 13.1 ± 0.68 | 1152.4 ± 25.9 | 59 ± 0.55 | |
| A* with pruning | 10.5 ± 0.62 | 11.4 ± 0.56 | 1024.7 ± 16.3 | 56 ± 0.5 | ||
| A* with smoothing | 8.7 ± 0.51 | 0 ± 0 | 934.5 ± 12.5 | 57.3 ± 0.55 | ||
| Environment | Algorithm | Time for Search (Mean ± Standard Deviation)/s | Total Turing Angle (Mean ± Standard Deviation) | Path Length (Mean ± Standard Deviation)/m | |
|---|---|---|---|---|---|
| Dynamic Unknown Scenario | Scenario 1 | Baseline DWA | 1.56 ± 0.15 | 382.4 ± 8.6 | 59.1 ± 0.53 |
| DWA with global path constraints | 1.47 ± 0.13 | 347.6 ± 6.5 | 55.8 ± 0.3 | ||
| DWA with optimisation of obstacle avoidance efficiency | 1.12 ± 0.09 | 344.2 ± 6 | 58.5 ± 0.48 | ||
| Scenario 2 | Baseline DWA | 2.1 ± 0.27 | 630.8 ± 11.5 | 62.6 ± 0.39 | |
| DWA with global path constraints | 1.89 ± 0.21 | 583.7 ± 9.75 | 60.1 ± 0.25 | ||
| DWA with optimisation of obstacle avoidance efficiency | 1.57 ± 0.19 | 577.3 ± 9.37 | 62 ± 0.38 | ||
| Environment | Algorithm | Number of Turning Points (Mean ± Standard Deviation) | Number of Nonsmooth Turning Points (Mean ± Standard Deviation) | Total Turning Angle (Mean ± Standard Deviation) | Path Length (Mean ± Standard Deviation)/m | |
|---|---|---|---|---|---|---|
| Static Known Scenario | Scenario 1 | A* | 7.2 ± 0.96 | 6.9 ± 0.64 | 642 ± 20.79 | 57.5 ± 0.8 |
| DWA | 7.6 ± 0.88 | 1.2 ± 0.1 | 615.4 ± 17.16 | 65.8 ± 0.6 | ||
| SOA-DWA | 5.4 ± 0.54 | 0 ± 0 | 550 ± 8.64 | 55.1 ± 0.4 | ||
| Scenario 2 | A* | 13.4 ± 0.85 | 13 ± 0.74 | 1153 ± 26.5 | 58.5 ± 0.6 | |
| DWA | 8.3 ± 0.73 | 0.9 ± 0.1 | 862.2 ± 18.7 | 61.9 ± 0.55 | ||
| SOA-DWA | 5.6 ± 0.46 | 0 ± 0 | 775.4 ± 10.5 | 55.2 ± 0.3 | ||
| Static Unknown Scenario | Scenario 1 | DWA | 8.2 ± 0.64 | 1.5 ± 0.3 | 614.7 ± 13.67 | 57.2 ± 0.4 |
| SOA-DWA | 7.9 ± 0.32 | 0 ± 0 | 575.4 ± 9.54 | 54.6 ± 0.2 | ||
| Scenario 2 | DWA | 10.6 ± 0.42 | 1.3 ± 0.25 | 626.8 ± 10.8 | 50.95 ± 0.42 | |
| SOA-DWA | 9.8 ± 0.25 | 0 ± 0 | 589.6 ± 7.6 | 49.1 ± 0.25 | ||
| Dynamic Unknown Scenario | Scenario 1 | DWA | 7.7 ± 0.52 | 2.1 ± 0.45 | 376.9 ± 8.2 | 58.6 ± 0.45 |
| SOA-DWA | 5.6 ± 0.38 | 0 ± 0 | 326.5 ± 5.8 | 55.2 ± 0.26 | ||
| Scenario 2 | DWA | 9.3 ± 0.73 | 1.8 ± 0.5 | 628.7 ± 10.54 | 62.23 ± 0.37 | |
| SOA-DWA | 7.9 ± 0.43 | 0 ± 0 | 510.5 ± 6.5 | 59.8 ± 0.15 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.; Tang, L.; Cao, S.; Sun, Q.; Zhou, G. Smooth Optimised A*-Guided DWA for Mobile Robot Path Planning. Appl. Sci. 2025, 15, 6956. https://doi.org/10.3390/app15136956
Cao L, Tang L, Cao S, Sun Q, Zhou G. Smooth Optimised A*-Guided DWA for Mobile Robot Path Planning. Applied Sciences. 2025; 15(13):6956. https://doi.org/10.3390/app15136956
Chicago/Turabian StyleCao, Liling, Lei Tang, Shouqi Cao, Qing Sun, and Guofeng Zhou. 2025. "Smooth Optimised A*-Guided DWA for Mobile Robot Path Planning" Applied Sciences 15, no. 13: 6956. https://doi.org/10.3390/app15136956
APA StyleCao, L., Tang, L., Cao, S., Sun, Q., & Zhou, G. (2025). Smooth Optimised A*-Guided DWA for Mobile Robot Path Planning. Applied Sciences, 15(13), 6956. https://doi.org/10.3390/app15136956




