MM-VSM: Multi-Modal Vehicle Semantic Mesh and Trajectory Reconstruction for Image-Based Cooperative Perception
Abstract
1. Introduction
Contributions
- A novel multi-modal (LiDAR and camera) and multi-view (single- and multiple-camera setups) Semantic Mesh Model reconstruction algorithm, which outperforms the original monocular version by a significant margin.
- A novel cooperative perception architecture specifically suitable for smart parking garages due to low-cost sensor integration and ease of deployment without context-specific 3D data annotation.
- A novel metric effectively identifying faulty pose estimates significantly improving reliability and safety in autonomous driving scenarios.
2. Related Works
2.1. Cooperative 3D Object Detection
2.2. Pose Estimation and Shape Reconstruction
2.3. Semantic Vertex Model Reconstruction
3. Materials and Methods
- The object reference shape is constructed using the LiDAR bounding box timeseries.
- The semantic keypoints are extracted, tracked and matched to the LiDAR bounding boxes throughout the trajectory.
- The shape and trajectory of the Semantic Mesh Model are optimized, minimizing 2D re-projection loss between the keypoints and vertices as well as 3D shape loss between the Semantic Mesh Model and the reference shape.
- The reconstructed Semantic Mesh Model can be used for single, or multi-image-based pose estimation.
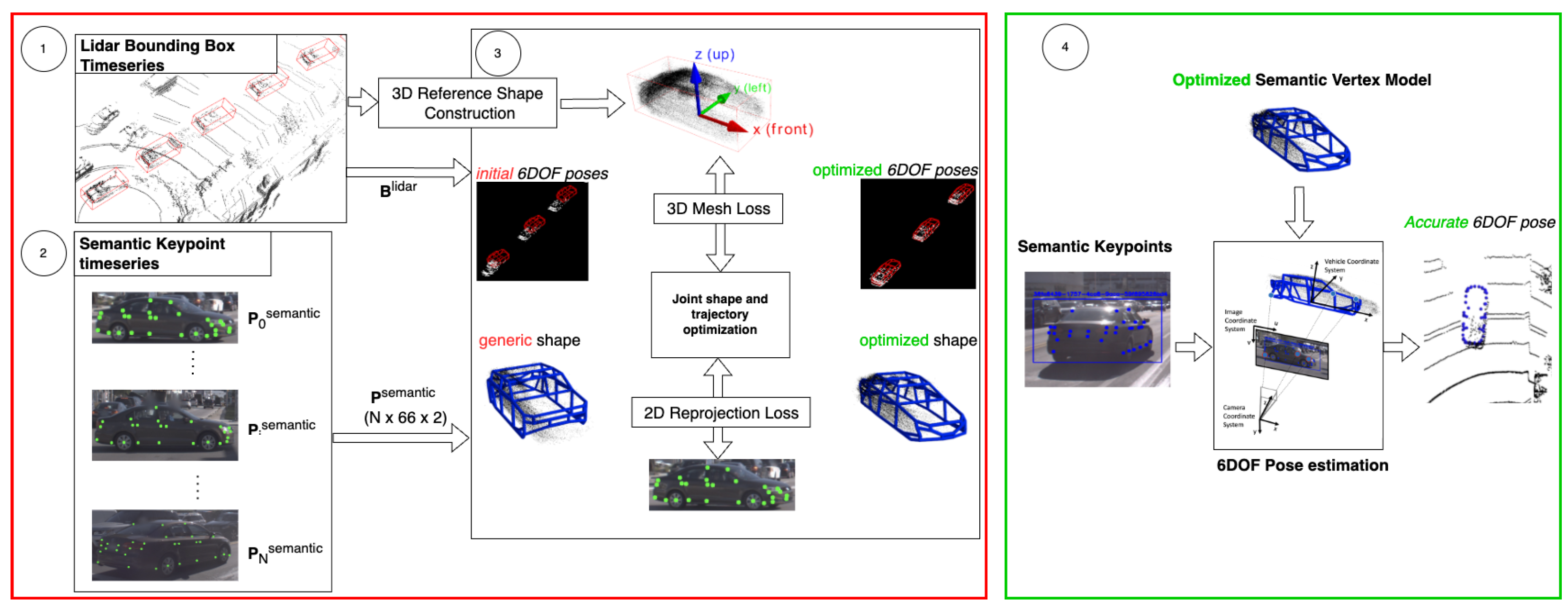
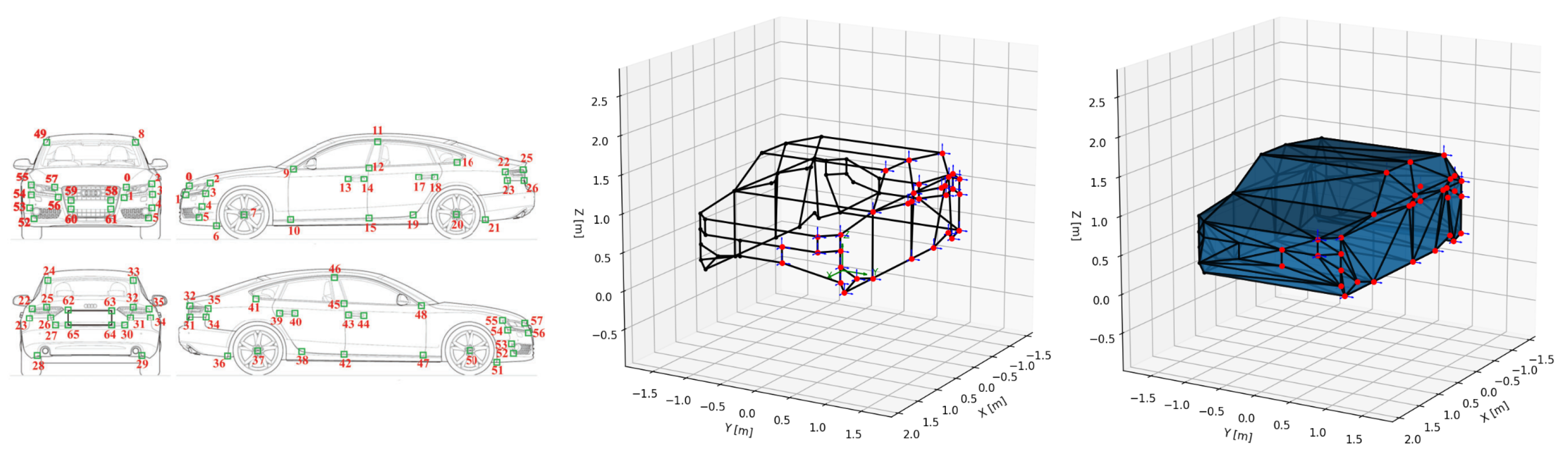
3.1. Problem Statement
- is the aforementioned vertex set.
- is the set of triangular faces defined by vertex indices, creating a watertight manifold mesh representing the vehicle’s surface:
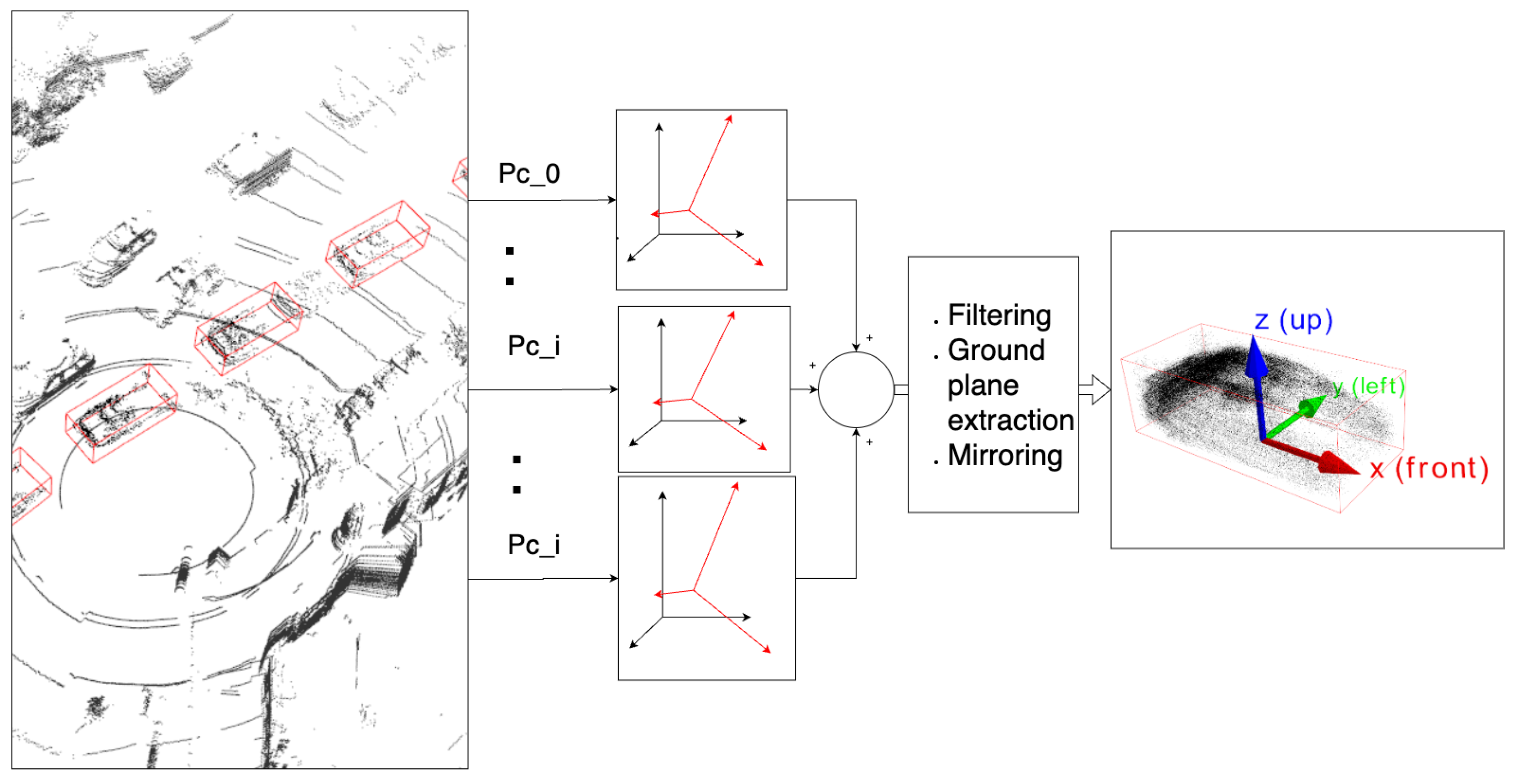
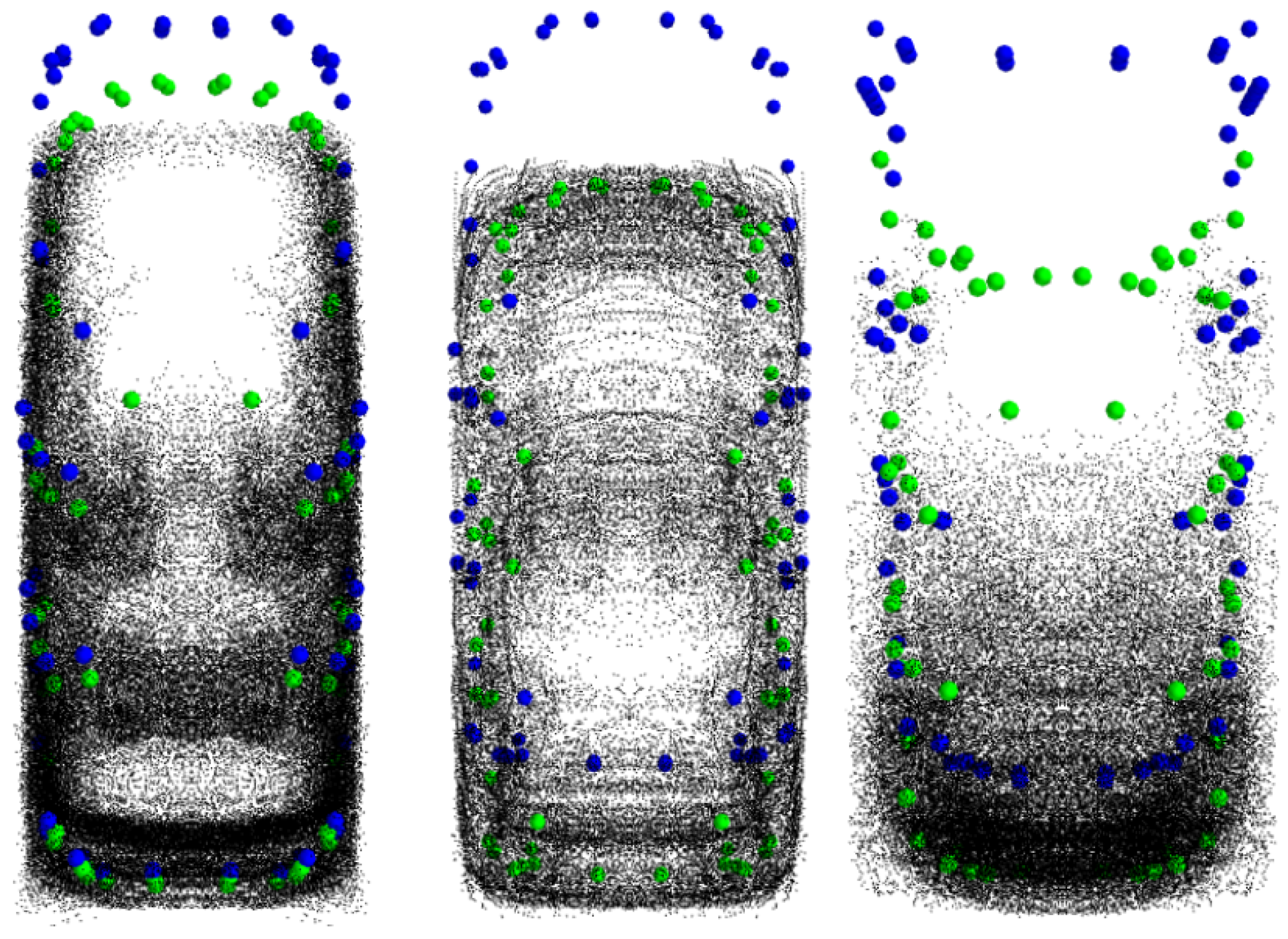
3.2. LiDAR-Based Reference Shape Reconstruction
3.3. Keypoint Extraction and Fault Detection
3.4. Semantic Mesh Shape Optimization
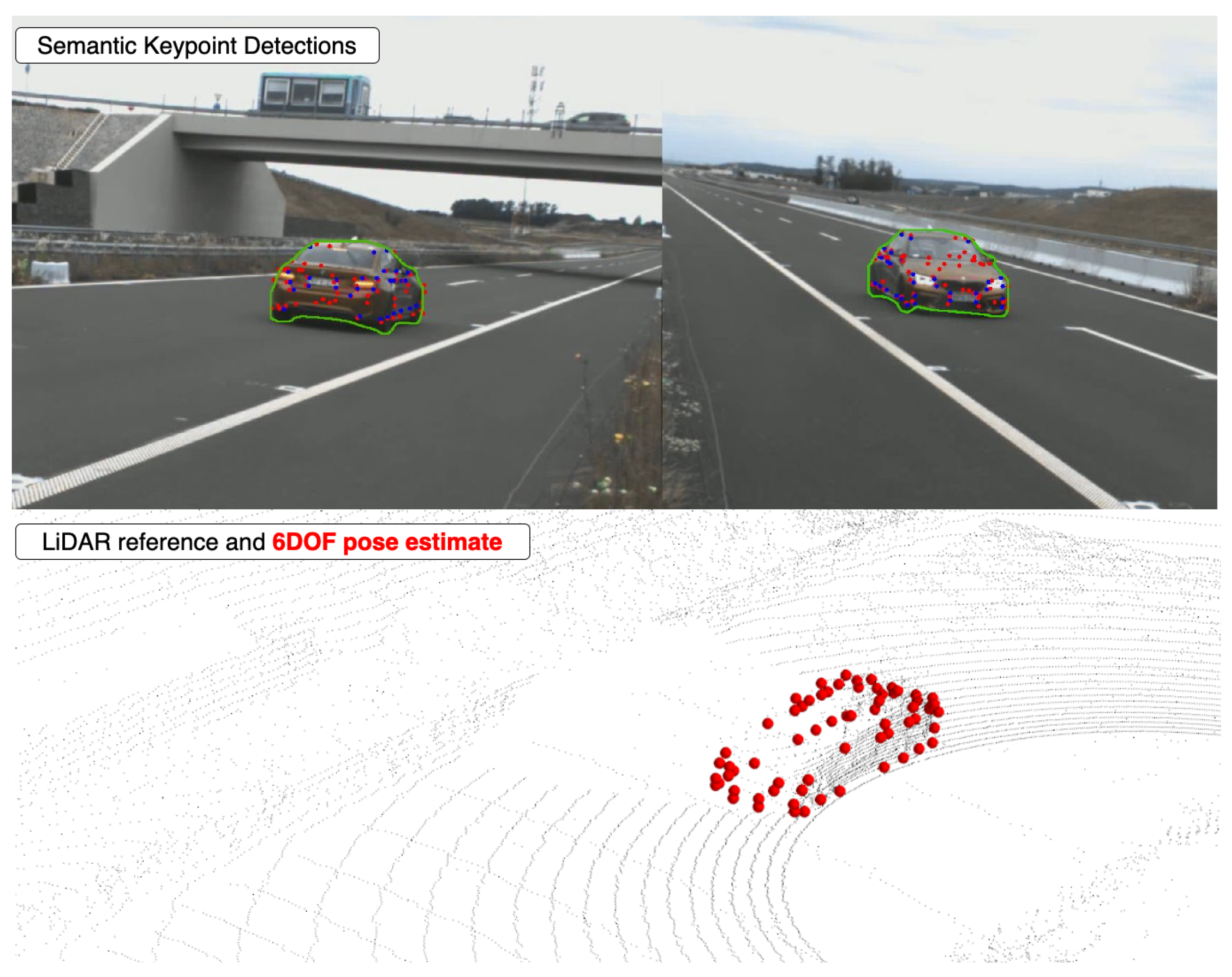
3.5. N–View Pose Estimation
4. Results
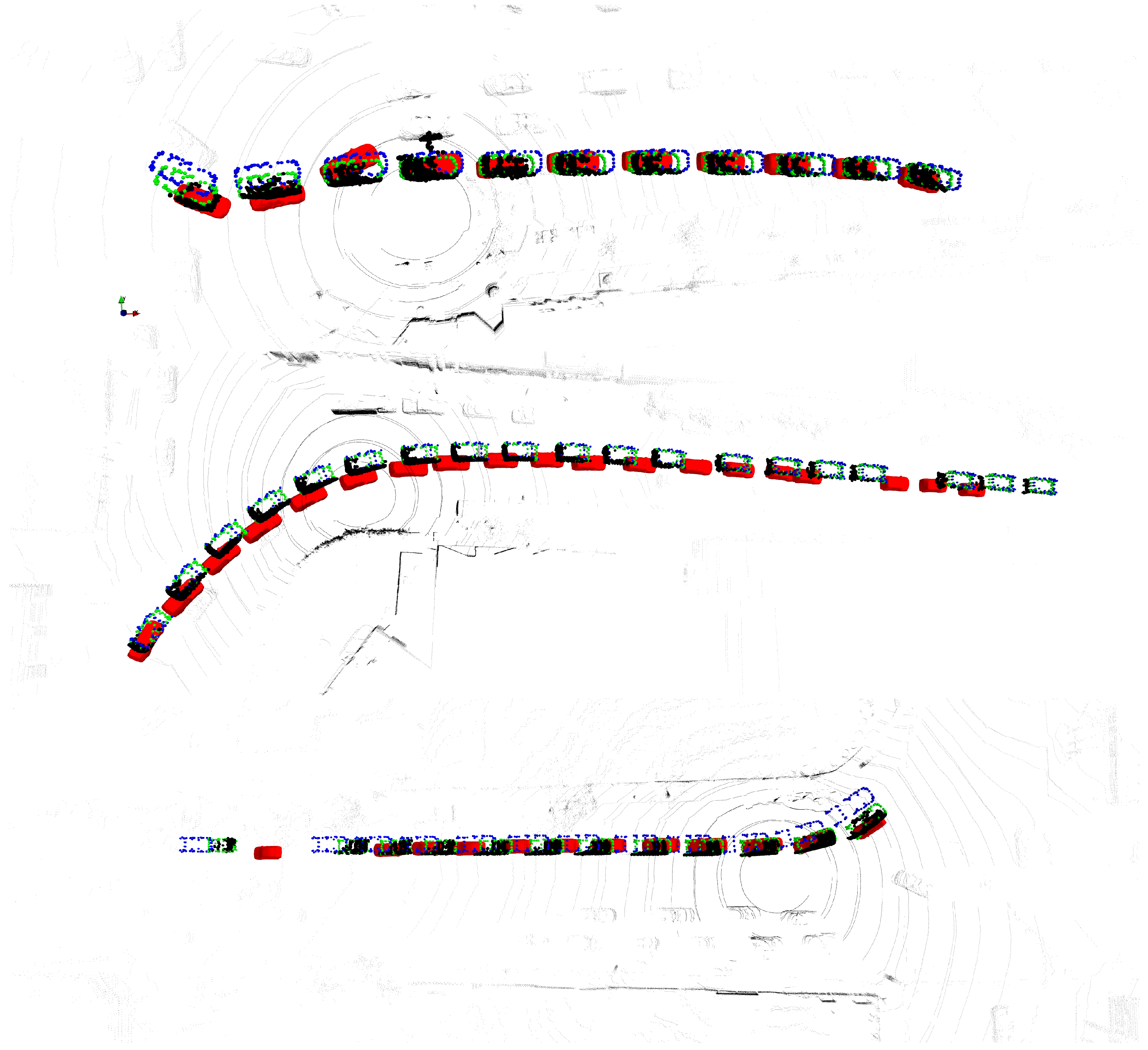
4.1. Evaluation Methodology
4.2. Improved Performance on the Argoverse Dataset
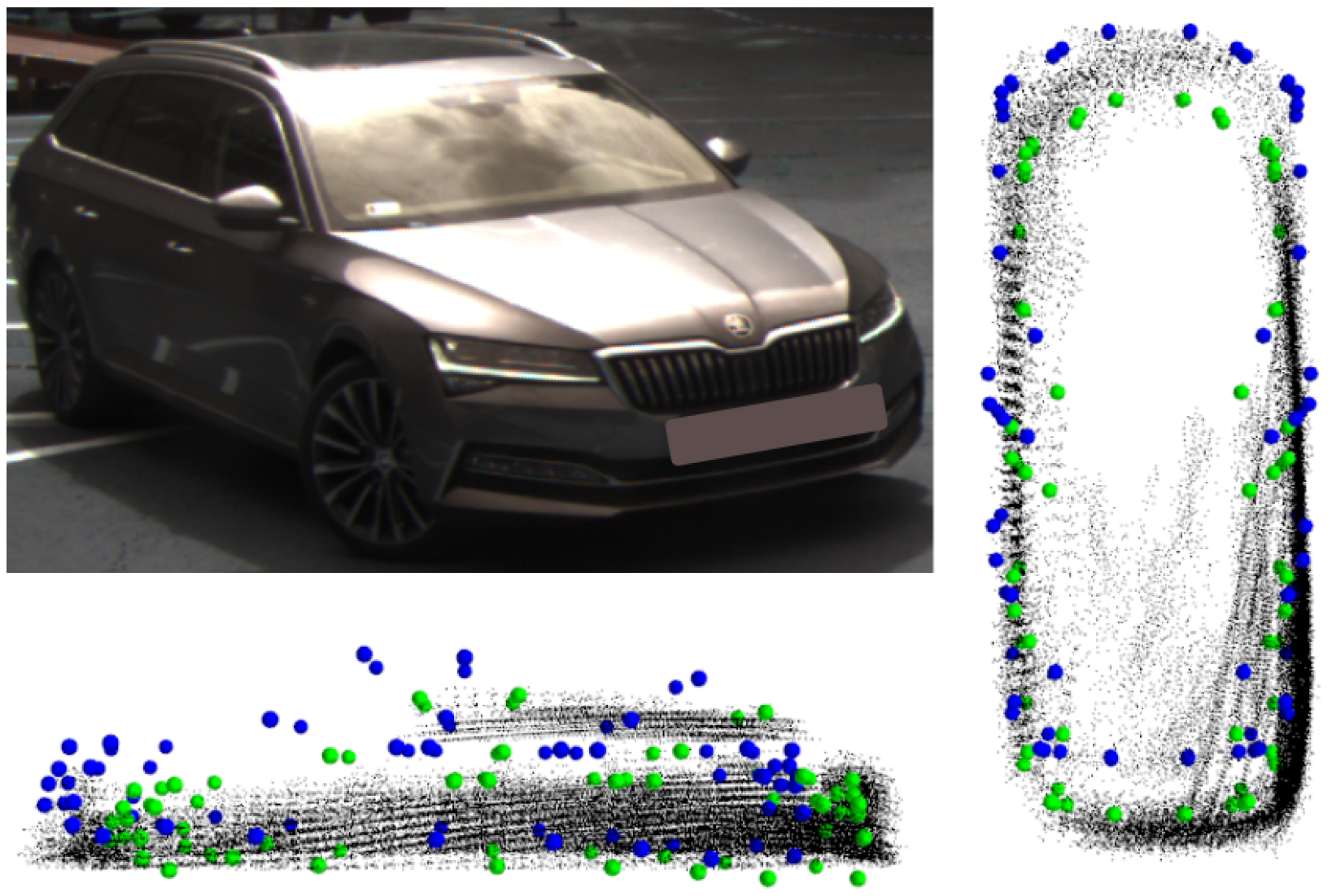
4.2.1. Qualitative Evaluation
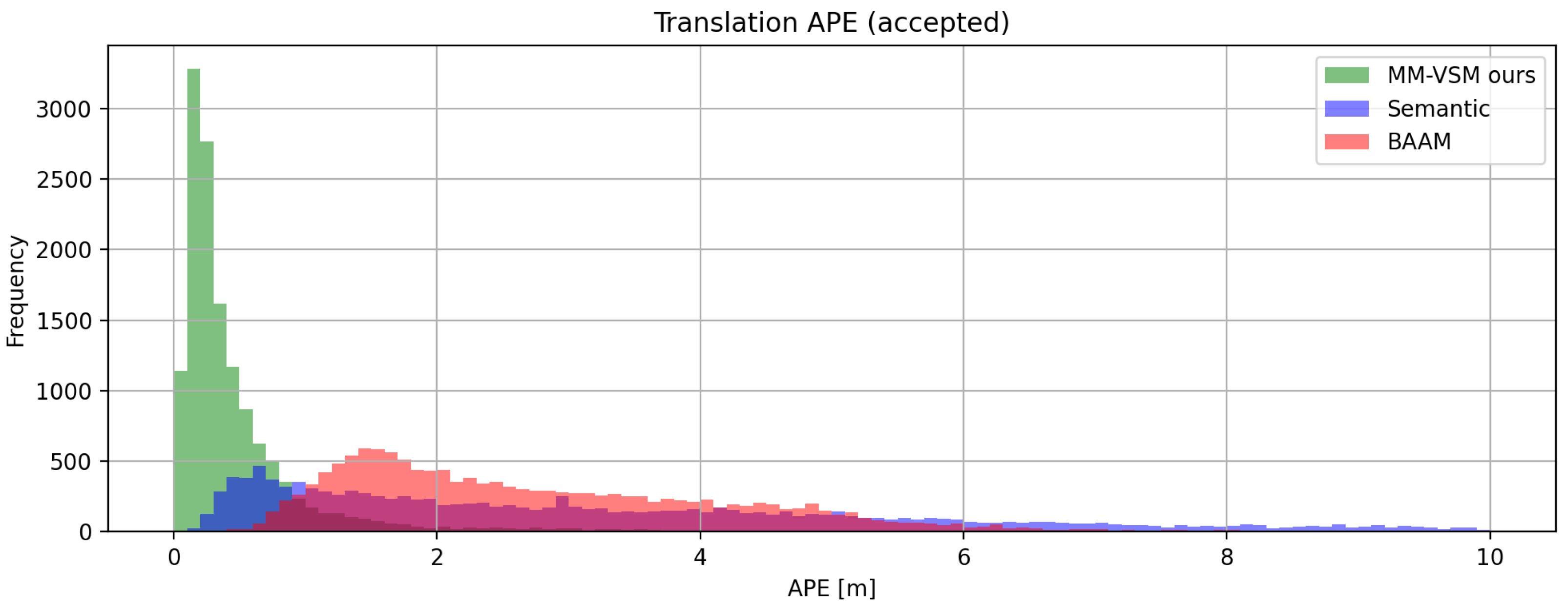
4.2.2. Quantitative Evaluation
- MM-VSM produces the most accurate pose estimates.
- Semantic produces the second-best peak accuracy with a large tail indicating many failed cases.
- BAAM produces larger but more consistent errors in APE than Semantic.
4.2.3. Findings
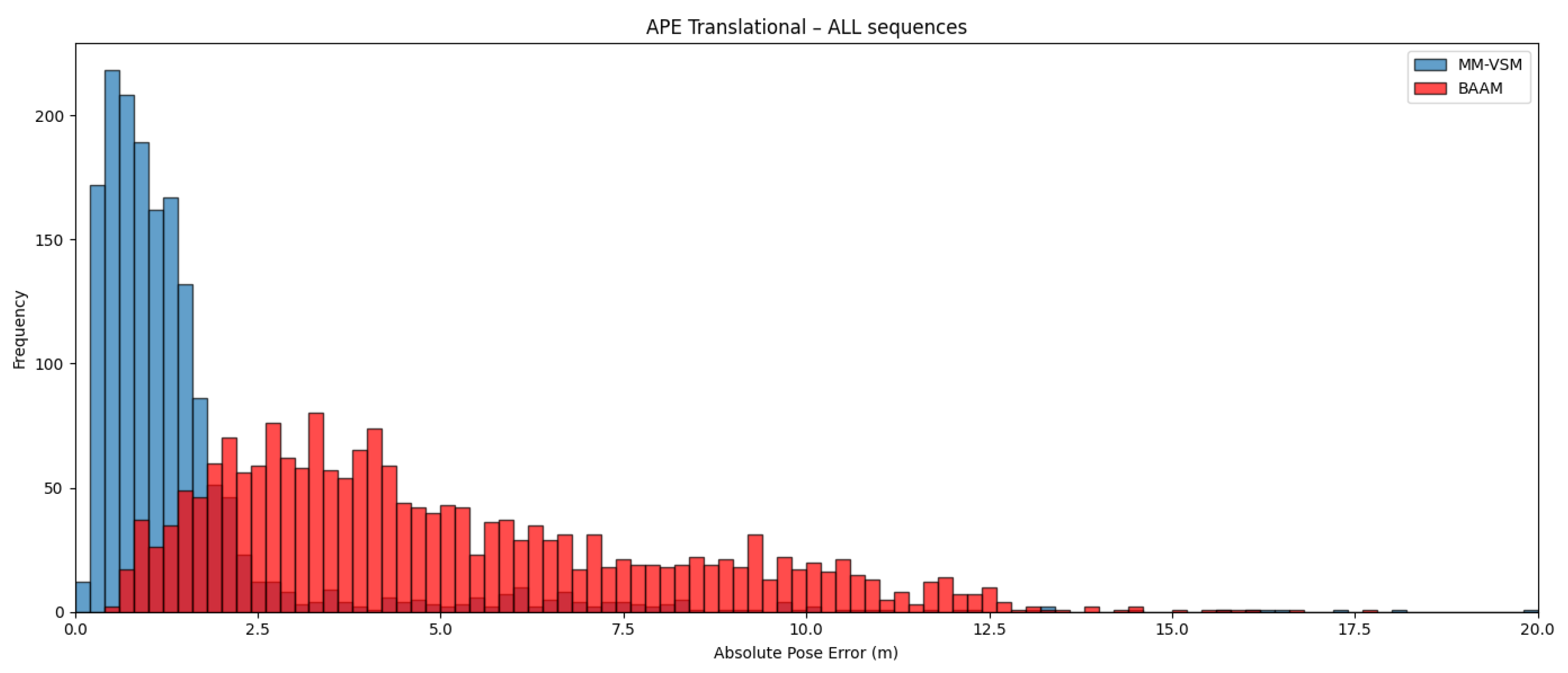
- Translational accuracy. MM-VSM significantly improves the robustness and accuracy of Semantic, producing the best translational APE on the evaluated frames, and also failing fewer times than BAAM.
- Rotational accuracy. In total rotational APE, MM-VSM outperforms BAAM and significantly improves Semantic.
- Local-frame RPY alignment. Using roll/pitch/yaw defined in the target’s own axes, MM-VSM is best on roll (2.60°) and pitch (3.28°), whereas BAAM is best on yaw (2.97°). Semantic sits consistently in the middle. Thus, BAAM’s overall rotation error stems primarily from roll–pitch misalignment, which is indicative of the training bias, due to the shifted camera position and viewpoint.
- Accuracy vs. robustness. MM-VSM delivers the best accuracy and passes the strict gate most often (lowest failure ). BAAM is the most robust under the default gate ( failures) but trades off accuracy; Semantic is weakest on both gates.
- Histograms. Looking at the head of the histograms, Semantic offers better peak accuracy compared to BAAM, and MM-VSM produces large improvements over both. This indicates that our LiDAR pipeline succesfully removes failures correcting Semantic’s errors.
- Axis-specific trends. MM-VSM excels at stabilizing vehicle roll and pitch; BAAM delivers the sharpest yaw on average, which benefits heading-aware downstream tasks.
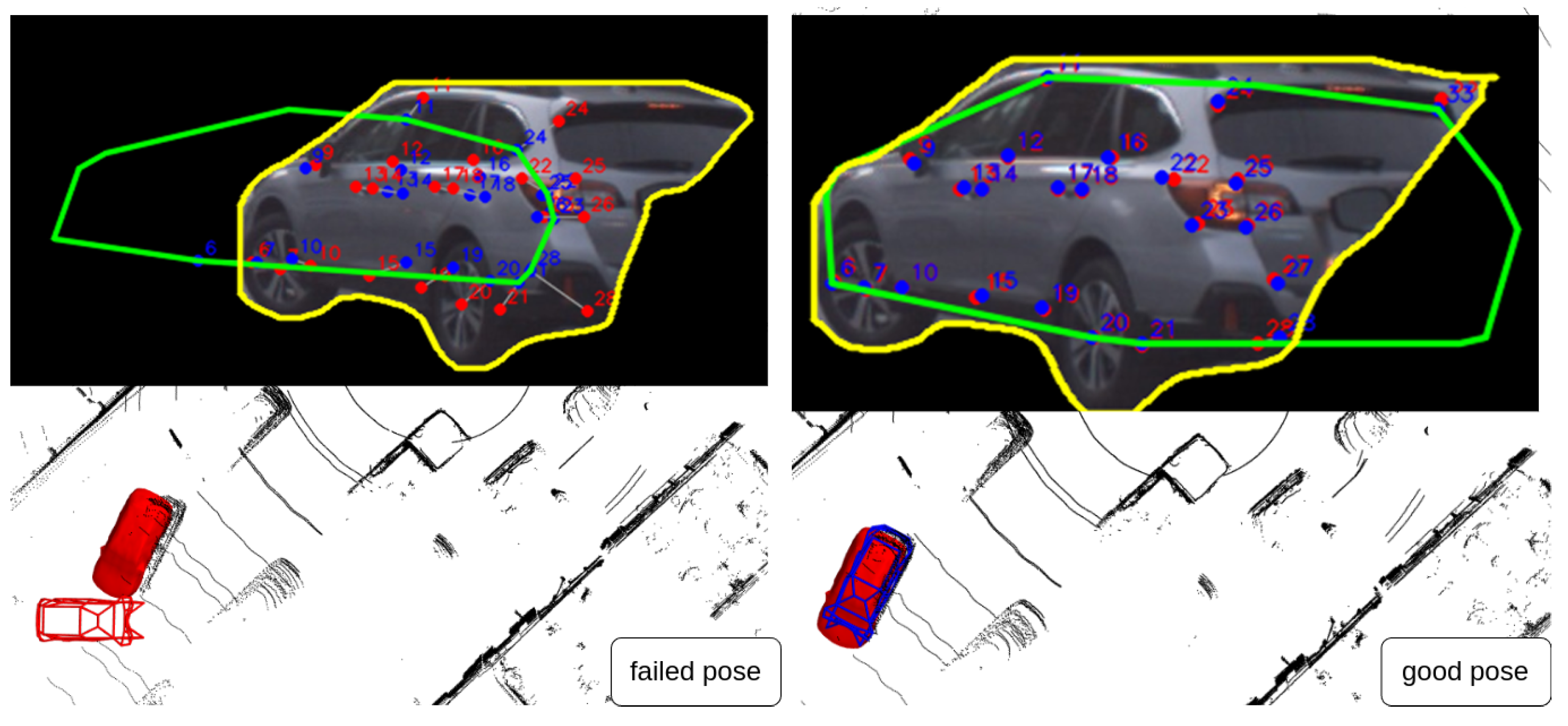
4.3. Failure Analysis and Failure Detecion
4.3.1. Failure Analysis-Occlusion
4.3.2. Pose Quality Metric
5. Ablation Study on ZalaZONE
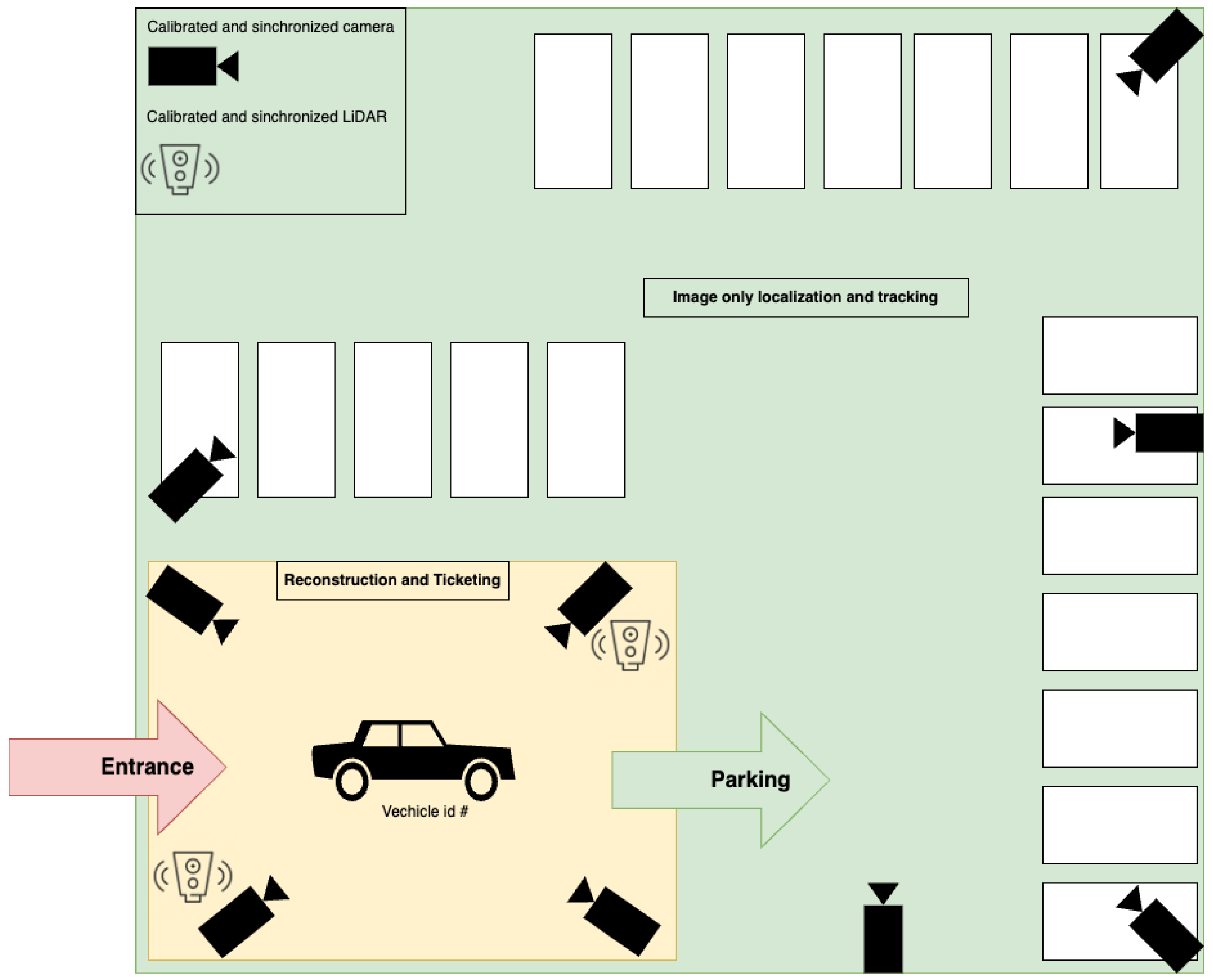
6. Real-World Application
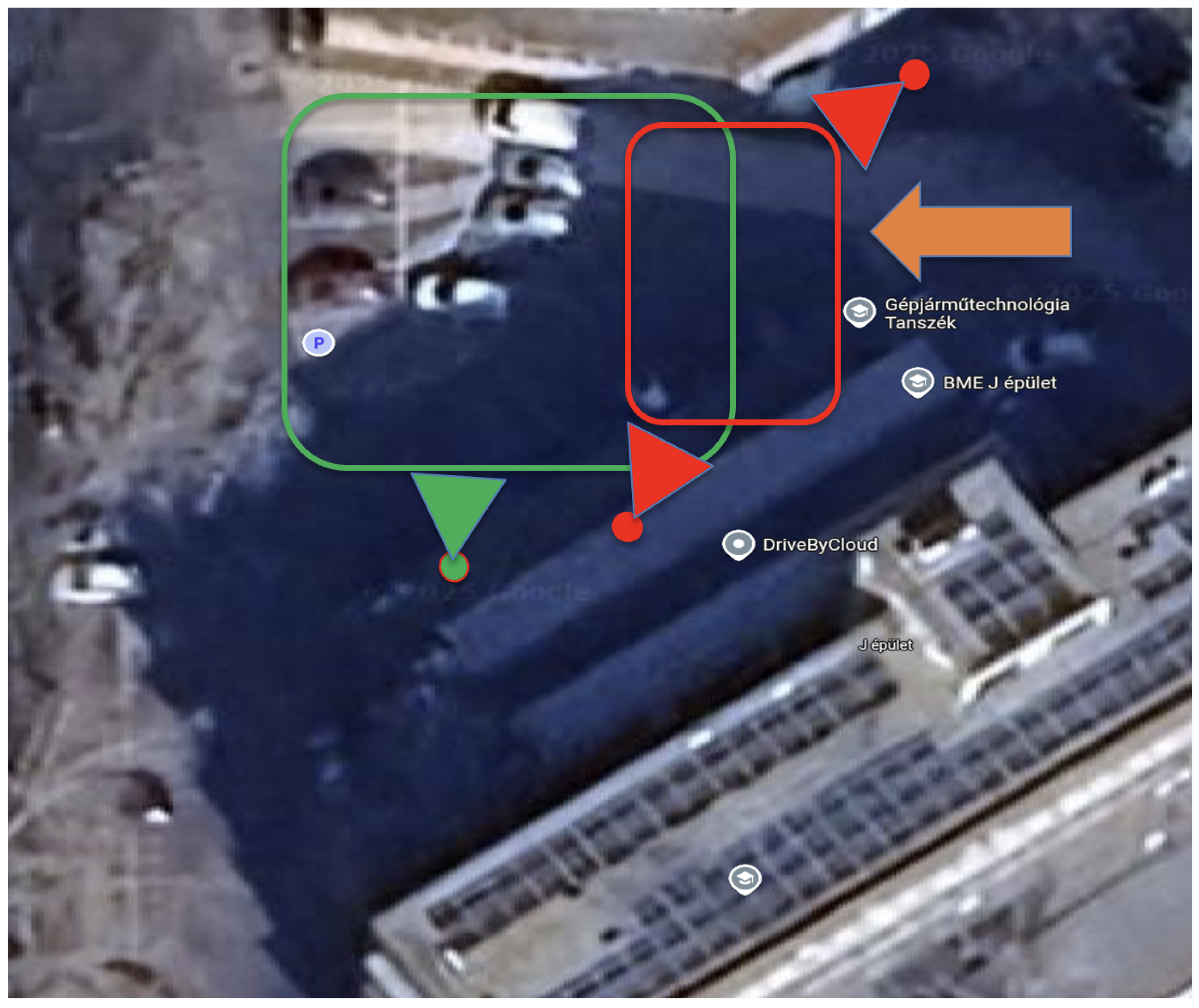
6.1. BME Parking Area
6.2. Experimental Setup
Evaluation
7. Discussion and Future Research
7.1. Advantages and Runtime Performance
7.2. Limitations
7.3. Future Research
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Definition of Mesh Faces
| (v1, v2, v3) | (v1, v2, v3) | (v1, v2, v3) | (v1, v2, v3) | (v1, v2, v3) |
|---|---|---|---|---|
| (2, 3, 0) | (9, 2, 0) | (48, 9, 0) | (57, 48, 0) | (0, 1, 59) |
| (0, 59, 57) | (1, 0, 3) | (1, 3, 4) | (1, 4, 5) | (1, 5, 59) |
| (59, 5, 61) | (9, 13, 2) | (2, 13, 10) | (13, 15, 10) | (15, 13, 14) |
| (4, 6, 5) | (18, 20, 19) | (2, 10, 7) | (2, 7, 3) | (6, 4, 7) |
| (3, 7, 4) | (41, 35, 33) | (33, 35, 32) | (33, 32, 24) | (24, 32, 25) |
| (24, 25, 22) | (24, 22, 16) | (9, 12, 13) | (13, 12, 14) | (17, 14, 12) |
| (14, 17, 15) | (15, 17, 19) | (12, 16, 17) | (16, 18, 17) | (18, 19, 17) |
| (16, 22, 18) | (18, 21, 20) | (18, 23, 21) | (8, 12, 9) | (11, 12, 8) |
| (11, 16, 12) | (8, 9, 48) | (8, 48, 49) | (11, 24, 16) | (24, 11, 46) |
| (22, 23, 18) | (23, 28, 21) | (23, 27, 28) | (22, 26, 23) | (22, 25, 26) |
| (23, 26, 27) | (24, 46, 33) | (55, 44, 48) | (11, 8, 49) | (11, 49, 46) |
| (57, 59, 58) | (57, 58, 56) | (59, 60, 58) | (59, 61, 60) | (48, 57, 55) |
| (58, 60, 52) | (58, 52, 56) | (56, 52, 53) | (53, 52, 51) | (50, 53, 51) |
| (56, 53, 54) | (57, 54, 55) | (57, 56, 54) | (54, 53, 50) | (55, 54, 50) |
| (44, 55, 47) | (55, 50, 47) | (49, 48, 45) | (44, 47, 42) | (48, 44, 45) |
| (43, 45, 44) | (42, 43, 44) | (40, 45, 43) | (49, 45, 46) | (46, 45, 41) |
| (46, 41, 33) | (43, 42, 40) | (40, 42, 38) | (40, 38, 39) | (40, 39, 41) |
| (45, 40, 41) | (38, 37, 39) | (39, 35, 41) | (37, 36, 39) | (39, 36, 34) |
| (36, 29, 34) | (34, 29, 30) | (39, 34, 35) | (35, 34, 31) | (35, 31, 32) |
| (34, 30, 31) | (65, 28, 27) | (64, 30, 29) | (63, 64, 65) | (63, 65, 62) |
| (30, 64, 63) | (27, 62, 65) | (64, 29, 28) | (64, 28, 65) | (31, 30, 63) |
| (62, 27, 26) | (32, 31, 25) | (25, 31, 26) | (31, 63, 26) | (63, 62, 26) |
| (36, 28, 29) | (36, 21, 28) | (36, 20, 21) | (36, 37, 20) | (37, 19, 20) |
| (37, 38, 19) | (38, 15, 19) | (38, 42, 15) | (42, 10, 15) | (42, 47, 10) |
| (6, 7, 10) | (47, 50, 51) | (47, 6, 10) | (47, 51, 6) | (51, 5, 6) |
| (51, 52, 5) | (5, 52, 61) | (61, 52, 60) |
References
- Ebrahimi Soorchaei, B.; Razzaghpour, M.; Valiente, R.; Raftari, A.; Fallah, Y.P. High-definition map representation techniques for automated vehicles. Electronics 2022, 11, 3374. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Zimmer, W.; Wardana, G.A.; Sritharan, S.; Zhou, X.; Song, R.; Knoll, A.C. Tumtraf v2x cooperative perception dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 22668–22677. [Google Scholar]
- Xiang, H.; Zheng, Z.; Xia, X.; Xu, R.; Gao, L.; Zhou, Z.; Han, X.; Ji, X.; Li, M.; Meng, Z.; et al. V2x-real: A largs-scale dataset for vehicle-to-everything cooperative perception. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 455–470. [Google Scholar]
- Yu, H.; Yang, W.; Ruan, H.; Yang, Z.; Tang, Y.; Gao, X.; Hao, X.; Shi, Y.; Pan, Y.; Sun, N.; et al. V2x-seq: A large-scale sequential dataset for vehicle-infrastructure cooperative perception and forecasting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5486–5495. [Google Scholar]
- Qu, D.; Chen, Q.; Bai, T.; Lu, H.; Fan, H.; Zhang, H.; Fu, S.; Yang, Q. SiCP: Simultaneous Individual and Cooperative Perception for 3D Object Detection in Connected and Automated Vehicles. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 8905–8912. [Google Scholar]
- Liu, J.; Wang, P.; Wu, X. A Vehicle–Infrastructure Cooperative Perception Network Based on Multi-Scale Dynamic Feature Fusion. Appl. Sci. 2025, 15, 3399. [Google Scholar] [CrossRef]
- Nagy, R.; Török, Á.; Petho, Z. Evaluating V2X-Based Vehicle Control under Unreliable Network Conditions, Focusing on Safety Risk. Appl. Sci. 2024, 14, 5661. [Google Scholar] [CrossRef]
- Chang, C.; Zhang, J.; Zhang, K.; Zhong, W.; Peng, X.; Li, S.; Li, L. BEV-V2X: Cooperative birds-eye-view fusion and grid occupancy prediction via V2X-based data sharing. IEEE Trans. Intell. Veh. 2023, 8, 4498–4514. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, P.; Li, X.; Sun, M.; Di, R.; Li, L.; Hong, W. MonoDFNet: Monocular 3D Object Detection with Depth Fusion and Adaptive Optimization. Sensors 2025, 25, 760. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Yan, P.; Xiong, S.; Xiang, X.; Tan, Y. Monocd: Monocular 3d object detection with complementary depths. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 10248–10257. [Google Scholar]
- Yang, L.; Zhang, X.; Yu, J.; Li, J.; Zhao, T.; Wang, L.; Huang, Y.; Zhang, C.; Wang, H.; Li, Y. MonoGAE: Roadside monocular 3D object detection with ground-aware embeddings. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17587–17601. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, H.; Choi, S.M.; Jeong, S.G.; Koh, Y.J. BAAM: Monocular 3D pose and shape reconstruction with bi-contextual attention module and attention-guided modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17-24 June 2023; pp. 9011–9020. [Google Scholar]
- Song, X.; Wang, P.; Zhou, D.; Zhu, R.; Guan, C.; Dai, Y.; Su, H.; Li, H.; Yang, R. Apollocar3d: A large 3d car instance understanding benchmark for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5452–5462. [Google Scholar]
- Cserni, M.; Rövid, A. Semantic Shape and Trajectory Reconstruction for Monocular Cooperative 3D Object Detection. IEEE Access 2024, 12, 167153–167167. [Google Scholar] [CrossRef]
- Chang, M.F.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; Lucey, S.; Ramanan, D.; et al. Argoverse: 3d tracking and forecasting with rich maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8748–8757. [Google Scholar]
- Chen, R.; Gao, L.; Liu, Y.; Guan, Y.L.; Zhang, Y. Smart roads: Roadside perception, vehicle-road cooperation and business model. IEEE Network 2024, 39, 311–318. [Google Scholar] [CrossRef]
- Yu, H.; Luo, Y.; Shu, M.; Huo, Y.; Yang, Z.; Shi, Y.; Guo, Z.; Li, H.; Hu, X.; Yuan, J.; et al. Dair-v2x: A large-scale dataset for vehicle-infrastructure cooperative 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 21361–21370. [Google Scholar]
- Xu, R.; Xia, X.; Li, J.; Li, H.; Zhang, S.; Tu, Z.; Meng, Z.; Xiang, H.; Dong, X.; Song, R.; et al. V2v4real: A real-world large-scale dataset for vehicle-to-vehicle cooperative perception. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 13712–13722. [Google Scholar]
- Bai, Z.; Wu, G.; Barth, M.J.; Liu, Y.; Sisbot, E.A.; Oguchi, K. Pillargrid: Deep learning-based cooperative perception for 3d object detection from onboard-roadside lidar. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 1743–1749. [Google Scholar]
- Qiao, D.; Zulkernine, F.; Anand, A. CoBEVFusion Cooperative Perception with LiDAR-Camera Bird’s Eye View Fusion. In Proceedings of the 2024 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Perth, Australia, 27–29 November 2024; pp. 389–396. [Google Scholar]
- Wei, S.; Wei, Y.; Hu, Y.; Lu, Y.; Zhong, Y.; Chen, S.; Zhang, Y. Asynchrony-robust collaborative perception via bird’s eye view flow. Adv. Neural Inf. Process. Syst. 2023, 36, 28462–28477. [Google Scholar]
- Eskandar, G. An empirical study of the generalization ability of lidar 3d object detectors to unseen domains. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 23815–23825. [Google Scholar]
- Zhi, P.; Jiang, L.; Yang, X.; Wang, X.; Li, H.W.; Zhou, Q.; Li, K.C.; Ivanović, M. Cross-Domain Generalization for LiDAR-Based 3D Object Detection in Infrastructure and Vehicle Environments. Sensors 2025, 25, 767. [Google Scholar] [CrossRef]
- Vincze, Z.; Rövid, A.; Tihanyi, V. Automatic label injection into local infrastructure LiDAR point cloud for training data set generation. IEEE Access 2022, 10, 91213–91226. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, Y.; Xu, R.; Xie, W.; Chen, S.; Wang, Y. Collaboration helps camera overtake lidar in 3d detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 9243–9252. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An accurate O(n) solution to the PnP problem. Int. J. Comput. Vis. 2009, 81, 155–166. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, X. Multi-View Metal Parts Pose Estimation Based on a Single Camera. Sensors 2024, 24, 3408. [Google Scholar] [CrossRef] [PubMed]
- Kreiss, S.; Bertoni, L.; Alahi, A. Openpifpaf: Composite fields for semantic keypoint detection and spatio-temporal association. IEEE Trans. Intell. Transp. Syst. 2021, 23, 13498–13511. [Google Scholar] [CrossRef]
- Jocher, G.; Chaurasia, A.; Qiu, J. Ultralytics YOLOv8 Software, Version 8.2.2; Ultralytics: London, UK, 2023. Available online: https://github.com/ultralytics/ultralytics (accessed on 14 June 2025).
- Pavlakos, G.; Zhou, X.; Chan, A.; Derpanis, K.G.; Daniilidis, K. 6-dof object pose from semantic keypoints. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2011–2018. [Google Scholar]
- Barowski, T.; Szczot, M.; Houben, S. 6DoF vehicle pose estimation using segmentation-based part correspondences. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 573–580. [Google Scholar]
- Ke, L.; Li, S.; Sun, Y.; Tai, Y.W.; Tang, C.K. Gsnet: Joint vehicle pose and shape reconstruction with geometrical and scene-aware supervision. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XV 16. pp. 515–532. [Google Scholar]
- He, T.; Soatto, S. Mono3d++: Monocular 3d vehicle detection with two-scale 3d hypotheses and task priors. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8409–8416. [Google Scholar]
- Liu, Z.; Zhou, D.; Lu, F.; Fang, J.; Zhang, L. Autoshape: Real-time shape-aware monocular 3d object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 15641–15650. [Google Scholar]
- Schörner, P.; Conzelmann, M.; Fleck, T.; Zofka, M.; Zöllner, J.M. Park my car! Automated valet parking with different vehicle automation levels by v2x connected smart infrastructure. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 836–843. [Google Scholar]
- Bradski, G.; Kaehler, A. OpenCV Library Software, Version 4.11; Intel Corporation: Santa Clara, CA, USA, 2000. Available online: https://opencv.org (accessed on 14 June 2025).
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- PyTorch3D Developers. PyTorch3D: Loss Functions. 2025. Available online: https://pytorch3d.readthedocs.io/en/latest/modules/loss.html (accessed on 7 June 2025).
- Chabot, F.; Chaouch, M.; Rabarisoa, J.; Teuliere, C.; Chateau, T. Deep manta: A coarse-to-fine many-task network for joint 2d and 3d vehicle analysis from monocular image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2040–2049. [Google Scholar]
- Rovid, A.; Tihanyi, V.; Cserni, M.; Csontho, M.; Domina, A.; Remeli, V.; Vincze, Z.; Szanto, M.; Szalai, M.; Nagy, S.; et al. Digital twin and cloud based remote control of vehicles. In Proceedings of the 2024 IEEE International Conference on Mobility, Operations, Services and Technologies (MOST), Dallas, TX, USA, 1–3 May 2024; pp. 154–167. [Google Scholar]

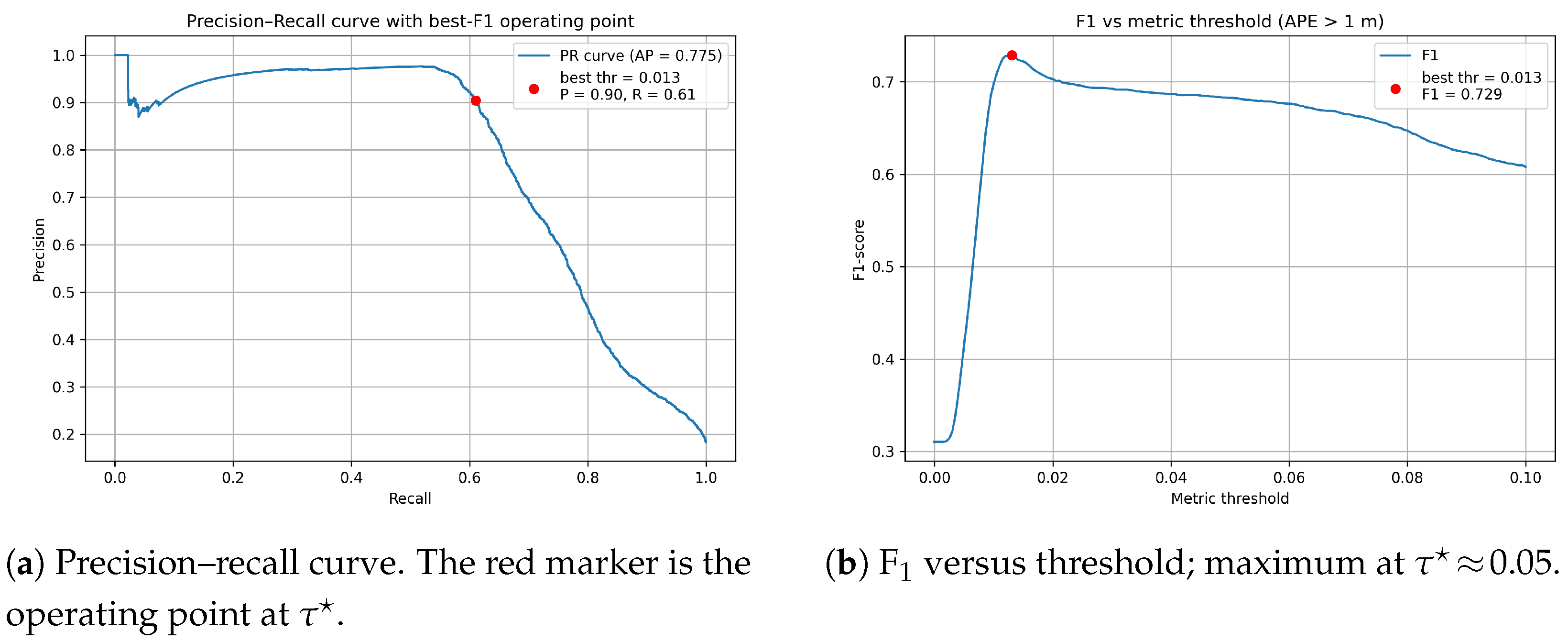
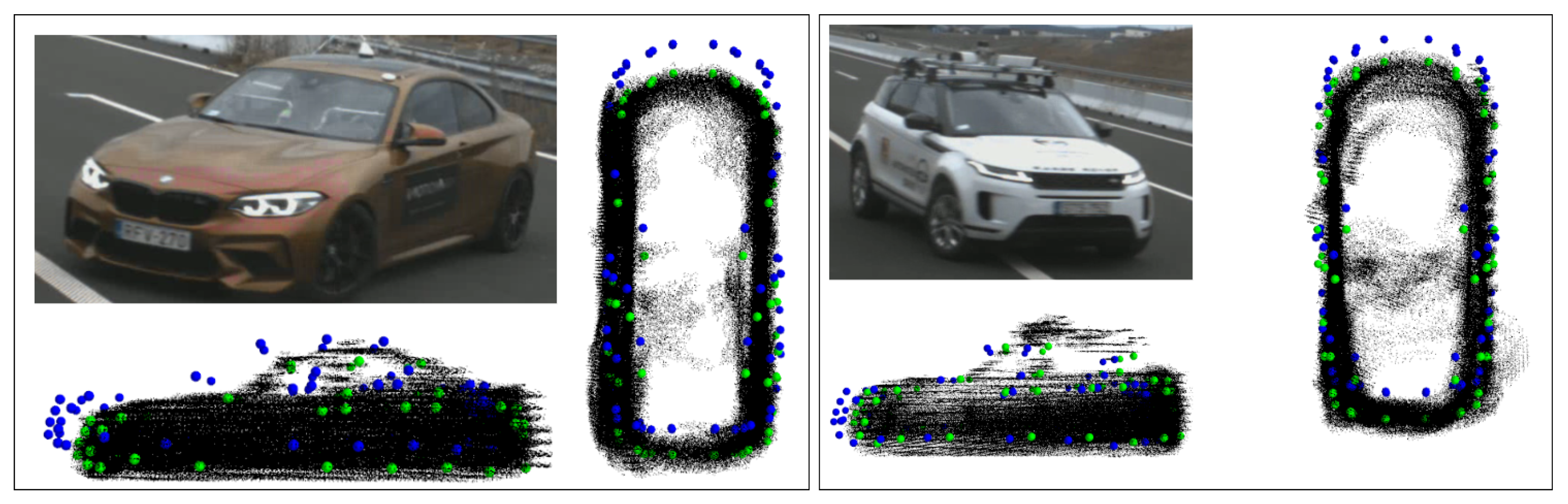

| Default Gate (10 m, 45°) | Strict Gate (5 m, 30°) | |||
|---|---|---|---|---|
| Method | Removed | Failure [%] | Removed | Failure [%] |
| MM-VSM (ours) | 1319 | 8.56 | 1781 | 11.56 |
| Semantic [15] | 2436 | 15.81 | 5527 | 35.87 |
| BAAM [13] | 834 | 5.41 | 2 204 | 14.31 |
| Translation [m] | Rotation [°] | |||||
|---|---|---|---|---|---|---|
| Method | Median | Median | ||||
| MM-VSM (ours) | 0.560.94 | 0.29 | 1.79 | 6.356.49 | 4.47 | 20.61 |
| Semantic [15] | 3.182.39 | 2.59 | 8.16 | 7.827.20 | 5.47 | 23.48 |
| BAAM [13] | 2.791.50 | 2.44 | 5.51 | 10.994.09 | 9.95 | 18.30 |
| Axis [°] | MM-VSM (Ours) | Semantic [15] | BAAM [13] |
|---|---|---|---|
| Roll | 2.603.23 | 2.783.26 | 2.881.87 |
| Pitch | 3.284.86 | 3.623.67 | 9.713.41 |
| Yaw | 3.094.66 | 4.786.73 | 2.973.43 |
| Method | Median | P95 | |
|---|---|---|---|
| MM-VSM (ours) | 1.401.48 | 1.02 | 4.85 |
| BAAM [13] | 4.422.37 | 3.97 | 9.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cserni, M.; Rövid, A.; Szalay, Z. MM-VSM: Multi-Modal Vehicle Semantic Mesh and Trajectory Reconstruction for Image-Based Cooperative Perception. Appl. Sci. 2025, 15, 6930. https://doi.org/10.3390/app15126930
Cserni M, Rövid A, Szalay Z. MM-VSM: Multi-Modal Vehicle Semantic Mesh and Trajectory Reconstruction for Image-Based Cooperative Perception. Applied Sciences. 2025; 15(12):6930. https://doi.org/10.3390/app15126930
Chicago/Turabian StyleCserni, Márton, András Rövid, and Zsolt Szalay. 2025. "MM-VSM: Multi-Modal Vehicle Semantic Mesh and Trajectory Reconstruction for Image-Based Cooperative Perception" Applied Sciences 15, no. 12: 6930. https://doi.org/10.3390/app15126930
APA StyleCserni, M., Rövid, A., & Szalay, Z. (2025). MM-VSM: Multi-Modal Vehicle Semantic Mesh and Trajectory Reconstruction for Image-Based Cooperative Perception. Applied Sciences, 15(12), 6930. https://doi.org/10.3390/app15126930







