Research on Dynamic Stability of Slopes Under the Influence of Heavy Rain Using an Improved NSGA-II Algorithm
Abstract
1. Introduction
2. Slope Survey and Monitoring
2.1. Engineering Geological Conditions
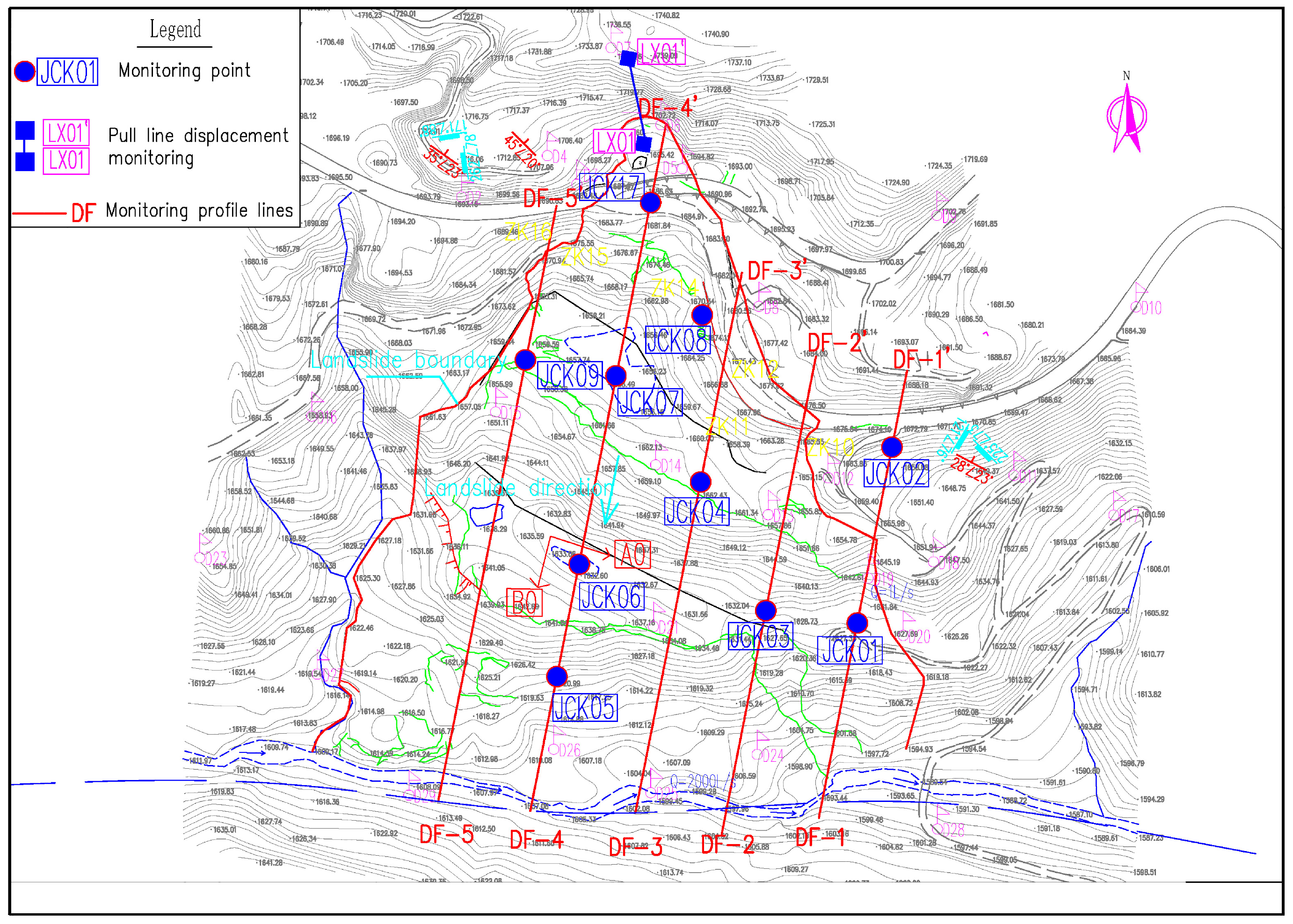
2.2. Slope Monitoring Arrangement
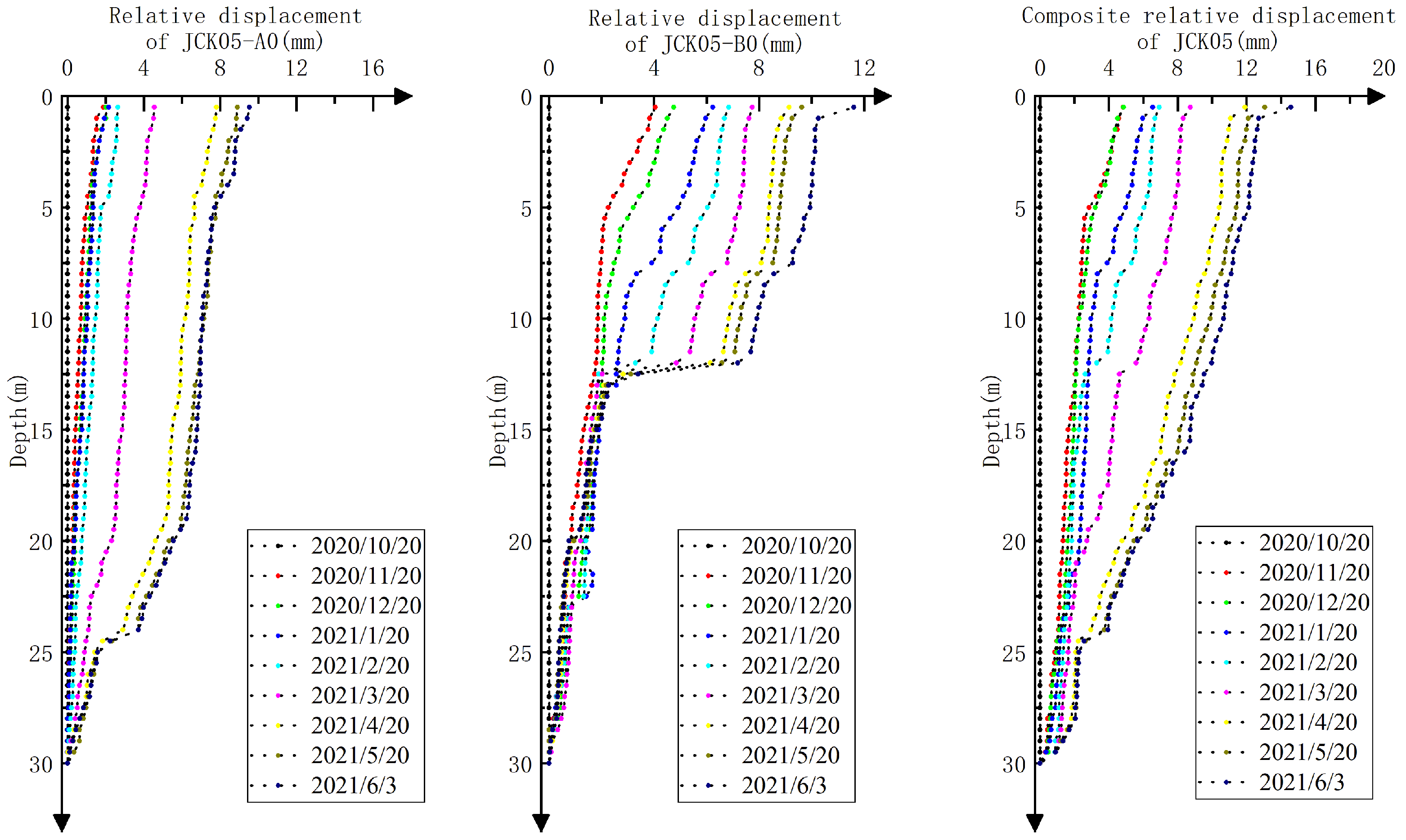
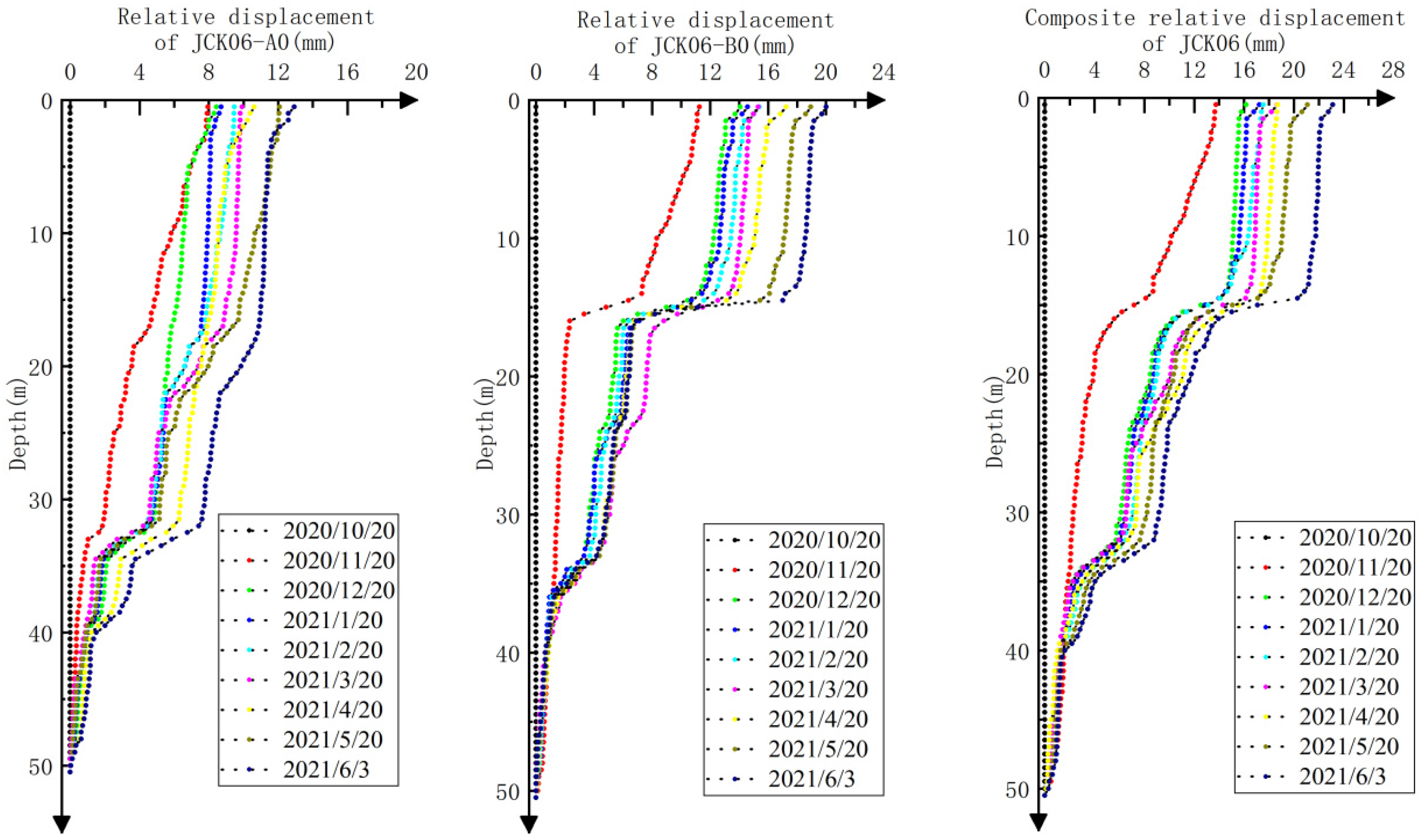
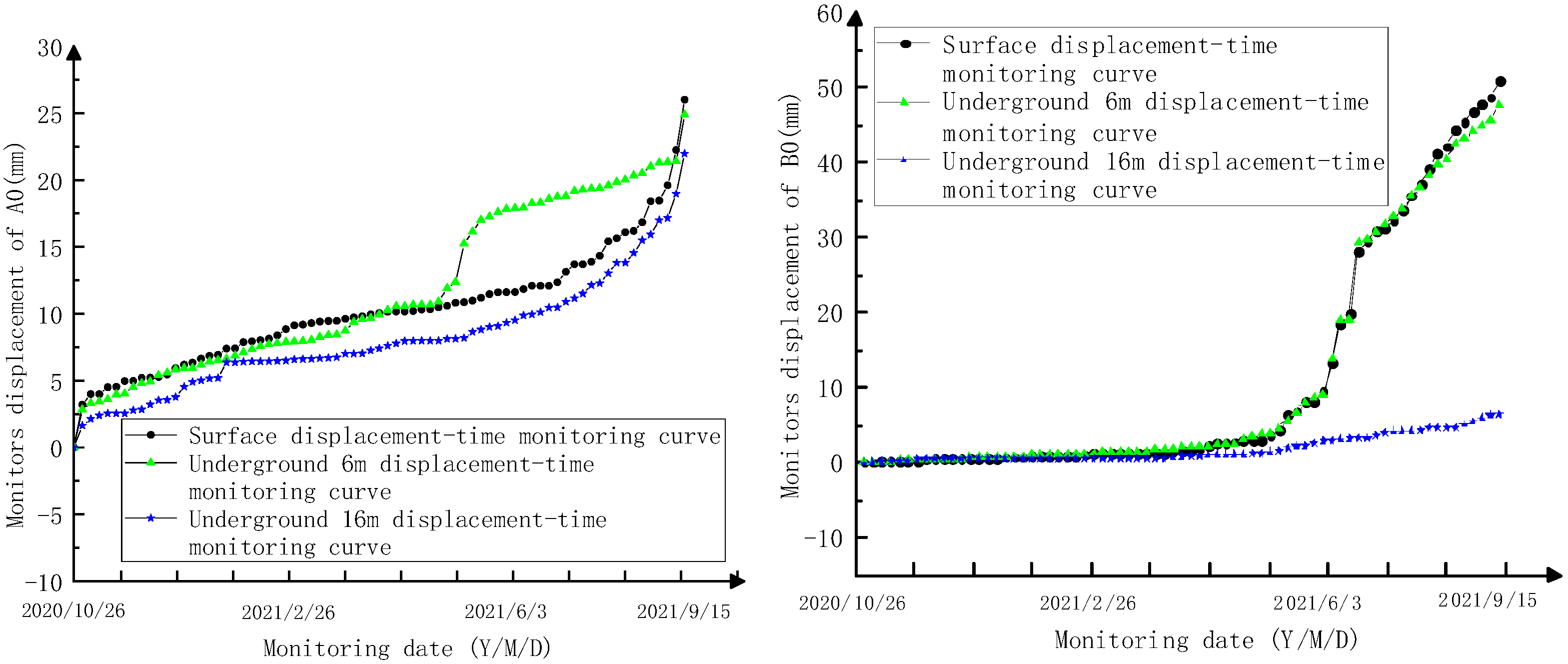
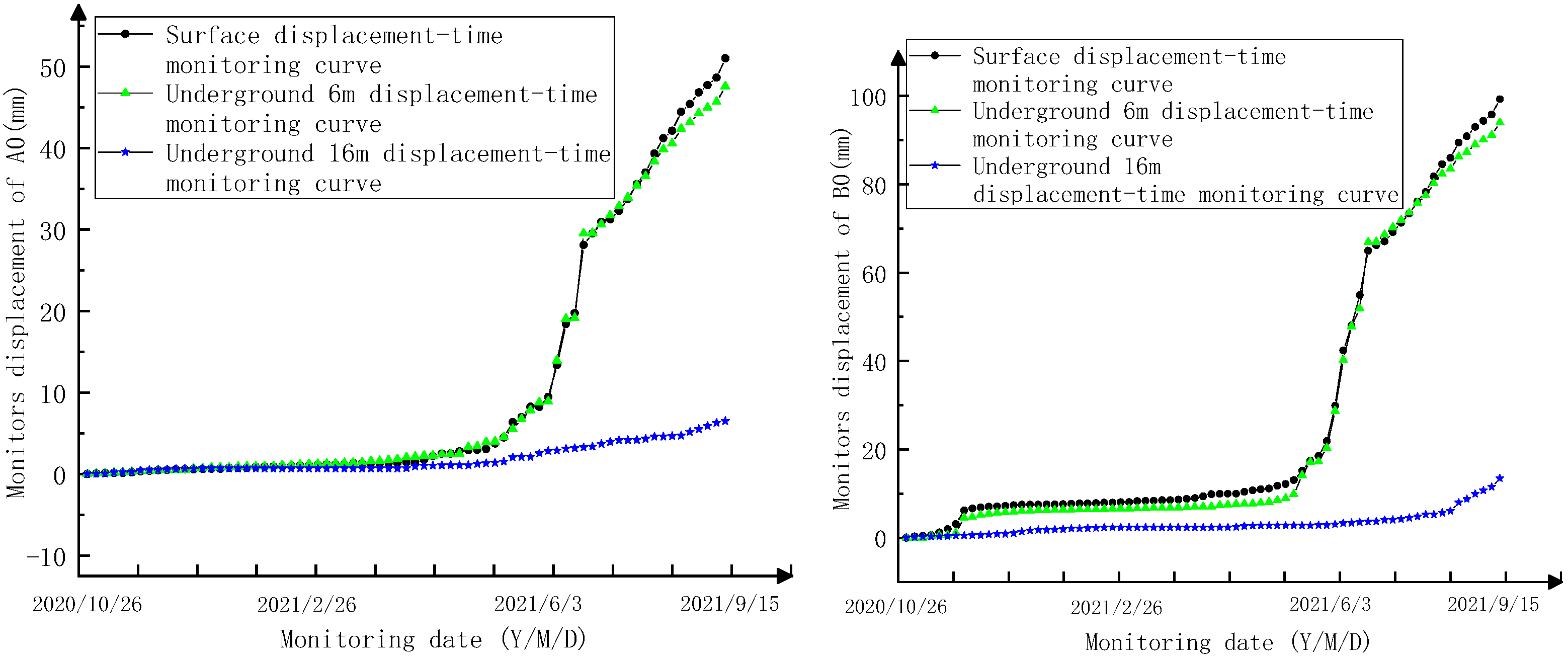
2.3. Analysis of Monitoring Data
3. Back Analysis of Slope Mechanical Parameters
3.1. Parameter Research of Inversion Model
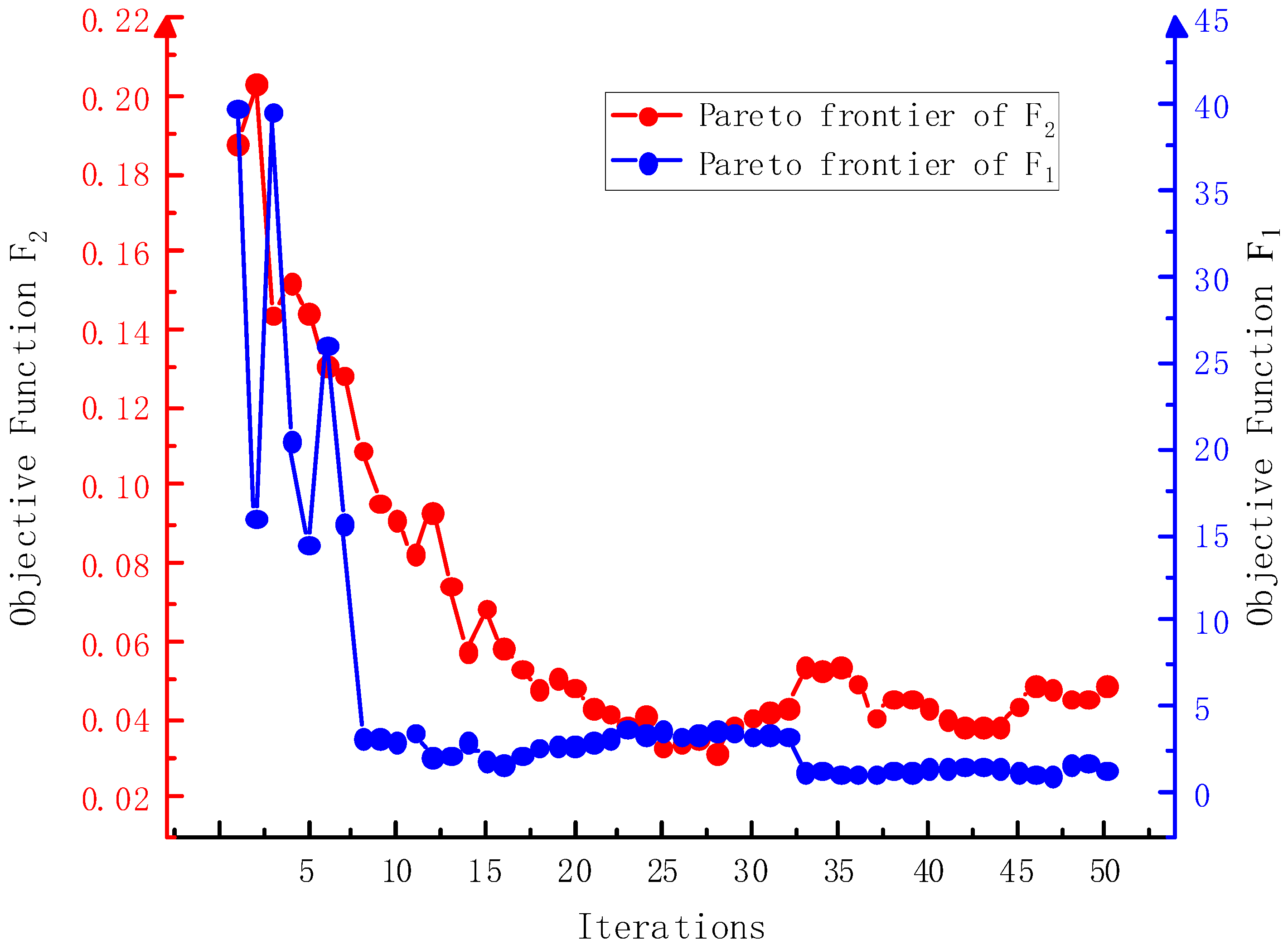
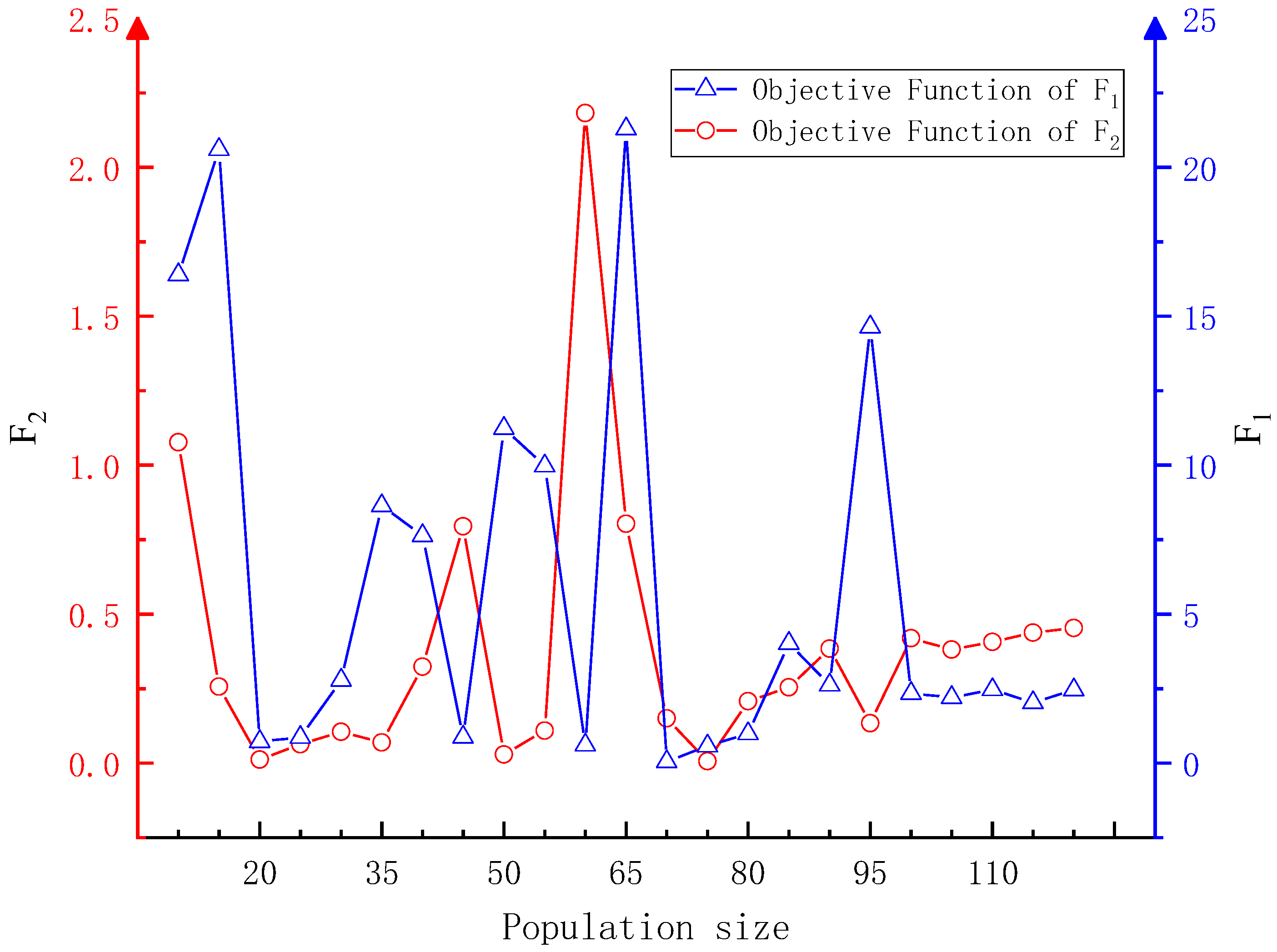
3.2. Inversion of Slope Mechanical Parameters
4. Slope Dynamic Stability Analysis
4.1. Slope Stability Calculation
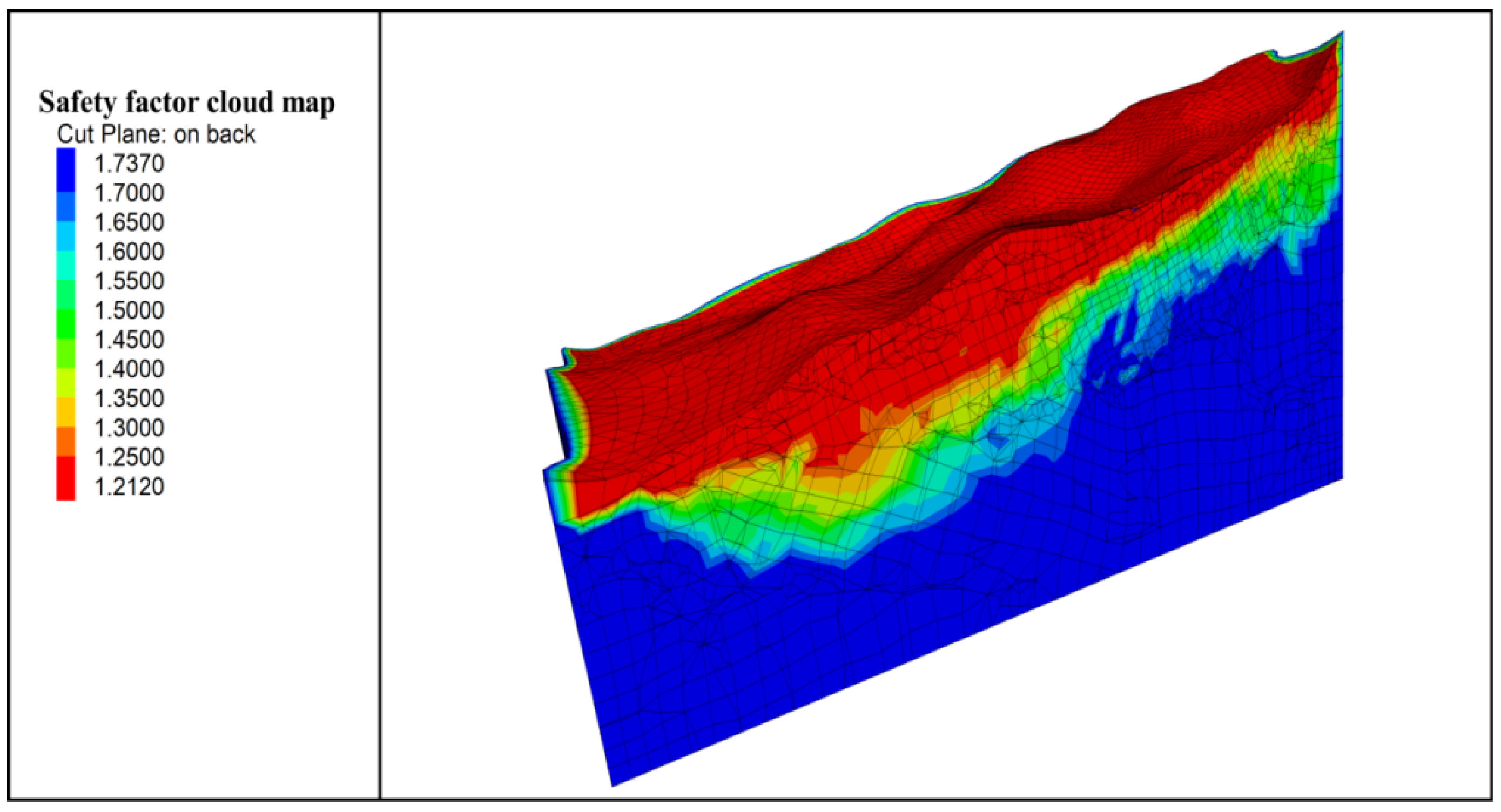
4.1.1. Calculation of Initial Slope Stability
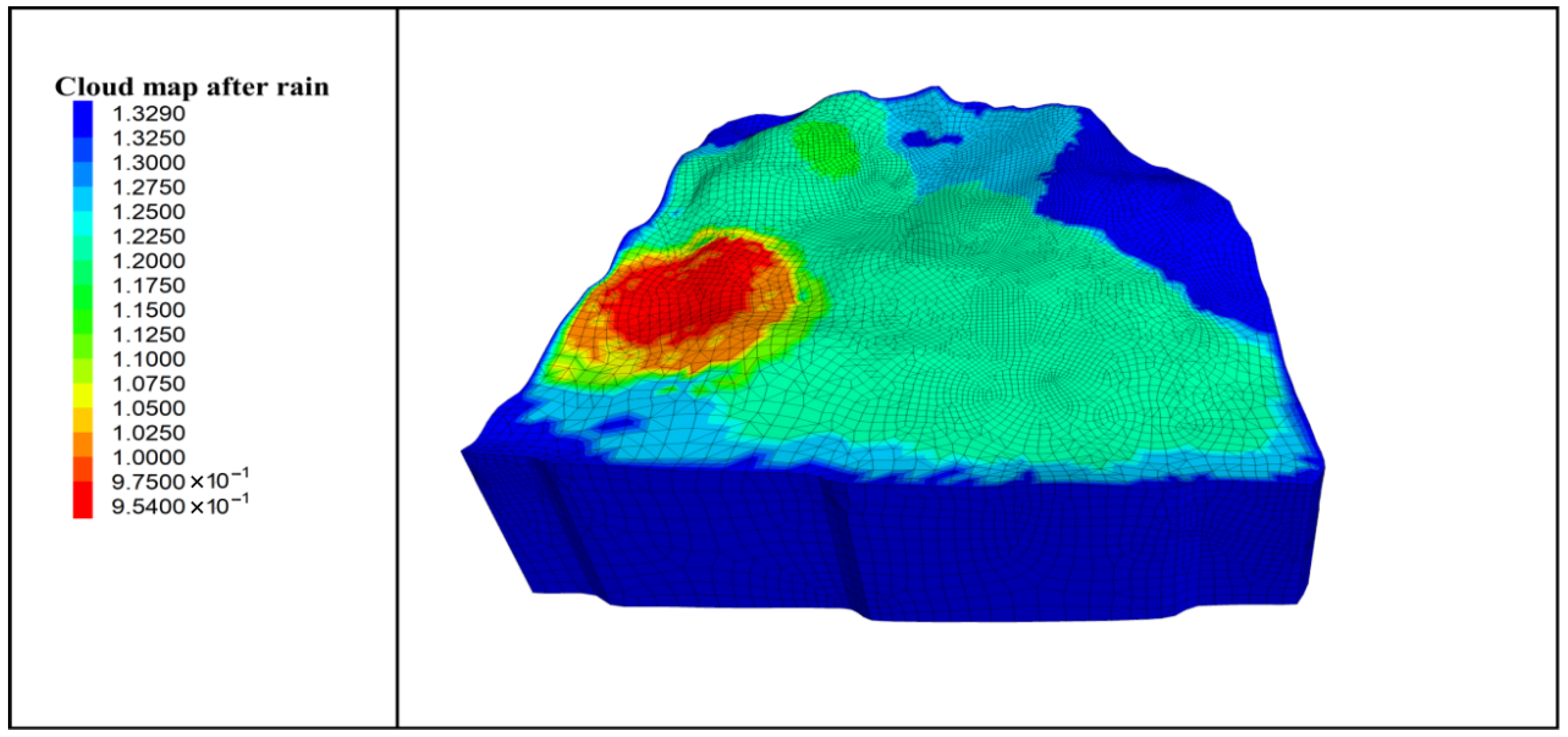
4.1.2. Real-Time Slope Stability Analysis
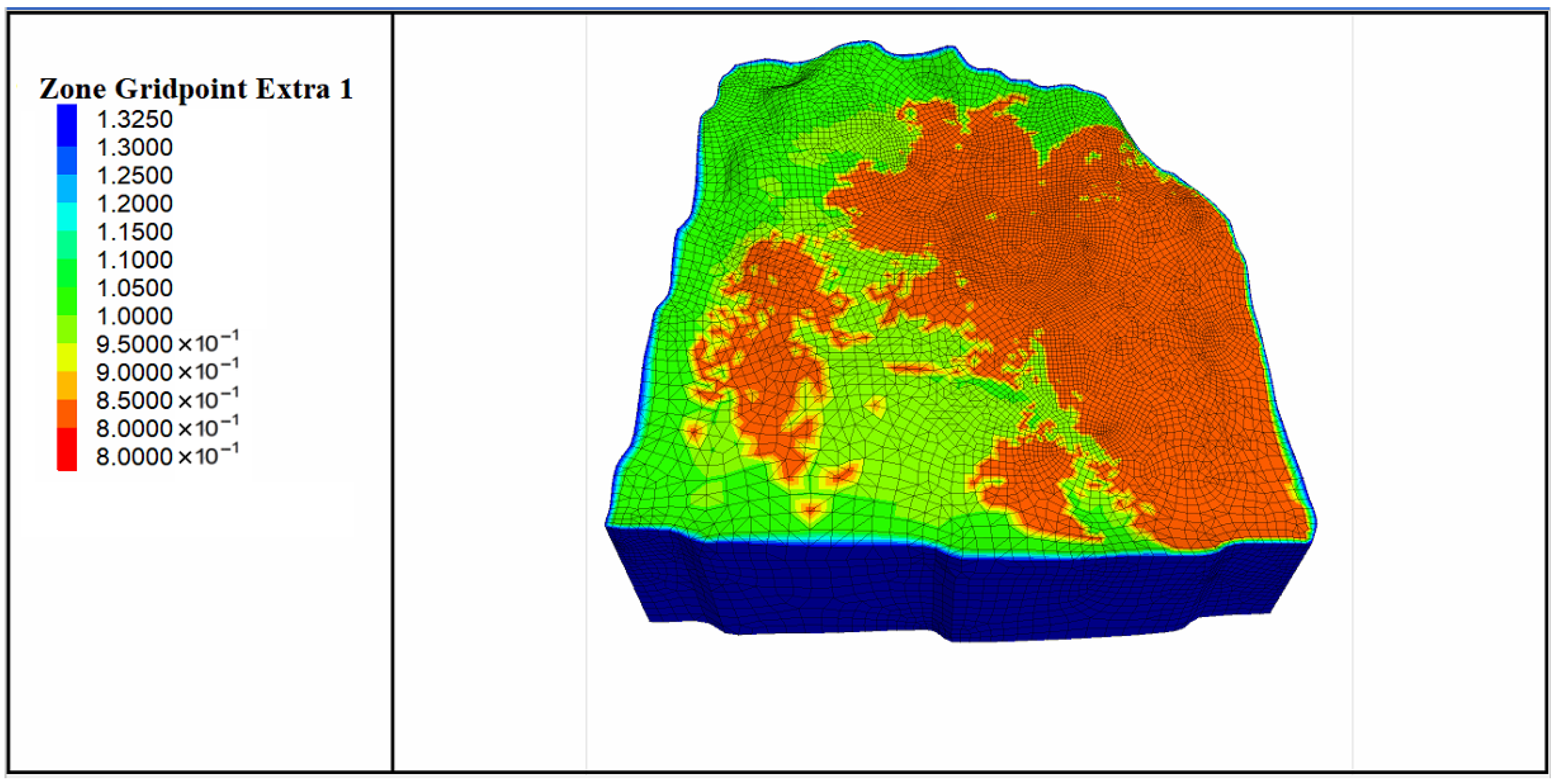
4.2. Slope Dynamic Monitoring
5. Conclusions
5.1. Research Results
5.2. Limitations and Future Work Plan
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, L.L.; He, K.Q.; Guo, L.; Zhang, J.; Sun, L.; Jia, Y. Research on the excavation stability evaluation method of Chaqishan ancient landslide in China. Eng. Fail. Anal. 2022, 141, 106664. [Google Scholar] [CrossRef]
- Lin, F.; Wu, L.Z.; Huang, R.Q.; Zhang, H. Formation and Characteristics of the Xiaoba Landslide in Fuquan, Guizhou, China. Landslides 2017, 15, 669–681. [Google Scholar] [CrossRef]
- Domínguez-Cuesta, M.J.; Quintana, L.; Valenzuela, P.; Cuervas-Mons, J.; Alonso, J.L.; Cortés, S.G. Evolution of a Human-induced Mass Movement Under the Influence of Rainfall and Soil Moisture. Landslides 2021, 18, 3685–3693. [Google Scholar] [CrossRef]
- Nguyen, L.C.; Tien, P.V.; Do, T.N. Deep-seated rainfall-induced landslides on a new expressway: A case study in Vietnam. Landslides 2020, 17, 395–407. [Google Scholar] [CrossRef]
- Martino, S.; Bozzano, F.; Caporossi, P.; D’Angiò, D.; Della Seta, M.; Esposito, C.; Fantini, A.; Fiorucci, M.; Giannini, L.M.; Iannucci, R.; et al. Impact of landslides on transportation routes during the 2016–2017 Central Italy seismic sequence. Landslides 2019, 16, 1221–1241. [Google Scholar] [CrossRef]
- Deng, E.; Xiang, Q.; Johnny, C.L.C.; Dong, Y.; Tu, S.; Chan, P.-W.; Ni, Y.-Q. Increasing temporal stability of global tropical cyclone precipitation. NPJ Clim. Atmos. Sci. 2025, 8, 11. [Google Scholar] [CrossRef]
- Zheng, Y.R. Development and application of numerical limit analysis for geological materials. Chin. J. Rock Mech. Eng. 2012, 31, 1297–1316. [Google Scholar]
- Wang, S.Y.; Tong, X.D. Stability analysis of slopes based on dynamic strength reductionimproved vector sum method. Chin. J. Geotech. Eng. 2023, 45, 1384–1392. [Google Scholar]
- Zhang, R.H.; Ye, S.H.; Tan, H. Stability analysis of multistage homogeneous loess slopes by improved limit equilibrium method. Rock Soil Mech. 2021, 42, 813–825. [Google Scholar]
- Lu, K.L.; Zhu, D.Y.; Gan, W.N. 3D limit equilibrium method for slope stability analysis and its application. Chin. J. Geotech. Eng. 2013, 35, 2276–2282. [Google Scholar]
- Liu, Z.P.; Yang, B.; Liu, J.; Ai, F. Three-dimensional limit equilibrium method based on GRASS GIS and TIN sliding surface. Rock Soil Mech. 2017, 38, 221–227. [Google Scholar]
- Nandi, S.; Santhoshkumar, G.; Ghosh, P. Development of limiting soil slope profile under seismic condition using slip line theory. Acta Geotech. 2021, 16, 3517–3531. [Google Scholar] [CrossRef]
- Bishop, A.W. The use of the slip circle in the stability analysis of slopes. Geotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Flaate, K.; Janbu, N. Soil exploration in a 500 m deep fjord, Western Norway. Mar. Geotechnol. 1975, 1, 117–139. [Google Scholar] [CrossRef]
- Spencer, E. A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Singh, J.; Verma, A.K.; Banka, H. Application of Biogeography based optimization to locate critical slip surface in slope stability evaluation. In Proceedings of the 4th International Conference on Recent Advances in Information Technology, Dhanbad, India, 15–17 March 2018; pp. 1–5. [Google Scholar]
- Meng, J.; Huang, J.; Sloan, S.W.; Sheng, D. Discrete modelling jointed rock slopes using mathematical programming methods. Comput. Geotech. 2018, 96, 189–202. [Google Scholar] [CrossRef]
- Chen, J.G.; Li, H.; He, Z.Y. Homogeneous soil slope stability analysis based on variational method. Rock Soil Mech. 2019, 40, 2931–2937. [Google Scholar]
- Zhou, X.P.; Huang, X.C.; Zhao, X.F. Optimization of the Critical Slip Surface of Three-Dimensional Slope by Using an Improved Genetic Algorithm. Int. J. Geomech 2020, 20, 04020120. [Google Scholar] [CrossRef]
- Zhou, F.X.; Zhu, S.W.; Liang, Y.W.; Zhao, W. Exact analysis of soil slope stability by using variational limit equilibrium method. Chin. J. Geotech. Eng. 2023, 45, 1341–1346. [Google Scholar]
- Lu, R.L.; Wei, W.; Shang, K.W.; Jing, X. Stability Analysis of Jointed Rock Slope by Strength Reduction Technique considering Ubiquitous Joint Model. Adv. Civ. Eng. 2020, 2020, 8862243. [Google Scholar] [CrossRef]
- Renani, H.R.; Martin, C.D. Factor of safety of strain-softening slopes. J. Rock Mech. Geotech. Eng. 2020, 12, 473–483. [Google Scholar] [CrossRef]
- Sengani, F.; Allopi, D. Accuracy of Two-Dimensional Limit Equilibrium Methods in Predicting Stability of Homogenous Road-Cut Slopes. Sustainability 2022, 14, 3872. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and non-associated visco-plasticity and plasticity in soil mechanics. Geotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Renani, H.R.; Martin, C.D.; Varona, P.; Lorig, L. Stability analysis of slopes with spatially variable strength properties. Rock Mech. Rock Eng. 2019, 52, 3791–3808. [Google Scholar] [CrossRef]
- Zhou, Y.; Cheng, X.H. High fill slope collapse: Stability evaluation based on finite element limit analyses. Transp. Geotech. 2024, 44, 101156. [Google Scholar]
- Sourav, S.; Manash, C. Stability analysis for two-layered slopes by using the strength reduction method. Int. J. Geo-Eng. 2021, 12, 24. [Google Scholar]
- Feng, S.; Zhao, Y.; Li, B.Y.; Wu, K. A Calculation Method of Double Strength Reduction for Layered Slope Based on the Reduction of Water Content Intensity. Comput. Model. Eng. Sci. 2024, 138, 221–243. [Google Scholar]
- Yu, M.D. Analysis on stability of mountain mass and numerical calculation of landslide resistance based on strength reduction method. Arab. J. Geosci. 2020, 13, 617. [Google Scholar] [CrossRef]
- Tayebeh, K.; Mohammad, R.A. Three-dimensional stability of locally loaded geocell-reinforced slopes by strength reduction method. Geomech. Geoengin.-Int. J. 2019, 14, 1581275. [Google Scholar]
- Hua, C.Y.; Yao, L.H.; Song, C.G.; Ni, Q.; Chen, D. A New Criterion for Defining Inhomogeneous Slope Failure Using the Strength Reduction Method. Comput. Model. Eng. Sci. 2022, 132, 413–434. [Google Scholar] [CrossRef]
- Du, Y.; Xie, M.W.; Lv, F.X.; Wang, Z.; Wang, G.; Liu, Q. New method for dynamic analysis of rock slope stability based on modal parameters. Chin. J. Geotech. Eng. 2015, 37, 1334–1339. [Google Scholar]
- Wang, C.; Zhang, R.R.; Zhang, F.H.; Du, C. A dynamic simulation analysis method of high-steep slopes based on real-time numerical model and its applications. Chin. J. Geotech. Eng. 2016, 37, 2383–2390. [Google Scholar]
- Song, L.F.; Xu, B.; Kong, X.J.; Zou, D.; Pang, R.; Yu, X.; Zhang, Z. Three-dimensional slope dynamic stability reliability assessment based on the probability density evolution method. Soil Dyn. Earthq. Eng. 2019, 120, 360–368. [Google Scholar] [CrossRef]
- Liu, H.Y.; Bai, M.Z.; Li, Y.J.; Yang, L.; Shi, H.; Gao, X.; Qi, Y. Landslide displacement prediction model based on multisource monitoring data fusion. Measurement 2024, 236, 115055. [Google Scholar] [CrossRef]
- Xiao, H.P.; Guo, G.L.; Chen, L.L. Research on Dynamic Evaluation Model of Slope Risk Based on Improved VW-UM. Math. Probl. Eng. 2019, 2019, 5813217. [Google Scholar] [CrossRef]
- Ai, Z.B.; Zhang, H.L.; Wu, S.C.; Jiang, C.; Yan, Q.; Ren, Z. Study on the slope dynamic stability considering the progressive failure of the slip surface under earthquake. Front. Earth Sci. 2022, 10, 981503. [Google Scholar] [CrossRef]
- Wu, J.; Guo, D.Y.; Zhang, L.W.; Wang, L. Stability analysis of arch dam and slope of the Xiluodu hydropower station on the Jinsha river. Chin. J. Rock Mech. Eng. 2023, 42, 2478–2494. [Google Scholar]
- Qu, X.L.; Chen, J.; Tang, H.; Dong, R.; Qi, C. Rock slope dynamic stability analysis based on coupling temporal domain numerical manifold method. Chin. J. Rock Mech. Eng. 2022, 41, 82–91. [Google Scholar]
- Wang, W.; Yang, Y.; Yang, X.; Gayah, V.V.; Wang, Y.; Tang, J.; Yuan, Z. A Negative Binomial Lindley Approach Considering Spatiotemporal Effects for Modeling Traffic Crash Frequency with Excess Zeros. Accid. Anal. Prev. 2024, 207, 107741. [Google Scholar] [CrossRef]
- Yang, Y.; Yin, Y.X.; Wang, Y.P.; Meng, R.; Yuan, Z. Modeling of Freeway Real-Time Traffic Crash Risk Based on Dynamic Traffic Flow Considering Temporal Effect Difference. J. Transp. Eng. Part A Syst. 2023, 149, 04023063. [Google Scholar] [CrossRef]
- He, B.H.; Du, X.L.; Bai, M.Z.; Yang, J.-W.; Ma, D. Inverse analysis of geotechnical parameters using an improved version of non-dominated sorting genetic algorithm II. Comput. Geotech. 2024, 171, 106416. [Google Scholar] [CrossRef]
- Baum, E.B.; Haussler, D. What size net gives valid generalization? Neural Comput. 1989, 1, 151–160. [Google Scholar] [CrossRef]







| Serial Number | Stratum | Rock Type | Thickness (m) |
|---|---|---|---|
| 1 | Quaternary artificial fill | 2~6.5 | |
| 2 | Quaternary collapse accumulation layer block stone soil | 3.1~23 | |
| 3 | Quaternary residual slope deposit silty clay | 1.7~9.3 | |
| 4 | Sandstone with mudstone | 3.3~10.5 | |
| 5 | Basalt | 9.2~20 |
| Monitoring Project | Point Number | Hole Depth (m) | Total (m) |
|---|---|---|---|
| Deep displacement monitoring | JCK01 | 28 | 312.5 |
| JCK02 | 16 | ||
| JCK03 | 33 | ||
| JCK04 | 33 | ||
| JCK05 | 29.5 | ||
| JCK06 | 50 | ||
| JCK07 | 35 | ||
| JCK08 | 29.5 | ||
| JCK09 | 30 | ||
| JCK17 | 28.5 | ||
| Surface displacement monitoring | 1 set of surface pull-wire intelligent displacement meter | ||
| Rainfall monitoring | 1 | ||
| Surface patrol | Once a month, with more frequent patrols during the rainy season | ||
| Layer | Quaternary Deposits | Weathered Layer | Interbedded Sandstone and Shale Layer | Moderately Weathered Basalt Layer | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Y1 | C1 | Y2 | C2 | Y3 | C3 | Y4 | C4 | ||||
| Unit | MPa | kPa | ° | MPa | kPa | ° | GPa | kPa | ° | GPa | kPa | ° |
| Original value | 32.8 | 19.7 | 30.3 | 19.3 | 23.1 | 23.4 | 30.6 | 53.9 | 29.9 | 64.2 | 76.2 | 42.6 |
| Improved value | 31.9 | 16.9 | 29.5 | 18.4 | 33.4 | 17.4 | 42.3 | 55.2 | 35.3 | 70.7 | 75.4 | 32.1 |
| Layer | Density (kg/m3) | Young’s Modulus (kPa) | Poisson’s Ratio | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|
| Quaternary deposits | 1850.00 | 2.00 × 104 | 0.30 | 23.00 | 24.00 |
| Weathered layer | 2200.00 | 1.00 × 106 | 0.28 | 40.00 | 15.00 |
| Moderately weathered sandstone with mudstone | 2300.00 | 3.00 × 107 | 0.25 | 70.00 | 35.00 |
| Moderately weathered basalt | 2900.00 | 4.00 × 107 | 0.20 | 75.00 | 55.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Du, X.; Bai, M.; Yang, J.; Ma, D. Research on Dynamic Stability of Slopes Under the Influence of Heavy Rain Using an Improved NSGA-II Algorithm. Appl. Sci. 2025, 15, 6914. https://doi.org/10.3390/app15126914
He B, Du X, Bai M, Yang J, Ma D. Research on Dynamic Stability of Slopes Under the Influence of Heavy Rain Using an Improved NSGA-II Algorithm. Applied Sciences. 2025; 15(12):6914. https://doi.org/10.3390/app15126914
Chicago/Turabian StyleHe, Bohu, Xiuli Du, Mingzhou Bai, Jinwen Yang, and Dong Ma. 2025. "Research on Dynamic Stability of Slopes Under the Influence of Heavy Rain Using an Improved NSGA-II Algorithm" Applied Sciences 15, no. 12: 6914. https://doi.org/10.3390/app15126914
APA StyleHe, B., Du, X., Bai, M., Yang, J., & Ma, D. (2025). Research on Dynamic Stability of Slopes Under the Influence of Heavy Rain Using an Improved NSGA-II Algorithm. Applied Sciences, 15(12), 6914. https://doi.org/10.3390/app15126914






