1. Introduction
As an emerging shaft construction technique, the mechanized shaft method integrates undrained excavation, overall suspended sinking, mechanical cutting using a milling drum, and prefabricated shaft assembly. This method exhibits strong adaptability to weak, disturbed, or otherwise unstable ground conditions. It significantly mitigates the impact of shaft construction on the surrounding strata, while reducing construction time and overall cost. Owing to these advantages, it has been increasingly adopted in modern shaft engineering practice.
Similar to other underground structures, mechanized shafts are inevitably subjected to earth and rock pressures from the surrounding strata, resulting in stress and deformation of the support system. Therefore, accurate estimation of the earth pressure acting on the support structure is essential in the structural design process. The classical Rankine and Coulomb earth pressure theories are widely applied in engineering practice due to their simplicity. However, their assumption of a linear earth pressure distribution often deviates from actual field conditions, leading to discrepancies between the theoretical and measured resultant earth pressures. Numerous laboratory tests have demonstrated that the active earth pressure behind plane retaining walls exhibits a nonlinear distribution [
1,
2]. Model tests on circular shafts have further confirmed this nonlinearity, revealing significant deviations from the classical Rankine earth pressure predictions [
3].
In recent years, extensive research has been carried out by both domestic and international scholars on the distribution of earth pressure behind retaining walls. Current analytical approaches for evaluating earth pressure on plane retaining walls primarily include the limit equilibrium method, slip-line theory, and limit analysis. Among these, the limit equilibrium method based on horizontal layer analysis has been widely adopted and has yielded numerous valuable results. For example, Handy [
4], Paik and Salgado [
5], as well as Goel and Patra [
6], incorporated the soil arching effect in the backfill and, based on the horizontal layer analysis method, derived the nonlinear distribution of active earth pressure in sandy soils. Since then, the earth pressure calculation method combining horizontal layer analysis with the soil arching effect has been further extended to various conditions, including seismic loading, limited-width backfills, seepage effects, and curved failure surfaces [
7,
8,
9,
10,
11,
12]. These developments have significantly advanced the understanding of earth pressure on plane retaining walls. Compared with the extensive research on plane retaining walls, studies on the calculation of earth pressure acting on curved retaining structures (e.g., circular shafts) remain relatively limited. Terzaghi [
13] was among the first to consider the effects of soil friction angle and the height-to-diameter ratio. Following an approach similar to Coulomb’s earth pressure theory, he derived an expression for the earth pressure on circular shafts based on the overall static equilibrium of the sliding soil mass. However, numerous studies have shown that under limit equilibrium conditions, stress redistribution in the soil behind the shaft gives rise to a vertical arching effect, similar to that observed in plane retaining walls. Additionally, a horizontal circular arching effect also develops. These two mechanisms, collectively referred to as the spatial arching effect, significantly influence both the magnitude and distribution of earth pressure [
14,
15].
To account for the influence of the circumferential arching effect, Berezantzev [
16] adopted the Haar–Karman assumption, which assumes that the circumferential stress
is always equal to the major principal stress
, and applied slip-line theory to derive the active earth pressure acting on circular shafts. However, subsequent studies [
17,
18,
19] have shown that the Haar–Karman assumption tends to overestimate the contribution of circumferential stress, as confirmed through extensive analytical and experimental investigations. For example, Prater [
17] introduced the concept of a circumferential stress coefficient
, defined as the ratio of circumferential stress to the major principal stress, and proposed that it should be taken as the static earth pressure coefficient
K0. Using the limit equilibrium method, he derived a formula for calculating the active earth pressure while accounting for the circumferential arching effect. The calculated results showed good agreement with experimental data in shallow soils but deviated significantly at greater depths. Furthermore, some researchers have considered both vertical and circumferential arching effects simultaneously. For instance, Chen and Zhou [
20] and Lu et al. [
21] incorporated the spatial arching effect and developed active earth pressure formulations for circular retaining walls based on the limit equilibrium approach. Zhang et al. [
22,
23] developed a calculation model for active earth pressure under various shaft wall displacement modes based on the horizontal layer analysis method, incorporating the influence of the spatial arching effect. Jia et al. [
24] adopted the Coulomb failure mechanism and derived a formulation for active earth pressure in circular shafts using the energy method, accounting for energy dissipation induced by circumferential stress. Recognizing that shaft wall displacement in practical applications is often insufficient to mobilize the active limit state, Pedro [
25] proposed a non-limit active earth pressure model that explicitly considers shaft wall displacement effects.
Most of the aforementioned studies assume that the circumferential stress coefficient
remains constant. However, its magnitude is, in fact, strongly dependent on the spatial location of the soil element [
26,
27]. Based on discrete element simulations, Chen and Zhou [
28] observed that the circumferential arching effect diminishes progressively with increasing distance from the wall, leading to a corresponding decrease in the circumferential stress coefficient
. Similarly, Xiong et al. [
29,
30] analytically derived the circumferential stress under axisymmetric active limit conditions and concluded that the influence of the circumferential arching effect decreases with radial distance. Therefore, assuming a constant circumferential stress coefficient inevitably introduces significant discrepancies between calculated and actual earth pressure distributions [
31]. In addition, due to the presence of soil arching in the vertical plane, the principal stress direction undergoes rotation, which induces horizontal shear stresses. These shear stresses significantly affect both the magnitude of the active earth pressure and the location of its resultant force [
32,
33]. However, this effect has not been adequately addressed in existing studies on shaft earth pressure.
Based on the above analysis, this study investigates the sliding soil mass behind the shaft wall, taking into account the radial variation of the circumferential stress coefficient. An analytical expression for the inclination angle of the sliding surface under active limit state conditions is derived. Incorporating the effects of spatial soil arching and interlayer shear, a calculation method for active earth pressure is established using a horizontal layer analysis approach combined with vertical and radial static equilibrium conditions. The proposed equation is validated through comparison with existing theoretical models and experimental results. Furthermore, an internal force calculation method for the shaft lining is developed based on elastic theory, considering the spatial effects of soil arching and interlayer shear. The proposed method is verified against field monitoring data, demonstrating its accuracy and practical applicability.
3. Analysis of Active Earth Pressure in Circular Shafts
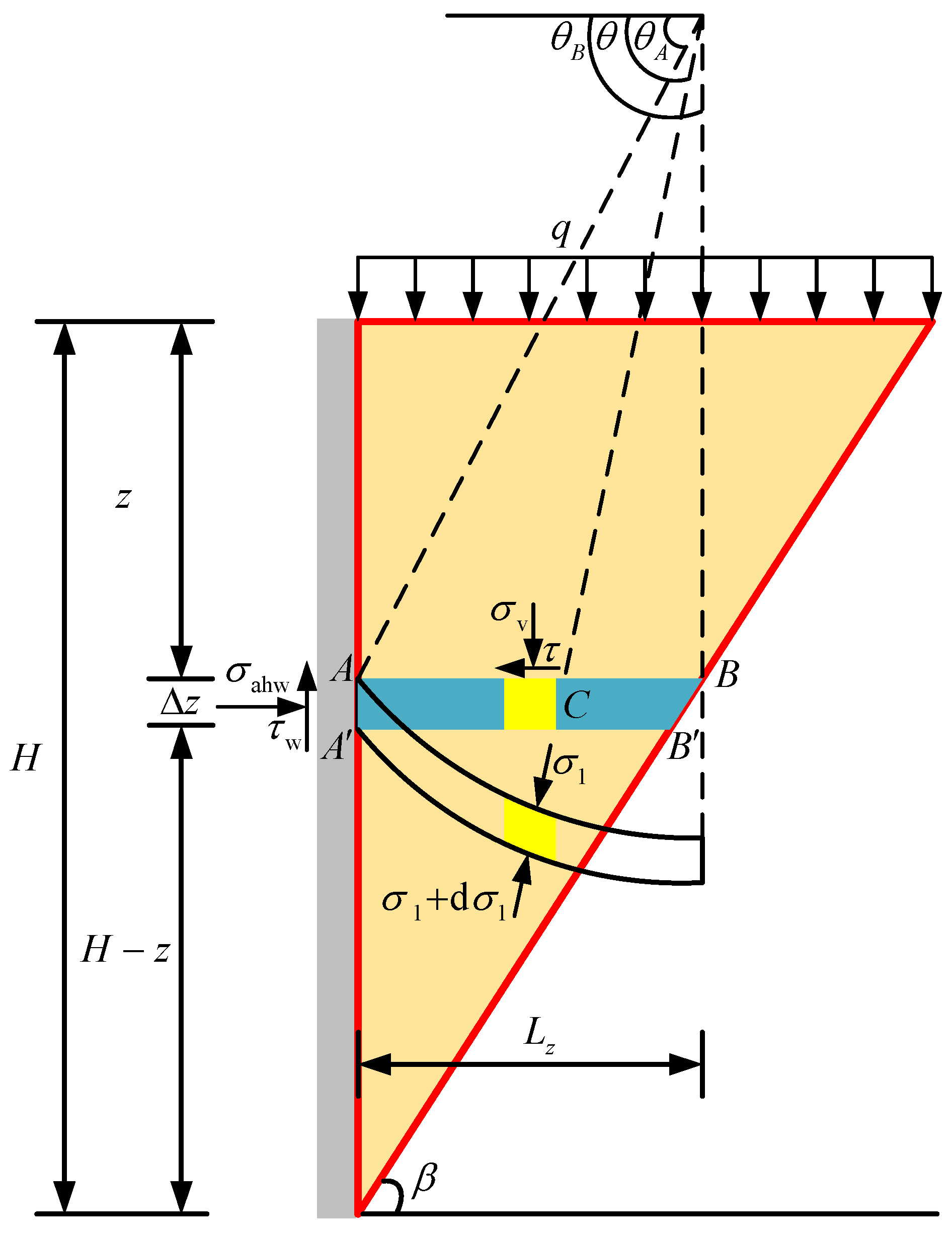
This study simultaneously considers the vertical arching effect and circumferential arching effect (i.e., the spatial arching effect) generated by the soil behind the shaft wall during deformation and incorporates the shear stress between horizontal soil layers to determine the active earth pressure distribution behind the circular shaft wall using the horizontal layer analysis method.
3.1. Vertical Arching Effect
Due to the presence of the vertical arching effect (i.e., the soil arch effect in the vertical plane), the direction of the minor principal stress in the soil is no longer horizontal but deflects to a certain extent. The trace of the minor principal stress within a soil element on the same horizontal layer forms a curve, as shown in
Figure 4, which can typically be approximated as an arc [
4].
According to the limit equilibrium condition, the deflection angles of the major principal stress at the wall–soil contact surface (point A) and at the sliding surface (point B) are given as follows:
The stress Mohr circle of the soil behind the shaft wall is translated leftward by
(i.e.,
) units, as shown in
Figure 5. The stress coordinates of any point in the equivalent coordinate system satisfy the following relationship:
Furthermore, as shown in
Figure 4, for the horizontal differential element
at depth
z under the active limit equilibrium state, assuming that the angle between the major principal stress direction at any point
C and the horizontal plane is
, the horizontal stress
, vertical stress
, and interlaminar shear stress
at this point are given as follows:
By substituting Equation (11) into Equation (13), the horizontal stress (i.e., the horizontal active earth pressure) at point
A on the wall–soil contact surface can be obtained as follows:
Furthermore, the average vertical stress
on the horizontal differential element
can be expressed as follows:
where
is the width of the upper surface of the horizontal differential element
, and
;
Similarly, the average shear stress
on the horizontal differential element
can be obtained as follows:
By combining Equations (14) and (15), the lateral active earth pressure coefficient
can be derived as follows:
where
;
Similarly, by combining Equations (15) and (16), the average shear stress coefficient
can be derived as follows:
3.2. Circumferential Arching Effect
When the soil behind the shaft wall reaches the active limit state, it is typically accompanied by centripetal displacement, generating a circumferential compression effect that increases the circumferential stress and enhances the stability of the soil. This phenomenon is referred to as the circumferential arching effect. The effect is unevenly distributed within the same horizontal soil layer and gradually weakens with an increase in radial distance, causing the circumferential stress to decrease progressively along the radial direction.
For the horizontal differential element
, the average circumferential stress
can be obtained using Equation (6) as follows:
Furthermore, by combining Equations (15) and (19), the average circumferential stress coefficient
can be obtained as follows:
In summary, considering the influence of the spatial arching effect, the relationships among the horizontal active earth pressure , the average shear stress between horizontal soil layers, the average circumferential stress , and the average vertical stress on the horizontal differential soil element have been established.
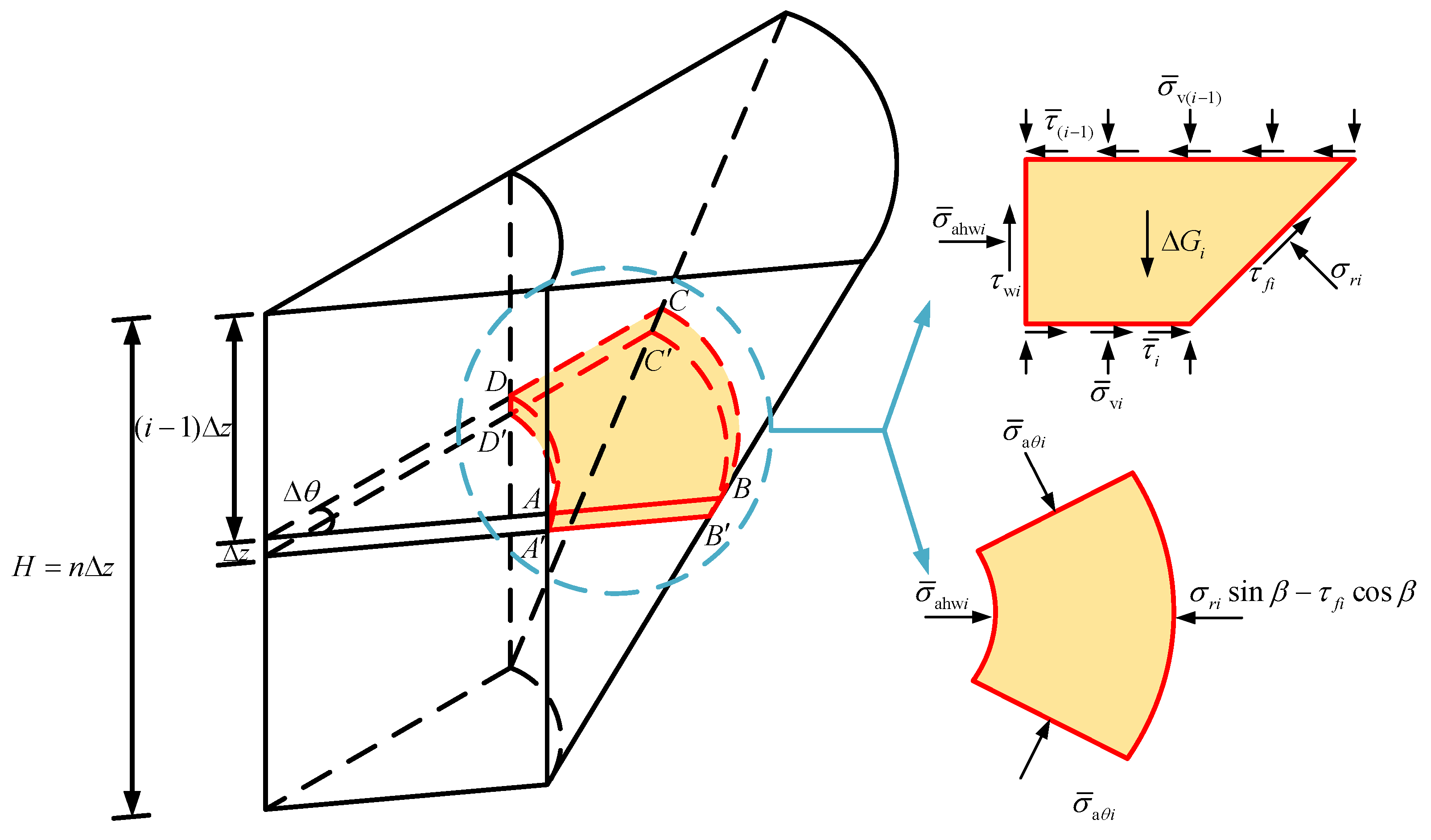
3.3. Numerical Iterative Solution for Active Earth Pressure
This study incorporates interlayer shear stress into the cohesive soil mechanics model. Due to the presence of
, it is not possible to obtain an explicit solution for the active earth pressure through integration; therefore, a numerical solution must be employed to derive the active earth pressure. This numerical solution divides the soil into horizontal sections based on the step length
, as shown in
Figure 6. By analyzing the
i-th layer of the horizontal differential soil element, the vertical and radial force equilibrium equations are derived as follows (in
Figure 6, the shear stress is considered only in the vertical force analysis).
where the action areas
,
,
,
, and
of each force can be obtained using Equation (23);
is the self-weight of the horizontal differential soil element of the
i-th layer, determined by Equation (24). Given the small thickness of the horizontal differential soil element, it is assumed that within the thickness
, the horizontal stress at the wall–soil contact surface and the circumferential stress of the soil element are approximately linearly distributed, which can be calculated using Equation (25). The remaining parameters can be determined using Equation (26), based on the stress relationships derived from the active limit equilibrium condition and the spatial arching effect.
By combining Equations (21)–(26), the iterative formula for a can be established:
where
;
;
; ;;
The active earth pressure of the horizontal differential soil elements below the critical depth and above the critical stress is summed to obtain the resultant active earth pressure:
where
is the
i value at the critical depth, which can be determined using Equation (29);
is the
i value at the critical stress at the bottom of the shaft; that is, the
i value corresponding to the point when Equation (27) is iterated to 0.
The total overturning moment caused by the active earth pressure on the wall heel is given by:
From Equation (30), the position of the active earth pressure resultant force can be finally obtained as:
3.4. Validation and Comparison with Other Theoretical and Experimental Results
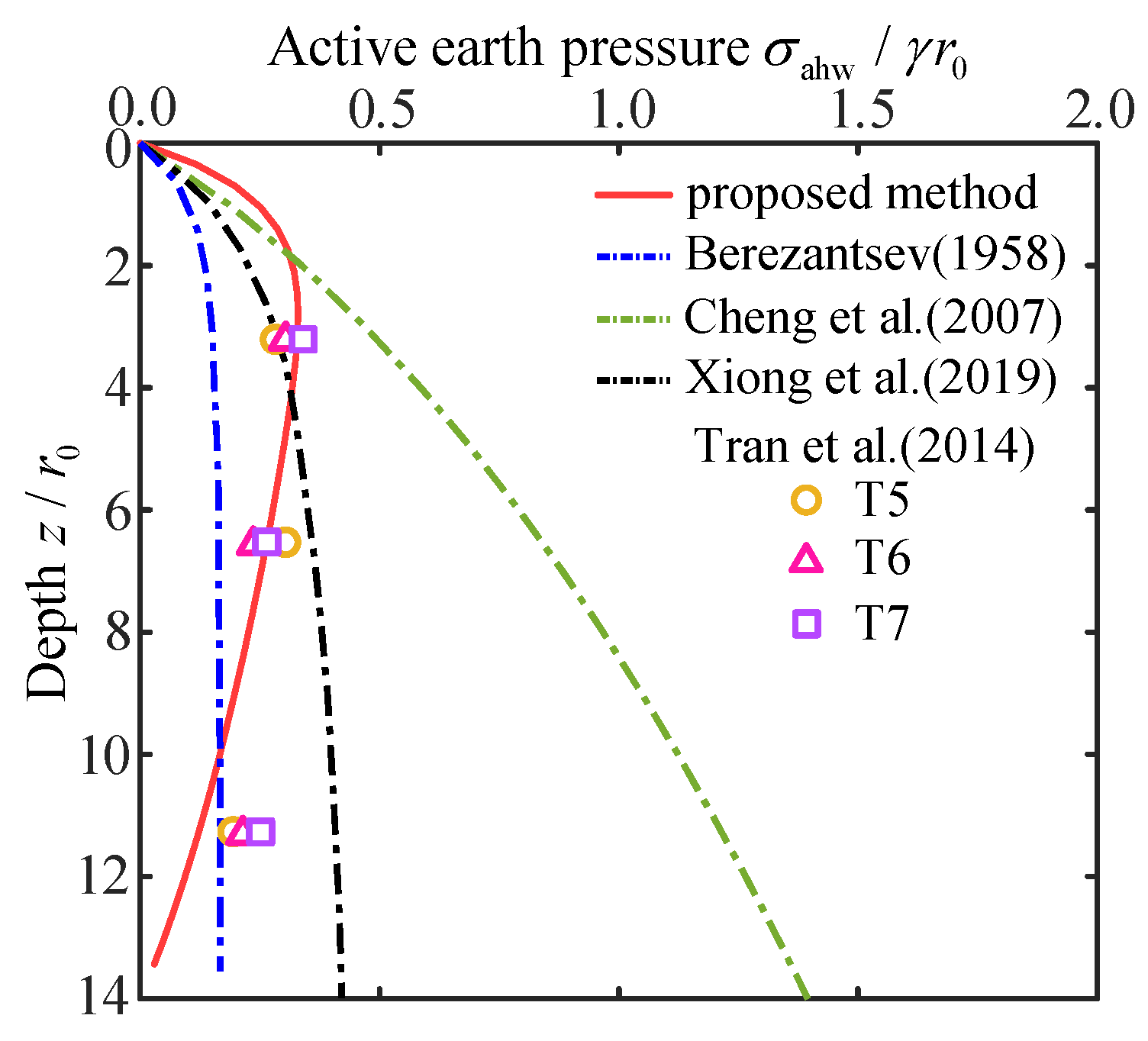
Tran et al. [
34] employed a circular shaft model with a uniformly decreasing diameter to investigate the distribution of active earth pressure on the shaft wall. The relevant parameters of the model test are:
.
Figure 7 compares the calculation results obtained in this study with the experimental results of Tran et al. [
34], and further compares and analyzes them alongside the theoretical predictions of Berezantsev [
16], Cheng et al. [
19], and Xiong et al. [
29].
As shown in
Figure 7, the calculated values from this study and those of Xiong et al. [
29] are generally consistent with the model test results. It is noteworthy that this study incorporates the spatial arching effect of the soil in the calculation, which allows for a more accurate representation of the trend where the soil pressure intensity first increases and then decreases with depth. In contrast, the calculation results of Berezantsev [
16] and Cheng et al. [
19] show significant deviations from the experimental values. The primary reason is that both studies assume the circumferential stress coefficient
to be constant (1 and
K0, respectively), neglecting the fact that the circumferential stress continuously varies with position. By comparison, this study accounts for the variation of the circumferential stress coefficient
along the radial coordinate, resulting in calculated values that are closer to the experimental results and thereby verifying the rationality and effectiveness of the proposed calculation method.
To further analyze the influence of the radius-to-height ratio and wall–soil friction angle on the distribution of active earth pressure intensity,
Figure 8 presents the distribution curves of active earth pressure intensity under different radius-to-height ratios and wall–soil friction angles. Additionally, to investigate the role of the interlayer shear effect of the soil, the calculation results of this study are compared with the values reported by Lu et al. [
21]. For ease of analysis, both the horizontal and vertical axes in the figure are normalized.
As shown in the figure, the active earth pressure intensity obtained in this study exhibits a curved distribution. The smaller the radius-to-height ratio and the larger the wall–soil friction angle, the more pronounced the influence of the soil arching effect on the distribution of active earth pressure intensity, and the more evident the curved distribution characteristics. In addition, when the radius-to-height ratio is less than 1, the calculated active earth pressure intensity in the middle and lower portions of the shaft is significantly lower than the theoretical value predicted by Rankine’s earth pressure theory. As the radius-to-height ratio increases, the circumferential arching effect gradually weakens, and the active earth pressure intensity at the same depth progressively increases; however, the rate of increase gradually diminishes.
Further comparative analysis of the calculation results of Lu et al. [
21] reveals that the shear stress between soil layers has a substantial impact on the distribution of active earth pressure along the depth direction. This effect is primarily reflected in the reduction of active earth pressure in the middle and upper portions of the shaft and the increase of active earth pressure at the shaft bottom. Moreover, the larger the radius-to-height ratio and the larger the wall–soil friction angle, the more pronounced the influence of interlayer shear on the active earth pressure distribution.
However, it should be noted that the assumption of a linear sliding surface extending to the bottom of the shaft results in a sudden drop in the calculated earth pressure to 0 at the base. As this discontinuity is distinctly localized and has a minimal effect on the overall distribution, a practical adjustment can be adopted in engineering applications by extrapolating the earth pressure value computed at 95% of the shaft depth to the bottom 5%.
5. A Case Study
To further validate the proposed calculation method, this study conducted a comparative analysis between the computed results and the field monitoring data.
5.1. Project Overview
The Mingyuan Forest Urban Green Underground Smart Garage Project is located at the southeast corner of Guangyan Road and Yonghe Road in Jingan District, Shanghai. The project comprised two circular shafts with an inner diameter of 21.0 m, constructed by mechanical excavation. In mechanical shaft construction, the segmental lining was installed by a top-down, ring-by-ring assembly synchronized with the shaft’s progressive sinking. The first ring was pre-assembled on the ground or in a shallow shaft. As excavation proceeded in stages and the shaft subsided, subsequent rings were installed sequentially within the sinking space. Each ring was bolted and sealed to ensure structural integrity and watertightness. Each shaft support structure consisted of three components: a 2.0 m thick cast-in-place bladed footing at the base, 22 rings of precast segmental linings totaling 44.0 m in height, and a 4.2 m high cast-in-place top section. For convenience in the following analysis, the blade foot was designated as Ring 0, and the precast segments were consecutively numbered from Ring 1 to Ring 22 in ascending order from bottom to top. The shaft excavation diameter was 23.0 m, with a segment thickness of 1.0 m. Each ring comprised 10 segments. The total excavation depth was approximately 50.2 m. The relevant geological parameters are listed in
Table 1.
The circular shaft case study aligns well with the calculation model proposed herein, and the comparative validation based on this case is both appropriate and robust. In addition, to verify the reliability of the analytical results, vibrating wire earth pressure gauges and steel reinforcement bar axial force gauges were installed to monitor the earth pressure on the Ring 3 and Ring 6 segments, as well as the axial forces in the inner and outer reinforcement bars, respectively. The locations of the monitoring points are shown in
Figure 10.
To facilitate subsequent analysis, based on the on-site construction plan and the stress characteristics of the support structure, the shaft construction process was divided into three stages.
Stage I: Excavation to the bottom under the condition that the outer wall was in contact with slurry and the inner wall was in contact with silty water. The unit weight of silty water on the inner wall was 12.5 kN/m3, and the unit weight of slurry on the outer wall was 11.0 kN/m3.
Stage II: Replacement of the slurry on the outer wall with plain concrete.
Stage III: Extraction of water from inside the shaft.
Since both the inner and outer sides of the segments were surrounded by fluid in Stage I, and therefore not subjected to earth pressure, the earth pressure analysis was conducted only for Stages II and III.
5.2. Analysis of the Internal and External Pressures on the Segment
Figure 11 compares the calculated active earth pressure, the theoretical value from Rankine’s earth pressure theory, and the monitoring data from Shaft No. 2 of the Jingan Garage. As shown in the figure, the theoretical values obtained from the method proposed in this study are in good agreement with the measured results. It can serve as a theoretical basis for the optimal design of circular shaft wall structures.
This is primarily attributed to the inclusion of soil arching effects in both the vertical and horizontal planes in the calculation. In particular, the consideration of the ring arching effect in the horizontal plane greatly improved the stability of the surrounding soil, thereby reducing the active earth pressure acting on the shaft wall. These results further validate the rationality and accuracy of the proposed calculation method.
For clarity and efficiency, Rings 3, 6, 10, 14, 18, and 22 were selected for analysis.
Table 2,
Table 3 and
Table 4 show the calculated internal and external pressures on the segments during the three construction stages.
5.3. Analysis of the Internal Forces and External Deformations
Figure 12 shows the contour plots of the analytical results for the radial internal forces, circumferential internal forces, and radial deformation of the Ring 3 segment during Stage I. As shown in the figure, the internal forces and deformations exhibited a clear symmetrical pattern, which is consistent with engineering practice.
Based on the assumptions of the plane section, linear elasticity, and uncracked concrete, the axial force in the steel bars and the circumferential stress at the section center, as obtained from monitoring, can be calculated using Equation (41):
where
σ′
φ is the circumferential internal stress;
Ns1 and
Ns2 are the monitored axial forces in the steel bars on the outer and inner sides of the segment, respectively;
Es is the elastic modulus of the steel bars; and
Ec is the elastic modulus of the reinforced concrete.
Figure 13 presents a comparison between the theoretical calculations and the monitored values of the annular internal forces for Rings 3 and 6. As shown in the figure, the relative error between the results obtained from earth pressure theory and the measured values was within 10%, with a correlation coefficient of 0.98, indicating a strong correlation between the analytical and monitored values. The error falls within a reasonable range, verifying the reliability of the proposed analysis.
Figure 14 shows the analysis results of internal forces. As observed from
Figure 13 and
Figure 14, the internal forces were positively correlated with the burial depth. When the internal pressure exceeded the external pressure, the maximum radial stress occurred at the inner arc surface, while the maximum radial deformation and circumferential stress occurred at the outer arc surface. Conversely, when the external pressure was greater than the internal pressure, the pattern was reversed. A large pressure difference between the inside and outside can result in excessive forces on the segment, while excessive internal pressure may cause the segment to undergo tension. In practical engineering, it is important to avoid both large pressure differences and excessive internal pressure.
Figure 15 presents the internal forces and deformation along the depth direction, where the solid line corresponds to the outcomes derived from the calculation method proposed herein, while the dotted line represents the results based on the Rankine earth pressure theory.
① During the first stage, the internal forces and deformations of the segment increased approximately linearly with burial depth, consistent with the linear growth of soil and fluid pressures acting on the segment at this stage. In contrast, segments in the second and third stages exhibited distinct nonlinear variations in force and deformation along the depth. This discrepancy primarily resulted from the fact that, in the first stage, the segment’s inner and outer surfaces were subjected to silt and slurry pressures respectively, both varying linearly with depth. However, the earth pressure model developed in this study incorporates the soil arching effect, producing a nonlinear earth pressure distribution, which in turn induces nonlinear responses in segment forces and deformations.
② In the second stage, the segment experienced maximum annular internal force and radial deformation at a burial depth near 38.0 m, while in the third stage, these maxima occurred closer to 23.0 m depth. This phenomenon was mainly driven by the evolving differential pressure across the segment. As construction advanced and surrounding ground conditions changed, the distribution of pressure difference was altered, leading to stage-dependent shifts in the locations of peak force and deformation. These results reveal the complex temporal and spatial evolution of segment stress states during construction, providing valuable guidance for the rational design of segment structures and effective construction control strategies.
6. Conclusions
In this study, the stress and deformation behavior of circular shafts was analyzed by explicitly incorporating the radial distribution of circumferential stress induced by the spatial arching effect. An analytical expression for the inclination angle of the sliding surface under active limit conditions was derived based on the global force equilibrium of the sliding soil. A novel method for calculating the active earth pressure on circular shafts was proposed, which accounts for both the spatial arching effect and interlayer shear interactions. The validity of the proposed approach was confirmed through comparisons with theoretical solutions, model test results, and field measurements. Furthermore, an elastic mechanics-based model was developed to evaluate the stress and deformation response of pipe segments during mechanical shaft excavation. The main conclusions are summarized as follows:
(1) Under active limit conditions, the inclination angle of the sliding surface behind the circular shaft wall is generally larger than that of the Coulomb sliding surface. As the radius-to-height ratio increases, the spatial arching effect—particularly the circumferential arching effect—gradually diminishes, leading to a decrease in the sliding surface angle that asymptotically approaches the theoretical prediction. Additionally, higher soil cohesion increases the shear stress required to satisfy limit equilibrium, thereby resulting in a greater sliding surface angle. This effect is more pronounced in soils with lower internal friction angles.
(2) The active earth pressure of circular shafts is significantly influenced by the radius-to-height ratio and interlayer shear stress: a smaller radius-to-height ratio enhances the circumferential arching effect, improving soil stability and reducing active earth pressure, while a larger diameter-to-height ratio amplifies the impact of interlayer shear stress on the pressure distribution. By accounting for the radial variation of the circumferential stress coefficient and the spatial arching effect, the proposed calculation method shows good agreement with model test results and effectively captures the depth-dependent variation of active earth pressure under the translation mode.
(3) The stress and deformation behavior of the shaft structure is fundamentally governed by the combined action of internal and external water and soil pressures. Owing to the spatial arching effect of the surrounding soil mass, the distribution of stresses and deformations in Stages II and III demonstrates a distinct nonlinear variation with depth. The analytical predictions show excellent agreement with the measured data, thereby confirming the validity and reliability of the proposed earth pressure calculation framework and the structural stress–deformation analysis approach developed in this study.
(4) The stresses experienced by the shaft structure are strongly governed by the pressure differential between its inner and outer sides. An excessive pressure differential can induce elevated structural stresses, while overly high internal pressures may subject the structure to significant tensile forces. Therefore, in practical engineering applications, it is crucial to carefully control both the pressure differential and the internal pressure to ensure the structural integrity and long-term safety of the shaft system.
In summary, the proposed calculation framework provides a theoretical basis for the optimization and safety evaluation of circular shaft wall structures under translational mode conditions. Moreover, the underlying concepts offer potential reference value for investigating displacement behavior under rotational failure modes, with prospects for broader application and further development.