Abstract
Facial wrinkles are a key indicator of aging and hold significant importance in skincare, cosmetics, and cosmetology. Their formation is closely linked to mechanical deformation, yet the underlying processes remain complex. This study integrates the Facial Action Coding System (FACS) with three-dimensional digital image correlation (3D-DIC) to dynamically capture and quantitatively analyze skin deformation during facial expression. Principal strains and their orientation are introduced as important parameters to investigate the relationship between mechanical behavior and wrinkle formation. To further explore these interactions, a four-layer finite element (FE) model incorporating a muscle layer is developed, simulating muscle contraction and its influence on skin deformation. The findings provide a mechanobiological framework for understanding wrinkle formation and may inspire the development of strain-sensitive sensors for real-time detection of microstructural deformations.
1. Introduction
Skin wrinkles, particularly on the face, are a key sign of aging and play an important role in the expanding fields of skincare, cosmetics, facial recognition, and dermatological treatments [1]. Moreover, wrinkles adversely affect facial recognition accuracy while playing a significant role in facial modeling and machine learning applications [2,3]. The image enhancement and denoising approach has driven the development of related fields such as facial modeling and wrinkle recognition [4]. Human skin develops two primary types of wrinkles: static wrinkles and dynamic wrinkles [5]. Static wrinkles result from age-related tissue volume loss, whereas dynamic wrinkles can form at any age due to the contraction of underlying skeletal muscles during facial expressions. Despite their differences, both types show similar wrinkling mechanisms. Campiche et al. [6] observed striking similarities in the facial wrinkle patterns of mothers and daughters when smiling or expressing anger. Wrinkles are an inherent feature of skin morphology, closely influenced by mechanical interactions with their surrounding environment [7]. To better understand wrinkle formation, it is essential to analyze the mechanical behavior of in vivo skin, as wrinkle development is strongly linked to deformation caused by repeated facial movements of both skin and muscles [6,8].
Both experimental and numerical methods are widely used to study skin wrinkles. Human skin typically consists of three layers: the epidermis, dermis, and hypodermis [9]. Skin exhibits nonlinear mechanical behavior across its stratified structure. Hyperelastic and viscoelastic constitutive models are employed to characterize this nonlinear mechanical behavior of biomaterials [10,11]. To investigate the formation of compressed skin folds, early studies employed a three-layer finite element (FE) model [12,13,14]. Recognizing the biomechanical contributions of sublayers, Zhao et al. [15] introduced a six-layer computational model to explore the relationship between aging and dynamic surface wrinkling. In their subsequent studies, they examined the potential mechanisms of three wrinkle formations [5]. Researchers extended earlier frameworks by developing enhanced FE models that integrated additional skin structural details. To investigate the effect of collagen fibers within the dermis, a multiscale four-layered 2D FE model was developed [16]. Considering the detailed geometry of a human finger, Yin et al. [17] utilized a multi-layered 3D FE simulation model to characterize wrinkling behavior in terms of wavelength, amplitude, and critical wrinkling stress/strain. Diosa et al. [18] incorporated realistic microscale topography into a multi-layered 3D model to examine its impact on the mechanical and tribological properties of human skin. To deepen our understanding of wrinkle formation with aging, Sun et al. [19] developed a four-layer skin model characterized by polygonal microrelief structures. Despite significant progress in modeling skin wrinkling, existing studies primarily focus on the structural composition of the skin itself while often overlooking the crucial role of underlying muscles. Dynamic wrinkles are directly induced by repeated muscle activity, and neglecting this factor limits the accuracy of simulations in capturing realistic wrinkle formation processes.
There has been notable advancement in experiments aimed at understanding the underlying mechanisms of wrinkle formation [20]. Flynn et al. [13] utilized an experimental setup, including a charged-coupled device (CCD) laser displacement sensor and a micro-translation stage, to investigate wrinkling on the volar forearm. To quantify the wrinkles on the knee and crow’s feet, Yoo et al. [21] employed an optical 3D capturing device and R-parameter. New optical methods are increasingly being adopted to study the formation of skin wrinkles. For example, the digital image correlation (DIC) technique has been widely applied because it enables measuring the deformation of the material surface [22,23,24,25,26]. Miura et al. [8] used the DIC method to assess strain around the eye during blinking and further explored the relationship between wrinkle formation and strain distribution. Moreover, a phase-contrast optical microscope was used by Youn et al. [27] to reconstruct an epithelial tissue folding model and examine the in situ biomechanical wrinkling. To directly obtain the internal wrinkling state of human skin, a novel in vitro technique that merges tissue engineering with 3D Swept Source-Optical Coherence Tomography imaging technology was introduced by Min et al. [28].
Existing studies show that in vitro experiments are often utilized in research on skin wrinkles. The formation of wrinkles is intrinsically linked to facial expressions, which are driven by underlying muscle contractions. Repeated facial movements and muscle contractions create dynamic stress on in vivo skin. However, limited research exists on the direct measurement in vivo for skin wrinkling. In addition, current FE models for wrinkling often overlook the role of the muscle and hypodermis layers, although skin wrinkling is the result of muscle contraction and layer-layer strain transmission to the skin surface.
Facial expressions can serve as a loading method to study the deformation characterization of in vivo skin, which is related to wrinkles [6]. This study aims to examine the potential relationship between deformation and skin wrinkling by introducing facial expressions. Moreover, how muscle-driven mechanical stress transmission through facial tissue layers governs wrinkle formation is still not clear. The skin movements during six basic facial expressions are generated according to FACS and recorded using two CCD cameras. The displacement and strain distributions on the skin’s surface during these expressions are obtained using the 3D-DIC method. The principal strains and their directions are introduced to qualitatively explain the wrinkle formation. To further quantitatively investigate the relationship between the mechanical parameters and wrinkle formation, a four-layer FE model considering muscle and hypodermis layers is proposed. The rest of this paper is organized as follows. The experimental and FE methods are described in detail in Section 2. The results of the mechanical deformation of the skin and wrinkle formation mechanisms are presented in Section 3. In Section 4, the influence of the loading method and the mechanical properties of skin and muscle on facial wrinkles is discussed. The important conclusions are summarized in Section 5.
2. Methods
2.1. Experiments
A series of experiments is carried out to measure skin deformation during various facial expressions based on a 3D-DIC system. This system comprises two CCD cameras (acA2500-20gm, Basler, Ahrensburg, Germany) and two illuminants to record human facial expressions, as illustrated in Figure 1a. Before the experiments, calibration procedures using Zhang’s method ensured three-dimensional reconstruction, meeting micro-level deformation measurement requirements [29].
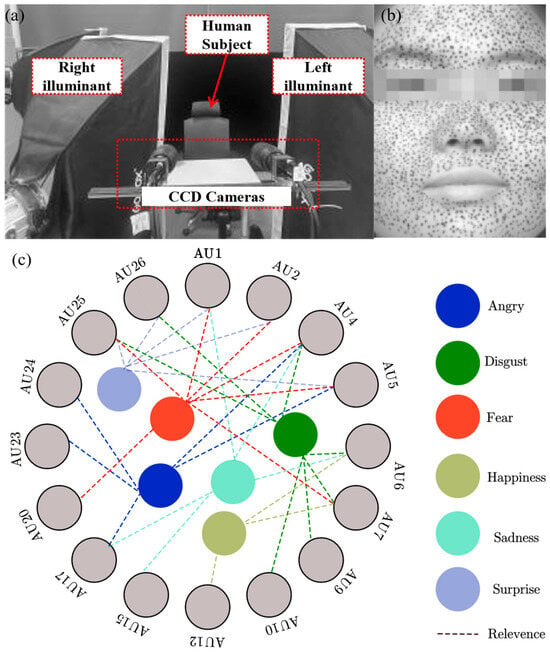
Figure 1.
(a) Experimental setup, (b) the cropped images of facial skin with irregular spots, and (c) relevance between facial expressions and Aus [30,31].
Before the experiments, healthy volunteers (20–30 years old) without skin diseases, burns, or surgical scars participated in this study. All participants provided written informed consent, and the experimental protocol was approved by the Ethics Committee of Tianjin Hospital of China. Irregular speckles are painted on the facial skin of human subjects using black skincare products. This procedure aims to enhance optical contrast and tracking accuracy.
A standardized procedure is implemented for facial expression experiments. Firstly, a pre-experiment is carried out. A neutral state is important to ensure high consistency both within and across subjects. To minimize physiological variability and ensure measurement consistency, participants undergo a 30 min acclimatization period in a controlled environment (25 °C) to achieve a relaxed baseline state. Secondly, trained professionals guide participants to produce six basic facial expressions: anger, disgust, fear, happiness, sadness, and surprise. These expressions are standardized based on the Facial Action Coding System (FACS), as proposed by Ekman and Friesen [30,31], which classifies facial muscle movements into distinct Action Units (AUs). In this study, the relevance between facial expressions and AUs is generated with some references [30,31] and shown in Figure 1c. The systematic identification of AUs ensured repeatable and anatomically consistent facial expressions. Subsequently, the experimental system captured high-resolution image sequences (1600 × 1200 pixels, 8-bit) at 30 frames per second, recording the transition from a neutral expression to the target expression states. The collected image sequences are pre-processed and segmented, ensuring optimal feature extraction for displacement analysis. Finally, the 3D-DIC technique is applied to compute full-field displacement distributions across the facial surface by referencing the neutral expression as an undeformed state. Using the 3D-DIC method, the subset size is set to 41 × 41 pixels, with a step size of 5 pixels, optimizing spatial resolution while maintaining computational efficiency. To ensure the reliability of measurements, the regions with a correlation coefficient above 0.98 are considered valid for displacement calculation.
2.2. Determination of Strain
Based on the computed displacements in Section 2.1, principal strains and their orientations are extracted to quantitatively characterize the mechanical response of facial skin under different expressive conditions. For small local regions of a 3D facial surface, the area can be approximated as a two-dimensional (2D) plane. Given the inherent curvature of the face, a local coordinate system is established for each local region to ensure accurate deformation analysis. The 3D displacement components, including horizontal, vertical, and normal displacements of the entire face during expressions, are obtained through coordinate transformations. The strain components within each local region are then computed using a first-order polynomial fitting method combined with a least-squares approach [32]. Due to variations in strain orientation across different facial points, a direct comparison of strain parameters across the entire face is not feasible. The principal strain analysis is employed to provide a unified comparative framework. The principal strains and their directions effectively characterize the deformation patterns and are expressed as follows:
where and are the maximum and minimum principal strains, respectively. and are the normal strain in the x direction and y direction, and is the shear strain. is the angle between the x-axis and the direction of one of the principal strains. The directions of the two principal strains are oriented at 90 degrees to each other. If , is the direction of the maximum principal strain . If , is the direction of the minimum principal strain . This direction represents the angle of clockwise rotation relative to the x-axis.
2.3. Establishment of the FE Model
The deformation of in vivo human skin is primarily influenced by muscle movement, contraction, and relaxation. This section focuses on simulating the mechanical response of skin layers under muscle-generated compression using Abaqus software (ver. 6.14, Dassault Systèmes, Paris, French). A two-dimensional (2D) finite element (FE) model is developed, incorporating both skin and muscle layers. Firstly, the skin structure with three distinct layers consisting of the epidermis, dermis, and hypodermis is established, as illustrated in Figure 2. The model spans a length of . Secondly, the mechanical behavior of each layer is endowed with material properties of a linear elastic model to ensure computational efficiency. The thicknesses and mechanical properties of each layer in the human skin and muscle models are summarized in Table 1 [33]. Thirdly, skin and muscle structure are discretized using four-node reduced integration elements (CPS4R). A mesh convergence study is conducted to verify that the grid resolution meets the convergence requirements. Each layer is then tied to the next layer through well-defined interfaces. Finally, critical buckling modes are determined via eigenvalue analysis of the Buckle step, followed by wrinkle morphology evolution tracking through the Static General step. The eigensolver employing the subspace iteration method is configured to compute 8 eigenvalues.
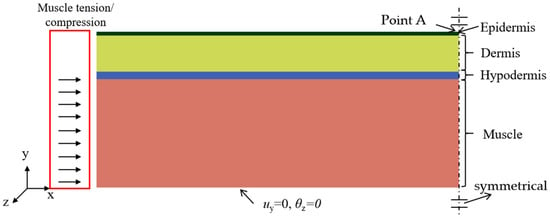
Figure 2.
A FE model of soft tissue that includes skin and muscle layers. The bottom of the muscle is fixed in the y-direction displacement and constrained against rotation about the z-axis. Symmetry constraints are applied to the right sides of both the skin and muscle. Muscle contraction is simulated by applying a horizontal displacement load to the left side of the muscle.

Table 1.
Mechanical parameters and thicknesses for each layer of soft tissue.
3. Results
3.1. Strain Parameters of Basic Expressions
As described in Section 2.1, facial images making six basic expressions were obtained. To analyze facial deformation patterns captured by CCD cameras, we focus on specific regions within the face images. An irregular region is selected from the cropped image for analysis. The eye and nose regions are excluded due to the absence of speckles, which prevent accurate deformation tracking. Additionally, the nose region is disregarded, as its high curvature and minimal deformation could introduce significant errors in the displacement calculations. Figure 3a–c depict the horizontal, vertical, and normal displacement distributions across the entire face during a happy facial expression, represented within the local coordinate system. The results reveal substantial movement at the corners of the mouth and cheeks, which is consistent with cheek bulging and mouth widening during laughter.
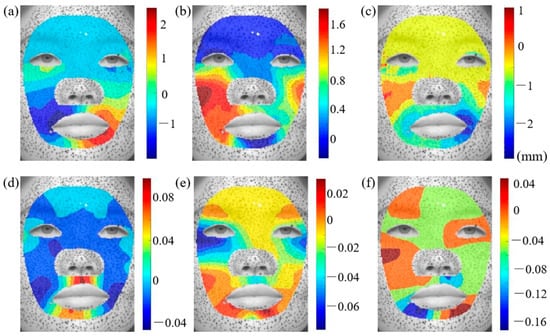
Figure 3.
Displacement and strain distributions during happy expression: (a) , (b) , (c) , (d) , (e) , and (f) . The color gradients in these figures indicate the magnitude of displacement values.
Since the measured displacement fields encompass both facial deformation and head movements (e.g., translation and rotation), a strain analysis is conducted to isolate the pure deformation effects. According to Equations (1)–(3), the strain distributions corresponding to the six basic facial expressions are evaluated. Figure 3d–f illustrates the , , and strain distributions for the happy expression. The strain around the eyes is predominantly in the y-direction, while the x-direction strain and shear strain are comparatively lower. In contrast, the mouth region exhibits significant variations in both linear and shear strain. To further achieve a consistent comparison of facial deformation, the principal strains and their corresponding directions are computed. Figure 4 presents the maximum and minimum principal strain distributions for the happy expression. Considering that wrinkle formation is predominantly associated with compressive deformation in biological tissues, our analysis primarily focuses on the direction of the minimum principal strain (). The principal strain distributions on the left and right sides of the face exhibit a general symmetry, though slight variations in strain magnitudes are observed. The greatest tensile strain occurs in the philtrum and lower jaw regions. The skin above the philtrum undergoes horizontal stretching. Conversely, the largest compressive strain is observed in the outer eye regions, corresponding to vertical uniaxial compression. Additionally, the principal strain and direction distributions for the remaining basic facial expressions are provided in Appendix A for further reference.
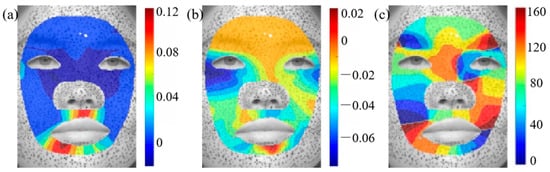
Figure 4.
Distributions of principal strain and principal direction during happy expressions: (a) , (b) , (c) .
3.2. Relationship Between the Principal Strain and Wrinkles
Wrinkles, especially those on the face, are a key indicator of human aging. These wrinkles primarily consist of forehead lines, glabellum lines, crow’s feet, et al. Their formation is closely related to skin deformation and surface stability. To investigate this correlation behavior, we identify regions of maximum compression during facial expressions, corresponding to regions of lowest minimum principal strain, to qualitatively analyze their relationship with wrinkle patterns.
Figure 5a highlights the regions of maximum compression during a surprised expression, with the minimum principal strain directions indicated by black arrows. The wrinkles shown in Figure 5b correspond to forehead lines [34], which predominantly appear horizontally on the foreheads of aged individuals. The results indicate that the formation of forehead lines coincides with the region of maximum compression during surprised expressions, with the principal direction being perpendicular to the forehead lines. Similarly, Figure 5c presents the minimum principal strain distribution during a fear expression, revealing significant compressive deformation in the forehead and glabellar regions. The strain direction in the forehead aligns with forehead lines. Figure 5d shows that the glabellum line relates to the minimum principal strain and its direction. Crow’s feet, one of the most common facial wrinkles, typically develop in this region with a distinctive fishtail pattern. A comparison between the strain distribution in Figure 5e and the crow’s feet formation in Figure 5f further confirms a strong correlation between mechanical strain and wrinkle development.
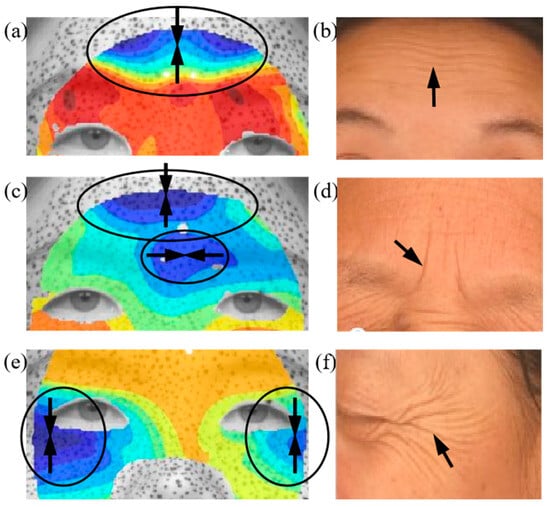
Figure 5.
Comparison of maximum compression and facial wrinkles: (a) the minimum principal strain distribution during a surprise expression, (b) forehead lines, (c) the minimum principal strain distribution during a fear expression, (d) glabellum lines, (e) the minimum principal strain distribution during a happy expression, (f) crow’s feet [34]. Arrows superimposed on the strain field denote the direction of the principal compressive, whereas those annotated on the wrinkle morphology highlight sites of surface buckles.
3.3. Wrinkle Analyses Based on the FE Method
Facial expressions significantly impact skin deformation, influencing both the distribution and orientation of facial wrinkles. The way the skin undergoes compression plays a crucial role in determining where and how wrinkles develop. Understanding the mechanical environment of the skin is key to investigating wrinkle formation. In this study, the FE method is employed to quantitatively examine the relationship between wrinkle formation and muscle-induced compression. Figure 6 presents the strain distributions of skin wrinkling across different skin models with hypodermis thicknesses of 0.2, 0.5, 1.0, and 2.0 mm. At low levels of muscle compression (approximately 5% compressive strain), the skin remains relatively smooth with minimal buckling. As muscle compression increases, wrinkles begin to form on the skin. These wrinkles create peaks and valleys, resulting in tensile and compressive strains, respectively.
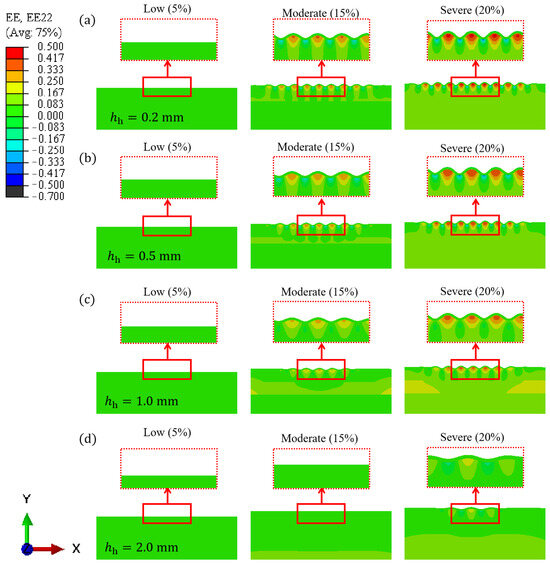
Figure 6.
FE simulation results of skin wrinkling under varying compression for models with different hypodermis thicknesses: (a) 0.2 mm, (b) 0.5 mm, (c) 1.0 mm, and (d) 2.0 mm.
As the hypodermis thickens, the skin becomes increasingly resistant to wrinkling under muscle compression. Figure 7a presents the x-direction strain at Point A in Figure 2 during wrinkle formation, comparing FE models with varying hypodermis thicknesses under identical muscle compression. The results indicate that as the hypodermis thickness increases, the strain transmitted to the skin surface decreases.
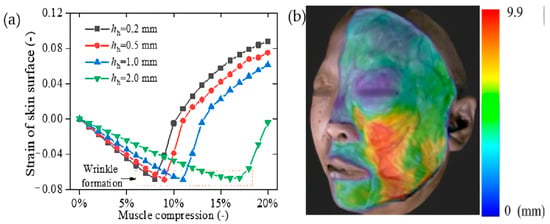
Figure 7.
(a) The strain of skin surface under muscle contraction, and (b) distribution of hypodermis thickness in the face [35].
4. Discussion
This study investigates the relationship between the formation mechanisms of skin wrinkling and the mechanical deformation of the skin, as well as the underlying muscles. The 3D-DIC method is employed to analyze strain distributions during facial expressions. The experimental results indicate that the formation of facial wrinkles is closely associated with both the magnitude and direction of the principal strain on the skin’s surface. The FE findings further support the experimental observations, revealing that maximum compressive strain occurs primarily around the eyes and forehead. Additionally, the results demonstrate that as the thickness of the hypodermis increases, the strain transmitted to the skin surface decreases. Notably, these results differ from previous studies, which predominantly focused on the epidermis and dermis for wrinkle formation [19]. However, our study highlights the crucial role of the hypodermis in the wrinkling process. Muscle deformation and strain are transmitted to the skin surface through interactions between skin layers and underlying muscles. Given the substantial variations in hypodermis thickness across different facial regions, its contribution to deformation transmission is significant. These findings provide new insights into the biomechanical factors influencing wrinkle formation and suggest that hypodermis should not be overlooked in future studies on facial wrinkling.
4.1. Comparison of Skin Wrinkles Between Muscle Compression and Skin Compression
Most existing models of skin wrinkle formation focus solely on the skin layer while neglecting the influence of underlying muscles [36]. In these models, uniaxial compression is directly applied to the skin to simulate muscle contraction, without the complex strain transfer mechanism of each layer. To address this limitation, this study compares two different loading methods: muscle compression (MC) and skin compression (SC), to accurately simulate the role of muscle contraction in skin wrinkling.
Figure 8a presents the FE results of skin wrinkling due to SC, with hypodermis thicknesses of 0.2 mm and 1.0 mm. The differences in wrinkle formation between models with varying hypodermis thicknesses are minimal. This is because the SC method does not account for the strain transfer effects between skin layers or between the skin and muscle. Furthermore, at higher compression levels (20%), the wrinkle patterns produced by SC and MC diverge significantly. As shown in Figure 9a, SC is more likely to generate wrinkles with pronounced tensile strain at the peak (Point A), whereas the MC method better replicates real-world observations of wrinkle formation.
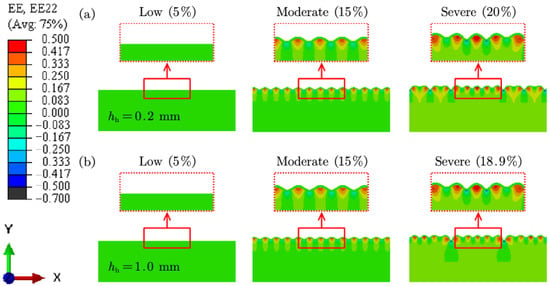
Figure 8.
FE results of skin wrinkling caused by (a) SC for young skin, and (b) MC for aged skin.
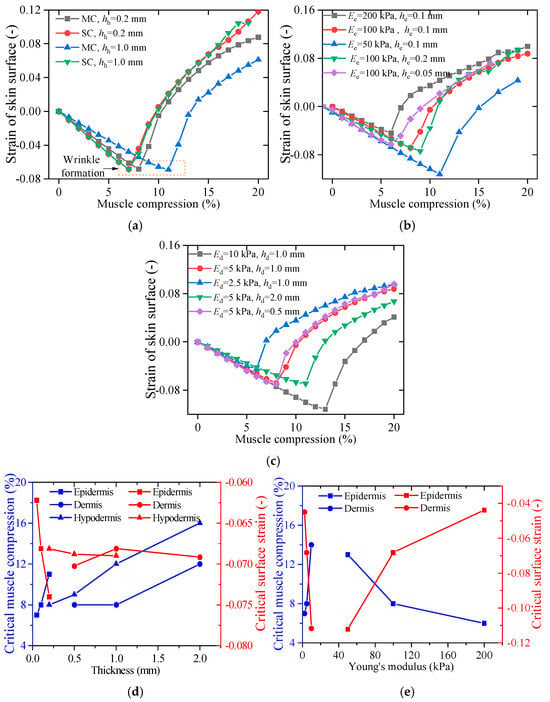
Figure 9.
Strain distribution on the skin surface under different conditions: (a) comparison between MC and SC, (b) effects of varying epidermis thickness and Young’s modulus, (c) effects of varying dermis thickness and Young’s modulus, and critical muscle compression and wrinkle strain related to (d) skin layer thickness and (e) Young’s modulus.
These findings underscore the importance of incorporating muscle compression into computational models of skin wrinkling. By considering the strain transfer between skin and muscle, this study provides a more realistic representation of wrinkle development, offering valuable insights into the biomechanical processes underlying facial aging.
4.2. Influence of Mechanical and Thickness Parameters
As humans age, the skin undergoes significant structural and mechanical changes, including the degradation of dermal elastic fibers and the denaturation of collagen bundles. These changes lead to substantial variations in Young’s modulus and tissue thickness compared to younger skin [37]. In this section, we explore how the mechanical properties and thickness of different skin layers influence wrinkle formation. Figure 9b presents the x-direction strain at Point A on the skin surface under varying epidermal thicknesses and Young’s moduli. The results indicate that a lower Young’s modulus in the epidermis reduces the likelihood of wrinkle formation. However, as shown in Figure 9c, the effect in the dermis is reversed, and wrinkles become more pronounced as Young’s modulus of the dermis decreases. In terms of thickness, both the epidermis and dermis follow a similar trend: thinner layers are more susceptible to wrinkle formation.
The x and y coordinates at the inflection points of the curves in Figure 9b–e correspond to the critical muscle compression and critical surface strain required for wrinkle formation. These critical parameters, influenced by variations in skin layer thickness and Young’s modulus, are further analyzed in Figure 9d,e. The results show that while dermis and hypodermis thickness significantly impact critical muscle compression, they have minimal influence on critical surface strain. Conversely, an increase in epidermal thickness leads to a decrease in critical surface strain. Regardless of the specific skin layer, a greater overall thickness results in higher critical muscle compression thresholds for wrinkle formation. Young’s modulus exerts a more pronounced effect than layer thickness among the examined factors. A stiffer epidermis decreases the critical muscle compression required for wrinkles to form when simultaneously reducing the critical surface strain. In contrast, a softer dermis facilitates wrinkle formation by lowering the required critical muscle compression and surface strain. These findings underscore the intricate biomechanical interplay between skin layers in the wrinkle formation process and highlight the importance of considering both mechanical properties and layer thickness when studying age-related skin deformation.
With human age, biomechanical alterations in skin structure collectively increase wrinkle susceptibility [37]. Epidermal stiffening and thinning, coupled with hypodermal fat loss, synergistically elevate critical surface strains while reducing the muscle compression required for wrinkle formation, as shown in Figure 9. This mechanistic triad explains why aging skin develops wrinkles more readily under smaller facial movements.
4.3. Application in Sensor Based on Skin Wrinkling
Facial wrinkles not only alter one’s appearance but also influence social perception, often affecting perceived attractiveness and interpersonal interactions [38]. As a result, understanding the mechanisms of wrinkle formation has become increasingly important, particularly in the fields of dermatology and cosmetics. Moreover, wrinkle structures play a crucial role in daily life. The tensile and compressive strain concentrations on the skin’s surface, which arise due to wrinkle formation, enhance sensitivity to external forces and improve tactile perception. Inspired by the micro-wrinkle structures of human skin, researchers have developed advanced strain sensors with heightened sensitivity and an extended range of strain detection [39]. A deeper understanding of the biomechanical principles behind skin wrinkling holds significant potential for practical applications, particularly in the design of next-generation wearable sensors for human motion detection and interactive technologies.
5. Conclusions
In this study, we investigated the relationship between facial deformation and wrinkle formation. The experimental findings demonstrate that the mechanical environment of in vivo skin, particularly the principal strain and its direction, plays a crucial role in wrinkle development. For example, the regions experiencing the highest compressive strains, specifically the periorbital area and central forehead, exhibit direct correspondence with typical wrinkle zones, while subcutaneous tissue thickening significantly suppresses wrinkle formation in these areas. The influence of muscle contractions and the transmission of strain between skin layers on the mechanical environment is further investigated by the FE method. Compared to models that exclude muscle effects, our four-layer tissue model provides a more comprehensive representation of strain transfer across skin-skin and skin-muscle interactions. Based on both experimental and finite element (FE) analysis, we draw the following conclusions: (1) the location and orientation of wrinkles correspond to the distribution and direction of the principal strain; (2) a thicker hypodermis reduces the strain transmitted to the skin surface, thereby decreasing the likelihood of wrinkle formation; and (3) a higher Young’s modulus of the epidermis decreases the critical muscle compression and the critical surface strain required for wrinkle formation, whereas the dermis layer exhibits the opposite effect. These insights enhance our understanding of the biomechanical factors influencing wrinkle formation, offering valuable implications for both cosmetic, sensor, and biomedical fields.
Author Contributions
Conceptualization, H.W. and Z.W.; methodology, H.W. and M.C.; software, B.L.; validation, W.H., B.L. and Z.W.; formal analysis, Z.L.; investigation, B.L.; resources, M.C.; data curation, Z.L.; writing—original draft preparation, H.W.; writing—review and editing, W.H.; visualization, L.H.; supervision, S.W.; project administration, S.W.; funding acquisition, H.W., S.W. and L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant numbers 12302242, 12472184, and 12462016) and the Jiangxi Provincial Natural Science Foundation (grant numbers 20224BAB201017 and 20212BAB211021).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of Tianjin Hospital of China (protocol code 2019-112 and date 2019.11.18 of approval).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Acknowledgments
The authors would like to acknowledge the Engineering Mechanics Experiment Center of Nanchang University for sharing the optical equipment. This support is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 3D-DIC | Three-dimensional digital image correlation |
| FACS | Facial Action Coding System |
| AUs | Action Units |
| FE | Finite element |
| MC | Muscle compression |
| SC | Skin compression |
Appendix A
The distributions of principal strain and principal direction for other basic facial expressions, including anger, disgust, fear, sadness, and surprise, are provided in Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5. Figure A1 shows the maximum principal strain, minimum principal, and their respective directions under anger expressions. The maximum tensile strain occurs in the skin around the mouth, while the maximum compressive strains are located around the eyebrows and corners of the mouth. The skin around the eyebrows is in a bidirectional compression state. Figure A2 shows that the maximum tensile strain under the disgust expression appears in the philtrum and chin. The maximum compressive strain occurs around the forehead and eyebrows. Under a disgusted expression, the skin at the chin position is in a bidirectional tension state.
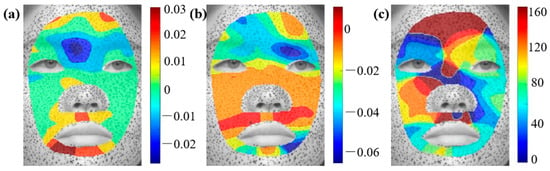
Figure A1.
Distributions of principal strain and principal direction during anger expressions: (a) , (b) , (c) .
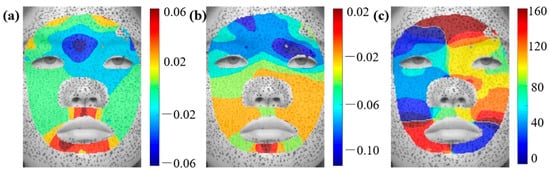
Figure A2.
Distributions of principal strain and principal direction during disgust expressions: (a) , (b) , (c) .
Under a fear expression, shown in Figure A3, there is a significant compressive strain on the forehead and a significant tensile strain at the nose bridge. The skin in the forehead area is basically in a bi-directional compression state. The strain distribution of sad expressions is similar to that of angry expressions, as shown in Figure A4. The difference is that under sad expressions, most of the skin around the eyes is in a compressed state, especially the corner of the eye. The maximum compression zone of the entire face is also observed in the middle of the forehead and the area between the eyebrows. Figure A5 shows that during the process of surprise, the skin between the middle of the eyebrows and between the eyes is in a stretched state, along the vertical direction. The maximum compression area is mainly located in the middle of the forehead, but the minimum principal strain in the middle of the eyes is almost zero. Through the strain distribution of the six basic facial expressions, we can find that the skin around the canthus, glabella, and forehead is the location where the maximum compressive strain occurs. These areas are prone to form skin wrinkling.
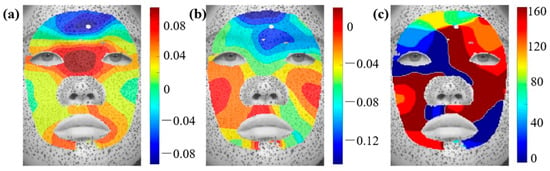
Figure A3.
Distributions of principal strain and principal direction during fear expressions: (a) , (b) , (c) .
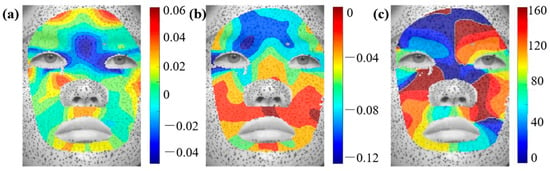
Figure A4.
Distributions of principal strain and principal direction during sad expressions: (a) , (b) , (c) .
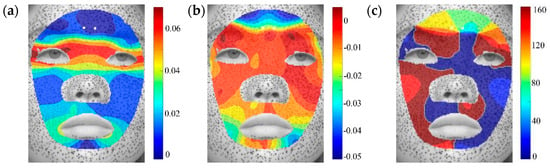
Figure A5.
Distributions of principal strain and principal direction during surprise expressions: (a) , (b) , (c) .
References
- Hillebrand, G. Facial Wrinkling: The Marquee Clinical Sign of Aging Skin. In Textbook of Aging Skin; Farage, M.A., Miller, K.W., Maibach, H.I., Eds.; Springer: Berlin/Heidelberg, Germay, 2016; pp. 1–10. [Google Scholar]
- Khan, S.A.; Hussain, A.; Basit, A.; Akram, S. Kruskal-Wallis-Based Computationally Efficient Feature Selection for Face Recognition. Sci. World J. 2014, 2014, 672630. [Google Scholar]
- Khan, A.; Alam, I.; Khan, M.F.; Ahmed, I.; Islam, Z.U.; Azam, M.; Akhtar, A. A comprehensive analysis of adaptive image restoration techniques in the presence of different noise models. Found. Univ. J. Eng. Appl. Sci. 2020, 1, 2. [Google Scholar] [CrossRef]
- Muslim, H.S.M.; Khan, S.A.; Hussain, S.; Jamal, A.; Qasim, H.S.A. A knowledge-based image enhancement and denoising approach. Comput. Math. Organ. Theory 2019, 25, 108–121. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, B.; Lee, J.; Lu, N.; Pierce, D.M. A multi-layered model of human skin elucidates mechanisms of wrinkling in the forehead. J. Mech. Behav. Biomed. Mater. 2020, 105, 103694. [Google Scholar] [CrossRef] [PubMed]
- Campiche, R.; Pascucci, F.; Jiang, L.; Vergne, T.; Cherel, M.; Gougeon, S.; Préstat-Marquis, E.; François, G.; Laurent, G.; Gempeler, M. Facial Expression Wrinkles and Their Relaxation by a Synthetic Peptide. Int. J. Pept. Res. Ther. 2021, 27, 1009–1017. [Google Scholar] [CrossRef]
- Franco, A.C.; Aveleira, C.; Cavadas, C. Skin senescence: Mechanisms and impact on whole-body aging. Trends Mol. Med. 2022, 28, 97–109. [Google Scholar] [CrossRef]
- Miura, N.; Arikawa, S.; Yoneyama, S.; Koike, M.; Murakami, M.; Tanno, O. Digital Image Correlation Strain Analysis for the Study of Wrinkle Formation on Facial Skin. J. Solid Mech. Mater. Eng. 2012, 6, 545–554. [Google Scholar] [CrossRef][Green Version]
- Celleno, L.; Tamburi, F. Chapter 1—Structure and Function of the Skin. In Nutritional Cosmetics; Tabor, A., Blair, R.M., Eds.; William Andrew Publishing: Boston, MA, USA, 2009; pp. 3–45. [Google Scholar]
- Holzapfel, G.A.; Ogden, R.W. On the tension–compression switch in soft fibrous solids. Eur. J. Mech.-A/Solids 2015, 49, 561–569. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Biomechanical relevance of the microstructure in artery walls with a focus on passive and active components. Am. J. Physiol.-Heart Circ. Physiol. 2018, 315, 540–549. [Google Scholar] [CrossRef]
- Magnenat-Thalmann, N.; Kalra, P.; Leveque, J.L.; Bazin, R.; Batisse, D.; Querleux, B. A computational skin model: Fold and wrinkle formation. IEEE Trans. Inf. Technol. Biomed. 2002, 6, 317–323. [Google Scholar] [CrossRef]
- Flynn, C.; McCormack, B. A three-layer model of skin and its application in simulating wrinkling. Comput. Methods Biomech. Biomed. Eng. 2008, 12, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Flynn, C.; McCormack, B.A.O. Simulating the wrinkling and aging of skin with a multi-layer finite element model. J. Biomech. 2010, 43, 442–448. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, B.; Lee, J.; Lu, N.; Pierce, D.M. A multi-layered computational model for wrinkling of human skin predicts aging effects. J. Mech. Behav. Biomed. Mater. 2020, 103, 103552. [Google Scholar] [CrossRef]
- Guissouma, I.; Hambli, R.; Rekik, A.; Hivet, A. A multiscale four-layer finite element model to predict the effects of collagen fibers on skin behavior under tension. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2021, 235, 1274–1287. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Gerling, G.J.; Chen, X. Mechanical modeling of a wrinkled fingertip immersed in water. Acta Biomater. 2010, 6, 1487–1496. [Google Scholar] [CrossRef]
- Diosa, J.; Moreno, R.; Chica, E.; Villarraga Ossa, J.; Buganza Tepole, A. Changes in the three-dimensional microscale topography of human skin with aging impact its mechanical and tribological behavior. PLoS ONE 2020, 16, 0241533. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Wang, B.; Yang, T.; Yin, R.; Wang, F.; Zhang, H.; Zhang, W. Three-Dimensional Bioprinted Skin Microrelief and Its Role in Skin Aging. Biomimetics 2024, 9, 366. [Google Scholar] [CrossRef]
- Yoneyama, S. Measuring Facial Displacements and Strains for Cosmetics Development and Beauty Care. In Gerontology as an Interdisciplinary Science; Shiozawa, T., Hirata, H., Inoue, T., Kanikowska, D., Takada, H., Eds.; Springer Nature: Singapore, 2024; pp. 175–189. [Google Scholar]
- Yoo, M.A.; Seo, Y.K.; Shin, M.K.; Koh, J.S. How much related to skin wrinkles between facial and body site? Age-related changes in skin wrinkle on the knee assessed by skin bioengineering techniques. Ski. Res. Technol. 2016, 22, 69–74. [Google Scholar] [CrossRef]
- Wang, Y.; Li, R.; Lu, M.; Fan, Z.; Chen, Y.; Xu, Y.; Jiang, Z.; Sun, T. Photo-crosslinking speckle patterns for large deformation measurement of hydrogels using digital image correlation. Appl. Phys. Lett. 2023, 123, 181904. [Google Scholar] [CrossRef]
- Jiang, Z. OpenCorr: An open source library for research and development of digital image correlation. Opt. Lasers Eng. 2023, 165, 107566. [Google Scholar] [CrossRef]
- Wang, L.; Lei, Z. Deep learning based speckle image super-resolution for digital image correlation measurement. Opt. Laser Technol. 2025, 181, 111746. [Google Scholar] [CrossRef]
- Zhan, N.; Zhang, X.; Ye, J.; Wang, T.; Dong, Z.; Song, Z. High-precision parameter-free optical distortion measurement and correction via digital image correlation. Opt. Laser Technol. 2024, 177, 111129. [Google Scholar] [CrossRef]
- Radi, K.; Allamand, F.; Kochmann, D.M. Deformation tracking of truss lattices under dynamic loading based on Digital Image Correlation. Mech. Mater. 2023, 183, 104658. [Google Scholar] [CrossRef]
- Youn, J.; Kim, D.; Kwak, H.; Lee, A.; Kim, D.S. Tissue-scale in vitro epithelial wrinkling and wrinkle-to-fold transition. Nat. Commun. 2024, 15, 7118. [Google Scholar] [CrossRef]
- Min, D.; Ahn, Y.; Lee, H.K.; Jung, W.; Kim, H.-J. A novel optical coherence tomography-based in vitro method of anti-aging skin analysis using 3D skin wrinkle mimics. Ski. Res. Technol. 2023, 29, 13354. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. Flexible camera calibration by viewing a plane from unknown orientation. In Proceedings of the Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 1, pp. 666–673. [Google Scholar]
- Ekman, P.; Friesen, W.V. Manual for the Facial Action Coding System; Consulting Psychologists Press: Palo Alto, CA, USA, 1978. [Google Scholar] [CrossRef]
- Barrett, L.F.; Adolphs, R.; Marsella, S.; Martinez, A.M.; Pollak, S.D. Emotional Expressions Reconsidered: Challenges to Inferring Emotion From Human Facial Movements. Psychol. Sci. Public Interest 2019, 20, 1–68. [Google Scholar] [CrossRef]
- Yoneyama, S. Computing Strain Distributions from Measured Displacements on a Three-dimensional Surface. J. Jpn. Soc. Exp. Mech. 2010, 10, 113–118. [Google Scholar]
- Wei, H.; Liu, X.; Li, L.; Li, C.; Chen, W.; Wang, S.; Wang, Z.; Ma, J. Visual indentation apparatus and finite element modelling as a method to characterize 3D mechanical properties of facial skin in vivo. Mech. Mater. 2021, 157, 103852. [Google Scholar] [CrossRef]
- Jiechen, Z.; Wei, H.; Suying, F.; Xiangsheng, C.; Hongwei, W. Classification of facial wrinkles among Chinese women. J. Biomed. Res. 2017, 31, 108–115. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, K.W.; Kim, J.S.; Gil, Y.C.; Tanvaa, T.; Shin, D.H.; Kim, H.J. Regional thickness of facial skin and superficial fat: Application to the minimally invasive procedures. Clin. Anat. 2019, 32, 1008–1018. [Google Scholar] [CrossRef]
- Limbert, G.; Kuhl, E. On skin microrelief and the emergence of expression micro-wrinkles. Soft Matter 2018, 14, 1292–1300. [Google Scholar] [CrossRef] [PubMed]
- Kuwazuru, O.; Saothong, J.; Yoshikawa, N. Mechanical approach to aging and wrinkling of human facial skin based on the multistage buckling theory. Med. Eng. Phys. 2008, 30, 516–522. [Google Scholar] [CrossRef] [PubMed]
- Hess, U.; Huppertz, D.; Mauersberger, H.; Kastendieck, T. Wrinkles are neither beautiful nor nice: The effect of facial wrinkles on person perception and interpersonal closeness. Acta Psychol. 2023, 241, 104077. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Chu, Z.; Fu, L.; Lv, Y.; Liu, X.; Fan, X.; Zhang, W. Thickness-induced gradient micro-wrinkle PDMS/MXene/rGO wearable strain sensor with high sensitivity and stretchability for human motion detection. Chem. Eng. J. 2024, 495, 153684. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).