Research on the Dynamic Characteristics of a Typical Medium–Low-Speed Maglev Train–Bridge System Influenced by the Transverse Stiffness of Pier Tops
Abstract
1. Introduction
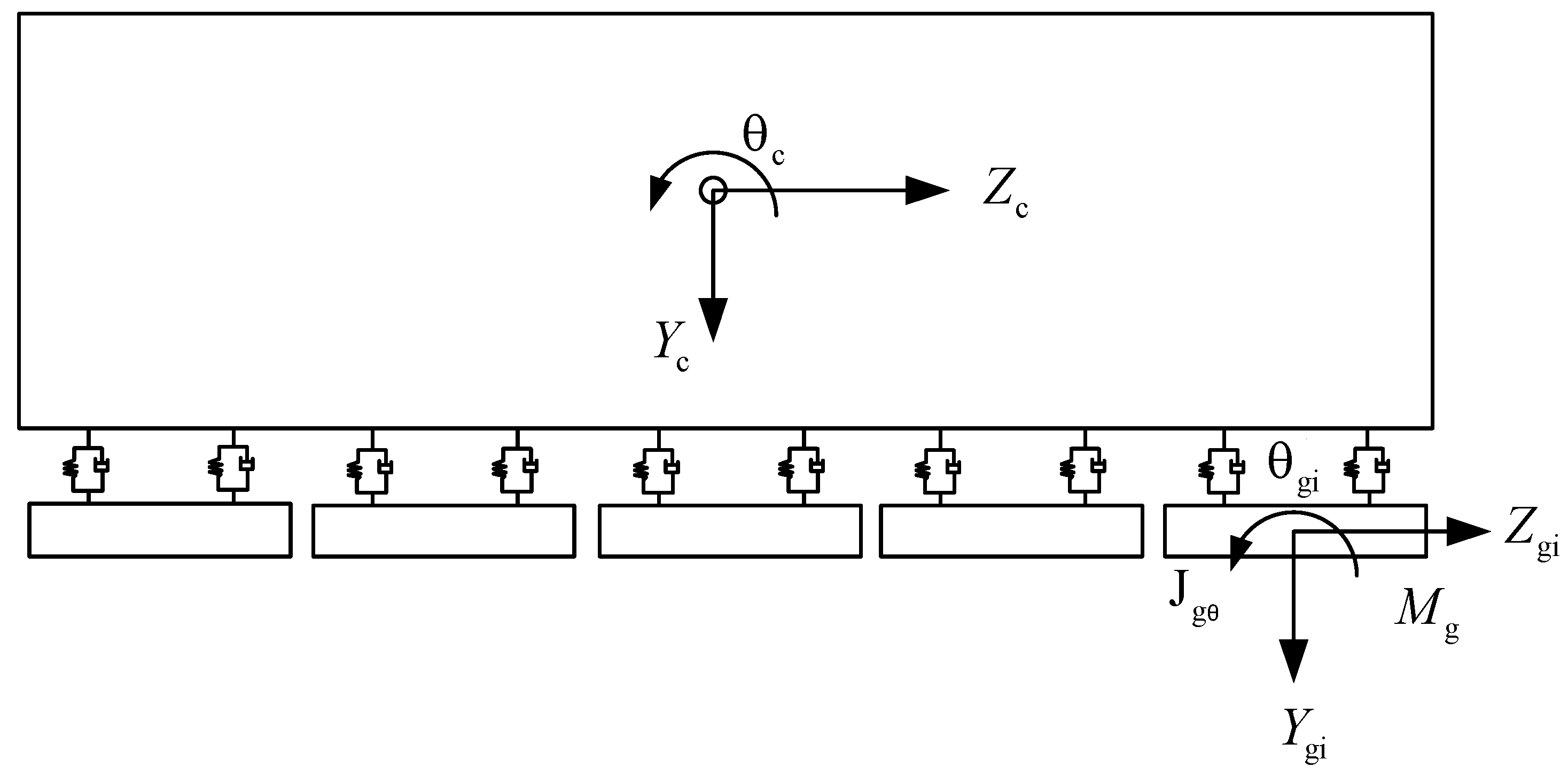
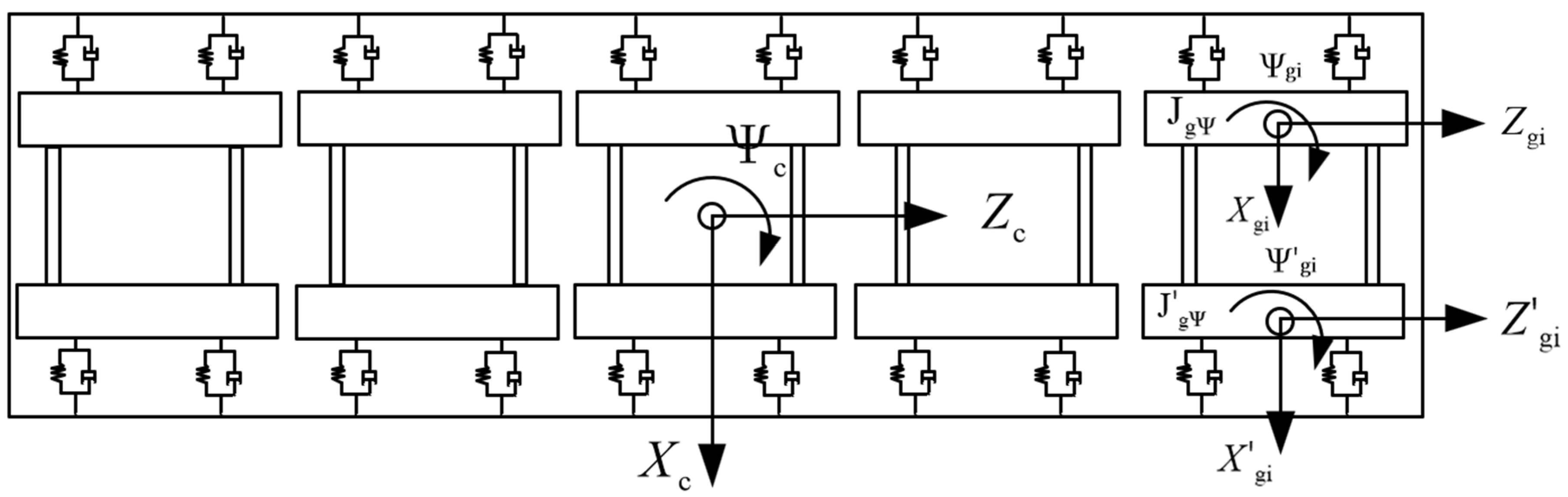
2. System Description
3. Modeling Approach
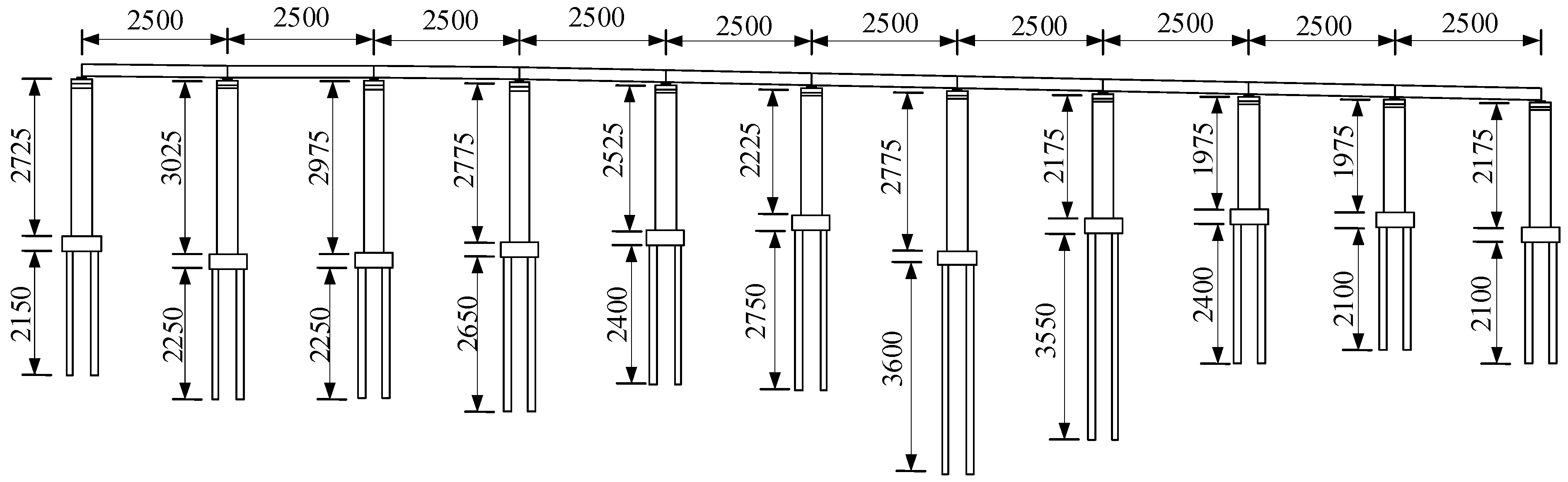
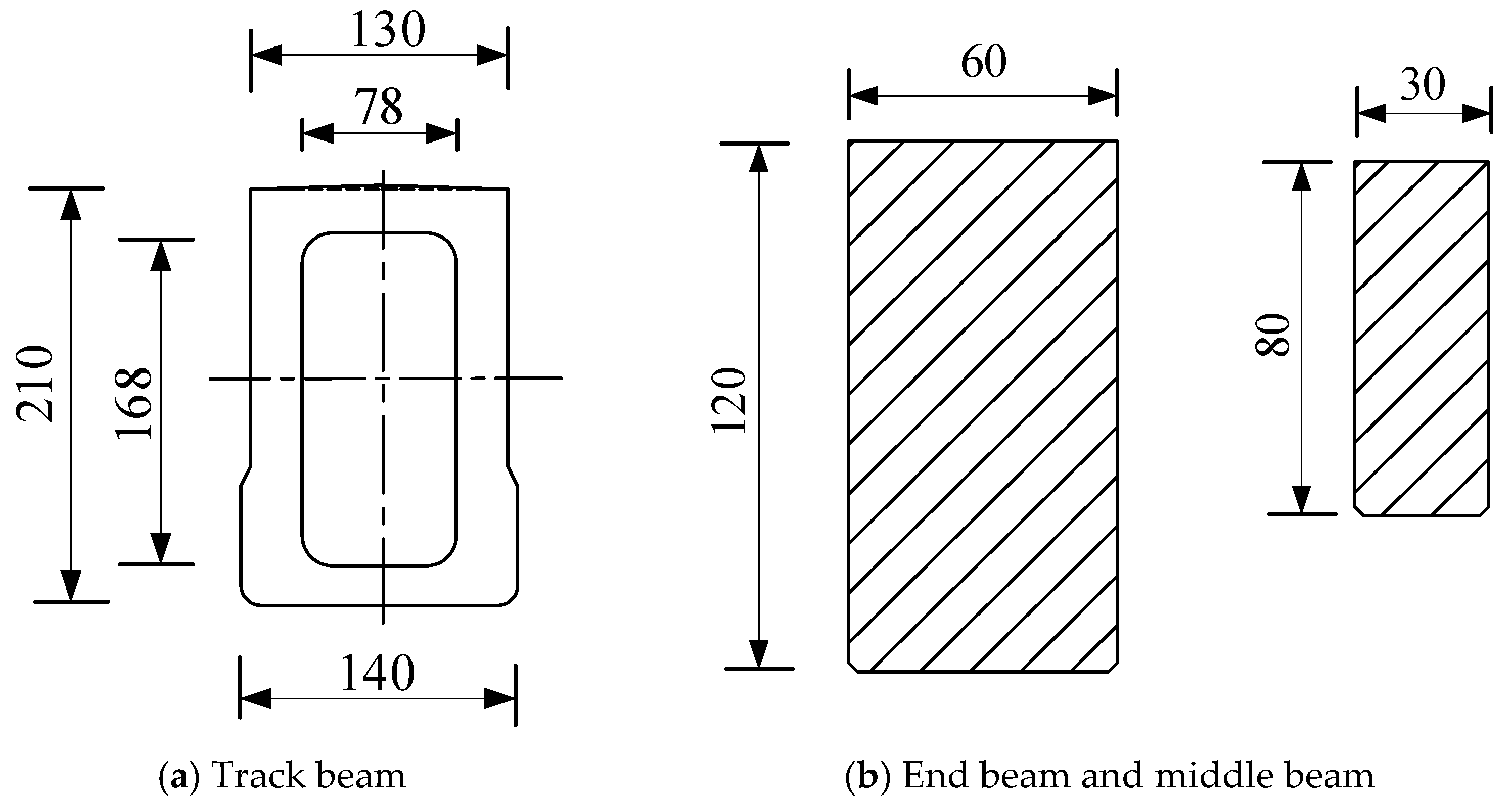
3.1. The Establishment of Finite Element Model of Bridge and the Calculation and Analysis of Its Natural Vibration Characteristics
3.2. Track Irregularity and Train Grouping
3.2.1. Track Irregularity
3.2.2. Train Mode Shape
3.3. Establishment of Spatial Vibration Analysis Model for Medium–Low-Speed Maglev Train
3.3.1. Basic Assumption
- Both structural components (carbody and levitation frame) are considered as rigid bodies, with their elastic demode shapes disregarded.
- Suspension elements are represented as linear springs, accompanied by equivalent viscous damping for energy dissipation modeling.
- System dynamics are analyzed within the small vibration range.
- Longitudinal vibrations along the guideway direction are deemed insignificant for medium–low-speed operations.
- The dynamic interaction from guideway longitudinal vibrations is not included in the current analysis scope.
3.3.2. Spatial Vibration Analysis Model of Medium–Low-Speed Maglev Train
3.4. Motion Equation of Medium- and Low-Speed Maglev Train
4. Calculation Results and Analysis of Dynamic Response of Medium–Low-Speed Maglev Train–Bridge System
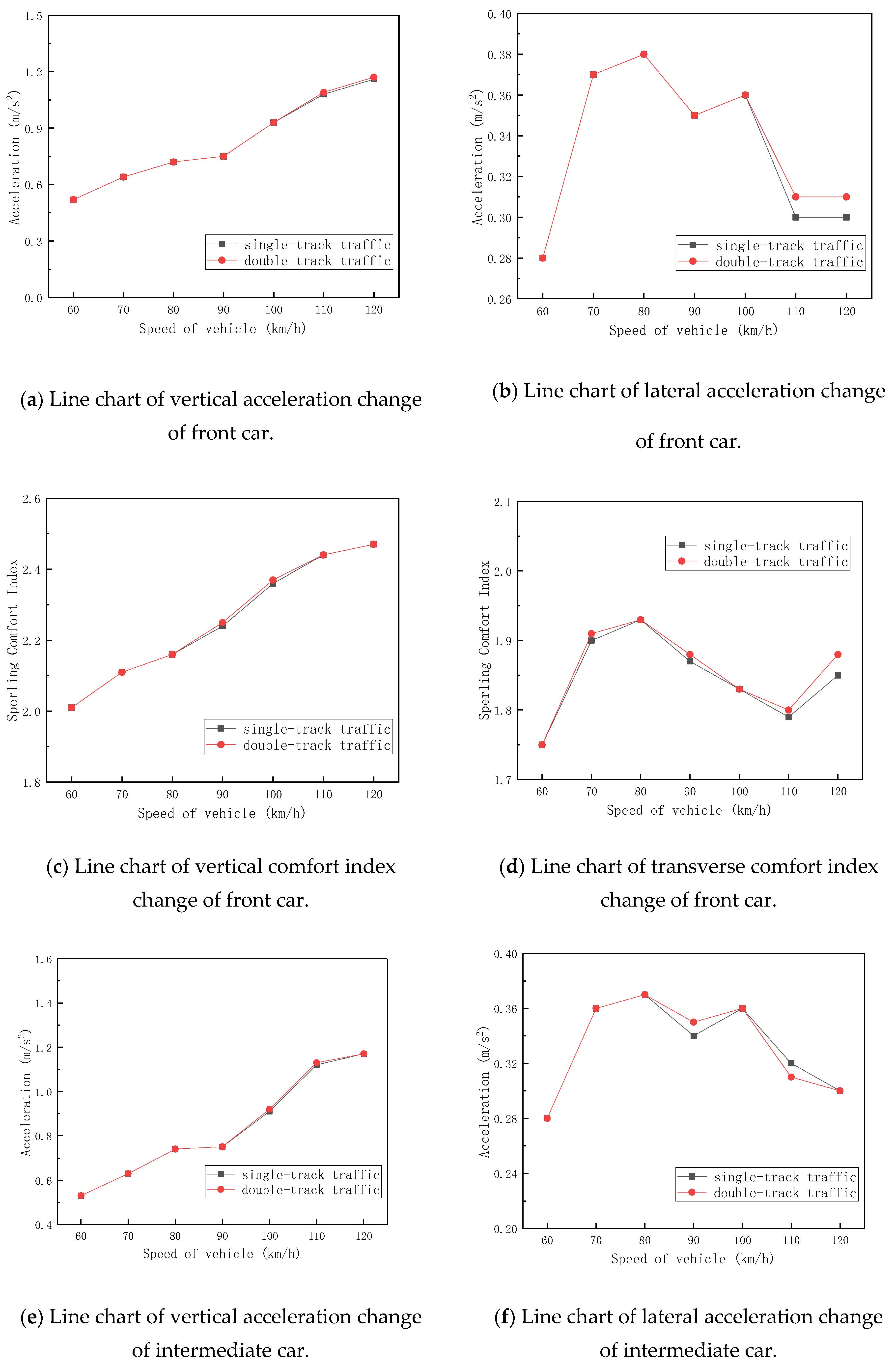
4.1. Calculation Results and Analysis of Bridge Dynamic Response
4.2. Calculation Results and Analysis of Train Dynamic Response
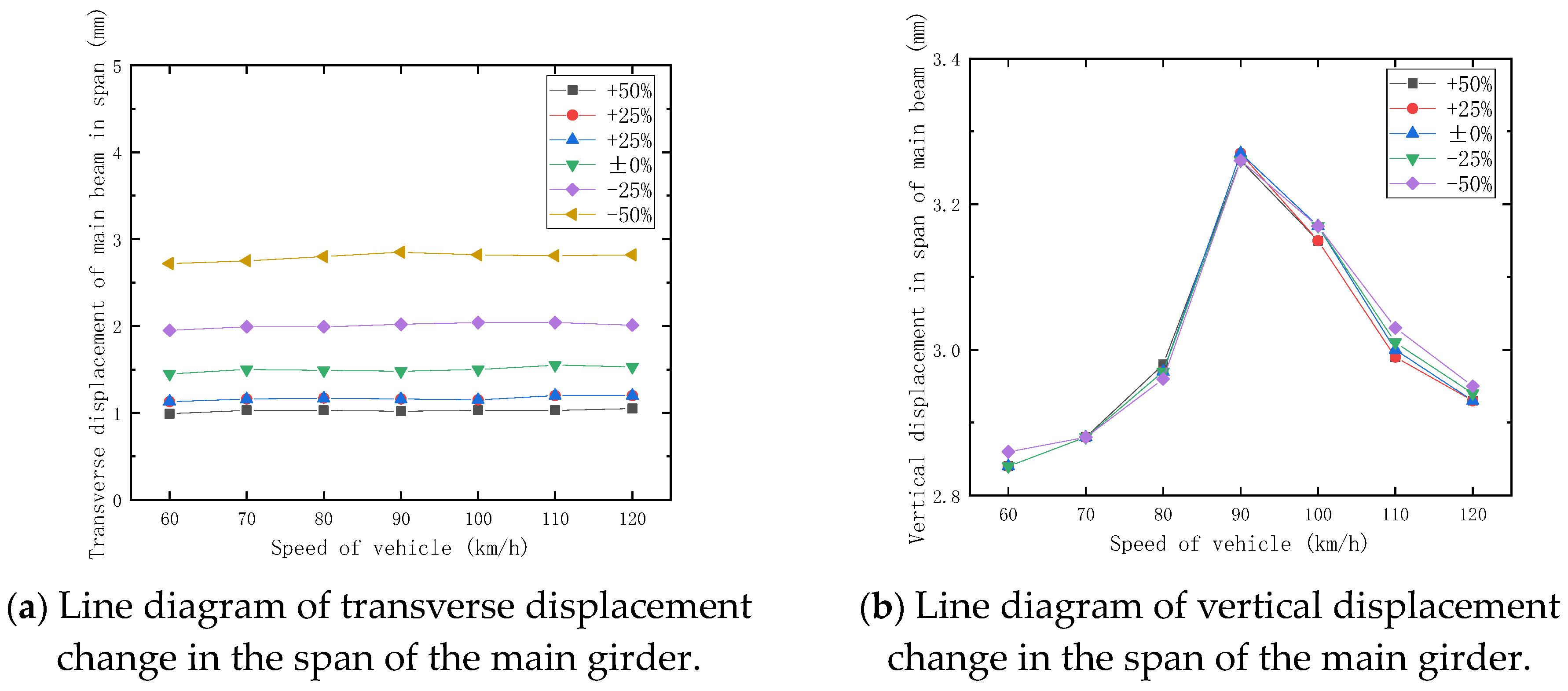
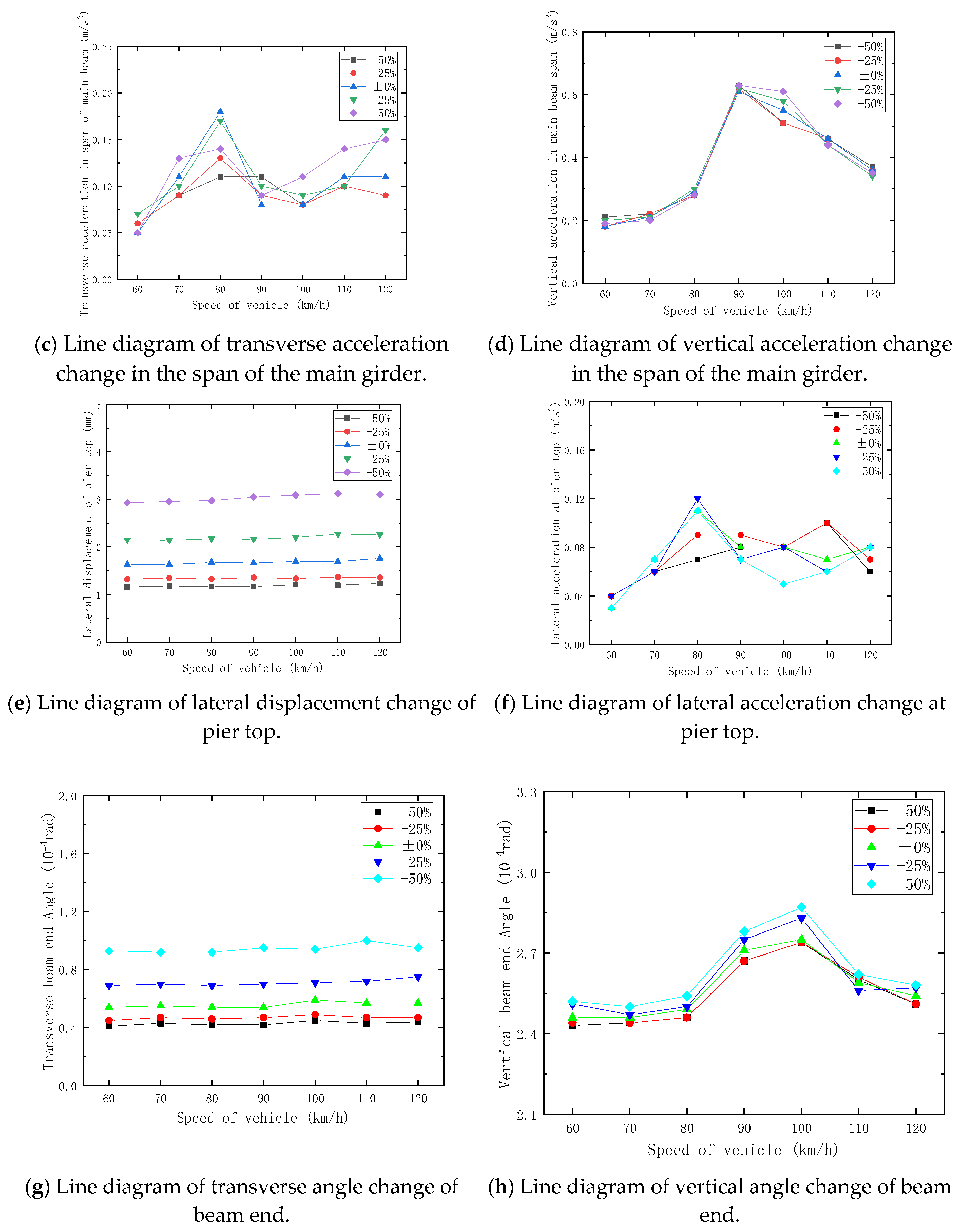
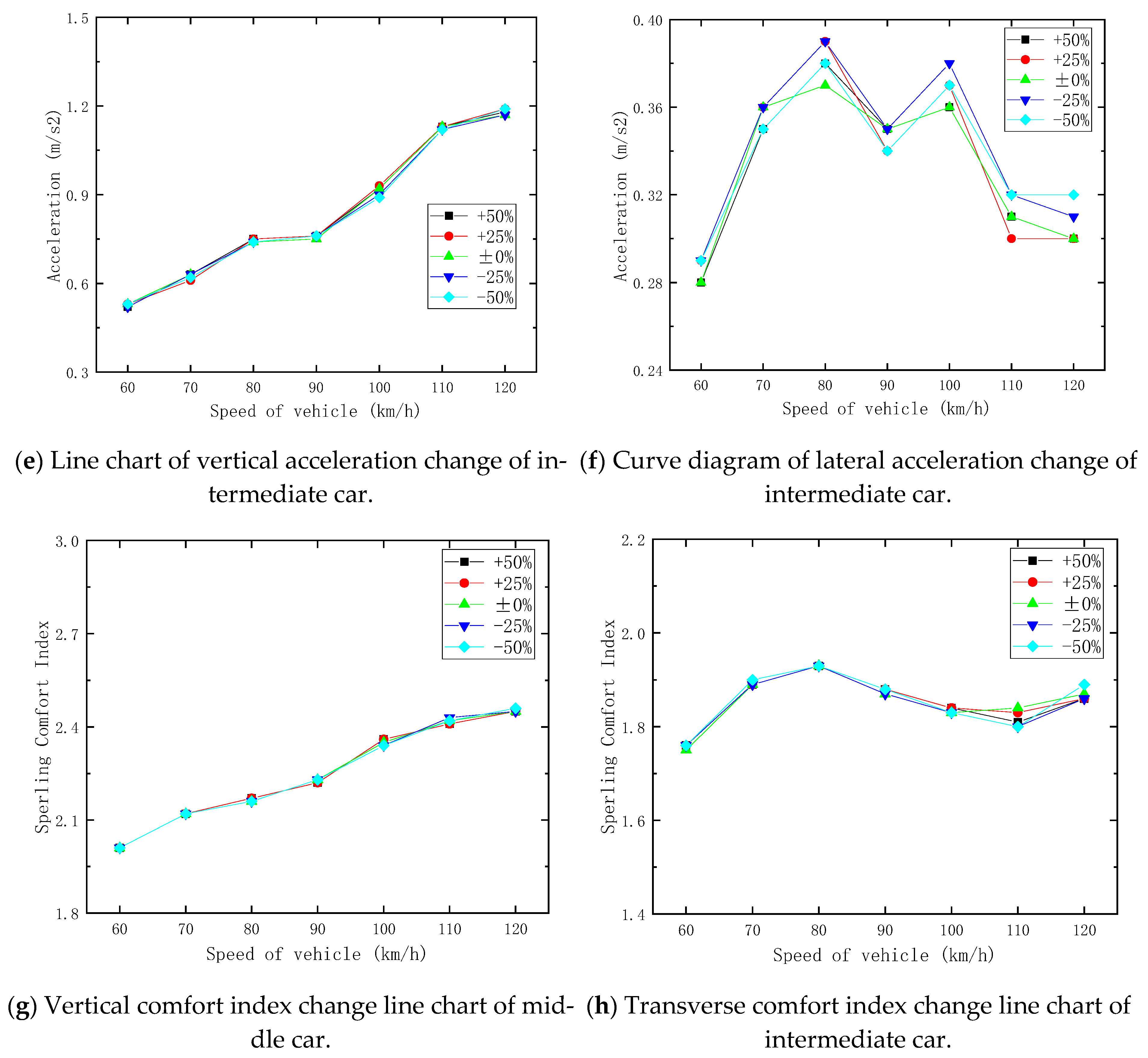
5. Influence of Lateral Stiffness Variation of Bridge on Dynamic Response of Maglev Vehicle–Bridge System
5.1. Influence of Lateral Line Stiffness of Pier Top on Natural Vibration Characteristics of Bridge
5.2. Influence of Lateral Line Stiffness of Pier Top on Dynamic Response of Bridge
5.3. Influence of Lateral Line Stiffness of Pier Top on Train Dynamic Response
6. Conclusions
- (1)
- The dynamic analysis of the 10 × 25 m simply supported beam bridge under various operating conditions shows that the lateral displacement of the main girder, lateral displacement and acceleration of the pier top, and lateral and vertical angle of beam end have little correlation with train speed (60–120 km/h) and show no clear pattern under single- or double-track conditions. However, the vertical displacement is significantly affected by track configuration, with the main girder’s vertical displacement being notably greater under double-track conditions compared to single-track conditions, while remaining largely unaffected by speed variations and showing no distinct regularity.
- (2)
- The pier top lateral stiffness exhibits a significant influence on the bridge’s dynamic characteristics. The lateral bending fundamental frequency increases progressively with stiffness enhancement, showing 61.8% growth when the lateral stiffness varies from −50% to +50%. Conversely, the longitudinal floating fundamental frequency decreases gradually, with a 29.2% reduction over the same stiffness variation range. These variations occur while the vertical linear stiffness at the control pier top remains constant throughout the analysis. Given the pronounced sensitivity of dynamic frequencies to lateral stiffness, precise stiffness control during construction is critical. While a higher lateral stiffness enhances transverse vibration resistance, its detrimental impact on longitudinal performance necessitates a balanced design approach, particularly in wind-prone regions, to mitigate resonance risks. These findings highlight the importance of early-stage parametric stiffness optimization to ensure structural safety and performance.
- (3)
- The pier top lateral linear stiffness significantly affects the following three key structural responses: the lateral displacement of the main girder, the lateral displacement of the pier top, and the lateral angle of beam end. As the lateral stiffness increases from −50% to +50% while maintaining a constant vertical linear stiffness at the control pier top, these responses demonstrate substantial reductions: a 63.2% decrease in main girder lateral displacement, a 60.3% decrease in pier top lateral displacement, and a 55% decrease in the angle of beam end.
- (4)
- Within the ±50% variation range of pier top lateral stiffness, the study reveals the following three key findings: the lateral vibration acceleration of the main girder shows no monotonic relationship with the pier top linear stiffness; the vertical vibration acceleration of the main girder remains relatively stable, with insignificant variations; and both transverse and vertical vibration accelerations exhibit minimal changes overall. Furthermore, the pier top lateral line stiffness demonstrates a negligible influence on the train’s lateral and vertical vibration accelerations.
- (5)
- According to the research findings, the pier top lateral stiffness has an insignificant impact on the lateral vibration acceleration of the main girder and also exerts minimal influence on the lateral and vertical vibration accelerations of the train. Therefore, in the process of code revision, it is advisable to consider relaxing the restrictions on the main girder’s vibration acceleration caused by variations in pier top lateral stiffness. Moreover, the provisions related to train vibration acceleration can also be optimized based on this conclusion, reducing the over-regulation of train vibration acceleration due to pier top lateral stiffness factors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, H.-S.; Kim, D.-S. Magnetic Levitation; Springer: Dordrecht, The Netherlands, 2016; 247p. [Google Scholar]
- Liu, Z.; Long, Z.; Li, X. Maglev Trains; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Sinha, P.K. Electromagnetic Suspension Dynamics & Control; Peter Peregrinus Ltd.: London, UK, 1987. [Google Scholar]
- Guobin, L.; Xiongwei, S. Application and further development of Maglev transportation in China. Mod. Transp. Syst. Technol. 2018, 4, 36–43. [Google Scholar]
- Kim, M.; Jeong, J.H.; Lim, J.; Kim, C.H.; Won, M. Design and control of levitation and guidance systems for a semi-high-speed maglev train. J. Electr. Eng. Technol. 2017, 12, 117–125. [Google Scholar] [CrossRef]
- Kwon, S.D.; Lee, J.S.; Moon, J.W.; Kim, M.Y. Dynamic interaction analysis of urban transit maglev vehicle and guideway suspension bridge subjected to gusty wind. Eng. Struct. 2008, 30, 3445–3456. [Google Scholar] [CrossRef]
- Nagashima, K. Update on basic research into superconducting maglev and research on application of maglev technology to conventional railway systems. Q. Rep. RTRI 2020, 61, 11–15. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.M.; Ni, Y.Q.; Sun, Y.G.; Lu, Y.; Duan, Y.F. Modelling dynamic interaction of maglev train–controller–rail–bridge system by vector mechanics. J. Sound Vib. 2022, 533, 117023. [Google Scholar] [CrossRef]
- Li, X.; Geng, J.; Wang, D. Dynamic responses of low–medium speed maglev train–simply supported beam interaction system. Urban Rail Transit 2017, 3, 136–141. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, C.; Ma, W.; Luo, S. Effect of suspension form on the vehicle-bridge coupled vibration of the maglev vehicle. Int. J. Veh. Mech. Mobil. 2024, 62, 511–532. [Google Scholar] [CrossRef]
- Zhou, F.; Li, X. Coupled Dynamics Modeling and Validation of Maglev Vehicle and Bridge Systems. Actuators 2025, 14, 107. [Google Scholar] [CrossRef]
- Cao, S.; Liu, C.; Wang, S.; Sun, L. Analysis of vibrational stability, bifurcation and resonance characteristics of the maglev train-bridge coupling system. Nonlinear Dyn. 2025, 113, 16135–16159. [Google Scholar] [CrossRef]
- Tian, X.; Xiang, H.; Li, Y. Modeling and analyzing of high-speed maglev train-bridge systems considering centrifugal force induced by bridge vertical demode shape. Structures 2025, 73, 108240. [Google Scholar] [CrossRef]
- Xia, W.; Zeng, J.; Dou, F.; Long, Z. Method of combining theoretical calculation with numerical simulation for analyzing effects of parameters on the maglev vehicle-bridge system. IEEE Trans. Veh. Technol. 2021, 70, 2250–2257. [Google Scholar] [CrossRef]
- Deng, Z.; Li, J.; Wang, H.; Li, Y.; Zheng, J. Dynamic simulation of the vehicle/bridge coupled system in high-temperature superconducting maglev. Comput. Sci. Eng. 2019, 21, 60–71. [Google Scholar] [CrossRef]
- Li, Y.-X.; Yu, Z.-W.; Xu, L. Stochastic resonance analysis of a coupled high-speed maglev vehicle-bridge coupled system under bounded noise. Sci. Rep. 2023, 13, 7519. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Ma, W.-h.; Gong, J.-h.; Li, W.-l.; Gao, D.-g.; Luo, S.-h. Dynamic performance test of medium and low speed maglev vehicle-bridge coupled system. J. Traffic Transp. Eng. 2022, 22, 141–154. [Google Scholar]
- Huang, F.; Wang, J.; Teng, N.; Cheng, B. Coupled vibration of low-medium-speed maglev vehicle-guideway system on isolated bridge with lead rubber bearings. Adv. Struct. Eng. 2024, 27, 2391–2408. [Google Scholar] [CrossRef]
- Song, Y.; Lin, G.; Ni, F.; Xu, J.; Chen, C. Study on Coupled Vertical Vehicle-Bridge Dynamic Performance of Medium and Low-Speed Maglev Train. Appl. Sci. 2021, 11, 5898. [Google Scholar] [CrossRef]
- Wang, L.; Bu, X.; Hu, P.; Han, Y.; Cai, C. Dynamic reliability analysis of running safety and stability of a high-speed maglev train on a guideway bridge. Int. J. Struct. Stab. Dyn. 2024, 24, 2450043. [Google Scholar] [CrossRef]
- Wang, L.; Bu, X.; Shen, Y.; Han, Y.; Hu, P.; Cai, C. Effect of control time delay on high-speed maglev vehicle-bridge-wind system. J. Vib. Control. 2025, 10775463251321726. [Google Scholar] [CrossRef]
- Bu, X.; Wang, L.; Han, Y.; Liu, H.; Hu, P.; Cai, C.S. Dynamic model of high-speed maglev train-guideway bridge system with a nonlinear suspension controller. Adv. Struct. Eng. 2024, 27, 1328–1348. [Google Scholar] [CrossRef]
- Bu, X.; Wang, L.; Han, Y.; Liu, H.; Hu, P.; Cai, C. A fast multi-objective optimization method for control parameters of high-speed maglev vehicle-bridge system. Int. J. Struct. Stab. Dyn. 2024, 2550206. [Google Scholar] [CrossRef]
- Li, X.; Wang, D.; Liu, D.; Xin, L.; Zhang, X. Dynamic analysis of the interactions between a low-to-medium-speed maglev train and a bridge: Field test results of two typical bridges. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 2039–2059. [Google Scholar] [CrossRef]
- Li, D.; Huang, J. Hierarchical model updating for high-speed maglev vehicle/guideway coupled system based on multi-objective optimization. Front. Struct. Civ. Eng. 2024, 18, 788–804. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, L.; Yin, J.H. Seismic and static stability analysis for rock slopes by a kinematical approach. Geotechnique 2004, 54, 543–549. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Upper bound solution for ultimate bearing capacity with a modified Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2005, 42, 550–560. [Google Scholar] [CrossRef]
- Yang, X.L.; Wang, J.M. Ground movement prediction for tunnels using simplified procedure. Tunn. Undergr. Space Technol. 2011, 26, 462–471. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Slope stability analysis with nonlinear failure criterion. J. Eng. Mech. 2004, 130, 267–273. [Google Scholar] [CrossRef]
- Hou, L.; Liang, S.; Chi, M. Research on vehicle-rail coupling vibration at turnout and suppression method of medium and low speed maglev vehicle. Electr. Drive Locomot. 2024, 5, 49–55. [Google Scholar]
- Tian, X.F.; Xiang, H.Y.; Chen, X.L.; Li, Y.L. Dynamic response analysis of high-speed maglev train-guideway system under crosswinds. J. Cent. South Univ. 2023, 30, 2757–2771. [Google Scholar] [CrossRef]
- Shan, J.T.; Wu, Y.M.; Yang, X.L. Three-dimensional stability of two-step slope with crack considering temperature effect on unsaturated soil. J. Cent. South Univ. 2025, 32, 1060–1079. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Guo, X.; Liu, J.; Cui, R. Research on Train-Induced Vibration of High-Speed Railway Station with Different Structural Forms. Materials 2024, 17, 4387. [Google Scholar] [CrossRef] [PubMed]
- CJJ/T 262–2017; Code for Design of Medium and Low Speed Maglev Transit. China Architecture & Building Press: Beijing, China, 2017.
- Zeng, Q. The principle of total potential energy with stationary value in elastic system dynamics. J. Huazhong Univ. Sci. Technol. 2000, 28, 1–3+14. [Google Scholar]
- Zeng, Q.Y.; Yan, G.P. The “set-in-right-position” rule forming structural method for space analysis of truss bridges. J. China Railw. Soc. 1986, 8, 48–59. [Google Scholar]
- Zeng, Q.Y.; Guo, X.R. Theory and Application of Vibration Analysis of Time-Varying Systems on Train Bridges; China Railway Publishing House: Beijing, China, 1999. [Google Scholar]



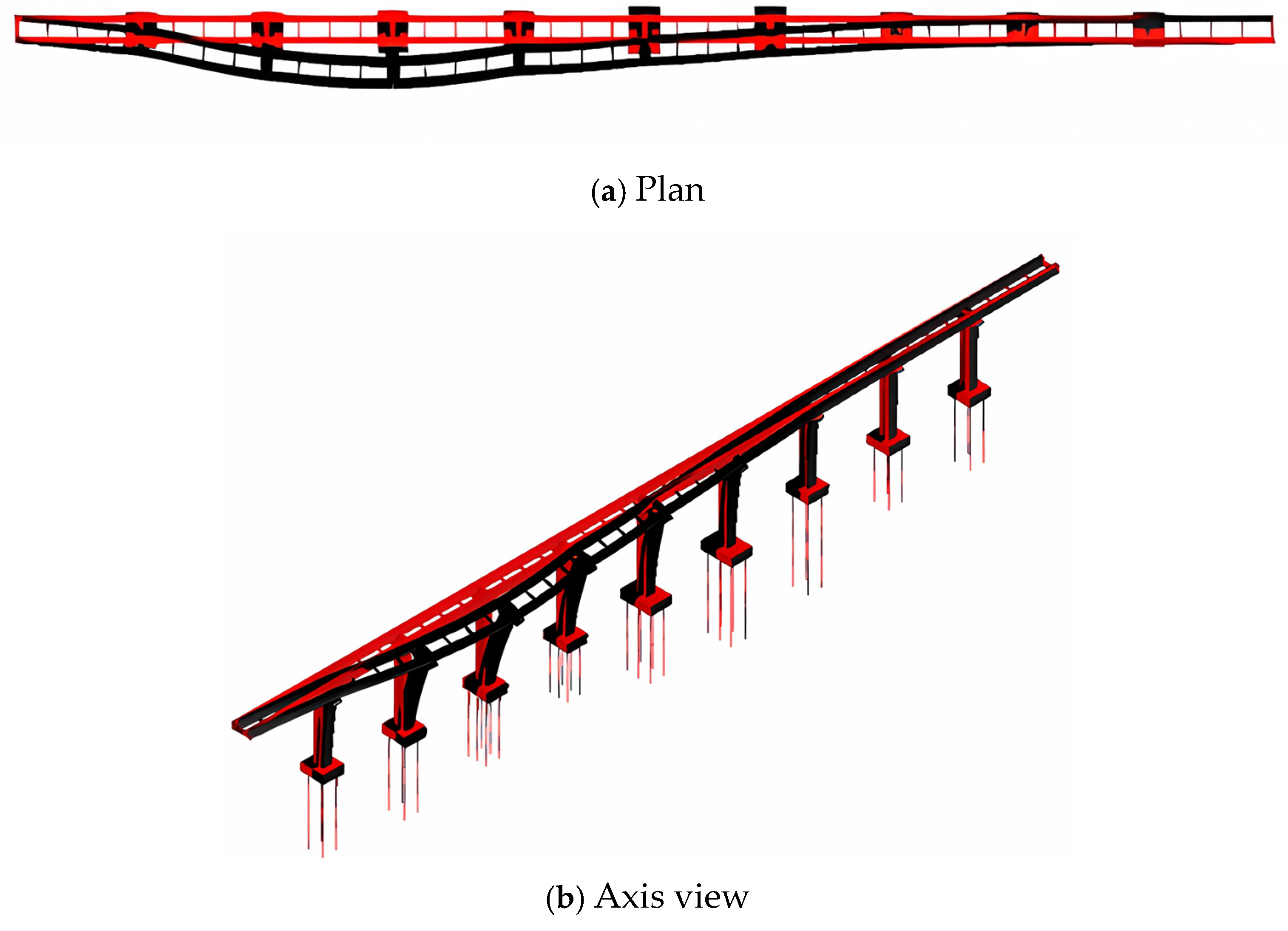

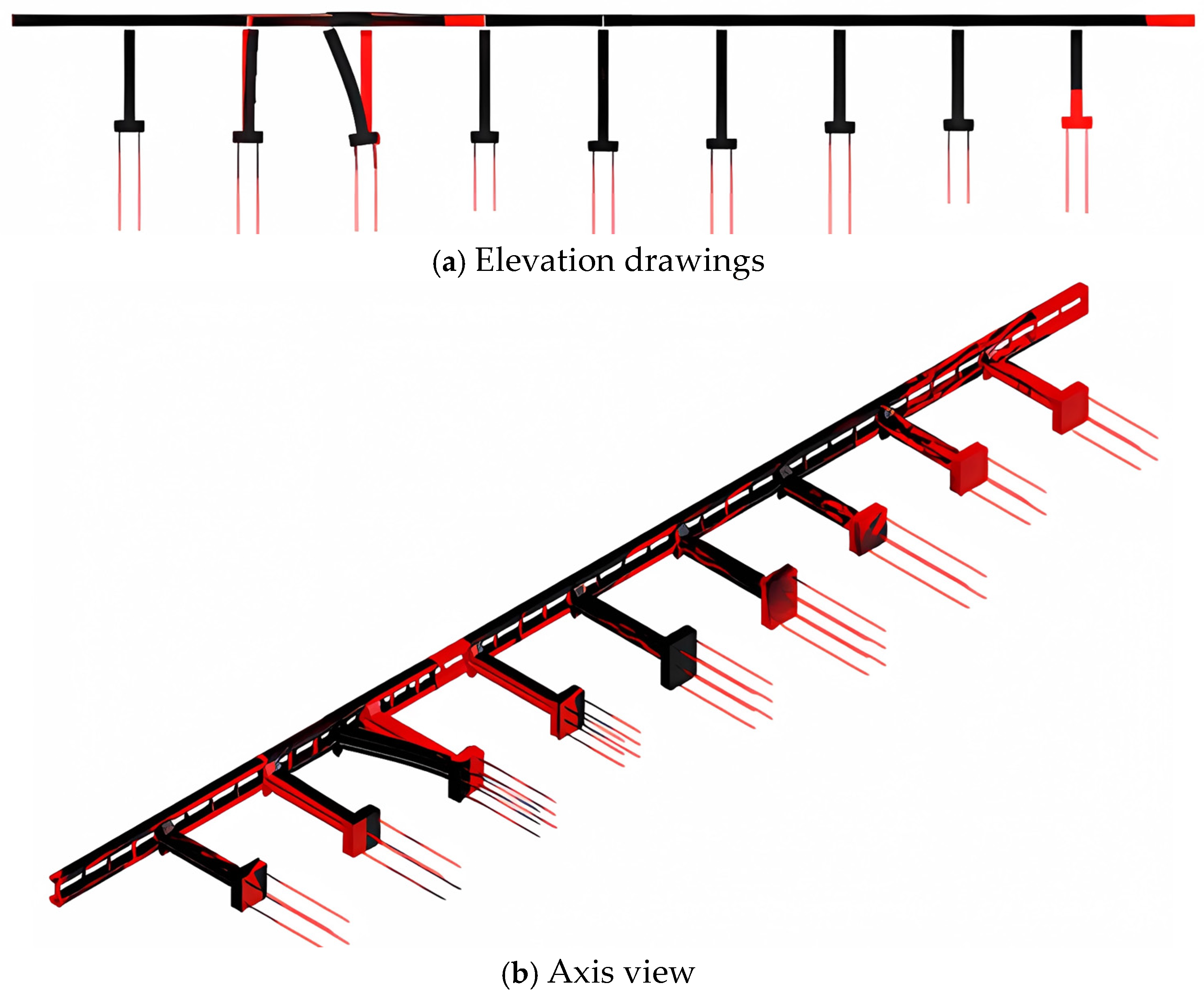





| Structural Mode Shape | The Order of the Mode Shape | Natural Frequency (Hz) | Characteristics of the Mode Shapes of a Structure |
|---|---|---|---|
| Lateral bending of the girder | 9 | 1.139 | Lateral flexural behavior of pier-girder system |
| 11 | 1.268 | ||
| 12 | 1.403 | ||
| Vertical flexure of the girder | 19 | 5.319 | Vertical flexural vibration of pier-girder assembly |
| 20 | 5.340 | ||
| 21 | 5.387 | ||
| Longitudinal deflection | 1 | 0.916 | Longitudinal floating behavior of pier–girder system |
| 2 | 0.918 | ||
| 3 | 0.940 |
| Train Type | Train Mode Shape | Calculated Speed (km/h) | Track Irregularity |
|---|---|---|---|
| Medium–low-speed maglev train | Three cars in groups (Lead car + middle car + lead car) | 60 70 80 90 100 110 120 | The German low-interference spectrum |
| Degree of Freedom | Vertical Displacement | Lateral Displacement | Yaw Rotation | Pitch Rotation | Roll Rotation |
|---|---|---|---|---|---|
| Maglev train body | |||||
| Left suspension module i (i = 1, 2, 3, 4, 5) | |||||
| Right suspension module i (i = 1, 2, 3, 4, 5) |
| Working Condition | Speed of Vehicle (km/h) | Impact Coefficient | Mid-Span Displacement of Main Girder (mm) | Main Girder Span Acceleration (m/s2) | Lateral Displacement of Pier Top (mm) | Lateral Acceleration at Pier Top (m/s2) | Angle of Beam End (10−4 rad) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Horizontal | Vertical | Horizontal | Vertical | Horizontal | Vertical | |||||
| Single track | 60 | 1.03 | 1.47 | 2.01 | 0.05 | 0.18 | 1.65 | 0.03 | 0.53 | 2.43 |
| 70 | 1.04 | 1.50 | 2.03 | 0.11 | 0.21 | 1.65 | 0.07 | 0.53 | 2.41 | |
| 80 | 1.06 | 1.49 | 2.07 | 0.14 | 0.23 | 1.63 | 0.09 | 0.53 | 2.41 | |
| 90 | 1.16 | 1.49 | 2.27 | 0.08 | 0.45 | 1.64 | 0.07 | 0.53 | 2.68 | |
| 100 | 1.13 | 1.50 | 2.21 | 0.09 | 0.55 | 1.63 | 0.08 | 0.56 | 2.75 | |
| 110 | 1.07 | 1.55 | 2.08 | 0.11 | 0.42 | 1.65 | 0.08 | 0.56 | 2.47 | |
| 120 | 1.05 | 1.54 | 2.06 | 0.09 | 0.36 | 1.68 | 0.06 | 0.56 | 2.46 | |
| Double track | 60 | 1.01 | 1.45 | 2.84 | 0.05 | 0.18 | 1.64 | 0.03 | 0.54 | 2.46 |
| 70 | 1.02 | 1.50 | 2.88 | 0.11 | 0.21 | 1.64 | 0.07 | 0.55 | 2.46 | |
| 80 | 1.06 | 1.49 | 2.97 | 0.18 | 0.29 | 1.68 | 0.11 | 0.54 | 2.49 | |
| 90 | 1.16 | 1.48 | 3.27 | 0.08 | 0.61 | 1.67 | 0.08 | 0.54 | 2.71 | |
| 100 | 1.12 | 1.50 | 3.17 | 0.08 | 0.55 | 1.70 | 0.08 | 0.59 | 2.75 | |
| 110 | 1.06 | 1.55 | 3.00 | 0.11 | 0.46 | 1.70 | 0.07 | 0.57 | 2.59 | |
| 120 | 1.04 | 1.53 | 2.93 | 0.11 | 0.36 | 1.76 | 0.08 | 0.57 | 2.54 | |
| Working Condition | Speed of Vehicle (km/h) | Lead Car | Middle Car | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Vertical Acceleration (m/s2) | Lateral Acceleration (m/s2) | Sperling Comfort Index | Vertical Acceleration (m/s2) | Lateral Acceleration (m/s2) | Sperling Comfort Index | ||||
| Horizontal | Vertical | Horizontal | Vertical | ||||||
| Single track | 60 | 0.52 | 0.28 | 2.01 | 1.75 | 0.53 | 0.28 | 2.01 | 1.76 |
| 70 | 0.64 | 0.37 | 2.11 | 1.90 | 0.63 | 0.36 | 2.12 | 1.89 | |
| 80 | 0.72 | 0.38 | 2.16 | 1.93 | 0.74 | 0.37 | 2.17 | 1.93 | |
| 90 | 0.75 | 0.35 | 2.24 | 1.87 | 0.75 | 0.34 | 2.23 | 1.87 | |
| 100 | 0.93 | 0.36 | 2.36 | 1.83 | 0.91 | 0.36 | 2.35 | 1.83 | |
| 110 | 1.08 | 0.30 | 2.44 | 1.79 | 1.12 | 0.32 | 2.42 | 1.80 | |
| 120 | 1.16 | 0.30 | 2.47 | 1.85 | 1.17 | 0.30 | 2.45 | 1.86 | |
| Double track | 60 | 0.52 | 0.28 | 2.01 | 1.75 | 0.53 | 0.28 | 2.01 | 1.75 |
| 70 | 0.64 | 0.37 | 2.11 | 1.91 | 0.63 | 0.36 | 2.12 | 1.89 | |
| 80 | 0.72 | 0.38 | 2.16 | 1.93 | 0.74 | 0.37 | 2.16 | 1.93 | |
| 90 | 0.75 | 0.35 | 2.25 | 1.88 | 0.75 | 0.35 | 2.23 | 1.87 | |
| 100 | 0.93 | 0.36 | 2.37 | 1.83 | 0.92 | 0.36 | 2.35 | 1.83 | |
| 110 | 1.09 | 0.31 | 2.44 | 1.80 | 1.13 | 0.31 | 2.42 | 1.84 | |
| 120 | 1.17 | 0.31 | 2.47 | 1.88 | 1.17 | 0.30 | 2.45 | 1.87 | |
| Mode Shape | Fundamental Lateral Flexural Mode | Fundamental Vertical Flexural Mode | Fundamental Longitudinal Floating Mode | ||||
|---|---|---|---|---|---|---|---|
| Condition | Mode | Frequency (Hz) | Mode | Frequency (Hz) | Mode | Frequency (Hz) | |
| +50% | 10 | 1.361 | 21 | 5.218 | 1 | 0.785 | |
| +25% | 10 | 1.245 | 22 | 5.250 | 1 | 0.785 | |
| ±0% | 9 | 1.139 | 19 | 5.319 | 1 | 0.916 | |
| −25% | 2 | 1.005 | 20 | 5.339 | 1 | 0.939 | |
| −50% | 1 | 0.841 | 22 | 5.343 | 4 | 1.109 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Guo, X.; Mao, H.; Liu, J. Research on the Dynamic Characteristics of a Typical Medium–Low-Speed Maglev Train–Bridge System Influenced by the Transverse Stiffness of Pier Tops. Appl. Sci. 2025, 15, 6628. https://doi.org/10.3390/app15126628
Cui Y, Guo X, Mao H, Liu J. Research on the Dynamic Characteristics of a Typical Medium–Low-Speed Maglev Train–Bridge System Influenced by the Transverse Stiffness of Pier Tops. Applied Sciences. 2025; 15(12):6628. https://doi.org/10.3390/app15126628
Chicago/Turabian StyleCui, Yanghua, Xiangrong Guo, Hongwei Mao, and Jianghao Liu. 2025. "Research on the Dynamic Characteristics of a Typical Medium–Low-Speed Maglev Train–Bridge System Influenced by the Transverse Stiffness of Pier Tops" Applied Sciences 15, no. 12: 6628. https://doi.org/10.3390/app15126628
APA StyleCui, Y., Guo, X., Mao, H., & Liu, J. (2025). Research on the Dynamic Characteristics of a Typical Medium–Low-Speed Maglev Train–Bridge System Influenced by the Transverse Stiffness of Pier Tops. Applied Sciences, 15(12), 6628. https://doi.org/10.3390/app15126628





