Abstract
This study aims to analyze electrocardiogram (ECG) data for the classification of five cardiac rhythms: sinus bradycardia (SB), sinus rhythm (SR), atrial fibrillation (AFIB), supraventricular tachycardia (SVT), and sinus tachycardia (ST). While SR is considered normal, the other four represent types of cardiac arrhythmias. A range of methods is utilized, including the supervised learning technique K-Nearest Neighbors (KNNs), combined with dimensionality reduction approaches such as Principal Component Analysis (PCA) and Uniform Manifold Approximation and Projection (UMAP), a modern method based in Riemannian topology. Additionally, logistic regression was applied using both maximum likelihood and Bayesian methods, with two distinct prior distributions: an informative normal prior and a non-informative Jeffreys prior. Performance was assessed using evaluation metrics such as positive predictive value (PPV), negative predictive value (NPV), specificity, sensitivity, accuracy, and F1-score. Ultimately, the UMAP-KNN method demonstrated the best overall performance.
1. Introduction
Cardiac arrhythmias are electrical disorders of the heart rhythm and are a leading cause of morbidity and mortality worldwide [1,2]. Common arrhythmias include sinus bradycardia (SB), atrial fibrillation (AFIB), supraventricular tachycardia (SVT), and sinus tachycardia (ST), each exhibiting distinct electrocardiographic signatures. The electrocardiogram (ECG) remains the gold standard for the non-invasive detection of such abnormalities, capturing key waveform elements such as the P wave, QRS complex, and T wave [3,4].
To enable automated and accurate ECG interpretation, the availability of robust, well-annotated databases is crucial, especially for training supervised machine learning (ML) models. Datasets such as the 2020 SPH ECG dataset [5] provide a large volume of labeled signals covering a broad spectrum of arrhythmias. Compared to the historically significant MIT-BIH Arrhythmia Database, SPH offers a considerably larger sample size and a wider diversity of rhythm classes, making it particularly suitable for modern classification pipelines. However, SPH remains less studied than MIT-BIH in classical ML settings, offering an opportunity to investigate lightweight alternatives to deep learning.
Over the past decade, several machine learning techniques—including support vector machines, decision trees, and deep learning models such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs)—have been explored for arrhythmia classification [6,7,8]. While deep learning models often achieve high classification accuracy, they require substantial computational resources, large volumes of raw data, and are typically difficult to interpret, challenges that limit their immediate applicability in clinical practice. In contrast, interpretable models such as logistic regression (LR) and K-Nearest Neighbors (KNNs), when coupled with dimensionality reduction techniques, can offer comparable performance with significantly lower complexity and enhanced transparency. This study investigates the classification of five clinically important heart rhythms: SB, SR (considered normal), AFIB, ST, and SVT. While some of these have been addressed independently in the literature, to our knowledge, their combined classification using low-dimensional models has not been extensively studied. Our work bridges this gap by comparing the performance of interpretable models under both classical and Bayesian frameworks.
Specifically, we evaluate two dimensionality reduction techniques—Principal Component Analysis (PCA) and Uniform Manifold Approximation and Projection (UMAP)—in combination with the KNN classifier. These are contrasted with logistic regression models implemented using both maximum likelihood estimation and Bayesian inference (with informative and non-informative priors). The choice of these methods is motivated by their computational efficiency, interpretability, and suitability for deployment in constrained environments such as point-of-care devices. We assess all models using common classification metrics, including positive predictive value (PPV), negative predictive value (NPV), sensitivity, specificity, accuracy, and F1-score.
2. Dataset Description and Processing
The ECG dataset used in this study was sourced from Chapman University and Shaoxing People’s Hospital (SPH) [5]. It consists of 10,646 labeled 12-lead ECG recordings, each sampled at 500 Hz over a duration of 10 s. These recordings are annotated with 1 of 11 cardiac rhythm classes and are accompanied by patient metadata such as age and diagnosis. The dataset includes both raw ECG signals and pre-extracted clinical features. In this work, we focus on a set of 11 derived features provided directly within the dataset, which serve as clinically meaningful summaries of cardiac activity. These include (1) QRS complex count, (2) atrial beat frequency, (3) ventricular beat frequency, (4) Q-wave onset, (5) Q-wave offset, (6) R-wave peak, (7) S-wave offset, (8) T-wave onset, (9) T-wave offset, (10) average RR interval, and (11) QT interval duration. All these features were used as input variables for the classification models. These engineered features were selected for their clinical interpretability and were precomputed by domain experts as part of the SPH dataset documentation. Table 1 presents the distribution of patients across the 11 rhythm classes, along with age statistics. Among the records, 17.15% were labeled as SR, while the remaining 82.85% correspond to various arrhythmias. The five rhythms retained for classification in this study—SB, SR, AFIB, ST, and SVT—were selected based on clinical relevance and class prevalence. Rarer classes such as AV re-entrant tachycardia or sinus to atrial wandering rhythm were excluded due to insufficient representation for robust model training. Given the class imbalance, particularly the under-representation of certain arrhythmias, it was essential to ensure a representative allocation across training and testing phases. To address this, we performed a stratified data split, allocating 60% of the samples for training and 40% for testing, while preserving the original class proportions. This ensures that minority classes are adequately represented during model training and evaluation. We did not apply oversampling or undersampling methods, opting instead for stratification to maintain the integrity of the dataset. While oversampling and undersampling techniques can improve balance, we opted to preserve the original data distribution to avoid introducing synthetic bias. All numeric features were standardized to have zero mean and unit variance using z-score normalization. This preprocessing step was applied to the entire dataset before performing the train–test split. This step reduces scale-related bias and ensures consistent convergence during model fitting. Standardization was conducted on the entire dataset prior to splitting to ensure consistent scaling of all features and comparability across folds. Subsequently, training data were used to build the classification models, while the test data were reserved exclusively for model evaluation. Figure 1 presents an overview of the full analytical pipeline, including preprocessing, dimensionality reduction, classification, and model evaluation. To further contextualize the classification task, Figure 2 provides a visual comparison between two representative ECG signal segments: one for SR and another for AFIB. The distinct morphological patterns in P-QRS-T sequences illustrate the need for reliable, feature-based discrimination.

Table 1.
Class distribution and age statistics for the SPH dataset.
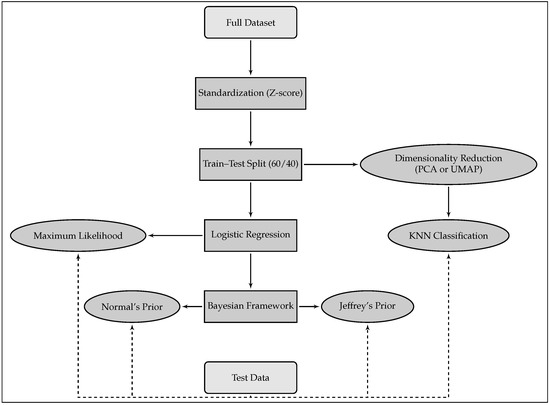
Figure 1.
Construction of models using the training data, followed by the evaluation of each model on test data. Note: Feature standardization was performed before data splitting, to ensure unified scaling across training and test subsets.
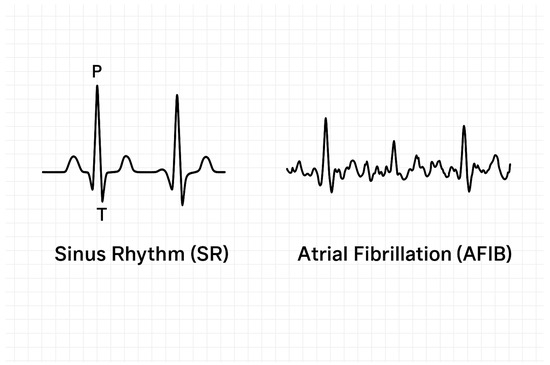
Figure 2.
Illustrative ECG waveforms. (Left): SR with regular morphology; (Right): AFIB with absent P waves and irregular R-R intervals.
3. Materials and Methods
This section details the machine learning methods used for ECG rhythm classification. The overall goal was to identify each rhythm class by comparing traditional and interpretable models using pre-engineered features. Two main strategies were explored: (i) K-Nearest Neighbors (KNNs) applied after dimensionality reduction, and (ii) logistic regression (LR) models under frequentist and Bayesian paradigms. Figure 1 (previous section) provides a schematic overview of the complete modeling pipeline.
3.1. Dimensionality Reduction
Dimensionality reduction helps to simplify high-dimensional ECG-derived features into a compact representation, facilitating classification and visualization. This also helps to reduce noise, eliminate redundancy, and mitigate overfitting [9].
3.1.1. Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a linear projection technique that transforms correlated input features into orthogonal components by maximizing variance [9]. The projection is defined by the eigenvectors of the covariance matrix. In our experiments, the first three principal components, explaining over 85% of the total variance, were retained to align with the 3D embedding used in the alternative method (UMAP) and ensure fair comparison.
3.1.2. Uniform Manifold Approximation and Projection
Uniform Manifold Approximation and Projection (UMAP) [10] is a nonlinear dimensionality reduction technique grounded in Riemannian geometry and algebraic topology. It begins by constructing a fuzzy topological structure that models the underlying manifold, under three key assumptions: the data are uniformly distributed on a Riemannian manifold, the Riemannian metric is locally constant, and the manifold is locally connected. UMAP then optimizes a low-dimensional projection by minimizing the cross-entropy between fuzzy topological representations, using stochastic gradient descent and negative sampling to enhance computational efficiency. UMAP is increasingly recommended in biomedical domains, including clinical data analysis, brain imaging, longitudinal proteomics, electronic health records (EHRs), and electrocardiogram (ECG) datasets [11], particularly for its ability to reveal complex data structures (see Figure 3). Comparative studies have shown that UMAP outperforms traditional methods such as PCA and t-SNE in preserving both local and global structures. In particular, Jain et al. [12] reported that UMAP significantly improved arrhythmia classification performance when integrated with ensemble classifiers. The main steps of the UMAP algorithm, originally introduced by McInnes et al. [13], are described below (Algorithm 1).
| Algorithm 1 UMAP Algorithm |
|
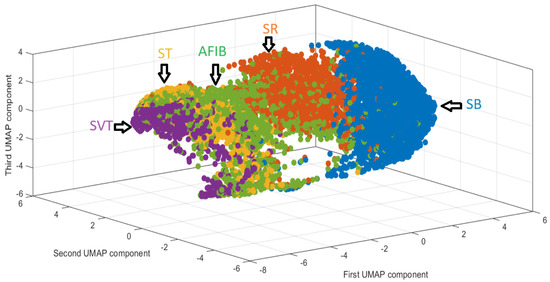
Figure 3.
Low-dimensional UMAP representation of ECG records colored by rhythm class.
For the validation step, both dimensionality reduction algorithms (PCA and UMAP) are combined with the k-Nearest Neighbor (KNN) algorithm as the supervised classification approach [14] for diagnostic decision. The classification of a new ECG record will be carried out by the most recurrent class of its k-Nearest Neighbors. The optimal number of neighbors, k, is a hyperparameter that has been estimated by cross-validation [15]. We used 3 dimensions for comparability and visualization purposes, and applied the standard parameters recommended in [10,11].
3.2. Logistic Regression (LR)
To provide a benchmark for linear and probabilistic modeling, we implemented logistic regression in both frequentist and Bayesian frameworks. All LR models were trained on the original 11-dimensional input space without dimensionality reduction to assess the impact of transformation on classification performance.
3.2.1. Frequentist Approach (LR-ML)
In the frequentist framework, we used a one-vs-rest multiclass logistic regression with maximum likelihood estimation. The method estimates the probability of each class based on a logistic link function. While interpretable, LR-ML assumes linear boundaries, which may not hold in complex ECG classification tasks [16].
3.2.2. Bayesian Logistic Regression
To incorporate parameter uncertainty and prior beliefs, we implemented two Bayesian logistic regression models. The first uses a non-informative Jeffreys prior [17], which is invariant to scale and suitable in the absence of expert knowledge. The second model (LR-BN) assumes a weakly informative multivariate normal prior, where large variance reflects prior neutrality. Both models were estimated using Metropolis–Hastings MCMC sampling [18], allowing posterior distributions over all 11 coefficients to be inferred.
The Bayesian framework proved useful in assessing the robustness of variable contributions and improved classification stability in low-prevalence classes. In particular, posterior summaries offered interpretable insights into the importance of individual ECG features across rhythm types. Though not novel methods per se, their use in this study highlights how Bayesian inference adds value to ECG analysis by quantifying uncertainty, an often-overlooked aspect in clinical decision systems.
3.2.3. Algorithm Comparison
Based on 10,646 ECG recordings, all models were trained on 6388 data items—60% of the dataset—and evaluated on the remaining 4258 (40%). Input features consisted of 11 ECG-derived variables. Dimensionality reduction output was fixed to 3D for both PCA and UMAP. The KNN classifier operated in the reduced space, while logistic regression was performed in the original 11-dimensional space. The main steps in applying the considered approaches are as follows:
- (a)
- Use of Dimensionality Reduction Techniques (PCA or UMAP): The first step involves applying a dimensionality reduction technique, such as Principal Component Analysis (PCA) or Uniform Manifold Approximation and Projection (UMAP), to project the ECG signals into a three-dimensional space. The associated heart rhythms from the training dataset are mapped into this reduced space, which helps to create a more manageable representation of the ECG signals for further analysis.
- (b)
- Identification of the Most Likely Class for Each ECG in the Validation Group: After the dimensionality reduction step, the next step is to classify the ECG signals in the validation group. Each ECG in this group is projected into the same lower-dimensional space. Using the KNN classification algorithm, with Euclidean distance, the model predicts the most likely class or heart rhythm for each ECG in the validation group.
- (c)
- Measurement of Classification Quality: Once the heart rhythm for each ECG in the validation set has been predicted, the next step is to evaluate how accurately the model has assigned the ECGs to the correct heart rhythm classes. This is achieved by comparing the predicted labels with the true labels of the ECGs in the validation set. The evaluation metrics for this task include Positive Predictive Value (PPV), Negative Predictive Value (NPV), Sensitivity, Specificity, Accuracy, and F1-score, which provide insights into the ability of these models to correctly classify heart rhythms compared to logistic regression approaches.
4. Results and Analysis
4.1. Overall Classification Performance
The proposed methods were evaluated on a held-out test set representing 40% of the dataset (n = 4258 records), ensuring class proportions matched the full dataset. All models were assessed based on six metrics: PPV, NPV, sensitivity, specificity, accuracy, and F1-score. Performance was analyzed separately for each of the five rhythm classes (SB, SR, AFIB, ST, SVT) and across five models: PCA-KNN, UMAP-KNN, LR-ML, LR-BJ, and LR-BN. Table 2 summarizes the classification metrics for each model and class.

Table 2.
Performance metrics for each diagnostic and model.
The UMAP-KNN model demonstrates the most balanced performance across all metrics and rhythm classes, outperforming logistic regression models particularly in more ambiguous or imbalanced cases such as SR, AFIB, and ST. Figure 3 shows the low-dimensional UMAP embedding of the ECG data. The spatial separation of rhythm clusters indicates the capacity of UMAP to uncover structure in high-dimensional ECG features.
The results demonstrate that UMAP-KNN outperforms other models in PPV, NPV, sensitivity, and F1-score for SB, SR, and ST, confirming its robustness in handling irregular and imbalanced classes. Although LR-ML leads in PPV for AFIB and in sensitivity for SVT, UMAP-KNN provides more balanced performance across all rhythms. Logistic regression models, especially LR-BJ and LR-BN, achieve high NPV and specificity, particularly in SB, SVT, and AFIB. Notably, LR-BJ shows perfect specificity (100%) for SR and ST. However, the logistic models fail to identify SR and ST in terms of sensitivity, with F1-scores close to zero. Overall, LR-BJ performs best for SB, with the highest F1-score (95.27%) and accuracy (96.43%). UMAP-KNN surpasses all others for SR and ST in F1-score (63.26% and 73.65%, respectively). LR-BN achieves the top F1-score for SVT (71.37%), although UMAP-KNN remains close. These outcomes are derived from confusion matrices of each model. As an illustration, Figure 4 presents the confusion matrix for UMAP-KNN on SB classification.
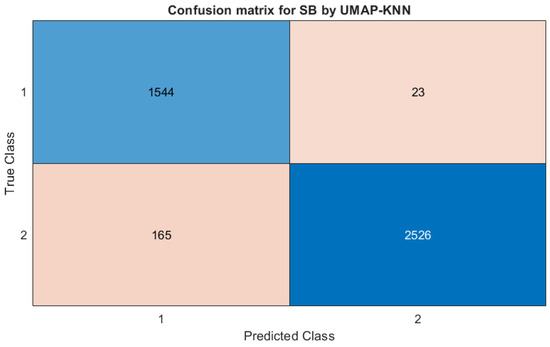
Figure 4.
Confusion matrix of UMAP-KNN on SB.
4.2. Related Work
Several recent deep learning-based studies have addressed ECG arrhythmia classification using the SPH dataset.
- Aziz et al. (2021) [19] proposed a hybrid CNN-LSTM architecture and reported an average F1-score of 94.2% on a multi-label classification task involving 11 rhythm classes.
- Gupta et al. (2024) [20] introduced a residual attention-based convolutional network that achieved over 96% accuracy and 95% F1-score across six arrhythmias.
- Ozpolat et al. (2023) [21] developed a temporal CNN with dilated convolutions, reaching 92.4% accuracy and 90.6% F1-score.
- Yildirim et al. (2020) [22] employed a bidirectional LSTM model and reported F1-scores above 94%, though the method required considerable computational time and resources.
Compared to these deep learning approaches, our best-performing models—particularly UMAP-KNN—achieved more modest F1-scores, ranging from 63% to 95% depending on the rhythm class. As illustrated in Figure 5, UMAP-KNN outperformed all logistic regression variants in challenging and imbalanced classes such as SR, AFIB, and ST, despite its conceptual simplicity.
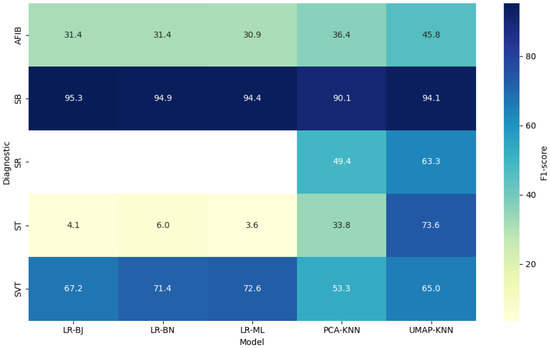
Figure 5.
F1-score per diagnostic class and classification model.
While deep learning models remain superior in terms of raw accuracy and generalization across classes, they come with significant limitations: high training costs, limited interpretability, and reduced feasibility for real-time deployment. In contrast, our approach offers a favorable trade-off between explainability, computational efficiency, and classification performance, especially in clinical decision support systems where transparency is essential.
5. Discussion and Conclusions
This study evaluated the performance of interpretable machine learning models for the classification of five clinically relevant cardiac rhythms—SB, SR, AFIB, ST, and SVT—using engineered features from the SPH ECG dataset. We focused on classical approaches such as K-Nearest Neighbors (KNNs) and logistic regression, both in frequentist and Bayesian frameworks, combined with dimensionality reduction techniques including Principal Component Analysis (PCA) and Uniform Manifold Approximation and Projection (UMAP). The results demonstrate that the UMAP-KNN model yielded the most balanced and robust performance across diverse rhythm types. It showed particular effectiveness in handling difficult and imbalanced classes such as SR, AFIB, and ST, achieving F1-scores of 63.26%, 45.95%, and 73.65%, respectively. By capturing nonlinear relationships in the feature space, UMAP improved the separability of rhythm classes and enhanced the performance of the KNN classifier. In contrast, logistic regression models, especially the Bayesian variants (LR-BJ and LR-BN), performed better in linearly separable classes such as SB and SVT, with F1-scores exceeding 91%. However, they struggled in overlapping or under-represented classes, which highlights the limitations of linear models in complex classification tasks. Compared to recent deep learning approaches applied to the same dataset [19,20,21,22], our models achieved more moderate performance levels. Nonetheless, they offer significant advantages in terms of interpretability, computational efficiency, and ease of implementation. Logistic regression provides transparent coefficient interpretation, while Bayesian models quantify predictive uncertainty, a key aspect in clinical decision-making. The use of dimensionality reduction, particularly UMAP, also adds interpretability by enabling the visual exploration of the data structure, an asset often lacking in deep neural networks. In contrast, our approach offers a favorable trade-off between explainability, computational efficiency, and classification performance, especially in clinical decision support systems where transparency is essential. Unlike end-to-end black-box models, our approach explicitly separates feature extraction and classification stages, allowing for diagnostic insight into both dimensionality structure and classification boundaries. This separation enhances transparency and supports clinical interpretability, features that are often lacking in deep learning pipelines. This work, however, presents certain limitations. First, only pre-engineered features were used, excluding raw ECG waveform data which could carry additional diagnostic information. Second, although stratified data splitting was employed, class imbalance persisted, affecting sensitivity and precision in minority classes. Third, no advanced tuning or ensemble techniques were applied, which may have limited the full potential of the tested models. To address these limitations, future research could explore hybrid approaches that combine deep representation learning with interpretable classification layers, such as CNN-based feature extraction followed by logistic regression. Attention mechanisms or rule-based modules could further enhance transparency. Including raw ECG signals may improve classification fidelity, and class imbalance could be addressed using resampling techniques or specialized loss functions. Moreover, for real-time clinical applications, deploying compressed or quantized versions of these models could ensure compatibility with constrained hardware environments. In conclusion, this study shows that interpretable, low-complexity models—especially UMAP-KNN—can provide a competitive and clinically meaningful performance for ECG rhythm classification. While they may not match the top accuracy of deep learning models, their transparency, efficiency, and ease of deployment make them particularly suitable for medical applications where interpretability and reliability are essential.
Author Contributions
S.L.T.: literature review, data analysis, writing—original draft, writing—review and editing. É.S.: literature review, data curation, statistical analysis, code development, writing—review and editing. I.B.: statistical analysis, writing—review and editing. J.J.: funding acquisition, medical analysis, writing—review. S.E.A.: supervision, methodology, validation, project administration, funding acquisition, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The author(s) declare that financial support was received for the research presented in this article. This study was supported through grant programs allocated to Dr. Jbilou from ResearchNB—Strategic Initiative Grant (SIG_2025_014) and to Drs. Jbilou and El Adlouni from the AI Pre-Voucher New Brunswick Innovation Fund (AIP_2023_013).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The database used in this study was sourced from Chapman University and Shaoxing People’s Hospital (Shaoxing Hospital, Zhejiang University School of Medicine) [5].
Acknowledgments
The authors would like to thank the New Brunswick Innovation Foundation (NBIF) for the financial support provided throughout this research project.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Al-mousa, A.; Baniissa, J.; Hashem, T.; Ibraheem, T. Enhanced electrocardiogram machine learning-based classification with emphasis on fusion and unknown heartbeat classes. Digit. Health 2023, 9, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Varvarousis, D.; Xenos, D.; Varvarousi, G.; Nakos, G. Atrial fibrillation in critical illness: Epidemiology and clinical significance. J. Crit. Care 2020, 58, 125–132. [Google Scholar] [CrossRef]
- Yi, H.; Wang, Y.; Zhang, Y.; Sun, Y. A review on automatic detection and classification of arrhythmias using ECG signals. Phys. Medica 2020, 72, 43–65. [Google Scholar] [CrossRef]
- Mantravadi, R.; Kim, H.; Moon, J. Explainable AI for ECG classification: Challenges and future directions. Comput. Biol. Med. 2024, 168, 107567. [Google Scholar]
- Zheng, J.; Zhang, J.; Danioko, S.; Yao, H.; Guo, H.; Rakovski, C. A 12-lead electrocardiogram database for arrhythmia research covering more than 10,000 patients. Sci. Data 2020, 7, 48. [Google Scholar] [CrossRef] [PubMed]
- Aziz, A.; Al-Ali, A.R.; Al-Nashash, H. Deep learning for electrocardiogram (ECG) analysis: A review. Biomed. Signal Process. Control 2021, 68, 102713. [Google Scholar] [CrossRef]
- Hassaballah, M.; Shaheen, S.I.; Aly, S. A survey of deep learning methods for ECG classification. Artif. Intell. Med. 2023, 140, 102500. [Google Scholar]
- Yildirim, O. A novel wavelet sequence based on deep bidirectional LSTM network model for ECG signal classification. Comput. Biol. Med. 2020, 96, 189–202. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Dadu, A.; Satone, V.K.; Kaur, R.; Koretsky, M.J.; Iwaki, H.; Qi, Y.A.; Ramos, D.M.; Avants, B.; Hesterman, J.; Gunn, R.; et al. Application of Aligned-UMAP to longitudinal biomedical studies. Patterns 2023, 4, 100741. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.; Sahu, P.; Jain, S. Dimensionality Reduction Using PCA and t-SNE for Analysis and Prediction of Cardiovascular Disease. J. Phys. Conf. Ser. 2022, 2161, 012003. [Google Scholar] [CrossRef]
- Meehan, C.; Ebrahimian, J.; Moore, W.; Meehan, S. Uniform Manifold Approximation and Projection (UMAP) [MATLAB Code]. 2023. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/71902 (accessed on 11 June 2025).
- Kononenko, I.; Kukar, M. Chapter 10—Statistical Learning. In Machine Learning and Data Mining; Woodhead Publishing: Sawston, UK, 2007; pp. 259–274. [Google Scholar] [CrossRef]
- Saporta, G. Probabilité, Analyse des Données et Statistique, 2nd ed.; Éditions Technip: Paris, France, 2006. [Google Scholar]
- MCCullagh, P. Generalized Linear Models; Routledge: London, UK, 2019. [Google Scholar]
- Chen, M.H.; Ibrahim, J.G.; Shao, Q.M. Properties and Implementation of Jeffreys’s Prior in Binomial Regression Models. J. Am. Stat. Assoc. 2008, 108, 1659–1664. [Google Scholar] [CrossRef] [PubMed]
- Robert, C.P. The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, 2nd ed.; Springer: New York, NY, USA, 2007; p. 303. [Google Scholar]
- Aziz, S.; Haider, S.U.; Yousaf, M.H.; Rauf, H.A.; Rehman, A. Automated cardiac arrhythmia classification using deep learning techniques. Sci. Rep. 2021, 11, 18738. [Google Scholar] [CrossRef]
- Gupta, U.; Singh, R.; Sharma, N. Arrhythmia classification using residual attention CNN on 12-lead ECGs. Heliyon 2024, 10, e26787. [Google Scholar] [CrossRef] [PubMed]
- Ozpolat, E.; Yildiz, O. A temporal CNN with dilated convolutions for ECG arrhythmia classification. Diagnostics 2023, 13, 1099. [Google Scholar] [CrossRef]
- Yildirim, O.; Talo, M.; Baloglu, U.B.; Aydin, G.; Acharya, U.R. Arrhythmia detection using deep bidirectional LSTM network. Comput. Methods Programs Biomed. 2020, 185, 105740. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).