Abstract
The prevalence of “building-bridge integrated” structures in station design is increasing. However, in stations where the mainline speed exceeds 160 km/h, structural joints are typically incorporated to ensure the integrity and functionality of the integrated system. The inspection and maintenance of these joints, which are critical for the long-term performance of such structures, can be particularly complex. Therefore, it is important to explore the feasibility of designing such stations without structural joints on the mainline. To address this issue, two six-line railway bridge-type stations are selected. The vibration simulation analysis model of the train-track-station coupling system is established, considering two structural types of the “building-bridge integrated” system: the arrival-departure line “building-bridge integrated” and the mainline “building-bridge integrated”. The vibration responses induced by trains passing through two types of “building-bridge integrated” station structures at speeds of 200~350 km/h on the mainline and 80 km/h on the arrival and departure tracks were simulated. The six-line operating conditions were selected as an example, and the influence of setting a structural joint on the mainline on the dynamic response of the “building-bridge integrated” station structure was analyzed. For both types of “building-bridge integrated” station structures, with and without a structural joint on the mainline, the dynamic responses of trains under operational loads show minimal differences. However, the structural joints on the mainline reduce the overall stiffness of the rail bearing floor slab and effectively isolate the train-induced responses transmitted to the platform slab during high-speed operation on the mainline. Therefore, the acceleration response of the platform slab is smaller in station structures with structural joints, while the acceleration and displacement response of the rail bearing floor slab is larger. Additionally, structural joints often lead to issues such as water leakage and seepage. Considering these factors, it is advisable to avoid setting structural joints on the mainline for such station structures.
1. Introduction
With the rapid economic development of China in recent years, the processes of urbanization and industrialization have accelerated significantly, leading to severe land wastage. In response, the state has increased its emphasis on intensive land use. Railway bridge-type stations, characterized by their land-saving nature, compact functional layout, efficient passenger flow lines, and streamlined structural form, are well-suited for intensive land use and meet the requirements for low-carbon urban spatial transformation. As a result, they are increasingly valued by construction entities [1,2,3].
As trains pass through stations, dynamic impact forces are generated, which may adversely affect the comfort of passengers waiting for or transferring trains. The vibration response of railway passenger stations induced by train operations has increasingly drawn attention. To tackle these issues, scholars both domestically and internationally have conducted research on this series of problems. In terms of numerical simulation, Feldmann et al. [4] developed a computational model for the new Berlin railway station building, predicting the structural vibrations and the impact of train-induced vibrations on the steel cables of the station roof. Deng et al. [5], aiming to study the train-induced vibration issues in large high-speed railway stations, decomposed the train–bridge–station system into two subsystems, namely “train–bridge” and “bridge–station”, and obtained the dynamic responses of the station structure while evaluating the comfort and safety of train operations. Zhu et al. [6,7,8], focusing on large railway passenger stations with an integrated bridge-and-building structure, established a coupled model of the train–track–station system. They verified the overall structure according to railway design codes and investigated the variation laws of station structure vibration responses under different train speed conditions. Fedorova et al. [9] developed an algorithm for analyzing the interaction between trains, tracks, and stations, highlighting the implementation process of the algorithm. Kim et al. [10,11] proposed an algorithm for controlling station vibrations and validated its accuracy and effectiveness through numerical examples. Zhang et al. [12,13] proposed a frequency-domain analysis model for predicting the vibration response of high-speed railway station structures and studied force and vibration transmission mechanisms. Guo et al. [14] investigated the lateral response variation laws of integrated bridge-and-building station structures under multi-line train operation conditions. Regarding field testing, Zhang et al. [15] conducted vibration tests on a typical bridge-type station building of a high-speed railway in China, measuring the vibration levels of the platform and waiting levels and calculating the Z-weighted vibration acceleration levels corresponding to the one-third octave band center frequencies at each measuring point. Xu et al. [16] performed train-induced vibration tests on the waiting level of Wuhan Station, further exploring the vibration effects of the station floor under the most unfavorable train load operation conditions. Xie et al. [17] measured the train-induced vibration response of a “bridge-building integrated” subway station and found that the vibration was more intense compared to “bridge-building separated” subway stations for this type of structure. Yang et al. [18] conducted on-site vibration tests on Tianjin West Station, obtaining the acceleration time responses of the station structure in the lateral, vertical, and longitudinal directions and finding that the structural vibration response increased with train speed. Guo et al. [19] verified the accuracy of the train–station finite element model using field measurement data, providing references for vibration control in similar double-deck high-speed railway stations. Ba et al. [20] tested the vibration transmission in the platform of a high-speed railway station with an integrated station-bridge structure, demonstrating a certain range of vibration rebound zones with increasing distance.
Currently, the “Code for Design of Railway Passenger Stations” (TB 10100-2018) in China states that the “building-bridge integrated” structure is not recommended for mainline passenger railways where train speeds exceed 160 km/h [21]. Therefore, in “building-bridge integrated” stations with high-speed trains passing through the mainline, structural joints are commonly implemented. However, these joints can cause issues such as water leakage and seepage, highlighting the need to explore whether it is feasible to design such stations without structural joints on the mainline. Existing literature on train-induced vibrations in “building-bridge integrated” railway bridge-type station structures primarily focus on vibration characteristics, safety, and comfort. It also summarizes the station structure’s vibration response, as well as the propagation and attenuation of wheel-rail noise. However, comparative research on the effects of setting versus not setting structural joints on the dynamic response, safety, and comfort of “building-bridge integrated” railway bridge-type stations is limited. To address this gap, this study selects two six-line railway bridge-type stations for analysis, considering two structural types of “building-bridge integrated” design: mainline “building-bridge integrated” and arrival-departure line “building-bridge integrated”. A comparative study is conducted to assess the impact of setting structural joints on the dynamic performance of “building-bridge integrated” railway bridge-type stations with mainline speeds exceeding 160 km/h. This study aims to provide valuable insights for bridge station design standards and future code revisions.
2. Project Overview
Railway bridge stations are divided into two types: “building-bridge integrated” and “building-bridge separated”. The “building-bridge integrated” type further splits into arrival-departure line and mainline versions, depending on structural joints. The arrival-departure version has joints between the mainline and arrival-departure line, while the mainline version has no joints. The “building-bridge separated” type has continuous joints, keeping the bridge and station structures independent. This type reduces vibrations but underutilizes space beneath the bridge. In contrast, the “building-bridge integrated” type is more widely used for better space utilization. A detailed comparison is given in Table 1.

Table 1.
Comprehensive Comparison of Different Structural Types.
For railway bridge-type stations, the utilization of the space under the bridge often needs to be considered. Although the “building-bridge separated” scheme makes the station structure and the bridge structure entirely independent, which can mitigate vibrations generated when trains pass at high speeds, the large size of the beams and columns results in inefficient use of the space under the bridge. Therefore, compared with the “building-bridge separated” scheme, the “bridge-building integrated” scheme is increasingly widely applied.
This paper investigates two types of “bridge-building integrated” station structures: the arrival and departure line “building-bridge integrated” structure and the mainline “building-bridge integrated” structure. The typical cross-sectional views of the station structures are illustrated in Figure 1. The former features a structural joint in the mainline, while the latter does not. Both station structures have a layout of two platforms and six tracks, comprising six operational lines. 3#, 4# are mainlines, and the remaining tracks are arrival and departure lines. The structural joint in the mainline is located between the mainlines (3#, 4#) and the arrival and departure lines (2#, 5#). The station buildings of both types have a length of 49 m in the direction perpendicular to the tracks and a length of 98.8 m in the direction parallel to the tracks. The structures have three spans in the direction perpendicular to the tracks: the arrival and departure line “building-bridge integrated” type has spans of 17.95 m + 9.9 m + 17.95 m, while the mainline “building-bridge integrated” type has spans of 18.75 m + 11.5 m + 18.75 m. In the direction parallel to the tracks, there are four spans with a length of 4 × 24.7 m. The platform level is at an elevation of 14.43 m, and the track-bearing level is at an elevation of 11.93 m. The waiting room is located at the ground level. To enhance the clarity and precision of the discussion, Station Type A and Station Type B are respectively used to denote the arrival-departure line “building-bridge integrated” Structure and mainline “building-bridge integrated” Structure.
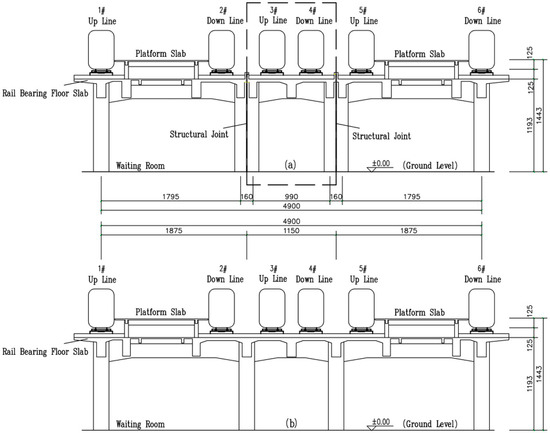
Figure 1.
Schematic diagram of “building-bridge integrated”. (a) section of Station Type A. (b) section of Station Type B.
3. Simulation and Analysis Model of Train-Track-Station Coupled Vibration
3.1. Train Model and Track Irregularity Simulation
When establishing the spatial vibration analysis model of the train, the basic assumptions about the train model in the work written by Zeng Qingyuan [22] are adopted: The train is regarded as a multi-rigid-body system composed of the car body, bogies, and wheelsets; the rigid bodies move at a constant speed in the direction along the bridge, and the longitudinal vibration of the rigid body system is neglected; it is assumed that each rigid body undergoes small vibrations; the springs in the primary and secondary suspensions are considered as linear elastic models with damping, and the influence of nonlinear creep is ignored; the wheelsets are always in close contact with the rails, and their vertical displacements are always the same.
A rigid body has six degrees of freedom (DOFs): three translational DOFs and three rotational DOFs. In the model established in this paper, since the longitudinal vibration of the train is neglected, the degree of freedom in the direction of vehicle travel is not considered. Therefore, a car body has five DOFs, including sway, heave, roll, pitch, and yaw. Since it is assumed that the wheelsets are always in vertical contact with the rails, the vertical displacement and roll displacement of the wheelsets are determined by the rails. Thus, the heave and pitch degrees of freedom of the wheelsets are ignored, and each wheelset only has two DOFs, namely sway and yaw. In summary, in the train model studied in this paper, one train car has one car body, two bogies, and four wheelsets, with a total of 23 degrees of freedom. The CRH3 vehicle dynamics analysis model is shown in Figure 2.
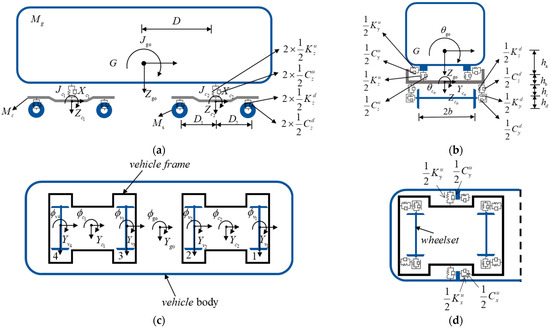
Figure 2.
Schematic Diagram of Train Dynamics Model. (a) elevation view; (b) side view; (c) plan view; (d) schematic diagram of the vehicle’s horizontal spring.
The specific details of the degrees of freedom are presented in Table 2, and the details of the remaining model parameters are shown in Table 3.

Table 2.
Summary of Degrees of Freedom (DOF) for Each Vehicle Model.

Table 3.
Vehicle Model Parameters.
The position of the train on the structure changes continuously as the train moves. First, it is necessary to calculate the total potential energy of a vehicle , then employing the elastic system dynamics principle of total potential energy conservation and the “set-in-right-position” rule that can form matrices, quickly proposed by Zeng Qingyuan [23,24], the stiffness matrix, damping matrix, and mass matrix of the vehicle system, namely , , in the following formula, can be rapidly established. By combining these matrices with the external load vector , the equation of motion for a single-vehicle model can be derived:
During the construction and service life of rails, deviations between the actual and theoretical track profiles arise due to factors such as construction tolerances, material de-fects, wear from service, and subgrade displacements. Given the complexity of the track conditions and the stochastic nature of track irregularities, it is highly challenging to de-fine track irregularities with a specific mathematical relationship. Therefore, statistical parameters are commonly employed to characterize track irregularities, and the power spectral density (PSD) function is utilized to elucidate the relationship between the track spectral density and frequency.
Track irregularities, primarily caused by construction errors and wear during opera-tion, result in deformations of the rail geometry. These irregularities significantly increase train vibrations and wheel-rail interaction forces and are the main excitation sources for train-structure coupled vibrations. Given their substantial impact on simulating train op-erations, effective simulation of track irregularities is essential. Track irregularities exhibit high uncertainty and are difficult to represent with specific formulas. However, their characteristics can be effectively described using statistical methods. Currently, the power spectral density function is widely used to describe the wavelength characteristics of track irregularities. Various countries have proposed different track irregularity spectra based on field measurements, such as the German low-disturbance track spectrum, the U.S. six-level spectrum, the Japanese spectrum, and the fitted spectrum for existing railway mainlines in China
This study investigates railway bridge-type stations with train speeds exceeding 160 km/h. It uses the German low-interference spectrum, which is suitable for high-speed applications, to simulate track irregularities. The randomly generated track irregularities based on the German low-interference spectrum are used as excitation for the track system. The power spectral density (PSD) functions for track direction, vertical alignment, horizontal alignment, and gauge irregularities are shown as follows, respectively:
where, , , , respectively, represent the power spectral densities (PSDs) corresponding to track alignment irregularity, vertical profile irregularity, and gauge irregularity, all units are (); represent the power spectral density of horizontal irregularities, and because of the use of an inclination angle measure, its unit is (); , , , respectively, represent roughness constant, its unit is (); , , represent cutoff frequency (); b represent half of the distance between the left and right rolling circles.
The roughness constants and cutoff frequencies for simulating track irregularities using the German low-interference spectrum are shown in Table 4.

Table 4.
German Low Interference Spectrum’s Cutoff Frequency and Roughness Coefficient.
3.2. Finite Element Models of Track-Station System
The software for vehicle-line-bridge-station coupled vibration dynamics simulation and analysis, which was independently developed by Professor Guo Xiangrong’s research team at Central South University, was used in this study. The modeling approach adopted by the software involves first obtaining the mass and stiffness matrices of each element of the track-station structure in the local coordinate system. Subsequently, these matrices are assembled into the overall structural matrices according to the “set-in-right-position” rule, integrating each element’s matrices into the global stiffness and mass matrices. This software has been successfully applied in the coupled vibration analysis of vehicle-line-bridge-station systems for structures such as Heze East Station, Dayanhe Street Station, and Yichang North Station. Reference [25] employing the same dynamic simulation calculation method as this study has verified the accuracy of the model and the feasibility of the vibration calculation approach by comparing the measured peak accelerations at the monitoring points with the theoretical calculation results.
Figure 3 and Figure 4 present the finite element analysis model of the track-station system developed using the self-developed finite element software GSAP-V2024 by Central South University. The model focuses solely on the main station structure that supports the mainline and arrival-departure tracks, excluding the canopy and pile-soil interaction. In the station structure model, beams and columns are modeled using two-node spatial beam elements, and floors are modeled using four-node plate elements. Each node of the two-node spatial beam element has three translational degrees of freedom and three rotational degrees of freedom. For the four-node plate element, each node has two translational degrees of freedom along the axial directions. The detailed parameters of the two types of “building-bridge integrated” station structures are shown in Table 5.

Figure 3.
Finite element model of Station Type A. (a) axonometric view; (b) front elevation.

Figure 4.
Finite element model of Station Type B (a) axonometric view; (b) front elevation.

Table 5.
Station Structure Parameters.
For such complex station structures, the structural damping is equally complex. In this study, Rayleigh damping is employed to simplify the simulation of the damping characteristics of the station structure, with a damping ratio of 2%. The finite element models of the two types of “building-bridge integrated” railway bridge station structures are shown in Figure 3 and Figure 4.
3.3. Establishment and Solution of the Coupled Vibration Equations for the Train-Track-Station System
This paper employs the method proposed by Zeng Qingyuan in Section 3.2 to establish the coupled vibration equations of the vehicle-track-station system. The process of establishing the equations is as follows:
- (1)
- The total potential energy of the spatial vibration of the vehicle-track-station system is obtained by calculating and summing the spatial vibration potential energies of the track-station and the train at a certain moment. The calculation formula is shown in Equation (6):
- (2)
- By applying the principle of constant total potential energy of elastic system dynamics, the variation of the total potential energy is set to zero, as shown in Equation (7):
- (3)
- The track irregularity is regarded as a self-excitation source. Based on the total potential energy variation equation and using the “position-matching” rule for forming matrices, the mass matrix , damping matrix , stiffness matrix , and load vector of the system at any time t are calculated. The vibration equation of the coupled vehicle-track-station system is established, as shown in Equation (8):
For the solution of linear structural vibration equations, the modal superposition method is generally adopted. On the one hand, the calculation process is relatively simple, and on the other hand, it allows for selective computation of any order of modes as needed. The train-track-station system investigated in this paper is a highly complex time-variant system. Although the vibration equations formed by the system are linear, the linear vibration equations formed are variable-coefficient equations due to the changes in spring and damping characteristics throughout the process. Therefore, the modal superposition method cannot be used. A more suitable approach is the step-by-step integration method. This method discretizes the entire time span during which the train passes through the system into numerous small time increments , assuming that the system properties remain constant within each time increment. The dynamic response of the system at the end of one time increment is then used as the initial condition for solving the response in the subsequent time increment. This process is iterated until the dynamic response of the system over the entire time history is obtained. The method implemented in this paper is an efficient, unique, and highly accurate explicit-explicit hybrid integration method: the diagonal elements of the system’s dynamic matrices are integrated using an implicit integration format with interpolated linear acceleration, while the off-diagonal elements are integrated explicitly using extrapolated linear acceleration. The combined solution of these two approaches enhances both the integration accuracy and computational efficiency.
4. Analysis of Dynamic Responses of Station Structures Under Various Working Conditions and Calculation Results of Dynamic Characteristics of the Model
4.1. Dynamic Characteristic Analysis of Station Structures
Based on the finite element analysis model of the track-station structure established earlier, modal analysis was performed on the two types of “building-bridge integrated” railway bridge station structures. The first 100 vibration modes were obtained for both types of structures. The first 10 natural frequencies of lateral bending, vertical bending, and longitudinal translation for both structures are presented in Table 6. The vibration mode shapes of the first-order lateral bending, vertical bending, and longitudinal drift for the two types of structural configurations are shown in Figure 5, Figure 6 and Figure 7.

Table 6.
The natural frequencies of the two types of “building-bridge integrated” station models.

Figure 5.
First-Order Lateral Bending Mode Shape Diagram of the Station (Side View). (a) Station Type A; (b) Station Type B.

Figure 6.
First-Order Vertical Bending Mode Shape Diagram of the Station (Front View). (a) Station Type A; (b) Station Type B.

Figure 7.
First-Order Longitudinal Drift Mode Shape Diagram of the Station (Front View). (a) Station Type A; (b) Station Type B.
According to Table 6, the first-order lateral translational and vertical natural frequencies of the Station Type A are lower than those of the Station Type B. The difference in the first-order longitudinal translational natural frequency between the two structures is very small. This indicates that the introduction of a separation joint in the mainline has led to an overall increase in the flexibility of the station structure.
4.2. Dynamic Response Results and Analysis of the Station Under Various Working Conditions
Based on the previous discussions, a coupled vibration analysis of the vehicle-track-station system was conducted. A CRH3 train formation consisting of 16 cars in a 4* (powered + trailer + trailer + powered) configuration was selected, and the German Low Interference Spectrum was used to simulate additional track irregularities during train operation. To investigate the dynamic response of the “building-bridge integrated” railway bridge station structure with and without the mainline separation joint, as well as the safety and comfort of the train, various track occupancy scenarios were considered: single line (3#), double lines (3#, 4#), triple lines (2#, 3#, 4#), quadruple lines (2#, 3#, 4#, 5#), quintuple lines (1#, 2#, 3#, 4#, 5#), and sextuple lines (1#, 2#, 3#, 4#, 5#, 6#). The dynamic responses of the structure induced by fully loaded trains running on the mainline at speeds of 200~350 km/h and on the arrival-departure lines at 80 km/h were calculated. The maximum dynamic responses of the rail bearing floor slab, platform slab, and train are presented in Table 7, Table 8 and Table 9. All vibration responses of the structures described below are measured relative to the initial equilibrium position.

Table 7.
Maximum Dynamic Response Results of the Rail Bearing Floor Slab.

Table 8.
Maximum Dynamic Response Results of the Platform Slab.

Table 9.
Maximum Dynamic Response Results of Train.
Table 7 summarizes the maximum dynamic responses of the rail bearing floor slab, for the two types of “building-bridge integrated” station structures under various operating conditions, including trains running on the mainline at speeds of 200~350 km/h and on the arrival/departure lines at 80 km/h. It can be observed that when a separation joint is introduced in the mainline, the direct connection between the mainline and the arrival/departure lines is severed. Since the interaction with the soil is not considered in this study, the maximum dynamic responses of the rail bearing floor slab, for the Station Type A, are identical for the double-line condition and the multi-line conditions (triple to sextuple lines). From Table 8, the maximum lateral accelerations for the rail bearing floor slabs of the Station Type A and Station Type B are 0.372 m/s2 and 0.312 m/s2, respectively. The maximum vertical accelerations are 1.593 m/s2 and 1.516 m/s2, respectively. These values meet the requirements of the Design Code for Railway Bridges and Culverts [26], which stipulates that the lateral and vertical vibration accelerations for ballastless track bridge decks should be less than 1.5 m/s2 and 5 m/s2, respectively.
Table 8 provides the maximum dynamic response values of the platform slab for the two types of station structures under various operating conditions. For the Station Type A, the dynamic response values for the single-line and double-line conditions are zero. This is because the separation joint in the mainline cuts off the direct connection between the mainline rail bearing floor slab and the platform slab. Therefore, the dynamic response of the platform slab in this station is only caused by the arrival/departure lines (1#, 2#, 5#, 6#).
Table 9 provides a summary of the maximum dynamic response values of trains under various operating conditions for the two types of “building-bridge integrated” structures. It can be observed that the lateral and vertical accelerations, derailment coefficients, and wheel load reduction rates of the trains all meet the limit values specified by the relevant standards, and the comfort indices in both lateral and vertical directions reach the “excellent” level.
To more intuitively illustrate the response time histories of trains passing through the two types of station structures, acceleration time-history diagrams are plotted for trains (taking the six-line condition with mainline speed at 200 km/h and arrival-departure line speed at 80 km/h as examples) as shown in Figure 8. It can be observed that under the same operating conditions, the acceleration time-history curves of the trains with the two different structural configurations are essentially consistent.
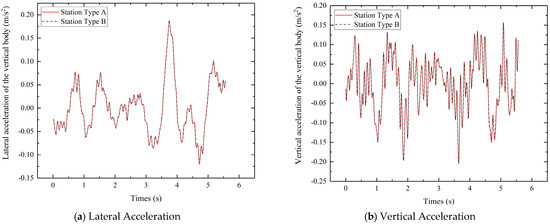
Figure 8.
Acceleration Time-History Diagram of the Train’s Leading Vehicle (v = 200 km/h).
In conclusion, when trains operate at speeds of 200~350 km/h on the mainline and 80 km/h on the arrival-departure lines, the dynamic responses of both the train and the rail bearing floor slab for the two types of “building-bridge integrated” structures—whether with or without a separation joint in the mainline—meet the regulatory limit values. The comfort indices of the trains reach the “excellent” standard, satisfying the requirements for safe and comfortable train operation. Therefore, both types of “building-bridge integrated” stations exhibit good dynamic performance.
5. The Impact of Mainline Structural Joint on the Dynamic Response of Station Structures
To better compare the impact of setting versus not setting a mainline structural joint on the dynamic response of station structures, a six-line condition (1#, 2#, 3#, 4#, 5#, 6#) with trains operating at speeds of 200~350 km/h on the mainline and 80 km/h on the arrival-departure lines is selected as an example. The maximum values of train response, rail bearing floor slab, response, and platform slab response under train action are compared and analyzed for the two types of “building-bridge integrated” station structures.
5.1. Comparison and Analysis of Train Response
To facilitate a more intuitive comparative analysis, the dynamic response of the train for the two types of “building-bridge” station structures is plotted as curves, as shown in the figure below.
As shown in Figure 9, the train’s dynamic response is nearly identical when passing through both types of “building-bridge integrated” station structures. Both lateral and vertical accelerations generally increase as speed increases. Regarding the Sperling comfort index, both the arrival-departure line “building-bridge integrated” station and the mainline “building-bridge integrated” station meet the excellent standard.
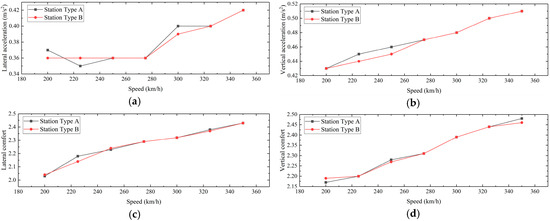
Figure 9.
Comparison of Train Dynamic Response. (a) Comparison of Train Lateral Acceleration; (b) Comparison of Train Vertical Acceleration; (c) Comparison of Train Lateral Comfort; (d) Comparison of Train Vertical Comfort.
5.2. Comparison and Analysis of the Rail Bearing Floor Slab Response
To provide a more intuitive comparison and analysis, the dynamic responses of the rail bearing floor slab for the two types of “building-bridge integrated” station structures are plotted as curves, as shown in the figure below.
As shown in Figure 10, the lateral and vertical displacements and accelerations of the rail bearing floor slab, in the Station Type A with a mainline structural joint, are greater than those in the Station Type B without such a joint. This is because the introduction of the mainline structural joint weakens the overall connectivity of the rail bearing floor slab structure, reducing both the lateral and vertical stiffness. As a result, the dynamic response of the rail bearing floor slab, in the Station Type A with a mainline structural joint, is larger.
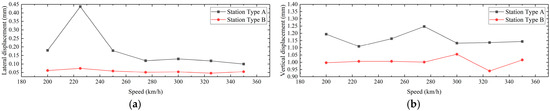
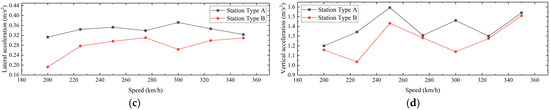
Figure 10.
Comparison Diagram of Dynamic Response of the Rail Bearing Floor Slab. (a) Comparison of Lateral Displacement; (b) Comparison of Vertical Displacement; (c) Comparison of Lateral Acceleration; (d) Comparison of Vertical Acceleration.
5.3. Comparison and Analysis of the Platform Slab Response
To facilitate a more intuitive comparison and analysis, the dynamic responses of the platform slab for the two types of “building-bridge integrated” station structures are plotted as curves, as shown in the figure below.
As shown in Figure 11, the lateral displacement of the platform floor in the Station Type B without a mainline structural joint is very close to that of the arrival-departure line “building-bridge integrated” station with a structural joint. The vertical displacement is slightly larger than that of the Station Type A. However, the lateral and vertical accelerations of the platform slab in the Station Type B are significantly greater than those in the Station Type A. This is attributed to the fact that the structural joints in the mainline severs the direct connection between the mainline rail bearing floor slab and the platform slab. As a result, the acceleration response transmitted to the platform slab during high-speed operation on the mainline is significantly reduced. Therefore, for station platforms with the “building-bridge integrated” configuration on arrival and departure tracks, the acceleration response of the platform slab is smaller.
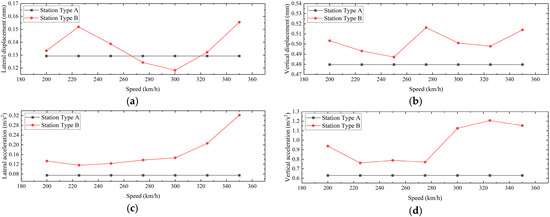
Figure 11.
Comparison Diagram of Dynamic Response of the Platform slab (a) Comparison of Lateral Displacement; (b) Comparison of Vertical Displacement; (c) Comparison of Lateral Acceleration; (d) Comparison of Vertical Acceleration.
6. Conclusions
This paper investigates the effect of introducing a mainline structural joint on the dynamic performance of “building-bridge integrated” railway bridge-type stations, where the mainline speeds exceed 160 km/h. A railway bridge-type station with two platforms and six tracks was selected for the study. Two types of “building-bridge integrated” structures were considered: one with a mainline structural joint (arrival-departure line “building-bridge integrated”) and one without (mainline “building-bridge integrated”). The spatially coupled vibration equations and analysis models for the train-track-station system were established, based on the elastic system dynamics principle of total potential energy conservation and the “set-in-right-position” rule for formulating matrices. The following conclusions were drawn:
- (1)
- When trains pass through the station structure at speeds of 200~350 km/h on the mainline and 80 km/h on the arrival-departure lines, the lateral and vertical accelerations of the rail bearing floor slab, for both the arrival/departure line “building-bridge integrated” and the mainline “building-bridge integrated” structures, remain within the permissible limits. Additionally, the lateral and vertical accelerations of the train, derailment coefficient, and wheel load reduction rate all satisfy the regulatory requirements. The comfort indices of the train comply with the current standards, indicating that both structures exhibit satisfactory dynamic performance.
- (2)
- When trains pass through the station structure, the presence or absence of a mainline structural joint has a minimal impact on the dynamic response of trains for the “building-bridge integrated” station structure. For both the arrival-departure line “building-bridge integrated” and the mainline “building-bridge integrated” structures, the lateral and vertical accelerations of the train generally increase with speed. Under the same working conditions, the acceleration time-history curves of the trains with the two different structural configurations are essentially consistent.
- (3)
- The discontinuity in the mainline structure reduces the overall stiffness of the rail bearing floor slab and isolates the train-induced responses transmitted to the platform slab during high-speed operation on the mainline. Therefore, under train loading, the arrival and departure track “building-bridge-integrated” structure with a mainline discontinuity exhibits smaller acceleration responses in the platform slab compared to the mainline “building-bridge integrated” structure without a discontinuity. However, the rail bearing floor slab in the structure with a discontinuity shows larger acceleration and displacement responses. Additionally, the implementation of structural joints often leads to issues such as water leakage and seepage. Thus, for such station structures, it may be considered not to set mainline structural joints.
Author Contributions
Conceptualization, X.G.; Methodology, Y.L.; Software, X.G. and Y.L.; Validation, X.G. and Y.L.; Formal analysis, J.L.; Investigation, Y.L.; Data curation, X.G. and Y.L.; Writing—original draft preparation, X.G. and Y.L.; Writing—review and editing, Y.L.; Visualization, Y.L.; Supervision, J.L.; Funding acquisition, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data included in this study are available upon request by contact with the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, S.T. Research for Space Pattern in Area of High-Speed Railway Station. Ph.D. Thesis, Tianjin University, Tianjin, China, 2010. [Google Scholar]
- Chen, C.L.; Wei, B. High-speed rail and urban transformation in China: The case of Hangzhou East Rail Station. Built Environ. 2013, 39, 385–398. [Google Scholar] [CrossRef]
- Shan, J.; Wu, Y.; Yang, X. Three-dimensional stability of two-step slope with crack considering temperature effect on unsaturated soil. J. Cent. South Univ. 2025, 32, 1–19. [Google Scholar] [CrossRef]
- Feldmann, M.; Heinemeyer, C.; Kühn, B.; Sedlacek, G. Prediction of the dynamic behavior of bridges and roof of the railway main station Berlin. ZEV Rail Glas. Ann. 2006, 130, 314–326. [Google Scholar]
- Deng, Z.M. Structural Vibration Analysis and Vibration Control Study on The New Changsha Railway Station. Ph.D. Thesis, Central South University, Changsha, China, 2010. [Google Scholar]
- Zhu, Z.; Davidson, M.T.; Harik, I.E.; Yu, Z. Train-induced vibration characteristics of an integrated high-speed railway station. J. Perform. Constr. Facil. 2017, 31, 04017010. [Google Scholar] [CrossRef]
- He, S.S. Research on Vehicle-Induced Vibration Response of High-Speed Railway Passenger Station. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2015. [Google Scholar]
- Fang, L.M.; Zhu, Z.H.; Wang, L.D.; Yu, Z. Analysis of train induced random vibration of high-speed railway station with integral station-bridge structure. J. China Railw. Soc. 2017, 39, 117–125. [Google Scholar]
- Fedorova, M.; Sivaselvan, M.V. An algorithm for dynamic vehicle-track-structure interaction analysis for high-speed trains. Eng. Struct. 2017, 148, 857–877. [Google Scholar] [CrossRef]
- Kim, M.; Choi, S. Vibration control of a railroad station using a multiple tuned mass damper technique. J. Korean Soc. Hazard Mitig. 2019, 20, 37–43. [Google Scholar] [CrossRef]
- Yoo, Y.; Kwon, S.J.; Choi, S. Development of vibration mitigation method for a railway station using a tunedmass-dampered platform. J. Korean Soc. Hazard Mitig. 2016, 16, 77–82. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, L.; Zhao, Y.; Zhou, X.; Li, X. A frequency domain model for analysing vibrations in large-scale integrated building–bridge structures induced by running trains. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 226–241. [Google Scholar] [CrossRef]
- Ran, W.; Li, Z.; Li, X.; Yi, B.; Zhang, X. Frequency-domain analysis method for vibration responses of a high-speed railway station structure under train load excitation. Vib. Shock 2018, 37, 218–224. [Google Scholar]
- Guo, X.; Wang, S. Research on the Dynamic Response of the Multi-Line Elevated Station with “Integral Station-Bridge System”. Buildings 2024, 14, 758. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.N.; Zhi, G.L.; Hu, W.L.; Guo, T.; Wang, S.L. Study on vehicle-induced vibration characteristics of high-speed railway bridge station structure. Earthq. Eng. Eng. Vib. 2023, 43, 222–231. [Google Scholar]
- Xu, W. Analysis of Vehicle-Induced Dynamic Effect of Long-Span Station Structure with Station-Bridge Integration. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2010. [Google Scholar]
- Xie, W.P.; Yang, Y.Z.; Li, W. Research on vibration and structural noise measurement of subway elevated station combi-nation of bridge and construction. J. Railw. Sci. Eng. 2021, 18, 1837–1845. [Google Scholar]
- Yang, N.; Guo, T.; Sun, G. Train-induced vibration on elevated railway station. J. Cent. South Univ. 2013, 20, 3745–3753. [Google Scholar] [CrossRef]
- Guo, T.; Zhi, G.; Zhu, R.; Zhang, L. Train-Induced Vibration Characteristics of a Double-Story High-Speed Railway Station. J. Perform. Constr. Facil. 2024, 38, 04024008. [Google Scholar] [CrossRef]
- Ba, Z.; Jiao, P.; Liang, J.; Liu, G.; Gao, Y. Actual measurement and analysis of station vibration induced by high-speed train. J. Tianjin Univ. 2020, 53, 1211–1217. [Google Scholar]
- TB 10100-2018; Code for Design of Railway Passenger Station. China Railway Publishing House: Beijing, China, 2018.
- Zeng, Q.Y.; Guo, X.R. Theory and Application of Vibration Analysis of Time-Varying Systems on Train Bridges; China Railway Publishing House: Beijing, China, 1999. [Google Scholar]
- Zeng, Q. The principle of total potential energy with stationary value in elastic system dynamics. J. Huazhong Univ. Sci. Technol. 2000, 28, 1–3+14. [Google Scholar]
- Zeng, Q.Y.; Yan, G.P. The “set-in-right-position” rule forming structural method for space analysis of truss bridges. J. China Railw. Soc. 1986, 8, 48–59. [Google Scholar]
- Guo, X.; Liu, J.; Wu, Y.; Jiang, Y. Research on the influencing parameters of the dynamic responses of the elevated station with “integral station-bridge system”. J. Railw. Sci. Eng. 2023, 20, 671–681. [Google Scholar]
- TB 10002-2017; Code for Design on Railway Bridge and Culvert. China Railway Publishing House: Beijing, China, 2017.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).