Research Advances in Large Deformation Analysis and Applications of the Material Point Method
Abstract
1. Introduction
2. Methodology of the MPM
2.1. Governing Equations
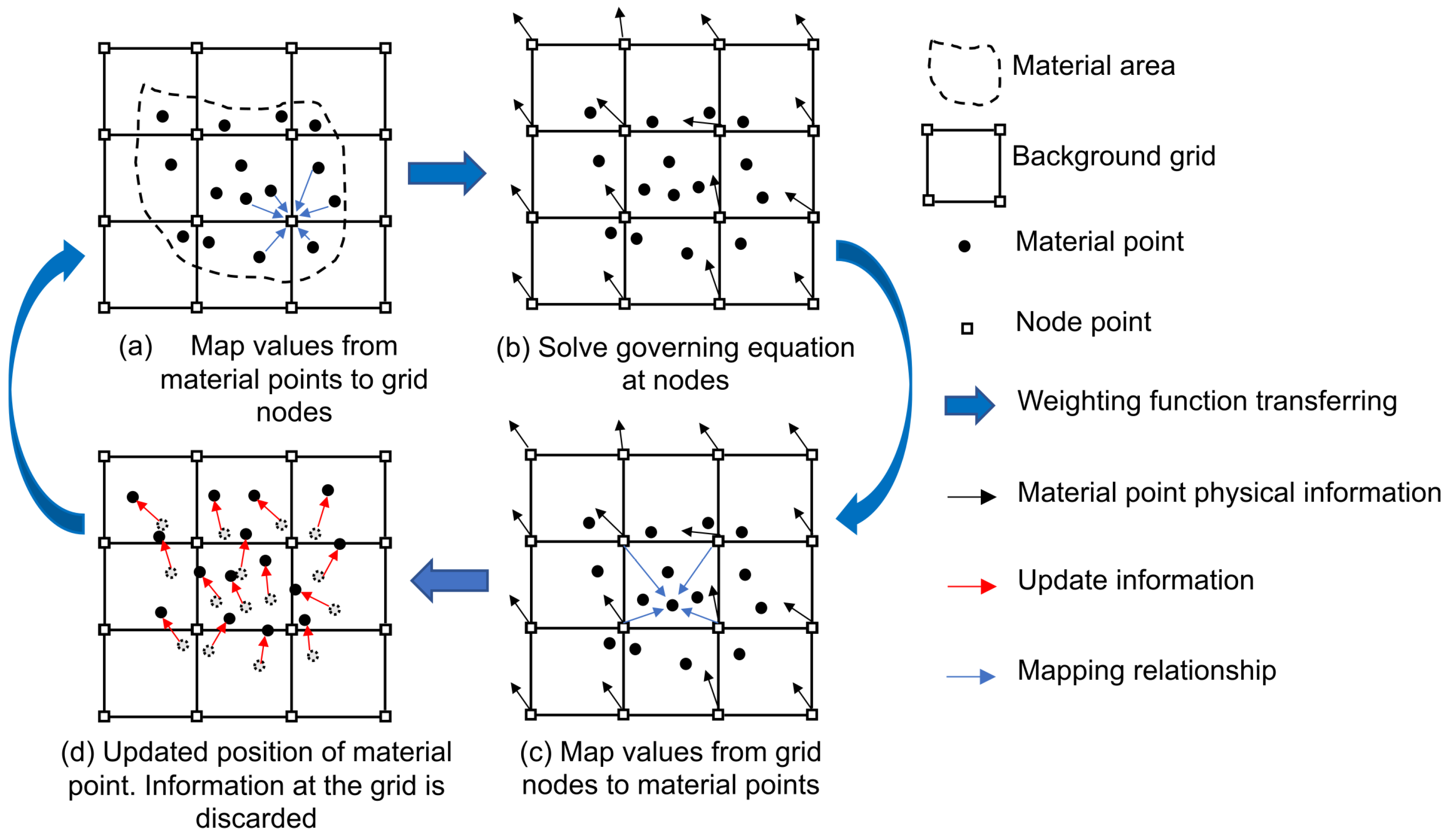
2.2. Discretization of the Governing Equations
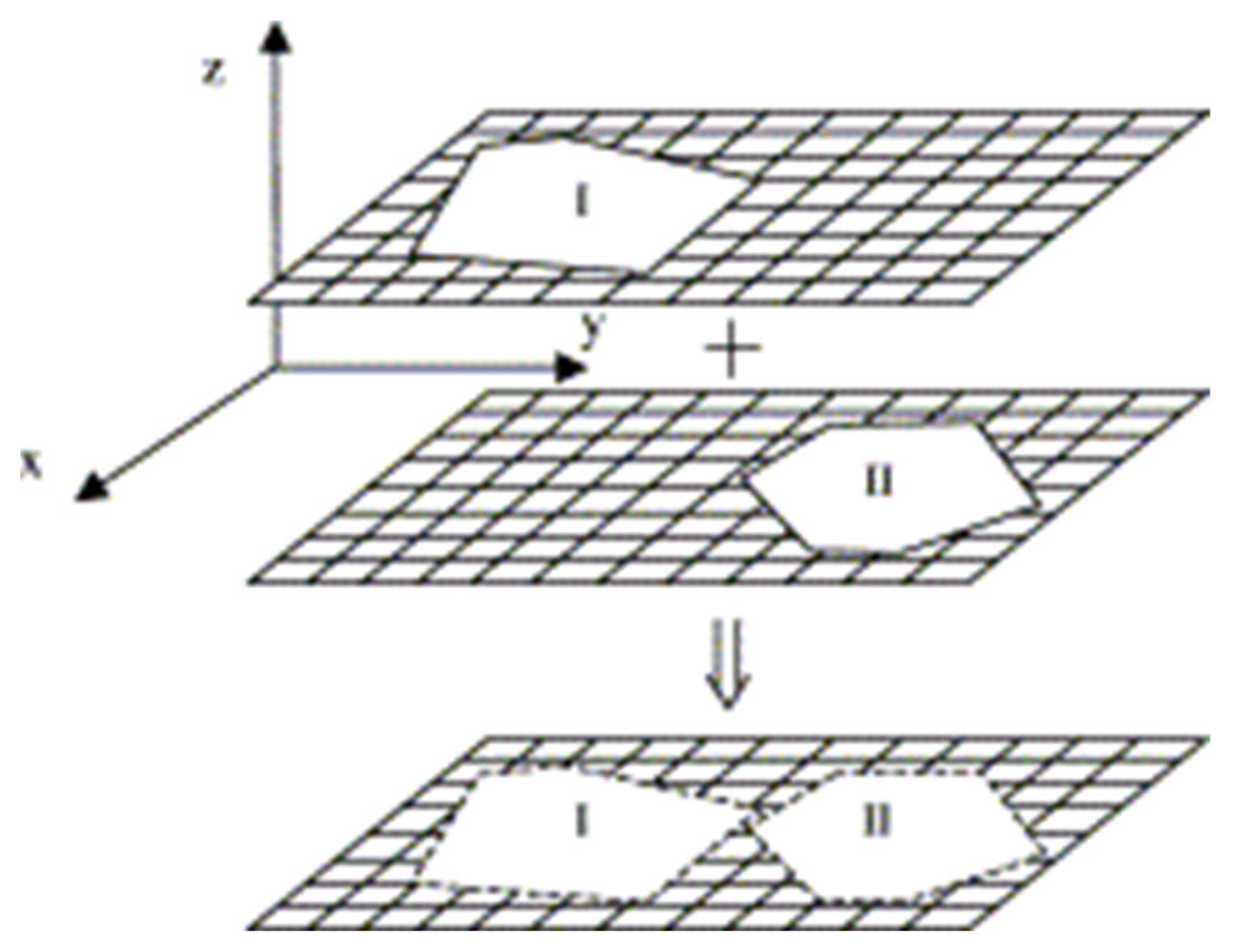
2.3. MPM Contact Model

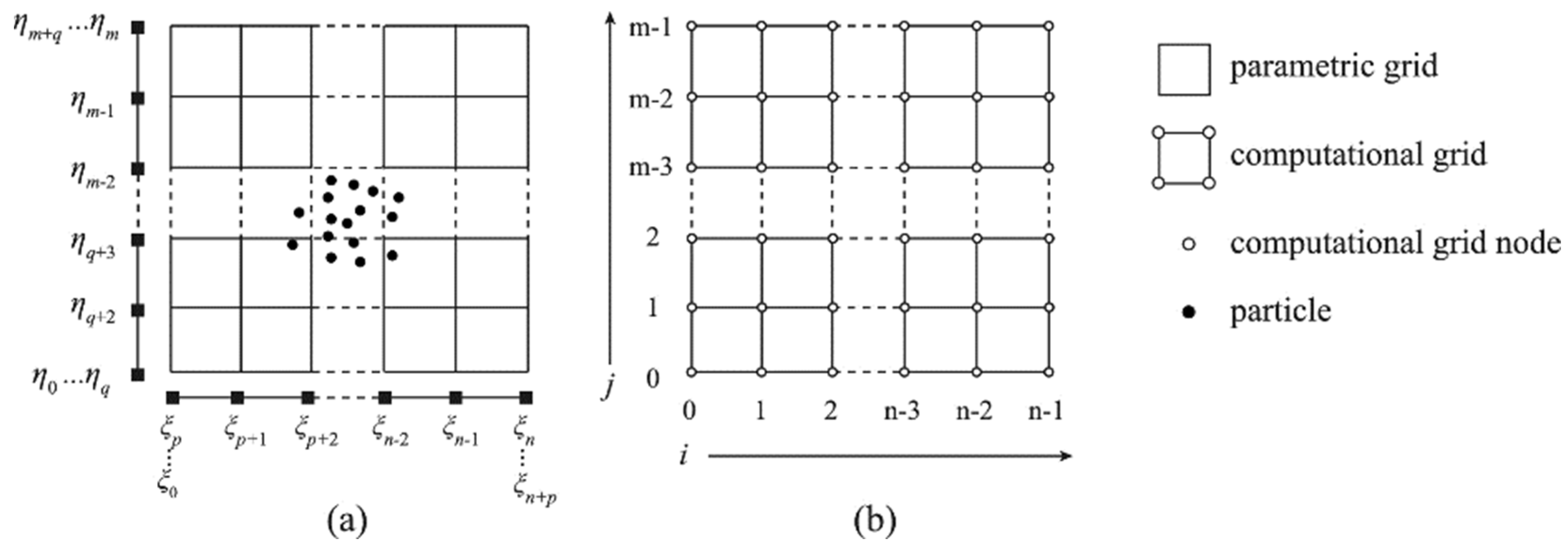
2.4. Relationship with Meshless Method
3. Application in High-Speed Impact
4. Application in Explosion
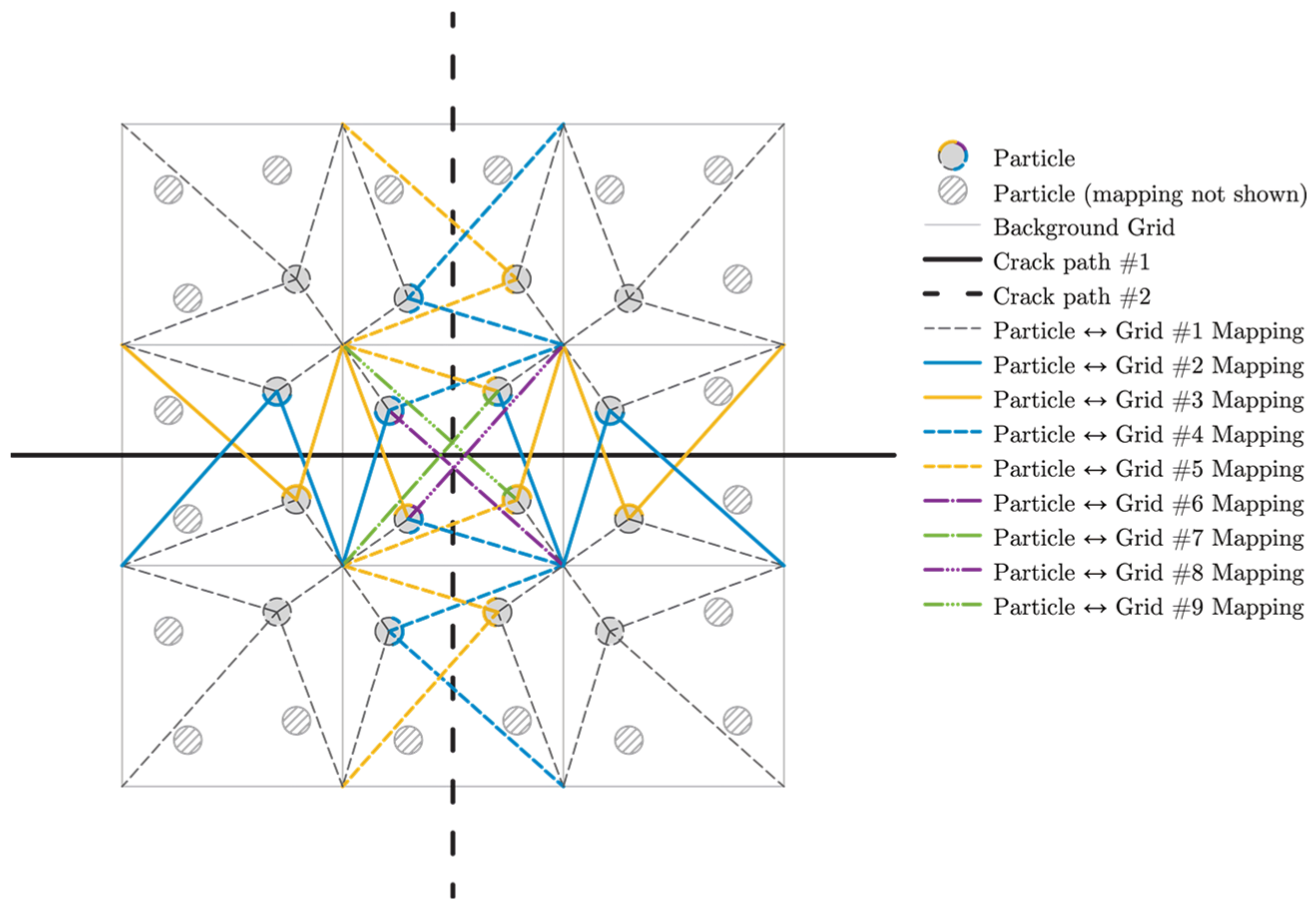
5. Application in Dynamic Cracking
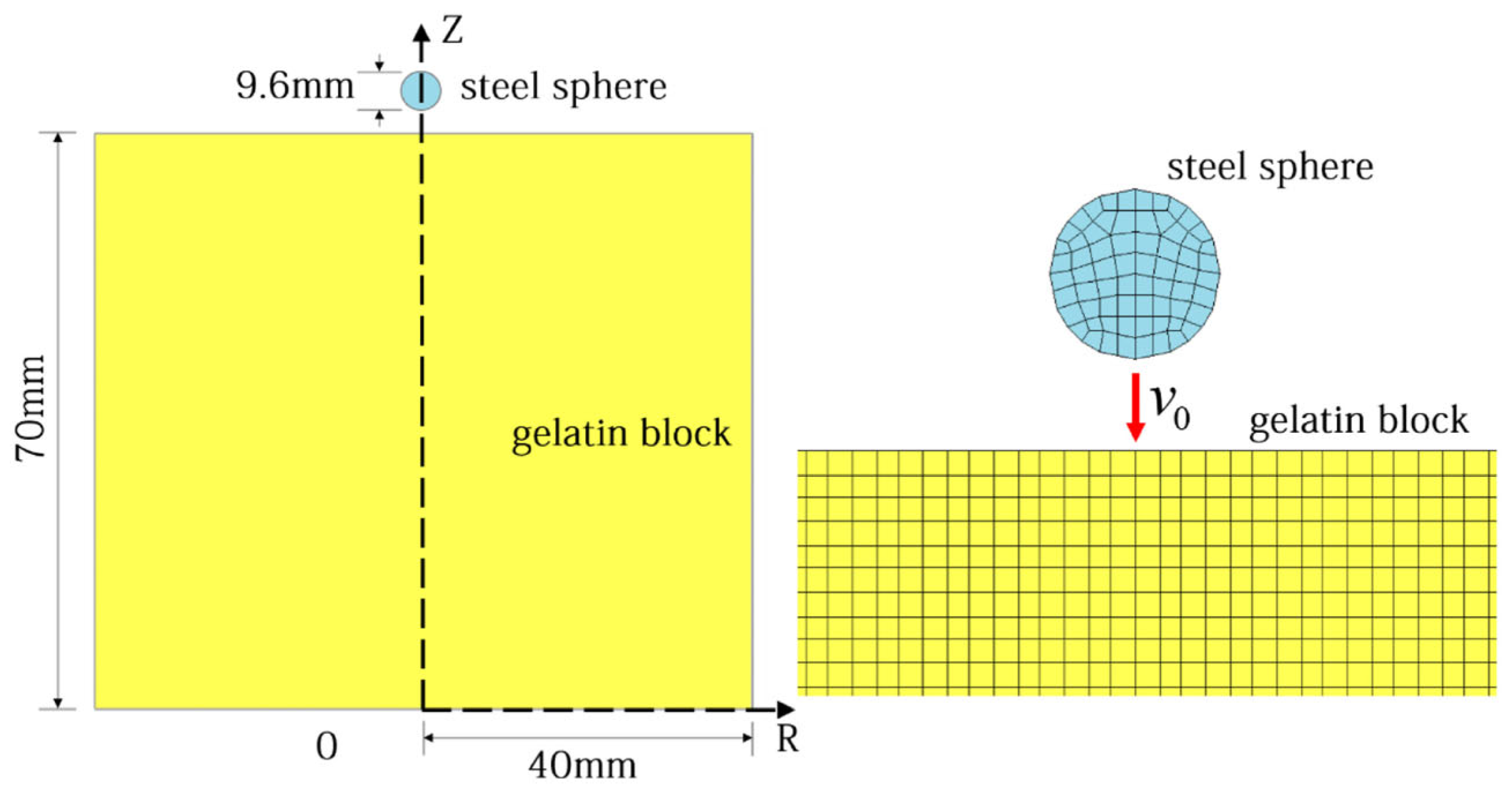
6. Application in Impact Penetration
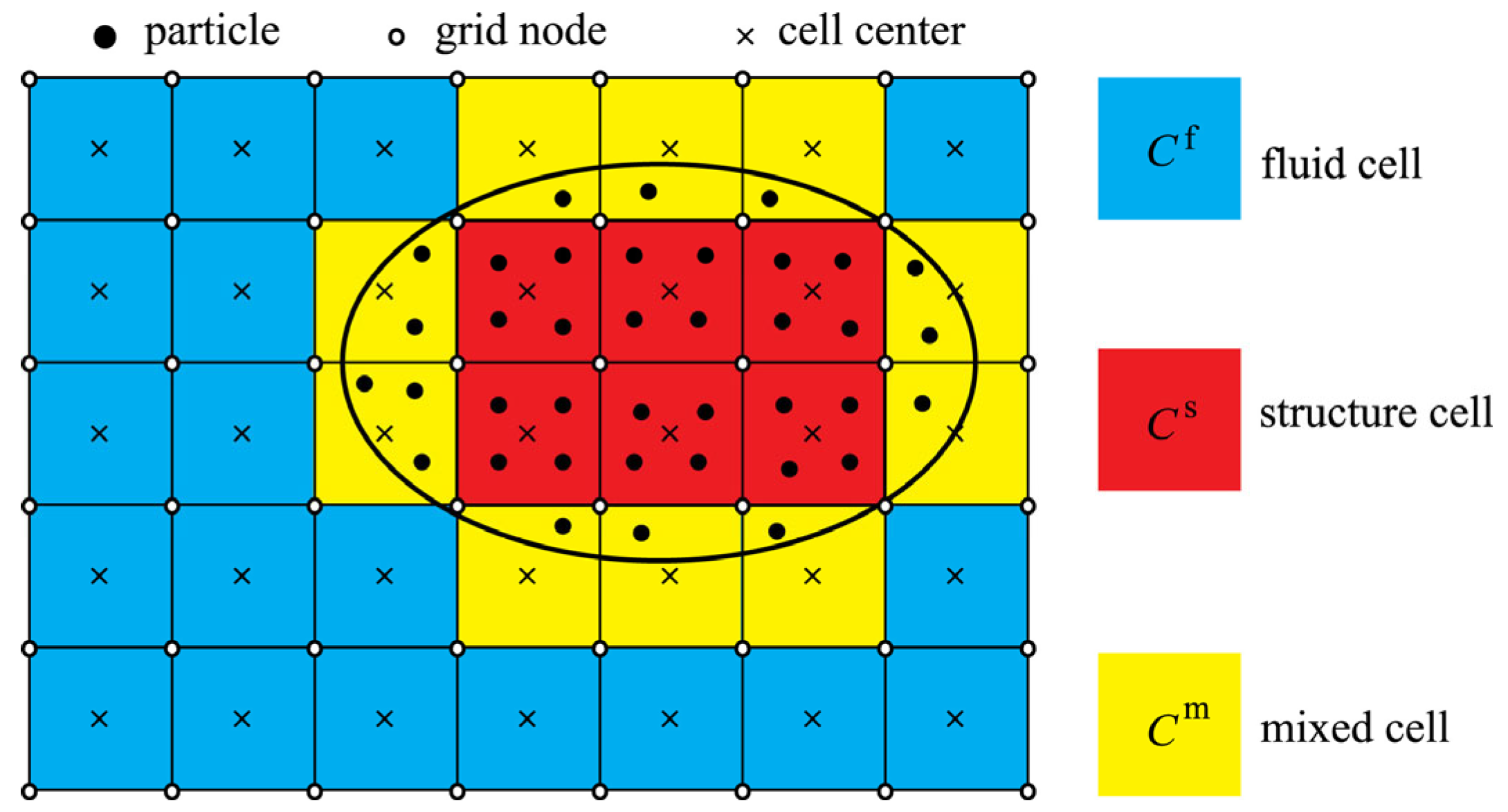
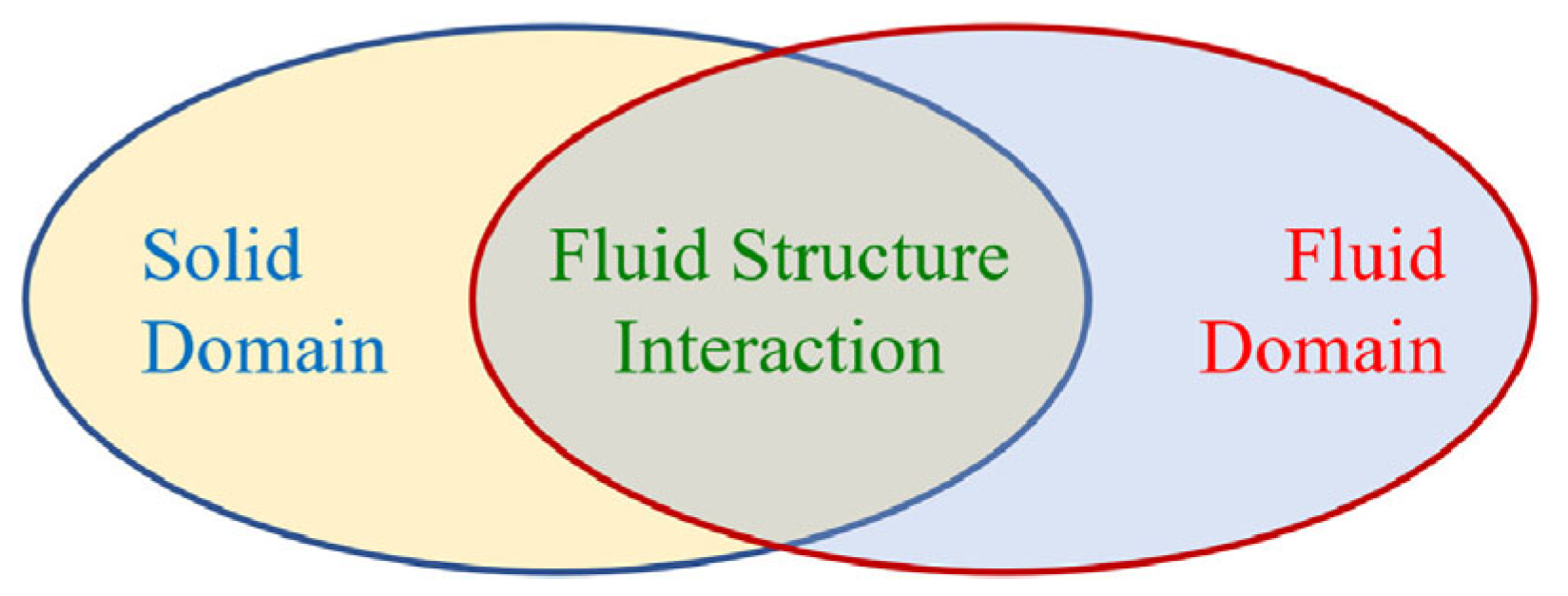
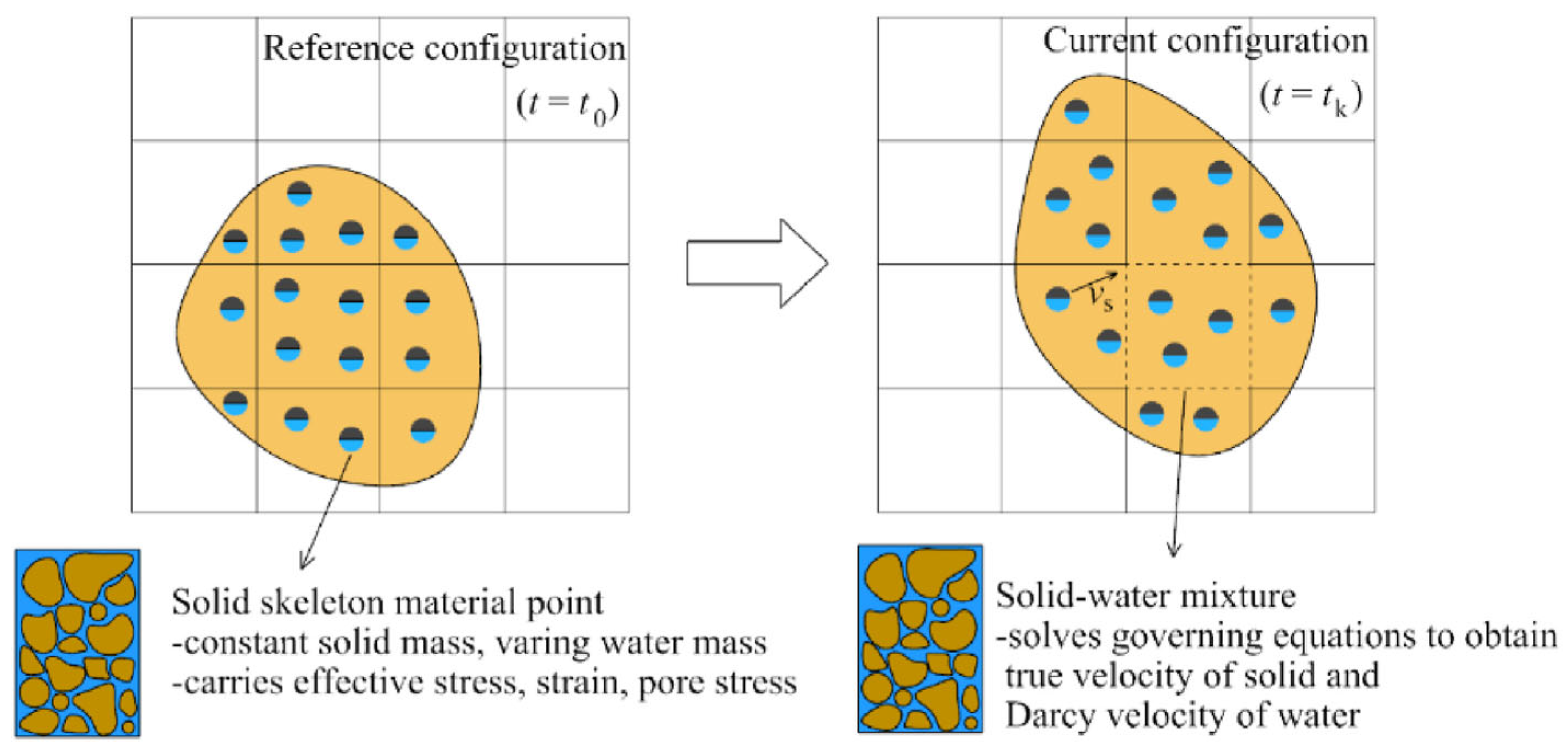
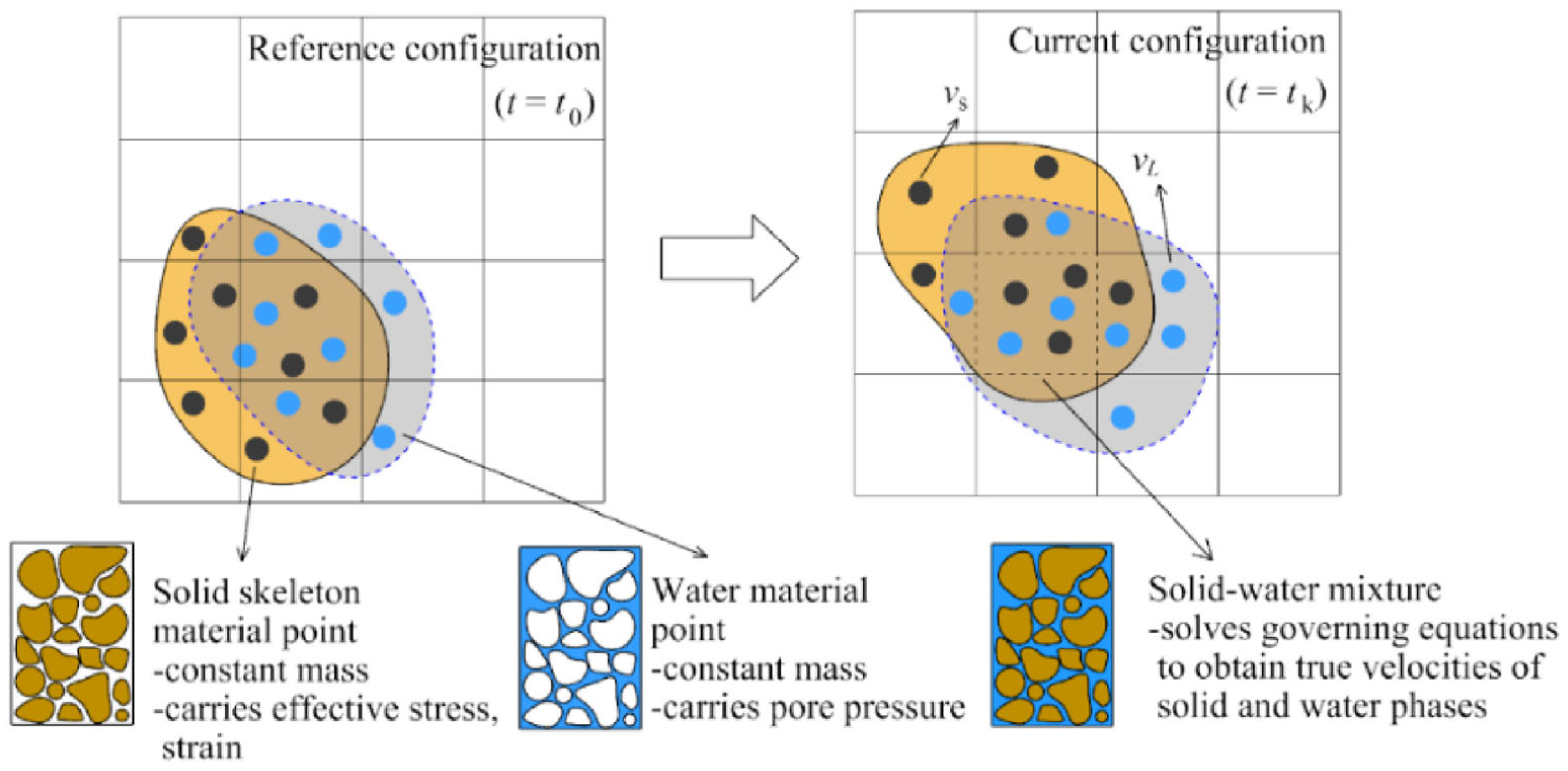
7. Application in Fluid–Structure Interaction
8. Conclusions and Outlook
- (1)
- Enhancing the computational efficiency of the MPM. Current developments in the MPM are primarily based on explicit time integration; although implicit integration schemes can improve the computational efficiency of the MPM in large deformation analysis, the computational cost can significantly increase when dealing with large-scale physical problems. Therefore, future research could focus on optimizing the distribution and quantity of material points, developing a three-dimensional MPM computational architecture with GPU parallel acceleration, and exploring intelligent MPM computation methods combined with neural networks.
- (2)
- Addressing the grid dependency of the MPM. Similarly to the FEM, the simulation results of the MPM are highly dependent on the background grid used, and in cases where strain localization phenomena are significant, pathological grid dependency may occur. Therefore, generating an appropriate grid is a time-consuming and challenging task, especially when dealing with problems of complex shapes and moving boundaries. It is recommended to introduce non-local grid regularization methods, dynamic grid methods, and overlapping grid methods to obtain objective and stable MPM solutions.
- (3)
- Refining boundary detection algorithms. In MPM computations, even when using a fixed background grid, grid nodes may not coincide perfectly with domain boundaries, which can lead to inaccurate boundary representation. Thus, the use of machine learning-assisted detection can be considered, such as employing CNNs to identify boundary features.
- (4)
- Expanding the MPM’s multi-field coupling capabilities. While enhancing MPM’s mechanical computation capabilities, it is essential to further expand the application scope of this method in multi-physical field problems, leveraging the MPM’s advantages in solving other physical fields such as heat transfer and electromagnetism. This will significantly promote the resolution of the complex engineering computation problems currently being faced.
- (5)
- In the field of fluid dynamics, there is a need to develop an efficient MPM coupling algorithm that can accurately solve problems involving highly compressible fluids, as well as to develop an MPM model capable of simulating high-viscosity non-Newtonian fluids.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MPM | Material Point Method |
| FDM | Finite Difference Method |
| FEM | Finite Element Method |
| SPH | Smoothed-Particle Hydrodynamics |
| PIC | Particle-in-Cell |
| FLIP | Fluid Implicit Particle |
| GIMP | Generalized Interpolation Material Point Method |
| MD | Molecular Dynamics |
| EOS | Equation of State |
| FSI | Fluid–Structure Interaction |
| CFDMP | Coupled Finite Difference Material Point Method |
| CDEM | Continuum Discontinuous Element Method |
| CRAMP | MPM with explicit cracks |
| PD | Peridynamics |
| IBM | Immersed Boundary Method |
| MMALE | Multi-Material ALE |
| PF-FEMPM | explicit finite element material point coupled with phase-field model |
| cBSMPM | B-spline MPM |
| CFEMP | Coupled Finite Element MPM |
| LBM | Lattice Boltzmann Method |
| LBMPM | Lattice Boltzmann-MPM |
References
- Liszka, T.; Orkisz, J. The finite difference method at arbitrary irregular grids and its application in applied mechanics. Comput. Struct. 1980, 11, 83–95. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite element method. In Wiley Encyclopedia of Computer Science and Engineering; Wiley Online Library: Hoboken, NJ, USA, 2007; pp. 1–12. [Google Scholar]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. In Handbook of Numerical Analysis; Elsevier B.V.: Amsterdam, The Netherlands, 2000; Volume 7, pp. 713–1018. [Google Scholar]
- Rizzo, F.J. An integral equation approach to boundary value problems of classical elastostatics. Q. Appl. Math. 1967, 25, 83–95. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Bićanić, N. Discrete element methods. In Encyclopedia of Computational Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Liu, J.; Kong, X.J. Development of three dimensional discontinuous deformation analyses. In Proceedings of the 6th International Conference on Analysis of Discontinuous Deformation, Trondheim, Norway, 5–8 October 2003; pp. 45–54. [Google Scholar]
- Ghasemi, M.; Falahatgar, S.; Mostofi, T. Mechanical and thermomechanical mesoscale analysis of multiple surface cracks in ceramic coatings based on the DEM-FEM coupling method. Int. J. Solids Struct. 2022, 236, 111336. [Google Scholar] [CrossRef]
- Zhou, C.; Zhong, Q.; Chen, M.; Wen, T.; Wu, X.; Meng, W.; Zhang, M. A continuous-discontinuous coupling computational method for multi-material mixtures. Int. J. Mech. Sci. 2024, 284, 109760. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Harlow, F.H. The particle-in-cell computing method for fluid dynamics. Methods Comput. Phys. 1964, 3, 319–343. [Google Scholar]
- Brackbill, J.U.; Ruppel, H.M. FLIP: A method for adaptively zoned, particle-in-cell calculations of fluid flows in two dimensions. J. Comput. Phys. 1986, 65, 314–343. [Google Scholar] [CrossRef]
- Sulsky, D.; Chen, Z.; Schreyer, H.L. A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
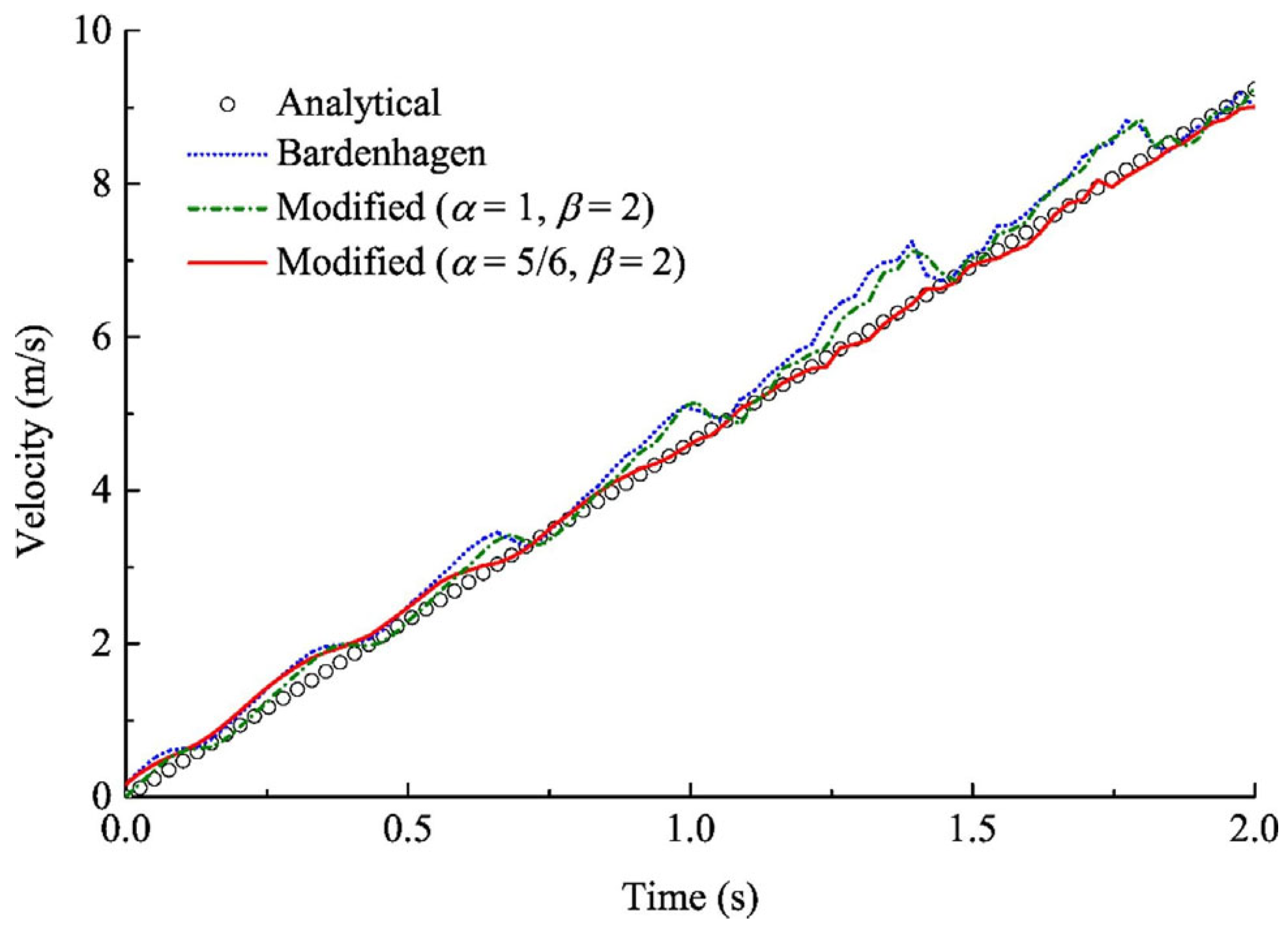
- Bardenhagen, S.; Brackbill, J.; Sulsky, D. The material-point method for granular materials. Comput. Methods Appl. Mech. Eng. 2000, 187, 529–541. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z. A multi-mesh MPM for simulating the meshing process of spur gears. Comput. Struct. 2003, 81, 1991–2002. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, X.; Ma, S.; Huang, X. Contact algorithms for the material point method in impact and penetration simulation. Int. J. Numer. Methods Eng. 2011, 85, 498–517. [Google Scholar] [CrossRef]
- Ma, J.; Wang, D.; Randolph, M.F. A new contact algorithm in the material point method for geotechnical simulations. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1197–1210. [Google Scholar] [CrossRef]
- Sang, Q.; Xiong, Y.; Zheng, R.; Bao, X.; Ye, G.; Zhang, F. A hybrid contact approach for modeling soil-structure interaction using the material point method. J. Rock Mech. Geotech. Eng. 2024, 16, 1864–1882. [Google Scholar] [CrossRef]
- Hammerquist, C.C.; Nairn, J.A. Modeling nanoindentation using the material point method. J. Mater. Res. 2018, 33, 1369–1381. [Google Scholar] [CrossRef]
- Gao, L.; Guo, N.; Yang, Z.; Jardine, R. MPM modeling of pile installation in sand: Contact improvement and quantitative analysis. Comput. Geotech. 2022, 151, 104943. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, S.; Zhao, J.; Zhou, X. DEM-enriched contact approach for material point method. Comput. Methods Appl. Mech. Eng. 2023, 404, 115814. [Google Scholar] [CrossRef]
- Nairn, J.A.; Hammerquist, C.C.; Smith, G.D. New material point method contact algorithms for improved accuracy, large-deformation problems, and proper null-space filtering. Comput. Methods Appl. Mech. Eng. 2020, 362, 112859. [Google Scholar] [CrossRef]
- Feng, R.; Fourtakas, G.; Rogers, B.D.; Lombardi, D. A general smoothed particle hydrodynamics (SPH) formulation for coupled liquid flow and solid deformation in porous media. Comput. Methods Appl. Mech. Eng. 2024, 419, 116581. [Google Scholar] [CrossRef]
- Dai, Z.; Lan, B.; Jiang, M.; Jiang, S. Numerical Modeling of Submarine Landslide Motion and Impact Behavior Based on the SPH Method. J. Ocean. Univ. China 2025, 24, 365–376. [Google Scholar] [CrossRef]
- Diao, Z.; Fang, D.; Xu, J. Numerical study of ice impacted by a vehicle launched underwater based on Smoothed Particle Hydrodynamics. Ships Offshore Struct. 2025, 1–21. [Google Scholar] [CrossRef]
- Liu, P.; Liu, Y.; Zhang, X.; Guan, Y. Investigation on high-velocity impact of micron particles using material point method. Int. J. Impact Eng. 2015, 75, 241–254. [Google Scholar] [CrossRef]
- Ye, Z.; Zhang, X.; Zheng, G.; Jia, G. A material point method model and ballistic limit equation for hyper velocity impact of multi-layer fabric coated aluminum plate. Int. J. Mech. Mater. Des. 2018, 14, 511–526. [Google Scholar] [CrossRef]
- Zhang, X.; Sze, K.Y.; Ma, S. An explicit material point finite element method for hyper-velocity impact. Int. J. Numer. Methods Eng. 2006, 66, 689–706. [Google Scholar] [CrossRef]
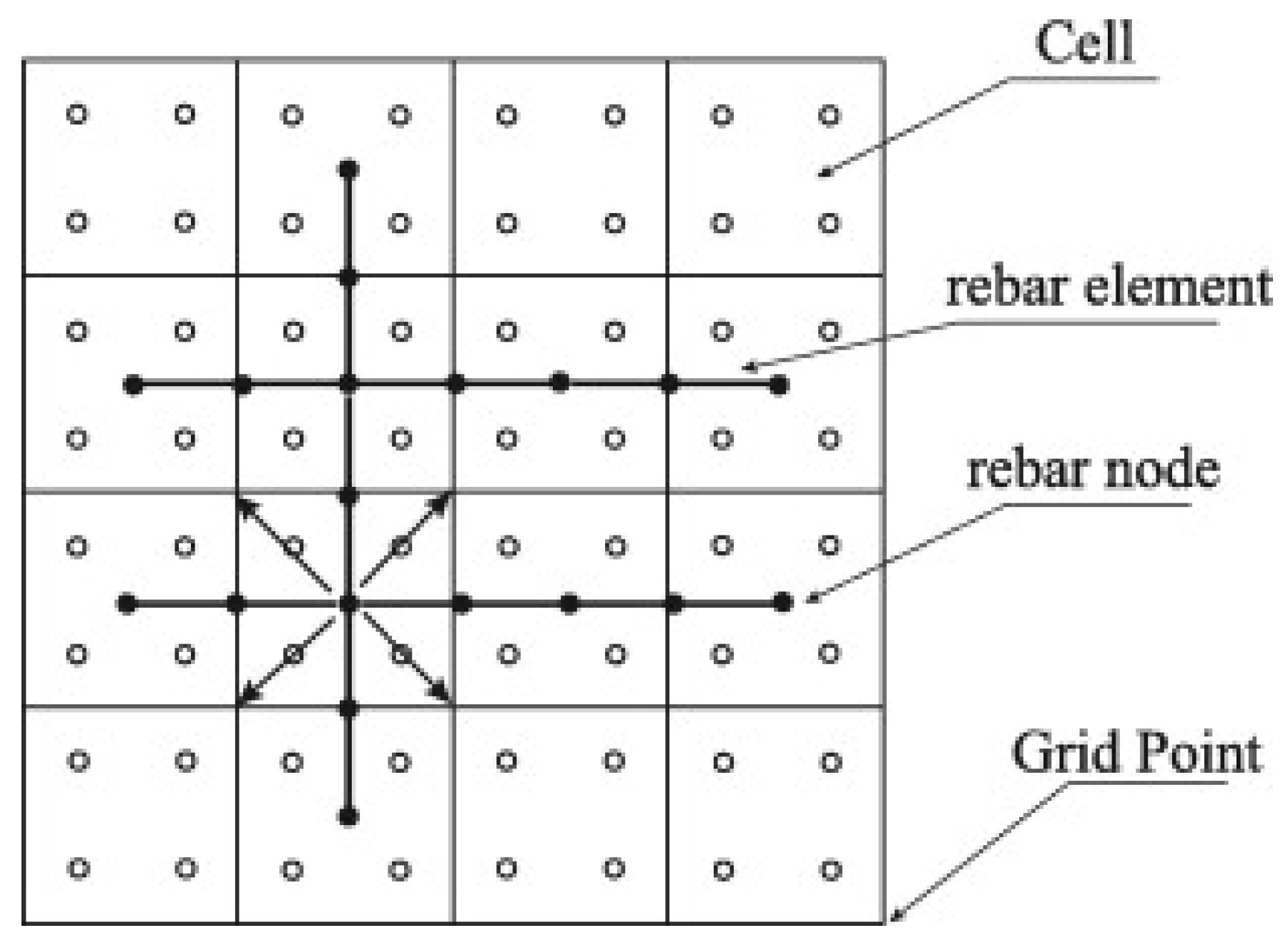
- Lian, Y.P.; Zhang, X.; Zhou, X.; Ma, Z.T. A FEMP method and its application in modeling dynamic response of reinforced concrete subjected to impact loading. Comput. Methods Appl. Mech. Eng. 2011, 200, 1659–1670. [Google Scholar] [CrossRef]
- Bardenhagen, S.G.; Kober, E.M. The generalized interpolation material point method. Comput. Model. Eng. Sci. 2004, 5, 477–496. [Google Scholar]
- Hu, Z.; Zhang, Z.; Zhou, X.; Cui, X.; Ye, H.; Zhang, H.; Zheng, Y. Explicit phase-field material point method with the convected particle domain interpolation for impact/contact fracture in elastoplastic geomaterials. Comput. Methods Appl. Mech. Eng. 2023, 405, 115851. [Google Scholar] [CrossRef]
- Jia, C.; Zhao, H.; Wan, H. A multi-scale model for use in hydrodynamic simulations of impacts and hypervelocity penetrations into porous silica aerogel. Mater. Today Commun. 2023, 37, 107374. [Google Scholar] [CrossRef]
- Kupchella, R.; Stowe, D.; Weiss, M.; Pan, H.; Cogar, J. SPH Modeling Improvements for Hypervelocity Impacts. In Proceedings of the 2015 Hypervelocity Impact Symposium (HVIS), Boulder, CO, USA, 26–30 April 2015; pp. 326–333. [Google Scholar]
- Liu, W.; Zhang, Q.; Long, R.; Gong, Z.; Wu, Q.; Ren, S.; Lu, Y.; Xu, J.; Zhong, X.; Ren, J. Ejecta velocity and motion model of spherical aluminum alloy projectile hypervelocity impact on basalt. Acta Astronaut. 2024, 224, 574–592. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Qiu, X.M. Comparison study of MPM and SPH in modeling hypervelocity impact problems. Int. J. Impact Eng. 2009, 36, 272–282. [Google Scholar] [CrossRef]
- Culp, D.B.; Ma, X. Modeling fragmentation within pagosa using particle methods. In Proceedings of the 2019 15th Hypervelocity Impact Symposium, Destin, FL, USA, 14–19 April 2019. [Google Scholar]
- Zhang, W.; Zhang, X.; He, L.; Li, P. The damage characteristics and formation mechanism of ultrahigh strength 7055 aluminum alloy under hypervelocity impact. Int. J. Impact Eng. 2023, 180, 104718. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, Z.; Yu, C.; Li, X.; Wang, X.; Yan, H. Numerical simulation of hypervelocity impact of the water-filled aluminum eggshell array structure using material point method. Phys. Fluids 2025, 37, 037104. [Google Scholar] [CrossRef]
- Romero, N.A.; Nakano, A.; Riley, K.M.; Shimojo, F.; Kalia, R.K.; Vashishta, P.; Messina, P.C. Quantum Molecular Dynamics in the Post-Petaflops Era. Computer 2015, 48, 33–41. [Google Scholar] [CrossRef]
- Su, Y.C.; Saffarini, M.H.; Sewell, T.; Chen, Z. Investigation of the Impact Response of Bi-Continuous Nanoporous Solids via the Material Point Method: Verification Against Molecular Dynamics Predictions. Int. J. Numer. Anal. Methods Geomech. 2025, 49, 1200–1215. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Z.; Liu, Y. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Liu, Y.; Wang, H.K.; Zhang, X. A multiscale framework for high-velocity impact process with combined material point method and molecular dynamics. Int. J. Mech. Mater. Des. 2013, 9, 127–139. [Google Scholar] [CrossRef]
- Kim, S.; Jang, Y.; Kim, Y.; Kim, B.-J.; Yun, G.J. Molecular dynamics-informed material point method for hypervelocity impact analysis. Int. J. Impact Eng. 2025, 195, 105124. [Google Scholar] [CrossRef]
- Erzincanli, B.; Eken, A.; Eken, S. Numerical Simulation of Hypervelocity Space Debris Impact. In Proceedings of the 10th International Conference on Recent Advances in Air and Space Technologies (RAST), Istanbul, Turkey, 7–9 June 2023. [Google Scholar]
- Hu, W.; Chen, Z. Model-based simulation of the synergistic effects of blast and fragmentation on a concrete wall using the MPM. Int. J. Impact Eng. 2006, 32, 2066–2096. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Lian, Y.; Zhou, X. Simulation of high explosive explosion using adaptive material point method. CMSE Comput. Model. Eng. Sci. 2009, 39, 101–123. [Google Scholar]
- Lian, Y.P.; Zhang, X.; Zhou, X.; Ma, S.; Zhao, Y.L. Numerical simulation of explosively driven metal by material point method. Int. J. Impact Eng. 2011, 38, 238–246. [Google Scholar] [CrossRef]
- Wang, Y.; Beom, H.G.; Sun, M.; Lin, S. Numerical simulation of explosive welding using the material point method. Int. J. Impact Eng. 2011, 38, 51–60. [Google Scholar] [CrossRef]
- Chen, W.D.; Yang, W.M.; Zhang, F. Numerical simulation of underwater explosion based on material point method. Key Eng. Mater. 2013, 525, 109–112. [Google Scholar] [CrossRef]
- Li, J.; Liang, Y.; Zeng, Z.; Zhang, X. A staggered grid shell particle method for shell structural damage subjected to underwater explosion. CMSE Comput. Methods Appl. Mech. Eng. 2025, 441, 117996. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, X.; Zhou, X.; Liu, Y.; Zhang, F. A coupled finite difference material point method and its application in explosion simulation. Comput. Model. Eng. Sci. 2014, 98, 565–599. [Google Scholar]
- Li, G.; Lu, F.; Li, Z. A coupled finite difference and material point method for simulation of gas-solid flow of thermobaric explosions. In Proceedings of the 2020 4th International Conference on Energy Material, Chemical Engineering and Mining Engineering (EMCEME 2020), Qingdao, China, 26–27 December 2020. [Google Scholar]
- Yue, Z.; Zhou, J.; Feng, C.; Wang, X.; Peng, L.; Cong, J. Coupling of material point and continuum discontinuum element methods for simulating blast-induced fractures in rock. Comput. Geotech. 2022, 144, 104629. [Google Scholar] [CrossRef]
- Tan, H.L.; Nairn, J.A. Hierarchical, adaptive, material point method for dynamic energy release rate calculations. Comput. Methods Appl. Mech. Eng. 2002, 191, 2095–2109. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, W.; Shen, L.; Xin, X.; Brannon, R. An evaluation of the MPM for simulating dynamic failure with damage diffusion. Eng. Fract. Mech. 2002, 69, 1873–1890. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, S.-L.; Zhou, A. Dynamic brittle fracture with eigenerosion enhanced material point method. Int. J. Numer. Methods Eng. 2020, 121, 3768–3794. [Google Scholar] [CrossRef]
- Wolper, J.; Fang, Y.; Li, M.; Lu, J.; Gao, M.; Jiang, C. CD-MPM: Continuum Damage Material Point Methods for Dynamic Fracture Animation. ACM Trans. Graph. 2019, 38, 119. [Google Scholar] [CrossRef]
- Xiao, M.; Liu, C.; Sun, W. DP-MPM: Domain partitioning material point method for evolving multi-body thermal-mechanical contacts during dynamic fracture and fragmentation. Comput. Methods Appl. Mech. Eng. 2021, 385, 114063. [Google Scholar] [CrossRef]
- Daphalapurkar, N.P.; Lu, H.; Coker, D.; Komanduri, R. Simulation of dynamic crack growth using the generalized interpolation material point (GIMP) method. Int. J. Fract. 2007, 143, 79–102. [Google Scholar] [CrossRef]
- Nairn, J.A. Material point method calculations with explicit cracks. CMSE Comput. Model. Eng. Sci. 2003, 4, 649–663. [Google Scholar]
- Adibaskoro, T.; Bordas, S.; Solowski, W.T.; Hostikka, S. Multiple discrete crack initiation and propagation in Material Point Method. Eng. Fract. Mech. 2024, 301, 109918. [Google Scholar] [CrossRef]
- Yang, D.; He, X.; Liu, X.; Deng, Y.; Huang, X. A peridynamics-based cohesive zone model (PD-CZM) for predicting cohesive crack propagation. Int. J. Mech. Sci. 2020, 184, 105830. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, H.; Zhang, X.; Liu, Y.; Chen, Z. An adaptive peridynamics material point method for dynamic fracture problem. Comput. Methods Appl. Mech. Eng. 2022, 393, 114786. [Google Scholar] [CrossRef]
- Lyu, Y.; Zhang, J.; Sarafopoulos, A.; Chang, J.; Guo, S.; Zhang, J.J. Integral-Based Material Point Method and Peridynamics Model for Animating Elastoplastic Material. In Transactions on Computational Science XXXVII: Special Issue on Computer Graphics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 91–108. [Google Scholar]
- Zeng, Z.; Su, Y.C.; Zhang, X.; Chen, Z. Combining peridynamics and generalized interpolation material point method via volume modification for simulating transient responses. Comput. Part. Mech. 2021, 8, 337–347. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Wang, L.; Xie, C.; Huang, W. A monolithic projection framework for constrained FSI problems with the immersed boundary method. Comput. Methods Appl. Mech. Eng. 2020, 371, 113332. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, L. A phase field-immersed boundary-lattice Boltzmann coupling method for fluid-structure interaction analysis. Ocean. Eng. 2024, 301, 117564. [Google Scholar] [CrossRef]
- Ni, R.; Li, J.; Zhang, X.; Zhou, X.; Cui, X. An immersed boundary-material point method for shock-structure interaction and dynamic fracture. J. Comput. Phys. 2022, 470, 111558. [Google Scholar] [CrossRef]
- Peery, J.S.; Carroll, D.E. Multi-Material ALE methods in unstructured grids. Comput. Methods Appl. Mech. Eng. 2000, 187, 591–619. [Google Scholar] [CrossRef]
- Kan, L.; Zhang, X. An immersed MMALE material point method for FSI problems with structure fracturing? Comput. Methods Appl. Mech. Eng. 2022, 396, 115099. [Google Scholar] [CrossRef]
- Kakouris, E.G.; Triantafyllou, S.P. Phase-field material point method for brittle fracture. Int. J. Numer. Methods Eng. 2017, 112, 1750–1776. [Google Scholar] [CrossRef]
- Kakouris, E.G.; Triantafyllou, S.P. Material point method for crack propagation in anisotropic media: A phase field approach. Arch. Appl. Mech. 2018, 88, 287–316. [Google Scholar] [CrossRef]
- Kakouris, E.G.; Triantafyllou, S.P. Phase-Field Material Point Method for dynamic brittle fracture with isotropic and anisotropic surface energy. Comput. Methods Appl. Mech. Eng. 2019, 357, 112503. [Google Scholar] [CrossRef]
- Peng, X.; Fu, Z.; Zhang, Z.; Chen, S.; Ji, E.; Zhong, Q. Two different phase field models of the explicit material point method for brittle dynamic fracture. Eng. Fract. Mech. 2023, 290, 109449. [Google Scholar] [CrossRef]
- Zeng, Z.; Ni, R.; Zhang, X.; Liu, Y. An explicit phase field material point method for modeling dynamic fracture problems. Int. J. Numer. Methods Eng. 2023, 124, 2680–2708. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiu, Y.; Hu, Z.; Ye, H.; Zhang, H.; Zheng, Y. Explicit phase-field total Lagrangian material point method for the dynamic fracture of hyperelastic materials. Comput. Methods Appl. Mech. Eng. 2022, 398, 115234. [Google Scholar] [CrossRef]
- Wang, R.; Wang, G.; Yang, X.; Sun, F.; Huang, J.; Liao, M.; Li, B. Explicit finite element material point method coupled with phase-field model for solid brittle fracture. Eng. Fract. Mech. 2025, 316, 110865. [Google Scholar] [CrossRef]
- Chihadeh, A.; Coombs, W.; Kaliske, M. A coupled implicit MPM-FEM approach for brittle fracture and fragmentation. Comput. Struct. 2023, 288, 107143. [Google Scholar] [CrossRef]
- Sulsky, D.; Schreyer, H.L. Axisymmetric form of the material point method with applications to upsetting and Taylor impact problems. Comput. Methods Appl. Mech. Eng. 1996, 139, 409–429. [Google Scholar] [CrossRef]
- Ikkurthi, V.; Rahulnath, P.; Mehra, V.; Warrier, M.; Dasgupta, K.; Savita, A.; Pahari, S.; Alexander, R.; Arya, A.; Malshe, U. Computational and experimental studies of penetration resistance of Ceramic-Metal composites. Mater. Today Proc. 2023, 87, 257–262. [Google Scholar] [CrossRef]
- Burghardt, J.; Leavy, B.; Guilkey, J.; Xue, Z.; Brannon, R. Application of Uintah-MPM to shaped charge jet penetration of aluminum. In Proceedings of the 9th World Congress on Computational Mechanics/4th Asian Pacific Congress on Computational Mechanics, Sydney, Australia, 19–23 July 2010. [Google Scholar]
- Li, L.; Lian, Y.; Li, M.J.; Gao, R.; Gan, Y. A contact method for B-spline material point method with application in impact and penetration problems. Comput. Mech. 2024, 73, 1351–1369. [Google Scholar] [CrossRef]
- Chen, F.; Chen, R.; Jiang, B. The adaptive finite element material point method for simulation of projectiles penetrating into ballistic gelatin at high velocities. Eng. Anal. Bound. Elem. 2020, 117, 143–156. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Layton, A. Numerical methods for fluid-structure interaction—A review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Liu, X. A Monolithic Lagrangian Meshfree Method for Fluid-Structure Interaction. Master’s Thesis, Case Western Reserve University, Cleveland, OH, USA, 2016. [Google Scholar]
- York, A.R.; Sulsky, D.; Schreyer, H.L. Fluid-membrane interaction based on the material point method. Int. J. Numer. Methods Eng. 2000, 48, 901–924. [Google Scholar] [CrossRef]
- Hu, P.G.; Xue, L.; Mao, S.; Kamakoti, R.; Zhao, H.; Dittakavi, N.; Wang, Z.; Li, Q.; Ni, K.; Brenner, M. Material point method applied to fluid-structure interaction (FSI)/aeroelasticity problems. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Sun, Z.; Ni, R.; Zeng, Z.; Zhang, X. A localized subdomain smoothing MMALE particle method for efficient modeling FSI problems. Comput. Methods Appl. Mech. Eng. 2024, 419, 116676. [Google Scholar] [CrossRef]
- Li, J.; Gao, Y.; Dai, J.; Li, S.; Hao, A.; Qin, H. MPMNet: A data-driven MPM framework for dynamic fluid-solid interaction. IEEE Trans. Vis. Comput. Graph. 2023, 30, 4694–4708. [Google Scholar] [CrossRef]
- Jassim, I.; Stolle, D.; Vermeer, P. Two-phase dynamic analysis by material point method. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2502–2522. [Google Scholar] [CrossRef]
- Zabala, F.; Alonso, E.E. Progressive failure of Aznalcóllar dam using the material point method. Géotechnique 2011, 61, 795–808. [Google Scholar] [CrossRef]
- Yerro, A.; Alonso, E.; Pinyol, N. The material point method for unsaturated soils. Géotechnique 2015, 65, 201–217. [Google Scholar] [CrossRef]
- Wang, D.; Wang, B.; Yuan, W.; Liu, L. Investigation of rainfall intensity on the slope failure process using GPU-accelerated coupled MPM. Comput. Geotech. 2023, 163, 105718. [Google Scholar] [CrossRef]
- Ceccato, F.; Yerro, A.; Girardi, V.; Simonini, P. Two-phase dynamic MPM formulation for unsaturated soil. Comput. Geotech. 2021, 129, 103876. [Google Scholar] [CrossRef]
- Wang, J.-H.; Xu, W.-J. Slope stability and failure dynamics of rainfall-induced landslide: Algorithm and applications. Comput. Geotech. 2025, 177, 106919. [Google Scholar] [CrossRef]
- Soga, K.; Alonso, E.; Yerro, A.; Kumar, K.; Bandara, S.; Kwan, J.S.H.; Koo, R.C.H.; Law, R.P.H.; Yiu, J.; Sze, E.H.Y.; et al. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method. Geotechnique 2018, 68, 457–458. [Google Scholar] [CrossRef]
- Du, W.; Sheng, Q.; Fu, X.; Chen, J.; Zhou, Y. Extensions of the two-phase double-point material point method to simulate the landslide-induced surge process. Eng. Anal. Bound. Elem. 2021, 133, 362–375. [Google Scholar] [CrossRef]
- Qin, T.; Song, Z.; Wang, C.; Liang, F. Two-point MPM study of fluidized grains in internal erosion around metro tunnel characterized by an erosion law. Comput. Geotech. 2025, 183, 107227. [Google Scholar] [CrossRef]
- Yao, Z.; Yuan, M.; Zhang, H.; Wang, K.; Zhang, Z. Material point method for numerical simulation of failure phenomena in multiphase porous media. In Proceedings of the International Symposium on Computational Mechanics, Beijing, China, 30 July–1 August 2007; pp. 36–47. [Google Scholar]
- Bandara, S.; Soga, K. Coupling of soil deformation and pore fluid flow using material point method. Comput. Geotech. 2015, 63, 199–214. [Google Scholar] [CrossRef]
- Liu, C.; Sun, Q.; Jin, F.; Zhou, G.G.D. A fully coupled hydro-mechanical material point method for saturated dense granular materials. Powder Technol. 2017, 314, 110–120. [Google Scholar] [CrossRef]
- Zhan, Z.Q.; Zhou, C.; Liu, C.Q.; Ng, C.W.W. Modelling hydro-mechanical coupled behaviour of unsaturated soil with two-phase two-point material point method. Comput. Geotech. 2023, 155, 105224. [Google Scholar] [CrossRef]
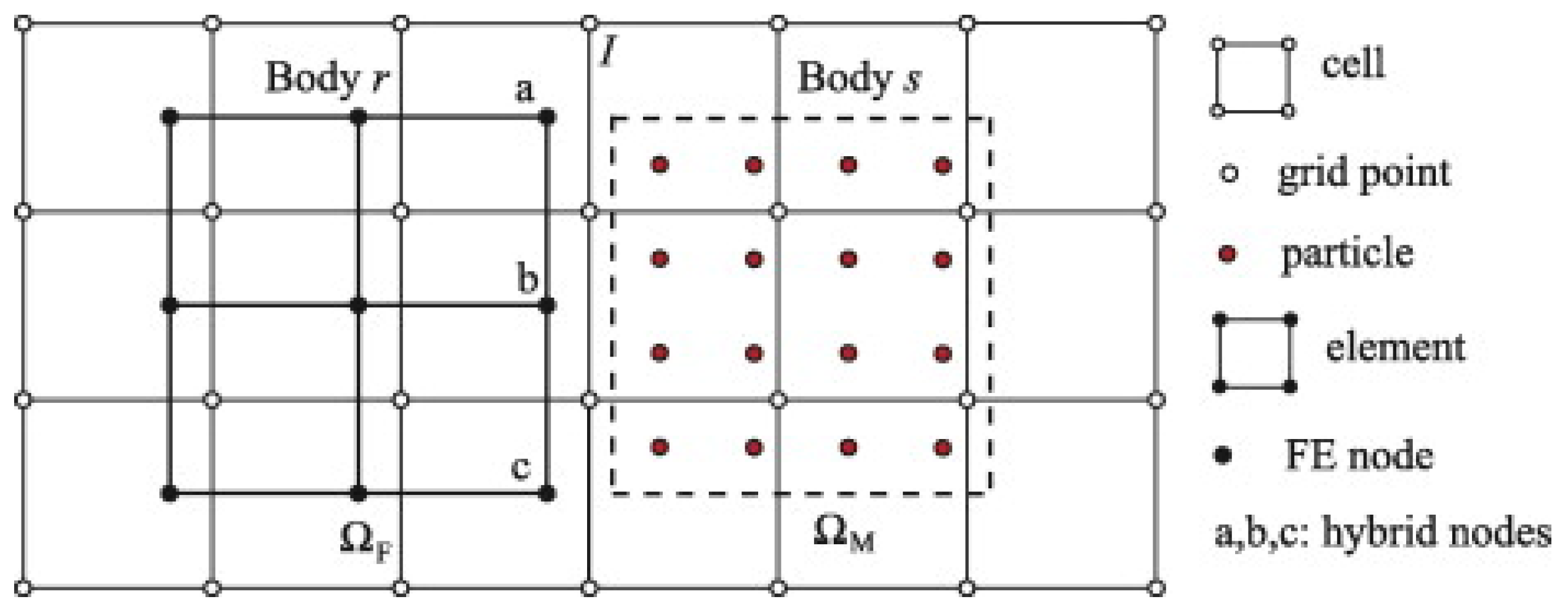
- Lian, Y.P.; Zhang, X.; Liu, Y. Coupling of finite element method with material point method by local multi-mesh contact method. Comput. Methods Appl. Mech. Eng. 2011, 200, 3482–3494. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, X.; Zhang, X.; Lian, Y. Improved coupling of finite element method with material point method based on a particle-to-surface contact algorithm. Comput. Methods Appl. Mech. Eng. 2015, 293, 1–19. [Google Scholar] [CrossRef]
- Cheon, Y.J.; Kim, H.G. An efficient contact algorithm for the interaction of material particles with finite elements. Comput. Methods Appl. Mech. Eng. 2018, 335, 631–659. [Google Scholar] [CrossRef]
- Chen, Z.P.; Zhang, X.; Sze, K.Y.; Kan, L.; Qiu, X.-M. vp material point method for weakly compressible problems. Comput. Fluids 2018, 176, 170–181. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Y.; Zhang, X. A non-penetration FEM-MPM contact algorithm for complex fluid-structure interaction problems. Comput. Fluids 2020, 213, 104749. [Google Scholar] [CrossRef]
- Li, M.; Lian, Y.; Zhang, X. An immersed finite element material point (IFEMP) method for free surface fluid-structure interaction problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114809. [Google Scholar] [CrossRef]
- Lei, Z.; Zeng, G.; Ren, H.; Wu, B.; Jie, Y. Effect of the sloping seabed on 3D soil-spudcan interaction using a material point-finite element (MPM-FEM) model. J. Rock Mech. Geotech. Eng. 2024, 16, 1436–1454. [Google Scholar] [CrossRef]
- Lei, Z.; Zhou, J.; Zhang, Z.; Zhang, J.-M.; Jie, Y.; Wu, B. Hydrodynamic responses of the triangle-shaped semi-submersible platform under wave loadings by an incompressible material point method and finite element method model. Ocean. Eng. 2024, 312, 119152. [Google Scholar] [CrossRef]
- Mazloomi, A.M.; Chikatamarla, S.S.; Karlin, I.V. Entropic Lattice Boltzmann Method for Multiphase Flows. Physical Review Letters 2015, 114, 174502. [Google Scholar] [CrossRef]
- Xie, C.; Raeini, A.Q.; Wang, Y.; Blunt, M.J.; Wang, M. An improved pore-network model including viscous coupling effects using direct simulation by the lattice Boltzmann method. Adv. Water Resour. 2017, 100, 26–34. [Google Scholar] [CrossRef]
- Boek, E.S.; Venturoli, M. Lattice-Boltzmann studies of fluid flow in porous media with realistic rock geometries. Comput. Math. Appl. 2010, 59, 2305–2314. [Google Scholar] [CrossRef]
- Chen, L.; Fang, W.; Kang, Q.; De’Haven Hyman, J.; Viswanathan, H.S.; Tao, W.-Q. Generalized lattice Boltzmann model for flow through tight porous media with Klinkenberg’s effect. Phys. Rev. E 2015, 91, 033004. [Google Scholar] [CrossRef] [PubMed]
- Dorschner, B.; Bösch, F.; Chikatamarla, S.S.; Boulouchos, K.; Karlin, I.V. Entropic multi-relaxation time lattice Boltzmann model for complex flows. J. Fluid Mech. 2016, 801, 623–651. [Google Scholar] [CrossRef]
- Ladd, A.J. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, H.; Zhang, H.; Zheng, Y. Coupling lattice Boltzmann and material point method for fluid-solid interaction problems involving massive deformation. Int. J. Numer. Methods Eng. 2020, 121, 5546–5567. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, H.; Zhang, H.; Zheng, Y. Coupling Phase-Field LB-MP Method for Multiphase Fluid-Deformable Solid Interaction Problems Involving Large Density and Viscosity Contrasts. Int. J. Appl. Mech. 2023, 15, 2350050. [Google Scholar] [CrossRef]
- Ren, S.; Zhang, P.; Galindo-Torres, S. A coupled discrete element material point method for fluid–solid–particle interactions with large deformations. Comput. Methods Appl. Mech. Eng. 2022, 395, 115023. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Wang, D.; Zhang, P.; Vardon, P.J. A coupled MPM-DEM method for modelling soil-rock mixtures. Comput. Geotech. 2023, 160, 105508. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, J.; Wu, H.; Soga, K. Multiscale, multiphysics modeling of saturated granular materials in large deformation. Comput. Methods Appl. Mech. Eng. 2023, 405, 115871. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, J.; Liang, W.; Zhao, S. Multiscale modeling of coupled thermo-hydro-mechanical behavior in ice-bonded granular media subject to freeze-thaw cycles. Comput. Geotech. 2024, 171, 106349. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Pan, P.; Chen, H.; Wang, D.; Chen, P. Failure analysis of soil-rock mixture slopes using coupled MPM-DEM method. Comput. Geotech. 2024, 169, 106226. [Google Scholar] [CrossRef]
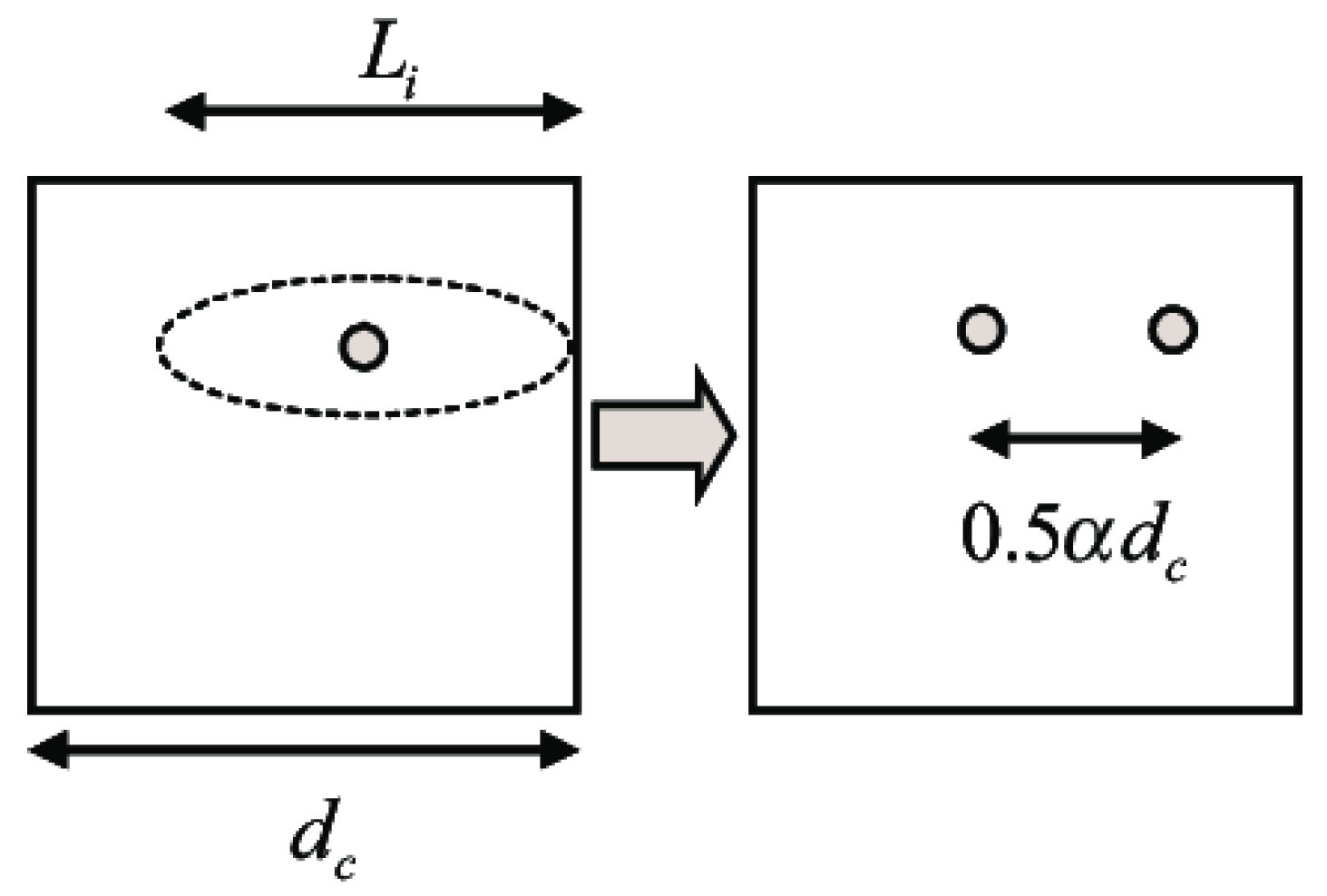
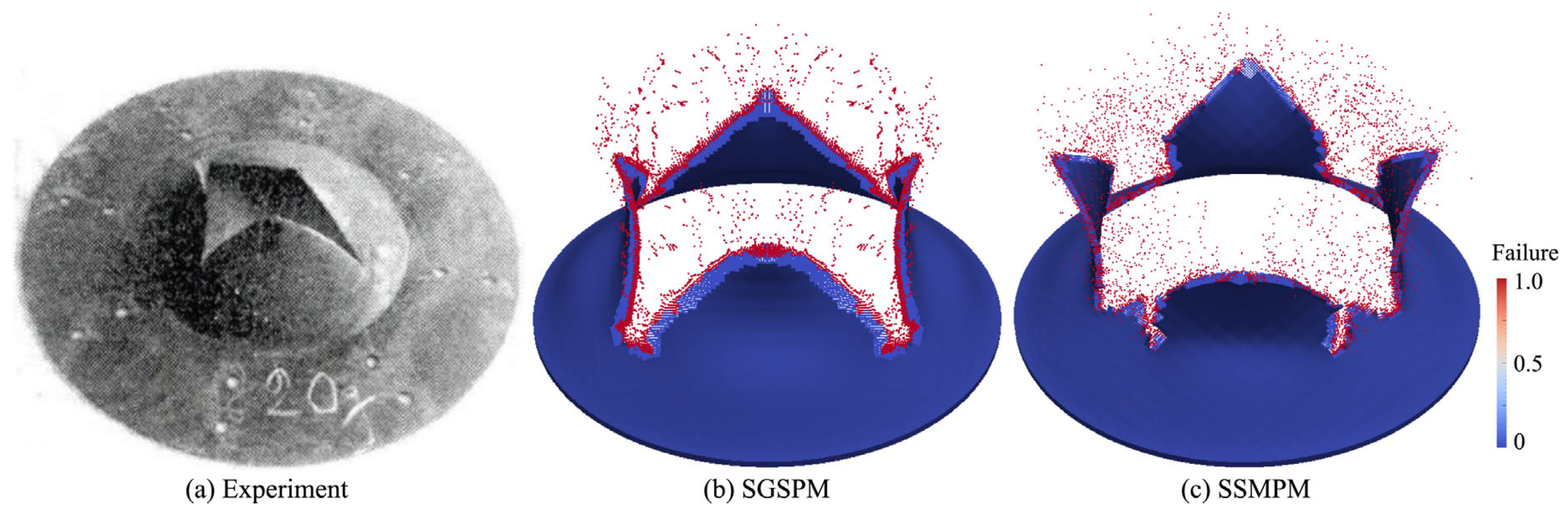
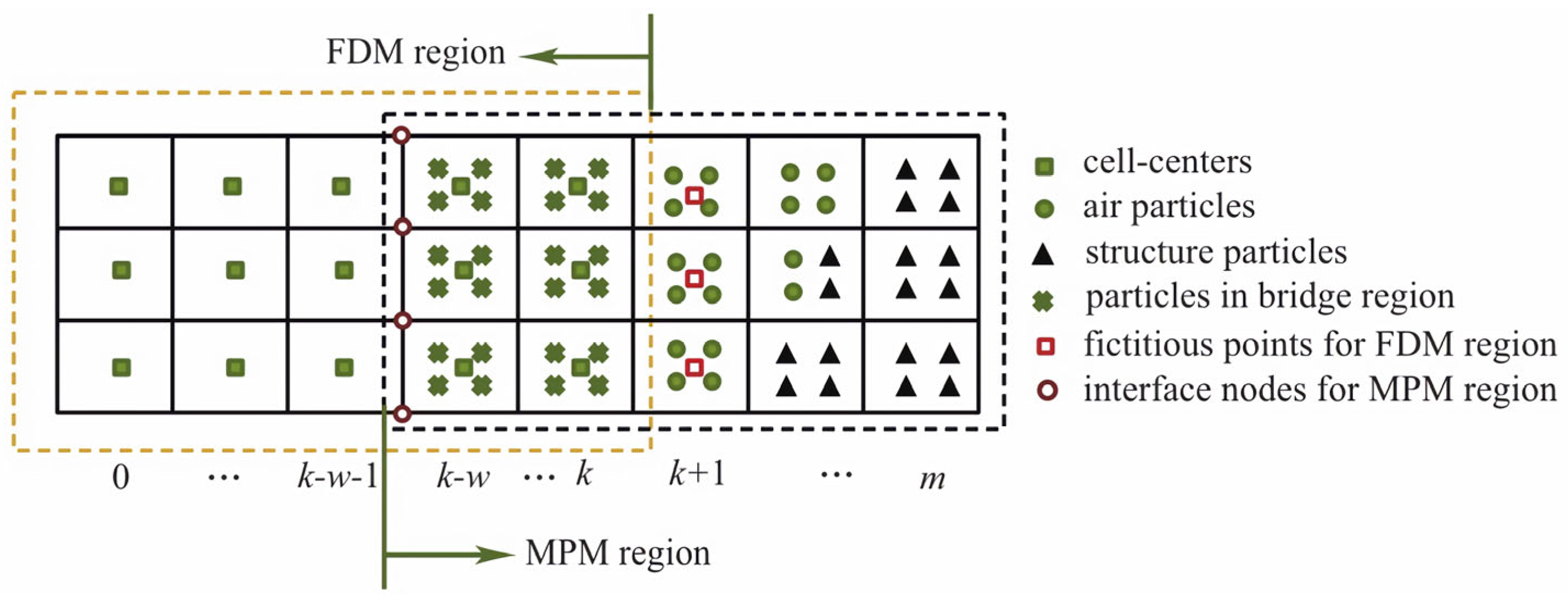
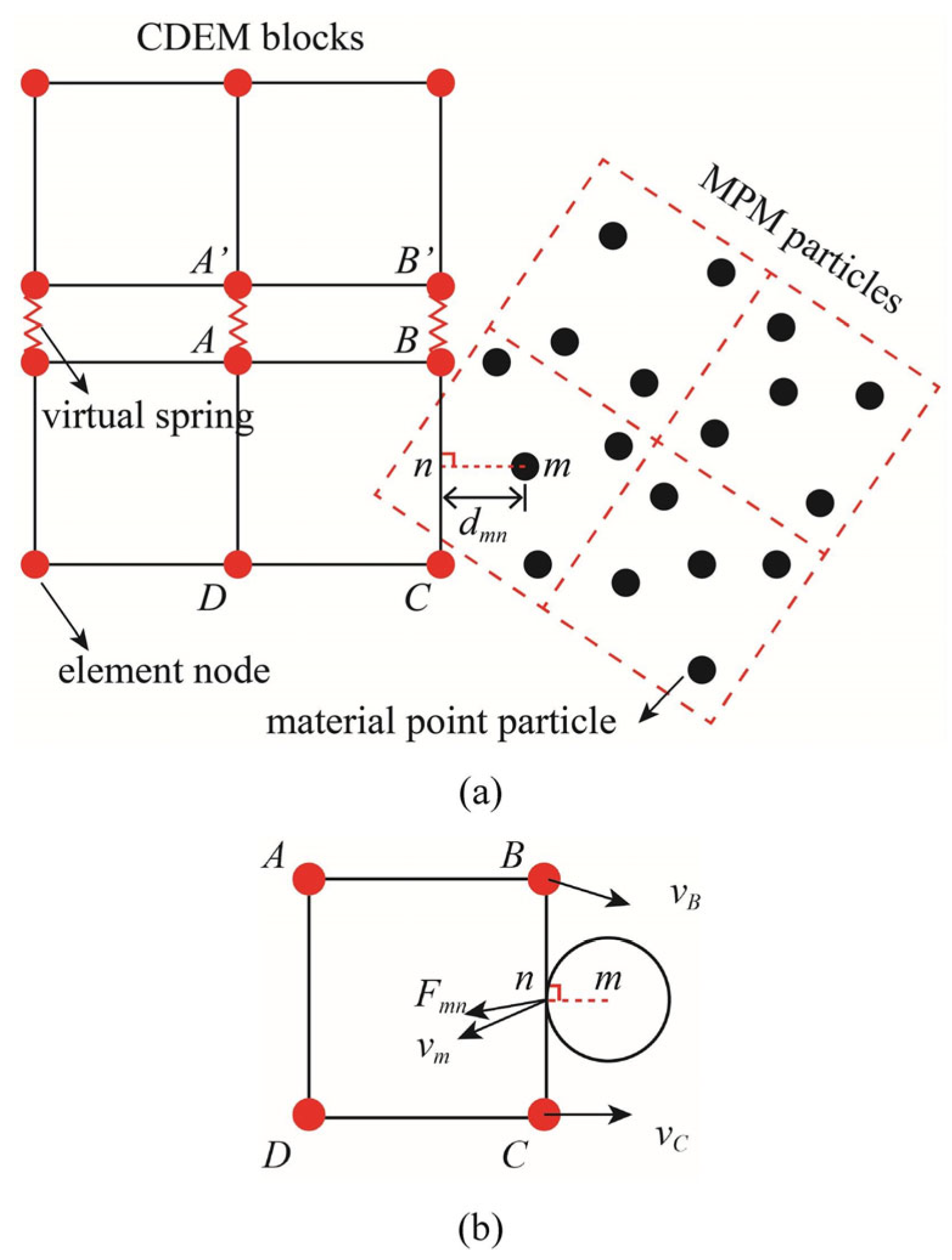





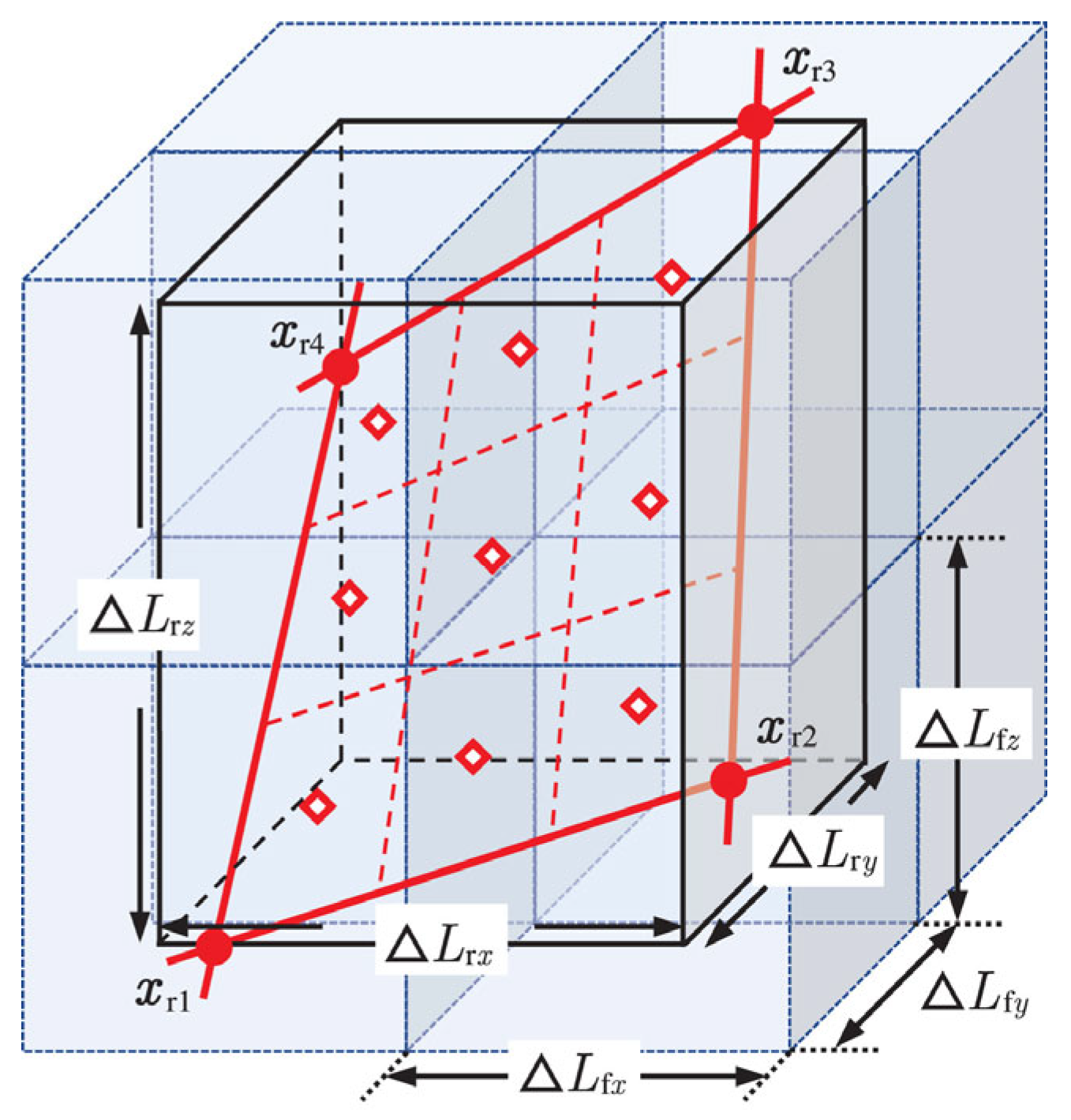
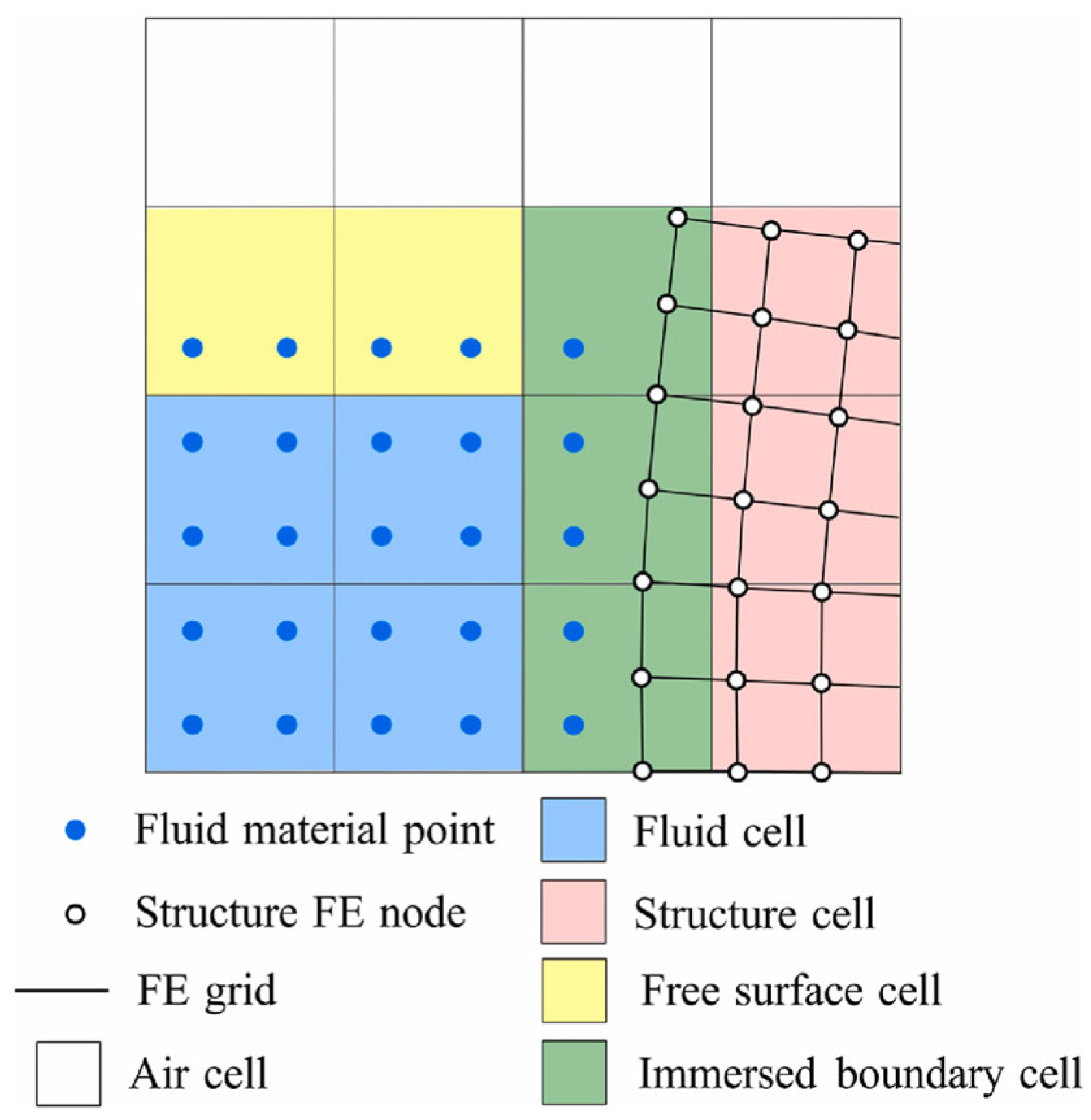
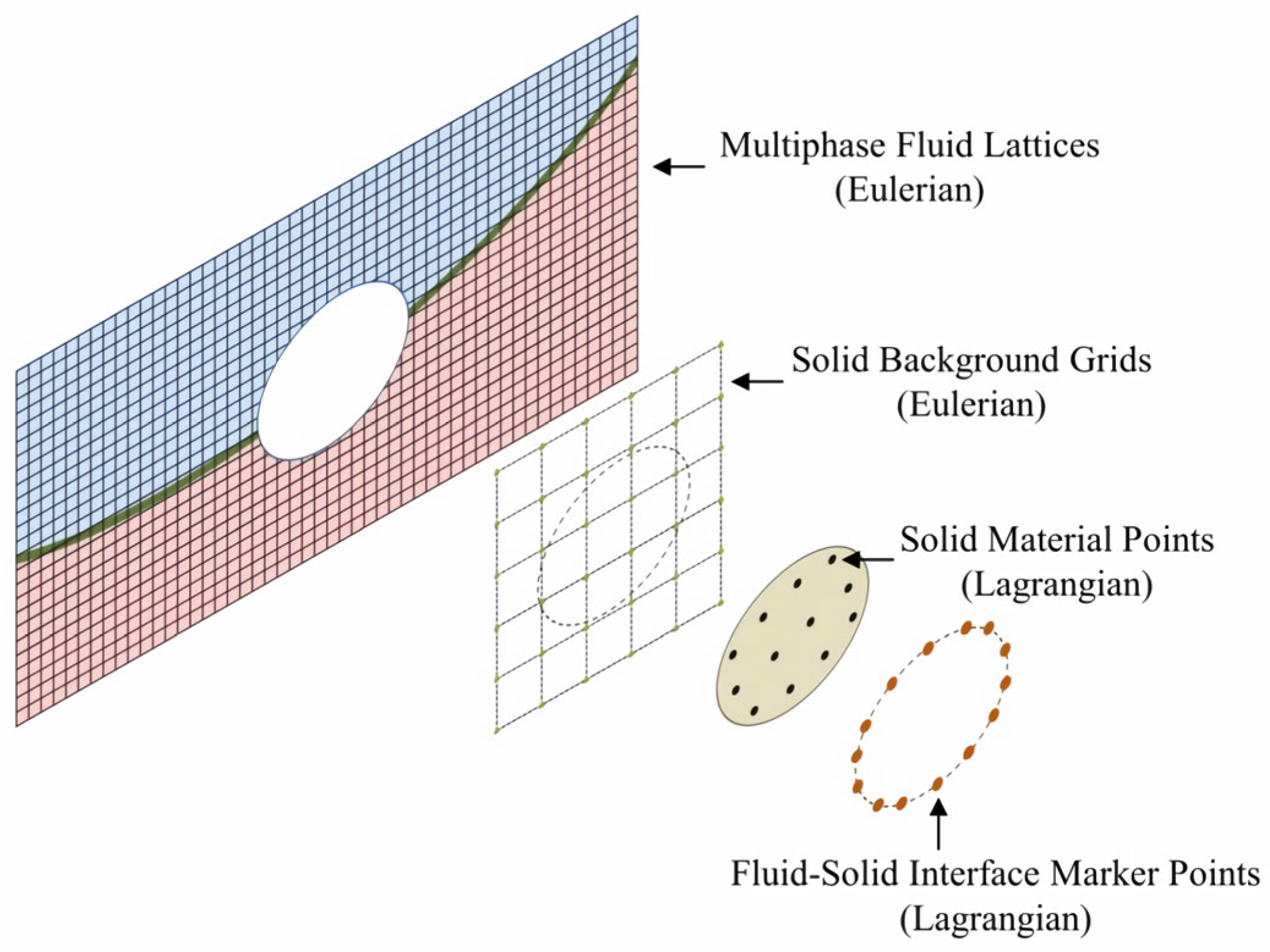
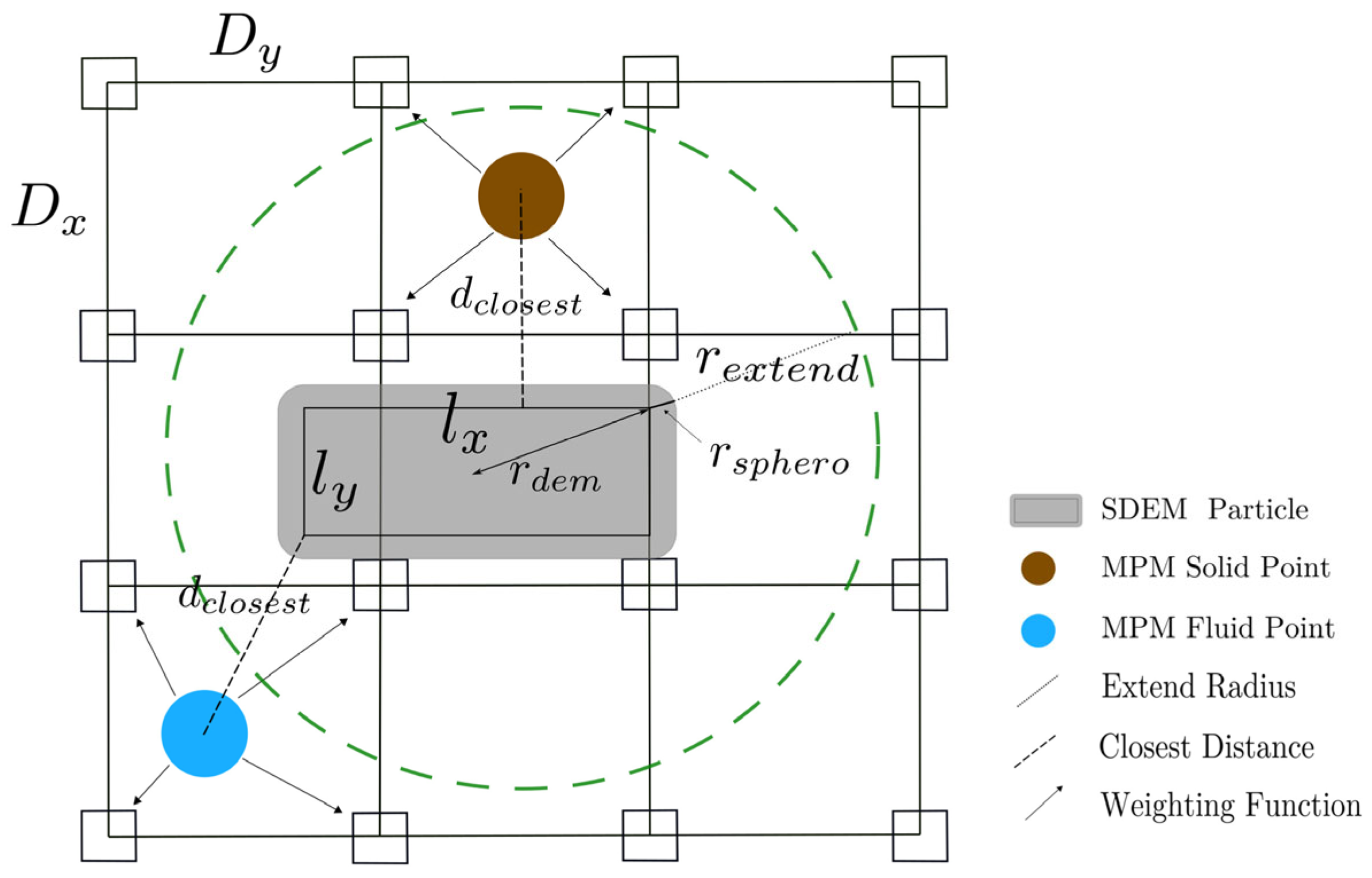
| Author | Method | Key Innovations | Limitations |
|---|---|---|---|
| Sulsky et al. (1994) [13] | Standard MPM | Firstly extended the FLIP method to solid mechanics, establishing a coupling framework between material points and background grids. | Significant numerical dissipation. Incomplete contact algorithms. |
| Hu and Chen (2003) [15] | multi-mesh MPM | Assigning independent background grids to different materials to address material interface issues. | Neglecting friction; inability to ensure non-penetration conditions at the particle level. |
| Bardenhagen and Kober (2004) [30] | GIMP | Introducing generalized interpolation shape functions to reduce grid-crossing noise. | The computational cost is slightly higher than that of the standard MPM. |
| Zhang et al. (2006) [28] | explicit material point FEM | Automatically converting FEM nodes to MPM particles in highly deformable regions. | The treatment of the coupling interface is complex. |
| Ma et al. (2009) [46] | adaptive MPM | Automatically splitting material points based on strain thresholds to improve simulation accuracy. | Particle splitting increases computational load, necessitating the optimization of multiple local background grids. |
| Lian et al. (2011) [104] | CFEMP | Coupling finite element truss elements with the material point method on a unified background grid to enhance computational efficiency and accuracy. | Consistent meshing between the FEM domain and the MPM domain is required, which may lead to over-meshing in the FEM domain. |
| Liu et al. (2013) [42] | multi-scale framework combining MD and MPM | Driving MPM macroscopic simulations with EOS data calculated from MD. | A large amount of MD state equation data needs to be precomputed. |
| Cui et al. (2014) [51] | CFDMP | More precise treatment of explosive multi-material interfaces. | The introduction of virtual points at the interface leads to interpolation errors, which necessitate precise boundary conditions. |
| Kakouris and Triantafyllou (2017) [72] | phase-field MPM | When combined with the phase-field fracture model, explicit crack tracking is not required. | The computational workload is significantly increased. |
| Ni et al. (2020) [69] | immersed boundary MPM | Incorporating the IBM avoids the need for FSI interface reconstruction. | The introduction of virtual fluid incurs additional computational costs. |
| Liu et al. (2020) [118] | LBMPM | Efficient simulation of large-deformation fluid–solid interaction without mesh reconstruction is achieved. | The computational efficiency in 3D is low. |
| Chen et al. (2020) [84] | adaptive finite element material point method | Dynamically converting finite elements to material points effectively avoids mesh distortion in extreme deformation problems. | The threshold for conversion needs to be set empirically. |
| Zeng et al. (2022) [63] | adaptive peridynamics MPM | Dynamically switching between MPM and peridynamics regions enables multi-scale fracture simulation. | It requires a preset threshold for conversion. |
| Yue et al. (2022) [53] | coupling of MPM and CDEM | The particle–surface contact model accurately simulates the entire process of rock transitioning from continuous deformation to fracture during blasting. | The contact criterion requires iterating through all material points. |
| Kan and Zhang (2022) [71] | IALEMPM | The contact criterion requires iterating through all material points. | The algorithm implementation is complex. |
| Li et al. (2022) [109] | immersed finite element material point | Incorporating weighted tracking points avoids the need for FSI interface reconstruction. | The computational cost is high, and it is difficult to apply boundary conditions. |
| Li et al. (2024) [83] | cBSMPM | Using B-spline background grids yields a smooth stress field. | Higher-order basis functions increase the computational workload. |
| Wang et al. (2025) [78] | PF-FEMPM | Mitigate mesh-crossing instabilities. | The efficiency is lower than that of the pure MPM phase-field method. |
| Application | Advantages | Disadvantages |
|---|---|---|
| High-speed impact | Effectively captures the physical phenomena of shock wave generation, debris cloud formation, and material damage; possesses robust handling capabilities for moving material interfaces and multi-material coupling issues. | The computational efficiency in regions of small deformation is inferior to the finite element method, necessitating the use of coupling methods (such as the CFEMP) to enhance efficiency; it struggles to accurately capture very fine details such as intricate fragmentation structures and vortex flow features. |
| Explosions | Has good adaptability for problems involving high pressure, high-speed flow, and solid deformation caused by explosions; capable of simulating the significant deformation, phase changes, and flow induced by blasts. | In handling high-speed flows, numerical dissipation and grid-crossing errors may occur, necessitating improvements with the GIMP method. |
| Dynamic cracking | Not constrained by the background mesh; it conveniently handles the significant topological changes during crack propagation; it can be combined with phase-field methods to further enhance simulation accuracy. | The precision of stress at the crack tip is dependent on the density of material points, and additional relationships are required to link the initiation of cracks with their propagation speed and direction, which increases computational costs and the complexity of the simulation. |
| Penetration | Effectively simulates the damage process of target plate materials under penetration; boundary conditions are readily applied, with no issues of tensile instability, offering high computational efficiency. | Complex contact determination necessitates the optimization of multiple local background grids. |
| Fluid–structure interaction | Uniformly handles fluid–solid interfaces (such as the coupling of explosive gases with structures); it can also be coupled with other methods (such as FEM, LBM, DEM, etc.) to enhance the capability of dealing with complex fluid–solid coupling problems. | Multiphase coupling computations are resource-intensive; applying boundary conditions is challenging; contact penetration is likely to occur when solid regions undergo small deformations while fluid regions experience large deformations. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Zhong, Q.; Zhou, X.; Wu, X.; Chen, S. Research Advances in Large Deformation Analysis and Applications of the Material Point Method. Appl. Sci. 2025, 15, 6617. https://doi.org/10.3390/app15126617
Zhou C, Zhong Q, Zhou X, Wu X, Chen S. Research Advances in Large Deformation Analysis and Applications of the Material Point Method. Applied Sciences. 2025; 15(12):6617. https://doi.org/10.3390/app15126617
Chicago/Turabian StyleZhou, Changhong, Qing Zhong, Xuejiao Zhou, Xionghua Wu, and Shiyi Chen. 2025. "Research Advances in Large Deformation Analysis and Applications of the Material Point Method" Applied Sciences 15, no. 12: 6617. https://doi.org/10.3390/app15126617
APA StyleZhou, C., Zhong, Q., Zhou, X., Wu, X., & Chen, S. (2025). Research Advances in Large Deformation Analysis and Applications of the Material Point Method. Applied Sciences, 15(12), 6617. https://doi.org/10.3390/app15126617







