Featured Application
This study offers scientific insights to optimize training strategies for elite Snowboard Big Air (SBA) athletes. By quantifying key biomechanical parameters during the takeoff phase, coaches and athletes can specifically target takeoff technique, rotational energy, and propulsion training to enhance trick difficulty and consistency. The kinematic and kinetic benchmarks established here can guide talent development, movement correction, and individualized training programs, supporting safer progression to high-difficulty tricks.
Abstract
Snowboard Big Air (SBA), recognized as an Olympic discipline since 2018, emphasizes maneuver difficulty as a key scoring criterion, requiring athletes to integrate technical skill with adaptive responses to dynamic environments in order to perform complex aerial rotations. The takeoff phase is critical, determining both flight trajectory and rotational performance through coordinated lower limb extension and upper body movements. Despite advances in motion analysis technology, quantitative assessment of key takeoff parameters remains limited. This study investigates parameters related to performance, joint kinematics, and rotational kinetics during the SBA takeoff phase to identify key factors for success and provide practical guidance to athletes and coaches. Eleven athletes from the Chinese national snowboard team performed multiple backside tricks (720°, 1080°, 1440°, and 1800°) at an outdoor dry slope with airbag landings. Three-dimensional motion capture with synchronized cameras was used to collect data on performance, joint motion, and rotational kinetics during takeoff. The results showed significant increases in most measured metrics with rising trick difficulty from 720° to 1800°. The findings reveal that elite SBA athletes optimize performance in high-difficulty maneuvers by increasing the moment of inertia, maximizing propulsion, and refining joint kinematics to enhance rotational energy and speed. These results suggest that training should emphasize lower limb power, core and shoulder strength, flexibility, and coordination to maximize performance in advanced maneuvers.
1. Introduction
Snowboard Big Air (SBA), which was officially introduced to the Winter Olympics in 2018, requires athletes to perform aerial maneuvers such as flips and spins from a large ramp. These maneuvers are judged based on execution, difficulty, amplitude, variety, and progression [1]. Maneuver difficulty plays a critical role in determining scores in SBA competitions [2,3]. Successfully completing high-difficulty tricks depends not only on external factors such as ramp design, weather conditions, and the athlete’s psychological preparation and equipment [4,5,6], but also—importantly—on the athlete’s technical skills, physical strength, and coordination [7,8,9]. These athlete-specific qualities underscore the need for precise monitoring and analysis of movement techniques, which are essential for optimizing performance and ensuring the safe execution of complex maneuvers.
The primary stages of SBA include the in-run, takeoff, flight, and landing. The takeoff stage is critical, as it determines the height, direction, and rotational velocity for the subsequent flight phase and is closely linked to the braking and absorption techniques employed during landing [10,11]. The takeoff phase is particularly important because it generates the majority of the angular momentum required for complex aerial maneuvers; errors during this stage often result in unsuccessful landings or incomplete rotations. By accumulating speed, performing explosive leg extensions, and coordinating upper body and arm movements to initiate and control rotation, athletes generate the necessary angular momentum to complete rotational maneuvers in the flight phase. This explains the positive correlations reported in previous studies between joint angles, angular velocities of the upper and lower limbs, center of mass velocity, and the number of rotational turns achieved [12]. Despite these insights, there remains a significant lack of technical analyses regarding how athletes execute maneuvers of varying—and especially high—difficulty.
Technical maneuvers in SBA are largely characterized by rotational elements, including horizontal spins, off-axis rotations, and flips. These movements share similarities with skill-based sports such as gymnastics, diving, and figure skating, where technical analysis frequently focuses on rotational parameters [13,14,15]. However, fundamental differences exist in takeoff mechanics and environmental conditions among these sports. For example, figure skaters generate ground reaction forces by extending the hip and knee joints and adjust their moment of inertia through limb positioning during flight to achieve rotational performance [14]. In contrast, SBA athletes initiate jumps with downhill speed and upper body rotation on snow, with environmental factors such as weather and snow surface conditions exerting significant influence, whereas figure skating takes place indoors on ice under highly controlled conditions. As a result, the generation and control of angular momentum in SBA require a combination of classic biomechanical principles and sport-specific adaptations.
While these differences limit the direct applicability of findings from figure skating and similar sports to SBA, the biomechanical principles established in those studies still provide valuable foundations for understanding and analyzing rotation in SBA. Therefore, it is essential to critically assess the limitations and relevance of research from related sports when exploring the unique biomechanics of SBA. Although previous studies have investigated general rotational variables—such as angular momentum and takeoff velocity—few have specifically quantified key SBA parameters like joint kinematics and rotational kinetics during takeoff, or addressed the impact of variable, outdoor environments. This research gap restricts a comprehensive understanding of the mechanisms underlying high-difficulty SBA maneuvers.
The integration of fixed-position and pan-tilt-zoom video cameras has enabled advanced multi-camera analyses of human movement in snowboarding and skiing maneuvers [16,17,18]. Machine vision technology further enhances the precise measurement of kinematic parameters such as joint angles, velocity, and acceleration [19], making it possible to identify the critical factors that influence maneuver success. High-difficulty maneuvers demand precise joint angle adjustments and greater speeds to achieve the intended rotations and flips. By assessing how rotational parameters change with increasing difficulty, athletes can optimize their use of rotational inertia while minimizing energy expenditure. This study examines key rotational parameters during the takeoff phase in snowboarding, including moment of inertia, angular momentum, and rotational energy. Through systematic analysis of these factors, our research offers a comprehensive understanding of the biomechanical characteristics that define this crucial performance phase. By focusing on the takeoff phase, we are able to identify the principal biomechanical factors that directly influence elite performance, thus providing a foundation for targeted training strategies.
This study aims to quantitatively analyze the takeoff phase of SBA by comparing performance, kinematic, and rotational kinetic parameters across tricks of increasing difficulty (720°, 1080°, 1440°, and 1800°). We hypothesize that higher-difficulty maneuvers are characterized by increased takeoff velocity, greater joint extension, and higher angular momentum. The objective is to identify key biomechanical adaptations that enable successful execution of high-difficulty tricks and to offer targeted recommendations for athlete training and coaching.
2. Materials and Methods
2.1. Participants and Measurement Protocol
In total, 11 athletes (7 males and 4 females; age: 20.4 ± 1.9 years; height: 165 ± 5.8 cm; weight: 54.4 ± 6.1 kg) from the Chinese national snowboard big air team voluntarily participated in this study, each providing informed consent. Inclusion criteria were (1) age between 18 and 30 years; (2) possession of at least the Chinese National First-Class Athlete qualification; (3) sufficient proficiency to perform the required experimental maneuvers; and (4) voluntary participation with informed consent. Exclusion criteria were (1) a history of significant upper or lower limb muscle injury within the past six months; (2) presence of neurological, cardiovascular, or psychiatric disorders; (3) pregnancy; and (4) inability to complete the experimental tasks. The experiment was conducted at an outdoor dry snowboard and ski airbag jump facility (Xindu JF-Dry Ski Four Season Resort, Chengdu, China).
Prior to the formal experiment, all participants completed a 15 min low-intensity warm-up that included grabs and low-difficulty spins, after which they proceeded with the performance trials in sequence. Participants executed backside 720°, 1080°, 1440°, and 1800° jumps (Bs 720, Bs 1080, Bs 1440, and Bs 1800), based on their proficiency in each maneuver. Each level of difficulty was performed 10 times. Maneuver completion was assessed by national team coaches and verified through video replay. To minimize fatigue, a rest interval of at least 5 min was provided between trials. The study protocol was approved by the Ethics Committee of Capital University of Physical Education and Sports (approval number: 2022A63). All procedures adhered to the Declaration of Helsinki (1964) and its most recent amendments (Finland, WMA, 19 October 2024).
2.2. Motion Capture and Data Processing
During the takeoff phase, 3D motion was captured, while 2D motion during the flight phase was recorded using three Z Cam E2 cameras (Shenzhen, China) positioned on both sides of the jump platform and at the referee stand (Figure 1A). Cameras were set to record at 50 Hz with a resolution of 1920 × 1080 and an exposure time of 1/800 s. Synchronization was achieved using sync cables. The jump platform was scanned using a terrestrial laser scanner (FARO Focus S150, Lake Mary, FL, USA), and point cloud data were processed with CloudCompare software (v2.12.4). Calibration was carried out with 28 existing platform markers (calibration volume: 9.4 × 7.9 × 4.2 m, Figure 1B). The known point on the top platform served as the origin of the coordinate system, with the x-axis pointing horizontally backward, the y-axis horizontally to the right, and the z-axis vertically upward (Figure 1A).
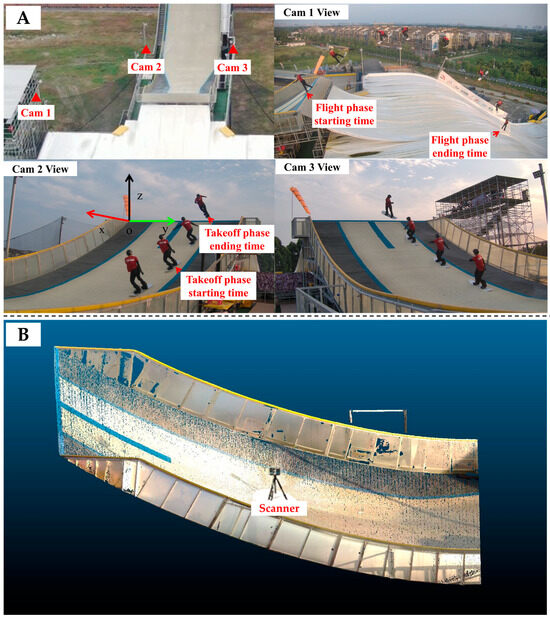
Figure 1.
Camera deployment and lidar-based SBA platform reconstruction. (A) Diagram of camera positions and perspectives of each camera. (B) Reconstructed SBA platform based on lidar point cloud technology.
A three-dimensional motion analysis software (FastMove 3D Motion, v1.1) was used to track 21 markers [20] placed on the athlete’s body during the takeoff phase. The 3D coordinates of these markers were derived using the direct linear transformation (DLT) method. Calibration accuracy showed small errors in reconstructing control point coordinates compared to known values (3.2, 3.7, −1.8 m) of the calibration frame, with mean square errors of 0.519% for X, 1.48% for Y, and 0.177% for Z coordinates. Identified marker trajectories were further smoothed using a Butterworth low-pass filter with a cutoff frequency of 6 Hz [21].
The takeoff phase was defined as beginning when a change was detected in the horizontal flexion/extension angle of the shoulder joint, signifying the initiation of the upper limb swing, and ending when the tail of the snowboard left the edge of the platform; the flight phase started at the moment the snowboard’s tail left the platform and concluded upon contact with the landing slope. Performance metrics were calculated as follows: takeoff time was defined as the interval from the start of the takeoff movement to the moment of platform departure; flight time was measured from takeoff to landing; flight height was identified as the maximum z-coordinate of the center of mass (COM) during the flight phase; departure combined velocity was calculated as the total velocity of the COM at the end of takeoff; departure anteroposterior velocity referred to the horizontal component of the resultant velocity (in the forward-backward direction) at the end of takeoff; departure vertical velocity was the vertical component of the resultant velocity at the end of takeoff; and departure angle was defined as the arctangent of the ratio between the vertical and anteroposterior velocities at takeoff completion.
The method for constructing body segments and joint angles in this study is consistent with previous research [22,23,24]. Anatomical coordinate systems for the upper arms, upper trunk, lower trunk, and thighs were established using unit vectors derived from key anatomical landmarks (shoulder, elbow, wrist, hip, knee, and ankle), with orthogonal axes determined via vector cross products. Joint angles were quantified as follows: the shoulder joint angle was defined as the Euler angle of the upper arm reference frame relative to the upper trunk reference frame, with the rotation sequence of horizontal adduction–abduction, adduction–abduction, and internal–external rotation; the hip joint angle was defined as the Euler angle of the thigh reference frame relative to the lower trunk reference frame, using the sequence of flexion–extension, adduction–abduction, and internal–external rotation; elbow and knee angles were defined as the angular deviation between the longitudinal axes of adjacent segments; the upper trunk twist angle was calculated as the angular displacement between the shoulder and hip transverse lines measured about their midpoint axis. This study specifically focused on the anterior joints, defined as the side of the athlete’s body facing the direction of travel during takeoff.
The moment of inertia for each body segment was calculated using a multi-step approach, in which the subject’s body parameters were first scaled based on a formula derived from standard human model data [25], incorporating adjustments for individual variations in weight and height.
where (kg·m2) is each body’s moment of inertia of the standard human model (kg) is the weight of the standard human model; M (kg) is the weight of the subject; (m) is the torso length of the standard human model; (m) is the torso length of the subject; (kg·m2) is the moment of inertia of the joint limb’s center of mass corresponding to the center of gravity; The rotation axes were identified by analyzing joint velocities, decomposed into components along the sagittal, coronal, and transverse planes. The dynamic calculation of the moment of inertia was performed throughout the motion sequence by applying the parallel axis theorem to each body segment at discrete time intervals, considering the segment’s mass and its position relative to the rotation axis.
where (kg·m2) is the moment of inertia of the joint limb’s center of mass corresponding to the center of gravity; (kg) is the mass of a particular limb; (m) is the distance from the limb’s center of gravity to the body’s center of gravity; (kg·m2) is the moment of inertia of the joint limb around the axis of rotation. The total body moment of inertia was then determined by summing the contributions of individual segments.
where (kg·m2) is the moment of inertia of the entire human body at a certain moment. The rotational kinetic energy of an athlete was calculated through the angular velocity and the moment of inertia of each body segment.
where (rad/s) is the angular velocity of the i-th segment and (J) is rotational kinetic energy of the human body.
2.3. Statistics
Means and standard deviations were calculated for all technical indicators across difficulty levels. A mixed linear model with subjects as a random effect was first used, but no significant subject-related effects were found. Therefore, one-way ANOVA (SPSS Inc., Chicago, IL, USA) was used to analyze the technical characteristics at different difficulty levels. The model treated difficulty level as the independent variable and technical indicators as dependent variables. The significance level α was set at 0.05. When the main effect of difficulty level reached statistical significance (p < 0.05), post hoc pairwise comparisons were performed using Tukey’s Honestly Significant Difference (HSD) test to identify specific differences between difficulty tiers. Homogeneity of variance was verified using Levene’s test prior to ANOVA. Effect sizes were quantified using partial eta-squared () values to assess the proportion of variance in technical indicators explained by difficulty level, with values of 0.01, 0.06, and 0.14 interpreted as small, moderate, and large effects, respectively.
3. Results
3.1. Performance Metrics
Performance metrics (Table 1) demonstrated systematic adaptations across increasing difficulty levels, with significant changes in temporal, spatial, and velocity parameters. Takeoff time and flight time progressively increased ( = 0.73 and 0.87, respectively), with the greatest percentage increment observed in takeoff time (44.3%). Flight height and takeoff angle also increased significantly ( = 0.77 and 0.53), while departure combined velocity and vertical velocity showed substantial gains ( = 0.83 and 0.91), with the latter exhibiting the strongest effect and a 25.8% increment. Notably, all these effect sizes are considered large, highlighting the practical relevance of these adaptations for snowboard performance. The intermediate difficulty transitions (1080–1440) were particularly crucial, as most parameters exhibited significant adaptations during this phase, highlighting the critical roles of takeoff time and departure vertical velocity in difficulty progression.

Table 1.
Performance metrics of SBA at different difficulty levels during takeoff and flight phases.
3.2. Joint Kinematics
The analysis of joint kinematics revealed significant effects of difficulty on various kinematic variables at both the start and end of the takeoff phase. At the start of the takeoff (Figure 2), significant changes were observed in the upper trunk twist angle (F3,36 = 3.6, p = 0.029, = 0.3), shoulder horizontal abduction angle (F3,36 = 8.2, p < 0.001, = 0.5), hip flexion angle (F3,36 = 7, p = 0.001, = 0.46), knee flexion angle (F3,36 = 23.7, p < 0.001, = 0.74), and elbow flexion angle (F3,36 = 8.2, p < 0.001, = 0.5). Specifically, the upper trunk twist angle and shoulder horizontal abduction angle increased significantly with difficulty, showing total gains of 121.1% and 98.6%, respectively. In contrast, the hip flexion angle, knee flexion angle, and elbow flexion angle decreased significantly, with total reductions of 61%, 37.3%, and 74.7%, respectively. These parameters all showed large effect sizes, indicating that changes in joint kinematics due to increased difficulty are not only statistically significant but also practically important for performance adaptation.
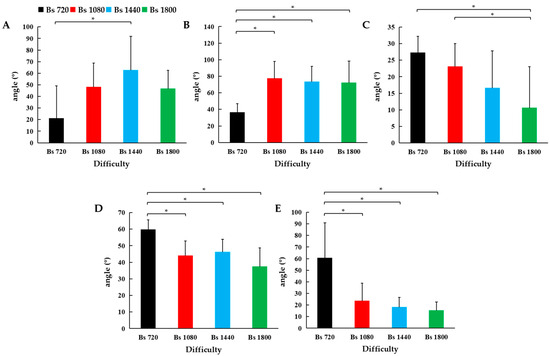
Figure 2.
The joint angles at various difficulty levels at the initial moment of the takeoff phase. (A) Upper trunk twist frontside angle. (B) Shoulder horizontal abduction angle. (C) Hip flexion angle. (D) Knee flexion angle. (E) Elbow flexion angle. Error bars represent the standard deviation (SD) and only show positive values. * indicates a significant difference compared to the previous difficulty level (p < 0.05).
At the end of the takeoff (Figure 3), significant effects were noted for the hip extension angle (F3,36 = 24.3, p < 0.001, = 0.74) and knee flexion angle (F3,36 = 23.7, p < 0.001, = 0.74), with the hip extension angle showing a remarkable total gain of 528%. The knee flexion angle also increased significantly, with a total gain of 55.4%. Both parameters demonstrated large effect sizes, further supporting the practical significance of these kinematic adaptations in response to increased difficulty.
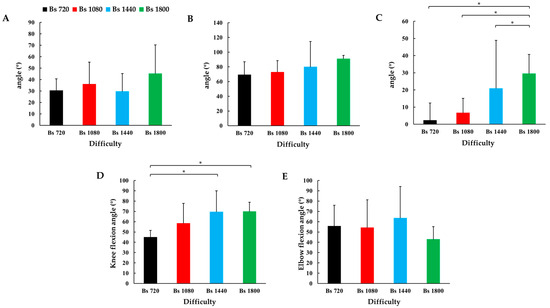
Figure 3.
The joint angles at various difficulty levels at the end of the takeoff phase. (A) Upper trunk twist backside angle. (B) Shoulder horizontal abduction angle. (C) Hip extension angle. (D) Knee flexion angle. (E) Elbow flexion angle. Error bars represent the standard deviation (SD) and only show positive values. * indicates a significant difference compared to the previous difficulty level (p < 0.05).
The range of motion (ROM, Figure 4) for several kinematic variables was significantly affected by difficulty, including the upper trunk twist angle (F3,36 = 11.4, p < 0.001, = 0.58), the shoulder horizontal angle (F3,36 = 13.6, p < 0.001, = 0.62), the hip sagittal angle (F3,36 = 20, p < 0.001, = 0.71), the knee angle (F3,36 = 6.4, p = 0.002, = 0.43), and the elbow angle (F3,36 = 5.7, p = 0.004, = 0.4). The upper trunk twist angle exhibited a total gain of 130.9%, while the shoulder horizontal angle showed a total gain of 98.5%. Similarly, the hip sagittal angle increased by 99.4%, the knee angle by 36.4%, and the elbow angle by 29.4%. All of these effects were large, underscoring the substantial impact of difficulty level on ROM adaptations.
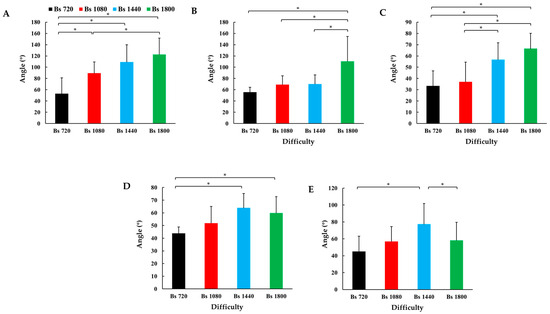
Figure 4.
The range of motion across various difficulty levels during the takeoff phase. (A) Upper trunk twist angle. (B) Shoulder horizontal angle. (C) Hip sagittal angle. (D) Knee angle. (E) Elbow angle. Error bars represent standard deviation (SD) and are displayed in the positive direction only. * indicates a significant difference compared to the previous difficulty level (p < 0.05).
Maximal angular velocities (Figure 5) were significantly influenced by difficulty, with the upper trunk twist angular velocity (F3,36 = 64, p < 0.001, = 0.88) increasing by 1309%. Other significant increases were observed in shoulder horizontal adduction angular velocity (F3,36 = 19.1, p < 0.001, = 0.7), shoulder horizontal abduction angular velocity (F3,36 = 8.41, p < 0.001, = 0.5), hip flexion angular velocity (F3,36 = 8.4, p < 0.001, = 0.5), knee flexion angular velocity (F3,36 = 10.4, p < 0.001, = 0.55) and knee extension angular velocity (F3,36 = 3.4, p = 0.033, = 0.3), indicating that as difficulty increased, the angular velocities of these joints also rose significantly. All these parameters exhibited large effect sizes, further emphasizing the strong influence of difficulty on joint angular velocity adaptations.
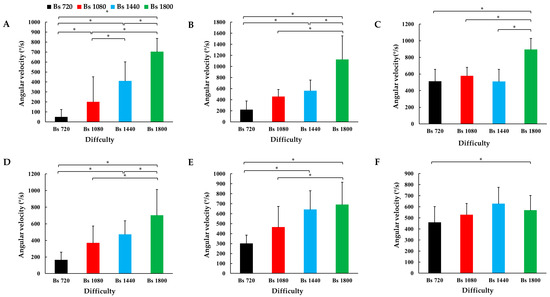
Figure 5.
The maximal angular velocities at different difficulty levels during takeoff phases. (A) Upper trunk twist angular velocity. (B) Shoulder horizontal adduction angular velocity. (C) Shoulder horizontal adduction angular velocity. (D) Hip flexion angular velocity. (E) Knee flexion angular velocity. (F) Knee extension angular velocity. Error bars represent standard deviation (SD) and are displayed in the positive direction only. * indicates a significant difference compared to the previous difficulty level (p < 0.05).
3.3. Moment of Inertia and Rotational Energy
Moment of inertia and rotational energy metrics (Table 2) demonstrated systematic adaptations across increasing difficulty levels, with significant changes in multiple kinematic variables during the takeoff phase. Moment of inertia parameters, including the maximum (F3,36 = 10.2, p < 0.001, = 0.55), range (F3,36 = 16.5, p < 0.001, = 0.66), and average (F3,36 = 29, p < 0.001, = 0.71) moments, progressively increased with difficulty elevation. The range of moment of inertia exhibited the most substantial gain at 152.5%, with significant increments observed across multiple transitions (720–1080, 1080–1440, and 1440–1800). All the moment of inertia parameters showed large effect sizes, highlighting the considerable practical impact of difficulty level on body rotational adaptations during takeoff.

Table 2.
Moments of inertia and rotational energies of SBA athletes across varying difficulty levels during the takeoff phase.
Rotational energy variables similarly showed significant progressive increases, with maximum rotational energy (F3,36 = 7.1, p < 0.001, = 0.37) gaining 139.2%, average rotational energy (F3,36 = 22, p < 0.001, = 0.65) increasing by 176.6%, and departure moment rotation energy (F3,36 = 10.1, p < 0.001, = 0.46) demonstrating a remarkable 310% total gain. The intermediate difficulty transitions, particularly between 1080 and 1440, were crucial, as most parameters exhibited significant adaptations during this phase. Notably, the moment of inertia to rotational energy ratio (F3,36 = 10.1, p < 0.001, = 0.46) decreased significantly by 52.7%, highlighting the complex biomechanical adaptations occurring with increased difficulty levels. These rotational energy-related parameters also showed medium to large effect sizes, underscoring their practical significance in the adaptation to difficulty increases.
4. Discussion
This study investigated adaptations in performance metrics, joint kinematics, moment of inertia, and rotational energy during the SBA takeoff phase across increasing difficulty levels.
The increase in takeoff and flight times reflects the greater preparation and adjustments athletes undertake at higher difficulty levels, requiring enhanced strength and coordination to achieve effective takeoff and flight stability [26]. This is consistent with findings in figure skating and trampoline studies [27,28], where longer takeoff and flight times are associated with more complex maneuvers that demand precise timing and body control. The rise in flight height suggests improved technical proficiency and strength adaptations, as athletes refine takeoff techniques and increase power output, likely attributable to enhanced muscle strength and explosive capacity [29]. Similar observations in ski jumping research indicate that higher flight heights are linked to better takeoff mechanics and superior lower-body power [30]. The observed increases in departure velocity and angle are indicative of dynamic adjustments during takeoff, with higher velocities representing greater force generation and optimal angles facilitating efficient energy transfer [12,26]. Supporting evidence from ski jumping and figure skating underscores the critical importance of accurately controlling both velocity and angle to maximize performance during complex jumps [31,32].
The analysis of joint kinematics during the takeoff initiation phase in SBA revealed key biomechanical adjustments as difficulty increased. The upper trunk twist angle and shoulder horizontal abduction angle increased significantly, indicating enhanced rotational momentum and stability. In contrast, hip, knee, and elbow flexion angles decreased, reflecting a more extended body posture to optimize force generation and propulsion. These adaptations are consistent with previous research, which emphasizes the importance of minimizing joint flexion to improve vertical force production and maximizing trunk rotation for better rotational control [12].
The kinematic changes observed at the end of the takeoff phase in SBA are critical for executing flight maneuvers. Increased hip extension enhances rotational dynamics and body alignment during spins and flips, optimizing force transfer from the lower to the upper body to achieve greater propulsion and flight height [33,34]. At the same time, increased knee flexion plays an important role in preparing for aerial maneuvers by refining motion control and ensuring stability and fluidity in the air [35]. These adjustments not only improve the efficiency of force transmission but also provide the necessary body coordination for complex technical movements, underscoring the importance of integrated lower and upper body actions in snowboard performance.
As maneuver difficulty increases, athletes significantly adjust the range of motion (ROM) of various kinematic variables to optimize performance. Enhanced ROM in upper trunk twist and shoulder horizontal abduction generates greater rotational momentum, thereby improving stability and fluidity during aerial maneuvers. For example, in gymnastics, increased ROM in the upper trunk and shoulders is essential for maintaining stability during flight [36]. Greater hip and knee ROM enable better force transfer and propulsion, resulting in higher takeoff height and faster rotational speed [37]. Adjustments in elbow ROM allow for more precise control during takeoff, contributing to stability and balance for subsequent flight actions [38]. These adaptations highlight the importance of coordinated upper and lower body movements when executing complex technical maneuvers at higher difficulty levels.
As maneuver difficulty increases, athletes demonstrate significant adaptive changes in joint angular velocities. The rise in upper trunk twist angular velocity enhances rotational momentum, thereby optimizing stability and fluidity during flight. Similarly, increased shoulder horizontal adduction angular velocity underscores the importance of coordinated upper limb movements for boosting rotational capacity and maintaining balance. These findings are consistent with previous research in high-performance sports such as gymnastics and figure skating, where effective management of joint angular velocity has been linked to improved performance [39,40]. Additionally, the increase in hip flexion angular velocity suggests that athletes optimize hip movements to improve force transfer and propulsion, leading to greater takeoff height and rotational speed [41]. Collectively, these adaptations highlight the critical role of coordinated joint actions in enabling high-difficulty maneuvers, providing essential biomechanical support for complex technical executions.
Contrary to conventional expectations, the moment of inertia during the takeoff phase increased as trick difficulty rose. This phenomenon can be attributed to two key biomechanical adjustments: greater body extension and more pronounced push-off actions. Traditionally, a smaller moment of inertia is associated with faster rotational speeds, as seen in figure skating and gymnastics [15,42]. However, most related research focuses on the flight phase rather than takeoff, making direct comparisons limited. Unlike other aerial sports, SBA takeoffs are uniquely influenced by an unstable, variable snow surface and high-speed approach, requiring athletes to constantly adjust posture and push-off mechanics to maintain balance and generate sufficient force for complex maneuvers. These sport-specific demands lead to increased body extension, push-off force, and moment of inertia during takeoff.
In SBA, a more extended body posture is adopted during takeoff to optimize force generation and propulsion [9], which naturally increases the moment of inertia by distributing mass farther from the axis of rotation [43]. Adjustments in limb and trunk positioning can independently affect both moment of inertia and performance [44], serving not just to manage inertia, but also to enhance stability, control, or safety in more difficult tricks. Thus, the increase in moment of inertia may reflect both the need for greater force and strategic adaptation. Furthermore, more pronounced push-off actions, with greater lower limb extension and force output, also contribute to increased inertia [45], which is essential for maximizing vertical force and takeoff height required for complex aerial maneuvers.
The increase in moment of inertia is closely associated with the observed enhancement in rotational energy. During takeoff, athletes generate greater force to overcome the larger moment of inertia, ensuring sufficient rotational momentum for complex tricks. Notably, the decreased ratio of moment of inertia to rotational energy indicates that athletes achieve higher rotational energy with a relatively smaller increase in inertia, thereby improving rotational efficiency. This finding underscores athletes’ ability to balance stability and rotational speed by optimizing body posture and push-off mechanics.
The stepwise analysis from performance metrics to kinematic characteristics, and further to moment of inertia and rotational energy, reveals a cohesive biomechanical strategy adopted by athletes during the takeoff phase. Enhanced outcomes such as longer flight times and greater flight heights are achieved through kinematic adjustments—like increased body extension and optimized joint angles—that improve force generation and propulsion. These changes, particularly in joint angular velocities, are closely interrelated: increased upper trunk twist velocity boosts rotational momentum for aerial maneuvers; higher shoulder adduction velocity refines in-air balance and body control; and greater hip flexion velocity enables a more powerful takeoff as well as efficient energy transfer from the lower to the upper body. The coordination among these joint actions ensures the upward transmission of kinetic energy and precise adjustment of rotational control, supporting both stability and rotational efficiency. These kinematic adaptations, in turn, impact moment of inertia and rotational energy—athletes balance increased rotational resistance with maximal force output to meet the demands of more difficult maneuvers. Altogether, these findings highlight the integrated and synchronized biomechanical adjustments that optimize SBA performance as trick difficulty increases.
The comparison between SBA and other sports such as gymnastics and figure skating is based on shared technical features in takeoff actions and similar requirements for strength, coordination, and flexibility. These overlaps suggest the potential for skill transfer and shared training insights across disciplines. However, the unique characteristics of SBA—such as the unstable snow surface and varying approach speeds—impose distinct biomechanical demands. Comparative analysis that identifies these sport-specific parameters can help refine training strategies and technical development for SBA athletes.
Based on these findings, we recommend that coaches and athletes implement targeted interventions to optimize performance in high-difficulty SBA maneuvers. Training should prioritize enhancing lower limb strength and explosive power through exercises such as squats, box jumps, and depth jumps to improve takeoff velocity and flight height [46,47]. Increasing trunk and shoulder flexibility and strength is also crucial; for shoulder conditioning, exercises such as dumbbell shoulder presses, lateral raises, bent-over reverse flyes, banded shoulder abductions, arm circles, and scapular wall slides are suggested to boost shoulder power, mobility, and stability [48,49]. Joint mobility exercises—including lunges with trunk rotation and dynamic stretching for the hips, knees, and elbows—can facilitate more effective force transfer and body coordination [50]. Additionally, incorporating drills such as agility ladder exercises and balance board training can help develop full-body coordination, timing, and precise body positioning required for complex tricks [51]. Finally, utilizing video analysis and slow-motion feedback during simulated takeoff and flight drills can further assist athletes in refining body posture and optimizing joint mechanics for both performance and safety [52].
This study has several limitations that should be acknowledged. First, the sampling frequency used may not have fully captured instantaneous peak acceleration and angular acceleration during snowboarding maneuvers. Although similar rates have been adopted in previous research [16,53,54], future studies are encouraged to utilize higher sampling frequencies to improve the accuracy of kinetic and kinematic measurements. Second, all experiments were conducted on dry ski slopes, which differ from natural snow in surface properties such as friction and hardness [55], so the findings may not be entirely representative of performance on natural snow. Future research should collect and compare data in real snow environments to enhance ecological validity. Third, potential learning or adaptation effects across the repeated trials cannot be completely ruled out, as participants may have improved their performance through practice, potentially influencing the results despite familiarization procedures. Fourth, this study focused exclusively on backside rotations, limiting the generalizability of the findings to other rotation directions or trick types. Finally, the relatively small number of female participants resulted in an unbalanced gender distribution, which may restrict the applicability of the findings to female snowboarders. To address these limitations, future research should employ higher-frequency motion capture systems, test under both dry slope and natural snow conditions, randomize trial orders to minimize learning effects, include a broader range of movements, and recruit larger and more gender-balanced samples to further validate and extend the current findings.
5. Conclusions
This study demonstrates that elite SBA athletes exhibit systematic biomechanical adaptations when performing increasingly difficult rotational tricks. Athletes increase the moment of inertia and optimize body positioning to enhance propulsion, leading to significant gains in rotational energy and efficiency. Joint kinematic changes, such as greater upper trunk twist angles and more extended postures, allow athletes to maintain both stability and rotational velocity during high-difficulty tricks. These findings offer new perspectives for snowboard training, highlighting the importance of control and propulsion in advanced maneuvers. Based on these results, we recommend that training prioritizes improvements in lower limb power, trunk and shoulder strength and flexibility, and overall coordination. Targeted strength, mobility, balance, and technique drills combined with video feedback can help athletes optimize performance and safety in high-difficulty maneuvers. Nevertheless, this study is limited by modest sampling frequency, testing only on dry slopes, possible learning effects from repeated trials, focus on backside rotations, and an unbalanced gender sample. Future research should address these issues to improve the validity and generalizability of the findings.
Author Contributions
Conceptualization, L.J., B.H. and Q.S.; methodology, L.J., B.H. and Q.S.; software, L.J. and Q.S.; validation, L.J. and Q.S.; formal analysis, L.J.; investigation, L.J.; resources, B.H.; data curation, L.J., X.C., X.G., Y.L. and T.G.; writing—original draft preparation, L.J.; writing—review and editing, L.J., B.H. and Q.S.; visualization, L.J.; supervision, B.H.; project administration, B.H.; funding acquisition, B.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China under Grant [2018YFF0300800] (BH).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the ethics committee of Capital University of Physical Education and Sports (protocol code: 2022A64, date of approval: 11 November 2022).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The datasets utilized and analyzed in this study are accessible from the corresponding authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SBA | Snowboard Big Air |
| Bs | Backside |
References
- FIS. Snowboard & Freeski Park & Pipe Judges Handbook; FIS, Ed.; FIS: Jacksonville, FL, USA, 2023. [Google Scholar]
- Harding, J.W.; James, D.A. Performance assessment innovations for elite snowboarding. Procedia Eng. 2010, 2, 2919–2924. [Google Scholar] [CrossRef]
- Tsai, M.; Chua, J.; Sheppard, J. Competition trick analysis in snowboard slopestyle and big air. J. Hum. Sport Exerc. 2023, 18, 526–533. [Google Scholar] [CrossRef]
- Thomson, C.; Morton, K.; Carlson, S.; Rupert, J.L. The Contextual Sensation Seeking Questionnaire for skiing and snowboarding (CSSQ-S) Development of a sport specific scale. Int. J. Sport Psychol. 2012, 43, 503–521. [Google Scholar]
- Schindelwig, K.; Platzer, H.; Mössner, M.; Nachbauer, W. Safety recommendations of winter terrain park jumps into airbags. J. Sci. Med. Sport 2019, 22, S50–S54. [Google Scholar] [CrossRef]
- Wolfsperger, F.; Meyer, F.; Gilgien, M. Towards more valid simulations of slopestyle and big air jumps: Aerodynamics during in-run and flight phase. J. Sci. Med. Sport. 2021, 24, 1082–1087. [Google Scholar] [CrossRef]
- Platzer, H.P.; Raschner, C.; Patterson, C.; Lembert, S. Comparison of physical characteristics and performance among elite snowboarders. J. Strength Cond. Res. 2009, 23, 1427–1432. [Google Scholar] [CrossRef]
- Staniszewski, M. Biomechanical conditions of maintaining balance in snowboarding. J. Sport Med. Phys. Fit. 2019, 59, 1870–1877. [Google Scholar] [CrossRef] [PubMed]
- Bacik, B.; Kurpas, W.; Marszalek, W.; Wodarski, P.; Sobota, G.; Starzyński, M.; Gzik, M. Movement Variability During the Flight Phase in a Single Back Sideflip (Wildcat) in Snowboarding. J. Hum. Kinet. 2020, 72, 29–37. [Google Scholar] [CrossRef]
- Hoholm, S.L. “Pop” and Its Relation to Performance Factors and Equivalent Fall Height in World Cup Slopestyle for Skiers and Snowboarders. Master’s Thesis, Norwegian School of Sport Sciences, Oslo, Norway, 2022. [Google Scholar]
- Linlokken, M. A Biomechanical Analysis of How Rider Behavior and Equivalent Fall Height Affect Landing Stability in World Cup Slopestyle for Freeski and Snowboard. Master’s Thesis, Norwegian School of Sport Sciences, Oslo, Norway, 2022. [Google Scholar]
- Piiparinen, M. The Effect of a Change in the Difficulty Level of the Big Air Jump Take-Off Phase in Joint Kinematics of Snowboarding Athletes. Master’s Thesis, University of Jyvaskyla, Jyvaskyla, Finland, 2022. [Google Scholar]
- Hao, W.; Wang, Z.; Ai, K. Changes of Moment of Inertia in Posture Control during Somersaults and Twists of Athletes. Chin. J. Sports Med. 2013, 32, 966–973. [Google Scholar]
- King, D.L.; Smith, S.L.; Brown, M.R.; McCrory, J.L.; Munkasy, B.A.; Scheirman, G.I. Comparison of split double and triple twists in pair figure skating. Sports Biomech. 2008, 7, 222–237. [Google Scholar] [CrossRef]
- Mikl, J.; Rye, D.C. Twist within a somersault. Hum. Mov. Sci. 2016, 45, 23–39. [Google Scholar] [CrossRef]
- Klous, M.; Müller, E.; Schwameder, H. Three-Dimensional Lower Extremity Joint Loading in a Carved Ski and Snowboard Turn: A Pilot Study. Comput. Math. Method Med. 2014, 2014, 340272. [Google Scholar] [CrossRef]
- Jonsson, M.; Welde, B.; Stoggl, T.L. Biomechanical differences in double poling between sexes and level of performance during a classical cross-country skiing competition. J. Sport Sci. 2019, 37, 1582–1590. [Google Scholar] [CrossRef]
- Ostrek, M.; Rhodin, H.; Fua, P.; Müller, E.; Spörri, J. Are Existing Monocular Computer Vision-Based 3D Motion Capture Approaches Ready for Deployment? A Methodological Study on the Example of Alpine Skiing. Sensors 2019, 19, 4323. [Google Scholar] [CrossRef] [PubMed]
- Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. DeepLabCut: Markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci. 2018, 21, 1281. [Google Scholar] [CrossRef]
- Hay, J.G. The Biomechanics of Sports Techniques; Prentice-Hall: Saddle River, NJ, USA, 1993; ISBN 9780130845344. [Google Scholar]
- Yu, B.; Gabriel, D.; Noble, L.; An, K.-N. Estimate of the optimum cutoff frequency for the Butterworth low-pass digital filter. J. Appl. Biomech. 1999, 15, 318–329. [Google Scholar] [CrossRef]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D’Lima, D.D.; Cristofolini, L.; Witte, H.; et al. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion—Part I: Ankle, hip, and spine. J. Biomech. 2002, 35, 543–548. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; van der Helm, F.C.T.; DirkJan Veeger, H.E.J.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef]
- Liu, H.; Leigh, S.; Yu, B. Sequences of upper and lower extremity motions in javelin throwing. J. Sports Sci. 2010, 28, 1459–1467. [Google Scholar] [CrossRef]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Wilson, C.; King, M.A.; Yeadon, M.R. The effects of initial conditions and takeoff technique on running jumps for height and distance. J. Biomech. 2011, 44, 2207–2212. [Google Scholar] [CrossRef]
- Albert, W.J.; Miller, D.I. Takeoff characteristics of single and double axel figure skating jumps. J. Appl. Biomech. 1996, 12, 72–87. [Google Scholar] [CrossRef]
- Heinen, T.; Krepela, F. Evaluating routines in trampoline gymnastics. Sci. Gymnast. J. 2016, 8, 229. [Google Scholar] [CrossRef]
- Eythorsdottir, I.; Gloersen, O.; Rice, H.; Werkhausen, A.; Ettema, G.; Mentzoni, F.; Solberg, P.; Lindberg, K.; Paulsen, G. The Battle of the Equations: A Systematic Review of Jump Height Calculations Using Force Platforms. Sports Med. 2024, 54, 2771–2791. [Google Scholar] [CrossRef]
- Vodicar, J.; Coh, M.; Jost, B. Kinematic Structure at the Early Flight Position in Ski Jumping. J. Hum. Kinet. 2012, 35, 35–45. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Elfmark, O.; Ettema, G.; Groos, D.; Ihlen, E.A.F.; Velta, R.; Haugen, P.; Braaten, S.; Gilgien, M. Performance Analysis in Ski Jumping with a Differential Global Navigation Satellite System and Video-Based Pose Estimation. Sensors 2021, 21, 5318. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, X.; Wang, X.; Chen, L.; Zhao, T. Performance and Biomechanics in the Flight Period of Ski Jumping: Influence of Ski Attitude. Biology 2022, 11, 671. [Google Scholar] [CrossRef]
- Kong, P.W. Hip extension during the come-out of multiple forward and inward pike somersaulting dives is controlled by eccentric contraction of the hip flexors. J. Sports Sci. 2010, 28, 537–543. [Google Scholar] [CrossRef]
- Kyselovicová, O.; Zemková, E. The effects of aerobic gymnastics training on performance-related variables in an elite athlete: A 2-year follow-up study. Front. Physiol. 2024, 15, 1380024. [Google Scholar] [CrossRef]
- Markström, J.L.; Grip, H.; Schelin, L.; Häger, C.K. Dynamic knee control and movement strategies in athletes and non-athletes in side hops: Implications for knee injury. Scand. J. Med. Sci. Sports 2019, 29, 1181–1189. [Google Scholar] [CrossRef]
- Mkaouer, B.; Jemni, M.; Amara, S.; Chaabène, H.; Tabka, Z. Kinematic and Kinetic Analysis of Two Gymnastics Acrobatic Series to Performing the Backward Stretched Somersault. J. Hum. Kinet. 2013, 37, 17–26. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Göpfert, C.; Holmberg, H.C.; Stöggl, T.; Müller, E.; Lindinger, S.J. Biomechanical characteristics and speed adaptation during kick double poling on roller skis in elite cross-country skiers. Sports Biomech. 2013, 12, 154–174. [Google Scholar] [CrossRef] [PubMed]
- Cabell, L.; Bateman, E. Biomechanics in Figure Skating. In The Science of Figure Skating; Routledge: Abingdon, UK, 2018; ISBN 9781315387741. [Google Scholar]
- Horri, Z.; Lenjannejadian, S.; Boroujeni, M.R.; Farazin, A. Kinematics of take-off phase in successful and unsuccessful performances of gymnastic somersault: An experimental study. Sport Sci. Health 2022, 18, 219–225. [Google Scholar] [CrossRef]
- Sands, W.A.; Kimmel, W.L.; McNeal, J.R.; Murray, S.R.; Stone, M.H. A comparison of pairs figure skaters in repeated jumps. J. Sports Sci. Med. 2012, 11, 102–108. [Google Scholar] [PubMed]
- Clark, K.P.; Meng, C.R.; Stearne, D.J. ‘Whip from the hip’: Thigh angular motion, ground contact mechanics, and running speed. Biol. Open 2020, 9, bio053546. [Google Scholar] [CrossRef]
- Ridge, S.T.; McLean, D.; Bruening, D.; Richards, J. Up in the air: The efficacy of weighted gloves in figure skating jumps. Sports Biomech. 2022, 23, 2637–2648. [Google Scholar] [CrossRef]
- Hora, M.; Soumar, L.; Pontzer, H.; Sládek, V. Body size and lower limb posture during walking in humans. PLoS ONE 2017, 12, e0172112. [Google Scholar] [CrossRef]
- Sasaki, S.; Nagano, Y.; Kaneko, S.; Sakurai, T.; Fukubayashi, T. The relationship between performance and trunk movement during change of direction. J. Sports Sci. Med. 2011, 10, 112–118. [Google Scholar]
- Turnbull, J.; Keogh, J.W.; Kilding, A.E. Strength and conditioning considerations for elite snowboard half pipe. Open Sports Med. J. 2011, 5, 1–11. [Google Scholar] [CrossRef]
- Markovic, G. Does plyometric training improve vertical jump height? A meta-analytical review. Br. J. Sports Med. 2007, 41, 349–355. [Google Scholar] [CrossRef]
- Bai, Y.; Zheng, Z.; Gong, B.; Shen, Y. Effects of different drop height training on lower limb explosive, anaerobic power, and change of direction performance in Chinese elite female wrestler. Heliyon 2024, 10, e38146. [Google Scholar] [CrossRef] [PubMed]
- Compos, Y.; Vianna, J.M.; Guimaraes, M.P.; Oliveira, J.L.D.; Hernández-Mosqueira, C.; da Silva, S.F.; Marchetti, P.H. Different Shoulder Exercises Affect the Activation of Deltoid Portions in Resistance-Trained Individuals. J. Hum. Kinet. 2020, 75, 5–14. [Google Scholar] [CrossRef]
- Ozdamar, S.; Agopyan, A.; Uzun, S. The effects of dumbbell versus TRX suspension training on shoulder strength, vertical jump, and spike speed in volleyball players. Isokinet. Exerc. Sci. 2024, 32, 109–123. [Google Scholar] [CrossRef]
- Skopal, L.K.; Drinkwater, E.J.; Behm, D.G. Application of mobility training methods in sporting populations: A systematic review of performance adaptations. J. Sports Sci. 2024, 42, 46–60. [Google Scholar] [CrossRef] [PubMed]
- González-Fernández, F.T.; Sarmento, H.; Castillo-Rodríguez, A.; Silva, R.; Clemente, F.M. Effects of a 10-Week Combined Coordination and Agility Training Program on Young Male Soccer Players. Int. J. Environ. Res. Public Health 2021, 18, 10125. [Google Scholar] [CrossRef]
- Barris, S.; Button, C. A Review of Vision-Based Motion Analysis in Sport. Sports Med. 2008, 38, 1025–1043. [Google Scholar] [CrossRef] [PubMed]
- Spoerri, J.; Kroell, J.; Schwameder, H.; Müller, E. The role of path length- and speed-related factors for the enhancement of section performance in alpine giant slalom. Eur. J. Sport. Sci. 2018, 18, 911–919. [Google Scholar] [CrossRef]
- Scheiber, P.; Seifert, J.; Mueller, E. Relationships between biomechanics and physiology in older, recreational alpine skiers. Scand. J. Med. Sci. Sports 2012, 22, 49–57. [Google Scholar] [CrossRef]
- Wolfsperger, F.; Meyer, F.; Gilgien, M. The Snow-Friction of Freestyle Skis and Snowboards Predicted from Snow Physical Quantities. Front. Mech. Eng. 2021, 7, 728722. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).