Identification of Structural Sealant Damage in Hidden Frame Glass Curtain Wall Based on Curvature Mode
Abstract
1. Introduction
2. Experimental Method
2.1. Theoretical Background
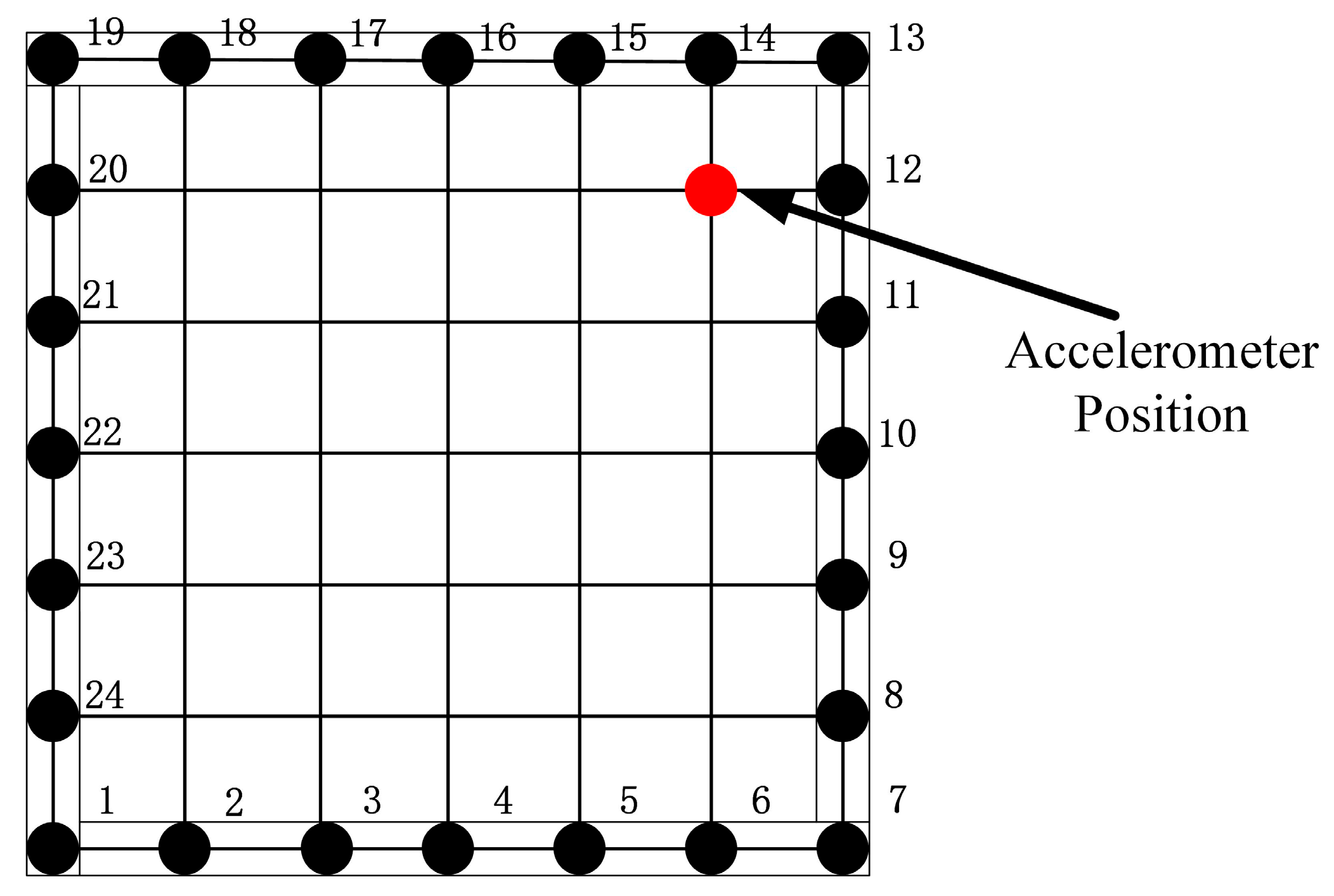
2.2. Experimental Program
3. Results and Discussions
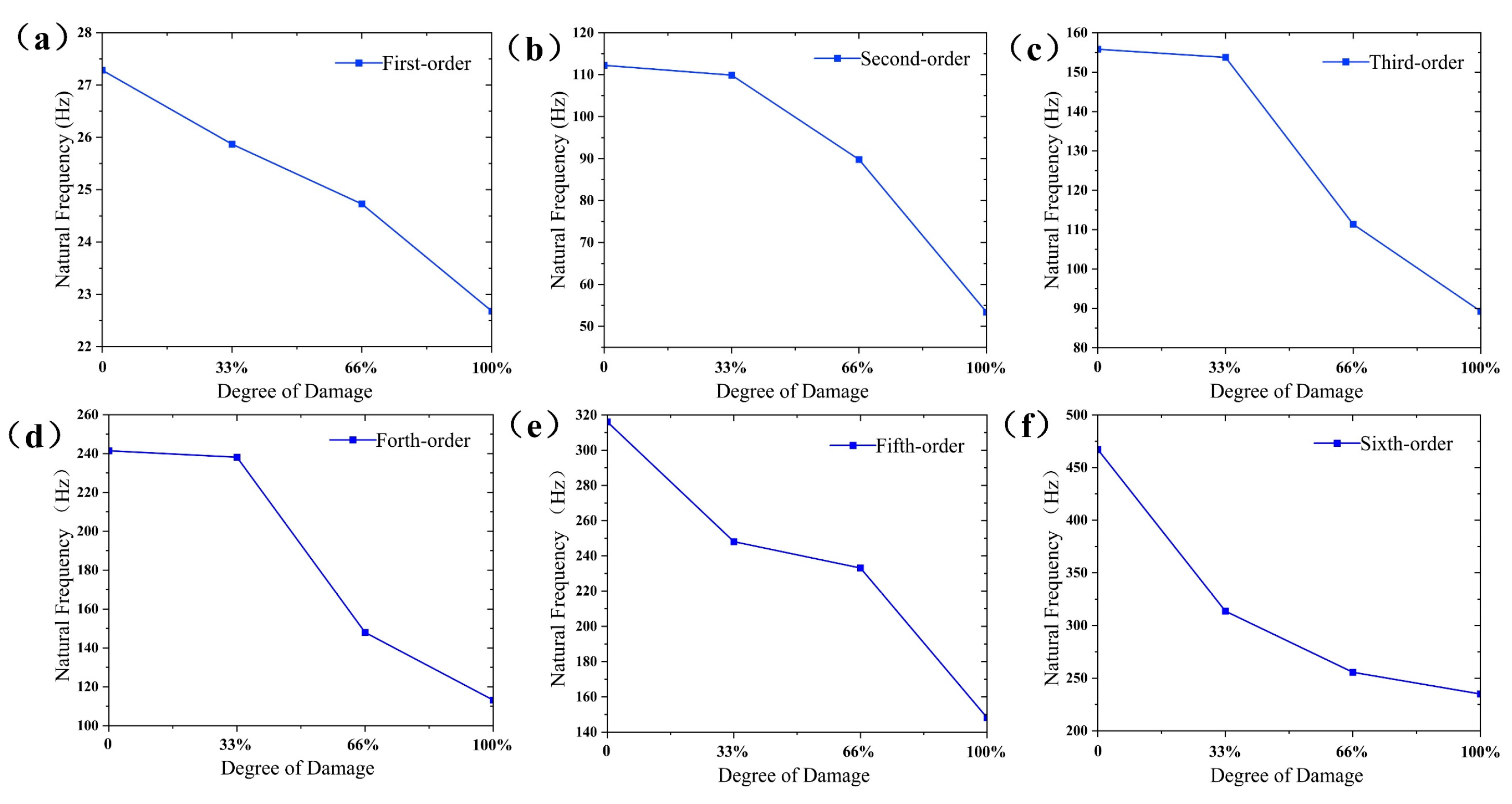
3.1. Damage Identification Based on Natural Frequency
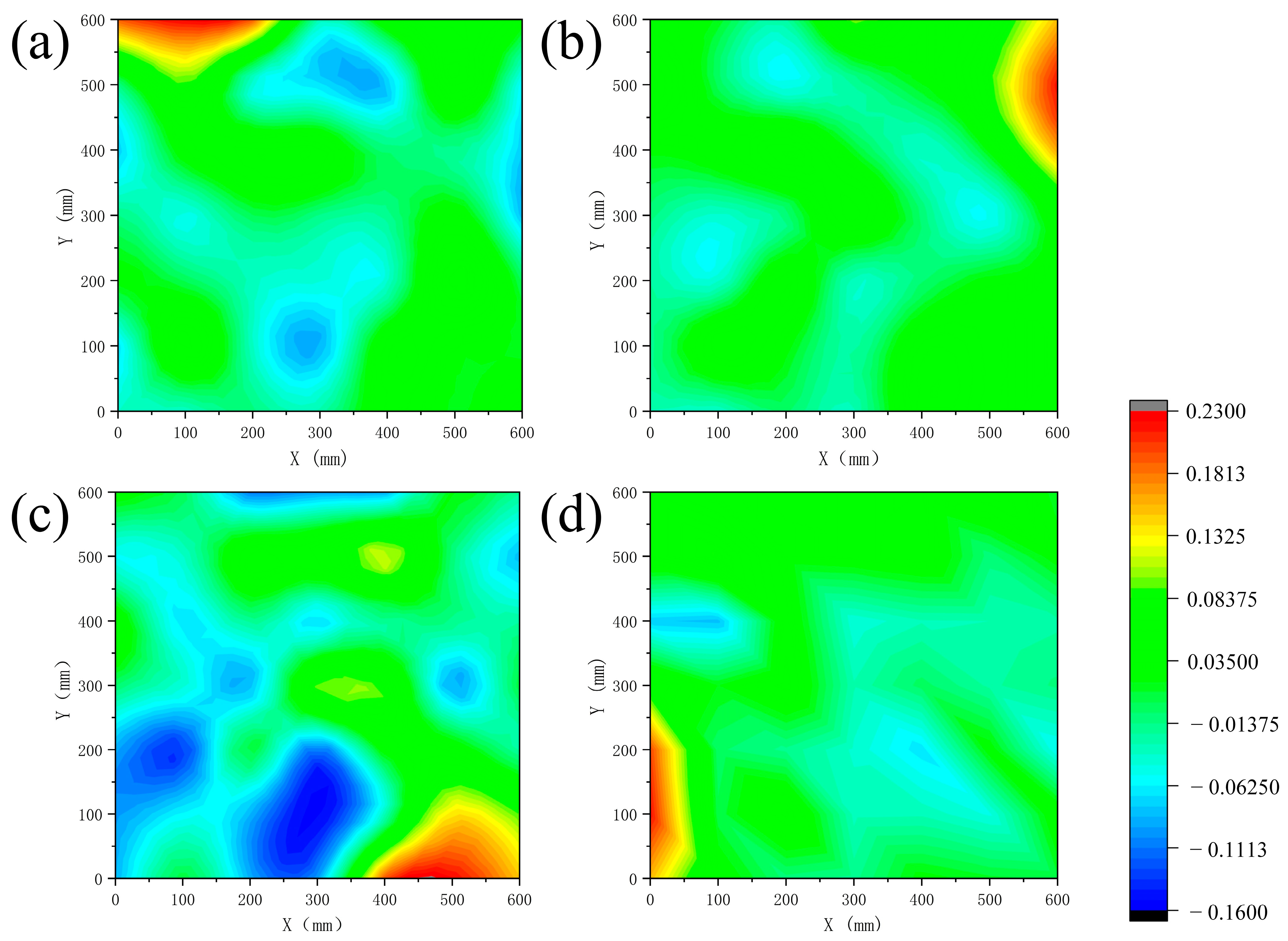
3.2. Damage Identification Based on Curvature Mode Difference
3.3. Quantitative Analysis of Curvature Mode Difference Damage Identification
3.4. Damage Identification Method Based on Boundary Modes
4. Conclusions
- (1)
- The FCMD values in damaged sealant regions are significantly higher than in intact areas, allowing accurate determination of damage extent and location through peak distribution analysis.
- (2)
- Based on boundary node FCMD distribution characteristics, a damage threshold of 0.1205 is established for quantitative damage detection. This threshold is validated using boundary modal data, achieving 100% verification accuracy. Specifically, structural sealant damage is confirmed when FCMD exceeds 0.1205.
- (3)
- Modal data classification reveals that boundary modes are more effective for damage identification than internal modes. Consequently, the modal test is optimized by reducing measurement points to 24 boundary nodes, halving the testing workload while maintaining FCMD accuracy. This boundary-specific approach enhances diagnostic reliability and practical applicability, streamlining structural sealant inspection in HFGCWs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Z.; Xie, M.; Chen, C.; Du, Y.; Zhao, J. Engineering application of a safety-state evaluation model for hidden frame-supported glass curtain walls based on remote vibration. J. Build. Eng. 2019, 26, 100915. [Google Scholar] [CrossRef]
- Huang, T.-T.; Zhang, D.-W.; Zhao, Y.-X.; Liu, J.-J.; Li, J.-H. Comprehensive appraisal of the safety of hidden frame glass curtain wall based on fuzzy theory. J. Build. Eng. 2019, 26, 100863. [Google Scholar]
- Liu, X.G.; Bao, Y.W. Reliability Evaluation of Glass Curtain Wall via Vibration Detection. Key Eng. Mater. 2012, 492, 410–414. [Google Scholar] [CrossRef]
- Hong, X.; Lin, J.; Liu, Y.; Xu, W. Active thermal sensing for bonding structure damage detection of hidden frame glass curtain wall. Sensors 2018, 18, 3594. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Guo, T.; Zhi, G.; Hu, Z. A Novel Debonding Damage Identification Approach of Hidden Frame-Supported Glass Curtain Walls Based on UAV-LDV System. Appl. Sci. 2024, 14, 5412. [Google Scholar] [CrossRef]
- Hong, X.; Liu, Y.; Liufu, Y.; Lin, P. Debonding detection in hidden frame supported glass curtain walls using the nonlinear ultrasonic modulation method with piezoceramic transducers. Sensors 2018, 18, 2094. [Google Scholar] [CrossRef]
- Hong, X.; Liu, Y.; Lin, P.; Xu, W. Interfacial adhesion–strength detection of structural silicone sealant for hidden frame–supported glass curtain wall based on nonlinear ultrasonic Lamb wave. J. Aerosp. Eng. 2018, 31, 04018047. [Google Scholar] [CrossRef]
- Lin, J.; Hong, X.; Ren, Z. Laser in-depth heating thermal wave detection of adhesive debonding in glass curtain walls: Numerical simulation and experiment. Measurement 2021, 177, 109268. [Google Scholar] [CrossRef]
- Xu, D.; Wang, Y.; Xie, J. Monitoring and Analysis of building curtain wall deformation based on optical fiber sensing technology. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 3081–3091. [Google Scholar] [CrossRef]
- Mojškerc, B.; Kek, T.; Grum, J. Pulse-Echo Ultrasonic Testing of Adhesively Bonded Joints in Glass Façades. J. Mech. Eng. 2016, 62, 147–153. [Google Scholar] [CrossRef]
- Brusa, E.; Bruzzone, F.; Delprete, C.; Di Maggio, L.G.; Rosso, C. Health indicators construction for damage level assessment in bearing diagnostics: A proposal of an energetic approach based on envelope analysis. Appl. Sci. 2020, 10, 8131. [Google Scholar] [CrossRef]
- Rucka, M. Non-destructive testing of structures. Materials 2020, 13, 4996. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Yu, F.; Qian, J.; An, B.; Duan, N. An Intelligent Fault Diagnosis Model for Rolling Bearings Based on IGTO-Optimized VMD and LSTM Networks. Appl. Sci. 2025, 15, 4338. [Google Scholar] [CrossRef]
- Liu, W.; Luo, Q.; Dai, G.; Tang, X. Experimental and Numerical Study on Dynamic Response of High-Pier Ballastless Continuous Beam Bridge in Mountainous Area. Appl. Sci. 2025, 15, 4341. [Google Scholar] [CrossRef]
- Yi, Q.; Wu, Z.; Zhao, L.; Li, Z.; Wang, S. Flexural Wave Propagation and Defect States of Periodic Slab Track Structure in High-Speed Railway. Appl. Sci. 2025, 15, 1070. [Google Scholar] [CrossRef]
- Zheng, H.; He, D.; Guo, T.; Chen, Z. A new damage identification approach of HFSGCW based on LDV and wavelet packet band energy method. J. Build. Eng. 2024, 95, 110113. [Google Scholar] [CrossRef]
- Jiang, K.; Pan, D.; Huang, Y.; Fu, X. Construction defect identification for structural sealant by statistical driving-point accelerance. Constr. Build. Mater. 2023, 392, 131817. [Google Scholar] [CrossRef]
- Pan, D.; Jiang, K.; Zhang, X.; Huang, Y. Sealant Delamination Detection of Structural Sealant Glazing Systems Based on Driving-Point Accelerance. Shock Vib. 2020, 2020, 7260438. [Google Scholar] [CrossRef]
- Gu, J.; Hao, W.; Luo, Y. Investigation of damage identification for glass curtain wall based on Hilbert-Huang transform and transmissibility function. Int. J. Model. Identif. Control 2011, 13, 38–45. [Google Scholar] [CrossRef]
- Yang, G.; Long, X.; Wang, X.; Liu, X.; Li, H.; Liu, Z. Structural adhesive damage identification of glass curtain wall. Nonlinear Dyn. 2022, 110, 2573–2587. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Nguyen, Q.B.; Bui-Tien, T.; De Roeck, G.; Wahab, M.A. Damage detection in girder bridges using modal curvatures gapped smoothing method and Convolutional Neural Network: Application to Bo Nghi bridge. Theor. Appl. Fract. Mech. 2020, 109, 102728. [Google Scholar] [CrossRef]
- Xiang, C.-S.; Li, L.-Y.; Zhou, Y.; Yuan, Z. Damage identification method of beam structure based on modal curvature utility information entropy. Adv. Civ. Eng. 2020, 2020, 8892686. [Google Scholar] [CrossRef]
- Chinka, S.S.B.; Putti, S.R.; Adavi, B.K. Modal testing and evaluation of cracks on cantilever beam using mode shape curvatures and natural frequencies. Structures 2021, 32, 1386–1397. [Google Scholar] [CrossRef]
- Khiem, N.T. Mode shape curvature of multiple cracked beam and its use for crack identification in beam-like structures. Vietnam J. Mech. 2020, 42, 123–132. [Google Scholar] [CrossRef]
- He, M.; Yang, T.; Du, Y. Nondestructive identification of composite beams damage based on the curvature mode difference. Compos. Struct. 2017, 176, 178–186. [Google Scholar] [CrossRef]
- Hakim, S.; Mhaya, A.; Noh, M.; Paknahad, M.; Tami, H.; Alshalif, A. Utilizing mode shape curvature and artificial neural networks for structural damage assessment in beam-like structures. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Langkawi, Malaysia, 18–19 September 2024; p. 012013. [Google Scholar]
- Pandey, A.; Biswas, M.; Samman, M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Wang, Q.-m.; Zhu, R.-h.; Zheng, J.-h.; Wang, N.; Luo, M.-y.; Che, Y.-f. A method for the damage detection of pile foundation in high-pile wharf based on a curvature mode deletion model. China Ocean Eng. 2020, 34, 871–880. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, K.; Pan, D.; Fu, X.; Hu, N. A Two-Stage Damage Localization Method for Structural Sealants Based on Boundary Modal Curvature. Appl. Sci. 2024, 14, 9641. [Google Scholar] [CrossRef]
- Li, W.; Liu, Y.; Yuan, X.; Li, Q.; Zhou, G. Rail hidden damage detection based on the modal curvature differences method. Adv. Mech. Eng. 2024, 16, 16878132241279500. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, J.; Xie, Y.; Xu, J. Warship damage identification using mode curvature shapes method. Appl. Ocean Res. 2022, 129, 103396. [Google Scholar] [CrossRef]
- Boscato, G.; Civera, M.; Zanotti Fragonara, L. Recursive partitioning and Gaussian process regression for the detection and localization of damages in pultruded glass fiber reinforced polymer material. Struct. Control Health Monit. 2021, 28, e2805. [Google Scholar] [CrossRef]
- Civera, M.; Boscato, G.; Fragonara, L.Z. Treed gaussian process for manufacturing imperfection identification of pultruded GFRP thin-walled profile. Compos. Struct. 2020, 254, 112882. [Google Scholar] [CrossRef]
- Rabiepour, M.; Zhou, C.; Chase, J.G. A Hysteresis Model Incorporating Varying Pinching Stiffness and Spread for Enhanced Structural Damage Simulation. Appl. Sci. 2025, 15, 724. [Google Scholar] [CrossRef]
- Chen, C.; Xie, M.; Du, Y.; Pang, W. A new method of safety detection in high-rise building curtain walls based on natural vibration frequency. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Zhuhai, China, 15–17 January 2021; p. 012092. [Google Scholar]
- Wang, Z.; Liu, X.; Cao, D.; Wan, D.; Wei, S. Detection and safety assessment of bonding defects in architectural decorative surface layer based on the variation of vibration acceleration amplitude. Case Stud. Constr. Mater. 2025, 22, e04278. [Google Scholar] [CrossRef]
- Back, J.H.; Bae, J.B.; Kang, J.H.; Kim, J.J. Comparing Bolt Implementation Methods in Vibration Testing for Accurate Dynamic Behavior Analysis. Appl. Sci. 2025, 15, 505. [Google Scholar] [CrossRef]
- Bagherkhani, A.; Baghlani, A. Enhancing the curvature mode shape method for structural damage severity estimation by means of the distributed genetic algorithm. Eng. Optim. 2021, 53, 683–701. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Wahab, M.A. Damage detection in slab structures based on two-dimensional curvature mode shape method and Faster R-CNN. Adv. Eng. Softw. 2023, 176, 103371. [Google Scholar] [CrossRef]
- Rucevskis, S.; Sumbatyan, M.A.; Akishin, P.; Chate, A. Tikhonov’s regularization approach in mode shape curvature analysis applied to damage detection. Mech. Res. Commun. 2015, 65, 9–16. [Google Scholar] [CrossRef]




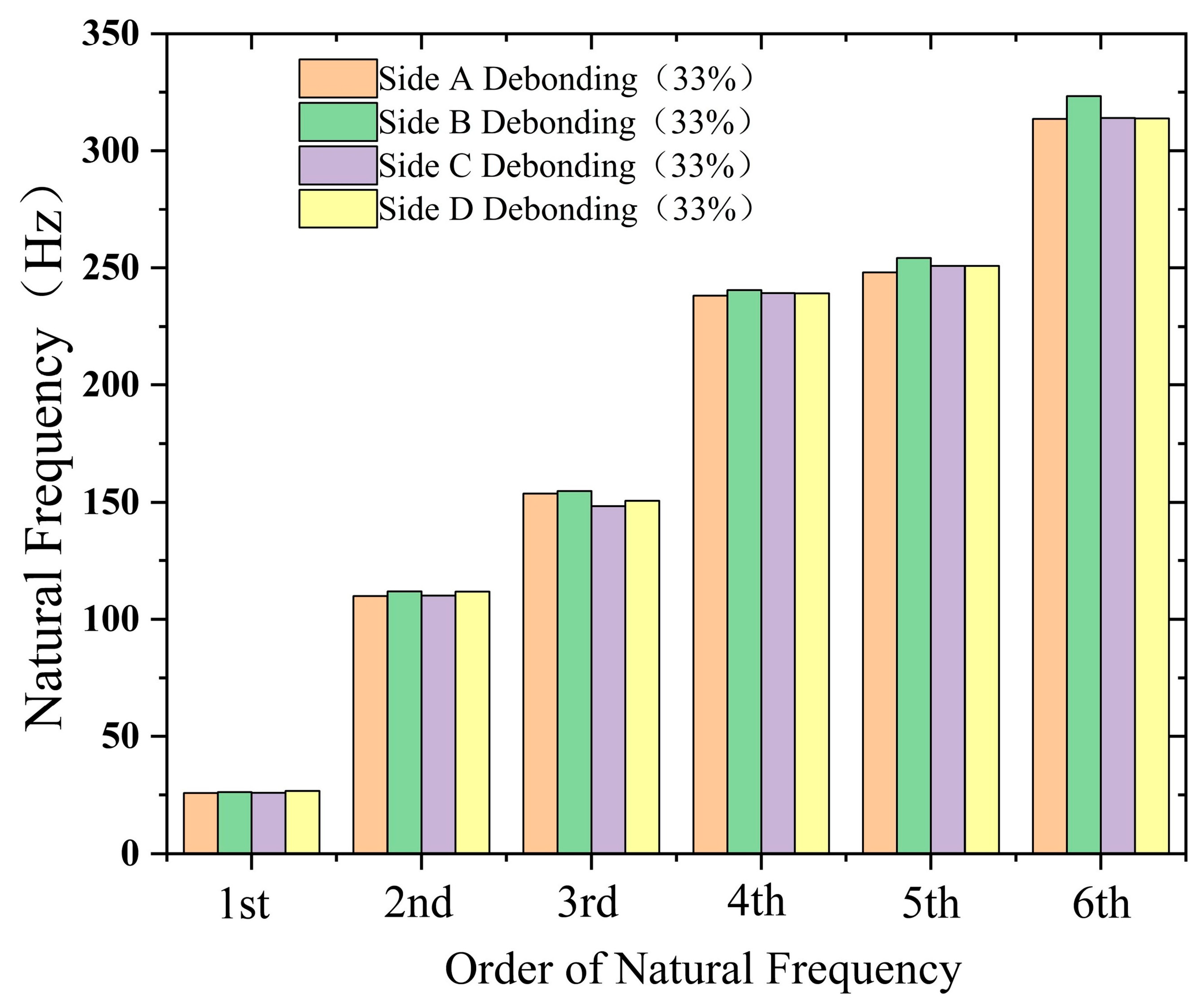



| Conditions | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | Condition 6 | Condition 7 |
|---|---|---|---|---|---|---|---|
| Damage scenario description | Undamaged | Side A debonding (33%) | Side B debonding (33%) | Side C debonding (33%) | Side D debonding (33%) | Side A debonding (66%) | Side A Debonding (100%) |
| Corresponding diagram | Figure 3a | Figure 3b | Figure 3c | Figure 3d | Figure 3e | Figure 3f | Figure 3g |
| Conditions | Average Value | Maximum Value | Minimum Value | Damage Threshold |
|---|---|---|---|---|
| Undamaged | −0.0034 | 0.11 | −0.11 | 0.1205 |
| Damaged | 0.194 | 0.272 | 0.131 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Wang, X.; Li, X.; Zhang, X.; Yang, F.; Sun, J. Identification of Structural Sealant Damage in Hidden Frame Glass Curtain Wall Based on Curvature Mode. Appl. Sci. 2025, 15, 6568. https://doi.org/10.3390/app15126568
Yan Y, Wang X, Li X, Zhang X, Yang F, Sun J. Identification of Structural Sealant Damage in Hidden Frame Glass Curtain Wall Based on Curvature Mode. Applied Sciences. 2025; 15(12):6568. https://doi.org/10.3390/app15126568
Chicago/Turabian StyleYan, Yuqin, Xiangcheng Wang, Xiaonan Li, Xin Zhang, Fan Yang, and Jie Sun. 2025. "Identification of Structural Sealant Damage in Hidden Frame Glass Curtain Wall Based on Curvature Mode" Applied Sciences 15, no. 12: 6568. https://doi.org/10.3390/app15126568
APA StyleYan, Y., Wang, X., Li, X., Zhang, X., Yang, F., & Sun, J. (2025). Identification of Structural Sealant Damage in Hidden Frame Glass Curtain Wall Based on Curvature Mode. Applied Sciences, 15(12), 6568. https://doi.org/10.3390/app15126568






