Quantitative Analysis of Explosion Characteristics Based on Ignition Location in an Ammonia Fuel Preparation Room Using CFD Simulation
Abstract
1. Introduction
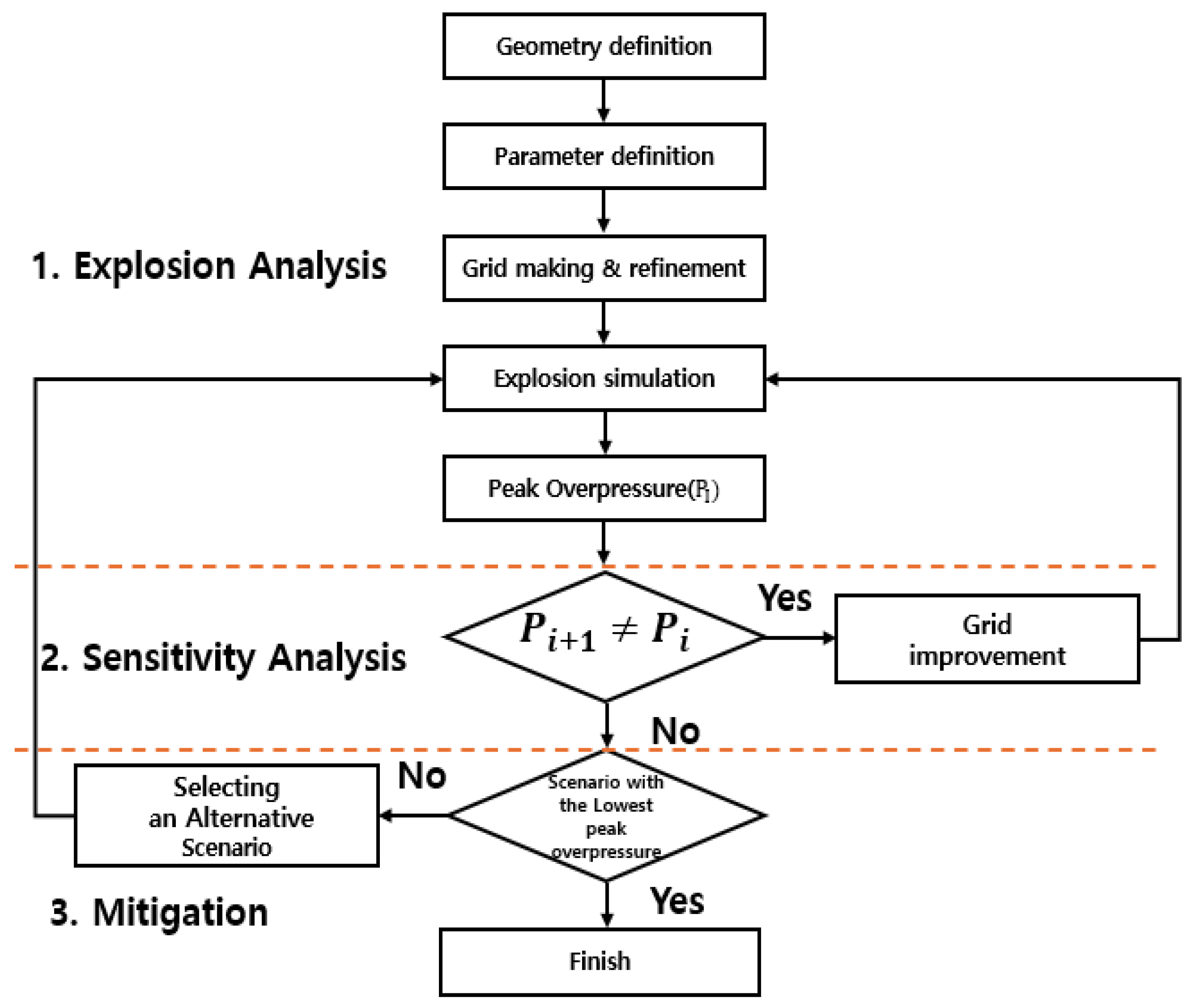
2. Methodology
2.1. Design of Ammonia Fuel Preparation Room
2.2. Scenario Description
2.3. Mathematical Model
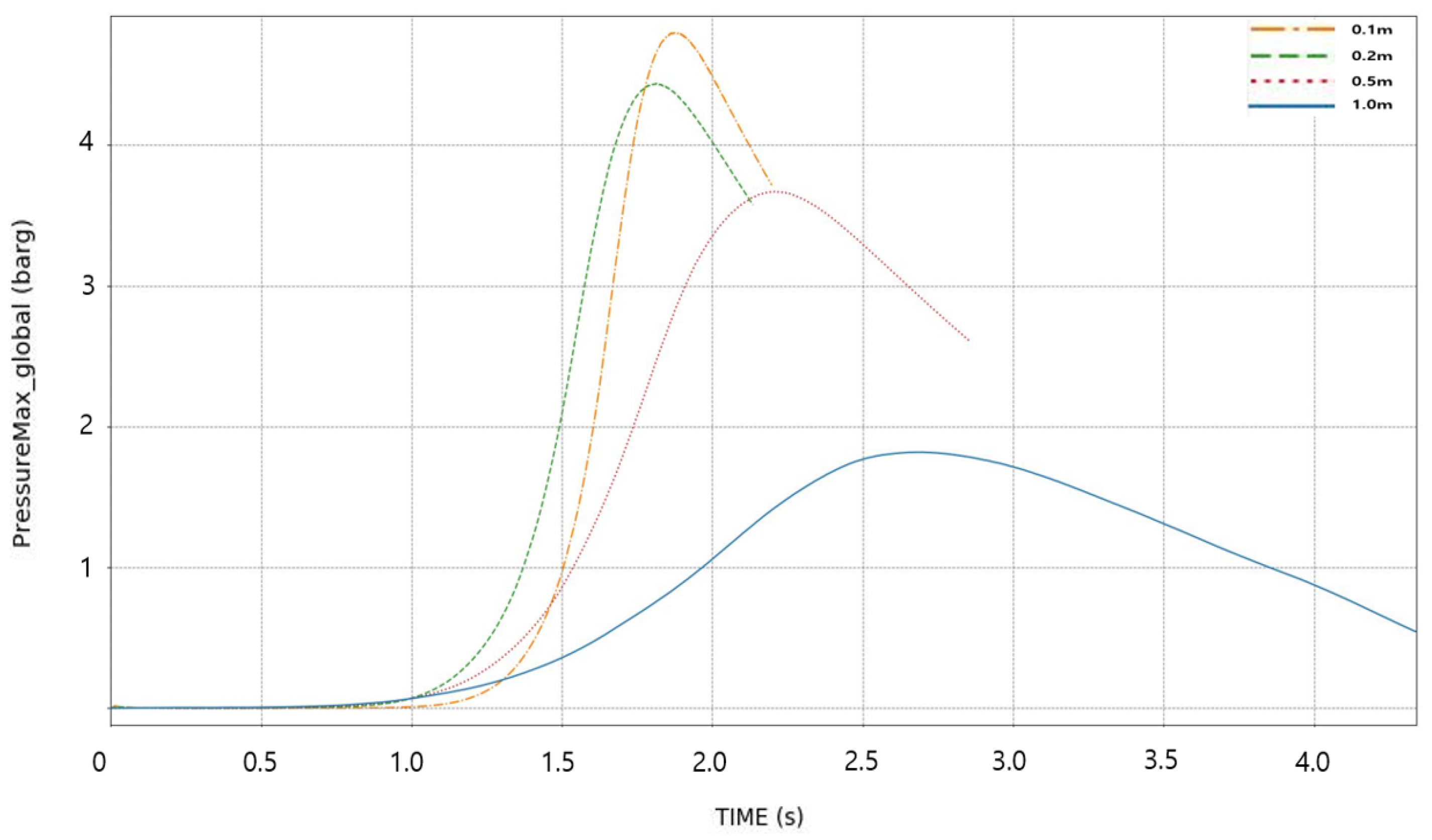
2.4. Simulation Domain and Mesh
3. Result and Discussion
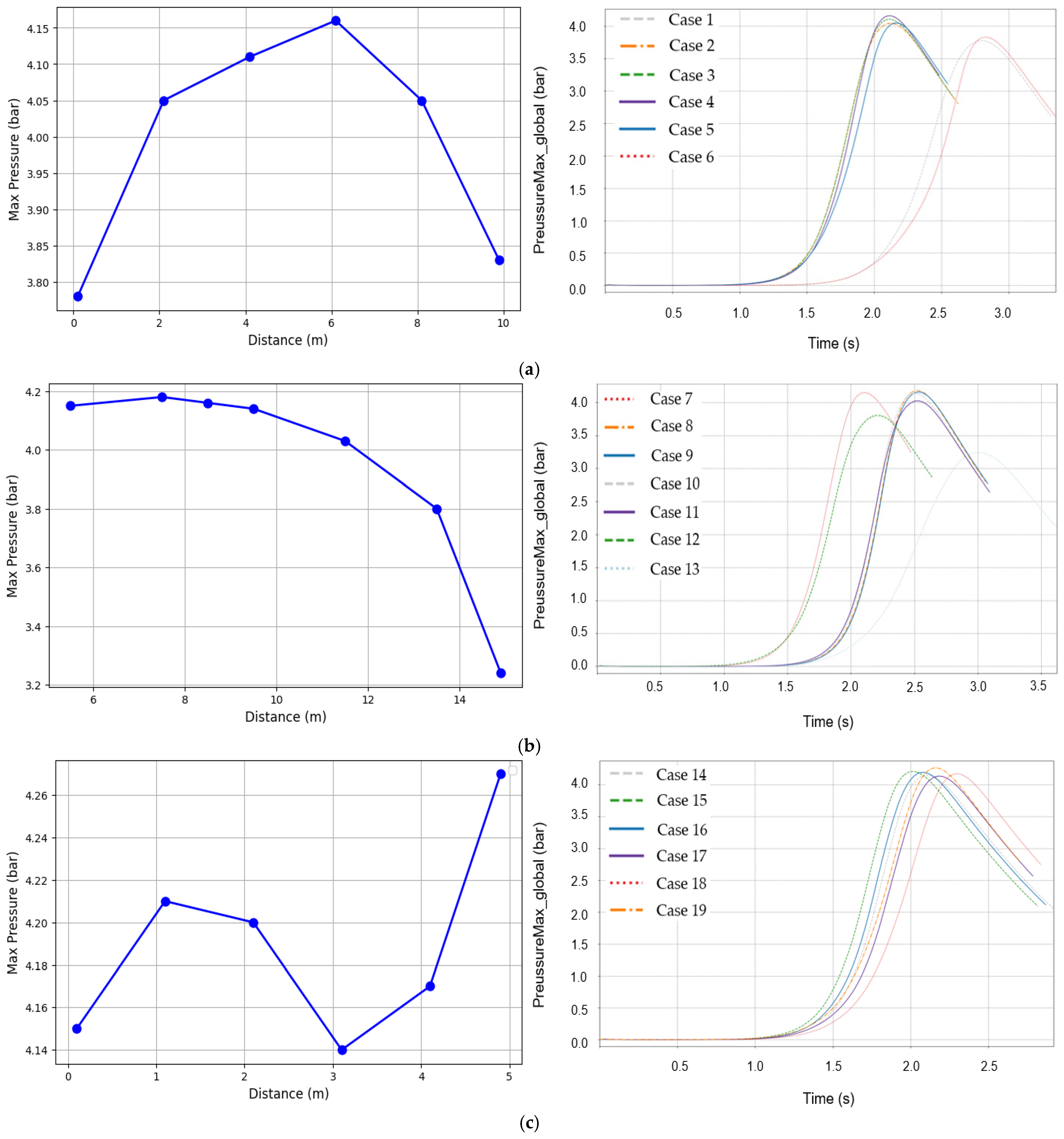
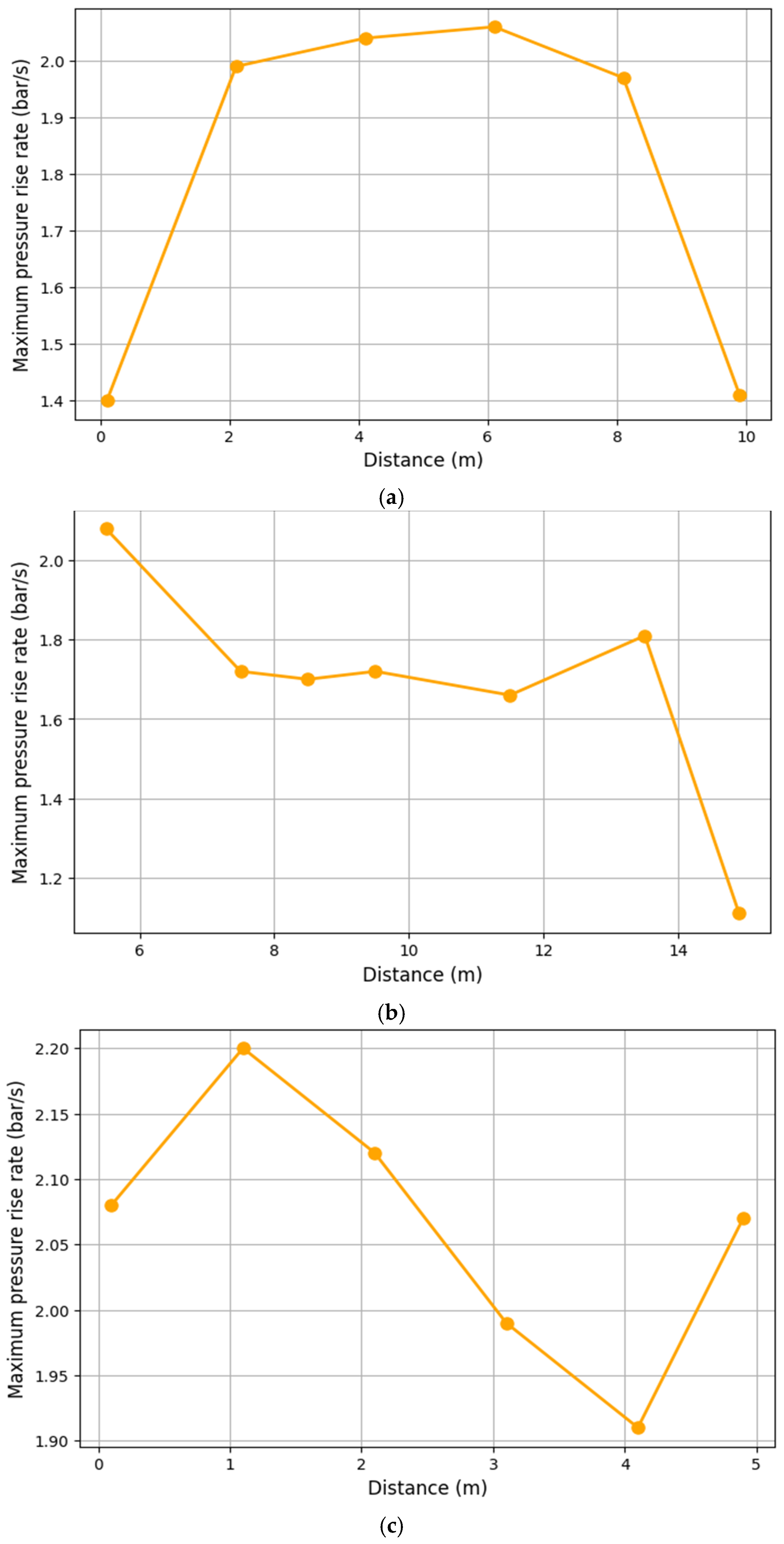
3.1. Analysis of Maximum Pressure and Maximum Pressure Rise Rate
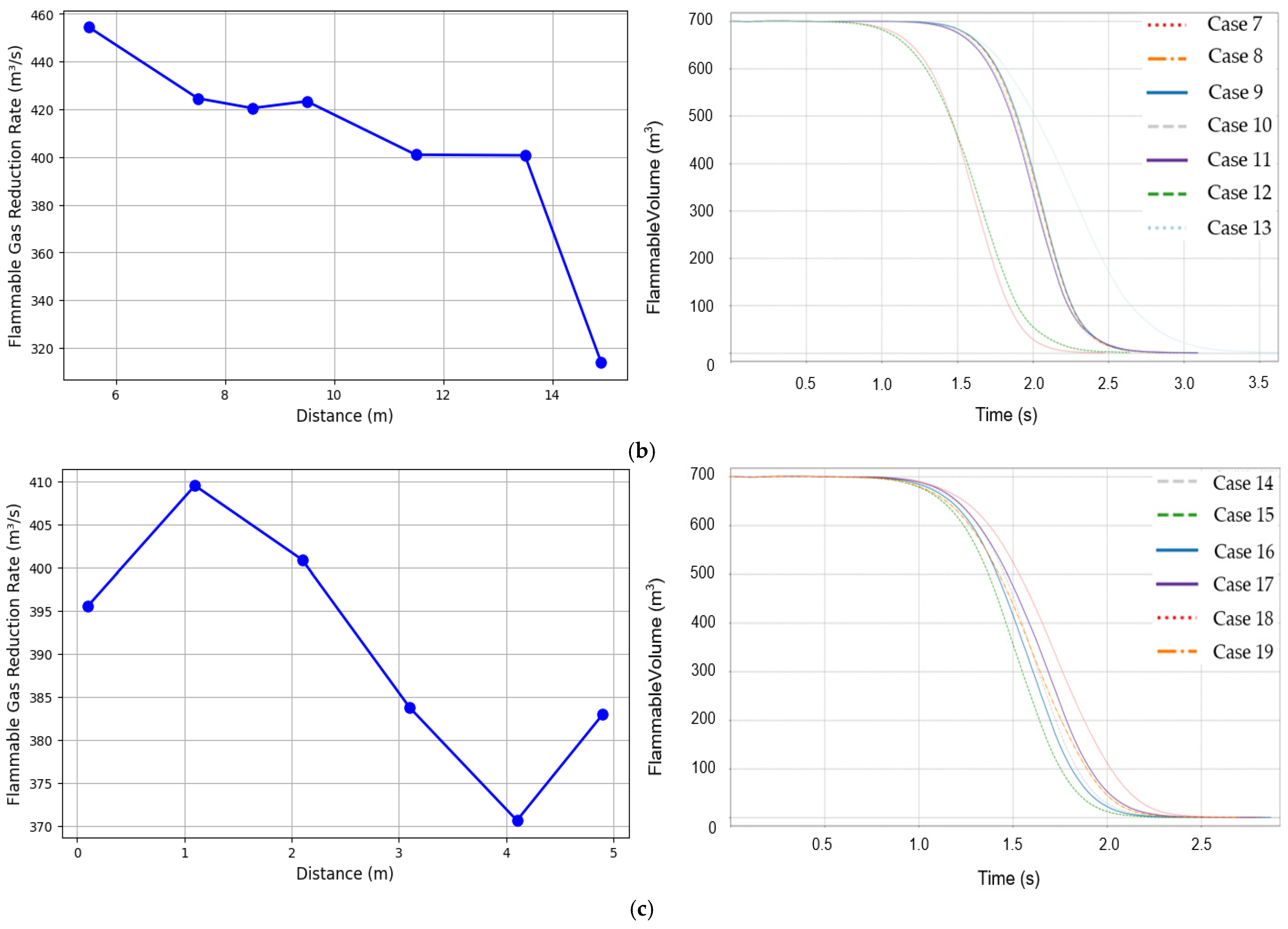
3.2. Variation in Flammable Gas Reduction Rate
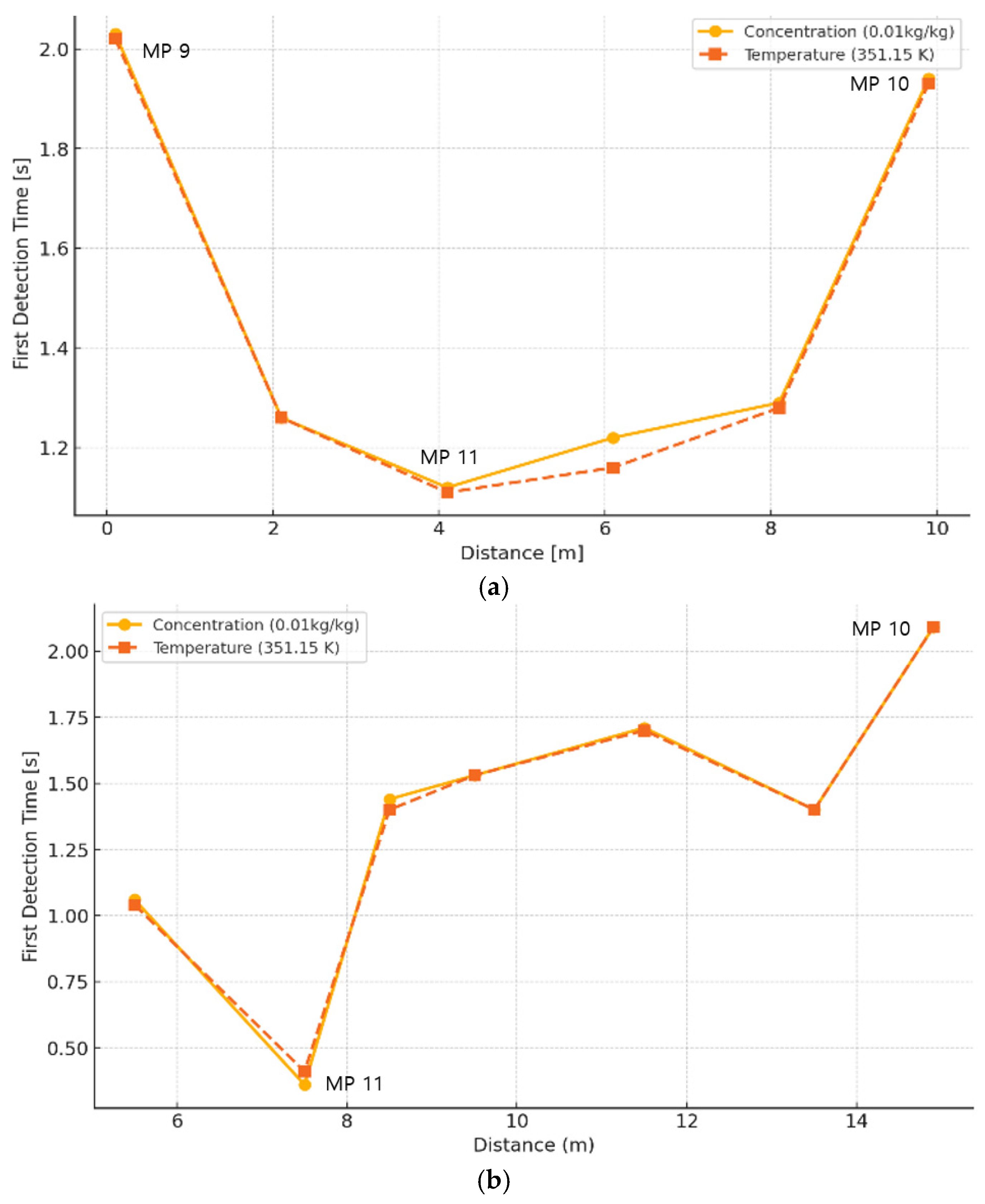
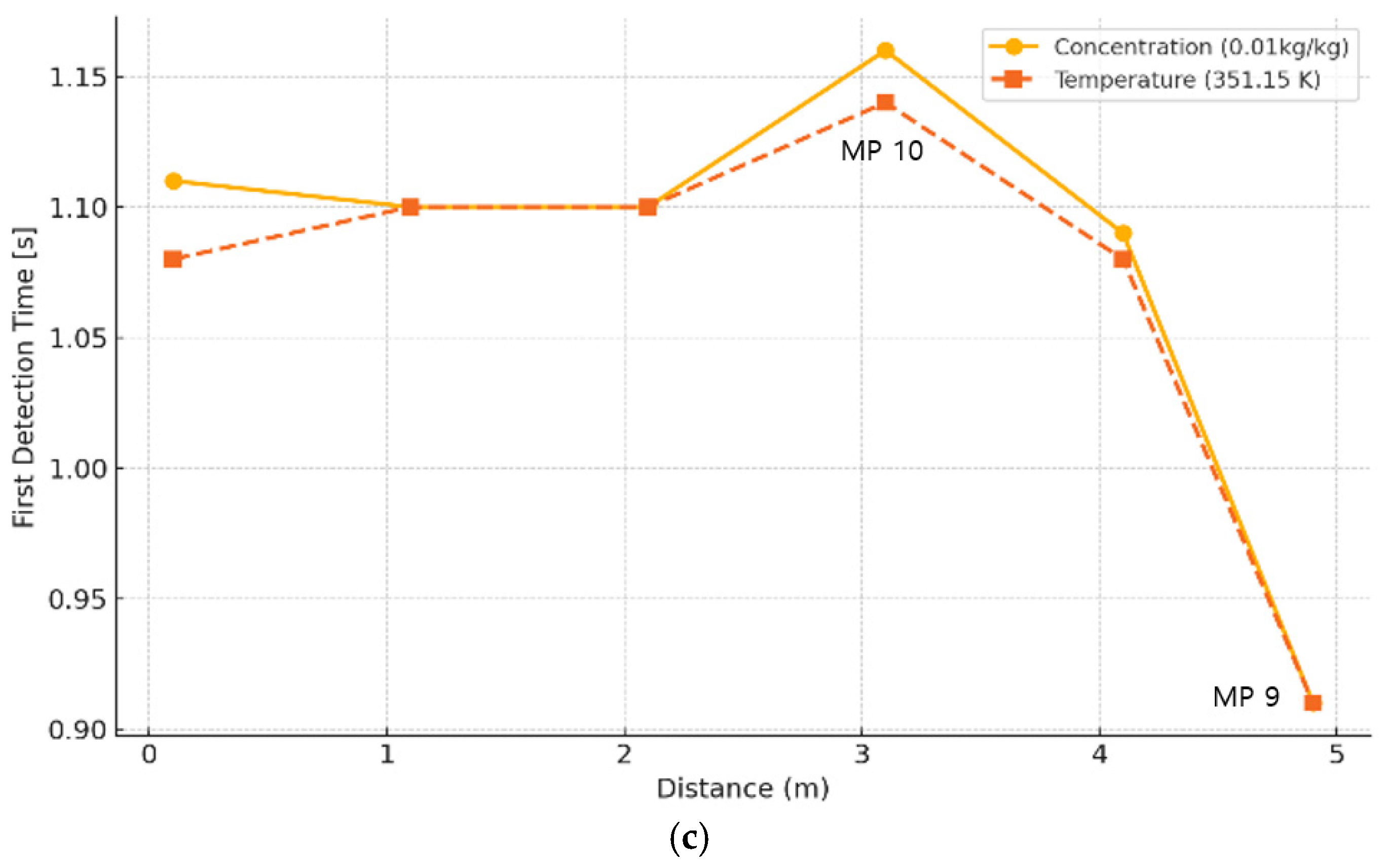
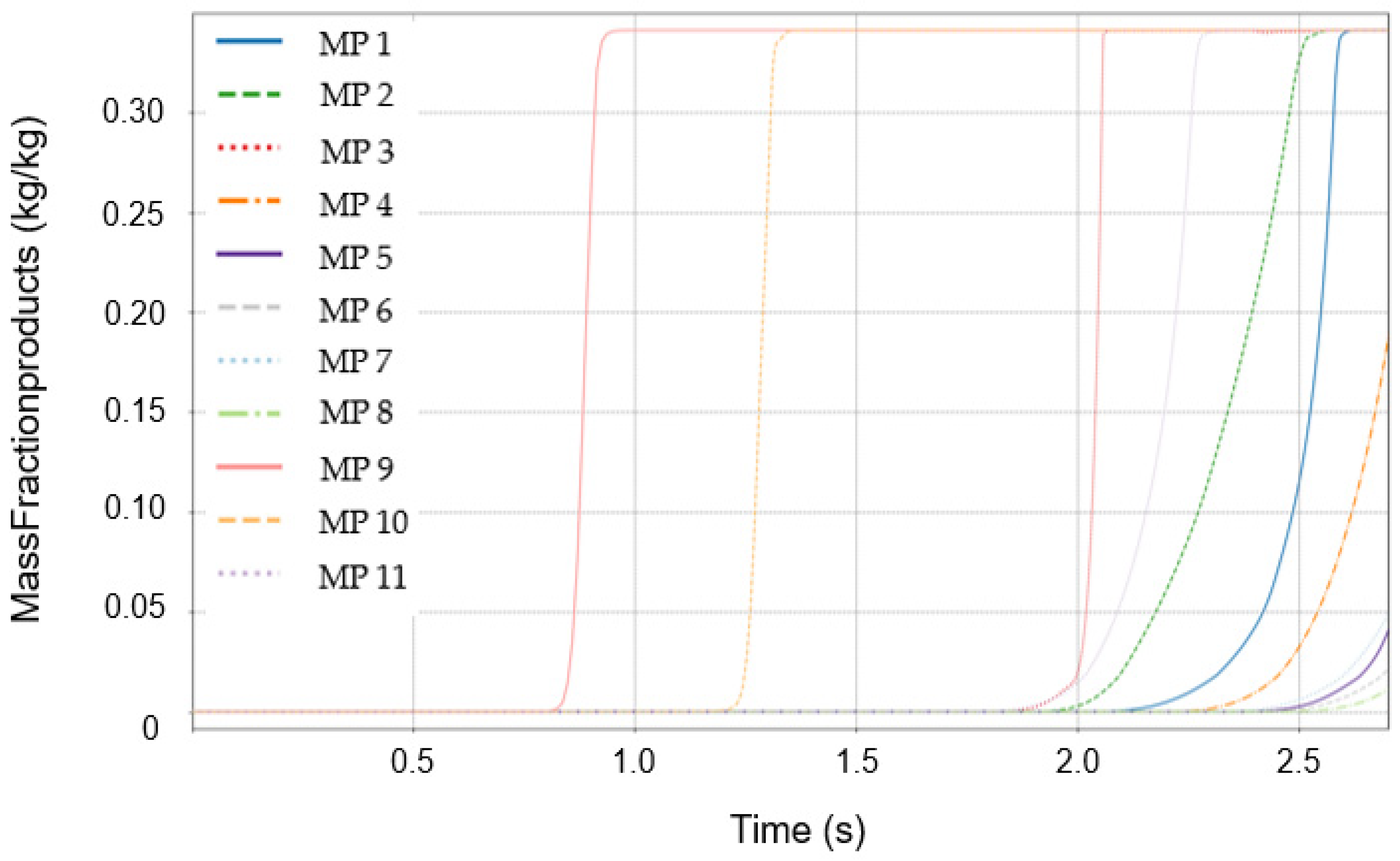
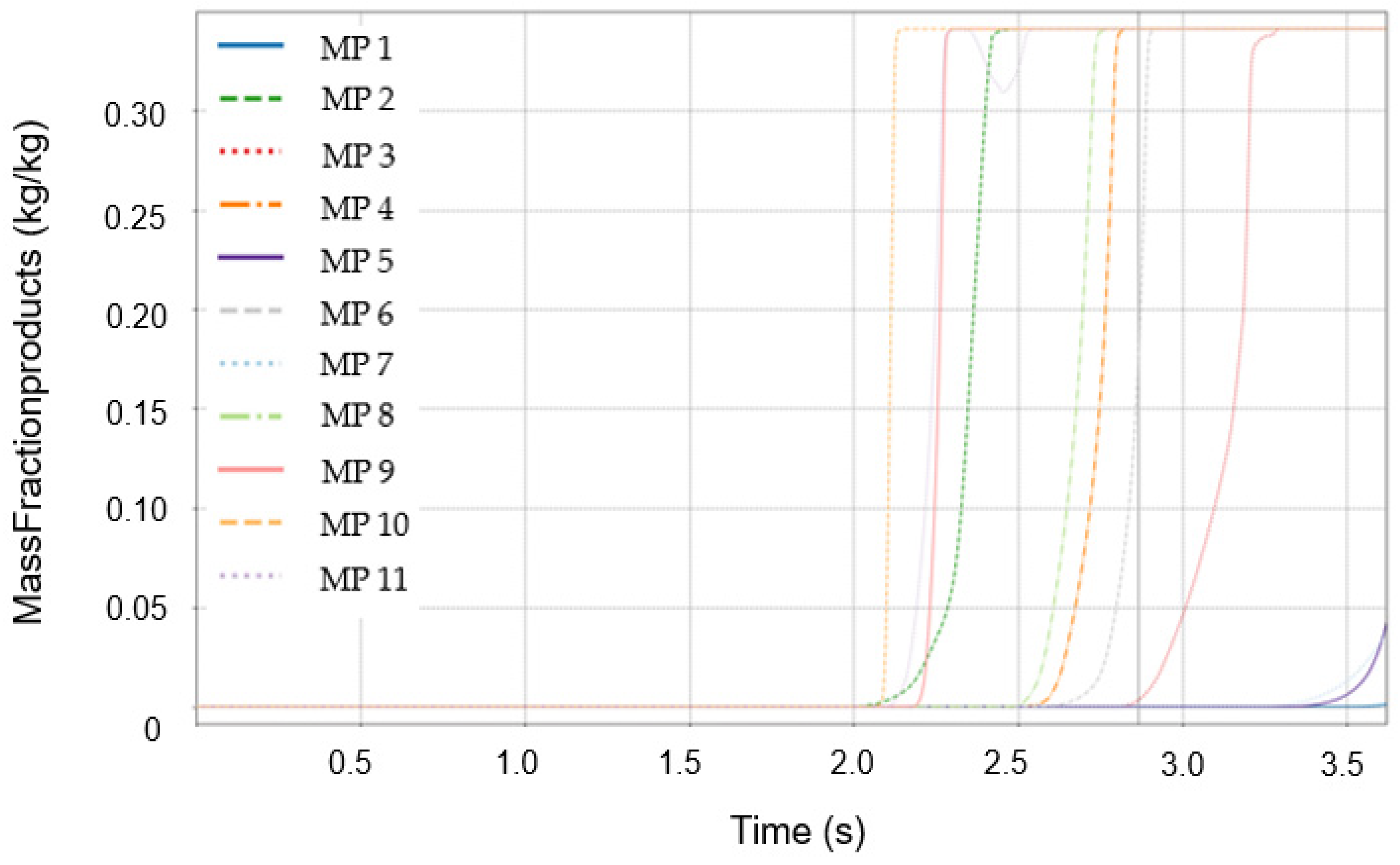
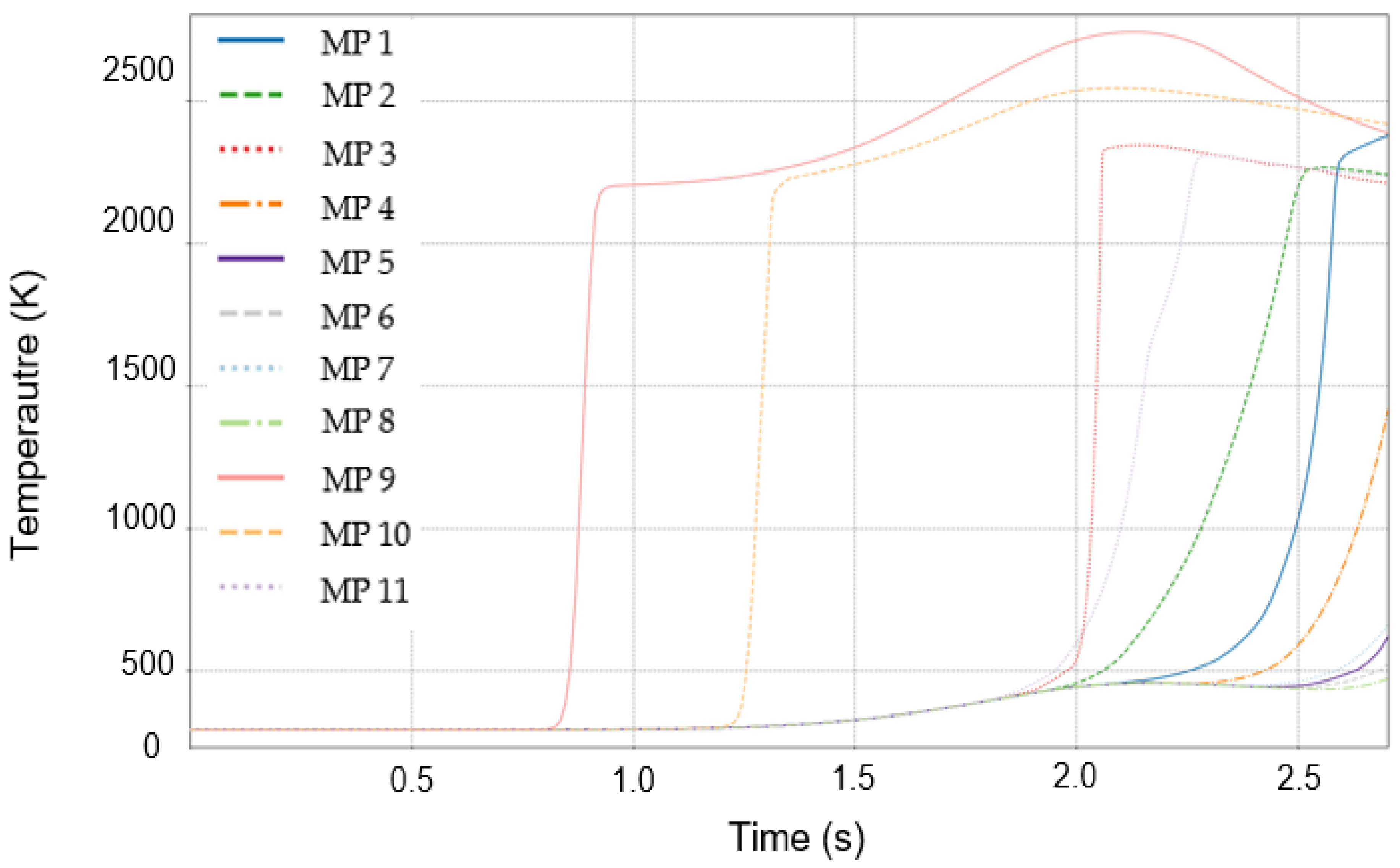
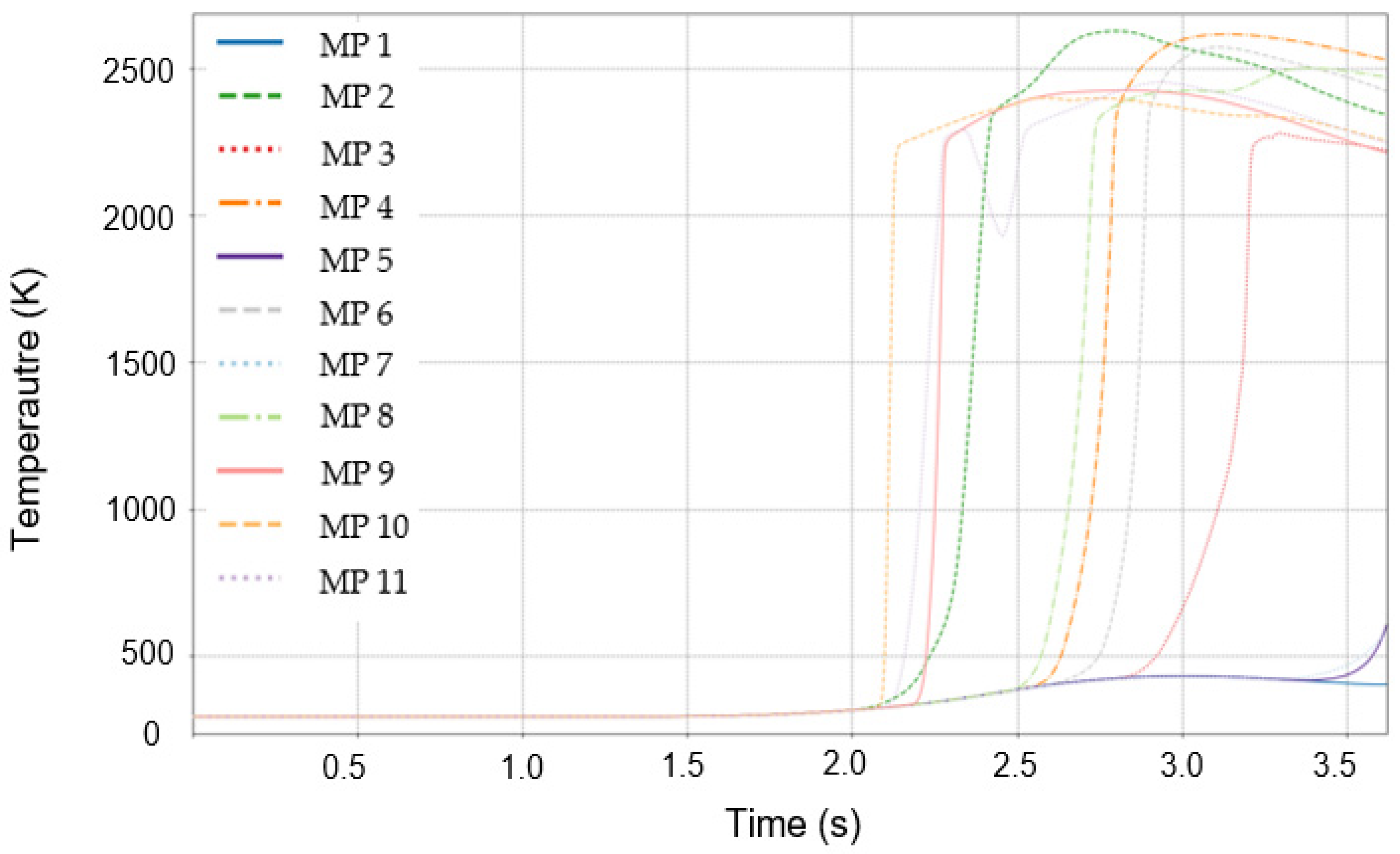
3.3. Initial Detection Characteristics of Temperature and Mass Fraction of Combustion Products
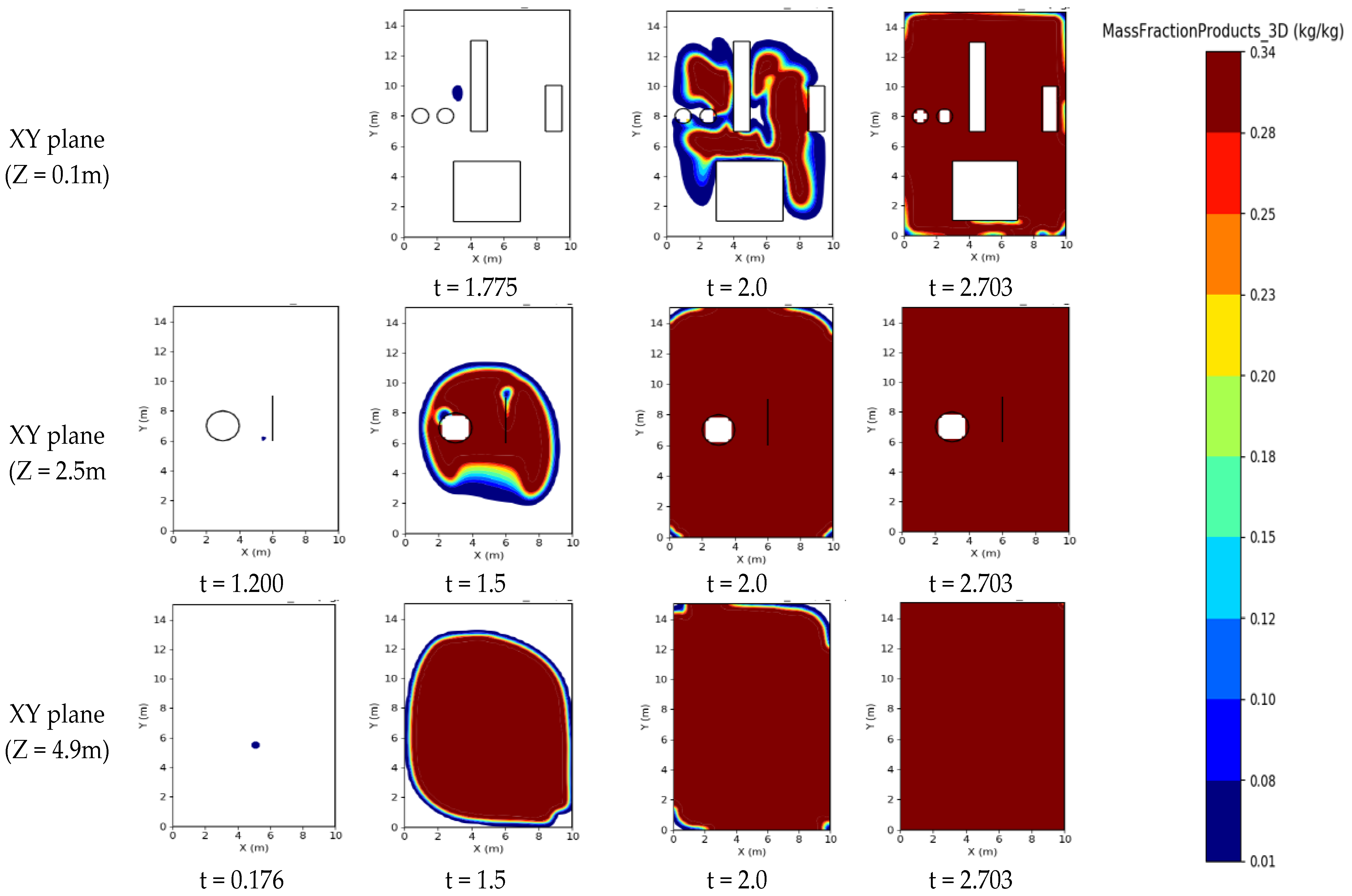
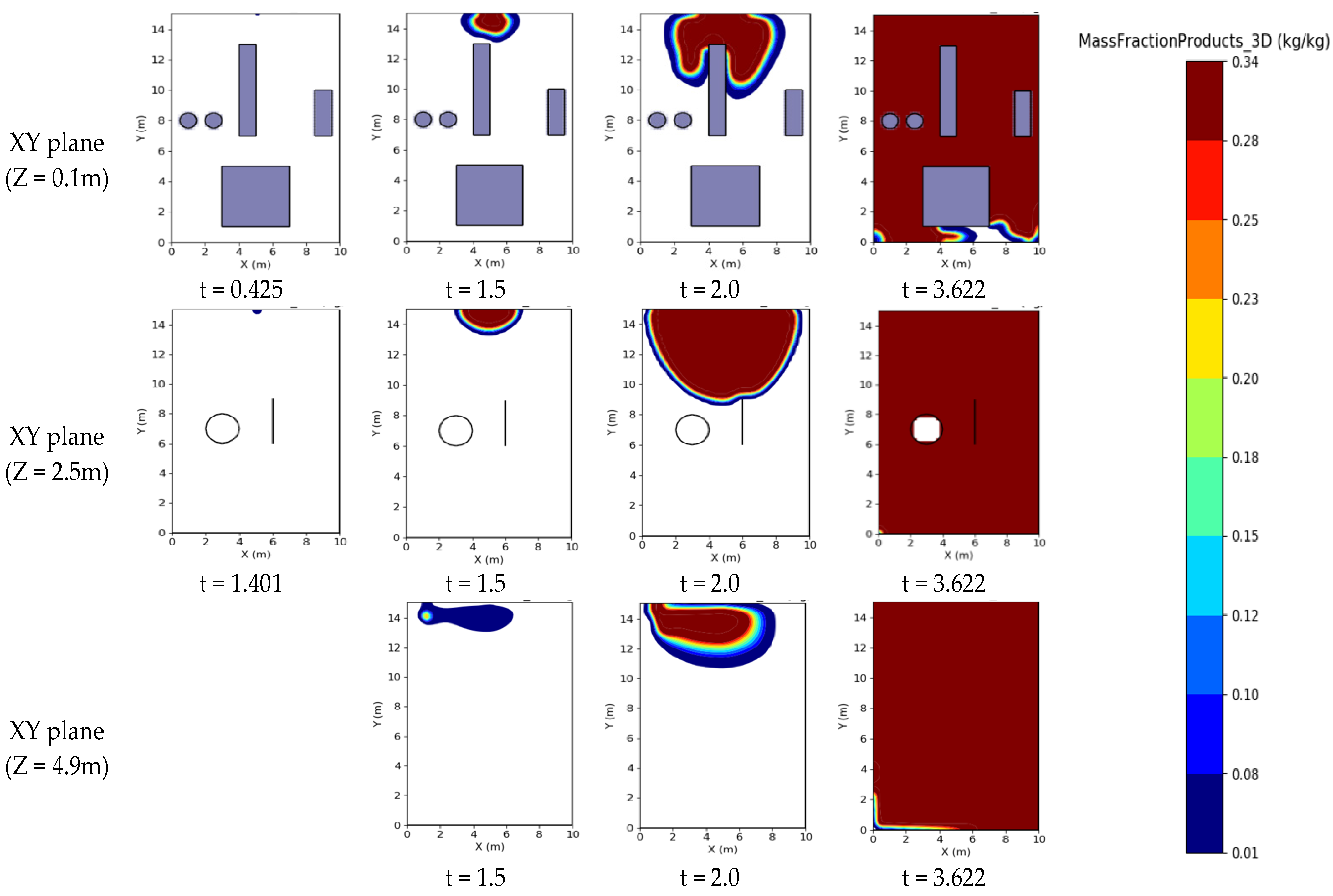
3.4. Distribution of Mass Fractions of Combustion Products
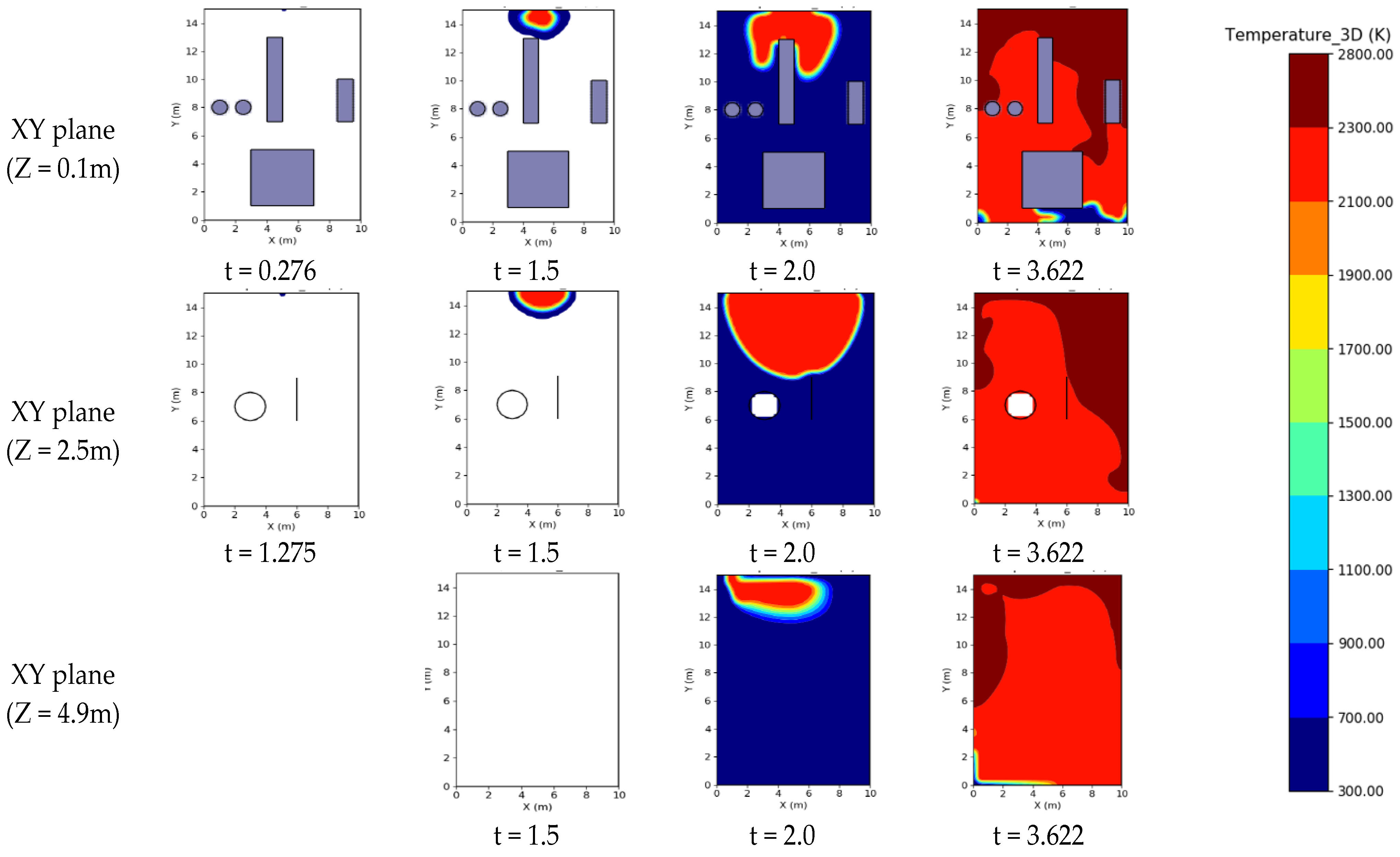
3.5. Distribution of Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BOG | Boil-Off Gas |
| CFD | Computational Fluid Dynamics |
| ER | Equivalence Ratio |
| FPR | Fuel Preparation Room |
| FSS | Fire Safety Systems |
| GHG | Greenhouse Gas |
| IEA | International Energy Agency |
| IMO | International Maritime Organization |
| ITF | International Transport Forum |
| LNG | Liquefied Natural Gas |
| MPRR | Maximum Pressure Rise Rate |
| MP | Monitoring Point |
| NH3 | Ammonia |
| OSHA | Occupational Safety and Health Administration |
| PWR | Pressurized Water Reactor |
References
- Armijo, J.; Philibert, C. Flexible production of green hydrogen and ammonia from variable solar and wind energy: Case study of Chile and Argentina. Int. J. Hydrogen Energy 2020, 45, 1541–1558. [Google Scholar] [CrossRef]
- Castellanos, G.; Roesch, R.; Sloan, A.; Gielen, D. A Pathway to Decarbonise the Shipping Sector by 2050; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2021.
- Fridell, E. Emissions and Fuel Use in the Shipping Sector. In Green Ports; Ng, A.K.Y., Becker, A., Cahoon, S., Chen, S.L., Earl, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 19–33. [Google Scholar]
- International Maritime Organization. Initial IMO Strategy on Reduction of GHG Emission from Ships. Resolution MEPC.304(72) (Adopted on 13 April 2018); International Maritime Organization: London, UK, 2018. [Google Scholar]
- Wang, S.; Zhen, L.; Psaraftis, H.N.; Yan, R. Implications of the EU’s inclusion of maritime transport in the emissions trading system for shipping companies. Engineering 2021, 7, 554–557. [Google Scholar] [CrossRef]
- Al-Aboosi, F.Y.; El-Halwagi, M.M.; Moore, M.; Nielsen, R.B. Renewable ammonia as an alternative fuel for the shipping industry. Curr. Opin. Chem. Eng. 2021, 31, 100670. [Google Scholar] [CrossRef]
- Valera-Medina, A.; Amer-Hatem, F.; Azad, A.K.; Dedoussi, I.C.; De Joannon, M.; Fernandes, R.X.; Costa, M. Review on ammonia as a potential fuel: From synthesis to economics. Energy Fuels 2021, 35, 6964–7029. [Google Scholar] [CrossRef]
- Valera-Medina, A.; Xiao, H.; Owen-Jones, M.; David, W.I.F.; Bowen, P.J. Ammonia for power. Prog. Energy Combust. Sci. 2018, 69, 63–102. [Google Scholar] [CrossRef]
- Thomas, G. Potential Roles of Ammonia in a Hydrogen Economy; U.S. Department of Energy: Washington, DC, USA, 2006. Available online: https://www.energy.gov/eere/fuelcells/articles/potential-roles-ammonia-hydrogen-economy (accessed on 24 March 2025).
- Park, H.S.; Kim, B.R.; Park, S.W.; Jeong, I.H. A Study on Policy Directions for Responding to IMO’s Regulation on GHG Emission; Korea Maritime Institute (KMI): Busan, Republic of Korea, 2020; pp. 1–249.
- Seo, Y.; Han, S. Economic evaluation of an ammonia-fueled ammonia carrier depending on methods of ammonia fuel storage. Energies 2021, 14, 8326. [Google Scholar] [CrossRef]
- Souissi, N. Fueling the Future: A Techno-Economic Evaluation of E-Ammonia Production for Marine Applications; OIES Paper: ET40; Oxford Institute for Energy Studies: Oxford, UK, 2024. [Google Scholar]
- Shin, I.; Cheon, J.; Lee, J. A study on the hazard area of bunkering for ammonia fueled vessel. J. Korean Soc. Mar. Environ. Saf. 2023, 29, 964–970. [Google Scholar] [CrossRef]
- Klerke, A.; Christensen, C.H.; Nørskov, J.K.; Vegge, T. Ammonia for hydrogen storage: Challenges and opportunities. J. Mater. Chem. 2008, 18, 2304–2310. [Google Scholar] [CrossRef]
- United States Department of Labor. Occupational Safety and Health Administration (OSHA). Available online: https://www.osha.gov/ords/imis/accidentsearch.search?sic=&sicgroup=&naics=&acc_description=&acc_abstract=&acc_keyword=%22Ammonia%22&inspnr=&fatal=&officetype=&office=&startmonth=&startday=&startyear=&endmonth=&endday=&endyear=&keyword_list=on&p_start=260& (accessed on 20 January 2025).
- NRK. En Død Etter Ammoniakkeksplosjon. Available online: https://www.nrk.no/vestfold/en-dod-etter-ammoniakkeksplosjon-1.272219 (accessed on 20 January 2025).
- ABC NEWS. Ammonia Leak China Caused by Detached Pipe Cap. Available online: http://www.abc.net.au/news/2013-09-02/an-china-ammonia-deaths-caused-by-detatched-cap/4928574 (accessed on 26 March 2025).
- French Ministry of the Environment. Explosion of an Ammonia Tank. Mar. 24, 1992, Dakar. Available online: https://www.aria.developpement-durable.gouv.fr/wp-content/files_mf/A3485_ips03485_002.pdf (accessed on 20 January 2025).
- Dharmavaram, S.; Pattabathula, V. The Dakar Ammonia Accident: Analysis of the Worst Incident at an Anhydrous Ammonia User; Utah Valley University: Orem, UT, USA, 2022. [Google Scholar]
- Li, C.; Lei, B.; Pang, R.; Xiao, J.; Kuznetsov, M.; Jordan, T. Effects of ignition location on CH4/air explosion characteristic in a spherical bomb. Therm. Sci. Eng. Prog. 2024, 50, 102539. [Google Scholar] [CrossRef]
- Wang, Q.; Wan, H.; Bi, M.; Gao, W.; Peng, B.; Luo, Z.; Xue, Y. Effects of ignition position and hydrogen concentration on the flame propagation characteristics of hydrogen–air deflagration. Fuel 2024, 359, 130349. [Google Scholar] [CrossRef]
- Hou, Z.; Wang, D.; Zhang, W.; Luo, S.; Lu, Y.; Tian, S.; Xu, Z. Study on the influence of ignition position on the explosion characteristics of methane–air premix in a semi-closed pipeline. Process Saf. Environ. Prot. 2023, 172, 642–651. [Google Scholar] [CrossRef]
- Chen, C.F.; Shu, C.M.; Ho, S.P.; Chang, H.P.; Ho, H.H.; Xie, B. Utilizing FLACS to Assess quantitative Analysis on Explosion Caused by Propylene Gas Leaks Within Drainage Culverts or Soil. In Proceedings of the World Conference on OIL, Gas and Infrastructure (WCOGI), Beijing, China, 26–29 October 2016. [Google Scholar]
- Middha, P.; Hansen, O.R.; Storvik, I.E. Validation of CFD-model for hydrogen dispersion. J. Loss Prev. Process Ind. 2009, 22, 1034–1038. [Google Scholar] [CrossRef]
- Evans, J.A.; Johnson, D.M.; Lowesmith, B.J. Explosions in Full Offshore Module Geometries (Work Carried Out under Contract to the HSE, MaTSU/8847/3522); Report No. R2422; BG Technology: Cheshire, UK, 1999. [Google Scholar]
- Ai-Hassan, T.; Johnson, D.M. Gas Explosions in Large Scale Offshore Module Geometries: Overpressures, Mitigation and Repeatability. In Proceedings of the 17th International Conference on Offshore Mechanics and Arctic Engineering (OMAE), American Society of Mechanical Engineers (ASME), Lisbon, Portugal, 5–9 July 1998; p. 12. [Google Scholar]
- Foisselon, P.; Hansen, O.R.; van Wingerden, K. Detailed Analysis of FLACS Performance in Comparison to Full Scale Experiments; Report No. 97-9; Gas Safety Programme: Singapore, 1998. [Google Scholar]
- Vyazmina, E.; Jallais, S. Validation and recommendations for FLACS CFD and engineering approaches to model hydrogen vented explosions: Effects of concentration, obstruction, vent area and ignition position. Int. J. Hydrog. Energy 2016, 41, 15101–15109. [Google Scholar] [CrossRef]
- Lv, D.; Tan, W.; Liu, L.; Zhu, G.; Peng, L. Research on maximum explosion overpressure in LNG storage tank areas. J. Loss Prev. Process Ind. 2017, 49, 162–170. [Google Scholar] [CrossRef]
- Hansen, O.R.; Johnson, D.M. Improved far-field blast predictions from fast deflagrations, DDTs and detonations of vapour clouds using FLACS CFD. J. Loss Prev. Process Ind. 2015, 35, 293–306. [Google Scholar] [CrossRef]
- Hansen, O.R.; Hinze, P.; Engel, D.; Davis, S. Using computational fluid dynamics (CFD) for blast wave predictions. J. Loss Prev. Process Ind. 2010, 23, 885–906. [Google Scholar] [CrossRef]
- Bleyer, A.; Taveau, J.; Djebaïli-Chaumeix, N.; Paillard, C.E.; Bentaïb, A. Comparison between FLACS Explosion Simulations and Experiments Conducted in a PWR Steam Generator Casemate Scale Down with Hydrogen Gradients. Nucl. Eng. Des. 2012, 245, 189–196. [Google Scholar] [CrossRef]
- Gexcon. FLACS-CFD v22.2 User’s Manual; Gexcon: Bergen, Norway, 2023. [Google Scholar]
- Jang, H.; Mujeeb-Ahmed, M.P.; Wang, H.; Park, C.; Hwang, I.; Jeong, B.; Sykaras, K. Safety Evaluation on Ammonia-Fueled Ship: Gas Dispersion Analysis through Vent Mast. Int. J. Hydrog. Energy 2024, 83, 1060–1077. [Google Scholar] [CrossRef]
- Tam, V.H.; Tan, F.; Savvides, C. A Critical Review of the Equivalent Stoichiometric Cloud Model Q9 in Gas Explosion Modelling. Eng 2021, 2, 156–180. [Google Scholar] [CrossRef]
- Li, Z.; Wu, J.; Liu, M.; Li, Y.; Ma, Q. Numerical analysis of the characteristics of gas explosion process in natural gas compartment of utility tunnel using FLACS. Sustainability 2019, 12, 153. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Wang, H.; Liu, X.; Jiao, Y.; Wu, Y. Dynamic process and damage evaluation subject to explosion consequences resulting from a LPG tank trailer accident. Processes 2023, 11, 1514. [Google Scholar] [CrossRef]
- Xu, H.; Deng, Q.; Huang, X.; Li, D.; Pan, F. Simulation and experimental verification of dispersion and explosion of hydrogen–methane mixture in a domestic kitchen. Energies 2024, 17, 2320. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, X.; Hao, Y.; Zhuang, S. Study on explosion venting characteristics of L-type venting duct. Processes 2024, 12, 2726. [Google Scholar] [CrossRef]
- Arntzen, B.J. Modelling of Turbulence and Combustion for Simulation of Gas Explosions in Complex Geometries. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1998. [Google Scholar]
- Zhang, H.; Jia, Z.; Ye, Q.; Cheng, Y.; Li, S. Numerical Simulation on Influence of Initial Pressures on Gas Explosion Propagation Characteristics in Roadway. Front. Energy Res. 2022, 10, 913045. [Google Scholar] [CrossRef]
- Razus, D.; Movileanu, C.; Oancea, D. The Rate of Pressure Rise of Gaseous Propylene–Air Explosions in Spherical and Cylindrical Enclosures. J. Hazard. Mater. 2007, 139, 1–8. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). International Code for Fire Safety Systems (FSS Code), Chapter 9, Section 2.4; Amendment 24 (Resolution MSC.108(73)); IMO: London, UK, 2001. [Google Scholar]
- March and McLennan. Large Property Losses in the Hydrocarbon-Chemical Industries: A Thirty-Year Review, 17th ed.; M&M Protection Consultants: New York, NY, USA, 1990. [Google Scholar]
- Carpenter, R.B. Lightning Protection for Flammables Storage Facilities; Lightning Eliminators Consultants: Boulder, CO, USA, 1996. [Google Scholar]




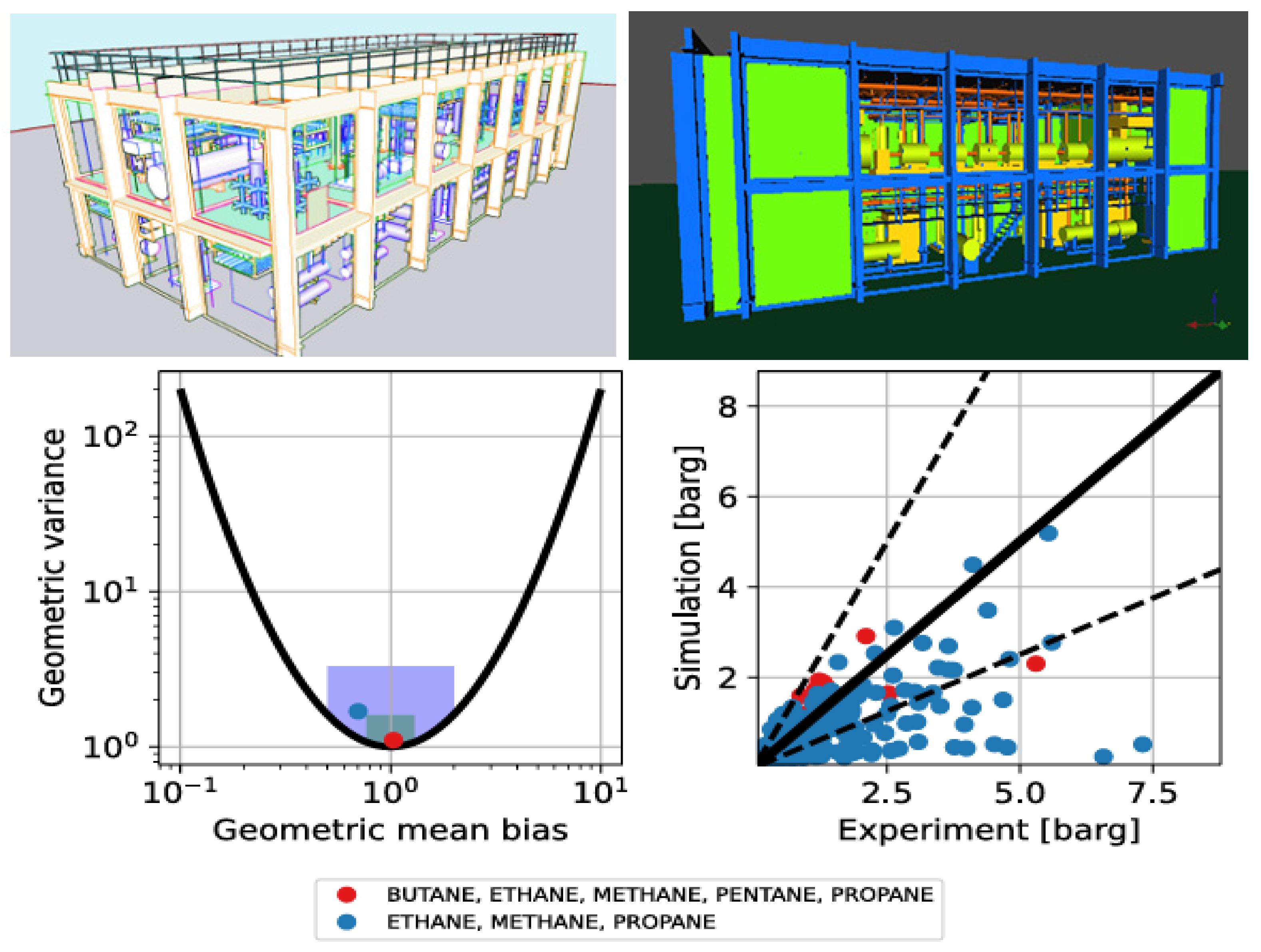
| Item | Specification |
|---|---|
| Vessel type | Bulk Carrier |
| Deadweight (ton) | 180,000 DWT |
| Tank type | IMO Type C |
| Volume | 15 m × 10 m × 5 m = 750 m3 (Width × Length × Height) |
| Diameter for ventilation inlet and outlet | 0.8 m |
| Equipment simplified | Fuel gas supply system including vaporizer and glycol water expansion tank, BOG compressor, degassing units, solenoid valve cabinet |
| Boundary Condition | |
| XLO | Euler |
| XLO | Euler |
| YLO | Euler |
| YHI | Euler |
| ZLO | Euler |
| ZHI | Euler |
| Initial Condition | |
| Ambient pressure [Pa] | 101325 |
| Environment temperature [K] | 288.15 |
| Gas composition ratio Gas cloud volume Shape of cloud volume | Ammonia 100% Equivalent volume(ER = 1) 10 × 15 × 5 cube |
| Case | Ignition Position X Axis (m) | Ignition Position Y Axis (m) | Ignition Position Z Axis (m) |
|---|---|---|---|
| 1. | 0.1 | 5.5 | 0.1 |
| 2. | 2.1 | 5.5 | 0.1 |
| 3. | 4.1 | 5.5 | 0.1 |
| 4. | 6.1 | 5.5 | 0.1 |
| 5. | 8.1 | 5.5 | 0.1 |
| 6. | 9.9 | 5.5 | 0.1 |
| 7. | 5.1 | 5.5 | 0.1 |
| 8. | 5.1 | 7.5 | 0.1 |
| 9. | 5.1 | 8.5 | 0.1 |
| 10. | 5.1 | 9.5 | 0.1 |
| 11. | 5.1 | 11.5 | 0.1 |
| 12. | 5.1 | 13.5 | 0.1 |
| 13. | 5.1 | 14.9 | 0.1 |
| 14. | 5.1 | 5.5 | 0.1 |
| 15. | 5.1 | 5.5 | 1.1 |
| 16. | 5.1 | 5.5 | 2.1 |
| 17. | 5.1 | 5.5 | 3.1 |
| 18. | 5.1 | 5.5 | 4.1 |
| 19. | 5.1 | 5.5 | 4.9 |
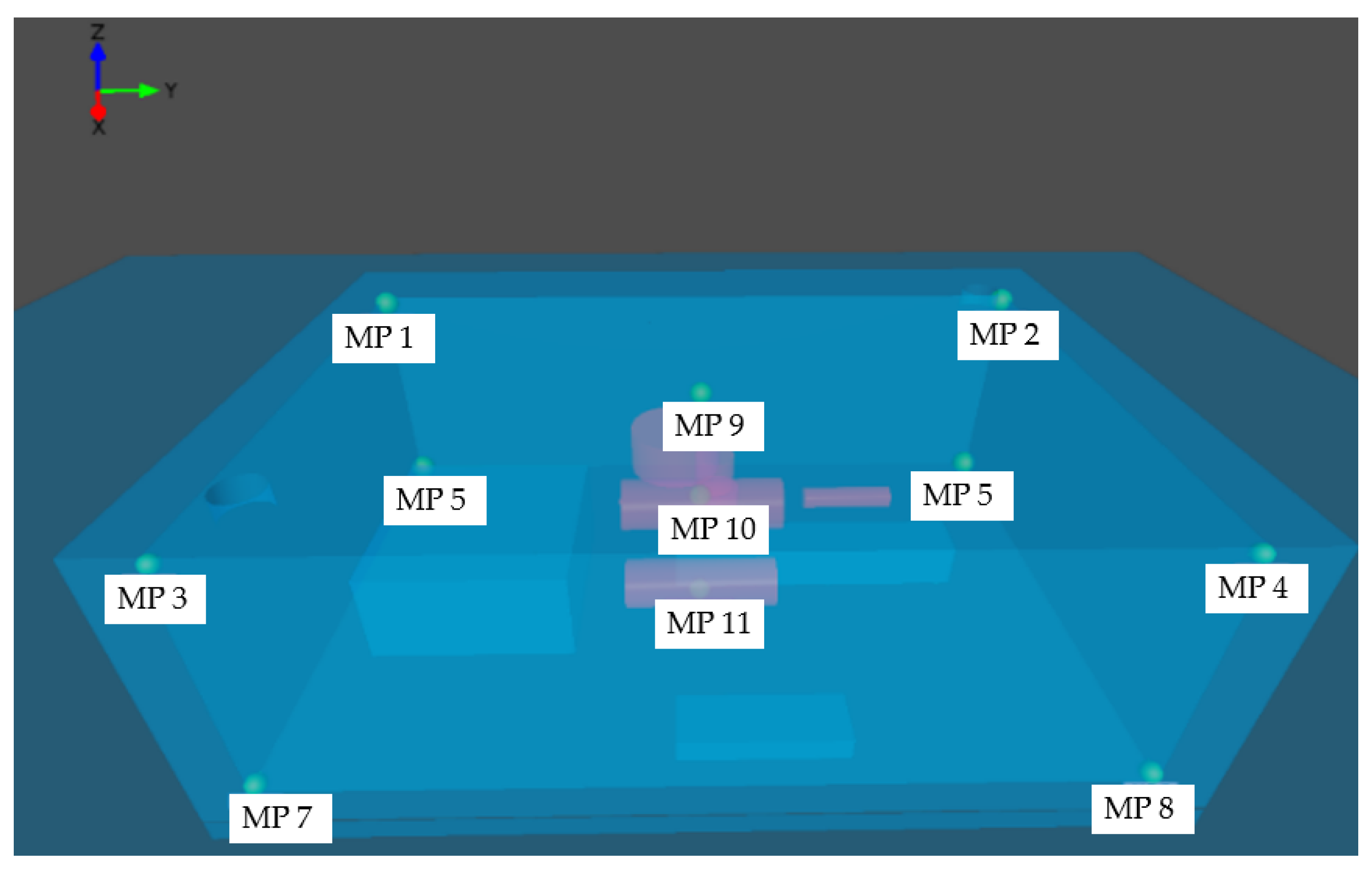
| Monitoring Point | Position X Axis (m) | Position Y Axis (m) | Position Z Axis (m) |
|---|---|---|---|
| 1. | 0.1 | 0.1 | 4.9 |
| 2. | 0.1 | 14.9 | 4.9 |
| 3. | 9.9 | 0.1 | 4.9 |
| 4. | 9.9 | 14.9 | 4.9 |
| 5. | 0.1 | 0.1 | 0.1 |
| 6. | 0.1 | 14.9 | 0.1 |
| 7. | 9.9 | 0.1 | 0.1 |
| 8. | 9.9 | 14.9 | 0.1 |
| 9. | 5.0 | 7.5 | 4.9 |
| 10. | 5.0 | 7.5 | 2.5 |
| 11. | 5.2 | 7.5 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, J.-W.; Noh, B.-S.; Lee, J.-W.; Choe, S.-J.; Park, K.-H.; Kim, J.-D.; Choi, J.-H. Quantitative Analysis of Explosion Characteristics Based on Ignition Location in an Ammonia Fuel Preparation Room Using CFD Simulation. Appl. Sci. 2025, 15, 6554. https://doi.org/10.3390/app15126554
Bae J-W, Noh B-S, Lee J-W, Choe S-J, Park K-H, Kim J-D, Choi J-H. Quantitative Analysis of Explosion Characteristics Based on Ignition Location in an Ammonia Fuel Preparation Room Using CFD Simulation. Applied Sciences. 2025; 15(12):6554. https://doi.org/10.3390/app15126554
Chicago/Turabian StyleBae, Jin-Woo, Beom-Seok Noh, Ji-Woong Lee, Su-Jeong Choe, Kweon-Ha Park, Jeong-Do Kim, and Jae-Hyuk Choi. 2025. "Quantitative Analysis of Explosion Characteristics Based on Ignition Location in an Ammonia Fuel Preparation Room Using CFD Simulation" Applied Sciences 15, no. 12: 6554. https://doi.org/10.3390/app15126554
APA StyleBae, J.-W., Noh, B.-S., Lee, J.-W., Choe, S.-J., Park, K.-H., Kim, J.-D., & Choi, J.-H. (2025). Quantitative Analysis of Explosion Characteristics Based on Ignition Location in an Ammonia Fuel Preparation Room Using CFD Simulation. Applied Sciences, 15(12), 6554. https://doi.org/10.3390/app15126554