Abstract
In the noisy medium-scale quantum era, quantum computers are constrained by a limited number of qubits, restricted physical topological structures, and interference from environmental noise, making efficient and stable circuit scheduling a significant challenge. To improve the feasibility of quantum computing, it is essential to optimize the scheduling of quantum gates and the insertion of SWAP gates, reducing running time and enhancing computational efficiency. We propose a collaborative optimization framework that integrates the Quantum Exchange Lock Parallel Scheduler (QELPS) with the Full-level Joint Optimization SWAP Algorithm (FJOSA). In QELPS, SWAP conflict characteristics are used to adjust the layout of quantum gates across different levels while considering physical constraints and dynamically adapting to the circuit’s execution state. Quantum lock parallel technology enables the selective postponement of certain quantum gates, minimizing circuit depth and mitigating inefficiencies caused by excessive SWAP gate insertions. Meanwhile, FJOSA employs a cross-layer optimization strategy that combines heuristic algorithms with cost functions to improve gate scheduling at a global level. This approach effectively reduces quantum gate conflicts found in traditional methods and optimizes execution order, leading to better computational efficiency and circuit performance. Experimental results show that, compared to the traditional 2QAN algorithm, QELPS and FJOSA reduce additional gate insertions by 85.59% and 89.38%, respectively, while decreasing running time by 56.32% and 66.47%. These improvements confirm that the proposed method significantly enhances circuit scheduling efficiency and reduces resource consumption, making it a promising approach for optimizing quantum computation.
1. Introduction
Compared to classical computing, quantum computing offers significant advantages in solving specific problems, particularly in complex optimization tasks and quantum system simulations. It has demonstrated strong potential in areas such as supply chain optimization [], simulation of quantum systems [], cryptography [], and drug development [], surpassing the capabilities of traditional computing. With ongoing advancements in quantum technology, research based on various quantum algorithms continues to expand its applications [,,]. Significant progress has been made across different quantum computing platforms, including ion traps [], superconductors [], topological quantum systems [], and quantum dots []. The manipulation of quantum bits and the implementation of quantum gates have also become increasingly refined, further enhancing the feasibility of quantum computing in practical applications.
Despite significant progress in the Noise Intermediate-Scale Quantum (NISQ) era, many challenges remain. In NISQ devices, quantum gate operations are inevitably affected by noise, reducing computational accuracy and reliability. Noise can corrupt both quantum bit states and gate executions, making large-scale quantum error correction infeasible. As a result, achieving high-fidelity calculations comparable to classical computing has remained difficult. With an increasing number of quantum gates, calculation accuracy gradually declines, further complicating the problem. In this context, performing efficient and accurate computations in a noisy environment has become a core challenge. Particularly in the NISQ era, quantum algorithms and computing models must operate under strict hardware and software constraints. Therefore, ensuring the efficient execution of quantum algorithms with limited hardware resources is a critical issue that must be addressed.
To address this challenge, quantum circuit scheduling has become a key research focus in quantum computing. Its primary goal is to reduce unnecessary qubit exchanges and operation delays by optimizing the execution order of quantum gates []. This approach improves computational efficiency and accuracy under limited hardware re-sources. Optimization at the hardware level is essential [] to ensure compatibility between quantum hardware and software. Additionally, the specific constraints of hardware resources must be carefully considered. Since different quantum hardware architectures have distinct characteristics, scheduling methods must be highly adaptable to meet the needs of various platforms. Quantum gate waveform optimization [] is also crucial. By fine-tuning gate execution, noise interference can be minimized, leading to improved computational accuracy and fidelity.
In existing NISQ devices, quantum programs are typically composed of single-qubit and two-qubit gates. Studies have shown that the error rate of two-qubit gates is usually 10 times higher than that of single-qubit gates []. As a result, two-qubit gates in quantum circuits face a significantly higher risk of errors during execution. To improve the fidelity and efficiency of quantum computing, various strategies have been explored, including optimizing quantum circuit design [], implementing quantum error mitigation techniques [], and developing more robust quantum algorithms []. The primary goal of these strategies is to reduce quantum gate error rates and improve qubit stability, thereby enhancing the overall performance and reliability of quantum computers.
To address the challenges of excessive SWAP gate insertion and insufficient parallelism in quantum circuit scheduling, we propose a new scheduling method. By integrating SWAP gate conflict avoidance with quantum gate parallelism optimization, a Quantum Exchange Lock Parallel Scheduler is designed, and a Full-level Joint Optimization SWAP Algorithm is implemented.
Our contributions focus on the following aspects:
- Introducing SWAP conflict optimization of traditional greedy algorithms: Reduce the conflict of SWAP gates through deep optimization, while balancing the relationship between local suboptimal solutions and global optimization. Using the idea of greedy algorithms, flexibly handle conflicts between quantum gates and avoid frequent insertion of SWAP gates.
- Quantum lock parallel time operation: Utilize the parallelism of quantum gates to reduce the execution time and depth of the circuit. It is based on the results of the first layering and further optimizes the execution order of SWAP gates and other quantum gates by dynamically inserting nonconflicting quantum gates.
- Full-level joint optimization algorithm: Through cross-level optimization, the FJOSA algorithm can more effectively reduce the insertion of SWAP gates and optimize the execution order of quantum gates.
- Cost function: The algorithm dynamically selects the optimal number of optimization layers through the cost function, balancing the relationship between reducing SWAP gate insertion and controlling algorithm complexity.
- Comprehensive experimental verification and algorithm comparison: The effectiveness and superiority of the QELPS algorithm and the FJOSA algorithm are experimentally verified and compared with the benchmark circuit and the 2QAN algorithm, providing a reliable solution for the quantum circuit scheduling problem.
2. Related Works
Quantum circuit scheduling has been systematically investigated through three principal dimensions: algorithmic innovation, hardware compatibility, and error mitigation strategies. Early developments include the FitCut methodology [], where quantum circuits were modeled as weighted graphs with a community-driven bottom-up cutting strategy to address qubit resource constraints. While effective in local optimization, this approach was observed to compromise global solution quality.
Wu et al. [] established an Integer Linear Programming (ILP)-based multi-circuit framework for fidelity maximization, though its practical implementation remains constrained due to exponentially escalating computational complexity. Bhoumik et al.’s heuristic approach [] effectively reduced SWAP gate insertions but frequently converged to local optima, particularly under complex topological constraints.
Recent progress in quantum circuit optimization has introduced novel techniques to address hardware limitations and improve scalability. Zhou et al. [] proposed a Monte Carlo Tree Search (MCTS) framework for quantum circuit transformation, which enables deeper solution space exploration and effectively reduces circuit depth and size overhead. Bouchmal et al. [] applied the Quantum Approximate Optimization Algorithm (QAOA) to routing in optical networks, demonstrating its potential for efficient, resource-aware scheduling in dynamic network environments. Kanno et al. [] introduced tensor-network-based quantum phase difference estimation techniques to facilitate scalable parameter estimation in large quantum circuits, supporting more efficient simulations and computations.
Advancements in quantum circuit design have spanned both algorithmic and hardware domains. Perriello et al. [] introduced a comprehensive quantum circuit to address the information set decoding problem, aiding quantum cryptanalysis. Grzesiak et al. [] showcased efficient quantum programming utilizing Efficient Advanced Synthesis Environment (EASE) gates on a trapped-ion platform, enhancing native gate synthesis. Lu et al. [] developed a reconfigurable silicon photonic processor based on Sidewall-Corrugated Optical Waveguide (SCOW) resonant structures, facilitating adaptive optical control. Kanaar et al. [] tackled always-on exchange in silicon spin qubits by crafting robust pulse sequences, improving gate fidelity under hardware constraints.
Advancements in quantum control and topological robustness have been achieved through various innovative approaches. Ding et al. [] designed baseband flux pulses to enhance controlled-phase gate fidelity in superconducting circuits. Yale et al. [] demonstrated all-optical spin control using coherent dark states in solid-state systems. Das Sarma et al. [] introduced a topological model based on Majorana zero-mode braiding, offering a path toward fault-tolerant quantum computing.
In the pursuit of enhancing quantum circuit performance and scalability, Che et al. [] introduced a rapid virtual gate extraction method for silicon quantum dot devices, streamlining calibration processes. Krantz et al. [] offered a comprehensive guide on superconducting qubits, detailing their design and operational principles. Sorourifar et al. [] explored Bayesian optimization priors to improve the efficiency of variational quantum algorithms. Murali et al. [] developed noise-adaptive compiler mappings tailored for noisy intermediate-scale quantum computers, optimizing circuit execution.
Distributed quantum computing scenarios introduce additional complexity in scheduling due to physical qubit separation. Cirac et al. [] demonstrated the feasibility of distributed quantum computation over long distances using optical fibers, laying the theoretical foundation for remote entanglement generation and inter-node gate operations. Altintas et al. [] investigated spatially separated quantum game systems through spin–photon interactions, providing early insights into the scheduling challenges in hybrid photonic-matter architectures.
Recent engineering efforts have focused on enabling reliable quantum communication between distant nodes. Koshino et al. [] proposed a bidirectional interface for state transfer between superconducting and microwave-photon qubits via single reflection, enabling efficient remote quantum communication. Ozaydin et al. [] achieved deterministic preparation of W states based on spin–photon interaction models, facilitating multi-node entanglement distribution. More recently, Main et al. [] demonstrated a functional optical link for distributed quantum computing, further underscoring the need for optimized SWAP scheduling in cross-node topologies.
Hietala et al. [] introduced Verified Optimizer for Quantum Circuits (VOQC), a formally verified quantum circuit optimizer built with the Coq proof assistant, ensuring correctness in circuit transformations. Chong et al. [] emphasized the necessity of quantum-specific programming languages and compilers to bridge the gap between high-level algorithms and quantum hardware constraints. Maslov [] proposed a comprehensive compilation strategy for ion-trap quantum machines, focusing on optimizing two-qubit gate usage and overall circuit efficiency.
Bravyi et al. [] demonstrated that shallow quantum circuits can outperform classical counterparts in solving specific problems, establishing a clear quantum advantage. Ryan-Anderson et al. [] achieved real-time fault-tolerant quantum error correction, marking a significant step toward practical quantum computing. Sivarajah et al. [] introduced t|ket⟩, a versatile compiler optimizing quantum circuits for NISQ devices, enhancing execution efficiency.
In the realm of quantum circuit optimization, Liu et al. [] focused on resource-efficient designs for discrete logarithms on binary elliptic curves under nearest-neighbor constraints. Choi et al. [] applied the Quantum Approximate Optimization Algorithm (QAOA) to wireless scheduling, showcasing its potential in addressing NP-hard problems. Misevičius et al. [] introduced a hybrid genetic-hierarchical algorithm to enhance solutions for the quadratic assignment problem. Jang et al. [] developed a depth-optimized quantum circuit for Gauss–Jordan elimination, crucial for accelerating information set decoding. Booth [] proposed constraint programming models for depth-optimal qubit assignment and SWAP-based routing, outperforming traditional ILP models in both solution quality and runtime.
Amy et al. [] proposed a meet-in-the-middle algorithm for synthesizing depth-optimal quantum circuits, achieving significant T-gate Depth (T-depth) reduction. Kaewpuang et al. [] introduced a stochastic model for managing entangled pairs and qubit resources in quantum cloud computing, optimizing cost and fidelity. Cross et al. [] presented Open Quantum Assembly Language (OpenQASM) 3, an enhanced quantum assembly language supporting advanced control flow and real-time classical-quantum interactions.
Peng et al. [] introduced Deep Dynamic Planning-enhanced Q-learning (Deep Dyna-Q), integrating planning into reinforcement learning for dialogue policy learning. Brandhofer et al. [] proposed optimal qubit reuse strategies to enhance quantum circuit efficiency. Zhang and Zhou [] developed a two-stage dynamic cloud task scheduling method to optimize resource allocation. Murali et al. [] addressed crosstalk issues in NISQ devices through software-level mitigation techniques.
Quetschlich et al. [] introduced Munich Quantum Toolkit Benchmark (MQT Bench), a benchmarking suite for evaluating quantum software tools across various abstraction levels. Wang et al. [] proposed a rejection sampling method to expedite ground-state energy estimation on early fault-tolerant quantum computers, offering a quadratic improvement in the ground state overlap parameter. Wan et al. [] developed a randomized phase estimation algorithm with complexity independent of the number of Hamiltonian terms, allowing error reduction through increased sampling without deeper circuits.
Xu et al. [] introduced Quantum-circuit Universal Extensible Synthesis Optimizer (QUESO), an automated framework for synthesizing quantum-circuit optimizers tailored to specific hardware architectures, outperforming existing compilers like Qiskit and TKET on diverse benchmarks. Zhang et al. [] developed a deep reinforcement learning algorithm for topological quantum compiling, generating near-optimal gate sequences for arbitrary single-qubit unitarizes without ancillary qubits.
To address multi-level challenges in quantum circuit scheduling—spanning architectural adaptation, dynamic noise response, and cross-layer optimization—a dual-engine collaborative framework (QELPS-FJOSA) is proposed. The QELPS module incorporates quantum swap lock parallelism to dynamically decouple circuit layer interdependencies thro-ugh gate conflict analysis, enabling co-optimization of SWAP gate reduction and circuit depth minimization. Simultaneously, the FJOSA algorithm introduces a unified optimization space integrating layout routing, gate scheduling, and resource allocation. Traditional hierarchical optimization limitations are overcome through an enhanced heuristic cost function and adaptive weight balancing between local refinement and global exploration.
This framework resolves critical conflicts involving topological constraints, noise propagation, and temporal competition while maintaining computational efficiency. A novel paradigm is thereby established for efficient quantum resource utilization in NISQ-era systems.
3. Quantum Circuit Scheduling Problem
Quantum gate scheduling and layering have been identified as critical components in quantum algorithm optimization, particularly for Hamiltonian simulation tasks [], where circuit depth reduction and hardware resource efficiency are prioritized.
The target Hamiltonian is systematically decomposed into quantum gate operations through a structured methodology that leverages its inherent spectral attributes and interaction topologies, as formalized in Equation (1). This decomposition process involves the analysis of the Hamiltonian’s spectral properties, including eigenvalue distributions and symmetry characteristics, alongside the interaction patterns encoded in its connectivity graph to generate efficient gate sequences. The resulting sequences are constructed to preserve unitary dynamics while minimizing circuit depth and gate complexity, adhering to physical constraints such as qubit connectivity and coherence time limitations. This ensures a high-fidelity realization of the target dynamics, addressing key challenges in quantum circuit design for practical hardware implementations.
The 5-qubit simulation architecture shown in Figure 1a provides the foundational hardware configuration for circuit implementation. Fundamental quantum operations including CNOT and Hadamard (H) gates are identified in Figure 1c, demonstrating the basic components of the quantum circuit. Initial qubit dependency relationships presented in Figure 1b reveal that CNOT and CNOT cannot be executed in parallel due to shared access to Qubit . Concurrent operations are enabled through the coordinated scheduling of CNOT, CNOT, and H in Layer , which maintain independent qubit utilization patterns.
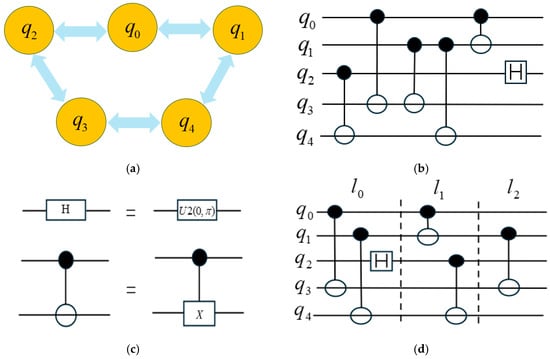
Figure 1.
Example of quantum circuit scheduling: (a) Quantum device architecture; (b) Initial quantum circuit; (c) Basic quantum gate; (d) Quantum circuit after scheduling.
Through systematic layering optimization, the dependent gates CNOT and CNOT are allocated to Layer , while CNOT is isolated in Layer to resolve cross-layer conflicts. The optimized quantum circuit architecture illustrated in Figure 1d achieves depth reduction by implementing hardware topology-aware scheduling. This improvement is accomplished through coordinated consideration of qubit coupling constraints during the compilation process, where gate sequences are reordered according to both dependency relationships and physical connectivity limitations.
The scheduling methodology confirms that parallel execution capabilities can be maximized through structured analysis of operational conflicts and hardware-specific constraints. Recent quantum compiler studies have demonstrated similar approaches for enhancing circuit efficiency through adaptive layering techniques []. Such optimizations become increasingly critical as quantum algorithms grow in complexity, requiring meticulous synchronization of computational requirements with device-specific architectural characteristics.
4. Quantum Exchange Lock Parallel Scheduler
The QELPS algorithm enhances quantum circuit layering through two optimized phases. First, a depth-prioritized greedy algorithm with SWAP conflict resolution is employed to balance local and global optimizations. Gate sequences are strategically reordered through temporary postponement, effectively resolving CNOT gate constraints without frequent SWAP insertions typically required by conventional methods.
Second, quantum lock parallelism is utilized to dynamically integrate non-conflicting operations. SWAP gate scheduling is optimized through temporal alignment with compatible gates, reducing both circuit depth and operational over-head. This dual-phase coordination enables improved hardware resource utilization compared to traditional layering approaches.
The methodology maintains circuit fidelity while demonstrating enhanced compatibility across NISQ device architectures. Experimental validations confirm these advantages through systematic comparisons under diverse quantum computing scenarios.
4.1. Deep Optimal Greedy Algorithm Layering Strategy Based on Swap Conflict
Theorem 1.
SWAP Conflict. Consider a quantum circuit that includes two CNOT gates, CNOT and CNOT. If CNOT fails to meet the topological constraint, a SWAP operation, SWAP, is introduced to alter the execution order of the qubits. However, this SWAP operation cannot operate on the same qubit simultaneously with both CNOT gates.
Theorem 2.
Local suboptimal solution. Consider a quantum circuit and a circuit layer that contain quantum gates CNOT and CNOT. Additionally, a quantum gate CNOT is present in layer . When CNOT fails to meet the topological constraint, the SWAP operation is introduced to alter the execution order of the qubits. However, SWAP cannot operate on the same qubit involved in both CNOT and CNOT within the layer. Consequently, CNOT is temporarily postponed to layer .
The first layering process employs a deep optimal greedy algorithm based on SWAP conflicts for quantum circuit partitioning. As shown in Equation (2), represents the total inserted SWAP gates, where corresponds to the SWAP count in the layer, ensuring equals the summation of across all layers. Traditional greedy algorithms are observed to resolve mapping conflicts immediately at each layering stage, leading to frequent insertions and increased circuit complexity. In contrast, the execution of specific quantum gates is intentionally postponed when conflicts are encountered in our approach, enabling temporary acceptance of local suboptimal configurations.
While immediate conflict resolution (a locally optimal strategy) substantially elevates in multilayered circuits, the proposed method strategically delays partial operations to prioritize global optimization. Conflicts in specific layers are purposefully maintained through controlled allocations to achieve this balance. The algorithm dynamically selects resolution strategies between optimal and suboptimal choices based on layer-specific parameters, thereby enhancing operational adaptability. This systematic compromise between localized SWAP gate management and circuit-wide efficiency ensures robust quantum circuit performance without logical integrity loss.
The specific operation steps are as follows:
Step 1: Quantum gates violating operational constraints are identified. The SWAP gate insertion schemes generated from these constrained gates are analyzed, forming the foundational basis for subsequent stratification.
Step 2: A local suboptimal solution is selected rather than enforcing immediate SWAP gate insertion, allowing strategic postponement of conflicting quantum operations.
Step 3: Residual quantum gates are progressively incorporated during layering iterations, with dual evaluation of both locally optimal and suboptimal configurations during insertion decisions.
Step 4: Non-conflicting quantum gates relative to existing components in the current layer are directly integrated; those exhibiting conflicts are systematically postponed for reprocessing.
Step 5: For quantum gates violating CNOT adjacency constraints, their SWAP insertion schemes are combined with prior configurations to establish optimized stratification baselines.
Step 6: The stratification cycle is completed when three conditions are met: All gates are optimally mapped to hierarchy levels through constraint-driven assignment; conflict resolutions are achieved via controlled postponement strategies; the layered architecture fulfills global optimization objectives.
4.2. Secondary Stratification Strategy Based on Quantum Lock Parallel Time
The quantum circuit structure is initially optimized using a deep greedy algorithm based on SWAP conflicts during primary layering, with residual conflicts addressed through secondary optimization. Temporal differences between SWAP execution times and shorter quantum gate durations enable refinement of layer allocation via quantum locking and gate movement mechanisms. By leveraging these timing differentials, the circuit schedule is improved while maintaining a balance between parallelism, optimization effectiveness, and computational complexity.
Step 1: Non-compliant quantum gates are identified through circuit mapping analysis. SWAP insertion candidates are simulated and selected based on conflict-free verification within current layer configurations.
Step 2: CNOT and H gate unlocking sequences are activated post-SWAP execution, exploiting quantum parallellism to insert executable gates in subsequent layers while maintaining temporal constraints established in primary layering.
Step 3: Full-circuit compliance is achieved through iterative traversal of non-compliant gates across hierarchical layers. Systematic gate allocation continues until archit-ectural constraints are satisfied through layer-wise insertion completion.
4.3. Quantum Circuit Hierarchical Strategy Based on Qelps
The QELPS algorithm includes a greedy layering strategy based on SWAP conflicts and a secondary layering strategy leveraging quantum lock parallelism. Together, they aim to reduce SWAP gate usage, optimize circuit depth, and enhance execution efficiency. Its main operation steps are as follows: Additionally, the algorithm dynamically adapts to the circuit’s evolving state to further refine the scheduling process.
- (1)
- Initial layering: First, identify all quantum gates that do not meet the CNOT constraints and analyze possible SWAP gate insertion schemes to ensure that the initial layer can meet the requirements of the hardware topology. Based on this analysis, build the first layer and use it as the basis for subsequent layering.
- (2)
- Intra-layer filling and conflict handling: Fill as many executable quantum gates as possible in the current layer to ensure maximum parallelism. If there is a conflict caused by topological restrictions or data dependencies, the conflicting quantum gates will be postponed to the next layer to avoid unnecessary SWAP gate overhead.
- (3)
- Dynamic adjustment of the number of layers: As the quantum gates are gradually filled in, the algorithm will flexibly increase or merge the layers according to the number of quantum gates in each layer, the execution parallelism and its conflict with the SWAP gate, thereby optimizing the circuit structure and improving the computing efficiency.
- (4)
- Screening micro-conflicting SWAP gates: In the first layer, simulated SWAP gate insertion is performed on all quantum gates that do not meet the quantum bit mapping requirements. By analyzing the impact of different SWAP gates, SWAP gates that only slightly conflict with the current layer are screened out to minimize the additional SWAP gate overhead.
- (5)
- Quantum locking and gate movement: The quantum gates in the first layer are locked to ensure the stability of circuit execution. In terms of execution order, CNOT gates are unlocked and executed before SWAP gates. Subsequently, quantum gates that will not conflict with the SWAP gates of the first layer and can be directly executed are selected in the subsequent layers to fill in the layer to optimize the entire scheduling process.
- (6)
- Constructing all levels: Repeat the optimization process of (4) and (5) for the subsequent levels, gradually fill in all quantum gates, and resolve mapping conflicts until the scheduling of the entire circuit is completed.
The pseudo code of the QELPS algorithm is as follows (Algorithm 1).
| Algorithm 1. Quantum Exchange Lock Parallel Scheduler | |
| Input: Output: that do not satisfy CNOT constraints do | |
| 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: | Else Break End If |
| 18:End While | |
| do | |
| 20: 21: 22: 23: 24: 25: 26: | ’s time End For |
28:Return C 29:End | |
4.4. Example AnalysisI
As shown in the quantum circuit diagram in Figure 2, the nodes represent quantum bits, while the edges indicate the connectivity between them. The input circuit consists of CNOT, CNOT, CNOT, CNOT, CNOT, and H. After introducing the QELPS algorithm, CNOT, which requires a mapping adjustment for execution, is selected as the benchmark and placed in layer The algorithm identifies both locally optimal and suboptimal solutions to resolve SWAP gate conflicts within the quantum circuit.
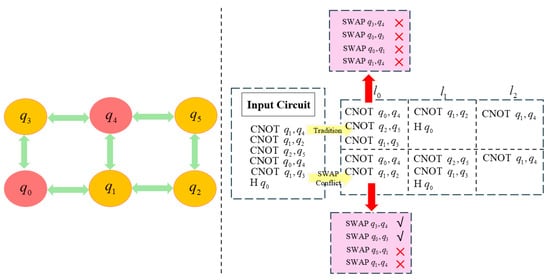
Figure 2.
The hardware architecture of a quantum circuit and the quantum circuit after the first layering.
During the layering process, a dynamic insertion and adjustment strategy for SWAP gates is applied to incrementally fill each layer with quantum gates while prioritizing gates in the front layers. Initially, the local optimal solution is considered, where CNOT, CNOT, and CNOT are placed in . However, after evaluating the insertion of four possible SWAP gates required to satisfy CNOT gate constraints, conflicts with qubits involved in the existing CNOT gates within the layer are detected. As a result, the local optimal solution is abandoned, and the local suboptimal solution is selected instead, consisting of CNOT and CNOT.
Following the SWAP conflict resolution process, the SWAP gates that satisfy the mapping conditions are SWAP and SWAP. This approach is consistently applied to all subsequent layers. As a result, contains CNOT and CNOT, consists of CNOT, CNOT, and H, while includes CNOT.
In the secondary layering process, it is assumed that multiple gates cannot act on a single qubit simultaneously. A qubit that participates in a certain gate operation is considered to be in a locked state and remains locked for a duration of before being unlocked. Based on this assumption, the operands of different quantum gates determine their locking durations, where the Hadamard (H) gate locks a qubit for , the CNOT gate for , and the SWAP gate for . Therefore, a reasonable assumption is made when , respectively.
Following these constraints, the gate CNOT in layer does not satisfy the mapping requirements for CNOT execution. As a result, a SWAP gate must be introduced to modify the quantum mapping. However, using SWAP and SWAP creates conflicts with CNOT and CNOT since these operations would act on qubits , and simultaneously. Therefore, these SWAP gates are not feasible and must be discarded. The only SWAP operations that satisfy the conflict constraints are SWAP and SWAP.
The introduction of SWAP gates increases execution time. In the upper coordinate diagram of Figure 3a, the parallel execution time for CNOT and SWAP is . After updating the quantum mapping, the execution time of the CNOT operation is . In layer , the parallel execution time for CNOT, CNOT, and H is also . The execution of CNOT in layer requires , leading to a total execution time of .
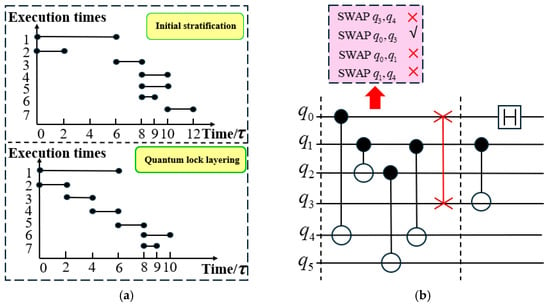
Figure 3.
Quantum circuit after secondary stratification: (a) Quantum gate duration diagram; (b) Quantum circuit after secondary stratification improvement.
With the introduction of the quantum locking mechanism, qubits and are initially locked and remain so for , as illustrated in the lower coordinate diagram of Figure 3a. When the SWAP gate is still executing, quantum gates that do not conflict with the qubits involved in the current SWAP operation can be identified from subsequent layers and inserted into the current layer. The inserted quantum gates must ensure that the execution time of this layer does not exceed its original execution time before stratification. Following this approach, when SWAP is executed, CNOT and CNOT are inserted into layer , maintaining an execution time of . After updating the mapping, the execution time of CNOT is . Finally, CNOT and H execute in parallel for , resulting in a total execution time of . The circuit structure after the second stratification is shown in Figure 3b, where one quantum circuit layer is eliminated, and the parallel execution of quantum gates is fully utilized to improve computational efficiency.
5. Full-Level Joint Optimization Swap Algorithm
5.1. Limitations of the QELPS Algorithm
The limitation of the QELPS algorithm is that, although parallel execution of quantum gates within each layer is ensured, dependencies and interactions across subsequent layers are not effectively handled. To address this, SWAP gate operations must be introduced to modify the quantum mapping. However, excessive SWAP insertions increase the gate error rate and prolong execution time. The FJOSA algorithm builds upon QELPS by more comprehensively considering gate dependencies and interactions, thereby improving scheduling efficiency and reducing unnecessary SWAP operations.
5.2. Algorithm Principle
We propose a Full-level Joint Optimization SWAP Algorithm based on a heuristic approach. Instead of strictly following the execution order of each layer, deep optimization is performed across multiple layers. Although breaking the layer structure may increase the complexity of circuit dependency management and reduce parallelism, the layers are not entirely broken. After completing the layering process using a deep optimal greedy algorithm based on SWAP conflicts, full-level joint optimization is further applied. However, when multiple layers are processed simultaneously, dependency complexity increases significantly. Therefore, the cost function must be carefully designed to select appropriate layers for joint optimization.
where represents the optimization, while denotes the number of optimized layers and the current total number of layers. The cost function, , evaluates the optimization impact from the layer to the layer during the optimization. The variable represents the number of SWAP gates used by the FJOSA algorithm for the to layer, whereas represents the number of SWAP gates used by the QELPS algorithm for the same range during the optimization. The difference between these values, , quantifies the reduction in SWAP gate usage achieved by the FJOSA algorithm compared to QELPS.
The parameters and serve as weights for different optimization indicators, ensuring a balanced contribution of each factor to the overall optimization goal. These weights are derived from experimental data. represents the scheduling complexity of quantum bits, defined as the number of optimized layers raised to the power after the optimization. The variable is a normalization factor used to balance the SWAP gate reduction effect across different layers, while is another normalization factor designed to assess the complexity of quantum bit scheduling.
The Full-level Joint Optimization SWAP Algorithm is executed in multiple rounds. In each round, optimization begins at the layer, and the circuit up to the layer is simulated to determine possible SWAP gate insertions . As the number of optimization rounds increases, more layers are included in the optimization process. After each round, the corresponding cost function value is computed, and the layer with the lowest cost function value is selected as the optimal choice. Once the current optimization is completed, the process proceeds to the next layer.
In Formula (4), represents the reduction in the number of SWAP gate insertions after optimizing layers starting from the layer during the optimization. As the number of optimized layers increases, the algorithm evaluates the potential reduction in SWAP gate insertions with each additional layer. However, since all possible SWAP gate insertion schemes must be explored, identifying the scheme with the fewest SWAP gate insertions significantly increases computational complexity as the number of optimization layers grows.
In order to control the computational cost caused by an increase in the number of optimization layers, a limiting factor is introduced in the cost function (Formula (3)). Quantum circuits are composed of multiple gates acting on quantum bits, and as the number of quantum bits increases, the overall circuit complexity increases. reflects the exponential growth in algorithm complexity as the number of optimization levels increases. Because the number of quantum bits involved in each optimization may vary with the number of levels, the insertion of SWAP gates and the scale of the search space are also affected. By incorporating , the effects of both the number of quantum bits and the number of optimization levels are dynamically combined to accurately model this complexity growth. In addition, normalization factors and are introduced into the cost function, as shown in Formulas (5) and (6), to balance complexity cost and optimization benefits within a unified scale. This improves both the versatility and interpretability of the cost function, allowing it to adapt to different circuit structures and optimization requirements.
Specifically, as the number of optimization layers increases, the number of SWAP gates that can be reduced by gradually decreases. However, the value of increases exponentially, causing the cost function value to rise rapidly. This exponential relationship reflects the characteristic of diminishing returns in optimization. Although optimizing more layers simultaneously can further reduce SWAP gate insertions, it also significantly increases computational complexity. Therefore, by employing , a restrictive effect is imposed. By reasonably selecting the number of optimized layers, a balance can be achieved between reducing the insertion of SWAP gates and controlling algorithm complexity. This approach ensures efficient circuit execution while minimizing computational overhead.
One critical aspect of the FJOSA algorithm is its computational scalability under increasing circuit depth and qubit count, which was not explicitly discussed in earlier sections. As the number of circuit layers increases, and more quantum bits are involved in optimization, the number of possible SWAP insertion combinations across multiple layers grows rapidly. Specifically, the search space complexity increases approximately as , since each additional layer allows for more interaction permutations among qubit pairs. This effect becomes even more pronounced when gate congestion or hardware constraints introduce dependency chains across layers, which further increase the cost of evaluating and selecting valid gate placements.
In FJOSA, the multi-layer scheduling process evaluates several candidate configurations to balance gate satisfaction and SWAP reduction. The algorithm’s complexity scales quadratically with both the number of active qubits and optimization layers. While this improves global performance, it also introduces overhead as circuit depth increases. Therefore, the number of layers per optimization round must be bounded in practice, particularly for circuits with over 20 qubits or 50 layers. This highlights the need for scalable heuristics when extending FJOSA to larger circuits.
The specific operations of the FJOSA algorithm are as follows:
- (1)
- Initial Stratification: The QELPS algorithm is used to stratify quantum circuits.
- (2)
- Screening the Optimal SWAP Combination: In the first layer, all SWAP gate combination solutions that solve the CNOT gate constraint are identified and compared. The solution with the least number of SWAP gates is selected.
- (3)
- Adjacent Layer Optimization: In the second layer, the best SWAP gate solution from the previous step is compared with the solutions in subsequent layers. The solution with the fewest SWAP gates is chosen.
- (4)
- Functional Judgment and Joint Optimization: Steps (2) and (3) are applied to the first () layers, where . If the cost function () for the layer is greater than zero, the first and layers are optimized. In this case, the optimization starts from the initial layer, specifically when .
- (5)
- Overall Layer Optimization: Once the mapping of the previous layer is satisfied, the optimization continues for all subsequent layers until the SWAP gate optimization for all layers is completed.
The pseudo code of the FJOSA algorithm is as follows (Algorithm 2).
| Algorithm 2. Full-level Joint Optimization SWAP Algorithm | |
| Input: Output: 1:Begin: 6: End for | |
| do | |
| 9: 10: 11: 12: 13: 14: 15: | End if End for |
| 16: End for | |
| do | |
| 18: 19: 20: 21: | End if |
| 22: End For | |
24:End | |
5.3. Example Analysis
As shown in Figure 4a, the original hardware architecture diagram illustrates the correlation between each quantum bit. Figure 4b presents the original logic circuit diagram, which must satisfy the quantum bit correlation shown in Figure 4a. The quantum gates enclosed by red dotted lines do not meet the physical constraints. The input circuits of the quantum circuit include CNOT, CNOT, CNOT, CNOT, CNOT, CNOT, and H, which are divided into four layers.
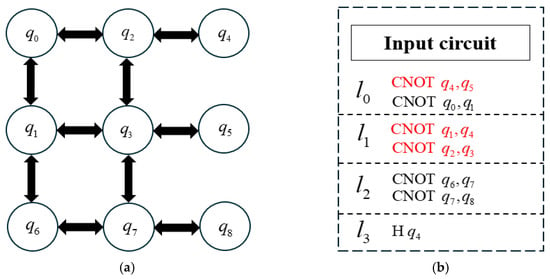
Figure 4.
Initial mapping quantum circuit diagram: (a) Original hardware architecture; (b) Original logic circuit diagram.
In the FJOSA algorithm, the value of is calculated during the optimization, and its positive or negative value determines whether to continue the optimization until the final layer is processed. The goal is to obtain the solution with the least number of inserted SWAP gates. When the number of optimizations is , the algorithm begins optimization from the initial layer (), with the minimum number of optimized layers set to . For each layer in the quantum circuit, represents the number of SWAP gates required. All possible SWAP insertion solutions are evaluated, revealing two feasible solutions that satisfy the constraints of the layer with a minimum of SWAP gates. The first solution consists of SWAP and SWAP , while the second includes SWAP and SWAP .
For each quantum mapping, the solution with the least number of SWAP gates in the layer is determined. In the first solution, as shown in Figure 5, , meaning two additional SWAP gates must be inserted. In contrast, in the second solution, as illustrated in Figure 6, means no SWAP gates are needed. This finding highlights that carefully selecting the SWAP insertion scheme can significantly reduce the total number of SWAP gates. Consequently, the FJOSA algorithm selects the second solution (), whereas the QELPS algorithm, which does not account for the impact of each solution on subsequent layer mappings, chooses the first solution ().
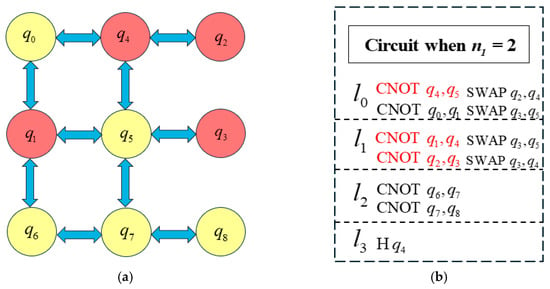
Figure 5.
Quantum circuit after optimization with : (a) Original hardware architecture with ; (b) Original logic circuit diagram with .
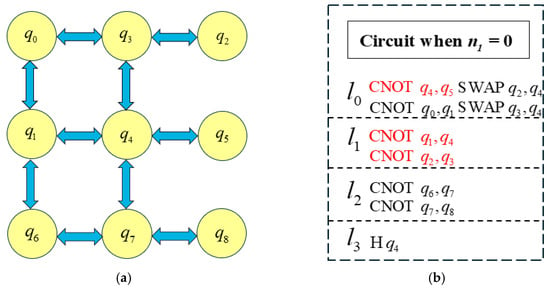
Figure 6.
Quantum circuit after optimization with : (a) Original hardware architecture with ; (b) Original logic circuit diagram with .
Formula (4) shows that , where Smax represents the number of SWAP gates along the longest path. The CNOT operations CNOT , CNOT , and CNOT correspond to paths , , and , respectively. After computing , Formula (5) yields . The first two layers involve six quantum bits and four CNOT gates, with and , leading to according to Formula (6). Through extensive experiments, is obtained, and Formula (4) results in . Since the cost function is less than zero, optimization continues.
When the number of optimizations is , the number of optimized layers increases to , while the current optimization starts from . In this case, all CNOT gates in the layer satisfy the mapping constraints. As a result, . The first three layers collectively utilize 10 quantum bits and 6 CNOT gates, with and . Using Formula (6), we obtain , and applying Formula (4) results in . Since the cost function value is greater than zero, the optimization process terminates.
For , the number of optimized layers is , and the current optimization begins from . In this case, all quantum gates in both the and layers satisfy the mapping constraints, leading to . These two layers involve a total of 4 quantum bits, 2 CNOT gates, and 1 Hadamard (H) gate. With and , Formula (6) yields , while Formula (4) computes . Since the cost function remains positive, the optimization process is again halted.
The FJOSA algorithm effectively minimizes the number of inserted SWAP gates while significantly reducing the overall circuit depth. Additionally, it enhances the mapping layout of quantum bits to a certain extent. When combined with a quantum gate parallel execution strategy, FJOSA can further decrease SWAP gate insertions while ensuring CNOT constraints are met. This ultimately leads to a more efficient and stable execution of quantum circuits, improving both computational accuracy and hardware resource utilization.
6. Experimental Evaluation
6.1. Evaluation Metrics
The experiments in this paper utilize the benchmark circuit library [,,,,,,], which is widely adopted for evaluating quantum circuit scheduling. All circuits consist of Clifford+T gates, with CNOT gates as the only two-qubit operations. The number of quantum bits in the circuits ranges from 4 to 16. To comprehensively analyze the execution performance and optimization effectiveness, IBM’s Qiskit compiler [] is integrated with superconducting quantum hardware [].
All algorithms presented in this paper are implemented using Python 3.9, and all compilation tasks are performed on a laptop equipped with an AMD Ryzen 7 processor (3.20 GHz, 16 GB RAM).
To further validate the effectiveness of the proposed method, the 2QAN (Quantum Annealing Network) algorithm [] is used as a comparative benchmark. The 2QAN algorithm optimizes quantum bit connectivity through quantum annealing techniques to minimize the number of SWAP gate insertions. By comparing our method with 2QAN, we provide a comprehensive evaluation of different optimization approaches in quantum circuits, particularly regarding their adaptability and optimization performance under complex hardware topologies. This analysis offers valuable insights for future quantum circuit optimization strategies.
6.2. Model Evaluation
We evaluate the performance of three quantum circuit scheduling and optimization algorithms—2QAN, QELPS, and FJOSA—in terms of compilation overhead through experiments on 30 benchmark circuits.
As shown in Table 1, all three algorithms effectively optimize the number of extra gates in quantum circuits, significantly reducing their count. However, their optimization effects vary. Compared with the benchmark circuit, the 2QAN algorithm achieves an optimization rate of 57.10%. Although it reduces a certain number of extra gates, its local optimization strategy does not fully consider the complexity of global optimization and inter-layer interactions. This limitation is particularly evident when dealing with complex circuits, where its performance is relatively inferior to the other two algorithms.

Table 1.
Comparison of the additional gate counts of 2QAN, QELPS, and FJOSA.
The optimization effect of the QELPS algorithm reaches 85.59%. Its deep optimal greedy strategy, based on SWAP conflict resolution, effectively handles CNOT gate constraint conflicts. By postponing the execution of certain quantum gates, it minimizes SWAP gate insertions, reducing circuit depth and overall complexity. Moreover, QELPS balances local suboptimal and optimal solutions, demonstrating strong optimization capabilities, particularly in large-scale circuits.
The FJOSA algorithm achieves the most significant optimization effect, reaching 89.38%, and demonstrates strong global optimization capabilities. By employing cross level deep optimization and a global perspective, it effectively reduces the insertion of SWAP gates. This algorithm excels in optimizing multi-layer circuits, minimizing redundant operations. Compared with the QELPS algorithm, the optimization effect of FJOSA improves by 26.29%. Although FJOSA incurs a higher computational cost, its enhanced optimization performance still makes it superior to the other two algorithms in terms of compilation overhead.
From the perspective of quantum bit count, the FJOSA algorithm achieves an optimization rate exceeding 80% for benchmark circuits with 4, 5, 12, 13, 14, and 15 qubits. In contrast, the QELPS algorithm exceeds 80% only in circuits with 4 and 14 qubits. This indicates that FJOSA demonstrates greater adaptability in large-scale circuits, particularly when handling complex structures. It effectively man-ages multi-level dependencies, enhances parallel execution, and improves overall circuit performance. In comparison, the QELPS algorithm shows limitations in optimizing larger-scale circuits.
As shown in Table 2, the execution time of the 2QAN, QELPS, and FJOSA algorithms on the benchmark circuits varies significantly. The 2QAN algorithm has the longest average runtime, while the QELPS and FJOSA algorithms reduce execution time by 56.32% and 66.47%, respectively, compared to 2QAN. The superior optimization of the FJOSA algorithm over QELPS is attributed to its use of a heuristic approach and a cost function to globally optimize SWAP gate insertion. Particularly in large-scale circuits, the FJOSA algorithm effectively balances local and global optimization through its cost function ().

Table 2.
Comparison of execution time of 2QAN, QELPS and FJOSA.
In small-scale circuits (four and five qubits), the QELPS algorithm reduces runtime by 60.53% compared to 2QAN, whereas the FJOSA algorithm achieves only a 6.05% reduction. This is because the global optimization strategy of FJOSA does not fully demonstrate its advantages in simpler circuits. In contrast, for circuits with more than 10 qubits, the FJOSA algorithm achieves a 66.49% runtime reduction, significantly outperforming the QELPS algorithm. This highlights its strong optimization capability in handling complex circuits.
6.3. Expanding the Number of Qubits
Since previous experiments primarily focused on datasets ranging from four to 16 qubits, we enhance the comprehensiveness of this study by expanding the range of quantum bits. As shown in Figure 7, the FJOSA algorithm builds upon the QELPS algorithm by incorporating a joint global hierarchical strategy. Experimental results indicate that when the parameter , the optimization of circuit overhead is particularly significant. This suggests that the weight assigned to SWAP gate overhead should be larger, while the weight of algorithm complexity should be relatively smaller due to its exponential relationship. By appropriately increasing algorithm complexity, the number of SWAP gate insertions can be effectively reduced.
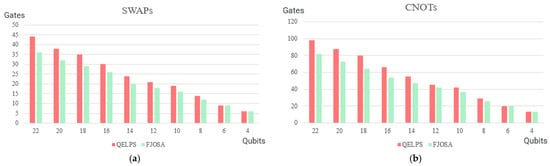
Figure 7.
Comparison of optimization results between QELPS and FJOSA: (a) Comparison of SWAP gate counts; (b) Comparison of CNOT gate counts.
Compared to the QELPS algorithm, the FJOSA algorithm reduces SWAP gate insertions by an average of 16.15% and CNOT gate insertions by an average of 16.2% in quantum circuits ranging from 22 to 12 qubits. In circuits with 10 to four qubits, SWAP gate insertions decrease by an average of 10.4%, while CNOT gate insertions are reduced by an average of 7.7%. These results demonstrate that the FJOSA algorithm is particularly well-suited for large-scale quantum circuits.
Experimental results indicate that the conflict problem of SWAP gates is effectively resolved by the QELPS algorithm through preliminary stratification. This approach results in a significant reduction in the number of inserted SWAP and CNOT gates, thereby improving the efficiency of quantum gate usage. Based on this, a secondary stratification strategy combined with quantum locks is employed, further reducing runtime overhead and enhancing scheduling efficiency. Finally, the FJOSA algorithm is applied within this stratified framework to further decrease the overhead of SWAP and CNOT gates, ultimately achieving a comprehensive optimization of quantum circuit depth and execution efficiency.
7. Conclusions
In response to the core challenges of quantum circuit scheduling in the NISQ era, we propose the QELPS–FJOSA framework. This framework integrates dynamic hierarchical optimization with global coordination strategies. In the QELPS component, SWAP conflict characteristics are employed to control the quantum gate layout in real time. The inter-layer coupling effect is decoupled via a quantum locking mechanism, thereby significantly optimizing circuit depth and reducing SWAP operation redundancy. The FJOSA component is based on cross-layer heuristic search driven by a cost function, which overcomes the limitations of traditional local optimization and achieves a globally optimal approximation of multi-level resource allocation.
The framework demonstrates strong generalization capabilities in heterogeneous architectures such as superconducting, photonic, and ion trap systems. Challenges related to the collaborative optimization of topological constraints, noise accumulation, and timing competition are effectively alleviated, while theoretical and methodological support is provided to improve the practical performance of quantum hardware. Future research will explore the integration of fault-tolerant mechanisms and verify the scalability of the framework in distributed quantum systems, thereby promoting the practical application of quantum computing in the NISQ era.
Author Contributions
Conceptualization, Z.D. and X.L.; Methodology, X.L. and H.L.; Software, Z.D.; Validation, Z.D., X.L. and H.L.; Formal analysis, X.L.; Investigation, Z.D., X.L. and H.L.; Resources, Z.D., X.L. and H.L.; Data curation, H.L.; Writing—original draft preparation, X.L.; Writing—review and editing, Z.D.; Visualization, H.L.; Supervision, Z.D.; Project administration, Z.D.; Funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Heilongjiang Province LH2024F042.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All values used in the study have been presented in the manuscript, but the complete recorded data are unavailable due to privacy restrictions.
Acknowledgments
We extend our sincere gratitude to Hui Li and Zuoqiang Du for their invaluable technical and administrative support throughout the study, which significantly facilitated its successful completion.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Montanaro, A. Quantum algorithms: An overview. npj Quantum Inf. 2016, 2, 1–8. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science (FOCS), Santa Fe, NM, USA, 20–22 November 1994; IEEE: New York, NY, USA, 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Blunt, N.S.; Camps, J.; Crawford, O.; Izsák, R.; Leontica, S.; Mirani, A.; Moylett, A.E.; Scivier, S.A.; Sünderhauf, C.; Schopf, P.; et al. A perspective on the current state-of-the-art of quantum computing for drug discovery applications. arXiv 2022, arXiv:2206.00551. [Google Scholar] [CrossRef] [PubMed]
- Gambetta, J.M.; Chow, J.M.; Steffen, M. Building logical qubits in a superconducting quantum computing system. npj Quantum Inf. 2017, 3, 2. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Cheng, J.; Karemore, G.; Zitnik, M.; Chong, F.T.; Liu, J.; Fu, T.; Liang, Z. Quantum-machine-assisted drug discovery: Survey and perspective. arXiv 2024, arXiv:2408.13479. [Google Scholar]
- Batra, K.; Zorn, K.M.; Foil, D.H.; Minerali, E.; Gawriljuk, V.O.; Lane, T.R.; Ekins, S. Quantum machine learning algorithms for drug discovery applications. J. Chem. Inf. Model. 2021, 61, 2641–2647. [Google Scholar] [CrossRef]
- Moses, S.A.; Baldwin, C.H.; Allman, M.S.; Ancona, R.; Ascarrunz, L.; Barnes, C.; Bartolotta, J.; Bjork, B.; Blanchard, P. A race-track trapped-ion quantum processor. Phys. Rev. X 2023, 13, 041052. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083–1159. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
- Kloeffel, C.; Loss, D. Prospects for spin-based quantum computing in quantum dots. Annu. Rev. Condens. Matter Phys. 2013, 4, 51–81. [Google Scholar] [CrossRef]
- Guerreschi, G.G.; Park, J. Two step approach to scheduling quantum circuits. arXiv 2018, arXiv:1708.00023. [Google Scholar] [CrossRef]
- Li, G.; Shi, Y.; Javadi-Abhari, A. Software-hardware co-optimization for computational chemistry on superconducting quantum processors. arXiv 2021, arXiv:2105.07127. [Google Scholar]
- Glaser, N.J.; Roy, F.A.; Tsitsilin, I.; Koch, L.; Bruckmoser, N.; Schirk, J.; Romeiro, J.H.; Huber, G.B.P.; Wallner, F.; Singh, M.; et al. Sensitivity-adapted closed-loop optimization for high-fidelity controlled-Z gates in superconducting qubits. arXiv 2024, arXiv:2412.17454. [Google Scholar]
- Barends, R.; Kelly, J.; Megrant, A.; Veitia, A.; Sank, D.; Jeffrey, E.; White, T.C.; Mutus, J.; Fowler, A.G.; Campbell, B.; et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500–503. [Google Scholar] [CrossRef]
- Murali, P.; Linke, N.M.; Martonosi, M.; Abhari, A.J.; Nguyen, N.H.; Alderete, C.H. Full-stack, real-system quantum computer studies: Architectural comparisons and design insights. In Proceedings of the 46th Annual International Symposium on Computer Architecture (ISCA), Phoenix, AZ, USA, 22–26 June 2019; ACM: New York, NY, USA, 2019; pp. 527–540. [Google Scholar] [CrossRef]
- Cai, Z.; Babbush, R.; Benjamin, S.C.; Endo, S.; Huggins, W.J.; Li, Y.; McClean, J.R.; O'Brien, T.E. Quantum error mitigation. Rev. Mod. Phys. 2023, 95, 045005. [Google Scholar] [CrossRef]
- Ravi, G.S.; Smith, K.N.; Gokhale, P.; Mari, A.; Earnest, N.; Javadi-Abhari, A.; Chong, F.T. VAQEM: A variational approach to quantum error mitigation. arXiv 2021, arXiv:2112.05821. [Google Scholar]
- Kan, S.; Du, Z.; Palma, M.; Stein, S.A.; Liu, C.; Wei, W.; Chen, J.; Li, A.; Mao, Y. Scalable circuit cutting and scheduling in a resource-constrained and distributed quantum system. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering (QCE), Montreal, QC, Canada, 15–20 September 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1077–1088. [Google Scholar]
- Wu, X.-C.; Ding, Y.; Shi, Y.; Alexeev, Y.; Finkel, H.; Kim, K.; Chong, F.T. ILP-based scheduling for linear-tape model trapped-ion quantum computers. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (SC19), Denver, CO, USA, 17–22 November 2019; Available online: https://sc19.supercomputing.org/proceedings/tech_poster/tech_poster_pages/rpost216.html (accessed on 1 February 2025).
- Bhoumik, D.; Majumdar, R.; Saha, A.; Sur-Kolay, S. Distributed scheduling of quantum circuits with noise and time optimization. arXiv 2023, arXiv:2309.06005. [Google Scholar]
- Zhou, X.Z.; Fang, Y.; Li, S.J. Quantum circuit transformation: A Monte Carlo tree search framework. In Proceedings of the 49th Annual International Symposium on Computer Architecture (ISCA), New York, NY, USA, 18–22 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1021–1034. [Google Scholar] [CrossRef]
- Bouchmal, O.; Cimoli, B.; Stabile, R.; Vegas Olmos, J.J.; Tafur Monroy, I. Quantum approximate optimization algorithm for routing optimization in 6G optical networks. In Proceedings of the 2024 International Conference on Optical Network Design and Modeling (ONDM 2024), Madrid, Spain, 6–9 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Kanno, S.; Sugisaki, K.; Nakamura, H.; Yamauchi, H.; Sakuma, R.; Kobayashi, T.; Gao, Q.; Yamamoto, N. Tensor-based quantum phase difference estimation for large-scale demonstration. arXiv 2024, arXiv:2408.04946. [Google Scholar]
- Perriello, S.; Barenghi, A.; Pelosi, G. A complete quantum circuit to solve the information set decoding problem. In Proceedings of the 2021 IEEE International Conference on Quantum Computing and Engineering (QCE), Broomfield, CO, USA, 17–22 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 366–377. [Google Scholar] [CrossRef]
- Grzesiak, N.; Maksymov, A.; Niroula, P.; Nam, Y. Efficient quantum programming using EASE gates on a trapped-ion quantum computer. Quantum 2022, 6, 634. [Google Scholar] [CrossRef]
- Lu, L.; Shen, L.; Gao, W.; Zhou, L.; Chen, J. Reconfigurable silicon photonic processor based on SCOW resonant structures. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Kanaar, D.W.; Wolin, S.; Güngördü, U.; Kestner, J.P. Single-tone pulse sequences and robust two-tone shaped pulses for three silicon spin qubits with always-on exchange. Phys. Rev. B 2021, 103, 235314. [Google Scholar] [CrossRef]
- Ding, Q.; Oppenheim, A.V.; Boufounos, P.T.; Gustavsson, S.; Grover, J.A.; Baran, T.A.; Oliver, W.D. Pulse design of baseband flux control for adiabatic controlled-phase gates in superconducting circuits. arXiv 2024, arXiv:2407.02722. [Google Scholar]
- Yale, C.G.; Buckley, B.B.; Christle, D.J.; Burkard, G.; Heremans, F.J.; Bassett, L.C.; Awschalom, D.D. All-optical control of a solid-state spin using coherent dark states. Proc. Natl. Acad. Sci. USA 2013, 110, 7595–7600. [Google Scholar] [CrossRef]
- Das Sarma, S.; Freedman, M.; Nayak, C. Majorana zero modes and topological quantum computation. npj Quantum Inf. 2015, 1, 15001. [Google Scholar] [CrossRef]
- Che, S.; Oh, S.W.; Qin, H.; Liu, Y.; Sigillito, A.; Li, G. Fast virtual gate extraction for silicon quantum dot devices. arXiv 2024, arXiv:2409.15181. [Google Scholar]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer's guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Sorourifar, F.; Chamaki, D.; Tubman, N.M.; Paulson, J.A.; Bernal Neira, D. Bayesian optimization priors for efficient variational quantum algorithms. arXiv 2024, arXiv:2406.14627. [Google Scholar]
- Murali, P.; Baker, J.M.; Javadi-Abhari, A.; Chong, F.T.; Martonosi, M. Noise-adaptive compiler mappings for noisy intermediate-scale quantum computers. In Proceedings of the 24th ACM International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS), Providence, RI, USA, 13–17 April 2019; pp. 1015–1029. [Google Scholar] [CrossRef]
- Cirac, J.I.; Ekert, A.K.; Huelga, S.F.; Macchiavello, C. Distributed quantum computation over noisy channels. Phys. Rev. A 1999, 59, 4249–4254. [Google Scholar] [CrossRef]
- Altintas, A.A.; Ozaydin, F.; Bayindir, C.; Bayrakci, V. Prisoners’ dilemma in a spatially separated system based on spin–photon interactions. Photonics 2022, 9, 617. [Google Scholar] [CrossRef]
- Koshino, K.; Inomata, K. Bidirectional state transfer between superconducting and microwave-photon qubits by single reflection. Phys. Rev. Appl. 2024, 21, 054049. [Google Scholar] [CrossRef]
- Ozaydin, F.; Yesilyurt, C.; Bugu, S.; Koashi, M. Deterministic preparation of W states via spin-photon interactions. Phys. Rev. A 2021, 103, 052421. [Google Scholar] [CrossRef]
- Main, D.; Drmota, P.; Nadlinger, D.P.; Ainley, E.M.; Agrawal, A.; Nichol, B.C.; Srinivas, R.; Araneda, G.; Lucas, D.M. Distributed quantum computing across an optical network link. Nature 2025, 629, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Hietala, K.; Rand, R.; Hung, S.-H.; Wu, X.; Hicks, M. A verified optimizer for quantum circuits. Proc. ACM Program. Lang. 2021, 5, 37. [Google Scholar] [CrossRef]
- Chong, F.T.; Franklin, D.; Martonosi, M. Programming languages and compiler design for realistic quantum hardware. Nature 2017, 549, 180–187. [Google Scholar] [CrossRef]
- Maslov, D. Basic circuit compilation techniques for an ion-trap quantum machine. New J. Phys. 2017, 19, 023035. [Google Scholar] [CrossRef]
- Bravyi, S.; Gosset, D.; König, R. Quantum advantage with shallow circuits. Science 2018, 362, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Ryan-Anderson, C.; Bohnet, J.G.; Lee, K.; Gresh, D.; Hankin, A.; Gaebler, J.P.; Francois, D.; Chernoguzov, A.; Lucchetti, D. Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X 2021, 11, 041058. [Google Scholar] [CrossRef]
- Sivarajah, S.; Dilkes, S.; Cowtan, A.; Simmons, W.; Edgington, A.; Duncan, R. t|ket⟩: A retargetable compiler for NISQ devices. Quantum Sci. Technol. 2020, 5, 034010. [Google Scholar] [CrossRef]
- Liu, J.; Wang, H.; Ma, Z.; Duan, Q.; Fei, Y.; Meng, X. Quantum circuit optimization for solving discrete logarithm of binary elliptic curves obeying the nearest-neighbor constrained. Entropy 2022, 24, 955. [Google Scholar] [CrossRef]
- Choi, J.; Oh, S.; Kim, J. Quantum approximation for wireless scheduling. Appl. Sci. 2020, 10, 7116. [Google Scholar] [CrossRef]
- Misevičius, A.; Andrejevas, A.; Ostreika, A.; Verenė, D.; Žekienė, G. An improved hybrid genetic-hierarchical algorithm for the quadratic assignment problem. Mathematics 2024, 12, 3726. [Google Scholar] [CrossRef]
- Jang, K.; Oh, Y.; Seo, H. Depth-optimized quantum circuit of Gauss–Jordan elimination. Appl. Sci. 2024, 14, 8579. [Google Scholar] [CrossRef]
- Booth, K.E.C. Constraint programming models for depth-optimal qubit assignment and SWAP-based routing. In Proceedings of the Leibniz International Proceedings in Informatics (LIPIcs), International Conference on Principles and Practice Constraint Program. (CP 2023), Dagstuhl, Germany, 22–29 September 2023; Volume 280, pp. 43:1–43:10. [Google Scholar] [CrossRef]
- Amy, M.; Maslov, D.; Mosca, M.; Roetteler, M. A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 818–830. [Google Scholar] [CrossRef]
- Kaewpuang, R.; Xu, M.; Hoang, D.T.; Niyato, D.; Yu, H.; Li, R.; Xiong, Z.; Kang, J. Elastic entangled pair and qubit resource management in quantum cloud computing. arXiv 2023, arXiv:2307.13185. [Google Scholar]
- Cross, A.W.; Javadi-Abhari, A.; Alexander, T.; De Beaudrap, N.; Bishop, L.S.; Heidel, S.; Ryan, C.A.; Sivarajah, P.; Smolin, J.A.; Gambetta, J.M.; et al. OpenQASM 3: A broader and deeper quantum assembly language. ACM Trans. Quantum Comput. 2022, 3, 1–32. [Google Scholar] [CrossRef]
- Peng, B.; Li, X.; Gao, J.; Liu, J.; Wong, K.-F. Deep Dyna-Q: Integrating planning for task-completion dialogue policy learning. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (ACL 2018), Melbourne, VIC, Australia, 15–20 July 2018; pp. 2184–2194. [Google Scholar] [CrossRef]
- Brandhofer, S.; Polian, I.; Krsulich, K. Optimal qubit reuse for near-term quantum computers. arXiv 2023, arXiv:2308.00194. [Google Scholar]
- Zhang, P.Y.; Zhou, M.C. Dynamic cloud task scheduling based on a two-stage strategy. IEEE Trans. Autom. Sci. Eng. 2018, 15, 772–783. [Google Scholar] [CrossRef]
- Murali, P.; McKay, D.C.; Martonosi, M.; Javadi-Abhari, A. Software mitigation of crosstalk on noisy intermediate-scale quantum computers. In Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS’20), Lausanne, Switzerland, 16–20 March 2020; pp. 1001–1016. [Google Scholar] [CrossRef]
- Quetschlich, N.; Burgholzer, L.; Wille, R. MQT Bench: Benchmarking software and design automation tools for quantum computing. Quantum 2023, 7, 1062. [Google Scholar] [CrossRef]
- Wang, G.; França, D.S.; Rendon, G.; Johnson, P.D. Efficient ground-state energy estimation and certification on early fault-tolerant quantum computers. arXiv 2023, arXiv:2304.09827. [Google Scholar] [CrossRef]
- Wan, K.; Berta, M.; Campbell, E.T. Randomized quantum algorithm for statistical phase estimation. Phys. Rev. Lett. 2022, 129, 030503. [Google Scholar] [CrossRef]
- Xu, A.; Molavi, A.; Pick, L.; Tannu, S.; Albarghouthi, A. Synthesizing quantum-circuit optimizers. In Proceedings of the ACM on Programming Languages; ACM: New York, NY, USA, 2023; Volume 7, p. 140. [Google Scholar] [CrossRef]
- Zhang, Y.-H.; Zheng, P.-L.; Zhang, Y.; Deng, D.-L. Topological quantum compiling with reinforcement learning. Phys. Rev. Lett. 2020, 125, 170501. [Google Scholar] [CrossRef]
- Lloyd, S. Universal quantum simulators. Science 1996, 273, 1073–1078. [Google Scholar] [CrossRef] [PubMed]
- Litteken, A. Adapting Compilation Strategies for Architecture-Specific Features in Quantum Computing. Ph.D. Thesis, University of Chicago, Chicago, IL, USA, 2022. Available online: https://knowledge.uchicago.edu/record/6411 (accessed on 4 February 2025).
- Bravyi, S.; Shaydulin, R.; Hu, S.; Maslov, D. Clifford circuit optimization with templates and symbolic Pauli gates. Quantum 2021, 5, 580. [Google Scholar] [CrossRef]
- Gheorghiu, V.; Huang, J.; Li, S.M.; Mosca, M.; Mukhopadhyay, P. Reducing the CNOT count for Clifford+T circuits on NISQ architectures. arXiv 2020, arXiv:2011.12191. [Google Scholar] [CrossRef]
- Li, S.; Zhou, X.; Feng, Y. Benchmarking quantum circuit transformation with QKNOB circuits. arXiv 2023, arXiv:2301.08932. [Google Scholar] [CrossRef]
- Niu, S.Y.; Suau, A.; Staffelbach, G.; Todri-Sanial, A. A hardware-aware heuristic for the qubit mapping problem in the NISQ era. IEEE Trans. Quantum Eng. 2020, 1, 3101614. [Google Scholar] [CrossRef]
- Zhu, P.; Cheng, X.; Guan, Z. An exact qubit allocation approach for NISQ architectures. Quantum Inf. Process. 2020, 19, 391. [Google Scholar] [CrossRef]
- Zhou, X.; Feng, Y.; Li, S. A Monte Carlo tree search framework for quantum circuit transformation. In Proceedings of the 39th International Conference on Computer-Aided Design, San Diego, CA, USA, 2–5 November 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Nam, Y.; Ross, N.J.; Su, Y.; Childs, A.M.; Maslov, D. Automated optimization of large quantum circuits with continuous parameters. npj Quantum Inf. 2018, 4, 23. [Google Scholar] [CrossRef]
- Wille, R.; Van Meter, R.; Naveh, Y. IBM’s Qiskit tool chain: Working with and developing for real quantum computers. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1234–1240. [Google Scholar] [CrossRef]
- IBM Quantum; Quantum Processing Units (QPUs). IBM Quantum Documentation; IBM: Armonk, NY, USA, 2025; Available online: https://docs.quantum.ibm.com/guides/qpu-information (accessed on 1 April 2025).
- Lao, L.; Browne, D.E. 2QAN: A quantum compiler for 2-local qubit Hamiltonian simulation algorithms. arXiv 2021, arXiv:2108.02099. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).