Comparative Analysis of Lower Limb Muscle Activity During Isometric External Rotation in Static and Dynamic Modeling Approaches

Abstract

This study investigates differences in lower limb muscle activity during isometric external hip rotation while standing using static and dynamic models within the AnyBody Modeling System. Thirty-three participants performed controlled isometric rotations using a custom-designed device capable of simultaneously measuring rotational moments and ground reaction forces. Both static and dynamic simulations were conducted for each subject using personalized biomechanical models. Muscle activity values at the point of peak rotational moment were analyzed for twelve key muscles involved in hip rotation and stabilization of the knee joint, and statistical differences were assessed for significance. Muscles from the gluteal group (Gluteus minimus, medius, and maximus) generally showed lower activation in dynamic simulations, although this trend was not statistically significant for all muscles or test conditions. The mean difference in muscle activity values between static and dynamic simulations was between 0.03 and 0.08 for the gluteal group muscles and up to 0.15 for the Iliopsoas. Static models overestimated the role of stabilizers. Significant differences (p ≤ 0.05, Wilcoxon signed-rank test) were observed between the two approaches in terms of predicted muscle activation. In conclusion, discrepancies in muscle activity predictions between static and dynamic simulations highlight the need for task-specific simulation design and careful result interpretation.

1. Introduction

Understanding the biomechanics of the lower limbs is crucial for preventing injuries and guiding rehabilitation, as even normal gait variations (for example, differences between genders) can alter joint loading and contribute to musculoskeletal disorders [1]. Isometric exercises—muscle contractions performed without joint movement—are widely used in strength training and therapy because they improve muscle performance and joint stability without imposing dynamic strain. Beyond orthopedic benefits, isometric regimens also confer general health advantages such as significantly reducing blood pressure in hypertensive patients (comparable to the effects of medication) [2]. Numerous studies underscore the value of isometric training for musculoskeletal health. For example, in sports medicine, isometric protocols (often combined with isotonic exercise) increase hamstring strength and flexibility, helping to reduce injury risk [3]. Isometric regimens provide effective pain relief in tendinopathies, comparable in the short term to isotonic training, making them integral to tendon rehabilitation [4]. In knee osteoarthritis, targeted isometric quadriceps exercises significantly improve muscle strength and reduce pain and disability, and their effectiveness in enhancing function has been shown to be on par with dynamic resistance training [5,6].

Researchers often measure muscle activation using surface electromyography (EMG) [7], but this technique has well-known limitations. Surface EMG primarily detects activity in superficial muscles, and the relationship between EMG signal amplitude and actual muscle force is nonlinear and complex [8,9], making direct force estimation from EMG unreliable. Advanced algorithms (including machine learning) can predict muscle forces from EMG with high accuracy [10], but these complexities underscore the need for computational musculoskeletal modeling to better estimate internal forces.

Musculoskeletal modeling enables the estimation of internal forces and muscle contributions during exercise, overcoming some limitations of direct measurement methods. For instance, a detailed shoulder model demonstrated that accounting for muscle architecture and moment arms can predict isometric force-generating capacity across different joint positions [11], illustrating how muscle structure influences functional capability. Experimental findings also help validate models; for example, trunk muscle activation patterns remain remarkably consistent across varying isometric postures [12], providing a valuable basis for verifying model predictions.

Modern musculoskeletal simulation software (e.g., the AnyBody Modeling System) supports both static and dynamic analyses [13]. Static optimization methods assume the body is in quasi-static equilibrium at each instant (neglecting inertia) and are computationally efficient [14], making them a cornerstone for analyzing postures or slow isometric tasks. A common approach is to use a min/max optimization criterion to distribute loads evenly among muscles, yielding physiologically realistic recruitment patterns [15]. Dynamic simulations, in contrast, account for inertial forces and time-dependent muscle behavior. They require motion capture data or predefined kinematic inputs and involve solving differential equations of motion, which is more computationally demanding. Careful scaling of a generic model to an individual’s anthropometry and strength—using data from both static reference poses and dynamic trials—can improve the accuracy of dynamic simulations [16]. Although more computationally intensive, dynamic analysis is essential for capturing momentum and other time-varying factors in movement (even during nominally “isometric” tests). It thus serves as a necessary complement to static modeling approaches.

Despite the broad utility of these modeling techniques, direct comparisons between static and dynamic musculoskeletal models during purely isometric exercises are scarce. Most prior studies either examine dynamic activities (e.g., gait or jumping) or apply static optimization to single postures, with few investigating how the two approaches differ under truly isometric conditions. One relevant study compared static optimization and a dynamic simulation (computed muscle control) during an athletic maneuver, finding generally similar muscle force patterns but significant differences for multi-joint (biarticular) muscles [17]. This suggests that dynamic models may capture certain intermuscular coordination complexities that static analyses miss, even when joint motion is minimal. More broadly, advanced simulations have proven valuable for revealing biomechanical insights beyond what is possible through experiments. For instance, large-scale models illuminate how muscles and the nervous system interact to produce coordinated movements [18]. Dynamic analyses have also shown how biarticular muscles redistribute energy during activities like jumping and pedaling [19]—phenomena that cannot be directly measured in vivo.

In light of this context, the present study aims to bridge the noted gap by comparing muscle activity predictions from static and dynamic models during an isometric external hip rotation task. By investigating a large sample (33 participants) in a single standardized task, this study aims to offer a novel contribution: understanding how static vs. dynamic modeling assumptions influence predicted muscle activity during isometric exercise. The findings are expected to inform model selection and highlight potential pitfalls when applying musculoskeletal models to rehabilitation exercise analysis. A custom-designed device was used to conduct controlled isometric rotations of the lower limb while measuring the generated moments and ground reaction forces. This provided a consistent dataset to drive both a static musculoskeletal model and a dynamic simulation in the AnyBody Modeling System. By analyzing the activation levels of key hip and knee stabilizer muscles at peak effort, we seek to determine how the static and dynamic approaches diverge in their predictions. Through this comparison, our goal is to highlight the unique contributions and limitations of each modeling method in the context of isometric exercise, thereby informing their appropriate application in biomechanical research and practical settings (such as ergonomic design, sports training, and rehabilitation).

2. Materials and Methods

2.1. Description of the Measuring Device

This study used a custom-built device (Figure 1) previously described in detail in [20]. The device is patented under the number PL243709. It enables simultaneous recording of the rotational moments of the lower limbs and the ground reaction forces for four anatomical support zones during standing. Force data is recorded over time, allowing use in both static and dynamic simulations. Measurement sensors with a maximum load of 200 N and an accuracy of ±0.03% were used to measure the moment of force. Sensors with a maximum load of 500 N and an accuracy of ±0.4% were used to measure the ground reaction forces.

2.2. Participants

A total of 33 healthy volunteers participated in the study (71 ± 18.5 kg, 166 ± 17.7 cm, mean age: 21 years). The research group consisted of people who did not complain about any ailments or injuries. All participants agreed to take part in the tests. This study was approved by the ethical committee of the Jerzy Kukuczka Academy of Physical Education in Katowice, Poland (protocol number 3/2019).

2.3. Test Setup

Isometric hip rotation was assessed in a standing position using the custom device and three 9-DoF inertial measurement units (IMU) sensors (Yost Labs, Portsmouth, OH, USA; orientation accuracy of ±1° for dynamic conditions, 360° orientation range for each axis). Isometric external rotation of the lower limbs applied to the hip joints was tested—foot movement was blocked by part of the device. The experimental research was conducted in accordance with previously published methodology [20].

Two IMUs were placed on the lateral knee ligaments to capture limb rotation; a third was mounted on the sacrum to detect pelvic tilt. Sensors were calibrated before use according to the manufacturer’s guidelines.

Prior to the commencement of measurements on the device, a standardized foot positioning procedure was implemented for each participant to ensure accurate measurement of pressure forces at the relevant anatomical points. Additionally, the foot was aligned in such a way that the limb’s axis of rotation consistently coincided with the platform’s axis of rotation.

To enhance measurement precision, the foot was divided into four segments, ensuring that each part maintained contact with a separate measurement platform. The division between the forefoot and hindfoot was determined based on the location of the Chopart joint, which, during the examination, was positioned along the line separating the anterior and posterior support platforms of the tested limb. Meanwhile, the distinction between the medial and lateral parts of the foot was established with reference to the center of the ankle joint in the frontal plane. During the measurement this center was positioned along the line separating the two platforms located on the left and right sides of the tested limb.

Each trial was preceded by a 10 s stabilization period in a habitual standing position. Participants were instructed to maintain an upright posture without altering the kinematics of the upper limbs, trunk, or head.

The subjects were instructed to rotate with the maximum force they could achieve. During this study, three trials were recorded successively:

• Maximum external isometric rotation of the right and left lower limbs simultaneously (RoRLLS, RoLLLS) applied in the hip joints for 10 s.
• Maximum external isometric rotation of the right lower limb (RoRLL) applied in the hip joint for 10 s.
• Maximum external isometric rotation of the left lower limb (RoLLL) applied in the hip joint for 10 s.

2.4. Description of Model Studies

This work uses an appropriate prepared model available in the AnyBody Managed Model Repository (AMMR) repository of the AnyBody environment (AnyBody Modeling System 5.2.0, AnyBody Technology A/S, Niels Jernes Vej 10, DK-9220 Aalborg Ø, Denmark). To conduct the model studies, 33 personalized models were prepared based on the FreePostureMove environment available in the AMMR repository. The FreePostureMove model is characterized by 69 rigid bodies, approximately 1000 muscle actions, a simple muscle model (AnyMuscleModel), and the ScalingLengthMassFat linear scaling method, which is based on the input body mass and height values [21,22]. The optimization criterion used is the minimization of the sum of the cubes of the ratios of muscle forces to their maximum values. The form of the optimization problem was identified using the following dependences:

• Objective function:

$$\begin{gathered} minG\left(f^{\left(M\right)}\right) \\ G\left(f^{\left(M\right)}\right)=\sum _{i=1}^{n^m}{\left({\displaystyle \frac{f_i^{\left(M\right)}}{N_i}}\right)}^3,i=1,\dots ,n^M \end{gathered}$$

• Limiting conditions:

$$\begin{gathered} Cf=d \\ 0\le f_i^{\left(M\right)}\le N_i,i\in 1,\dots ,n^{\left(M\right)} \end{gathered}$$

where the following apply:

• f^M—muscular force;
• N_i—maximum muscle forces;
• n^M—number of muscles;
• C—matrix of arms of muscular strength action and reactions in relation to a given joint;
• f—matrix of muscular forces and reactions present in the system;
• d—resultant moments of external forces determined in relation to a given joint.

FreePostureMove is a dynamic model controlled by angles that can be implemented in the MannequinInterpolation.any file. The MannequinInterpolation.any file is a crucial part of the AnyBody Modeling System and is specifically used for dynamic models where joint angles need to be controlled over time [22].

The FreePosture model was validated using in vivo force data by Ehreiser et al. and Dupré et al. [23,24].

For each case studied, the model was scaled by inputting the body height and mass of the individual. The dynamic simulation using the FreePostureMove model lasted 8 s and was conducted at a frequency of 20 Hz. The input data for the model over time included

• pelvic tilt in the sagittal plane,
• rotational moments of the left and right limbs,
• load on the inner forefoot of the left and right limbs,
• load on the outer forefoot of the left and right limbs,
• load on the hindfoot of the left and right limbs.

The kinematics of the lower limbs were excluded due to the recorded values being smaller than the measurement error of the device. This was attributed to the characteristics of the movement. Twelve muscles were analyzed due to their functional importance in generating external hip rotation torque and in stabilizing the pelvis and knee during upright posture. The examined muscles included the knee joint stabilizers—Sartorius and Tensor fasciae latae—and the primary and secondary lower limb rotators: Iliopsoas, Gluteus minimus, Gluteus medius, Gluteus maximus, Piriformis, Quadratus femoris, Obturator internus, Obturator externus, Gemellus inferior, and Gemellus superior. As reported by Semciw et al. (2013), the gluteal muscles—particularly Gluteus medius and minimus—along with the deep external rotators, play a crucial role in maintaining pelvic control and lower limb alignment during stance and locomotion [25]. In addition, the Iliopsoas, although primarily a hip flexor, has been shown to contribute to lumbopelvic stability and to assist in hip external rotation in postural contexts [26].

The muscle activity values at the time point where the rotational moment in the experimental studies was highest were compared with previously published results of a static simulation, using input data from the same time point [20]. Muscle activity in AnyBody was defined as the ${\displaystyle \raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$N$}\right.}$ property that we minimized as a square sum over all the muscles. In other words, muscle activity is a measure of the force in a muscle relative to its strength [22].

Muscle activity was chosen as the primary parameter for analysis due to its universal applicability in scaled models. In these models, muscle forces were scaled relative to body weight, resulting in individual variations in maximum force values. Given this context, muscle activity was deemed the most universal parameter for comparative analysis.

2.5. Statistics

Data distribution for each muscle’s activation difference between static and dynamic conditions was first evaluated for normality using the Shapiro–Wilk test. The significance of differences in muscle activation between static and dynamic simulations was tested for each muscle using either a paired Student’s t-test or a non-parametric Wilcoxon signed-rank test (paired, two-tailed).

3. Results

To compare the muscle activity values in both static and dynamic models, Figure 2 presents the results for a single subject across three types of simulations: rotation with both limbs, rotation with the right limb, and rotation with the left limb. These values are shown for the time point in the dynamic simulation at which the rotational moment for the respective limb was the greatest. This time frame from the dynamic simulation corresponded to the input data for the static simulation. Values are normalized to a maximum of 1. Confidence intervals may exceed the range [0, 1] due to statistical variation and normalization. These deviations reflect the uncertainty of the estimates and do not imply invalid or out-of-range measurements.

Average differences in muscle activity values were determined for tests carried out on 33 static models and 33 dynamic models. The differences in the average values for selected muscle groups are presented in the

Table 1. The mean difference between muscle activity values for static and dynamic simulation.

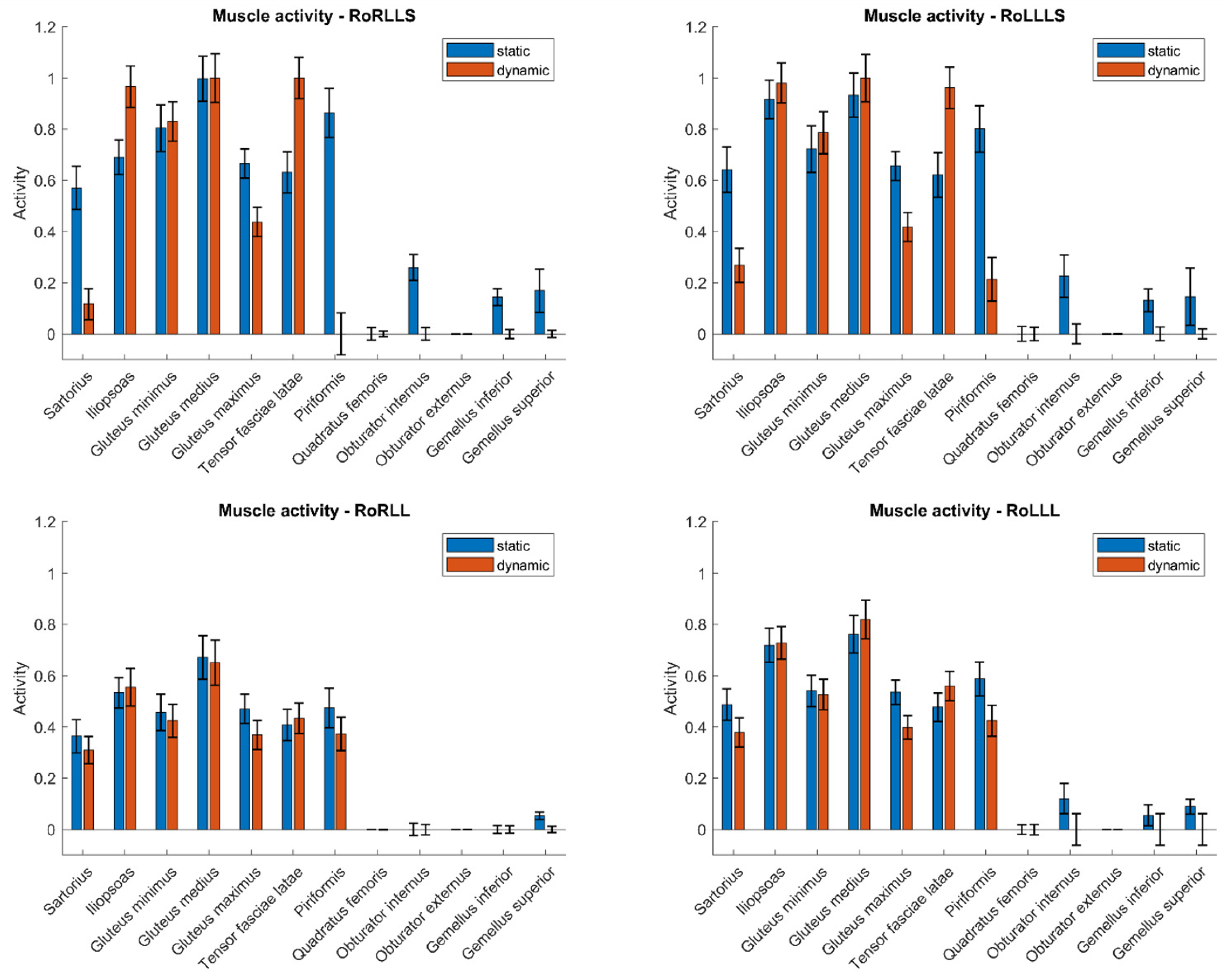
	RoRLLS			RoLLLS			RoRLL			RoLLL
	Mean	Std	95% CI	Mean	Std	95% CI	Mean	Std	95% CI	Mean	Std	95% CI
Sartorius	0.12	0.16	0.06 to 0.17	0.1	0.11	0.06 to 0.14	0.07	0.11	0.03 to 0.11	0.03	0.03	0.02 to 0.05
Iliopsoas	0.17	0.2	0.1 to 0.24	0.12	0.17	0.06 to 0.18	0.1	0.09	0.07 to 0.14	0.03	0.02	0.03 to 0.04
Gluteus minimus	0.08	0.13	0.03 to 0.13	0.04	0.05	0.02 to 0.06	0.03	0.06	0.01 to 0.06	0.01	0.02	0.01 to 0.02
Gluteus medius	0.11	0.12	0.07 to 0.16	0.12	0.08	0.09 to 0.14	0.11	0.07	0.08 to 0.13	0.13	0.06	0.11 to 0.15
Gluteus maximus	0.24	0.16	0.18 to 0.29	0.2	0.12	0.16 to 0.24	0.16	0.1	0.12 to 0.19	0.14	0.08	0.11 to 0.17
Piriformis	0.15	0.23	0.07 to 0.23	0.09	0.14	0.04 to 0.14	0.05	0.11	0.01 to 0.09	0.04	0.06	0.02 to 0.06
Quadratus femoris	0.02	0.04	0 to 0.03	0.01	0.05	0 to 0.03	0	0	0 to 0	0	0.01	0 to 0.01
Obturator internus	0.11	0.10	0.07 to 0.15	0.16	0.18	0.1 to 0.22	0.05	0.06	0.03 to 0.08	0.05	0.06	0.03 to 0.08
Obturator externus	0	0	0 to 0	0	0	0 to 0	0	0	0 to 0	0	0	0 to 0
Gemellus inferior	0.07	0.07	0.05 to 0.09	0.07	0.07	0.05 to 0.1	0.03	0.04	0.02 to 0.05	0.04	0.07	0.02 to 0.07
Gemellus superior	0.13	0.22	0.05 to 0.2	0.17	0.29	0.07 to 0.27	0.03	0.03	0.01 to 0.04	0.04	0.1	0.01 to 0.08
Tensor fasciae latae	0.07	0.13	0.03 to 0.12	0.07	0.1	0.04 to 0.11	0.02	0.06	0 to 0.04	0.01	0.03	0.01 to 0.02

.

A significance level of α = 0.05 was used for all statistical tests, and the resulting p-values for each muscle comparison are presented in

Table 2. Wilcoxon signed-rank test p-values for muscle activation differences between static and dynamic simulations.

		Sartorius	Iliopsoas	Gluteus minimus	Gluteus medius	Gluteus maximus	Piriformis	Quadratus femoris	Obturator internus	Obturator externus	Gemellus inferior	Gemellus superior	Tensor fasciae latae
RoRLLS	p-value	0.38	0.00	0.00	0.00	0.00	0.01	0.01	0.15	0.01	0.17	0.02	0.03
RoLLLS	p-value	0.05	0.00	0.00	0.06	0.00	0.02	0.20	0.13	0.01	0.55	0.03	0.13
RoRLL	p-value	0.00	0.00	0.00	0.00	0.00	0.75	0.34	0.00	0.99	0.00	0.01	0.00
RoLLL	p-value	0.60	0.00	0.00	0.00	0.00	0.08	0.04	0.86	0.12	0.66	0.87	0.89

.

Paired comparisons were conducted for each muscle to assess whether the difference in activation between dynamic and static models was statistically significant. The Shapiro–Wilk test was initially applied to assess the normality of the distribution of differences. Due to the non-normal distribution observed in all cases, the Wilcoxon signed-rank test was used for all statistical comparisons (Table 2).

The analysis revealed a number of muscles with statistically significant differences in activation between the two simulation types. Muscles from the gluteal group (Gluteus minimus, medius, and maximus) generally exhibited lower activation in dynamic simulations. However, this trend was not statistically significant across all test configurations. For instance, while the Gluteus maximus consistently showed significant differences, the Gluteus medius did not reach statistical significance under certain conditions (e.g., RoLLLS). These findings suggest that although a pattern of reduced activation in dynamic models is apparent for gluteal muscles, the consistency of this trend may vary depending on the specific muscle and task configuration. These findings demonstrate that static models may consistently overestimate the involvement of postural stabilizers and underestimate dynamic contributors such as the Iliopsoas. This insight is particularly relevant when using such models in rehabilitation or ergonomic applications, where accurate estimation of muscle loading is critical for designing exercise regimens or work environments. The observed activation differences suggest that muscle function (e.g., stabilization vs. movement initiation) influences a muscle’s sensitivity to modeling assumptions—an important consideration when interpreting or generalizing simulation outputs across tasks.

In contrast, certain deep rotators of the hip, such as the Obturator externus, exhibited minimal differences in activation between static and dynamic models. However, others, including the Obturator internus and Gemellus superior, showed statistically significant differences in selected test configurations. This suggests that while some deep rotators maintain a stable activation pattern regardless of simulation type, others may be sensitive to the modeling approach or task variation. These findings highlight the need to consider individual muscle characteristics when interpreting simulation outputs.

4. Discussion

This study compared lower-limb muscle activation during isometric rotation using static and dynamic simulations in the AnyBody Modeling System. Activation values were analyzed at the peak moment of force generation. Rather than establishing the superiority of one model over another, the aim was to examine how modeling assumptions influence predicted muscle activity.

The results revealed significant discrepancies between muscle activity predictions in static and dynamic simulations. These discrepancies were particularly notable in several hip and thigh muscles, such as the Gluteus maximus, Iliopsoas, and Sartorius, whereas muscles like the Piriformis showed more stable activation between models, while the Tensor fasciae latae exhibited some statistically significant differences, suggesting partial sensitivity to simulation type. These differences were further confirmed by statistical analyses, which showed that, for most muscles, the variations in activation were statistically significant (Table 2).

Such variability in muscle activation predictions can be attributed to several factors. First, the sensitivity of musculoskeletal systems to modeling inputs and assumptions has been well documented [27,28,29]. Even slight variations in segmental mass, joint stiffness, or muscle parameters can produce measurable differences in estimated loads and activations. In the current study, although the same individual anthropometrics and force inputs were applied to both simulations, the mathematical treatment of time-varying inputs and muscle recruitment strategies differed between the two models. This likely contributed to the observed differences in activation patterns.

Similar observations have been made in previous validation studies involving musculoskeletal modeling. For instance, Wibawa et al. compared EMG measurements with muscle activations predicted by the AnyBody Modeling System during walking, hopping, and side-jumping [30]. Their results showed poor agreement between simulated and measured activations (mean kappa < 0.20), particularly in unconstrained tasks such as normal gait. The discrepancies were attributed to model simplifications such as the absence of antagonist co-contraction, the use of idealized joints, and lack of neuromuscular delays.

In another study, Jessup et al. validated an OpenSim/Moco muscle-driven model against EMG during hopping tasks [31]. They observed that muscle activation predictions were highly muscle-specific; while extensors like the vastus lateralis and soleus matched well with EMG, predictions for flexors and bi-articular muscles such as the rectus femoris were much less accurate. They noted that the optimization objective function (e.g., minimizing squared excitations) and the absence of electromechanical delay in the model could partly explain the timing and amplitude mismatches.

The role of task specificity has also been emphasized by Imani Nejad et al., who found that generic models calibrated for gait performed poorly in predicting joint loading and muscle activation during high-load tasks such as squats [32]. Their findings support the notion that muscle activity predictions are not universally transferable across tasks and that validation must be task-specific.

This idea is echoed in Mokhtarzadeh et al., who compared muscle forces predicted using static optimization and forward dynamics during a single-leg hop [33]. While major extensors yielded relatively consistent results, bi-articular muscles like the gastrocnemius and hamstrings showed large discrepancies in activation profiles, highlighting how methodological choices can influence output.

Additional insights into model-to-model variability were offered by Jing et al., who compared six different musculoskeletal models using the same pediatric gait dataset [34]. Although general trends in joint kinematics and kinetics were preserved across models, predicted muscle activity varied substantially. Four of six models captured EMG-like activation in the rectus femoris, while others did not. These differences were attributed to differences in muscle path definitions and anatomical assumptions.

Taken together, the present results align with and expand on previous literature suggesting that muscle activity predictions in musculoskeletal simulations are highly sensitive to model structure, optimization strategy, and the nature of the task being simulated. These factors may explain why certain muscles demonstrated consistent activation levels while others did not. Moreover, the variation in statistical significance across muscles suggests that some may be more robust to model assumptions than others.

Importantly, this study focused on muscle activity as the primary parameter of interest. As defined in AnyBody, muscle activity reflects the ratio of a muscle’s force to its maximum force capacity and serves as a normalized indicator of muscle effort. While this metric allows for comparisons across models and individuals, it should be noted that it does not incorporate time delays, co-contraction behavior, or subject-specific neuromuscular strategies. As discussed by Wibawa et al. and Jessup et al., this limitation may contribute to the differences in timing and magnitude observed between simulated and experimental data.

Musculoskeletal simulations of an isometric external hip rotation often show different muscle activation patterns between static and dynamic models. These differences arise from several biomechanical factors. First, individual muscles have distinct functions and moment arms that can change with joint position. For example, the Gluteus maximus is a powerful external rotator with a large moment arm [35], but its contraction also produces hip extension that must be counteracted by a hip flexor (such as Iliopsoas). A static optimization model (solving one static posture) tends to favor muscles with the most effective moment arms and minimal antagonist involvement [36]. It may therefore under-utilize stabilizing muscles or co-contraction. In contrast, a dynamic simulation (which accounts for time-dependent motion and stability) often recruits a broader set of muscles. The Iliopsoas, for instance, may be more active in dynamic models to stabilize the hip joint and center the femoral head during the external rotation effort [37], even though static models might not engage it if no net flexion torque is required. Likewise, the Gluteus medius and minimus—primarily hip abductors—contribute to dynamic hip stability by compressing the joint and preventing unwanted pelvis motion [38]. Dynamic conditions (even during an isometric task) demand such co-activation to maintain joint alignment and resist perturbations, whereas static analyses omit these requirements.

Furthermore, the treatment of input data differs between static and dynamic simulations. In static models, calculations are based on instantaneous equilibrium, whereas dynamic models incorporate continuous changes in external forces and joint angles. Although both simulations in this study were aligned at the same time point, the way the two models interpreted input data over time may have contributed to divergence in predicted activation.

Although direct validation using EMG was initially considered, it was ultimately excluded from the study for both methodological and practical reasons. A substantial proportion of the analyzed muscles—particularly the deep external rotators of the hip, such as the Piriformis, Obturator internus, and Obturator externus—are inaccessible to surface electromyography (sEMG), which only records signals from superficial muscle layers. Using intramuscular EMG (needle electrodes) in a large sample of healthy participants would raise ethical concerns and introduce considerable logistical complexity. Moreover, surface EMG is associated with well-documented limitations, including cross-talk from adjacent muscles and the integration of signals from multiple motor units within the same recording area. These factors diminish the specificity of EMG and hinder its use for accurately estimating muscle force. EMG amplitude also requires normalization to subject-specific maxima, which introduces additional variability and potential bias in between-subject comparisons [39]. Previous studies have shown limited agreement between EMG recordings and muscle activations predicted by musculoskeletal models, especially during complex or unconstrained tasks. For example, Wibawa et al. reported poor correspondence between measured and simulated activity during walking and jumping [28], while Jessup et al. observed significant discrepancies between modeled and recorded activation in a hopping task [29]. Given these challenges, and considering that the primary objective of this study was to compare static and dynamic simulation approaches—not to validate model outputs against EMG—we concluded that musculoskeletal modeling alone provides a sufficient framework for comparative analysis. This is particularly relevant for muscles whose activation patterns cannot be measured noninvasively, such as the deep hip rotators that play a central role in isometric external rotation. Future work could incorporate EMG data to validate simulation outcomes for superficial muscles. For instance, Xu et al. recently demonstrated that a rigorous EMG acquisition and preprocessing protocol (utilizing a 16-channel wireless system at 1000 Hz, with band-pass filtering between 10–400 Hz, full-wave rectification, low-pass filtering ~6 Hz, and normalization to maximal voluntary contractions) can enable the direct comparison of measured muscle activity with model-predicted activations [40]. Notably, their musculoskeletal model’s output closely matched the normalized EMG activation levels across multiple lower-limb muscles, underscoring the potential of EMG-based validation for confirming model reliability. Adopting a similar approach in a prospective study could thus strengthen confidence in the simulation outcomes for accessible muscle groups. Additionally, testing other modeling environments or control strategies, such as those driven by motion capture systems, may enhance the understanding of how methodological choices influence simulation outcomes. The integration of more detailed muscle–tendon models, such as Hill-type or three-element models, could also improve physiological accuracy, particularly in tasks involving complex joint coordination or rapid loading. Additionally testing other modeling environments or control strategies, such as those driven by motion capture systems, may enhance the understanding of how methodological choices influence simulation outcomes.

Another important consideration is the exclusion of ankle muscles, such as the peroneus longus and peroneus brevis, which can contribute to outward foot rotation. These muscles were not included in the musculoskeletal model, as their primary functions are foot eversion and ankle stabilization rather than generating hip rotation [41]. Moreover, with the feet securely fixed in our isometric setup, their ability to influence axial limb rotation is minimal [42]. Therefore, the analysis focused on the major hip external rotators and knee-stabilizing muscles described above.

It should be noted that the model’s predictions depend on certain underlying assumptions, particularly the anthropometric scaling approach and the muscle force constraints used. In this study, we applied a standard linear scaling based on each subject’s height and mass to personalize the model, a method that is widely adopted for musculoskeletal simulations. While this ensures subject-specific segment geometry and strength, different scaling techniques or calibrations could alter these parameters and thereby influence the muscle activation outcomes [27]. Similarly, muscle recruitment in our simulations was determined by an optimization criterion (minimizing the sum of cubed muscle forces normalized by their maxima) under the constraint that no muscle exceeds its maximum force capacity. This common approach to resolving muscle redundancy provides physiologically plausible load-sharing, but the distribution of predicted muscle forces can vary if alternative cost functions or strength assumptions are used [27]. In the present comparison, we maintained consistent scaling and recruitment settings across both static and dynamic models in order to focus on the effects of dynamic versus static simulation. Consequently, no additional sensitivity analysis of these modeling assumptions was performed. We acknowledge that this is a limitation of our study, and the results should be interpreted within the context of the chosen scaling method and force constraints. Future work may explore how alternative scaling strategies or variations in muscle strength parameters affect the robustness of the observed differences [28].

Ultimately, the present comparison provides a framework for interpreting variability in muscle activity predictions, underscoring the importance of critical model evaluation and task-specific validation in musculoskeletal research.

5. Conclusions

The presented study examined differences in muscle activity during isometric hip rotation using static and dynamic simulations performed in the AnyBody Modeling System. By analyzing a large sample of 33 individuals and focusing on peak moments of rotational effort, the research enabled a detailed investigation of muscle engagement patterns for key stabilizers and rotators of the hip joint.

Findings showed noticeable variability in predicted muscle activity between the two types of simulations, with several muscles exhibiting statistically significant differences. These discrepancies emphasize how modeling assumptions, particularly in the treatment of force dynamics and time-dependent variables, influence the resulting activation profiles. Muscles with different biomechanical roles—such as primary movers versus stabilizers—responded differently to the simulation methods, suggesting that their functional characteristics may affect sensitivity to the modeling approach. This observation highlights the value of task-specific simulation design and careful interpretation of output, especially when translating results to clinical or performance-oriented applications.

These results have direct implications for clinical and practical settings. In rehabilitation, static models may overemphasize postural stabilizers (e.g., gluteals), while dynamic models may better reflect activation of primary movers like the Iliopsoas. This suggests that static models might misrepresent true muscular demands during isometric exercises. In ergonomics, incorporating dynamic modeling can improve estimation of muscular load during sustained postures, reducing injury risk. In sports, dynamic simulations help tailor training programs to reinforce the muscles truly responsible for force generation in static-like tasks, enhancing injury prevention and performance.

Despite the methodological differences between the static and dynamic approaches, both modeling strategies provided meaningful insights into the behavior of the musculoskeletal system during isometric loading. When appropriately applied and interpreted, these models can support the exploration of muscle function in scenarios where in vivo measurement is limited or impractical.

The observed patterns align with previous literature highlighting the complexity of predicting muscle activation and the influence of model configuration on outcomes [30,32]. This underscores the importance of context-specific model selection and critical evaluation of input data, optimization strategies, and output interpretation in musculoskeletal research. Future investigations may benefit from expanding model validation with experimental data, particularly for deep or less-accessible muscles, and by exploring the integration of different modeling paradigms depending on the task and research question.