Fine-Tuned Visual Transformer Masked Autoencoder Applied for Anomaly Detection in Satellite Images
Abstract
:1. Introduction
1.1. Related Work
1.2. Contribution
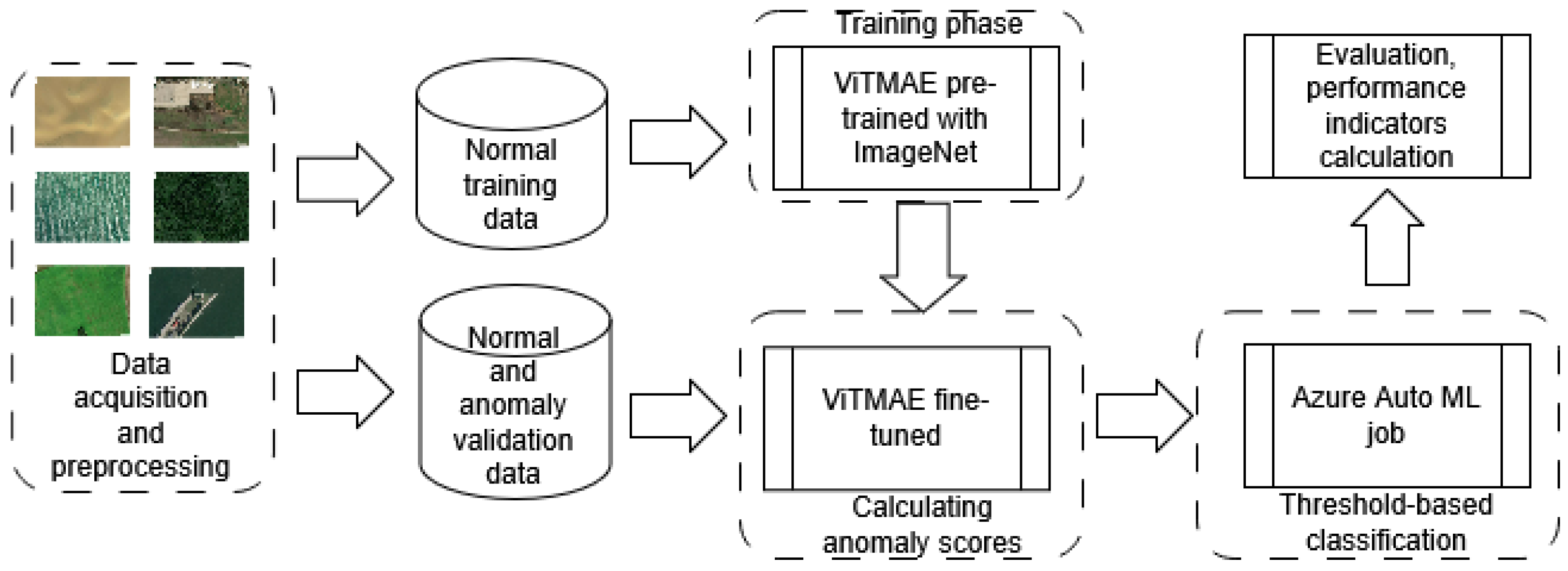
2. Materials and Methods
2.1. Dataset
2.2. Proposed Approach
2.3. Grad-CAM Method
3. Results and Discussion
3.1. Trained Architecture
- TP (True Positive) = a sample classified as an anomaly that is truly an anomaly;
- FP (False Positive) = a sample classified as an anomaly, but in fact is from the normal class;
- FN (False Negative) = a sample classified as normal, but in fact is an anomaly;
- TN (True Negative) = a sample classified as normal that truly belongs to the normal class.
3.2. Results Obtained by the Grad-CAM Method
3.3. Additional Experiments
3.4. Grad-CAM Results Obtained for Revisited Dataset
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Autoencoder |
| Grad-CAM | Gradient-based Class Activation Mapping |
| MAE | Masked Autoencoder |
| ViT | Vision Transformer |
| ViTMAE | Vision Transformer with Masked Autoencoder |
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December2017; Volume 2017.
- ChatGPT. 2023. Available online: https://openai.com/chatgpt (accessed on 17 October 2014).
- DALL-E. 2023. Available online: https://openai.com/dall-e-3 (accessed on 17 October 2014).
- What Is a Transformer Model? 2023. Available online: https://blogs.nvidia.com/blog/2022/03/25/what-is-a-transformer-model/ (accessed on 17 October 2014).
- Yang, J.; Xu, R.; Qi, Z.; Shi, Y. Visual anomaly detection for images: A survey. arXiv 2021, arXiv:2109.13157. [Google Scholar]
- Patcha, A.; Park, J.M. An overview of anomaly detection techniques: Existing solutions and latest technological trends. Comput. Netw. 2007, 51, 3448–3470. [Google Scholar] [CrossRef]
- Barnett, V.; Lewis, T. Outliers in Statistical Data; Wiley: New York, NY, USA, 1994; Volume 3. [Google Scholar]
- Elmrabit, N.; Zhou, F.; Li, F.; Zhou, H. Evaluation of machine learning algorithms for anomaly detection. In Proceedings of the IEEE Cyber Security, Dublin, Ireland, 15–19 June 2020; pp. 1–8. [Google Scholar]
- Spillner, A.; Linz, T. Software Testing Foundations: A Study Guide for the Certified Tester Exam-Foundation Level-ISTQB® Compliant; Rocky Nook: San Rafael, CA, USA, 2021. [Google Scholar]
- Eskin, E. Anomaly Detection over Noisy Data using Learned Probability Distributions. In Proceedings of the International Conference on Machine Learning (ICML ’00), San Francisco, CA, USA, 29 June–2 July 2000; pp. 255–262. [Google Scholar]
- Klerx, T.; Anderka, M.; Büning, H.K.; Priesterjahn, S. Model-based anomaly detection for discrete event systems. In Proceedings of the IEEE International Conference on Tools for Artificial Intelligence (ICTAI), Limassol, Cyprus, 10–12 November 2014; pp. 665–672. [Google Scholar]
- Ruff, L.; Vandermeulen, R.A.; Gornitz, N.; Binder, A.; Muller, E.; Kloft, M. Deep support vector data description for unsupervised and semi-supervised anomaly detection. In Proceedings of the International Conference on Machine Learning (ICML) Workshop on Uncertainty and Robustness in Deep Learning, Long Beach, CA, USA, 14 June 2019; pp. 9–15. [Google Scholar]
- Lesouple, J.; Baudoin, C.; Spigai, M.; Tourneret, J.Y. Generalized isolation forest for anomaly detection. Pattern Recognit. Lett. 2021, 149, 109–119. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, J.; Miner, A. Anomaly intrusion detection using one class SVM. In Proceedings of the 5th IEEE Systems, Man, and Cybernetics (SMC) Information Assurance Workshop, New York, NY, USA, 10–11 June 2004; pp. 358–364. [Google Scholar]
- Sheridan, K.; Puranik, T.G.; Mangortey, E.; Pinon-Fischer, O.J.; Kirby, M.; Mavris, D.N. An application of dbscan clustering for flight anomaly detection during the approach phase. In Proceedings of the American Institute of Aeronautics and Astronautics Scitech Forum, Orlando, FL, USA, 6–10 January 2020; p. 1851. [Google Scholar]
- Wibisono, S.; Anwar, M.T.; Supriyanto, A.; Amin, I.H.A. Multivariate weather anomaly detection using DBSCAN clustering algorithm. In Journal of Physics: Conference Series (JPCS); IOP Publishing: Bristol, UK, 2021; Volume 1869, p. 012077. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long Short Term Memory Networks for Anomaly Detection in Time Series. In Proceedings of the European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 22–24 April 2015; Volume 2015, p. 89. [Google Scholar]
- An, J.; Cho, S. Variational autoencoder based anomaly detection using reconstruction probability. Spec. Lect. IE 2015, 2, 1–18. [Google Scholar]
- Xia, X.; Pan, X.; Li, N.; He, X.; Ma, L.; Zhang, X.; Ding, N. GAN-based anomaly detection: A review. Neurocomputing 2022, 493, 497–535. [Google Scholar] [CrossRef]
- Vareldzhan, G.; Yurkov, K.; Ushenin, K. Anomaly detection in image datasets using convolutional neural networks, center loss, and mahalanobis distance. In Proceedings of the IEEE Ural-Siberian Conference on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 13–14 May 2021; pp. 387–390. [Google Scholar]
- Sarafijanovic-Djukic, N.; Davis, J. Fast distance-based anomaly detection in images using an inception-like autoencoder. In Proceedings of the Discovery Science (DS2019), Split, Coratia, 28–30 October 2019; Springer: Cham, Switzerland, 2019; pp. 493–508. [Google Scholar]
- Staar, B.; Lütjen, M.; Freitag, M. Anomaly detection with convolutional neural networks for industrial surface inspection. CIRP 2019, 79, 484–489. [Google Scholar] [CrossRef]
- Togo, R.; Watanabe, H.; Ogawa, T.; Haseyama, M. Deep convolutional neural network-based anomaly detection for organ classification in gastric X-ray examination. Comput. Biol. Med. 2020, 123, 103903. [Google Scholar] [CrossRef] [PubMed]
- Siddalingappa, R.; Kanagaraj, S. Anomaly detection on medical images using autoencoder and convolutional neural network. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 148–156. [Google Scholar] [CrossRef]
- Zhou, Z.; Sodha, V.; Siddiquee, M.M.R.; Feng, R.; Tajbakhsh, N.; Gotway, M.B.; Liang, J. Models genesis: Generic autodidactic models for 3d medical image analysis. In Proceedings of the Medical Image Computing and Computer Assisted Interventions (MICCAI), Shenzhen, China, 13–17 October 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 384–393. [Google Scholar]
- Khan, A.S.; Ahmad, Z.; Abdullah, J.; Ahmad, F. A spectrogram image-based network anomaly detection system using deep convolutional neural network. IEEE Access 2021, 9, 87079–87093. [Google Scholar] [CrossRef]
- Goh, J.; Adepu, S.; Tan, M.; Lee, Z.S. Anomaly detection in cyber physical systems using recurrent neural networks. In Proceedings of the IEEE HASE, Singapore, 12–14 January 2017; pp. 140–145. [Google Scholar]
- Huang, H.; Wang, P.; Pei, J.; Wang, J.; Alexanian, S.; Niyato, D. Deep Learning Advancements in Anomaly Detection: A Comprehensive Survey. arXiv 2025, arXiv:2503.13195. [Google Scholar]
- Zhang, X.; Li, N.; Li, J.; Dai, T.; Jiang, Y.; Xia, S.T. Unsupervised Surface Anomaly Detection with Diffusion Probabilistic Model. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 6759–6768. [Google Scholar] [CrossRef]
- Li, D.; Chen, D.; Goh, J.; Ng, S.K. Anomaly detection with generative adversarial networks for multivariate time series. arXiv 2018, arXiv:1809.04758. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In Proceedings of the Information Processing in Medical Imaging (IPMI), Boone, NC, USA, 25–30 June 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 146–157. [Google Scholar]
- Zhang, J.; Wang, C.; Li, X.; Tian, G.; Xue, Z.; Liu, Y.; Pang, G.; Tao, D. Learning Feature Inversion for Multi-class Anomaly Detection under General-purpose COCO-AD Benchmark. arXiv 2024, arXiv:2404.10760. [Google Scholar]
- Seeböck, P.; Waldstein, S.; Klimscha, S.; Gerendas, B.S.; Donner, R.; Schlegl, T.; Schmidt-Erfurth, U.; Langs, G. Identifying and categorizing anomalies in retinal imaging data. arXiv 2016, arXiv:1612.00686. [Google Scholar]
- Richter, C.; Roy, N. Safe visual navigation via deep learning and novelty detection. In Robotics: Science and Systems XIII; Massachusetts Institute of Technology: Cambridge, MA, USA, 2017. [Google Scholar]
- Xia, Y.; Cao, X.; Wen, F.; Hua, G.; Sun, J. Learning discriminative reconstructions for unsupervised outlier removal. In Proceedings of the International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1511–1519. [Google Scholar]
- ViTMAE Document Page. 2023. Available online: https://huggingface.co/docs/transformers/main/model_doc/vit_mae (accessed on 10 December 2024).
- Castillo-Villamor, L.; Hardy, A.; Bunting, P.; Llanos-Peralta, W.; Zamora, M.; Rodriguez, Y.; Gomez-Latorre, D.A. The Earth Observation-based Anomaly Detection (EOAD) system: A simple, scalable approach to mapping in-field and farm-scale anomalies using widely available satellite imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102535. [Google Scholar] [CrossRef]
- Wang, H.; Yu, W.; You, J.; Ma, R.; Wang, W.; Li, B. A unified framework for anomaly detection of satellite images based on well-designed features and an artificial neural network. Remote Sens. 2021, 13, 1506. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Mapbox. Available online: https://www.mapbox.com/ (accessed on 5 August 2024).
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R.B. Masked Autoencoders Are Scalable Vision Learners. arXiv 2021, arXiv:2111.06377. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. In Proceedings of the International Conference on Learning Representations (ICLR), Vienna, Austria, 4 May 2021. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]









| Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|
| 0.49 | 0.49 | 0.67 | 0.57 |
| Predicted Anomaly | Predicted Normal | |
|---|---|---|
| True anomaly | 7 | 63 |
| True normal | 29 | 60 |
| Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|
| 0.81 | 0.32 | 0.8 | 0.46 |
| Predicted Anomaly | Predicted Normal | |
|---|---|---|
| True anomaly | 8 | 2 |
| True normal | 17 | 73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajda, J.; Kwiecień, J. Fine-Tuned Visual Transformer Masked Autoencoder Applied for Anomaly Detection in Satellite Images. Appl. Sci. 2025, 15, 6286. https://doi.org/10.3390/app15116286
Gajda J, Kwiecień J. Fine-Tuned Visual Transformer Masked Autoencoder Applied for Anomaly Detection in Satellite Images. Applied Sciences. 2025; 15(11):6286. https://doi.org/10.3390/app15116286
Chicago/Turabian StyleGajda, Jakub, and Joanna Kwiecień. 2025. "Fine-Tuned Visual Transformer Masked Autoencoder Applied for Anomaly Detection in Satellite Images" Applied Sciences 15, no. 11: 6286. https://doi.org/10.3390/app15116286
APA StyleGajda, J., & Kwiecień, J. (2025). Fine-Tuned Visual Transformer Masked Autoencoder Applied for Anomaly Detection in Satellite Images. Applied Sciences, 15(11), 6286. https://doi.org/10.3390/app15116286






