Comparative Analysis of Lab-Data-Driven Models for International Friction Index Prediction in High Friction Surface Treatment (HFST)
Abstract
1. Introduction
2. Materials and Methods
2.1. Aggregate
2.2. Binder
2.3. Preparing High Friction Surface Treatment Slabs
2.4. Performance Tests for Frictional Properties
2.4.1. Accelerated Three-Wheel Polishing Device
2.4.2. Dynamic Friction Test (DFT)
2.4.3. Circular Track Meter (CTM)
2.5. Prediction of IFI for Skid-Resistance Analysis
2.5.1. Model Development and Evaluation
2.5.2. Logarithmic Model
2.5.3. Power Model
2.5.4. Polynomial Model
2.5.5. Parameter Estimation
2.5.6. Models’ Validation
3. Results and Discussion
3.1. Relationship Between Sliding Speed and Polishing Cycles
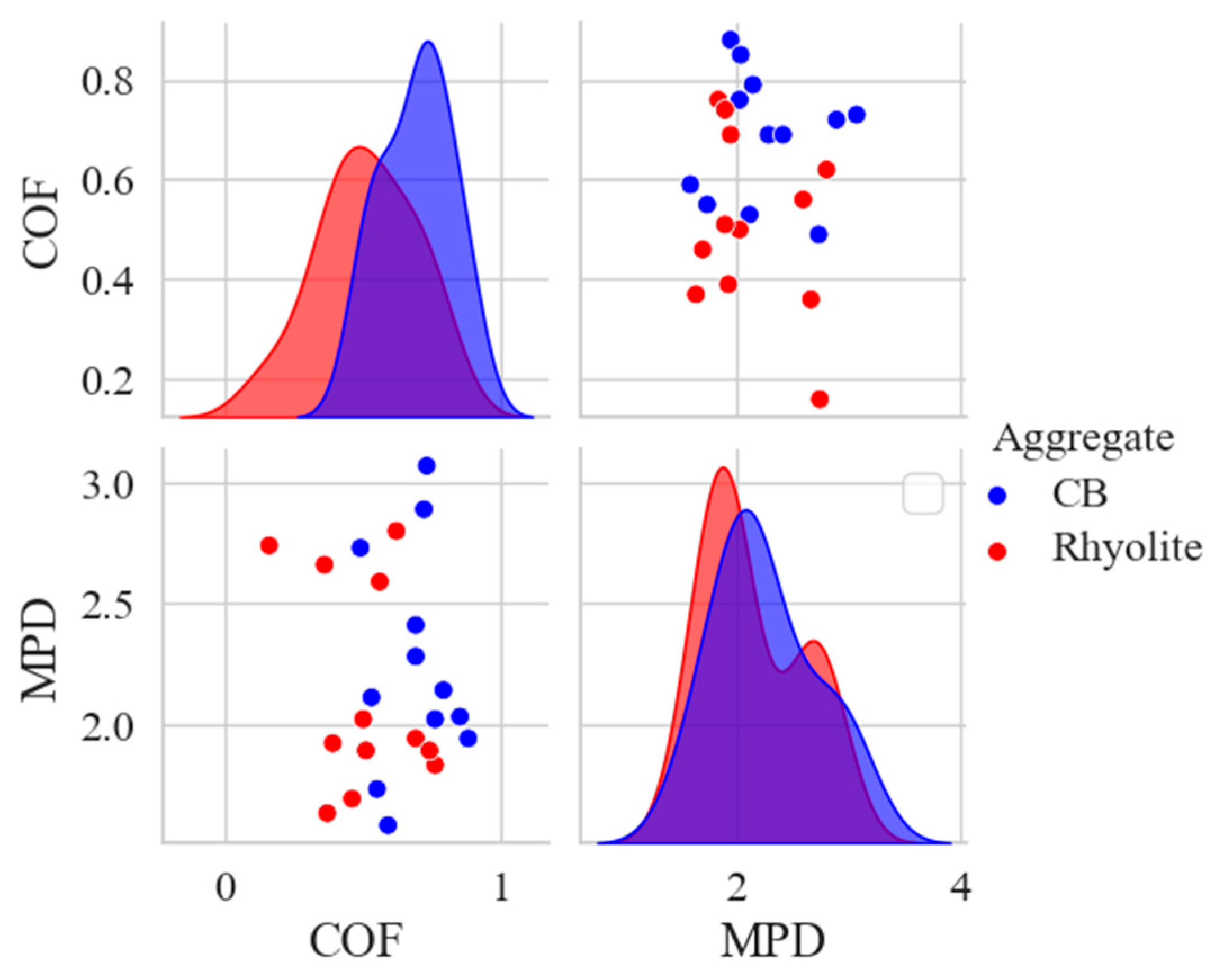
3.2. Data Preparation
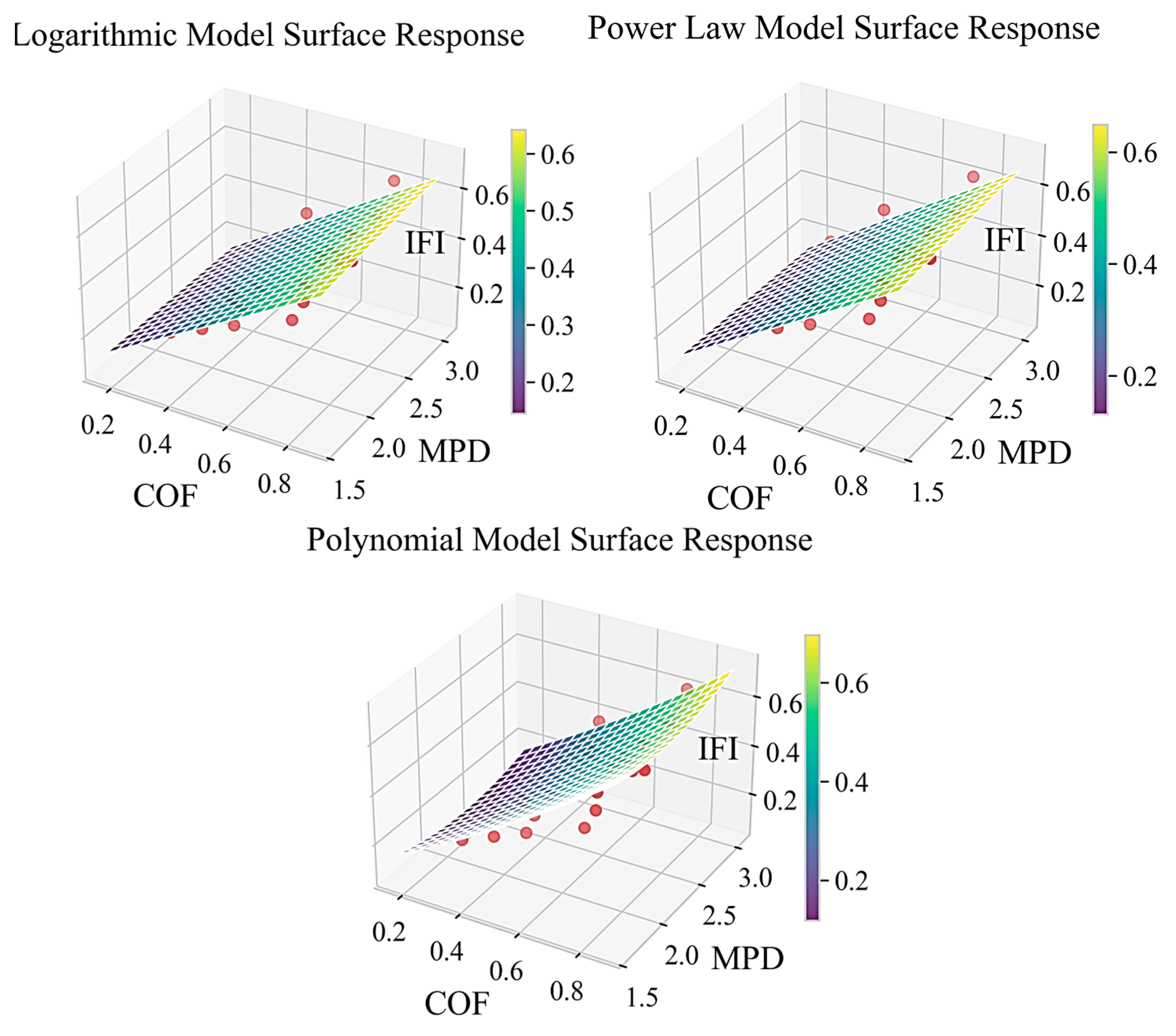
3.3. Model Performance and Comparative Analysis
Model Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roshan, A.; Abdelrahman, M. Friction Enhancements to Asphalt Pavement Surfaces; Report No. cmr 24-015; Missouri Department of Transportation, Construction and Materials Division: Jefferson City, MO, USA, 2024. Available online: https://rosap.ntl.bts.gov/view/dot/77701 (accessed on 15 April 2025).
- de León Izeppi, E.; Flintsch, G.W.; McGhee, K.K. Field Performance of High Friction Surfaces; Virginia Center for Transportation Innovation and Research: Blacksburg, VA, USA, 2010. [Google Scholar]
- Merritt, D.K.; Lyon, C.; Persaud, B. Evaluation of Pavement Safety Performance; United States Federal Highway Administration: Austin, TX, USA, 2015. [Google Scholar]
- Federal Highway Administration (FHWA). EveryDay Counts Program (EDC-2) Innovation. 2020. Available online: https://www.fhwa.dot.gov/innovation/everydaycounts/edc-2.cfm (accessed on 15 April 2025).
- Roshan, A.; Abdelrahman, M. Evaluating Friction Characteristics of High Friction Surface Treatment Application Under Varied Polishing and Slippery Conditions. Transp. Res. Rec. 2024, 2679, 1847–1860. [Google Scholar] [CrossRef]
- Li, S.; Hu, J.; Tan, Y.; Xiao, S.; Han, M.; Li, S.; Li, J.; Wang, W. A review of non-contact approach for pavement skid resistance evaluation based on texture. Tribol. Int. 2024; 8, 109737. [Google Scholar]
- Roshan, A.; Abdelrahman, M. Influence of Aggregate Properties on Skid Resistance of Pavement Surface Treatments. Coatings 2024, 14, 1037. [Google Scholar] [CrossRef]
- Athiappan, K.; Kandasamy, A.; Mohamed, M.J.; Parthiban, P.; Balasubramanian, S. Prediction modeling of skid resistance and texture depth on flexible pavement for urban roads. Mater. Today Proc. 2022, 52, 923–929. [Google Scholar] [CrossRef]
- Kanafi, M.M.; Tuononen, A.J. Application of Three-Dimensional Printing to Pavement Texture Effects on Rubber Friction. Road Mater. Pavement Des. 2017, 18, 865–881. [Google Scholar] [CrossRef]
- Roshan, A.; Abdelrahman, M. Developing an effective approach to assess pavement condition for high friction surface treatment (HFST) installation. Acta Polytech. 2024, 64, 571–581. [Google Scholar] [CrossRef]
- Chen, C.; Gu, F.; Heitzman, M.; Powell, B.; Kowalski, K. Influences of Alternative Friction Aggregates on Texture and Friction Characteristics of High Friction Surface Treatment. Constr. Build. Mater. 2022, 314, 125643. [Google Scholar] [CrossRef]
- Ueckermann, A.; Wang, D.; Oeser, M.; Steinauer, B. Calculation of Skid Resistance from Texture Measurements. J. Traffic Transp. Eng. (Eng. Ed.) 2015, 2, 3–16. [Google Scholar] [CrossRef]
- Zhu, S.; Ji, X.; Yuan, H.; Li, H.; Xu, X. Long-term skid resistance and prediction model of asphalt pavement by accelerated pavement testing. Constr. Build. Mater. 2023, 375, 131004. [Google Scholar] [CrossRef]
- Plati, C.; Pomoni, M.; Stergiou, T. Development of a Mean Profile Depth to Mean Texture Depth Shift Factor for Asphalt Pavements. Transp. Res. Rec. 2017, 2641, 156–163. [Google Scholar] [CrossRef]
- Roshan, A.; Abdelrahman, M. Improving aggregate abrasion resistance prediction via Micro-Deval test using ensemble machine learning techniques. Eng. J. 2024, 28, 15–24. [Google Scholar] [CrossRef]
- Wambold, J.C.; Antle, C.E.; Henry, J.J.; Rado, Z. International PIARC Experiment to Compare and Harmonize Texture and Skid Resistance Measurements; PIARC: Paris, France, 1995; p. 346. [Google Scholar]
- Fuentes, L.G.; Gunaratne, M. Evaluation of the Speed Constant and Its Effect on the Calibration of Friction-Measuring Devices. Transp. Res. Rec. 2010, 2155, 134–144. [Google Scholar] [CrossRef]
- ASTM E1960-07; Standard Practice for Calculating International Friction Index of a Pavement Surface, Annual Book of ASTM Standards. ASTM International: West Conshohocken, PA, USA, 2011.
- D’Apuzzo, M.; Evangelisti, A.; Nicolosi, V. An exploratory step for a general unified approach to labelling of road surface and tyre wet friction. Accid. Anal. Prev. 2020, 138, 105462. [Google Scholar] [CrossRef] [PubMed]
- Rajaei, S.; Chatti, K.; Dargazany, R. A Review: Pavement Surface Micro-Texture and Its Contribution to Surface Friction. In Proceedings of the Transportation Research Board 96th Annual Meeting; Transportation Research Board, Washington, DC, USA, 8–12 January 2017. [Google Scholar]
- Pereira, P.A.; Pais, J.C.; Trichês, G.; Fontes, L.P. Skid resistance and texture of compacted asphalt mixes evaluated from the IFI in laboratory preparation. In Proceedings of the 4th Eurasphalt and Eurobitume Congress, Copenhagen, Denmark, 21–23 May 2008; 2008; pp. 1–14. [Google Scholar]
- Wilson, B.; Saca, M. High Friction Surface Treatment (HFST) Synthesis for Florida Pavements; FHWA/FL-21/BE923 Final Report; Texas A&M Transportation Institute: College Station, TX, USA, 2021. [Google Scholar]
- High Friction Surface Treatment Site Selection and Installation Guide; FHWA-SA-21-093; FHWA: Washington, DC, USA, 2024.
- Roshan, A.; Abdelrahman, M.; Ragab, M. Performance Evaluation of Highly Modified Asphalt-Based Binders in High Friction Surface Treatment: Comparative Study with Epoxy-Based System. Buildings 2025, 15, 1425. [Google Scholar] [CrossRef]
- AASHTO MP41-22; Standard Specification for High Friction Surface Treatment for Asphalt and Concrete Pavements Using Calcined Bauxite. American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2022. Available online: https://dnr.mo.gov/document-search/rhyolite-pub2927/pub2927 (accessed on 15 November 2023).
- Missouri Geological Survey, Geological Survey Program. Rhyolite—PUB2927; Missouri Department of Natural Resources: Rolla, MO, USA, 2020. [Google Scholar]
- NJSP-15-13B; High Friction Surface Treatment. Standard Specifications. Missouri Department of Transportation: Jefferson City, MO, USA, 2015.
- Pranav, C.; Tsai, Y.C. High Friction Surface Treatment Deterioration Analysis and Characteristics Study. Transp. Res. Rec. 2021, 2675, 370–384. [Google Scholar] [CrossRef]
- Wei, F.; Xing, M.; Li, S.; Shan, J.; Guan, B. Physical and Mechanical Properties of Epoxy–Bauxite Mortar of High-Friction Surface Treatment. J. Mater. Civ. Eng. 2020, 32, 04020146. [Google Scholar] [CrossRef]
- Roshan, A.; Abdelrahman, M. Performance and Economic Evaluation of Asphalt-Based High Friction Surface Treatment (HFST) Applications. Appl. Sci. 2025, 15, 873. [Google Scholar] [CrossRef]
- Heitzman, M.; Turner, P.; Greer, M. High Friction Surface Treatment Alternative Aggregates Study; NCAT Report; National Center for Asphalt Technology, Auburn University: Auburn, AL, USA, 2015. [Google Scholar]
- ASTM E1911-19; Standard Test Method for Measuring Paved Surface Frictional Properties Using the Dynamic Friction Tester. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM E2157-15; Standard Test Method for Measuring Pavement Macrotexture Properties Using the Circular Track Meter. ASTM International: West Conshohocken, PA, USA, 2019.
- Sezen, H.; Fisco, N. Evaluation and comparison of surface macrotexture and friction measurement methods. J. Civ. Eng. Manag. 2013, 19, 387–399. [Google Scholar] [CrossRef]
- Fuentes, L.G.; Gunaratne, M.; de León Izeppi, E.; Flintsch, G.W.; Martinez, G. Determination of Pavement Macrotexture Limit for Use in International Friction Index Model. Transp. Res. Rec. 2012, 2306, 138–143. [Google Scholar] [CrossRef]
- Paji, M.K.; Gordan, B.; Bedon, C.; Faridmehr, I.; Valerievich, K.; Hwang, H.J. Artificial Neural Network Levenberg–Marquardt Based Algorithm for Compressive Strength Estimation of Concrete Mixed with Magnetic Salty Water. Eng. Sci. 2023, 23, 878. [Google Scholar] [CrossRef]
- Polushkina-Merchanskaya, O.; Armstrong, M.D.; Gómez-Llorente, C.; Ferrer, P.; Fernandez-Gonzalez, S.; Perez-Cruz, M.; Gómez-Roig, M.D.; Camacho, J. Considerations for missing data, outliers and transformations in permutation testing for ANOVA with multivariate responses. Chemom. Intell. Lab. Syst. 2025, 258, 105320. [Google Scholar] [CrossRef]
- Amini, K.; Rostami, F.; Caristi, G. An efficient Levenberg–Marquardt method with a new LM parameter for systems of nonlinear equations. Optimization 2018, 67, 637–650. [Google Scholar] [CrossRef]
- Khan, M.A.; Farooq, F.; Javed, M.F.; Zafar, A.; Ostrowski, K.A.; Aslam, F.; Malazdrewicz, S.; Maślak, M. Simulation of Depth of Wear of Eco-Friendly Concrete Using Machine Learning Based Computational Approaches. Materials 2021, 15, 58. [Google Scholar] [CrossRef]
- Aghaee, K.; Roshan, A. Predicting Time to Cracking of Concrete Composites Subjected to Restrained Shrinkage: A Review with Insights from Statistical Analysis and Ensemble Machine Learning Approaches. J. Build. Eng. 2024, 110856. [Google Scholar] [CrossRef]
- Shinde, S.N.; Christa, S.; Grover, R.K.; Pasha, N.; Harinder, D.; Nakkeeran, G.; Alaneme, G.U. Optimization of waste plastic fiber concrete with recycled coarse aggregate using RSM and ANN. Sci. Rep. 2025, 15, 7798. [Google Scholar] [CrossRef] [PubMed]
- Jumabekova, A.; Berger, J.; Foucquier, A. An Efficient Sensitivity Analysis for Energy Performance of Building Envelope: A Continuous Derivative Based Approach. Build. Simul. 2021, 14, 909–930. [Google Scholar] [CrossRef]
- Tsvetkova, O.; Ouarda, T.B. A Review of Sensitivity Analysis Practices in Wind Resource Assessment. Energy Convers. Manag. 2021, 238, 114112. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, H. Machine learning based pavement performance prediction for data-driven decision of asphalt pavement overlay. Struct. Infrastruct. Eng. 2025, 21, 940–955. [Google Scholar] [CrossRef]
- Clemmensen, A.; Wang, H. Airfield pavement performance prediction using clustered Markov chain models. Road Mater. Pavement Des. 2025, 26, 658–678. [Google Scholar] [CrossRef]
- Radwan, M.M.; Zahran, E.M.; Dawoud, O.; Abunada, Z.; Mousa, A. Comparative Analysis of Asphalt Pavement Condition Prediction Models. Sustainability 2025, 17, 109. [Google Scholar] [CrossRef]

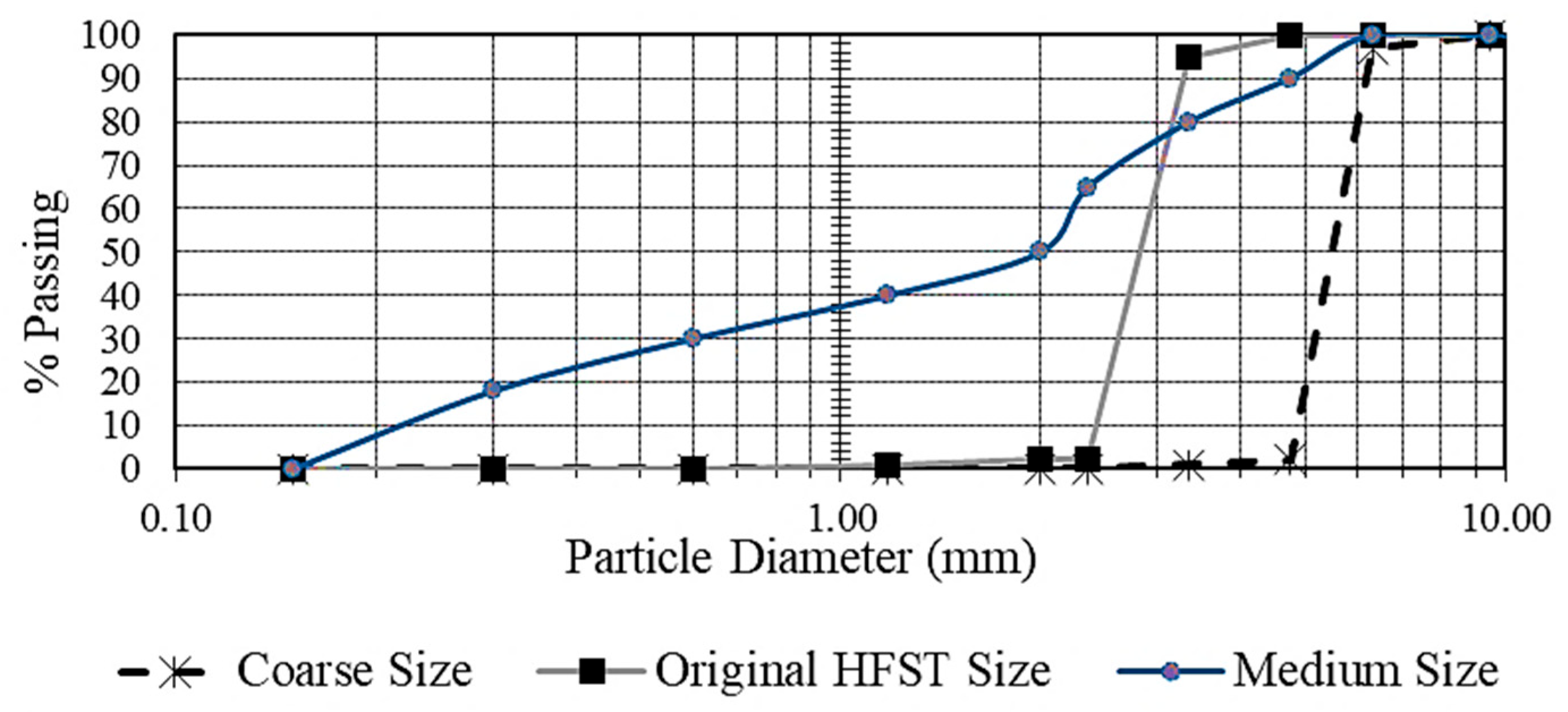


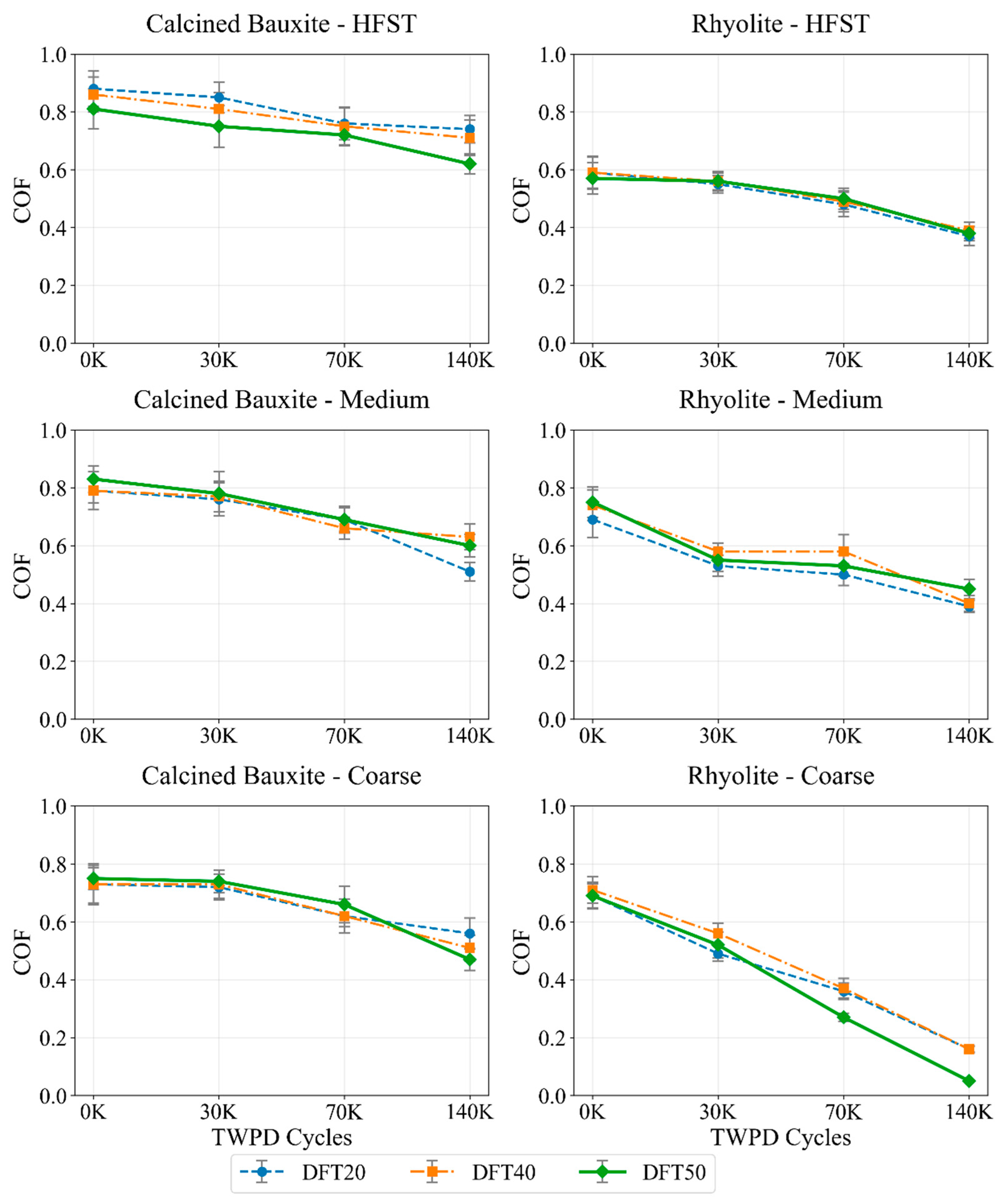
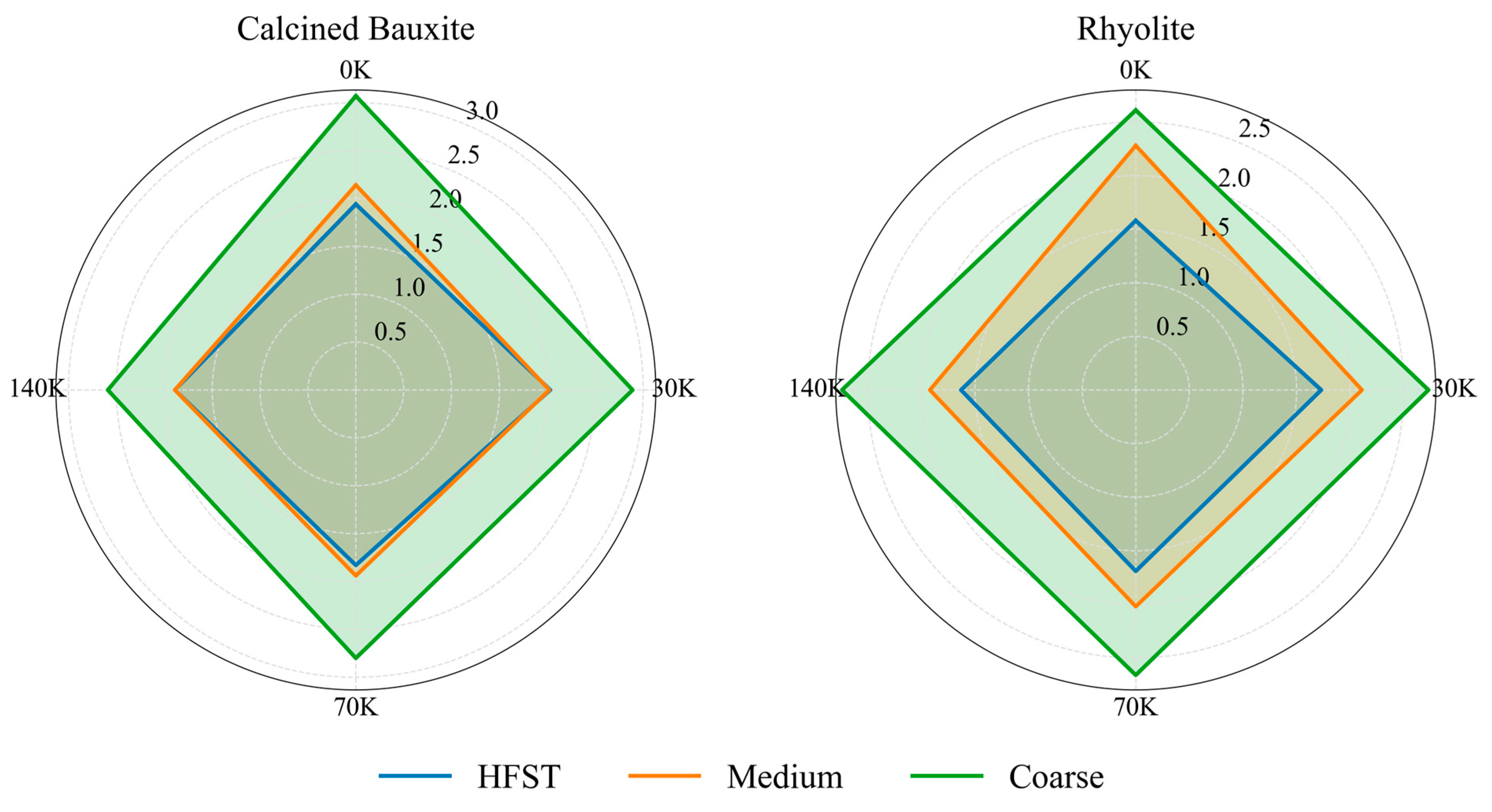
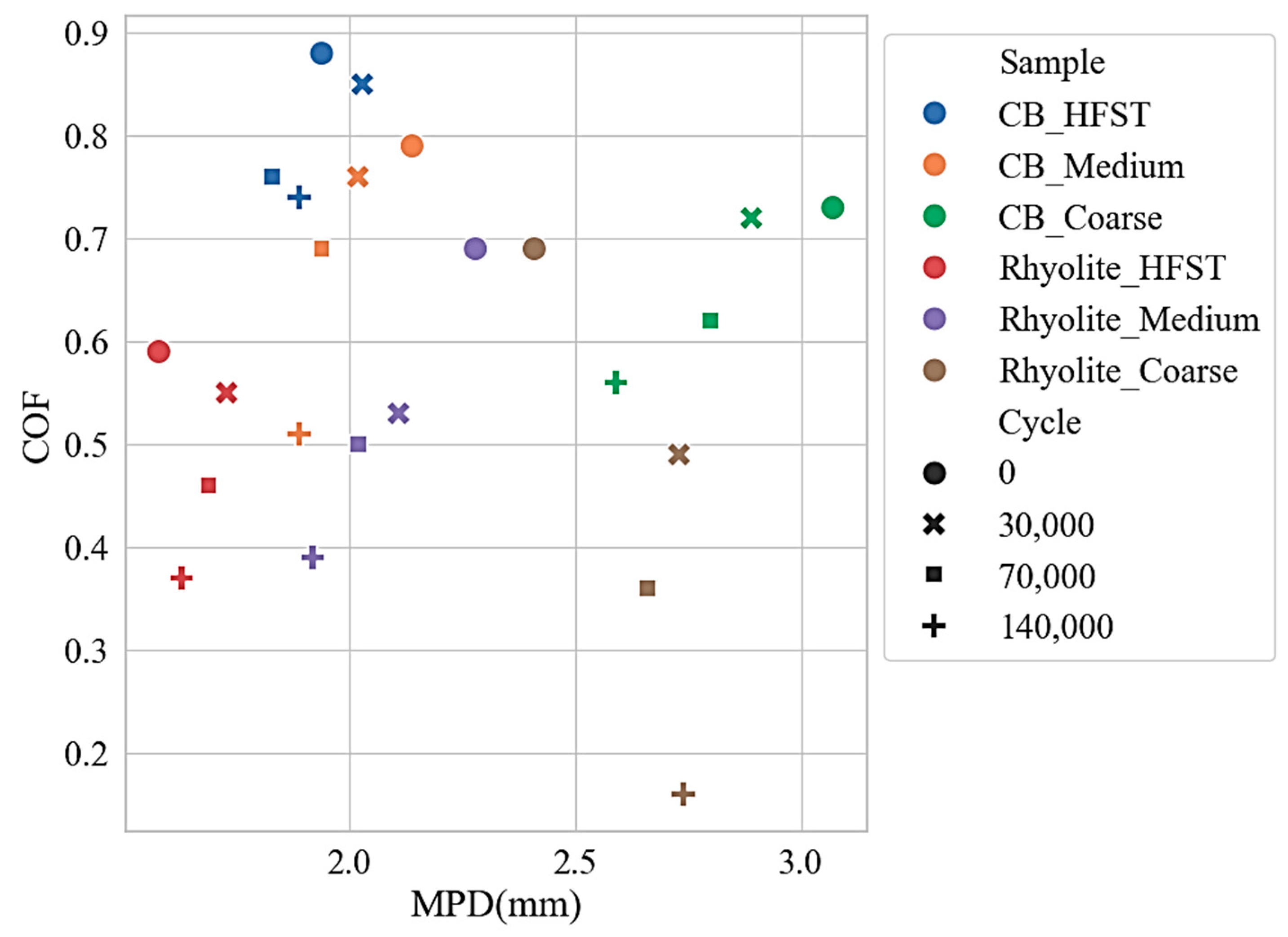

| Properties | CB | Rhy |
| Bulk specific gravity | 3.25 | 2.57 |
| Water absorption (%) | 1.5 | 1.7 |
| LAA value (%) | Grade D | D |
| MDA value (%) | 16.01 15 min 2.45 | 15.11 15 min 2.6 |
| Uncompacted void content (UVC) | 45% | 43% |
| Property | Test Result | AASHTO Requirement |
|---|---|---|
| Gel time (min) | 10 | 10 |
| Ultimate tensile strength (MPa) | 22 | 17.2–34.4 |
| Compressive strength, 3 h (MPa) | 43.5 | 6.9 (minimum) |
| Adhesive strength, 24 h (MPa) | 5 | 1.7 (minimum) |
| Water absorption, 24 h (%) | 0.1 | 1 (maximum) |
| Model | Equation | Coefficients |
|---|---|---|
| Logarithmic | F (60) = a + b × COF | a = 0.0257, b = 1, c = 50, d = 50 |
| Power law | F (60) = a + b × COF | a = 0.0056, b = 1, c = 50, d = 50, e = 0.5017 |
| Polynomial | F (60) = a + b × COF + c × MPD + d × COF2 + e × MPD2 + f × COF × MPD | a = 0.4970, b = 0.50, c = −0.4145, d = 0.1856, e = 0.0883, f = −0.0294 |
| Model | COF (Max ΔIFI, %) | MPD (Max ΔIFI, %) |
|---|---|---|
| Logarithmic | 14.3 | 1.8 |
| Power law | 14.7 | 1.5 |
| Polynomial | 17.7 | 6.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roshan, A.; Abdelrahman, M. Comparative Analysis of Lab-Data-Driven Models for International Friction Index Prediction in High Friction Surface Treatment (HFST). Appl. Sci. 2025, 15, 6249. https://doi.org/10.3390/app15116249
Roshan A, Abdelrahman M. Comparative Analysis of Lab-Data-Driven Models for International Friction Index Prediction in High Friction Surface Treatment (HFST). Applied Sciences. 2025; 15(11):6249. https://doi.org/10.3390/app15116249
Chicago/Turabian StyleRoshan, Alireza, and Magdy Abdelrahman. 2025. "Comparative Analysis of Lab-Data-Driven Models for International Friction Index Prediction in High Friction Surface Treatment (HFST)" Applied Sciences 15, no. 11: 6249. https://doi.org/10.3390/app15116249
APA StyleRoshan, A., & Abdelrahman, M. (2025). Comparative Analysis of Lab-Data-Driven Models for International Friction Index Prediction in High Friction Surface Treatment (HFST). Applied Sciences, 15(11), 6249. https://doi.org/10.3390/app15116249





