Sensitivity Analysis of the Influence of Heavy-Intensity Rain Duration on the Stability of Granular Soil Slopes Under Unsaturated Conditions
Abstract
1. Introduction
2. Materials and Methods
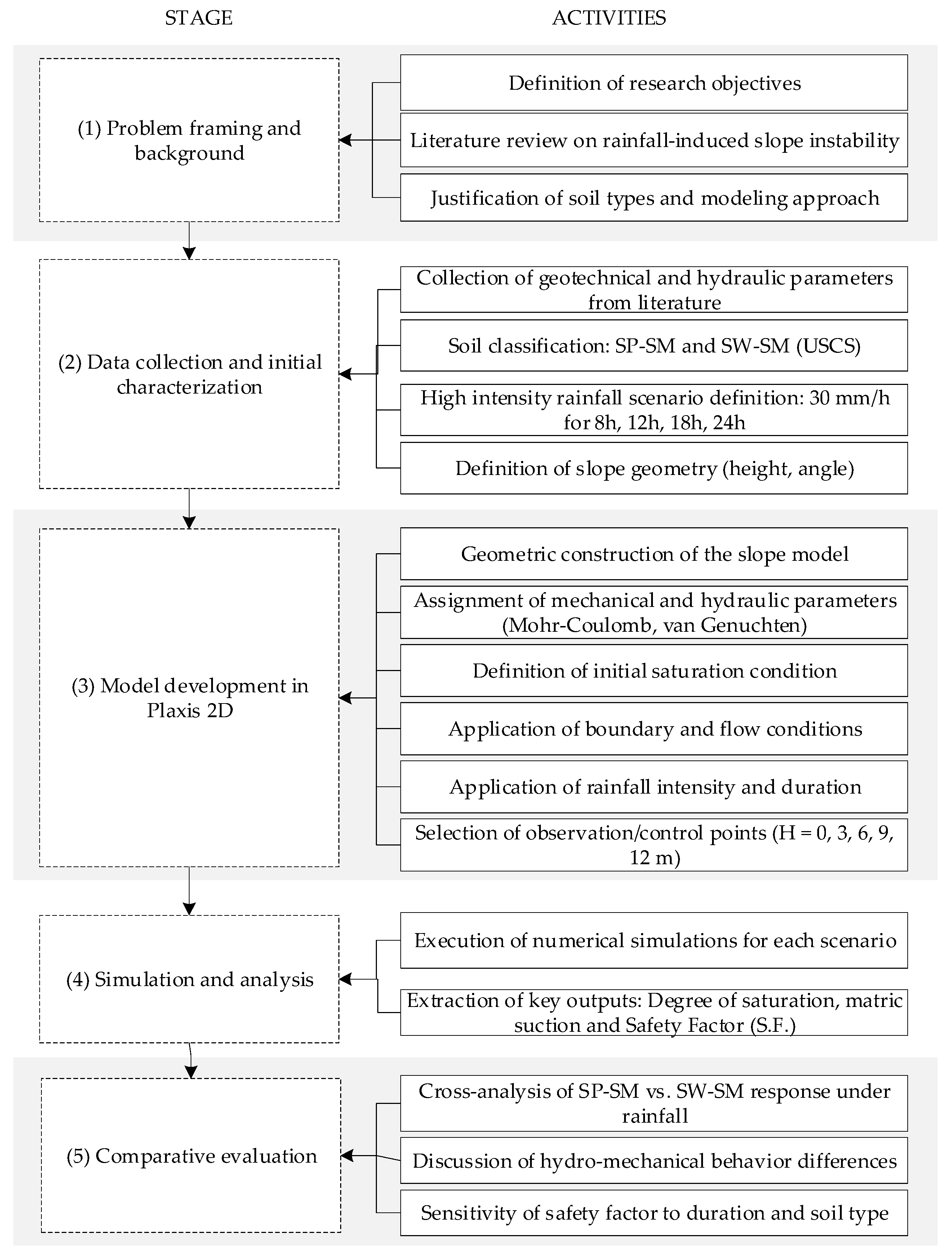
2.1. Research Method
2.2. Constitutive Model
2.3. Soil Properties
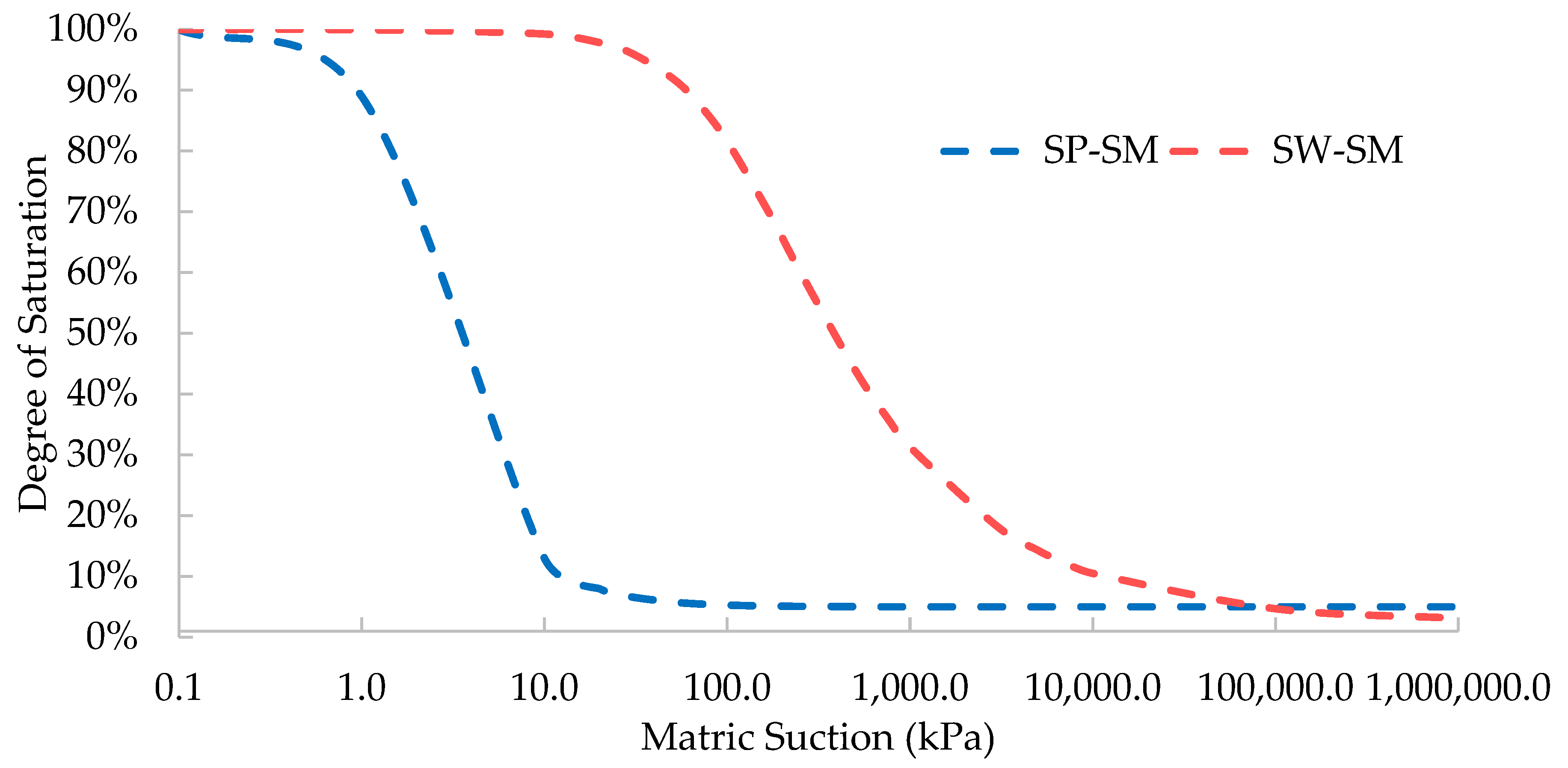
2.4. Hydraulic Model
2.5. Rain Characterization
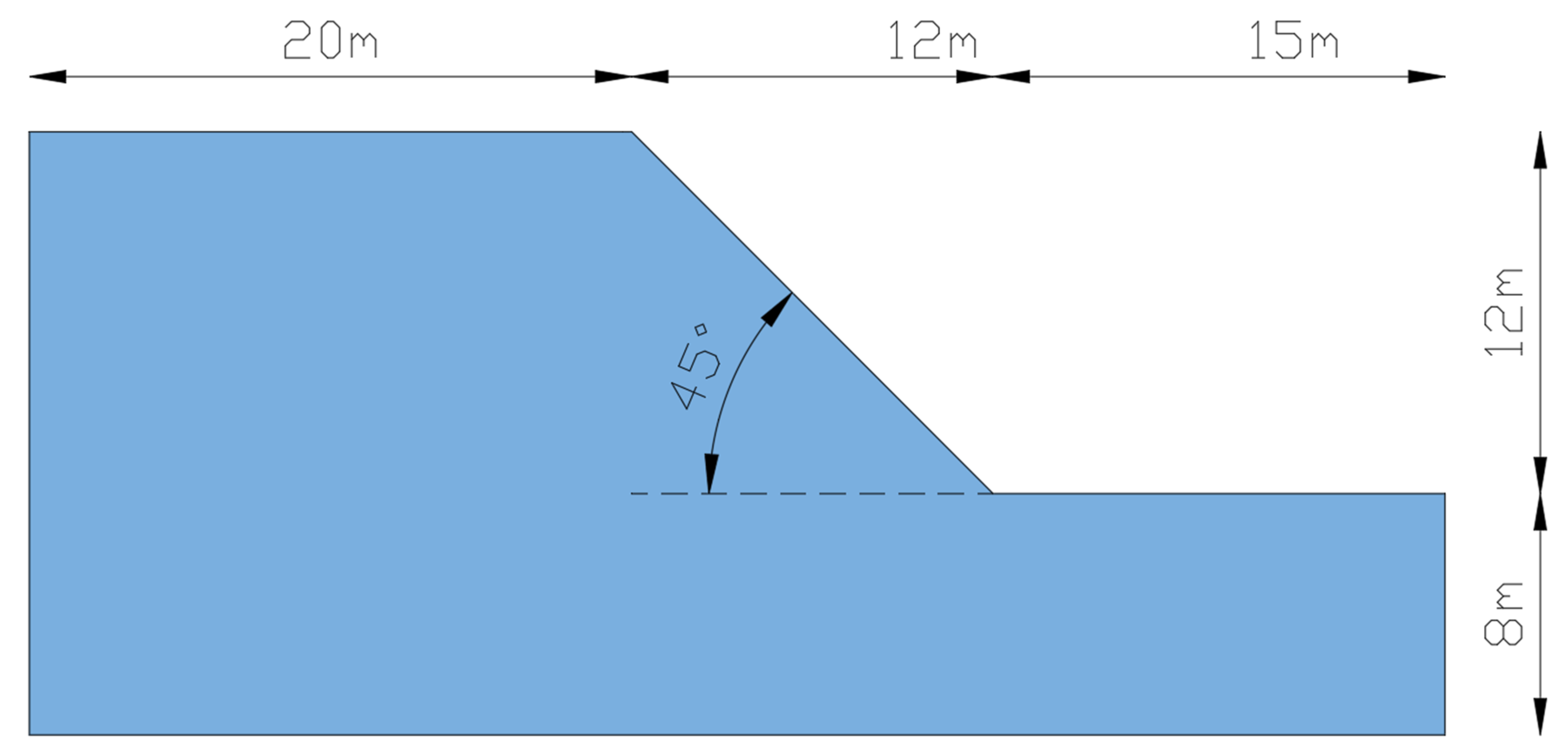
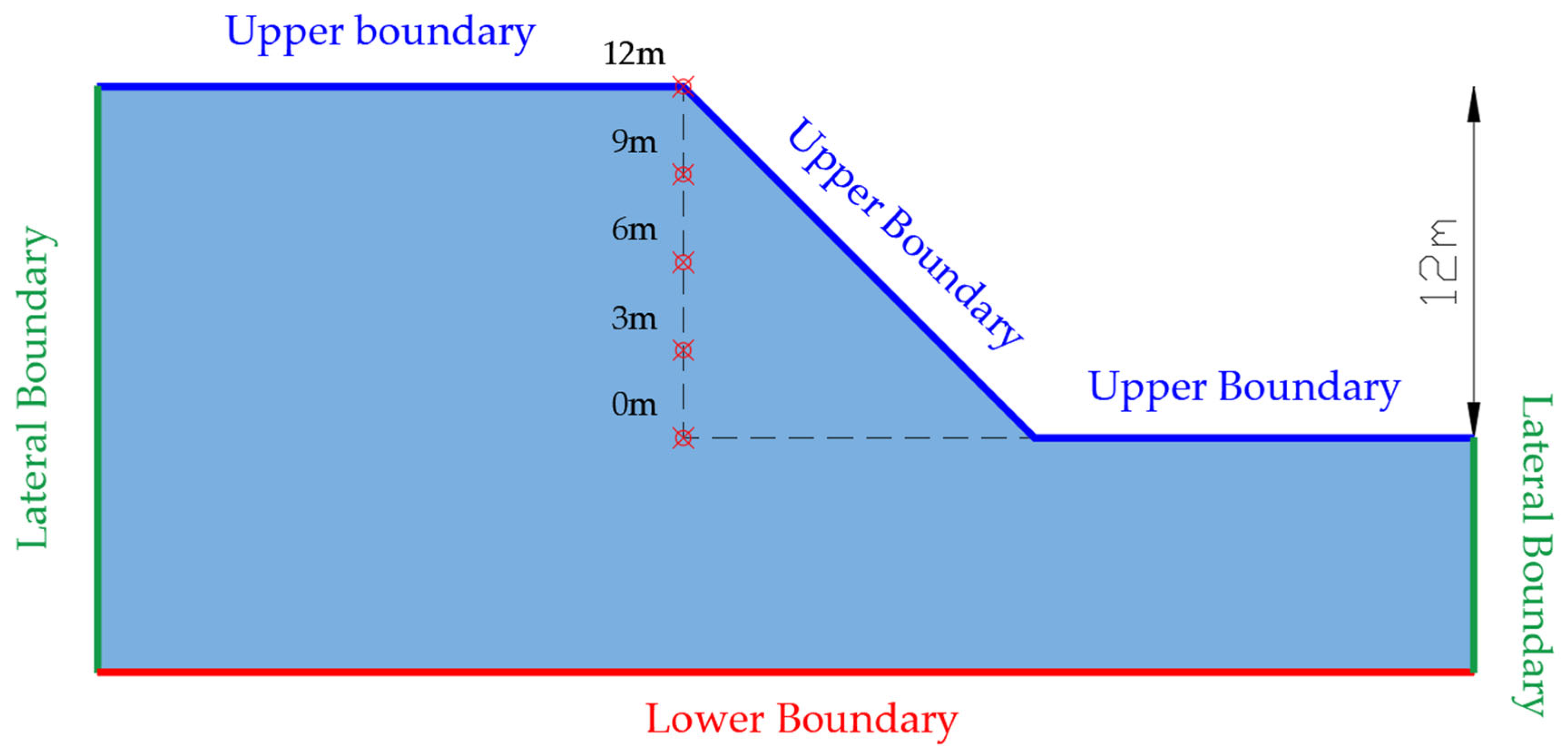
2.6. Slope Geometry and Boundary and Flow Conditions
3. Results and Discussion
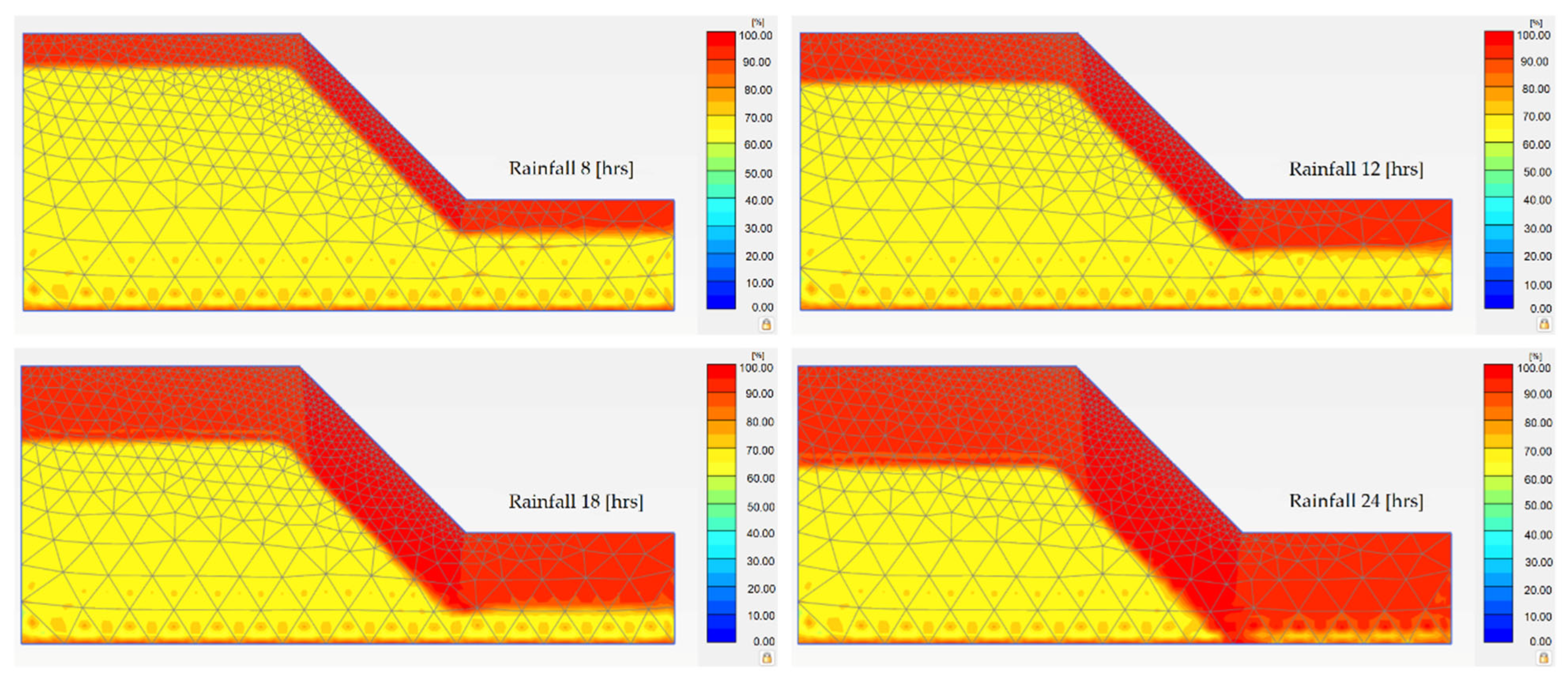
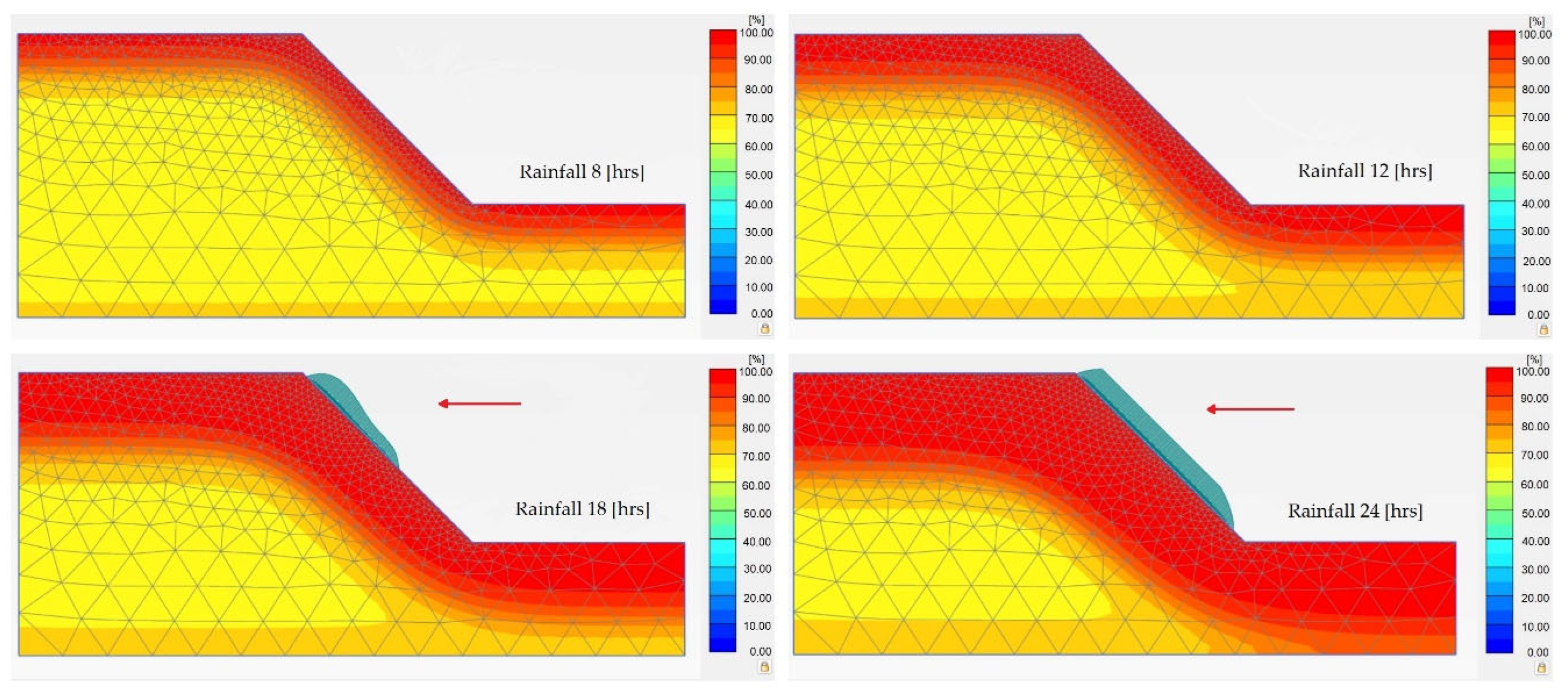
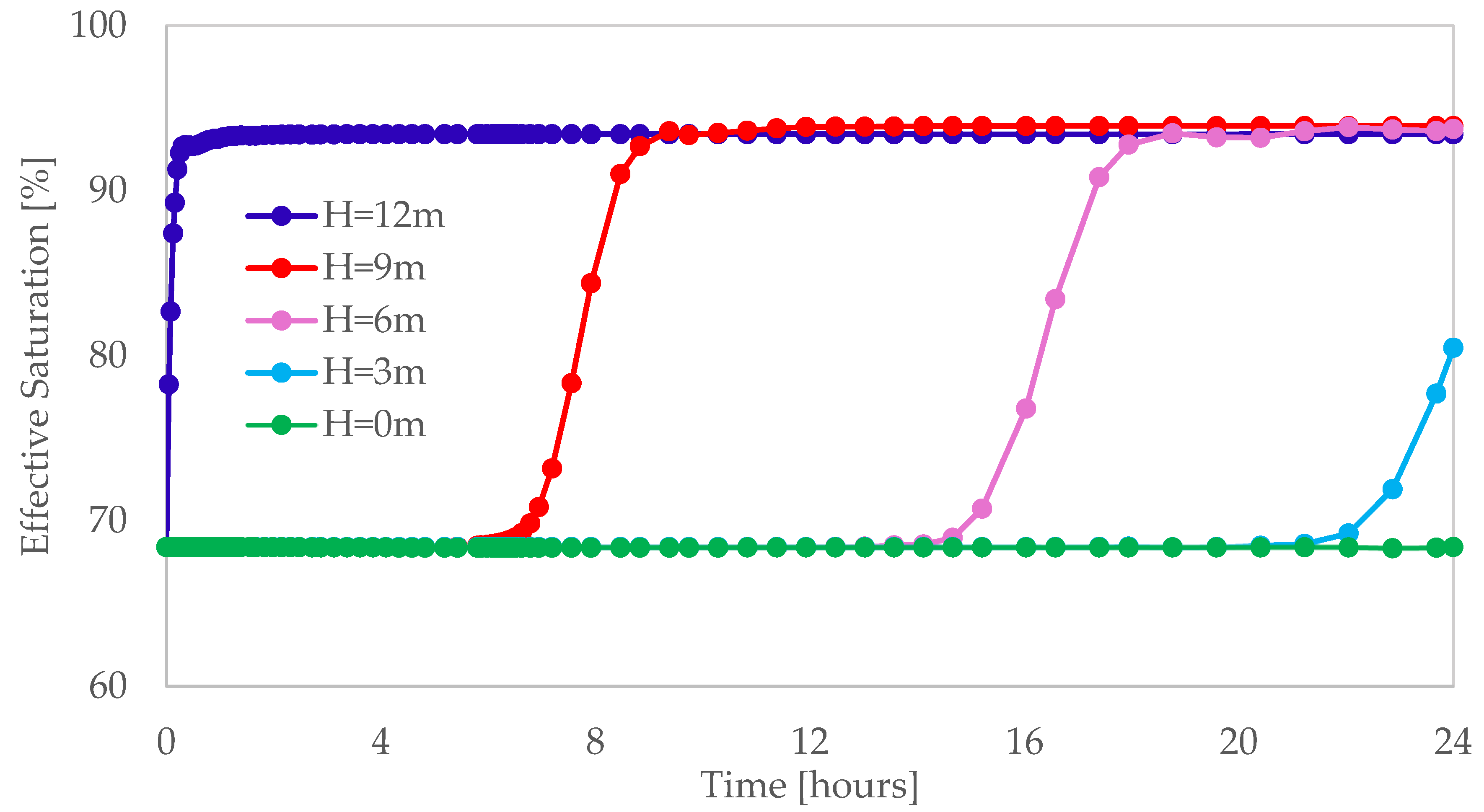
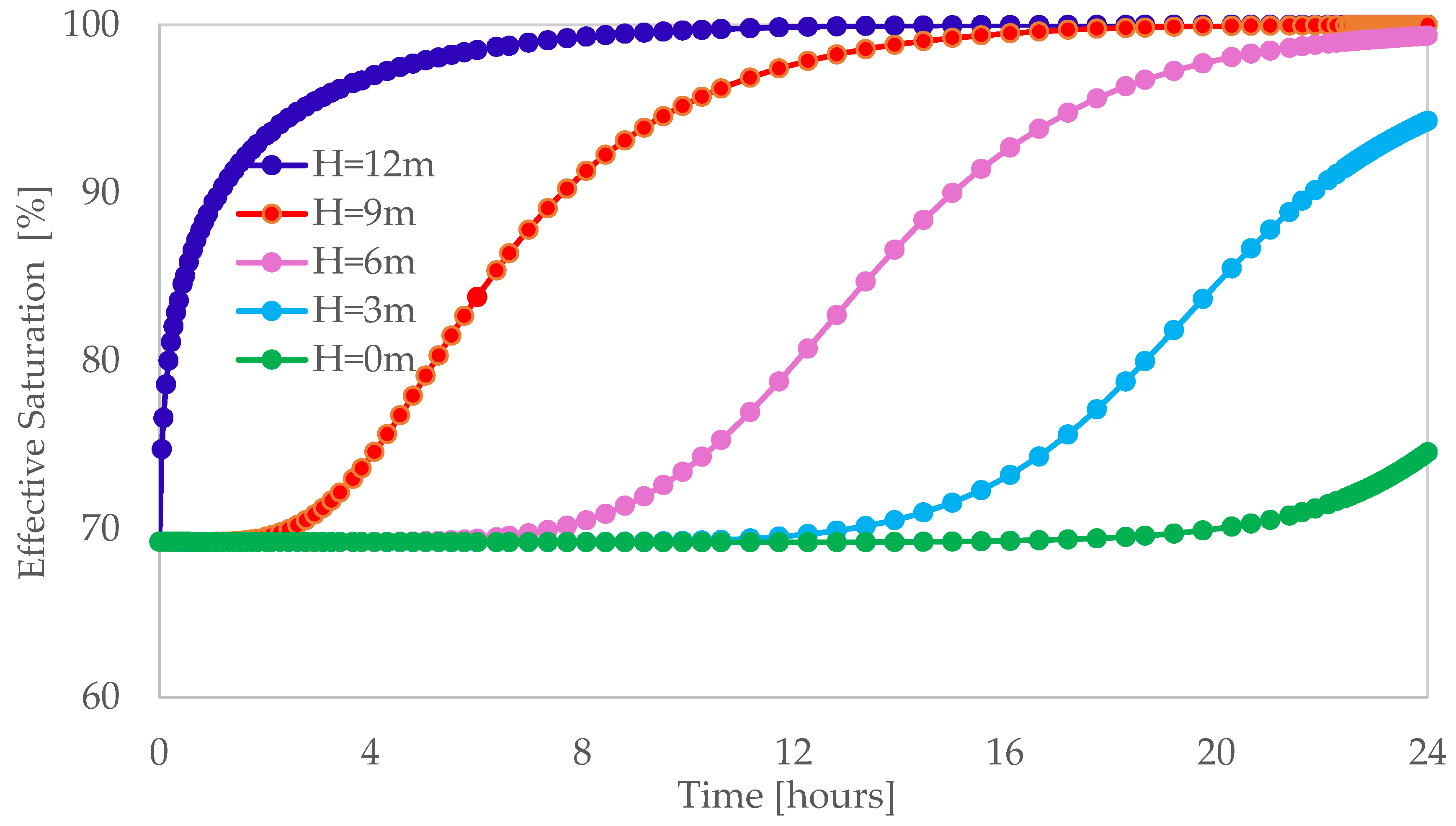
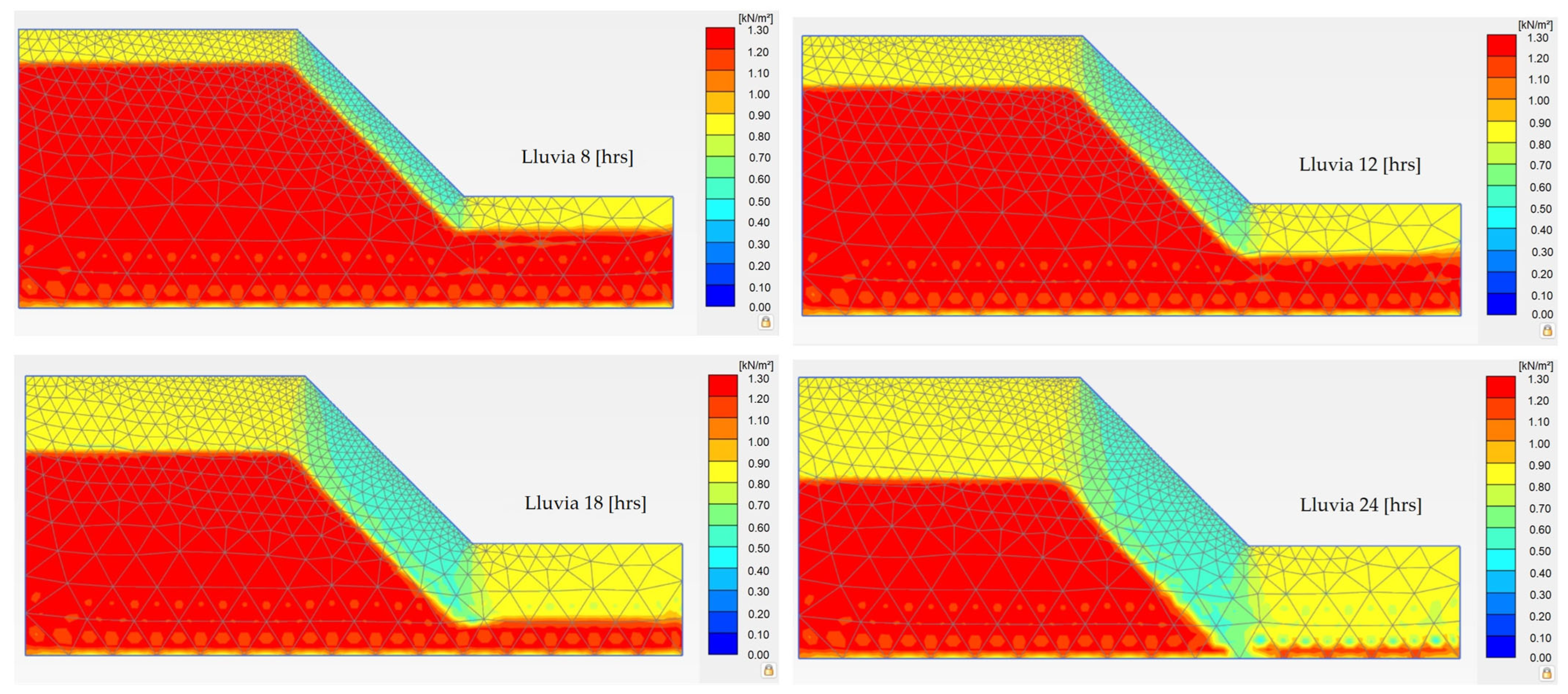
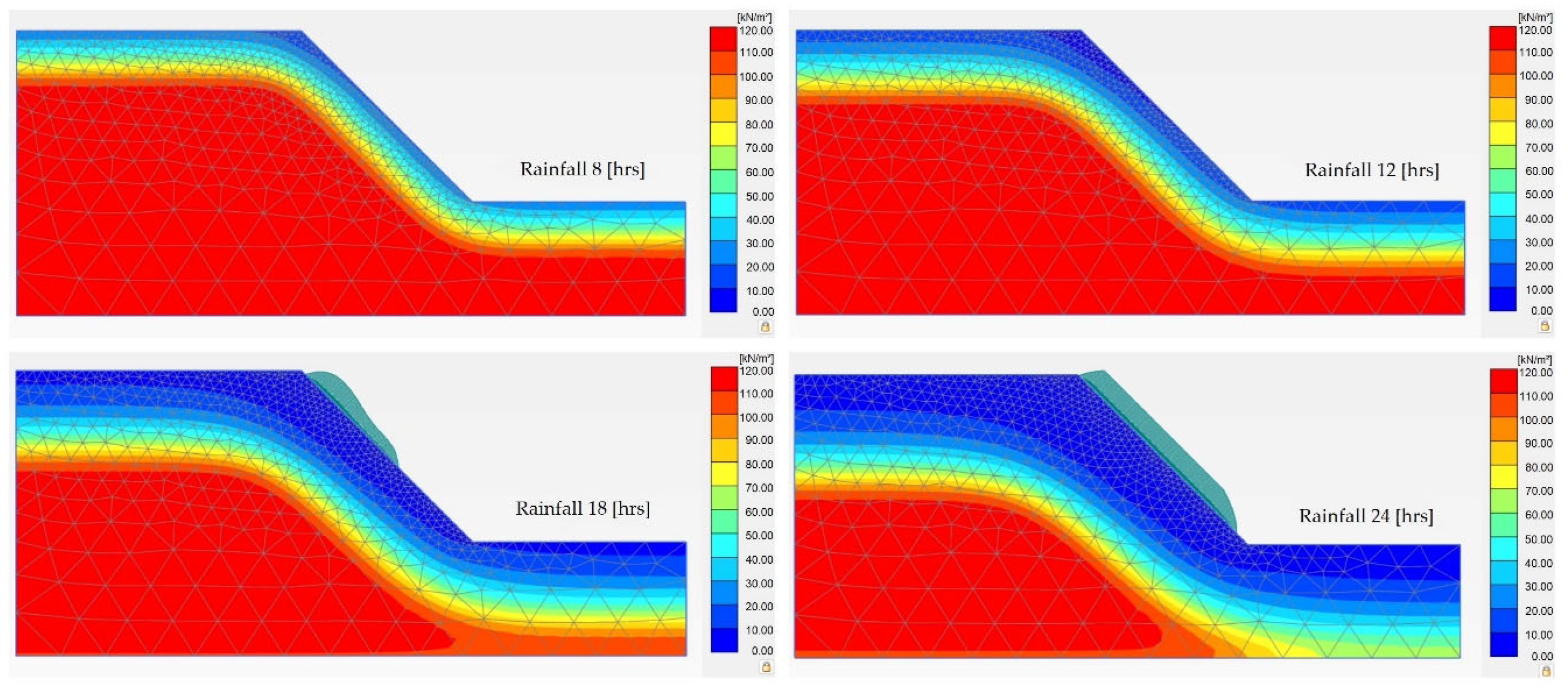
3.1. Effect of Rainfall Duration on the Degree of Saturation
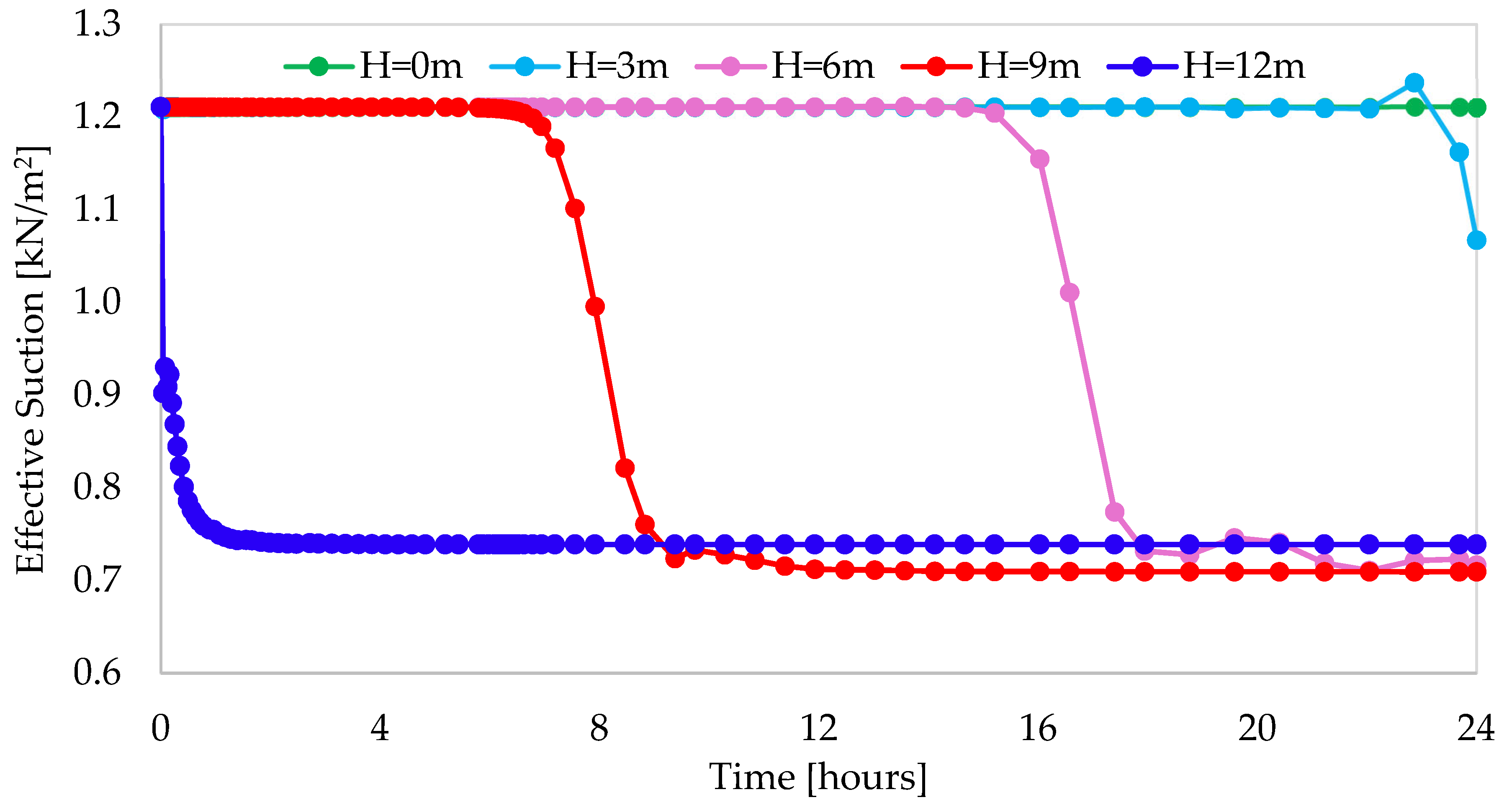
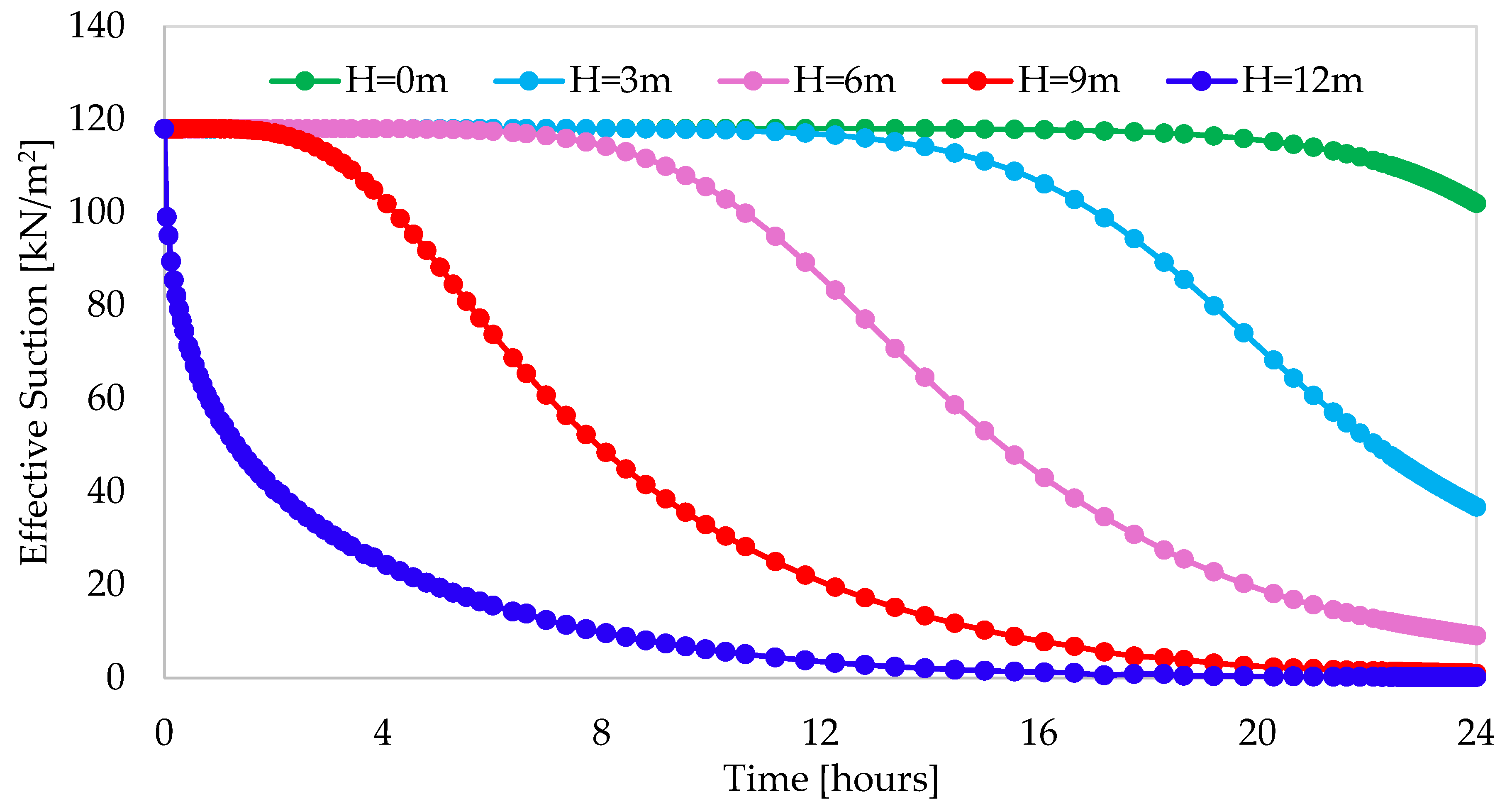
3.2. Effect of Rainfall Duration on Matric Suction
3.3. Effect of Rainfall Duration on the Safety Factor
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fukuoka, M. Landslides Associated with Rainfall. Geotech. Eng. 1980, 11, 1–29. [Google Scholar]
- Wolle, C.M.; Hachich, W. Rain-Induced Landslides in Southeastern Brazil. In Proceedings of the International Conference on Soil Mechanics and Foundation Engineering, Rio de Janeiro, Brazil, 13–18 August 1989; Volume 3, pp. 1639–1642. [Google Scholar]
- Lim, T.T.; Rahardjo, H.; Chang, M.F.; Fredlund, D.G. Effect of Rainfall on Matric Suctions in a Residual Soil Slope. Can. Geotech. J. 1996, 33, 618–628. [Google Scholar] [CrossRef]
- Josifovski, J.; Lenart, S. Some Experience in Numerical Modelling of Unsaturated Slope Instabilities. In Proceedings of the 3rd European Conference on Unsaturated Soils—“E-UNSAT 2016”, E3S Web of Conferences, Paris, France, 12–14 September 2016. [Google Scholar]
- Tsai, T.L.; Hung-En, A.E.; Ae, C.; Yang, J.-C.; Chen, H.-E.; Yang, J.-C. Numerical Modeling of Rainstorm-Induced Shallow Landslides in Saturated and Unsaturated Soils. Environ. Geol. 2008, 55, 1269–1277. [Google Scholar] [CrossRef]
- Li, Z.; Yin, Z. Failure Pattern of Dispersive Soil Slopes under the Action of Rainfall Conditions. Alexandria Eng. J. 2024, 104, 193–210. [Google Scholar] [CrossRef]
- Fei, C.; Keizo, U. Numerical Analysis of Rainfall Effects on Slope Stability. Int. J. Geomech. 2004, 4, 69–78. [Google Scholar] [CrossRef]
- García, J.; Cobelo, W.D.; Quevedo, G.J.; Flores, I.; Rodríguez, C.M. Análisis Del Comportamiento Tenso-Deformacional de Un Suelo Parcialmente Saturado Para Un Cimiento Circular Bajo Carga Axial. Ing. Desarro. 2020, 38, 181–196. [Google Scholar]
- Mongil-Manso, J.; Jiménez-Ballesta, R.; Navarro-Hevia, J.; Martín, R.S. Soil Infiltration Rates in Mediterranean Mountain Areas: Relationship with Soil Properties and Different Land-Use. Eur. J. For. Res. 2024. [Google Scholar] [CrossRef]
- Chen, H.; Lee, C.F.; Law, K.T. Causative Mechanisms of Rainfall-Induced Fill Slope Failures. Geotech. Geoenviron. Eng. 2004, 130, 593–602. [Google Scholar] [CrossRef]
- Naseer, S.; Evans, R. Effect of Rainfall Intensity and Duration on Stability of Natural Slopes of Unsaturated Fine Soils. In Proceedings of the 4th Conference on Sustainability in Civil Engineering (CSCE’22), Hanoi, Vietnam, 25–27 November 2022; pp. 405–411. [Google Scholar]
- Taher, N.R.; Aksoy, H.S.; Gor, M. Numerical Investigation on the Effect of Slope Angle on Slope Stability Subjected to Rainfall. In Proceedings of the 7th International Erciyes Conference on Scientific Research, Kayseri, Turkey, 9–10 March 2022. [Google Scholar]
- Travis, Q.B.; Houston, S.L.; Marinho, F.A.M.; Schmeeckle, M. Unsaturated Infinite Slope Stability Considering Surface Flux Conditions. J. Geotech. Geoenviron. Eng. 2010, 136, 963–974. [Google Scholar] [CrossRef]
- Fourie, A.B.; Rowe, D.; Blight, G.E. The Effect of Infiltration on the Stability of the Slopes of a Dry Ash Dump. Géotechnique 1999, 49, 1–13. [Google Scholar] [CrossRef]
- Jin, L.; Wei, J.; Luo, C.; Qin, T. Slope Stability Analysis Based on Improved Radial Movement Optimization Considering Seepage Effect. Alexandria Eng. J. 2023, 79, 591–607. [Google Scholar] [CrossRef]
- Farahmand, A.; Aghakouchak, A. A Satellite-Based Global Landslide Model. Nat. Hazards Earth Syst. Sci. 2013, 13, 1259–1267. [Google Scholar] [CrossRef]
- Banu, S.; Attom, M.; Abed, F.; Vandanapu, R.; Astillo, P.V.; Al-Lozi, N.; Khalil, A. Numerical Analysis of the Ultimate Bearing Capacity of Strip Footing Constructed on Sand-over-Clay Sediment. Buildings 2024, 14, 1164. [Google Scholar] [CrossRef]
- Cheng, H.; Wu, Z.; Chen, H.; Zhou, X. Stability Analysis of Unsaturated–Saturated Soil Slopes under Rainfall Infiltration Using the Rigorous Limit Equilibrium Method. Bull. Eng. Geol. Environ. 2024, 83, 147. [Google Scholar] [CrossRef]
- Khan, A.Q.; Asadullah; Alam, M.; Shahkar, M.; Aslam, M.A. Numerical Investigation of the Slope Stability under the Rainfall Infiltration of Different Intensities and Duration Using Finite Element Code. Sustain. Struct. Mater. 2023, 6, 12–16. [Google Scholar] [CrossRef]
- Ullah, R.; Abdullah, R.A.; Kassim, A.; Yunus, N.Z.M.; Sendo, H. Assessment Of Residual Soil Properties For Slope Stability Analysis. Int. J. GEOMATE 2021, 21, 72–80. [Google Scholar] [CrossRef]
- Ali, T.; Rana, H.; Babu, G.L.S. Analysis of Rainfall-Induced Shallow Slope Failure. In Lecture Notes in Civil Engineering; Springer Science and Business Media Deutschland GmbH: Berlin, Germany, 2021; pp. 679–691. [Google Scholar]
- Massey, C.I.; Petley, D.N.; McSaveney, M.J. Patterns of Movement in Reactivated Landslides. Eng. Geol. 2013, 159, 1–19. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, Q. Influence of Rainfall Intensity and Duration on Slope Stability in Unsaturated Soils. Q. J. Eng. Geol. 1998, 31, 105–113. [Google Scholar] [CrossRef]
- Ramadhani, S.; Martini; Oktaviana, D.A. The Effect of Rain Intensity and Soil Saturation Levels on Slope Stability in Kebun Kopi Area KM 49+635. Proc. IOP Conf. Ser. Earth Environ. Sci. 2024, 1355, 012026. [Google Scholar] [CrossRef]
- Llasat, M. An Objective Classification of Rainfall Events on the Basis of Their Convective Features: Application to Rainfall Intensity in the Northeast of Spain. Int. J. Climatol. 2001, 21, 1385–1400. [Google Scholar] [CrossRef]
- Chen, C.W.; Saito, H.; Oguchi, T. Rainfall Intensity–Duration Conditions for Mass Movements in Taiwan. Prog. Earth Planet. Sci. 2015, 2, 14. [Google Scholar] [CrossRef]
- Heriberto, M. Comparación de Modelos Constitutivos En Análisis Estáticos de Un Tranque de Relaves. Master’s Thesis, Pontificia Universidad Católica de Chile, Santiago, Chile, 2016. [Google Scholar]
- El-Din Fawzy, H.; Basha, A.M.; Botross, M.N. Estimating a Mathematical Formula of Soil Erosion under the Effect of Rainfall Simulation by Digital Close Range Photogrammetry Technique. Alexandria Eng. J. 2020, 59, 5079–5097. [Google Scholar] [CrossRef]
- Pradel, D.; Raad, G. Effect of Permeability on Surficial Stability of Homogeneous Slopes. J. Geotech. Eng. 1993, 119, 315–332. [Google Scholar] [CrossRef]
- Au, S.W.C. Rain-Induced Slope Instability in Hong Kong. Eng. Geol. 1998, 51, 1–36. [Google Scholar] [CrossRef]
- Van Genuchten, M. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Lizana, D.; Aguilar, Z.; Calderon, D. Estimation of the Soil-Water Characteristic Curve in Sandy Soils Using the Filter Paper Test. Tecnia 2023, 33, 42–51. [Google Scholar] [CrossRef]
- Kaushalya, A.A.S.; Pallewattha, M.A.; Ansar, F.S.A.; Nawagamuwa, U.P. Use of Chilled Mirror /Dew-Point Method (WP4C) to Develop Soil Water Characteristic Curve for Coastal Silty Sand with a Comparison of the Existing Analytical Models. Eng. J. Inst. Eng. Sri Lanka 2024, 57, 13–20. [Google Scholar] [CrossRef]
- Bentley PLAXIS 2D, Material Models Manual, Van Genuchten Model Section. Available online: https://www.bentley.com/wp-content/uploads/FS-PLAXIS-2D-Matrix-LTR-EN-LR.pdf (accessed on 11 December 2024).
- Griffiths, D.V.; Lane, P.A. Slope Stability Analysis by Finite Elements. Géotechnique 2001, 51, 653–654. [Google Scholar] [CrossRef]
- Ke, Z.; Hong, W.; Jianxing, L.; Yuguang, Z.; Fangping, C.; Zhengjun, Y. Deformation and Failure Mechanism of Colluvial Landslide under Sustained Rainfall—A Case Study of Xinzhan Landslide in Tongzi County, China. Alexandria Eng. J. 2023, 71, 89–103. [Google Scholar] [CrossRef]
- Qiu, D.; Xu, R.; Wu, C.; Mu, X.; Zhao, G.; Gao, P. Effects of Vegetation Restoration on Soil Infiltrability and Preferential Flow in Hilly Gully Areas of the Loess Plateau, China. CATENA 2023, 221, 106770. [Google Scholar] [CrossRef]
- Hidayat, M.; Djufri, D.; Basri, H.; Ismail, N.; Idroes, R.; Ikhwali, M.F. Influence of Vegetation Type on Infiltration Rate and Capacity at Ie Jue Geothermal Manifestation, Mount Seulawah Agam, Indonesia. Heliyon 2024, 10, e25783. [Google Scholar] [CrossRef] [PubMed]
- Tobon, W.; García, E.; Carlos Alberto, V.-P. Análisis Numérico del Proceso de Infiltración de Agua y Localización de Deformación en Suelos Parcialmente Saturados. Rev. EIA 2016, 13, 53. [Google Scholar] [CrossRef]
- Flores Berenguer, I.; Nápoles, O.; Jacobo Rodríguez, O.; Glez Haramboure, Y.; García Tristá, J. Efecto de La Porosidad y La Permeabilidad En La Estabilidad de Taludes Bajo El Efecto de La Lluvia. Ing. Hidráulica Ambient. 2023, 44, 31–43. [Google Scholar]
- Varas, P.; Noviembre, D. Simposio Internacional de Geología Ambiental Para Planificación Del Uso Del Territorio. In Proceedings of the Simposio Internacional de Geología Ambiental para Planificación del Uso del Territorio, Puerto Varas, Chile, 4–6 November 2002; pp. 169–172. [Google Scholar]
- Húmerez, A.; Balboa, A. Estudio Fundado de Riesgos; Plan Regulador Metropolitano de Valparaíso: Valparaíso, Chile, 2012. [Google Scholar]
- Timalsina, A.; Rokaya, D.K.; Dumre, P.; Paudel, M.R. Estimate of Safe Angle for Cut Slopes Under Different Geology and Rainfall Intensity in Central Nepal. Am. J. Geosci. 2024, 13, 1–12. [Google Scholar] [CrossRef]
- Kardena, E.; Helmy, Q.; Funamizu, N. Biosurfactants and Soil Bioremediation. In Biosurfactants; CRC Press: Boca Raton, FL, USA, 2014; pp. 372–381. [Google Scholar]
- Gitirana, G.; Fredlund, D. Statistical Assessment of Hydraulic Properties of Unsaturated Soils. Soils Rocks 2016, 39, 81. [Google Scholar] [CrossRef]
- Vickneswaran, T.; Ravichandran, N. Multi Hazard Analysis of Earth Slopes Using Coupled Geotechnical-Hydrological Finite Element Model. En Geo-Congress; American Society of Civil Engineers: Reston, VA, USA, 2020; pp. 60–69. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Gonzalez, N.A.; Galavi, V.; Bonnier, P.G. Fully Coupled Hydro-Mechanical Analysis of Unsaturated Soils. In Proceedings of the Computational Geomechanics I (ComGeo I), Juan-les-Pins, France, 29 April–1 May 2009. [Google Scholar]
- Bowles, J.E. Foundations Analysis and Design, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Leij, F.J.; Alves, W.J.; Van Genuchten, M.T.; Williams, J.R. The UNSODA Unsaturated Soil Hydraulic Database User’s Manual Version 1.0; UNSODA: New York, NY, USA, 1996. [Google Scholar]
- van Zuidam, R.A.; Zuidam-Cancelado, F.I.; International Institute for Aerospace Survey and Earth Sciences. Aerial Photo-Interpretation in Terrain Analysis and Geomorphologic Mapping; Smits Publishers: Eindhoven, The Netherlands, 1986; ISBN 9789070043247. [Google Scholar]
- Fu, H.; Song, K.; Ma, Z.; Zhao, Y.; Liang, L.; Guo, H. An Accurate Identification and Spatial Characterization Method for the Development Degree of Preferential Flow Paths in Water-Flooded Reservoir. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 141. [Google Scholar] [CrossRef]
- Imre, E.; Bálint, Á.; Houng, D.Q.; López, L.; Kollár, C.S.; Répássy, L.; Mwinken, D.K.; Illés, Z.S.; Datcheva, M.; Baille, W.; et al. Using Grain Size Distribution to Estimate Permeability. In Geotechnical Engineering Challenges to Meet Current and Emerging Needs of Society; CRC Press: London, UK, 2024; pp. 2987–2990. [Google Scholar]
- Díaz-Curiel, J.; Miguel, M.J.; Biosca, B.; Arévalo-Lomas, L. New Granulometric Expressions for Estimating Permeability of Granular Drainages. Bull. Eng. Geol. Environ. 2022, 81, 397. [Google Scholar] [CrossRef]
| Properties | SP-SM | SW-SM |
|---|---|---|
| Saturated unit weight [kN/m3] | 18.9 | 18 |
| Unsaturated unit weight [kN/m3] | 15.7 | 16 |
| Deformation modulus [kN/m2] | 30,000 | 15,000 |
| Poisson’s ratio | 0.3 | 0.35 |
| Friction angle [°] | 38 | 36 |
| Cohesion [kN/m2] | 5 | 10 |
| Sand percentage | 93.5 | 87.8 |
| Fines percentage | 6.5 | 11.9 |
| Gravel percentage | 0 | 0.3 |
| Initial degree of saturation | 70 | 70 |
| Parameters | SP-SM | SW-SM |
|---|---|---|
| Permeability [m/day] | 1.572 | 0.864 |
| Sres | 0.050 | 0.025 |
| Ssat | 1.000 | 1.000 |
| ga | 5.411 | 0.085 |
| gn | 2.449 | 1.561 |
| gl | −0.592 | −0.359 |
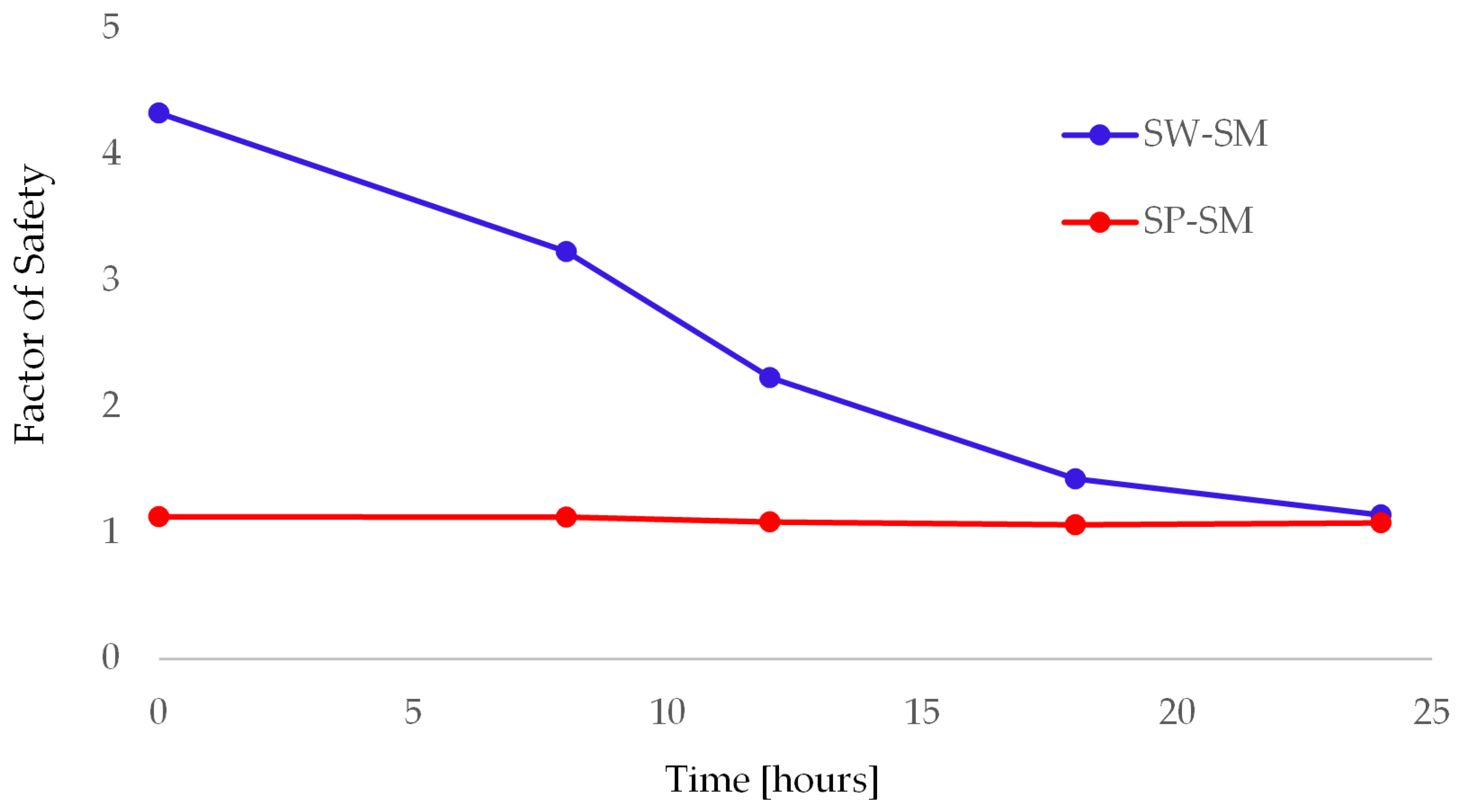
| Safety Factor (S.F.) | ||
|---|---|---|
| SW-SM | SP-SM | |
| No rainfall | 4.329 | 1.126 |
| Rainfall duration 8 [h] | 3.229 | 1.123 |
| Rainfall duration12 [h] | 2.229 | 1.085 |
| Rainfall duration18 [h] | 1.427 | 1.063 |
| Rainfall duration24 [h] | 1.140 | 1.078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bustamante, J.; Gallardo-Sepúlveda, R.; Atencio, E.; Parra, P.F. Sensitivity Analysis of the Influence of Heavy-Intensity Rain Duration on the Stability of Granular Soil Slopes Under Unsaturated Conditions. Appl. Sci. 2025, 15, 6074. https://doi.org/10.3390/app15116074
Bustamante J, Gallardo-Sepúlveda R, Atencio E, Parra PF. Sensitivity Analysis of the Influence of Heavy-Intensity Rain Duration on the Stability of Granular Soil Slopes Under Unsaturated Conditions. Applied Sciences. 2025; 15(11):6074. https://doi.org/10.3390/app15116074
Chicago/Turabian StyleBustamante, Javier, Ricardo Gallardo-Sepúlveda, Edison Atencio, and Pablo F. Parra. 2025. "Sensitivity Analysis of the Influence of Heavy-Intensity Rain Duration on the Stability of Granular Soil Slopes Under Unsaturated Conditions" Applied Sciences 15, no. 11: 6074. https://doi.org/10.3390/app15116074
APA StyleBustamante, J., Gallardo-Sepúlveda, R., Atencio, E., & Parra, P. F. (2025). Sensitivity Analysis of the Influence of Heavy-Intensity Rain Duration on the Stability of Granular Soil Slopes Under Unsaturated Conditions. Applied Sciences, 15(11), 6074. https://doi.org/10.3390/app15116074









