Flowability-Dependent Anisotropic Mechanical Properties of 3D Printing Concrete: Experimental and Theoretical Study

Abstract

Three-dimensional printing concrete (3DPC) has garnered significant attention for its construction efficiency and complex geometric capabilities. However, its mechanical properties differ markedly from cast-in-place concrete due to interlayer/intralayer interface weakening and pore anisotropy. Flowability directly regulates printability and pore distribution, thereby influencing mechanical properties. This study systematically examines flowability’s effects on 3DPC mechanical properties through compressive, flexural, and interfacial splitting tensile tests, integrated with Griffith’s fracture theory and stress intensity factor calculations. The key findings are as follows: (1) 3DPC exhibits pronounced anisotropy—compressive strength (X > Y > Z), flexural strength (Y ≈ Z > X2 > X1), and splitting tensile strength (C > T). Increased flowability enables compressive and Y/Z direction flexural strengths to approach cast concrete levels. (2) The anisotropy coefficient $I_{\mathrm{a}}$ decreases significantly with flowability (66.7% for compressive, 66.8% for flexural strength). Flexural strength shows greater sensitivity to interfacial defects than compressive strength. (3) The aspect ratio of ellipsoidal pores directly influences the anisotropic compressive behavior. Increased flowability promotes morphological transformation of elliptical pores toward more spherical geometries with reduced flattening, thereby mitigating the anisotropy in compressive performance. These results establish a theoretical framework for optimizing and predicting 3DPC mechanical performance, supporting its practical application in construction.

1. Introduction

Against the backdrop of rapid global industrial automation and digitalization, 3D printing concrete (3DPC) employs a layer-by-layer deposition method to enable efficient fabrication of complex geometries, significantly reducing formwork usage and labor costs [1]. However, the mechanical properties of 3DPC differ markedly from those of cast-in-place concrete, primarily manifested as interlayer interfacial weakening and an anisotropic pore structure [2]. These differences not only compromise the structural load-bearing capacity but may also induce early-age cracking and durability issues [3,4]. Therefore, an in-depth investigation of 3DPC’s mechanical behavior is critical for advancing its engineering applications.

Flowability, a critical workability parameter for 3DPC, directly governs material extrudability, interlayer bond strength, and pore structure distribution [5,6,7]. Insufficient flowability leads to excessively high yield stress and plastic viscosity of cementitious materials, impairing filament extrudability and preventing dense packing during layer deposition. This results in detrimental interfacial pores [8], adversely affecting mechanical performance [9]. Moreover, 3DPC exhibits pronounced mechanical anisotropy along three axes, significantly compromising structural load uniformity and stability. Existing studies on flowability’s influence remain limited, predominantly focusing on shape retention [10,11], while systematic investigations into unfavorable pore structures under low flowability and their mechanical implications are scarce.

Existing studies on 3DPC’s compressive behavior generally report the highest strength along the X-axis (printing direction), though conclusions on Y- and Z-axis strengths remain inconsistent [12,13,14,15,16,17,18,19,20]. Some researchers have analyzed this anisotropy: For instance, Liu [21] employed simulation and theoretical modeling to reveal stress concentration effects in homogenized single-pore 3DPC specimens, explaining the X > Y > Z strength hierarchy. Liu [22] investigated the correlation between pore geometry and interlayer interfacial bond strength. In parallel, Xiao [23] investigated the influence of interfacial bonding properties on the anisotropic mechanical behavior of 3DPC through FE modeling incorporating traction-separation laws at interlayer interfaces. Flexural and splitting tensile strengths follow a clearer trend [7,24,25], with interfacial loading yielding minimum strength due to high interfacial porosity-induced defects [26]. As demonstrated by Chen [27], the flexural strength of 3DPC is the lowest along the interlayer direction and the highest in the direction perpendicular to the layers. Zhang [28] further developed an interfacial constitutive model based on material co-deformation theory and pore inclusion analysis, revealing that while the interlayer interfacial bond strength exceeds that of intralayer, both remain inferior to the bond strength observed in cast-in-place concrete. However, current studies about compressive strength anisotropy of 3DPC primarily focus on interfacial pores while neglecting bulk pore distribution effects [29]. Theoretical analyses typically rely on single-pore compressive stress concentration models [30], failing to explain anisotropic mechanical behavior from the perspectives of tensile stress concentration and stress intensity factors. In addition, current analysis predominantly relied on finite element modeling of weak interfacial zones, lacking mathematical formulations from fracture mechanics perspectives (e.g., stress intensity factor calculations or energy-based crack propagation criteria [31]). This methodological gap limits the quantitative linkage between microcosmic defects and macroscopic anisotropy. Moreover, current research on the anisotropic flexural strength of 3DPC often overlooks critical distinctions within X direction loading: the interlayer and intralayer orientations have rarely been differentiated in reported studies, despite their fundamentally distinct failure mechanisms [32]. Additionally, the size effects of large pores induced by low flowability on failure mechanisms remain insufficiently investigated. Meanwhile, the influence of flowability-induced microstructural improvements (e.g., pore spheroidization and interfacial densification) on compressive, flexural, and splitting tensile strengths has not been systematically reported.

To address these gaps, this study conducted compression, flexural, and interfacial splitting tensile tests to analyze failure processes and morphological characteristics of 3DPC specimens with varying flowability. Anisotropy coefficients for compressive and flexural strengths were calculated, while Griffith’s fracture theory and critical fracture stress calculations were employed to quantify mechanical performance trends. This approach elucidates the origins of compressive anisotropy and clarifies flowability-dependent anisotropic evolution. The findings provide theoretical insights into flowability’s influence on 3DPC mechanical properties.

2. Materials and Methods

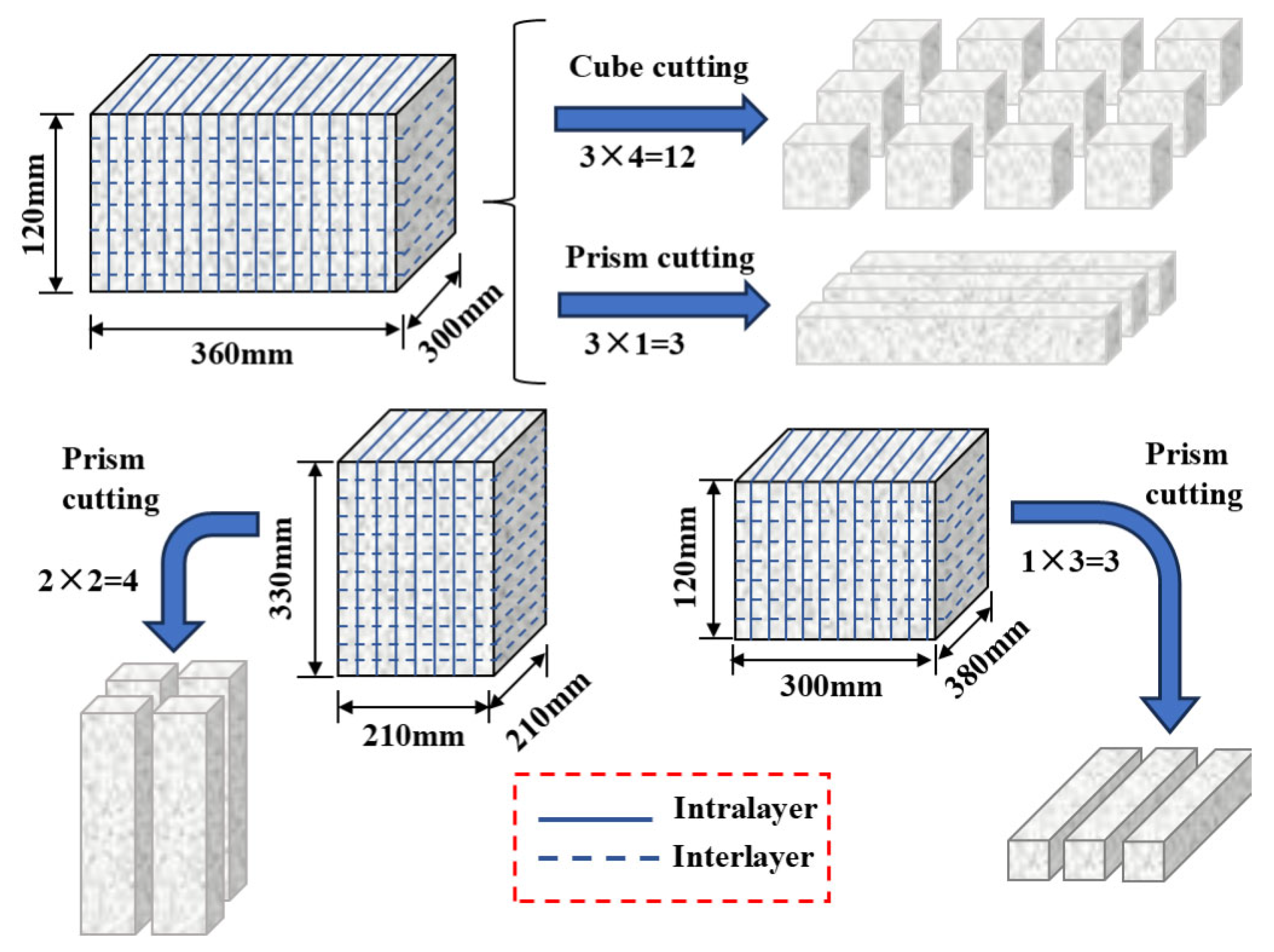
2.1. Raw Materials and Printing Processes

The 3DPC mixture consisted of 42.5 rapid hardening sulfoaluminate cement, silica fume, natural river sand, polypropylene (PP) fibers, a polycarboxylate-based high-performance superplasticizer (PCE-SP), a retarder, a defoamer, and a thixotropic agent, as demonstrated in

Table 1. Mass proportion of 3DPC mix.

Cement	Silica Fume	Natural River Sand	Water	PCE-SP (%)	Tartaric Acid	Defoamer (%)	Thixotropic Agent (%)	PP Fiber (%)
1	0.11	1.11	0.39	0.5–1	0.01	0.22	0.11	0.56

. The PCE-SP was employed to modulate flowability without altering the water–cement ratio, ensuring consistency in mixture composition, mixing procedures, and printing parameters. This approach strictly adheres to the single-variable principle, isolating flowability effects while minimizing perturbations to the mechanical strength development of 3DPC [33].

The 3D printer used for this experiment is a gantry-type laboratory-grade printer with dimensions of 2.8 m (length) × 1.5 m (width) × 1.8 m (height). The print head was equipped with a screw to control the extrusion speed. After mixing, the concrete was added to the hopper of the printer and extruded through the print head by rotating the screw. During the printing process, the print nozzle diameter was 30 mm, the printing speed was 20 mm/s, and the extrusion speed was 2 r/s. In this work, the width of all printed filaments was set to 30 mm, and the height was set to 15 mm.

2.2. Mechanical Test

Following the applicable flowability range for 3DPC established by Zhang et al. [34] and Sun et al. [35], compressive strength tests, flexural strength tests, and interfacial splitting tensile strength tests were conducted at 28 days for nine groups with flowability values ranging from 153 to 191 mm. Testing procedures complied with the standard “Test methods for basic mechanical properties of 3D printed concrete” (T/CBMF 183-2022) [36]. Mechanical testing was conducted using a 200-ton universal testing machine (UTM) under force control mode, applying constant loading rates until specimen failure. The compressive strength tests employed a loading rate of 0.30–0.50 MPa/s, while flexural and interfacial splitting tensile tests utilized a reduced rate of 0.05–0.10 MPa/s to accommodate brittle failure modes. This protocol ensures standardized failure progression while minimizing dynamic effects, aligning with the standard for test methods of concrete physical and mechanical properties (GB/T 50081-2019) [37].

Cast specimens were tested without directional distinction, while printed specimens required directional loading due to anisotropy (Figure 1): Compressive test specimens (70.7 mm × 70.7 mm × 70.7 mm) were loaded along X, Y, and Z directions; flexural test specimens (70.7 mm × 70.7 mm × 300 mm) were loaded along X1, X2, Y, and Z directions; and interfacial splitting tensile test specimens (70.7 mm × 70.7 mm × 70.7 mm) were loaded along X1, X2, Y, and Z directions. X1 and Y directions represented interlayer interfacial splitting failure, while X2 and Z directions represented intralayer interfacial splitting failure. The final interlayer and intralayer splitting tensile strengths were determined by averaging the respective directional results. The representative value for each test group was determined as the average of three specimens, totaling 324 specimens (108 groups). Data processing followed the standard for test methods of concrete physical and mechanical properties (GB/T 50081-2019) [37]: if either the maximum or minimum value deviated from the median by more than 15%, the maximum or minimum values should be discarded, and the median value was adopted as the test result; the results were deemed invalid if both extremes exceeded this threshold.

Test specimens for mechanical evaluation were obtained through precision cutting of printed structures, while cast specimens were produced using identical batch materials in standard molds. To minimize structural disturbance during cutting, printed specimens underwent 24 h curing to achieve full hardening prior to sectioning. The cutting procedure (Figure 2) involved three printed configurations to prepare cubic and prismatic specimens. All specimens received in situ film membrane curing before and after cutting, with pre-curing surface hydration achieved through uniform water spraying (laboratory conditions: 65–75% relative humidity, 18–20 °C).

2.3. X-CT Test

Cubic specimens cured for 28 days under different flowability conditions were subjected to X-CT testing using an XTH255/320LC industrial X-CT system. The specimen dimensions were 70.7 mm × 70.7 mm × 70.7 mm. Projections with varying X-ray signal intensities at different spatial positions provided non-destructive characterization of pore characteristics [38].

The X-ray emission parameters were set to 180 kV and 180 μA, with an exposure time of 708 ms. A complete scan generated 1400 X-ray projections, yielding X-ray images with a pixel resolution of 57 μm. Before the rigorous 3D structural reconstruction, a region of interest (ROI) was selected for each sample to represent the structure of the material. Here, a 60 × 60 × 60 mm ROI was carefully chosen, encompassing the interlayer and intralayer regions of each 3DPC sample, to analyze the overall 3D pore structure. The projections were then processed using CT3dpro software, where qualified projections were selected and stacked for three-dimensional reconstruction to obtain comprehensive pore information within the specimens.

3. Results and Discussion

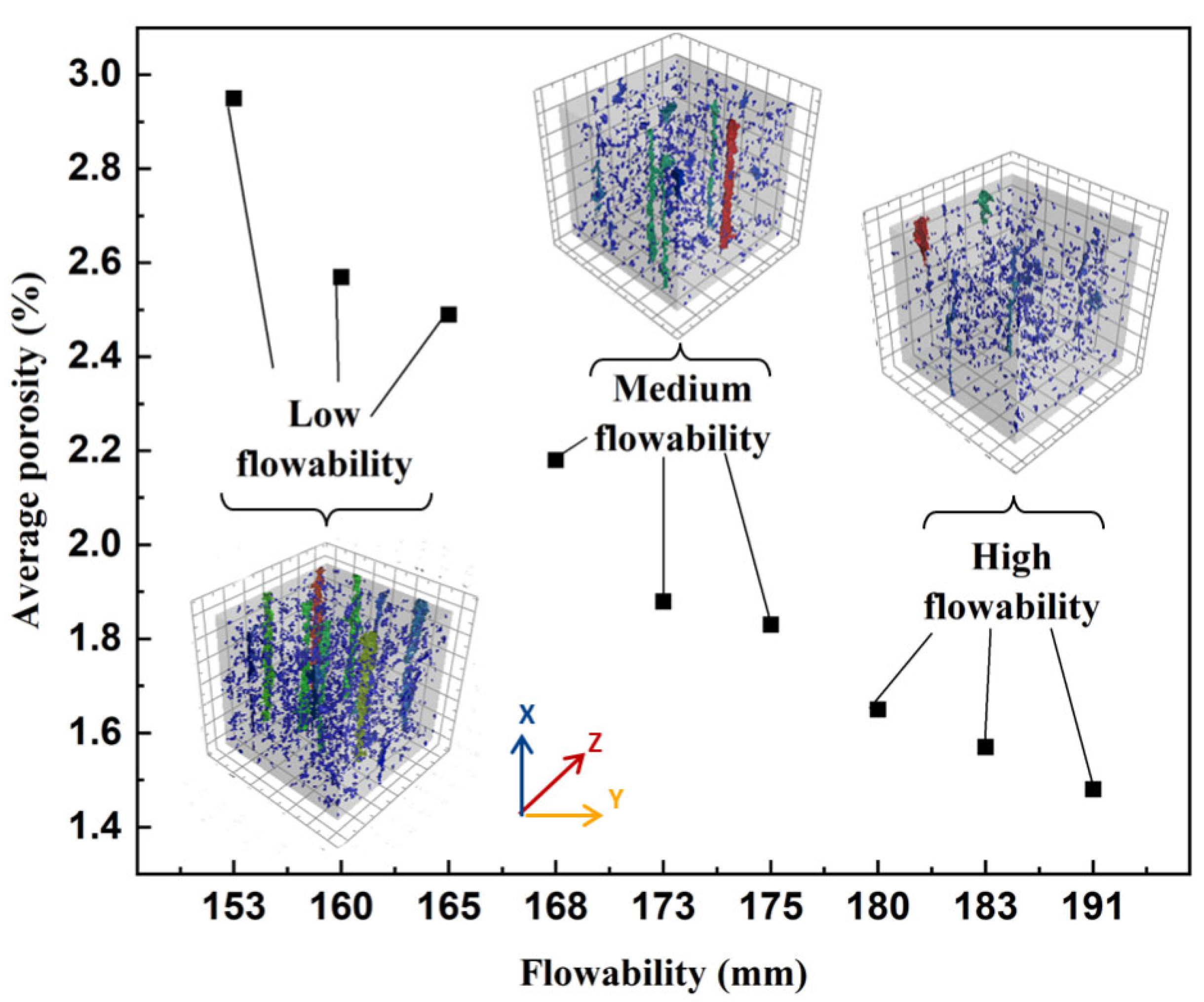
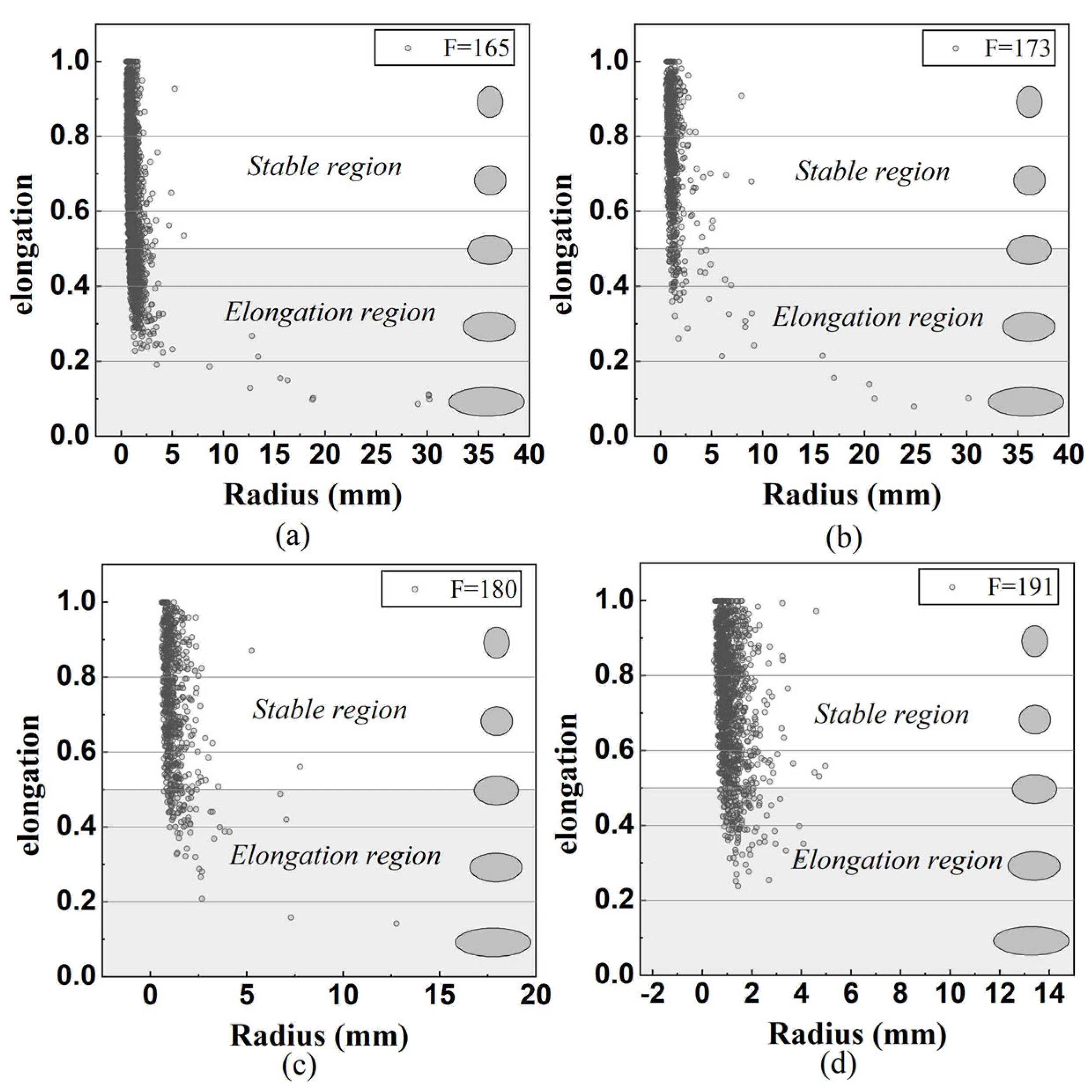
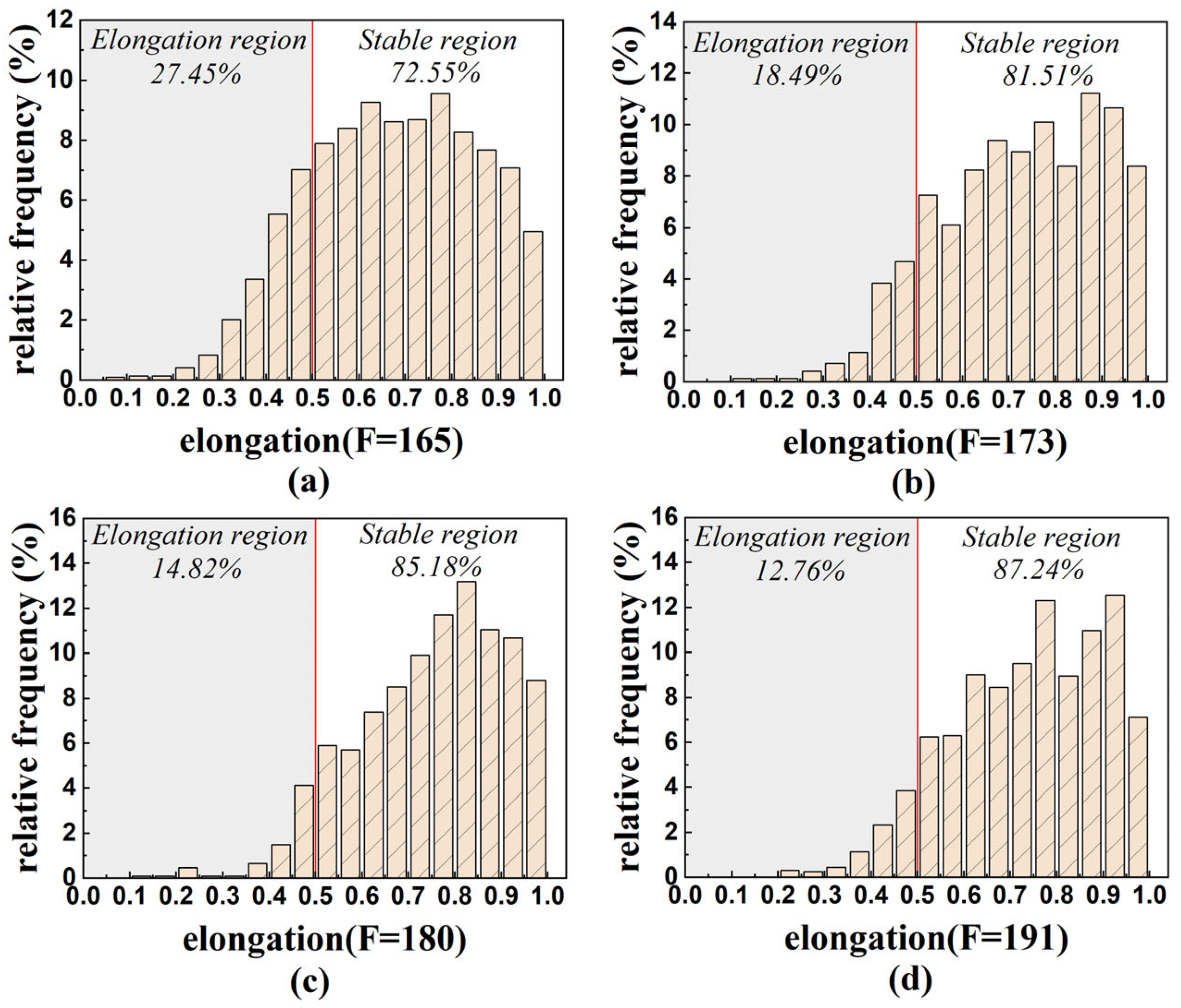
3.1. X-CT Test Results

Compared to cast concrete, 3DPC exhibits significant spatial anisotropy in pore morphology. While pores in cast concrete are randomly distributed and predominantly spherical [39], the extrusion–deposition process of 3DPC imparts distinct directional characteristics to pore geometry and distribution [40]. In the X direction (printing path), pores are elongated into aligned ellipsoids due to extrusion shear forces and nozzle dragging effects. The Z direction pores become flattened under layer-by-layer compaction from self-weight pressure. For the Y direction, interfacial compression between filaments results in intermediate pore sizes (X > Y > Z), collectively forming spatially anisotropic ellipsoidal pore configurations. This anisotropic pore architecture (X > Y > Z) provides critical microstructural insights into the mechanistic origins of 3DPC’s mechanical anisotropy.

As shown in Figure 3, the average porosity of 3DPC decreased with increasing flowability, exhibiting a steeper gradient in the low- and medium-flowability ranges, while the decline moderated and stabilized in the high-flowability range. This indicates that flowability exerts a more pronounced regulatory effect on porosity at low to medium levels, whereas porosity approaches the densification limit of the material under high-flowability conditions. The connected pores at the intersections of the interlayer and intralayer zones decreased substantially with increasing flowability. Owing to the unique extrusion–deposition mechanism of 3DPC, the pore morphology and spatial distribution demonstrate distinct directional characteristics. Specifically, the pores were observed to be significantly elongated along the printing direction (X-axis).

The evaluation of pore defect elongation ratios was conducted across four representative flowability groups (F = 165, 173, 180, and 191 mm), as illustrated in Figure 4, where the elongation ratio was defined as the ratio of the median to maximum axis lengths in pore projections, with values approaching 0 indicating more elongated pore geometries. The stable region (elongation ratio > 0.5) and elongation region (elongation ratio ≤ 0.5) were divided to characterize the elongated state of the pore geometry according to the elongation distribution. As the pore size increases, the number of elongated pores in 3DPC progressively rises while stable pores decrease, demonstrating that pore geometry becomes more elongated and approaches an ellipsoidal shape with increasing pore dimensions. As shown in Figure 5, the majority of pores reside within the stable region (cumulative frequency ≥ 72.55%), while a smaller fraction occupies the elongated region (cumulative frequency ≤ 27.45%). Notably, specimens with low flowability exhibit the highest relative frequency of elongated pores (27.45% at 165 mm flowability), indicating pronounced pore elongation. As flowability increases, the proportion of elongated pores progressively decreases, reaching 12.76% at 191 mm flowability. This 14.69% reduction demonstrates that enhanced flowability effectively reduces ellipsoidal pore populations and improves pore characteristics.

3.2. Failure Modes

Taking compressive strength testing as a representative case, this study systematically analyzed the failure modes of printed and cast specimens under different loading directions across varying flowability ranges (

Table 2. Failure modes of cubic specimens under compressive loading.

Type	Loading Direction
	X	Y	Z	Cast
Low flowability
Medium flowability
High flowability

). The results demonstrate that the failure patterns of cast specimens showed minimal dependence on flowability, primarily exhibiting vertical and diagonal cracks along edges and outer surfaces. This behavior correlates strongly with the 45° principal tensile stress trajectories induced by the confinement effect [41].

In contrast, printed specimens displayed distinct anisotropic failure characteristics. Under X direction compression, the failure mode resembled that of cast specimens, dominated by vertical and diagonal cracks. However, at low flowability, vertical cracking prevailed due to the parallel orientation of interlayer and intralayer interfaces relative to loading direction. The insufficient interfacial filling caused by high yield stress and plastic viscosity at low flowability resulted in weak interfacial bonding strength, facilitating crack propagation along interfaces when principal tensile stresses encountered interlayer and intralayer defects. This phenomenon diminished significantly with increasing flowability and improved interfacial bonding. For Y and Z direction compression, stress concentration around connected pores at interlayer and intralayer junctions [42] in low-flowability specimens led to pore-connecting cracks. Medium-flowability specimens exhibited reduced pore connectivity, making weak interfaces the dominant factor. Since both Y and Z direction loading involved interfaces either perpendicular or parallel to the load, the interaction between principal tensile stresses and interfaces induced transverse or vertical shear failures, forming step-shaped cracks. High-flowability specimens showed enhanced interfacial bonding and reduced porosity, resulting in more uniform stress distribution and ultimately demonstrating cast-like 45° diagonal cracking patterns.

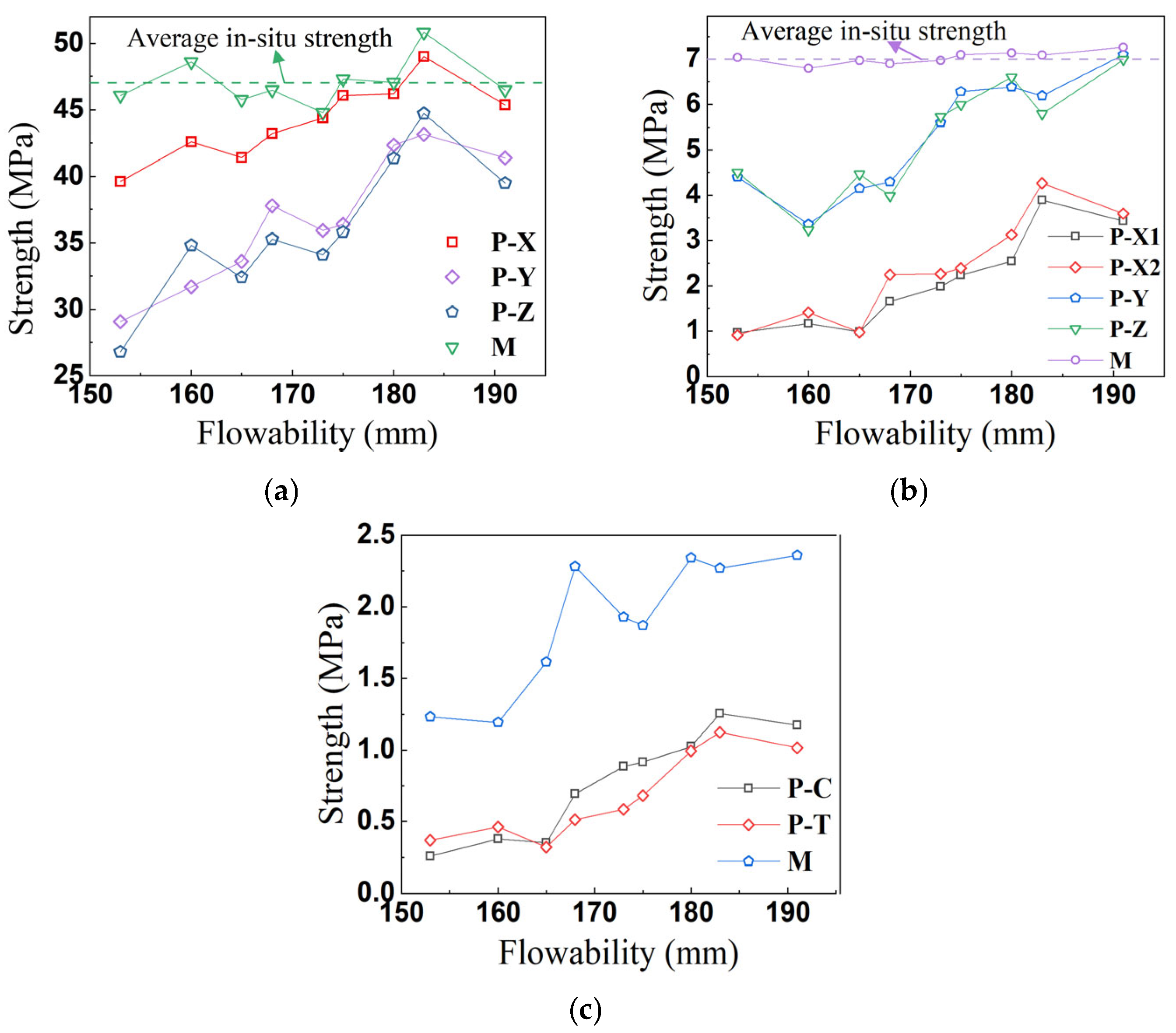
3.3. Mechanical Test Results

Figure 6a shows the 28-day compressive strength of printed (P-X/P-Y/P-Z) and cast (M) specimens at different flowabilities. Printed specimens exhibited lower strength than cast ones, especially at low flowability (153 mm): X, Y, and Z direction strengths were 13.9%, 36.7%, and 41.7% lower, respectively. Strength increased with flowability before stabilizing, approaching cast specimen values due to reduced porosity. In addition, printed specimens showed clear anisotropy: X direction strength exceeded Y and Z directions, with Y generally higher than Z. However, exceptions occurred in some groups at low and high flowability levels, where the Z direction strength exceeded the Y direction strength. This phenomenon may be attributed to the interlocking effect of staggered intralayer interfaces at low flowability, which hinders crack propagation. At high flowability, improved interfacial compaction and significantly reduced porosity minimized the strength disparity between the Y and Z directions. Nevertheless, random errors during the loading process could occasionally alter the relative strength relationship between these directions.

Figure 6b shows the 28-day flexural strength of printed (P-X1/P-X2/P-Y/P-Z) and cast (M) specimens under different flowability conditions. The printed specimens exhibited lower strength than the cast ones with marked anisotropy. The Y and Z directions showed significantly higher strength than the X1 and X2 directions, with minimal difference between Y and Z strengths. The X2 direction strength slightly exceeded X1 at medium-high flowability but was lower at low flowability. This behavior stems from fundamental failure mechanisms. In the Y and Z directions, loading primarily engages the bulk material without interface weakness. In contrast, the X1 and X2 directions fail along intralayer and interlayer interfaces, respectively, due to tensile stresses perpendicular to loading (Figure 7). Additionally, while the directional alignment of fibers enhances the tensile strength and crack resistance of 3DPC [43], interfacial regions exhibit minimal fiber content. Consequently, the Y and Z directions benefit from increased fiber presence within the bulk matrix, resulting in superior mechanical performance relative to the X1/X2 directions. At low flowability, irregular intralayer interfaces in the X1 direction hinder crack propagation, making X1 stronger than X2. However, at higher flowability, gravity-compacted interlayer interfaces in the X2 direction demonstrate superior strength. Notably, while the Y and Z direction strengths approached cast specimen values (within 5% at 191 mm flowability), the X1 and X2 directions remained below 50% of cast strength even at maximum flowability. These observations corroborate Nerella et al.’s findings [7] that interface bonding strength governs 3DPC mechanical performance, with tensile stresses preferentially propagating cracks along weaker interfaces. The persistent strength deficit in the X1/X2 directions confirms the critical role of interfacial quality in 3DPC’s structural performance.

Figure 6c presents the 28-day interfacial splitting tensile strength of printed specimens (C: interlayer, T: intralayer) and cast specimens (M) at different flowabilities. The results reveal that printed specimens exhibited significantly lower strength than cast specimens due to splitting along these weaker interfaces. At low flowability, T showed slightly higher splitting tensile strength than C, attributed to interlocking effects between staggered filaments. As flowability increased, this interlocking diminished, causing C to regain higher strength than T. Both interfacial strengths stabilized at higher flowability but remained substantially lower than M. For instance, at 191 mm, the strengths of C and T were 32.5% and 37.7% lower than M, respectively. This persistent strength reduction demonstrates that even with improved flowability, interfacial weaknesses remain a critical limitation for 3DPC’s tensile performance compared to conventional cast concrete. The data further confirms that interface quality, rather than material properties, governs the splitting tensile behavior of 3DPC.

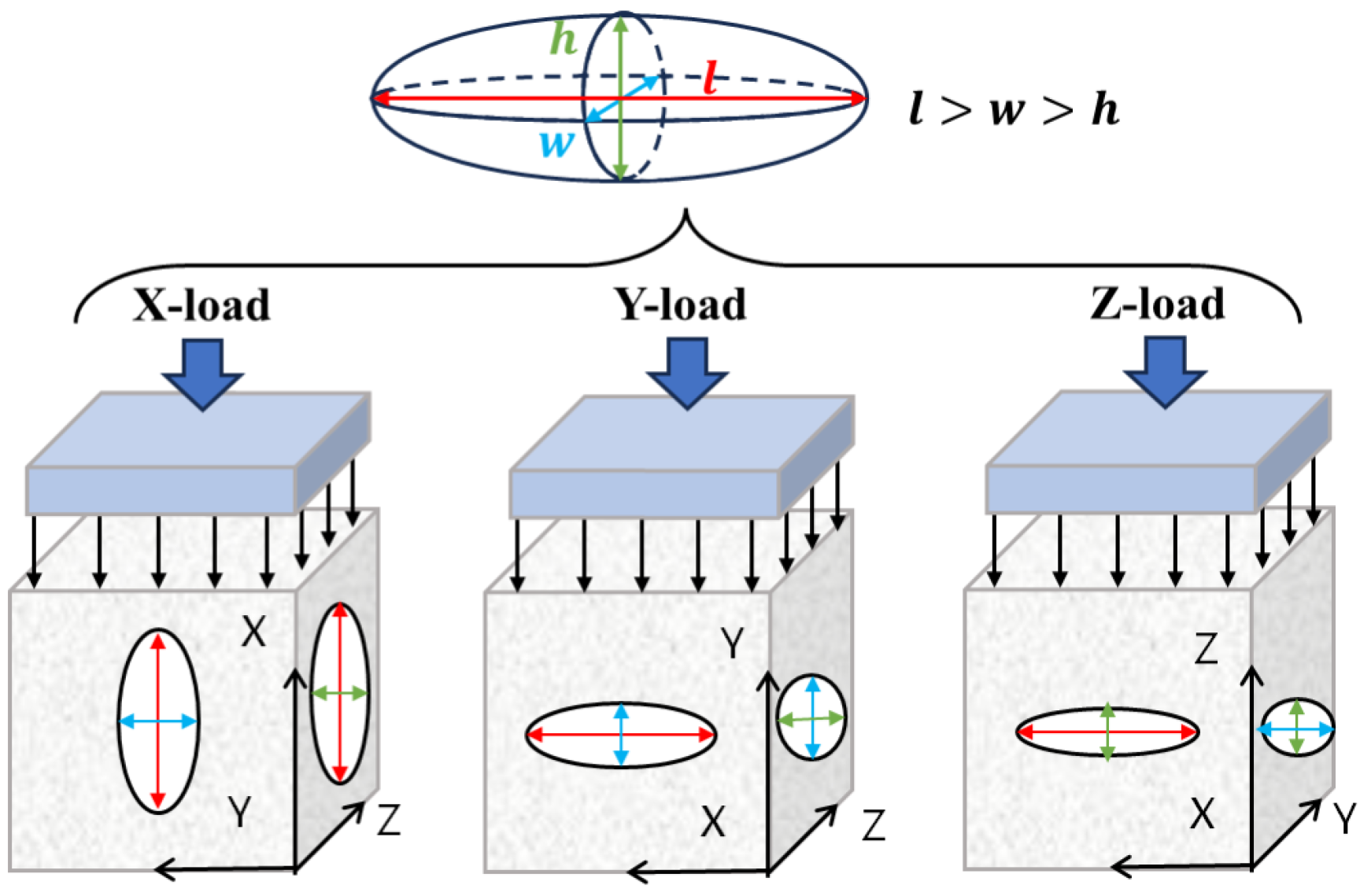
4. Anisotropy Analysis

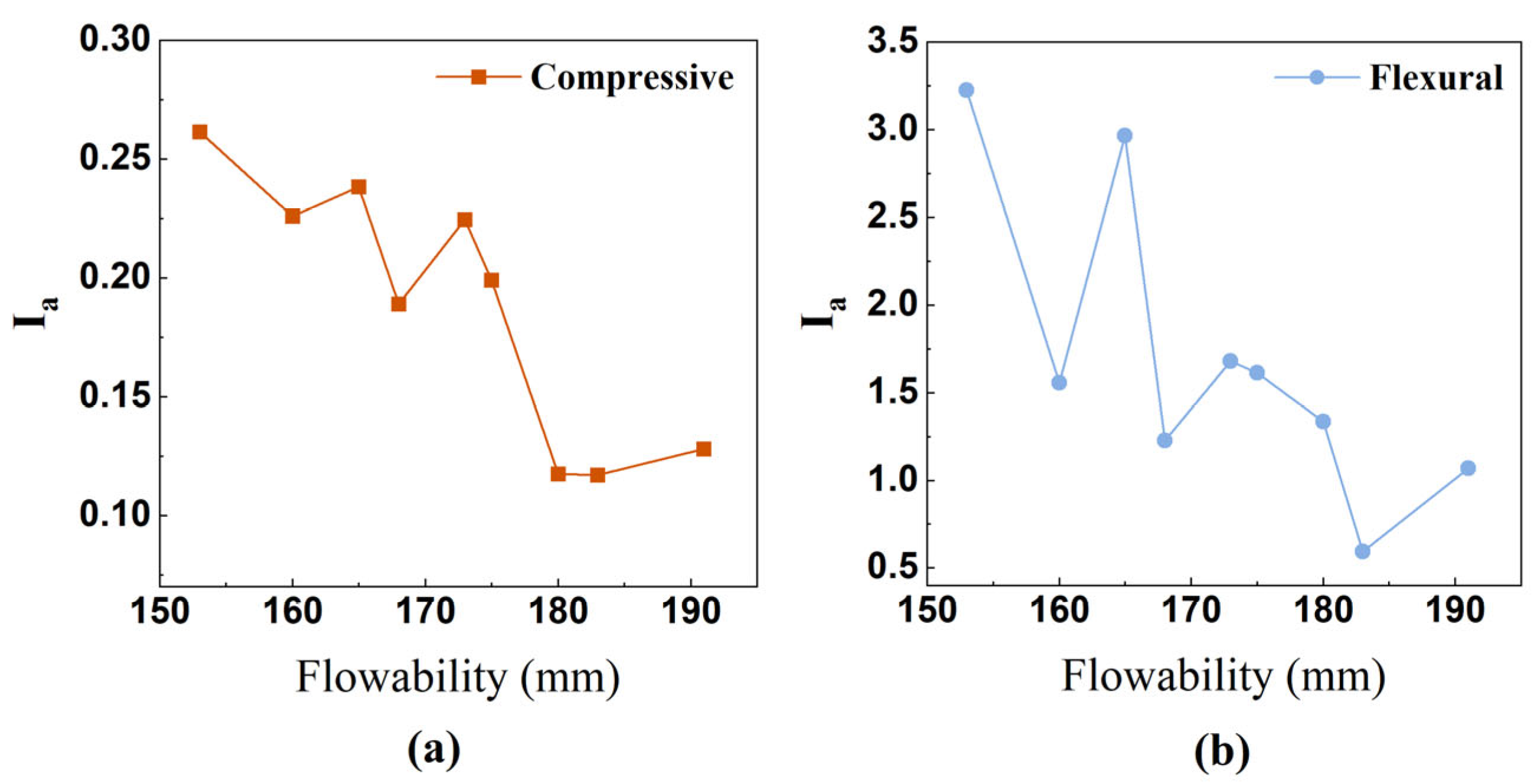
4.1. Evaluation of Anisotropic Mechanical Properties

The strength variations of 3DPC under different loading directions reflect the degree of mechanical anisotropy, quantified using the anisotropy coefficient ($I_{\mathrm{a}}$) [44]. For compressive strength, $I_{\mathrm{a}}$ is calculated via Equations (1) and (2), while flexural strength anisotropy is evaluated using Equations (3) and (4). Splitting tensile strength anisotropy is not discussed, as it involves only two loading directions (C and T).

$$I_{\mathrm{direction}}=\sqrt{{\left(f_{\mathrm{X}}-f_{\mathrm{direction}}\right)}^2+{\left(f_{\mathrm{Y}}-f_{\mathrm{direction}}\right)}^2+{\left(f_{\mathrm{Z}}-f_{\mathrm{direction}}\right)}^2}/f_{\mathrm{direction}}$$

(1)

$$I_{\mathrm{a}}=\left(I_{\mathrm{X}}+I_{\mathrm{Y}}+I_{\mathrm{Z}}\right)/3$$

(2)

$$I_{\mathrm{direction}}={\displaystyle \frac{\sqrt{{\left(f_{\mathrm{X}1}-f_{\mathrm{direction}}\right)}^2+{\left(f_{\mathrm{X}2}-f_{\mathrm{direction}}\right)}^2+{\left(f_{\mathrm{Y}}-f_{\mathrm{direction}}\right)}^2+{\left(f_{\mathrm{Z}}-f_{\mathrm{direction}}\right)}^2}}{f_{\mathrm{direction}}}}$$

(3)

$$I_a=\left(I_{\mathrm{X}1}+I_{\mathrm{X}2}+I_{\mathrm{Y}}+I_{\mathrm{Z}}\right)/4$$

(4)

Here, $I_{\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$ represents strength in a specific direction, and $f_{\mathrm{X}},f_{\mathrm{Y}},f_{\mathrm{Z}}$ (or $f_{\mathrm{X}1},f_{\mathrm{X}2},f_{\mathrm{Y}},f_{\mathrm{Z}}$) denote compressive/flexural strengths along respective axes.

The anisotropy coefficient $I_{\mathrm{a}}$ quantitatively reflects the directional strength disparity in 3DPC, where a higher $I_{\mathrm{a}}$ indicates greater anisotropy. As demonstrated in Figure 8, increasing the flowability from 153 mm to 191 mm substantially reduced anisotropy in both compressive and flexural strengths. Specifically, the compressive strength $I_{\mathrm{a}}$ decreased from 0.42 to 0.14 (66.7% reduction), while the flexural strength $I_{\mathrm{a}}$ declined from 3.22 to 1.07 (66.8% for reduction). This improvement suggests that enhanced flowability optimizes the material’s rheological properties and pore microstructure, effectively mitigating interfacial defects induced during printing and consequently improving structural uniformity and stability.

Notably, the flexural strength exhibited significantly higher anisotropy than compressive strength (3.5–10 times greater $I_{\mathrm{a}}$ values) at the same flowability. This difference arises because flexural loading generates tensile stresses concentrated at the interlayer and intralayer interfaces (X1/X2 directions), where insufficient pore filling and weak interfacial bonding readily initiate cracks, leading to substantial strength reduction and pronounced directional disparities. In contrast, compressive strength benefits from multiaxial stress constraints, resulting in lower sensitivity to interfacial defects.

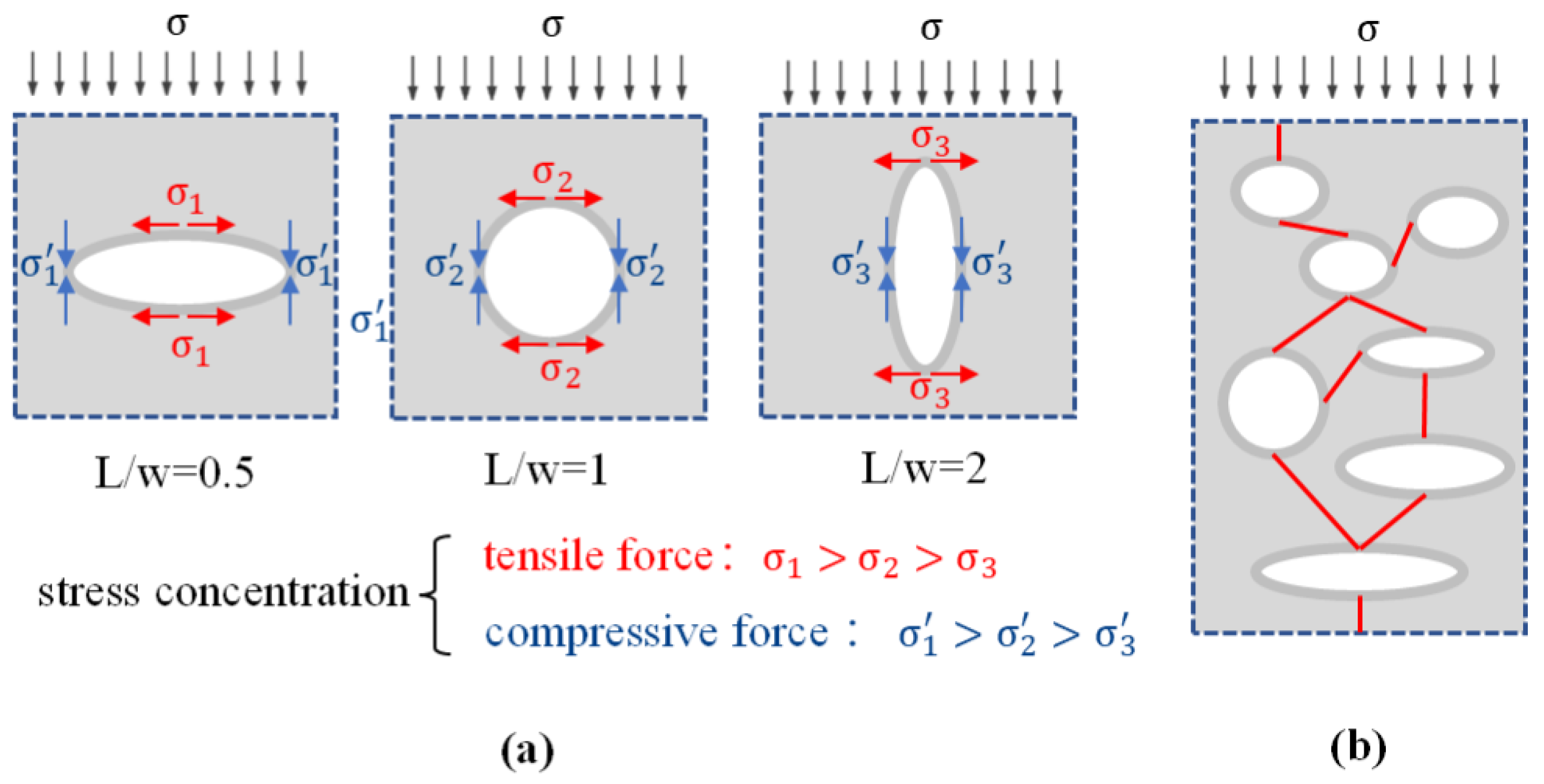
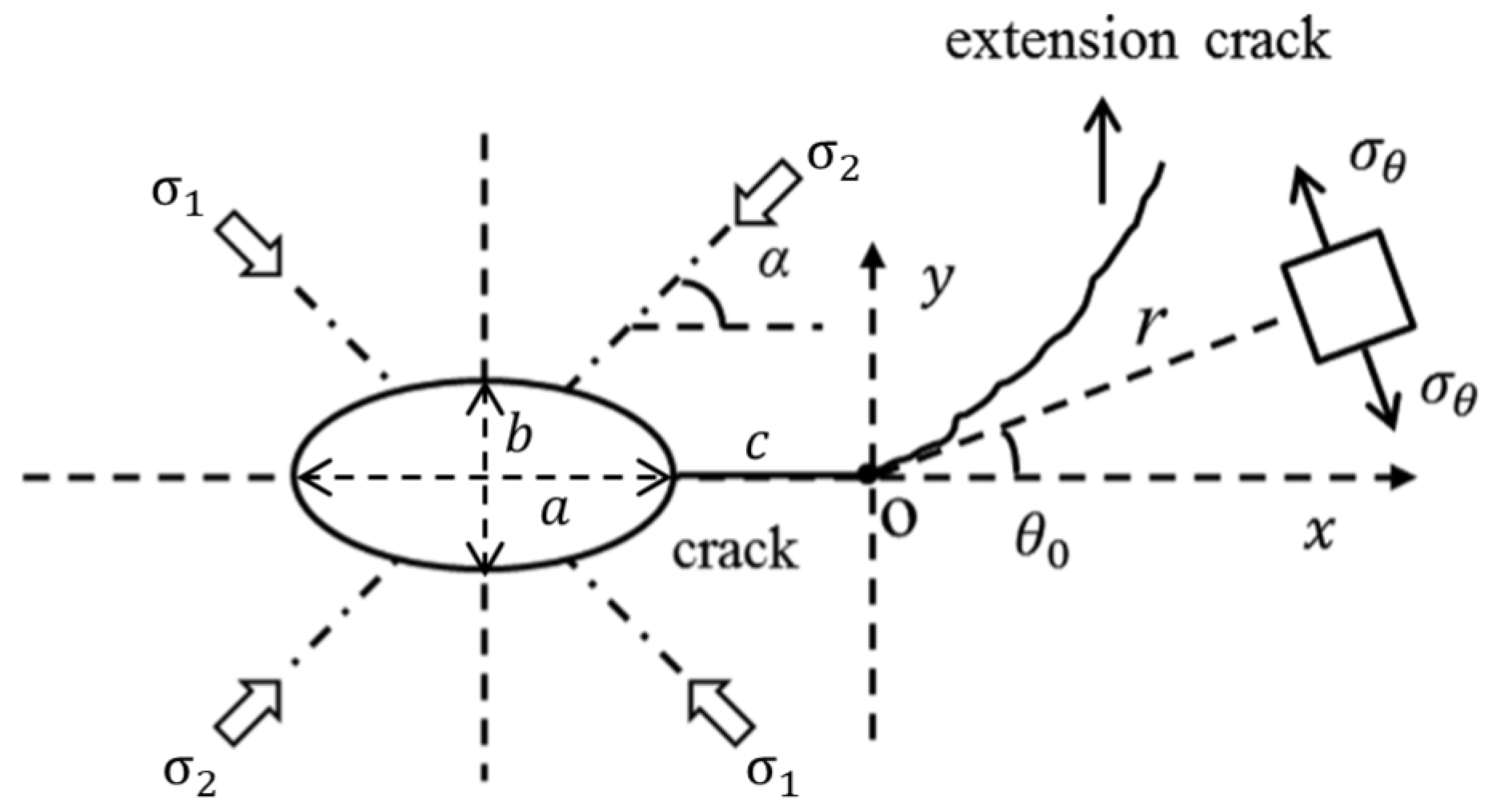
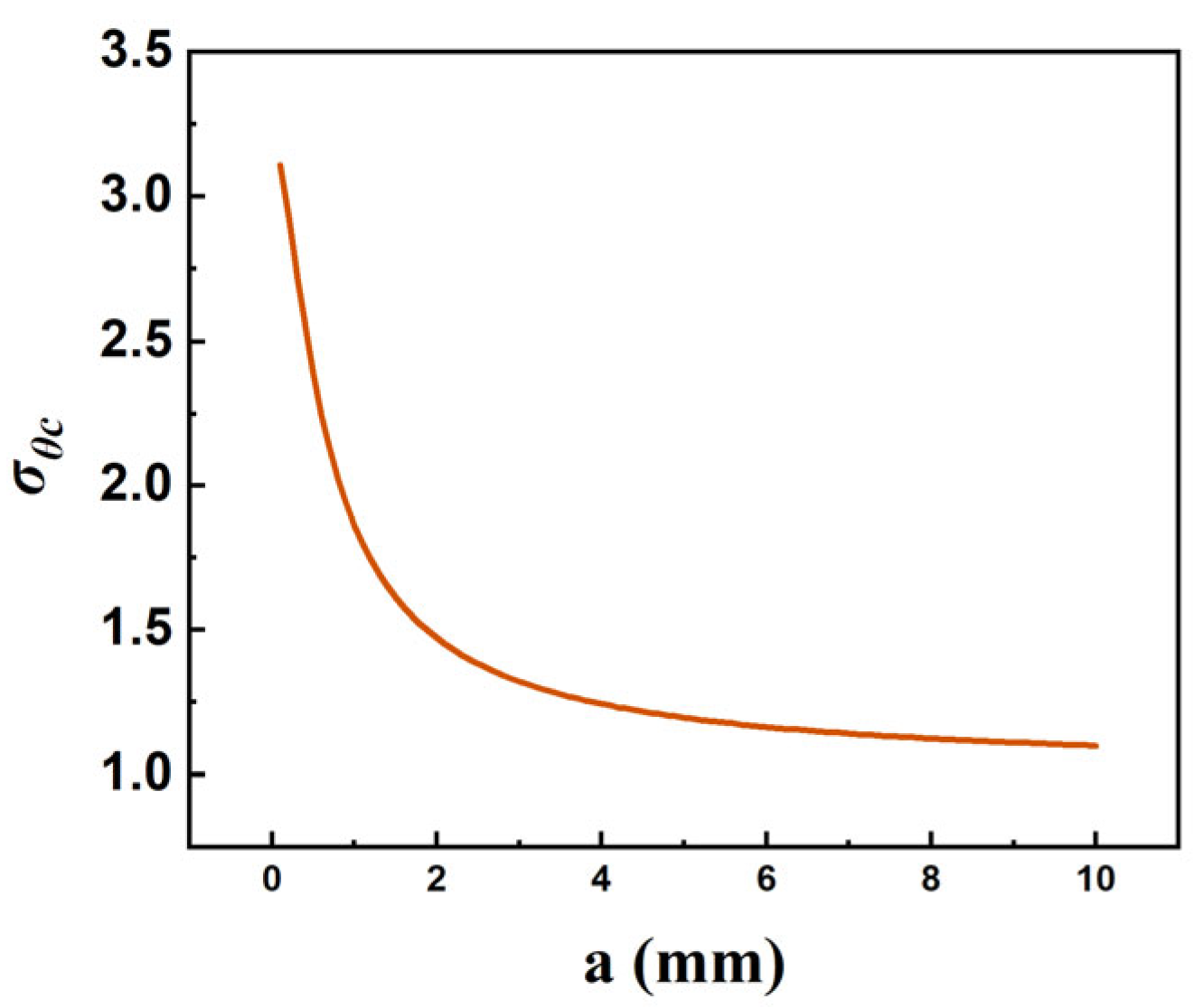
4.2. Fracture Theory of Ellipsoidal Pores Based on Stress Intensity Factor

Under external loading, the stress distribution at pore boundaries is significantly influenced by their geometric morphology [42]. According to Griffith’s microcrack theory [45], when the aspect ratio (L/w) of a pore along the loading direction is small, stress concentration preferentially occurs at the boundary, inducing crack initiation. As illustrated in Figure 9a, compressive stress concentration at the left and right tips of an elliptical pore may lead to local crushing, while tensile stress concentration at the upper and lower tips tends to initiate tensile cracking. Given that the tensile strength of concrete is substantially lower than its compressive strength, failure typically occurs via brittle tensile cracking.

Once stress concentration triggers crack formation at a pore, the stress field redistributes, altering the mechanical state of adjacent pores and promoting continuous crack propagation [21] (Figure 9b). Furthermore, such pore-induced microcrack evolution ultimately governs the macroscopic mechanical behavior of the material [46].

The stress intensity factor ($K$) serves as a fundamental parameter for evaluating material fracture. When $K$ reaches the material’s fracture toughness ($K_c$), the fracture initiates and propagates until complete specimen failure occurs. This mechanism is equally applicable for analyzing concrete fracture behavior [47]. For ellipsoidal pores in concrete, theoretical analytical models have been developed to calculate the stress intensity factor at crack tips under complex stress states [48], with the mechanical schematic shown in Figure 10. In the figure, $a$ represents the major axis of the elliptical pore, $b$ denotes the minor axis of the elliptical pore, and $c$ indicates the crack length at the tip of the elliptical pore. The far-field compressive stresses are designated as ${\sigma }_1$ and ${\sigma }_2$, while $\alpha$ represents the angle between ${\sigma }_1$ and the major axis. The crack initiation angle is ${\theta }_0$, $r$ is the initiation radius, and ${\sigma }_{\theta }$ signifies the tangential stress at the fracture point. For calculation purposes, compressive stresses are defined as positive and tensile stresses as negative.

The stress intensity factor is calculated using Equations (5) and (6):

$$K_{\mathrm{I}}=\sqrt{{\displaystyle \frac{\pi {(d+1)}^2(d^2-1){(a+b)}^2}{4d\left[(d^2-1)a+{(d+1)}^{2}b\right]}}}\left[-{\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}}+{\displaystyle \frac{{\sigma }_1-{\sigma }_2}{2}}\cos 2\alpha \right]$$

(5)

$$K_{\mathrm{II}}=\sqrt{{\displaystyle \frac{\pi (d^2+1)(d^2-1){(a+b)}^2}{4d\left[(d^2-1)a+(d^2+1)b\right]}}}\left[{\displaystyle \frac{{\sigma }_1-{\sigma }_2}{2}}\sin 2\alpha \right]$$

(6)

Here, $K_{\mathrm{I}}$ and $K_{\mathrm{II}}$ correspond to Mode I (opening) and Mode II (sliding) crack types, respectively, where $d={\displaystyle \frac{c+\mathrm{a}+\sqrt{{(c+a)}^2-a^2+b^2}}{a+b}}$.

The crack initiation angle is determined by Equation (7):

$${\theta }_0=\left\{\begin{array}{ll}0,\hfill & K_{\mathrm{II}}=0\hfill \\ 2\mathrm{arctg}\left[{\displaystyle \frac{1-\sqrt{1+8{\left(\frac{K_{\mathrm{II}}}{K_{\mathrm{I}}}\right)}^2}}{4\frac{K_{\mathrm{II}}}{K_{\mathrm{I}}}}}\right],\hfill & K_{\mathrm{II}}\ne 0\hfill \end{array}\right.$$

(7)

Based on this, the maximum tensile force at impending crack initiation can be calculated using Equation (8):

$${\sigma }_{\theta c}={\displaystyle \frac{1}{2\sqrt{2\pi r}}}\cos {\displaystyle \frac{{\theta }_0}{2}}\left[K_{\mathrm{I}}\left(1+\cos {\theta }_0\right)-3K_{\mathrm{II}}\sin {\theta }_0\right]$$

(8)

A fracture occurs when ${\sigma }_{\theta c}$ exceeds the concrete’s tensile strength ${\sigma }_t$. As the cracks propagate, microcracks induced by adjacent pores interconnect, ultimately leading to macroscopic failure of the specimen. Here, ${\sigma }_t$ represents an intrinsic material property that depends exclusively on the mix proportion and curing duration. For practical testing, ${\sigma }_t$ can be derived by referencing the tensile strength of cast-in-place concrete under equivalent flowability conditions. The magnitude of ${\sigma }_{\theta c}$ serves as a direct indicator of the concrete specimen’s mechanical performance. A higher ${\sigma }_{\theta c}$ value signifies that the material reaches its ultimate tensile strength under lower external loading, which macroscopically manifests as reduced material strength.

4.3. Mechanism of Compressive Strength Anisotropy Based on Maximum Critical Tangential Stress

This study systematically elucidates the intrinsic mechanism by which pore defects induce anisotropic compressive strength in 3DPC, based on variations in critical tangential stress (${\sigma }_{\theta c}$) across different loading directions. It should be noted that flexural strength and interfacial splitting tensile strength are primarily governed by interfacial bond strength and porosity, with their mechanisms being relatively well established and thoroughly discussed in Section 3.3, and thus will not be reiterated here.

Under vertical compressive stress (where ${\sigma }_1$ = 0 and α = 0°), for comparative purposes, we set ${\sigma }_2$ = 1 MPa and $r$ = 0.05 mm. Under these conditions, the expression for ${\sigma }_{\theta c}$ can be simplified to

$${\sigma }_{\theta c}=-{\displaystyle \frac{1}{2\sqrt{0.2\pi }}}\left(\sqrt{{\displaystyle \frac{\pi (d^2+1)(d^2-1){(a+b)}^2}{d\left[(d^2-1)a+(d^2+1)b\right]}}}\right)$$

(9)

In Figure 10, the stress convention follows compression-positive and tension-negative notation. Equation (9) yields ${\sigma }_{\theta c}$< 0, indicating tensile stress concentration that aligns with the concrete’s characteristic brittle tensile failure mode. To investigate pore geometry effects, we maintained a constant crack length ($c$ = 0.1 mm) and minor axis ($b$ = 1 mm) while systematically varying the major axis ($a$ = 0.1~10 mm), obtaining the ${\sigma }_{\theta c}$-$a$ relationship shown in Figure 11. The results demonstrate that the tensile ${\sigma }_{\theta c}$ decreases with increasing $a$, indicating that elliptical pores with more elongation along the load direction exhibit reduced the maximum tensile force at impending crack initiation. Consequently, such pore geometries require higher stress levels to reach the ultimate tensile strength and initiate crack formation, thereby enhancing the specimen’s resistance to failure.

Based on the theoretical analysis in Section 4.1, the aspect ratios of ellipsoidal pores vary significantly under different loading directions, as shown in Figure 12. Cross-sectional observations reveal distinct pore morphology characteristics across orientations: The Z direction exhibits the most flattened pores, followed by the Y direction, while the X direction shows minimal flattening. This geometric anisotropy directly governs the magnitude of critical tangential stress ${\sigma }_{\theta c}$. Under Z direction compression, ${\sigma }_{\theta c}$ reaches its maximum value, most readily attaining the concrete’s tensile strength and initiating failure. In contrast, X direction loading, where pore long axes align with the loading direction, demonstrates the weakest stress concentration and the lowest ${\sigma }_{\theta c}$, resulting in optimal load-bearing capacity. The Y direction displays intermediate ${\sigma }_{\theta c}$ values, with compressive strength lower than the X direction but higher than the Z direction.

In addition, failure modes further differ between orientations: Y direction failure primarily involves interlayer sliding, whereas Z direction failure is dominated by intralayer sliding [23]. Although both originate from interfacial weak zones formed during printing, the gravitational compaction of upper layers enhances interlayer bonding strength compared to intralayer interfaces. Consequently, the Y direction requires greater loading to induce interfacial sliding failure than the Z direction under compression.

Notably, increased flowability in fresh concrete significantly improves material homogeneity. As demonstrated in Section 3.1, higher flowability promotes transformation of elliptical pores toward more spherical geometries with reduced flattening, while simultaneously enhancing interfacial packing density and decreasing large pore content. These microstructural improvements progressively mitigate material anisotropy with increasing flowability.

5. Conclusions

This study systematically investigates the influence of flowability on the mechanical properties of 3DPC through combined experimental and theoretical analyses, with particular emphasis on evaluating and explaining anisotropic behavior under different flowabilities. The main findings are summarized as follows:

• All 3DPC specimens exhibited lower compressive, flexural, and splitting tensile strengths compared to cast concrete, along with significant anisotropy: compressive strength (X > Y > Z), flexural strength (Y ≈ Z > X2 > X1), and splitting tensile strength (C > T). With increasing flowability, reduced porosity and enhanced interfacial bonding improved the compressive strength in all directions and flexural strength in the Y/Z directions, approaching cast concrete levels. However, the flexural strength in the X1/X2 directions and interfacial splitting tensile strength remained substantially lower due to interfacial weaknesses.
• The anisotropy coefficient $I_{\mathrm{a}}$ decreased significantly with increasing flowability by 66.7% for compressive strength and 66.8% for flexural strength. Notably, flexural strength demonstrated 3.5–10 times greater anisotropy than compressive strength, reflecting its higher sensitivity to interfacial defects.
• The aspect ratio of ellipsoidal pores significantly affects the compressive performance of 3DPC, as quantified through Griffith’s fracture theory and stress intensity factor calculations. Flatter pores induce greater stress concentration and lower critical fracture stress, with X direction specimens exhibiting the most elongated pore geometries and consequently the highest compressive strength, followed by Y direction and then Z direction specimens. Notably, increased flowability promotes the transformation of elliptical pores toward more spherical morphologies with reduced flattening, thereby progressively mitigating the anisotropy in compressive performance.