Abstract
This study introduces a state transition simulated annealing algorithm that incorporates integrated destruction operators and backward learning strategies (DRSTASA) to address complex challenges in UAV path planning within multidimensional environments. UAV path planning is a critical optimization problem that requires smooth flight paths, obstacle avoidance, moderate angle changes, and minimized flight distance to conserve fuel and reduce travel time. Traditional algorithms often become trapped in local optima, preventing them from finding globally optimal solutions. DRSTASA improves global search capabilities by initializing the population with Latin hypercube sampling, combined with destruction operators and backward learning strategies. Testing on 23 benchmark functions demonstrates that the algorithm outperforms both traditional and advanced metaheuristic algorithms in solving single and multimodal problems. Furthermore, in eight engineering design optimization scenarios, DRSTASA exhibits superior performance compared to the STASA and SNS algorithms, highlighting the significant advantages of this method. DRSTASA is also successfully applied to UAV path planning, identifying optimal paths and proving the practical value of the algorithm.
1. Introduction
Unmanned aerial vehicles (UAVs) are widely used in various fields such as military operations, agriculture, disaster relief, environmental monitoring, and communications due to their low cost, high maneuverability, and adaptability [1,2,3]. However, path planning in complex and dynamic environments remains a significant challenge, as it must ensure obstacle avoidance, flight safety, and energy efficiency. Finding the optimal path has become a key issue in UAV applications [4].
Traditional path planning methods such as the A* algorithm [5,6], ant colony optimization (ACO) [7], and particle swarm optimization (PSO) [8] have been widely used but often struggle to balance real-time performance, global optimality, and obstacle avoidance. Therefore, researchers have worked to refine or integrate these methods with new approaches to improve their performance.
For instance, Jie Chen, Fang Ye, and Tao Jiang proposed a UAV trajectory planning strategy that leverages the rapid optimization capabilities of ant colony optimization (ACO), though it did not account for complex factors like flight angles [9]. Luji Guo, Chenbo Zhao, and Jiacheng Li optimized the cost function weights of the A* algorithm and introduced virtual target points in the artificial potential field (APF) method, improving both path smoothness and obstacle avoidance [10]. Hongbo Xiang, Xiaobo Liu, and their team combined enhanced particle swarm optimization (EPSO) with genetic algorithms, adaptively tuning the acceleration coefficients of EPSO based on fitness values, which enhanced global search [11]. Dongcheng Li, Wangping Yin, and W. Eric Wong applied Q-learning to dynamically adjust factors such as step size and cost function in the A* algorithm, creating a hybrid method that effectively balances global and local search [12]. Bo Li, Xiaogang Qi, and Baoguo Yu incorporated the Metropolis criterion from simulated annealing into ACO, reducing the likelihood of getting trapped in local optima. They also employed an inscribed circle smoothing method to optimize trajectories, enhancing both feasibility and effectiveness [13].
In recent years, the rapid development of artificial intelligence and intelligent optimization algorithms has led to the increasing application of advanced algorithms and deep learning methods in UAV path planning. Hui Li, Teng Long, and Guangtong Xu proposed a coupling degree-based heuristic priority planning method (CDH-PP), which enhances the efficiency of cooperative path planning for UAV swarms through coupling degree heuristics [14]. Ronglei Xie, Zhijun Meng, and Lifeng Wang addressed path planning challenges in complex dynamic environments using deep learning, introducing the RQ method and an adaptive sampling mechanism to improve obstacle avoidance capabilities [15]. Liguo Tan, Yaohua Zhang, and Jianwen Huo combined the rapidly-exploring random tree (RRT) algorithm with driver visual behavior to propose an RRT path planning method that simulates driver vision. They optimized the path using a greedy algorithm; however, while this method is effective in complex scenarios, it exhibits high computational complexity [16]. Xing Wang, Jeng-Shyang Pan, and Qingyong Yang introduced an improved mayfly algorithm (modMA), which optimizes UAV layout and reduces overall costs through exponentially decreasing inertia weights (EDIW), adaptive Cauchy mutations, and enhanced crossover operators [17]. Jingfan Tian, Yankai Wang, and Dongdong Yuan improved the global optimization capability of the elastic rope algorithm by enhancing the node update mechanism and introducing paths composed of m-dimensional nodes to increase its applicability [18].
Additionally, other studies have proposed innovative strategies for algorithm improvement. Xiaohui Cui, Yu Wang, and Shijie Yang effectively addressed two-point and multi-point path planning problems by employing a chaotic initialization method combined with genetic algorithms (GA) and simulated annealing (SA) [19]. Xiaobing Yu, Chenliang Li, and Jiafang Zhou introduced an adaptive selection mutation-constrained differential evolution algorithm, which shows promising application prospects in disaster scenarios [20]. Xiangyin Zhang, Shuang Xia, and Xiuzhi Li developed a quantum theory-improved firefly algorithm (QFOA), utilizing wave functions to replace random search, thereby enhancing population diversity and outperforming the traditional firefly algorithm (FQA) in terms of search capability, stability, and robustness [21]. The combination of simplified grey wolf optimization (SGWO) and the mutual symbiotic organism search (MSOS) algorithm has also demonstrated potential in UAV path planning [22]. To improve path planning efficiency and ensure the smoothness and safety of UAV operations, Yaqing Chen, Qizhou Yu, and Dan Han proposed a hybrid algorithm that integrates grey wolf optimization (GWO) with the artificial potential field method (APF), significantly enhancing path planning capabilities, particularly in scenarios with short distances and high safety requirements [23]. Despite the widespread application of intelligent algorithms and neural networks in UAV path planning, most algorithms remain limited to two-dimensional path planning, failing to adequately consider factors such as obstacle height and flight slope, while some methods exhibit high computational complexity.
The state transition simulated annealing algorithm (STASA), a hybrid intelligent optimization algorithm proposed by Han et al. [24]. It combines the strengths of the state transition algorithm (STA) [25] and simulated annealing (SA) [26], achieving significant results in various application areas, such as PM2.5 prediction [27] and the optimization of methane production conditions in coal-to-gas processes [28]. Compared to traditional algorithms such as genetic algorithm (GA) [29], particle swarm optimization (PSO) [30], and grey wolf optimizer (GWO) [31], STASA demonstrates greater efficiency and flexibility. STASA offers greater efficiency and flexibility. However, its performance declines when addressing complex, high-dimensional problems.
To address the shortcomings of the state transition simulated annealing algorithm (STASA), this paper introduces the state transition simulated annealing algorithm with destructive perturbation operators and reverse learning strategies (DRSTASA). This algorithm enhances population diversity using Latin hypercube sampling and incorporates destructive perturbation and reverse learning strategies to improve global search, speed up convergence, and avoid local optima. Experimental results show that DRSTASA outperforms other algorithms on 23 benchmark test functions and 8 engineering optimization problems. It has also been successfully applied to three-dimensional UAV path planning, demonstrating strong practical feasibility [32].
The rest of this paper is structured as follows: Section 2 covers the objective function for UAV path planning, Section 3 explains the original STASA algorithm, Section 4 describes the enhancements made by DRSTASA, and Section 5 presents a comparison with other algorithms and experimental results. Finally, a summary is provided.
2. UAV Three-Dimensional Path Planning
With the rapid advancement of unmanned aerial vehicle (UAV) technology, these systems have found widespread applications in military operations, agriculture, logistics, and environmental monitoring. To ensure that UAVs can safely and effectively execute tasks in complex environments, path planning has emerged as a critical issue. The objective of UAV path planning is to identify an optimal route in three-dimensional space that enables the UAV to travel from a starting point to a destination while avoiding obstacles and adhering to safety and energy consumption requirements. The UAV three-dimensional path planning problem aims to find an optimal trajectory that satisfies the following objectives:
- The Shortest Path: The total flight distance from the starting point to the endpoint should be minimized.
- Obstacle Avoidance: The flight path must navigate around all obstacles to ensure safety.
- Flight Altitude: The flight path must comply with the specified altitude restrictions.
- Path Smoothness: The trajectory should be as smooth as possible, avoiding sharp turns and steep inclines.
Therefore, this problem primarily considers four key factors. The specific cost function and objective function for UAV path planning are defined in the following subsection.
2.1. Path Optimality
Path planning must achieve optimality under specific criteria to ensure the efficient operation of UAVs. For applications such as aerial photography, surveying, and surface inspection, minimizing the path length is a primary objective.
The cost function for path length can be expressed as follows:
represents the list of n waypoints that the flight path needs to traverse, with the coordinates of each waypoint denoted as .
2.2. Safety and Feasibility Constraints
In path planning, ensuring the safe operation of the UAV is crucial. This involves avoiding obstacles in the environment while maintaining flight within a specified altitude range. Furthermore, the flight path should be as smooth as possible to prevent abrupt ascents and descents. Consequently, the remaining cost functions include threat cost, flight altitude cost, and path smoothness cost.
Threat Cost:
where
In the problem, it is assumed that the set K contains several cylindrical obstacles, each defined by a center coordinate and a radius . The diameter of the UAV is represented by D. The vertical distance from adjacent path nodes to the origin is denoted as , and S represents the danger zone of the obstacles. The experimental parameters were set as k = 6, = 80, = [200,100,150], and = [800;800;150]. The obstacle layout is illustrated in Figure 1.
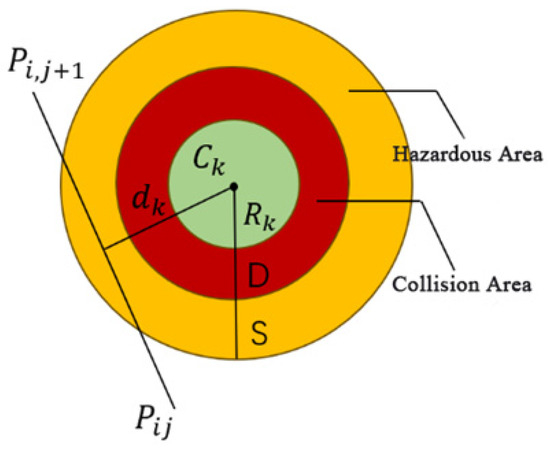
Figure 1.
Schematic diagram of obstacles.
In practice, there are usually specific altitude requirements for UAVs, which stipulate that the UAV must operate within a defined range between a minimum and maximum height. The cost associated with flight altitude can be calculated using the following formula:
The total altitude cost can be calculated using the following formula:
where represents the current altitude of the UAV, and and denote the maximum and minimum allowable flight altitudes, respectively. The experimental parameters were configured as = 200; = 100.
Smoothness Cost:
The smoothness cost evaluates the turning and ascent angles of the path. The turning angle and the ascent angle are calculated using the following formulas:
Turning Angle:
Ascent Angle:
The total smoothness cost can be calculated using the following formula:
and are the penalty coefficients for the horizontal turning angle and the vertical pitch angle, respectively. The experimental parameters were set as = 1; = 1.
3. STASA
The state transition simulated annealing algorithm (STASA) integrates discrete and continuous state transition operators derived from the state transition algorithm (STA), thereby improving its search capabilities. In both STA and STASA, the solution to an optimization problem is represented as a “state”, and the process of refining the solution is analogous to a “state transition”. This refinement occurs through local and global searches using update operators, followed by the application of a criterion to determine whether the solution has improved.
The general framework for generating candidate solutions using the state transition algorithm is as follows:
where represent the current and the new generation solution, respectively, is a function that relates the current state to historical states, and and are matrices for random transformations. denotes the fitness function for the problem being solved, and represents the fitness value of .
3.1. State Transition Operators
In continuous optimization problems, STASA employs four types of state transition operators: rotation, translation, scaling, and axis transformation. Each operator plays a distinct role in improving the search process.
- (a)
- Rotation Operator
- (b)
- Translation Operator
- (c)
- Scaling Operator
- (d)
- Axis Transformation Operator
3.2. Update Strategy of the STASA
STASA does not rely on a greedy update criterion. Instead, it uses the Metropolis criterion, similar to the simulated annealing algorithm, to refine solutions. The update process is as follows:
where η is a random number in the range [0, 1]. When the fitness value of the next-generation solution is less than that of the current solution, the new solution is accepted. When the next-generation solution is not better than the current solution, the simulated annealing temperature is calculated using formula: . If the temperature is greater than η, the new solution is accepted; otherwise, the current solution is retained.
4. DRSTASA
4.1. Population Initialization Based on Latin Hypercube Sampling
In intelligent algorithms, the initialization of the population plays a crucial role in determining the performance and convergence speed of the algorithm. A well-initialized population ensures diversity, which facilitates a more efficient exploration of the search space and accelerates convergence towards the global optimal solution. As a result, this improves the algorithm’s stability and efficiency. Traditional approaches, such as STA and STASA, typically rely on random initialization functions. However, this randomness can hinder the uniform distribution of solutions within the search space, ultimately reducing search efficiency.
To overcome this issue, the Latin hypercube sampling (LHS) method [33] is employed. LHS divides the multidimensional parameter space into non-overlapping intervals, randomly selecting samples from each interval to ensure uniform distribution and better coverage of the parameter space. The key steps of LHS involve determining the number of samples, dividing the parameter range for each dimension into NNN intervals, selecting values from each interval for every dimension, mapping these values to the desired distribution, and shuffling the order to maintain randomness.
Figure 2 illustrates a comparison between the population distributions generated using random initialization and Latin hypercube sampling (LHS) for two- and three-dimensional populations. The comparison demonstrates that unlike random initialization, LHS uniformly partitions each dimension and independently selects sample points from each partition, ensuring an even distribution of points throughout the sample space while maintaining uniqueness across all dimensions. This approach enhances initial population coverage, effectively mitigates the “curse of dimensionality” commonly encountered in high-dimensional spaces with conventional methods, and increases initial population diversity. As a result, it significantly improves the algorithm’s global exploration capability within the solution space.
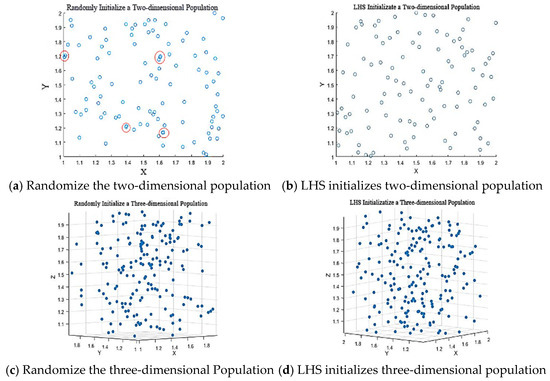
Figure 2.
Initialize population comparisons.
4.2. Disruption Operator
Inspired by the gravitational destruction phenomenon observed in astrophysics, the interference operator (DO) was first introduced in the gravitational search algorithm (GSA) [34,35]. Its main objective is to improve exploration and exploitation capabilities that will prevent premature convergence and maintain population diversity. Over time, DO has been widely used in heuristic algorithms, such as elite particle swarm optimization algorithms [36].
The DO simulates the disruption of smaller-mass particles as they approach a larger-mass object. Here, the current optimal solution is treated as the large-mass object, and the remaining solutions are considered smaller-mass particles. When specific conditions are met, disruptive perturbations are applied to these solutions. Formula (15) describes the activation of the DO, which occurs when the Euclidean distance between neighboring solutions exceeds a predefined threshold C. The distance between a candidate solution and the current optimal solution is used to determine the degree of disruption.
The algorithm activates the disruption operator to update the current solution only when the condition in Formula (15) is satisfied, where represents the Euclidean distance between neighboring candidate solutions i and j, and is the Euclidean distance between the particle and the current optimal solution. C is a preset threshold.
To improve the efficacy of the DO, the threshold C is dynamically adjusted throughout the algorithm’s iterations. A larger initial C value facilitates broad exploration early in the process, while a gradually decreasing C encourages convergence during the later stages. Formula (16) details this dynamic threshold adjustment.
is the manually defined initial threshold, typically set between 1 and 3. Iter represents the current iteration count, and T denotes the total number of iterations set for the algorithm. It is important to note that, aside from the current optimal solution, all other solutions will be evaluated according to Formula (16). Only the solutions that meet the criteria of this formula will activate the disruption operator, which is defined as follows:
Here, is a randomly distributed number, with its range defined based on the Euclidean distance between neighboring candidate solutions i and j. When , it indicates that the solution is far from the optimal solution, and the disruption operator explores a broader range. In other cases, when the distance is closer, the disruption operator conducts a more localized search around the current solution.
Finally, for solutions that meet the conditions, a disruptive perturbation is applied, and the solution is updated according to the following formula:
In Formula (18), represents the solution after applying the disruptive perturbation. The first part of the formula retains some information from the current solution, while the second part incorporates the influence of the disruption operator. The impact of the disruption operator gradually diminishes as the algorithm progresses, allowing for broader exploration of the search space in the early stages to avoid local optima, and accelerating convergence in the later stages.
In STASA, the disruption operator is executed after the application of the four update operators. This sequence allows the algorithm to conduct extensive exploration during the early stages and prevent falling into local optima in later stages, ultimately increasing the chances of finding the global optimal solution.
4.3. Reverse Learning Strategy
To enhance optimization performance and accelerate convergence, a dynamic reverse learning strategy is introduced. Reverse learning compares the current solution with its reverse point , selecting the better option to improve the algorithm’s search capability and exploration range [37]. Here, , and represent the upper and lower bounds of the variables, respectively. The formula for calculating the reverse point is as follows:
Reverse learning expands the search space of the algorithm, improving both convergence accuracy and speed. To enhance flexibility, a dynamic reverse learning strategy is employed, where the upper and lower bounds of the reverse point change with each iteration. The formula for calculating the dynamic reverse point is as follows:
In the equation, represents the position of the j-th solution in the i-th dimension during the t-th iteration.
and are the minimum and maximum values of the current population in the i-th dimension, respectively, and is a random number in the range [0, 1]. The decision to perform reverse learning is made by comparing with the control parameter , and the specific form is as follows:
where t represents the number of iterations, is the current solution, and is the corresponding reverse solution. Both and rand are random numbers in the range [0, 1], and is the population in the t+1th iteration. In the subsequent experiments, the control parameter is set to 0.5. The opposition-based learning strategy activates when meeting predefined stochastic conditions, utilizing opposition solutions to expand search space diversity and balance exploration versus exploitation capabilities. Through fitness comparison between original and opposition solutions, this approach accelerates convergence while enhancing solution quality. Moreover, the opposition mechanism assists in escaping premature stagnation, thereby markedly improving algorithm robustness and optimization efficiency.
4.4. Basic Process of DRSTASA
The overall structure and pseudocode for DRSTASA are presented in Figure 3 and Algorithm 1. The algorithm begins by initializing the population using the Latin hypercube sampling method and evaluating the initial solutions. The best population members and optimal objective values are selected. During each iteration, four transformation operators are applied first to update the population, followed by the Metropolis criterion from simulated annealing to determine whether to replace the current solution. After assessing the distance between current solutions, the disruption operator is applied as needed, and the reverse learning strategy is probabilistically executed to further refine the search process.
| Algorithm 1: The Proposed Algorithm DRSTASA |
| 1: Set the initial parameters 2: LHS generate the initial population u, Evaluate the fitness value: f, the current optimal solution: Best 3: while the set stop temperature value is not reached 4: Update the xk through four transformation operators by Equations (2)–(5) and obtain xk+1. 5: Calculate the fitness value of the current solution and new solution: f(xk), f(xx+1). 6: Update Best and fBest with Metropolis Criteria by Equation (6). 7: Calculate threshold C using Equation (16). 8: Judging by Equation (15), the condition is updated using Equation (17). 9: if rand > p Use Equation (21) to update. 10: T = α*T, k = k + 1 and return to step 4. |
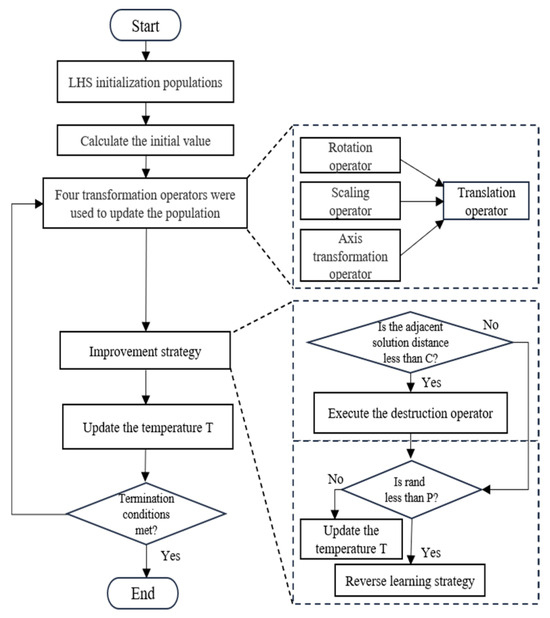
Figure 3.
DRSTASA algorithm flowchart.
5. Experimental Testing and Analysis
To evaluate the performance of DRSTASA, a total of 23 standard benchmark functions were selected for experimentation. The results were compared with those of nine other recent algorithms, including STA, STASA, AOA, SCA, AHA, FDA, AVOA, GWO, and the improved ASTASA, to analyze the testing performance of each algorithm. The experiments were conducted on a standard PC running Windows 10 64-bit, equipped with a 12th Gen Intel® Core™ i5-12490F processor operating at 3.00 GHz and 16 GB of RAM. The implementation was based on MATLAB 2020a. For all algorithms, the population size and search intensity were set to 50, with parameter configurations either consistent with the original publications or based on classical settings, as detailed in Table 1.

Table 1.
Compare algorithm parameter settings.
5.1. Benchmark Test Functions
In this section, 23 fundamental benchmark functions are used to evaluate DRSTASA and eight comparison algorithms. The test functions cover both unimodal and multimodal problems. Specifically, functions are unimodal, and are bimodal. The dimensionality of the functions is variable; for these tests, it is set to 30. Detailed definitions can be found in Table 2 and Table 3.

Table 2.
Unimodal benchmarking function definition.

Table 3.
Multimodal benchmarking function definition.
Each algorithm was independently executed 30 times, during which the optimal values, mean values, and standard deviations (std) were recorded. The optimal values of each algorithm were compared: if an algorithm outperformed the comparison algorithm, it was assigned a score of 1; if the results were equal, it received a score of 0; and if it underperformed, it was assigned a score of −1. In cases where the optimal values were identical, the mean values and standard deviations were sequentially compared. Ultimately, the total scores were tallied for each algorithm across all test functions, clearly demonstrating the performance of DRSTASA in relation to other algorithms.
The results of DRSTASA, compared to nine other algorithms, are presented in Table 4. Apart from its weaker performance on the multimodal functions F21, F22, and F23—where the mean values were suboptimal and stability was lacking—DRSTASA exhibited stable performance on the other test functions, with minimal differences between the minimum and mean values. In functions F6, F12, F13, F16, F21, F22, and F23, DRSTASA did not achieve the optimal value; however, it reached the theoretical optimal values in other test functions, demonstrating adequate solution accuracy.

Table 4.
Test results of nine algorithms on benchmark functions (Among them, the values in bold are the optimal values).
Overall, DRSTASA shows advantages over other algorithms in most tests, with results surpassing those of recent algorithms. Specifically, when compared to STASA and ASTASA, which scored 13 and 11 points, respectively, it is evident that DRSTASA achieved superior results in the majority of test cases. Although DRSTASA successfully escaped local optima in the multimodal test functions F21, F22, and F23, there remains a significant gap when compared to more robust algorithms such as AHA, FDA, and AVOA. While DRSTASA performed exceptionally well in unimodal tests, it slightly underperformed in multimodal tests relative to these stronger algorithms.
5.1.1. Convergence Analysis
Due to space limitations, Figure 4 illustrates the convergence behavior of various algorithms on selected test functions, highlighting the best results from each algorithm. The blue curve represents the convergence trajectory of the DRSTASA algorithm, with the horizontal axis indicating the number of iterations and the vertical axis representing the optimal objective function value. In the F3 and F4 tests, although DRSTASA achieved the theoretical optimal value, the convergence speed was slower compared to other algorithms, especially in unimodal test functions where the AVOA algorithm demonstrated the fastest convergence. In the F7 and F9 tests, DRSTASA also reached the minimum objective function value; however, significant oscillations were observed during the early iterations. This suggests that the algorithm likely employed techniques such as simulated annealing and perturbation to escape local optima and search for the global optimum. In the F12 and F13 tests, while DRSTASA did not surpass the FDA algorithm in finding the optimal value, it still exhibited a faster convergence speed compared to the other algorithms.
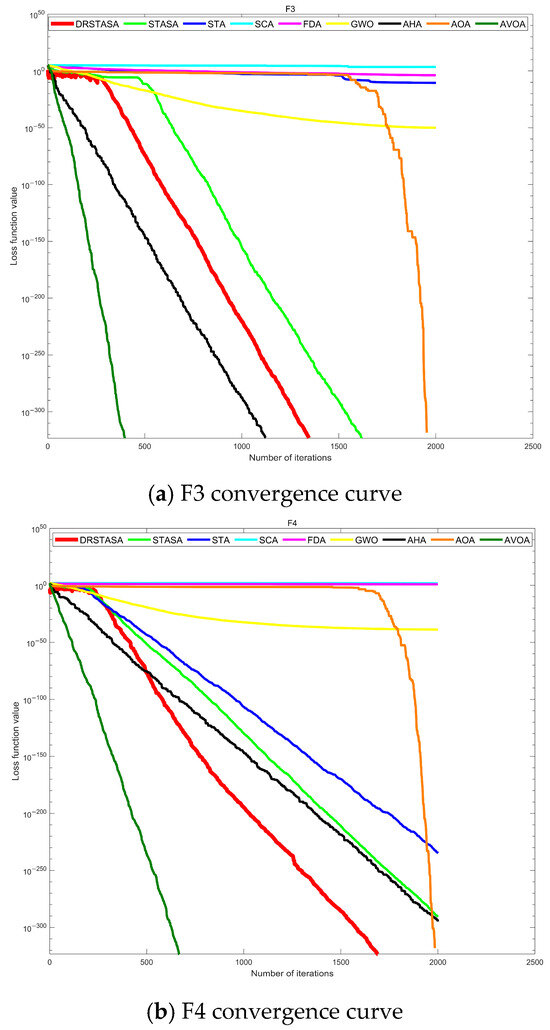
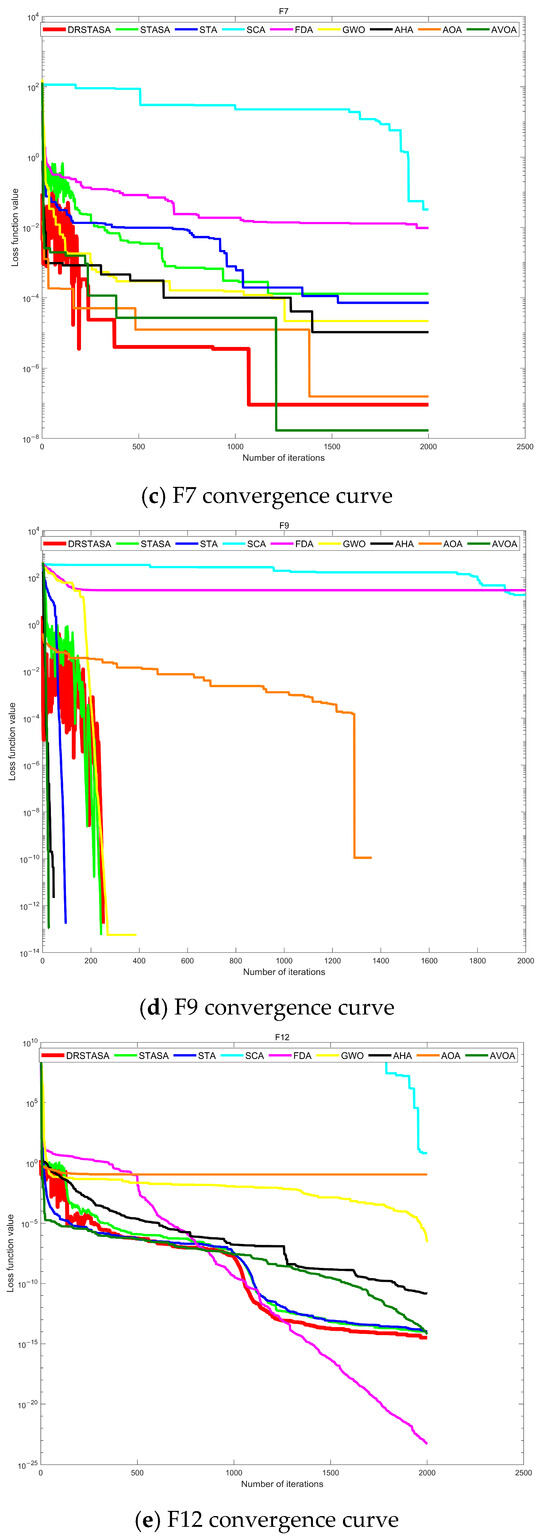
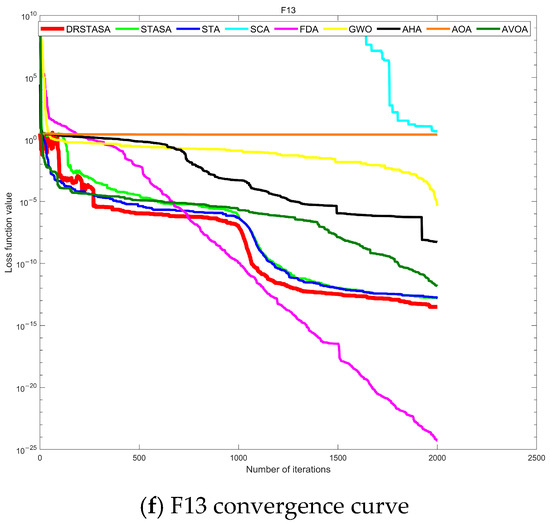
Figure 4.
Convergence curves for each algorithm.
5.1.2. Time Complexity Analysis
Time complexity reflects the efficiency of an algorithm, and as the problem size increases, it directly influences both time and resource costs. The time complexity of the proposed algorithm is primarily determined by the population size, the number of iterations, the dimensionality of the problem, and the time required to update the operators. Let N represent the population size, T denote the number of iterations, and D signify the problem dimensionality. Ignoring the time complexity of the operators, the overall time complexity of the algorithm is as follows:
In a single iteration, let the time complexity of evaluating the objective function for a single solution be , and the time complexity of updating a solution using the four operators be . Without incorporating any improvement strategies, the time complexity of the algorithm is as follows:
When introducing destruction operators and opposition-based learning strategies, let the time complexities of the destruction operator and opposition-based learning be denoted as and , respectively. Consequently, the time complexity of the algorithm incorporating these improvements becomes the following:
From the analysis, it can be concluded that the time complexity of DRSTASA does not increase by an order of magnitude compared to the original STASA. Additionally, the destruction operator and opposition-based learning strategies enhance the efficiency of the algorithm, resulting in faster convergence.
Figure 5 shows the average runtime of nine algorithms across 23 test functions. It is observed that the SCA, AOA, and AHA algorithms have the shortest runtimes, but they exhibit slightly lower accuracy compared to the others. AVOA and GWO fall into the second tier, characterized by higher time costs but with improved accuracy. STA, STASA, and DRSTASA are in the third tier, where DRSTASA has a slightly longer runtime than STASA but achieves significantly higher accuracy, making the additional time acceptable. The FDA requires the longest runtime but offers greater stability, albeit at a considerable time.
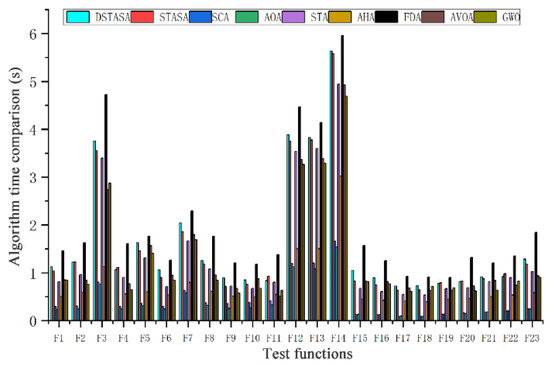
Figure 5.
Algorithmic average time.
To evaluate the effectiveness and stability of DRSTASA, eight engineering design optimization problems were selected for testing. The DRSTASA, STASA, and social network search (SNS) algorithms were employed to solve each problem, with 30 independent runs and 2000 iterations per run. The performance of each algorithm was assessed by comparing the optimal values, mean values, and standard deviations. Table 5 provides details of the eight engineering problems, while Table 6 presents the comprehensive results of each algorithm.

Table 5.
Eight classic engineering design problems.

Table 6.
Comparison of the three algorithms.
From Table 6, it is clear that the performance of DRSTASA in the string design problem is not as strong as that of the other two algorithms; however, the algorithm excels in the remaining engineering challenges. In the cantilever beam, tubular column, and welded beam design problems, although DRSTASA achieves optimal values, the average performance and standard deviation still show a gap compared to the other algorithms, suggesting that further improvements in stability are needed. The comparison results indicate that DRSTASA demonstrates significant improvements over STASA in various engineering problems and surpasses the SNS algorithm, highlighting the potential of this approach for solving real-world engineering challenges.
5.2. Experimental Results
By considering path optimality, safety, and feasibility constraints, specific weights are assigned to each cost function to determine the overall objective function value for the problem.
The variables represent the weight coefficients, while to denote the values of the objective function corresponding to the aforementioned constraints. In the experiment, the parameters were configured as = 5, = 1, = 1, and = 5, while the remaining parameters are given in Section 2.
In this study, the DRSTASA, STASA, SNS, and PSO algorithms were each executed 30 times within the hardware system environment previously described, using a population size of 500 and a maximum of 2000 iterations. Table 7 presents the optimal, worst, and average fitness values obtained from these 30 runs. Figure 6 shows the three-dimensional view, top view, and side view of the optimal path planning results achieved by the algorithms, while Figure 7 illustrates the fitness iteration curves.

Table 7.
Algorithm running results.
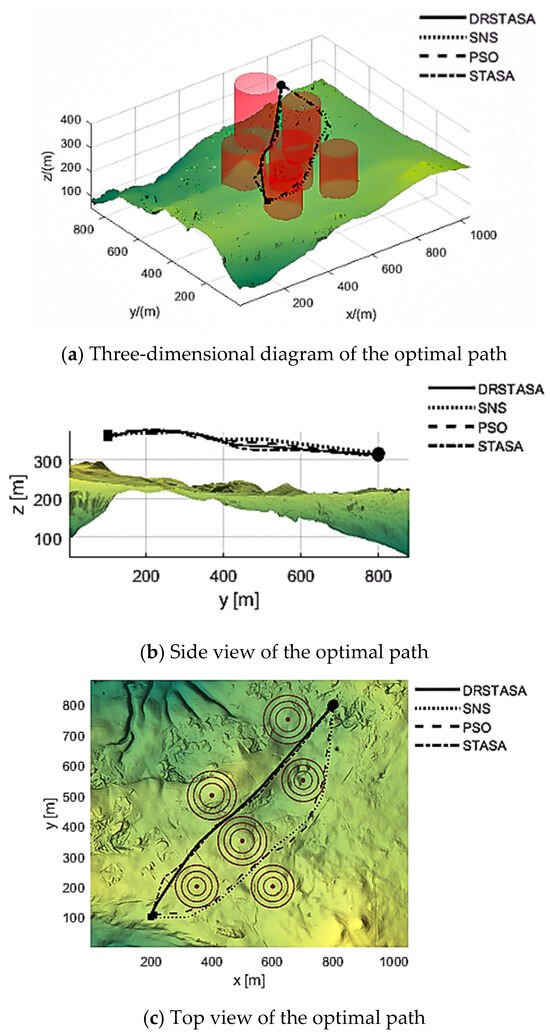
Figure 6.
Optimal path planning diagram.
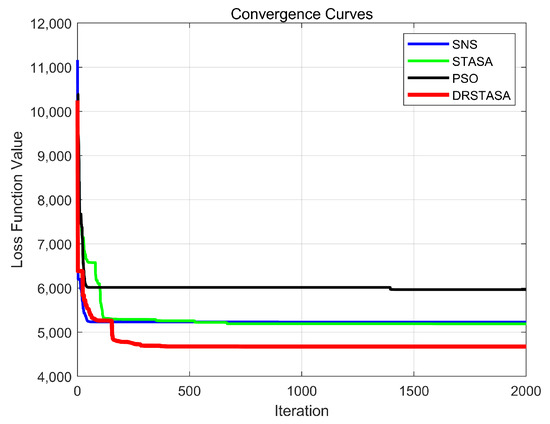
Figure 7.
Fitness iteration curve.
From Table 7, it is clear that this algorithm demonstrates relatively high stability across multiple runs, with both the optimal and worst fitness values being lower than those achieved by other algorithms. This suggests a strong capability for escaping local optima. Figure 5 shows that the optimal path generated by the algorithm successfully avoids obstacles, ensuring a smooth transition from the starting point to the destination. Compared to the other three algorithms, it identifies a safer and faster flight route. Figure 6 illustrates the rapid convergence of the algorithm during iterations, allowing it to find the optimal solution efficiently.
6. Summary
This paper presents an enhancement to the STASA algorithm by introducing a state transition simulated annealing algorithm (DRSTASA) that incorporates the use of destruction perturbation operators and opposition-based learning strategies. During the initialization phase, the super-Latin hypercube sampling method is employed to ensure a more uniform distribution of initial solutions. Subsequently, the integration of destruction operators and opposition-based learning strategies helps to accelerate the convergence process and improve the algorithm’s capacity for escaping local optima. The effectiveness of these enhancements is validated through comparisons with eight other algorithms across 23 standard test functions and eight classical engineering design problems.
DRSTASA is further applied to the UAV path planning problem, demonstrating greater stability in the solutions compared to three other algorithms. The paths produced by DRSTASA are more feasible, safer, and more efficient, thus showcasing the practical value of the algorithm. However, the comparative results indicate that there is room for improvement in terms of reducing time costs for complex problems and enhancing stability in multimodal scenarios. Future research will focus on increasing the convergence speed of the algorithm and reducing computational time.
Author Contributions
Conceptualization, J.L. and X.H.; methodology, J.L.; software, J.L.; validation, F.L., J.W. and W.Z.; formal analysis, J.L.; investigation, F.L.; resources, J.W.; data curation, W.Z.; writing—original draft preparation, J.L.; writing—review and editing, X.H.; visualization, F.L.; supervision, J.W.; project administration, W.Z.; funding acquisition, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China Funding Project grant number (62176176).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author, Xiaoxia Han, upon reasonable request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Fang, Z.; Savkin, A.V. Strategies for Optimized UAV Surveillance in Various Tasks and Scenarios: A Review. Drones 2024, 8, 193. [Google Scholar] [CrossRef]
- Torrero, L.; Seoli, L.; Molino, A.; Giordan, D.; Manconi, A.; Allasia, P.; Baldo, M. The Use of Micro-UAV to Monitor Active Landslide Scenarios. In Engineering Geology for Society and Territory—Volume 5; Lollino, G., Manconi, A., Guzzetti, F., Culshaw, M., Bobrowsky, P., Luino, F., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Yan, C.; Fu, L.; Zhang, J.; Wang, J. A Comprehensive Survey on UAV Communication Channel Modeling. IEEE Access 2019, 7, 107769–107792. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Korf, R.E. Depth-First Iterative-Deepening: An Optimal Admissible Tree Search. Artif. Intell. 1985, 27, 97–109. [Google Scholar] [CrossRef]
- Cen, Y.; Song, C.; Xie, N.; Wang, L. Path planning method for mobile robot based on ant colony optimization algorithm. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 298–301. [Google Scholar] [CrossRef]
- Qin, Y.-Q.; Sun, D.-B.; Li, N.; Cen, Y.-G. Path planning for mobile robot using the particle swarm optimization with mutation operator. In Proceedings of the 2004 International Conference on Machine Learning and Cybernetics (IEEECat. No. 04EX826), Shanghai, China, 26–29 August 2004; Volume 4, pp. 2473–2478. [Google Scholar] [CrossRef]
- Chen, J.; Ye, F.; Jiang, T. Path planning under obstacle-avoidance constraints based on ant colony optimization algorithm. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; pp. 1434–1438. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, C.; Li, J.; Yan, Q.; Li, W.; Chen, P. UAV path planning based on improved A * and artificial potential field algorithm. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 5471–5476. [Google Scholar] [CrossRef]
- Xiang, H.; Liu, X.; Song, X.; Zhou, W. UAV Path Planning Based on Enhanced PSO-GA. In Artificial Intelligence; Fang, L., Pei, J., Zhai, G., Wang, R., Eds.; CICAI 2023; Lecture Notes in Computer Science; Springer: Singapore, 2024; Volume 14474. [Google Scholar] [CrossRef]
- Li, D.; Yin, W.; Wong, W.E.; Jian, M.; Chau, M. Quality-Oriented Hybrid Path Planning Based on A* and Q-Learning for Unmanned Aerial Vehicle. IEEE Access 2022, 10, 7664–7674. [Google Scholar] [CrossRef]
- Li, B.; Qi, X.; Yu, B.; Liu, L. Trajectory Planning for UAV Based on Improved ACO Algorithm. IEEE Access 2020, 8, 2995–3006. [Google Scholar] [CrossRef]
- Li, H.; Long, T.; Xu, G.; Wang, Y. Coupling-Degree-Based Heuristic Prioritized Planning Method for UAV Swarm Path Generation. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 3636–3641. [Google Scholar] [CrossRef]
- Xie, R.; Meng, Z.; Wang, L.; Li, H.; Wang, K.; Wu, Z. Unmanned Aerial Vehicle Path Planning Algorithm Based on Deep Reinforcement Learning in Large-Scale and Dynamic Environments. IEEE Access 2021, 9, 24884–24900. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, Y.; Huo, J.; Song, S. UAV Path Planning Simulating Driver’s Visual Behavior with RRT algorithm. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 219–223. [Google Scholar] [CrossRef]
- Wang, X.; Pan, J.-S.; Yang, Q.; Kong, L.; Snášel, V.; Chu, S.-C. Modified Mayfly Algorithm for UAV Path Planning. Drones 2022, 6, 134. [Google Scholar] [CrossRef]
- Tian, J.; Wang, Y.; Yuan, D. An Unmanned Aerial Vehicle Path Planning Method Based on the Elastic Rope Algorithm. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 137–141. [Google Scholar] [CrossRef]
- Cui, X.; Wang, Y.; Yang, S.; Liu, H.; Mou, C. UAV path planning method for data collection of fixed-point equipment in complex forest environment. Front. Neurorobot. 2022, 16, 1105177. [Google Scholar] [CrossRef]
- Yu, X.; Li, C.; Zhou, J. A constrained differential evolution algorithm to solve UAV path planning in disaster scenarios. Knowl.-Based Syst. 2020, 204, 106209. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, S.; Li, X. Quantum Behavior-Based Enhanced Fruit Fly Optimization Algorithm with Application to UAV Path Planning. Int. J. Comput. Intell. Syst. 2020, 13, 1315–1331. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhang, J.; Zhong, M. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning. Knowl.-Based Syst. 2020, 194, 105530. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Q.; Han, D.; Jiang, H. UAV path planning: Integration of grey wolf algorithm and artificial potential field. Concurr. Comput. Pract. Exp. 2024, 36, e8120. [Google Scholar] [CrossRef]
- Han, X.; Dong, Y.; Yue, L.; Xu, Q. State Transition Simulated Annealing Algorithm for Discrete-Continuous Optimization Problems. IEEE Access 2019, 7, 44391–44403. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, C.; Gui, W. State Transition Algorithm. J. Ind. Manag. Optim. 2012, 8, 1039–1056. [Google Scholar] [CrossRef]
- Aarts, E.H.L. Simulated Annealing: Theory and Applications; Springer Nature: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Chu, J.; Dong, Y.; Han, X.; Xie, J.; Xu, X.; Xie, G. Short-term prediction of urban PM2. 5 based on a hybrid modified variational mode decomposition and support vector regression model. Environ. Sci. Pollut. Res. 2021, 28, 56–72. [Google Scholar] [CrossRef]
- Shen, Y.; Dong, Y.; Han, X.; Wu, J.; Xue, K.; Jin, M.; Xie, G.; Xu, X. Prediction model for methanation reaction conditions based on a state transition simulated annealing algorithm optimized extreme learning machine. Int. J. Hydrog. Energy 2023, 48, 24560–24573. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intel. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61, ISSN 0965-9978. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Dige, N.; Diwekar, U. Efficient sampling algorithm for large-scale optimization under uncertainty problems. Comput. Chem. Eng. 2018, 115, 431–454. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Sarafrazi, S.; Nezamabadi-pour, H.; Saryazdi, S. Disruption: A new operator in gravitational search algorithm. Sci. Iran. 2011, 18, 539–548. [Google Scholar] [CrossRef]
- Liu, H.; Ding, G.; Wang, B. Bare-bones particle swarm optimization with disruption operator. Appl. Math. Comput. 2014, 238, 106–122. [Google Scholar] [CrossRef]
- Shekhawat, S.; Saxena, A. Development and applications of an intelligent crow search algorithm based on opposition based learning. ISA Trans. 2020, 99, 210–230. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. A hybrid self-adaptive sine cosine algorithm with opposition based learning. Expert Syst. Appl. 2019, 119, 210–230. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).