Abstract
The rapid advancement of modern megapolises has led to a dearth of surface space, and, in response, engineers have begun to trial substitutes below ground level. Shafts are generally used to provide temporary access and permanent work to the subsurface for tunnelling, as well as for lifts or ventilation purposes. In urban areas, one important design issue is the prediction of the excavation-induced displacements by open caisson shaft construction. Settlements and ground movements associated with open caisson shafts are influenced by the choice of construction method, soil composition, and excavation geometry. Compared with other geotechnical construction events, for instance, tunnelling, the literature relating to the ground deformations induced from open caisson shafts are comparatively limited. This review offers an evaluation of several case studies that utilize experimental and computational modeling techniques to provide clearer insights into earth pressure distribution and induced surface and subsurface soil displacements, as well as the associated ground deformations during open caisson shaft construction. The modeling test results are compared to the state of the practice ground deformation prediction theories and measured results from field monitoring data. Findings indicate that the lateral earth pressure distribution aligns closely with the theoretical predictions based on Terzaghi’s and Berezantzev’s models, and lateral earth pressure diminishes gradually until the onset of active wall displacement. Current modeling techniques generally fail to properly represent in situ stress states and large-scale complexities, emphasizing the need for hybrid approaches that combine physical and numerical methodologies. In future studies, modern approaches, including artificial intelligence (AI) monitoring (e.g., PINNs, ACPP), multi-field coupling models (e.g., THMC), and transparent soil testing, hold profound potential for real-time prediction, optimization, and visualization of soil deformation. Numerical–physical coupling tests will integrate theory and practice. Improving prediction reliability in complicated soil conditions such as composite and heterogenous strata using different modeling techniques is still unclear, and further investigation is therefore needed.
1. Introduction
In subsurface excavations in urban areas, shafts are currently gaining renewed significance as the growing demand for an upgraded transportation infrastructure and environmental pressures continue to increase. For the traditional retaining structure for deep excavation in soft soil distribution area, confined water induces serious problems. During the dewatering process, serious risks and emergency measures can result in uncertainty in construction; this process can also face serious environmental influences. To solve these problems, press-in open caisson modeling and continuous combinations to form large-scale deep excavation methods have been proposed and promoted in the Shanghai Subway of China. The development of potential continuous combined open caisson requires systematic modeling methods to simulate and understand the working conditions under extreme conditions. However, there is a distinct gap in the literature regarding large-diameter open caisson shafts. In the existing literature, there seems to be a scarcity of well-documented case studies examining the performance of open caissons. This scarcity was not unexpected while considering the difficulties and costs associated with monitoring construction sites. Potential issues like sinking difficulties, excessive inclination, or instability of the cutting surface are expected to occur during the construction of a deep open caisson [1,2,3].
In urban areas, shafts are generally built by caisson sinking or underpinning. Allenby and Kilburn [4] described underpinning as a construction technique which involves incremental excavations and the installations of a pre-cast concrete segmental ring, which includes watertight gaskets. This process occurs when the grouting behind the annulus is completed, as shown in Figure 1a. In this traditional open caisson construction technique, during excavation, a concrete surface collar is cast to support the shaft. Advancement of the excavation is carried out in stages, with structural floors and stepping or benching installed as the caisson descends. Grout is used to prevent seepage and stabilize the base, while the permanent roof slab and surface treatments ensure the structural integrity of the completed shaft. This method is well-suited for shallow shafts and soil conditions that remain stable without extensive lateral support.
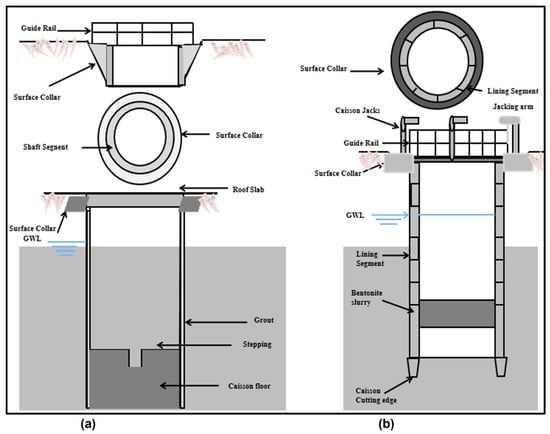
Figure 1.
(a,b) Construction technique of underpinning and press in caisson sinking modified after [4].
Figure 1b shows another approach using the press-in method, which is particularly advantageous in soft or unstable soil conditions. A surface collar and jacking arms are utilized to press the caisson segments into the ground, reducing reliance on traditional excavation methods. Bentonite slurry fills the annulus, providing lateral support and minimizing the risk of soil collapse during the sinking process. The base of the caisson is stabilized using a concrete tremie plug and single-size stone. This method enhances construction safety and precision in densely populated urban areas where minimal ground disturbance is essential. Essentially, caisson-sinking as described by [5], involving progressively lowering the shaft structure either by self-weight or with the assistance of jacks in a controlled manner from the surface level, as shown in Figure 1b. A cutting edge is connected to the first caisson ring to aid the sinking operation in this technique. Regardless of the method employed, any underground construction project induces ground movements that can damage existing structures. Current practices in geotechnical engineering strive to minimize these movements, emphasizing the significance of accurate assessments for successful project outcomes.
For the Heathrow express trial tunnel constructed in London clay, Arthur et al. [6] investigated the ground movements during shaft construction. The study validated ground movement prediction methods using monitored data. Additionally, novel methods for the construction of caissons with a large diameter in boulder clay have been explored [7]. Later, the study focused on predictive modeling of soil deformation behind the open caisson caused by pipe jacking execution, as carried out by [8], emphasizing factors like stratum loss rate and overburden load.
Scholars have extensively investigated the sinking process of open caissons through various methods, including theoretical analysis, laboratory tests, numerical analysis, and field monitoring data. Their aim is to understand the mechanical responses and deformation properties of the surrounding soil caused by the installation of these caissons [2,9,10,11,12].
Many case studies of caissons are presented by [13,14], used for bridge piers in Bangladesh, of which the largest were over 100 m deep. Significant ground subsidence became evident during the construction process, primarily attributed to the upward heave of soil inside the caisson, leading to potential damage to nearby infrastructure. Through four construction case studies, Allenby et al. [5] documented the process of sinking both dry and wet open caissons. They highlighted the critical role of control measures in ensuring caisson verticality and structural integrity during the construction process.
Large-diameter open caisson shafts serve as essential portals for underground construction sites. They are commonly used for launching and receiving zones for tunnel boring machines, as well as providing subsurface storage and attenuation. Caissons are a type of support before excavation (SBE) construction, which involves the controlled sinking of the caisson walls into the ground, coordinated with alternating excavation stages to extract the soil from inside the caisson. During this sinking stage, a delicate balance exists between the descending weight of the caisson walls and the upward resistance generated by soil–structure interaction [15]. The unique construction method of sinking caisson structure, relying on their own weight, introduces complexity to the structural stress and displacement in the construction process. Large caissons, in particular, are susceptible to issues such as cracking, partial settling and sudden settling during the initial stage of sinking. Additionally, achieving successful sinking in the final stage can be challenging. Thus, real-time monitoring and stress analysis of the caisson structure during construction are essential for ensuring safety and optimizing performance [5,10,16]. In the abovementioned cases, it can be seen that successful operation of the open caisson depends on the modeling method used before installation. The current accumulation of literature provided fruitful material and support for the new requirements for press-in open caisson modeling in urban-intensive areas. However, the lack of system summarization of the current open caisson modeling method cannot provide enough support for a direct solution to the new requirement problem. To solve this gap, this study collected and evaluated multiple case studies that employed different modeling approaches to investigate the surface and subsurface soil displacements due to excavation and the corresponding ground deformations. The current problem and discussions about future direction were presented to fulfill this task. This review discusses the gap which needs to be covered, and provides an effective framework for understanding the new requirements, which will drive future study.
2. Methodological Route for Study Selection
The study selection criteria were established to ensure transparency and reproducibility in the selection of evaluated papers. The methodological route for study selection is provided in Figure 2. Considering both physical and computational modeling techniques, the goal to concentrate on open caisson construction in soft urban underground space was established. Relevant literature was retrieved from Web of Science, Google Scholar, Scopus, and CNKI, targeting research articles from 1940 to 2025. Specific keywords like open caisson and physical and numerical modeling were utilized as a search strategy. Based on relevancy, methodologically sound and well documented studies were included, while irrelevant and methodologically lacking details were excluded from the study. The screening and selection process was adopted based on abstract and full text reviews, with cross verifications from multiples authors. Finally, selected datasets including physical modeling, numerical modeling, theoretical advancements, and case studies were compared, and challenges and future directions were provided.
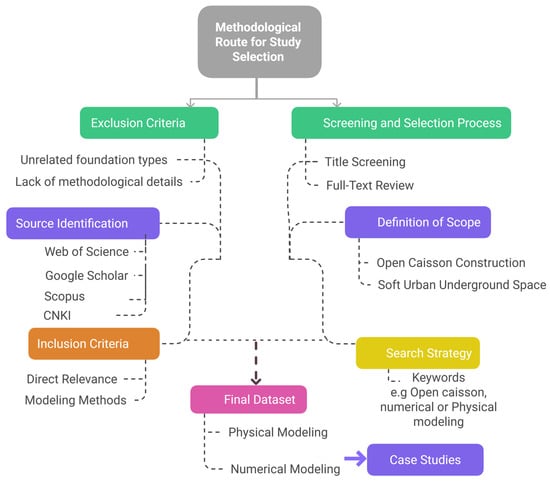
Figure 2.
Methodological route for study selection.
Open caisson shaft construction is an important engineering technology utilized in deep foundation systems, especially in soft urban underground spaces (UUSs) with high groundwater levels. Recent developments in modeling techniques have greatly improved the accuracy, efficiency, and dependability of open caisson design and construction. These innovations are powered by the combination of physical model testing, numerical tools, and data-driven approaches. In the upcoming section, a detailed review of some of these developments, with an emphasis on their practical implications in open caisson modeling, is presented. The framework for this study is shown in Figure 3. The influence of these modeling techniques and their integration, as well as their limitations, will be explored as along with the advances in the whole design and construction process.
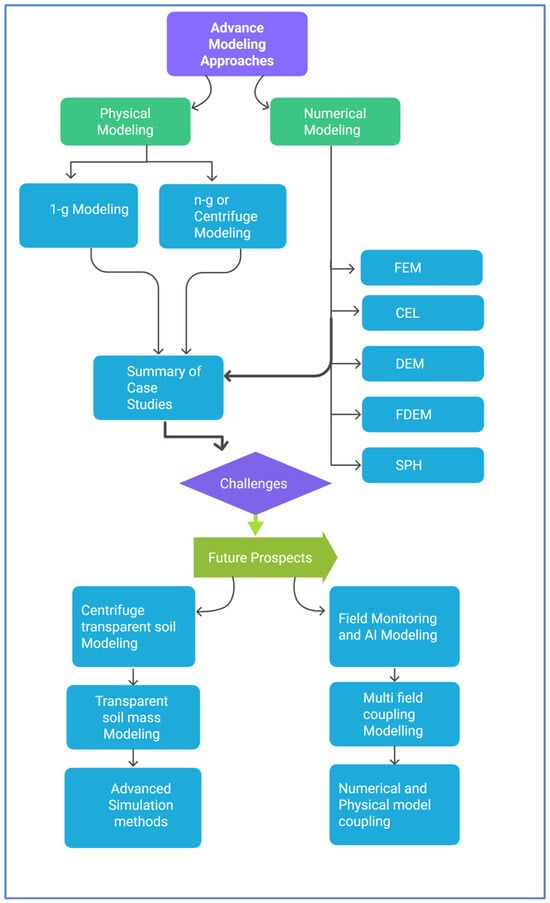
Figure 3.
Framework for review of advance modeling approaches.
3. Advances in Physical Modeling Method
Physical model tests in the geotechnical engineering field played a crucial and fundamental role in studying complex geo-structure problems [17]. Physical modeling involves creating scaled-down models that simulate the behavior of various geotechnical problems/prototypes. By using appropriately sized models, researchers have gained valuable insights [18,19].
Physical models play a vital role in evaluating complex open caisson systems. These systems are often dependent on factors such as construction techniques, non-linear soil–structure interactions, and variable geometries. These tests can serve as substitutes for numerical models or as valuable supplements. To verify the validity of the various assumptions and approaches of the numerical models, data from physical model tests are often used. Moreover, physical model results can also be used to rectify numerical models to better represent anticipated loading conditions.
The initial physical model was offered by [20], which utilized sand to simulate and explain the subsidence phenomenon. While numerical and analytical tunneling research has expanded due to advancements in computational techniques, geotechnical engineering researchers continue to use physical modeling to explore different facets of tunneling, such as failure mechanisms and deformation patterns. The important goal of any model testing is to extend model behavior to the corresponding behavior of the prototype. However, in most physical models, prototypes are based on proposed excavations. It is therefore usually not possible to directly compare the behavior of a model with that of a field. To evaluate how well physical models represent field behavior, the model findings should be contrasted to field data that have features similar to theoretical prototypes and to existing prediction approaches for ground deformation associated with excavations. The physical model findings were assessed using the projected settlement profiles provided by [21,22], which are two reputable methods for predicting excavation-induced deformation.
In open caisson construction, 1-g modeling is typically used because it is less expensive [21,22,23,24,25,26]; however, because the simulated stress state was reasonable [27,28,29], the n-g type grows quickly. Also, 1-g modeling can be carried out at a greater scale than n-g modeling. According to [21,30], 1-g model tests exhibited the following characteristics: (1) they can be carried out with more control over the model’s parameters, (2) eliminate adverse impacts linked to small models, such as the grain size impact, (3) allow information about the expected patterns of reaction to be received more quickly, (4) provide more space for monitoring components while causing the least disruption to soil behavior, and (5) can potentially be repeated at a relatively low cost.
The effectiveness of 1-g models was constrained by their inability to simulate in situ stresses realistically. Notwithstanding this constraint, 1-g models have been utilized in soft ground tunneling studies [31]. Numerical models can be calibrated and validated using data from physical models. Many researchers worldwide have created and applied a range of methods to replicate the deep excavation process over the course of several decades. Tests conducted on a smaller scale in 1-g conditions provide complete control over the excavation process.
Physical modeling has recently been used at various scales and study domains, from the laboratory scale to full scale, to calibrate behavior under real-world conditions [32,33]. The technical and economic aspects of the physical modeling influenced the test efficiency and the quality of the results [18,33]. Finally, it is usually not practicable to fully comply with scaling laws. When compared to centrifuge modeling, physical modeling under single gravity (1-g) is typically more cost-effective. The next step was to develop scale factors, which enable the parameters at the prototype scale (such as displacements, strains, stresses, and forces) to be calculated from model-scale observations.
Physical modeling has been successfully employed for many decades [34], enabling visualization of the problem, as well as validation and verification of numerical modeling [35]. Several 1-g physical models have been presented, and many useful results have been obtained, examining soil–structure interaction [30,36,37,38,39,40,41], failure models and mechanisms [21,22,23], ground movements, structure stability and collapse, arching effect [28,29,42], ground displacements [43,44,45,46,47], reinforcement effect [48,49], and pile behaviors [50,51]. Overall, 1-g models are often employed for soft ground tunneling, mining, geomorphology, and soil–structure interaction. Centrifuge tests were conducted by [52,53] on shafts to simulate the half excavation profile (i.e., the plan shape of the excavation was semicircular). The purpose of these soil models was to analyze the subsurface earth movements caused by the construction. The excavation was driven up against a poly-methyl methacrylate (PMMA) window in huge rectangular boxes. The researchers used physical models in order to comprehend the processes occurring during excavation in the soil. A series of physical model case studies and their results are described in this paper for better understanding of the deformation induced by the shaft construction.
A widespread review of the literature on shafts conducted by [54] revealed that only eighteen case studies on circular shaft construction were published between 1980 and 2016. In 2017, further case studies were reported [54,55]. The majority of these case studies were directed at surface settlement, with only three cases presenting subsurface soil displacements and one example reporting surface horizontal displacement.
3.1. Classification of Physical Modeling Based on Gravitational Acceleration
Based on gravitational acceleration, g, physical modeling can be divided into two groups: n-g (centrifuge) and 1-g (laboratory on a small size and filed on a full scale). Centrifuge tests (n-g modeling) increased the effective gravitational acceleration to n times Earth’s gravity by spinning a model at high speeds. By improving stress conditions in small-scale models, this technique made it possible to simulate full-scale behavior realistically. By comparison, 1-g modeling comprises small-scale laboratory testing and full-scale field investigations and works under typical Earth gravity. Laboratory models at 1-g were cost-effective and widely used for fundamental studies, while field tests provided real-world validation of geotechnical principles. In physical modeling, scaling laws based on dimensional analysis and the governing equations of engineering problems were very important to replicate the prototype conditions. Scaling factors such as geometry, stress, time, and others played significant role to ensure similitude between model and prototype [56], validating that model behavior faithfully reflected the prototype behavior [57]. Variability in model and prototype behaviors encountered due to scaling process arose from various factors such as grain size of soil mass relative to model size [58], time scaling affected pore pressure reduction and consolidation processes [59] and size and capacity of model box resulting in incomplete similitude [60]. Overall, 1-g models had limitations in replicating the in situ stress conditions of prototype and therefore suitable for problems or processes that were not dependent on stress [61] as scale effects were significant for phenomenon influenced by stress levels [62]. However, centrifuge models can effectively replicate in situ stress state of prototype [57] and provided high level of control due to capability of gravity manipulation [60]. The comparison between 1-g and n-g modeling used for open caisson excavation studies including experimental setup, scale effects, and experimental constraints is discussed in detail by reviewing existing case studies. Table 1 provides a summary of the physical modeling approaches in this section, along with information on ground conditions, shaft geometries, and modeling techniques.

Table 1.
Summary of physical modeling approaches.
3.2. 1-g Modeling
Physical modeling under 1-g can offer a reliable data source, enabling numerical modeling and back analysis with well-defined and controlled boundary conditions. The model size can be large, resulting in a small linear scale for typical prototypes; however, it was typically impossible to fully replicate the prototype. Some case studies of recently performed 1-g modeling tests to simulate open caisson shafts are discussed in detail in upcoming sections.
3.2.1. Lateral Earth Pressure Resulting from the Radial Displacement of Shaft Linings
Tobar and Meguid (2009) [63] performed several tests under normal gravity conditions to examine variations in lateral earth pressure resulting from the radial displacement of shaft linings. The apparatus they developed enabled the modeling of both the complete geometry of the shaft and the radial displacement of the lining. It was constructed using six curved lining segments held vertically in place by segment holders; the model setup is shown in Figure 4. The model shaft was 0.15 m in diameter and 1 m in length, filled with coarse dry sand, and having ϕ = 41°; γ = 14.7 kN/m3.
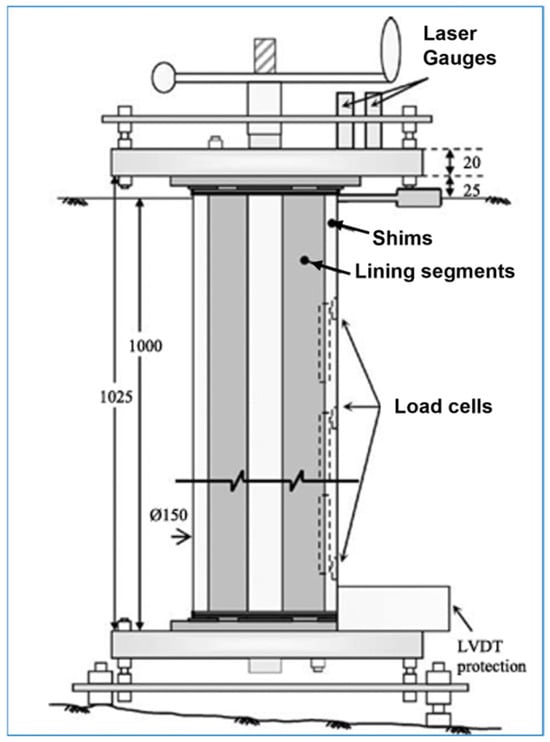
Figure 4.
Detail of shaft test setup [63].
The measured and calculated earth pressures at S ≥ 0.1% and H S ≥ 0.3%H were in good agreement within the range predicted by Cheng and Hu, as well as Terzaghi’s and Berezantzev’s theories, respectively. At the upper part of the shaft, Prater’s theory also provided a strong relationship with the measured values. However, at the lower part of the shaft, the predicted zero value did not align with the range of the experimental findings.
3.2.2. Soil Deformation During Caisson Construction in Dry Sand
By using a small-scale laboratory study, Song and Sheil (2023) [64] investigated the processes of soil deformation during caisson construction in dry sand; the setup for the experiment is depicted in Figure 5. To assess the influence of critical caisson geometric parameters and the efficiency of external cofferdams in reducing soil displacement, the results of seven tests were analyzed. The findings revealed that a compressive “bearing” front below the cutting face and a “frictional” contribution above the cutting face are the main mechanisms causing ground movements.
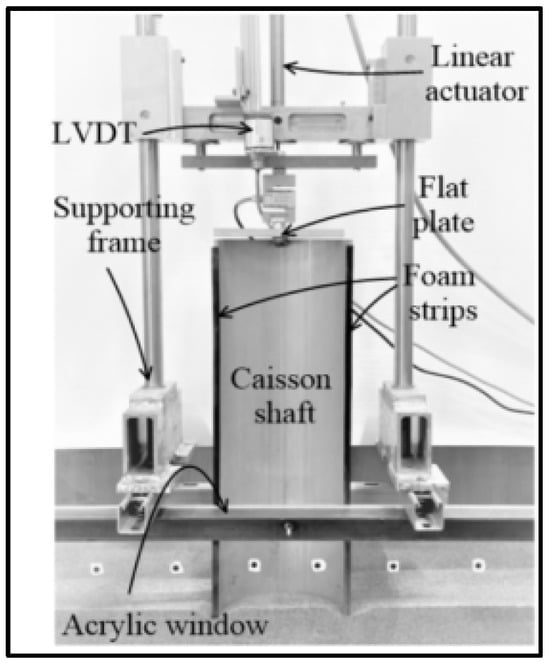
Figure 5.
Shows experimental setup after [64].
Furthermore, it was demonstrated that the normalized radial settlement profile was insensitive to the normalized caisson embedment depth, and that the settlement zone of effect reached a maximum of 0.25 diameters below the caisson cutting edge. Moreover, studies have demonstrated the significant efficacy of an exterior cofferdam in mitigating soil settlements. With an increase in cofferdam depth from 0.25 to 0.5, quantitative analysis shows a considerable decrease in soil settling; the results were consistent across soil elevations.
The laboratory findings identified two principal mechanisms causing construction-induced ground motions outside the caisson: (1) a compressive bearing front largely beneath the cutting face, and (2) a frictional contribution above the cutting face. The current free-field test revealed that the bearing mechanism causes the majority of soil settlement, with a secondary, but consistent, influence of friction as the caisson passes the elevation of interest. Ref. [26] provided useful insights into open caisson-induced ground movements, but further work was required, particularly for understanding the magnitude and distribution of induced ground movement during the installation of caissons in heterogeneous soils.
3.2.3. Load–Penetration Behavior and Soil Flow Dynamics in Sandy Soil
To explore the load–penetration behavior and the soil flow dynamics in sandy soil surrounding the cutting edge of a circular open caisson, [65] a series of 1-g model studies were conducted; the test setup is shown in Figure 6. A square tank with a height and width of 350 and 450 mm, respectively, was used to carry out the test in order to minimize boundary effects and provide an accurate depiction of the soil–structure interaction. Different caisson models with radii ratios of 0.615, 0.737 and 0.783, cutting-edge widths of 25, 12.5 and 16.5 mm, respectively, and various tapered angles of 30, 45, 60, 75 and 90° were used. These tests considered both full and half open caissons, varying the tapered angles of the cutting edge. Utilizing image-based deformation measurement techniques, the study evaluated the soil flow mechanism and concluded that during sinking, both slope angle and blade foot depth significantly affect the resistance of the foot blade and the flow behavior of the soil adjacent to the blade foot.

Figure 6.
Schematic of experimental setup [65].
Although the research was restricted to 1-g model tests, which may not adequately capture the complexities of field conditions and the study only examined sandy soils, leaving the behavior in other soil types unexplored. However, the results offer important insights into the mechanics of caisson penetration and can be helpful in the design and construction of circular open caissons in sandy environments. The study discovered that the resistance provided by the soil to the cutting edge and the soil flow surrounding it varied continuously during the sinking process.
3.3. n-g Modeling
According to Craig et al. (2015) [66], geotechnical centrifuge modeling technology has undergone multiple stages of development over the previous century. The first documented tests were performed in the United States and the Soviet Union in the 1930s, and across the next four decades, early pioneers from all across the world made significant achievements. In the years between 1970 and 1980, rapid developments were made in centrifuge instruments and modeling methods, resulting in increased application and understanding of centrifuge modeling potential in the wider civil engineering domain. Centrifuge modeling resolved a significant difficulty in geotechnical structure modeling by maintaining true stress conditions, as most soil attributes rely on effective confining stress. Models evaluated at 1-g provided only qualitative details because their soil attributes (such as stiffness, strength, and dilatancy) varies greatly from full-scale situations. Increasing the gravitation field in centrifuge tests assured that the model and full-scale prototype have similar stress responses, making the model’s response to diverse loadings more reflective of real-world situations. Some examples of recently performed centrifuge modeling tests to simulate open caisson shafts are discussed in detail in the upcoming sections.
3.3.1. Earth Pressure During Excavation Within Granular Soil
Kim et al. (2013) [67] used two overlapped semi-cylindrical aluminum segments with a length and outer diameter of 200 mm and 80 mm, respectively, to construct a physical model. It was constructed at a scale of 1:75 and tested at 75 g acceleration in a centrifuge. The model has the equivalent size to a 15 m long, 6 m diameter reinforced concrete prototype shaft, as shown in Figure 7. In the model, granular soil was used.
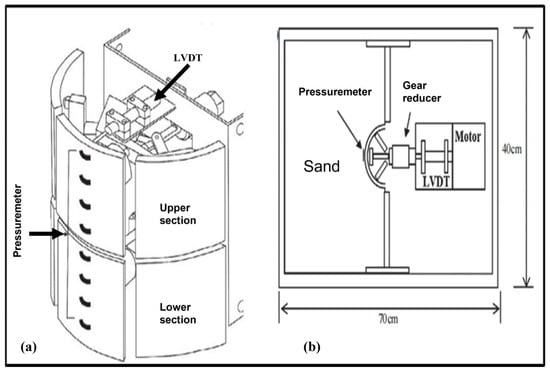
Figure 7.
(a) Physical experimental model—vertical section. (b) Plan view [67].
In order to simulate soil excavation, a multi-gear motor has been used to move the semi-cylindrical segment at a rate of 1.0 mm per 140 s. Two LVDTs have been attached with the semi-cylindrical portions, one at the top and one at the bottom of the shaft, and eight soil pressure transducers were fixed on the exterior of the shaft.
The tests revealed that for the first level of excavation the earth pressure progressively reduced corresponding to the height of the first segment, unless an active displacement of δℎ/H = 0.2 × 10−2 was accomplished. Afterward, there was no additional variation in the pressure. Earth pressure dropped until it reached 30% of its original value, after the active displacement state was achieved. However, at the same time, recorded earth pressure on the bottom portion remained constant.
Furthermore, in the second phase, the movement of the lower segment, the earth pressure declined until it reached 80% of its primary value, once the active displacement was reached. With the displacement of the lower segment, earth pressures in the upper segment area began to increase concurrently until they approached the initial pressure. For a deeper excavation level, during the second stage of the excavation, the arching effect was more effectively produced. From the test, it was revealed that the plastic zone ranges across a distance of 1D and the vertical displacements were noted as 13 mm.
3.3.2. Ground Movements During Excavation Within Dry Dense Sand
To examine the shaft excavation and the associated ground movements in dry dense sand, Faustin et al. (2021) [68] conducted several centrifuge tests under an experimental system at a scale of 1:80, which is shown in Figure 8. Excavation was simulated by removing sand from the center of the shaft, which can replicate the actual stress changes. The excavation procedures (installing the excavation system and then removing the soil) were analogous to SBE shaft construction. They plotted the settlement results by analyzing ground surface displacement against the distance from the shaft and concluded that, initially, when the excavation proceeds, the extent of the settlement is found to be at maximum near the shaft and reduces progressively when moving farther away from the shaft. They observed that within 20 mm from the shaft wall, small settlements occurred.
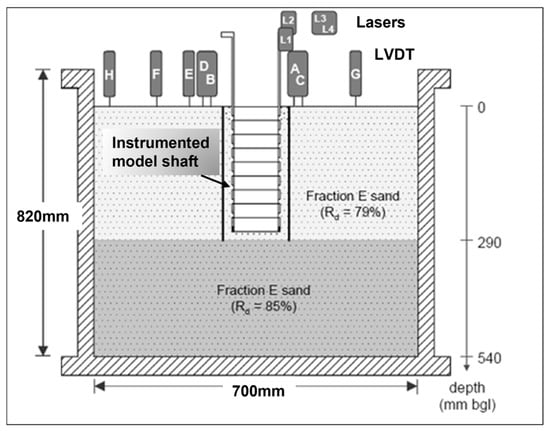
Figure 8.
Illustration of the centrifuge model system [68].
These experiments focused on a single soil layer, assuming homogeneity with idealized boundary conditions for testing. However, in real-world scenarios, shafts interact with surrounding soil, water, and structures, and soil conditions vary significantly; moreover, this study does not account for variations in soil properties or layering. These interactions affect performance, but cannot be fully captured in the experiments.
3.3.3. Ground Failure During Excavation Within Granular Soil
An experimental model using duralumin semi-cylinders was developed by Imamura, S. et al. (2000) [69]. The model consists of two semi-cylinders; one is fixed, and the other is capable of moving horizontally. To investigate the mechanism of the ground failure, these two semi-cylinders were spaced 40 mm apart. The dimensions of the modelled shafts were 500 mm in height and 120 mm in diameter, equivalent to the prototype shaft with a depth of 50 m and a diameter of 12 m. Granular soil was used in the model for centrifuge model testing at 100× g acceleration. The mobile semi-cylinder underwent horizontal displacement at a constant velocity of 0.75 mm/min. Four tests were performed, out of which three of the tests resulted in maximum horizontal displacements of 3.6 mm and 10 mm in another test. The earth pressure was monitored at ten evenly spaced points along the shaft lining. For the measurement of the ground surface movement, three laser displacement meters were used.
In the vicinity of shaft, a narrow failure zone was formed at a consistent range of 0.3D as depicted in Figure 9. To approximate the failure surfaces, a logarithmic curve can be used at deeper depths. The resulting pressure corelates strongly with the soil pressure obtained through the usage of the finite element method and Berezantzev’s theory that relates to 0.2% of the wall height, and 1.6% of the shaft radius (H).
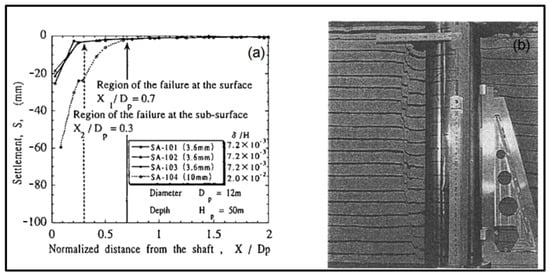
Figure 9.
(a) Settlement profiles at ground surface; (b) failure surface [69].
3.3.4. Surface and Subsurface Soil Displacements During Excavation Within Cohesive Soil
To investigate both surface and subsurface soil displacements caused by shaft construction, Le, B.T., Goodey, R.J., and Divall, S. (2019) [70] designed a bespoke centrifuge model by back analysis of four available case studies; the system setup is illustrated in Figure 10.
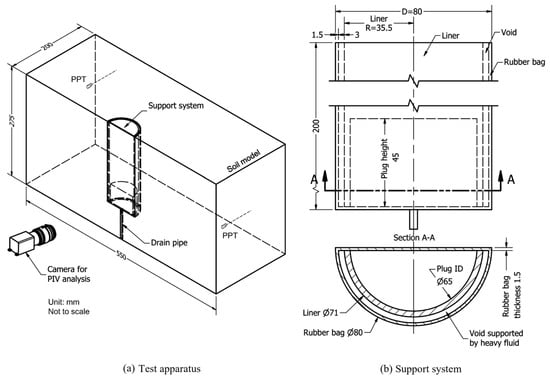
Figure 10.
Schematic of the experimental apparatus [70].
A shaft liner that measured 200 mm in height and 71 mm in outer diameter was employed. The shaft liner was surrounded by a 1.5 mm thick latex bag, creating a 3 mm space among the liner and the bag. This space was filled with a dense fluid that could be drained to replicate the excavation process.
Both the radial and vertical strains decreased with the draining of the heavy fluid. A centrifuge model was used to evaluate the experimental model at 100× g of acceleration by using cohesive soil. The soil displacements exhibit symmetry, with both vertical and horizontal displacements decreasing as the distance from the center of the shaft increases. In this study, to gain understanding of the surface and subsurface displacements of soil, [70] measurements from centrifuge tests were analyzed based on available field data. However, there was limited guidance for estimating ground movements due to the excavation of circular shafts due to the scarcity of published case studies related to circular shaft construction. Representative input parameters and validation against field observations were required for finite element analysis. This study emphasizes the need for further empirical data and improved prediction methods for subsurface soil displacements caused by circular shaft construction.
Scholars attempt to integrate and improve the benefits of numerical and physical modeling [71,72,73,74]. Even as computer capacity increased, the complexity and uncertainty of engineering issues posed a significant challenge to numerical methods, prompting some experts to wonder about the limits of numerical modeling. Therefore, physical modeling has been reproduced.
4. Advances in Computational Modeling Method
To replicate the related physical models, computational modeling comprising numerical simulation approaches was established. The basis for the validation of numerical models was the outcome of the physical model testing. Both computational models and enhanced monitoring techniques have the potential to be used in field investigations to accurately forecast the performance of real construction projects. Computational modeling has a wide range of approaches, as shown in Figure 11. Although fewer particular computational simulations of in situ assembled caisson technology are currently being undertaken, earlier research on the excavation of deep foundations and conventional caissons has significant implications.
Figure 11.
Illustration of various types of numerical modeling approaches.
4.1. FEM
Using COMSOL Multiphysics 5.3, in the excavation process, researchers [75] investigated rigidity and the settlement of the retaining wall deformation. They also conducted a comparative study with monitoring data collected from the excavation of a deep foundation pit in Shanghai. In order to investigate the impact of caisson structure dimensions on internal forces during the early sinking phase, Li et al. [76] created a 3D finite element method (FEM) model for soil–structure interaction. Furthermore, Jiang et al. [77] examined the impact of excavation on the sinking process of open caissons using numerical simulations based on FEM. Xiao-qing et al. [78] used both physical model testing and numerical simulations in Plaxis 3D to carry out an extensive investigation into the stress and deformation properties of anchor caisson foundations on sandy soils. A thorough examination of the mechanics behind the interaction between soil and structure was also included in the study. To more precisely model installation impacts, Lai et al. [79] used sophisticated kinematic and continuous three-dimensional numerical approaches in a different investigation. These methods used the normal Lagrangian finite element (FE) approach and the large deformation finite element (LDFE) method, respectively, to integrate coupled interactions between the excavation and penetration processes. However, there were considerable time constraints and high computational expenses involved with both approaches. Yang et al. [80] examined how deep excavations behaved close to flexible retaining walls, using the numerical tool Plaxis 3D to evaluate how wall depth, excavation depth, and bending rigidity affected the retaining structures’ mechanical reaction. Through numerical simulation using ABAQUS, Dong et al. [81] analyzed the deformation characteristics and stress distribution of the caisson structure and surrounding soil. The reliability of the finite element model was validated by field monitoring data collected during the construction process that confirmed the strong correlation between simulation and monitoring data. Kumar et al. [82] also employed ABAQUS for simulation of laboratory-scale caisson models by changing base dimensions and embedment depth while holding other factors constant. The results revealed that lateral load resistance increased with both parameters.
Using the numerical code Plaxis 3D, De Falco et al. [83] validated and extended the work of conducted by Le et al. (2019) which utilized a geotechnical centrifuge to estimate the depth-dependent distribution of soil movements induced throughout shaft construction. Numerical modeling is divided into three distinct calculation phases, as shown in Figure 12: (a) the phase of consolidation; (b) the phase of pre-excavation; and (c) the phase of excavation. During the first phase, the speswhite kaolin clay employed in the centrifuge test is over consolidated by applying uniform vertical load of up to 500 kPa, followed by the establishment of the gravity-induced stress profile. This step was performed to replicate the test conditions of CR500 carried out by Le et al. (2019) [70]. To avoid soil displacement during soil removal, the excavation support system which included a basement and a cylinder liner, was constructed in the physical model during the pre-excavation phase (Figure 12b). In order to simulate this phase, which was carried out quickly in tests, very rigid elements (whose dimensions are shown in Figure 12c) were activated, and the interior clay elements were removed.
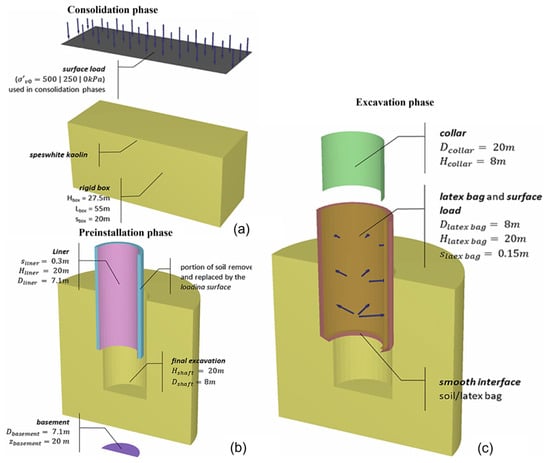
Figure 12.
Phases of building in stages using FEM numerical models: (a) consolidation; (b) pre-installation; (c) excavation [83].
The largest displacements occur at the shaft wall. These displacements were primarily horizontal and were most significant at a depth of nearly 0.6 times the shaft diameter. Beyond a distance of 1.5 times the shaft diameter (which corresponds to 30 m), the displacements become negligible. This study provided insights into the behavior of ground displacements during circular shaft construction, emphasizing the significance of depth and distance from the excavation wall.
During the shaft construction in soft grounds of Shanghai, Zhou et al. [84] conducted comparative analysis between the theoretical calculations and numerical simulations to evaluate ground settlements and deep layered displacements. The study concentrated on horizontal displacements and lateral earth pressures, comparing field measurements and simulation findings at depths varying from 15 to 35 m from the shaft center. Field results were compared with the numerical analysis, showing variation in the results since the model does not simulate this process. Shaft excavation has a minor impact on the lateral earth pressure. During construction, the lateral earth pressure was somewhat decreased by roughly 7%. Caisson installation usually entails an intricate relationship of significant deformation, caisson penetration, and soil excavation, which is challenging to simulate with computational simulations [79,85]. For example, interface issues and mesh distortions are constant in the FEM, which further contributes to the non-convergence of numerical outcomes [8,77,86,87,88].
4.2. FDM
The finite difference method (FDM) is among the earliest numerical methods to address differential equations with specified initial and boundary conditions. It simulates plastic deformation in soil, rock, and other materials when yield limits are exceeded, utilizing a user-defined grid of discrete components that mimic structural geometry [89]. With parametric studies showing the relevance of compaction pressure on wall displacement, FDM has been effectively used to replicate retaining structure [90]. Lin et al. [91] used FLAC 3D to create a numerical simulation model that includes excavation time under various computational ranges to account for creep and seepage effects in order to study pile displacement and ground settlement. Shah et al. [92] simulated mechanized tunneling by incorporating sequential excavation, face support, grouting pressure, and lining installation in Plaxis 3D and FLAC 3D. They evaluated the inconsistencies caused by intricate soil–structure interactions and tunneling mechanics in modeling outcomes. The results demonstrated considerable agreement in ground movement predictions among both methods under stiff soil conditions, highlighting their reliability despite diverse numerical methods. DEM, which characterized soil as an assemblage of discrete interacting particles, provides an effective representation of soil behavior during the failure of a caisson foundation as soils within the failure zone undergo large deformations, rendering continuum mechanics ineffective. However, DEM models were proven to be computationally expensive, especially when applied to boundary value problems like caisson foundation analysis [93].
4.3. ALE and CEL
To overcome the limitations in FEM, various computing techniques, such as the Arbitrary Lagrangian–Eulerian (ALE) and coupled Eulerian–Lagrangian (CEL) approaches, have been developed to model penetration-related problems. Severe mesh distortion complications can be somewhat sorted by these methods [94,95,96,97]. Lai et al. [79] used the 3D large deformation finite-element (LDFE) method based on the Coupled Eulerian–Lagrangian (CEL) approach to explored the soil deformation characteristics and installation mechanism of GDCO caissons. Dong et al. [98] created an innovative static simulating method for caisson sinking that successfully models complex seepage circumstances by combining the coupled Euler-Lagrange method. As CEL was time-consuming, to increase computational efficiency and accuracy in complicated soil conditions to simulate open caisson shafts, future research should concentrate on improving these techniques.
4.4. DEM
Using the discrete element approach (DEM) and physical model experiments, Zhou et al. [99] investigated the effects of asymmetrical excavation adjacent to a metro station, assessing the impact of excavation depth and station width. Chen et al. [100] created a three-dimensional numerical model to examine how surface settlement and tunnel stability are affected by triangular-distribution tunnel excavation. To analyze the distribution of stress and lateral earth pressure around a cylindrical shaft, Tran et al. [101] used both FEM and DEM, showing good agreement between the two approaches and validation with well-established predicted theories. However, the discussion did not include detailed assessment of the merits and weaknesses of each approach, mainly concerning performance, sensitivity to input variables, and practical relevance to actual conditions. By clarifying these strengths and limitations, the study’s capabilities could be improved in the domain of open caisson shaft–soil interactions. Particle-based approaches like the DEM were likely to be suitable for large deformation problems [102]. However, these approaches have constraints caused by their high computing cost and implausible simplifications, such as 2D models.
4.5. FDEM
To analyze the gradual failure of sand caisson foundations, Yin [93] used the coupled finite difference method–discrete element method (FDM-DEM). He represented the caisson with FDM shell components, while the surrounding soils in a small region were modelled with DEM spherical particles, with the remaining parts of the soil modelled by FDM. The macro and micro features of the surrounding caisson soils were evaluated using simulations, thereby enhancing insights into the micro-mechanisms in the progressively occurring failure process of caisson foundations. For caisson construction in soft soils, soils can be considered as discrete particles, allowing the numerical DEM to investigate failure processes and mechanical characteristics at the micro level. However, during the failure process, soils within the failure zone often experience significant deformation, making continuum mechanics ineffective. Consequently, in these settings, the DEM, which represented soils as an assemblage of separate particles, effectively depicts the actual aspect of the soils. However, the DEM model is generally computationally expensive, especially for the study of boundary value problems such as caisson foundation. By taking into consideration the advantages and disadvantages of DEM- and FDM-based continuum approaches, it was preferable to combine the two methods. The literature presented numerous examples of successful couplings between DEM and FDM [103,104,105,106] in other studies. The coupling method can offer a potential approach to explore the deformation mechanism of open caisson shafts, which has yet to be covered in the existing literature.
4.6. SPH
In view of significant soil deformation, mesh distortion, and computation errors, conventional techniques such as FEM have limited application when dealing with numerical simulations of sinking caissons. The Lagrangian-based smoothed-particle hydrodynamics (SPH) approach, on the other hand, is a possible substitute since it manages interface migration and large deformations effectively. Wang et al. [107] used a single-phase soil particle and the SPH method to model the sinking process of open caissons. However, the method’s inability to precisely reproduce the conditions of wading engineering construction limited its usefulness. Even though the modeling accounted for the significant soil deformation, the intricate soil–water relation was, however, neglected, making it impossible to determine the fluctuation rule of pore water pressure (PWP). In order to examine the changing failure of caisson foundations in sand, Jin et al. [108] used a combined Lagrangian–SPH technique, examining different loading combinations and caisson dimensions. Using SPH, Rogers et al. [109] modeled floating bodies in the surf zone, showing good agreement with experimental data for caisson breakwater displacement and realistic behavior for a floating box. These investigations demonstrate SPH’s adaptability and efficiency in simulating intricate caisson-related events. To overcome this limitation and to simulate the whole sinking and excavation process of open caisson, Zhang [110] presented a coupled soil–water–caisson interaction algorithm. The δ-SPH approach was used to address support domain truncation close to the blade, which ensured precise pore water pressure distribution and reduced pressure fluctuations from density oscillations. Furthermore, realistic underwater soil excavation was made possible by the dynamic particle birth and death technique, which successfully captured the intricate interactions that take place during the caisson sinking process. A small time step determines the algorithm’s stability, which raises the computational cost and necessitates a certain particle resolution. Performance can be increased by particle refining and GPU parallel processing.
In geotechnical engineering, numerical simulations rely on soil constitutive models that differ in complexity, parameter requirements, and computational demands. Mohr–Coulomb models use fundamental parameters like cohesion and friction angle, are computationally effective, and are employed for broad applications [111], but may not perform well under complicated stress [112]. According to [113], comparative study revealed that despite increased parameter requirements and calibration difficulties, modified Mohr–Coulomb models yielded more reliable forecasts in pipeline–soil interactions than the Drucker–Prager model. This model considered a linear stress–strain relationship until failure, followed by plastic deformation without hardening [114]. Inaccurate predictions of soil deformation may result from the model’s assumption of a linear elastic response and failure to take into consideration non-linear stress–strain behavior or small-strain stiffness, particularly in stiff or soft soils [115,116]. Also, this model did not take into account the anisotropic behavior of soils, which can be crucial for clays and other deposited soils [117]. The elastoplastic Hardening Soil (HS) model took stress-dependent stiffness and non-linear stress–strain behavior into consideration. It was frequently used for deep excavation analyses and was especially appropriate for soils that showed strain hardening, including sands and clays [118]. In order to simulate deep excavations in Warsaw’s pre-consolidated clays, [119] the Hypoplastic Clay model and Hardening Soil models were employed. He concluded that the Hypoplastic Clay model was most effective in properly predicting wall behavior and ground displacements, even if basal heave was slightly underestimated. Hardening Soil models, on the other hand, greatly overestimated wall deformations and displacements. The modified Calm Clay (MCC) model was commonly utilized in geotechnical engineering and offered a conceptual framework for engineering applications and numerical analysis [120]. The MCC model was especially effective in clays due to accurate depiction of the anisotropic nature and critical state behavior of clays. However, a drawback in practice can be its complexity and the need for accurate parameter calibration [121]. Despite its widespread application, the Modified Cam Clay model had several other drawbacks, including the assumption of isotropic hardening [122], an inherent tendency for overestimating dilatancy [123], and a failure to account for small-strain stiffness [124]. The constitutive models had unique advantages and drawbacks, making their selection crucial for accurate soil behavior forecasts in deep excavations. The Hardening Soil model, due to its capability to capture dynamic stress–strain behavior and small-strain stiffness, was suitable for deep excavations in sands and clays. The Cam Clay model was preferable for clays that exhibit considerable critical state behavior and anisotropy. However, the Mohr–Coulomb model was ineffective for complicated soil conditions and should only be used for preliminary studies. While selecting a model, the project’s specific needs, soil conditions, and required level of accuracy should all be considered. Comparative summary of the numerical modeling methods including their strength shortcomings and applications are provided in Table 2.

Table 2.
Comparative summary of the numerical modeling methods including their strength, shortcomings, and applications.
The numerical models described in the paper, while advantageous, offer certain drawbacks. Particularly, unexpected shifts in soil characteristics and the thixotropic behavior of soft clay at geological contacts were not properly recorded, resulting in differences between simulated and actual data, especially at depths of 15–20 m. Furthermore, the lack of important constructing activities, such as bentonite grouting, reduces the model’s ability to correctly mimic field circumstances, limiting its applicability to real-world situations. The study also concentrated on certain depth ranges (15–40 m) and distances (within 30 m of the shaft center), which limited its relevance to other geotechnical scenarios. Changes in lateral earth pressure were simplified, with local disparities along with construction dynamics understudied. These limitations emphasized the necessity for more thorough and precise modeling in order to increase accuracy and applicability under a variety of scenarios. A summary of the advanced modeling approaches, physical and numerical modeling, including their advantages and shortcomings, is provided in Table 3.

Table 3.
Summary of the advanced modeling approaches.
5. Challenges and Future Directions
5.1. Challenges
Open caisson excavation comprises the removal of soil or rock material to form a cavity for constructing foundations, tunnels, or other underground structures. For safe and efficient construction, the understanding of the underlying mechanisms causing deformation during this process is critical. By installing the liner segments and excavating the soil beneath and inside the caisson, the building process uses a combined structure that enables the caisson to sink into the soil either by jacking pressure or by self-weight. Unexpectedly, there was a scarcity of literature on the design and performance of large-diameter caissons. The initial investigations into the sinking process were presented by [125,126], and some case studies have been documented by [127,128]. More recently, the mechanisms related to the sinking process have been explored through real-time monitoring [2], numerical simulations [15,85,129], and laboratory testing [130]. Here, a review of some of the key mechanisms occurring during the sinking and excavation process of open caisson shafts is provided below.
5.1.1. Soil–Structure Interaction (SSI) Mechanism
Soil–structure interactions involve the interplay between soils and structures in transmitting forces from one to the another via contact surfaces. The deformation patterns during the caisson excavation and sinking are determined by the interactions between the caisson and the surrounding soil. SSI influences both the soil behavior and the caisson response under loading.
During the sinking process into earth, the cutting face located under the bottom of the caisson wall played a key role. This was achieved by exploiting the self-weight of the caisson wall. The cutting face of the cutting edge was critical during the sinking process as it reduced the vertical bearing capacity and enhanced the soil failure mechanism advancement toward the central area of the caisson [15,126]. Numerous studies in the literature have concentrated on defining the cutting face angle, symbolized as “β”, within ranges such as 30–90° [131] or 30–45° [132], demonstrating numerous methods.
During the sinking stage of the caisson construction process, the self-weight of the structure and upwards resistance produced from soil–structure interaction (SSI) should be carefully balanced [2,133]. Caisson-bearing stresses at the base, v, and frictional stresses on the exterior surface of the caisson walls, τ, were exerted by the surrounding soil. To minimize design inefficiencies and construction risks, accurate assessment of these contact stresses is critical. Unexpected or excessive caisson movements might result from over-prediction [2]. Additionally, heterogeneity of ground conditions or poor excavation leads to non-uniform resistance, which can cause a loss of verticality or tilting [128].
However, under-estimation of the contact stresses during caisson sinking was the main risk, which might cause the caisson to become wedged and unable to achieve the desired formation level. In this scenario, potential remedial measures can be very expensive, having substantial associated risks, and remain largely unconfirmed. Presently, increasing caisson wall thickness was used to ensure sufficient self-weight W to comfortably overcome the sinking resistances. In terms of both cost and environmental impact, this had obvious inefficiencies, as excessive material utilization exceeds the structural requirements.
During construction, particular features were included in the caisson’s design to reduce and regulate the contact stresses between the surrounding soil and the structure. As shown in Figure 13, the cross section of the RC caisson wall is tapered at the base to form a cutting face. This was commonly accomplished by means of an angled bearing pad cast from concrete under the wall, which was broken out to start the shaft sinking [134].
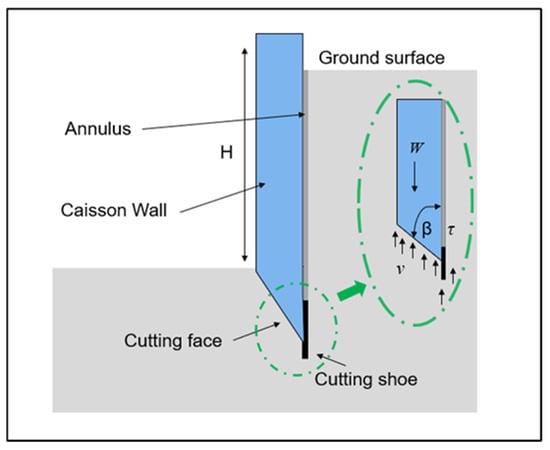
Figure 13.
Illustration of an open caisson shaft section, demonstrating distinctive construction features and the contact stresses acting on the walls during sinking.
Based on the gathered site experience, a footing taper angle, β, of 45° is frequently used in industry [130]. Tomlinson et al. [135] mentioned that β adjustment depended on the ground conditions: for stiff clays, and angle of 30° was recommended, and for sands and soft clays 45° was recommended. By cutting into the soil, minimizing the vertical bearing capacity, and moving the soil failure mechanism inside the caisson for excavation, the employment of a tapered cutting face was thought to facilitate the sinking process [130,136,137].
In 1945, Ozerov [138] designed and patented external over-cuts as an additional important construction feature. Usually, the radius of excavation was 30–100 mm larger than the shaft itself [128]. This was typically accomplished by casting a thicker piece of the RC wall, e.g., [126,128], or, more commonly, by inserting a steel ‘cutting shoe’ at the front edge of the caisson wall [2,5,139]. Identical to pipe-jacked tunnelling, this created a gap among the caisson and the adjacent soil as the caisson lowers, known as the ‘annulus’. This was filled with a support fluid, generally a bentonite slurry, which stabilizes the excavation and lubricates the interface [15,134]. The resulting behavior of the soil–lubricant–structure interface (SLSI) at the caisson exterior had a considerable impact on the formation of frictional forces while sinking. Once the caisson had reached the foundation depth, the annulus was normally injected with grout to evacuate the lubricant, stabilize the excavation, and serve as a permanent frictional resistance [5].
5.1.2. Earth Pressure During Sinking
The main concern when sinking a caisson foundation had been ensuring that it sinks safely. Because the end resistance distribution characteristics differ from those of medium- small-sized caisson foundations, different sinking construction regulating methods are inevitably required for different caisson foundation sizes [140]. The studies on the distribution of the earth’s pressure on circular shafts were first performed by [141] and enhanced by Terzaghi [142] later on. He expanded Westergaard’s theory to lined shafts, using the Mohr–Coulomb criterion to estimate the minimum earth pressure on shaft liners with σθ = σv = σ1 and σr = σ3 in the plastic zone. To take into consideration the effects of non-zero shear stress, he proposed to decrease the friction angle of sand from 30° < Ø < 40°. It was demonstrated that in granular soils, radial and hoop stresses decline as the radial distance to the shaft decreases, known as the arching effect. Meanwhile, radial stress progressively increases with depth. The arching effect makes the standard earth pressure theories developed for plane strain situations by [143,144] inappropriate, and results in overly conservative earth pressure predictions [145]. Since then, other researchers have developed techniques based on different models to determine the axisymmetric earth pressure acting on a shaft [142,146,147,148,149,150]. Prater [151] proposed a conical failure surface for axisymmetric conditions. He adopted Coulomb wedge theory by using limit equilibrium theory, suggesting that lateral earth pressure initially increases up to a peak value and then gradually decreases to a value of zero. He considered that the value of earth pressure coefficient should lie between Ka and K0, not equal to 1 as assumed in Terzaghi’s theory. To evaluate the earth pressure acting on the cylindrical shafts, Derezantzev [146] expanded the slip line method by assuming that σθ = σv = σ1 and σr = σ3 within the plastic zone, under active conditions, thus making the stress ratio λ = = 1. He also argued that within the plastic zone, the hoop and radial stresses are equivalent to the major and the minor principal stresses. The hoop and redial stresses, acting along the shaft circumference and in the radial direction, respectively, are the normal stresses. The major and the minor principal stresses represent the maximum and minimum normal stresses, acting along principal directions where the shear stress is zero. Based on these assumptions, he concluded that, λ = = 1. He used the Mohr–Coulomb failure criterion and approximated the failure surface as a straight line. Berezantzev’s theory was extended by [152]; considering λ as a variable, it was proven that for λ = 1, the minimum value of the lateral earth pressure can be obtained, suggesting the use of λ = K0 = 1 − sinϕ.
The evolution of the normalized earth pressure () with the normalized depth () is presented in Figure 14, which provides comparative summary of earth pressure distributions calculated using various methods for a specific shaft geometry: height (h), radius (a), and soil properties (ϕ). As all methods predicted pressures below at-rest and active values, their depth-wise pressure distributions varied significantly. Terzaghi’s and Berezantzev’s methods assume a unit earth pressure coefficient λ = 1, resulting in the minimum active earth pressure that aligns with predictions from the plastic equilibrium and slip-line methods producing constant earth pressures at depths below the surface. However, Prater’s method predicted a distinct distribution characterized by a rapid earth pressure increasement to a depth of 4.5 times of the shaft radius, followed by a reduction to zero at a depth of 8.5 times the shaft radius.
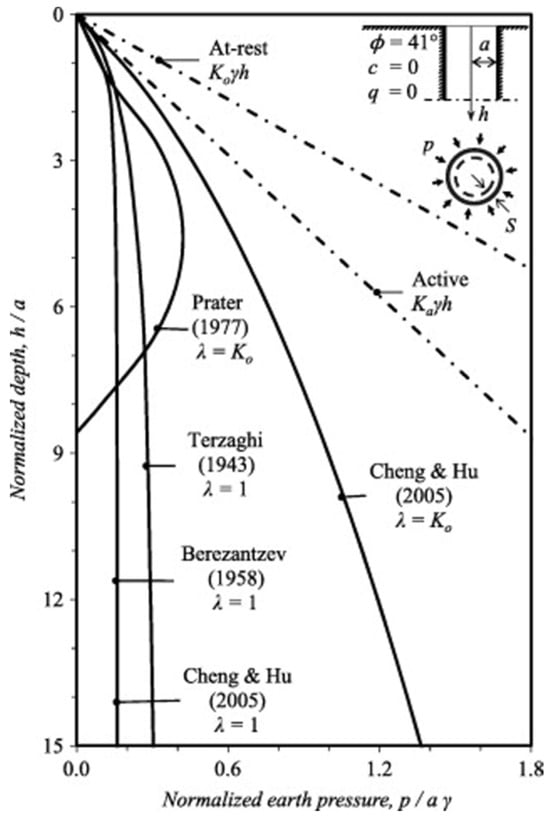
Figure 14.
Earth pressure distribution around a shaft with depth h, radius a in cohesionless soil without surcharge [142,146,151,152,153].
Cheng and Hu’s solution provided both lower and upper bounds for lateral earth pressure, corresponding to λ = 1 and λ = K0, respectively. Notably, for λ = 1, the earth pressure aligned well with Berezantzev’s predictions. For shallow shafts, where the height ranged between one and two times of the shaft radius, negligeable differences among the theoretical methods are revealed, as shown in Figure 14. Currently, due to the dependence of the sinking and soil excavation construction of caisson foundations on the engineering experience, earth pressure distribution is unclear during soil excavation, resulting in limited control of the sinking operation [154]. Based on prior studies, it can be summarized that, unlike under plane strain conditions, earth pressure on the cylindrical walls did not rise linearly with depth for axisymmetric excavations conducted under active conditions. The normalized pressure falls and eventually approaches a depth-independent constant as soil movement increases. However, since the lateral stress coefficient cannot be accurately determined, theoretical solutions reflect notable differences.
Terzaghi’s model assumed that the distribution of earth pressure is triangular and s increases linearly with depth. Although this simplification works well in many real-world situations, it might not take into account the non-linear soil behavior or intricate soil–structure interactions. The theories Westergaard (1940) [141] and Terzaghi (1943) [142] are based on Rankine-based plastic equilibrium along horizontal planes under presumptions to minimize stress singularities at elastic–plastic boundaries. Although the earth pressure calculations align well with other theoretical findings, one major shortcoming of the theory is its unrealistic prediction of the plastic zone form, which, according to Terzaghi, expands with depth and asymptotically approaches a constant radius, revealing theoretical limitations [151]. The safety of the sinking caisson foundation structure and its reliability is significantly impacted by soil excavation that solely relies on engineering expertise; therefore, more research is required to fully understand the sinking process through soil excavation. The earth pressure at the foot blade is an essential factor in determining the sinking resistance of a caisson foundation, and it serves as a crucial foundation for developing a soil excavation plan. An estimated computation model of the ultimate soil resistance of a caisson foundation during sinking was constructed based on the slip line field theory by [155], and equations for calculating the ultimate load capacity for the plane strain problem and the axisymmetric conditions were derived. Guo et al. [16] employed identical methods to figure out the annular caisson foundation’s ground pressure distribution properties, which were confirmed by practical examples. Using the centrifugal model test, they investigated the earth pressure beneath the foot blade and discovered that the ratio of earth pressure remains nearly constant between the foot blade’s horizontal and oblique positions. Zhang et al. [156] and Mu et al. [157] investigated the process of the caisson foundation’s abrupt sinking and discovered that the foot blade’s earth pressure will drop noticeably prior to the caisson foundation’s abrupt sinking. A couple of investigations have been conducted on the end resistance of medium-sized or super large caisson foundations, while the rarer of current research has been on small- and medium-sized caisson foundations.
Qin et al. [158] observed that the ratio of end resistance to side friction resistance has progressively become the key component to safe sinking of the caisson foundation as the dimension of caisson foundation continually increases. The behavior of lateral earth pressure on circular shafts was studied using the shaft sinking technique [159]. In this model study, a miniature model caisson equipped with a cutting edge advanced at a recess distance from the lining surface, which was intended to represent induced soil movement during construction. To replicate soil displacement throughout the excavation process, Tobar and Meguid [160] employed a mechanical device to move the rigid shaft lining to explore the earth pressure distribution on cylindrical shafts. The results revealed that with the minor wall movement, the lateral earth pressure decreased rapidly, and the shaft movement required to achieve the full active state was determined to be 1.5% and 2.5% of the shaft radius, respectively, aligning well with the findings of [161,162].
The presented assumptions and simplifications have had a considerable impact on outcomes in theoretical approaches, whereas the choice of constitutive models and parameters in numerical methods has significantly influenced the results. Physical modeling provides more advantages than theoretical and numerical approaches in establishing real conditions to examine ground pressure distribution in open caisson shafts. Many existing studies have adopted small-scale models in 1-g and centrifuge modeling to determine the distribution of earth pressure and the induced surface and subsurface soil displacements, which will be explained in the upcoming sections.
5.1.3. Soil Variability and Unpredictable Subsurface Conditions
Another significant challenge in open caisson excavation is interactions with extremely variable subsurface conditions, ranging from cohesive clay layers to lose sands and silts. These subsurface variations may induce excessive friction along the caisson walls, differential settlement, and difficulties in maintaining verticality during sinking. During open caisson excavation, Yan et al. [163] conducted the field study on the deformation and stress characteristics of large open caissons in deep marine soft clay. They analyzed the deviations of caisson geometric posture, cone tip resistance, and lateral soil pressure. The findings provide valuable technical guidance for accurate modeling to predict ground movement and stress redistribution.
Open caisson encounters various heterogeneous soil layers during the process of sinking. The inherent uncertainty and construction complexity often results in accidents such as deflection, sudden sinking, and sand gushing [164]. In recent years, researchers have extensively investigated the stress characteristics of caisson during excavation [10]. Gerolymos et al. [165], through field experiments, studied the force of the blade foot during the sinking process. Chiou et al. [166] evaluated a laterally loaded bridge caisson foundation in gravel using an in situ lateral load test. Abdrabbo and Gaaver [128] documented a case history of a caisson with a 20 m diameter, which became wedged due to the development of excessive soil–structure frictional stresses during sinking. Additionally, more recently, researchers [167,168,169] have investigated the settlement and performance monitoring utilizing diaphragm walls associated with the construction of a deep shaft. During caisson construction in dry sand, Song and Sheil [64] investigated soil deformation mechanisms from a small-scale laboratory study by analyzing data from seven tests to recognize the impact of significant caisson geometric properties and the competence of exterior cofferdams in controlling soil displacement. Two key mechanisms were identified as a driving ground movement: a compressive bearing zone beneath the cutting face and frictional forces contributions above the cutting face. Chen et al. [170] conducted structural stress analyses based on automated caisson monitoring data and revealed that at the bottom four corners of the caisson, the vertical earth pressure was significantly greater than the other positions, depicting that at the four corners there was an apparent stress concentration phenomenon. Furthermore, the measured horizontal earth pressure at the base of the monitoring section was lower compared to pressures recorded at the middle and bottom regions of the caisson. This observation indicated the existence of a stress displacement region in the vicinity of the cutting face. During the sudden sinking process of an open caisson, Zhang et al. [156] investigated the soil disturbance and damage behaviors through the numerical simulation method. They found that the unequal distribution of soil damage was found to adversely impact the open caisson attitude and cause open caisson tilting. Periodic monitoring of caisson deformation and stress characteristics is crucial to ensure construction safety and to optimize design [164]. Using machine learning (ML) algorithms and monitoring data from the Changtai Yangtze River Bridge Project, Dong et al. [171] estimated open caisson inclination. Several machine learning methods were evaluated to determine the most precise and productive prediction models. The findings provide ideal approaches with great accuracy and a low computation time. In engineering applications, these outcomes can improve the safety, stability, and control of open caisson sinking processes.
Due to uncertain subsurface conditions and soil property variability, the excavation of open caissons presents key challenges, which can result in increased friction, differential settling, and verticality problems. To overcome these issues, future research should focus on the integration and strengthening of prediction model resilience by including more varied datasets, such as various soil types and caisson geometries, as well as exploring the impact of groundwater water levels and temperature. Furthermore, adaptive prediction systems and real-time monitoring could improve caisson’s dynamic response to abrupt changes in subsurface conditions.
Examining the influence of heterogeneous soil layers on the sinking process and subsequent ground movements can yield significant insights for future endeavors. Factors such as soil–structure interaction, caisson geometry, and construction sequence play a crucial role in determining ground movements. The complex interaction between the caisson and the surrounding soil requires detailed investigation.
There is a critical need to explore the earth pressure distribution on ultra-deep shafts in complicated soil conditions such as composite, heterogenous soil strata using different modeling techniques to address the existing gap in this area.
Experimental modeling has evolved significantly, yet it often faces limitations in replicating in situ conditions. For instance, 1-g models are cost-effective and allow larger-scale experimentation, but they struggle to simulate realistic stress states compared to n-g (centrifuge) models. There is a dire need to improve the fidelity of stress representation in 1-g models while addressing scaling challenges inherent in n-g models. Techniques to reconcile these limitations could include hybrid modeling approaches that integrate both 1-g and n-g methodologies, as well as innovations in material and boundary condition simulations. A comparative summary of parametric aspects, predictive discrepancies and their causes across various modeling approaches is shown in Table 4.

Table 4.
Comparative summary of parametric aspects, predictive discrepancies and their causes across various modeling approaches.
5.2. Future Directions
The scarcity of significant-quality literature in field measurements from shaft construction was most likely due to the high cost of monitoring schemes particularly for deep shaft construction projects. These costs resulted from the need for deep drilling to install casings for inclinometers and extensometers below the shaft plug level in order to gather representative data. Furthermore, shaft construction sites were frequently associated with high levels of activity, which might interfere with measurement accuracy, resulting in data that are not genuinely typical. Furthermore, the existence of pre-existing subsurface structures might alter soil deformation mechanisms, confounding measurement results and reducing the availability of valid field data. Future research should focus on addressing the existing gaps in understanding earth pressure distribution and ground movements during open caisson shaft construction, particularly in complex, heterogeneous soil conditions. Large-scale experiments and advanced physical modeling techniques, such as centrifuge modeling, are crucial for achieving more accurate insights into soil behavior and the effects of gravity in geotechnical events. The development of ultra-deep shafts in composite soil strata required further exploration, with emphasis on soil–structure interactions, caisson geometry, and construction sequences. These factors significantly influence ground movements and earth pressure mechanisms, yet they remain insufficiently understood.
To overcome the limitations of modeling techniques, future efforts should improve the stress representation in 1-g models while addressing scaling challenges in n-g centrifuge models. Hybrid modeling approaches that combine the advantages of both techniques, alongside advancements in material simulation and boundary condition replication, hold promise for achieving more reliable and realistic results. Key future research directions are given in the following sections.
5.2.1. Real-Time Field Monitoring and AI Methods
Current real-time monitoring systems for open caissons have shown remarkable progress, providing instantaneous visualization of the sinking process; however, they still fall short of adequately assisting in construction decision-making. This is largely due to the complexity and heterogeneity of the foundation soils and rock formations, which makes it challenging for open caissons to consistently maintain uniform descent during sinking operations. Thus, there is a critical need for timely adjustments and corrections to prevent deviation. This implied a necessity for prompt decision-making regarding the construction status throughout the process. ACPP is an actively controlled technology, where sinking and excavation operations are automatically controlled by the adopting (AI) system employing the monitoring sensors data, shown in Figure 15. So far, the ACPP technology was recently used for the first time on the west expansion of Shanghai Metro Line 13 to construct the escape shaft project at Yunle Road Station, demonstrating the effectiveness of this cutting-edge innovation. Measurements gathered throughout the project yielded remarkable results. The inclination of the sinking well achieved 0.65% precision, with an ultimate soil settlement of 4.95 mm and a corner height variability of only 2 mm. Additionally, the segment lining demonstrated no evidence of leakage or incorrect alignment, reflecting great overall reliability [172].
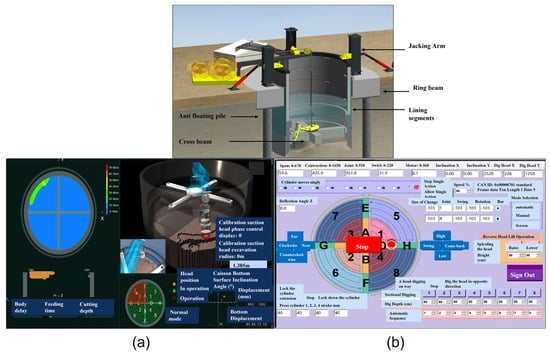
Figure 15.
Schematic diagram of ACPP excavation system: (a) automatic trajectory record; (b) excavation interface [173].
Advancements in information technologies and artificial intelligence technologies have enabled the application of data-driven approaches in auxiliary decision-making in civil engineering [174]. Using the convolutional neural network, Dong et al. [175] studied the stress characteristics of an open caisson structure, which can effectively predict the sinking speed of the open caisson to provide a basis for safe construction. The soil pressure data from foot blades can accurately depict the stress level during sinking. The excavation scheme was designed based on the stress level at various stages of sinking [176]. By comparison of machine learning models, Tian et al. [177] revealed that the multilabel K-nearest neighbor (MLKNN) was the best successful model predicting open caisson excavation instructions. Improvements to MLKNN, such as enhanced normalization and distance measures, increased its accuracy to 89.04% for excavation predictions and 98.63% for non-excavation decisions. However, these data-driven methods for open caisson excavation were highly accurate in the middle and later stages of construction, but they were less effective in the initial phase. Addressing this constraint required additional study to improve algorithmic decision-making at the early stages, when uncertainties were the largest. The empiricism-constrained neural network (ECNN) was utilized by [178] for prescriptive design; this was calibrated and compared to classic empirical models using reduced-scale laboratory data. It was concluded that both methods effectively anticipate surface and subsurface settlement troughs, but the neural network approach was more accurate in capturing the impact of caisson depth on soil settlements.
AI model performance in predicting caisson settlement is heavily influenced by training needs and data quality. Robust model development requires high-quality data and suitable preprocessing procedures, like feature selection. There are pros and cons to using AI with conventional geotechnical design techniques, and the anisotropic and heterogeneous character of soil–rock media made these predictions more challenging. A selection of related features can help in reducing noise and improving the model’s predictive power to improve model accuracy [179,180]. For the development of a successful model, large and high-quality training datasets are essential. To develop viable models, geotechnical data must be handled carefully because they are commonly inadequate [181]. According to [182], in order to increase their accuracy, AI models must account for the complicated behavior of soil–rock mediums, such as discontinuities and elastic–plastic behavior. He concluded that relative to conventional methods, advanced AI algorithms can provide better prediction capabilities by modeling the non-linear and discontinuous nature of geotechnical materials. To ensure accuracy of these models, they are validated using real-world data, and to evaluate the impact of different factors on model predictions, sensitivity analysis is crucial [183]. Incorporating advanced field monitoring systems with AI techniques, such as Physics-Informed Neural Networks (PINN) and use of actively controlled prefabricated caisson technology (ACPP), can revolutionize real-time analysis and prediction of soil behavior. Although shafts and underground structures primarily involved complex soil–structure interaction problems, the application of advanced artificial intelligence (AI) techniques offered significant potential for enhancing predictive and analytical capabilities in this domain. Significant domains under this subject could include evaluating the stresses and deformations of lining, predicting vertical and horizontal deformations due to open caisson excavation, and optimizing the selection of open caisson shaft construction technique on basis of soil profile and shaft depth.
Future studies should focus on the automated evaluation of the entire process which can be achieved by integrating the proposed model and monitoring system, which could offer improved accuracy in assessing soil displacements, stress distributions, and deformation patterns. As a result, more efficient and safe construction operations will be possible if their engineering application and level of intelligence are improved.
5.2.2. Multi-Field Coupling Modeling
Multi-field coupling models, particularly those integrating thermal–hydraulic–mechanical–chemical (THMC) interactions, are critical for grasping the difficulties of open caisson shaft excavations. These models can aid in forecasting soil–structure behavior under a variety of environmental and loading circumstances. Recent advances in THMC modeling are aimed at dealing with the complicated interactions between the thermal, hydraulic, mechanical, and chemical fields. To accurately simulate ground behavior during excavations, several physical processes must be integrated, according to the studies referenced. In frozen soils, Li et al. [184] carried out studies that showed that temperature gradients on the surface can influence hydraulic conductivity and pore pressure, changing soil stability and deformation. The results of these investigations have led to an improved numerical model that can replicate related processes in various circumstances, such as seasonal shifts.
The coupled THMC processes in geological media are important for a variety of subsurface engineering applications [185,186,187]. Recent advances in modeling THMC interactions included the creation of fully coupled frameworks that combined various codes to simulate complicated subsurface systems. Experiments have also been carried out to investigate THMC coupling in frozen vertical shafts, revealing the spatiotemporal evolution of temperature, moisture, and stress fields [188]. The use of coupled THMC modeling in open caisson shaft design was still unexplored. Open caissons, prone to complex subsurface interactions such as heat effects, groundwater movement, mechanical loads, and chemical reactions, could benefit from THMC modeling to enhance stress distribution, soil deformation, and ecological impact.
Geothermal variations and groundwater flow might impact the rigidity of soil and pressure within pores, whereas mechanical stress and chemical responses can change soil properties gradually. The incorporation of chemical remedies such as grouting can improve the stability of soil through minimizing permeability and enhancing strength. However, chemical processes could cause dissolution and precipitation of minerals, which can change soil structure over time, influencing both mechanical and hydraulic performance. Establishing THMC models for open caissons could improve construction accuracy, safety, and long-term viability, especially in difficult ground conditions. Additional research and simulations are required to bridge this gap.
5.2.3. Advanced Simulation Methods
Numerical simulation techniques, including FEM, SPH, FDM, DEM, FDEM, and CEL, offer advanced tools for studying soil–structure interactions. These methods enable precise analysis of stress, displacement, and failure mechanisms in both homogeneous and heterogeneous soil conditions as discussed in the computational section. However, the coupling between different simulation methods in scenario of open caisson remains unexplored. Understanding the relationships between soil behavior and structural responses during excavation operations requires the integration of mechanical and hydraulic analysis into numerical simulation methods for open caisson excavation shafts.
In future research, these methods should be coupled, for example, using FEM for structural mechanics and FDM for fluid dynamics. Engineers can more accurately forecast how caissons will behave in various scenarios by using these coupled numerical techniques, which will improve safety and construction approaches.
5.2.4. Transparent Soil Mass Modeling
Geotechnical model testing primarily monitors the internal deformation of the model using pre-embedded sensors that provide point-specific data. However, this method has limitations in capturing continuous stress and strain distributions over lines or surfaces. As a result, there is an urgent need for the development of non-intrusive geotechnical models [189] that may observe the continuous deformation of rock and soil without the requirement for sensor implantation, which is intrinsically limited in non-transparent materials. While it is possible to monitor deformation at the interface between the soil and the model box by replacing the box sidewalls with transparent glass, this method does not provide information about the soil’s interior deformation. The idea of transparent soil had emerged as a result of this limitation. Transparent soil not only ensures the geotechnical attributes of soil, but also allows for the visualization of the internal deformation. A newly developed sort of material for model research is transparent soils [190]. Finding an analogous material for transparent soil has emerged as an innovative field of study for natural soil simulation. About 40 years ago, the study of transparent soil was initiated. Initially, Allersma [191] started with broken glass pieces as a transparent material to investigate the stress and strain distribution of materials under shear conditions. Subsequently, similar materials [192] were employed to analyze the stress variations in saturated dykes subjected to seismic loadings. However, due to the lack of absorption capacity in broken glass, it was impossible to remove the entrapped air from the glass voids. This limitation caused poor transparency and an inability to accurately replicate the strength and deformation characteristics of natural soils. To address these challenges, Iskander et al. [193] proposed the use of consolidating suspensions of amorphous silica as transparent soils which were synthesized by a pore fluid with a matched refractive index. Later on, Sadek et al. [194] investigated that amorphous silica and transparent silica gels have macroscopic geotechnical properties comparable to natural sands and clays, making them suitable for simulating soil behavior in model studies.
Transparent soil is a two-phase medium composed of synthesized aggregate and fluid parts with matched refractive indices (RIs), intended to create optical transparency in the concluding soil [168]. For the successful manufacturing of a transparent soil that allows the entire penetration of visible light, it is essential that the refractive indices (RIs) of aggregate materials and pore fluids are similar [193,195]. This transparency enables the direct visualization of soil behavior and continuum deformation in experimental models. When integrated with innovative photogrammetry and image processing techniques, transparent soils facilitate the accurate measurement of the spatial deformation, displacement and multi-phase flow in experimental model tests. These manufactured soils have been effectively utilized in geotechnical model tests, as their measured geotechnical properties replicate those of natural soils, making them a viable solution for simulating prototype behavior.
The most commonly used aggregate materials for transparent synthetic soils include silica gel, amorphous silica powder, fused silica, fused quartz, aqua beads and gel beads. These constituents are matched with various fluids or fluid blends including white oil, mineral oils, paraffinic oil, brine mixture, sucrose solution and water. Previous studies have extensively explored the geotechnical properties of these transparent soils and verified that their properties align closely with those of natural soils [195,196,197,198,199].
Nowadays, transparent soils are widely utilized in laboratory settings to simulate soil–structure interaction problems, [200,201,202,203] including soil deformation measurements [204,205,206], and tunnelling-induced movements [207,208]. Hence, in geotechnical engineering, transparent soils are widely employed to execute experimental tests. Advances in image processing techniques, such as particle image velocimetry (PIV) or digital image correlation (DIC) [195,209], has significantly enhanced their ability to analyze and compare images of deformed soils captured by digital cameras during these experiments. However, there are many challenges like transparency issues, the restricted applicability of model tests, and the use of homogenous soil conditions. Future studies should focus on developing transparent soil mass that could be used in a wider range of soil types and conditions; more significantly, transparent soil masses can be used in their layered form in a single model box to mimic the real ground conditions.
5.2.5. Centrifuge Transparent Soil Modeling
In view of its advantages in modeling soil behavior in geotechnical events, the centrifuge modeling technique can overcome the challenges of identifying representative soil displacements caused by shaft construction [210]. Modern technological advancements have enabled precise monitoring of soil deformations anywhere in small-scale centrifuge models [211,212]. Transparent soils were utilized in centrifuge experiments to investigate different mechanism like pullout capability, anchor rotation of VDPA and embedment loss during keying [213,214]. Black [60] created a centrifuge modeling method that combines transparent soil with laser imaging technologies and was verified by conducting experiments on a strip foundation. Future advancements in centrifuge testing allowed for the accurate simulation of gravity effects and realistic stress states in small-scale models using transparent soil masses. This technique held significant potential for studying ultra-deep shafts and addressing the complexities of heterogeneous soil strata. Another interesting approach could be to incorporate real-time monitoring and multi-sensor systems into centrifuge transparent soil models. Combining technologies such as fiber-optic sensors, piezoelectric transducers, and particle image velocimetry (PIV) allowed for simultaneous monitoring of displacement, strain, and pore pressure during testing. This multi-parameter method generated a larger dataset for verifying numerical models and expanding prediction competencies. Future research should also look into the effects of factors like variations in temperature and the flow of groundwater on soil dynamics in transparent models, specifically in the setting of climate change implications on infrastructure, which has remained unexplored.
5.2.6. Numerical and Physical Model Coupling (n-p Coupling)
Numerical–physical coupling (n-p coupling) tests represent a promising avenue for combining the strengths of numerical simulations and physical experiments. By integrating the accuracy of numerical models with the practicality of physical tests, this approach can bridge the gap between theoretical predictions and practical observations, leading to more robust geotechnical designs. Composite modeling has several advantages, including the capability to simulate complex problems which neither physical nor numerical modeling can replicate alone. Additionally, it also increased model accuracy without increasing or decreasing costs and without compromising accuracy. Moreover, it contributed to reductions in uncertainty at the same cost, signifying that reducing uncertainty is inherently linked to enhancing model quality.
Hybrid testing employed the substructure approach used by Blakeborough et al. [215] by integrating the physical model with a numerical model that enables more comprehensive analysis of complex systems. The physical test examined essential elements of one domain, whereas the numerical simulation accurately simulated the influence of an adjacent domain. By combining these approaches, physical modeling capabilities were enhanced because the combined findings explained the behavior of the entire domain with better precision than ordinary physical modeling with simplified boundary conditions. Real-time coupling between the physical and numerical domains was an important feature of hybrid testing as it ensures continuous data flow and allows the response from one domain to drive the other. This real-time connection was especially important for time-dependent problems because it ensured integrity in boundary conditions, such as forces or displacements, between the two domains. The application of coupling within geotechnical centrifuge modeling has emerged recently; for example, Kong et al. [216] employed displacement-controlled boundary conditions in a geotechnical centrifuge model that were derived based on numerical analyses. In previous studies, hydraulic boundaries which were kept constant or within the domain of the model box can be defined on the base of N-P coupling analyses to replicate the original ground water conditions in future research.
5.3. Prioritize Direction
To address current challenges and research gaps, the future directions on open caisson construction in soft urban underground spaces discussed above could be prioritize based on potential impact and technical feasibility. The most important research direction was real-time field monitoring combined with artificial intelligence (AI) approaches. Technologies such as ACPP and machine learning algorithms offered high potential for immediate use in optimizing shaft construction operations and improving dynamic risk analysis. Because of their high viability and profound impact, integrating AI with field data collecting systems was expected to substantially enhance smart construction practices such as combination of caissons for large underground space. For the accurate prediction of the intricate soil–caisson interactions under various environmental and operational situations, the development of multi-field coupling models, incorporating thermal, hydraulic, mechanical, and chemical (THMC) processes were crucial. These models had significant scientific influence despite being technically difficult and requiring collaborative teamwork. Advancement of coupled simulation techniques, such as FEM-DEM and SPH-FEM methods, held significant potential in enhancing the modeling of soil–structure interactions, stress analysis and deformation mechanism. However, their use may be constrained by numerical stability and computational cost. Additionally, centrifuge modeling by using transparent soil mass offered a novel experimental technique. This method provided internal visualization of deformation and failure processes, thus providing new validation routes for numerical simulations. However, replicating the behavior of natural cohesive soils within transparent analog material remained challenging. Finally, numerical and physical model coupling approaches (n-p coupling) that incorporate real-time interactions between simulations and physical models represented a highly novel but technically challenging research direction. Considering the existing limits in monitoring, processing, and synchronization tools, future improvements were expected to improve feasibility and develop highly precise hybrid modeling systems.
6. Conclusions
This review paper highlighted the status of various modeling tools in understanding the complicated dynamics of ground displacement during open caisson construction. The construction of open caisson shafts in soft urban contexts was a complicated process influenced by a number of factors, including soil–structure interaction, earth pressure distribution, and excavation methods. This paper emphasized the importance of physical modeling, such as 1-g and centrifuge models, as well as numerical modeling, in capturing the mechanisms of deformation and ground motions that occur during caisson building. The key findings included the following: the examined results verified theoretical models given by Terzaghi, Berezantzev, and Prater, demonstrating that earth pressure falls with depth and reaches active conditions with wall displacements ranging from 0.2 to 1.6% of shaft height. However, considerable variation in earth pressure patterns remained due to changes in experimental settings, shaft geometry, and soil qualities.
Current 1-g and centrifuge modeling tools were extremely useful for studying the behavior of open caissons under controlled settings, but they frequently failed to properly recreate in situ stress states and large-scale complexity. Hybrid techniques that combine physical and numerical models represented a possible route for tackling these difficulties.
Large-scale physical tests and enhanced numerical models were crucial for better understanding the sinking behavior of ultra-deep caissons in a variety of geotechnical conditions. Improvements in real-time monitoring techniques and better modeling materials will improve the accuracy of this research.
The advancement of geotechnical engineering in complicated and diverse soil conditions depends on the research of ground movements and earth pressure distribution under open caisson shaft construction. This review highlighted the significant potential of combining advanced monitoring systems, numerical modeling, and physical experiments to address existing knowledge gaps. Field monitoring associated with AI approaches, such as PINNs and ACPP, provided a robust tool for real-time prediction and optimization of construction operations. Multi-field coupling models, such as THMC coupling, offer a comprehensive understanding of soil–structure interactions, while advanced numerical methods allowed precise analysis of soil behavior under various scenarios. Transparent soil testing and centrifuge transparent testing have emerged as valuable approaches for visualizing and validating soil deformation mechanisms, especially in ultra-deep shafts and complex strata. Additionally, numerical–physical coupling tests have bridged theoretical and experimental studies, enhancing the reliability of predictions and practical applications.
Future studies have to focus on improving these approaches, combining their advantages, and overcoming their constraints. By embracing these advanced methodologies, the geotechnical community can improve construction safety, optimize design strategies, and better tackle the challenges posed by soft urban underground spaces in heterogeneous soil conditions.
Author Contributions
Methodology, J.W., N.S.A., W.P., W.W. and X.Z.; Software, S.N.A., A.A., B.A. and H.L.; Validation, S.N.A., J.W., A.A., B.A. and H.L.; Formal analysis, N.S.A., J.W., W.P., H.L. and W.W.; Investigation, J.W., N.S.A., W.P., H.L., W.W., X.Z., P.G., B.A. and H.L.; Resources, J.W., W.P., P.G. and W.W.; Data curation, S.N.A. and J.W.; Writing—original draft, N.S.A. and J.W.; Writing—review and editing, J.W., W.P. and W.W.; Supervision, J.W.; Project administration, J.W., W.P., P.G., H.L., W.W. and X.Z.; Funding acquisition, J.W., W.P. and W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanghai Tunnel Engineering Co., Ltd. (2022-SK-02); Shanghai Tunnel Engineering Rail Transit Design and Research Institute. (ST-TY020-2024); Research Project of Shanghai Housing and Urban Rural Development Management Committee (2024-Z02-007); Shanghai Shallow Geothermal Energy Engineering Technology Research Center (DRZX-202302); Shanghai Municipal Science and Technology Project (18DZ1201301; 19DZ1200900); Guangzhou Metro Design and Research Institute Co., Ltd.; Ministry of Housing and Urban-Rural Development of Research and Development Program of the People’s Republic of China (2022-K-044); Suzhou Rail Transit Line 1 Co., Ltd. (SURT01YJ1S10002); Shanghai Institute of Geological Survey (2023(D)-003(F)-02); Key Laboratory of Land Settlement Monitoring and Prevention, Ministry of Natural Resources of the People’s Republic of China (KLLSMP202101; KLLSMP202201); China Railway 15 Bureau Group Co., Ltd. (CR15CG-XLDYH7-2019-GC01).
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
This study did not involve humans.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We want to express our thanks to the authors whose publications we cited and the efficient editor.
Conflicts of Interest
Authors Weiqiang Pan and Hao Li were employed by the company Shanghai Tunnel Engineering Co., Ltd. Authors Weifeng Wu, Xiaofei Zhang, Panfeng Guan were employed by the company Shanghai Tunnel Engineering and Rail Transit Design and Research Institute. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sheil, B. Prediction of microtunnelling jacking forces using a probabilistic observational approach. Tunn. Undergr. Space Technol. 2021, 109, 103749. [Google Scholar] [CrossRef]
- Royston, R.; Sheil, B.B.; Byrne, B.W. Monitoring the construction of a large-diameter caisson in sand. Proc. Inst. Civ. Eng.-Geotech. Eng. 2022, 175, 323–339. [Google Scholar] [CrossRef]
- Royston, R.; Sheil, B.B.; Byrne, B.W. Undrained bearing capacity of the cutting face for an open caisson. Géotechnique 2022, 72, 632–641. [Google Scholar] [CrossRef]
- Allenby, D.; Kilburn, D. Overview of underpinning and caisson shaft-sinking techniques. Proc. Inst. Civ. Eng.-Geotech. Eng. 2015, 168, 3–15. [Google Scholar] [CrossRef]
- Allenby, D.; Waley, G.; Kilburn, D. Examples of open caisson sinking in Scotland. Proc. Inst. Civ. Eng.-Geotech. Eng. 2009, 162, 59–70. [Google Scholar] [CrossRef]
- Arthur, L.; Darby, A.; Rafoneke, B.; Daws, G.; MacDonald, D.; Innaurato, N.; Mancini, R.; Rondena, E.; Zaninetti, A.; Coutts, A. Ground movement model validation at the Heathrow Express trial tunnel. In Tunnelling’94: Papers Presented at the Seventh International Symposium,‘Tunnelling’ 94’, London, UK, 5–7 July 1994; Springer US: New York, NY, USA, 1994; pp. 301–329. [Google Scholar]
- Ho, C.E. Settlement performance of large diameter friction caissons in bouldery clay. In Proceedings of the Deep Foundations 2002: An International Perspective on Theory, Design, Construction, and Performance, Orlando, FL, USA, 14–16 February 2002; pp. 525–541. [Google Scholar]
- Sun, Y.; Shen, S.; Xu, Z.; Xia, X. Prediction of lateral displacement of soil behind the reaction wall caused by pipe jacking operation. Tunn. Undergr. Space Technol. 2014, 40, 210–217. [Google Scholar] [CrossRef]
- Guo, M.; Dong, X.; Yang, Z. Settlement analysis of the giant open caisson during the construction of the Changtai Yangtze River Bridge. Front. Earth Sci. 2023, 10, 1056695. [Google Scholar] [CrossRef]
- Jiang, B.-N.; Wang, M.-T.; Chen, T.; Zhang, L.-L.; Ma, J.-L. Experimental study on the migration regularity of sand outside a large, deep-water, open caisson during sinking. Ocean Eng. 2019, 193, 106601. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, K.; Luo, C.; Yang, B. Centrifugal model test study of caisson sinking resistance. Rock Soil Mech. 2019, 40, 3969–3976. [Google Scholar]
- Templeman, J.O.; Phillips, B.M.; Sheil, B.B. Cutting shoe design for open caissons in sand: Influence on vertical bearing capacity. Proc. Inst. Civ. Eng.-Geotech. Eng. 2023, 176, 58–73. [Google Scholar] [CrossRef]
- Chandler, J.; Hinch, L.; Fair, R.; Hughes, D.; Peraino, J.; Rowe, P. Jamuna river 230 kV crossing, Bangladesh. Part 2: Construction. In IEE Proceedings C (Generation, Transmission and Distribution); IET: Stevenage, UK, 1984; pp. 319–332. [Google Scholar]
- Safiullah, A. Geotechnical problems of bridge construction in Bangladesh. In Proceedings of the Japan-Bangladesh Joint Seminar on Advances in Bridge Engineering, Dacca, Bangladesh, 10 August 2005; pp. 135–146. [Google Scholar]
- Sheil, B.; Royston, R.; Byrne, B. Real-time monitoring of large-diameter caissons. In Springer Series in Geomechanics and Geoengineering, Proceedings of the China-Europe Conference on Geotechnical Engineering, Vienna, Austria, 13–16 August 2016; Springer: Berlin/Heidelberg, Germany, 2018; Volume 1, pp. 725–729. [Google Scholar]
- Guo, M.; Dong, X.; Li, J. Study on the earth pressure during sinking stage of super large caisson foundation. Appl. Sci. 2021, 11, 10488. [Google Scholar] [CrossRef]
- Wood, D.M. Geotechnical Modelling; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wood, D.M. Physical modelling. In Prediction and Simulation Methods in Geomechanics: State-of-the-Art Report on Selected Topics by TC-34; Japanese Geotechnical Society: Bunkyo City, Tokyo, 2005; pp. 7–11. [Google Scholar]
- Askarinejad, A.; Laue, J.; Zweidler, A.; Iten, M.; Bleiker, E.; Buschor, H.; Springman, S.M. Physical modelling of rainfall induced landslides undercontrolled climatic conditions. In Proceedings of the Eurofuge 2012, Delft, The Netherlands, 23–24 April 2012. [Google Scholar]
- Knothe, S. Observations of surface movements under influence of mining and their theoretical interpretation. In Proceedings of the European Congress on Ground Movement, Leeds, UK, 9–12 April 1957; pp. 210–218.
- Wu, L.; Huang, R.; Xu, Q.; Zhang, L.; Li, H. Analysis of physical testing of rainfall-induced soil slope failures. Environ. Earth Sci. 2015, 73, 8519–8531. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Li, L.; Tang, H.; Li, Y. Centrifuge model test on the retrogressive landslide subjected to reservoir water level fluctuation. Eng. Geol. 2018, 245, 169–179. [Google Scholar] [CrossRef]
- Chueasamat, A.; Hori, T.; Saito, H.; Sato, T.; Kohgo, Y. Experimental tests of slope failure due to rainfalls using 1g physical slope models. Soils Found. 2018, 58, 290–305. [Google Scholar] [CrossRef]
- Zhang, Q.; Duan, K.; Jiao, Y.; Xiang, W. Physical model test and numerical simulation for the stability analysis of deep gas storage cavern group located in bedded rock salt formation. Int. J. Rock Mech. Min. Sci. 2017, 94, 43–54. [Google Scholar] [CrossRef]
- Cho, H.I.; Bang, E.S.; Yi, M.J.; Kim, D.S. Physical modeling of land subsidence due to underground cavity and its monitoring by electrical resistivity survey in geotechnical centrifuge. Jpn. Geotech. Soc. Spec. Publ. 2016, 2, 2469–2472. [Google Scholar] [CrossRef]
- He, M.-C.; Gong, W.-L.; Li, D.-J.; Zhai, H.-M. Physical modeling of failure process of the excavation in horizontal strata based on IR thermography. Min. Sci. Technol. 2009, 19, 689–698. [Google Scholar] [CrossRef]
- Vardoulakis, P.; Stavropoulou, M.; Exadaktylos, G. Sandbox modeling of the shallow tunnel face collapse. Riv. Itall. Geotech. 2009, 1, 9–22. [Google Scholar]
- Moradi, A. Plasmon modes of spherical nanoparticles: The effects of quantum nonlocality. Surf. Sci. 2015, 637, 53–57. [Google Scholar] [CrossRef]
- Xie, Q.; Cao, Z.; Shi, X.; Fu, X.; Ban, Y.; Wu, Z. Model test of interaction between load-caused landslide and double-row anti-slide piles by transparent soil material. Arab. J. Sci. Eng. 2021, 46, 4841–4856. [Google Scholar] [CrossRef]
- Chen, H.-M.; Yu, H.-S.; Smith, M.J. Physical model tests and numerical simulation for assessing the stability of brick-lined tunnels. Tunn. Undergr. Space Technol. 2016, 53, 109–119. [Google Scholar] [CrossRef]
- Meguid, M.; Saada, O.; Nunes, M.; Mattar, J. Physical modeling of tunnels in soft ground: A review. Tunn. Undergr. Space Technol. 2008, 23, 185–198. [Google Scholar] [CrossRef]
- White, D.; Gaudin, C.; Take, W. General report for TC104 physical modelling in geotechnics. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering: Challenges and Innovations in Geotechnics, ICSMGE 2013, Paris, France, 2–6 September 2013; IOS Press: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Green, D. Modelling geomorphic systems: Scaled physical models. In Geomorphological Techniques; British Society for Geomorphology: London, UK, 2014. [Google Scholar]
- Garnier, J. Modèles physiques en géotechnique-I–Évolution des techniques expérimentales et des domaines d’application. Rev. Franç. Géotech. 2001, 97, 3–29. [Google Scholar] [CrossRef]
- Shiau, J.; Sams, M.; Lamb, B. Introducing advanced topics in geotechnical engineering teaching–tunnel modelling. GEOMATE J. 2016, 10, 1698–1705. [Google Scholar] [CrossRef]
- Beguin, R.; Fry, J.-J.; Picault, C.; Courivaud, J.-R.; Faure, Y.-H.; Philippe, P. Control of the risk of dike failure caused by contact erosion. In Proceedings of the 6th International Conference on Scour and Erosion, Paris, France, 29–31 August 2012; pp. 1551–1558. [Google Scholar]
- Al Heib, M.; Emeriault, F.; Nghiem, H.-L. On the use of 1g physical models for ground movements and soil-structure interaction problems. J. Rock Mech. Geotech. Eng. 2020, 12, 197–211. [Google Scholar] [CrossRef]
- Ganasan, R.; Lim, A.; Wijeyesekera, D. Physical and software modelling for challenging soil structure interaction. ARPN J. Eng. Appl. Sci. 2016, 11, 3668–3676. [Google Scholar]
- Houda, M.; Jenck, O.; Emeriault, F.; Briançon, L.; Gotteland, P. Development of a threedimensional small scale model to simulate soil improvement by rigid piles. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013. [Google Scholar]
- Sreelakshmi, G.; Asha, M.; Suraj, S. Application of the particle image velocimetry to study pile soil interaction. In Proceedings of the Indian Geotechnical Conference (IGC), Chennai, India, 15–17 December 2016; Indian Institute of Technology (IIT) Madras: Chennai, India, 2016. [Google Scholar]
- Giardina, G.; Marini, A.; Hendriks, M.A.; Rots, J.G.; Rizzardini, F.; Giuriani, E. Experimental analysis of a masonry façade subject to tunnelling-induced settlement. Eng. Struct. 2012, 45, 421–434. [Google Scholar] [CrossRef]
- Xu, C.; Liang, L.; Chen, Q.; Luo, W.; Chen, Y.F. Experimental study of soil arching effect under seepage condition. Acta Geotech. 2019, 14, 2031–2044. [Google Scholar] [CrossRef]
- Son, M.; Cording, E.J. Estimation of building damage due to excavation-induced ground movements. J. Geotech. Geoenviron. Eng. 2005, 131, 162–177. [Google Scholar] [CrossRef]
- Laefer, D.F.; Hong, L.T.; Erkal, A.; Long, J.H.; Cording, E.J. Manufacturing, assembly, and testing of scaled, historic masonry for one-gravity, pseudo-static, soil-structure experiments. Constr. Build. Mater. 2011, 25, 4362–4373. [Google Scholar] [CrossRef]
- Marini, A.; Giuriani, E.; Riva, P. Comportamento Sperimentale di Una Facciata in Muratura su Archi Nell’Ipotesi di Cedimento Differenziale di un Pilastro. In Proceedings of the Atti Convegno Nazionale Sperimentazione su Materiali e Strutture, Venice, Italy, 6–7 December 2006. [Google Scholar]
- Moussaei, N.; Khosravi, M.H.; Hossaini, M.F. Physical modeling of tunnel induced displacement in sandy grounds. Tunn. Undergr. Space Technol. 2019, 90, 19–27. [Google Scholar] [CrossRef]
- Chapman, D.; Ahn, S.; Hunt, D.V. Investigating ground movements caused by the construction of multiple tunnels in soft ground using laboratory model tests. Can. Geotech. J. 2007, 44, 631–643. [Google Scholar] [CrossRef]
- Tang, H.; Hu, X.; Xu, C.; Li, C.; Yong, R.; Wang, L. A novel approach for determining landslide pushing force based on landslide-pile interactions. Eng. Geol. 2014, 182, 15–24. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Tang, H.; Hu, X.; Liu, X.; Wang, C.; Liu, T.; Zhang, Y. Model testing of the response of stabilizing piles in landslides with upper hard and lower weak bedrock. Eng. Geol. 2016, 204, 65–76. [Google Scholar] [CrossRef]
- Guo, W.D.; Qin, H. Thrust and bending moment of rigid piles subjected to moving soil. Can. Geotech. J. 2010, 47, 180–196. [Google Scholar] [CrossRef]
- Hu, X.; Liu, D.; Zheng, W.; Tannant, D.; Kang, C. 1-g physical modeling in engineering geology and its application of pile-reinforced reservoir landslides. Eng. Geol. 2024, 331, 107450. [Google Scholar] [CrossRef]
- Phillips, R. Ground Deformation in the Vicinity of a Trench Heading; University of Cambridge: Cambridge, UK, 1986. [Google Scholar]
- Britto, A.M.; Kusakabe, O. Stability of axisymmetric excavations in clays. J. Geotech. Eng. 1983, 109, 666–681. [Google Scholar] [CrossRef]
- Faustin, N.E. Performance of Circular Shafts and Ground Behaviour During Construction. PhD Thesis, University of Cambridge, Cambridge, UK, 2017. [Google Scholar]
- New, B. Settlements due to shaft construction. Tunn. Tunn. Int. 2017, 16–17. [Google Scholar]
- Garnier, J.; Gaudin, C.; Springman, S.M.; Culligan, P.; Goodings, D.; Konig, D.; Kutter, B.; Phillips, R.; Randolph, M.; Thorel, L. Catalogue of scaling laws and similitude questions in geotechnical centrifuge modelling. Int. J. Phys. Model. Geotech. 2007, 7, 1–23. [Google Scholar] [CrossRef]
- Taylor, R. Centrifuges in modelling: Principles and scale effects. In Geotechnical Centrifuge Technology; CRC Press: Boca Raton, FL, USA, 2018; pp. 19–33. [Google Scholar]
- Bhattacharya, S.; Demirci, H.E.; Nikitas, G.; Prakhya, G.K.V.; Lombardi, D.; Alexander, N.A.; Aleem, M.; Amani, S.; Mylonakis, G. Physical modeling of interaction problems in geotechnical engineering. In Modeling in Geotechnical Engineering; Elsevier: Amsterdam, The Netherlands, 2021; pp. 205–256. [Google Scholar]
- Tobita, T.; Iai, S.; von der Tann, L.; Yaoi, Y. Application of the generalised scaling law to saturated ground. Int. J. Phys. Model. Geotech. 2011, 11, 138–155. [Google Scholar] [CrossRef]
- Black, J.A. Centrifuge modelling with transparent soil and laser aided imaging. Geotech. Test. J. 2015, 38, 631–644. [Google Scholar] [CrossRef]
- Bradshaw, A.; Giampa, J.; Gerkus, H.; Jalilvand, S.; Fanning, J.; Nanda, S.; Gilbert, R.; Gavin, K.; Sivakumar, V. Scaling considerations for 1-g model horizontal plate anchor tests in sand. Geotech. Test. J. 2016, 39, 1006–1014. [Google Scholar] [CrossRef]
- Gibson, A.D. Physical Scale Modeling of Geotechnical Structures at One-G; California Institute of Technology: Pasadena, CA, USA, 1997. [Google Scholar]
- Meguid, M.; Tobar, T. Distribution of Active Earth Pressure on Vertical Shafts. 2009. Available online: https://www.geogroup.mcgill.ca/Research/Conferences/13-Distribution%20of%20Active%20Earth%20Pressure%20on%20Vertical%20Shafts_Tobar_Meguid_CGC_2009.pdf (accessed on 5 January 2025).
- Song, G.; Sheil, B.B. Laboratory Testing of Construction-Induced Ground Displacements for Open Caisson Shafts in Sand. J. Geotech. Geoenviron. Eng. 2023, 149, 04023086. [Google Scholar] [CrossRef]
- Chavda, J.T.; Dodagoudar, G.R. Experimental studies on a circular open caisson. Int. J. Phys. Model. Geotech. 2022, 22, 70–87. [Google Scholar] [CrossRef]
- Craig, W.H.; Vinogradov, V.V.; Frolovsky, Y.K.; Zaytsev, A.A. Pioneers of centrifuge modelling. Int. J. Phys. Model. Geotech. 2015, 15, 3–18. [Google Scholar] [CrossRef]
- Kim, K.-Y.; Lee, D.-S.; Cho, J.; Jeong, S.-S.; Lee, S. The effect of arching pressure on a vertical circular shaft. Tunn. Undergr. Space Technol. 2013, 37, 10–21. [Google Scholar] [CrossRef]
- Faustin, N.; Mair, R.; Elshafie, M. Development of a new excavation technique for centrifuge testing in sand. In Geotechnical Aspects of Underground Construction in Soft Ground; CRC Press: Boca Raton, FL, USA, 2021; pp. 275–282. [Google Scholar]
- Imamura, S.; Nomoto, T.; Fujii, T.; Hagiwara, T.; Kusakabe, O. Earth pressures acting on a deep shaft and the movements of adjacent ground in sand. In Proceedings of the Geotechnical Aspects of Underground Construction on Soft Ground, Tokyo, Japan, 19–21 July 1996; pp. 647–652. [Google Scholar]
- Le, B.T.; Goodey, R.J.; Divall, S. Subsurface ground movements due to circular shaft construction. Soils Found. 2019, 59, 1160–1171. [Google Scholar] [CrossRef]
- Nakai, T.; Xu, L.; Yamazaki, H. 3D and 2D model tests and numerical analyses of settlements and earth pressures due to tunnel excavation. Soils Found. 1997, 37, 31–42. [Google Scholar] [CrossRef]
- Pang, P. Physical and numerical modelling. In Geotechnical Aspects of Underground Construction in Soft Ground; CRC Press: Boca Raton, FL, USA, 2008; pp. 125–136. [Google Scholar]
- Aydan, Ö.; Ohta, Y.; Geniş, M.; Tokashiki, N.; Ohkubo, K. Response and stability of underground structures in rock mass during earthquakes. Rock Mech. Rock Eng. 2010, 43, 857–875. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Liu, S.; Zhu, Y.; Pan, W.; Zhou, J. Physical model test of transparent soil on coupling effect of cut-off wall and pumping wells during foundation pit dewatering. Acta Geotech. 2019, 14, 141–162. [Google Scholar] [CrossRef]
- Ma, J. Numerical simulation of retaining wall in deep foundation based on COMSOL Multiphysics. Highw. Eng 2018, 1, 256–260. [Google Scholar]
- Li, P.; Song, E.; Zheng, T. Initial sinking method for large open caisson in a highway bridge project. In Proceedings of the China-Europe Conference on Geotechnical Engineering, Vienna, Austria, 13–16 August 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 2, pp. 1692–1696. [Google Scholar]
- Jiang, B.-n.; Ma, J.-l.; Chu, J.-l. The influence of soil surrounding the caisson cutting edge to excavation and sinking. In Proceedings of the International Conference on Geotechnical and Earthquake Engineering 2018, Austin, TX, USA, 10–13 June 2018; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 435–448. [Google Scholar]
- Xiao-qing, Z.; Wei, Z.; Xin, Y.; Jin-chang, W.; Zhong-xuan, Y.; Xiao-nan, G. Experimental study and simulation on deformation characteristics of caissons in sand under horizontal loads. Chin. J. Geotech. Eng. 2021, 43, 80–83. [Google Scholar]
- Lai, F.; Liu, S.; Deng, Y.; Sun, Y.; Wu, K.; Liu, H. Numerical investigations of the installation process of giant deep-buried circular open caissons in undrained clay. Comput. Geotech. 2020, 118, 103322. [Google Scholar] [CrossRef]
- Yang, Q.-R.; Li, M.-G.; Chen, J.-J. Influence of a flexible retaining wall on performance of an adjacent deep excavation. KSCE J. Civ. Eng. 2022, 26, 661–672. [Google Scholar] [CrossRef]
- Dong, X.; Tu, J.; Xu, J.; Cai, L.; Wu, B.; Cai, L. Based on Abaqus finite element analysis software to assist the construction of super large caisson. In Proceedings of the 2023 International Seminar on Computer Science and Engineering Technology (SCSET), New York, NY, USA, 29–30 April 2023; pp. 627–631. [Google Scholar]
- Kumar, M.; Chatterjee, K. A numerical study on lateral load response of caissons in static conditions. In Geo-Congress 2020; American Society of Civil Engineers: Reston, VA, USA, 2020; pp. 15–22. [Google Scholar]
- De Falco, N.; Bilotta, E.; Divall, S.; Goodey, R. Numerical analysis of deep ground movements induced by circular shaft construction. In Proceedings of the 20th International Conference on Soil Mechanics and Geotechnical Engineering, Sydney, Australia, 1–5 May 2023. [Google Scholar]
- Zhou, J.; Liu, C.; Xu, J.; Zhang, Z.; Li, Z. Deformation Mechanism and Control of In-Situ Assembling Caisson Technology in Soft Soil Area under Field Measurement and Numerical Simulation. Materials 2023, 16, 1125. [Google Scholar] [CrossRef]
- Lai, F.; Zhang, N.; Liu, S.; Sun, Y.; Li, Y. Ground movements induced by installation of twin large diameter deeply-buried caissons: 3D numerical modeling. Acta Geotech. 2021, 16, 2933–2961. [Google Scholar] [CrossRef]
- Georgiannou, V.N.; Serafis, A.; Pavlopoulou, E.-M. Analysis of a vertical segmental shaft using 2D & 3D finite element codes. GEOMATE J. 2017, 13, 138–146. [Google Scholar]
- Peng, F.-L.; Wang, H.-L.; Tan, Y.; Xu, Z.-L.; Li, Y.-L. Field measurements and finite-element method simulation of a tunnel shaft constructed by pneumatic caisson method in Shanghai soft ground. J. Geotech. Geoenviron. Eng. 2011, 137, 516–524. [Google Scholar] [CrossRef]
- Sun, Y.; Su, J.-B.; Xia, X.-H.; Xu, Z.-L. Numerical analysis of soil deformation behind the reaction wall of an open caisson induced by horizontal parallel pipe-jacking construction. Can. Geotech. J. 2015, 52, 2008–2016. [Google Scholar] [CrossRef]
- Suwansawat, S.; Einstein, H.H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling. Tunn. Undergr. Space Technol. 2006, 21, 133–150. [Google Scholar] [CrossRef]
- Yu, Y.; Bathurst, R.J.; Allen, T.M.; Nelson, R. Physical and numerical modelling of a geogrid-reinforced incremental concrete panel retaining wall. Can. Geotech. J. 2016, 53, 1883–1901. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, B.-Y.; Yang, D. Simulation study on foundation pit excavation in soft soil considering effect of creep and seepage. Mod. Tunn. Technol. 2020, 57, 91–98. [Google Scholar]
- Shah, R.; Zhao, C.; Lavasan, A.A.; Peila, D.; Schanz, T.; Lucarelli, A. Influencing factors affecting the numerical simulation of the mechanized tunnel excavation using FEM and FDM techniques. In Proceedings of the EUROTUN, Innsbruck, Austria, 18–20 April 2017. [Google Scholar]
- Yin, Z.-Y. Three-dimensional numerical modelling of progressive failure of caisson foundation in sand using a coupled FDM–DEM method. Ocean Eng. 2022, 253, 111332. [Google Scholar] [CrossRef]
- Hamann, T.; Qiu, G.; Grabe, J. Application of a Coupled Eulerian–Lagrangian approach on pile installation problems under partially drained conditions. Comput. Geotech. 2015, 63, 279–290. [Google Scholar] [CrossRef]
- Ko, J.; Jeong, S.; Lee, J.K. Large deformation FE analysis of driven steel pipe piles with soil plugging. Comput. Geotech. 2016, 71, 82–97. [Google Scholar] [CrossRef]
- Grabe, J.; Heins, E. Coupled deformation–seepage analysis of dynamic capacity tests on open-ended piles in saturated sand. Acta Geotech. 2017, 12, 211–223. [Google Scholar] [CrossRef]
- Wang, D.; Bienen, B.; Nazem, M.; Tian, Y.; Zheng, J.; Pucker, T.; Randolph, M.F. Large deformation finite element analyses in geotechnical engineering. Comput. Geotech. 2015, 65, 104–114. [Google Scholar] [CrossRef]
- Dong, Z.; Jin, S.; Cao, X.; He, Z.; Yan, H. Enhanced static simulation process of caisson sinking using the coupled Euler-Lagrange method. Ocean Eng. 2023, 286, 115453. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, P.; Li, J.; Lin, J.; Ge, T.; Deng, S.; Ren, R.; Wang, Z. Deformation characteristics and failure evolution process of the existing metro station under unilateral deep excavation. Eng. Fail. Anal. 2022, 131, 105870. [Google Scholar] [CrossRef]
- Chen, T.; Zhou, K.; Wei, J.; Liu, X.-C.; Lin, Y.-L.; Zhang, J.; Shen, Q. Excavation influence of triangular-distribution tunnels for wind pavilion group of a metro station. J. Cent. South Univ. 2020, 27, 3852–3874. [Google Scholar] [CrossRef]
- Tran, V.D.; Yacoub, T.E.; Meguid, M.A. On the Analysis of Vertical Shafts in Soft Ground: Evaluating Soil-Structure Interaction Using Two Different Numerical Modeling Techniques. 2013. Available online: https://geogroup.mcgill.ca/Research/Conferences/23-On%20the%20analysis%20of%20vertical%20shafts%20in%20soft%20ground_Tran_et_al_GeoMon2013.pdf (accessed on 24 December 2024).
- Zhang, N.; Arroyo, M.; Ciantia, M.O.; Gens, A.; Butlanska, J. Standard penetration testing in a virtual calibration chamber. Comput. Geotech. 2019, 111, 277–289. [Google Scholar] [CrossRef]
- Long, Y.-Y.; Tan, Y. Soil arching due to leaking of tunnel buried in water-rich sand. Tunn. Undergr. Space Technol. 2020, 95, 103158. [Google Scholar] [CrossRef]
- Zhu, H.-X.; Yin, Z.-Y. Grain rotation-based analysis method for shear band. J. Eng. Mech. 2019, 145, 04019073. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E.; Mack, M. Fully coupled simulation of a hydraulic fracture interacting with natural fractures with a hybrid discrete-continuum method. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1430–1452. [Google Scholar] [CrossRef]
- Zhu, H.X.; Yin, Z.Y.; Zhang, Q. A novel coupled FDM-DEM modelling method for flexible membrane boundary in laboratory tests. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 389–404. [Google Scholar] [CrossRef]
- Wang, J.; Hua, H.; Lian, W. Penetration simulation for an open caisson using mesh-free SPH method. In Proceedings of the Computer Methods and Recent Advances in Geomechanics, Kyoto, Japan, 22–25 September 2014; pp. 105–109. [Google Scholar]
- Jin, Z.; Yin, Z.-Y.; Kotronis, P.; Jin, Y.-F. Numerical investigation on evolving failure of caisson foundation in sand using the combined Lagrangian-SPH method. Mar. Georesour. Geotechnol. 2019, 37, 23–35. [Google Scholar] [CrossRef]
- Rogers, B.D.; Dalrymple, R.A.; Stansby, P.K. Simulation of caisson breakwater movement using 2-D SPH. J. Hydraul. Res. 2010, 48, 135–141. [Google Scholar] [CrossRef]
- Zhang, J. Numerical simulation on the whole sinking process of open caisson with an improved SPH method. Math. Probl. Eng. 2021, 2021, 6699880. [Google Scholar] [CrossRef]
- Coombs, W. Finite Deformation of Particulate Geomaterials: Frictional and Anisotropic Critical State Elasto-Plasticity; Durham University: Durham, UK, 2011. [Google Scholar]
- Huang, B.; Bathurst, R.J.; Hatami, K. Numerical study of reinforced soil segmental walls using three different constitutive soil models. J. Geotech. Geoenviron. Eng. 2009, 135, 1486–1498. [Google Scholar] [CrossRef]
- Robert, D.; Soga, K.; Britto, A. Soil constitutive models to simulate pipeline-soil interaction behaviour. In Proceedings of the International Conference on Geotechnical Engineering ICGE, Colombo, Sri Lanka, 10–11 August 2015; pp. 347–350. [Google Scholar]
- Do, N.V.; Nghia, D.T.; Tu, P.Q. Stiffness of Soil in Excavation-Induced Deformation Analysis in Vietnam. In Geotechnics for Sustainable Infrastructure Development; Springer: Berlin/Heidelberg, Germany, 2019; pp. 351–354. [Google Scholar]
- Dahal, B.K.; Regmi, S.; Paudyal, K.; Dahal, D.; KC, D. Enhancing Deep Excavation Optimization: Selection of an Appropriate Constitutive Model. CivilEng 2024, 5, 785–800. [Google Scholar] [CrossRef]
- Lim, A.; Ou, C.-Y.; Hsieh, P.-G. Evaluation of clay constitutive models for analysis of deep excavation under undrained conditions. J. Geoengin. 2010, 5, 9–20. [Google Scholar]
- Dawd, S.; Trygg, R. FE analyses of horizontal deformations due to excavation processes in deep layers of soft Gothenburg clay. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2013; p. 80. [Google Scholar]
- Huynh, Q.T.; Lai, V.Q.; Tran, V.T.; Nguyen, M.T. Back analysis on deep excavation in the thick sand layer by hardening soil small model. In Proceedings of the ICSCEA 2019: International Conference on Sustainable Civil Engineering and Architecture, Ho Chi Minh, Vietnam, 24–26 October 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 659–668. [Google Scholar]
- Mitew-Czajewska, M. Parametric study of deep excavation in clays. Bull. Pol. Acad. Sciences. Tech. Sci. 2018, 66, 747–754. [Google Scholar] [CrossRef]
- Miranda, P.; Vargas Jr, E.; Moraes, A. Evaluation of the Modified Cam Clay model in basin and petroleum system modeling (BPSM) loading conditions. Mar. Pet. Geol. 2020, 112, 104112. [Google Scholar] [CrossRef]
- Carter, J.P. Constitutive modelling in computational geomechanics–61st Rankine lecture, British Geotechnical Association, 2023. Géotechnique 2024, 74, 1511–1535. [Google Scholar] [CrossRef]
- Wheeler, S.J.; Näätänen, A.; Karstunen, M.; Lojander, M. An anisotropic elastoplastic model for soft clays. Can. Geotech. J. 2003, 40, 403–418. [Google Scholar] [CrossRef]
- Yu, H.-S. CASM: A unified state parameter model for clay and sand. Int. J. Numer. Anal. Methods Geomech. 1998, 22, 621–653. [Google Scholar] [CrossRef]
- Atkinson, J. Experimental determination of stress-strain-time characteristics in laboratory and-in-situ tests. General report. In Proceedings of the 10th Soil Mechanics & Foundation Engineering, Florence, Italy, 26–30 May 1991; pp. 915–956. [Google Scholar]
- Tomlinson, M. Foundation Design and Construction Longman Scientific & Technical; Longman Scientific & Technical: Harlow, UK, 1986. [Google Scholar]
- Nonveiller, E. Open caissons for deep foundations. J. Geotech. Eng. 1987, 113, 424–439. [Google Scholar] [CrossRef]
- Puller, M. Deep Excavation; ICE Publishing: London, UK, 2015. [Google Scholar]
- Abdrabbo, F.; Gaaver, K. Challenges and uncertainties relating to open caissons. DFI J. -J. Deep Found. Inst. 2012, 6, 21–32. [Google Scholar] [CrossRef]
- Wang, J.; Chai, L.S.; Wu, H. Numerical simulation on the sinking process of open caisson with particle flow code (PFC). Adv. Mater. Res. 2014, 838, 831–834. [Google Scholar] [CrossRef]
- Royston, R.; Phillips, B.; Sheil, B.; Byrne, B. Bearing capacity beneath tapered blades of open dug caissons in sand. Civ. Eng. Res. Irel. 2016, 2016, 473–478. [Google Scholar]
- Sheil, B.; Templeman, J. Bearing capacity of open caissons embedded in sand. Géotechnique 2021, 73, 495–505. [Google Scholar] [CrossRef]
- Chavda, J.T.; Dodagoudar, G. Finite element evaluation of bearing capacity factors for cutting face of open caissons. Int. J. Geotech. Eng. 2022, 16, 951–961. [Google Scholar] [CrossRef]
- Wu, W.; Yu, H.-S. Proceedings of China-Europe Conference on Geotechnical Engineering; Springer: Berlin/Heidelberg, Germany, 2018; Volume 2. [Google Scholar]
- Royston, R. Investigation of Soil-Structure Interaction for Large Diameter Caissons; University of Oxford: Oxford, UK, 2018. [Google Scholar]
- Tomlinson, M.J.; Boorman, R. Foundation Design and Construction; Pearson Education: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Chavda, J.T.; Mishra, S.; Dodagoudar, G.R. Experimental evaluation of ultimate bearing capacity of the cutting edge of an open caisson. Int. J. Phys. Model. Geotech. 2020, 20, 281–294. [Google Scholar] [CrossRef]
- Fischer, G.R.; Gerszewski, W.L.; Barchok, F.J.; Yavarow, M.K. Deep Caisson Sinking in Soft Soils, Grand Forks, North Dakota. 2004. Available online: https://scholarsmine.mst.edu/icchge/5icchge/session01/42/ (accessed on 15 November 2024).
- Ter-Galustov, S.; Ponomarenko, A.; Opershtein, V.; Ivanov, V. Experience in sinking an open caisson in a thixotropic lining. Soil Mech. Found. Eng. 1966, 3, 128–131. [Google Scholar] [CrossRef]
- Newman, T.; Wong, H. Sinking a jacked caisson within the London Basin geological sequence for the Thames Water Ring Main extension. Q. J. Eng. Geol. Hydrogeol. 2011, 44, 221–232. [Google Scholar] [CrossRef]
- Shi, Z.; Li, S.; Yang, S.; Feng, C. Study on the characteristics of friction resistance and the mechanism of sudden sinking in the middle and late sinking stages of super large caisson foundation. Chin. J. Geotech. Eng 2019, 38, 3894–3904. [Google Scholar]
- Westergaard, H.M. Plastic State of Stress Around a Deep Well; Harvard University: Cambridge, MA, USA, 1939. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1943. [Google Scholar]
- Coulomb, C.A. Essai sur une Application des Regles de Maximis et Minimis a Quelques Problemes de Statique Relatifs a L’architecture (Essay on Maximums and Minimums of Rules to Some Static Problems Relating to Architecture)–TRID; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1973. [Google Scholar]
- Rankine, W.J.M., II. On the Stability of Loose Earth; Philosophical Transactions of the Royal Society of London: London, UK, 1857; pp. 9–27. [Google Scholar]
- Liu, F.; Wang, J. A generalized slip line solution to the active earth pressure on circular retaining walls. Comput. Geotech. 2008, 35, 155–164. [Google Scholar] [CrossRef]
- Derezantzev, V. Earth pressure on the cylindrical retaining walls. In Proceedings of the Brussels Conference on Earth Pressure Problems, II, Brussels, Belgium, September 1958; pp. 21–27. [Google Scholar]
- Cheng, Y.M.; Au, S.; Hu, Y.; Wei, W. Active pressure for circular cut with Berezantzev’s and Prater’s theories, numerical modeling and field measurements. Soils Found. 2008, 48, 621–631. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Zhang, L. Axi-symmetric active earth pressure obtained by the slip line method with a general tangential stress coefficient. Comput. Geotech. 2009, 36, 352–358. [Google Scholar] [CrossRef]
- Guojun, X.; Jianhua, W. A rigorous characteristic line theory for axisymmetric problems and its application in circular excavations. Acta Geotech. 2020, 15, 439–453. [Google Scholar] [CrossRef]
- Wong, R.; Kaiser, P. Design and performance evaluation of vertical shafts: Rational shaft design method and verification of design method. Can. Geotech. J. 1988, 25, 320–337. [Google Scholar] [CrossRef]
- Prater, E. An examination of some theories of earth pressure on shaft linings. Can. Geotech. J. 1977, 14, 91–106. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, Y. Active earth pressure on circular shaft lining obtained by simplified slip line solution with general tangential stress coefficient. Chin. J. Geotech. Eng. 2005, 27, 110–115. [Google Scholar]
- Tobar, T.; Meguid, M.A. Comparative evaluation of methods to determine the earth pressure distribution on cylindrical shafts: A review. Tunn. Undergr. Space Technol. 2010, 25, 188–197. [Google Scholar] [CrossRef]
- Luo, C. Settlement Monitoring and Numerical Simulation Analysis of Super-Deep and Large Caisson Foundation. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Yan, F.; Shi, G. Analysis of limiting soil resistance beneath cutting curb during sinking of open caisson. Rock Soil Mech. 2013, 34, 80–87. [Google Scholar]
- Zhang, Z.; Deng, Y.; Zheng, F.; Wang, J. Analysis on sudden sinking behaviors of massive open caisson in deep-thick soft clay area. Chin. J. Undergr. Space Eng. 2020, 16, 933–943. [Google Scholar]
- Mu, B.; Wang, Y.; Zhu, J.; Gong, W.; Ouyang, Z. Analysis of large caisson sinking measured resistance. J. Civ. Archit. Environ. Eng. 2012, 33, 107–115. [Google Scholar]
- Qin, S.; Yuan, R.; Zheng, Q.; Fu, Z.; Ma, R.; Xu, L. Research on structural systems for very long-span rail-cum-road cable-stayed bridge. Bridge Constr. 2020, 50, 1–8. [Google Scholar]
- Walz, B. Left bracket apparatus for measuring the three-dimensional active soil pressure on a round model caisson right bracket. Baumasch. Bautech. 1973, 20, 339–344. [Google Scholar]
- Tobar, T.; Meguid, M.A. Experimental study of the earth pressure distribution on cylindrical shafts. J. Geotech. Geoenviron. Eng. 2011, 137, 1121–1125. [Google Scholar] [CrossRef]
- Tran, V.D.; Meguid, M.A.; Chouinard, L.E. A discrete element study of the earth pressure distribution on cylindrical shafts. In Proceedings of the Tunnelling Association of Canada (TAC) Conference 2012, Montreal, QC, Canada, 17–20 October 2012. [Google Scholar]
- Tran, V.D.; Meguid, M.A.; Chouinard, L.E. Discrete element and experimental investigations of the earth pressure distribution on cylindrical shafts. Int. J. Geomech. 2014, 14, 80–91. [Google Scholar] [CrossRef]
- Yan, X.; Zhan, W.; Hu, Z.; Xiao, D.; Yu, Y.; Wang, J. Field study on deformation and stress characteristics of large open caisson during excavation in deep marine soft clay. Adv. Civ. Eng. 2021, 2021, 7656068. [Google Scholar] [CrossRef]
- Jiang, B.; Ma, J.; Li, M.; Chu, J. Experiments on spatial stress of foot blade during caisson sinking in water. Rock Soil Mech. 2019, 40, 1693–1703. [Google Scholar]
- Gerolymos, N.; Gazetas, G. Development of Winkler model for static and dynamic response of caisson foundations with soil and interface nonlinearities. Soil Dyn. Earthq. Eng. 2006, 26, 363–376. [Google Scholar] [CrossRef]
- Chiou, J.-S.; Ko, Y.-Y.; Hsu, S.-Y.; Tsai, Y.-C. Testing and analysis of a laterally loaded bridge caisson foundation in gravel. Soils Found. 2012, 52, 562–573. [Google Scholar] [CrossRef]
- Schwamb, T. Performance Monitoring and Numerical Modelling of a Deep Circular Excavation. 2014. Available online: https://www.repository.cam.ac.uk/items/04ec45a9-4b8b-4ece-b848-7806d4636412 (accessed on 5 December 2024).
- Schwamb, T.; Elshafie, M.Z.; Soga, K.; Mair, R.J. Considerations for monitoring of deep circular excavations. Proc. Inst. Civ. Eng.-Geotech. Eng. 2016, 169, 477–493. [Google Scholar] [CrossRef]
- Schwamb, T.; Soga, K.; Mair, R.J.; Elshafie, M.Z.; Sutherden, R.; Boquet, C.; Greenwood, J. Fibre optic monitoring of a deep circular excavation. Proc. Inst. Civ. Eng.-Geotech. Eng. 2014, 167, 144–154. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, R.; Li, Z. Automatic monitoring and structural stress analysis during ultra-large onshore caisson sinking construction. Results Eng. 2024, 21, 101951. [Google Scholar] [CrossRef]
- Dong, X.; Guo, M.; Wang, S. Inclination prediction of a giant open caisson during the sinking process using various machine learning algorithms. Ocean Eng. 2023, 269, 113587. [Google Scholar] [CrossRef]
- Zhi, W. This ACPP technology system provides a new solution for underground space construction [N]. Securities Times, 30 October 2024. [Google Scholar]
- Wang, J.; Abbasi, N.S.; Pan, W.; Alidekyi, S.N.; Li, H.; Ahmed, B.; Asghar, A. A Review of Vertical Shaft Technology and Application in Soft Soil for Urban Underground Space. Appl. Sci. 2025, 15, 3299. [Google Scholar] [CrossRef]
- Zar, A.; Hussain, Z.; Akbar, M.; Rabczuk, T.; Lin, Z.; Li, S.; Ahmed, B. Towards vibration-based damage detection of civil engineering structures: Overview, challenges, and future prospects. Int. J. Mech. Mater. Des. 2024, 20, 591–662. [Google Scholar] [CrossRef]
- Dong, X.; Guo, M.; Wang, S. Advanced prediction of the sinking speed of open caissons based on the spatial-temporal characteristics of multivariate structural stress data. Appl. Ocean Res. 2022, 127, 103330. [Google Scholar] [CrossRef]
- Guo, M.; Dong, X.; Shen, K.; Wang, S.; Lan, G.; Chen, Z. Study on the variation of the bottom resistance during sinking stage of super large caisson foundation. Chin. J. Rock Mech. Eng. 2021, 40, 2976–2985. [Google Scholar]
- Tian, W.; Li, H.; Wang, Y.; Zhu, Y.; Zhu, H.; Li, K. Data-Driven Decision Algorithm for Open Caisson Foundation Construction. Adv. Civ. Eng. 2024, 2024, 9373931. [Google Scholar] [CrossRef]
- Song, G.; He, Y.; Sheil, B.; Morris, J. Ground settlement prediction for open caisson shafts in sand using a neural network constrained by empiricism. Comput. Geotech. 2024, 166, 106001. [Google Scholar] [CrossRef]
- Shuman, N.M.; Khan, M.S.; Amini, F. Efficient machine learning model for settlement prediction of large diameter helical pile in c—Φ soil. AI Civ. Eng. 2024, 3, 10. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.-Y.; Jin, Y.-F. Machine learning-based modelling of soil properties for geotechnical design: Review, tool development and comparison. Arch. Comput. Methods Eng. 2021, 29, 1229–1245. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, H.-M. Digital geotechnics: From data-driven site characterisation towards digital transformation and intelligence in geotechnical engineering. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2024, 18, 8–32. [Google Scholar] [CrossRef]
- Shahin, M.A. A review of artificial intelligence applications in shallow foundations. Int. J. Geotech. Eng. 2015, 9, 49–60. [Google Scholar] [CrossRef]
- Bozorgzadeh, N.; Feng, Y. Evaluation structures for machine learning models in geotechnical engineering. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2024, 18, 52–59. [Google Scholar] [CrossRef]
- Li, K.-Q.; Yin, Z.-Y. State of the art of coupled thermo–hydro-mechanical–chemical modelling for frozen soils. Arch. Comput. Methods Eng. 2024, 32, 1039–1096. [Google Scholar] [CrossRef]
- Huang, Y.; Lei, Z.; Lipnikov, K.; Moulton, J.; Sweeney, M.; Hyman, J.; Knight, E.; Stauffer, P. Modeling Coupled Thermo-Hydro-Mechanical-Chemical Processes in Subsurface Geological Media. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023; ARMA: Atlanta, GA, USA, 2023. [Google Scholar]
- Jing, L.; Feng, X. Numerical modeling for coupled thermo-hydro-mechanical and chemical processes (THMC) of geological media—International and Chinese experiences. Chin. J. Rock Mech. Eng. 2003, 22, 1704–1715. [Google Scholar]
- Wang, J.; Ahmed, B.; Huang, J.; Nong, X.; Xiao, R.; Abbasi, N.S.; Alidekyi, S.N.; Li, H. Physical and Mechanical Properties and Constitutive Model of Rock Mass Under THMC Coupling: A Comprehensive Review. Appl. Sci. 2025, 15, 2230. [Google Scholar] [CrossRef]
- Chen, G.; Li, D.; Chen, J.; Chen, H.; Wang, J.; Jia, Z.; Sun, Q.; Xia, M. Experimental analysis of the thermo-hydro-mechanical (THM) coupling in freezing vertical shafts of unsaturated sandy soil. Cold Reg. Sci. Technol. 2024, 228, 104254. [Google Scholar] [CrossRef]
- Qi, C.; Fan, G.; Cui, Y.; Zhang, Q. Geotechnical physical model test using artificial synthetic transparent soil. Rock Soil Mech. 2015, 36, 3157–3163. [Google Scholar]
- Iskander, M. Transparent soils turn 25: Past, present, and future. In Physical Modelling in Geotechnics; CRC Press: Boca Raton, FL, USA, 2018; Volume 1, pp. 389–394. [Google Scholar]
- Allersma, H.G. Determination of the stress distribution in assemblies of photoelastic particles: Theoretical and experimental description of the application of the photoelasticity method to three-dimensional assemblies of glass particles. Exp. Mech. 1982, 22, 336–341. [Google Scholar] [CrossRef]
- Konagai, K.; Tamura, C.; Rangelow, P.; Matsushima, T. Laser-aided tomography: A tool for visualization of changes in the fabric of granular assemblage. Doboku Gakkai Ronbunshu 1992, 1992, 25–33. [Google Scholar] [CrossRef]
- Iskander, M.G.; Liu, J.; Sadek, S. Transparent amorphous silica to model clay. J. Geotech. Geoenviron. Eng. 2002, 128, 262–273. [Google Scholar] [CrossRef]
- Sadek, S.; Iskander, M.G.; Liu, J. Geotechnical properties of transparent silica. Can. Geotech. J. 2002, 39, 111–124. [Google Scholar] [CrossRef]
- Ganiyu, A.A.; Rashid, A.S.A.; Osman, M.H. Utilisation of transparent synthetic soil surrogates in geotechnical physical models: A review. J. Rock Mech. Geotech. Eng. 2016, 8, 568–576. [Google Scholar] [CrossRef]
- Zhao, H.; Ge, L. Dynamic properties of transparent soil. In Dynamic Response and Soil Properties; ASCE: Reston, VA, USA, 2007; pp. 1–9. [Google Scholar]
- Liu, J.; Iskander, M.G.; Sadek, S. Consolidation and permeability of transparent amorphous silica. Geotech. Test. J. 2003, 26, 390–401. [Google Scholar] [CrossRef]
- Zhao, H.; Ge, L. Investigation on the shear moduli and damping ratios of silica gel. Granul. Matter 2014, 16, 449–456. [Google Scholar] [CrossRef]
- Guzman, I.L.; Iskander, M. Geotechnical properties of sucrose-saturated fused quartz for use in physical modeling. Geotech. Test. J. 2013, 36, 448–454. [Google Scholar] [CrossRef]
- Toiya, M.; Hettinga, J.; Losert, W. 3D Imaging of particle motion during penetrometer testing: From microscopic to macroscopic soil mechanics. Granul. Matter 2007, 9, 323–329. [Google Scholar] [CrossRef]
- Zhao, H. Development and Assessment of Transparent Soil and Particle Image Velocimetry in Dynamic Soil-Structure Interaction; Missouri University of Science and Technology, Center for Infrastructure: Rolla, MO, USA, 2007. [Google Scholar]
- Liu, J.; Liu, M.; Gao, H. Influence of pile geometry on internal sand displacement around a laterally loaded pile using transparent soil. In Deep Foundations and Geotechnical In Situ Testing; ASCE: Westford, MA, USA, 2010; pp. 104–110. [Google Scholar]
- Lwti, N.K. Assessment of Disturbance Impact of Hydraulic Jack in Pile Penetration Using Artificial Transparent Clay; Universiti Teknologi Malaysia: Johor Bharu, Malaysia, 2015. [Google Scholar]
- Liu, J. Visualization of Three-Dimensional Deformations Using Transparent “Soil” Models; Polytechnic University: Toronto, ON, Canada, 2003. [Google Scholar]
- White, D.J.; Take, W.A.; Bolton, M.D. Discussion of “Accuracy of digital image correlation for measuring deformations in transparent media” by Samer Sadek, Magued G. Iskander, and Jinyuan Liu. J. Comput. Civ. Eng. 2005, 19, 217–219. [Google Scholar] [CrossRef]
- Beckett, C.; Augarde, C. A novel image-capturing technique for the experimental study of soil deformations during compaction. Geotech. Test. J. 2011, 34, 571–578. [Google Scholar] [CrossRef]
- Ahmed, M. Investigation of Tunnel Face Stability and Ground Movements Using Transparent Soil Models; Polytechnic Institute of New York University: New York, NY, USA, 2011. [Google Scholar]
- Ahmed, M.; Iskander, M. Tunnel face support pressure and associated risk. In Geo-Risk 2011: Risk Assessment and Management; ASCE: Reston, VA, USA, 2011; pp. 939–947. [Google Scholar]
- Sadek, S.; Iskander, M.G.; Liu, J. Accuracy of digital image correlation for measuring deformations in transparent media. J. Comput. Civ. Eng. 2003, 17, 88–96. [Google Scholar] [CrossRef]
- Taylor, R.N. Geotechnical Centrifuge Technology; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Stanier, S.A.; Blaber, J.; Take, W.A.; White, D. Improved image-based deformation measurement for geotechnical applications. Can. Geotech. J. 2016, 53, 727–739. [Google Scholar] [CrossRef]
- Le, B.; Nadimi, S.; Goodey, R.; Taylor, R. System to measure three-dimensional movements in physical models. Géotech. Lett. 2016, 6, 256–262. [Google Scholar] [CrossRef]
- Song, Z.; Hu, Y.; Wang, D.; O’Loughlin, C. Pullout capacity and rotational behaviour of square anchors. In Pullout Capacity and Rotational Behaviour of Square Anchors; Taylor & Francis: Abingdon, UK, 2006; pp. 1325–1331. [Google Scholar]
- Song, Z.; Hu, Y.; O’Loughlin, C.; Randolph, M.F. Loss in anchor embedment during plate anchor keying in clay. J. Geotech. Geoenviron. Eng. 2009, 135, 1475–1485. [Google Scholar] [CrossRef]
- Blakeborough, A.; Williams, M.; Darby, A.; Williams, D. The development of real–time substructure testing. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 359, 1869–1891. [Google Scholar] [CrossRef]
- Kong, V.; Cassidy, M.J.; Gaudin, C. Development of a real-time hybrid testing method in a centrifuge. Int. J. Phys. Model. Geotech. 2015, 15, 169–190. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).