Wave-Screening Methods for Prestress-Loss Assessment of a Large-Scale Post-Tensioned Concrete Bridge Model Under Outdoor Conditions
Abstract
1. Introduction
2. Methods
2.1. The CWI Analysis
2.2. CWI of Seismic Interferometry
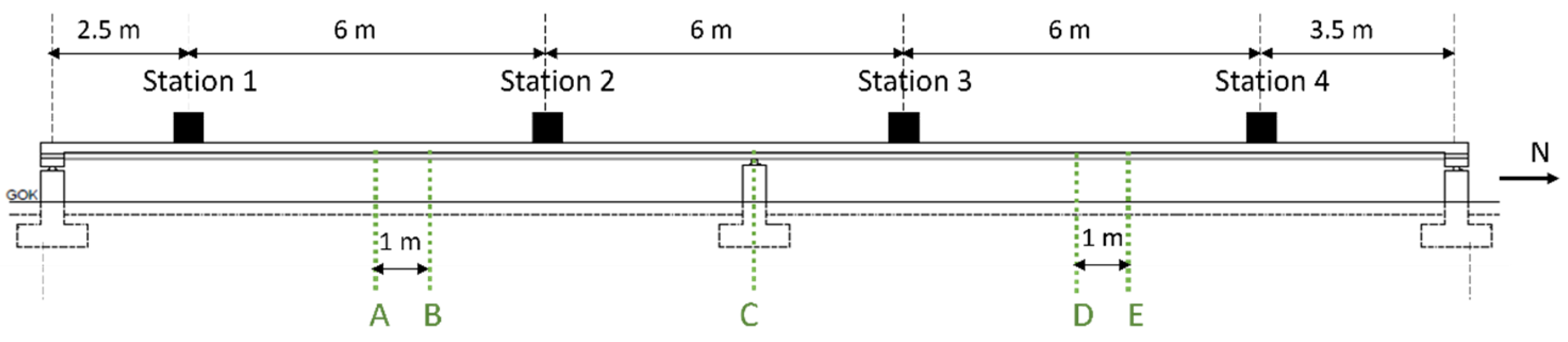
3. Experimental Setup and Instrumentation
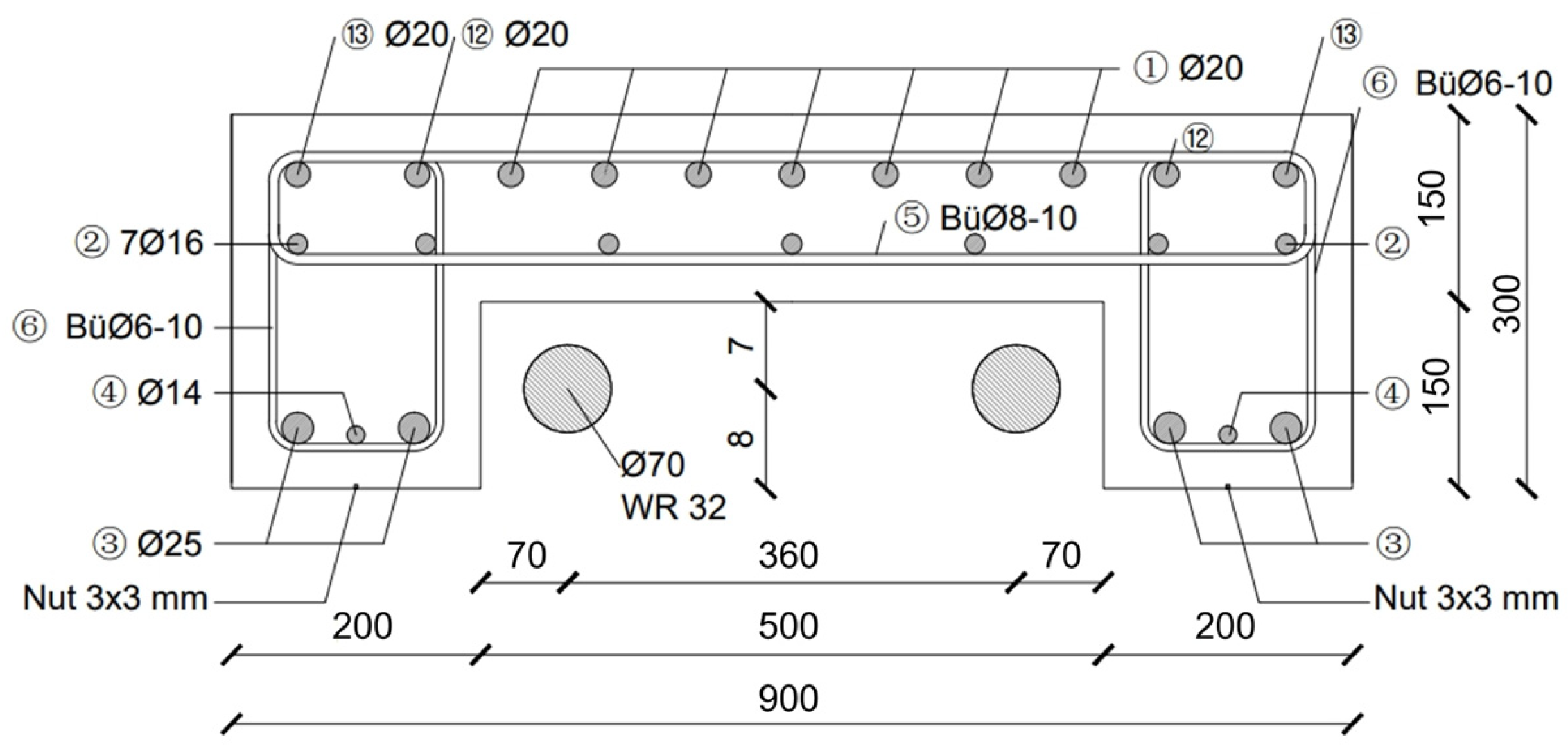
3.1. Bridge Model Description
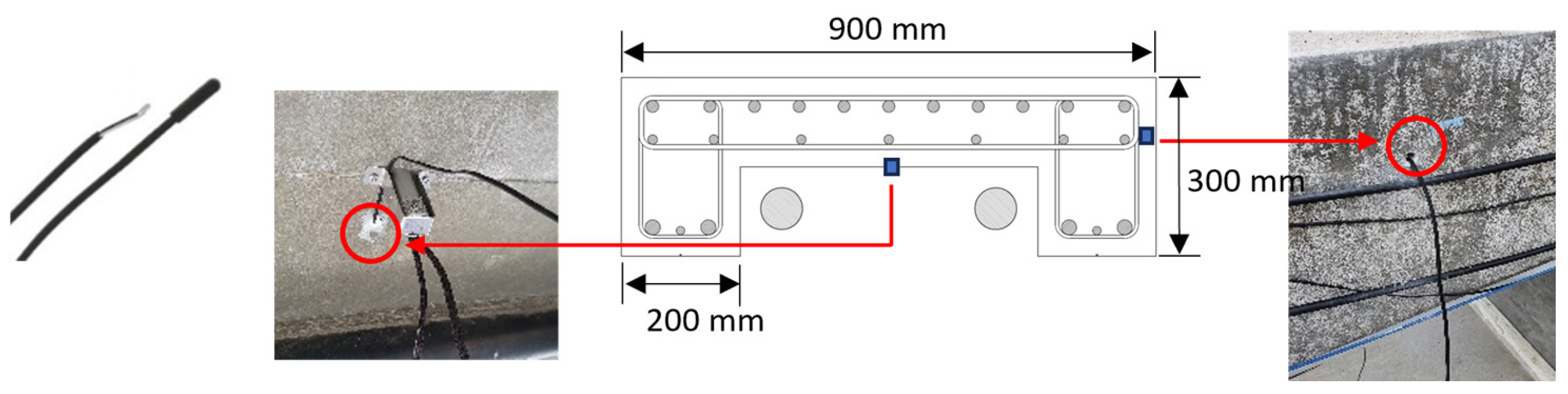
3.2. Sensor Deployment and Measurement Techniques
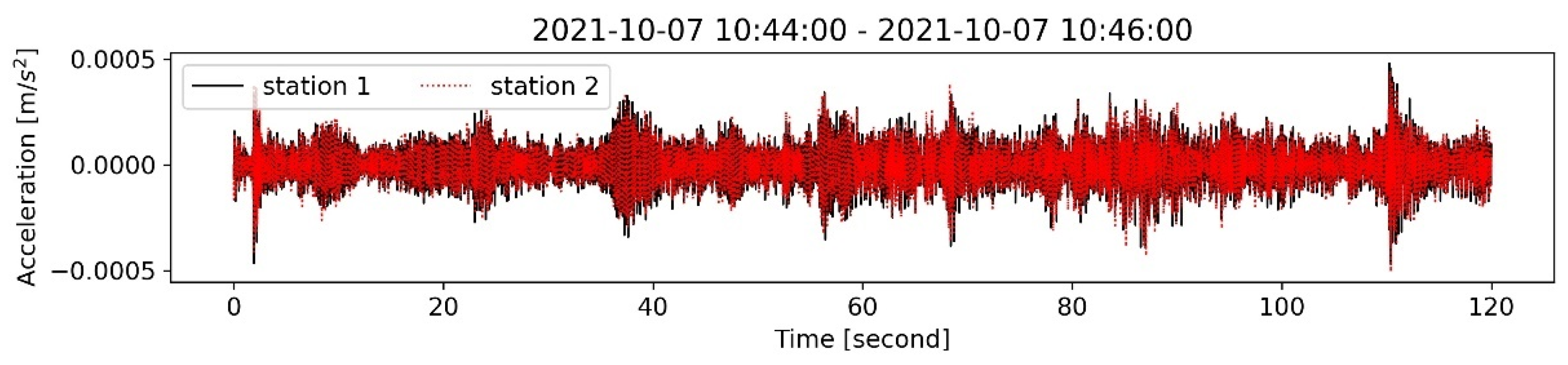
4. Vibration Measurements
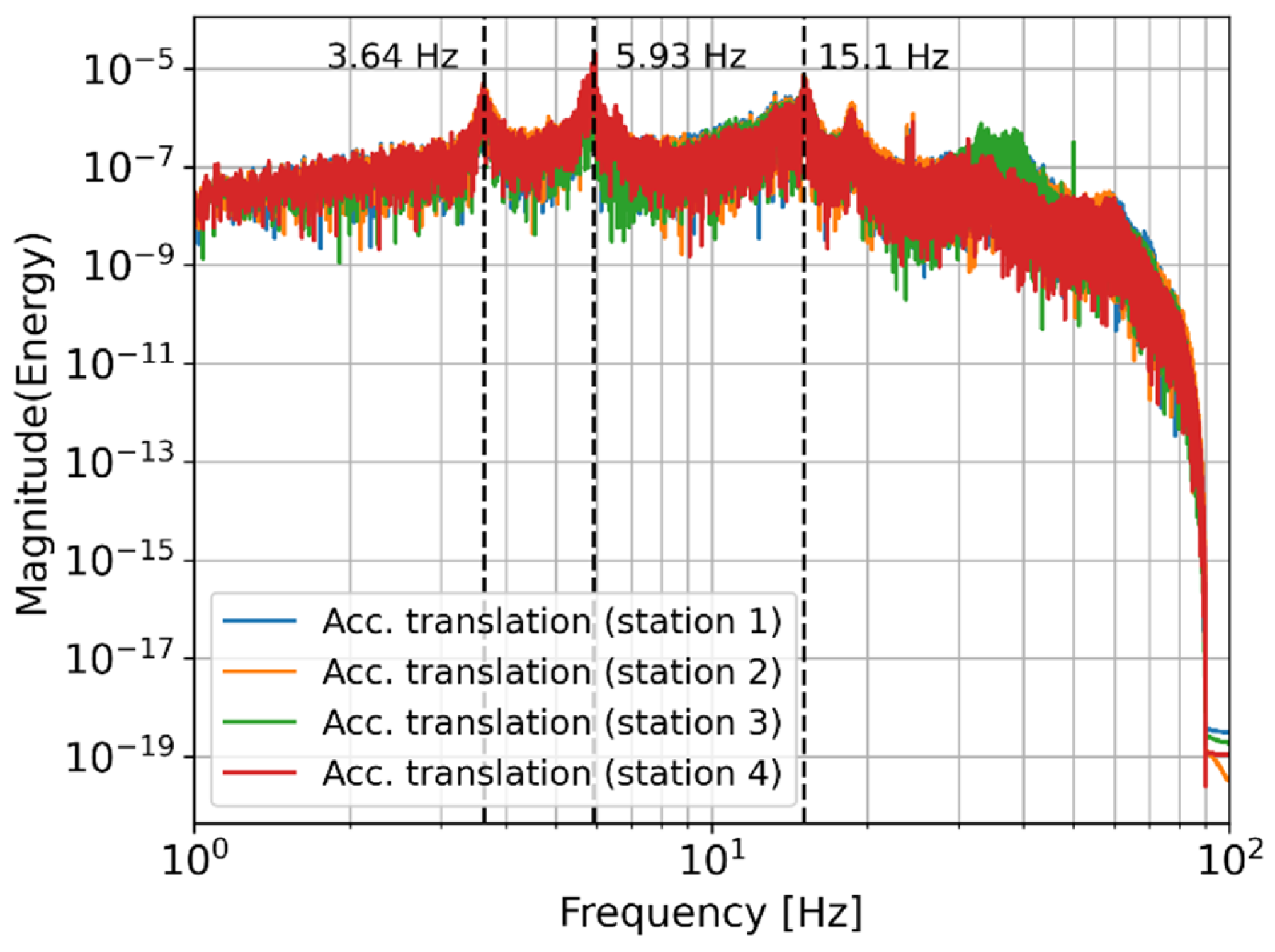
4.1. Frequency Domain Analysis
4.2. CCFs
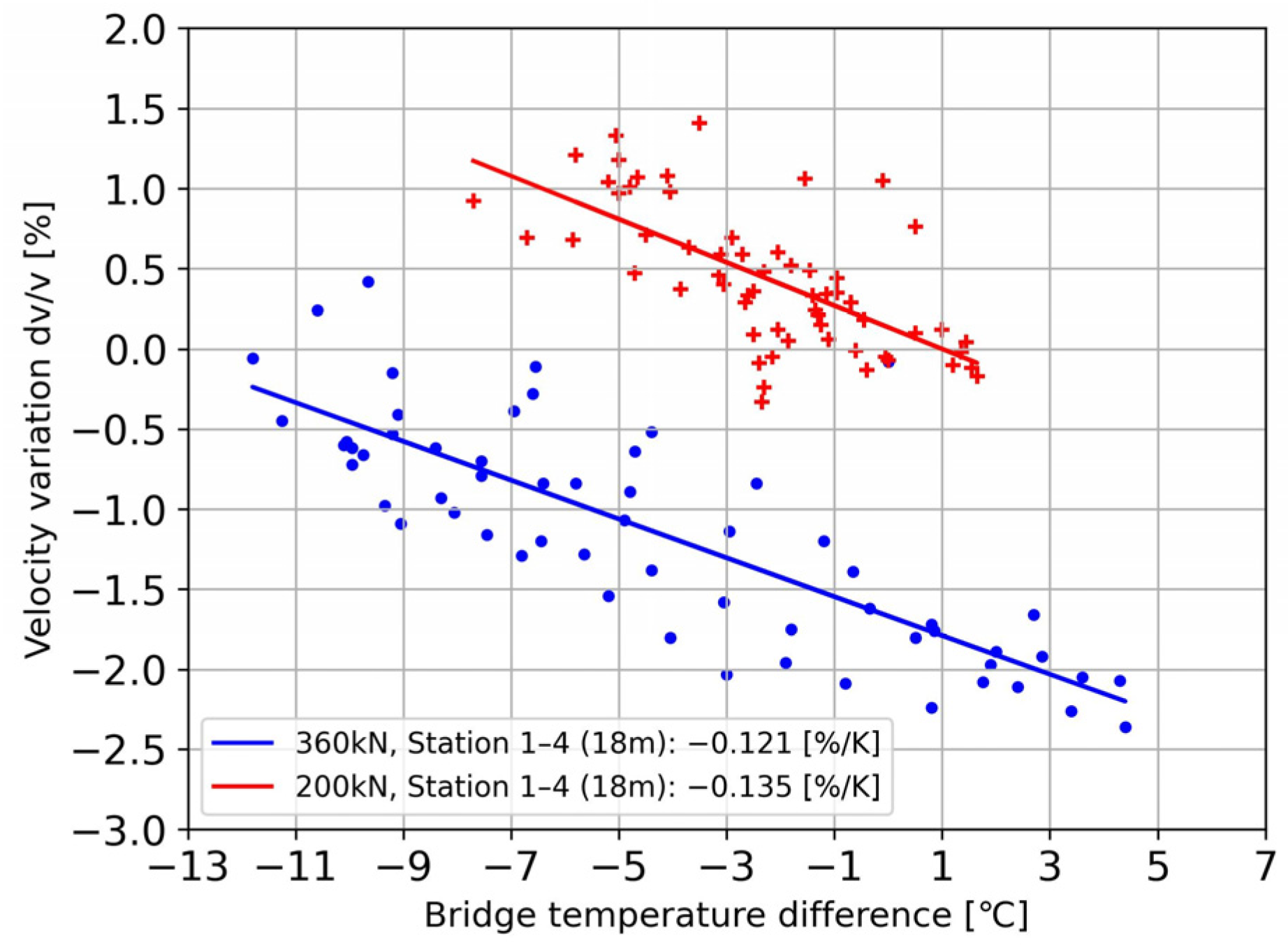
4.3. Long-Term Monitoring Results
5. Prestress Loss Tests
5.1. Prestressing Force Setup
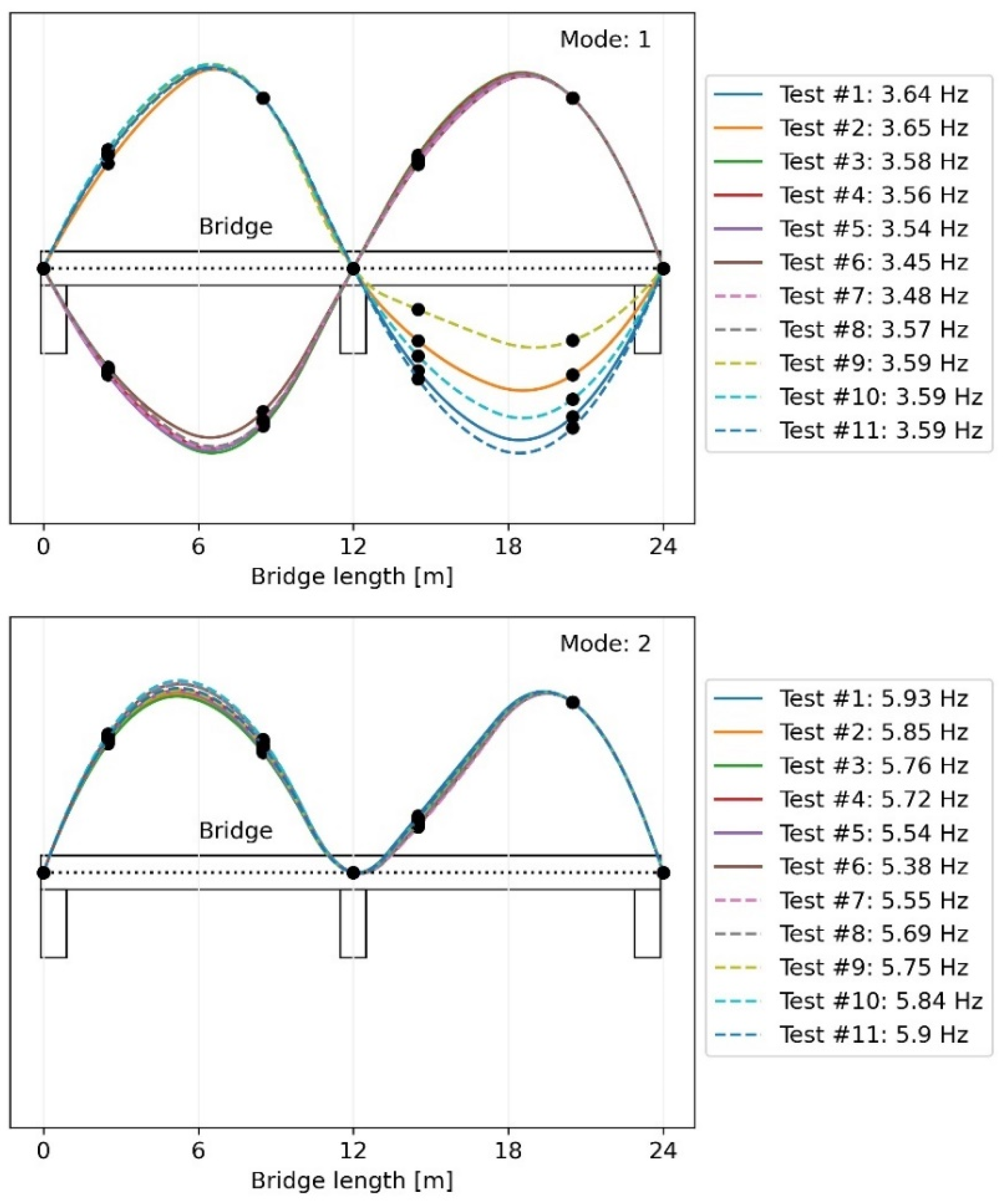
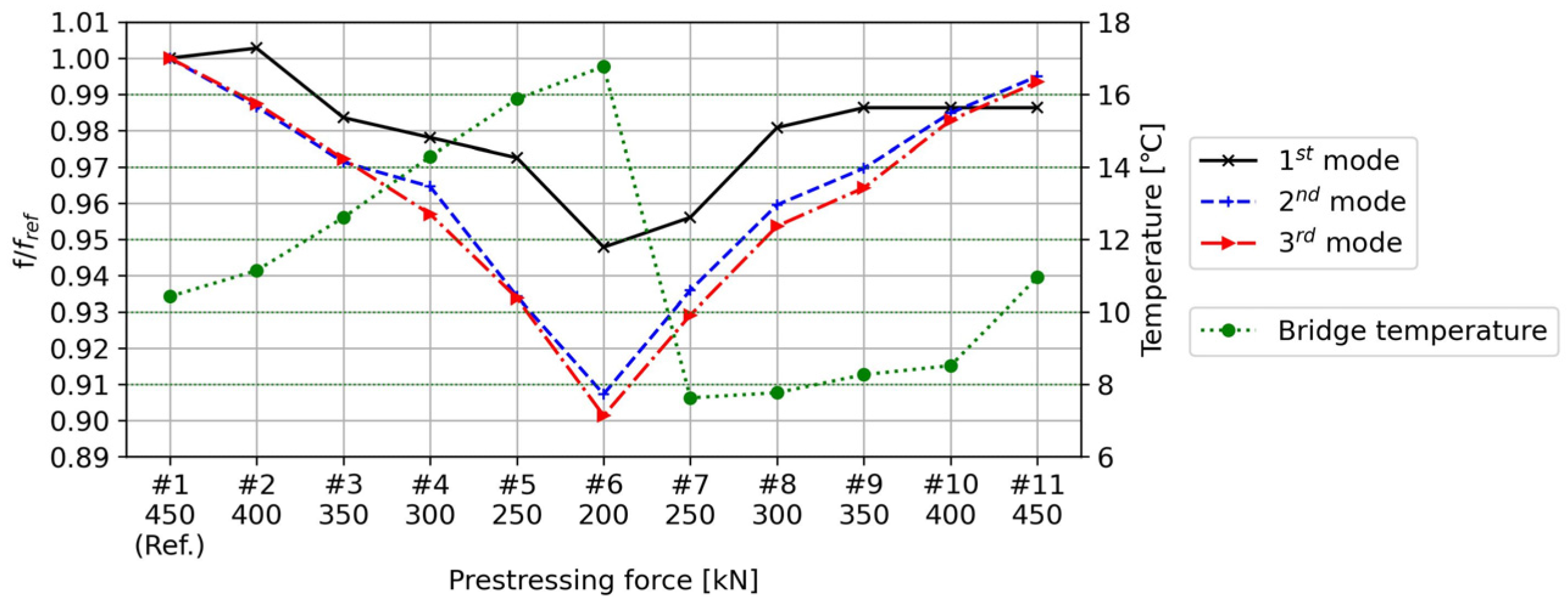
5.2. Modal Analysis Results
5.3. CWI Analysis Results
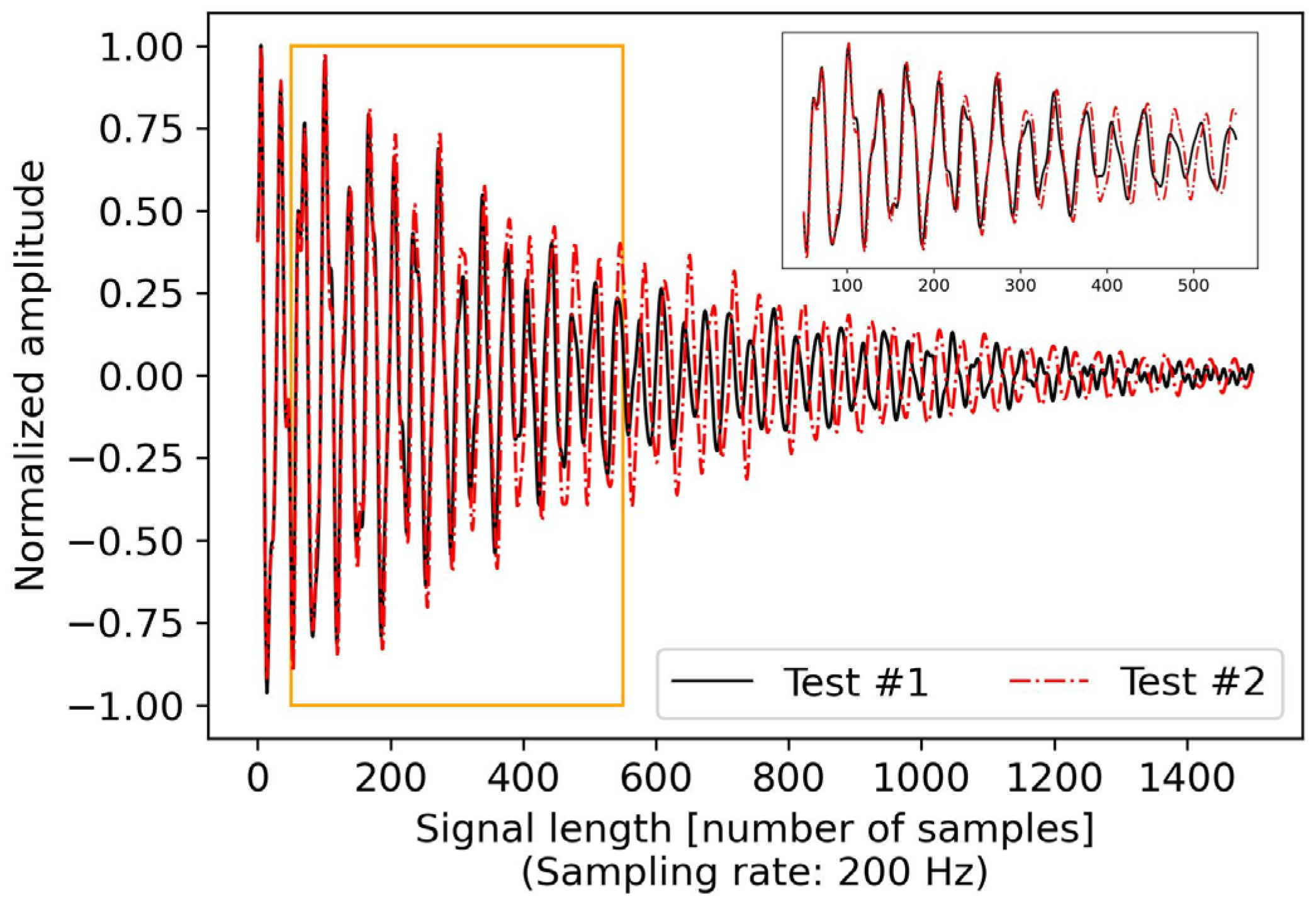
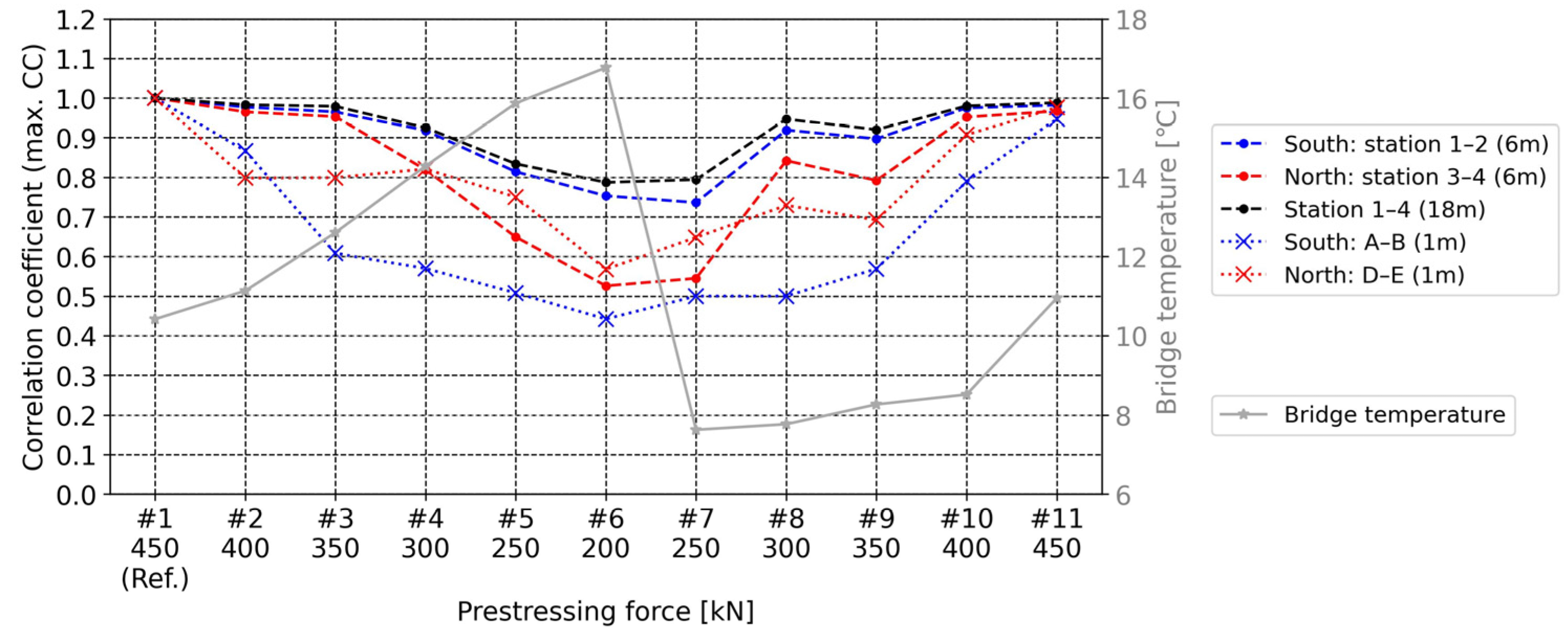
5.3.1. Max. CC Values
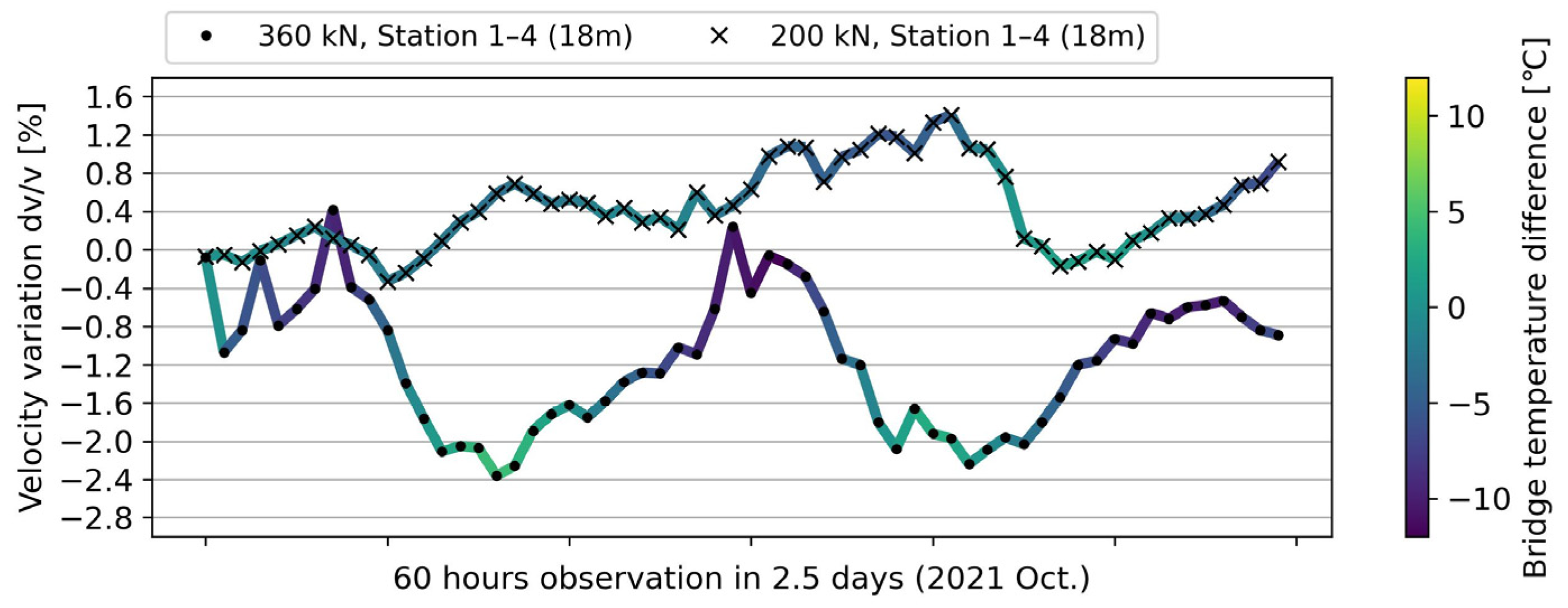
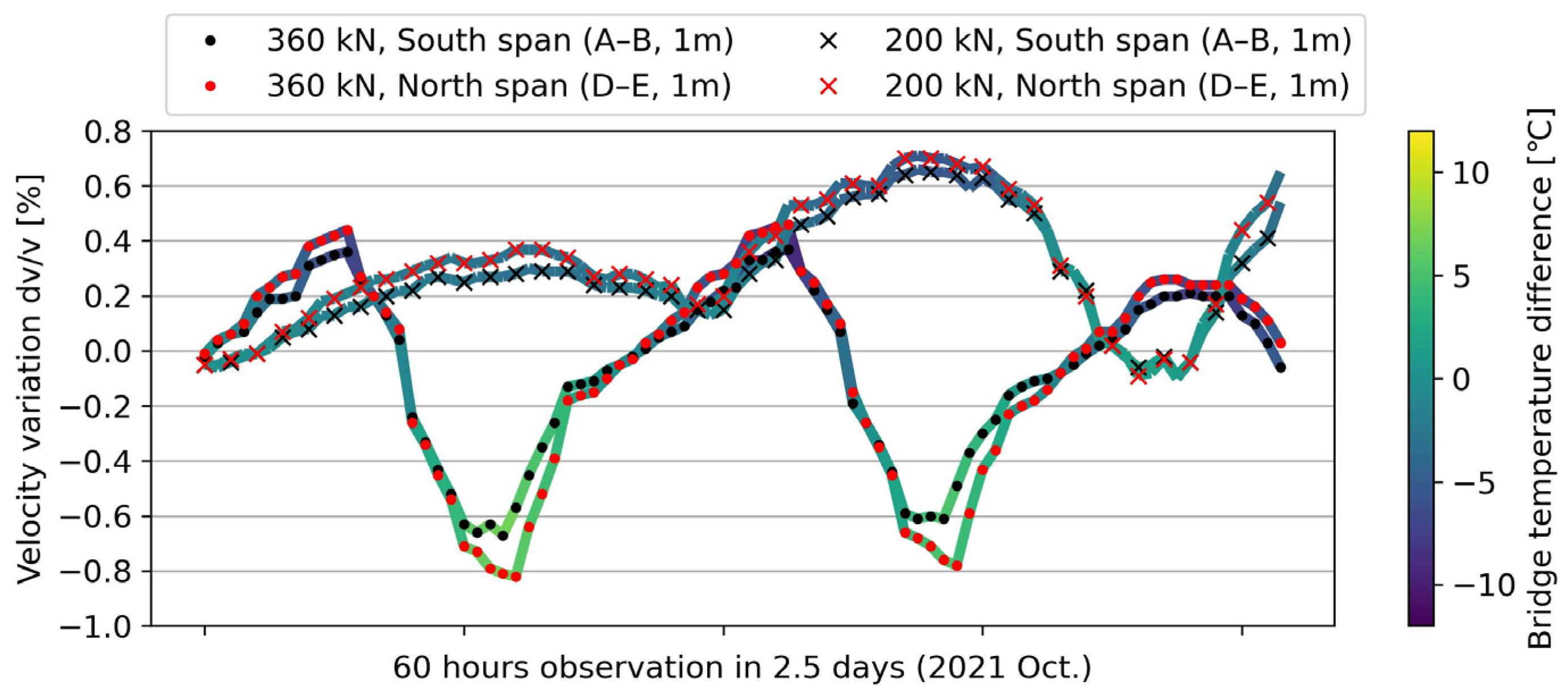
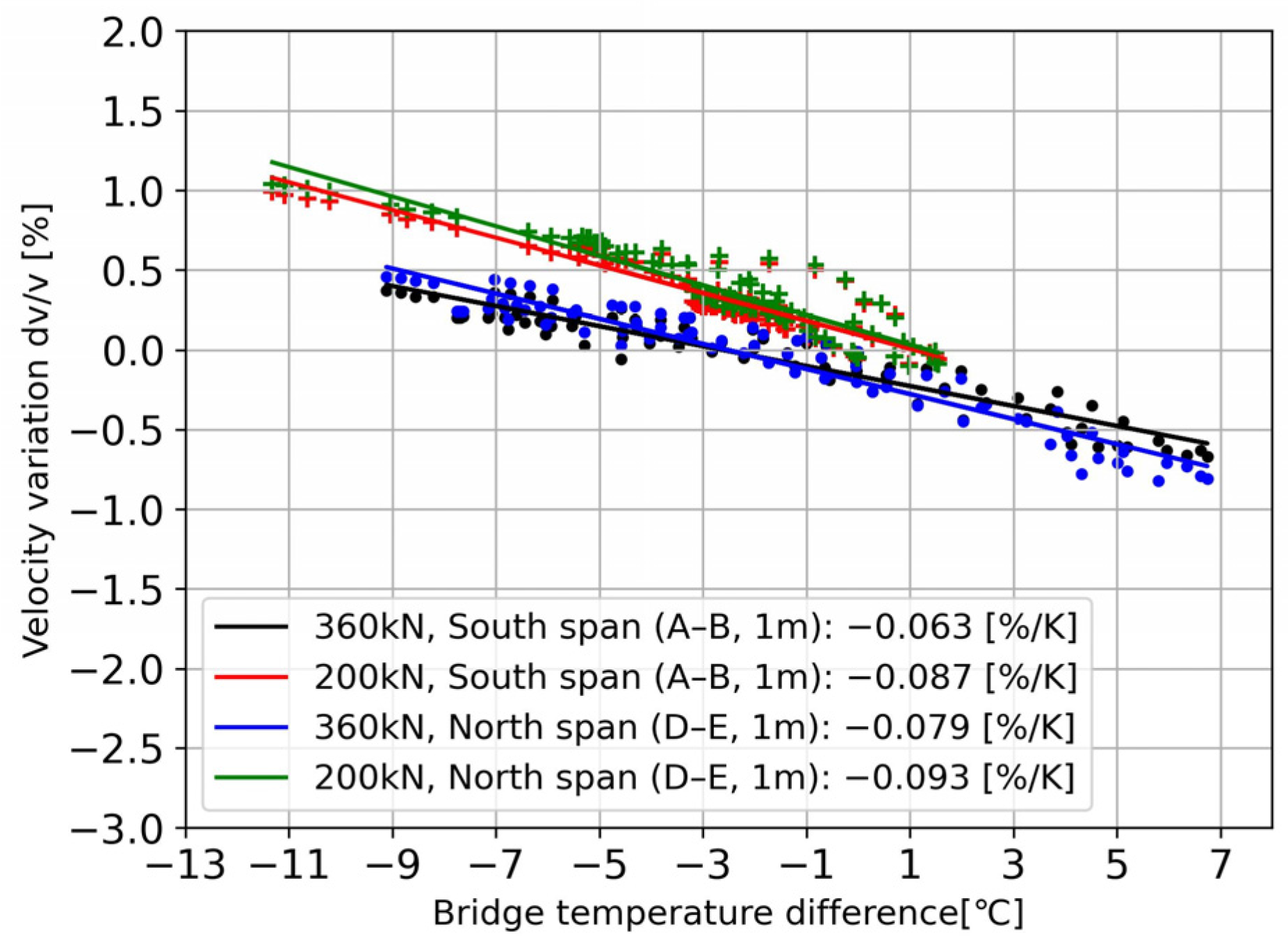
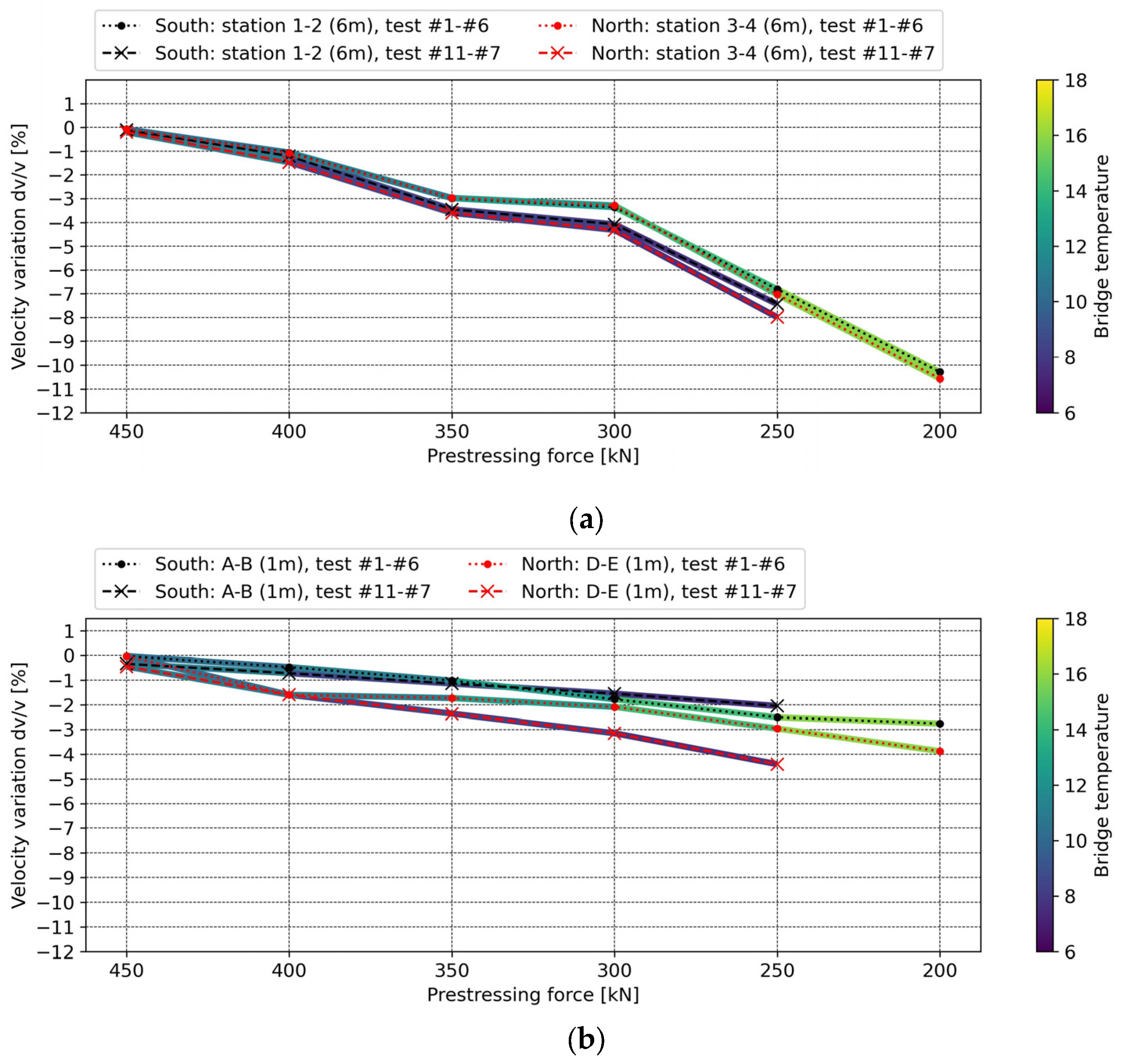
5.3.2. Wave Velocity Variations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CWI | Coda wave interferometry |
| FDD | Frequency Domain Decomposition |
| Max. CC | Maximum cross-correlation |
| NSR | Noise signal ratio |
| OMA | Operational modal analysis |
| PC | Prestressed concrete |
| PP | Peak picking |
| SHM | Structural health monitoring |
| UPV | Ultrasonic pulse velocity |
References
- Soyoz, S.; Feng, M.Q. Long-term monitoring and identification of bridge structural parameters. Comput.-Aided Civ. Infrastruct. Eng. 2009, 24, 82–92. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014; Volume 142, p. 143. [Google Scholar]
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Han, Q.; Ma, Q.; Xu, J.; Liu, M. Structural health monitoring research under varying temperature condition: A review. J. Civ. Struct. Health Monit. 2021, 11, 149–173. [Google Scholar] [CrossRef]
- Zhang, C.; Mousavi, A.A.; Masri, S.F.; Gholipour, G.; Yan, K.; Li, X. Vibration feature extraction using signal processing techniques for structural health monitoring: A review. Mech. Syst. Signal Process. 2022, 177, 109175. [Google Scholar] [CrossRef]
- Alampalli, S. Effects of testing, analysis, damage, and environment on modal parameters. Mech. Syst. Signal Process. 2000, 14, 63–74. [Google Scholar] [CrossRef]
- Wickramasinghe, W.R.; Thambiratnam, D.P.; Chan, T.H.; Nguyen, T. Vibration characteristics and damage detection in a suspension bridge. J. Sound Vib. 2016, 375, 254–274. [Google Scholar] [CrossRef]
- De Angelis, A.; Losanno, D.; Parisi, F.; Pecce, M.R. Identification of Modal Parameters of Scaled Bridge PC Beams by OMA Dynamic Tests. J. Bridge Eng. 2024, 29, 04024051. [Google Scholar] [CrossRef]
- Gandelli, E.; Rossini, G.; Mantelli, S.G.; Minelli, F. Damage detection of prestressed concrete beams affected by shear and flexure cracks through vibration monitoring. Eng. Struct. 2024, 304, 117572. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.C.; Lee, Z.K. State-of-the-art review on determining prestress losses in prestressed concrete girders. Appl. Sci. 2020, 10, 7257. [Google Scholar] [CrossRef]
- Zanini, M.A.; Faleschini, F.; Pellegrino, C. New trends in assessing the prestress loss in post-tensioned concrete bridges. Front. Built Environ. 2022, 8, 956066. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Alvandi, A.; Cremona, C. Assessment of vibration-based damage identification techniques. J. Sound Vib. 2006, 292, 179–202. [Google Scholar] [CrossRef]
- Carden, E.P.; Fanning, P. Vibration based condition monitoring: A review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Zahid, F.B.; Ong, Z.C.; Khoo, S.Y. A review of operational modal analysis techniques for in-service modal identification. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 398. [Google Scholar] [CrossRef]
- Niederleithinger, E.; Wolf, J.; Mielentz, F.; Wiggenhauser, H.; Pirskawetz, S. Embedded ultrasonic transducers for active and passive concrete monitoring. Sensors 2015, 15, 9756–9772. [Google Scholar] [CrossRef]
- Schumacher, T.; Niederleithinger, E. Combining Passive and Active Ultrasonic Stress Wave Monitoring Techniques: Opportunities for Condition Evaluation of Concrete Structures. In Proceedings of the NDT-CE 2022-The International Symposium on Nondestructive Testing in Civil Engineering, Zurich, Switzerland, 16–18 August 2022. [Google Scholar]
- Karaiskos, G.; Deraemaeker, A.; Aggelis, D.G.; Van Hemelrijck, D. Monitoring of concrete structures using the ultrasonic pulse velocity method. Smart Mater. Struct. 2015, 24, 113001. [Google Scholar] [CrossRef]
- Gholizadeh, S. A review of non-destructive testing methods of composite materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Smith, S.T.; Soh, C.K. Wave propagation based monitoring of concrete curing using piezoelectric materials: Review and path forward. NDT E Int. 2018, 99, 50–63. [Google Scholar] [CrossRef]
- Hassan, M.; Burdet, O.; Favre, R. Ultrasonic measurements and static load tests in bridge evaluation. NDT E Int. 1995, 28, 331–337. [Google Scholar] [CrossRef]
- Epple, N.; Sanchez-Trujillo, C.A.; Niederleithinger, E. Ultrasonic monitoring of large-scale structures-input to engineering assessment. In Life-Cycle of Structures and Infrastructure Systems; CRC Press: Boca Raton, FL, USA, 2023; pp. 1805–1812. [Google Scholar]
- Hassani, S.; Dackermann, U. A systematic review of advanced sensor technologies for non-destructive testing and structural health monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Gorgin, R.; Luo, Y.; Wu, Z. Environmental and operational conditions effects on Lamb wave based structural health monitoring systems: A review. Ultrasonics 2020, 105, 106114. [Google Scholar] [CrossRef] [PubMed]
- Snieder, R.; Miyazawa, M.; Slob, E.; Vasconcelos, I.; Wapenaar, K. A comparison of strategies for seismic interferometry. Surv. Geophys. 2009, 30, 503–523. [Google Scholar] [CrossRef]
- Niederleithinger, E.; Wang, X.; Herbrand, M.; Müller, M. Processing ultrasonic data by coda wave interferometry to monitor load tests of concrete beams. Sensors 2018, 18, 1971. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Jaber, H.; Glisic, B. Monitoring of prestressing forces in prestressed concrete structures—An overview. Struct. Control Health Monit. 2019, 26, e2374. [Google Scholar] [CrossRef]
- Snieder, R.; Grêt, A.; Douma, H.; Scales, J. Coda wave interferometry for estimating nonlinear behavior in seismic velocity. Science 2002, 295, 2253–2255. [Google Scholar] [CrossRef]
- Obermann, A.; Planès, T.; Larose, E.; Sens-Schönfelder, C.; Campillo, M. Depth sensitivity of seismic coda waves to velocity perturbations in an elastic heterogeneous medium. Geophys. J. Int. 2013, 194, 372–382. [Google Scholar] [CrossRef]
- Planès, T.; Larose, E. A review of ultrasonic Coda Wave Interferometry in concrete. Cem. Concr. Res. 2013, 53, 248–255. [Google Scholar] [CrossRef]
- Grabke, S.; Clauß, F.; Bletzinger, K.U.; Ahrens, M.A.; Mark, P.; Wüchner, R. Damage detection at a reinforced concrete specimen with coda wave interferometry. Materials 2021, 14, 5013. [Google Scholar] [CrossRef]
- Zhong, B.; Zhu, J. Applications of stretching technique and time window effects on ultrasonic velocity monitoring in concrete. Appl. Sci. 2022, 12, 7130. [Google Scholar] [CrossRef]
- Wapenaar, K.; Draganov, D.; Snieder, R.; Campman, X.; Verdel, A. Seismic Interferometry: Tutorial on seismic interferometry: Part 1—Basic principles and applications. Geophysics 2010, 75, 75A195–75A209. [Google Scholar] [CrossRef]
- Hadziioannou, C.; Larose, E.; Coutant, O.; Roux, P.; Campillo, M. Stability of monitoring weak changes in multiply scattering media with ambient noise correlation: Laboratory experiments. J. Acoust. Soc. Am. 2009, 125, 3688–3695. [Google Scholar] [CrossRef] [PubMed]
- ETA-05/0123; European Technical Assessment. DIBt: Berlin, Germany, 2023. Available online: https://dywidag.com/downloads/eta-05-0123-dywidag-pt-bar-tendon-system-with-bars-o-175-to-47-mm/de (accessed on 16 April 2025).
- Kee, S.H.; Zhu, J. Using piezoelectric sensors for ultrasonic pulse velocity measurements in concrete. Smart Mater. Struct. 2013, 22, 115016. [Google Scholar] [CrossRef]
- Dumoulin, C.; Deraemaeker, A. Design optimization of embedded ultrasonic transducers for concrete structures assessment. Ultrasonics 2017, 79, 18–33. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, J. Thermal modulation of nonlinear ultrasonic wave for concrete damage evaluation. J. Acoust. Soc. Am. 2019, 145, EL405–EL409. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441. [Google Scholar] [CrossRef]
- Lorenzo, G.W.F.; Mercerat, D.; d’Avila, M.P.S.; Bertrand, E.; Deschamps, A. Operational modal analysis of a high rise rc building and modelling. In Proceedings of the IOMAC’15-The 6th International Operational Modal Analysis Conference, Gijon, Spain, 12–14 May 2015. [Google Scholar]
- Pasca, D.P.; Aloisio, A.; Rosso, M.M.; Sotiropoulos, S. PyOMA and PyOMA_GUI: A Python module and software for Operational Modal Analysis. Softw. X, 2022, in press. [CrossRef]
- Yang, Y.; Cascante, G.; Polak, M.A. Depth detection of surface-breaking cracks in concrete plates using fundamental Lamb modes. NDT E Int. 2009, 42, 501–512. [Google Scholar] [CrossRef]
- Stähler, S.C.; Sens-Schönfelder, C.; Niederleithinger, E. Monitoring stress changes in a concrete bridge with coda wave interferometry. J. Acoust. Soc. Am. 2011, 129, 1945–1952. [Google Scholar] [CrossRef]
- Zhong, B.; Zhu, J.; Morcous, G. Measuring acoustoelastic coefficients for stress evaluation in concrete. Constr. Build. Mater. 2021, 309, 125127. [Google Scholar] [CrossRef]
- Aloisio, A. Aspects of vibration-based methods for the prestressing estimate in concrete beams with internal bonded or unbonded tendons. Infrastructures 2021, 6, 83. [Google Scholar] [CrossRef]
- Bolborea, B.; Baera, C.; Dan, S.; Gruin, A.; Burduhos-Nergis, D.D.; Vasile, V. Concrete compressive strength by means of ultrasonic pulse velocity and moduli of elasticity. Materials 2021, 14, 7018. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, C.-M.; Bernauer, F.; Niederleithinger, E.; Igel, H.; Hadziioannou, C. Wave-Screening Methods for Prestress-Loss Assessment of a Large-Scale Post-Tensioned Concrete Bridge Model Under Outdoor Conditions. Appl. Sci. 2025, 15, 6005. https://doi.org/10.3390/app15116005
Liao C-M, Bernauer F, Niederleithinger E, Igel H, Hadziioannou C. Wave-Screening Methods for Prestress-Loss Assessment of a Large-Scale Post-Tensioned Concrete Bridge Model Under Outdoor Conditions. Applied Sciences. 2025; 15(11):6005. https://doi.org/10.3390/app15116005
Chicago/Turabian StyleLiao, Chun-Man, Felix Bernauer, Ernst Niederleithinger, Heiner Igel, and Céline Hadziioannou. 2025. "Wave-Screening Methods for Prestress-Loss Assessment of a Large-Scale Post-Tensioned Concrete Bridge Model Under Outdoor Conditions" Applied Sciences 15, no. 11: 6005. https://doi.org/10.3390/app15116005
APA StyleLiao, C.-M., Bernauer, F., Niederleithinger, E., Igel, H., & Hadziioannou, C. (2025). Wave-Screening Methods for Prestress-Loss Assessment of a Large-Scale Post-Tensioned Concrete Bridge Model Under Outdoor Conditions. Applied Sciences, 15(11), 6005. https://doi.org/10.3390/app15116005







