Modern Methods for Diagnosing Faults in Rotor Systems: A Comprehensive Review and Prospects for AI-Based Expert Systems
Abstract
1. Introduction
2. Research Methodology
2.1. Analysis of the Most Common Problems in the Diagnostics of the Rotor System
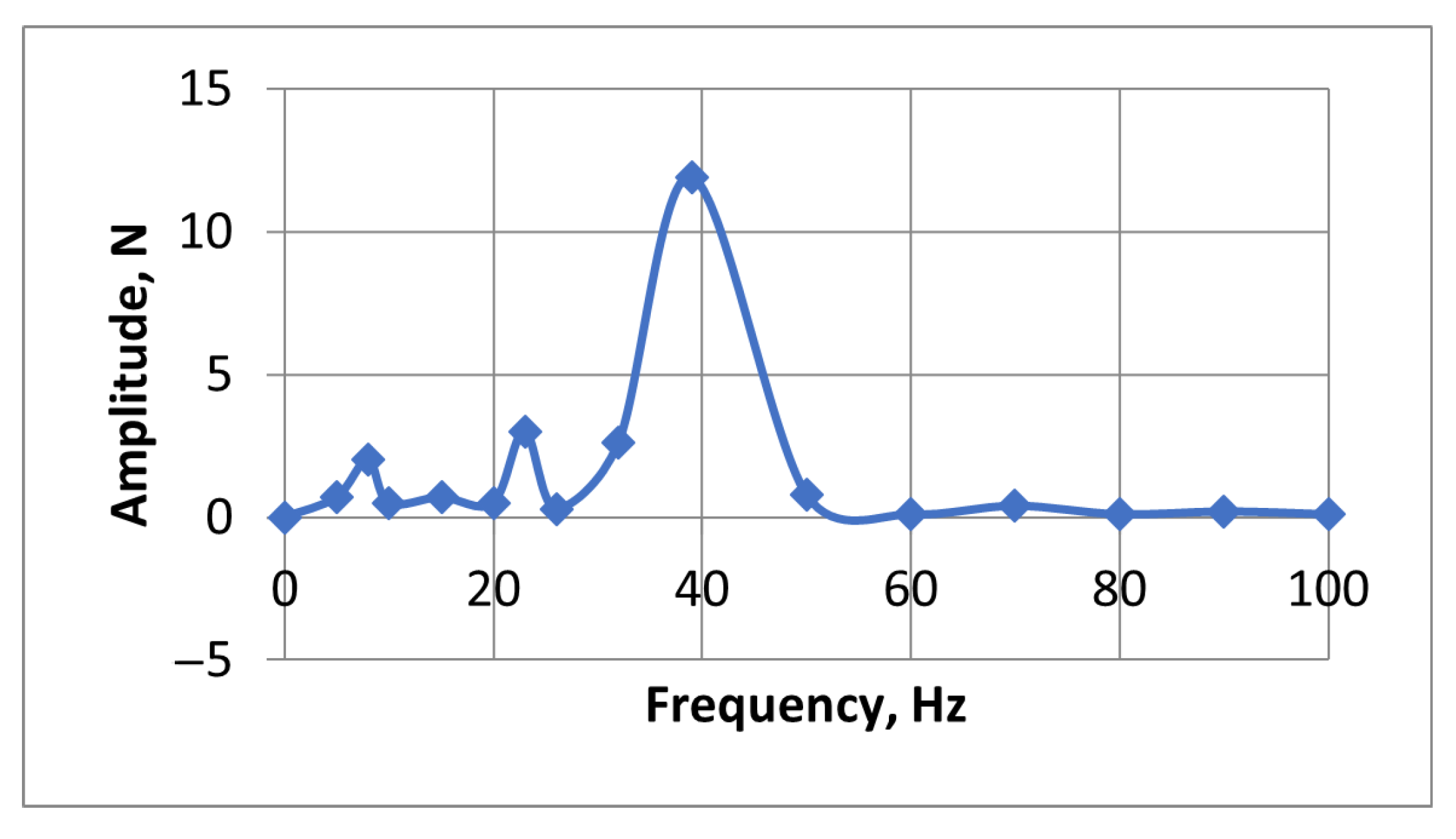
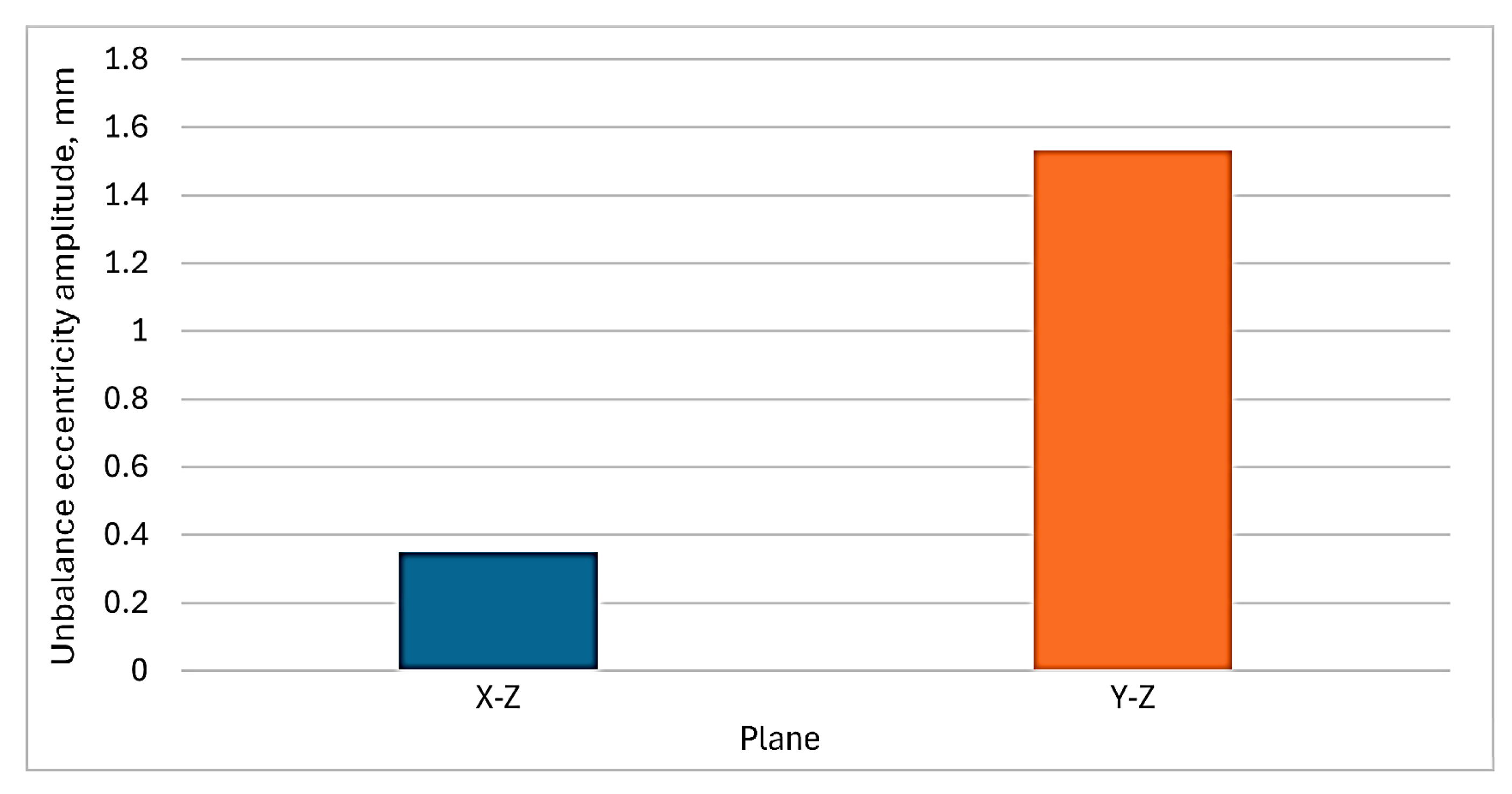
2.2. Unbalance
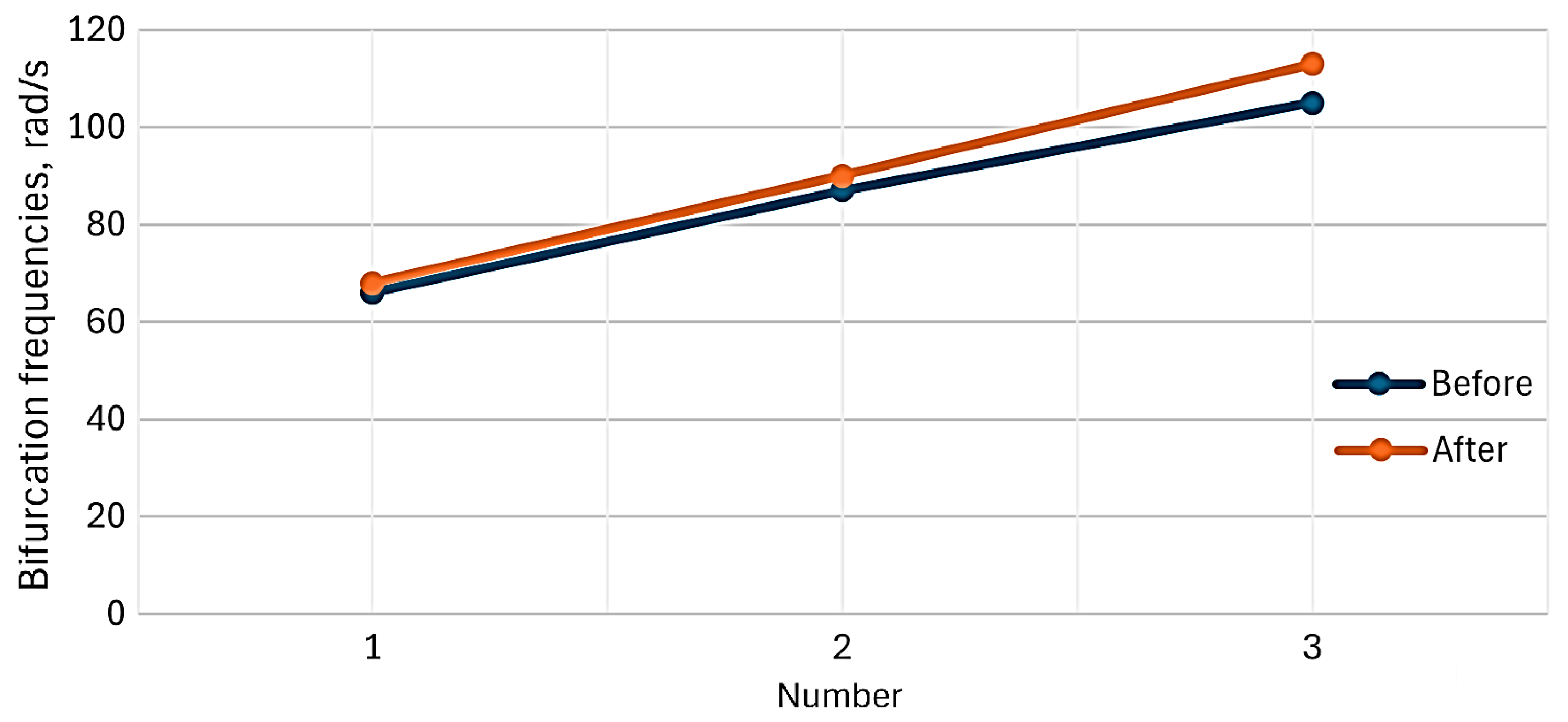
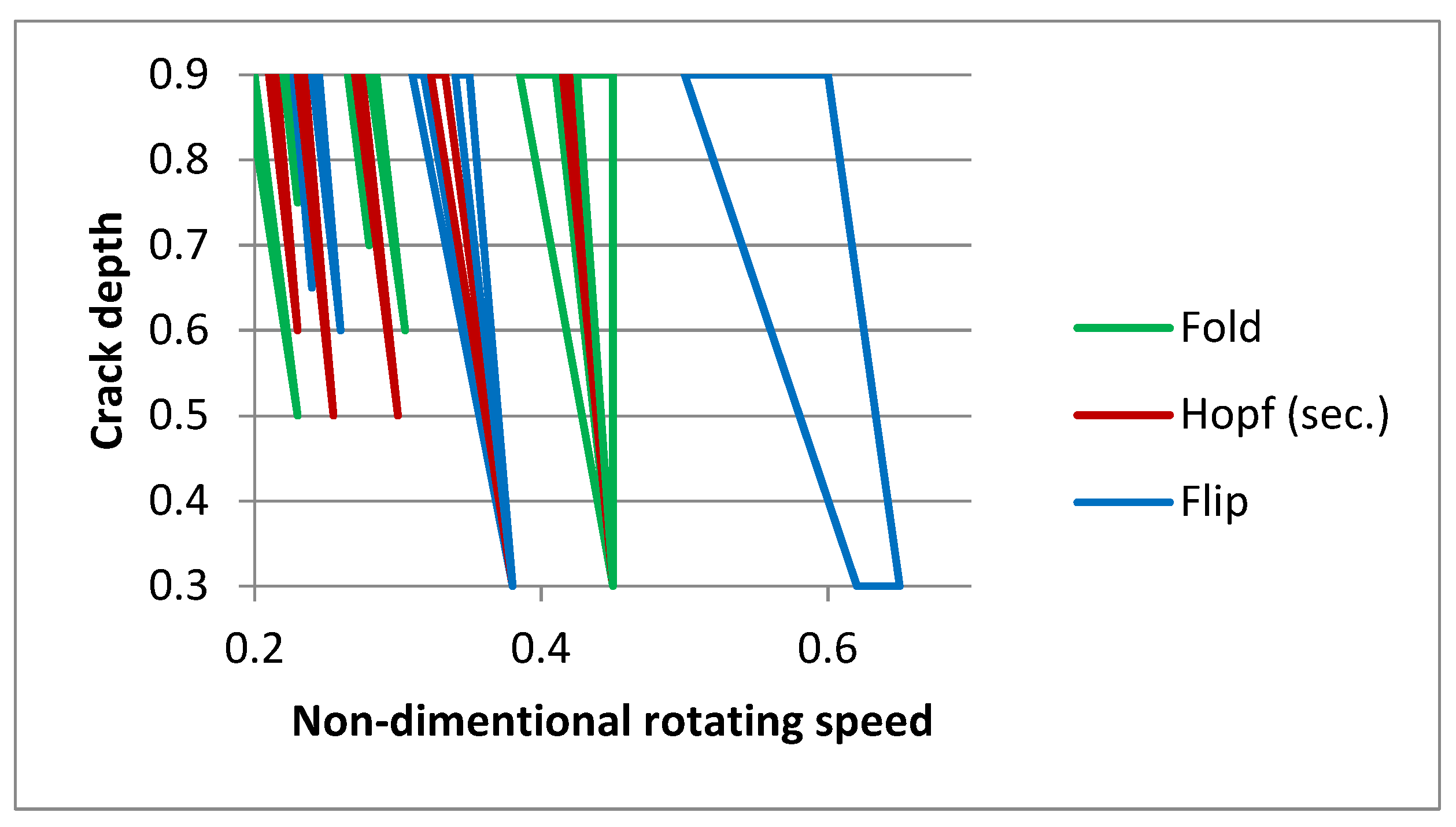
2.3. Cracks
2.4. Misalignment
2.5. Residual Rotor Bending
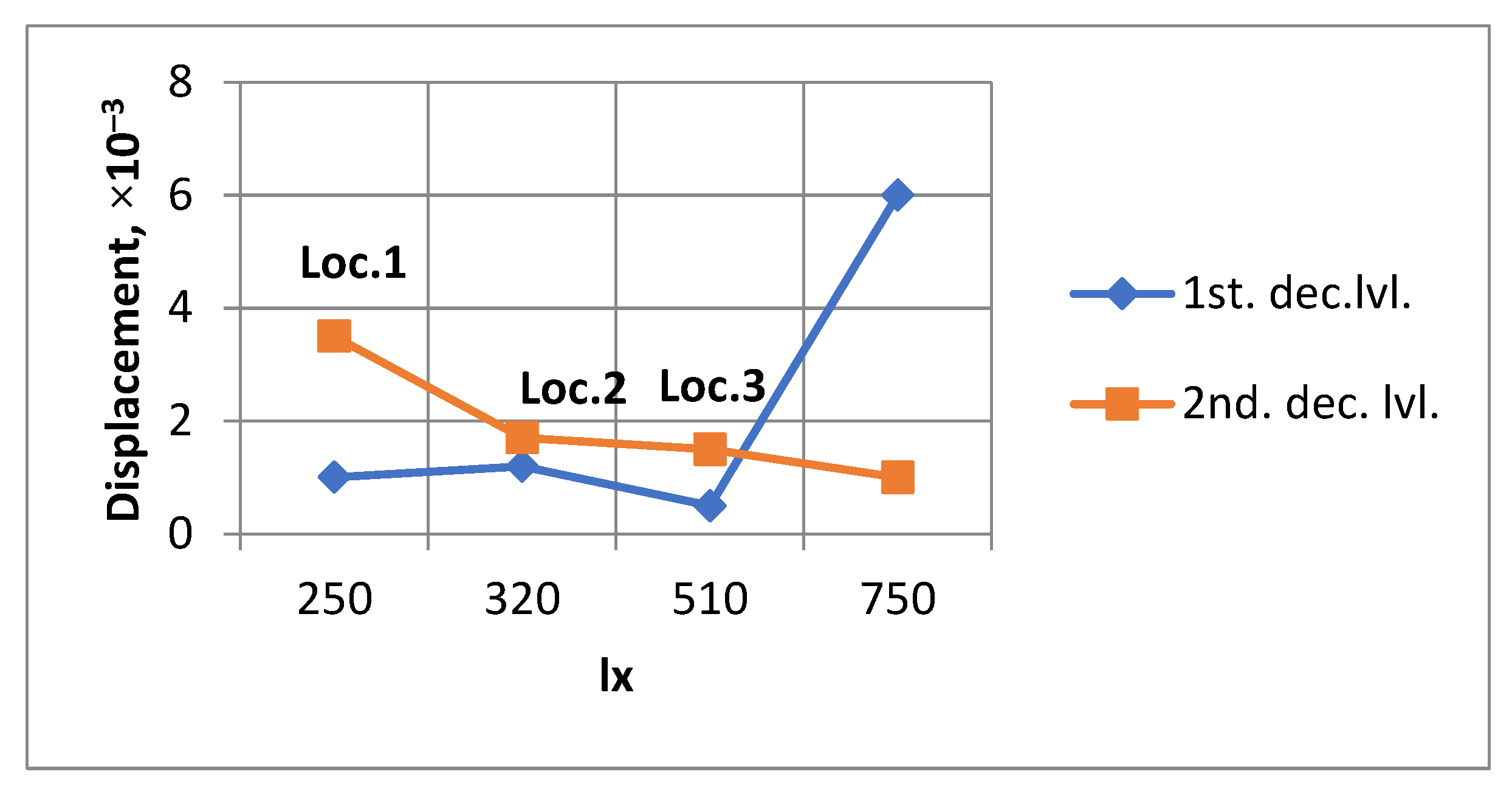
2.6. Rotor–Stator Interaction
2.7. Bearing Faults
2.8. Combined Faults
2.9. Modeling Methods Improvements
3. Results
3.1. The Most Common Attendant Issues in the Diagnostics of Rotor Systems
3.2. Measurement Noises and Computational Complexity
3.3. Comparative Information of Reviewed Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| ANM | asymptotic numerical method |
| ANN | artificial neural network |
| APEWT | adaptive parameter-free empirical wavelet transform |
| BHO | Bayesian hyperparameter optimization |
| BP | backpropagation |
| CIM | Chebyshev interval method |
| CNN | convolutional neural network |
| CPU | central processing unit |
| CWT | continuous wavelet transform |
| Db6 | Debes wavelet transform |
| DCGAN | generative adversarial neural network |
| DE | differential evolution |
| DFT | discrete Fourier transform |
| DIRS | dynamic improved reduced system |
| DOF | degree of freedom |
| DT | decision tree |
| DWT | discrete wavelet transform |
| EEMD | ensemble empirical mode decomposition |
| EKF | extended Kalman filter |
| ELMM | equivalent load minimization method |
| EMA | experimental modal analysis |
| EMD | empirical mode decomposition |
| ESM | empirical selection method |
| EWT | empirical wavelet transform |
| FCC | full connected cascade |
| FDM | finite difference method |
| FEA | finite element analysis |
| FEM | finite element modeling |
| FEMU | finite element model updating |
| FFEM | fuzzy finite element method |
| FFT | fast Fourier transform |
| FNN | feedforward neural network |
| FRF | frequency response function |
| FST | Fourier synchrosqueezed transform |
| FTG | full tensor grid |
| GA | genetic algorithm |
| GAN | generative adversarial networks |
| GPU | graphics processing unit |
| GR | Guyan reduction |
| GRU | gated recurrent unit |
| GT | Gabor transform |
| HB | harmonic balance |
| HBM | harmonic balance method |
| HHT | Hilbert–Huang transform |
| HT | Hilbert transform |
| IES | inverse eigensensitivity |
| IHBM | incremental harmonic balance method |
| IIR | infinite impulse response |
| IMSM | interval modal superposition method |
| IPM | interval perturbation module |
| ISOMAP | isometric mapping |
| ITEO | improved Teager energy operator |
| JISEA | joint input-state estimation algorithm |
| KF | Kalman filter |
| KL | Karhunen–Loève discretisation |
| KNN | k-nearest neighbors |
| LCD | local characteristic-scale decomposition |
| LEM | linearized equation method |
| LLM | large language model |
| LSTM | long short-term memory |
| MAC | modal assurance criterion |
| MAE | mean absolute error |
| MAF | moving average filter |
| MB | modal balancing |
| MCS | Monte Carlo simulation |
| MCMC | Markov-chain Monte Carlo |
| MDS | multidimensional scaling |
| MEA | modal expansion algorithm |
| MHA | multi-head attention |
| ML | machine learning |
| MLP | multilayer perceptron |
| MoE | mixture-of-experts approach |
| NARX | nonlinear autoregressive with exogenous input |
| NAS | neural acceleration subsystem |
| NCA | neighborhood component analysis |
| NDE | nonlinear differential equation |
| NFD | natural frequency difference |
| NHT | normalized Hilbert transform |
| NN | neural network |
| NOFRF | nonlinear output frequency response function |
| NREM | nonlinear equation reduction method |
| ODS | operating deflection shape |
| ODSR | operating deflection shape ratio |
| OMA | operational modal analysis |
| ORM | over-relaxation method |
| PCA | principal component analysis |
| PCE | polynomial chaos expansion |
| POD | proper orthogonal decomposition |
| PSO | particle swarm optimization |
| QDNHT | quadrature-derivative-based normalized Hilbert transform |
| RBFNN | radial basis function neural network |
| RF | random forest |
| RMSC | regional mode shape curvature |
| RNN | recurrent neural network |
| ROM | reduced-order model |
| SEREP | system equivalent reduction expansion process |
| SERR | strain energy release rate |
| SFEM | stochastic finite element method |
| SFT | synchronized Fourier transform |
| SIS | sub-interval similarity |
| SNN | spiking neural network |
| STFDD | short-time frequency domain decomposition |
| STFT | short-term Fourier transform |
| SVD | singular value decomposition |
| SVM | support vector machine |
| TEO | Teager energy operator |
| TFA | time-frequency analysis |
| TF-DLGAN | deep long short-term memory convolutional generative adversarial network |
| TFMRA | topological fractal multi-resolution analysis |
| TM | transfer matrix |
| TPR | temporal pattern recognition |
| TRAC | time response agreement criterion |
| UKF | unscented Kalman filter |
| UQ | uncertainty-quantification |
| WPT | wavelet packet transformation |
| WT | wavelet transform |
| WVD | Wigner–Ville distribution |
References
- Li, J.T.; Lu, H.H.; Feng, K.P.; Liu, Y.; Zhao, Y.L. Research on a new diagnosis index for fixed-point rub-impact of rotor system. Eng. Fail. Anal. 2021, 125, 105394. [Google Scholar] [CrossRef]
- Makivskyi, O.; Kondus, V.; Pitel, J.; Sotnyk, M.; Andrusiak, V.; Polkovnychenko, V.; Musthai, M. The influence of the design features of the submersible pump rotor on the vibration reliability. J. Eng. Sci. 2024, 11, D1–D9. [Google Scholar] [CrossRef]
- Nasar, R.A.; Alzarooni, T.; Al-Shudeifat, M.A. On modeling and damage detection methodologies in rotor systems. Nonlinear Dyn. 2024, 112, 16657–16710. [Google Scholar] [CrossRef]
- Gao, P.; Hou, L.; Yang, R.; Chen, Y. Local defect modelling and nonlinear dynamic analysis for the inter-shaft bearing in a dual-rotor system. Appl. Math. Model. 2019, 68, 29–47. [Google Scholar] [CrossRef]
- Pineda-Sanchez, M.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Riera-Guasp, M.; Perez-Cruz, J. Partial inductance model of induction machines for fault diagnosis. Sensors 2018, 18, 2340. [Google Scholar] [CrossRef]
- Alberto, C.; Alves, D.S.; Machado, T.H. Linear and nonlinear performance analysis of hydrodynamic journal bearings with different geometries. Appl. Sci. 2022, 12, 3215. [Google Scholar] [CrossRef]
- Phadatare, H.P.; Pratiher, B. Nonlinear modeling, dynamics, and chaos in a large deflection model of a rotor-disk-bearing system under geometric eccentricity and mass unbalance. Acta Mech. 2019, 231, 907–928. [Google Scholar] [CrossRef]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassõlkin, A.; Iqbal, M.N. The cluster computation-based hybrid FEM–analytical model of induction motor for fault diagnostics. Appl. Sci. 2020, 10, 7572. [Google Scholar] [CrossRef]
- Cao, X.; Zeng, N.; Chen, B.; He, W. Sparsity enhanced topological fractal decomposition for smart machinery fault diagnosis. IEEE Access 2018, 6, 51886–51897. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Marques Cardoso, A.J.; Antonino-Daviu, J.A. Introducing the filtered park’s and filtered extended park’s vector approach to detect broken rotor bars in induction motors independently from the rotor slots number. Mech. Syst. Signal Process. 2017, 93, 30–50. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Burriel-Valencia, J.; Pineda-Sanchez, M.; Puche-Panadero, R.; Riera-Guasp, M. The harmonic order tracking analysis method for the fault diagnosis in induction motors under time-varying Conditions. IEEE Trans. Energy Convers. 2017, 32, 244–256. [Google Scholar] [CrossRef]
- Yang, Z.; Hong, J.; Wang, D.; Cheng, R.; Ma, Y. Vibration analysis of rotor systems with bearing clearance using a novel conformal contact model. Nonlinear Dyn. 2024, 112, 7951–7976. [Google Scholar] [CrossRef]
- Singh, V.; Gangsar, P.; Porwal, R.; Atulkar, A. Artificial intelligence application in fault diagnostics of rotating industrial machines: A state-of-the-art review. J. Intell. Manuf. 2021, 34, 931–960. [Google Scholar] [CrossRef]
- Nath, A.G.; Udmale, S.S.; Singh, S.K. Role of artificial intelligence in rotor fault diagnosis: A comprehensive review. Artif. Intell. Rev. 2020, 54, 2609–2668. [Google Scholar] [CrossRef]
- De Rezende, S.W.F.; Barella, B.P.; Moura, J.R.V.; Tsuruta, K.M.; Cavalini, A.A.; Steffen, V. ISHM for fault condition detection in rotating machines with deep learning models. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 212. [Google Scholar] [CrossRef]
- Liao, H.; Xie, P.; Deng, S.; Wang, H. Intelligent Early Fault Diagnosis of Space Flywheel Rotor System. Sensors 2023, 23, 8198. [Google Scholar] [CrossRef]
- Zhang, D.; Li, S.; Hong, T.; Zhang, C.; Zhao, W. Enhanced fault prediction for synchronous condensers using LLM-optimized wavelet packet transformation. Electronics 2025, 14, 308. [Google Scholar] [CrossRef]
- Bechiri, M.B.; Allal, A.; Naoui, M.; Khechekhouche, A.; Alsaif, H.; Boudjemline, A. Effective diagnosis approach for broken rotor bar fault using Bayesian-based optimization of machine learning hyperparameters. IEEE Access 2024, 12, 139923–139936. [Google Scholar] [CrossRef]
- Fu, C.; Sinou, J.-J.; Zhu, W.; Lu, K.; Yang, Y. A state-of-the-art review on uncertainty analysis of rotor systems. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Arnst, M.; Ponthot, J.-P.; Boman, R. Comparison of stochastic and interval methods for uncertainty quantification of metal forming processes. C. R. Méc. 2018, 346, 634–646. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, Z.; Chen, M.; Hong, J. Interval analysis of rotor dynamic response with uncertain parameters. J. Sound Vib. 2013, 332, 3869–3880. [Google Scholar] [CrossRef]
- Deepthikumar, M.B.; Sekhar, A.S.; Srikanthan, M.R. Modal balancing of flexible rotors with bow and distributed unbalance. J. Sound Vib. 2013, 332, 6216–6233. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, Y.; Xiang, J. Quantitative detection of multiple damages in wind turbine blade based on the operating deflection shape and natural frequencies. Ocean Eng. 2023, 278, 114387. [Google Scholar] [CrossRef]
- Gohari, M.; Eydi, A.M. Modelling of shaft unbalance: Modelling a multi discs rotor using k-nearest neighbor and decision tree algorithms. Measurement 2020, 151, 107253. [Google Scholar] [CrossRef]
- Pavlenko, I.; Ivanov, V.; Kuric, I.; Gusak, O.; Liaposhchenko, O. Ensuring vibration reliability of turbopump units using artificial neural networks. In Advances in Manufacturing II. MANUFACTURING 2019. Lecture Notes in Mechanical Engineering; Trojanowska, J., Ciszak, O., Machado, J., Pavlenko, I., Eds.; Springer: Cham, Switzerland, 2019; pp. 165–175. [Google Scholar] [CrossRef]
- Walker, R.B.; Vayanat, R.; Perinpanayagam, S.; Jennions, I.K. Unbalance localization through machine nonlinearities using an artificial neural network approach. Mech. Mach. Theory 2014, 75, 54–66. [Google Scholar] [CrossRef]
- Sinha, J.K.; Lees, A.W.; Friswell, M.I. Estimating unbalance and misalignment of a flexible rotating machine from a single run-down. J. Sound Vib. 2004, 272, 967–989. [Google Scholar] [CrossRef]
- Sanches, F.D.; Pederiva, R. Simultaneous identification of unbalance and shaft bow in a two-disk rotor based on correlation analysis and the SEREP model order reduction method. J. Sound Vib. 2018, 433, 230–247. [Google Scholar] [CrossRef]
- Phadatare, H.P.; Pratiher, B. Large deflection model for rub-impact analysis in high-speed rotor-bearing system with mass unbalance. Int. J. Non-Linear Mech. 2021, 132, 103702. [Google Scholar] [CrossRef]
- Corbally, R.; Malekjafarian, A. Bridge damage detection using operating deflection shape ratios obtained from a passing vehicle. J. Sound Vib. 2022, 537, 117225. [Google Scholar] [CrossRef]
- Maes, K.; Iliopoulos, A.; Weijtjens, W.; Devriendt, C.; Lombaert, G. Dynamic strain estimation for fatigue assessment of an offshore monopile wind turbine using filtering and modal expansion algorithms. Mech. Syst. Signal Process. 2016, 76–77, 592–611. [Google Scholar] [CrossRef]
- Antonino-Daviu, J. Electrical monitoring under transient conditions: A new paradigm in electric motors predictive maintenance. Appl. Sci. 2020, 10, 6137. [Google Scholar] [CrossRef]
- Gerdes, M.T.; Wang, Y.; Wei, X.; Wang, G.C.; Liu, R.; Gross, K.C. Vibration resonance spectrometry (VRS) for the advanced streaming detection of rotor unbalance. Machines 2023, 11, 639. [Google Scholar] [CrossRef]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassolkin, A.; Van Khang, H. The modeling and investigation of slot skews and supply imbalance on the development of principal slotting harmonics in squirrel cage induction machines. IEEE Access 2021, 9, 165932–165946. [Google Scholar] [CrossRef]
- Pavlenko, I.; Verbovyi, A.; Neamţu, C.; Ivanov, V.; Ciszak, O.; Trojanowska, J. Fractional-order mathematical model of single-mass rotor dynamics and stability. Alex. Eng. J. 2023, 76, 91–100. [Google Scholar] [CrossRef]
- Sudhakar, G.N.D.S.; Sekhar, A.S. Identification of unbalance in a rotor bearing system. J. Sound Vib. 2011, 330, 2299–2313. [Google Scholar] [CrossRef]
- Qiu, Y.; Rao, S.S. A fuzzy approach for the analysis of unbalanced nonlinear rotor systems. J. Sound Vib. 2005, 284, 299–323. [Google Scholar] [CrossRef]
- Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Burriel-Valencia, J.; Riera-Guasp, M. Fault diagnosis in the slip–frequency plane of induction machines working in time-varying conditions. Sensors 2020, 20, 3398. [Google Scholar] [CrossRef]
- Costa, C.C.O.; Costa, C.D. Quantification and analysis of uncertainties in parameters of rotors supported by bearings. Eur. J. Eng. Technol. Res. 2021, 6, 88–95. [Google Scholar] [CrossRef]
- Han, B.; Liu, Z.; He, P.; Yan, P. Rotor crack breathing under unbalanced disturbance. J. Sound Vib. 2024, 574, 118236. [Google Scholar] [CrossRef]
- Kulesza, Z.; Sawicki, J.T. Damping by parametric excitation in a set of reduced-order cracked rotor systems. J. Sound Vib. 2015, 354, 167–179. [Google Scholar] [CrossRef]
- Guo, C.; Al-Shudeifat, M.A.; Yan, J.; Bergman, L.A.; McFarland, D.M.; Butcher, E.A. Stability analysis for transverse breathing cracks in rotor systems. Eur. J. Mech.-A/Solids 2013, 42, 27–34. [Google Scholar] [CrossRef]
- Cherif, B.D.E.; Rahali, H.; Seninete, S. Enhanced diagnosis and monitoring of broken rotor bar faults in induction motors using a combined Ceemdan-MLP approach. Metrol. Meas. Syst. 2024, 31, 73. [Google Scholar] [CrossRef]
- Sivaraj, N.; Rajagopal, B. Performance analysis of neural networks for fault detection in induction motor. Int. J. Electr. Electron. Eng. 2025, 12, 129–141. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Spyropoulos, D.V.; Mitronikas, E. Advanced detection of rotor electrical faults in induction motors at start-up. IEEE Trans. Energy Convers. 2021, 36, 1101–1109. [Google Scholar] [CrossRef]
- de las Morenas, J.; Moya-Fernández, F.; López-Gómez, J.A. The edge application of machine learning techniques for fault diagnosis in electrical machines. Sensors 2023, 23, 2649. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, X.; Xiong, Y.; Zhang, Y. Intelligent fault diagnosis of turbine blade cracks via multiscale sparse filtering and multi-kernel support vector machine for information fusion. Adv. Eng. Inform. 2023, 56, 101979. [Google Scholar] [CrossRef]
- Kumar, P.; Tiwari, R. Finite element modelling, analysis and identification using novel trial misalignment approach in an unbalanced and misaligned flexible rotor system levitated by active magnetic bearings. Mech. Syst. Signal Process. 2021, 152, 107454. [Google Scholar] [CrossRef]
- Ma, X.; Li, Z.; Xiang, J.; Chen, C.; Huang, F. Vibration characteristics of rotor system with coupling misalignment and disc-shaft nonlinear contact. Mech. Syst. Signal Process. 2025, 223, 111839. [Google Scholar] [CrossRef]
- Sun, X.; Chocholaty, B.; Liu, Y.; Marburg, S. Nonlinear dynamic behavior of a rotor-bearing system considering time-varying misalignment. Int. J. Mech. Sci. 2024, 284, 109772. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Z.; Lin, J.; Han, Q.; Liu, Y. A novel nonlinear spectrum estimation method and its application in on-line condition assessment of bearing-rotor system. Measurement 2023, 221, 113497. [Google Scholar] [CrossRef]
- Bentrad, M.B.; Ghoggal, A.; Bahi, T. Advanced diagnosis of air gap eccentricity in three-phase induction motor using DWT decomposition and AI techniques. J. Eur. Syst. Autom. 2024, 57, 1249–1257. [Google Scholar] [CrossRef]
- Nityananda, R.H.; Srivatsa, S.R.; Somaskanda, S.; Taj, A.P. Finite element model updating of boring bar and determination of chatter stability. Mater. Today Proc. 2021, 45, 165–171. [Google Scholar] [CrossRef]
- Huang, S.-C.; Octaviani, S.; Najibullah, M. A novel hybrid approach to the diagnosis of simultaneous imbalance and shaft bowing faults in a jeffcott rotor-bearing system. Appl. Sci. 2024, 14, 3269. [Google Scholar] [CrossRef]
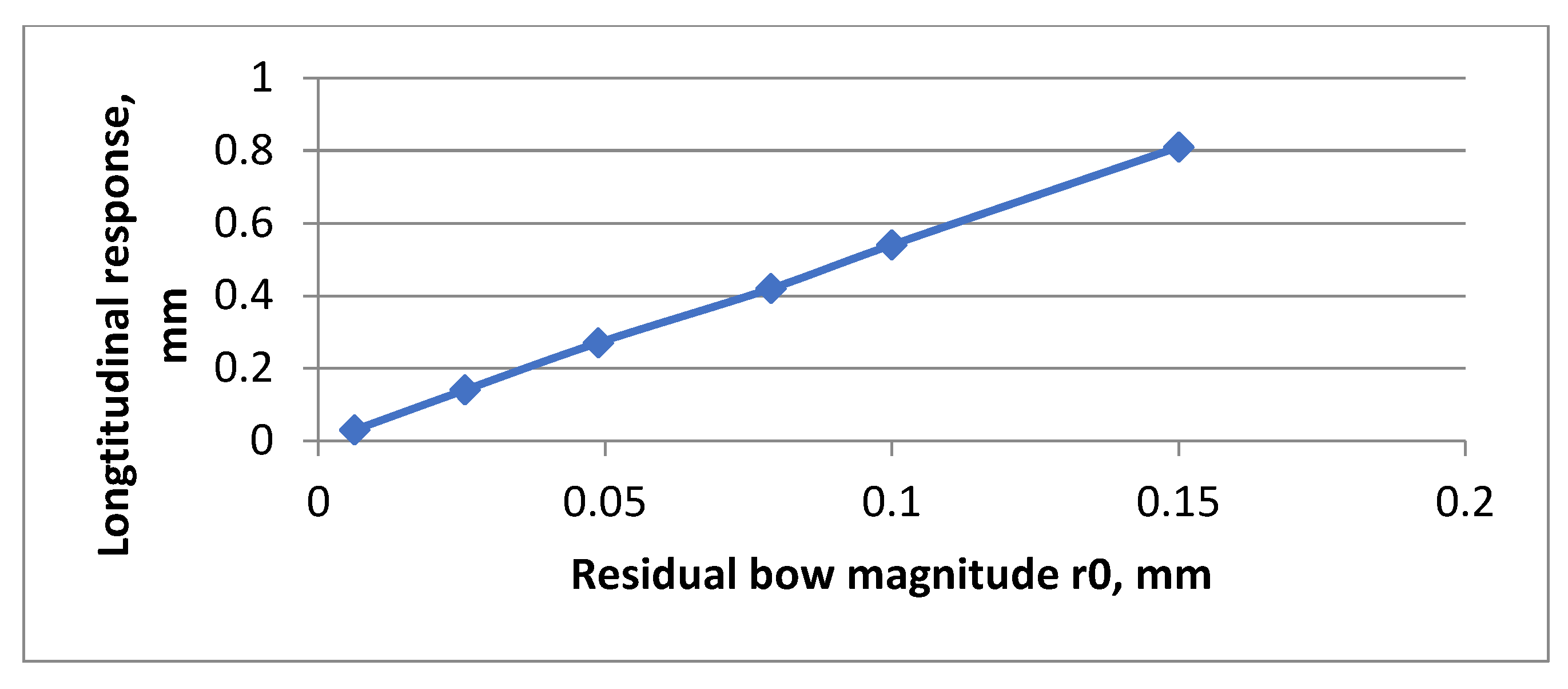
- Song, G.F.; Yang, Z.J.; Ji, C.; Wang, F.P. Theoretical–experimental study on a rotor with a residual shaft bow. Mech. Mach. Theory 2013, 63, 50–58. [Google Scholar] [CrossRef]
- Muszynska, A.; Goldman, P. Chaotic responses of unbalanced rotor/bearing/stator systems with looseness or rubs. Chaos Solitons Fractals 1995, 5, 1683–1704. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Yang, S.; Cheng, J. Adaptive parameterless empirical wavelet transform based time-frequency analysis method and its application to rotor rubbing fault diagnosis. Signal Process. 2017, 130, 305–314. [Google Scholar] [CrossRef]
- Li, Q.; Hu, H.; Liao, M.; Jing, X. A nonlinear transmissibility function-based diagnosis approach for multi-disks rub-impact faults in rotor systems with nonlinear supports. Mech. Syst. Signal Process. 2025, 228, 112418. [Google Scholar] [CrossRef]
- Pavlenko, I.; Simonovskiy, V.; Ivanov, V.; Zajac, J.; Pitel, J. Application of artificial neural network for identification of bearing stiffness characteristics in rotor dynamics analysis. In Advances in Design, Simulation and Manufacturing. DSMIE 2019. Lecture Notes in Mechanical Engineering; Ivanov, V., Rong, R., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2019; pp. 325–335. [Google Scholar] [CrossRef]
- Feng, Z.; Wang, T.; Zuo, M.J.; Chu, F.; Yan, S. Teager energy spectrum for fault diagnosis of rolling element bearings. J. Phys. Conf. Ser. 2011, 305, 012129. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, W.; Chen, F.; Huang, G.; Wang, X.; Yuan, W.; Xiong, X. Fault diagnosis of nuclear power plant sliding bearing-rotor systems using deep convolutional generative adversarial networks. Nucl. Eng. Technol. 2024, 56, 2958–2973. [Google Scholar] [CrossRef]
- Barusu, M.R.; Sethurajan, U.; Deivasigamani, M. Diagnosis of bearing outer race faults using a low-cost non-contact method with advanced wavelet transforms. Elektron. Ir Elektrotech. 2019, 25, 44–53. [Google Scholar] [CrossRef]
- Bae, I.; Lee, S. A multi-input convolutional neural network model for electric motor mechanical fault classification using multiple image transformation and merging methods. Machines 2024, 12, 105. [Google Scholar] [CrossRef]
- Ma, J.; Fu, C.; Zheng, Z.; Lu, K.; Yang, Y. The effects of interval uncertainties on dynamic characteristics of a rotor system supported by oil-film bearings. Lubricants 2022, 10, 354. [Google Scholar] [CrossRef]
- Masrol, S.R.; Madlan, M.A.; Salleh, S.M.; Ismon, M.B.; Roslan, M.N. Vibration analysis of unbalanced and misaligned rotor system using laser vibrometer. Appl. Mech. Mater. 2013, 315, 681–685. [Google Scholar] [CrossRef]
- Dang, P.V.; Do, L.H.T.; Vo, N.T.; Ngo, T.N.; Le, H.N. Identification of unbalance in rotating machinery using vibration analyse solution. IOP Conf. Ser. Mater. Sci. Eng. 2020, 841, 012011. [Google Scholar] [CrossRef]
- Abubakar, I.M.; Farid, B.J.M. Generalized Den Hartog tuned mass damper system for control of vibrations in structures. WIT Trans. Built Environ. 2009, 104, 185–193. [Google Scholar] [CrossRef]
- Domínguez-Nicolás, S.M. Signal conditioning system for real-time monitoring of unbalanced mass and angular position in helicopter propeller rotor balancing. Measurement 2025, 242, 116150. [Google Scholar] [CrossRef]
- Wu, X.; Meagher, J. A two-disk extended Jeffcott rotor model distinguishing a shaft crack from other rotating asymmetries. Int. J. Rotating Mach. 2008, 2008, 846365. [Google Scholar] [CrossRef]
- Patel, T.H.; Darpe, A.K. Vibration response of a cracked rotor in presence of rotor-stator rub. J. Sound Vib. 2008, 317, 841–865. [Google Scholar] [CrossRef]
- Nishimura, H.; Horiguchi, H.; Suzuki, T.; Sugiyama, K.; Tsujimoto, Y. Sub- and super-synchronous self-excited vibrations of a columnar rotor due to axial clearance flow. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 072001. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Feng, G.Q.; Zhou, B.Z.; Lin, L.J.; Han, Q.K. Transverse vibration measurement and analysis of a three-point supported dual-span rotor system with angle misaligned flexible coupling. Adv. Mater. Res. 2011, 301, 790–796. [Google Scholar] [CrossRef]
- Ma, X.; Song, Y.; Cao, P.; Li, J.; Zhang, Z. Self-excited vibration suppression of a spline-shafting system using a nonlinear energy sink. Int. J. Mech. Sci. 2023, 245, 108105. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, K.; Zhang, W.; Fu, C. Investigation on dynamic behaviors of rotor system with looseness and nonlinear supporting. Mech. Syst. Signal Process. 2022, 166, 108400. [Google Scholar] [CrossRef]
- Inoue, T.; Ishida, Y.; Kondo, K. Chaotic vibration and internal resonance phenomena in rotor systems (in the vicinity of the major critical speed). Trans. Jpn. Soc. Mech. Eng. Part C 2000, 66, 370–377. [Google Scholar] [CrossRef][Green Version]
- Kurvinen, E.; Viitala, R.; Choudhury, T.; Heikkinen, J.; Sopanen, J. Simulation of subcritical vibrations of a large flexible rotor with varying spherical roller bearing clearance and roundness profiles. Machines 2020, 8, 28. [Google Scholar] [CrossRef]
- Bachschmid, N.; Pennacchi, P.; Vania, A. Thermally induced vibrations due to rub in real rotors. J. Sound Vib. 2007, 299, 683–719. [Google Scholar] [CrossRef]
- Wu, F.; Hong, J.; Chen, X.; Ma, Y. Analysis of high-speed rotor vibration failure due to sudden angular deformation of bolt joints. Symmetry 2023, 15, 1937. [Google Scholar] [CrossRef]
- Tian, Y.-W.; Yang, J.-G. Research on vibration induced by the coupled heat and force due to rotor-to-stator rub. J. Vib. Control 2010, 17, 549–566. [Google Scholar] [CrossRef]
- Pacheco-Chérrez, J.; Fortoul-Díaz, J.A.; Cortés-Santacruz, F.; Aloso-Valerdi, L.M.; Ibarra-Zarate, D.I. Bearing fault detection with vibration and acoustic signals: Comparison among different machine leaning classification methods. Eng. Fail. Anal. 2022, 139, 106515. [Google Scholar] [CrossRef]
- Wang, C.; Aldakheel, F.; Zhang, C.; Gu, L.; Wriggers, P. Failure of high-speed bearing at cyclic impact-sliding contacts: Numerical and experimental analysis. Int. J. Mech. Sci. 2023, 253, 108410. [Google Scholar] [CrossRef]
- Zhou, G.; Li, P.; Liao, D.; Zhang, Y.; Zhong, P. The friction-induced vibration of water-lubricated rubber bearings during the shutdown process. Materials 2020, 13, 5818. [Google Scholar] [CrossRef] [PubMed]
- Sawaqed, L.S.; Alrayes, A.M. Bearing fault diagnostic using machine learning algorithms. Prog. Artif. Intell. 2020, 9, 341–350. [Google Scholar] [CrossRef]
- Hongjun, W.; Hongfeng, W.; Yongjian, J. Orbit identification method based on ISOMAP for rotor system fault diagnosis. In Proceedings of the 2013 IEEE 11th International Conference on Electronic Measurement & Instruments, Harbin, China, 16–19 August 2013; pp. 668–671. [Google Scholar] [CrossRef]
- Mishra, R.K.; Choudhary, A.; Fatima, S.; Mohanty, A.R.; Panigrahi, B.K. A generalized method for diagnosing multi-faults in rotating machines using imbalance datasets of different sensor modalities. Eng. Appl. Artif. Intell. 2024, 132, 107973. [Google Scholar] [CrossRef]
- Tang, Q.; Huang, J.; Zhu, B.; Yu, J.; Liang, C.; Li, J. Time-varying harmonic analysis method based on adaptive frequency-shift filtering for power systems. Electr. Power Syst. Res. 2025, 238, 111177. [Google Scholar] [CrossRef]
- Sastry, C.V.S.; Mahapatra, D.R.; Gopalakrishnan, S.; Ramamurthy, T. An iterative system equivalent reduction expansion process for extraction of high frequency response from reduced order finite element model. Comput. Methods Appl. Mech. Eng. 2003, 192, 1821–1840. [Google Scholar] [CrossRef]
- MacNeil, P.E.; Schultz, S.R. A genetic algorithm approach to the solution of a differential equation. In Proceedings of the IEEE SoutheastCon 2010 (SoutheastCon), Concord, NC, USA, 18–21 March 2010; pp. 448–450. [Google Scholar] [CrossRef]
- Li, Y.L.; Huang, J.L.; Zhu, W.D. A generalized incremental harmonic balance method by combining a data-driven framework for initial value selection of strongly nonlinear dynamic systems. Int. J. Non-Linear Mech. 2024, 169, 104951. [Google Scholar] [CrossRef]
- Lara-Molina, F.A.; De Piemonte Dourado, A.; Cavalini, A.A.; Steffen, V. Uncertainty analysis techniques applied to rotating machines. Rotating Mach. 2019, 2, 83828. [Google Scholar] [CrossRef]
- Peradotto, E.; Panunzio, A.M.; Salles, L.; Schwingshackl, C. Stochastic methods for nonlinear rotordynamics with uncertainties. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; p. GT2015-43534. [Google Scholar] [CrossRef]
- Xu, B.; Ning, P.; Wang, G.; Zang, C. Steady-state response analysis of an uncertain rotor based on Chebyshev orthogonal polynomials. Appl. Sci. 2024, 14, 10698. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, J.; Faes, M.G.R.; Bi, S.; Wang, Y. The sub-interval similarity: A general uncertainty quantification metric for both stochastic and interval model updating. Mech. Syst. Signal Process. 2022, 178, 109319. [Google Scholar] [CrossRef]

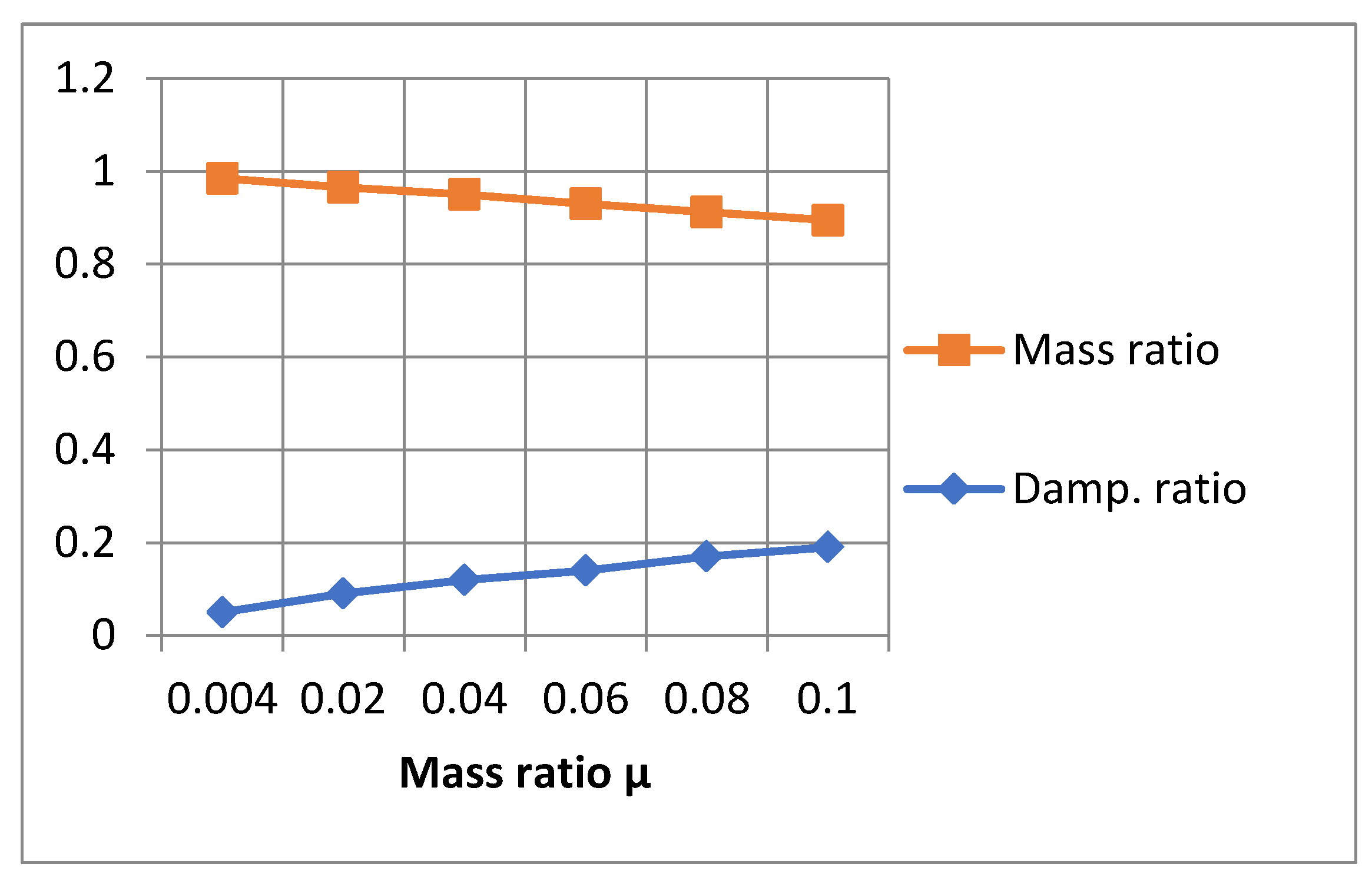
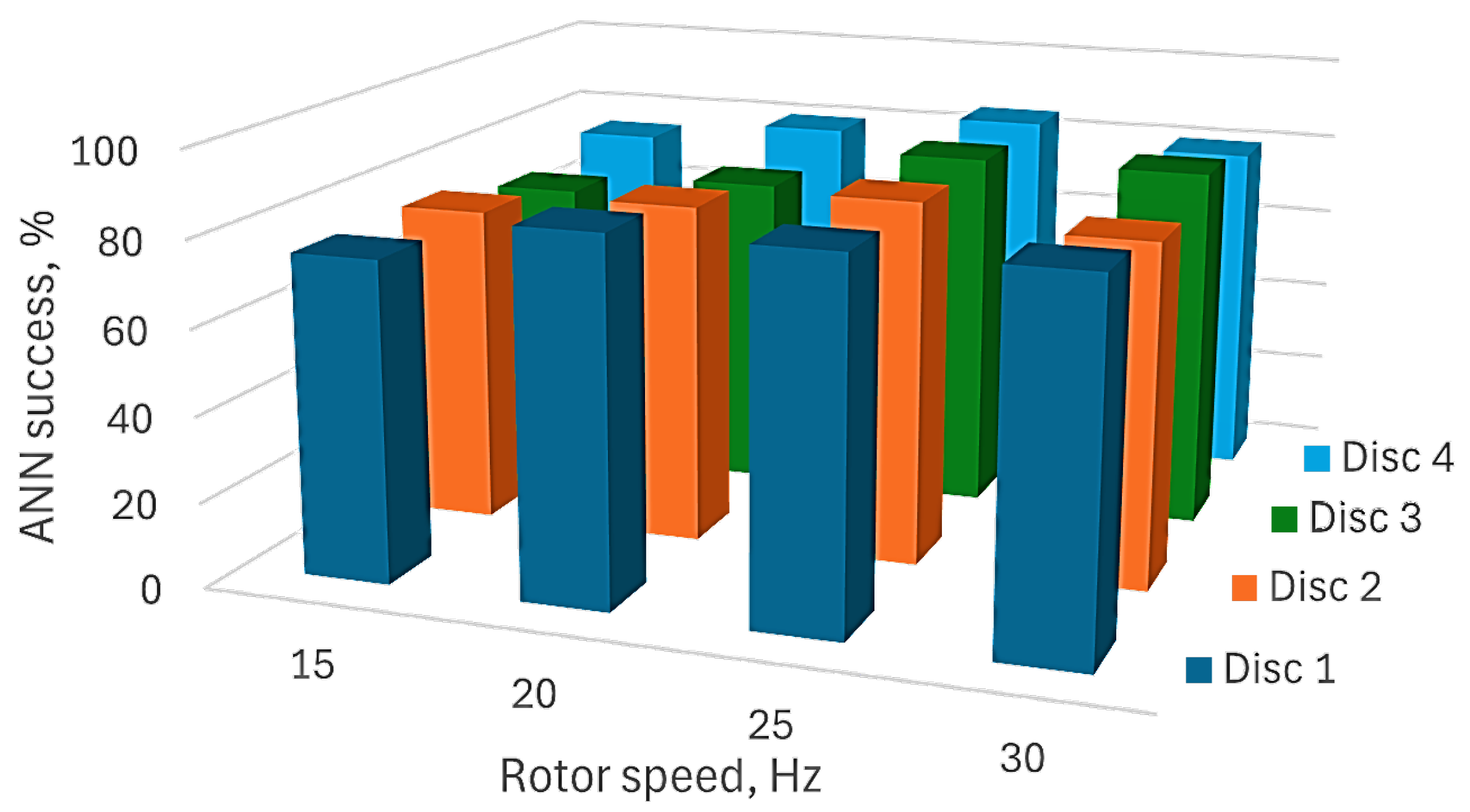
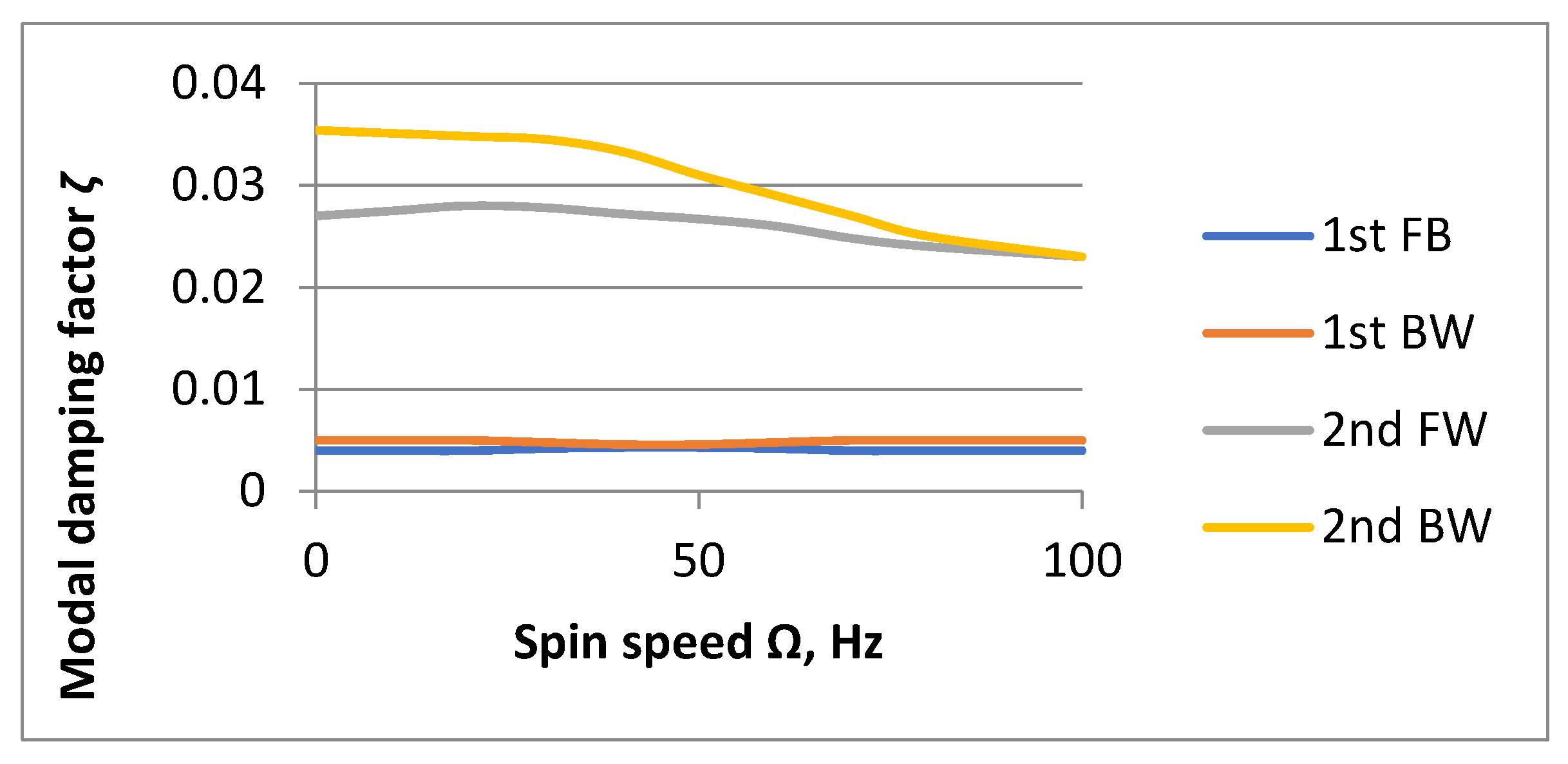

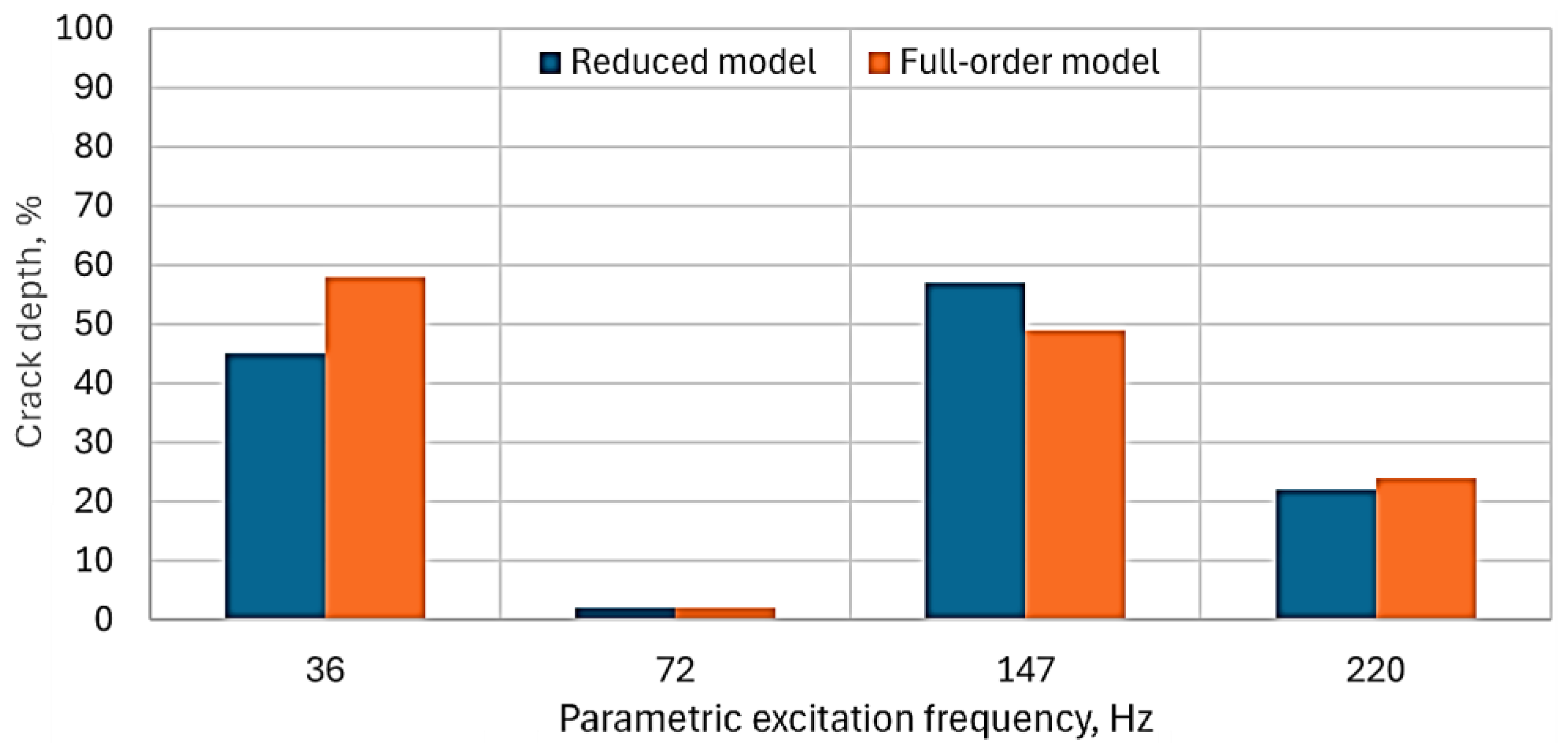


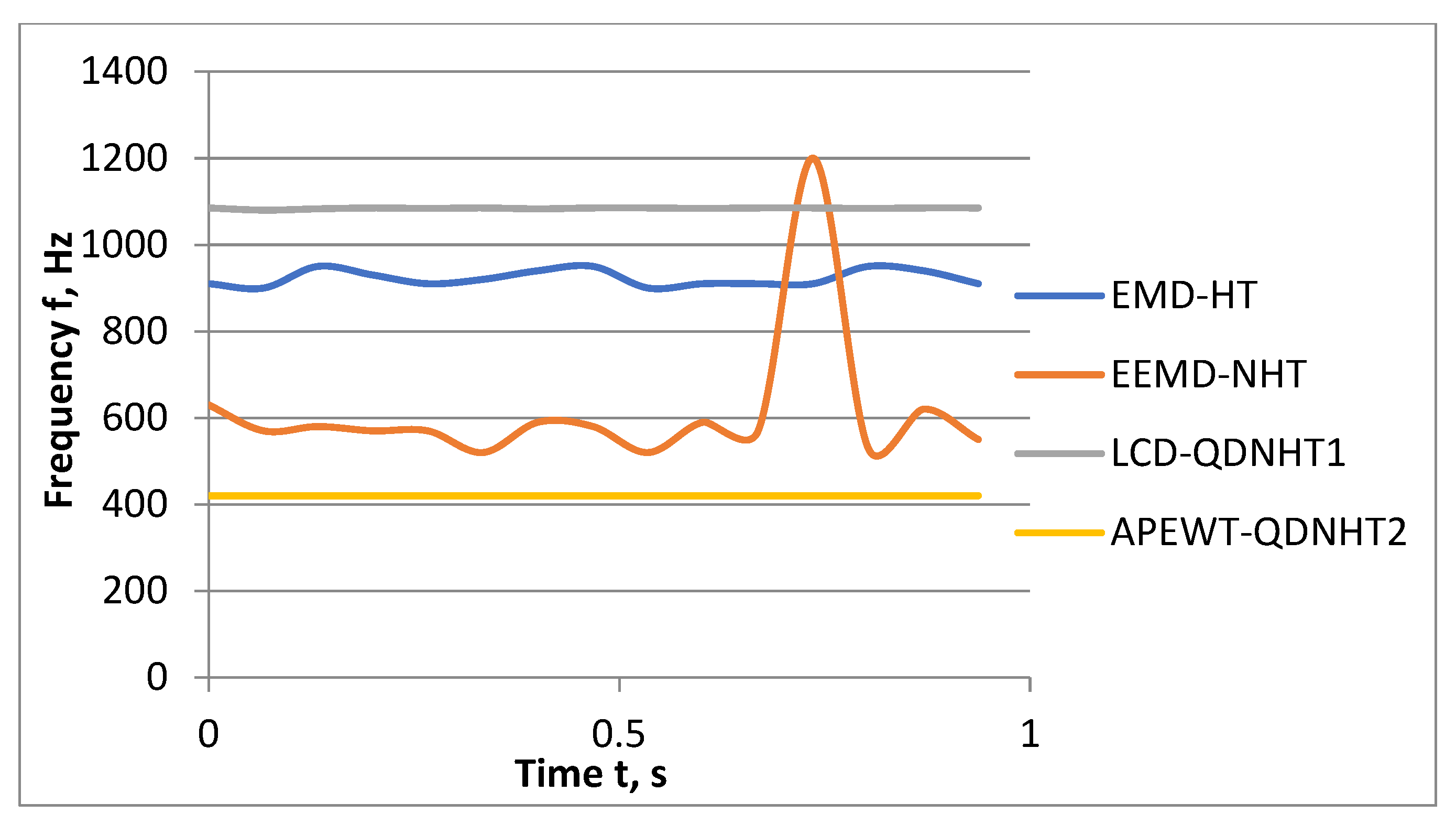
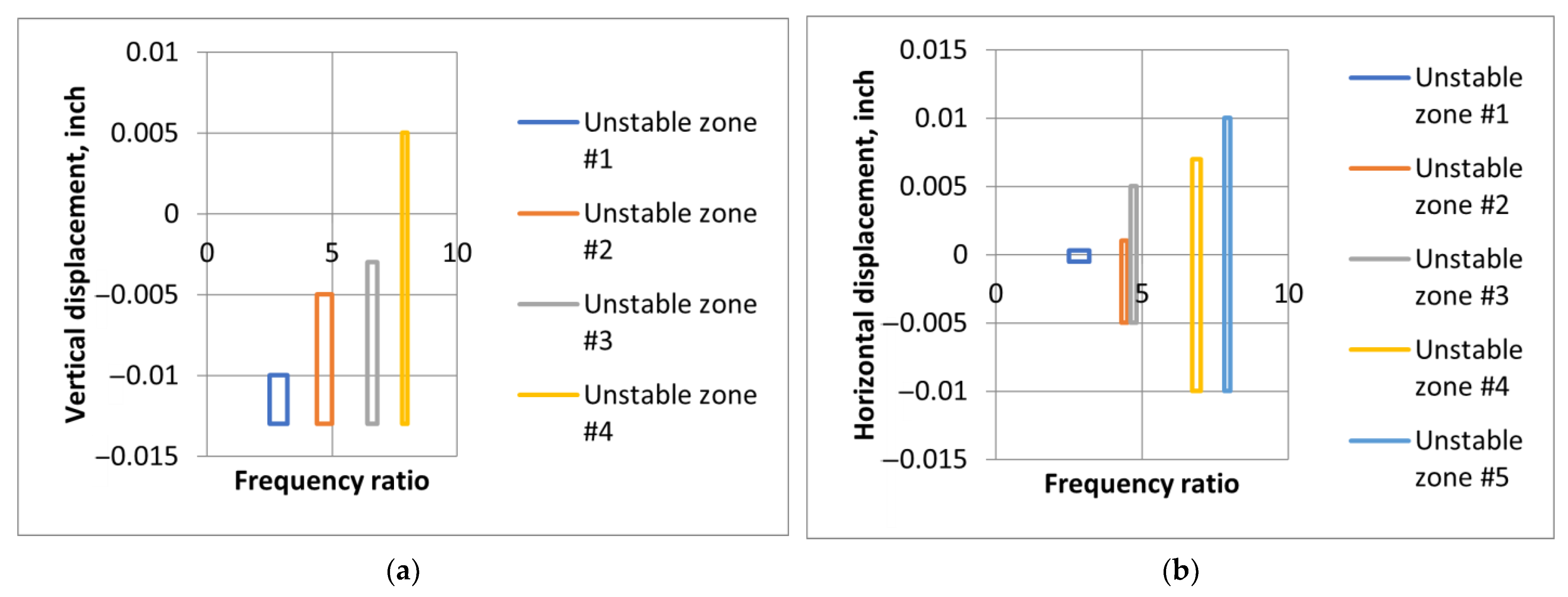
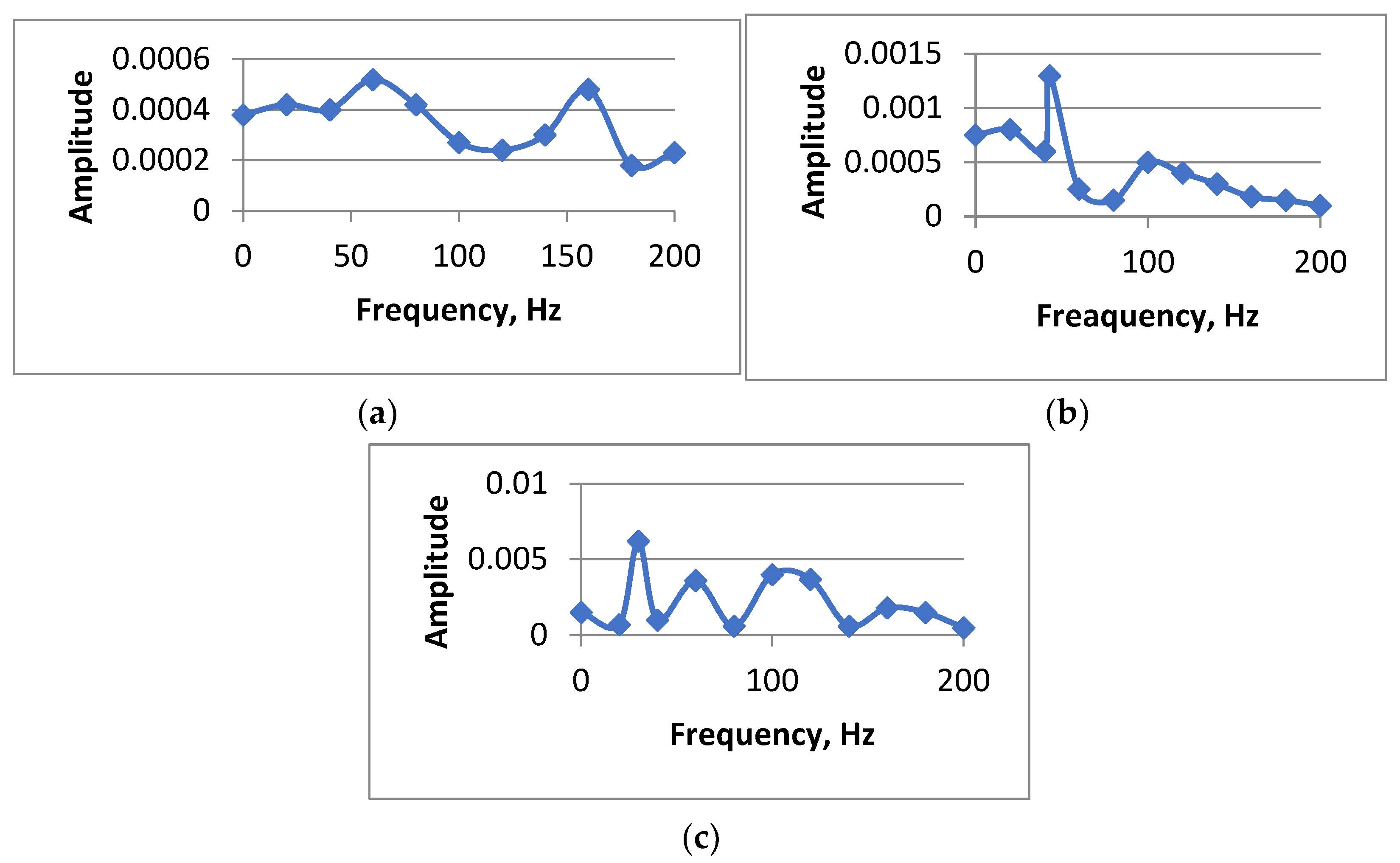
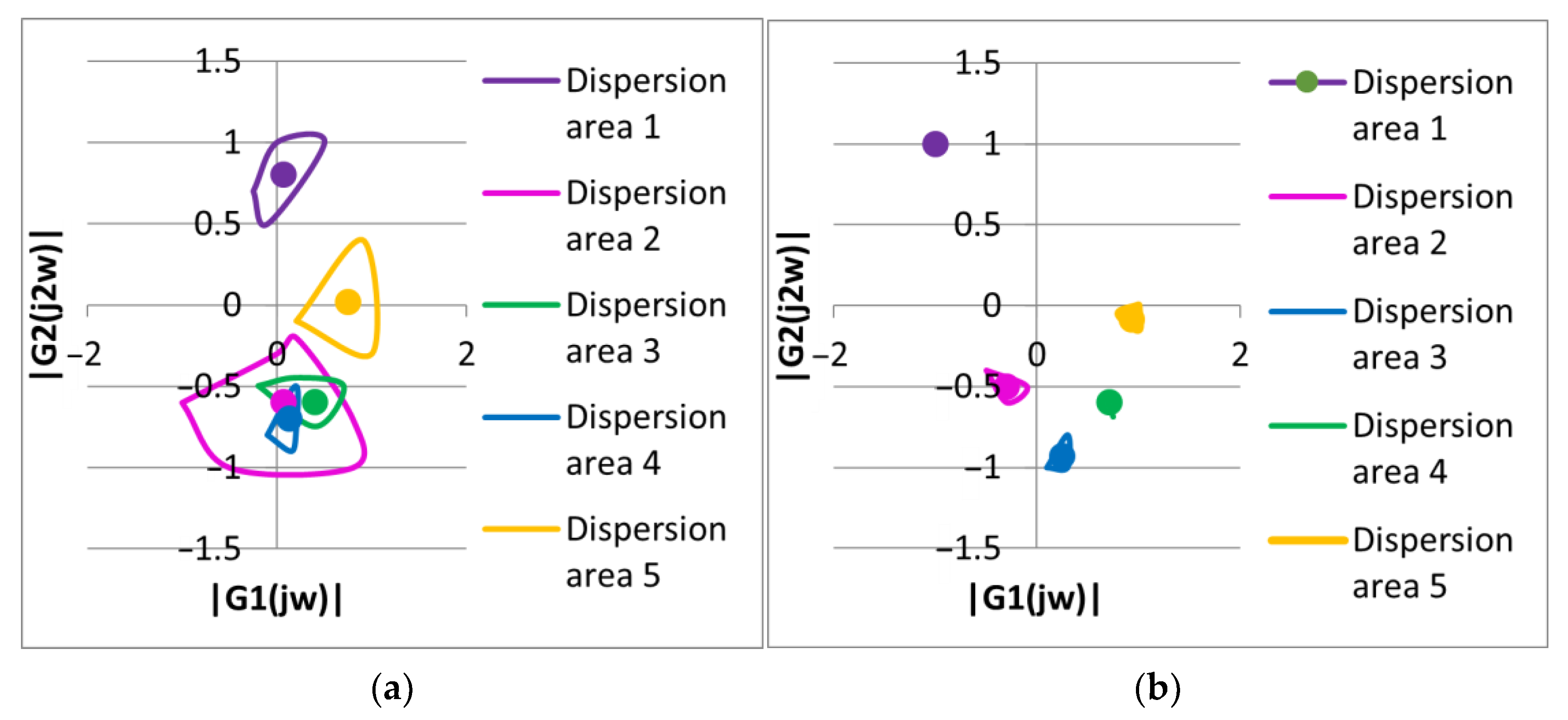
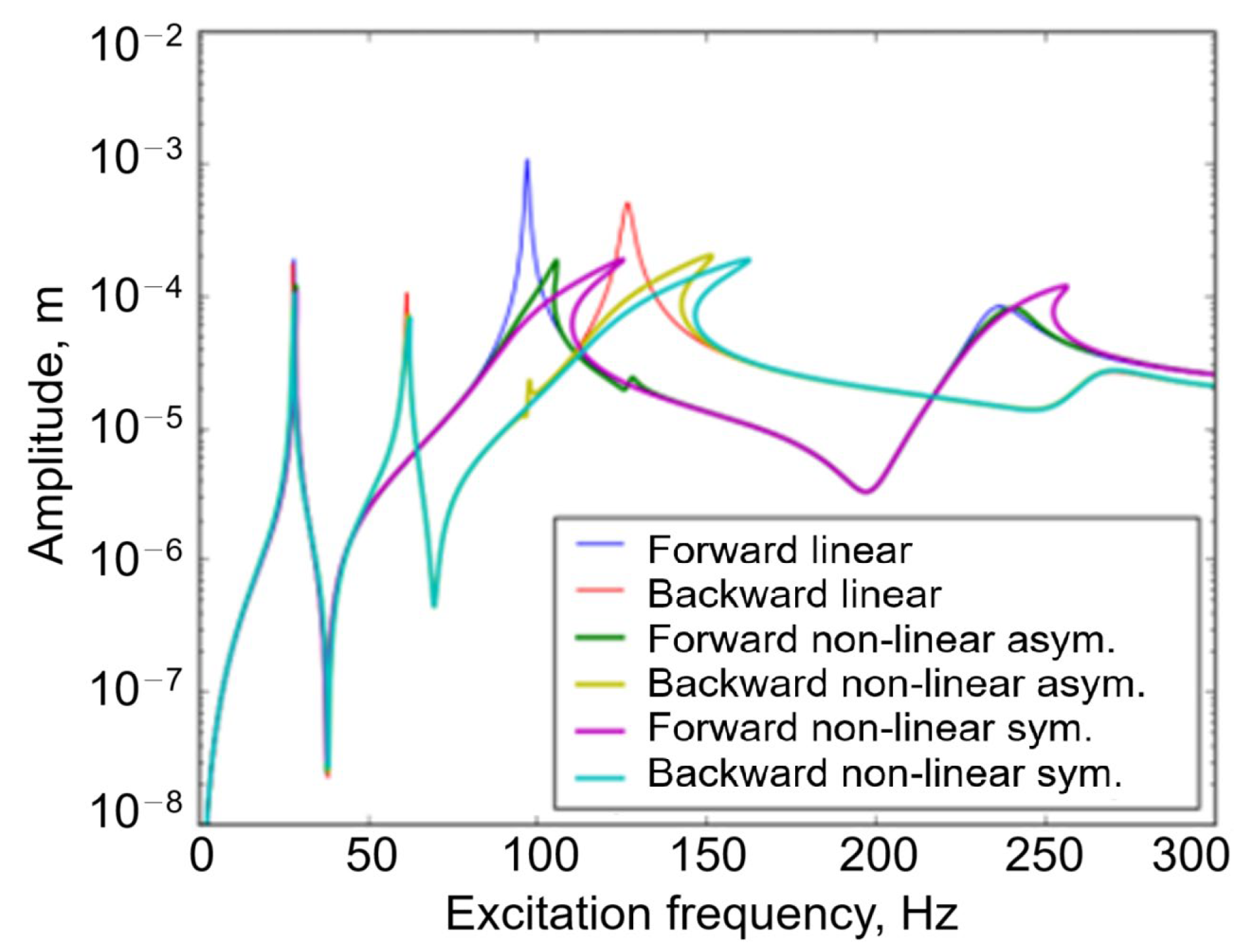

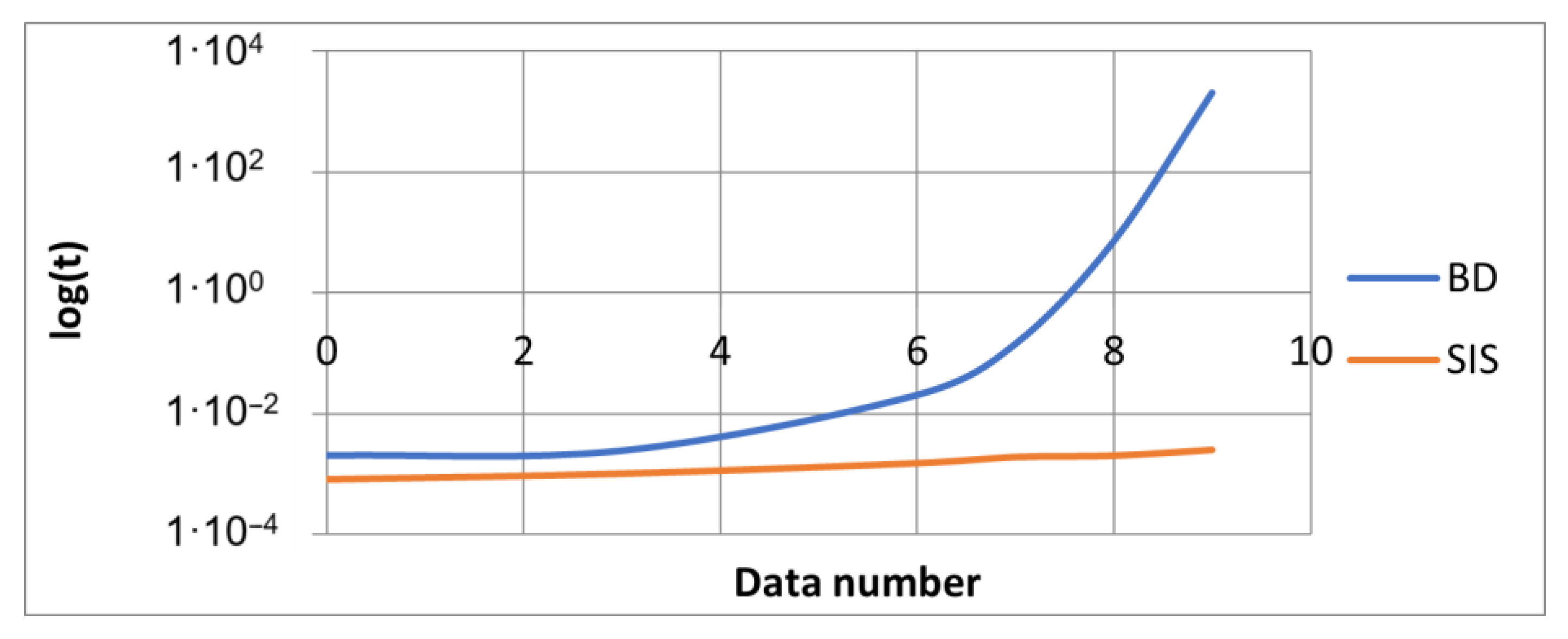

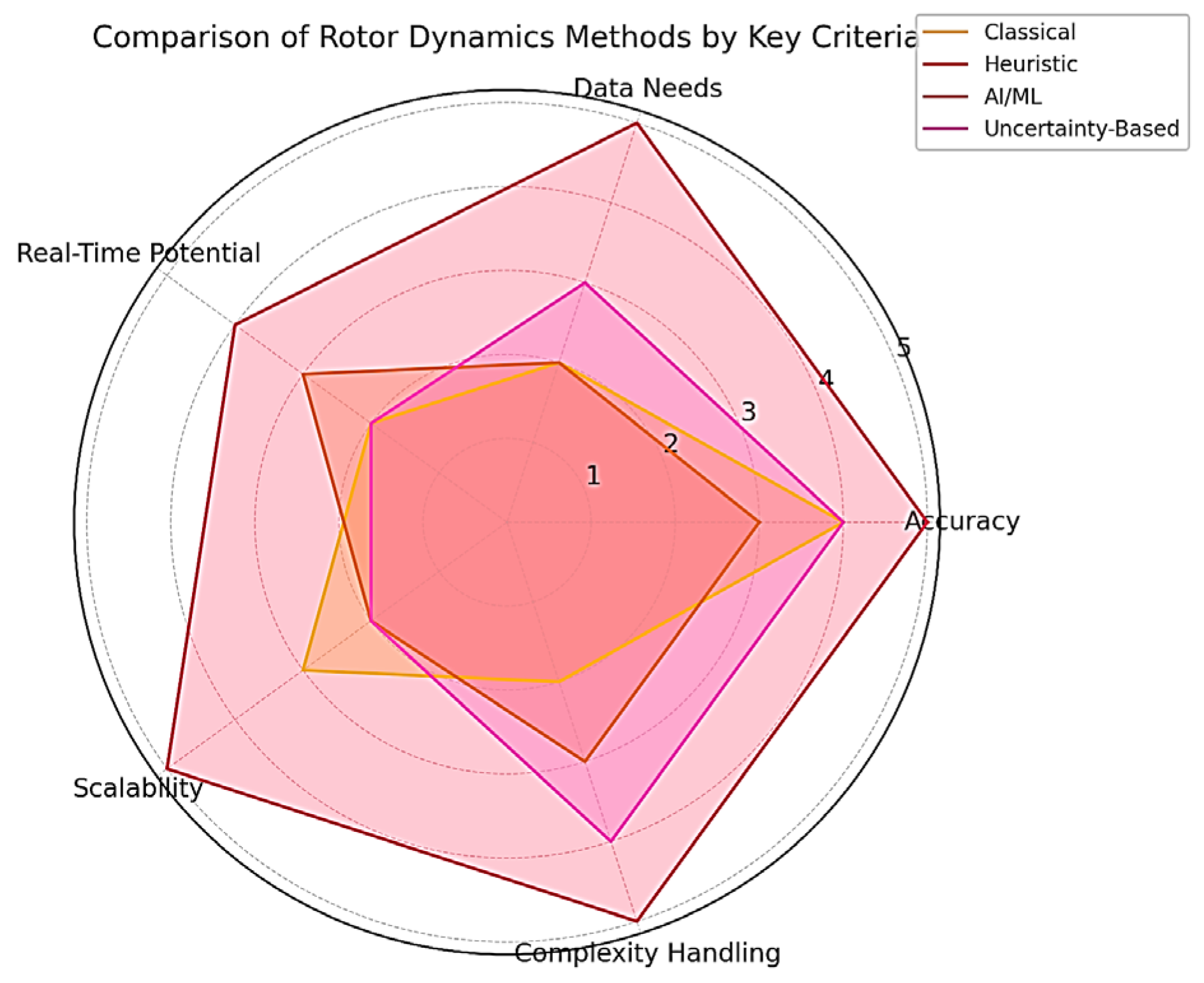
| Issue | Identification Methods | References |
|---|---|---|
| Unbalance | Finite element method (FEM) | [22,23,24,25,26,27,28,29] |
| Operating deflection shape (ODS) method | [23,30] | |
| Fast Fourier transform (FFT) | [14,24,28,31,32,33,34] | |
| Short-term Fourier transform (STFT) | [27,32] | |
| Fractional-order analysis (Pavlenko’s approach) | [35] | |
| Equivalent load minimization method (ELMM) | [14] | |
| Joint input-state estimation algorithm (JISEA) | [31] | |
| Modal balancing (MB) | [22] | |
| Differential evolution (DE) | [28] | |
| Singular value decomposition (SVD) | [22,27] | |
| Newton–Raphson method | [25,28,36] | |
| Runge–Kutta methods | [28,29,37] | |
| Least squares method | [25,27,31,36] | |
| Continuous wavelet transform (CWT) | [32,38] | |
| Random forest (RF) | [23] | |
| k-nearest neighbors (KNN) | [24] | |
| Principal component analysis (PCA) | [33] | |
| Artificial neural network (ANN) | [25,30] | |
| Monte Carlo simulation (MCS) | [39] | |
| Cracks | Finite element method (FEM) | [40,41,42] |
| Hilbert–Huang transform (HHT) | [40,43,44] | |
| Fast Fourier transform (FFT) | [40,42,43,44,45] | |
| Strain energy release rate (SERR) | [40] | |
| Discrete wavelet transform (DWT) | [32,46] | |
| Support vector machine (SVM) | [46,47] | |
| Artificial neural network (ANN) | [44,47] | |
| Decision tree (DT) | [46] | |
| Random forest (RF) | [46] | |
| k-nearest neighbors (KNN) | [46] | |
| Newmark-β method | [40,41] | |
| Misalignment | Finite element method (FEM) | [27,48,49,50] |
| Finite difference method (FDM) | [50] | |
| Orbit analysis | [48,49,50] | |
| Phase measurement | [27,48] | |
| Time-frequency analysis (TFA) | [51] | |
| Singular value decomposition (SVD) | [27] | |
| Support vector machine (SVM) | [52] | |
| Discrete wavelet transform (DWT) | [52] | |
| Short-term Fourier transform (STFT) | [52] | |
| Decision tree (DT) | [52] | |
| Newton–Raphson Method | [49] | |
| Runge–Kutta Methods | [48,49] | |
| Least squares method | [27,48,51] | |
| Newmark-β method | [49,50] | |
| Rotor bending | Finite element method (FEM) | [28,29,53] |
| Finite element model updating (FEMU) | [53] | |
| Fast Fourier transform (FFT) | [29] | |
| Artificial neural network (ANN) | [54] | |
| Feedforward neural network (FNN) | [54] | |
| Short-term Fourier transform (STFT) | [54] | |
| Wavelet transform (WT) | [28,55] | |
| Rotor bending | System equivalent reduction expansion process (SEREP) | [53] |
| Isometric mapping (ISOMAP) | [55] | |
| Inverse eigensensitivity (IES) method | [53] | |
| Principal component analysis (PCA) | [28,55] | |
| Natural frequency difference (NFD) | [29,53,55] | |
| Characteristic equation method | [53] | |
| Newton–Raphson method | [55] | |
| Runge–Kutta methods | [29] | |
| Least squares method | [28,53] | |
| Rotor–stator rub | Finite element method (FEM) | [49,56] |
| Time-frequency analysis (TFA) | [57] | |
| Fast Fourier transform (FFT) | [9,49,57] | |
| Hilbert transform (HT) | [9,57] | |
| Wavelet transform (WT) | [57,58] | |
| Gabor transform (GT) | [9,16] | |
| Topological fractal multi-resolution analysis (TFMRA) | [9] | |
| Empirical mode decomposition (EMD) | [57] | |
| Method of small parameter | [56] | |
| Newton–Raphson method | [49,56,57] | |
| Runge–Kutta methods | [49] | |
| Convolutional neural network (CNN) | [16,58] | |
| Teager energy operator (TEO) | [58] | |
| Newmark-β Method | [49,57] | |
| Bearing faults | Finite element method (FEM) | [59] |
| Time-frequency analysis (TFA) | [51,60,61] | |
| Wavelet transform (WT) | [17,60,61] | |
| Fast Fourier transform (FFT) | [11,17,32,38,46,51,60,62,63] | |
| Hilbert–Huang transform (HHT) | [11,32,38] | |
| Discrete wavelet transform (DWT) | [32,38] | |
| Short-term Fourier transform (STFT) | [38,62] | |
| Gabor transform (GT) | [11,16,46] | |
| Chebyshev interval method (CIM) | [64] | |
| Full tensor grid (FTG) | [64] | |
| Principal component analysis (PCA) | [17,51,62] | |
| Decision tree (DT) | [46] | |
| Random forest (RF) | [46] | |
| Support vector machine (SVM) | [46] | |
| Teager energy operator (TEO) | [60] | |
| Artificial neural network (ANN) | [59,61,62] | |
| Convolutional neural networks (CNN) | [16,38,44,61,63] | |
| Continuous wavelet transform (CWT) | [61] | |
| Long short-term memory (LSTM) | [61] | |
| Generative adversarial networks (GAN) | [61] | |
| Least squares method | [51,59] |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Finite element method (FEM) | High accuracy in modeling complex mechanical systems [22,23,24]. | High computational costs can be a limitation for real applications [25,26]. | N/A |
| Ability to consider nonlinear effects and complex boundary conditions [27,28]. | Sensitivity to the quality of input parameters and the need for careful calibration [27,28]. | ||
| Operating deflection shape (ODS) method | It can be used to determine the location of damage in structures [23,40]. | Sensitive to noise in measurements, which can affect the accuracy of the results [30]. | TD/FD |
| It does not require knowledge of input forces, as it is based only on vibration measurements [23]. | Determining local changes can be difficult due to the scaling of defective forms [30]. | ||
| Fast Fourier transform (FFT) | Fast and efficient signal conversion to the frequency domain [24,36]. | Inability to accurately analyze nonstationary signals without additional methods [5,28]. | FD |
| Works well for harmonic analysis and resonance detection [36]. | Loss of temporal information complicates the analysis of transient processes [31,34]. | ||
| Short-term Fourier transform (STFT) [26] | It allows analyzing nonstationary signals and obtaining time-frequency characteristics. | Limited resolution due to the trade-off between time and frequency. | TFD |
| Sensitive to window selection, which affects the accuracy of the analysis. | |||
| Equivalent load minimization method (ELMM) [36] | It reduces the error in fault detection, even with a few measurements. | Sensitive to FEM modeling quality, it can cause errors in case of inaccurate definitions of boundary conditions. | N/A |
| High computational complexity due to the need to minimize errors in theoretical models. | |||
| Joint input-state estimation algorithm (JISEA) [31] | Provides simultaneous estimation of both system states and unknown excitatory forces. | High sensitivity to noise and errors in input data. | N/A |
| It is more efficient than the classical Kalman filter for structural dynamics problems. | Requires significant computing power, especially for complex systems. | ||
| Modal balancing (MB) method [22] | Allows effective compensation for a distributed unbalanced load. | Requires accurate modeling and experimental verification. | TD/FD |
| It may require complex calculations and multi-stage testing. | |||
| Artificial neural network (ANN) | High accuracy in estimating or identifying [25,26]. | Depends on reliable FEM input or experimental data [25,26]. | N/A |
| It supports virtual balancing without trial runs [25]. | ANN performance is sensitive to architecture [25]. | ||
| Suitable for nonlinear and implicit process modeling [25,26]. | Less effective under noise or with linear-only models [26]. | ||
| Modal balancing (MB) method [22] | Allows adequate compensation for a distributed unbalanced load. | Requires accurate modeling and experimental verification. | TD/FD |
| It may require complex calculations and multi-stage testing. | |||
| Differential evolution (DE) method [28] | Good results with nonlinear and multidimensional problems. | It may require many iterations to achieve an accurate solution. | N/A |
| Singular value decomposition (SVD) [22] | It allows the isolation of the main components and reduces low and medium noise levels. | It is sensitive to high noise levels in the input data, which can distort the results. | N/A |
| Newton–Raphson method | Fast convergence to roots with a good initial approximation [25,36]. | It may not converge, or it gives incorrect results with a poor initial approximation [25]. | N/A |
| Runge–Kutta methods | High accuracy in solving differential equations without calculating higher-order derivatives [28,37]. | Sensitive to the choice of integration step, which can affect the accuracy of the results [29]. | N/A |
| Least squares method | It is suitable for regularizing problems with many variables [27]. | Requires the correct choice of regularization parameters to avoid over-computation [31]. | N/A |
| Monte Carlo simulation (MCS) [39] | Provides complete statistics (mean, variance, skewness, kurtosis) of critical speeds and stability thresholds. | Quickly becomes computationally expensive | N/A |
| Scales naturally when additional random variables or nonlinearities are introduced. | Supplies no derivatives or analytical expressions |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Finite element method (FEM) | Ability to take nonlinear effects into account [40]. | Sensitivity to the quality of initial parameters and boundary conditions [41]. | N/A |
| Hilbert–Huang transform (HHT) [40] | Efficient analysis of nonstationary and nonlinear signals. | High computational costs when calculating complex signals. | TFD |
| Better resolution compared to classical methods of spectral analysis. | Noise can affect the accuracy of the results. | ||
| Fourier expansion | It approximates periodic signals with high accuracy [40,42]. | It is unsuitable for analyzing nonstationary signals without additional modifications [42]. | FD |
| Facilitates the calculation of complex functions by representing them as series [40]. | It requires many harmonics to represent complex waveforms accurately [40]. | ||
| Strain energy release rate (SERR) [40] | It allows us to determine the stress level and predict the cracks’ development. | Sensitive to geometric parameters and measurement accuracy. | N/A |
| Newmark-β method | It provides a stable numerical solution for effective analysis of vibrations [41]. | It requires a small step for accuracy, increasing computational costs [40]. | N/A |
| Sensitive to the choice of integration parameters, which affects the accuracy of the results [41]. |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Finite element method (FEM) | Ability to consider nonlinear contacts and imbalances [48,50]. | Sensitivity to model parameters and accuracy of the input data [49]. | N/A |
| Suitable for modeling both flexible and rigid rotors [27,48]. | Difficulty in choosing suitable element partitioning and boundary conditions [50]. | ||
| Finite difference method (FDM) [50] | More straightforward to implement and calculate in comparison with FEM. | Poor accuracy in coarse mesh partitioning. | N/A |
| High computational speed for few-dimensional problems. | Problems with solution stability for rigid systems. | ||
| Convenient for solving problems of hydrodynamic lubrication and analysis of film bearings. | It is difficult to use for complex geometries due to the need for a regular mesh. | ||
| Orbit analysis | It allows the analysis of nonlinear effects and motion instabilities [50]. | Requires high-precision sensors for data collection [48,50]. | TD/FD |
| An effective method for detecting rotor imbalance and misalignment [48,49]. | Limited efficiency at low rotor speeds [49]. | ||
| Convenient for diagnosing the condition of bearings and contact zones [49]. | It is challenging to interpret orbits with complex defects [50]. | ||
| Phase measurement | It allows the evaluation of the dynamic characteristics of a rotor system in real time [27]. | Requires accurate calibration of measuring equipment [27]. | TD/FD |
| High sensitivity to changes in the system state [48]. | Difficult to use for complex rotor systems with multiple disturbance sources [27]. | ||
| Time-frequency analysis (TFA) [51] | An effective method for analyzing transients in rotary systems. | High computational complexity, especially for large datasets. | TFD |
| Allows for the detection of frequency components that are not visible in conventional spectral analysis. | |||
| Singular value decomposition (SVD) [27] | Reduces data dimensionality and highlights the most important system characteristics. | High computational costs for large matrices. | N/A |
| Newmark-β method | Allows controlling accuracy and stability by selecting the parameters β and γ [50]. | Sensitive to choosing initial parameters [50]. | N/A |
| Suitable for analyzing both linear and nonlinear systems [49]. | |||
| Newton–Raphson method [49] | Provides fast convergence for finding the roots of nonlinear equations. | It does not work if the derivative of the function is close to zero, which can cause instability. | N/A |
| Runge–Kutta methods | High accuracy in solving differential equations without calculating derivatives at each point [48]. | Adaptive step selection may be required, complicating implementation [49]. | N/A |
| Stability in solving equations [49]. | |||
| Least squares method [51] | Effective for solving overdetermined equation systems. | It may not work well for very sparse data. | N/A |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Finite element method (FEM) | Ability to consider complex geometries and material properties [29]. | Sensitivity to boundary conditions and grid-partitioning parameters [29]. | N/A |
| Suitable to analyze resistance to self-oscillations and the effect of defects [53]. | |||
| Finite element model updating (FEMU) [53] | Improves the correspondence of the numerical model to real experimental data. | The dependence on the accuracy of experimental data to adjust the model. | N/A |
| Fast Fourier transform (FFT) [29] | Fast and efficient signal conversion to the frequency domain. | It loses temporal resolution and is not suitable for analyzing nonstationary processes. | FD |
| Sensitive to the choice of window length and interpolation methods. | |||
| Wavelet transform (WT) | Allows analyzing nonstationary signals with high time-frequency resolution [55]. | Higher computational costs compared to FFT [28]. | TFD |
| Effective for detecting local signal features and short-term anomalies [28]. | The choice of the wave basis significantly affects the accuracy of the results [55]. | ||
| System equivalent reduction expansion process (SEREP) [53] | Preserves the physical content of the model while reducing its dimensionality. | Sensitive to the choice of base modes. | N/A |
| Provides accurate results within the selected frequency range. | Loss of accuracy outside the specified frequency range. | ||
| ISOMAP [55] | Allows nonlinear data dimensionality reduction while preserving global geometry. | High computational costs for large samples. | N/A |
| Effective for detecting hidden structures in complex multidimensional data. | Sensitive to the choice of the number of neighbors, which affects the results. | ||
| Inverse eigensensitivity method (IES) | Effective for updating finite element models by adjusting parameters [53]. | Sensitive to initial assumptions about model parameters [26]. | N/A |
| Principal component analysis (PCA) | Reduces data dimensionality while saving the most significant characteristics [28,55]. | Loss of information with rejecting insignificant components [55]. | N/A |
| Reduces noise in data and improves the interpretability of results [28]. | Assumes linearity of data, which can be a limitation for complex nonlinear dependencies [28]. | ||
| Natural frequency difference (NFD) | Improves the accuracy of updated finite element models [53]. | Sensitive to noise in measurements [55]. | FD |
| Suitable for identifying differences between experimental and numerical modal characteristics [55]. | It does not consider the shape of the vibration modes, which can lead to an incomplete picture of the discrepancy [53]. | ||
| Characteristic equation method [53] | Accurately determines the natural frequencies and oscillation forms of the system. | Sensitive to errors in system parameters, which can affect the accuracy of the results. | N/A |
| Newton–Raphson method [55] | Converges quickly to a solution with a good initial approximation. | It can cause instability if the function’s derivative is close to zero. | N/A |
| Runge–Kutta methods [29] | Provides high accuracy in solving a wide range of problems in numerical modeling. | Sensitive to the choice of the integration step: a too-significant step can reduce accuracy, and a too-small step can increase computational costs. | N/A |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Finite element method (FEM) | Allows for modal analysis and determination of natural frequencies of structures [56]. | High computational costs, especially when using models with many degrees of freedom [49]. | N/A |
| The accuracy of calculations depends on the correct choice of boundary conditions and material parameters [56]. | |||
| Time-frequency analysis (TFA) [57] | Comparison with other methods showed a higher accuracy of signal feature extraction. | Sensitivity to noise and parameter selection when analyzing nonstationary signals. | TFD |
| Fast Fourier transform (FFT) | A fast method of spectral analysis that allows estimating the frequency composition of signals in rotary systems [49]. | Not suitable for analyzing rapidly changing signals [57]. | FD |
| Effective for detecting fundamental harmonics and resonant frequencies in vibration analysis [57]. | |||
| Hilbert transform (HT) [57] | An effective demodulation method for mono-component signals. | Prone to energy losses at the edges of the signal and the appearance of negative frequencies. | TD/FD |
| Suitable for estimation of the instantaneous frequency and the instantaneous amplitude of signals. | Violates the conditions of Bedrosian’s theorem, which may affect the accuracy of the analysis. | ||
| Wavelet transform (WT) [57] | High time-frequency resolution for analyzing nonstationary signals. | Requires the selection of an appropriate wave base, which may affect the analysis results. | TFD |
| Empirical mode decomposition (EMD) [57] | An adaptive method for decomposing a signal into internal modal functions (IMFs) allows for analyzing complex nonstationary processes. | Lack of rigorous mathematical justification, which complicates its formal analysis. | TFD |
| Small parameter method [56] | Allows analytical evaluation of the influence of minor nonlinear effects on the behavior of rotor systems. | It does not always accurately describe transient transitions, as it is based on approximations. | N/A |
| Newton–Raphson method | Used for the iterative solution of kinetic equations in rotary systems, which allows considering nonlinear contact forces between the disk and the shaft [49]. | For complex mechanical systems, additional refinement of the Jacobi matrix is required to achieve stable convergence [55]. | N/A |
| Allow to improve the accuracy of numerical modeling by combining with the Newmark-β method [49]. | Sensitive to the choice of the initial approximation [57]. | ||
| Provides fast convergence in solving nonlinear equations [57]. | |||
| Newmark-β method | It allows effectively modeling the bearing parameters’ impact on the rotor vibration characteristics [49]. | Sensitive to the choice of initial conditions, which can affect the accuracy of the numerical solution [57]. | N/A |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Finite element method (FEM) [59] | Allows accurate modeling of critical frequencies and rotor vibration shapes. | There is a need to determine the stiffness of bearings to obtain accurate results. | N/A |
| Time-frequency analysis (TFA) | It allows the detection of short-term anomalies in the signal [51]. | Sensitive to the choice of transformation parameters, which can affect the diagnostic accuracy [60]. | TFD |
| Wavelet transform (WT) [60] | High time-frequency resolution allows the detection of short-term anomalies in the signal. | The wave base’s choice affects the accuracy, which may require additional adjustment. | TFD |
| Fast Fourier transform (FFT) | Fast and efficient signal conversion to the frequency domain [60]. | Sensitive to the choice of window length and averaging methods [51,63]. | FD |
| Principal component analysis (PCA) [51] | Efficiently highlighting the main patterns in large sets of vibration data. | Assumes linearity of data, which can be a limitation for complex nonlinear dependencies. | N/A |
| Teager energy operator (TEO) [60] | Effective for detecting short-term pulses in vibration signals. | Sensitive to noise. | TD/FD |
| Requires additional signal preprocessing to improve the quality of results. | |||
| Artificial neural network (ANN) [59] | It can effectively model nonlinear dependencies and adapt to complex problems. | Sensitivity to the quality of input data. | N/A |
| High accuracy with enough training data. | Requires a large amount of training data to work effectively. | ||
| Convolutional neural networks (CNN) [16,61,63] | Automatically detects significant signal features without the need for manual processing. | Uninterpretable: It is difficult to explain what features the network uses for classification. | N/A |
| High classification accuracy with enough training data. | |||
| Continuous wavelet transform (CWT) [61] | Effective for detecting local features and short-term anomalies in vibration signals. | The choice of the wave base affects the accuracy of the analysis and requires customization. | TFD |
| Long short-term memory (LSTM) [61] | It can effectively detect long-term dependencies in data. | Requires a large amount of data for training to avoid overfitting. | N/A |
| It can be used in combination with CNN to improve fault diagnosis. | |||
| Generative adversarial networks (GAN) [61] | Improves classification accuracy by combining actual and generated data. | Poor tuning can cause training instability. | N/A |
| Capable of detecting hidden patterns in complex multidimensional data. | Generated data may contain artifacts that affect the quality of analysis. | ||
| Least squares method [59] | It reduces errors in the correlation of modal characteristics when updating the model. | It can produce physically incorrect model parameters if no constraints or regularization are applied. | N/A |
| Chebyshev interval method (CIM) [64] | It works with bounded uncertainties only—no PDFs are needed. | Accuracy hinges on the chosen polynomial order and grid level; tuning remains empirical. | TD/FD |
| Clearly separates the influence of globaland local (bearing length, unbalance phase) parameters. | Ignoring parameter correlations and fault-driven nonlinearities. | ||
| Full tensor grid (FTG) [64] | Captures all interactions among interval variables exactly at sampled points. | A large number of FEA runs. | TD/FD |
| Offers a direct benchmark for validating surrogate methods like CIM. | May miss the true extrema between grid nodes. |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Joint input-state estimation algorithm (JISEA) [31] | Provides simultaneous estimation of both system states and unknown excitatory forces. | High sensitivity to noise and errors in input data. | N/A |
| Modal expansion algorithm (MEA) [31] | Does not require knowledge of natural frequencies or damping ratios. | Not suitable for low-frequency (quasi-static) strain estimation. | FD |
| ISOMAP-based orbit identification [85] | Captures nonlinear features from high-dimensional orbit data. | It requires careful parameter tuning and may be sensitive to sampling density. | N/A |
| Digital filter method [85] | It allows for the effective reduction of noise and extracts the rotor orbit’s basic shape. | It is not effective for nonlinear or complex signals. | TD/FD |
| RBFNN [86] | Achieves good accuracy on balanced and imbalanced datasets across three sensor modalities (acoustic, vibration, current). | It requires careful choice of window size and overlap, as well as careful ANN architecture design planning. | N/A |
| Synchronized Fourier transform (SFT) [86] | Allows reconstruction. | Requires proper tuning of squeezing parameters. | TFD |
| Preserves phase information. | |||
| Operating deflection shape (ODS) method [30] | It does not require knowledge of input forces, as it is based only on vibration measurements. | Determining local changes can be difficult due to the scaling of defective forms. | TD/FD |
| Artificial neural network (ANN) | High accuracy in estimating or identifying [59,86]. | Depends on reliable FEM input or experimental data [59]. | N/A |
| Suitable for nonlinear and implicit process modeling [59]. | Sensitive to class imbalance ratios [86]. | ||
| Works with limited sensor setups [86]. | Performance depends heavily on careful feature engineering and parameter tuning [59,86]. |
| Method | Advantages | Disadvantages | Domain * |
|---|---|---|---|
| Fractional-order model | Allows for more accurate consideration of hydrodynamic and viscoelastic effects in rotor systems [35]. | Requires more complex computational methods than classical models [35]. | N/A |
| Improves the assessment of the stability of rotor dynamic modes by using fractional derivatives [35]. | Difficult to interpret results [56]. | ||
| Incremental harmonic balance method (IHB) and ANN [90] | Using a neural network to select initial values can significantly improve the convergence of the method. | High computational complexity with an increasing number of harmonics. | FD |
| Suitable for calculating nonlinear dynamic systems with many degrees of freedom. | Requires high-quality neural network training to determine the initial values accurately. | ||
| Genetic algorithm (GA) for differential equations [89] | Allows for the obtaining of reasonable approximate solutions for differential equations. | It does not guarantee the finding of an optimal global solution. | N/A |
| It makes it possible to estimate challenging parameters by using analytical methods. | It may require significant computing resources, especially when the number of parameters is large. | ||
| Iterative system equivalent reduction expansion process (SEREP) [88] | Using an iterative approach improves accuracy in the high-frequency range. | High computational complexity in calculating the eigenvectors of the system. | N/A |
| This allows for reducing the model dimension without significant loss of accuracy. | A reasonable choice of frequency range is required to reduce the model order effectively. | ||
| Time-varying harmonic analysis [87] | Improved adaptive frequency-shift filtering allows for more efficient harmonic analysis. | Requires complex algorithms for adaptive signal processing. | TFD |
| Reduces the loss of spectral information within the standard Fourier transform. | Sensitive to the choice of filtering parameters, which affects the accuracy. | ||
| Stochastic finite element method (SFEM) [91] | Provides full statistical information—means, variances, and confidence bands. | Requires reliable probability-density functions for every uncertain parameter; scarce or poor statistics can distort the results. | TD/FD |
| Non-intrusive: the existing FE model is reused, with randomness introduced via a Karhunen–Loève expansion of material fields. | Assumes Gaussian, independent inputs in the paper; real-world correlations or non-Gaussian tails may lead to over- or under-estimating risk. | ||
| Fuzzy finite element method (FFEM) [91] | No probability-density functions are required; triangular fuzzy numbers can be elicited from expert judgment or sparse test data. | Produces conservative (potentially over-wide) response bounds, which may mask useful sensitivity information. | TD/FD |
| Guarantees that the true response lies within the α-level envelopes—valuable when only epistemic uncertainty is present. | The choice of membership-function shape and spread is subjective; inconsistent expert inputs can skew the results. | ||
| Polynomial chaos expansion (PCE) [92] | Provides a full probabilistic output. | Requires a reliable PDF for every uncertain parameter. | FD |
| Non-intrusive and differentiable, enabling variance-based sensitivity analysis and robust optimization. | “Curse of dimensionality”: accuracy and grid size grows rapidly beyond 4–5 random variables. | ||
| Monte Carlo simulation (MCS) | Scales naturally with added random variables and nonlinearities [92,93]. | Requires 1000+ FEM runs even for a moderate problem [92,93]. | TD/FD |
| It provides a statistical picture of the response distribution, which helps validate interval surrogates [93]. | Impractical for iterative design loops or real-time monitoring due to computational burden [92]. | ||
| Chebyshev interval method (CIM) [93] | Requires no probability-density functions. | Empirical tuning. | TD/FD |
| A relatively small number of FEM evaluations. | It ignores correlations among parameters and has not been tested with defect-induced nonlinearities. | ||
| Markov-chain Monte Carlo (MCMC) on sub-interval similarity (SIS) metric [94] | Integrates SIS directly into the likelihood, enabling consistent treatment of sparse, irregular experimental data without assuming Gaussian errors. | Needs prior PDFs; posterior sampling can still be expensive for high-dimensional parameter spaces. | N/A |
| Universally applicable: the same metric works when data are intervals, single samples, or complete distributions. | Performance and convergence depend on the empirical choice of the sub-interval number. | ||
| Particle swarm optimization (PSO) sub-interval similarity (SIS) metric [94] | It requires only upper/lower bounds for measurements and delivers guaranteed parameter intervals. | Correlations between parameters are not represented. | N/A |
| High-speed efficiency. | Provides no probabilistic ranking. |
| Issue | Features | Causes | Detection Methods | References |
|---|---|---|---|---|
| Unbalance | Excessive vibration and noise; increased bearing loads. | Uneven mass distribution. | Vibration analysis; balancing tests. | [65,66] |
| Misalignment | High vibration; increased bearing temperature; coupling wear. | Improper installation; thermal expansion. | Laser alignment tools; vibration spectrum analysis. | [66,73] |
| Resonance | High-amplitude vibrations at critical speeds. | Structural design flaws; improper damping. | Modal analysis; frequency-response testing. | [76,77] |
| Rotor cracks | Subharmonic vibrations; unexpected frequency changes. | Fatigue stress; corrosion. | Non-destructive testing (NDT); modal analysis. | [69,70] |
| Bearing failures | Noise, irregular vibrations, increased temperature. | Lubrication failure; contamination. | Shock pulse monitoring; envelope analysis. | [81,82,83,84] |
| Oil whirl/whip | Self-excited vibrations at sub-synchronous frequencies. | Insufficient bearing stiffness; excessive lubrication. | Vibration analysis; bearing design assessment. | [71,72] |
| Rotor–stator rub | Sudden vibration spikes, high noise levels, and heat spots. | Thermal expansion; misalignment. | Acoustic emission; temperature monitoring. | [78,79,80] |
| Looseness | Impact-like vibration; irregular waveform signals. | Loose fasteners; foundation problems. | Time waveform analysis; visual inspection. | [74,75] |
| Issue | Solution Methods |
|---|---|
| Measurement noise | Kalman filter (KF), discrete Fourier transform (DFT), Fourier synchro-squeezed transform (FST), joint input-state estimation algorithm (JISEA), modal expansion, moving average filter (MAF), wavelet transform (WT), equivalent loads minimization method, generative-competitive networks (GAN). |
| Computational complexity | Proper orthogonal decomposition (POD), Krylov subspace methods, ISOMAP, system equivalent reduction expansion process (SEREP), Guyan reduction (GR), iterative SEREP, modal truncation, inverse eigensensitivity (IES) method, dynamic condensation, differential evolution (DE), phase-locked loop. |
| Conception | Achievements | Problems | Methods, Techniques, and Algorithms | Domain * |
|---|---|---|---|---|
| Abubakar I.—Generalized Den Hartog tuned mass damper system for control of vibrations in structures [67]. | ||||
| Including the damping characteristics of a pedestal in the Den Hartog model. | Den Hartog’s model, which considers the damping characteristics of a pedestal, is much more accurate. | Considers a linear model that is not suitable in the case of random or impulse excitations. | The Den Hartog’s method. | Classical |
| Andres Lara-Molina, F.—Uncertainty Analysis Techniques Applied to Rotating Machines [91]. | ||||
| Provides the first side-by-side, test-rig-validated comparison of stochastic and fuzzy uncertainty quantification for a flexible rotor-bearing system. | Confirmed both stochastic and fuzzy frameworks’ predictive reliability. | Both schemes assume independent Gaussian or triangular inputs and become computationally heavy as the number of uncertain variables grows. | Stochastic finite element method (SFEM); fuzzy finite element method (FFEM). | Uncertain |
| Corbally R.—Bridge damage detection using operating deflection shape ratios obtained from a passing vehicle [30]. | ||||
| Quantification of continuous values to instantaneous values using Hilbert’s transformation. | Using a dimensionless operating deflection shape ratio allows for the detection of damage to construction, regardless of external load intensity. | The external load model is not oscillatory; besides, in the scope of the research, the load should be moving along the construction. | Operating deflection shape ratios (ODSR); mel-frequency cepstrum; Kullback–Leibler divergence; wavelet transform; Hilbert transform; short time-frequency domain decomposition (STFDD); regional mode-shape curvature (RMSC); Dirac delta function. | Classical |
| Deepthikumar M.—Modal balancing of flexible rotors with bow and distributed unbalance [22]. | ||||
| Conception of imbalance distributed along the rotor length. | Derived criteria for rotor suitability for further work; methodology of balancing of distributed imbalance with point masses. | The required uniform distribution of sensors is often not possible; the model represents a vertical rotor, so it does not consider the influence of gravity on an imbalanced rotor. | Modal balancing (MB) method; transfer matrix (TM) method; singular decomposition. | Classical |
| Domingues-Nicolas S.—Signal conditioning system for real-time monitoring of unbalanced mass and angular position in helicopter propeller rotor balancing [68]. | ||||
| Synchronization of rotation and vibration phases to reduce signal noise. | Geometry parametrization allows for building and researching systems with various geometry configurations. | Model, in terms of statics, does not allow for studying oscillation processes of rotor systems; only the angular coordinates of imbalance are identified. | Kalman filter; phase-locked loop. | Classical |
| Feng Z.—Teager energy spectrum for fault diagnosis of rolling element bearings [60]. | ||||
| The Teager energy spectrum received from impulses’ repeating frequency is obtained with the Fourier transform on the instantaneous Teager energy series. | The proposed method successfully extracts characteristic frequencies of bearing element faults while effectively detecting weaker inner race and rolling element fault symptoms. | Sensitivity to noise and initial parameters: a simple model that does not consider complex nonlinear vibration processes. | Teager energy operator (TEO); Teager energy spectrum; fast Fourier transform (FFT). | Classical |
| Gohari M.—Modeling of shaft imbalance: Modeling a multi discs rotor using k-nearest neighbor and decision tree algorithms [24]. | ||||
| Applying heuristic clustering and decision-making algorithms for rotor systems diagnostics. | Performed a comparison of efficiency for k-nearest neighbor and decision tree methods. | kNN method means clusterization by discrete values (here, it is a disk number), so it is impossible to evaluate the imbalance position as a continuous value; the angular coordinate of imbalance is not considered for calculations; it is not clear what are input and output structures. | k-nearest neighbors method (KNN); decision tree (DT); fast Fourier transform (FFT); Hanning window. | Heuristic |
| Guo C.—Stability analysis for transverse breathing cracks in rotor systems [42]. | ||||
| A model with changing cross-section moment of inertia and eccentricity values depending on the rotation angle. | Performed detailed analysis of the stability of the faulty rotor system under different conditions. | The model is validated only for specific crack positions, so there must be additional research to scale the approach for the identification of an arbitrarily placed crack. | Floquet theory; Bolotin’s method. | Classical |
| Han B.—Rotor crack breathing under unbalanced disturbance [40]. | ||||
| A consideration is that after some specific value of the rotation speed, a crack stops breathing and freezes in some half-open position, which leads to a constant value of cross-section moment of inertia. | The approach suggests markers of cracks’ existence; it allows the diagnosis of cracks at any angle-to-axis. | The model does not consider nonlinear effects in crack breathing. | Strain energy release rate (SERR). | Classical |
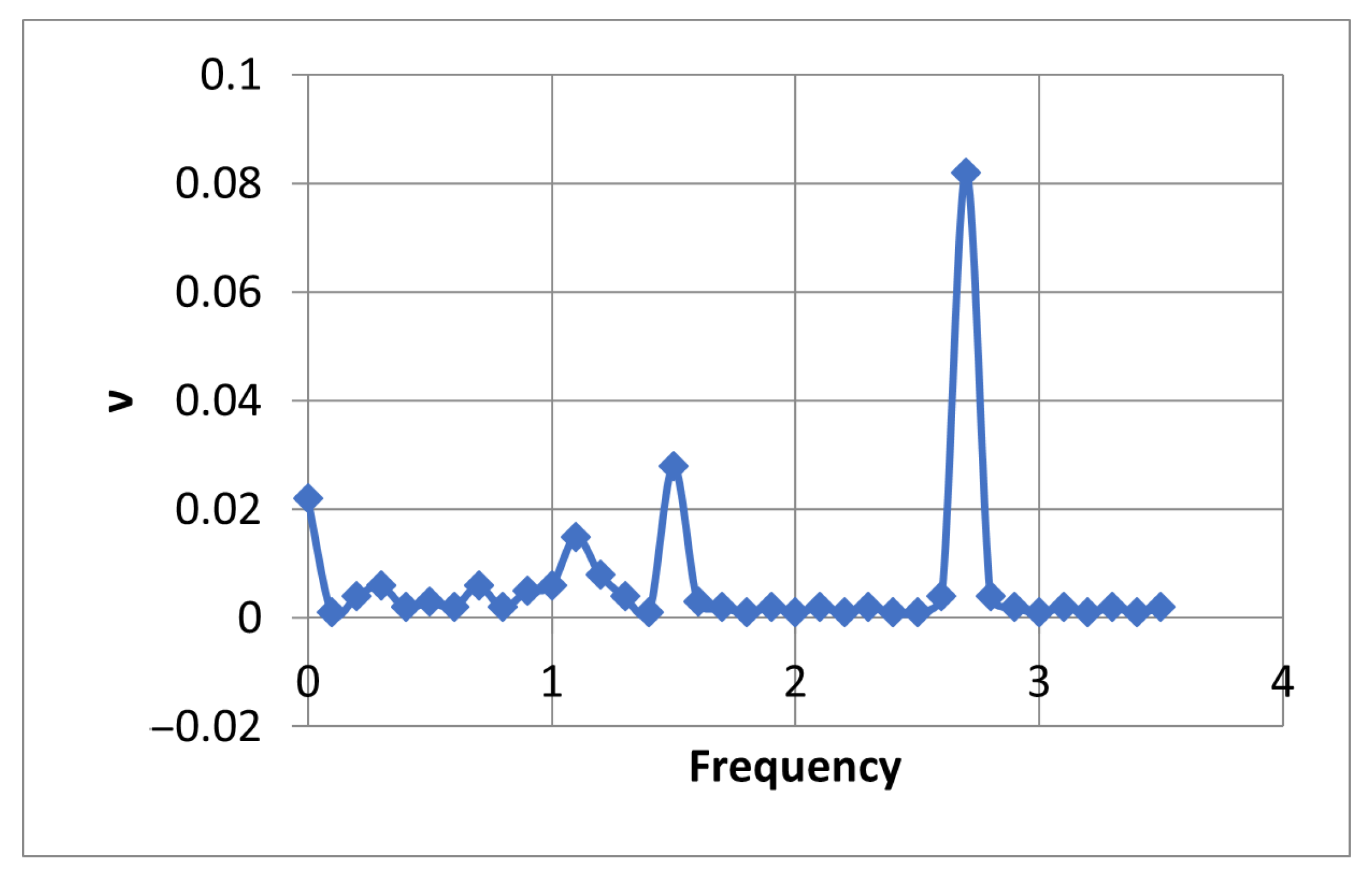
| Hongjun W.—Orbit identification method based on ISOMAP for rotor system fault diagnosis [85]. | ||||
| Augmentation of the orbit single position with additional data to a high-dimensional point in high-dimensional space and scaling it with ISOMAP to a 2D map. | Result maps provide clear patterns of different rotor faults. | It is not clear what actual data were added to an orbit point and what the structure of such a point and space is. | ISOMAP; k-nearest neighbors method (KNN); Dijkstra’s algorithm. | Classical/ Heuristic |
| Jiang H.—Quantitative detection of multiple damages in wind turbine blades based on the operating deflection shape and natural frequencies [23]. | ||||
| Using wavelet transformation of natural oscillation forms for damage localization and the random forest algorithm to identify the damage rate | The approach allows the localization and assessment of the damage rate of the turbine blade. | Since the source of knowledge of the approach is statistical databases for specific elements, the approach has poor scalability and requires separate data for even slightly different geometries. | Random forest; operating deflection shape method (ODS); Daubechies wavelet. | Classical/ Heuristic |
| Kulesza Z.—Damping by parametric excitation in a set of reduced-order cracked rotor systems [41]. | ||||
| Representation of a crack as two planes uniformly connected with elastic elements. | It was found regularly in anti-resonance appearance and the existence of cracks. | Validation was performed on the static rotor with an artificial crack breathing simulation. | Floquet theory; Bolotin’s method. | Classical |
| Kumar P.—Performance prediction and Bayesian optimization of screw compressors using Gaussian process regression [48]. | ||||
| Equation system reduction with novel trial misalignment approach. | According to the authors, the approach allows for determining a considerable number of different parameters in real-time. | MATLAB Simulink was performed with no experimental verification. | Dynamic reduction; finite element analysis (FEA). | Classical |
| Li Q.—Fault diagnosis of nuclear power plant sliding bearing-rotor systems using deep convolutional generative adversarial networks [61]. | ||||
| Combining several methods of AI and ML to achieve high accuracy in journals and rotor fault identification. | The method shows sufficient accuracy compared with other AI methods; the method requires a minimal input dataset. | A necessity to retrain the system for even minor changes with high computational costs. | Convolutional neural networks (CNN); continuous wavelet transform (CWT); deep long short-term memory convolutional generative adversarial network (TF-DLGAN); generative adversarial networks (GANs); long short-term memory (LSTM). | AI/ML |
| Li Y.—A generalized incremental harmonic balance method by combining a data-driven framework for initial value selection of strongly nonlinear dynamic [90]. | ||||
| Optimal initial data for the iteration harmonic balance method selection with ANN. | Significantly decreases the chance of iteration divergence and reduces iteration costs. | The proposed algorithm is weak for systems with high nonlinearity. | Harmonic balance (HB) method; incremental harmonic balance (IHB) method; Newton–Raphson method; multiple scales method; Runge–Kutta methods; Newmark-β method; fast Fourier transform (FFT); Powel dogleg algorithm; linearized equation method (LEM); nonlinearity reduced equation method (NREM); empirical selection method (ESM). | Classical/AI |
| Ma X.—Vibration characteristics of rotor system with coupling misalignment and disc-shaft nonlinear contact [49]. | ||||
| Improvement of the Newmark-β method by combining it with the Newton–Raphson method. | Simulated processes in disk–rotor interference fit in conditions of shaft misalignment in a coupling connection. | The suggested model is more about the influence of common interference values and poorly considers the impact of nonlinear contact. | Newton–Raphson method; Newmark-β method. | Classical |
| MacNeil P.—A genetic algorithm approach to the solution of a differential equation [89]. | ||||
| Using genetic algorithms for solving differential equations. | Solved the physical problem of the interaction of particles, which is described by a different equation. | There are no details about crossover, mutation, and selection functions; the approach is extremely sensitive to changes in initial conditions. | Genetic algorithm. | Heuristic |
| Maes K.—Dynamic strain estimation for fatigue assessment of an offshore monopile wind turbine using filtering and modal expansion algorithms [31]. | ||||
| Applying different methods (JISEA, MEA, Kalman filter) to estimate the strain of wind turbine construction. | Construction strain estimation without direct strain measurement using only accelerometers. | Direct strain measurement is required for an approach based on the Kalman filter. | State-space form; time-domain deconvolution approach; Kalman filter; recursive least squares estimation; modal expansion algorithm (MEA); unscented Kalman filter (UKF); extended Kalman filter (EKF); particle filter; joint input-state estimation algorithm (JISEA); operational modal analysis (OMA); fast Fourier transform (FFT); time response assurance criterion (TRAC); mean absolute error (MAE). | Classical |
| Mishra R.—A generalized method for diagnosing multi-faults in rotating machines using imbalance datasets of different sensor modalities [86]. | ||||
| Creating a spectrum of analog signals with frame-by-frame signal transformation and using an ANN to analyze a spectrum. | The approach shows high accuracy in the identification of different types of failures. | Result accuracy is sensitive to system parameter selection, e.g., window size and overlap ratio. | Short-time Fourier transform (STFT); wavelet transform (WT); Wigner–Ville distribution (WVD); adaptive sparse denoising; periodicity weighted spectrum separation; wavelet-autoregressive model; support vector machine (SVM); k-nearest neighbors (KNN); long short-term memory (LSTM); Fourier synchro-squeezed transform (FST); full connected cascade (FCC); radial basis function neural networks (RBFNN); generative adversarial network (GAN); invertible mapping; Levenberg–Marquardt algorithm; neuron-by-neuron algorithm. | Classical/ML Heuristic/AI |
| Muzhynska A.—Chaotic responses of unbalanced rotor/bearing/stator systems with looseness or rubs [56]. | ||||
| Model of viscous–dry friction between rotor and stator, considering gaps in bearings. | Determined stable work regimes and influence of geometry factors on system stability in conditions of viscous–dry frictions due to gaps in bearings. | The proposed algorithm is weak for systems with high nonlinearity. | Method of small parameters; restitution coefficients. | Classical |
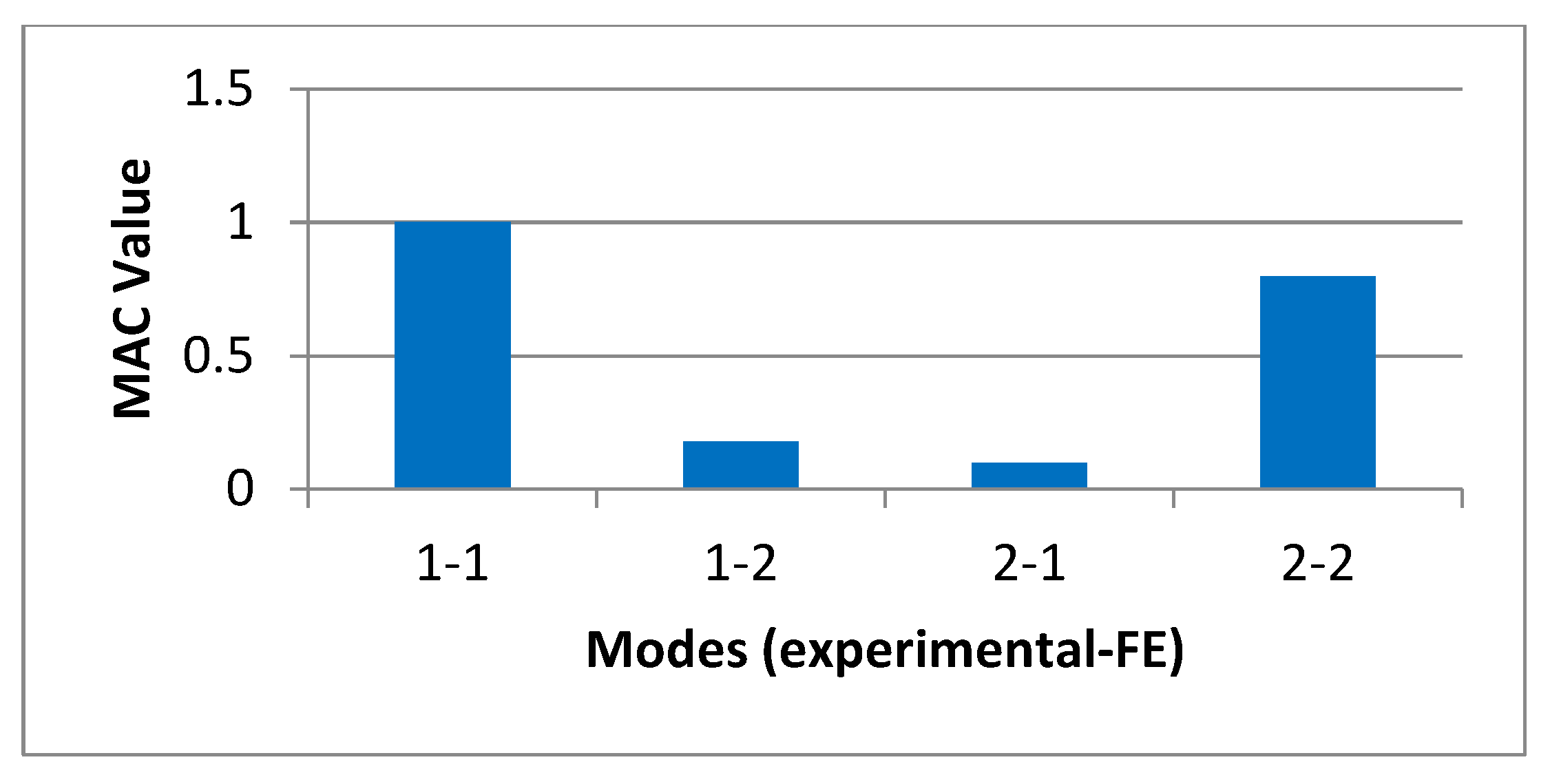
| Nityananda R.—Finite element model updating of boring bar and determination of chatter stability [53]. | ||||
| Iterative update of the FE model with the inverse eigensensitivity method. | Achieved a significant increase in FEA simulation accuracy. | The approach does not consider damping effects. | Iterative inverse eigensensitivity method (IES); system equivalent reduction expansion process (SEREP); natural frequency difference (NFD) correlation coefficient; modal assurance criterion (MAC); characteristic equation method; experimental modal analysis (EMA). | Classical/ Reduction |
| Pavlenko I.—Application of artificial neural network for identification of bearing stiffness characteristics in rotor dynamics analysis [59]. | ||||
| A model that considers the nonlinear relation between bearing stiffness and rotation speed using ANN for system parameters identification. | Compared the accuracy of parameter identification with ANN and linear regression, where the first approach demonstrated much better efficiency compared to the second one. | Poor scalability of the ANN-based approach. | Least squares method; linear regression. | Classical/AI |
| Pavlenko I.—Ensuring vibration reliability of turbopump units using artificial neural networks [25]. | ||||
| A model that considers the nonlinear relation between bearing stiffness, rotation speed, and rotor bow using ANN for system parameters identification. | Determined the imbalance masses for the rotor, which works in the condition of the rotor bow using ANN. | Limited scalability of the ANN-based approach; the approach is based on using influence coefficients, but due to the heuristic nature of the algorithm, they remain hidden under the neuron link. | Least squares method; linear regression. | Classical/AI |
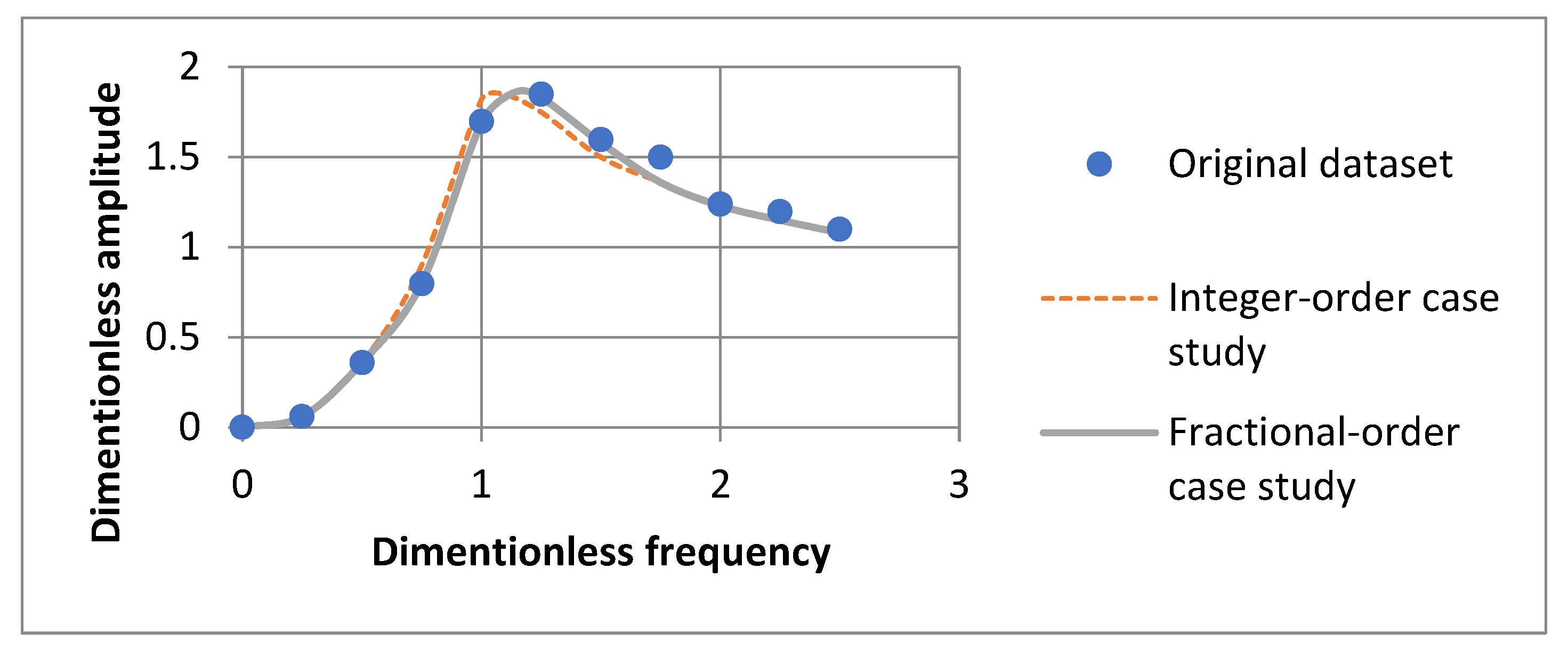
| Pavlenko I.—Fractional-order mathematical model of single-mass rotor dynamics and stability [35]. | ||||
| Considering the fractional-order origin of the damping force. | A variation in the fractional-order value of rotor system parameters was identified and evaluated for unstable regimes for different cases. | The results depend significantly on the fractional damping factor, which cannot be determined analytically, so experimental calibration is required. | Riemann–Liouville integral; Basset force; fractional-order derivative. | Classical |
| Peradotto E.—Stochastic Methods for Nonlinear Rotordynamics with Uncertainties [92]. | ||||
| Introduces a non-intrusive PCE surrogate coupled with HB and ANM that slashes stochastic rotor dynamic runtime by one to two orders of magnitude. | Reproduces 95% Monte Carlo envelopes for FRF and stochastic Campbell diagrams. | Accuracy degrades beyond four to five random variables. | Polynomial chaos expansion (PCE); Monte Carlo simulation (MCS); Smolyak sparse-grid integration. | Uncertain |
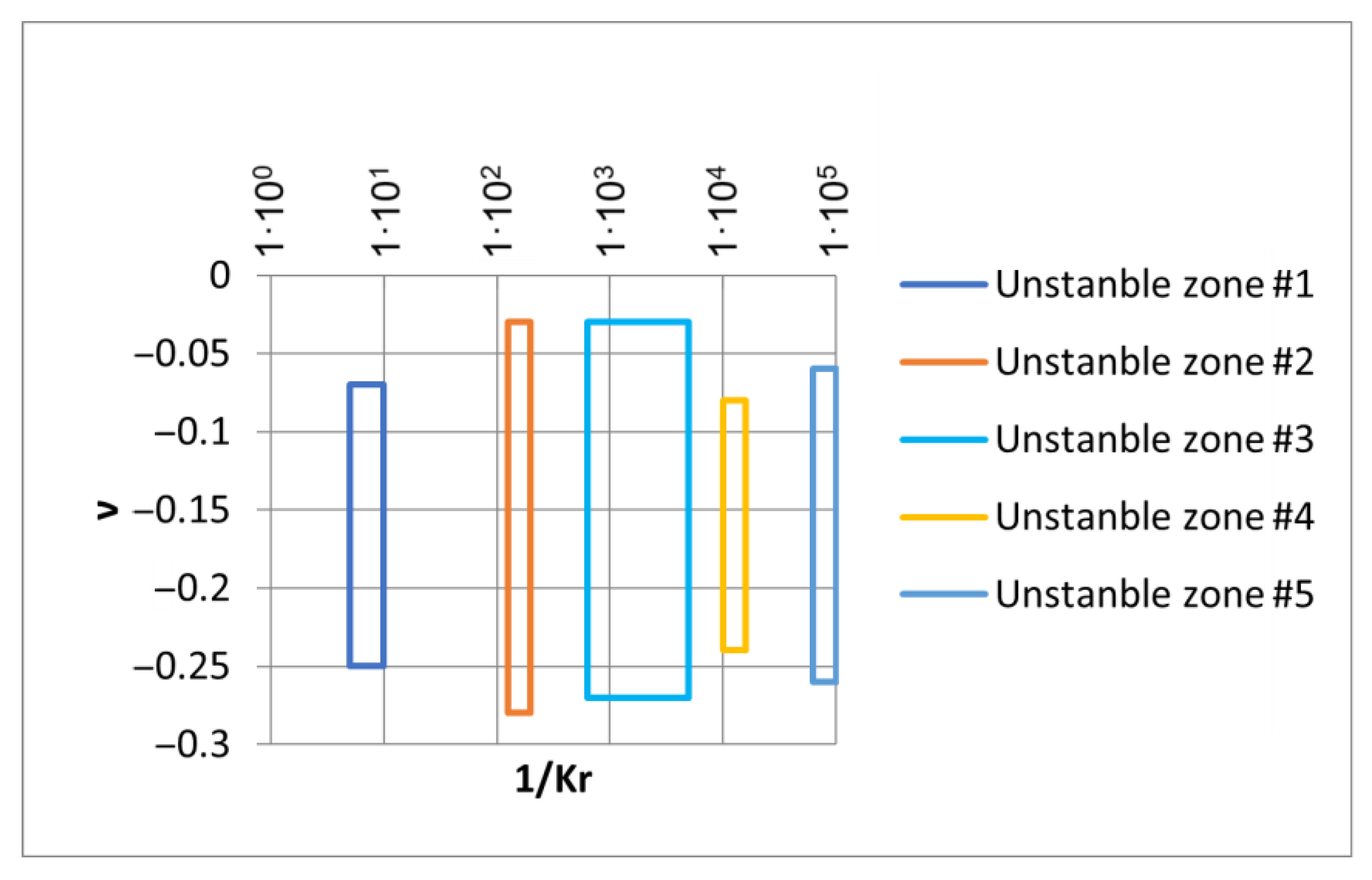
| Phadatare H.—Large deflection model for rub-impact analysis in high-speed rotor-bearing system with mass unbalance [29]. | ||||
| Non-dimensional governing equations of movement. | Derived signs of friction due to imbalance on the spectrum and phase diagrams; found unstable zones. | The model works for relatively large deflections of a rotor under imbalance forces. | Hamilton’s principle; Runge–Kutta method; Poincare’s section. | Classical |
| Sanches F.—Theoretical and experimental identification of the simultaneous occurrence of unbalance and shaft bow in a Laval rotor [28]. | ||||
| Approach to model residual rotor bow; model reduction techniques. | The method allows the identification of rotor bow and imbalance with high accuracy; nevertheless, it has noise effects. | It is a straightforward rotor model that does not consider many factors like shaft weight and stiffness or system damping. | Finite element method (FEM); Guyan reduction; Laval rotor; differential evolution (DE); Newton–Raphson method; fourth-order Runge–Kutta method; fast Fourier transform. | Classical/ Reduction |
| Sastry C.—An iterative system equivalent reduction expansion process for extraction of high frequency response from reduced order finite element model [88]. | ||||
| An accurate and effective method of reducing the number of system’s DOFs. | The accuracy after system reduction with the proposed method is much better than for other considered reduction methods. | Accuracy and computation efficiency depend on the proper selection of the initial frequency range. | System equivalent reduction expansion process (SEREP); dynamic improved reduced system (DIRS); Guyan reduction. | Classical/ Reduction |
| Sinha J.—Estimating unbalance and misalignment of a flexible rotating machine from a single run-down [27]. | ||||
| Regularization and filtering methods increase the stability of calculations. | This method allows for identifying misalignment and imbalance with high accuracy. | The accuracy of the method critically depends on the correct definition of model parameters. | Singular value decomposition (SVD); least squares method. | Classical |
| Song G.—Theoretical–experimental study on a rotor with a residual shaft bow [55]. | ||||
| Effective isolation of residual rotor bow features from other signals. | The method shows adequately accurate results in residual bending identification. | The accuracy of the method critically depends on the accuracy of the sensor installation. | Daubechies wavelet; ISOMAP; principal component analysis (PCA). | Classical/ Reduction/ ML |
| Sudhakar G.—Identification of unbalance in a rotor bearing system [36]. | ||||
| Improvements to the method of equivalent load minimization. | Ability to determine imbalance with a minimum number of measurements and to extend the method to other types of defects. | Approximation is required for unmeasured positions, which can lead to an accumulation of errors and inaccuracy in determining the defect parameters. | Modal expansion method; Newton–Raphson method; least squares method; fast Fourier transform (FFT). | Classical |
| Sun X.—Nonlinear dynamic behavior of a rotor-bearing system considering time-varying misalignment [50]. | ||||
| Considering rotor time-dependent deformation caused by misalignment; the model of oil-film behavior. | Identified the distribution of lubricant pressure in bearings caused by misalignment and its impact on stability. | Only laminar lubricant flow is considered; lubricant viscosity is considered independent of temperature. | FEM; FDM; over-relaxation method (ORM); Newmark-β method. | Classical |
| Qiu Y.—A fuzzy approach for the analysis of unbalanced nonlinear rotor systems [37]. | ||||
| Performing fuzzy logic on uncertain processes that are hard or impossible to model analytically. | Designed membership functions based on equations of motion to determine imbalance value in natural language terms. | The approach does not allow for determining concrete values and the location of imbalance. | Fuzzy set; Runge–Kutta method. | Classical/ Uncertain |
| Tang Q.—Time-varying harmonic analysis method based on adaptive frequency-shift filtering [87]. | ||||
| Using the Teager energy operator for harmonic interval identification. | The algorithm can effectively determine the stability of each harmonic and automatically segment of its steady-state interval. | High sensitivity to system parameters, detecting time delays. | Kalman filter; Prony-based algorithms; wavelet transform (WT); fast Fourier transform (FFT); infinite impulse response (IIR) filter; improved Teager energy operator (ITEO). | Classical |
| Walker R.—Unbalance localization through machine nonlinearities using an artificial neural network approach [26]. | ||||
| Applying ANN for an imbalance diagnosis. | The approach can localize imbalance with high accuracy while requiring a minimal number of sensors. | Does not identify imbalance causes; ANN must be retrained after minor system changes. | Butterworth low-pass filters; short-term Fourier transform (STFT). | Classical/AI |
| Xu B.—Steady-State Response Analysis of an Uncertain Rotor Based on Chebyshev Orthogonal Polynomials [93]. | ||||
| Develops a Chebyshev-polynomial interval surrogate with Smolyak sparse-grid sampling that makes multi-parameter interval analysis of steady rotor response. | Using only a few finite element evaluations reproduces Monte Carlo envelopes for FRF and steady orbits; cuts CPU time by ~96%. | Bounds remain conservative; parameter correlations are ignored. | Chebyshev interval method (CIM); Monte Carlo simulation (MCS); Smolyak sparse-grid integration. | Uncertain |
| Zhao Y.—A novel nonlinear spectrum estimation method and its application in online condition assessment of bearing-rotor system [51]. | ||||
| Using nonlinear output frequency-response functions (NOFRFs) to identify the types and severity of faults. | The method demonstrates stable diagnostic results, even in the presence of noise and structural changes. | Needs more research to recognize different types of faults and combined faults. | Support vector machine (SVM); nonlinear output frequency-response functions (NOFRFs); principal component analysis (PCA); neighborhood component analysis (NCA); nonlinear autoregressive with exogenous input (NARX); discrete Fourier transform (DFT). | Heuristic/ML |
| Zhao Y.—The sub-interval similarity: A general uncertainty quantification metric for both stochastic and interval model updating [94]. | ||||
| Proposes the sub-interval similarity (SIS) metric that unifies stochastic (Bayesian) and interval model updating. | SIS cuts parameter errors below 1% and runs ~500 times faster than high-order probabilistic methods. | Performance hinges on an empirically chosen number of sub-intervals. | Markov-chain Monte Carlo (MCMC); sub-interval similarity (SIS) metric; particle swarm optimization (PSO). | Uncertain/ Heuristic |
| Zheng J.—Adaptive parameterless empirical wavelet transform-based time-frequency analysis method and its application to rotor rubbing fault diagnosis [57]. | ||||
| Improved wavelet transformation method. | The proposed methodology shows better results on the problem with rotor friction than the empirical mode decomposition (EMD), and ensemble empirical mode decomposition (EEMD) methods. | The approach is extremely sensitive to the spectral portioning method. | Empirical mode decomposition (EMD); ensemble empirical mode decomposition (EEMD); Hilbert transform (HT); normalized Hilbert transform (NHT). | Classical |
| Method | Description | Advantages | Disadvantages | NN Type(s) |
|---|---|---|---|---|
| Mixture of Experts (MoE) | A technique where multiple specialized subnetworks (experts) are trained, and a gating network determines which experts to activate for a given input. | Scales efficiently by activating only relevant experts per input, reducing overall computation. Improves specialization as different experts learn different aspects of the data. | High memory usage, as all experts need to be stored. Complex training due to the gating mechanism and balancing expert utilization. | BP, RNN |
| Neural Architecture Search (NAS) | An automated method to design optimal neural network architectures using reinforcement learning or evolutionary algorithms. | Optimized model architectures improve performance with minimal manual tuning. Adaptability across various tasks by selecting the best structure. | Extremely computationally expensive, requiring vast amounts of graphics processing unit (GPU) power. Difficult to interpret, as the resulting architecture may not provide intuitive insights. | BP, CNN, RNN, LSTM |
| Sparse Neural Networks (SNN) | Networks where a significant portion of weights are zero, reducing the number of active connections and improving efficiency | Reduces computational cost and memory footprint without significant loss in accuracy. Speeds up inference, making models suitable for edge computing. | Training sparse networks is challenging, often requiring specialized pruning techniques. Potential accuracy degradation, especially if sparsification is too aggressive. | BP, CNN, RNN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roshchupkin, O.; Pavlenko, I. Modern Methods for Diagnosing Faults in Rotor Systems: A Comprehensive Review and Prospects for AI-Based Expert Systems. Appl. Sci. 2025, 15, 5998. https://doi.org/10.3390/app15115998
Roshchupkin O, Pavlenko I. Modern Methods for Diagnosing Faults in Rotor Systems: A Comprehensive Review and Prospects for AI-Based Expert Systems. Applied Sciences. 2025; 15(11):5998. https://doi.org/10.3390/app15115998
Chicago/Turabian StyleRoshchupkin, Oleksandr, and Ivan Pavlenko. 2025. "Modern Methods for Diagnosing Faults in Rotor Systems: A Comprehensive Review and Prospects for AI-Based Expert Systems" Applied Sciences 15, no. 11: 5998. https://doi.org/10.3390/app15115998
APA StyleRoshchupkin, O., & Pavlenko, I. (2025). Modern Methods for Diagnosing Faults in Rotor Systems: A Comprehensive Review and Prospects for AI-Based Expert Systems. Applied Sciences, 15(11), 5998. https://doi.org/10.3390/app15115998







