Hyperband-Optimized CNN-BiLSTM with Attention Mechanism for Corporate Financial Distress Prediction
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. CNN-BiLSTM-AT
3.2. CNN
- (1)
- The convolutional layer operation extracts the local features of the input data by convolution operation, i.e., the convolution kernel sliding dot product operation on the input data.where is the output of the convolutional layer, is the input data, is the weight of the convolutional kernel, b is the bias of the convolutional kernel, and f is the activation function.
- (2)
- Pooling layer operation uses a maximum pooling operation to divide the input data into non-overlapping rectangular regions. It selects the maximum value within each rectangular region as the representative value for that region.where the above formula is for a maximum pooling window of 2 × 2 and a step size of 2, indicating the value of the position in the output region after the pooling operation.
- (3)
- Fully connected layer operations, where the multi-dimensional feature maps output from the convolutional or pooling layers are spread into one-dimensional vectors and fed into one or more fully connected layers, and the classification results are outputted using the softmax activation function.where is the weight of the fully connected layer, is the output of the last pooling layer, is the bias of the fully connected layer, and is the activation function.
3.3. BiLSTM
- (1)
- Positive processing sequence. The input sequence is processed step by step from the first to the last time step. For each time step, t, the positive hidden layer state, , is computed according to the positive formula.
- (2)
- The reverse processes the sequence. The input sequence is processed step by step from the last time step to the first-time step. For each time step, t, the reverse hidden layer state, , is computed according to the reverse formula.
- (3)
- Connect the forward and backward hidden states. For each time step t, the forward and backward hidden states are concatenated. The concatenated hidden state is then passed through the fully connected layer to produce the final output .
3.4. Attention Mechanism
- (1)
- Calculating the attention score. For each time step t, the attention score is calculated via the activation function.
- (2)
- Calculating the attention weights. For each time step t, calculate the attention weights, , using the softmax function; these weights represent the importance of each time step.
- (3)
- Calculating the weighted summation. Based on the calculated attention weights , for the i-th hidden state , at time step t, the input sequence , is weighted and summed to obtain the context vector of the output of the current time step.
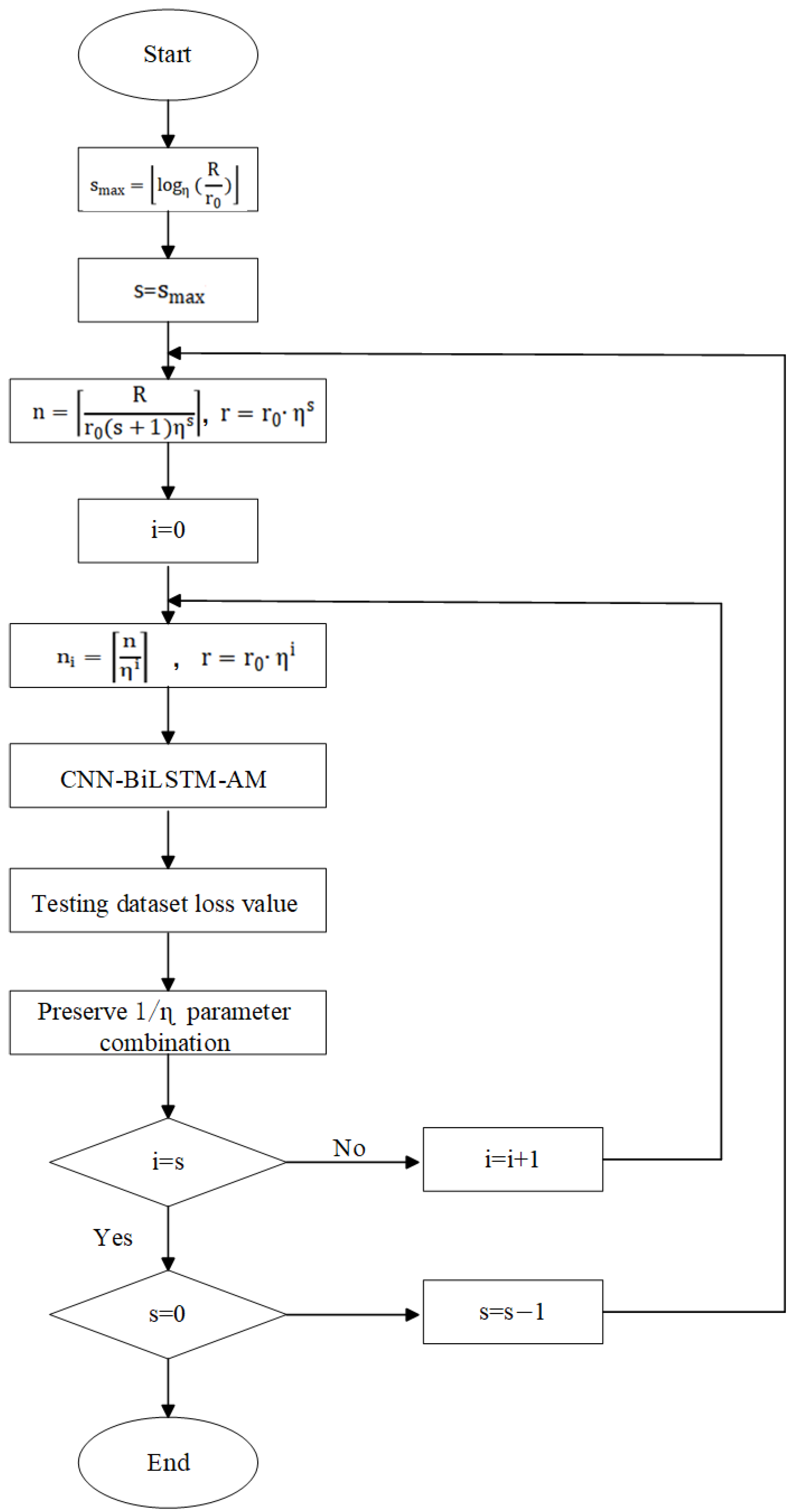
3.5. Hyperband Algorithm
- (1)
- Initialization parameters. Set the resource budget R (the total number of training rounds), set the bandwidth factor (a parameter controlling the elimination speed of hyper-parameter configurations; the default is 3), and set the initial amount of resources (the amount of resources used by each configuration in the initial evaluation).
- (2)
- Calculate maximum rounds. is the maximum number of rounds that can be performed with the current resource budget R, and initial resource amount .where stands for the downward rounding sign.
- (3)
- Perform multiple rounds of hyperparameter configuration and the elimination process. Multiple rounds are performed from to .For each round s, the number of configurations and the amount of resources are initialized, and n hyperparameter configurations are generated, each of which receives a training resource amount r, at the beginning.In each round s, obtain the number of hyperparameter configurations , and the amount of resources , used for each configuration in the ith subphase (from 0 to s).Allocate resources evenly to all hyperparameter configurations and perform initial training. According to the Successive Halving algorithm, eliminate the underperforming configurations and concentrate the resources on the best-performing configurations, at which point the elimination ratio is , and the best-performing configurations are retained.
- (4)
- Selection of the optimal configuration. At the end of all rounds, the best-performing hyperparameter configuration is selected from the final configuration.
4. Experiment
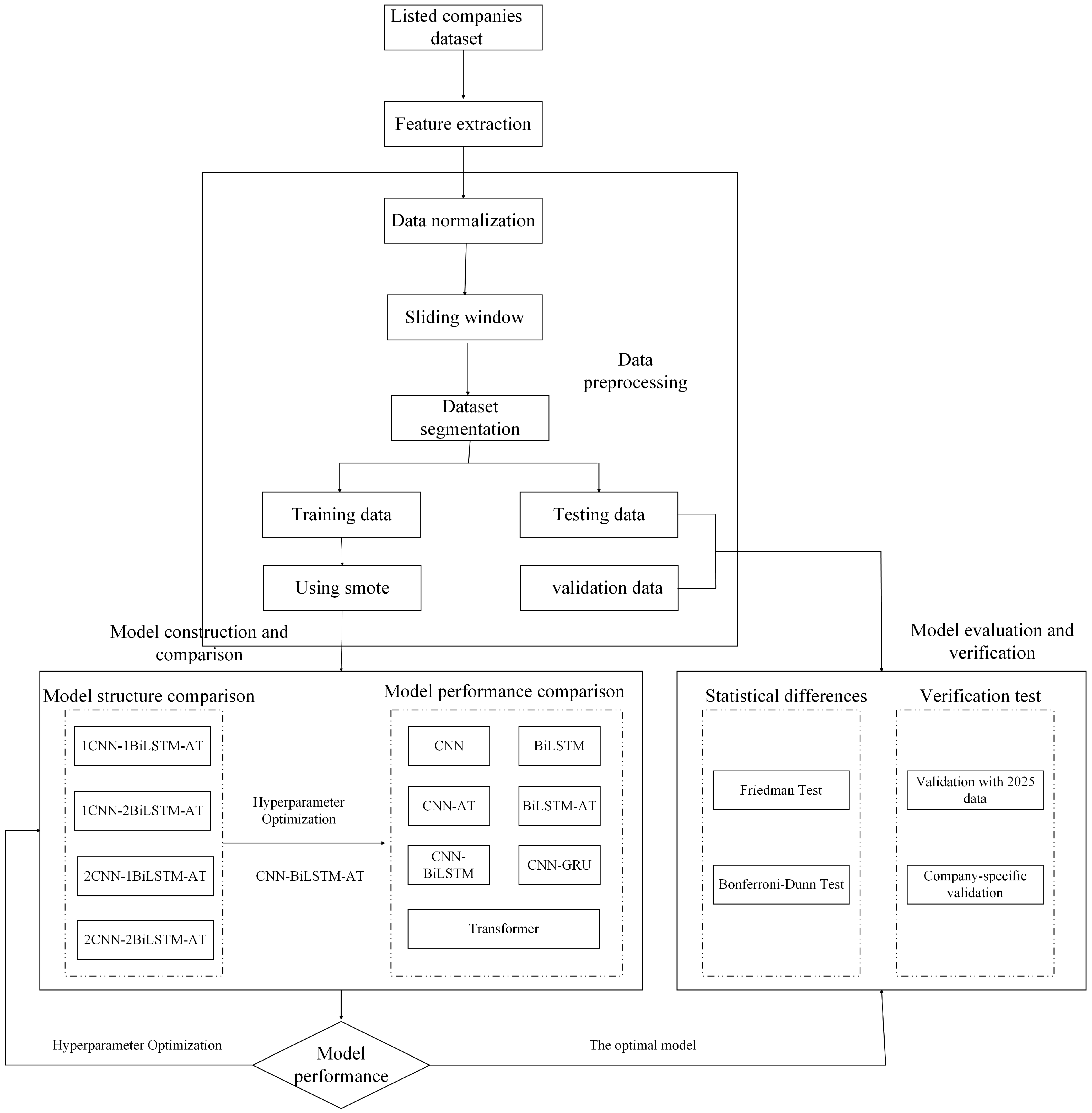
4.1. Overview of Experimental Process
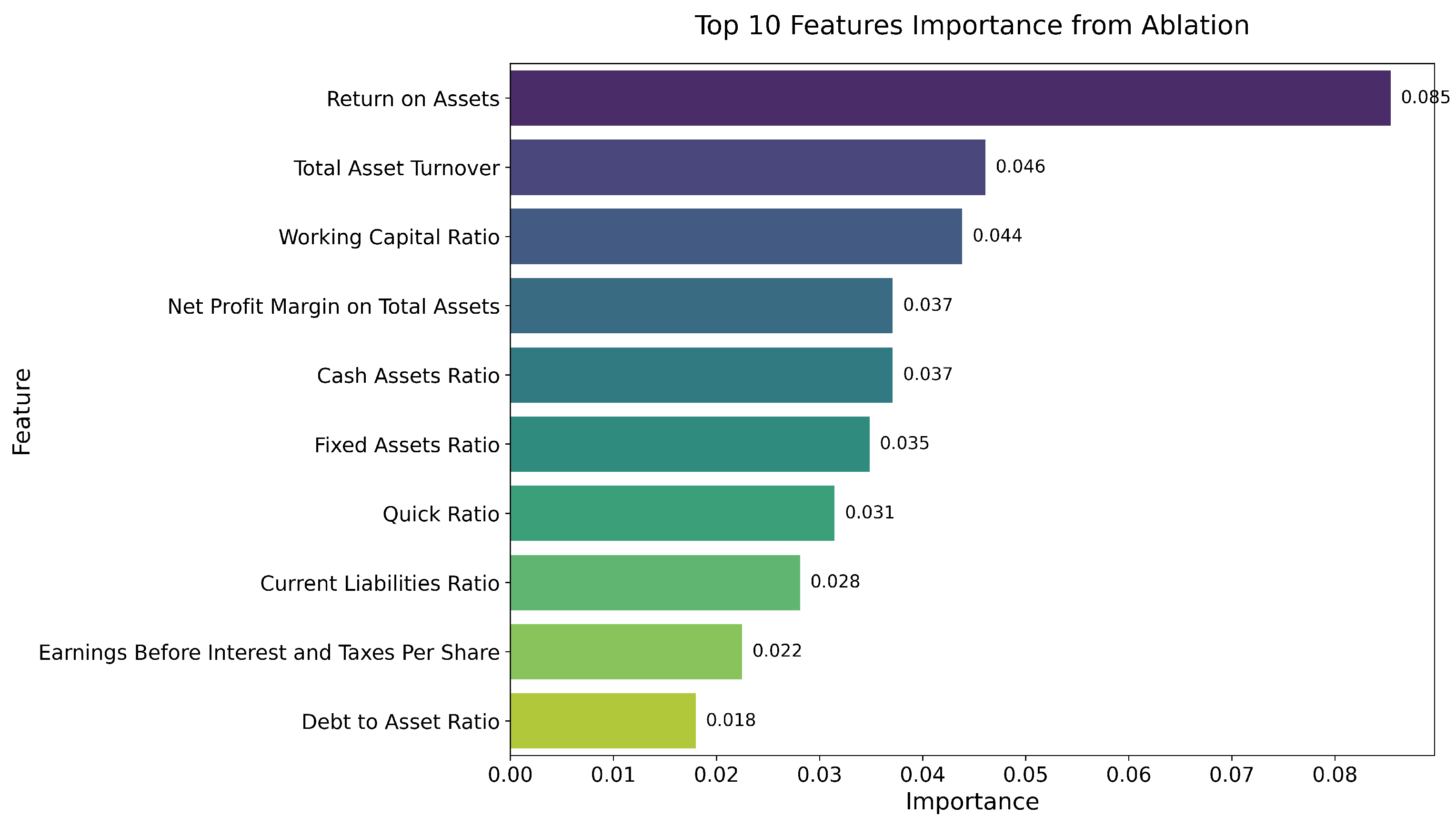
4.2. Sample and Indicator Selection
4.3. Data Preprocessing
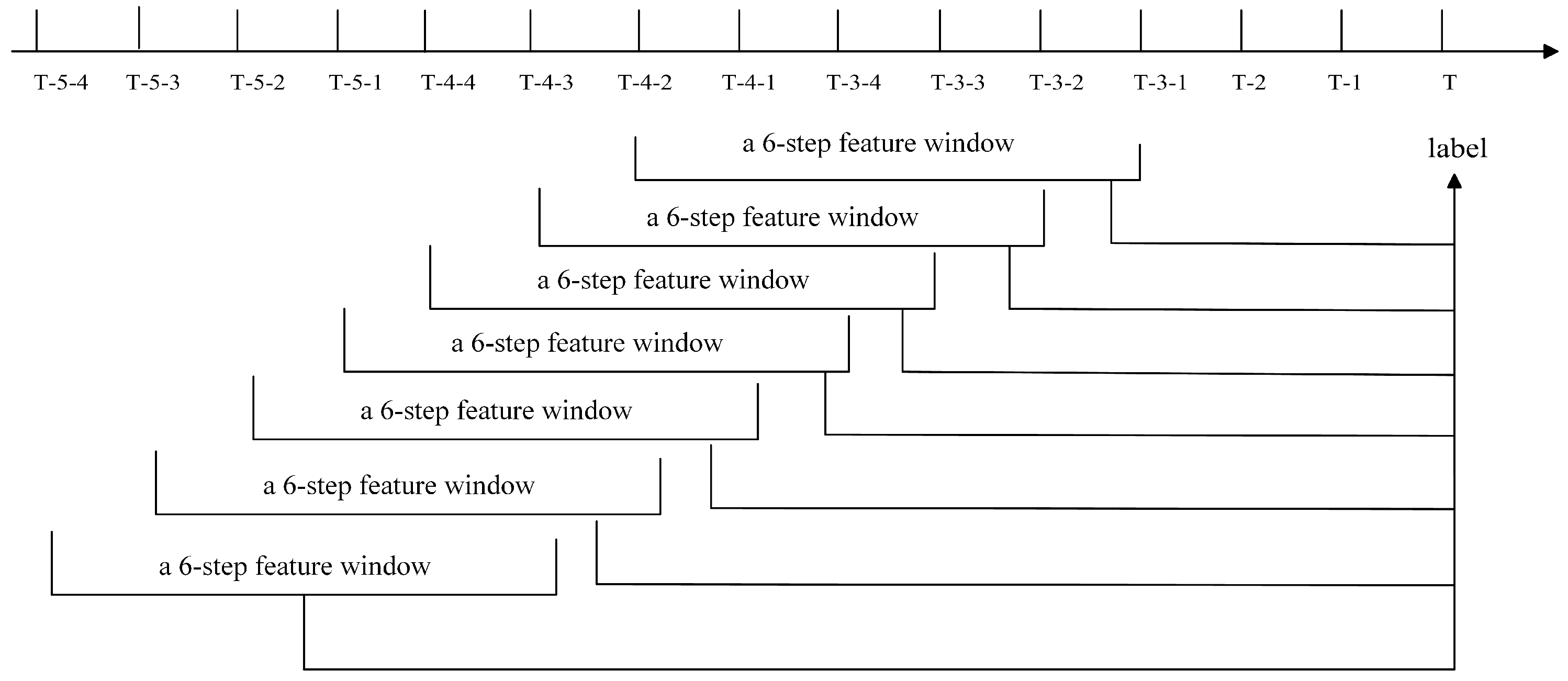
4.3.1. Sliding Window
4.3.2. SMOTE Oversampling
5. Results
5.1. Analysis of the Prediction Effect of Hyperband-CNN-BiLSTM-AT Model
5.1.1. Hyperband Algorithm Application
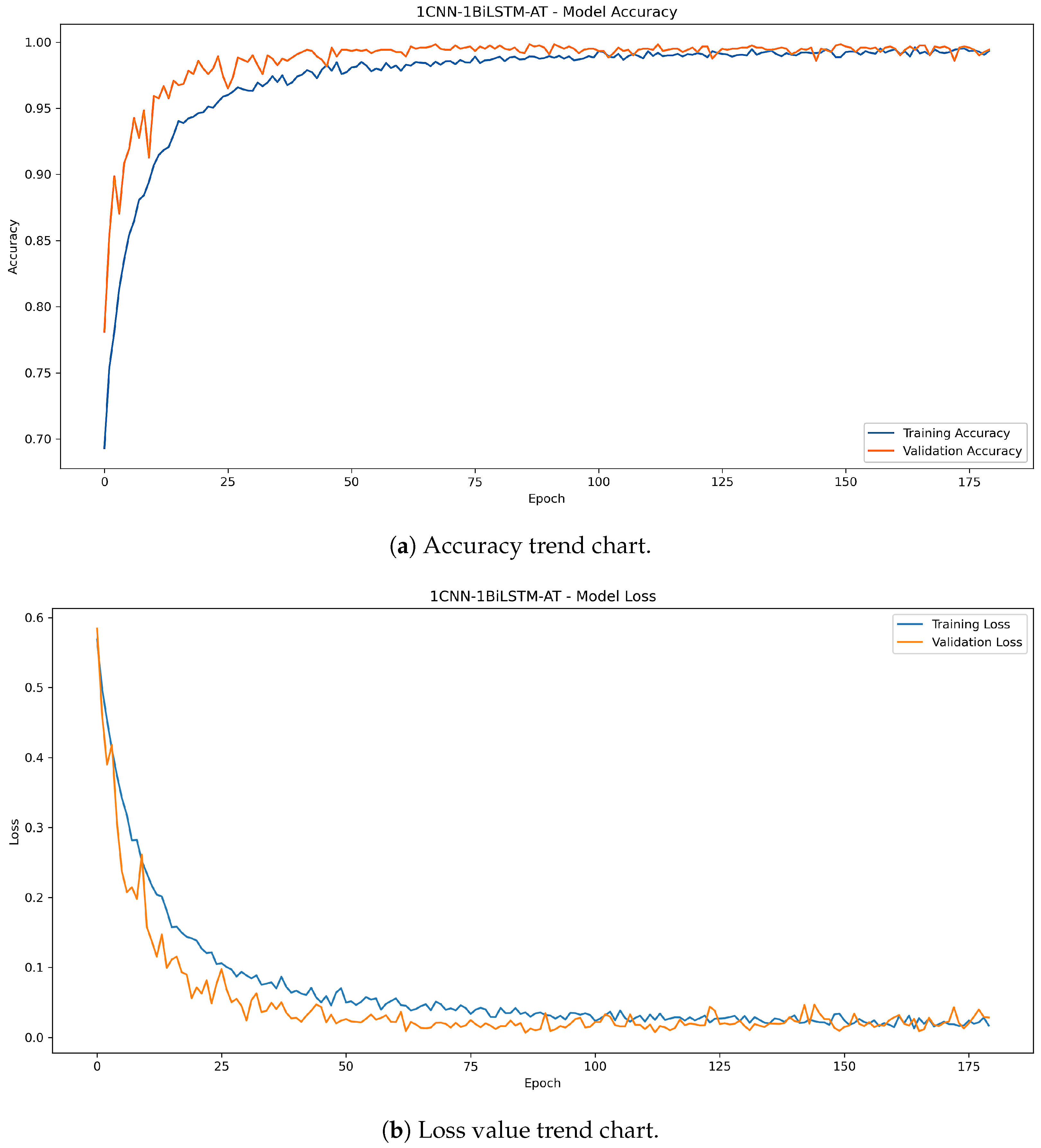
5.1.2. Comparative Analysis of CNN-BiLSTM-AT Model Structure
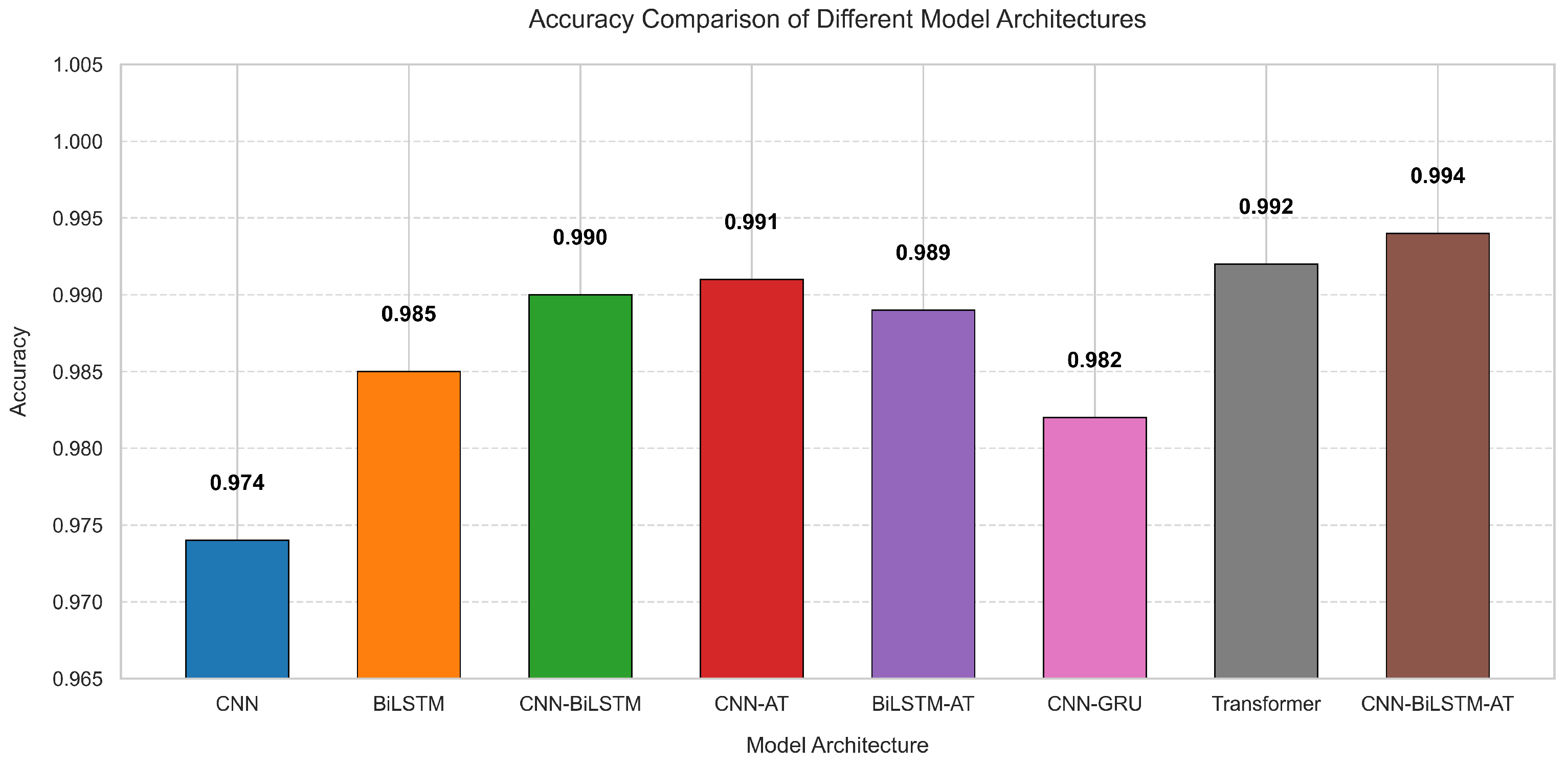
5.1.3. Comparison of Results from Different Models
- (1)
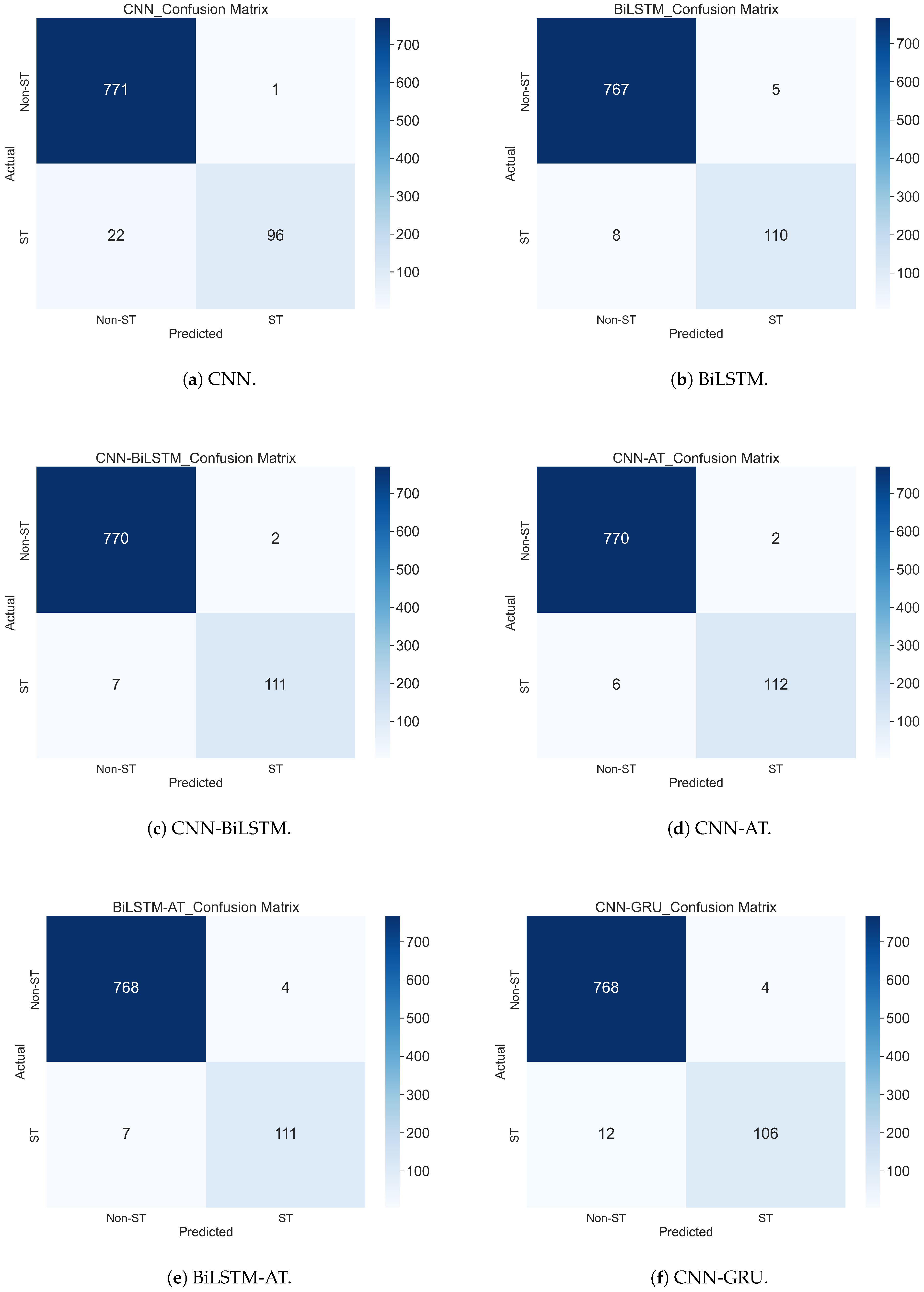
- CNN model. The accuracy of this model was 0.974, showing it performed relatively well. However, it had the lowest accuracy among all models, mainly when predicting ST companies. Among the 118 actual ST sequence data points, 22 were mispredicted, and the recall rate was only 0.814. This indicates that using the CNN alone may not achieve optimal results when dealing with specific tasks. In addition, the model had a training time of 162.52 s, the shortest training time, and therefore is mainly suitable for use in scenarios with limited computing resources or requiring fast training.
- (2)
- BiLSTM model. The accuracy of this model was 0.985, which is significantly improved compared with the simple CNN model. The recall rate of ST samples was increased to 0.932, indicating that the model performs stably in identifying ST samples and performs better for time series data. In addition, the model took 1279.94 s to train, the longest training time. Although it performed well, the training time was relatively long, making it suitable for use in scenarios where resources are abundant or time is not tight.
- (3)
- CNN-BiLSTM model. This model’s accuracy was 0.990, performing better than CNN or BiLSTM. It also improved the accuracy and recall of predicting ST companies. In addition, the model’s training time was 798.16 s, which was shorter than the training time of the BiLSTM model alone. This indicates that the CNN can effectively extract features in the model, reduce the computational burden of BiLSTM, and thus accelerate the training speed.
- (4)
- CNN-AT model. The accuracy of this model was 0.991, which was better than using the CNN alone. The accuracy and recall of predicting ST companies were significantly improved, indicating that the combination of the CNN and attention mechanism gave a good performance in handling tasks that require attention to important features. Although the training time was 163.34 s, which was slightly longer than CNN, the performance improvement proved the effectiveness of this combination in enhancing the model’s predictive ability.
- (5)
- BiLSTM-AT model. This model’s accuracy was 0.989, outperforming BiLSTM used alone. It combines the advantages of BiLSTM and the attention mechanism and performs well in tasks that require long-term dependencies and important feature attention. In addition, the model’s training time was 1064.18 s. Although the performance improved, the training time was relatively long and unsuitable for fast iteration scenarios.
- (6)
- CNN-GRU model. The accuracy of this model was 0.982, which is an improvement compared with the standalone CNN model, but still lower than more complex structures such as CNN-BiLSTM and CNN-AT. Among 118 actual ST samples, the model had 12 prediction errors and a recall rate of 0.898, indicating that it still has some shortcomings in identifying ST companies. The training time was 418.58 s, which is at a moderate level.
- (7)
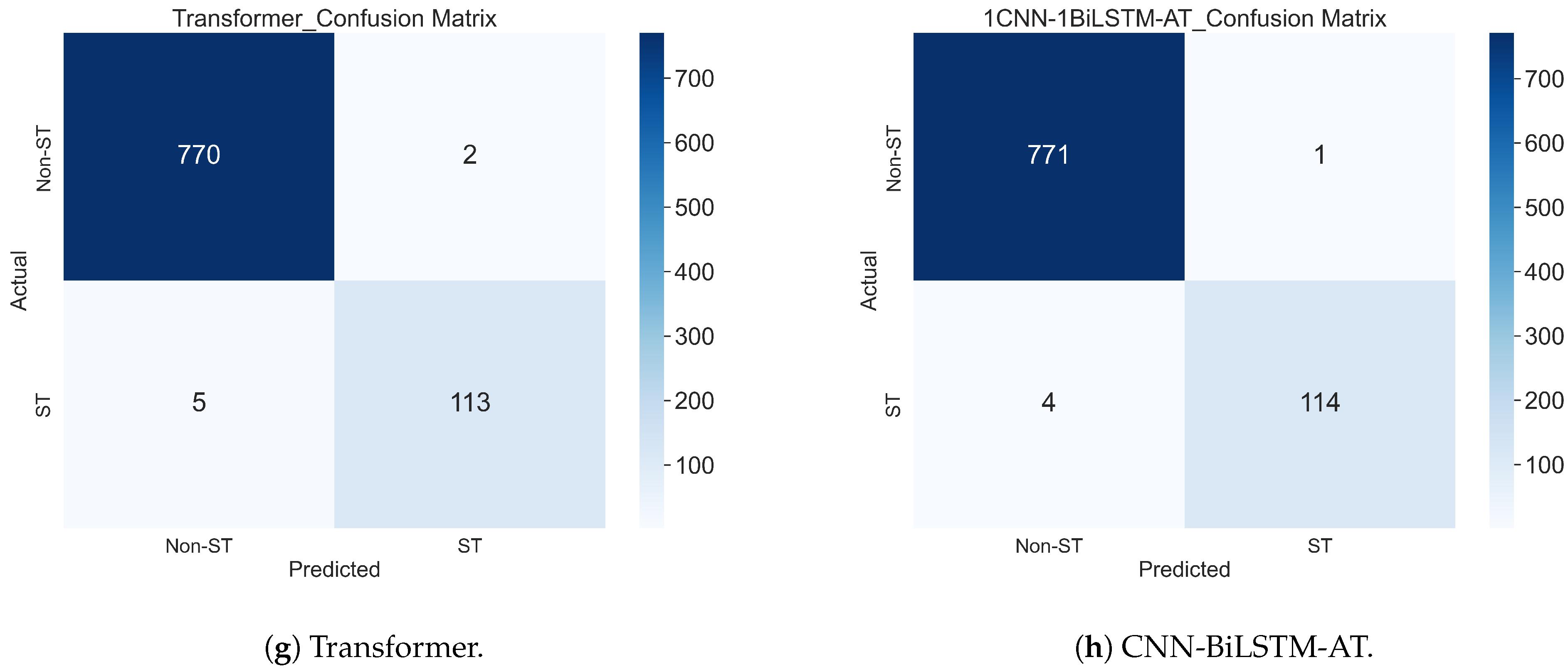
- Transformer model. The accuracy of this model was 0.992, ranking high among all models, second only to the CNN-BiLSTM-AT model. This model utilized a self-attention mechanism to model the relationships between time points in the sequence, effectively capturing the global dependency features of the data and improving overall prediction performance. However, when predicting ST samples, its performance was slightly inferior to CNN-BiLSTM-AT, indicating that sensitivity to small sample categories still needs to be strengthened. The training time was 151.87 s, one of the shortest among all models.
- (8)
- CNN-BiLSTM-AT model. The accuracy of this model was 0.994, and only five time data points were mispredicted. This indicates that this comprehensive model can fully utilize the features extracted by the convolutional layer, the time series information processed by BiLSTM, and the important features focused on by the attention mechanism to achieve the best results. Although the training time was 430.97 s, slightly longer than the CNN and CNN-AT models, its training time was still relatively short compared with the other models, and its overall performance was the best, making it an ideal choice for achieving a good balance between accuracy and efficiency.
5.2. Optimal Model Validation Analysis
5.2.1. Data Validation in 2025
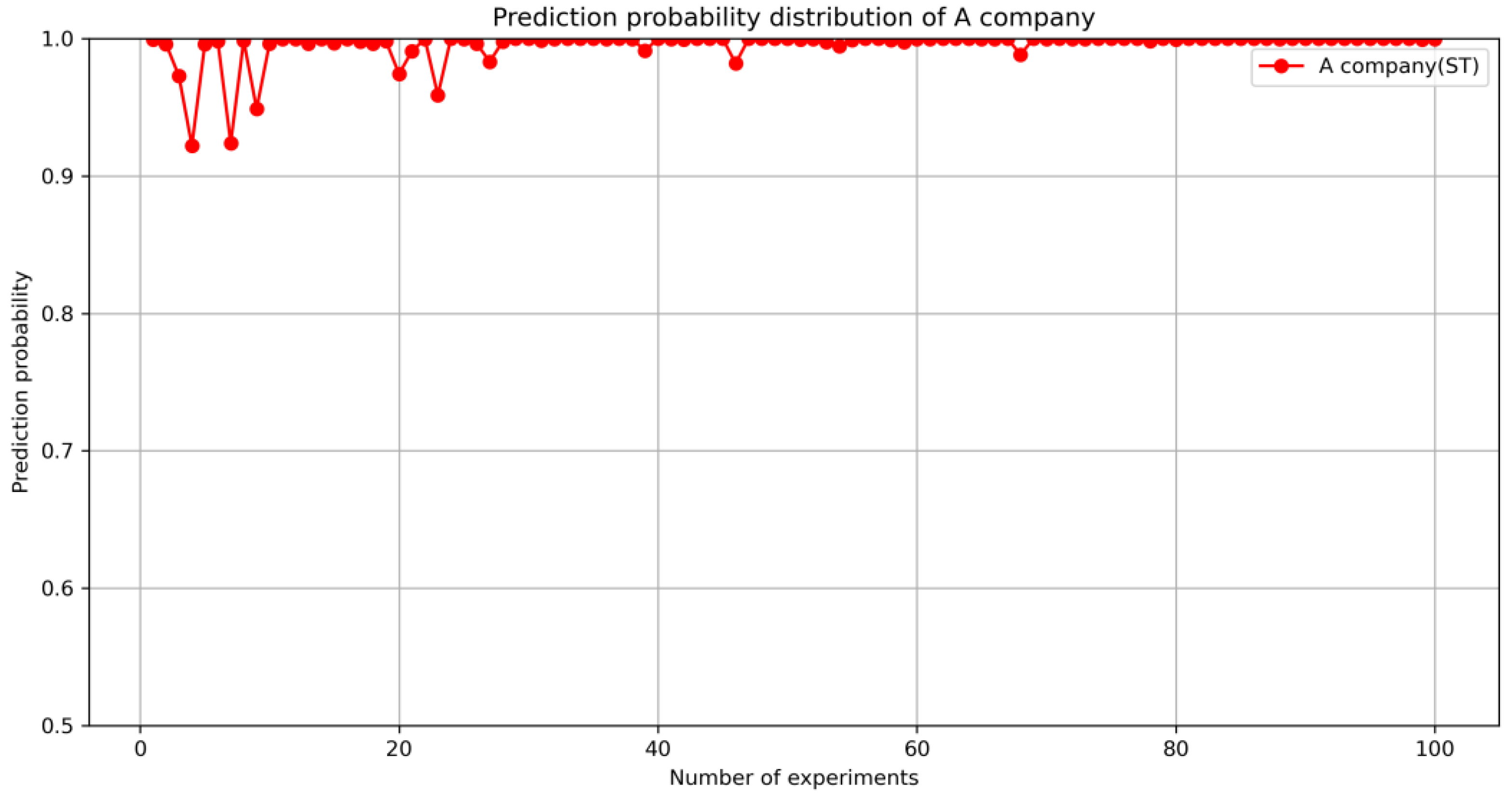
5.2.2. Case Application Analysis
6. Conclusions
6.1. Research Conclusions
6.2. Research Limitations and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNN | Convolutional neural network |
| BiLSTM | Bidirectional long short-term memory |
| AT | Attention mechanism |
| GRU | Gated recurrent unit |
| RNN | Recurrent neural network |
| LSTM | Long short-term memory |
| ST | Special treatment |
| SMOTE | Synthetic minority over-sampling technique |
| SVM | Support vector machine |
References
- Kuen, J.; Lim, K.M.; Lee, C.P. Self-taught learning of a deep invariant representation for visual tracking via temporal slowness principle. Pattern Recognit. 2015, 48, 2964–2982. [Google Scholar] [CrossRef]
- Gu, S.; Kelly, B.; Xiu, D. Empirical asset pricing via machine learning. Rev. Financ. Stud. 2020, 33, 2223–2273. [Google Scholar] [CrossRef]
- Hosaka, T. Bankruptcy prediction using imaged financial ratios and convolutional neural networks. Expert Syst. Appl. 2019, 117, 287–299. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, H.; Long, H. Forecasting the equity premium: Do deep neural network models work? Mod. Financ. 2023, 1, 1–11. [Google Scholar] [CrossRef]
- Li, S.; Chen, X. Research on Enterprise Financial Crisis Warning Model Based on Deep Learning Neural Network. Modern Inf. Technol. 2021, 5, 101–103+107. [Google Scholar]
- Aslam, S.; Rasool, A.; Jiang, Q.; Qu, Q. LSTM based model for real-time stock market prediction on unexpected incidents. In Proceedings of the 2021 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Xining, China, 15–19 July 2021; pp. 1149–1153. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar]
- Tao, L.H. Research on the Early Warning of Enterprise Financial Crisis Based on Transformer. Master’s Thesis, Hunan University of Science and Technology, Xiangtan, China, 2022. [Google Scholar]
- Ouyang, Z.S.; Lai, Y. Systemic financial risk early warning of financial market in China using Attention-LSTM model. N. Am. J. Econ. Financ. 2021, 56, 101383. [Google Scholar] [CrossRef]
- Zhao, Y. Design of a corporate financial crisis prediction model based on improved ABC-RNN+ Bi-LSTM algorithm in the context of sustainable development. PeerJ Comput. Sci. 2023, 9, e1287. [Google Scholar] [CrossRef]
- Chen, J.; Sun, B. Enhancing Financial Risk Prediction Using TG-LSTM Model: An Innovative Approach with Applications to Public Health Emergencies. J. Knowl. Econ. 2024, 16, 2979–2999. [Google Scholar] [CrossRef]
- Lu, W.; Li, J.; Wang, J.; Qin, L. A CNN-BiLSTM-AM method for stock price prediction. Neural Comput. Appl. 2021, 33, 4741–4753. [Google Scholar] [CrossRef]
- Kavianpour, P.; Kavianpour, M.; Jahani, E.; Ramezani, A. A CNN-BiLSTM model with attention mechanism for earthquake prediction. J. Supercomput. 2023, 79, 19194–19226. [Google Scholar] [CrossRef]
- Han, P.; Chen, H.; Rasool, A.; Jiang, Q.; Yang, M. MFB: A generalized multimodal fusion approach for bitcoin price prediction using time-lagged sentiment and indicator features. Expert Syst. Appl. 2025, 261, 125515. [Google Scholar] [CrossRef]
- Chen, J.; Liu, W. A study on stock price prediction based on Hyperband-LSTM model. Fin. Manag. Res. 2023, 1, 65–85. [Google Scholar]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2018, 18, 1–52. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple comparisons using rank sums. Technometrics 1964, 6, 241–252. [Google Scholar] [CrossRef]



| Indicator Name | Description |
|---|---|
| Debt Service Capacity | Current ratio, quick ratio, cash ratio, working capital, debt-to-asset ratio, equity ratio, multiplier equity ratio |
| Ratio Structure | Current assets ratio, cash assets ratio, working capital ratio, non-current assets ratio, current liabilities ratio, fixed assets ratio, operating profit margin |
| Operating Capacity | Accounts receivable turnover, inventory turnover, accounts payable turnover, current asset turnover, fixed asset turnover, total asset turnover |
| Earnings Capacity | Return on assets, net profit margin on total assets, net profit margin on current assets, net profit margin on fixed assets, return on equity, operating profit rate |
| Cash Flow Capacity | Operating index |
| Development Capability | Capital preservation and appreciation rate, fixed asset growth rate, revenue growth rate, sustainable growth rate, owners’ equity growth rate |
| Per Share Metrics | Earnings per share, earnings before interest, taxes per share |
| Company Type | Number of Company Samples | Number of Time Series Data Points |
|---|---|---|
| ST | 135 | 1620 |
| Non-ST | 755 | 9060 |
| Total | 890 | 10,680 |
| Time Step | Training Data | Testing Data | ||||
|---|---|---|---|---|---|---|
| Non-ST | ST | Total | Non-ST | ST | Total | |
| 5346 | 972 | 6318 | 1359 | 243 | 1602 | |
| 4832 | 864 | 5696 | 1208 | 216 | 1424 | |
| 4228 | 756 | 4984 | 1057 | 189 | 1246 | |
| 3624 | 648 | 4272 | 906 | 162 | 1068 | |
| 3020 | 540 | 3560 | 772 | 118 | 890 | |
| 2416 | 432 | 2848 | 604 | 108 | 712 | |
| 1811 | 325 | 2136 | 454 | 80 | 534 | |
| 1204 | 220 | 1424 | 306 | 50 | 356 | |
| 603 | 109 | 712 | 152 | 26 | 178 | |
| Time Step | Original Training Data | Oversampled Training Data | ||
|---|---|---|---|---|
| ST | Non-ST | ST | Non-ST | |
| 972 | 5346 | 5346 | 5346 | |
| 864 | 4832 | 4832 | 4832 | |
| 756 | 4228 | 4228 | 4228 | |
| 648 | 3624 | 3624 | 3624 | |
| 540 | 3020 | 3020 | 3020 | |
| 432 | 2416 | 2416 | 2416 | |
| 325 | 1811 | 1811 | 1811 | |
| 220 | 1204 | 1204 | 1204 | |
| 109 | 603 | 603 | 603 | |
| Method | Time (Seconds) | Test Accuracy |
|---|---|---|
| Hyperband | 2186.32 | 0.9876 |
| Random search | 628.25 | 0.9798 |
| Bayesian optimization | 591.74 | 0.9764 |
| Hyperparameter | Search Scope | Step | Optimal Value |
|---|---|---|---|
| Conv_filters | [16, 128] | 16 | 64 |
| CNN_Dropout | [0.1, 0.5] | 0.1 | 0.5 |
| Bilstm_units1 | [32, 128] | 32 | 64 |
| Bilstm_Dropout1 | [0.1, 0.5] | 0.1 | 0.2 |
| Bilstm_units2 | [32, 128] | 32 | 128 |
| Bilstm_Dropout2 | [0.1, 0.5] | 0.1 | 0.1 |
| Dense_units1 | [32, 256] | 32 | 128 |
| Dense_Dropout1 | [0.1, 0.5] | 0.1 | 0.1 |
| Dense_units2 | [32, 256] | 32 | 128 |
| Dense_Dropout2 | [0.1, 0.5] | 0.1 | 0.3 |
| Layer | m1: 1CNN-1BiLSTM-AT | m2: 1CNN-2BiLSTM-AT | m3: 2CNN-1BiLSTM-AT | m4: 2CNN-2BiLSTM-AT |
|---|---|---|---|---|
| Conv1D | 3 × 64 (ReLU) | 3 × 64 (ReLU) | 3 × 64 (ReLU) | 3 × 64 (ReLU) |
| MaxPool | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 |
| Conv1D | - | - | 3 × 128 (ReLU) | 3 × 128 (ReLU) |
| MaxPool | - | - | 2 × 2 | 2 × 2 |
| BiLSTM | 64 (Tanh) | 64 (Tanh) | 64 (Tanh) | 64 (Tanh) |
| BiLSTM | - | 128 (Tanh) | - | 128 (Tanh) |
| Attention | ✔ | ✔ | ✔ | ✔ |
| Dense | 128 (ReLU) | 128 (ReLU) | 128 (ReLU) | 128 (ReLU) |
| Time Step | Batch Size = 32 | Batch Size = 64 | ||||||
|---|---|---|---|---|---|---|---|---|
| m1 | m2 | m3 | m4 | m1 | m2 | m3 | m4 | |
| 0.948 | 0.947 | 0.917 | 0.923 | 0.956 | 0.946 | 0.917 | 0.908 | |
| 0.963 | 0.958 | 0.946 | 0.928 | 0.955 | 0.961 | 0.946 | 0.935 | |
| 0.984 | 0.987 | 0.953 | 0.967 | 0.984 | 0.983 | 0.972 | 0.960 | |
| 0.982 | 0.980 | 0.968 | 0.966 | 0.978 | 0.977 | 0.969 | 0.970 | |
| 0.994 | 0.987 | 0.987 | 0.981 | 0.985 | 0.987 | 0.980 | 0.976 | |
| 0.993 | 0.993 | 0.973 | 0.976 | 0.990 | 0.985 | 0.979 | 0.987 | |
| 0.983 | 0.979 | 0.983 | 0.968 | 0.987 | 0.981 | 0.974 | 0.981 | |
| 0.941 | 0.958 | 0.916 | 0.924 | 0.952 | 0.941 | 0.930 | 0.955 | |
| 0.820 | 0.787 | 0.792 | 0.781 | 0.798 | 0.792 | 0.798 | 0.815 | |
| Model | m1 | m2 | m3 | m4 |
|---|---|---|---|---|
| Mean Rank | 1.0000 | 2.3000 | 3.3333 | 3.3667 |
| Friedman statistic | 34.3061 | |||
| p-value | 0.000 | |||
| Comparison | Z-Score | Bonferroni-Corrected p-Value |
|---|---|---|
| m1 and m2 | 2.7577 | 0.0349 |
| m1 and m3 | 4.9497 | 0.0000 |
| m1 and m4 | 5.0205 | 0.0000 |
| m2 and m3 | 2.1920 | 0.1703 |
| m2 and m4 | 2.2627 | 0.1419 |
| m3 and m4 | 0.0707 | 1.0000 |
| Sampling Method | Type | Precision | Recall | F1-Score | Accuracy |
|---|---|---|---|---|---|
| SMOTE | Non-ST | 0.995 | 0.998 | 0.997 | 0.994 |
| ST | 0.991 | 0.966 | 0.979 | ||
| Non-SMOTE | Non-ST | 0.985 | 0.992 | 0.988 | 0.979 |
| ST | 0.946 | 0.898 | 0.922 |
| Model | ST | Non-ST | Training Time (s) | ||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | F1-Score | Precision | Recall | F1-Score | ||
| CNN | 0.990 | 0.814 | 0.893 | 0.972 | 0.999 | 0.985 | 162.52 |
| BiLSTM | 0.957 | 0.932 | 0.944 | 0.990 | 0.994 | 0.992 | 1279.94 |
| CNN-BiLSTM | 0.982 | 0.941 | 0.961 | 0.991 | 0.997 | 0.994 | 798.16 |
| CNN-AT | 0.982 | 0.949 | 0.966 | 0.992 | 0.997 | 0.995 | 163.34 |
| BiLSTM-AT | 0.958 | 0.958 | 0.958 | 0.994 | 0.994 | 0.994 | 1064.18 |
| CNN-GRU | 0.964 | 0.898 | 0.939 | 0.985 | 0.995 | 0.990 | 418.58 |
| Transformer | 0.982 | 0.957 | 0.970 | 0.994 | 0.997 | 0.995 | 151.87 |
| CNN-BiLSTM-AT | 0.991 | 0.966 | 0.979 | 0.995 | 0.999 | 0.997 | 430.97 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| 0 | 0.994 | 0.988 | 0.991 | 341 |
| 1 | 0.905 | 0.950 | 0.927 | 40 |
| Macro Avg | 0.949 | 0.969 | 0.959 | 381 |
| Weighted Avg | 0.985 | 0.984 | 0.984 | 381 |
| Accuracy | 0.984 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Chiangpradit, M.; Busababodhin, P. Hyperband-Optimized CNN-BiLSTM with Attention Mechanism for Corporate Financial Distress Prediction. Appl. Sci. 2025, 15, 5934. https://doi.org/10.3390/app15115934
Song Y, Chiangpradit M, Busababodhin P. Hyperband-Optimized CNN-BiLSTM with Attention Mechanism for Corporate Financial Distress Prediction. Applied Sciences. 2025; 15(11):5934. https://doi.org/10.3390/app15115934
Chicago/Turabian StyleSong, Yingying, Monchaya Chiangpradit, and Piyapatr Busababodhin. 2025. "Hyperband-Optimized CNN-BiLSTM with Attention Mechanism for Corporate Financial Distress Prediction" Applied Sciences 15, no. 11: 5934. https://doi.org/10.3390/app15115934
APA StyleSong, Y., Chiangpradit, M., & Busababodhin, P. (2025). Hyperband-Optimized CNN-BiLSTM with Attention Mechanism for Corporate Financial Distress Prediction. Applied Sciences, 15(11), 5934. https://doi.org/10.3390/app15115934







