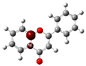
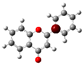
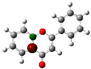
3.1. Stability of Mono-Substituted Flavones (n-Hydroxyflavones)
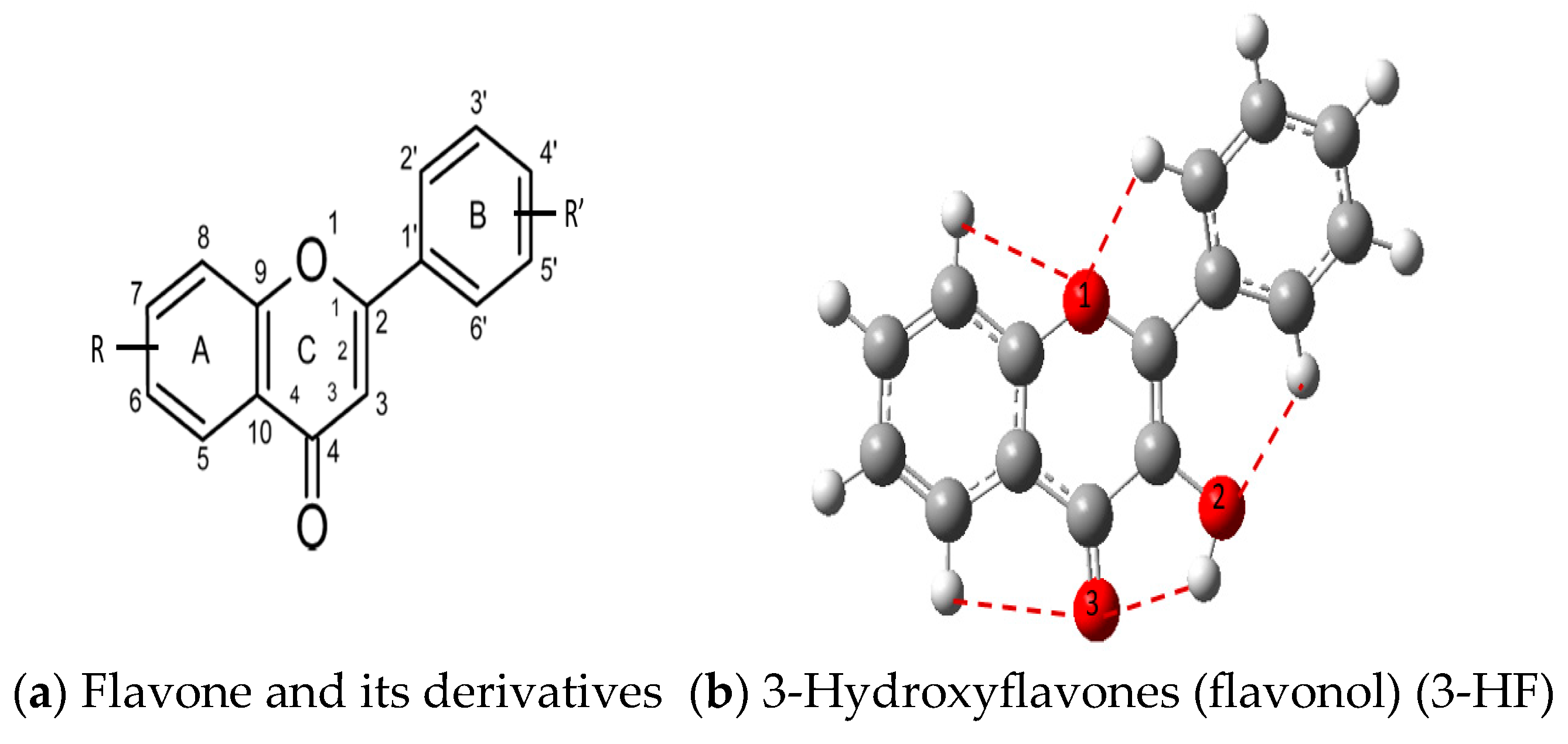
The structure of 3-HF (C
15H
10O
3) consists of a phenyl benzopyrone skeleton with fifteen carbon atoms, in which two benzene rings (A and B) are linked through a γ-pyrone ring C, as shown in
Figure 1, together with its nomenclature. All the hydrogens of the ten C-H bonds of the unsubstituted flavone (0-HF, C
15H
10O
2) can be replaced by a hydroxyl group (-OH) as mono-hydroxyflavones. As a result, in addition to the unsubstituted flavone (0-HF), there are seven unique mono-hydroxyflavones, 3-HF, 5-HF, 6-HF, 7-HF, 8-HF, 2′/6′-HF, 3′/5′-HF, and 4′-HF. Here, 5-HF was the most stable mono-hydroxyflavone in the gas phase, in agreement with an earlier study [
10], and it was also the most stable mono-hydroxyflavone in DMSO solvent obtained from the present study. 3-HF is unique because its -OH group replaces a single hydrogen atom on the γ-pyrone C-ring. Among the intramolecular hydrogen bonds (HBs) formed, the one within the γ-pyrone C-ring was the most significant, as highlighted in the structure shown at the bottom right of
Figure 1.
The stability and electronic properties of mono-substituted hydroxyflavones (n-HFs) have been systematically calculated using DFT calculations. The ground electronic states of mono-substituted flavones (n-HF where n=0 for unsubstituted flavone, n = 2–8 for n-hydroxyflavones) were optimized in DMSO solvent. Due to the symmetry and the rotations around the C2-C1′ single bond at room temperature, the mono-substituted flavones on the phenyl B-ring would be practically the same in the measurements, although they are theoretically not identical [
13]. For example, the 2′-HF and 6′-HF and the 3′-HF and 5′-HF pairs are hardly distinguished by room-temperature NMR measurements. As a result, we only studied 2′-HF (for 6′-HF) and 3′-HF (for 5′-HF). It was noted that the 2′-HF/6′-HF pair could be more different from the 3′-HF/5′-HF pair, as the former on the B-ring may engage with intramolecular interactions with the C-ring, forming certain hydrogen-bond networks, theoretically [
10].
Figure 2 compares the stability of the n-HF compounds, such as the total energies and dipole moments. Here, the unsubstituted flavone is presented as a reference. The total electronic energies of these eight n-HFs provide insights into their relative stability, which follows the following order: 5-HF > 4′-HF ≈ 7-HF > 3′-HF > 6-HF > 2′-HF > 3-HF > 8-HF.
The most stable n-HF was 5-HF, with the hydroxyl group substitution in the benzopyrone system (specifically in the A- and C-rings). In contrast, 8-HF, which was the least stable, also resides in the same benzopyrone framework (opposite the C5 position (para) in the A-ring). This trend indicates that the stability of n-HFs is influenced by the position of the hydroxyl (-OH) substitution and the ability to form hydrogen bonds within the molecular framework. Notably, the differences in the total electronic energy between conformers are relatively small, especially for the n-HFs where hydroxyl rotation does not significantly affect intramolecular hydrogen bonding, as observed for 6-HF, 7-HF, 3′-HF, and 4′-HF. This stability trend is consistent with earlier gas-phase calculations by Meyer [
10] (as shown in
Figure S1) and correlates well with the distribution of dipole moments, which reflects the electronic environment and intermolecular interactions of these molecules. For example, the energy differences due to hydroxyl group rotation for 2′-HF and 6′-HF are small, calculated at ΔE ≈ 3.73 kJ/mol, while for 3′-HF and 5′-HF, the difference is as low as ΔE ≈ 0.29 kJ/mol (Meyer, HF/6-31G(d)) [
10]. These small energy differences indicate the flexibility of certain hydroxyl groups in these n-HFs, suggesting that the stabilization effect of intramolecular hydrogen bonding can be a key factor in their conformational preferences. The results support the fact that most naturally occurring flavones have a hydroxyl group at the C5 position of the A-ring, while hydroxylation at other positions, such as C7 (A-ring) or C3′ and C4′ (B-ring), varies across different plant species [
5].
The dipole moment distributions further support the stability trend. The dipole moments of n-HFs range from 4.61 Debye for 3-HF (the smallest) to 7.81 Debye for 7-HF (the largest) in DMSO solvent. This significant variation in dipole moments correlates with the molecular geometry and the position of the hydroxyl group, which affect the electronic distribution within the molecule. High dipole moments, such as in 7-HF, suggest stronger interactions with the solvent and other molecules, which can enhance stability in solution. Conversely, lower dipole moments, such as in 3-HF, reflect less-pronounced charge separation, potentially resulting in lower stabilization through dipole–dipole interactions.
The stability of n-HFs is primarily influenced by the position of the hydroxyl group and the ability to form intramolecular hydrogen bonds. The ability of specific hydroxyl positions to enhance the stability and dipole moments suggests opportunities for tuning molecular properties through selective substitutions. To further explore the intramolecular hydrogen-bonding networking associated with these n-HFs,
Table 1 provides selected geometric properties of the flavones. While all the n-HFs are non-planar, with the phenyl B-ring deviating from the plane of the benzopyrone system (A- and C-rings), 3-HF and 4′-HF stand out by having the smallest dihedral angles between the B-ring and the benzopyrone, at 15.4° and 13.3°, respectively. More details of the geometric parameters obtained in the present study, with literature, for 0-HF and 3-HF are given in
Tables S1 and S2, respectively.
The results in
Table 1 demonstrate that, among the mono-substituted n-HFs, 3-HF stood out due to its unique geometric and electronic properties. While other n-HFs, such as 5-HF, 8-HF, and 2′-HF, exhibited intramolecular hydrogen bonding, their structural arrangements do not support the formation of a two-ring intramolecular hydrogen-bonding network as observed in 3-HF (see
Figure 1). For instance, 5-HF forms a single strong hydrogen bond between the hydroxyl group at the C5 position and the carbonyl oxygen, but the absence of a secondary hydrogen bond limits the molecule’s planarity. Similarly, 8-HF exhibits hydrogen bonding within the benzopyrone system; however, this interaction does not extend to the B-ring, reducing its overall stabilization (making 8-HF the most unstable mono-substituted n-HF). In the case of 2′-HF, the hydroxyl group on the B-ring primarily interacts within the B-ring itself, with minimal interaction with the benzopyrone system, further distinguishing it from 3-HF.
A distinctive feature of 3-HF is its ability to form two strong intramolecular hydrogen-bonding network connecting rings B and C. As shown in
Figure 1b, the hydroxyl group at the C3 position of the γ-pyrone C-ring interacts with the carbonyl oxygen (O3), -C3-O2H···O3=C4, and the hydrogen atom on C6′ of the phenyl B-ring, -C3-(H)O2···HC6′. These interactions result in the formation of pentagonal and hexagonal hydrogen-bonded ring structures of -C3-O2H···O3=C4- and -C3-(H)O2··· HC6′-C1′-C2-, respectively, which stabilize the molecule. The hexagon ring in 3-HF also exhibits an additional H···O bond, which stops the phenyl ring B from free rotations along the C2-C1′ bond. The O2H···O3 distance of 3-HF was very short, underscoring their strength. Specifically, the O2H···O3 and H···O2H distances in 3-HF were among the shortest calculated, with the bond distances being 1.95 Å and 2.21 Å, respectively. This dual hydrogen-bonding network not only increases the geometric rigidity of the molecule but also plays a pivotal role in defining its electronic properties. It was also noted that 5-HF exhibited a dual hydrogen-bonding network, but the O2H···O3 and H···O2H distances in 5-HF were 1.64 Å and 2.61 Å, respectively. Thus, the dual hydrogen-bonding network of 5-HF may contribute to the total energy stabilization, and 5-HF was the most stable mono-flavone derivative, as indicated in
Figure 2.
The near-planarity in 3-HF required for the hydrogen-bonding network, however, may impose geometric constraints, leading to an increased strain energy. The constrained arrangement around the hydroxyl group and the carbonyl oxygen introduces torsional and angular strain, which counterbalances the stabilizing effect of the strong hydrogen bonding. For instance, the relatively small dihedral angle, ∠321′6′, in 3-HF indicates a more planar structure compared to other n-HFs (except for 4′-HF). This increased planarity facilitates better conjugation between the B-ring and the benzopyrone system, thereby enhancing electronic delocalization. While 4′-HF also exhibits a small dihedral angle, its hydroxyl group at the C4′ position of the phenyl B-ring is more isolated and interacts minimally with other parts of the molecule. In contrast, the hydroxyl group in 3-HF, strategically positioned at the C3 site of the γ-pyrone C-ring, engages in critical intramolecular hydrogen-bonding interactions. This unique placement allows 3-HF to achieve a balance between electronic delocalization and structural stabilization, distinguishing it from other mono-hydroxyflavones.
Despite its extensive hydrogen-bonding network, the stability of 3-HF is determined by a delicate balance between geometric strain, electronic delocalization, and solvation effects. The strain imposed by maintaining a near-planar configuration, combined with the localization of electron density in specific regions, appears to counteract the stabilizing influence of the hydrogen bonds. This interplay explains why 3-HF, despite possessing the most intramolecular hydrogen bonding, ranks as the second least stable among mono-hydroxyflavones.
3.3. C-NMR Chemical Shifts Indicating Intermolecular Interactions of n-Hydroxyflavones
Table 3 reports the calculated
13C-NMR chemical shifts (δ
C) of the flavones. The accuracy of the calculated δ
C for n-HFs can be evaluated by comparing the root mean square deviation (RMSD) values between the calculated and experimental data [
6] for each isomer. The RMSD values of the eight compounds ranged from 0.85 ppm (0-HF) to 1.56 ppm (5-HF). Note that the “experimental” δ
Cs for 8-HF are the estimated averaged data from reference [
17], as there are no available NMR measurements for this compound to our knowledge. As a result, it is no surprise that the error for this 8-HF was as large as 2.15 ppm. Other RMSD values for the n-HFs where a hydroxyl group replaced the Hs on the benzopyrone (A- and C-) rings exhibited smaller variations. The simulated individual H-NMR spectra of all the n-HFs are given in
Figure S2 in the Supplementary Materials, which provides direct visualization of the patterns.
The real RMSD values for carbons in the phenyl B-ring are likely smaller than the tabulated values. A significant factor contributing to this discrepancy is the rotational flexibility of the C2–C1′ single bond. At room temperature, this bond allows for dynamic averaging of the chemical environments of carbons C2′/C6 and C3′/C5 in ring B [
13]. Experimental NMR captures this averaged state, whereas computational models treat these environments as distinct [
13]. Consequently, this difference inflates the RMSD values, suggesting larger deviations than may actually exist under experimental conditions. For example, the mono-substituted n-HFs on the B-ring exhibited both the smallest RMSD values, such as 0.92 ppm for 4′-HF and 0.98 ppm for 3′-HF, and the largest RMSD value of 2.13 ppm for 2′-HF. The notable RMSD for 2′-HF, which was significantly higher than those of 3′-HF and 4′-HF, can be attributed to the dynamic averaging of the carbon chemical shifts, δ
C, in the experimental measurements. Specifically, the δ
C for 2′-HF reflects an averaged state between 2′-HF and its isomer, 6′-HF, due to the “free” flip of the phenyl B-ring, while the computational calculations accounted only for 2′-HF. As illustrated in
Figure 1, the structural differences between the 2′-HF and 6′-HF isomers were more pronounced compared to those of the 3′-HF and 5′-HF isomers. In contrast, 4′-HF, located at the para-position on the phenyl B-ring, has no isomer, resulting in a reduced variability and the smallest RMSD among the B-ring-substituted flavones.
Another key factor influencing the RMSD is the substitution pattern across the flavone structure. Unsubstituted flavone (0-HF) exhibited the lowest RMSD values, showing an excellent agreement with the experimental data. This was likely due to its structural rigidity, which minimizes conformational variability. In contrast, mono-substituted flavones on the A- and C-rings showed larger RMSD values. The flexibility of the hydroxyl group in these compounds introduces variability in the local chemical environment, as the hydroxyl group can rotate or “flip,” leading to deviations between the calculated and experimentally observed values [
18]. Despite these discrepancies, an RMSD analysis provides a valuable tool for benchmarking computational predictions. The observed deviations emphasize the need to account for conformational flexibility, intramolecular interactions, and the inherent limitations of static computational models. These factors must be considered when interpreting RMSD values to ensure accuracy.
The systematically calculated δ
C values of the n-HFs presented in
Table 3 reveal an intriguing pattern. The δ
C values for the flavones ranged from 100.64 ppm (C8 in 7-HF) to 182.96 ppm (C4 in 5-HF), spanning approximately 82 ppm. This wide range reflects the diverse chemical environments of the carbon atoms. Notably, the carbonyl carbon (C4) consistently exhibited the largest δ
C (>170 ppm) across all isomers, with 3-HF showing the smallest δ
C (C4) at 172.22 ppm and 5-HF exhibiting the largest δ
C (C4) at 182.96 ppm. The carbon chemical shifts also revealed three consistently prominent carbons—C4, C2, and C9—that displayed significantly higher δ
C values compared to the others. The fourth largest δ
C corresponded to the carbon bonded to the hydroxyl group in each n-HF isomer. For unsubstituted flavone, there were only three such carbons due to the absence of a hydroxyl group. Interestingly, the smallest δ
C was almost always associated with the C3 carbon in the n-HF isomers, except for 3-HF and 7-HF. In these two cases, the smallest δC was observed for C8. The unique position of C3 in the flavone structure contributes to its low chemical shift. It is the only carbon atom in the γ-pyrone C-ring that is not part of the phenyl ring (unlike C9 and C10) and does not directly bond with oxygen (unlike C2, C4, and C9), except in 3-HF. This structural uniqueness likely explains the consistently low δ
C values for C3 in most n-HF isomers. The remaining δ
C values corresponded to the phenyl carbons, which typically fell within the 110–140 ppm range, depending on their specific positions. Notably, 8-HF emerged as an outlier, as its experimental NMR values were based on literature estimates rather than direct measurements. This introduced additional uncertainty in the comparison and inflated the RMSD values.
Half of the n-HF isomers, such as 3-HF, 5-HF, 8-HF, and 2′-HF, were able to form intramolecular hydrogen bonding with oxygens (O1 or O3 on the γ-pyrone C-ring) on adjacent carbon atoms, which was reflected by the chemical shifts of the isomers. The environment of a
13C nucleus can also be affected in an inductive, through-space (field effect), or resonance-based manner by substituents that are bonded to its carbon framework (skeleton). These effects, which became apparent in the
13C substituent chemical shift analyses, caused the associated chemical shifts to vary in a systematic and predictable manner.
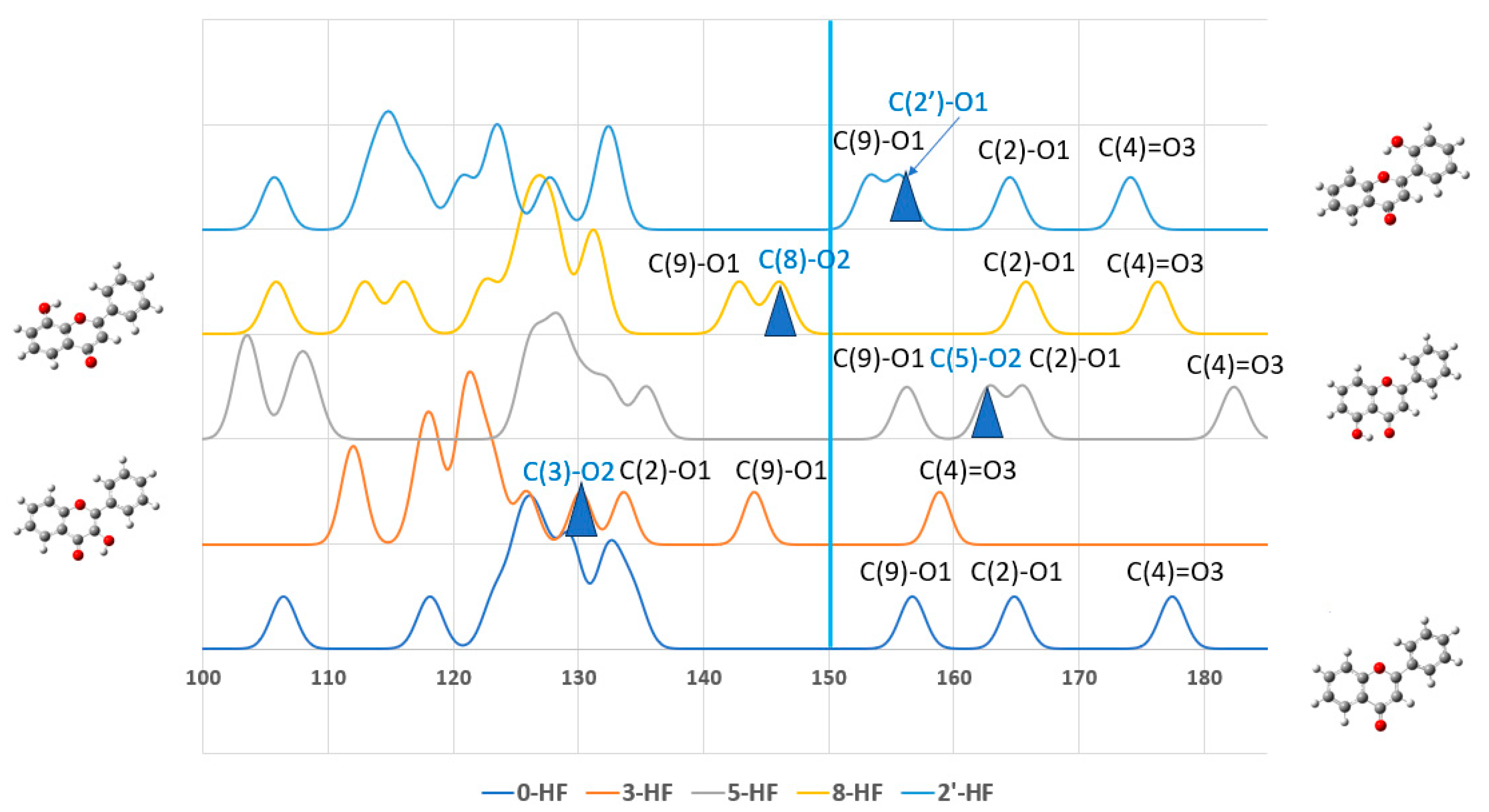
Figure 3 plots the
13C-NMR spectra of these n-HFs with respect to 0-HF. The full width at half maximum (FWHF) of the spectra was given by 0.20 ppm. The
13C-NMR spectra of all the n-HF isomers are given in
Figure S3 in the Supplementary Materials.
The carbons with the largest chemical shifts across all flavones were typically those forming C=O or C-O bonds, including C(4), C(2), and C(9), as well as the hydroxyl-substituted C(n) carbons. This indicates that chemical shifts are more influenced by the carbon–oxygen bonding environment than by their positions within the A-, B-, or C-rings. For the unsubstituted flavone (0-HF), only three chemical shifts occurred above 135 ppm, corresponding to its three C-O bonds. However, all the n-HF derivatives showed four chemical shifts above 135 ppm, which is attributable to the presence of an additional C-OH bond introduced by hydroxyl substitution. This further emphasizes the strong impact of oxygen bonding on the chemical shifts of carbons in flavones. As expected, all the flavones showed the C(4)=O carbonyl group as the one with the highest chemical shift, which aligns with its highly deshielded nature due to strong electron-withdrawing effects. The C-NMR chemical shifts (δC) of C4 in the most stable isomer, 5-HF, exhibited the largest δC for its carbonyl carbon C(4), consistent with its strong electron-withdrawing effects and stability and the hydrogen-bonding interaction of C5-O-H···O3=C4. The hydroxyl-substituted C-OH carbons exhibited δC values that were intermediate, but closer to the higher end of the chemical shift range, reflecting their partially deshielded environment. These carbons consistently had δC values above 135 ppm, which aligns with their attachment to electron-withdrawing oxygen atoms.
The specific δ
C ordering for various carbons provides insight into the electronic environments. For unsubstituted flavone, 0-HF, the chemical shift order is as follows:
For most n-HF derivatives, the order is slightly modified to the following:
where n = 5, 8, ad 2′. However, in 3-HF, the order is unique:
This unique δC ordering in 3-HF further highlights the distinct electronic effects of its extended hydrogen-bonding network and near-planar geometry. The deshielding effect on C(9) surpasses that on C(2) in 3-HF, reflecting the strong influence of hydrogen bonding and electronic delocalization in this isomer.
3.4. Quantum Mechanical Insights of the Uniqueness of 3-HF
The
13C-NMR chemical shifts of mono-hydroxyflavones are primarily influenced by their local electronic environments, including inductive effects, lone-pair resonance, and conjugation, which are accurately captured through DFT-based quantum mechanical calculations. This highlights the importance of computational approaches for reliably predicting
13C-NMR shifts. While empirical methods, such as curve fitting or machine learning (ML), provide estimates, they lack the ability to fully capture the fundamental quantum mechanical principles that dictate these chemical environments. For example, a recently developed ML model failed to accurately predict
13C-NMR chemical shifts for up to six classes of natural products, including flavonoids, lignans, sesquiterpenoids, steroids, alkaloids, and chromans [
19]. These classes of natural products contain a delocalized conjugation framework.
To highlight the unique electronic structure of 3-HF,
Figure 4 presents the calculated electronic charge (natural bond orbital (NBO)) distributions of 3-HF compared to those of 5-HF, the most stable isomer, and 0-HF, the unsubstituted flavone. The analysis of NBO atomic charges and bonding in the flavones revealed significant variations in the electronic environments and roles of individual carbons and hydrogens. According to the NBO charge distribution, all hydrogens are positively charged (green), while carbons are generally negatively charged, except for those involved in C–O bonds, which exhibit positive charges (red). This distinction underscores the influence of oxygen’s strong electronegativity on neighboring carbons. In the case of 0-HF (unsubstituted flavone), the carbons C3 and C9 within the γ-pyrone C-ring are negatively charged. However, C3 is more negatively charged than C9 due to its position between two highly electronegative oxygen atoms. In contrast, C9 is part of the aromatic A-ring, where its negative charge is partially delocalized into the aromatic system, reducing its overall negative character. Notably, 0-HF lacks any C(n)–OH bonds, which sets its NBO charge distribution apart from its hydroxylated derivatives. An interesting observation is that the positively charged (green-colored) carbons bonded directly to oxygen atoms do not form C–H bonds. In 0-HF, C3 is the only carbon within the γ-pyrone C-ring that forms a C–H bond, further highlighting its unique electronic environment within the γ-pyrone C-ring of unsubstituted flavone.
In 3-HF and 5-HF, hydroxyl substitution introduces a fourth positively charged carbon, corresponding to the hydroxylated carbon (C3 in 3-HF and C5 in 5-HF, respectively). The substitution significantly alters the local electronic environment, highlighting the differences in the charge distribution compared to unsubstituted flavone. In 3-HF, the hydroxyl group at C3 enables the formation of a robust intramolecular hydrogen-bonding network. This group participates in multiple hydrogen bonds, including H···O(3)=C and C(6′)–H···O(2), forming a pentagonal ring, and C(2′)–H···O(1), constituting a hexagonal ring. These hydrogen-bonding interactions contribute to the geometric rigidity of 3-HF, although they also introduce additional electronic strain, as discussed earlier. The distinct charge distributions and bonding environments in flavones are primarily determined by the presence and positioning of hydroxyl groups and the resulting C–O bonds. Hydroxyl substitution not only influences the local electronic properties of flavones, but also enhances the negative charge on specific carbons. Furthermore, it enables hydrogen bonding, which plays a crucial role in determining their structural stability and energetic properties. Such quantum mechanical effects of flavones are well predicted using pattern-recognition methods such as machine learning [
19]. The chemical shifts δ
C of the carbons with C-O bonding for these n-HFs are further compared in
Figure S4. For the three δ
Cs with single C-O bonding (that is, C2, C9, and Cn for n-HFs), they all follow the same trend that C9 has the smallest δ
C among these carbons, except for 3-HF, where C9 has the second largest δ
C after δ
C (C4=O). This is in good agreement with the measurement of Burns et al. [
6].
From a structural point of view, the unsubstituted 0-HF and mono-substituted 3-HF share the same molecular skeleton with the same number carbon atoms, but 3-HF has one more oxygen atom. The uniqueness of 3-hydroxyflavone (3-HF) compared to flavone (0-HF) can be attributed to the significant changes in the carbon core electron density distributions (C1s) caused by the presence of the hydroxyl group at the C3 position.
Table 4 compares the top six C1s orbitals of 3-HF and 0-HF (out of 15 C1s core orbitals). The DFT calculations reveal that the local energy C1s orbitals, 4a-12a for 3-HF and 3a-11a for 0-HF, exhibited minimal changes in their local density distributions. This is because these core C1s electrons are primarily dominated by the aromatic phenyl rings in the A-ring and B-ring, as shown in
Figure S5. However, the top six C1s core electrons in
Table 4 demonstrate noticeable reordering in 3-HF (13a-18a) compared to 0-HF (12a-17a). All these top six carbon C1s core orbitals are located in the γ-pyrone C-ring, plus the C1′ in the B-ring and C2 in the γ-pyrone C-ring. Specifically, the hydroxyl group at C3 introduces a significant electronic perturbation, causing a pair-swapping in the order of the six top C1s electron densities (see
Table 4 by matching colors). For instance, the sixth highest C1s state in 0-HF (12a on C3, blue) shifts to become the third highest C1s state (17a on C3) in 3-HF. This reordering is directly attributed to the C3-OH group, which alters the local electronic environment and increases the electron density around the C3 carbon, as indicated in their
13C-NMR chemical shifts. These changes reflect the strong electronic influence of the hydroxyl group in 3-HF, distinguishing it from unsubstituted flavone and highlighting its unique electronic structure and reactivity.
The mono-substitution on C3 for 3-HF also caused the C1s electron density reordering of the highest C1s orbitals on C4 and C2 in 0-HF, which was switched in 3-HF as C2 and C4 in 3-HF. It was also noted that a certain amount of electron density sharing between C4 and C3 of 3-HF was observed, and this was not seen in 0-HF under the same conditions.