Abstract
This paper presents a novel control strategy employing a deep reinforcement learning (DRL) scheme for online selection of optimal weighting factors in cost functions of the finite control set model predictive current controller of a permanent magnet synchronous motor (PMSM). Indeed, when designing predictive controllers for PMSMs’ phase currents, competing objectives appear, such as managing current convergence and switching transitions. These objectives result in an asymmetric cost function where they have to be balanced through weighting factors in order to enhance the inverter and motor performance. Leveraging the twin delayed deep deterministic policy gradient algorithm, the optimal weighting factor selection policy is obtained for online balancing of the choice between current deviation in the frame and inverter commutations. For comparison, a metaheuristic-based artificial neural network is trained on static data obtained through a multi-objective genetic algorithm to predict the weights. The key performance markers, such as torque ripple, total harmonic distortion, switching frequency, steady-state, and dynamic performance, are provided through numerical simulations to verify the effectiveness of the proposed tuning scheme. The results of these simulations confirm that the proposed dynamic control scheme effectively resolves the challenges of weighting factor choice, meeting inverter performance requirements, and delivering better dynamic and steady-state performance.
1. Introduction
With growing concerns over the greenhouse effect, the energy efficiency of industrial plants has become a critical priority. The automotive and aerospace industries are thus shifting toward greater efficiency, increasingly replacing hydraulic actuators with permanent magnet synchronous motors (PMSMs), which offer better energy performance [1,2]. Indeed, PMSMs are widely preferred in industrial applications for their compact design, high power density, exceptional efficiency, low inertia, and elimination of field windings.
The predominant control methods for surface PMSM (SPMSM) drive systems are vector control and direct torque control (DTC) [3]. These methods often include a linear proportional–integral (PI) controller in the control loop. Such a controller has limitations, particularly in applications that require minimal overshoot and high dynamic performance. Traditional DTC also suffers from significant torque fluctuations at low speeds [4,5]. As a result, researchers are actively seeking advanced control strategies to enhance the performance of the PMSM drive system. Among other advanced control strategies, model predictive control (MPC) has gained much attention in the control of power electronics and motor drives due to its ability to handle multivariable problems with constraints and nonlinearities [6]. MPC has been extensively used in various industrial applications, including wind power generation systems, computer numerical control machine drive systems, and high-speed rail traction drive systems [7,8,9].
As a result, the last decade has seen the study of various types of MPC for drive applications based on fixed or randomly distributed switching frequencies across converters. These predictive strategies can be classified into two categories, namely continuous control set (CCS) MPC and finite control set (FCS) MPC. In CCS-MPC, a constant switching frequency can be achieved through the modulation stage. However, the prediction process involved is complex [10]. On the other hand, FCS-MPC has become more popular among other predictive control strategies due to its intuitive nature and straightforward implementation. Indeed, it optimizes the switching states directly without needing an external modulation stage, resulting in a randomly distributed switching frequency [11]. Various approaches have been proposed to achieve a constant switching frequency with FCS-MPC in the literature [12,13,14]. Furthermore, a data-driven predictive controller has been employed to achieve gating without requiring the explicit model of the plant, helping to improve robustness and transient response [15].
Although FCS-MPC offers impressive advantages, such as high-performance multi-objective control with inherent constraints, it faces several challenges. In addition, this control strategy can lead to variable switching frequency in the inverter output, which is often undesirable, as it can cause the risk of triggering an unexpected resonance and affect the power efficiency of the inverter [16]. Then, the central element of the FCS-MPC strategy is its cost function, essential to balance various control objectives, including tracking error, control effort, total harmonic distortion (THD), switching frequency, and torque ripple, all under state constraints. All or part of these conflicting objectives can appear simultaneously in an asymmetric cost function, each weighted by a different factor, balancing their relative importance. One of the most critical issues is therefore the choice of optimal weights within the asymmetric cost function, which can significantly impact the overall effectiveness of the controller [17]. It is important to note that the weighting factors within the cost function directly impact the control performance of PMSM drives, particularly regarding total harmonic distortion (THD) and switching frequency, as they manage the trade-offs between the different objectives. In addition, current convergence ensures accurate tracking of the reference current, which directly affects torque precision and dynamic response. However, achieving fast convergence often requires fast inverter switching, which leads to increased switching frequency, power losses, and thermal stress on the semiconductor devices (IGBT, MOSFET). On the other hand, minimizing switching transitions improves inverter efficiency, reduces electromagnetic interference, and enhances the reliability and lifespan of power electronics, but may compromise current tracking performance and introduce torque ripples.
Incorrectly set weighting factors can lead to misalignment in prioritizing control targets, ultimately reducing control effectiveness [18]. It is consequently important to choose appropriate weighting factors in the FCS-MPC’s cost function, reflecting the relative importance of each control objective, as the accuracy of these factors significantly influences the overall performance of the control strategy. The online calculation of the weights in MPC’s cost function is highly challenging due to the complexity and coupling between multiple control objectives [19]. Furthermore, online solutions often use observer-based approaches to dynamically optimize the weighting coefficients, but these methods significantly increase the computational burden on MPC-based systems [20,21]. To address this, researchers have proposed alternative methods, such as using a symmetric cost function, where each term has equal priority and focuses solely on tracking errors [17]. Another approach is the use of sequential model predictive control (SMPC), which decomposes multiple control objectives into separate sub-cost functions, evaluated sequentially [22]. This method simplifies the control structure, reduces computational load, and offers flexibility. However, SMPC performance is dependent on the execution order of the sub-cost functions, making it difficult to guarantee optimal performance and preventing simultaneous optimization of all targets [23]. Furthermore, offline tuning schemes have been proposed in the literature [24]. While these schemes are straightforward, they are time-consuming and computationally expensive. Additionally, using a fixed weighting factor does not ensure optimal performance across various operating conditions.
Recently, data-driven strategies have become more popular in the field of power conversion applications. It has been applied successfully in power electronic systems for model-free control approaches, particularly with the use of an artificial neural network (ANN)-based controller and estimator for the identification and control of power electronics and motor drives [25,26]. Furthermore, data-driven schemes are used for the design of weighting factors [27]. Intelligent approaches for optimizing cost functions include heuristic methods and fuzzy logic, which often increase computational complexity. Heuristic approaches such as genetic algorithms (GAs) have been applied to optimize weighting factors in MPC, but they significantly increase computational complexity due to their iterative nature [28]. Similarly, fuzzy decision-making models, which replace the cost function to bypass weighting factor selection, are mainly suitable for online optimization and add complexity, particularly in multilevel inverters. Although both methods can improve accuracy, they impose a high computational burden on MPC systems [29]. However, data-driven designs based on ANN give a significant advantage due to their strong capabilities in nonlinear regression, prediction, and classification [30,31]. Data-driven design reduces computational complexity, as the training and testing of the model is done offline, and when integrated online, it dynamically updates the weighting factors of the cost function to enhance the performance of the MPC, which is better than fixed weighting factors in the cost function.
This paper then presents a novel method for online optimization of weighting factors in the asymmetric cost function of an FCS model predictive current controller (MPCC), targeting reduced computational complexity and enhanced dynamic performance. The approach leverages a twin delayed deep deterministic policy gradient (TD3) [32] reinforcement learning (RL) agent to formulate an optimal policy for weighting factor design, with plant dynamics and inverter nonlinearities modeled within the control environment. Through agent–environment interaction, the TD3 agent adaptively optimizes the weighting factors by maximizing a reward function, effectively addressing multi-objective control requirements. Furthermore, to the authors’ knowledge, this study represents the first effort to establish a dynamic, data-driven tuning framework using deep reinforcement learning (DRL) for an asymmetric cost function. The proposed tuning scheme aims to optimize control objectives by balancing multiple competing criteria and enhancing control system performance.
For comparative analysis, we propose a multiobjective GA (MOGA)-based neural network scheme that is employed to optimize the weighting factors. MOGA constructs a Pareto front of optimal weights [33] from which a dataset under varied operating conditions is established. These datasets are used as training data for a feedforward neural network (NN). This network provides a baseline data-driven approach for online tuning of the weighting factors across variable conditions. Test cases using a DRL-based dynamic tuning scheme and an NN-based static tuning approach are presented to validate the proposed method, demonstrating an improved weighting factor design in MPC for voltage source inverter (VSI)-fed PMSMs.
The remainder of the paper is structured as follows. Section 2 presents the mathematical model of the considered electric drives. In addition, the general formulation of FCS-MPCC with an asymmetric cost function is presented. Then, Section 3 delves into a detailed explanation of the static and dynamic data-based training methods for the weighting factors’ optimization strategies. Section 4 is dedicated to the evaluation of the effectiveness of the reinforcement learning approach, where we compare its performance under various test conditions with the baseline MOGA-NN-based method for the online selection of weighting factors in the asymmetric cost function. Finally, the significant findings of the proposed DRL online tuning scheme are summarized in Section 5.
2. Mathematical Modeling
The mathematical model of the considered plant and its control strategy are established in the following.
2.1. Modeling of a Three-Phase Two-Level Voltage Source Inverter
A three-phase VSI consisting of six switches and a DC rail, as presented in Figure 1, is commonly used in industrial applications.
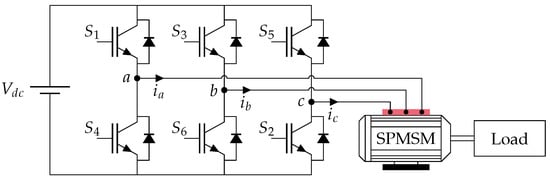
Figure 1.
The schematic representation of VSI-fed SPMSM.
A modulation scheme modulates the DC input voltage from the DC link to generate a three-phase AC output for driving electric machines by providing appropriate sequences of gate signals to the transistors. To prevent shoot-through, the gate signals for the upper and lower transistors in each inverter leg are complementary, and their transitions are managed with dead time intervals to avoid shoot-through phenomena; see Chapter 10 in [1]. The instantaneous stator voltage of the three-phase inverter is expressed as
Here, , , and represent the switching states of the upper transistors of the three inverter legs at time t, such that , with , if the transistor i is closed and 0 otherwise. The output voltage vectors of a two-level VSI in the coordinate frame are given in Table 1. For ease of representation and analysis, the time dependency in the equations is omitted in further discussions.

Table 1.
Output voltage vectors of a two-level three-phase inverter.
To simplify the control process, three-phase voltages are transformed into two-phase components in both stationary () and synchronous rotating () reference frames using Clarke and Park transformations, respectively. These transformations are respectively expressed as
where is the angle between the and frames, i.e., in the case of a motor, between the stator and the rotor. The possible switching configurations for a two-level VSI in the frame are shown in Figure 2. In this figure, the , with , correspond to the projection of the voltage vectors of Table 1 on the axes.
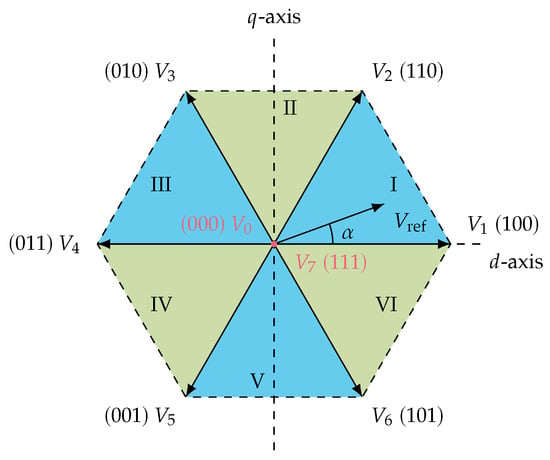
Figure 2.
Inverter possible switching configuration.
2.2. Modeling of Surface Permanent Magnet Synchronous Motor
The mathematical modeling of the three-phase SPMSM is considered in the rotating reference frame. Due to the non-salient characteristic of the motor drive, we consider that the d- and q-axis inductances and of the motor satisfy . To ensure model simplicity and real-time implementation feasibility, high-frequency effects such as magnetic saturation, core losses, and temperature variations were neglected. The direct-axis and quadrature-axis currents, and , respectively, are obtained from the following equations, as given in Chapter 6 in [1],
where and are the voltage components in the frame, is the stator resistance, is the electrical angular velocity, and is the magnetic flux due to permanent magnets. The voltages and fed to the SPMSM are obtained through the VSI described in the previous section, as shown in Figure 1.
For a given sampling period , we use the explicit forward Euler discretization approach [34] to derive a discrete-time prediction model of the frame currents as
This equation describes the updated current values and at the next time step in terms of the different signal values and system parameters at the current time step k.
The motor speed is considered to remain constant over several time steps, as the electromechanical time constant of the motor drive is significantly smaller than the mechanical time constant [35]. This leads to the approximation . The electromagnetic torque produced by the SPMSM is
where p is the number of pole pairs of the motor. This model provides a fundamental understanding of the motor’s operation employed in this paper, enabling effective design and analysis of control systems for SPMSMs.
2.3. Decision Function
The FCS-MPCC control strategy relies on the principle that a static power converter can only produce a finite set of switching states, each impacting the system variables differently. This is the case for the VSI described above, where we have eight possible switching states and the associated values of the voltages and . Using the control plant model (5), we can predict the behavior of the currents and in each of these switching states.
The selection of the optimal switching state is then based on a selection criterion, specifically a cost function. In classical FCS-MPCC, the cost function is evaluated at each time step for all possible switching states, and the optimal state is selected as the one yielding the minimal cost function. The same is done in this paper, with the cost function being composed of three elements.
The first element of the cost function aims to minimize the deviation of the currents and from their respective references and . This deviation is evaluated over a given prediction horizon N by considering
where and are the predictions of and obtained by applying N times the dynamical model (5) from the knowledge of and for a given choice of voltage vectors and , with , assuming remains constant and equal to . In the following, we consider .
Remark 1.
In this paper, we consider, for current prediction, that and remain constant over the prediction horizon in order to minimize the number of cost function evaluations made at each time instant. Indeed, as seen in Table 1, there are eight possible choices for the pair at each time step, leading to (since in this paper) possible combinations to test over the prediction horizon. It follows that when evaluating , we only choose voltages and while and .
Due to the lack of a modulator in the control design, the switching frequency is variable, leading to increased commutation between the consecutive sampling periods. As a result, this causes switching losses and reduces the converter’s efficiency. To limit this issue, a second element
aiming to reduce the switching frequency is added to the decision function to reduce the commutation burden on the transistors at each sampling time. We introduce in (8) the quantity , corresponding to the number of legs of the VSI where a commutation occurred between two time instants and k.
Remark 2.
Following Remark 1, we have, in this paper, for any .
Finally, a third term
playing the role of a constraint on the maximum current that can pass through the SPMSM is added to the decision function. Indeed, the function is defined as
adding an infinite penalty to the cost in case the predicted currents get higher than the rated phase current.
Finally, the total cost function has three objectives: reducing the deviation of the current from the reference, reducing the total amount of switches between transistor states, and limiting the maximum current through the SPMSM, and is expressed as
where and are weighting factors of current tracking and switching frequency regulation, respectively.
We see that the cost function (11) is asymmetric. Indeed, reducing the switching frequency affects the current tracking error , as the chosen switching states influence the voltage sent to the motor. On the other hand, getting a better current tracking has an impact , as it imposes switching states and, as a consequence, a switching frequency on the VSI. To overcome this complexity, this paper presents an optimization algorithm using a multi-objective approach as well as a data-driven approach employing static and dynamic data to find the balance between current tracking error and variable frequency reduction, which gives overall enhanced drive performance.
3. Proposed Intelligent Weighting Factors Design Approach
Based on what precedes, Figure 3 illustrates the proposed control system structure. The FCS-MPCC block encapsulates the minimization strategy described in Section 2.3, providing the appropriate gating pulses to the VSI. Indeed, it receives the values , , , and the gate pulses at time in order to predict the different and for the eight possible values of and of Figure 2 and the associated gate pulses. The goal of this section is then to describe a DRL approach to determine the optimal weighting factors and of the asymmetric decision function (11). Reinforcement learning effectively manages a dynamic set of data online to update the weights of a neural network, aiding both transient and steady-state responses of the control system. To assess the efficiency of the proposed DRL approach, we propose running a multiobjective genetic algorithm to generate static data [33] to tune a neural network providing the weighting factors as a baseline for comparison with the proposed method.
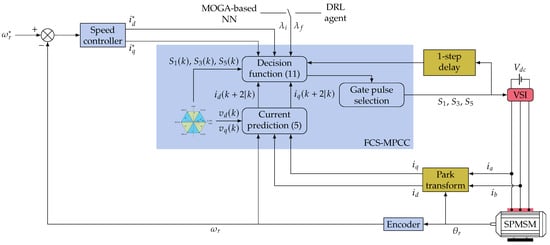
Figure 3.
FCS-MPCC-based control design of SPMSM.
3.1. MOGA-Based NN Weighting Factor Tuning Approach
As explained, the DRL-based strategy has to be compared to a baseline method to assess its efficiency. The baseline considered in this paper is the neural network presented in Figure 4. This network has two hidden layers, the first one having 15 neurons using the poslin activation function and the second one having 10 neurons using the tansig activation function. The inputs of the network are the q-axis current error at time instant k, the integral of this error, and the number of commutations between time instants and k. The outputs are the weighting factors and .
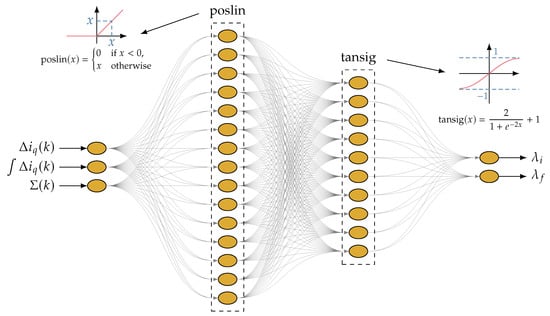
Figure 4.
Neural network architecture.
Remark 3.

To select the best set of signals as the neural network inputs, several combinations were tried. For each set of input signals, the performance of the control strategy of Figure 3 was evaluated using the neural network resulting from the supervised learning procedure described below. For test cases, the integral square error (ISE), integral time-weighted square error (ITSE), integral absolute error (IAE), and integral time-weighted absolute error (ITAE) of the errors and were evaluated. As can be seen on Table 2 on one example of input signals, the set of inputs we selected always performed better, hence its selection.

Table 2.
Performance metrics for neural network input features.
To train this neural network, an optimal value of the weighting factors is first obtained using a MOGA implemented through the Matlab 2024a function gamultiobj. This algorithm uses a population of individuals. To each individual is assigned a pair of weighting factors drawn randomly such that and . For each individual, a simulation using the structure Figure 3 is run by fixing the weighting factors to those of the individual and using the parameters Table 3 for the different elements in the structure. The speed controller is a PI controller whose parameters are also given in Table 3. The best individuals are selected based on two objectives:
- The total number of transitions over the simulation, i.e., the sum of the ;
- The ITAE of the q-axis current where N is the total number of time steps in the simulation.
Based on the obtained results, a new generation of individuals is generated using the default methods of the gamultiobj function. This process is then repeated over a maximum of generations.

Table 3.
Simulation model parameters.
Table 3.
Simulation model parameters.
| Parameter | Description | Value |
|---|---|---|
| Sampling period | ||
| Switching frequency reference | ||
| Stator resistance | ||
| Stator inductance | ||
| Flux linkage | ||
| Torque constant | ||
| p | Pole pairs | 4 |
| J | Rotor inertia | |
| Speed proportional gain | ||
| Speed integral gain |
Through the use of MOGA, a Pareto front of weighting factors balancing the two objectives is obtained. The structure of Figure 3 is then simulated under different conditions using different pairs from the Pareto front as weighting factors and the parameters of Table 3. The different conditions include varied steady-state and transient conditions, load variations, external disturbances, noise, parameter variations, and sampling time changes. The results of these simulations are gathered to constitute a comprehensive dataset used to train the neural network of Figure 4. The variety of simulation conditions helps enhance the network’s overall robustness and generalization capabilities by simulating varied realistic operating environments.
The neural network is then trained using a supervised learning approach with the dataset. The performance of the neural network is evaluated over its training phase by using the mean squared error of the predicted values with respect to the ones from the dataset.
The flowchart presented in Figure 5 summarizes the procedure described in this section for the training of a neural network based on the use of MOGA.
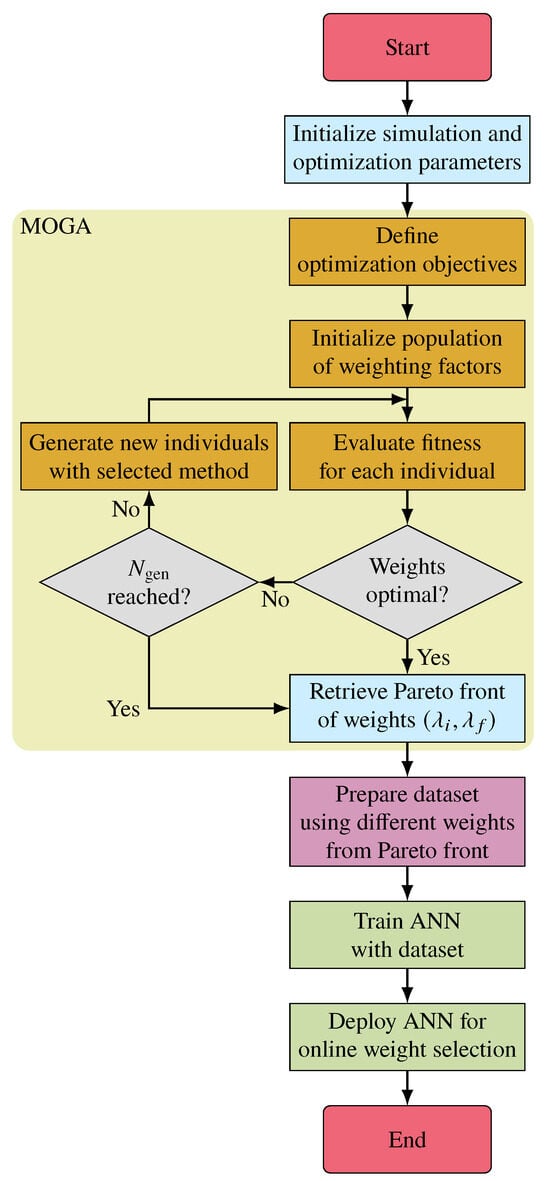
Figure 5.
Process flowchart of MOGA-based NN training for weighting factor selection of FCS-MPCC for SPMSM.
3.2. Proposed Weighting Factor Tuning Scheme Based on DRL
The baseline data-driven approach we previously described has one important limitation. Indeed, in order to be able to train the neural network, we first obtained a Pareto front of weighting factors on the nominal operating conditions. Then, we generated a dataset through test cases, and even though we included many different cases in order for the network to be able to generalize its choice of weighting factors, some unforeseen possibilities or operating conditions might have been overlooked. These omissions might lead to poor weight selection in some situations. The data-driven method we propose is then based on deep reinforcement learning, since in this case, the neural network used for weighting factor selection is trained online, directly on the simulation of the structure of Figure 3. The remainder of this section describes the proposed method.
3.2.1. Generalities
Reinforcement learning is a distinct paradigm within the field of machine learning [36]. It focuses on teaching an agent how to make sequences of decisions by interacting with an environment in order to solve a so-called sequential decision problem. The sequential decision problem can be represented using a Markov decision process (MDP). An MDP is defined by a list of components, which are described as follows:
- The state space corresponding to the set of all possible values of the states describing the environment with which the agent interacts;
- The action space corresponding to the set of all possible choices the agent can make to act on the environment;
- The transition dynamics characterizing the dynamics of the environment by giving the probability of obtaining a state at time knowing a state-action pair at time k;
- The reward function quantifying the desirability for the agent to perform action when the environment is in some state ;
- The discount factor determining the relative importance of future rewards compared to immediate ones, therefore influencing the agent’s consideration of long-term consequences when selecting an action to perform.
Remark 4.
When the transition dynamics are stochastic as described above, the state at time is a random variable following the probability distribution depending on the values at the time k of the state and the action . It is often denoted . When these transition dynamics are deterministic, there is only one possible value for the random variable with probability . To simplify the notations, such a case is often denoted .
The RL aims to solve the sequential decision problem described above by constructing a policy function that can be either stochastic or deterministic. This policy function corresponds to the probability for the agent to perform a given action at time k while being in a given state at the same time instant. In other words, it is defined such that for any and , we have, at time k, that . This policy defines the agent’s behavior so that, if the environment is in state at time k, the action is a random variable following the probability distribution , denoted by . The goal of RL is then to find the optimal policy achieving the maximum expected reward from all states,
where denotes the expected value of when the pair is sampled from the distribution of trajectories induced by a given policy .
Remark 5.
As is the case for the transition dynamics as presented in Remark 4, the policy can also be deterministic. In this case, there is only one possible value for the random variable with probability . To simplify the notations, such a case is often denoted .
It is worth highlighting that RL can be model-free or model-based depending on the use of a model of the environment (an approximation or the exact transition dynamics ) in the training process. While the algorithm discussed in the upcoming sections outlines an RL agent interacting with a model-based system, the agent itself is designed without direct access to the system’s model. Consequently, the agent’s implementation aligns with the model-free RL paradigm.
3.2.2. Twin Delayed Deep Deterministic Policy Gradient
As presented above, the overarching goal of RL is to find the policy maximizing the objective (12). Such a policy often has an intractable mathematical expression. For this reason, we often replace it by a neural network parameterized by a vector of real parameters that we denote by . One of the purposes of the RL research field is then to define algorithms allowing us to find the optimal vector of parameters such that .
One such algorithm is the TD3 [32]. It is an actor–critic algorithm for continuous action spaces aiming to find a deterministic policy represented by the neural network , also called the actor. Since the resulting policy is deterministic, we can adopt the notation of Remark 5 such that the action at time k is , with the state of the environment at time k. The critic is another neural network parameterized by a vector of real parameters denoted by , approximating the action-value function of the agent, that is the expected return when taking action in state . Like the policy, the true action-value function is often intractable for large MDPs. To maximize the objective (12) with the TD3 algorithm, a policy iteration, which is a method of alternating between policy evaluation and policy improvement within the actor–critic framework, is used.
In the policy evaluation step, the critic parameter vector is obtained by minimizing the Bellman error
where is a replay buffer of past experiences—triplets containing a state of the environment that the agent observed during its training—associated with the action it performed following its policy, and the subsequent environment’s state – and Y is the Bellman regression target defined, for any and , as
In TD3, two critic networks and , with and their respective vectors of parameters, are trained simultaneously using (13) by replacing by either or . To reduce overestimation bias, TD3 uses the minimum of the two Q-values to compute the Bellman regression target as
for both critics and .
In the policy improvement step, the actor parameter vector is updated to maximize the expected return according to the current critic estimates, that is, to maximize
3.2.3. Comparison of TD3 with Other Reinforcement Learning Algorithms
To show the efficacy of TD3 in optimizing the weighting factors in the MPC asymmetric decision function, we summarize a comprehensive qualitative analysis from the literature comparing TD3 with other state-of-the-art RL methods, such as deep deterministic policy gradient (DDPG) [37] and soft actor–critic (SAC) [38], in Table 4. TD3 provides a good trade-off between control performance, computational complexity, and stability, which is essential for real-time applications.

Table 4.
Qualitative comparison of RL algorithms for weighting factor tuning in MPC [37,38].
While SAC shows superior robustness and sample efficiency, its computational complexity and memory requirements during training and inference make it less effective for deployment in embedded systems. TD3, on the other hand, addresses the overestimation bias in DDPG and uses delayed policy updates and target smoothing to improve training stability without introducing significant complexity.
Furthermore, TD3 achieved faster convergence to optimal weights and demonstrated improved transient and steady-state performance compared to DDPG, while being computationally lighter than SAC. These qualities make TD3 particularly suitable for industrial motor control applications.
3.2.4. Problem Formulation
Based on what precedes, we propose a TD3-based method to train an RL agent to learn the best policy for tuning the weighting factors of the decision function (11). After training, the resulting actor network is then used in real-time to provide the weighting factors and in the control strategy of Figure 3.
To be able to apply the TD3 algorithm, some elements presented in Section 3.2.1 have to be reformulated in terms of the control objective of the paper. We mentioned that the goal of the RL agent’s policy is to provide the weighting factors to the predictive controller of Figure 3. It follows naturally that the action space is then where , , , and are as in Section 3.1, with the actions being and . The environment on which the RL agent acts is the structure Figure 3, except for the weighting factors, as they are defined to be the action of the RL agent. Finally, to describe the environment, a set of states has to be chosen. Numerous possibilities arise from the structure of Figure 3. However, as for the inputs of the MOGA-based neural network of Figure 4, the environment’s states were chosen by trial and error, resulting in
where is the instantaneous total harmonic distortion of the SPMSM’s phase a current , , with the phase a current reference obtained from and using the transforms (2) and (3), and , with the switching frequency reference for the VSI at time k and the switching frequency of the VSI at time k.
We see in the state vector the appearance of the switching frequency , its reference , and its error . This information might seem redundant as the error is directly obtained from the values of the switching frequency and its reference. However, the fact that the agent performs better by using the three input features at the same time might indicate that it is unable to infer their relationship by itself.
In addition, we see that the set of states, that is, the set of inputs to the neural network approximating the agent’s policy, is not the same as the one considered in Section 3.1. This is due to the trial and error performed to select the set of inputs for both methods and the learning strategies (supervised learning in Section 3.1 and DRL here), which are relatively sensitive to the information they receive in their input layer. However, we can see that they are related:
- The number of commutations of the VSI’s legs is directly linked to the switching frequency;
- The information contained in the q-axis current and its error is contained, at least partly, in the SPMSM’s phase a current, its error, and its harmonic distortion.
It therefore makes sense to compare the method of Section 3.1 and the proposed one, as the chosen set of inputs is the one giving the best performance for each strategy.
With the state space and the action space described (albeit implicitly in the case of ), one element remains to learn the weighting factor selection policy: the reward function. It plays a central role in guiding the agent’s learning process and influencing its behavior. It has to be designed in order for the resulting weighting factors to balance multiple objectives in the asymmetric decision function, including accurate current tracking, minimizing switching frequency, maintaining stability in control actions, and ensuring smooth control transitions. These different objectives can be split into three reward terms:
- The current tracking reward which incentivizes the SPMSM’s phase a current to follow its reference within a given tolerance margin and is expressed as
- The switching frequency reward ensuring that the switching frequency of the VSI follows its reference and is expressed as
- The specific goal reward increasing the reward if some specific performance thresholds are achieved, that is expressed as
and two penalty terms:
- The weighting factor variation penalty discourages rapid changes in the weighting factors’ values to increase stability and is expressed as
- The control unbalance penalty penalizing the gap between the values of the two weighting factors, having for expression
Combining these components results in the global reward function
to achieve the objectives mentioned above.
The content of Figure 6 is a rewriting of the structure of Figure 3, aiming to highlight the position of the RL agent and its interaction with the environment according to what we defined in this section.
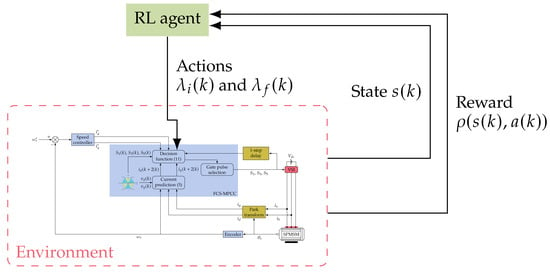
Figure 6.
Schematic representation of the interactions between the RL agent and its environment.
3.2.5. Learning Scheme
The proposed approach to train the RL agent with the TD3 algorithm is summarized in Algorithm 1. The algorithm’s inputs are three vectors of real parameters, , , and , used to parameterize the two critics and and the actor , the discount factor , and the structure of Figure 3 using the parameters from Table 3 for the environment’s simulation. We use two critic networks as presented in Section 3.2.2 to take advantage of the clipped double-Q learning trick [32], allowing us to reduce the overestimation bias by using the minimum of the two Q-values when updating the policy. From these initial parameters, we initialize two vectors and and use them to parameterize two target critic networks and . To stabilize the learning process, these target networks are updated slowly as a weighted average of the critic and target critic parameters and , with , through a hyperparameter as shown on line 20 of Algorithm 1. We finally initialize a set , the replay buffer, that is used to store past experiences. After training, the algorithm outputs are , , and , the optimized values of the parameter vectors , , and .
| Algorithm 1: TD3 training algorithm. |
 |
The learning scheme runs in an episodic fashion for a given number of episodes of time steps each. For each episode, the system, i.e., the SPMSM controlled in a rotation speed closed loop of Figure 3, starts with the same given initial conditions and parameters from Table 3. At each time step of the episode, the agent receives the current value of the state of the system and applies the action to the environment using the current value of the parameter vector . This action is used as the weighting factors of the FCS-MPCC decision function (11) so that the correct gating pulses can be selected to be applied to the VSI. Using them, the system evolves to the next time step. The resulting reward and next state are stored in the replay buffer as the 4-tuple .
This process is run as long as the number of 4-tuples in the replay buffer is below a given threshold . Whenever this threshold is reached, an update of the parameter vectors , , , , and is performed according to the procedure described in Section 3.2.2. The only difference that can be seen in Algorithm 1 is that the Bellman regression target and the actor loss are computed using the minimum of both target critics and . As explained before, this stabilizes the learning process. At the same time, the losses , , with , and are not directly calculated from the current values of the state and action as was presented in Section 3.2.2, but as an average of their values on past experiences to improve the learning process. This is accomplished by sampling tuples from the replay buffer into a so-called mini-batch . The gradients used to update , , and are calculated using deep deterministic policy gradient [37].
To summarize key elements of Section 3, Table 5 provides a qualitative comparison of the DRL method we propose with the MOGA-NN one on some crucial aspects for real-life implementation of the methods.

Table 5.
Qualitative comparison of DRL and MOGA-based ANN for weighting factor optimization in MPCC.
4. Test Results and Discussion
To verify the efficiency of the proposed data-driven weighting factor tuning approach, numerical simulations of varied motor operating conditions were run. The main objective of this work is to achieve high-performance control of PMSMs used in spindles or servo drive applications that are commonly used in industry. A comprehensive comparative study between a baseline MOGA-based neural network and a TD3-based DRL agent, detailed in Section 3, was performed using a laptop running Windows 11 with an Intel i7, 32 GB RAM, and an NVIDIA RTX 3000 GPU. The parameters used for the MOGA and training of the RL agent are presented in Table 6.

Table 6.
MOGA and TD3 learning parameters.
Using the learning strategy described in Section 3.2, the evolution of the cumulative reward obtained per episode and the average reward are presented in Figure 7. Although the reward is initially high, it shows notable fluctuations as a result of the agent’s exploratory behavior and early policy selection. These variations show the agent’s effort to learn from the dynamic system environment while balancing between switching transition reduction and current convergence. After episode 300, the agent has converged on an ideal tuning strategy, as the reward stabilizes with fewer oscillations. Both the per-episode cumulative reward and average reward become consistent, reflecting the successful learning of weighting factor adjustments for robust MPCC performance.
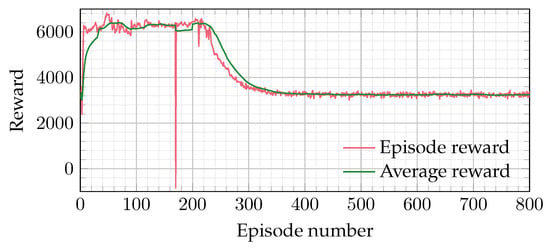
Figure 7.
Training process of TD3 agent.
We start by evaluating rotor speed, phase current, and torque responses of the drive motor during acceleration and deceleration at a constant load torque of , as presented in Figure 8. The results obtained with the DRL-based strategy show a significant improvement on the current response with respect to the MOGA-NN-based approach, with reduced harmonic content. Indeed, it can be seen on the phase current response using DRL of Figure 8b that the total harmonic distortion (THD) is of while it is of for the MOGA-NN in Figure 8a. Furthermore, torque ripple is observed to have a total amplitude higher with the MOGA-NN approach than with the DRL approach, which achieves smoother torque transitions.
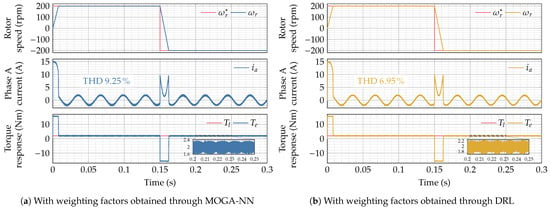
Figure 8.
Performance evaluation under a load torque during motor acceleration and deceleration.
We now consider a case where the rotor shaft speed is fixed at and a load variation from to is introduced at . We then study the same outputs as before, as presented in Figure 9. First, without even evaluating the THD, we can see in the phase current responses of Figure 9a,b that the phase currents obtained with the DRL approach present a reduced harmonic content with respect to the currents obtained through the MOGA-NN approach. In the same way, we see in Figure 9a,b that the rotation speed and electromagnetic torque responses obtained with the DRL approach present fewer ripples, even after load variation, than what we obtained with the other approach. It shows that the DRL approach achieves better current convergence and demonstrates enhanced robustness to system variations, ensuring smoother transitions and improved overall stability under dynamic load changes.
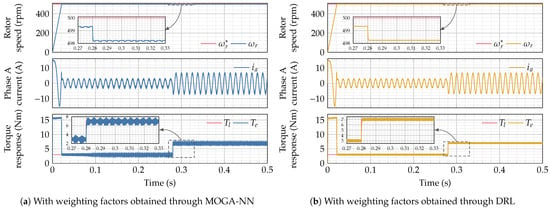
Figure 9.
Performance evaluation under load variation at a shaft speed of .
This conclusion is further emphasized by the results presented in Figure 10. In this case, the motor has a fixed shaft speed with different loads of , , , , , , , and applied sequentially at the respective times , , , , , , , and . As expected, the torque and current ripples obtained with the DRL approach have a constant and reduced amplitude compared to those obtained with the MOGA-NN approach. In addition, Figure 11 gives more information regarding the operation of the proposed control strategies. First, we see that the DRL-based approach reduces the number of switch transitions compared to the MOGA-NN method. Fewer switch transitions directly implies an overall lower switching frequency, which not only minimizes switching losses but also improves the overall efficiency and thermal performance of the inverter. This reduction in switching activity is critical for extending the lifespan of the power electronic components, making the DRL method more practical for long-term applications. Furthermore, the reduced current errors and in the DRL approach ensure better electromagnetic torque stability, reduced harmonic content, and overall improved dynamic and steady-state performance of the PMSM drive. We also see that the DRL-based approach demonstrates better consistency and adaptability in the values of the weighting factors and , maintaining a stable and optimal profile compared to the fluctuating and unstable adjustments of MOGA-NN. This stability enhances MPCC robustness, enabling reliable performance under dynamic conditions. Additionally, the DRL method adapts efficiently to system variations in real time, offering faster response times and better control performance compared to the static MOGA-NN approach.
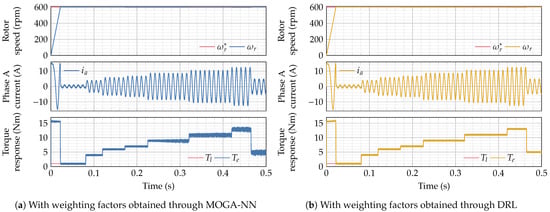
Figure 10.
Performance evaluation under different load variations at a shaft speed of .
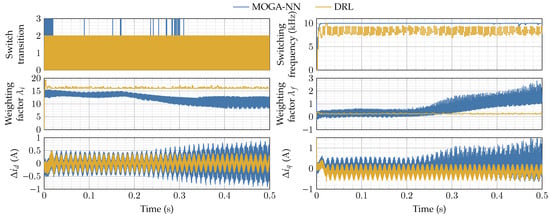
Figure 11.
Model predictive current controller performance under different load variations at a shaft speed of .
For the operation of electrical machines, it is also interesting to study what happens when the electrical parameters, that is, the stator resistance and inductance, do not match the values for which the controller is tuned. To this end, we first considered operations under nominal parameter values, and we then increased them by and of their nominal values with respect to their nominal values, as illustrated in Figure 12a. In addition, we considered operations under nominal parameter values, and we then decreased them by and of their nominal values with respect to their nominal values, as illustrated in Figure 12b. Once again, the results demonstrate the superiority of the proposed DRL-based weighting factor tuning approach. Indeed, the current and torque responses are more stable and present fewer ripples with the DRL approach than with the MOGA-NN approach. In addition, the MOGA-NN approach tends to be unstable for important mismatches in electrical parameters, as can be seen in Figure 12a.
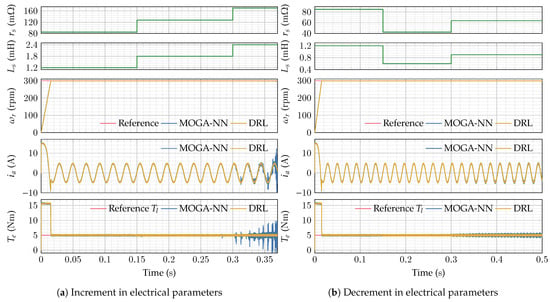
Figure 12.
Performance analysis for mismatched electrical parameters.
As in the previous case, Figure 13 gives more information regarding the operation of the proposed control strategies. The same overall behavior of the DRL and MOGA-NN approaches as the ones of Figure 11 can be observed. Indeed, the DRL approach gives fewer switch transitions and, as a consequence, a reduced switching frequency, except in the case of increased electrical parameter values. However, even in this last case, we observe a stable and consistent value for the weighting factors and reduced current errors and with the DRL approach, while the MOGA-NN approach exhibits unstable behaviors. These results therefore validate the proposed DRL approach as a superior solution for MPCC optimization, ensuring stable and efficient motor operation even in the presence of significant parameter variations. The proposed approach effectively handles the external disturbance and parametric variation due to its capability to explore and exploit under a wide range of operating conditions during training. By dynamically adapting the cost function weights, the controller maintains a balanced response between competing objectives such as current tracking accuracy and switching transition minimization, improving the overall performance of the control system.
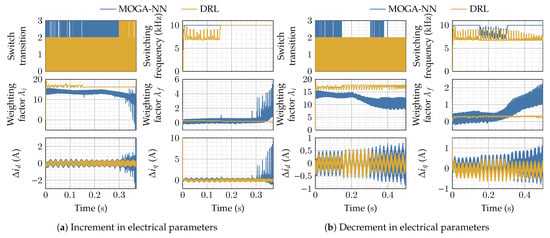
Figure 13.
Model predictive current controller performance under mismatched electrical parameters.
Finally, while maintaining a constant load and motor speed of and , respectively, we measured the instantaneous THD of the motor phase currents. Figure 14 presents the THD values at , , and . We can observe that the DRL-based controller achieves consistently lower THD compared to the MOGA-NN-based one as we obtain at the different time instants, respectively, , , and , while the MOGA-NN approach gives , , and . This reduction in THD showcases the DRL-based controller’s enhanced capacity to mitigate harmonics dynamically, contributing to improved drive performance and reduced harmonic distortion in varying operational conditions. The results once again affirm the effectiveness of the DRL approach in maintaining a cleaner current waveform, which is critical for robust and efficient motor operation.
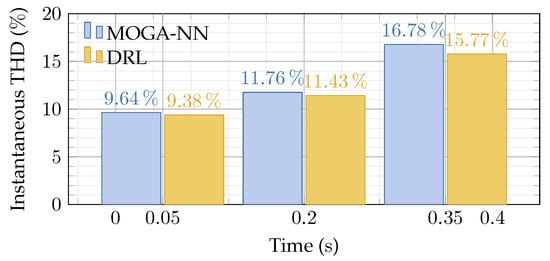
Figure 14.
Total harmonic distortion under a load of and shaft speed of .
5. Conclusions
This paper presents an online approach for tuning weighting factors in the finite control set model predictive current control of permanent magnet synchronous motor drive systems. The proposed method effectively tackles the challenge of designing weighting factors for asymmetric cost functions to achieve a balance among multiple control objectives inherent in traditional model predictive current control. By using a TD3-based deep reinforcement learning agent to choose the weighting factors online, we enable real-time tuning across various operating conditions and multiple objectives, ensuring optimal control performance. The method is specifically designed to optimize weighting factors for multi-objective system performance, allowing for efficient real-time adjustments to meet dynamic operational requirements. Comparative validation test results confirm the effectiveness of the proposed approach in determining optimal weighting factors for the asymmetric cost function.
Furthermore, the proposed TD3-based algorithm, by allowing online optimization of the weighting factors in an asymmetric cost function, effectively adapts to varying operating conditions without requiring manual tuning. However, due to the lack of a general theoretical framework to ensure the stability of RL algorithms, extensive validation remains essential prior to industrial deployment. The proposed DRL-based control strategy represents a significant step forward in intelligently addressing multiple conflicting objectives within the model predictive control framework. By learning to dynamically tune the weighting factors, the algorithm improves both steady-state and transient performance, demonstrated through reduced torque ripple, lower current harmonics, and smoother switching transitions. This intelligent weighting approach allows the control system to balance performance trade-offs more effectively than static or manually tuned approaches. The proposed design is capable of incorporating multiple additional objectives, such as voltage constraints and efficiency optimization, which will be key directions in future work. This enables the development of a more adaptive control strategy capable of maintaining optimal performance across a wide range of operating conditions.
Author Contributions
Conceptualization, M.U.; methodology, M.U.; validation, M.U.; writing—original draft preparation, M.U. and A.S.; writing—review and editing, M.U., A.S., T.C. and N.L.; supervision, T.C. and N.L.; funding acquisition, N.L. All authors have read and agreed to the submitted version of the manuscript.
Funding
This work was supported by ANR and Région Normandie through the HAISCoDe (ANR-20-THIA-0021) and PAMAP projects.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no competing interests.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial neural network |
| CCS | Continuous control set |
| DDPG | Deep deterministic policy gradient |
| DRL | Deep reinforcement learning |
| FCS | Finite control set |
| IAE | Integral absolute error |
| ISE | Integral squared error |
| ITAE | Integral time-weighted absolute error |
| ITSE | Integral time-weighted squared error |
| MOGA | Multi-objective genetic algorithm |
| MDP | Markov decision process |
| MPC | Model predictive control |
| MPCC | Model predictive current control |
| NN | Neural network |
| PI | Proportional–integral |
| PMSM | Permanent magnet synchronous motor |
| RL | Reinforcement learning |
| SAC | Soft Actor Critic |
| SMPC | Sequential model predictive control |
| SPMSM | Surface permanent magnet synchronous motor |
| TD3 | Twin Delayed Deep Deterministic Gradient |
| THD | Total harmonic distortion |
| VSI | Voltage source inverter |
References
- Nam, K.H. AC Motor Control and Electrical Vehicle Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Xu, W.; Ismail, M.M.; Islam, M.R. Permanent Magnet Synchronous Machines and Drives: Flux Weakening Advanced Control Techniques; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Bida, V.M.; Samokhvalov, D.V.; Al-Mahturi, F.S. PMSM vector control techniques–A survey. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering, Moscow, Russia, 29 January–1 February 2018; pp. 577–581. [Google Scholar]
- Yao, H.; Yan, Y.; Shi, T.; Zhang, G.; Wang, Z.; Xia, C. A novel SVPWM scheme for field-oriented vector-controlled PMSM drive system fed by cascaded H-bridge inverter. IEEE Trans. Power Electron. 2021, 36, 8988–9000. [Google Scholar] [CrossRef]
- Sun, X.; Diao, K.; Lei, G.; Guo, Y.; Zhu, J. Direct torque control based on a fast modeling method for a segmented-rotor switched reluctance motor in HEV application. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 232–241. [Google Scholar] [CrossRef]
- Yu, Z.; Long, J. Review on advanced model predictive control technologies for high-power converters and industrial drives. Electronics 2024, 13, 4969. [Google Scholar] [CrossRef]
- Mahmoud, H.; Mohamed, M.A.; Hassan, A.A.; Mossa, M.A. Optimal predictive voltage control of a wind driven five phase PMSG system feeding an isolated load. e-Prime Adv. Electr. Eng. Electron. Energy 2024, 9, 100697. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Kazmierkowski, M.P.; Rodríguez, J.; Kennel, R. Robust predictive control of three-level NPC back-to-back power converter PMSG wind turbine systems with revised predictions. IEEE Trans. Power Electron. 2018, 33, 9588–9598. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Li, H.; Zhang, Z. A model independent predictive control of PMSG wind turbine systems with a new mechanism to update variables. Energies 2023, 16, 3764. [Google Scholar] [CrossRef]
- Karimi, M.H.; Rostami, M.A.; Zamani, H. Continuous control set model predictive control for the optimal current control of permanent magnet synchronous motors. Control Eng. Pract. 2023, 138, 105590. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T. Guidelines for the design of finite control set model predictive controllers. IEEE Trans. Power Electron. 2020, 35, 7434–7450. [Google Scholar] [CrossRef]
- Tomlinson, M.; du Toit Mouton, H.; Kennel, R.; Stolze, P. A fixed switching frequency scheme for finite-control-set model predictive control – Concept and algorithm. IEEE Trans. Ind. Electron. 2016, 63, 7662–7670. [Google Scholar] [CrossRef]
- Xu, S.; Sun, Z.; Yao, C.; Zhang, H.; Hua, W.; Ma, G. Model predictive control with constant switching frequency for three-level T-type inverter-fed PMSM drives. IEEE Trans. Ind. Electron. 2022, 69, 8839–8850. [Google Scholar] [CrossRef]
- Mossa, M.A.; Mohamed, R.A.; Al-Sumaiti, A.S. Performance enhancement of a grid connected wind turbine-based PMSG using effective predictive control algorithm. IEEE Access 2025, 13, 64160–64185. [Google Scholar] [CrossRef]
- Usama, M.; Kim, J. Model-free current control solution employing intelligent control for enhanced motor drive performance. Sci. Rep. 2025, 15, 60. [Google Scholar] [CrossRef] [PubMed]
- Dragičević, T.; Novak, M. Weighting factor design in model predictive control of power electronic converters: An artificial neural network approach. IEEE Trans. Ind. Electron. 2019, 66, 8870–8880. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Babayomi, O.; Li, Z. Weighting factor design techniques for predictive control of power electronics and motor drives. Symmetry 2023, 15, 1219. [Google Scholar] [CrossRef]
- Cortes, P.; Kouro, S.; La Rocca, B.; Vargas, R.; Rodriguez, J.; Leon, J.I.; Vazquez, S.; Franquelo, L.G. Guidelines for weighting factors design in Model Predictive Control of power converters and drives. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, Australia, 10–13 February 2009. [Google Scholar]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F.; Elmorshedy, M.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest advances of model predictive control in electrical drives—Part II: Applications and benchmarking with classical control methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Caseiro, L.M.A.; Mendes, A.M.S.; Cruz, S.M.A. Dynamically weighted optimal switching vector model predictive control of power converters. IEEE Trans. Ind. Electron. 2019, 66, 1235–1245. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Shadmand, M.B.; Balog, R.S. Model predictive control of a voltage-source inverter with seamless transition between islanded and grid-connected operations. IEEE Trans. Ind. Electron. 2017, 64, 7906–7918. [Google Scholar] [CrossRef]
- Norambuena, M.; Rodriguez, J.; Zhang, Z.; Wang, F.; Garcia, C.; Kennel, R. A very simple strategy for high-quality performance of AC machines using model predictive control. IEEE Trans. Power Electron. 2019, 34, 794–800. [Google Scholar] [CrossRef]
- Zhang, J.; Li, L.; Norambuena, M.; Rodriguez, J.; Dorrell, D.G. Sequential model predictive control of direct matrix converter without weighting factors. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1477–1482. [Google Scholar]
- Arshad, M.H.; Abido, M.A.; Salem, A.; Elsayed, A.H. Weighting factors optimization of model predictive torque control of induction motor using NSGA-II with TOPSIS decision making. IEEE Access 2019, 7, 177595–177606. [Google Scholar] [CrossRef]
- Li, S.; Won, H.; Fu, X.; Fairbank, M.; Wunsch, D.C.; Alonso, E. Neural-network vector controller for permanent-magnet synchronous motor drives: Simulated and hardware-validated results. IEEE Trans. Cybern. 2020, 50, 3218–3230. [Google Scholar] [CrossRef]
- Fu, X.; Li, S. A novel neural network vector control technique for induction motor drive. IEEE Trans. Energy Convers. 2015, 30, 1428–1437. [Google Scholar] [CrossRef]
- Guazzelli, P.R.U.; de Andrade Pereira, W.C.; de Oliveira, C.M.R.; de Castro, A.G.; de Aguiar, M.L. Weighting factors optimization of predictive torque control of induction motor by multiobjective genetic algorithm. IEEE Trans. Power Electron. 2019, 34, 6628–6638. [Google Scholar] [CrossRef]
- Zanchetta, P. Heuristic multi-objective optimization for cost function weights selection in finite states model predictive control. In Proceedings of the 2011 Workshop on Predictive Control of Electrical Drives and Power Electronics, Munich, Germany, 14–15 October 2011; pp. 70–75. [Google Scholar]
- Villarroel, F.; Espinoza, J.R.; Rojas, C.A.; Rodriguez, J.; Rivera, M.; Sbarbaro, D. Multiobjective switching state selector for finite-states model predictive control based on fuzzy decision making in a matrix converter. IEEE Trans. Ind. Electron. 2013, 60, 589–599. [Google Scholar] [CrossRef]
- Novak, M.; Xie, H.; Dragicevic, T.; Wang, F.; Rodriguez, J.; Blaabjerg, F. Optimal cost function parameter design in predictive torque control (PTC) using artificial neural networks (ANN). IEEE Trans. Ind. Electron. 2021, 68, 7309–7319. [Google Scholar] [CrossRef]
- Vazquez, S.; Marino, D.; Zafra, E.; Peña, M.D.V.; Rodríguez-Andina, J.J.; Franquelo, L.G.; Manic, M. An artificial intelligence approach for real-time tuning of weighting factors in FCS-MPC for power converters. IEEE Trans. Ind. Electron. 2022, 69, 11987–11998. [Google Scholar] [CrossRef]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR: New York, NY, USA, 2018; pp. 1587–1596. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Atkinson, K.E. An Introduction to Numerical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Zhang, Y.; Xu, D.; Liu, J.; Gao, S.; Xu, W. Performance improvement of model-predictive current control of permanent magnet synchronous motor drives. IEEE Trans. Ind. Appl. 2017, 53, 3683–3695. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR: New York, NY, USA, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).