Abstract
Advanced Persistent Threats (APTs) challenge cybersecurity due to their stealthy, multi-stage nature. For the provenance graph based on fine-grained kernel logs, existing methods have difficulty distinguishing behavior boundaries and handling complex multi-entity dependencies, which exhibit high false positives in dynamic environments. To address this, we propose a Hypergraph Attention Network framework for APT detection. First, we employ anomaly node detection on provenance graphs constructed from kernel logs to select seed nodes, which serve as starting points for discovering overlapping behavioral communities via node aggregation. These communities are then encoded as hyperedges to construct a hypergraph that captures high-order interactions. By integrating hypergraph structural semantics with nodes and hyperedge dual attention mechanisms, our framework achieves robust APT detection by modeling complex behavioral dependencies. Experiments on DARPA and Unicorn show superior performance: 97.73% accuracy, 98.35% F1-score, and a 0.12% FPR. By bridging hypergraph theory and adaptive attention, the framework effectively models complex attack semantics, offering a robust solution for real-time APT detection.
1. Introduction
Nowadays, with the widespread application of digital technologies, APTs (Advanced Persistent Threats) pose a core challenge to the cybersecurity of enterprises, governments, and individuals through zero-day exploit utilization, customized malware, and multi-stage penetration strategies. Because it is characterized by high stealth and destructiveness, building a provenance graph based on kernel logs to detect and trace APTs has become mainstream. However, the provenance graph-based method still has many challenges in apt detection. Data-driven detection methods rely on prior attack patterns and struggle to identify new variants; the rule-driven detection methods lag behind the real-time update mechanisms, failing to adapt to the dynamically evolving structure of attack behaviors. Therefore, the method combining data and rules has become the mainstream of APT detection.
Moreover, traditional provenance graph methods are inherently limited by their edge structure, which fails to accurately characterize hierarchical behavioral patterns like interactions among processes, files, and networks [1,2,3]. As shown in Figure 1, attack techniques such as T1588 (Data Encrypted), T1588.002 (Abuse of Certificates), and T1490 (Indirect Communication) manifest as overlapping-node interaction networks in provenance graphs [4]. Traditional sub-graph discovery methods strictly partition node membership, leading to a loss of critical semantic information and severely degrading behavioral analysis accuracy, which leads to high false positive and negative rates. Additionally, the high computational complexity caused by large-scale log data further restricts the real-time detection applications of traditional graph analysis methods [5].
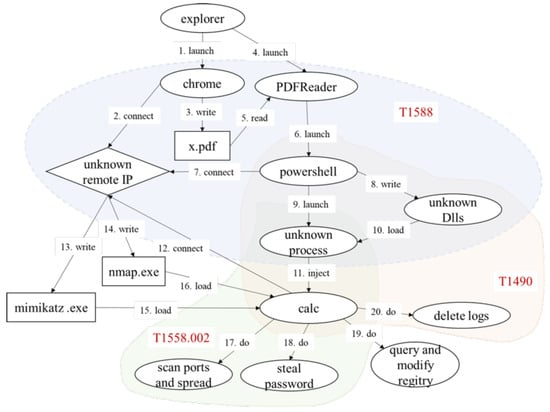
Figure 1.
Provenance graph of high-level technical and tactical behaviors.
As a generalized graph structure, hypergraphs offer a new path to overcoming these bottlenecks through their ability to connect multiple vertices via hyperedges [6]. A single hyperedge can naturally represent composite operations involving multiple entities (e.g., a process creating a file and initiating a network connection), and its hierarchical modeling capability can more accurately capture the high-order semantic correlations of attack behaviors. Transforming provenance graphs into hypergraphs for representation learning is expected to break through the expressive limitations of traditional models and improve the accuracy and efficiency of APT detection.
Nonetheless, hypergraph modeling and attack detection for kernel logs still face three core challenges:
- Behavior Boundary Division (C1): In the provenance graph, there is no clear boundary between which behavior a node or edge belongs to. Data-driven and rule-driven methods cannot accurately distinguish them, resulting in further aggravation of false positives and false negatives.
- High-level Behavioral Modeling (C2): Hyperedges need to integrate spatiotemporal features of multi-entity interactions like timestamps, process attributions, and network parameters, but existing methods cannot generalize complex behavioral patterns in dynamic contexts. Traditional rule matching and shallow machine learning struggle to capture deep correlations in cross-modal data.
- Heterogeneous Data Fusion (C3): Kernel logs contain multiple entity types (processes, files, registries, network sockets, etc.) which have interactive behaviors featuring heterogeneity and temporal dependencies. Designing targeted approaches to efficiently extract key features and map them into hyperedges remains necessary.
To tackle these challenges, we present an approach to APT detection via a Hypergraph Attention Network with community-based behavioral mining. For Challenge 1 (C1), we use the improved LFM algorithm [7] for overlapping community discovery to divide the behavior boundaries and generate different behavior subgraphs. For Challenge 2 (C2), we employ a hypergraph to represent behavioral communities, where a hyperedge denotes a behavioral pattern. For Challenge 3 (C3), we devise a two-layer attention mechanism: node-level attention to focus on key entities within hyperedges and edge-level attention to filter discriminative hyperedges, aiming at hypergraph representation learning and attack behavior detection. The main contributions of this paper are outlined as follows:
- 1
- This paper proposes a hypergraph construction method based on overlapping community discovery: by adapting LFM to the provenance graph to discover behavioral subgraphs, multi-dimensional features are integrated into weighted hyperedges, and high-order multi-entity behaviors are modeled, breaking through the limitations of traditional binary relationships in graphs.
- 2
- This paper improves the overlapping community detection algorithm to achieve more efficient behavioral community mining. Because of the instability of the starting point of overlapping community discovery, this paper selects the initial point of overlapping community discovery through an abnormal node detection method to avoid the high overhead and behavioral mining uncertainty caused by the randomness of community discovery.
- 3
- This paper proposes a HyperGAT model based on a dual attention mechanism: design node-level and edge-level attention mechanisms, focus on key entities and discriminative hyperedges, improve the accuracy of feature aggregation and attack behavior detection, and optimize the misjudgment rate to 0.12% through graph-level classification.
2. Related Works
2.1. Behavioral Community Mining Techniques
In the domain of behavioral community mining for cybersecurity, several studies have leveraged graph theory and community detection algorithms to model complex attack patterns.
HERCULE [8] formulates multi-stage intrusion analysis as a community detection problem, constructing dynamic community sequences from contaminated log entries (e.g., malware binary analysis or website blacklists) via global graph modeling. By building multi-dimensional weighted graphs to correlate lightweight log entries, this approach identifies “attack communities” through community detection, enabling structured representation of multi-phase attack behaviors. T-Trace [9] introduces a tensor decomposition-based method for log community detection, extracting key behavioral patterns via event saliency scoring. This technique identifies abnormal communities associated with APT attacks in provenance graphs, providing fine-grained support for attack tracing by quantifying temporal and causal relationships in log data. KAIROS [10] employs a novel GNN-based encoder–decoder architecture to model the temporal evolution of provenance graph structures, quantifying the anomaly degree of each system event. Community detection is then used to reconstruct attack footprints from fine-grained anomaly scores, generating compact summary graphs that accurately describe the temporal correlation of malicious activities. DEPCOMM [11] addresses the dependency explosion problem in large-scale logs by partitioning provenance graphs into process-centric communities, compressing redundant edges from insignificant or repetitive system activities. Analyzing inter-community information flows generates semantic summaries for each community, refining high-value behavioral patterns from dependency graphs to facilitate lightweight representation for subsequent detection.
However, these methods rely on rule-based or learning-driven strict community assignments, neglecting the overlapping semantic interactions where nodes may participate in multiple behavioral communities simultaneously. This oversight leads to higher false positives and negatives in complex attack scenarios, particularly when handling fine-grained kernel-level log semantics.
2.2. Graph-Based APT Attack Detection Methods
In APT detection, researchers have integrated log analysis, graph models, and machine learning to improve detection precision:
Sleuth [12] proposes a two-stage machine learning framework that identifies abnormal inter-cluster invocation patterns by analyzing the spatiotemporal correlations between program execution paths and system events, effectively detecting collaborative attacks across hosts. UNICORN [2] develops Unicorn, a real-time APT detection system that converts audit logs into provenance graphs and extracts temporal-causal features. Capable of detecting APTs without prior attack knowledge, Unicorn achieves high accuracy and low false positive rates by leveraging dynamic feature engineering. Holmes [13] constructs a real-time detection system based on the kill chain model, mapping low-level system events to high-level attack scenarios via a High-Level Scenario Graph (HSG). This semantic mapping enables effective identification of multi-stage attack chains by bridging technical details with tactical-level behaviors. Bhatt et al. [14] proposed a kill chain detection framework based on a layered architecture, which improves detection targeting by reducing the probability of cross-layer vulnerability reuse. However, this method relies on partial data and preset rules, and its generalization ability is limited in complex and dynamic network attack and defense environments, making it difficult to deal with new attack variants.
These studies provide a multi-layer solution for APT detection from log modeling to semantic enhancement, but there is still room for optimization in terms of heterogeneous data fusion, dynamic environment adaptability, and low resource consumption. The Hypergraph Attention Network proposed in this paper further enhances the modeling ability of high-order behavior associations through a node-edge bidirectional attention mechanism, making up for the shortcomings of traditional graph models in complex semantic representation.
In summary, existing APT detection methods face critical limitations in behavioral modeling and community analysis, including vague behavior boundary division where traditional graph methods rely on strict community partitioning and overlook nodes’ participation in overlapping multi-stage attack behaviors, leading to semantic information loss and high false positive rates. Additionally, binary edge-based graph models fail to represent composite operations involving multiple entities, making capturing high-order semantic correlations of attack behaviors difficult. Meanwhile, the spatiotemporal dependencies of multi-modal data in kernel logs are inadequately handled, and traditional rule-based matching or shallow learning cannot mine deep cross-modal correlations. Furthermore, the random seed selection in traditional community detection for large-scale log processing causes instability and high computational overhead, making it challenging to meet real-time detection requirements.
3. Preliminary
3.1. Provenance Graph
A provenance graph [15] is defined as , where the node set V denotes all system entities, and the edge set E represents all system events. Each edge signifies that a system entity u (termed the subject) performs an operation p on a system entity v (termed the object).
3.2. Hypergraph
A hypergraph [16] is defined as , where the node set V denotes all entities, and the hyperedge set H represents multi-variate relationships among entities. Each hyperedge signifies a complex interaction involving k nodes (), where the cardinality of h captures the order of the relationship. Hyperedges may be weighted (denoted by ) or labeled to encode additional semantic information about the interactions.
3.3. Threat Model
The threat model adopted in this paper is consistent with existing provenance graph-based APT detection research [1,17,18]. First, we assume the OS kernel and audit module maintain data integrity, ensuring provenance data provides a trustworthy foundation for analysis. Second, while attackers may use various strategies to execute APT attacks, their malicious activities are assumed to generate observable traces in audit logs.
We further assume kernel-level APT behaviors exhibit statistical regularities and semantic correlations amenable to quantitative and semantic modeling. Specifically, as Figure 1 shows, entity interaction patterns in APTs, such as multi-level associations among processes, files, and network entities—reveal latent behavioral dependencies through semantic analysis. These dependencies are aggregated into behavioral units encoding high-order attack semantics, a premise validated by prior works, including T-Trace [9] and Hercule [8].
4. System Overview
As shown in Figure 2, the proposed system comprises four core modules: provenance graph construction, abnormal behavioral community detection, hypergraph construction, and attack behaviors detection.
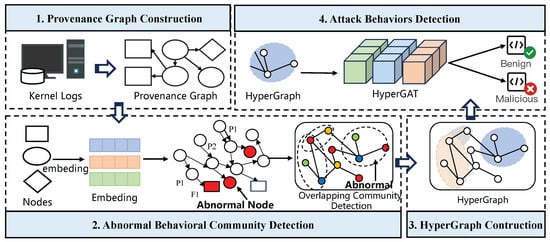
Figure 2.
Different Modules of the System.
Provenance Graph Construction. This module transforms kernel logs into a provenance graph, enabling subsequent context feature extraction and method implementation by modeling entities as nodes and their interactions as edges to capture behavioral dependencies and temporal sequences in audit data.
Abnormal Behavioral Community Detection. It first extracts multi-dimensional node attributes and uses GNNs to learn node representations for classifying abnormal nodes from benign ones. It then detects overlapping communities to model complex multi-entity interactions, leveraging an improved LFM algorithm that starts with abnormal nodes to cluster behaviors.
Hypergraph Construction. Nodes clustered into abnormal behavior communities serve as the basis for hyperedge construction, resulting hypergraph that captures high-order behavioral correlations that traditional binary graphs cannot represent, providing a rich semantic foundation for subsequent analysis.
Attack Behaviors Detection. We use a Hypergraph Attention Network to classify attack behaviors. Hyperedges in the hypergraph preserve detailed spatiotemporal and semantic features of entity interactions, which are processed through a two-layer attention mechanism with node-level and edge-level attention.
5. Provenance Graph Construction
During the first step, we use Kellect [19] to collect kernel logs and convert them into provenance graphs for analysis. In the graphs, nodes represent entities like processes, files, and network connections. Edges show entity interactions. Edge directions indicate operation flows, presenting system data and behavior relationships.
6. Abnormal Behavioral Community Detection
Based on the above analysis, APT attack behaviors exhibit structured patterns that can be modeled by aggregating entity interaction features. Entities involved in multiple behaviors require mining overlapping subgraphs in provenance graphs to capture cross-behavior correlations, for which overlapping community detection is well-suited [20].
The LFM algorithm is a classic method for overlapping community detection [7]. However, when applied to behavioral community detection in provenance graphs, its random initial node selection leads to unstable community partitions. This instability harms the reproducibility of detection results and the reliability of behavioral analysis, especially in scenarios requiring precise network structures for in-depth attack pattern mining.
To address this, we improve the LFM that overcomes these inherent flaws. We extract the node features and generate a vector with GNNs, and use classification methods to discover abnormal nodes. Then, we design a rule to assign weight to edges and calculate the fitness to discover behavior communities with the LFM algorithm. Here are the details of the method.
6.1. Seed Node Selection
The LFM first selects seed nodes as the initial nodes for community detection. The seed nodes of the traditional LFM are randomly selected, which directly affects the quality of community detection. Therefore, we use node-level detection to discover potential abnormal nodes first in the provenance graph as seed nodes.
Firstly, we extract the initial value of the feature for each node. The features of the node should reflect its behavior pattern in the provenance graph. Compared with benign nodes, abnormal nodes usually have different interaction patterns.
The nodes in the provenance graph are classified into four types (process, file, registry, and socket). Interactions between different types of nodes can form 18 types of edges, as shown in Table 1.

Table 1.
Different Types of Edges in Provenance Graph.
For each node in the provenance graph, a vector in 36-dimensional is created as the initial feature of , where the first 18 dimensions are the features of incoming edges, and the last 18 dimensions are the features of outgoing edges.
The first-order interaction pattern of nodes cannot capture the semantic causal relationship of the context, thus, it cannot be used for the judge of node states. Therefore, to learn the causal association of nodes, it is necessary to use a GNN to aggregate contextual information of each node to learn node features. Using the node type as a supervision signal, and classifying nodes into process, file, registry, or socket to train the GNN. The training formula is as follows:
GNN can be trained through multiple layers. At layer t, the node feature matrix is updated, where G is the topological structure of the provenance graph (usually represented by an adjacency matrix), is the trainable parameter matrix, and is the calculation result of the formula for layer .
On the provenance graph G, stack t GNN layers to learn the final feature matrix , and then input it into a softmax classifier to classify node types according to the following formula:
where P is the probability distribution of node type, is the parameter matrix of the classifier, and is the final feature matrix. The GNN is trained using gradient descent.
Given the initial feature matrix of the node in the provenance graph, input into the trained encoder GNN. The encoder will output the final feature matrix of the provenance graph.
After obtaining the final feature matrix of each node in the provenance graph, seed node detection is considered as an outlier mining problem. Here, the outlier mining algorithm Isolation forest is used to detect outliers in all process nodes in the provenance graph [21], and these abnormal outlier nodes are selected as seed nodes. This algorithm has been proven to be an effective outlier mining algorithm for detecting outlier nodes in the provenance graph.
6.2. Overlapping Behavioral Community Detection
Based on the abnormal seed nodes, we will then divide the overlapping behavior communities. As mentioned earlier, there are no clear boundaries for behaviors in the provenance graph. So, we set a series of weight rules, calculate the weight for each edge and each node in the provenance graph, and reconstruct the provenance graph into a weighted heterogeneous graph, and then divide behaviors through fitness calculation.
Assign a 21-dimensional feature vector, as shown in Table 2, and calculate the weights for each node in the provenance graph. The weight corresponding to a node is the sum of the values of all bits of the initial feature vector corresponding to the node.

Table 2.
Rules of 21-Dimensional Feature Vector.
For two vertices u and v connected by an edge, the explanations for different characteristics are as follows:
- : if and only if the time difference between u and v is less than the threshold t, where the threshold t can be customized by the user.
- : if and only if u and v have the same process id.
- : if and only if the destination IP of u and v are the same.
- : if and only if the ports of u and v are the same.
- to : if and only if the corresponding characteristics of u and v in the socket logs are the same.
- to : if and only if u and v are sibling processes or parent-child processes.
- : if and only if u and v access the same object.
- : if and only if u and v have the same process name.
- and : if and only if the outbound/inbound network requests are related to DNS queries.
- to : if and only if DNS query behaviors are related to web browsing behaviors.
Calculate the weight of each edge according to the above rules to obtain a set of edge weights. After obtaining the set of node weights and the set of edge weights, reconstruct the provenance graph, add weighted attributes to each node and each edge, and form the corresponding heterogeneous graph.
Based on the obtained weighted heterogeneous graph, the improved LFM algorithm is then used for overlapping community detection. Since the initial nodes of the algorithm have been obtained through anomaly node detection, the main idea of LFM is: based on the initial abnormal nodes, detect the natural community of node a, and remove a from the seed node set. Repeat the operation until all nodes are assigned to at least one group or the seed node set is empty, and then the detection algorithm is completed. The details are shown in Algorithm 1.
| Algorithm 1 Overlapping Behavioral Community Detection Algorithm |
Input:
Output:
|
In this algorithm, the relationship between nodes and natural communities is expressed by fitness. The algorithm process will be described in detail below. The meaning of the formulas used in the process is shown in Table 3.

Table 3.
Definitions of Fitness Calculation Formulas.
If a node a is selected as a community C, at this time, both the internal fitness and the external fitness of community C are 0. Firstly, select any neighbor node j (not including the nodes in community C) from the set of neighbor nodes of community C and add it to community C, and calculate the internal fitness and external fitness of community C at this time. The formula for internal fitness is as follows:
Among them, represents the internal fitness of the original community C, initially is 0; represents the internal fitness of community C after node j is added; represents the fitness of node j in community C, and the calculation formula is as follows:
The node i represents the node inside community C, represents the weight of the edge connecting node i and node j, and represents the weight of node j. This formula represents the sum of the products of the weights of all edges connected to node j inside the community and the weight of node j.
where u represents a node outside community C, denotes the weight of the edge connecting node u and node j, and is the weight of node u. This formula represents the sum of the products of the weights of all nodes outside the community connected to node j and the corresponding edge weights.
Secondly, evaluate the community quality using . If the value of increases, retain node j in the community; otherwise, remove j from the community and also remove j from the set of neighbor nodes of community C. The calculation formula for is as follows:
where is the community quality, is the internal fitness of community C after node j is added to community C, is the external fitness of community C after node j is added to community C, and is a positive real-valued parameter representing community resolution. Here, is taken as 1 because it is a comparison between the internal degree and the social area.
Thirdly, if the set of neighbor nodes of community C is not empty, repeat steps one and two; otherwise, obtain the community expanded from its neighbors by community C and the final quality of community .
Fourthly, if the community quality of community is equal to the community quality of community C, that is, no neighbor node of any community C is added to community C, end the algorithm. Otherwise, extract the set of neighbor nodes of community , and repeat steps one to four. If the set of neighbor nodes of community is empty, end the algorithm.
After the above algorithm ends, an expanded community G is obtained, which is called the community of node a. By iterating through the abnormal nodes and applying the aforementioned procedure to each, we ultimately derive the community set of abnormal behavioral patterns
7. Hypergraph Construction
In the set of behavioral communities, provenance graphs struggle to model high-order interactions between entity groups. We use hypergraphs, where hyperedges connect multiple nodes, to naturally represent these multi-variate relationships. Community detection identifies related entity groups, which are modeled as hyperedges to analyze group-level associations efficiently.
Specifically, define the community set as , where each community is a subset of the entity set E (i.e., ). For each community , a corresponding hyperedge is constructed in the hypergraph, with its node set given by . This mapping upgrades the representation from “entity-entity binary relationships” to “entity-group multi-variate relationships”, encapsulating the collective semantics of the community within a single hyperedge.
To further quantify the strength of the relationships represented by hyperedges, we introduce the concept of hyperedge weight . This weight is calculated using a specific formula to characterize the tightness or functional correlation among entities within the community, providing a quantitative basis for subsequent complex network analyses based on hypergraphs.
where represents the number of entities in community , and represents the metric value between entities. In this paper, the weight composed of features is used as the metric value.
Through the above definitions of nodes and hyperedges, the hypergraph constructed in this paper can be expressed as , where V is the set of nodes, is the set of hyperedges, and is the set of hyperedge weights. By constructing a hypergraph, the complex relationships in the provenance graph are represented by more expressive hyperedges, providing further high-level behavioral representations for subsequent attack detection.
8. Attack Behaviors Detection
8.1. HyperGAT
The GAT algorithm has been applied in graph machine learning and proven to have good effects [22]. To support hypergraph machine learning in the constructed hypergraph, this subsection applies the HyperGAT model, and the model architecture is shown in Figure 3. Differently from traditional GNN models, HyperGAT uses two aggregation functions to learn node representations so as to capture the heterogeneous high-order contextual information of behaviors among nodes on the behavior hypergraph. Among them, a HyperGAT layer can be defined as
where is the set of hyperedges connected to node , and is the representation of hyperedge in layer l. aggregates hyperedge features to nodes, and aggregates node features to hyperedges. In this paper, these two functions are implemented based on a dual-attention mechanism of node-level attention and edge-level attention.
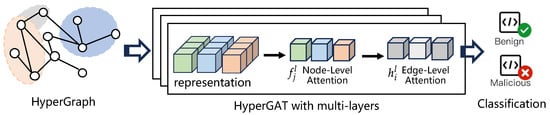
Figure 3.
The framework of HyperGAT.
8.2. Attention in HyperGAT
To effectively capture high-order semantic correlations in hypergraphs and enhance discriminative feature learning, HyperGAT constructs a hierarchical mechanism of node-level attention and edge-level attention, achieving multi-level semantic modeling of “entity-behavior-context” by focusing on key entities within hyperedges and filtering discriminative hyperedges across communities.
8.3. Node-Level Attention
Within a hyperedge , nodes contribute differently to the behavioral pattern (e.g., malicious process nodes carry higher weights for attack definitions). Node-level attention quantifies the relative importance of nodes within hyperedges to emphasize core entities. For the node set in hyperedge , the attention coefficient for node is defined as:
where is the feature representation of node at layer , is a node feature transformation matrix mapping raw features to the attention space, and is a node-level attention parameter vector quantifying the contribution of nodes to hyperedge semantics. After softmax normalization, node features are aggregated by attention coefficients to generate the semantic representation of hyperedge :
This operation strengthens the feature weights of critical nodes like abnormal processes, suspicious files and suppresses interference from redundant entities lile routine system files, enabling precise encoding of multi-entity interaction patterns within hyperedges.
8.4. Edge-Level Attention
A node is typically associated with multiple hyperedges, which differ in their discriminative contributions to node behavior (e.g., cross-community hyperedges are more likely to contain attack features). Edge-level attention filters discriminative hyperedges by measuring their semantic relevance to nodes. For the hyperedge set associated with node , the attention coefficient for hyperedge is calculated as
where is the feature representation of hyperedge at layer l, is the historical feature of node denotes feature concatenation, is a cross-modal feature fusion matrix mapping hyperedge and node features to a joint semantic space, and is an edge-level attention parameter vector measuring the importance of hyperedges to node semantics. Node representations are updated by aggregating hyperedge features based on attention coefficients:
where is the Sigmoid activation function. This mechanism prioritizes feature propagation from cross-community hyperedges involving abnormal network connections like unknown remote IP communications or sensitive registry operations like permission modifications, suppressing interference from routine system behavior hyperedges and enhancing the semantic discrimination ability of node representations for attack patterns.
8.5. Behavior Detection
For each hyperedge, after L HyperGAT layers, all node representations on the constructed hypergraph can be calculated. Then, an average pooling operation is applied to the learned node representations to obtain the behavior representation z, and it is input into a softmax layer for behavior representation classification, which can be formally expressed as:
where is a parameter matrix that maps the provenance graph behavior representation to the output space, is the bias term. represents the predicted behavior representation classification score. In particular, the loss function for provenance graph behavior representation classification is defined as binary cross-entropy loss:
Here, y is the result, is the predicted probability of being benign. Therefore, HyperGAT can be trained by minimizing the above loss function on all labeled provenance graphs.
9. Evaluation
This paper implements this method in Python 3.8. The graph data are constructed using the graph processing library networkx and stored in the format of JSON and triples <subject, behavior, object>. Among them, LFM is implemented in native Python. HyperGAT is implemented by PyTorch which is 2.6.0 of version. Based on the prior research in [6,23], the Hypergraph Attention Network consists of 2 layers with 300 and 100 embedding dimensions. We also apply the dropout mechanism and set the dropout rate to 0.5. We update the model parameters using the Adam algorithm, with a learning rate set to 0.0005 and a batch size of 32. And this part of the core codes is available at https://github.com/SongQijie/APTHyperGAT (accessed on 18 May 2025).
Among them, the experimental host environment includes Windows 10 Professional Workstation version, equipped with an Intel i5-10400 processor (2.9GHz, 6 cores, 32GB memory). The operating system version is 21H2. The training environment is equipped with an Intel Xeon Gold 5218 processor (2.30GHz, 16 cores, 128GB memory), the graphics card is NVIDIA RTX 4090, and the operating system is Ubuntu 20.04.
9.1. Dataset
The Unicorn Wget [2] dataset detailed in Table 4 includes simulated attacks generated by the Unicorn framework, comprising 150 log batches collected via Camflow. Of these, 125 batches are benign, and 25 contain supply chain attacks designed to mimic legitimate system workflows, classified as stealth attacks due to their ability to evade detection by emulating benign behavior. This dataset is the most challenging among the experimental datasets herein, attributed to its large volume, complex log structure, and the stealthy nature of embedded attacks.

Table 4.
Details of the Dataset.
The DARPA Engagement 3 (E3) dataset was collected in enterprise network environments during adversarial engagements as part of the DARPA Transparent Computing Program. It captures Red Team operations exploiting diverse vulnerabilities to execute Advanced Persistent Threat (APT) attacks for sensitive data exfiltration, alongside Blue Team efforts to identify these attacks through network host auditing and causal analysis.
9.2. Abnormal Nodes Detection
In this experiment, we evaluate the detection effect of abnormal nodes by comparing it with two SOTA models.
(1) StreamSpot [24]: It is a clustering-based anomaly detector. It abstracts the provenance graph into a vector based on the relative frequency of local substructures and detects abnormal provenance graphs through a clustering algorithm. To detect abnormal nodes, the second-order local graph of the node is used as input.
(2) ThreaTrace [25]: It is a prediction-based anomaly detector. It learns a representation of each benign system entity in a provenance graph and detects abnormal nodes based on the deviation of the predicted node type from its actual type.
This experiment uses the Unicorn dataset. In this experiment, since it is assumed that there are no abnormal nodes in the benign samples, based on relevant experience in network security and discussions with experts, some nodes suspected to be unsafe were selected from the benign samples, labeled, and then the experiment was conducted. The experimental results are shown in Table 5.

Table 5.
Comparison of Related Work on Abnormal Nodes Detection.
ThreaTrace’s performance is significantly better than StreamSpot [24]. This is because ThreaTrace uses GNNs to learn node representations in a self-supervised manner, while ThreaTrace outlines the provenance graph in an unsupervised way. Supervised signals can better optimize the representation model. But overall, our method performs well in terms of recall, F1-score, FPR, and AUC, and achieves the best results.
9.3. Ablation Experiment
In the first experiment, we compared attention-based network models similar to the hypergraph attention mechanism. In the “w/o attention” operation, convolutional operations were used to replace the node-level and edge-level attention mechanisms. In the “w/o behavior semantic” operation, the adaptability calculation for overlapping communities was based on the in-degree and out-degree of nodes to construct the hypergraph. In the experiment, we also added GCN and GAT as baseline methods for comparison.
The experimental results are shown in Table 6. The experiment was conducted on the Theia and Cadets datasets. The provenance graph contains the host’s behavior features, which are crucial for accurate classification.

Table 6.
Comparison of Ablation Results.
HyperGAT significantly outperforms the other four experimental groups. It achieved accuracy scores of 0.9773 ± 0.0018 on the Theia dataset and 0.9253 ± 0.0006 on the Cadets dataset, far surpassing “w/o attention” and “w/o behavior semantic”, which demonstrates its distinct advantage in handling hypergraph classification tasks.
Further analysis reveals the pivotal roles of the attention mechanism and the constructed hypergraph’s semantic information in the recognition process. HyperGAT’s unique dual-attention mechanism enables it to learn features of nodes and edges within hyperedges, thus better capturing node relationships and behavior patterns for accurate behavior recognition. Meanwhile, graph contextual semantics help the model understand the position and meaning of nodes and edges in the overall graph structure, further improving classification accuracy.
Also, false positives (FPRs) are crucial in graph-level detection tasks. Experimental results show HyperGAT has low FPRs of 0.0012 ± 0.0010 on Theia and 0.0016 ± 0.0011 on Cadets, rarely misclassifying negative instances and effectively controlling false positives. In contrast, “w/o attention” and “w/o behavior semantic” have higher FPRs, being more prone to misjudging positive and negative instances. The lower FPR makes HyperGAT more reliable and practical in real-world applications, delivering more accurate results for provenance graph classification.
9.4. Runtime Overhead
The performance of runtime overhead is shown in Table 7. In this experiment, we repeated the experiment and took the average value as the experimental result. Each stage’s time consumption and memory usage reflect the differences in the complexity of different operations and resource requirements.

Table 7.
The Result of Performance Overhead.
The overlapping community detection stage consumes less time and memory because this stage mainly performs a preliminary analysis of data based on relatively simple algorithms and does not involve complex model training. In this stage, only some basic features in the data are extracted and a preliminary community division is carried out, without the need to handle a large number of parameters and complex calculations like in subsequent stages.
During training, the process takes 1285 s and uses 2.71 GB of memory, mainly due to the hypergraph-based dual-attention mechanism. Hypergraphs effectively model high-order relationships and complex structures, where node-level attention highlights critical nodes and edge-level attention emphasizes key hyperedges. The mechanism’s complex computations on numerous nodes/edges for importance weights, combined with parameter optimization and large-scale dataset iterations, drive resource consumption.
During testing, it takes 875 s with memory usage rising to 3.87 GB. Despite no parameter updates, the model’s complexity and hypergraph structure require complex inference computations, including loading trained parameters, processing input data, and generating predictions.
Notably, the dataset was collected over 24 h. For shorter data collection windows like sub-hourly snapshots, the volume of data is correspondingly smaller. In such scenarios, the method’s computational overhead decreases significantly due to the reduced scale of input data.
We conducted a sustained overhead experiment, as shown in Figure 4. The malicious node detection system maintains low CPU usage with 14% and memory with 0.9 GB in the idle state, but CPU usage rises to 43% and memory to 3.87 GB during testing, and we found there is a slight rise in memory. This is due to storing behavior community hypergraphs for inference. However, as malicious behaviors are rare in large datasets, the memory increase remains minimal.
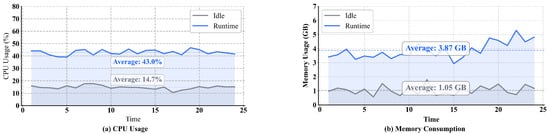
Figure 4.
Runtime overhead.
In the comparison of overhead with the latest work, we select the recent works of Magic and Prographer for comparison. Under the same laboratory environment, the memory and execution time during the testing phase are compared. The experimental results are shown in Table 8. Prographer’s time consumption is only 164 s, far less than the other two. Because it stores snapshots in memory for fast retrieval, it leads to a larger memory footprint, and as the data volume increases, the memory usage continues to rise. Magic’s time consumption is the largest among the three, as it needs to perform compression, feature mining, and representation during graph processing, while its memory usage is comparable to this work. Overall, although this work’s time consumption is not the least, compared with Prographer’s memory overhead and Magic’s time consumption, it has more practical overhead characteristics.

Table 8.
Comparing the overhead with related work.
10. Conclusions and Future Work
10.1. Conclusions
This paper introduces an APT attack detection framework based on hypergraph representation learning, addressing traditional methods’ limitations in modeling complex attack patterns. By enhancing community detection, constructing behavioral hypergraphs, and using the HyperGAT model with dual attention, the approach effectively captures hierarchical system interactions. Experimental results show superior accuracy, F1-score, and false positive control, establishing its potential for detecting stealthy APT attacks.
10.2. Future Work
Future research will focus on three key directions to improve practicality and scalability. First, develop specialized methods for high-order behavior mining in hypergraphs to detect complex attack patterns by modeling hyperedge-level dependencies. Second, optimize hypergraph construction through automated log processing and heterogeneous data integration, reducing manual effort and enhancing structural mapping efficiency. Third, reduce computational overhead via algorithmic optimizations like sparse representations and approximate attention to enable deployment in resource-constrained environments. Balancing performance and detection accuracy will be critical, ensuring the method adapts to diverse security scenarios. These advancements aim to bridge theory and practice, strengthening this method’s role in robust APT defense systems and finally applying it in the real world.
Author Contributions
Methodology, Q.S. and T.C.; Software, M.L. and X.Q.; Validation, T.Z.; Investigation, T.Z.; Resources, T.C. and Z.Z.; Data curation, M.L.; Writing—original draft, Q.S.; Funding acquisition, T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the “Pioneer” and “Leading Goose” R&D Program of Zhejiang under Grant No. 2025C01082; National Natural Science Foundation of China under Grant No. 62002324, U22B2028, and U1936215.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rehman, M.U.; Ahmadi, H.; Hassan, W.U. Flash: A comprehensive approach to intrusion detection via provenance graph representation learning. In Proceedings of the 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 3552–3570. [Google Scholar]
- Han, X.; Pasquier, T.; Bates, A.; Mickens, J.; Seltzer, M. Unicorn: Runtime provenance-based detector for advanced persistent threats. arXiv 2020, arXiv:2001.01525. [Google Scholar]
- Jia, Z.; Xiong, Y.; Nan, Y.; Zhang, Y.; Zhao, J.; Wen, M. MAGIC: Detecting advanced persistent threats via masked graph representation learning. In Proceedings of the 33rd USENIX Security Symposium (USENIX Security 24), Philadelphia, PA, USA, 14–16 August 2024; pp. 5197–5214. [Google Scholar]
- Xiong, W.; Legrand, E.; Åberg, O.; Lagerström, R. Cyber security threat modeling based on the MITRE Enterprise ATT&CK Matrix. Softw. Syst. Model. 2022, 21, 157–177. [Google Scholar]
- Lv, M.; Gao, H.; Qiu, X.; Chen, T.; Zhu, T.; Chen, J.; Ji, S. TREC: APT tactic/technique recognition via few-shot provenance subgraph learning. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Copenhagen, Denmark, 26–30 November 2024; pp. 139–152. [Google Scholar]
- Jia, J.; Yang, L.; Wang, Y.; Sang, A. Hyper attack graph: Constructing a hypergraph for cyber threat intelligence analysis. Comput. Secur. 2025, 149, 104194. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z. A Fast Method of Detecting Overlapping Community in Network Based on LFM. J. Softw. 2015, 10, 825–834. [Google Scholar] [CrossRef][Green Version]
- Pei, K.; Gu, Z.; Saltaformaggio, B.; Ma, S.; Wang, F.; Zhang, Z.; Si, L.; Zhang, X.; Xu, D. Hercule: Attack story reconstruction via community discovery on correlated log graph. In Proceedings of the 32nd Annual Conference on Computer Security Applications, Los Angeles, CA, USA, 5–9 December 2016; pp. 583–595. [Google Scholar]
- Li, T.; Liu, X.; Qiao, W.; Zhu, X.; Shen, Y.; Ma, J. T-Trace: Constructing the APTs Provenance Graphs Through Multiple Syslogs Correlation. IEEE Trans. Dependable Secur. Comput. 2024, 21, 1179–1195. [Google Scholar] [CrossRef]
- Cheng, Z.; Lv, Q.; Liang, J.; Wang, Y.; Sun, D.; Pasquier, T.; Han, X. Kairos: Practical intrusion detection and investigation using whole-system provenance. In Proceedings of the 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 3533–3551. [Google Scholar]
- Xu, Z.; Fang, P.; Liu, C.; Xiao, X.; Wen, Y.; Meng, D. Depcomm: Graph summarization on system audit logs for attack investigation. In Proceedings of the 2022 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–26 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 540–557. [Google Scholar]
- Hossain, M.N.; Milajerdi, S.M.; Wang, J.; Eshete, B.; Gjomemo, R.; Sekar, R.; Stoller, S.; Venkatakrishnan, V. SLEUTH: Real-time attack scenario reconstruction from COTS audit data. In Proceedings of the 26th USENIX Security Symposium (USENIX Security 17), Vancouver, BC, Canada, 16–18 August 2017; pp. 487–504. [Google Scholar]
- Milajerdi, S.M.; Gjomemo, R.; Eshete, B.; Sekar, R.; Venkatakrishnan, V. Holmes: Real-time apt detection through correlation of suspicious information flows. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1137–1152. [Google Scholar]
- Bhatt, P.; Yano, E.T.; Gustavsson, P. Towards a framework to detect multi-stage advanced persistent threats attacks. In Proceedings of the 2014 IEEE 8th International Symposium on Service Oriented System Engineering, Oxford, UK, 7–11 April 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 390–395. [Google Scholar]
- Li, Z.; Chen, Q.A.; Yang, R.; Chen, Y.; Ruan, W. Threat detection and investigation with system-level provenance graphs: A survey. Comput. Secur. 2021, 106, 102282. [Google Scholar] [CrossRef]
- Bretto, A. Hypergraph theory. In An Introduction. Mathematical Engineering; Springer: Cham, Switzerland, 2013; Volume 1, pp. 209–216. [Google Scholar]
- Hassan, W.U.; Guo, S.; Li, D.; Chen, Z.; Jee, K.; Li, Z.; Bates, A. Nodoze: Combatting threat alert fatigue with automated provenance triage. In Proceedings of the Network and Distributed Systems Security Symposium, San Diego, CA, USA, 24–27 February 2019. [Google Scholar]
- Li, S.; Dong, F.; Xiao, X.; Wang, H.; Shao, F.; Chen, J.; Guo, Y.; Chen, X.; Li, D. Nodlink: An online system for fine-grained apt attack detection and investigation. arXiv 2023, arXiv:2311.02331. [Google Scholar]
- Chen, T.; Song, Q.; Zhu, T.; Qiu, X.; Zhu, Z.; Lv, M. Kellect: A Kernel-based efficient and lossless event log collector for windows security. Comput. Secur. 2025, 150, 104203. [Google Scholar] [CrossRef]
- Xie, J.; Kelley, S.; Szymanski, B.K. Overlapping community detection in networks: The state-of-the-art and comparative study. ACM Comput. Surv. (CSUR) 2013, 45, 1–35. [Google Scholar] [CrossRef]
- Djidjev, C. siForest: Detecting Network Anomalies with Set-Structured Isolation Forest. arXiv 2024, arXiv:2412.06015. [Google Scholar]
- Yan, N.; Wen, Y.; Chen, L.; Wu, Y.; Zhang, B.; Wang, Z.; Meng, D. Deepro: Provenance-based APT campaigns detection via GNN. In Proceedings of the 2022 IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Wuhan, China, 9–11 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 747–758. [Google Scholar]
- Ding, K.; Wang, J.; Li, J.; Li, D.; Liu, H. Be More with Less: Hypergraph Attention Networks for Inductive Text Classification. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; Webber, B., Cohn, T., He, Y., Liu, Y., Eds.; pp. 4927–4936. [Google Scholar]
- Manzoor, E.; Milajerdi, S.M.; Akoglu, L. Fast memory-efficient anomaly detection in streaming heterogeneous graphs. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1035–1044. [Google Scholar]
- Wang, S.; Wang, Z.; Zhou, T.; Sun, H.; Yin, X.; Han, D.; Zhang, H.; Shi, X.; Yang, J. Threatrace: Detecting and tracing host-based threats in node level through provenance graph learning. IEEE Trans. Inf. Forensics Secur. 2022, 17, 3972–3987. [Google Scholar] [CrossRef]
- Yang, F.; Xu, J.; Xiong, C.; Li, Z.; Zhang, K. PROGRAPHER: An anomaly detection system based on provenance graph embedding. In Proceedings of the 32nd USENIX Security Symposium (USENIX Security 23), Anaheim, CA, USA, 9–11 August 2023; pp. 4355–4372. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).