Explainable Two-Layer Mode Machine Learning Method for Hyperspectral Image Classification

Abstract

Explainable machine learning methods with a specific mathematical model provide insights into how the model works. We propose a new mode that contains a two-layer architecture for hyperspectral image (HSI) classification. In the front-end learning layer, superpixel segmentation and mathematical models are combined to achieve the band selection, which obtains the data re-expression in a lower dimension. The mathematical model uses the $l_{\mathrm{2,1}}$ norm and graph regularized term, which helps induce sparsity, improve robustness to outliers and noise, and enhance the explainability of the data re-expression. We employ the support vector machine or the K-nearest neighbor algorithms in the back-end layer to classify low-dimensional data. Finally, the two-layer mode classification method is applied to the three real HSI dataset classifications. Numerical results show that the overall classification accuracy of our method is improved.

1. Introduction

Hyperspectral images (HSIs) are obtained through an imaging spectrometer with hundreds of continuous spectral bands, and they integrate spectral and image information. They have multi-band and high spectral resolution characteristics [1]. Hyperspectral technology has become an effective tool for remote sensing applications, recognizing and learning multidimensional information from hyperspectral images to achieve corresponding research goals [2]. HSI classification has been used in agriculture for crop identification and health monitoring [3], environmental protection for land cover mapping [4], and water quality assessment [5]. In practical applications, the multi-band characteristics of hyperspectral remote sensing data enable a more comprehensive description of the reflection characteristics of ground objects and have a strong ability to identify ground object attributes [6]. However, the large amount of redundant information in the data can lead to high computational complexity, which is not conducive to subsequent image analysis and weakens the classifier’s generalization ability [7]. The curse of dimensionality and the Hughes phenomenon affect classification performance [8].

In recent years, HSI classification research has made significant progress [9]. Traditional machine learning methods, such as support vector machine (SVM) [10] and random forest [11], effectively handle high-dimensional spectral data by leveraging the unique spectral signatures of materials. However, these methods often struggle with capturing complex spatial–spectral relationships in HSI data, which led to the exploration of more advanced techniques.

With the advent of deep learning, convolutional neural networks (CNNs) emerged as a powerful tool for HSI classification. CNNs can automatically extract features from spectral and spatial dimensions of HSI data, significantly improving classification accuracy [12]. For example, 3D-CNNs have been particularly effective in capturing spatial–spectral information by applying convolutional operations across both dimensions. Also, hybrid models that combine CNNs with other architectures, such as recurrent neural networks (RNNs) or graph neural networks (GNNs) [9], have been developed to enhance performance. Due to their ability to handle non-Euclidean data and capture complex relationships between pixels, GNNs perform well.

The decision-making process of deep learning models remains a black box, making it challenging to understand how and why certain classifications are made [13]. Explainable artificial intelligence (EXI) methods [14,15] address this issue by providing interpretability to complex models.

Developing EXI methods based on integrating deep learning and mathematical models can help analyze the model’s decision-making basis and further optimize its performance. The HSI classification methods are divided into two categories: one is the end-to-end learning approach, for example, using deep learning algorithms [16,17,18,19,20,21] to directly train models from input data to classification results; another type has the characteristics of two-layer mode [22,23,24,25,26,27], which completes the data representation through front-end learning and then uses classifiers to determine the classification model in back-end learning.

A new two-layer mode machine learning method for HSI classification is proposed in this paper, which is shown in Figure 1.The classification method contains two layers: the front-end learning layer and the back-end learning layer. The former layer achieves HSI re-expression, which combines superpixel segmentation technology and a regularized subspace clustering method for band selection. The latter layer uses SVM or K-nearest neighbor (KNN) classification algorithms to classify the re-expressed HSI data. Finally, the evaluation metrics from the back-end learning help adjust the number of bands in the front-end learning layer.

To sum up, our main contributions are as follows. First, a two-layer mode machine learning method for HSI classification is proposed, combining the data re-expression and classification layers. Second, entropy-rate superpixel segmentation is used to reduce the impact of homogeneity and heterogeneity caused by different geographical locations. Third, an explainable mathematical model employs the $l_{\mathrm{2,1}}$ norm, the graph regulation term, which maintains the robustness and inherent geometric local structure of HSI data. Fourth, numerical comparison on three HSI data sets, i.e., TeaFarm, Salinas, and Indian Pines datasets, with the existing HSI classification methods indicate that the proposed method works well.

2. Band Selection with Sparse Space Clustering

This section summarizes the classical Sparse Space Clustering (SSC) method [28,29] for hyperspectral data analysis given the HSI dataset $H\in {\mathbb{R}}^{m\times n\times b}$, where $m,n$, and $b$ denote the width, height, and the number of bands, respectively. We reshape the original HSI cube $H$ into matrix form $X$, where $X=(x_1,x_2,\dots ,x_b)\in {\mathbb{R}}^{mn\times b}$. The SSC method assumes that all bands (i.e., band vectors) of the $X$ lie in a union of low-dimensional subspace, and a linear or affine combination of several bands can represent every band vectors. Accordingly, each band vector $x_i\in {\mathbb{R}}^{mn}, i=\mathrm{1,2}, ...,b$ can be represented as

$$x_i=z_{1i}{x}_1+z_{2i}{x}_2+\dots +z_{bi}{x}_b,$$

(1)

where $z_{ij}$ in (1) is the $ij$ th element of matrix $Z\in {\mathbb{R}}^{b\times b}$. It should be noted that $x_i$ cannot be represented by itself, which indicates that $z_{ii}=0, i=\mathrm{1,2},...b$.

We combine $b$ band vectors into a matrix format so that (1) can be organized as

$$X=XZ, diag\left(Z\right)=0,$$

(2)

where $Z$ is the coefficient matrix of all band vectors and $diag\left(Z\right)$ denotes the diagonal vector of matrix $Z$. By minimizing the following optimization Problem (3), the solution of (2) can be found [29].

$$\widehat{Z}=argmin{‖Z‖}_q^2 \mathrm{s}.\mathrm{t}. \mathrm{X} = \mathrm{XZ}, \mathrm{diag}(\mathrm{Z}) = 0.$$

(3)

where ${‖Z‖}_q$ represents the $l_q$ norm of $Z$, which is defined as ${‖Z‖}_q={\left(\sum _{i=1}^b\sum _{j=1}^b{\left|z_{ij}\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}$. For $q=0$, the $l_0$ norm counts the number of nonzero elements of $Z$, and it helps to maintain sparse property of $Z$. The $l_1$ norm is usually considered as a relaxation $l_0$ norm.

Then, the sparse matrix $\widehat{Z}$ is used to construct the similarity matrix $W$, that is, $W=(\widehat{Z}+{\widehat{Z}}^T)/2$. With $W$, the spectral clustering method [30] clusters all band vectors into their underlying subspaces.

We convert the band selection problem into the general form

$$\mathit{min}{‖X-XZ‖}_q^2+\lambda J\left(Z\right)$$

(4)

where $J(·)$ represents the regularized term and $\lambda >0$ is a regularized parameter. The regularized term $J\left(Z\right)$ can depend on certain properties of the data, such as geometrical information and physical meaning [22].

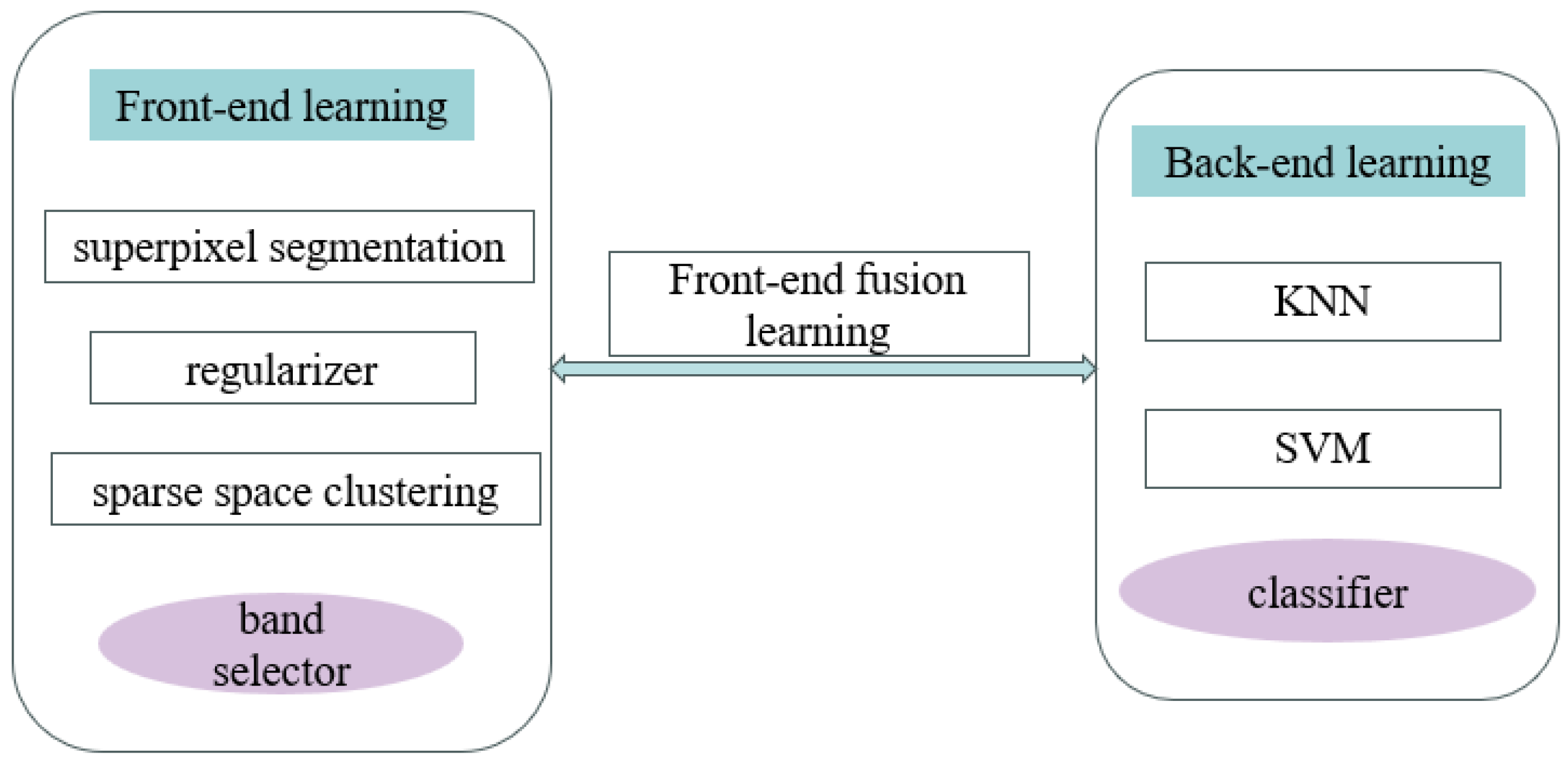
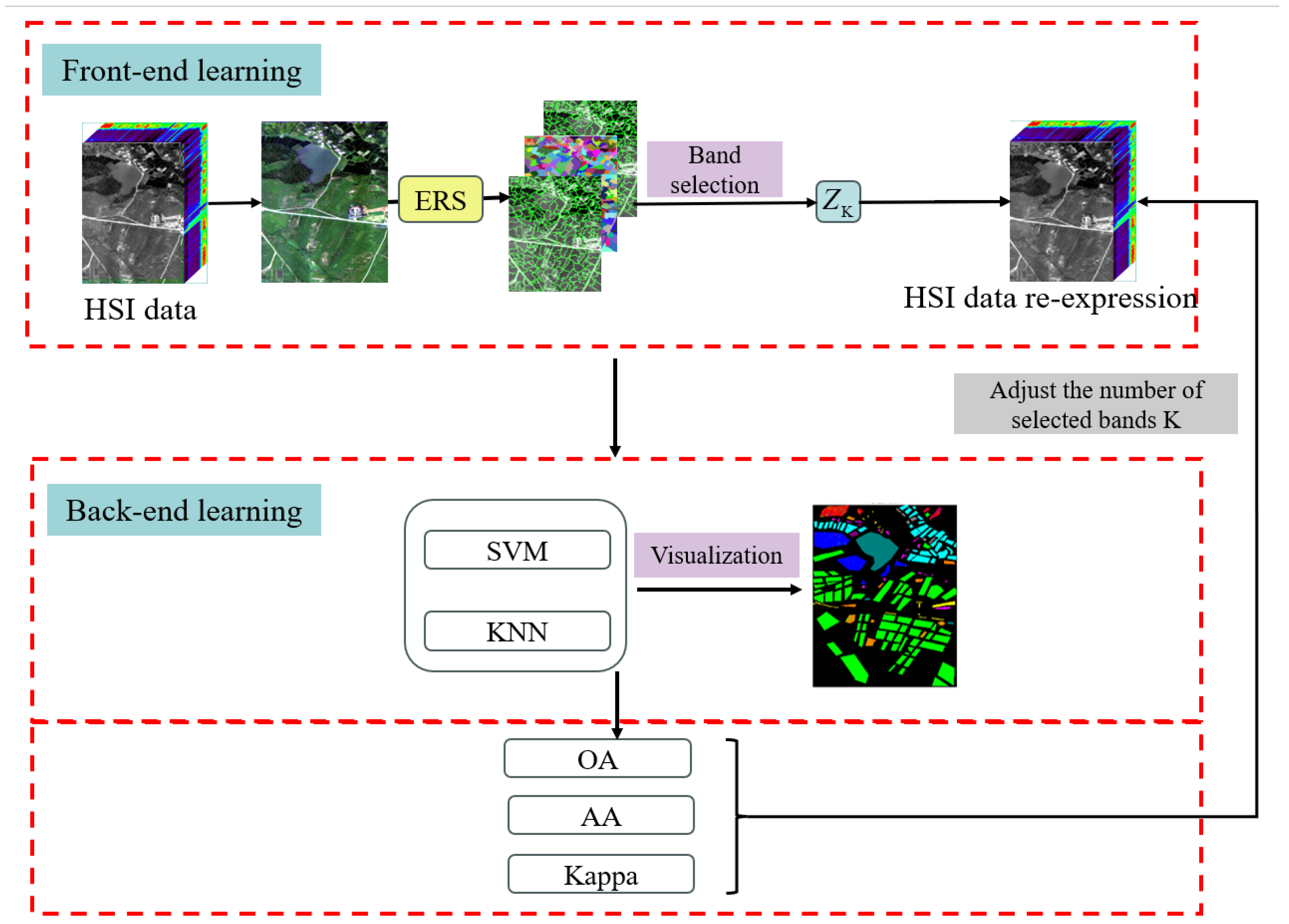
3. HSI Classification Method in Explainable Two-Layer Mode

This section introduces a new paradigm for HSI classification: explainable two-layer mode. We divide the classification algorithm into two layers: front-end learning and back-end learning [31]. In the front-end learning layer, the band selection is realized by combining superpixel segmentation and SSC, resulting in a low-dimensional HSI data re-expression. In the back-end learning layer, support vector machine (SVM) or K-nearest neighbor (KNN) is employed to classify low-dimensional data. Band selection and classification tasks are combined through the front-end and back-end integration strategy.

3.1. Front-End Learning Layer for Data Re-Expression

The front-end learning layer completes the band selection task, which gives HSI data a low-dimension re-expression. Our sparse SSC method combines the superpixel segmentation strategy, the $l_{\mathrm{2,1}}$ norm, and graph regularization to explore HSI information fully.

3.1.1. Segment HSI with Superpixel Segmentation

When interpreting HSI, the same land cover type is affected by geographical location, growth conditions, and other factors, presenting different spectral curves in regions, resulting in the same object with a different spectrum. The sensor resolution may yield the same spectral curve containing spectral information of multiple land cover types simultaneously.

Entropy-rate superpixel segmentation is used to reduce the impact of the above issues. It constructs a graph for the HSI image and defines the objective function for superpixel segmentation with two components: the entropy rate of a random walk on the graph and a balance term. The entropy rate favors compact and homogeneous clusters, while the balancing term encourages clusters of similar size. The superpixel segmentation provides spatial support for region-based features [32,33].

Given the HSI cube $H\in {\mathbb{R}}^{m\times n\times b}$, where m and n represent the spatial width and height, respectively, and $b$ denotes the number of bands, superpixel segmentation cuts an image into $N$ parts, where each piece is called a superpixel. We divide $H$ into $N$ non-overlapping parts and obtain $N$ pixel set $S_i$, where $S_i$ is the index set of the $i$ th superpixel and $i=\mathrm{1,2},\dots ,N$. Each superpixel is a group of adjacent pixels that share similar characteristics.

3.1.2. Explainable Minimization Problem for SSC

We compute the average spectral values at each band of $N$ superpixels. The original matrix $X\in {\mathbb{R}}^{mn\times b}$ transfers into $F\in {\mathbb{R}}^{N\times b}$. Then, the minimization problem for SSC can be formulated as follows:

$$min{‖F-FZ‖}_F^2+\lambda {‖Z‖}_1$$

where ${‖Z‖}_1=\underset{1\le j\le b}{max}\sum _{i=1}^b\left|Z_{ij}\right|$ and $J\left(Z\right)$ in (4) is set to ${‖Z‖}_1$, which helps to maintain a sparse coefficient matrix $Z$.

As described in (1), each band vector is written as a linear combination of other band vectors. It is reasonable in the re-expression procedure to preserve the inherent geometric local structure among the data in order to design a model that can reflect the relationship between the data $f_1,f_2,\dots ,f_N$, where $F={\left({f_1}^T,{f_2}^T,\dots ,{f_N}^T\right)}^T$ and the re-expressed data ${\tilde{f}}_1,{\tilde{f}}_2,\dots ,{\tilde{f}}_N$, where $FZ={\left({{\tilde{f}}_1}^T,{{\tilde{f}}_2}^T,\dots ,{{\tilde{f}}_N}^T\right)}^T$. The assumption is that if $f_i$ and $f_j$ are in close relationship, their corresponding re-expressed data ${\tilde{f}}_i,{\tilde{f}}_j$ should also be close. According to this discussion, we suppose that $S=\left(s_{ij}\right)\in {\mathbb{R}}^{N\times N}$ represents a matrix where $s_{ij}$ quantifies the similarity between the data point $f_i$ and $f_j$. The problem of learning local structure can be formulated as

$$\begin{array}{c} min{\displaystyle \frac{1}{2}}\sum _{i,j=1}^N{‖{\tilde{f}}_i-{\tilde{f}}_j‖}_2^2{s}_{ij}={\displaystyle \frac{1}{2}}{\displaystyle {\sum }_{i,j=1}^N}\left({\tilde{f}}_i-{\tilde{f}}_j\right){\left({\tilde{f}}_i-{\tilde{f}}_j\right)}^T{s}_{ij}\hfill \\ ={\displaystyle \frac{1}{2}}{\displaystyle {\sum }_{i,j=1}^N}\left({\tilde{f}}_i{{\tilde{f}}_i}^T+{\tilde{f}}_j{{\tilde{f}}_j}^T-{\tilde{f}}_j{{\tilde{f}}_i}^T-{\tilde{f}}_i{{\tilde{f}}_j}^T\right)s_{ij}={\displaystyle {\sum }_{i,j=1}^N}\left({\tilde{f}}_i{{\tilde{f}}_i}^T-{\tilde{f}}_i{{\tilde{f}}_j}^T\right)s_{ij}\hfill \\ =\sum _{i=1}^N{\tilde{f}}_i{d}_{ii}{{\tilde{f}}_i}^T-{\displaystyle {\sum }_{i=1}^N}{\tilde{f}}_i{s}_{ij}{{\tilde{f}}_j}^T=tr\left(Z^T{F}^{T}DFZ\right)-tr\left(Z^T{F}^{T}SFZ\right)=tr\left(Z^T{F}^{T}LFZ\right)\hfill \end{array}$$

where $L=D-S$ is the Laplacian matrix related to the data, $S={\left(s_{ij}\right)}_{N\times N},$ and $D$ is a diagonal matrix with diagonal elements $d_{ii}=\sum _{j=1}^N{s}_{ij}$ for $i=1,2,\dots ,N$.

$$s_{ij}=exp\left(-{‖{\tilde{f}}_i-{\tilde{f}}_j‖}^2/2{\sigma }^2\right),i=\mathrm{1,2},...N,$$

(5)

The explainable minimization problem for SSC is defined as follows:

$$\mathit{min}{‖F-FZ‖}_{\mathrm{2,1}}^2+{\lambda }_{1}tr\left(Z^T{F}^{T}LFZ\right)+{\lambda }_2{‖Z‖}_{\mathrm{2,1}}^2,$$

(6)

where ${‖·‖}_{\mathrm{2,1}}$ denotes the $l_{\mathrm{2,1}}$ norm, ${‖Z‖}_{\mathrm{2,1}}={\sum _{j=1}^b\left(\sum _{i=1}^b{z_{ij}}^2\right)}^{{\displaystyle \frac{1}{2}}}$.

The gradient of the objective function in (6) is

$$\mathsf{\nabla }f\left(Z\right)=F^T{P}_{1}FZ-F^T{P}_{1}F+{\lambda }_1{F}^{T}LFZ+{\lambda }_2{P}_{2}Z$$

(7)

We let $df\left(Z\right)/dZ=0$; therefore, we have

$$Z={\left(F^T{P}_{1}F+{\lambda }_1{F}^{T}LF+{\lambda }_2{P}_2\right)}^{-1}\left(F^T{P}_{1}F\right)$$

(8)

where $P_1$ and $P_2$ are diagonal matrices. The diagonal elements are

$${\left(P_1\right)}_{ii}=1/\sqrt{{\sum }_{j=1}^b{\left(F-FZ\right)}_{ij}^2}, {\left(P_2\right)}_{ii}=1/\sqrt{{\sum }_{j=1}^b{Z}_{ij}^2}$$

We set $W=(\widehat{Z}+{\widehat{Z}}^T)/2$ where $\widehat{Z}$ is the estimated solution of (5); then, we cluster all band vectors into $k$ underlying subspaces with the spectral clustering method. Finally, we obtain the selected band set $B_k$; then, after feature selection, the input data to the second layer are $F_{B_k}{\in \mathbb{R}}^{N\times k}$, obtained with band selection.

3.2. Back-End Learning Layer for HSI Classification

Front-end learning obtains HSI data re-expression in a lower dimension, while back-end learning starts up the classification procedure.

KNN or SVM is used to complete the classification task for back-end learning. Given a new sample point to be classified, KNN searches for the nearest training samples in the training set and predicts the new sample point’s category based on the neighbors’ categories. In our numerical test, the distance between samples is calculated with Euclidean distance. The basic idea of SVM is to find hyperplanes that maximize the interval between different categories. In the numerical test, we call Matlab’s function KKN-Classifier or SVM-Classifier to complete the classification work.

3.3. Two-Layer Mode HSI Classification Method

The two-layer mode HSI classification method proposed in this paper fuses the front-end and back-end through the optimal indicators. We set the number of selected bands $K$ to 5, 10, and 15. The indicator is calculated using the classification results. Finally, the optimal indicator determines the number of selected bands. Figure 2 shows the two-layer mode of our method.

Now, we are ready to give Algorithm 1, which contains our band selection method for HSI data.

Algorithm 1: Classification Algorithm under two-Layer Mode (CALM)

Input: HSI data $H\in {\mathbb{R}}^{m\times n\times b}, \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{the} \mathrm{selected} \mathrm{band} K, \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{segmented} \mathrm{region} N, \mathrm{parameters} {\lambda }_1 \mathrm{and} {\lambda }_2, Z^0=randn\left(b\right),k≔0, \epsilon .$

Output: The index set of the selected band ZK.

Step 1: Segment H into N regions with the index set s1, s2, ..., sN via ERS.

Step 2: Compute F with the index set S1, S2, ..., SN.

Step 3: Compute $\nabla f\left(Z\right) \mathrm{with} \left(7\right), \mathrm{if} ‖\nabla f\left(Z\right)‖<\epsilon$ then goto Step 6, else, go to Step 4.

Step 4: Update Z with (5).

Step 5: Update S with (8), go to step 3.

Step 6: Let Z = (Z + ZT)/Z, and generate ZK with spectral clustering algorithm.

Step 7: Using ZK as input, train a classification model using SVM or KNN, andcalculate the evaluation metrics obtained by selecting K bands.

Step 8: $\mathrm{If} K<50, \mathrm{then} K≔K+5; \mathrm{go} \mathrm{to} \mathrm{Step} 6. \mathrm{Otherwise}, OA=\max \left({OA}_K\right),K≔\underset{K}{\arg }max\left({OA}_K\right)$

4. Experiments

Having presented the explainable two-layer mode HSI classification method, we are ready to test its performance on three HSI datasets.

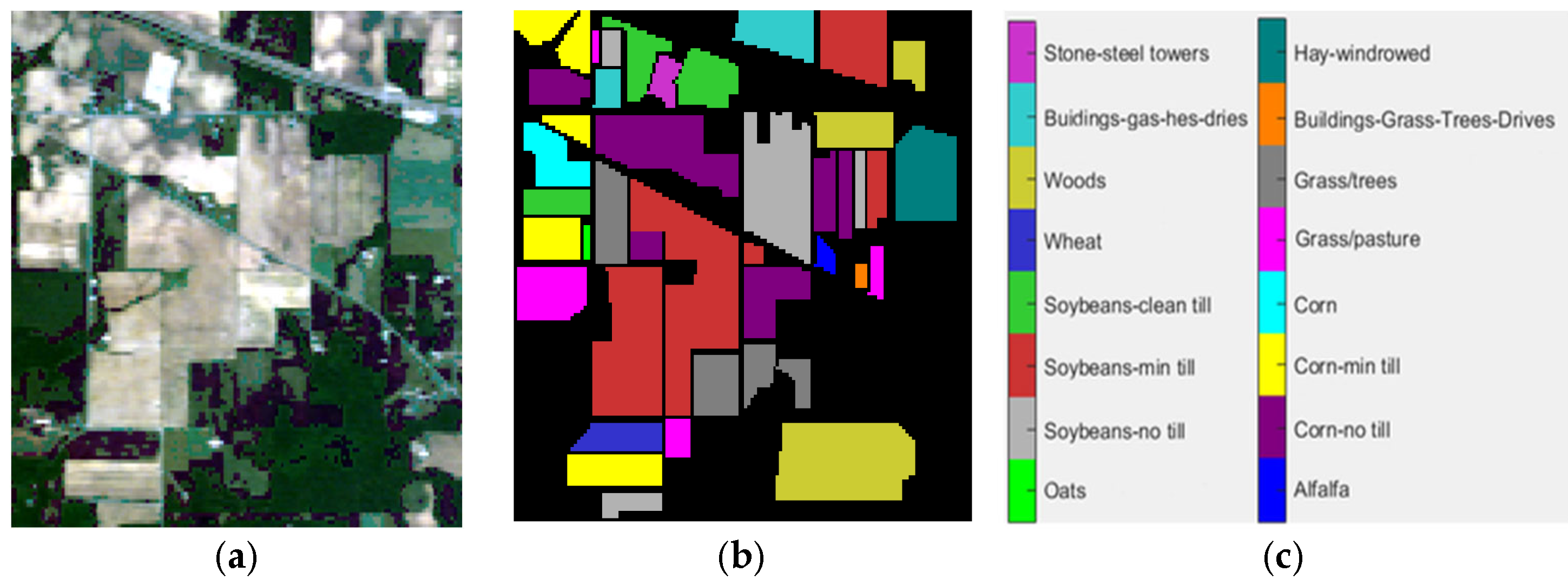
4.1. Datasets

The three HSI datasets in our experiments are TeaFarm, Salinas, and Indian Pines, whose pseudo-color and ground-truth images are shown in Figure 3, Figure 4 and Figure 5.

TeaFarm: Located in the tea tree planting base of Fanglu village, Changzhou, Jiangsu Province, the data contain 348 × 512 pixels with a spatial resolution of 2.25 m. The dataset consists of 80 spectral bands covering a spectral range of 417–855 nm.

It includes 10 types of land cover classes, which is available at https://www.geodoi.ac.cn/edoi.aspx?DOI=10.3974/geodb.2017.03.04.V1 (access on 21 May 2025).

Salinas: The data have a size of 512 × 217 with a spatial resolution of 3.7 m. The dataset contains 224 contiguous spectral bands. After removing 20 water absorption bands (108–112, 154–167, 224), 204 bands are actually used for training. The dataset includes 16 types of land cover classes.

Indian Pines: Imaged by the AVIRIS spectrometer, with a wavelength range of 0.4–2.5 μm, the data size is 145 × 145, and there are 224 spectral bands, of which 200 are used for experiments. The dataset contains 16 types of land cover classes.

4.2. Comparison Algorithms

The algorithm proposed in this article is compared numerically with the following four band selection algorithms. After implementing band selection for front-end learning, we use the same classifier for classification and compare the performance of five band selection algorithms. The information for all of these methods is summarized as follows.

ASPS_MN [34]: The core idea is to divide the HSI cube into multiple sub-cubes via an adaptive subspace partition strategy and then select the band with minimum noise in each sub-cube as the representative band to reduce the data dimension while retaining more useful information.

SEASP [35]: By calculating the correlation coefficient between adjacent bands to identify the orderliness between bands, a subset of characteristic bands is selected from the partitioned subspace using information entropy as the metric.

S⁴P [36]: The spatial structure of HSI is captured through superpixel segmentation, and the spectral correlation between bands is learned using a self-representation model. An adaptive and weighted multi-graph fusion term is designed to generate a unified similarity graph between different superpixels, and the importance of the bands is measured by imposing an $l_{\mathrm{2,1}}$ norm on the self-representation coefficient matrix.

RLFFC [37]: Spatial information is obtained through superpixel segmentation, and the separability among bands is enhanced by a latent feature fusion strategy, thereby improving the performance of band selection.

GRSC [22]: The spatial information of HSI is preserved through superpixel segmentation, and representative bands are selected by combining spectral correlation and spatial structure information using a self-representation subspace clustering model, thereby reducing data redundancy and noisy bands.

4.3. Experimental Setup

In the experiments, three metrics, OA, AA, and Kappa, are used as the evaluation criteria, and two typical traditional classifiers, KNN and SVM, are also used. The number of selected bands is systematically varied from 5 to 50, with increments of 5, to observe the impact of band selection on classification performance. The parameter $k$ of KNN is set to 5 in our experiments. As for the SVM classifier, the cross-validation process determines that the Radial Basis Function (RBF) with the kernel parameter γ = 0.5 performs best for our classification tasks. In order to reduce the sampling random bias, each classification algorithm is run 10 times, and the average classification accuracy is reported.

There are two critical parameters, ${\lambda }_1$ and ${\lambda }_2,$ in our model. We meticulously tune these parameters within a wide range of values, specifically from ${10}^{-4}$ to ${10}^4$. The optimal settings of these parameters that yield the best classification results are determined, that is, ${\lambda }_1$ = 0.5 and ${\lambda }_2$ = 0.1.

4.4. Experimental Results

Table 1. Classification results of different methods with three metrics on different datasets.

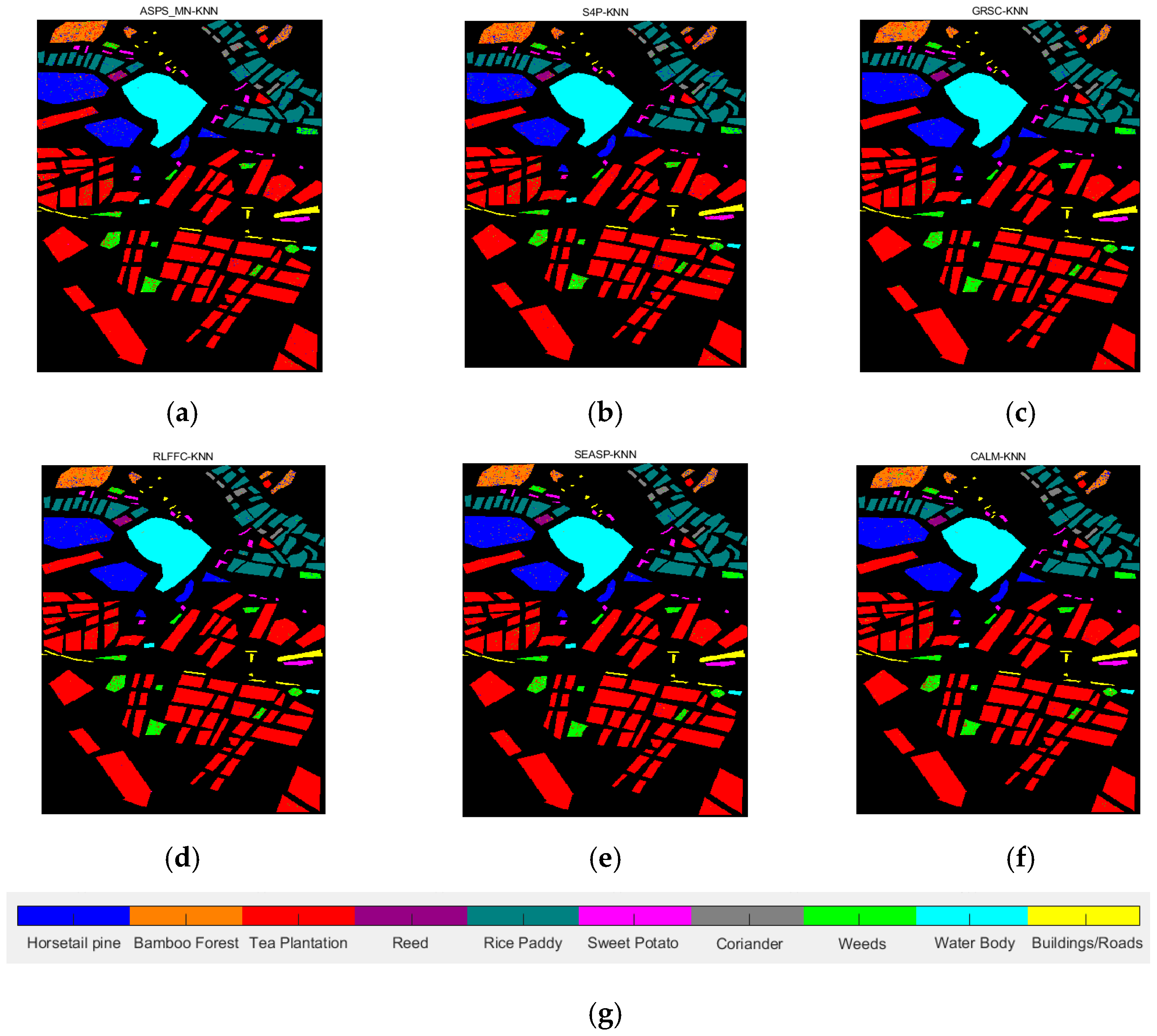
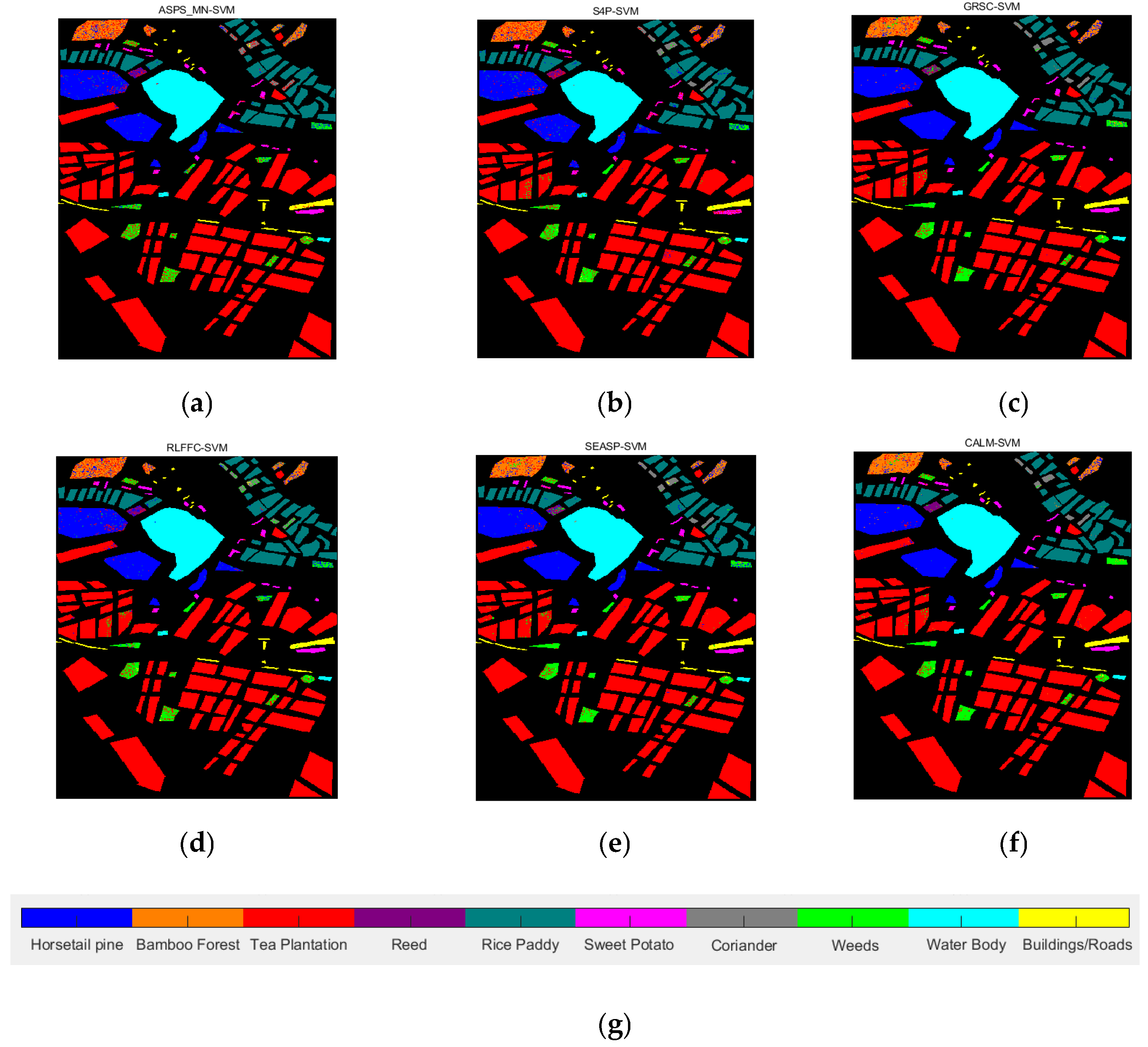
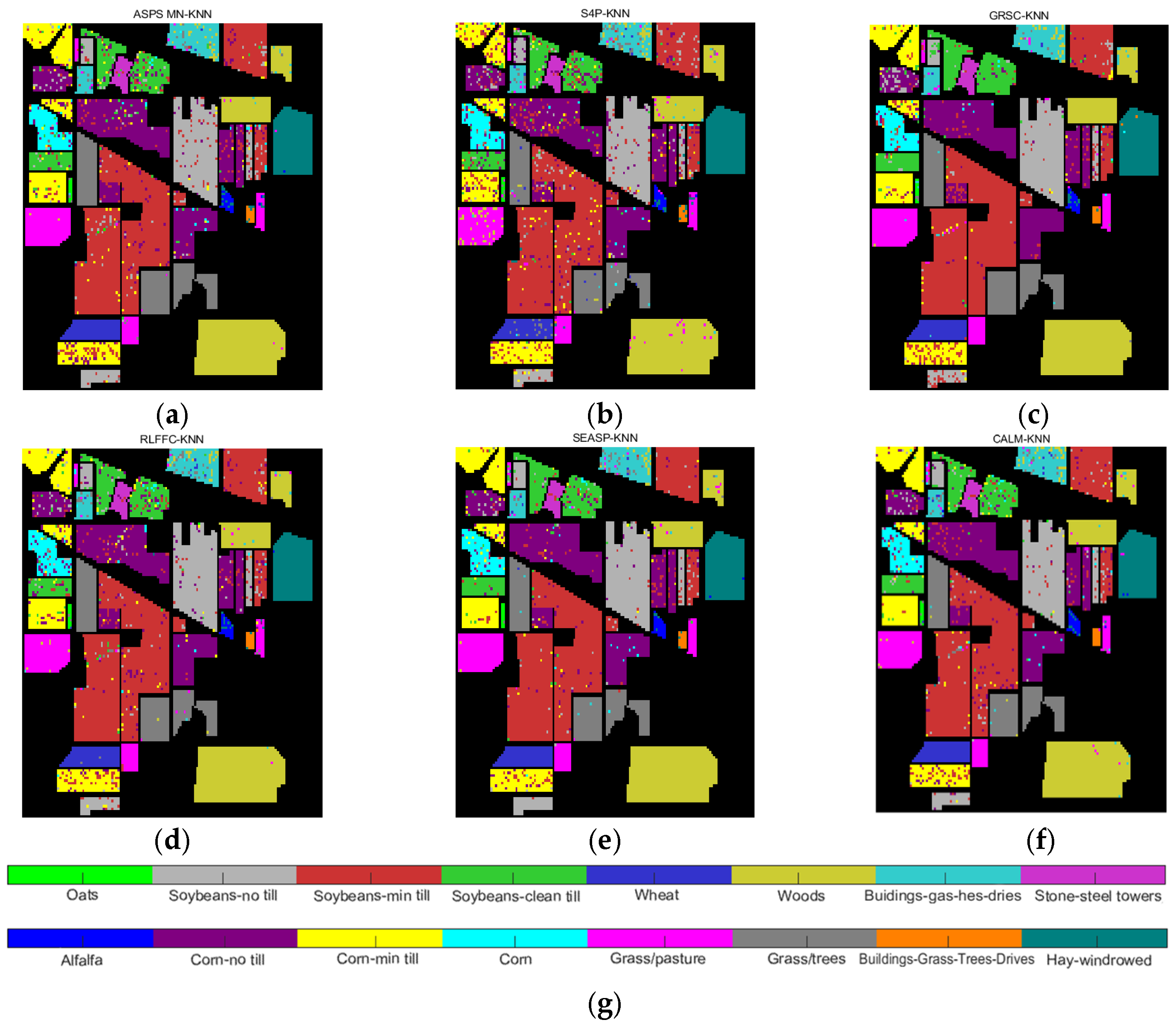
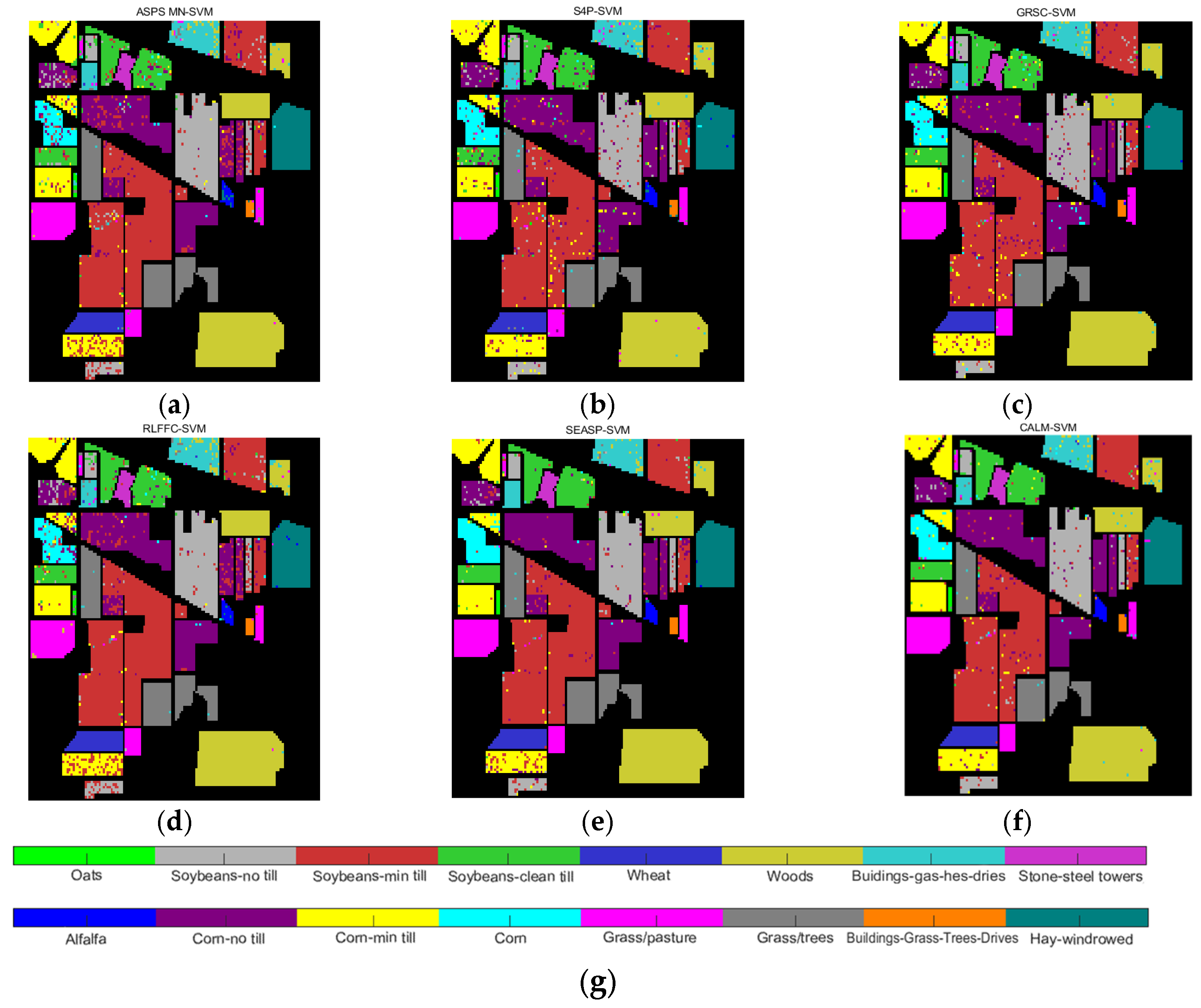
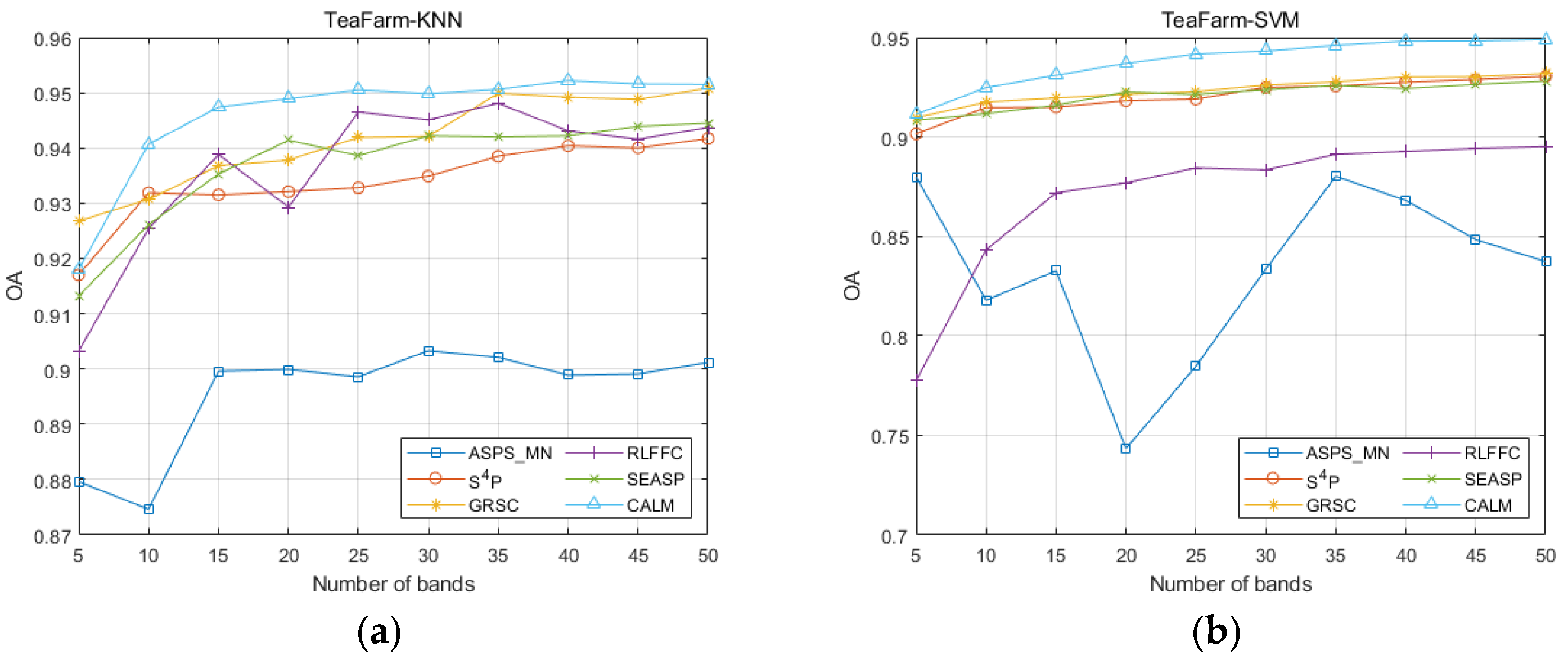
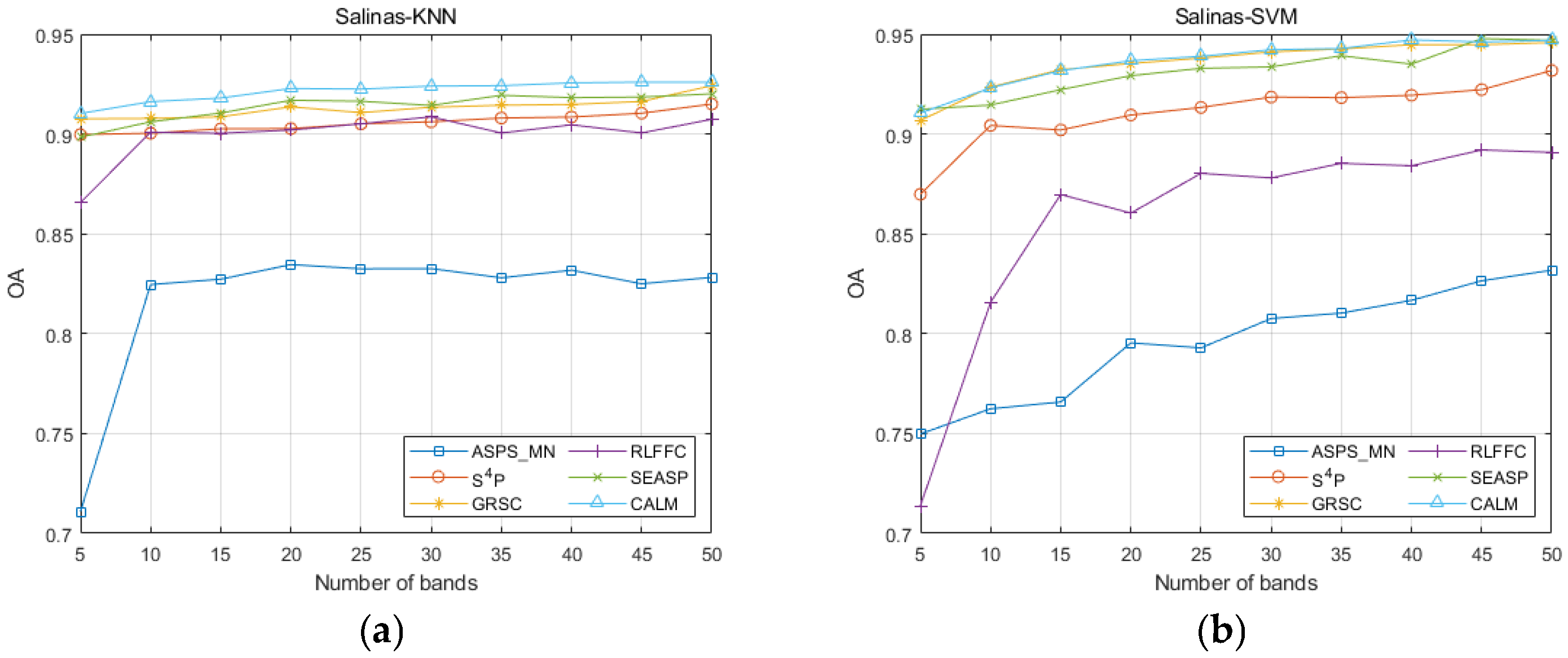
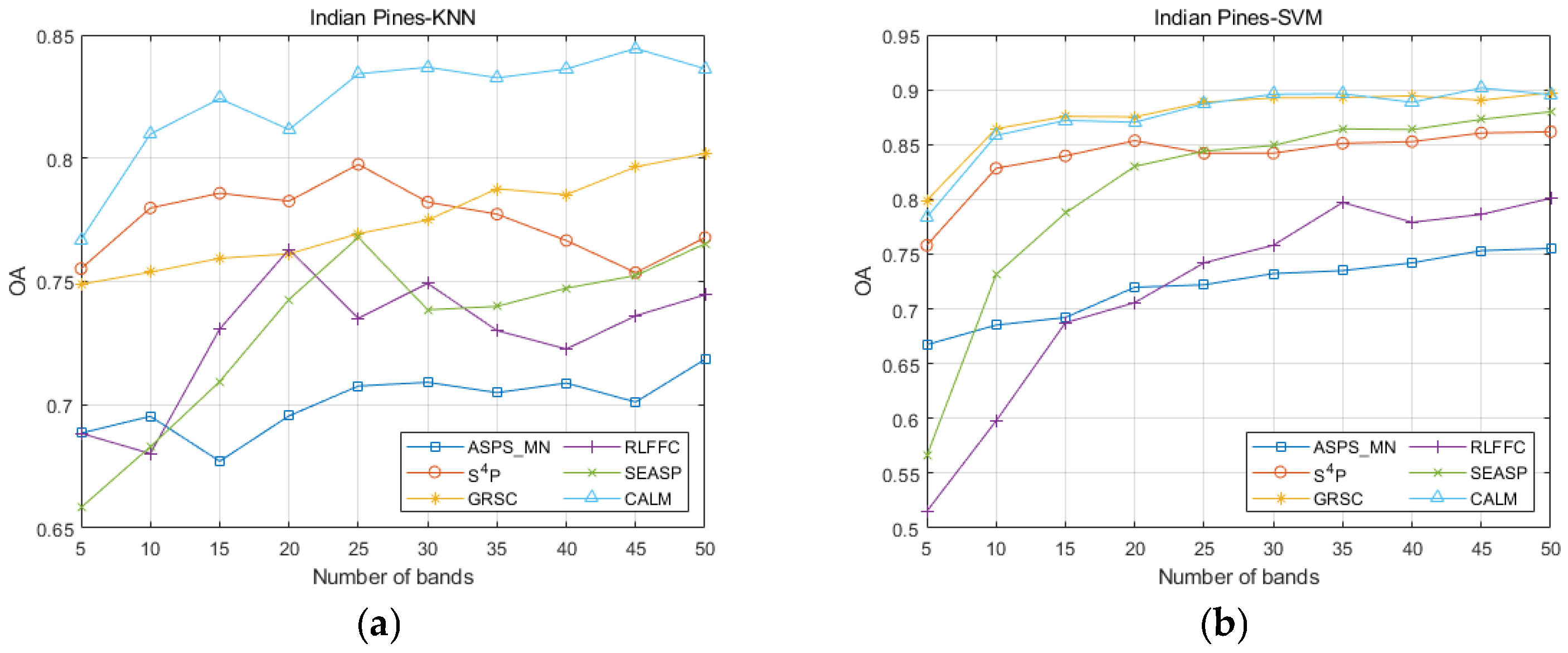
Datasets	Classifier	Metrics	ASPS_MN	S4P	GRSC	RLFFC	SEASP	CALM
TeaFarm	KNN	OA	0.9012	0.9417	0.9508	0.9437	0.9445	0.9522
		AA	0.7747	0.8576	0.8638	0.8633	0.8647	0.8902
		Kappa	0.8932	0.9152	0.9140	0.9180	0.9194	0.9302
	SVM	OA	0.8802	0.9304	0.9319	0.8951	0.9281	0.9490
		AA	0.7479	0.7491	0.7480	0.6 851	0.7397	0.8632
		Kappa	0.6747	0.8987	0.9007	0.8472	0.8953	0.9255
Salinas	KNN	OA	0.8282	0.9150	0.9242	0.9074	0.9201	0.9260
		AA	0.8830	0.9565	0.9629	0.9537	0.9610	0.9637
		Kappa	0.8172	0.9075	0.9174	0.8994	0.9129	0.9193
	SVM	OA	0.8318	0.9318	0.9458	0.8908	0.9478	0.9469
		AA	0.8849	0.9673	0.9738	0.9320	0.9721	0.9757
		Kappa	0.8210	0.9255	0.9259	0.8812	0.9418	0.9417
Indian Pines	KNN	OA	0.7184	0.7678	0.8644	0.7446	0.7653	0.8363
		AA	0.7324	0.7678	0.8000	0.6824	0.7150	0.8285
		Kappa	0.6885	0.7479	0.7807	0.7234	0.7449	0.8285
	SVM	OA	0.7552	0.8616	0.8971	0.8009	0.8799	0.9016
		AA	0.7284	0.8626	0.8976	0.7412	0.8852	0.8989
		Kappa	0.7352	0.8477	0.8857	0.7821	0.8671	0.8907

NOTE: The best results on the quality index are labeled in bold.

provides a detailed list of OA, AA, and Kappa values obtained using different band selection algorithms on different datasets.

During the classification stage, the stratified sampling approach helps construct training and testing sets. To form the training set, 70% of the samples from each class for each frequency band are randomly selected. This ensures that the training data are representative of the entire dataset. The remaining 30% of the samples are allocated to the testing set, which is used to evaluate the model’s performance on unseen data.

The results show that CALM showed a certain degree of improvement after introducing the regularization term compared to S⁴P and GRSC in all three evaluation metrics. Compared with ASPS_MN, introducing superpixel segmentation technology makes the band selection results more effective. Under all classifiers and conditions, the OA value of CALM is generally high, with values generally approaching or exceeding 0.9. As shown in Table 1, the new method, CALM, consistently outperforms other methods in terms of different metrics, i.e., OA, AA, Kappa. Taking TeaFarm datasets as an example, the OA of CALM with the SVM classifier increases by 6.88%, 1.86%, 1.71%, 5.39%, and 2.09%; the value of AA increases by 11.53%, 11.41%, 11.52%, 17.81%, and 12.35%; the value of Kappa increases by 25.08%, 2.68%, 2.48%, 7.83%, and 3.02%.

As Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 demonstrates the visualization result graph under different classification methods. Taking the TeaFarm dataset as an example, from Figure 6 and Figure 7, the areas classified as bamboo forest (red area) and grassland (orange area) are less affected by other categories and exhibit higher color category purity in the classification map. In the tea tree area, the distribution range of tea trees can be more accurately identified, reducing the occurrence of misclassification and missed classification. Compared with other methods, the CALM algorithm has higher classification accuracy in complex regions and significantly reduces speckle noise. The classification results indicate the effectiveness of the CALM method, which is more suitable for subsequent hyperspectral data classification.

As is well known, raw hyperspectral images often contain noise and a large amount of redundant information, which can significantly negatively impact classification accuracy [38]. Therefore, it is not easy to consistently achieve optimal performance for HSI classification using a complete set of bands. On the contrary, selecting the appropriate number of bands can improve classification performance to a certain extent.

The optimal number of bands for 3 HSI datasets is obtained with the OA curves, which is shown in Figure 12, Figure 13 and Figure 14. The OA curves describe the OA values with different numbers of selected bands.

Figure 12, Figure 13 and Figure 14 show that the OA values increase obviously when the number of selected bands increases from 5 to 10 for all six band selection methods. The CALM method stays stable, and its OA values are better than those of the other methods.

5. Conclusions

This paper proposes a two-layer mode HSI classification method divided into front-end and back-end learning stages. To reduce the dimensionality of HSI data, the representation learning in the front end combines superpixel segmentation techniques and the minimization model defined with norm and graph regularization, which yields the re-expression of HSI data for the back-end classification. After the back-end procedure implements classification, the number of bands selected by the front-end procedure is determined by classification accuracy.

Introducing a two-layer mode machine learning method helps further develop the interpretability of end-to-end deep learning models, and so does the use of certain mathematical models to achieve data re-expression, providing explainable features for analyzing numerical results of related applications.