Experimental Study of the Air Demand of a Spillway Tunnel with Multiple Air Vents
Abstract
1. Introduction
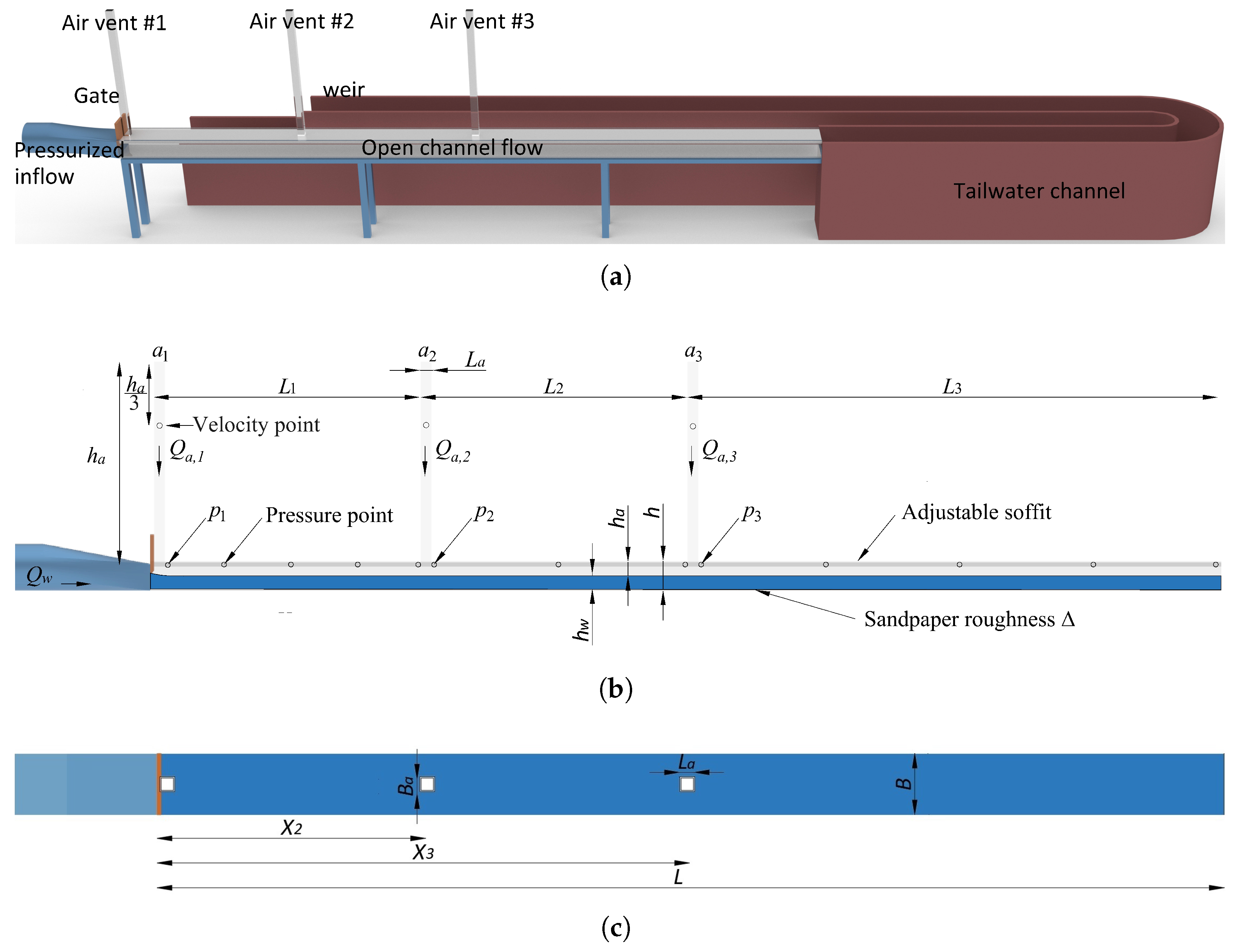
2. Experimental Setup
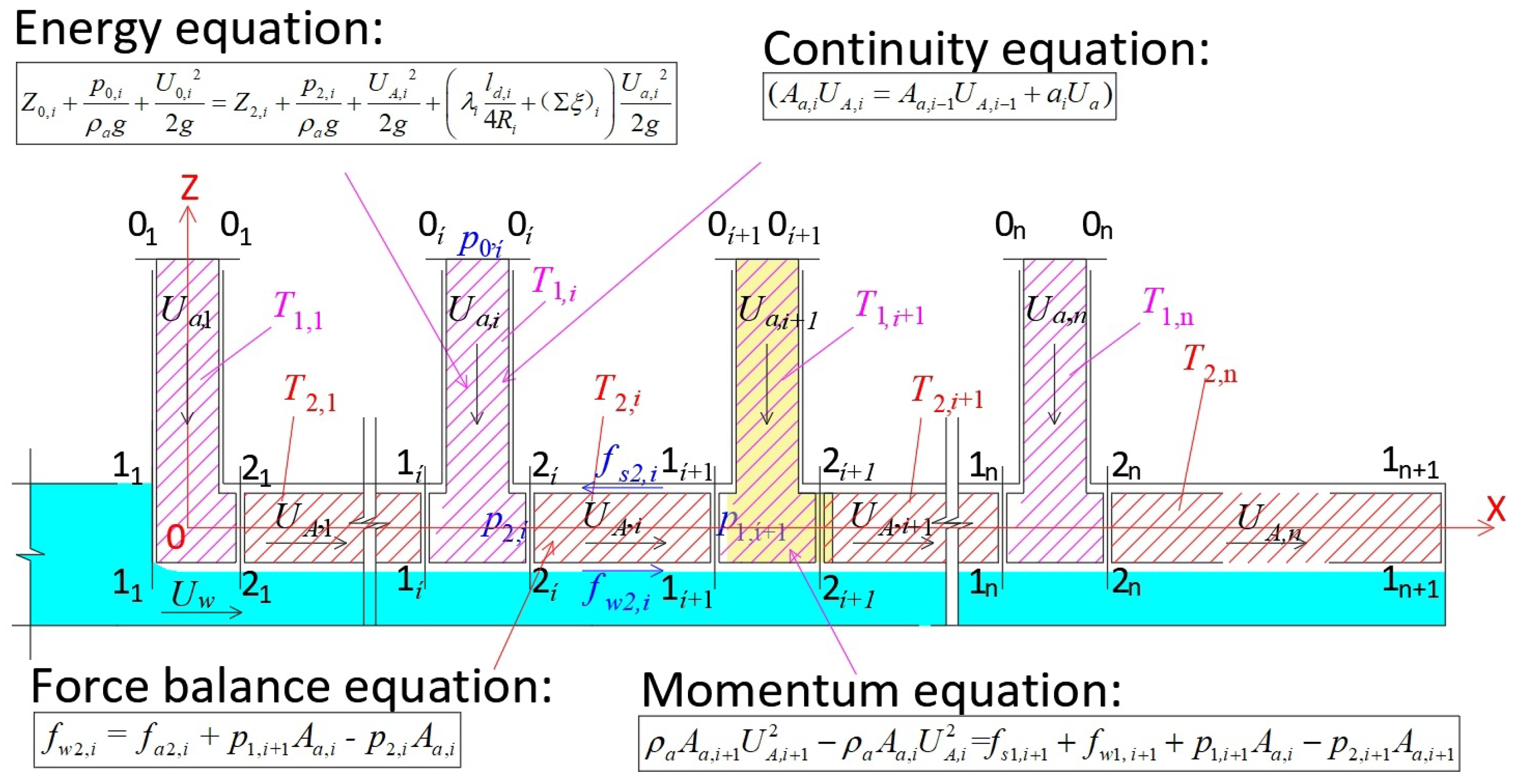
2.1. Model and Instrumentation
2.2. Test Program and Procedure
3. Results and Discussion
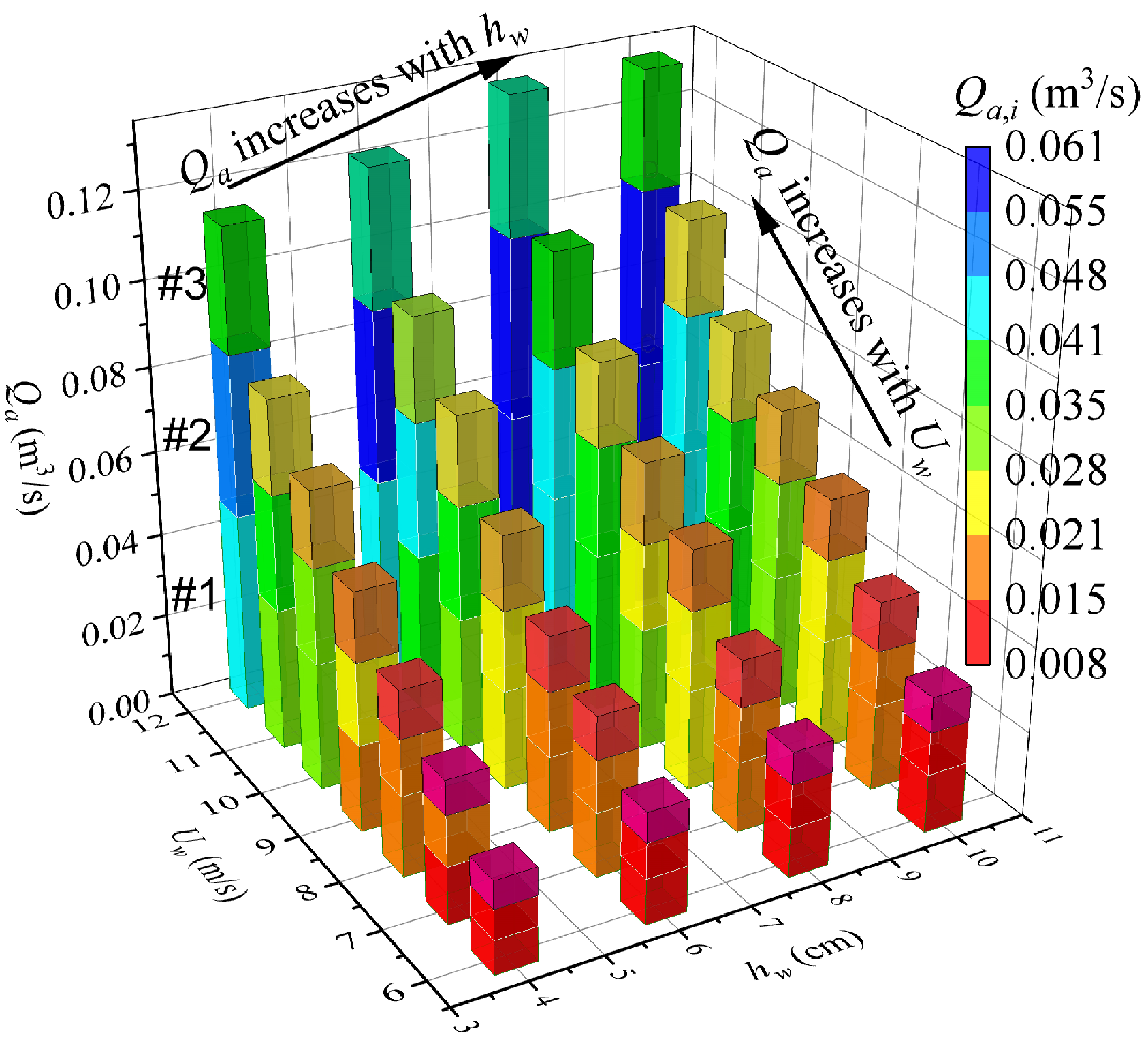
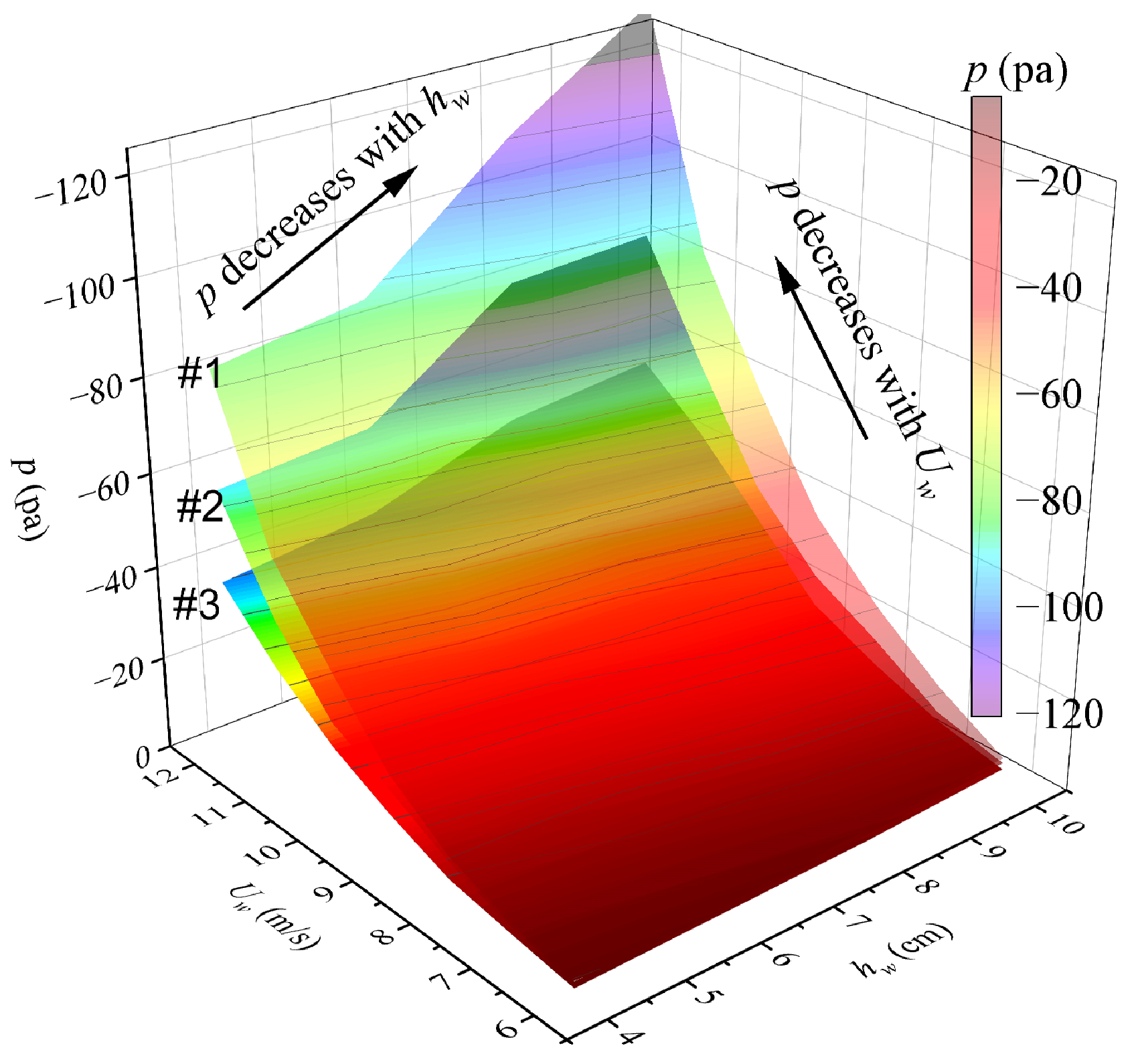
3.1. Effects of Water Velocity and Flow Depth on Air Demand
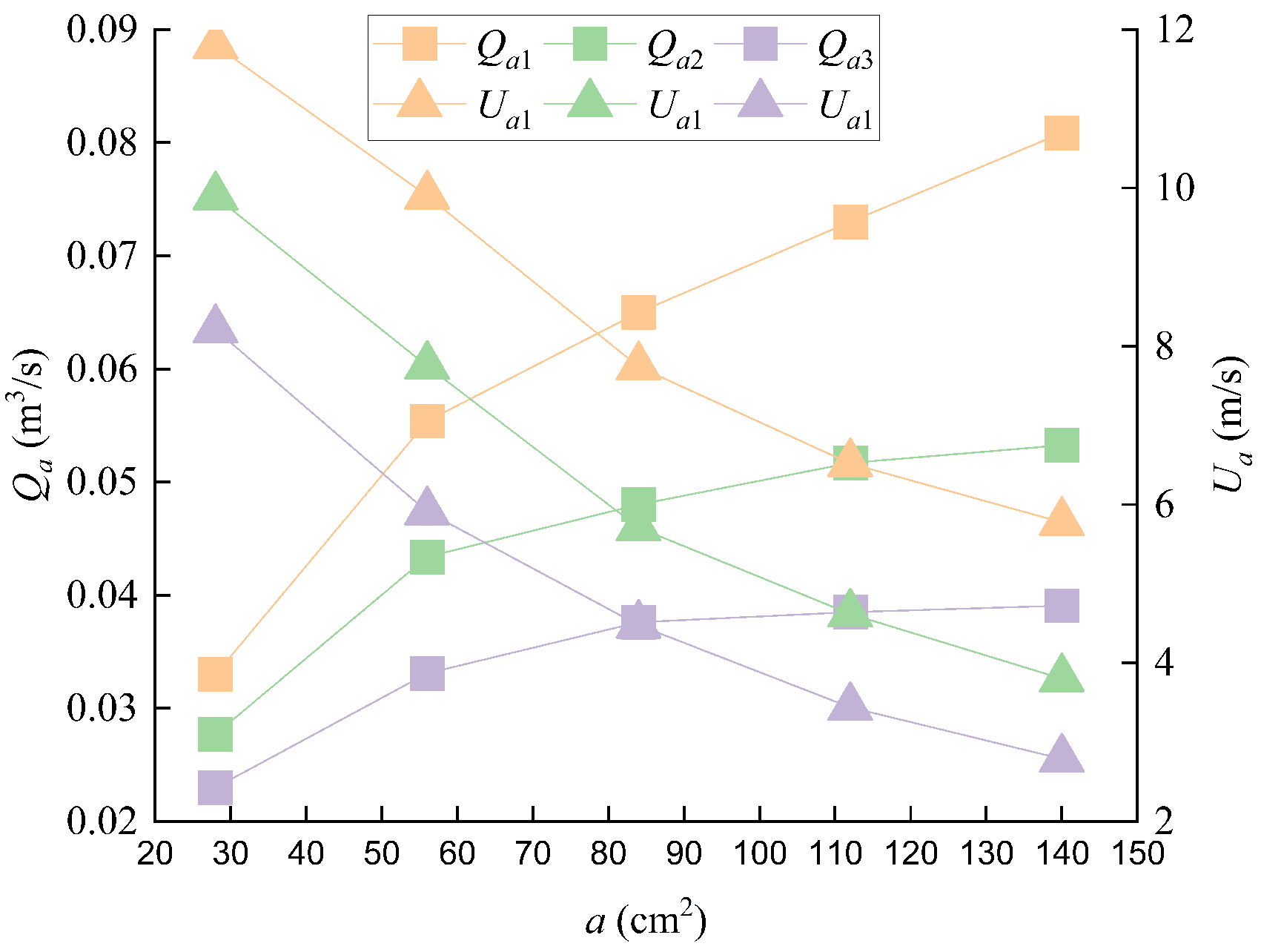
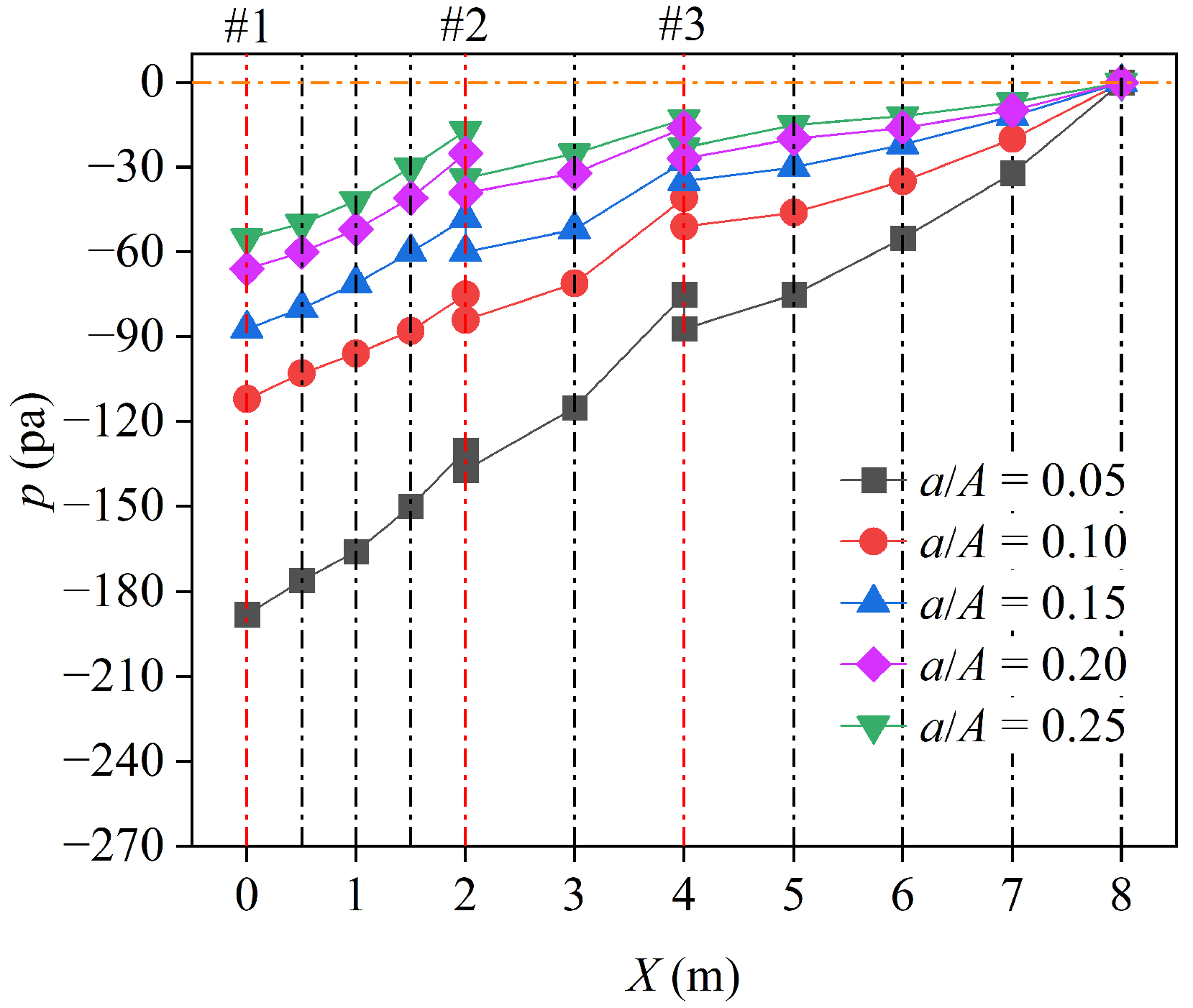
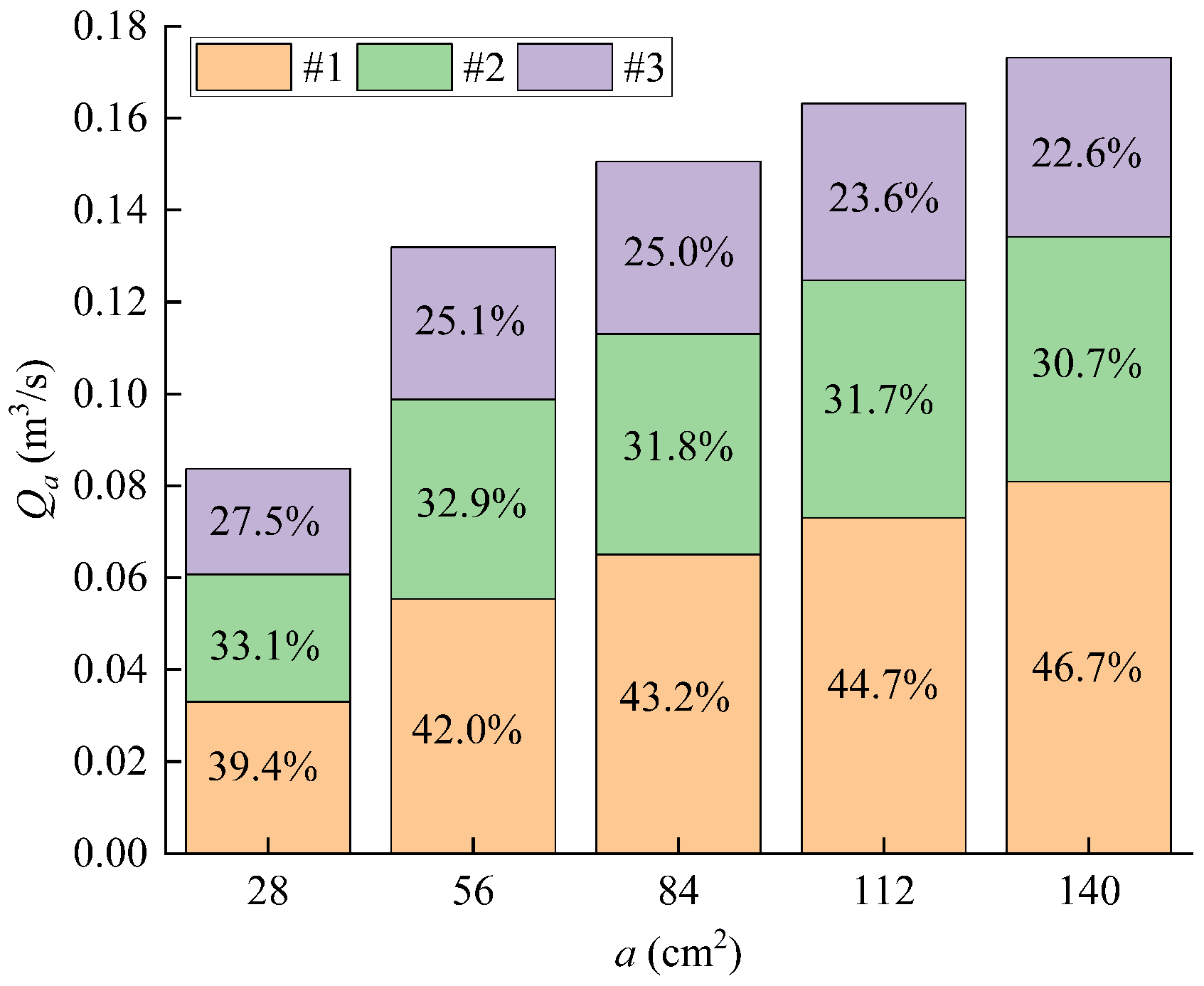
3.2. Effect of the Air Vent Area on the Air Demand
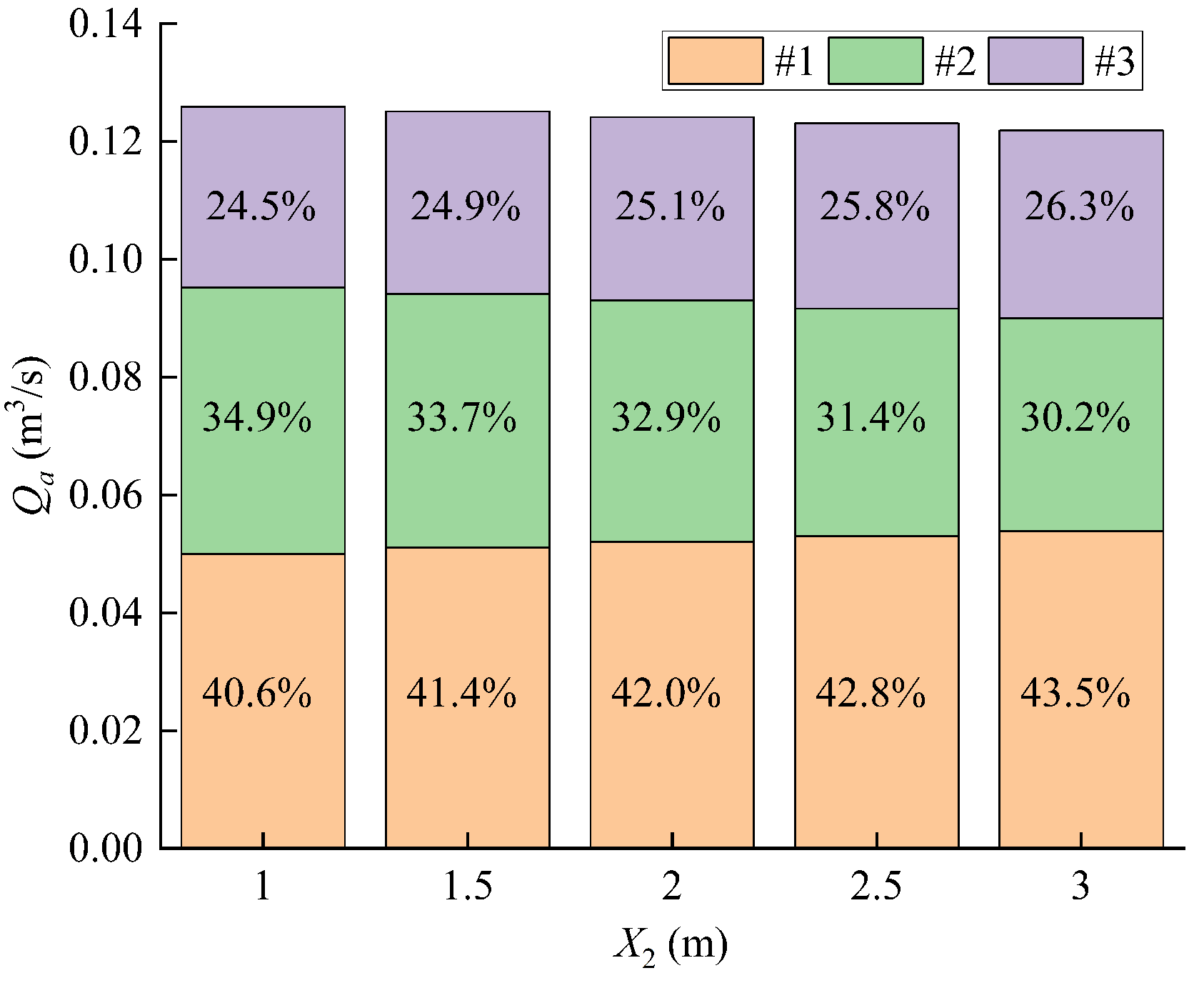
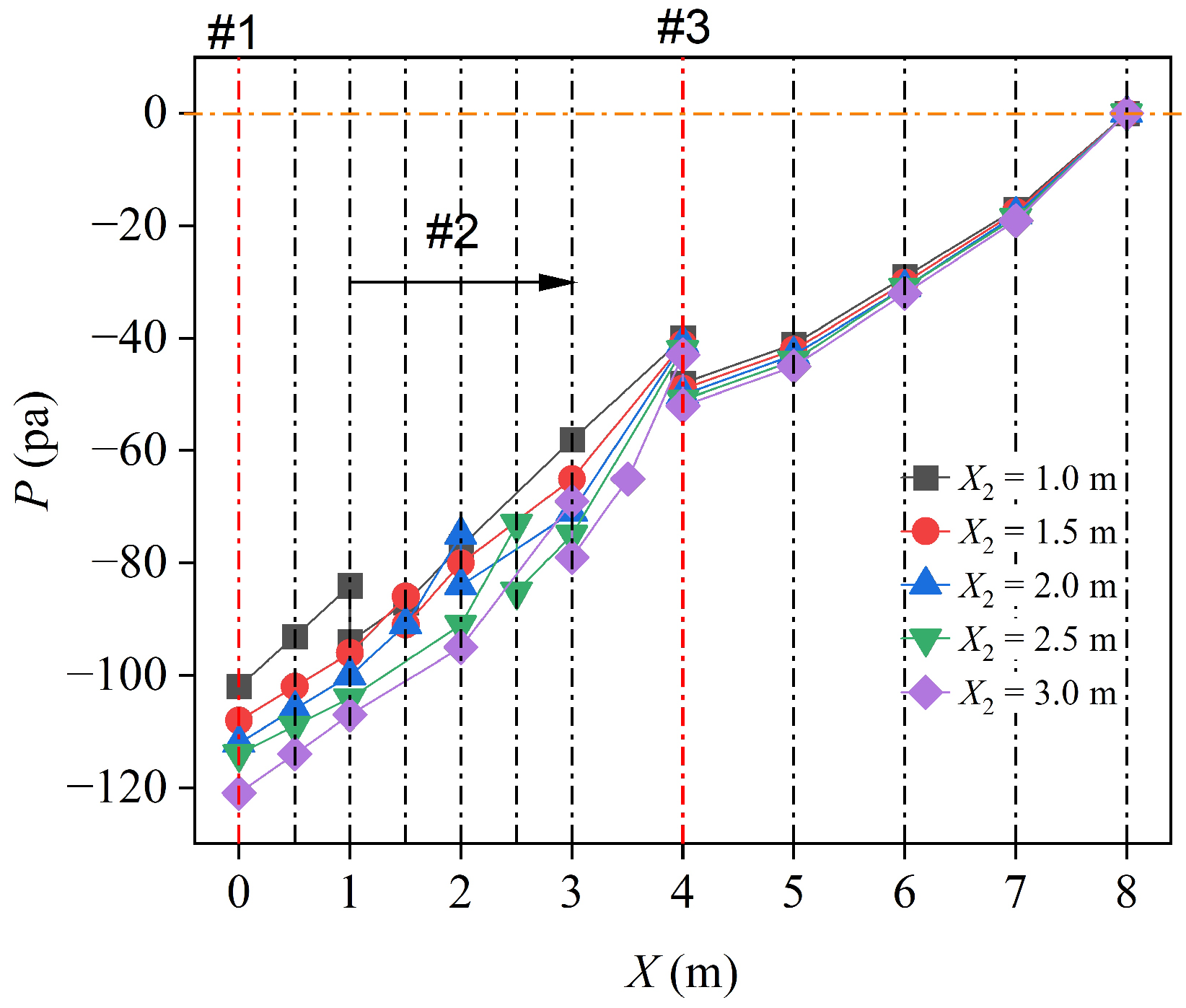
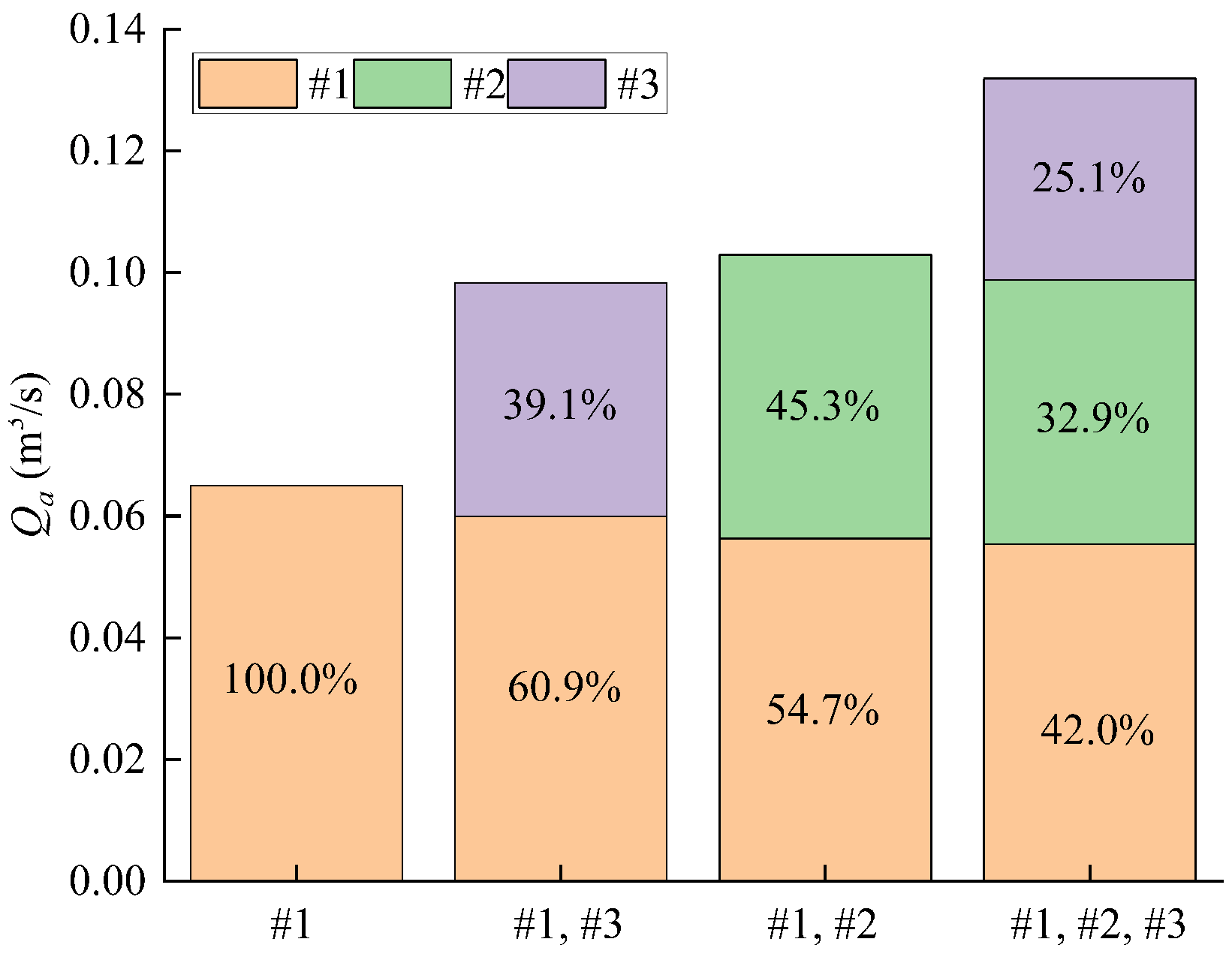
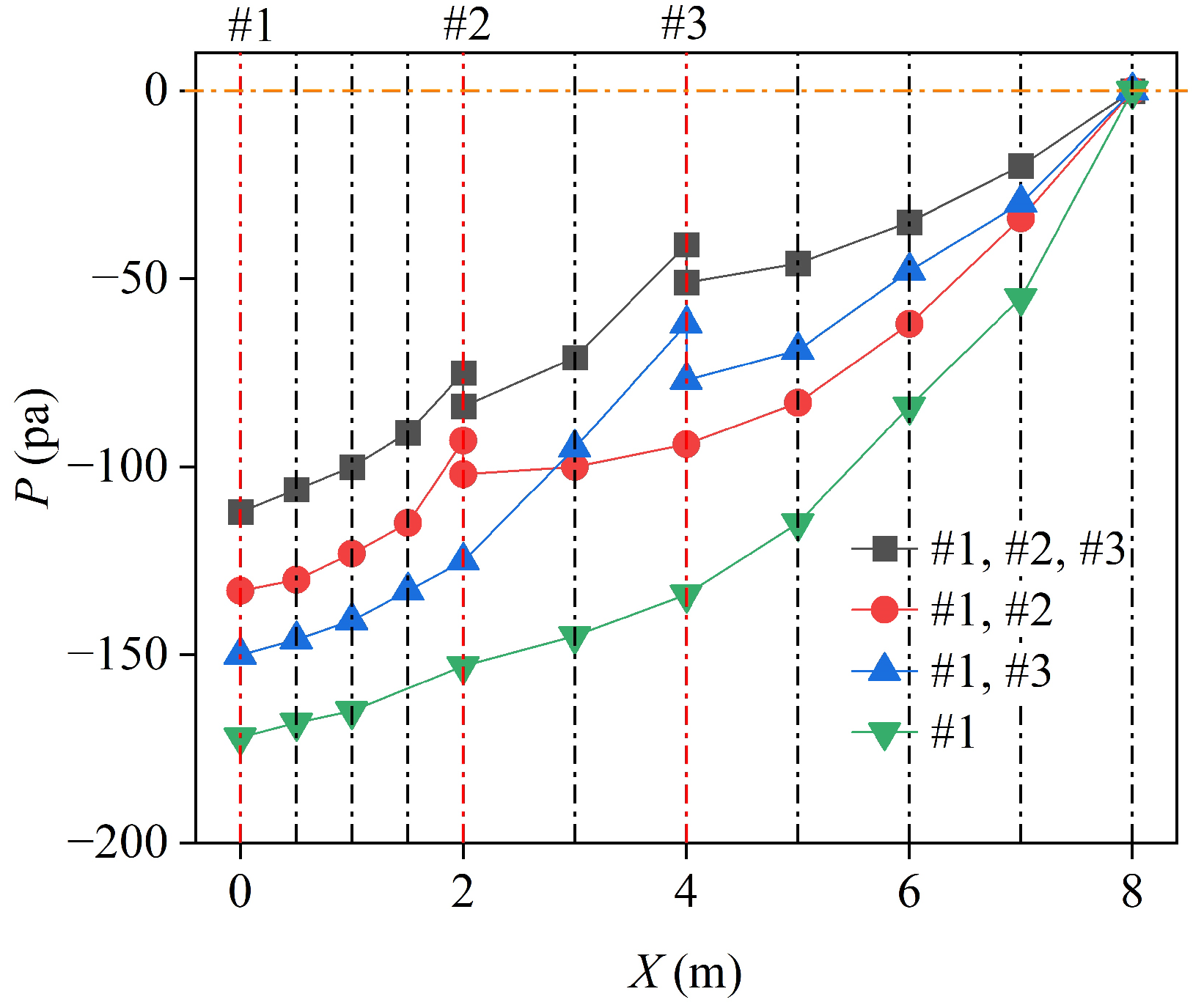
3.3. Effects of the Air Vent Location and Number on the Air Demand
4. Calculation Equation for Air Demand
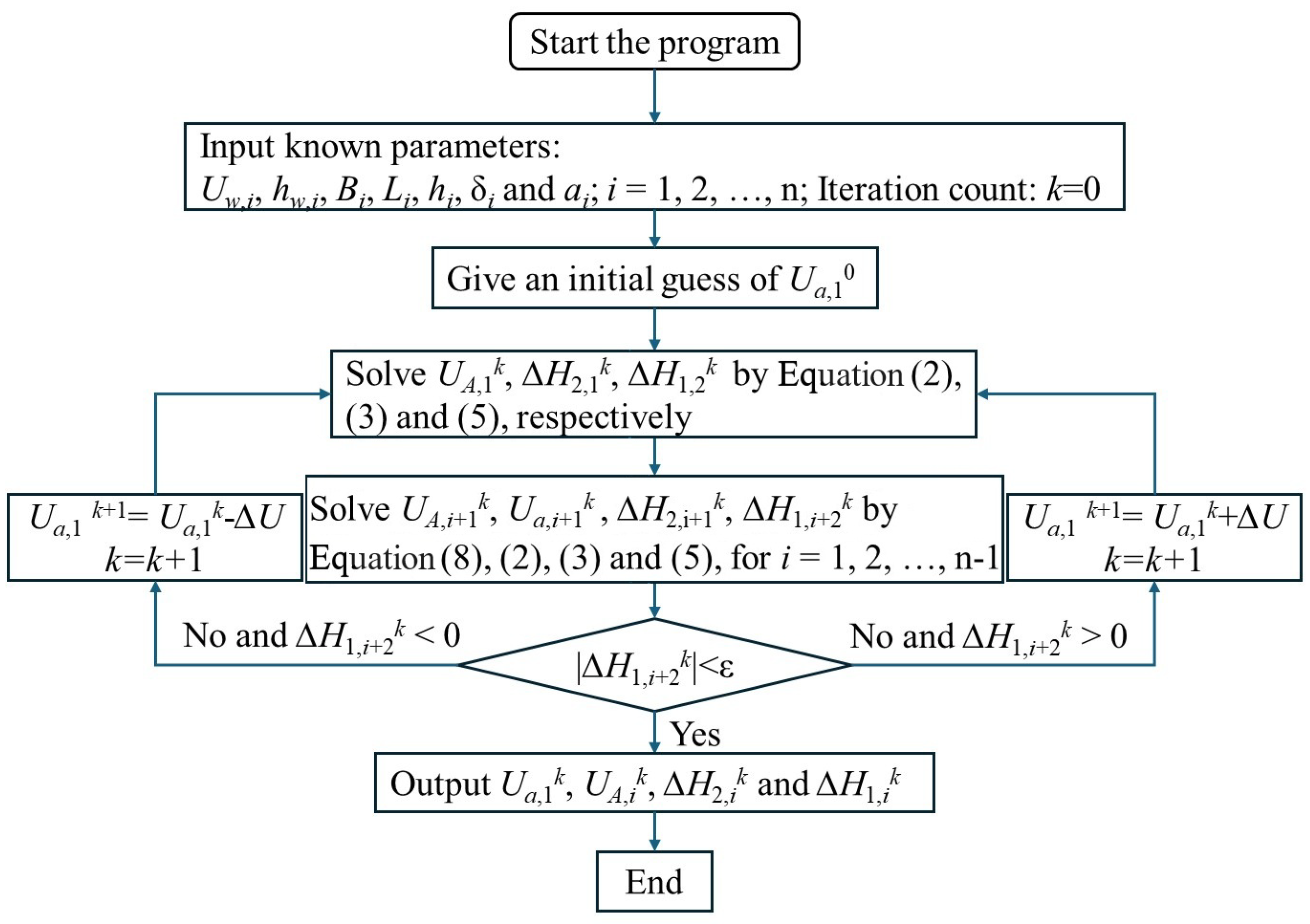
4.1. Solution Procedure for Air Demand
4.2. Analysis of the Interfacial Shear Stress Formulation
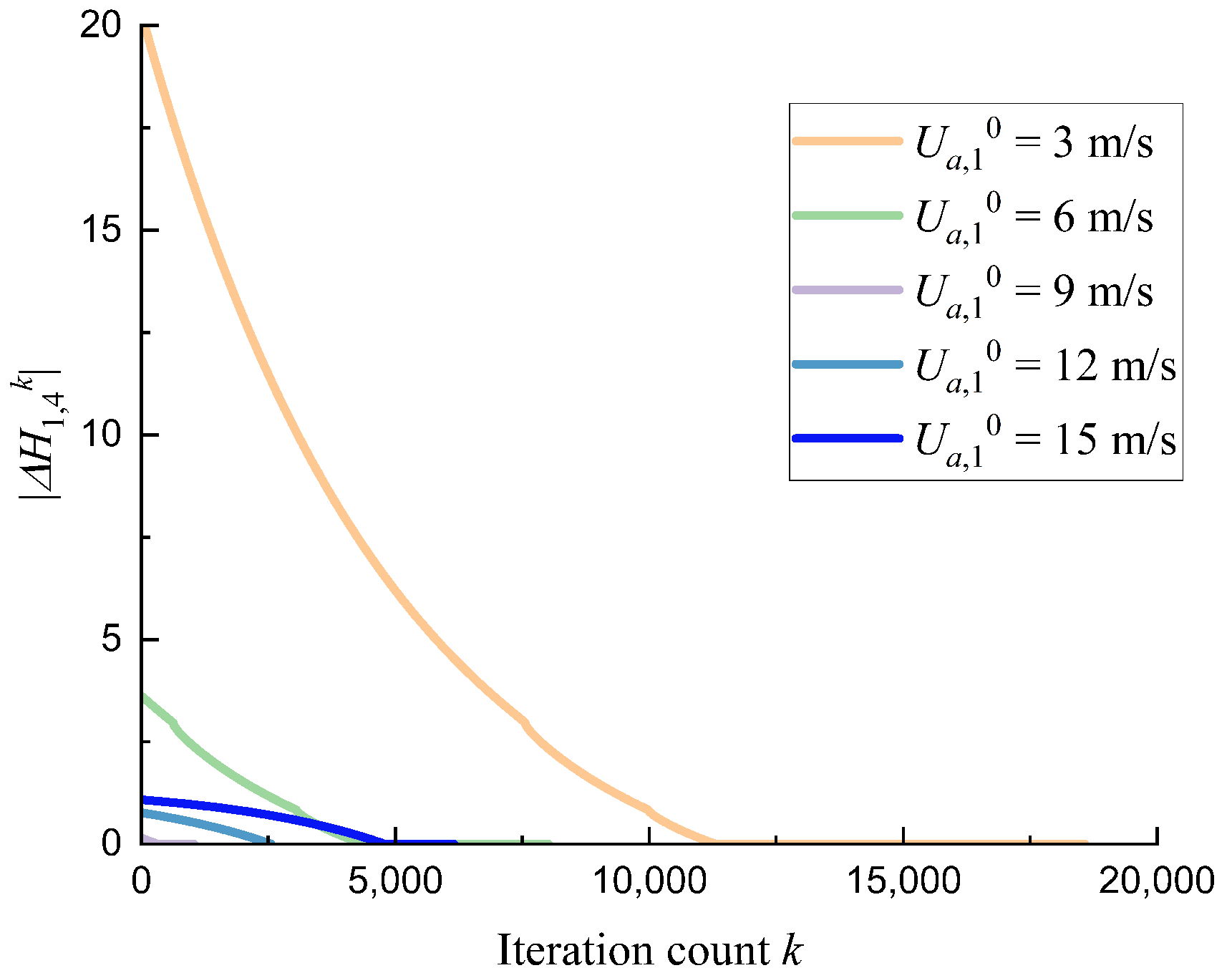
4.3. Convergence and Sensitivity Analysis
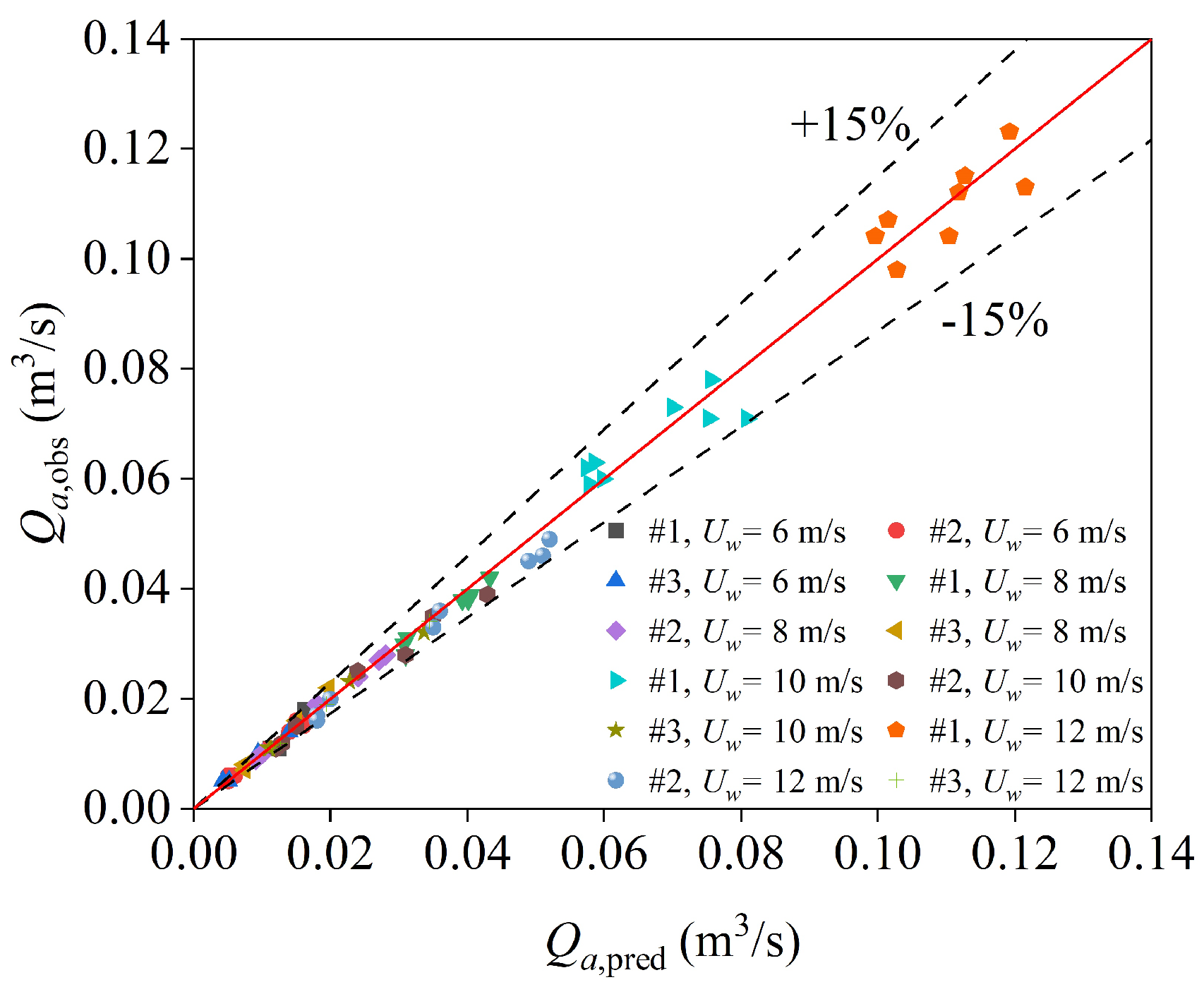
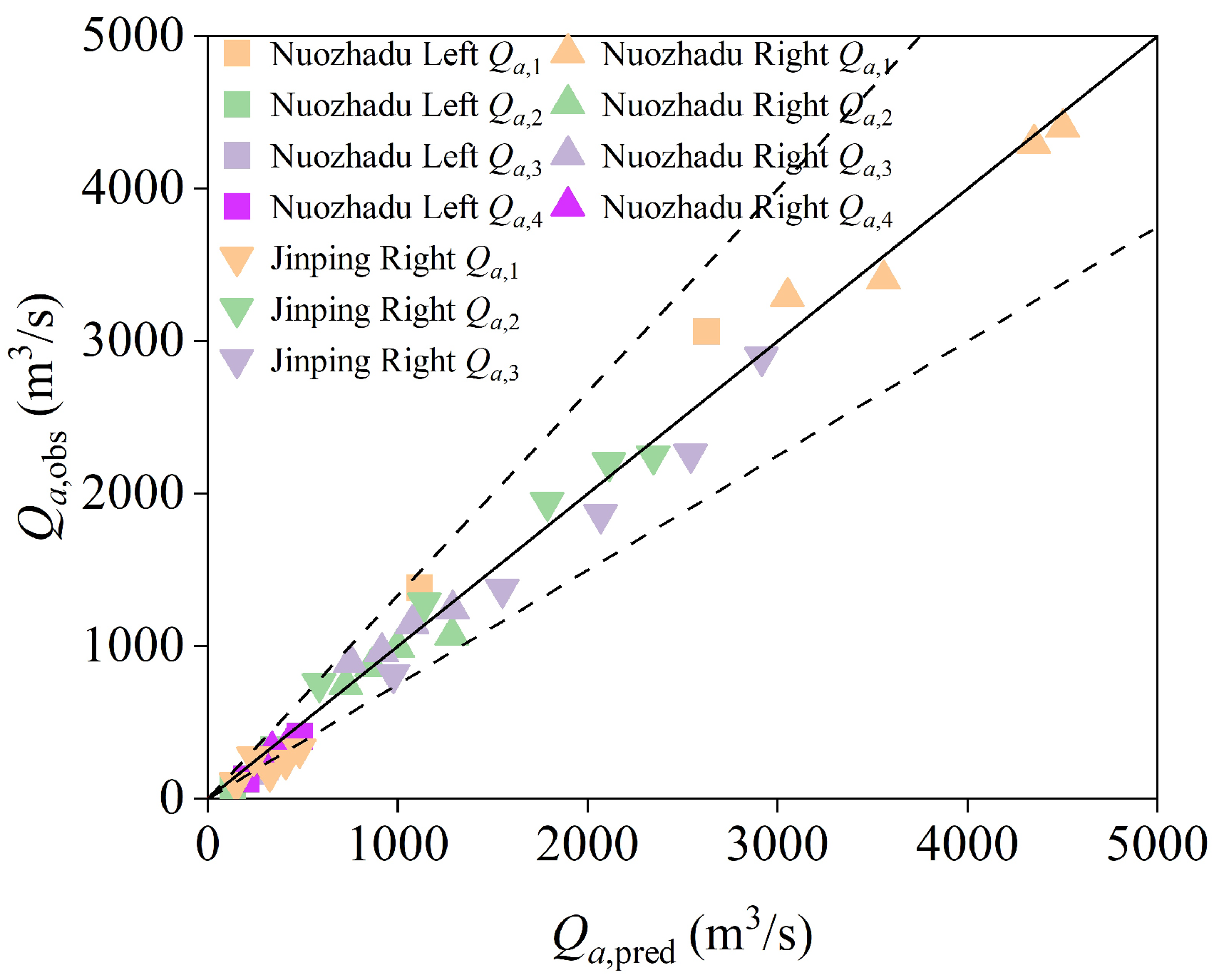
4.4. Comparison of the Prototype and Model Test Dates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pagliara, S.; Hohermuth, B.; Boes, R.M. Air–Water Flow Patterns and Shockwave Formation in Low-Level Outlets. J. Hydraul. Eng. 2023, 149, 06023002. [Google Scholar] [CrossRef]
- Speerli, J.; Hager, W.H. Air-water flow in bottom outlets. Can. J. Civ. Eng. 2000, 27, 454–462. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, H. Experimental study on pressurized and free-surface flow of discharge tunnel. J. Hydraul. Eng. 1964, 4, 52–57. [Google Scholar] [CrossRef]
- Crookston, B.M.; Erpicum, S. Hydraulic engineering of dams. J. Hydraul. Res. 2022, 60, 184–186. [Google Scholar] [CrossRef]
- Falvey, H.T. Air-water flow in hydraulic structures. NASA STI/Recon Tech. Rep. N 1980, 81, 26429. [Google Scholar]
- Hohermuth, B.; Vetsch, D.F.; Schmocker, L.; Felder, S.; Boes, R.M. Air-Water Flow Downstream of High-Head Sluice Gates: Experimental and Numerical Investigations. In Proceedings of the 38th IAHR World Congress—Water: Connecting the World, Panama City, Panama, 1–6 September 2019. [Google Scholar]
- Wei, W.R.; Deng, J.; Xu, W. Numerical investigation of air demand by the free surface tunnel flows. J. Hydraul. Res. 2021, 59, 158–165. [Google Scholar] [CrossRef]
- Kalinske, A.A.; Robertson, J.M. Entrainment of Air in Flowing Water: A Symposium: Closed Conduit Flow. Trans. Am. Soc. Civ. Eng. 1943, 108, 1435–1447. [Google Scholar] [CrossRef]
- Campbell, F.; Guyton, B. Air Demand In Gated Outlet Works. In Proceedings of the Minnesota International Hydraulic Convention, Minneapolis, MN, USA, 1–4 September 1953; pp. 529–533. [Google Scholar]
- Wisner, P. Hydraulic design for flood control by high head gated outlets. In Proceedings of the 9th ICOLD Congress, Istanbul, Turkey, 4–8 September 1967; pp. 495–507. [Google Scholar]
- Sharma, H.R. Air Demand for High Head Gated Conduits. Ph.D. Thesis, Norwegian Institute of Technology, University of Trondheim, Trondheim, Norway, 1973. [Google Scholar]
- Hohermuth, B.; Schmocker, L.; Boes, R.M. Air Demand of Low-Level Outlets for Large Dams. J. Hydraul. Eng. 2020, 146, 04020055. [Google Scholar] [CrossRef]
- Gao, Y. Ventilation of closed drain pipes. In Progress in Water Conservancy and Hydropower Science and Technology; Water Resources Press: Beijing, China, 1963; Volume 1, pp. 138–148. [Google Scholar]
- Luo, H. Study of air intake problems in drainage pipes. J. Hydraul. Eng. 1984, 64–70. [Google Scholar]
- Lian, J.; Wang, X.; Liu, D. Air demand prediction and air duct design optimization method for spillway tunnel. J. Hydraul. Res. 2021, 59, 448–461. [Google Scholar] [CrossRef]
- Wang, X.; Lian, J. Numerical Investigation on Air–Water Two-Phase Flow of Jinping-I Spillway Tunnel. Appl. Sci. 2022, 12, 4311. [Google Scholar] [CrossRef]
- Yazdi, J.; Zarrati, A.R. An algorithm for calculating air demand in gated tunnels using a 3D numerical model. J. Hydro-Environ. Res. 2011, 5, 3–13. [Google Scholar] [CrossRef]
- Fan, W.; Anglart, H. A new set of volume of fluid solvers for turbulent isothermal multiphase flows in OpenFOAM. Comput. Phys. Commun. 2020, 247, 106876. [Google Scholar] [CrossRef]
- Almeland, S.K.; Mukha, T.; Bensow, R.E. An improved air entrainment model for stepped spillways. Appl. Math. Model. 2021, 100, 170–191. [Google Scholar] [CrossRef]
- Bertolotti, L.; Jefferson Loveday, R.; Ambrose, S.; Korsukova, E. A comparison of volume of fluid and Euler–Euler approaches in computational fluid dynamics modeling of two-phase flows with a sharp interface. J. Turbomach. 2021, 143, 121005. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Zhang, X.T.; Lou, Y.L.; Xing, W.P. Comparative Analysis of Wind Speed in Ventilation Hole Simulated by VOF and Euler Model. Appl. Mech. Mater. 2014, 624, 643–646. [Google Scholar] [CrossRef]
- González, F.S.; Saiz, J.S.M.; Jordana, M.Á.C.; de Navarra, E.O.I. Air demand estimation in bottom outlets with the particle finite element method. Susqueda Dam case study. Comput. Part. Mech. 2017, 4, 345–356. [Google Scholar]
- Yue, S.; Diao, M.; Zhao, J. Analysis and Research of Aeration Capacity of the Spillway Tunnel with High Speed Flows. Adv. Eng. Sci. 2013, 45, 7–12. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, W.; Ye, S. A study of prototype law of air demand in flood control conduits. Hydro-Sci. Eng. 1986, 1, 1–18. [Google Scholar] [CrossRef]
- Wang, W.; Liao, W.; Qi, L. Experiment of turbulent characteristics of flow in wide-and-narrow channels. Adv. Water Sci. 2020, 31, 394–403. [Google Scholar] [CrossRef]
- Liu, C.; Li, D.; Wang, X. Experimental study on friction velocity and velocity profile of open channel flow. J. Hydraul. Eng. 2005, 8, 950–955. [Google Scholar]
- Nezu, I.; Rodi, W. Open-channel Flow Measurements with a Laser Doppler Anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Yang, C. Research of Roughness Coefficient and Turbulence Character in Uniform Flow of Open Channel. Master’s Thesis, Northwest A&F University, Xianyang, China, 2010. [Google Scholar]
- Liu, D. Hydraulic Modelling of Air Demand of Aerators on High Velocity Sluicing Structures. J. Change River Sci. Res. Inst. 1995, 1, 1–10. [Google Scholar]
- Lv, H.; Yu, J. Experimental Research on Sudden Rising of Wall Roughness in Open Channels on the Effect of Turbulent Velocity and Turbulence Intensity. China Rural. Water Hydropower 2011, 1, 97–99. [Google Scholar]
- Ramesh, B.; Kothyari, U.C. Turbulence characteristics in an open channel flow over transitionally rough bed. ISH J. Hydraul. Eng. 2014, 20, 169–176. [Google Scholar] [CrossRef]
- Zhong, L.; Jiang, T.; Zhang, J.; Liu, J. PIV Experimental Study on Velocity Fluctuations of Turbulent Flow in Open Channel. Adv. Eng. Sci. 2019, 51, 84–93. [Google Scholar] [CrossRef]
- Brater, E.F.; King, H.W.; Lindell, J.E.; Wei, C.Y. Handbook of Hydraulics for the Solution of Hydraulic Engineering Problems, 7th ed.; McGraw-Hill Professional: New York, NY, USA, 1996. [Google Scholar]
- Yoosefdoost, A.; Lubitz, W.D. Sluice Gate Design and Calibration: Simplified Models to Distinguish Flow Conditions and Estimate Discharge Coefficient and Flow Rate. Water 2022, 14, 1215. [Google Scholar] [CrossRef]
- Zheng, D.; Chen, Y. Report on the Study of Ventilation and Noise Reduction in the Spillway Tunnel of Yunnan Lancangjiang River Nuozhadu Hydropower Project; Technical Report 1; Kunming Engineering Corporation Limited: Kunming, China, 2015. [Google Scholar]
- Lian, J.; Qi, C.; Liu, F.; Gou, W.; Pan, S.; Ouyang, Q. Air Entrainment and Air Demand in the Spillway Tunnel at the Jinping-I Dam. Appl. Sci. 2017, 7, 930. [Google Scholar] [CrossRef]
- Rabben, S.; Rouve, G. Air demand of high head gates-model-family studies to quantify scale effects. In Proceedings of the IAHR Symposium on Scale Effects in Modelling Hydraulic Structures, Esslingen am Neckar, Germany, 3–6 September 1984; pp. 4–9. [Google Scholar]
- Rabben, S. Untersuchung der Belüftung an Tiefschützen Unter besonderer Berücksichtigung von Maßstabseffekten. Ph.D. Thesis, Institut für Wasserbau und Wasserwirtschaft, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 1984. Available online: https://publications.rwth-aachen.de/record/68562 (accessed on 1 May 2025).

| Reference | Equation | Flow Pattern |
|---|---|---|
| Kalinske [8] | Hydraulic jump | |
| Campbell [9] | Free-surface flow | |
| Wisner [10] | Hydraulic jump | |
| Hydraulic jump | ||
| Free-surface flow | ||
| Sharma [11] | Free-surface flow | |
| Hydraulic jump | ||
| Speerli [2] | Free-surface flow | |
| Hohermuth [12] | Free-surface flow | |
| Gao [13] | with | Free-surface flow |
| Luo [14] | with | Free-surface flow |
| Lian [15] | with | Free-surface flow |
| Case | Condition 1 | Condition 2 | Comment |
|---|---|---|---|
| (1) | = 6, 7, 8, 9, 10, 11, 12 m/s | = 4, 6, 8, 10 cm | |
| m, m | |||
| (2) | m, | m/s, cm | |
| m | |||
| (3) | m/s, cm | ||
| m; | |||
| m; | |||
| m; | |||
| m; | |||
| m | |||
| (4) | m/s, cm | ||
| m; | |||
| m; | |||
| m; | |||
| m | |||
| (5) | m/s | = 12, 45, 60, 70, 110, 180, m | , cm, |
| m |
| % | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −10 | −5 | 5 | 10 | −10 | −5 | 5 | 10 | −10 | −5 | 5 | 10 | −10 | −5 | 5 | 10 | −10 | −5 | 5 | 10 | |
| −19.97 | −10.24 | 10.73 | 21.94 | −3.38 | −1.69 | 1.67 | 3.31 | 3.32 | 1.61 | −1.52 | −2.97 | −0.32 | −0.16 | 0.15 | 0.30 | −1.72 | −0.86 | 1.68 | 0.85 | |
| −18.95 | −9.66 | 10.01 | 20.33 | −1.73 | −0.79 | 0.60 | 0.95 | 2.69 | 1.32 | −1.26 | −2.47 | −0.29 | −0.14 | 0.14 | 0.27 | 0.44 | 0.22 | −0.43 | −0.21 | |
| −18.14 | −9.20 | 9.44 | 19.07 | −0.38 | −0.05 | −0.29 | −1.01 | 2.15 | 1.06 | −1.03 | −2.04 | −0.25 | −0.13 | 0.12 | 0.24 | 0.49 | 0.24 | −0.48 | −0.24 | |
| Project | Spillway Tunnel | Air Vent Area () | (m) | (m) | (m/s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | #1 | #2 | #3 | #4 | |||||||
| Nuozhadu Left | 12 | 16 | 497.8 | 31 | 8 | 9.6 | 12 | 1.7 | 35.6 | 44.7 | 10.8 | 18.8 | 10.8 |
| 9.0 | 34.8 | 98.8 | 40.6 | 21.7 | 32.5 | ||||||||
| Nuozhadu Right | 12 | 16.5 | 382.7 | 36 | 9.42 | 9.42 | 9.42 | 3.4 | 36.5 | 91.4 | 79.0 | 94.5 | 10.8 |
| 5.1 | 36.4 | 94.5 | 92.0 | 101.7 | 15.3 | ||||||||
| 6.8 | 36.2 | 119.3 | 105.1 | 121.7 | 15.3 | ||||||||
| 8.5 | 36.1 | 122.2 | 113.7 | 131.5 | 15.3 | ||||||||
| JinPing-I Right | 13 | 17 | 1407 | 85 | 36 | 36 | / | 1.1 | 22.0 | 19.5 | 23.8 | 22.6 | / |
| 3.5 | 18.8 | 32.2 | 44.0 | 38.2 | |||||||||
| 7.0 | 17.4 | 46.7 | 54.0 | 51.8 | |||||||||
| 10.5 | 16.9 | 61.1 | 61.3 | 62.8 | |||||||||
| 14.0 | 19.0 | 52.2 | 62.5 | 80.4 | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Fan, Q.; Tian, Z.; Wang, W. Experimental Study of the Air Demand of a Spillway Tunnel with Multiple Air Vents. Appl. Sci. 2025, 15, 5831. https://doi.org/10.3390/app15115831
Yang H, Fan Q, Tian Z, Wang W. Experimental Study of the Air Demand of a Spillway Tunnel with Multiple Air Vents. Applied Sciences. 2025; 15(11):5831. https://doi.org/10.3390/app15115831
Chicago/Turabian StyleYang, Hao, Qiang Fan, Zhong Tian, and Wei Wang. 2025. "Experimental Study of the Air Demand of a Spillway Tunnel with Multiple Air Vents" Applied Sciences 15, no. 11: 5831. https://doi.org/10.3390/app15115831
APA StyleYang, H., Fan, Q., Tian, Z., & Wang, W. (2025). Experimental Study of the Air Demand of a Spillway Tunnel with Multiple Air Vents. Applied Sciences, 15(11), 5831. https://doi.org/10.3390/app15115831







