Abstract
In existing traffic simulation software or studies related to traffic flow at signalized intersections, the treatment of yellow lights is often simplified or overlooked. However, driving behavior during the yellow phase is characterized by significant uncertainty, which can lead to discrepancies between simulation results and real-world conditions. To address this issue, this paper develops a driving behavior model based on risk perception and fuzzy decision-making and integrates it into a simulation framework to replicate continuous driving behaviors at isolated signalized intersections. The performance of intersections under varying yellow light durations is analyzed, yielding some key findings. For instance, when vehicles strictly adhere to the designed speed, increasing the yellow light duration from 3 s to 5 s results in higher traffic volumes under high traffic density. Furthermore, real-time traffic speed fluctuations stabilize, and the occurrence of unsafe driving behaviors decreases. The concept of risk perception is employed to explain the underlying mechanisms behind these phenomena. This paper provides both a theoretical foundation and a simulation framework for more detailed representations of driving behaviors and for explaining the fundamental principles governing intersection performance.
1. Introduction
Simulation is an effective means of replicating the real world or envisioning future scenarios, particularly in studies involving complex systems, multiple variables, uncertain and dynamic environments, or high-cost experiments [1,2,3]. For traffic flow simulation, many software tools have been developed and widely applied, such as VISSIM, SUMO, and others [4,5,6]. These tools use various micro driving behavior models to describe traffic performance with different levels of accuracy, ranging from microscopic analysis of driver behavior to macroscopic modeling of traffic flow [7].
In scenarios involving signalized intersections, the signal light is a key factor influencing both efficiency and safety, because the decision-making behavior of drivers during the yellow light phase is characterized by randomness and uncertainty [8,9,10]. However, these simulation tools rarely provide a detailed description of driving behavior during the yellow phase and struggle to explore the impact of yellow phase settings on driving behavior and traffic flow. Instead, they define driver decision-making through simple response parameters. This does not align with real-world traffic conditions, especially conditions that are typical in China. Furthermore, the micro driving behavior models used in the simulation tools are typically developed separately based on the characteristics of road spatial structure, such as car-following models, lane-changing models, and yielding models at intersections. When these different knowledge-driven or data-driven models are integrated into a simulation environment, they need to be switched at the junctions of different road spatial structures to ensure that the driving behavior model a vehicle follows aligns with the road spatial structure it is currently in. This transition can negatively affect the smoothness of the simulation between different road spatial structures.
Therefore, there is a clear need for a driving behavior model developed with unified logic. Our previous research focused on modeling driving behavior based on the subjective risk perception of drivers under “risk prediction–motion planning” logic, which includes car-following and lane-changing, as well as behavior at both signalized and unsignalized intersections [8,11,12,13,14] and will be described in detail in Section 3. It is particularly important to highlight that we have developed a refined model for stop/go decision-making behavior during the yellow phase, capturing the heterogeneity in drivers’ risk acceptance [8]. However, each driver’s risk acceptance level has been assumed to be fixed, with his/her inherent uncertainty overlooked.
Although broad insights are available about the effects of signal timing characteristics on traffic flow performance [15,16,17], little is known about the exact effects of the perception processes involved which may have indirect effects on traffic flow by influencing driver-related characteristics. In this paper, we improve our previous model by incorporating a fuzzy decision-making approach and integrating it into a simulation framework with a particular focus on the setting of yellow light duration. By simulating continuous vehicle movement in an upstream road segment and within an intersection, we investigate the impact of yellow light duration on driver performance at isolated signalized intersections and explain the underlying mechanisms based on risk perception theory. This study extends our previous research, aiming to establish the connection between driving behavior mechanisms and observed traffic phenomena, thereby providing a theoretical foundation and simulation tool for explaining the underlying logic of driver behavior and improving safety and efficiency at signalized intersections.
The contributions of this study are reflected in the following three aspects:
- By enhancing the previous risk-perception-based driving behavior model with fuzzy decision-making theory, the micro-level influence of yellow light duration is incorporated into the simulation, further narrowing the gap between simulated and actual driving behaviors.
- A simulation framework employing a set of driving behavior models based on unified modeling logic is integrated, which attempts to eliminate the complexity of switching between different driving behavior models across various road areas and traffic scenarios.
- The process of risk perception grounded in risk homeostasis theory is suggested to explain the underlying mechanisms of traffic flow performance at isolated signalized intersections.
This paper is organized as follows: Section 2 provides a brief review of related work; Section 3 introduces the risk perception and fuzzy decision-based driving behavior model; Section 4 describes the simulation framework and sets the simulation parameters for modeling continuous driving behavior at an isolated signalized intersection under different yellow light durations; Section 5 and Section 6 analyze and discuss the simulation results of traffic flow performance in four aspects: traffic volume, queue length, average speed, and safety; and the final section presents the study’s conclusions and limitations.
2. Literature Review
Due to the inherent uncertainty in driver decision-making behavior when approaching signalized intersections during the yellow light phase, most researchers have adopted statistical models to describe stop-or-go decisions and to estimate the likelihood of different choices. Discrete Choice Models [18,19] have been widely used to establish the relationship between driver decisions and various influencing factors after the onset of the yellow signal, most commonly through binary logistic regression models. In addition, Fuzzy Logic Models [20], Bayesian Networks [21], and Agent-based Models [22] have also been employed to capture and predict driver behavior. However, the hesitation of human drivers to enter an intersection during the yellow phase can affect traffic flow, potentially increasing the risk of collisions, fuel consumption, and travel time [23,24,25]. This calls for greater attention on models of uncertain driving behavior during the yellow phase to bridge the gap between simulated environments and actual traffic conditions. The above models primarily focus on data-driven approaches to identifying decision-making patterns, without incorporating the risk perception process or exploring the fundamental causes behind decisions.
In current research involving human-driven or autonomous vehicles, scholars often use models such as the IDM (Intelligent Driver Model) [26,27], Gipps model [28,29,30], optimal velocity model [31,32], and Newell’s car-following model [26,33] to simulate the behavior of human-driven vehicles following other vehicles. However, when describing behavior when approaching signalized intersections, only a few studies have considered the yellow light phase. For instance, Ma et al. considered a yellow duration of 3 s, allowing vehicles to pass the stop line within the first second of the yellow phase during trajectory planning [33]. Yao et al. separated the yellow duration into effective green and red phases [28,29]. Cheng et al. allowed human-driven vehicles to stop before the stop line during the yellow phase [34]. These studies typically simplify or idealize the treatment and assumptions regarding the yellow phase. In fact, many researchers overlook the impact of the yellow phase on driving behavior, assuming that vehicles can only pass through the intersection during the green phase. However, this assumption does not align with real-world traffic conditions and may lead to errors in simulation results.
In existing simulation software, driving behavior models built on different logical frameworks have been applied to various traffic scenarios. Table 1 presents a comparative overview of the models adopted by several widely used traffic simulation tools, highlighting the diversity in modeling strategies. However, this may hinder consistency and scalability when applying the same simulation across multiple scenarios. In contrast, models developed under a unified logical framework may be more conducive to smoother and more convenient transitions between structured simulation scenarios, as they enable standardized interpretation of driving behaviors, especially when studying complex, multi-phase traffic conditions.

Table 1.
Driving behavior models used in major traffic simulation software.
3. Risk Perception and Fuzzy Decision-Based Driving Behavior Model
Under the unified logic of “risk prediction–motion planning”, a driving behavior model based on subjective risk perception has been established and rigorously validated in scenarios such as car-following on road segments and approaching signalized intersections. This section provides a brief introduction to the modeling process, with detailed steps available in previous studies [8,11]. Furthermore, to characterize the uncertainty in driver decision-making during the yellow light phase, we enhance our previous model by integrating risk perception theory with fuzzy decision-making theory, as detailed in Section 3.3.
3.1. Risk Quantification
We successively introduced a risk field model framework that uniformly defines the risks posed by traffic elements, including moving vehicles and signal lights [8,11]. The model posits that the risk generated by an element varies within a range of 0 to 1.
For a vehicle, the risk value within its coverage area is equal to 1. At the same speed, as the relative distance from the vehicle increases, the risk in each direction decreases from 1 and gradually approaches 0. Conversely, at the same position, the risk increases with speed but never exceeds 1. Equations (1)–(6) provide the method for quantifying the risk of a moving vehicle in both the lateral and longitudinal directions, characterizing the risk imposed by vehicle k on (x, y) as follows:
where αvehicle,k,x and βvehicle,k,x represent the influence of the lateral speed and relative distance of the k-th vehicle on its lateral risk, respectively; αvehicle,k,y and βvehicle,k,y represent the influence of the longitudinal speed and longitudinal relative distance, respectively, of the k-th vehicle on its longitudinal risk; k,x(t) and k,y(t) represent the lateral and longitudinal speeds, respectively, of the k-th vehicle at time t; and Lk and Wk represent the length and width of the k-th vehicle, respectively.
Figure 1 illustrates the risk generated by moving vehicles, exhibiting a spatial pattern that radiates outward from the vehicle coverage area and gradually decreases. The higher the speed of vehicles, the greater the risk imposed at a given location.
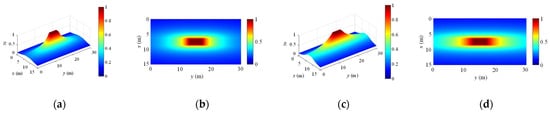
Figure 1.
Spatial morphology of risk arising from an individual moving vehicle: (a) risk arising from individual moving vehicle ( = 5 m/s, = 0); (b) risk arising from individual moving vehicle ( = 5 m/s, = 0, top view); (c) risk arising from individual moving vehicle ( = 10 m/s, = 0); and (d) risk arising from individual moving vehicle ( = 10 m/s, = 0, top view).
Similarly, risks arising from traffic lights are regarded as risks arising from virtual static obstacles at the stop line. Equations (7)–(10) describe the risk field model of traffic lights, which is a form of multiplying time and spatial variation functions.
where li and di represent the length and width of the i-th stop line; βi,x and βi,y represent the influence degree of the relative spacing of the i-th stop line on the longitudinal and lateral risk; tj,g, tj,y, tj,r, Tj are the durations of green light, yellow light, red light, and signal cycle at the j-th traffic light; and n is a natural number.
Visually, at a certain moment, the risks at signal lights present a spatial pattern with the stop line as the center, radiating outwardly and gradually decreasing, as shown in Figure 2.
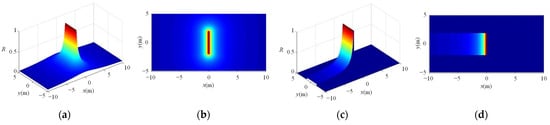
Figure 2.
Spatial morphology of risk arising at traffic lights: (a) all-round spatial variation; (b) all-round spatial variation (top view); (c) spatial variation only considering the actual area; and (d) spatial variation only considering the actual area (top view).
When the risks generated by different objects at the same time and space overlap, we take the largest value among them.
3.2. Risk Prediction
According to preview-follower theory [53], a driver will predict the state of the subject vehicle in the following time based on the current state. We assume that the vehicle travels at a constant speed during the preview time. The position and speed of the subject vehicle after the preview time can be calculated by Equation (11):
where T is preview time; xs(t) and s(t) are the position and speed, respectively, of the subject vehicle at the time t; and xs,p(t + T) represents the predicted position of the subject vehicle at the time t + T.
Then, the risk generated by the traffic elements after the preview time can be calculated by plugging t + T into Equations (6) and (10). Finally, by substituting the predicted position of the subject vehicle into the risk field model, the risk borne by the subject vehicle after the preview time can be obtained. The predicted risk is the basis on which the subject driver makes motion decisions at this time step.
3.3. Fuzzy Decision
Fuzzy decision-making theory is intended to handle decision-making problems characterized by uncertainty, vagueness, and subjectivity. It has been effectively applied to the modeling of driving behavior [54,55,56]. When the leading vehicle approaches a signalized intersection during the yellow light phase, a decision must be made whether to proceed or stop. In our previously developed risk-perception-based model, each driver’s desired risk was assumed to be a fixed value. However, this assumption overlooks the inherent uncertainty influenced by various factors, such as individual personality traits and road environment conditions. Therefore, in this study, we improve the model by incorporating fuzzy decision-making based on the distance to the stop line, current speed, and perceived risk of the traffic signal. For following vehicles, which are not responsible for leading decisions, their motion decisions are simplified by considering only the perceived risk induced by the preceding vehicle.
We used 2303 yellow phase-approaching cases extracted from high-resolution event-based data collected at six intersections along Trunk Highway 55 in the Twin Cities area, as shown in Figure 3. The data were gathered using the SMART-SIGNAL system developed by the University of Minnesota, which continuously records vehicle detector actuations and signal phase changes [57,58]. The cases were investigated from west to east in the direction of the particular phase, in which the green phase time is 110 s, yellow phase time is 5.5 s, and the total cycle length is 210 s, including detailed timestamps of vehicle arrivals at the stop line after yellow onset. The data did not include information on the speed limit at the intersection entrance or on the upstream road segment. However, analysis of the 2303 cases shows that the approach speeds follow a normal distribution, with a mean of 22.94 m/s and a standard deviation of 3.57 m/s and values ranging from 6.40 m/s to 29.92 m/s. The acceleration data also follow a normal distribution, with a mean of 0.61 m/s2, a standard deviation of 1.41 m/s2, and a range from −7.92 m/s2 to 3.93 m/s2. Among the cases, 1833 involved accelerations through the intersection, while 470 involved decelerations.
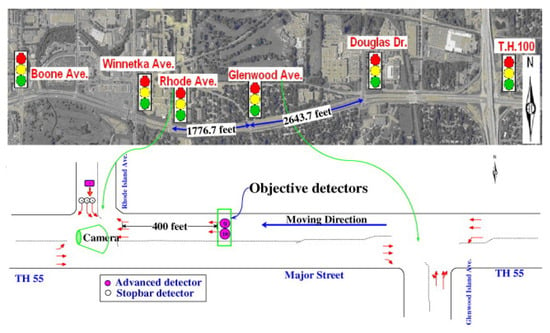
Figure 3.
Data collection site.
As observed from the cases, even when a vehicle is very close to the stop line, there are instances where a deceleration decision is still made due to the predicted signal risk being high and approaching 1. This occurs even though the remaining distance to the stop line may be insufficient to meet the braking requirements, potentially resulting in a yellow-running outcome despite the driver’s intention to stop. Therefore, in addition to the commonly considered factors, i.e., distance to the stop line and vehicle speed at the onset of the yellow phase, we introduced the perceived signal risk calculated using Equation (9) as the third factor in the decision-making process. The marginal histograms illustrating the distributional relationships among these three factors are shown in Figure 4.
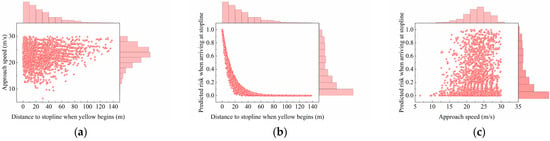
Figure 4.
Distributional relationships among three factors: (a) approach speed vs. distance to stop line; (b) predicted risk vs. distance to stop line; and (c) predicted risk vs. approach speed.
Based on the 2303 yellow phase-approaching cases, membership functions for the three input factors were constructed, as shown in Figure 5. Subsequently, through fuzzy inference and defuzzification (the principles and procedures for creating fuzzy rules are not elaborated here), a fuzzy decision tree representing driver behavior during the yellow phase was developed, as illustrated in Figure 6. The output of the model is the probability of passing or not passing the stop line. An overall prediction accuracy of 80% was achieved for classifying pass and no-pass decisions. Accordingly, we characterize the driver’s behavior approaching intersections during the yellow phase through the lens of risk perception and fuzzy decision-making, without limiting the analysis to whether the vehicle was located within the dilemma zone.
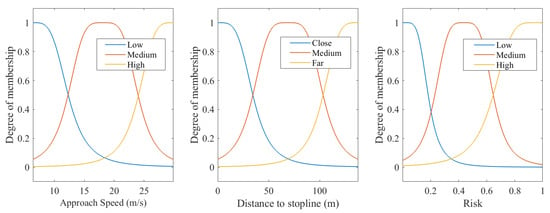
Figure 5.
Membership functions of the three factors.
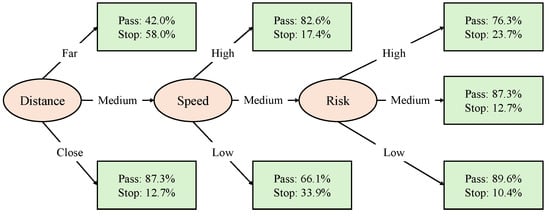
Figure 6.
Fuzzy decision model of driving behavior during yellow phase.
3.4. Motion Planning
For the motion path of vehicles inside the intersection, we use the path planning model based on the third-order Bezier curve proposed by Lu et al. [59].
For leading vehicles approaching the intersection and directly affected by signal risk during the yellow phase, trajectory planning should be performed at each time step following the fuzzy decision-making process. Similarly, following vehicles, although not subject to fuzzy decision-making, also carry out trajectory planning based on the risk induced by their respective preceding vehicles. According to the risk homeostasis theory [60], a driver has a relatively fixed desired risk and makes decisions based on the difference between subjectively perceived risk and desired risk while driving. Therefore, the key point of vehicle trajectory planning is to find the desired position after the preview time according to the predicted risk.
We need to look for the desired position xs,d(t + T) in the predicted risk field that matches the driver’s desired risk. Then the acceleration s(t) required to reach the desired position can be calculated by Equation (12), thus completing trajectory planning within a time step.
4. Simulation Framework
4.1. Building Simulation Environment
A traffic flow simulation environment for an isolated signalized intersection was built in MATLAB 2024a on a system equipped with Windows 10, an Intel Core i7-10700 2.90 GHz processor, and 16.0 GB RAM. The driving behavior models were embedded within this environment. The specific architecture is shown in Figure 7.
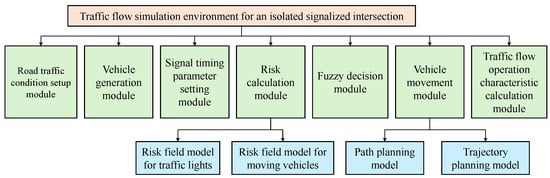
Figure 7.
Simulation environment architecture.
The simulation environment primarily includes modules for road traffic condition setup, vehicle generation, signal timing parameter settings, risk calculation, fuzzy decision-making, vehicle movement, and traffic flow operation characteristic calculation.
4.2. Setting Simulation Parameters
Setting the yellow light at the signalized intersection serves as a buffer and warning for passing vehicles [61]. If a driver decides to decelerate and stop upon seeing the yellow light, he/she needs to stop in front of the stop line before the red light is activated. Therefore, the design method for the yellow light duration (ty) at an isolated signalized intersection typically follows Equation (13):
where t0 represents the reaction time (s) for a driver to make a decision after seeing the yellow light; v denotes the vehicle speed (m/s); and b indicates the vehicle braking deceleration (m/s2).
Vehicle speed is a key variable in determining yellow phase duration and is generally taken as the speed limit at the intersection. According to the European agreement on road traffic signs and signals, Li [62] provides recommended yellow light durations for different speed limits, as shown in Table 2. Additionally, Li et al. [63] have suggested minimum yellow phase durations based on a comprehensive comparison of yellow phase duration calculation methods in Germany, the United States, and Japan, in conjunction with actual conditions in China. Therefore, this paper considers yellow phase durations of 3 s, 4 s, and 5 s in the simulation, which represent commonly adopted values in international practice. Specifically, 3 s is typical for low-speed urban roads (≤40 km/h), 4 s is widely used for medium-speed roads (40–70 km/h), and 5 s accounts for higher-speed or safety-enhanced settings. These values ensure the simulation reflects representative traffic control standards.

Table 2.
Recommended yellow light durations.
Variability in driving behavior is one of the main reasons for poor stability and safety in traffic flow [64]. To analyze the impact of differences in driver behavior under varying yellow phase durations on traffic efficiency and safety at signalized intersections, a scenario for a specific approach direction at an isolated signalized intersection was set up in the constructed simulation environment, with specific simulation parameters as follows:
- The total length of the upstream segment of the signalized intersection is 2000 m.
- To intuitively analyze the traffic volume for each direction and specifically observe the impact of yellow phase duration, the approach direction was individually configured with three lanes, with vehicle departure proportions for left-turn, straight, and right-turn lanes set at 30%, 30%, and 40%, respectively, without considering lane-changing behavior on the upstream segment.
- It is assumed that vehicle departures follow a Poisson curve, with the number of departing vehicles per unit time (λ) set at 0.2 veh/s, 0.3 veh/s, and 0.4 veh/s. For all vehicles, the departure speed was set as equal to the intersection design speed.
- The simulation duration is 3600 s. The signal cycle length is 123 s, with a constant green duration, and three signal timing schemes are set:
- ✧
- Green light lasts for 60 s, yellow light lasts for 3 s, and red light lasts for 60 s.
- ✧
- Green light lasts for 60 s, yellow light lasts for 4 s, and red light lasts for 59 s.
- ✧
- Green light lasts for 60 s, yellow light lasts for 5 s, and red light lasts for 58 s.
- It is assumed that vehicles strictly adhere to the intersection design speed, meaning they always travel at the speed limit in a free-flowing state. Since the observed maximum acceleration rate is nearly 4 m/s2 and the maximum deceleration rate is about 8 m/s2, the range of vehicle acceleration is from −8 to 4 m/s2, and overtaking is not allowed during travel.
Additionally, the effects of signal timing at upstream consecutive intersections on vehicle departures and the impacts of other conflicting vehicles at the intersection are not considered, as well as non-motorized vehicles and pedestrians.
The specific parameter settings for different simulation experimental groups are shown in Table 3.

Table 3.
Simulation parameter settings under different ty.
5. Results
5.1. Traffic Volume
Under conditions where λ is set to 0.2 veh/s, 0.3 veh/s, and 0.4 veh/s, and Vmax is 60 km/h, the simulation yielded left-turn and straight traffic volumes for ty of 3 s, 4 s, and 5 s, corresponding to Groups 1, 2, and 3, respectively, as shown in Table 4. When the number of departing vehicles is relatively low (λ = 0.2 veh/s and 0.3 veh/s), no distinct patterns in traffic volumes on the entrance lane were observed in the simulation with different yellow phase durations. However, as λ increased to 0.4 veh/s, the traffic volumes on both the left-turn and straight lanes exhibited rising trends as ty increased from 3 s to 5 s.

Table 4.
Traffic volumes on left-turn and straight lanes under different ty (Vmax = 60 km/h).
Under conditions where Vmax is set to 50 km/h, 60 km/h, and 70 km/h, and λ is 0.3 veh/s, the simulation results for left-turn and straight traffic volumes at ty of 3 s, 4 s, and 5 s, corresponding to Groups 4, 5, and 6, are shown in Table 5. At a constant λ = 0.3 veh/s and Vmax, the effect of yellow phase durations on traffic volumes remains inconspicuous, consistent with the findings presented in Table 4. This suggests that under relatively low traffic densities, the impact of yellow duration on traffic efficiency is minimal.

Table 5.
Traffic volumes on left-turn and straight lanes under different ty (λ = 0.3 veh/s).
5.2. Queue Length
Under conditions where λ is set to 0.2 veh/s, 0.3 veh/s, and 0.4 veh/s, with Vmax of 60 km/h, the simulated queue lengths for left-turn and straight lanes per signal cycle with ty of 3 s, 4 s, and 5 s, corresponding to Groups 1, 2, and 3, are shown in Figure 8a–c. Similarly, under conditions where Vmax is set to 50 km/h, 60 km/h, and 70 km/h and λ is 0.3 veh/s, the statistical results for queue lengths in left-turn and straight lanes per signal cycle with ty of 3 s, 4 s, and 5 s, corresponding to Groups 4, 5, and 6, are shown in Figure 8d–f. As the simulation includes 30 signal cycles, each box plot contains 30 data points with each representing the queue length (veh) within an individual signal cycle.
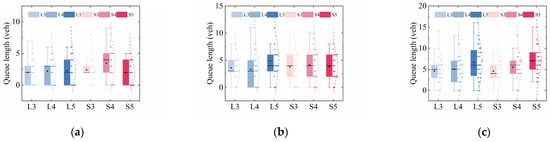
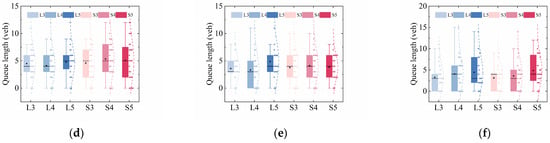
Figure 8.
Queue lengths at left-turn lanes and straight lanes under different ty (L = left-turn lane, S = straight lane; 3, 4, and 5 represent ty = 3 s, 4 s, and 5 s, respectively): (a) Vmax = 60 km/h and λ = 0.2 veh/s; (b) Vmax = 60 km/h and λ = 0.3 veh/s; (c) Vmax = 60 km/h and λ = 0.4 veh/s; (d) Vmax = 50 km/h and λ = 0.3 veh/s; (e) Vmax = 60 km/h and λ = 0.3 veh/s; (f) Vmax = 70 km/h and λ = 0.3 veh/s.
As shown in Figure 8c, under high traffic volume conditions (λ = 0.4 veh/s), the queue lengths per signal cycle when ty is set to 4 s or 5 s is slightly longer compared to that when ty is set to 3 s in most cycles. That is, for ty of 3 s, 4 s, and 5 s, the average queue lengths per cycle in the left-turn lane are 4.6 veh, 5.1 veh, and 6.6 veh, respectively, while in the straight lane, the average queue lengths per cycle are 4.6 vehicles, 5.4 vehicles, and 7.0 vehicles, respectively.
Similarly, as seen in Figure 8f, when the speed limit is relatively high (Vmax = 70 km/h), the queue lengths per signal cycle are slightly longer at ty of 4 s and 5 s than at 3 s in most cycles. Specifically, for ty of 3 s, 4 s, and 5 s, the average queue lengths per cycle in the left-turn lane are 3.2 veh, 4.0 veh, and 4.4 veh, respectively, while in the straight lane, the average queue lengths per cycle are 3.1 veh, 3.6 veh, and 4.9 veh.
Additionally, as shown in Figure 8a,b,d,e, when the traffic volume is low, and when Vmax is set to 50 km/h and 60 km/h, yellow light duration has no significant impact on queue length.
5.3. Average Speed
When λ is 0.2 veh/s, 0.3 veh/s, and 0.4 veh/s respectively, and Vmax is 60 km/h, the simulation results indicate that for ty of 3 s, 4 s, and 5 s (corresponding to Groups 1, 2, and 3), the real-time average speeds of left-turning and straight-going vehicles at each time step are shown in Figure 9. Similarly, when Vmax is 50 km/h, 60 km/h, and 70 km/h, and λ is 0.3 veh/s, the simulation results for ty of 3 s, 4 s, and 5 s (corresponding to Groups 4, 5, and 6) are presented in Figure 10, which illustrate the real-time average speeds of left-turning and straight-going vehicles at each time step.
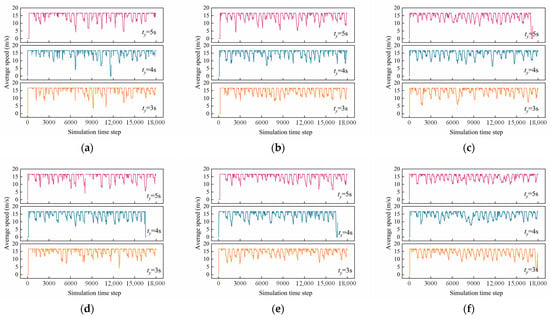
Figure 9.
Average vehicle speed under different ty (Vmax = 60 km/h): (a) left-turning vehicles, λ = 0.2 veh/s; (b) left-turning vehicles, λ = 0.3 veh/s; (c) left-turning vehicles, λ = 0.4 veh/s; (d) straight-going vehicles, λ = 0.2 veh/s; (e) straight-going vehicles, λ = 0.3 veh/s; and (f) straight-going vehicles, λ = 0.4 veh/s.
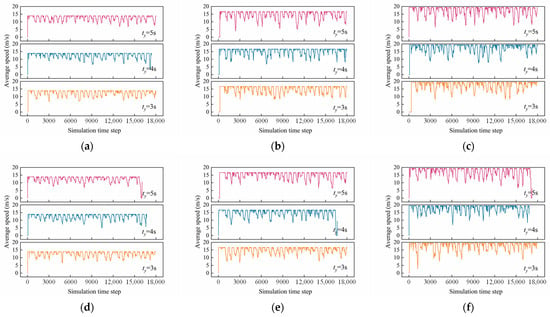
Figure 10.
Average vehicle speed under different ty (λ = 0.3 veh/s): (a) left-turning vehicles, Vmax = 50 km/h; (b) left-turning vehicles, Vmax = 60 km/h; (c) left-turning vehicles, Vmax = 70 km/h; (d) straight-going vehicles, Vmax = 50 km/h; (e) straight-going vehicles, Vmax = 60 km/h; and (f) straight-going vehicles, Vmax = 70 km/h.
As observed in Figure 9 and Figure 10, when the traffic flow does not reach a saturated state, the real-time average vehicle speed exhibits periodic fluctuations over signal cycles. During red phases, vehicle queuing leads to lower average speeds, while during green phases, the average speed recovers to the maximum speed. From Figure 9, as the traffic flow gradually increases (without reaching saturation), the amplitude of average speed fluctuations within each signal cycle decreases. Figure 10 shows that as the speed limit increases, the amplitude of average speed fluctuations within each signal cycle also increases.
5.4. Safety
Under the conditions where λ is 0.2 veh/s, 0.3 veh/s, and 0.4 veh/s and Vmax is 60 km/h, the numbers of yellow- and red-running vehicles on left-turn and straight lanes for ty of 3 s, 4 s, and 5 s are presented in Table 6. Similarly, under the conditions where Vmax is 50 km/h, 60 km/h, and 70 km/h and λ is 0.3 veh/s, the corresponding numbers for ty of 3 s, 4 s, and 5 s are shown in Table 7. In the simulations, vehicles that decelerated upon encountering a yellow light but failed to stop before the stop line during the yellow phase were also considered as engaging in red running. In reality, however, vehicles that have crossed the stop line may still choose to wait. This discrepancy causes the simulated number of red-running vehicles to be higher than the real-world situation. Nonetheless, the focus is to compare the impact of different yellow durations to vehicles crossing the stop line during the red phase, so the statistical bias in red-running vehicle counts is disregarded.

Table 6.
Number of yellow- and red- running vehicles on left-turn and straight lanes under different ty (Vmax = 60 km/h).

Table 7.
Number of yellow- and red-running vehicles on left-turn and straight lanes under different ty (λ = 0.3 veh/s).
From Table 6, it can be observed that under a given speed limit and a longer yellow duration (ty = 5 s), the number of yellow-running vehicles gradually decreases as traffic flow increases (without reaching saturation). For higher traffic volumes (λ = 0.4 veh/s), increasing ty from 3 s to 5 s results in fewer yellow- and red-running vehicles, consistent with the conclusions in the study of Ma et al. [65]. As shown in Table 7, under a fixed departure rate, a lower speed limit (Vmax = 50 km/h) and an increase in ty from 3 s to 5 s significantly reduce the numbers of both yellow- and red-running vehicles.
6. Discussion
6.1. Traffic Volume
The observed finding that traffic volume increases as yellow light duration extends from 3 s to 5 s under high departure rates can be attributed to the following reasons: When departure rate is low, the signal state encountered by vehicles near the intersection is highly influenced by the randomness of vehicle departure time sequences [66]. As a result, the probability of vehicles arriving at the intersection during the yellow phase is relatively low, and thus the impact of yellow light duration on traffic volume is minimal. However, under higher departure rates, more vehicles are required to make stop/go decisions during the yellow phase. From the perspective of driver risk perception, the decision-making process during the yellow phase involves assessing the trade-off between perceived risk and the potential benefit of crossing the intersection. With an extended yellow phase duration, drivers are more likely to perceive a lower signal risk at the onset of a yellow light (assuming equal vehicle speed and distance to the stop line). This perceived risk may also fall below their desired threshold, increasing the likelihood of vehicles crossing the stop line during the yellow phase.
Furthermore, a longer yellow duration not only reduces perceived risk but also creates a psychological buffer that allows drivers to anticipate their movements more confidently. This aligns with risk homeostasis theory, which suggests that drivers continuously adjust their behavior to maintain an acceptable risk level based on real-time traffic conditions. The extended yellow phase helps drivers recalibrate their risk perception dynamically, thereby facilitating smoother traffic flow and reducing abrupt stopping decisions.
Studies support the idea that an extended yellow phase duration provides traffic with additional passing and buffer time, enhancing intersection performance during high traffic volumes [37,67,68]. However, this must be balanced against safety concerns, as excessively long yellow light durations could encourage aggressive driving behavior or undermine the predictability of traffic signals. Therefore, within the context of design speed and intersection geometry, it is recommended to moderately extend the yellow phase duration within the range of 3–5 s during high traffic volumes.
6.2. Queue Length
Simulation results also revealed that under high traffic volume conditions, the queue length of vehicles during most signal cycles is slightly longer for yellow light durations of 4 s and 5 s compared to 3 s. This may be attributed to the lower perceived risk by drivers at the onset of a longer yellow phase duration (assuming equal vehicle speed and distance to the stop line). This perception reduces the gap between the actual perceived risk and the driver’s desired risk threshold, meaning the perceived risk is only marginally greater than what drivers find acceptable. As a result, drivers exhibit lower deceleration rates, maintaining higher speeds for longer periods before deciding to stop or proceed. Consequently, vehicles arrive at higher speeds, leading to a cascading effect where subsequent vehicles in the queue adjust their behavior accordingly, maintaining a higher overall approach speed for the following queue. This increases the likelihood of more vehicles arriving during a subsequent short red phase [69], particularly under high departure rates where arrival patterns are less random. This phenomenon aligns with findings by Liu et al. [58], which suggest that such cumulative effects are more pronounced under high traffic volumes.
Another observation is that this phenomenon also occurs under higher speed limits for similar reasons. However, over the long term, yellow phase duration does not have a significant impact on traffic delays in approach lanes. This indicates that while queue lengths may vary across signal cycles due to risk perception and behavioral adjustments, the system tends to stabilize as drivers adapt to consistent traffic conditions, underscoring the importance of considering both short-term behavioral responses and long-term system-level impacts when optimizing signal timings.
6.3. Average Speed
The fluctuations in average speed can reflect the stability of traffic flow on a road segment [70]. One finding is that as traffic flow increases but does not reach saturation, the amplitude of average speed fluctuations within each signal cycle gradually decreases. This is consistent with the conclusions drawn in the study of Ma et al. [65]. However, a unique perspective may be to explain this phenomenon from the viewpoint of risk perception. Specifically, this may be because, at lower traffic volumes, there are more vehicles traveling freely, and when these vehicles are constrained by dynamic signal risks, they are more likely to experience sudden risk changes, leading to abrupt acceleration or deceleration. This results in unstable vehicle speeds [71,72]. In contrast, at higher traffic volumes, the traffic flow tends to stabilize into steady following behavior during each signal cycle, which reduces the amplitude of average speed fluctuations.
Another finding is that as the road speed limit increases, the amplitude of average speed fluctuations within each signal cycle also increases. This could be due to the higher vehicle speeds associated with higher speed limits. When vehicles approach the intersection during the yellow phase (assuming the distance to the stop line remains the same), the perceived signal risk increases. As a result, greater deceleration and longer deceleration time are required to either safely pass through the intersection or stop before the red light turns on [73]. This leads to greater speed variations in the vehicles following, which in turn affects the overall average speed of the vehicle queue [74].
A further observation is that, under the same departure rate, shorter yellow phase durations (e.g., 3 s) result in slightly larger average speed fluctuations compared to longer durations (4 s or 5 s). This could be explained by the fact that with a shorter yellow phase duration, drivers perceive a higher risk at the onset of the yellow light (assuming equal vehicle speed and distance to the stop line). The larger gap between the perceived and desired risks compels drivers to decelerate more aggressively, causing abrupt changes in individual vehicle speeds. These sudden adjustments ripple through the traffic flow, increasing real-time speed fluctuations and reducing overall stability. Therefore, when traffic volume has not reached saturation, appropriately increasing the yellow duration within the range of 3–5 s can stabilize the fluctuations in real-time vehicle speeds, thereby reducing the potential risks associated with sudden acceleration or deceleration [57].
The interplay between traffic volume, speed limits, and yellow phase duration underscores the importance of understanding driver risk perception in optimizing signal control strategies. Moderate increases in yellow phase duration can contribute to smoother traffic flow by reducing abrupt speed fluctuations and enhancing stability. However, the impact of these adjustments should be carefully balanced against operational constraints and intersection characteristics to ensure that stability gains do not compromise traffic efficiency.
6.4. Safety
The finding that the number of yellow-running vehicles gradually decreases as traffic volume increases (without reaching saturation) under certain speed limits and longer yellow phase durations can be explained by the interaction between driver risk perception and following behavior. In dense traffic conditions, most vehicles upstream are in a following state, with their movement significantly influenced by the one ahead [75,76]. According to Knoflacher’s “Mitschlepp” effect [77], this following state diminishes individual drivers’ autonomy, as risk perception is partly transferred from the leading driver to the followers. If the lead driver during the yellow phase opts to stop, downstream vehicles, regardless of their own risk preferences, are often compelled to do the same, reducing the likelihood of yellow-running behavior.
In contrast, under sparse traffic conditions, vehicles operate more freely, and drivers’ decisions are dominated by their individual risk thresholds. Drivers who perceive a higher risk may stop, while those who find the risk acceptable are more likely to continue through the yellow light. This disparity in behavior results in higher yellow-running frequencies, as fewer vehicles are constrained by the actions of others. Furthermore, due to situations where vehicles decelerate during the yellow phase but fail to stop completely before the stop line, leading to red-running behavior, when yellow-running behavior decreases, the associated red-running behavior also decreases for the reason mentioned above. Therefore, under longer yellow phase durations, the number of red-running vehicles also decreases as traffic volume increases. This conclusion has also been confirmed in past research [78,79]. For instance, Bonneson and Zimmerman [78] made a finding that an increase of 1 s in yellow phase duration (such that it does not exceed 5.5 s) would decrease the red-running frequency by at least 50%.
Another important finding is that at lower speed limits (e.g., 50 km/h), increasing the yellow duration from 3 s to 5 s significantly reduces both the number of yellow- and red-running vehicles. This could be explained by the fact that under longer yellow light durations, drivers perceive a lower risk at the onset of the yellow light or as the green light is about to end, and the perceived risk is more likely to be smaller than their desired risk. In this case, if the vehicle speed is relatively high when the yellow light turns on (assuming the distance to the stop line is the same), the vehicle may maintain a high speed as it approaches the intersection, making it more likely to cross the stop line during the yellow phase. The following vehicles, also moving at higher speeds, may be unable to stop in time before the yellow or red light turns on, thus increasing the likelihood of yellow- or red-running behavior. A study that reached a finding that 71% of those who passed an intersection after yellow light onset were platoon leaders and 23% were first followers can support this conclusion [80]. On the other hand, if a vehicle’s approaching speed is lower, the occurrence of this behavior may decrease.
The number of yellow- and red-running vehicles was also observed to decrease as the yellow light duration extended from 3 s to 5 s under higher traffic volume. This finding is consistent with the conclusions in the study of Ma et al. [60]. However, the study of Ren et al. [81] found that when the yellow light duration is longer (e.g., 5 s), a smaller following distance makes it more likely for the first yellow-running vehicle in a queue to lead the following vehicles to do the same, thus increasing the number of yellow- and red-running vehicles. This phenomenon is closely related to factors such as traffic volume, following distance, and vehicle speed [82,83,84]. According to the simulation results in this study, due to the randomness of departure sequences and differences in drivers’ desired risks, even with a yellow duration of 5 s, it is rare for two or more vehicles to run a yellow light within the same signal cycle. As a result, the situation described in the study of Ren et al. [81] did not occur in this study. If we consider the total number of yellow- and red-running vehicles under the same departure rate, speed limit, and yellow light duration as a measure of unsafe driving behavior, the analysis suggests that when traffic flow evolves from sparse to dense conditions, increasing the yellow light duration within the range of 3–5 s can help suppress the occurrence of unsafe driving behaviors. Therefore, traffic managers may consider appropriately extending yellow phase duration within this range under high traffic volumes at intersections, which is consistent with the conclusions in Section 6.1 and offers a pragmatic solution for traffic managers seeking to enhance safety at intersections.
However, traffic volume and speed limits should be jointly considered when optimizing yellow phase duration. While longer yellow light durations may improve safety at lower speeds, they must be carefully calibrated under higher speed limits to prevent unintended risk-taking behaviors. Combining these insights with advanced traffic signal control technologies and driver assistance systems can further enhance safety outcomes.
7. Conclusions
This study first introduces a subjective risk-perception-based driving behavior model built under the unified framework of “risk prediction–motion planning” and further refines it using fuzzy decision-making theory. The improved model is then embedded into a simulation environment for isolated signalized intersections, where the functions of each module and the associated input–output parameters are explicitly defined. Subsequently, simulations are conducted to analyze the efficiency and safety performance of isolated signalized intersections under varying yellow durations. The findings reveal that, assuming that vehicles strictly adhere to the designed speed, an increase in yellow light duration from 3 s to 5 s leads to greater traffic volume under high traffic density. Meanwhile, real-time fluctuations in traffic speed stabilize and the occurrence of unsafe driving behaviors is mitigated. Finally, the study explains these phenomena through the lens of risk-perception theory, recommending that traffic managers consider appropriately extending yellow phase durations within the range of 3–5 s during periods of high traffic volume. A comparative discussion with other research findings also supports the feasibility of the proposed model in simulating the impact of yellow phase duration on traffic flow performance. Furthermore, the study emphasizes the importance of accounting for both short-term behavioral responses and long-term system-level impacts when optimizing signal timing strategies.
This study provides a simulation environment to evaluate traffic performance at isolated intersections under various signal timing schemes. By analyzing traffic phenomena from the perspective of risk perception and driving behavior mechanisms, the study explores the application of risk-based driving behavior models in improving overall intersection efficiency and safety. It offers a theoretical foundation for describing driving behaviors at signalized intersections in greater detail and for explaining the underlying logic behind intersection performance. Additionally, it serves as a decision-making tool for the design of signal timing schemes. For traffic simulation, the approach also facilitates the development of more refined driving behavior models and reduces the complexity of switching between different models across diverse road spaces and traffic scenarios.
However, this study has several limitations. First, the simulation results are inherently stochastic, necessitating an increased number of iterations to support more reliable conclusions. Meanwhile, comparing the proposed model with simplified driver behavior models and other existing models is necessary to further demonstrate its validity and reliability, as well as to examine the sensitivity of yellow phase duration to traffic flow performance. Second, only isolated intersections were considered, without accounting for the influence of upstream intersections. Third, the simulation process involves stepwise computation of risk fields, making it time-consuming and computationally intensive, which poses challenges for conducting larger-scale or more extensive simulations. Finally, future research could further explore the impact of yellow phase duration on mixed traffic with both human-driven vehicles and autonomous vehicles.
Author Contributions
Conceptualization, J.H., B.L.; methodology, J.H.; software, J.H., P.L. and W.Z.; validation, J.H. and W.Z.; formal analysis, J.H.; writing—original draft preparation, J.H.; writing—review and editing, B.L.; visualization, P.L.; supervision, B.L.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Key Lab of Intelligent Transportation System under Project No. 2024-Z001.
Data Availability Statement
The data presented in this study is available on request from the corresponding author. The data is not publicly available due to the requirements of the data provider.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Banks, J. Principles of simulation. In Handbook of Simulation; Oxford University Press: Oxford, UK, 1998; Volume 12, pp. 3–30. [Google Scholar]
- Bossel, H. Modeling and Simulation; AK Peters: Natick, MA, USA; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Turner, B.L. Model laboratories: A quick-start guide for design of simulation experiments for dynamic systems models. Ecol. Model. 2020, 434, 109246. [Google Scholar] [CrossRef]
- Saidallah, M.; El Fergougui, A.; Elalaoui, A.E. A comparative study of urban road traffic simulators. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2016; Volume 81, p. 05002. [Google Scholar]
- Vrbanić, F.; Čakija, D.; Kušić, K.; Ivanjko, E. Traffic flow simulators with connected and autonomous vehicles: A short review. Transform. Transp. 2021, 15–30. [Google Scholar] [CrossRef]
- Silgu, M.A.; Erdağı, İ.G.; Göksu, G.; Celikoglu, H.B. Combined control of freeway traffic involving cooperative adaptive cruise controlled and human driven vehicles using feedback control through SUMO. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11011–11025. [Google Scholar] [CrossRef]
- Wang, T.; Hussain, A.; Bhutta, M.N.M.; Cao, Y. Enabling bidirectional traffic mobility for ITS simulation in smart city environments. Future Gener. Comput. Syst. 2019, 92, 342–356. [Google Scholar] [CrossRef]
- Hua, J.; Lu, G.; Liu, H.X. Modeling and simulation of approaching behaviors to signalized intersections based on risk quantification. Transp. Res. Part C Emerg. Technol. 2022, 142, 103773. [Google Scholar] [CrossRef]
- Liu, P.; Zhao, J.; Zhang, F.; Yeo, H. Modeling decision-making process of drivers during yellow signal phase at intersections based on drift–diffusion model. Transp. Res. Part F Traffic Psychol. Behav. 2024, 105, 368–384. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Nikolaidou, A.; Lilis, E.; Politis, I.; Papaioannou, P. Extending the decision-making process during yellow phase from human drivers to autonomous vehicles: A microsimulation study with safety considerations. J. Traffic Transp. Eng. (Engl. Ed.) 2024, 11, 362–379. [Google Scholar] [CrossRef]
- Tan, H.; Lu, G.; Liu, M. Risk field model of driving and its application in modeling car-following behavior. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11605–11620. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, G.; Tan, H.; Liu, M. A risk-field based motion planning method for multi-vehicle conflict scenario. IEEE Trans. Veh. Technol. 2023, 73, 310–322. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, G.; Tan, H. Driving behavior model for multi-vehicle interaction at uncontrolled intersections based on risk field considering drivers’ visual field characteristics. IEEE Trans. Intell. Transp. Syst. 2024, 25, 15532–15546. [Google Scholar] [CrossRef]
- Tan, H.; Lu, G.; Wang, Z.; Hua, J.; Liu, M. A unified risk field-based driving behavior model for car-following and lane-changing behaviors simulation. Simul. Model. Pract. Theory 2024, 136, 102991. [Google Scholar] [CrossRef]
- Al-Turki, M.; Jamal, A.; Al-Ahmadi, H.M.; Al-Sughaiyer, M.A.; Zahid, M. On the potential impacts of smart traffic control for delay, fuel energy consumption, and emissions: An NSGA-II-based optimization case study from Dhahran, Saudi Arabia. Sustainability 2020, 12, 7394. [Google Scholar] [CrossRef]
- Qadri, S.S.S.M.; Gökçe, M.A.; Öner, E. State-of-art review of traffic signal control methods: Challenges and opportunities. Eur. Transp. Res. Rev. 2020, 12, 1–23. [Google Scholar] [CrossRef]
- Eom, M.; Kim, B.I. The traffic signal control problem for intersections: A review. Eur. Transp. Res. Rev. 2020, 12, 1–20. [Google Scholar] [CrossRef]
- Pawar, D.S.; Pathak, D.; Patil, G.R. Modeling dynamic distribution of dilemma zone at signalized intersections for developing world traffic. J. Transp. Saf. Secur. 2022, 14, 886–904. [Google Scholar] [CrossRef]
- Wu, Y.; Abdel-Aty, M.; Ding, Y.; Jia, B.; Shi, Q.; Yan, X. Comparison of proposed countermeasures for dilemma zone at signalized intersections based on cellular automata simulations. Accid. Anal. Prev. 2018, 116, 69–78. [Google Scholar] [CrossRef]
- Tang, K.; Xu, Y.; Wang, F.; Oguchi, T. Exploring stop-go decision zones at rural high-speed intersections with flashing green signal and insufficient yellow time in China. Accid. Anal. Prev. 2016, 95, 470–478. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y.; Ma, J.; Zhang, G.; Walton, C.M. Driver behavior formulation in intersection dilemma zones with phone use distraction via a logit-Bayesian network hybrid approach. J. Intell. Transp. Syst. 2018, 22, 311–324. [Google Scholar] [CrossRef]
- Kim, S.; Son, Y.J.; Chiu, Y.C.; Jeffers, M.A.B.; Yang, C.D. Impact of road environment on drivers’ behaviors in dilemma zone: Application of agent-based simulation. Accid. Anal. Prev. 2016, 96, 329–340. [Google Scholar] [CrossRef]
- Bao, J.; Chen, Q.; Luo, D.; Wu, Y.; Liang, Z. Exploring the impact of signal types and adjacent vehicles on drivers’ choices after the onset of yellow. Phys. A Stat. Mech. Its Appl. 2018, 500, 222–236. [Google Scholar] [CrossRef]
- Wolfgram, J. A Safety and Emissions Analysis of Continuous Flow Intersections. Master’s Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 2018. [Google Scholar]
- Du, M.; Yang, S.; Chen, Q. Impacts of vehicle-to-infrastructure communication on traffic flows with mixed connected vehicles and human-driven vehicles. Int. J. Mod. Phys. B 2021, 35, 2150091. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, J.; An, S.; Wang, M.; Park, B.B. Eco approaching at an isolated signalized intersection under partially connected and automated vehicles environment. Transp. Res. Part C Emerg. Technol. 2017, 79, 290–307. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Y.; Wang, X.; Yang, S.; Chen, T. Hierarchical longitudinal control for connected and automated vehicles in mixed traffic on a signalized arterial. Sustainability 2021, 13, 8852. [Google Scholar] [CrossRef]
- Yao, H.; Li, X. Decentralized control of connected automated vehicle trajectories in mixed traffic at an isolated signalized intersection. Transp. Res. Part C Emerg. Technol. 2020, 121, 102846. [Google Scholar] [CrossRef]
- Yao, H.; Li, X. Lane-change-aware connected automated vehicle trajectory optimization at a signalized intersection with multi-lane roads. Transp. Res. Part C Emerg. Technol. 2021, 129, 103182. [Google Scholar] [CrossRef]
- Yu, M.; Long, J. An eco-driving strategy for partially connected automated vehicles at a signalized intersection. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15780–15793. [Google Scholar] [CrossRef]
- Zhao, W.; Ngoduy, D.; Shepherd, S.; Liu, R.; Papageorgiou, M. A platoon based cooperative eco-driving model for mixed automated and human-driven vehicles at a signalised intersection. Transp. Res. Part C Emerg. Technol. 2018, 95, 802–821. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Xu, Q.; Wang, J.; Li, K. Mixed platoon control of automated and human-driven vehicles at a signalized intersection: Dynamical analysis and optimal control. Transp. Res. Part C Emerg. Technol. 2021, 127, 103138. [Google Scholar] [CrossRef]
- Ma, C.; Yu, C.; Yang, X. Trajectory planning for connected and automated vehicles at isolated signalized intersections under mixed traffic environment. Transp. Res. Part C Emerg. Technol. 2021, 130, 103309. [Google Scholar] [CrossRef]
- Cheng, Y.; Chen, C.; Hu, X.; Chen, K.; Tang, Q.; Song, Y. Enhancing mixed traffic flow safety via connected and autonomous vehicle trajectory planning with a reinforcement learning approach. J. Adv. Transp. 2021, 2021, 6117890. [Google Scholar] [CrossRef]
- Lin, D.; Yang, X.; Gao, C. VISSIM-based simulation analysis on road network of CBD in Beijing, China. Procedia-Soc. Behav. Sci. 2013, 96, 461–472. [Google Scholar] [CrossRef]
- Ma, X.; Jin, J.; Lei, W. Multi-criteria analysis of optimal signal plans using microscopic traffic models. Transp. Res. Part D Transp. Environ. 2014, 32, 1–14. [Google Scholar] [CrossRef]
- Paul, M.; Ghosh, I.; Haque, M.M. The effects of green signal countdown timer and retiming of signal intervals on dilemma zone related crash risk at signalized intersections under heterogeneous traffic conditions. Saf. Sci. 2022, 154, 105862. [Google Scholar] [CrossRef]
- Smith, D.; Djahel, S.; Murphy, J. A SUMO based evaluation of road incidents’ impact on traffic congestion level in smart cities. In Proceedings of the 39th Annual IEEE Conference on Local Computer Networks Workshops, Edmonton, AB, Canada, 8–11 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 702–710. [Google Scholar]
- Flötteröd, Y.P.; Behrisch, M. Improving SUMO’s Signal Control Programs by Introducing Route Information. EPiC Ser. Eng. 2018, 2, 162–172. [Google Scholar]
- Zhang, Y.; Su, R. An optimization model and traffic light control scheme for heterogeneous traffic systems. Transp. Res. Part C Emerg. Technol. 2021, 124, 102911. [Google Scholar] [CrossRef]
- Varga, B.; Doba, D.; Tettamanti, T. Optimizing vehicle dynamics co-simulation performance by introducing mesoscopic traffic simulation. Simul. Model. Pract. Theory 2023, 125, 102739. [Google Scholar] [CrossRef]
- Ronaldo, A. Comparison of the Two Micro-Simulation Software Aimsun & Sumo for Highway Traffic Modelling. Master’s Thesis, Linköping University, Linköping, Sweden, 2012. [Google Scholar]
- Sun, B.; Appiah, J.; Park, B.B. Practical guidance for using mesoscopic simulation tools. Transp. Res. Procedia 2020, 48, 764–776. [Google Scholar] [CrossRef]
- Abedian, S.; Mirsanjari, M.M.; Salmanmahiny, A. Investigating the effect of suburban buses on traffic flow and carbon monoxide emission by Aimsun simulation software. J. Indian Soc. Remote Sens. 2021, 49, 1319–1330. [Google Scholar] [CrossRef]
- Ansariyar, A.; Taherpour, A. Investigating the accuracy rate of vehicle-vehicle conflicts by LIDAR technology and microsimulation in VISSIM and AIMSUN. Adv. Transp. Stud. 2023, 61, 37–52. [Google Scholar]
- Wang, Q.; Li, L.; Hou, D.; Li, Z.; Hu, J. Simulation study on the effect of automated driving in a road network environment. IET Intell. Transp. Syst. 2020, 14, 228–232. [Google Scholar] [CrossRef]
- Raju, N.; Farah, H. Evolution of traffic microsimulation and its use for modeling connected and automated vehicles. J. Adv. Transp. 2021, 2021, 2444363. [Google Scholar] [CrossRef]
- Coropulis, S.; Berloco, N.; Gentile, R.; Intini, P.; Ranieri, V. The use of microscopic simulators for safety assessment in automated and partially automated scenarios: A comparison. Transp. Res. Procedia 2023, 69, 313–320. [Google Scholar] [CrossRef]
- Sagaama, I.; Kchiche, A.; Trojet, W.; Kamoun, F. Energy consumption models in VANET simulation tools for electric vehicles: A literature survey. Int. J. Ad Hoc Ubiquitous Comput. 2023, 42, 30–46. [Google Scholar] [CrossRef]
- Laubenbacher, R.; Jarrah, A.S.; Mortveit, H.S.; Ravi, S.S. Agent-based modeling, mathematical formalism for. In Complex Social and Behavioral Systems: Game Theory and Agent-Based Models; Springer: Berlin/Heidelberg, Germany, 2020; pp. 683–703. [Google Scholar]
- Tzouras, P.G.; Mitropoulos, L.; Stavropoulou, E.; Antoniou, E.; Koliou, K.; Karolemeas, C.; Karaloulis, A.; Mitropoulos, K.; Tarousi, M.; Vlahogianni, E.I.; et al. Agent-based models for simulating e-scooter sharing services: A review and a qualitative assessment. Int. J. Transp. Sci. Technol. 2023, 12, 71–85. [Google Scholar] [CrossRef]
- Othman, N.B.; Jayaraman, V.; Chan, W.; Loh, Z.X.K.; Rajendram, R.; Mepparambath, R.M.; Agrawal, P.; Ramli, M.A.; Qin, Z. SUMMIT: A multi-modal agent-based co-simulation of urban public transport with applications in contingency planning. Simul. Model. Pract. Theory 2023, 126, 102760. [Google Scholar] [CrossRef]
- Gao, Z.; Guan, X.; Guo, K. Driver directional control model and the application in the research of intelligent vehicle. China J. Highw. Transp. 2000, 13, 106–109. [Google Scholar]
- Almadi, A.I.; Al Mamlook, R.E.; Almarhabi, Y.; Ullah, I.; Jamal, A.; Bandara, N. A fuzzy-logic approach based on driver decision-making behavior modeling and simulation. Sustainability 2022, 14, 8874. [Google Scholar] [CrossRef]
- Hurwitz, D.S.; Wang, H.; Knodler Jr, M.A.; Ni, D.; Moore, D. Fuzzy sets to describe driver behavior in the dilemma zone of high-speed signalized intersections. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 132–143. [Google Scholar] [CrossRef]
- Yang, Z.; Tian, X.; Wang, W.; Zhou, X.; Liang, H. Research on driver behavior in yellow interval at signalized intersections. Math. Probl. Eng. 2014, 2014, 518782. [Google Scholar] [CrossRef]
- Lu, G.; Wang, Y.; Wu, X.; Liu, H.X. Analysis of yellow-light running at signalized intersections using high-resolution traffic data. Transp. Res. Part A Policy Pract. 2015, 73, 39–52. [Google Scholar] [CrossRef]
- Liu, H.X.; Wu, X.; Ma, W.; Hu, H. Real-time queue length estimation for congested signalized intersections. Transp. Res. Part C Emerg. Technol. 2009, 17, 412–427. [Google Scholar] [CrossRef]
- Lu, G.; Hua, J.; Zhao, H.; Liu, M.; Xu, J.; Zong, F. Modeling Vehicle Paths at Intersections: A Unified Approach Based on Entrance and Exit Lanes. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14097–14110. [Google Scholar] [CrossRef]
- Wilde, G.J.S. The theory of risk homeostasis: Implications for safety and health. Risk Anal. 1982, 2, 209–225. [Google Scholar] [CrossRef]
- Hurwitz, D.; Abadi, M.G.; McCrea, S.; Quayle, S.; Marnell, P. Smart Red Clearance Extensions to Reduce Red-Light Running Crashes; No. FHWA-OR-RD-16-10; Oregon. Dept. of Transportation: Salem, OR, USA, 2016. [Google Scholar]
- Li, K. Guidelines for Traffic Signal Control—Current German Regulations (RiLSA); China Construction Industry Press: Shanghai, China, 2006. [Google Scholar]
- Li, K.; Yang, P.; Ni, Y. Amber interval design at urban signalized intersections. Urban Transp. China 2010, 8, 67–72. [Google Scholar]
- Chen, Y.; Kong, D.; Sun, L.; Zhang, T.; Song, Y. Fundamental diagram and stability analysis for heterogeneous traffic flow considering human-driven vehicle driver’s acceptance of cooperative adaptive cruise control vehicles. Phys. A Stat. Mech. Its Appl. 2022, 589, 126647. [Google Scholar] [CrossRef]
- Ma, J.; Xu, Y.; Ji, H.; Su, B. Multi-agent microsimulation of urban intersections considering yellow light driving behavior. J. Syst. Eng. 2015, 30, 394–405. [Google Scholar]
- Comert, G.; Khan, Z.; Rahman, M.; Chowdhury, M. Grey models for short-term queue length predictions for adaptive traffic signal control. Expert Syst. Appl. 2021, 185, 115618. [Google Scholar] [CrossRef]
- Chiou, Y.C.; Chang, C.H. Driver responses to green and red vehicular signal countdown displays: Safety and efficiency aspects. Accid. Anal. Prev. 2010, 42, 1057–1065. [Google Scholar] [CrossRef]
- Fayazi, S.A.; Vahidi, A. Mixed-integer linear programming for optimal scheduling of autonomous vehicle intersection crossing. IEEE Trans. Intell. Veh. 2018, 3, 287–299. [Google Scholar] [CrossRef]
- Kaul, R.; Jipp, M. Influence of cognitive processes on driver decision-making in dilemma zone. Transp. Res. Interdiscip. Perspect. 2023, 19, 100805. [Google Scholar] [CrossRef]
- Hoogendoorn, S.; Knoop, V. Traffic flow theory and modelling. In The Transport System and Transport Policy: An Introduction; Edward Elgar Publishing: Cheltenham, UK, 2013; pp. 125–159. [Google Scholar]
- Durrani, U.; Lee, C.; Shah, D. Predicting driver reaction time and deceleration: Comparison of perception-reaction thresholds and evidence accumulation framework. Accid. Anal. Prev. 2021, 149, 105889. [Google Scholar] [CrossRef] [PubMed]
- Adavikottu, A.; Velaga, N.R. Analysis of speed reductions and crash risk of aggressive drivers during emergent pre-crash scenarios at unsignalized intersections. Accid. Anal. Prev. 2023, 187, 107088. [Google Scholar] [CrossRef]
- El-Shawarby, I.; Rakha, H.; Inman, V.W.; Davis, G.W. Evaluation of driver deceleration behavior at signalized intersections. Transp. Res. Rec. 2007, 2018, 29–35. [Google Scholar] [CrossRef]
- Adavikottu, A.; Velaga, N.R.; Mishra, S. Modelling the effect of aggressive driver behavior on longitudinal performance measures during car-following. Transp. Res. Part F Traffic Psychol. Behav. 2023, 92, 176–200. [Google Scholar] [CrossRef]
- Sharma, A.; Zheng, Z.; Kim, J.; Bhaskar, A.; Haque, M.M. Assessing traffic disturbance, efficiency, and safety of the mixed traffic flow of connected vehicles and traditional vehicles by considering human factors. Transp. Res. Part C Emerg. Technol. 2021, 124, 102934. [Google Scholar] [CrossRef]
- Maiti, N.; Chilukuri, B.R. Does anisotropy hold in mixed traffic conditions? Phys. A Stat. Mech. Its Appl. 2023, 632, 129336. [Google Scholar] [CrossRef]
- Knoflacher, H. Der Einfluß des Grünblinkens auf die Leistungsfähigkeit und Sicherheit lichtsignalgeregelter Straßenkreuzungen. Strassenforschung 1973, 8, 1–4. [Google Scholar]
- Bonneson, J.A.; Zimmerman, K.H. Effect of yellow-interval timing on the frequency of red-light violations at urban intersections. Transp. Res. Rec. 2004, 1865, 20–27. [Google Scholar] [CrossRef]
- Prasetijo, J.; Musa, I.; Sulaiman, N.A.; Mustafa, M.A.; Putranto, L.S.; Hamid, N.B.; Siang Alvin John, L.M.; Abd Latif, M.F. Red-light running vehicles behaviour based on linear regression approach at traffic lights along Bakau Condong Road, Batu Pahat, Johor. Int. J. Road Saf. 2020, 1, 4–8. [Google Scholar]
- Papaioannou, P.; Papadopoulos, E.; Nikolaidou, A.; Politis, I.; Basbas, S.; Kountouri, E. Dilemma zone: Modeling drivers’ decision at signalized intersections against aggressiveness and other factors using uav technology. Safety 2021, 7, 11. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Y.; Wu, X.; Yu, G.; Ding, C. Influential factors of red-light running at signalized intersection and prediction using a rare events logistic regression model. Accid. Anal. Prev. 2016, 95, 266–273. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Fu, C.; Hu, L. Yellow light dilemma zone researches: A review. J. Traffic Transp. Eng. (Engl. Ed.) 2014, 1, 338–352. [Google Scholar] [CrossRef]
- Palat, B.; Delhomme, P. A simulator study of factors influencing drivers’ behavior at traffic lights. Transp. Res. Part F Traffic Psychol. Behav. 2016, 37, 107–118. [Google Scholar] [CrossRef]
- Chen, P.; Yu, G.; Wu, X.; Ren, Y.; Li, Y. Estimation of red-light running frequency using high-resolution traffic and signal data. Accid. Anal. Prev. 2017, 102, 235–247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).