Determination of Atmospheric Gusts Using Integrated On-Board Systems of a Jet Transport Airplane—3D Problem
Abstract
1. Introduction
2. Theoretical Background
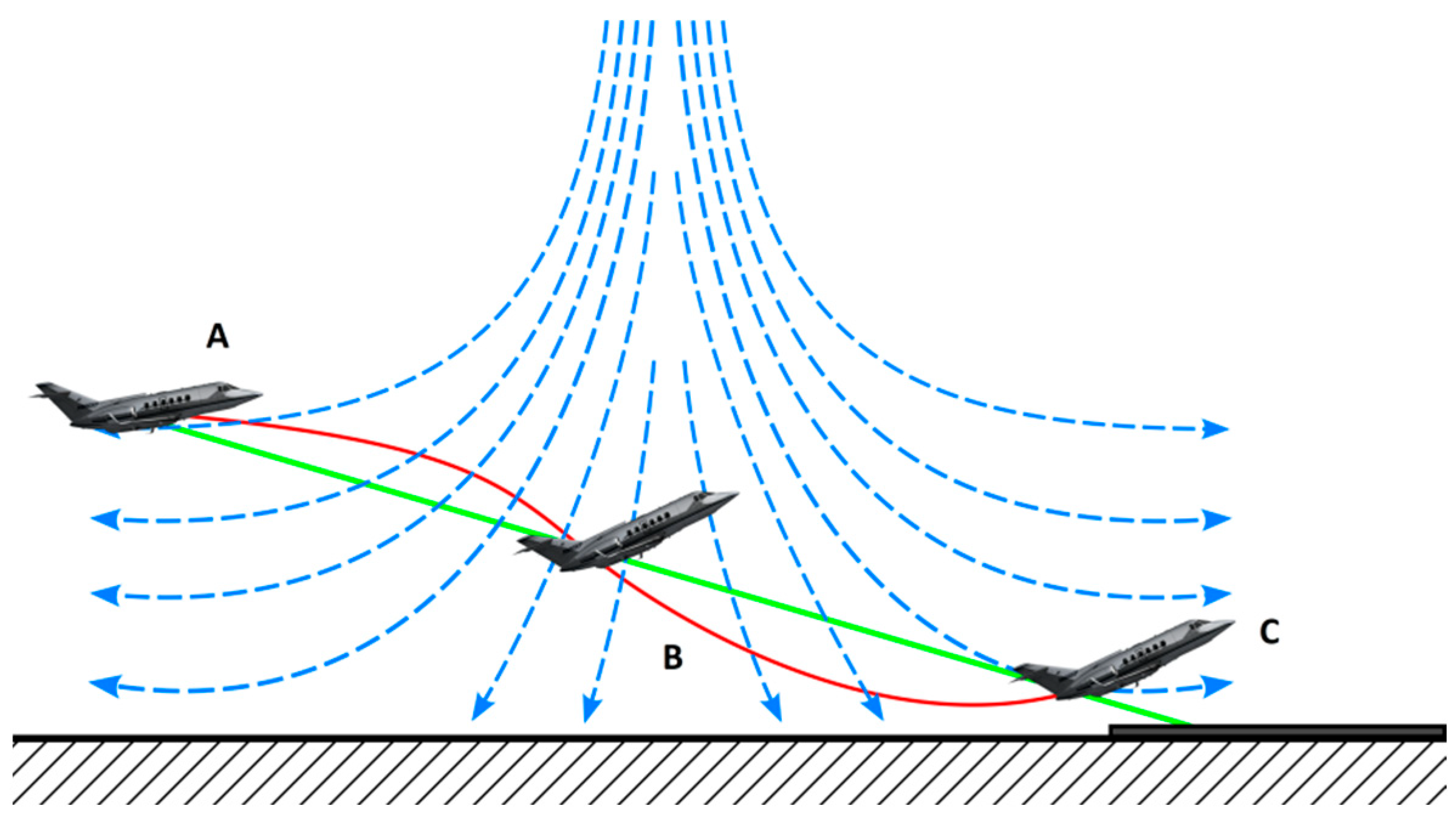
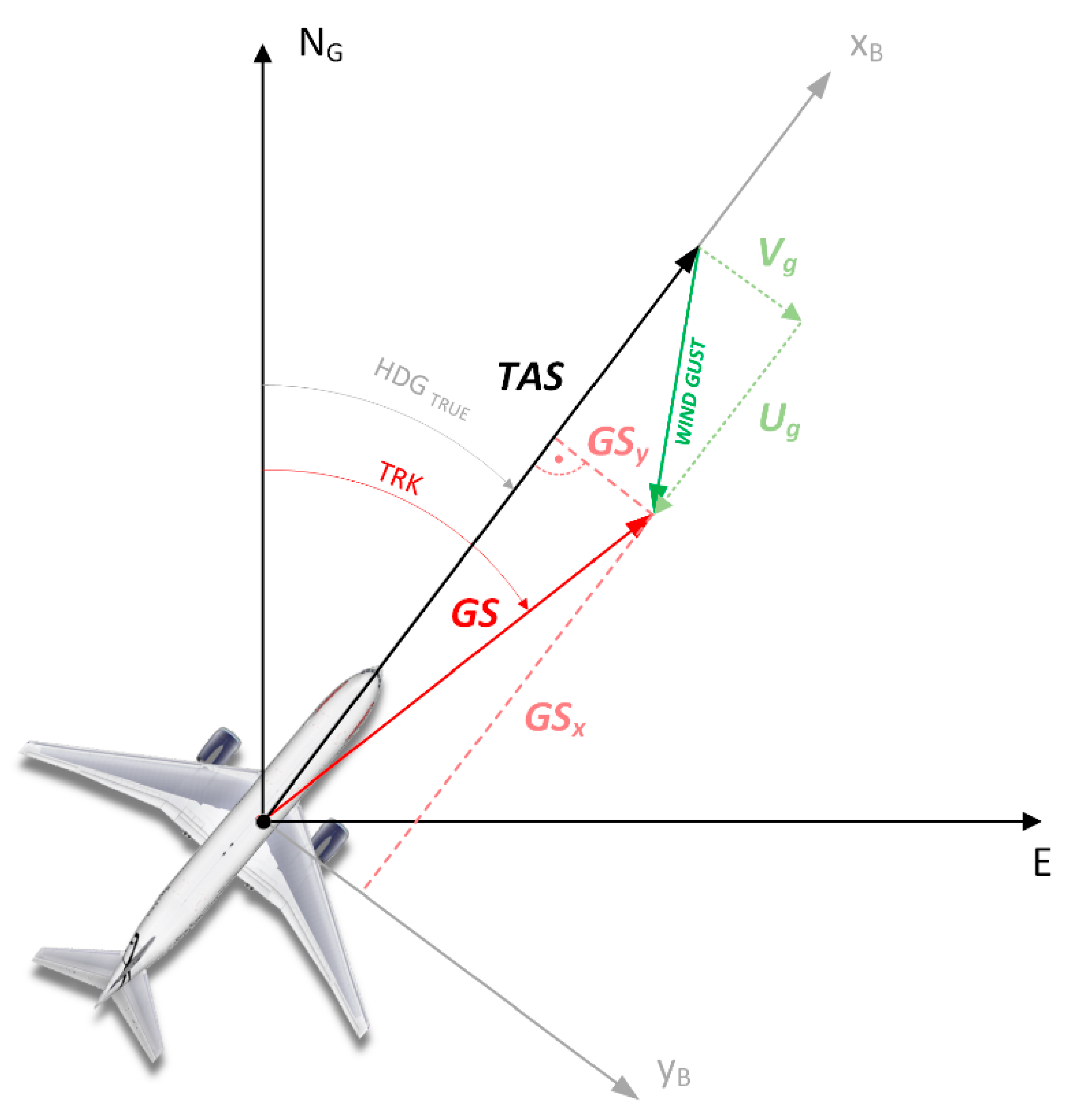
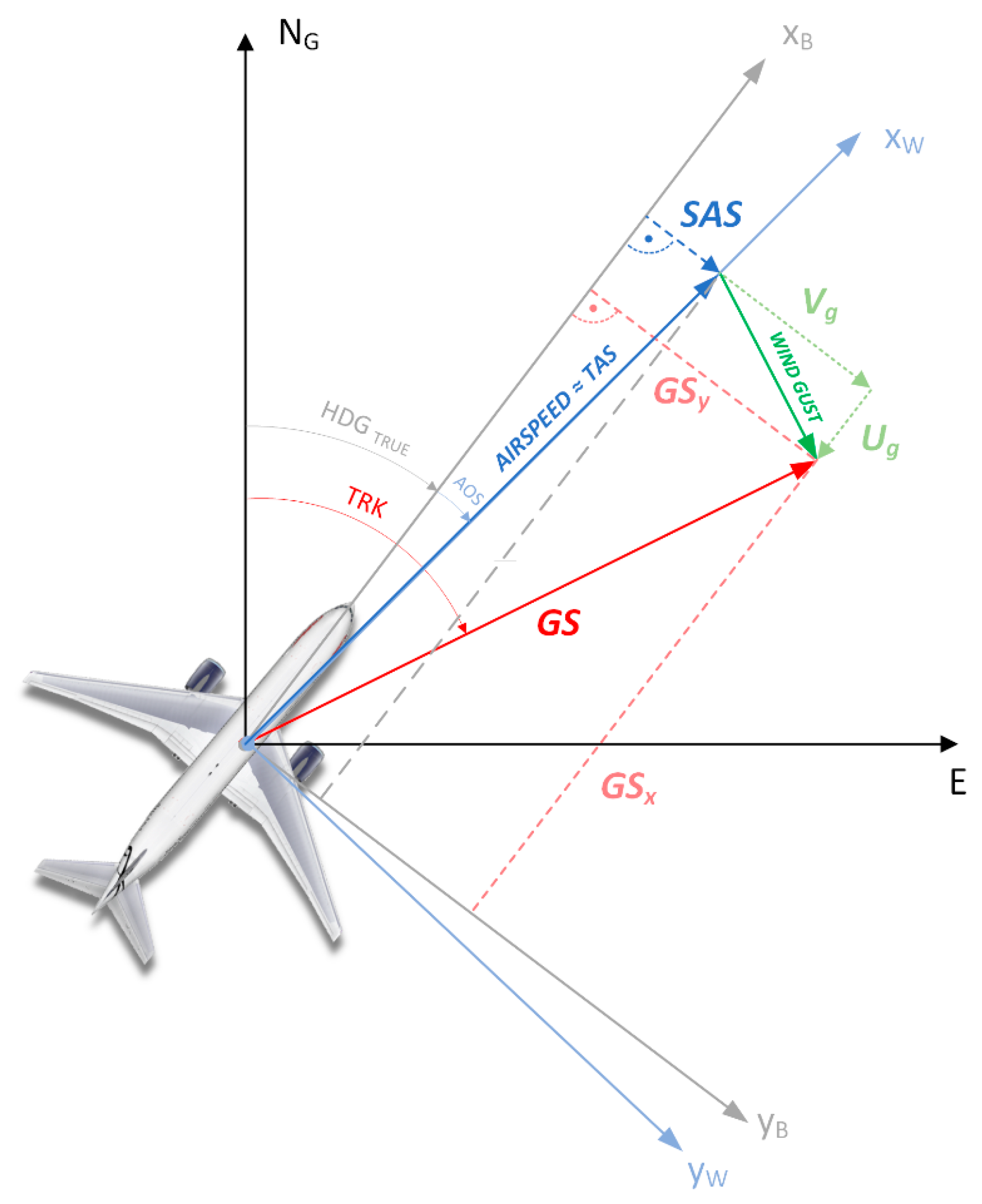
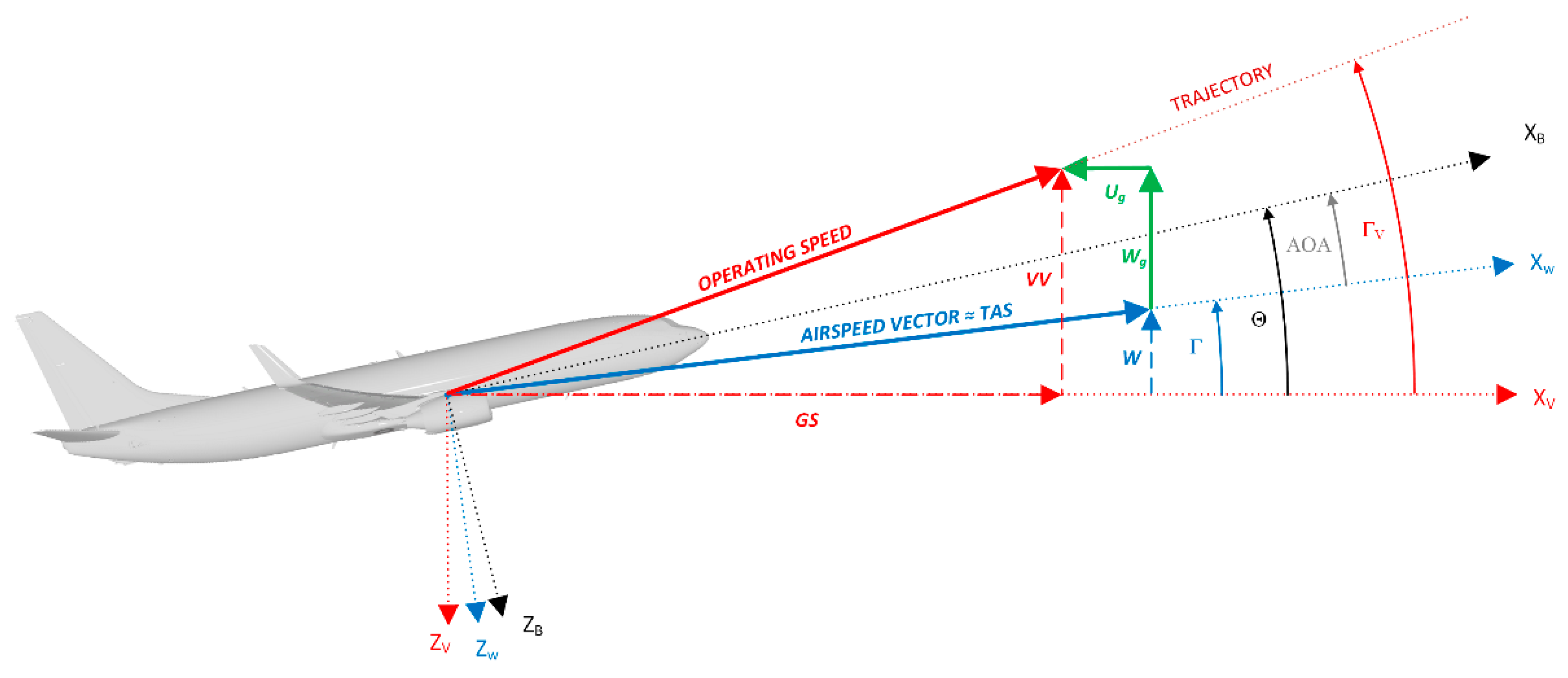
2.1. Analysis of the Possibilities of Wind Gusts Estimation (3D Problem)
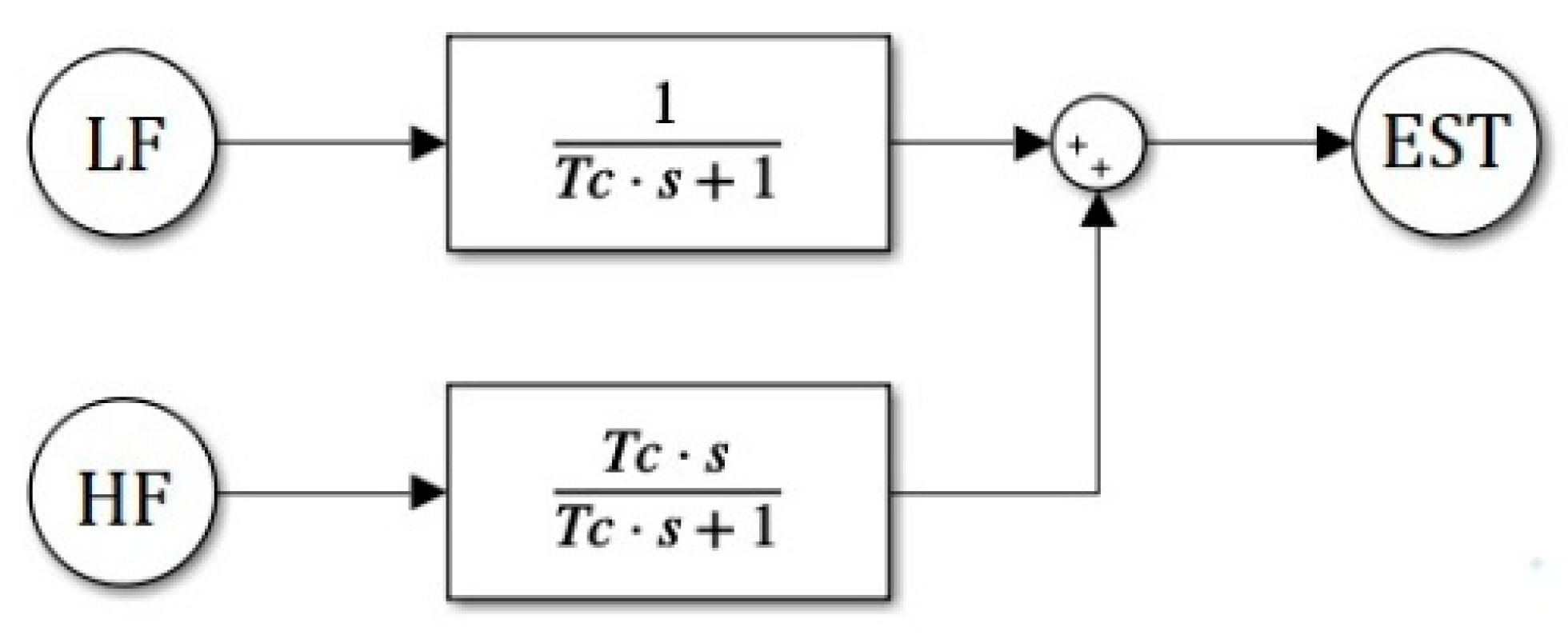
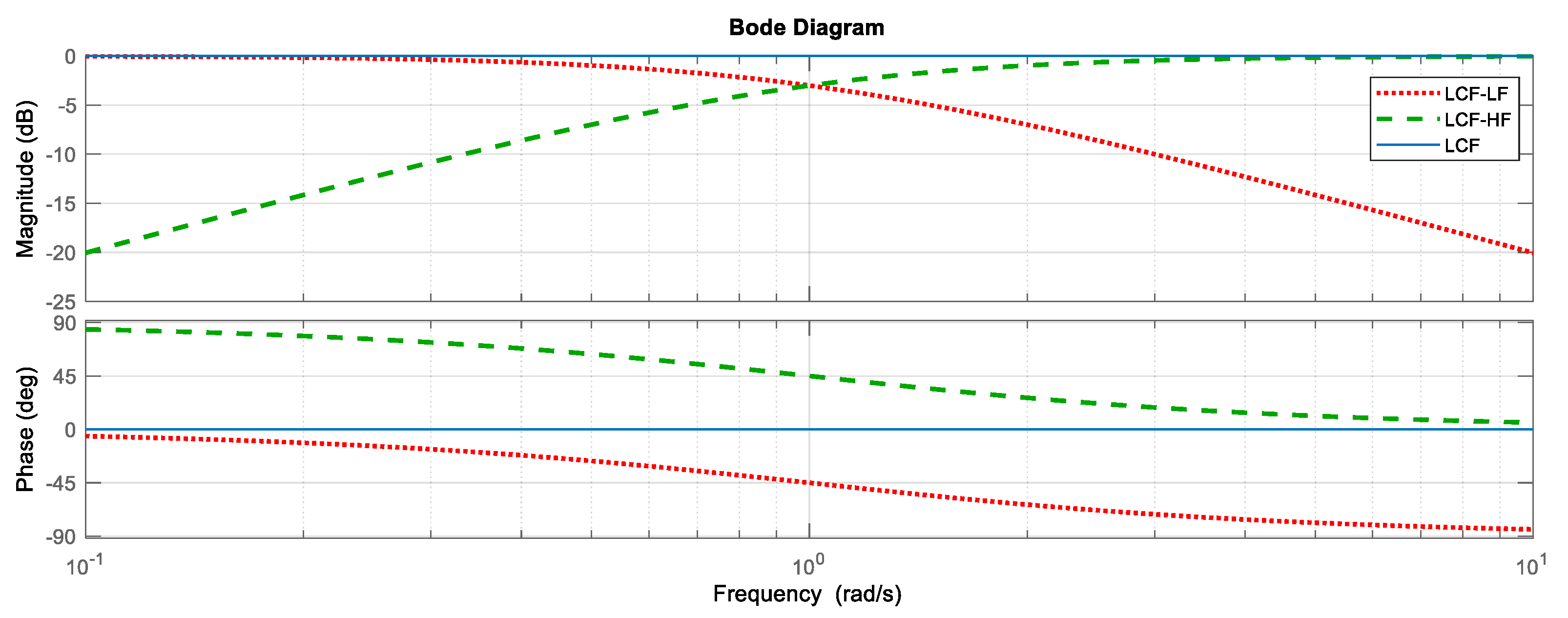
2.2. Proposed Methods for Estimating Head-On Gusts
- LF—low-frequency signal,
- HF—high-frequency signal,
- EST—output of CF.
2.3. Proposed Methods for Estimating Side Gusts
2.4. Proposed Methods for Estimating Vertical Gusts
3. Research Environment and Plan of Experiment
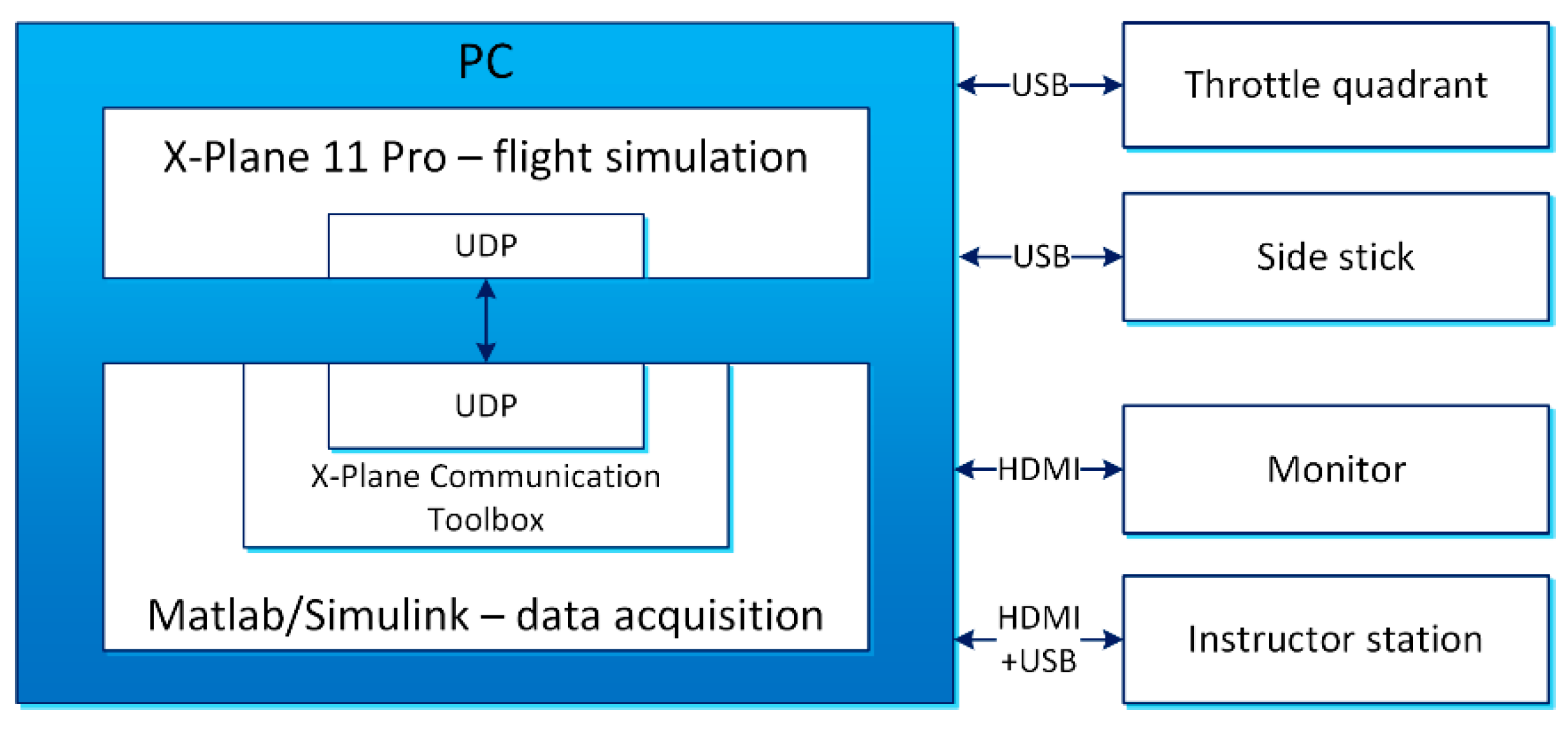
3.1. Flight Simulation Environment and Data Acquisition
- Data from simulated avionics systems (flight model controls and flight model position),
- Real-time gust parameters generated by predefined wind layers (simulation weather).
3.2. Simulation Assumptions
- Aircraft weight: 65,000 kg,
- Automatic flight with a layer of atmospheric gusts
- Three flight phases: descent, level flight and climb
- Simulation performed by a pilot holding a current type rating for the B737.
- LVL CHG (Level Change). This mode coordinates pitch and thrust commands to perform automatic climbs and descents to preselected altitudes at specified airspeeds. During descent, the autothrottle mode annunciates RETARD, followed by ARM, and then maintains the idle thrust. During the climb, the autothrottle mode annunciates N1 for climb and holds limit thrust for CLB from FMC. In both cases, the Autopilot Flight Director System (AFDS) holds the selected airspeed [45]. The rate of climb is a resulting parameter. This mode allows for the assumption of approximately constant thrust during simulation (the VS—Vertical Speed mode maintains a constant vertical speed, adjusting thrust and pitch to hold the selected IAS and vertical speed VVI).
- ALT HLD (Altitude Hold). In this mode, the autopilot commands pitch to hold the uncorrected barometric altitude at which the switch was pressed or MCP (Mode Control Panel) selected altitude after climb or descent. The autothrottle system holds the selected speed indicated in the IAS/MACH display on the MCP by adjusting the throttle control and thrust accordingly.
- HDG SEL (Heading Select). This mode commands roll to turn to and maintain the heading set on the MCP HEADING display. The maximum bank angle limit is limited by the bank angle selector [45].
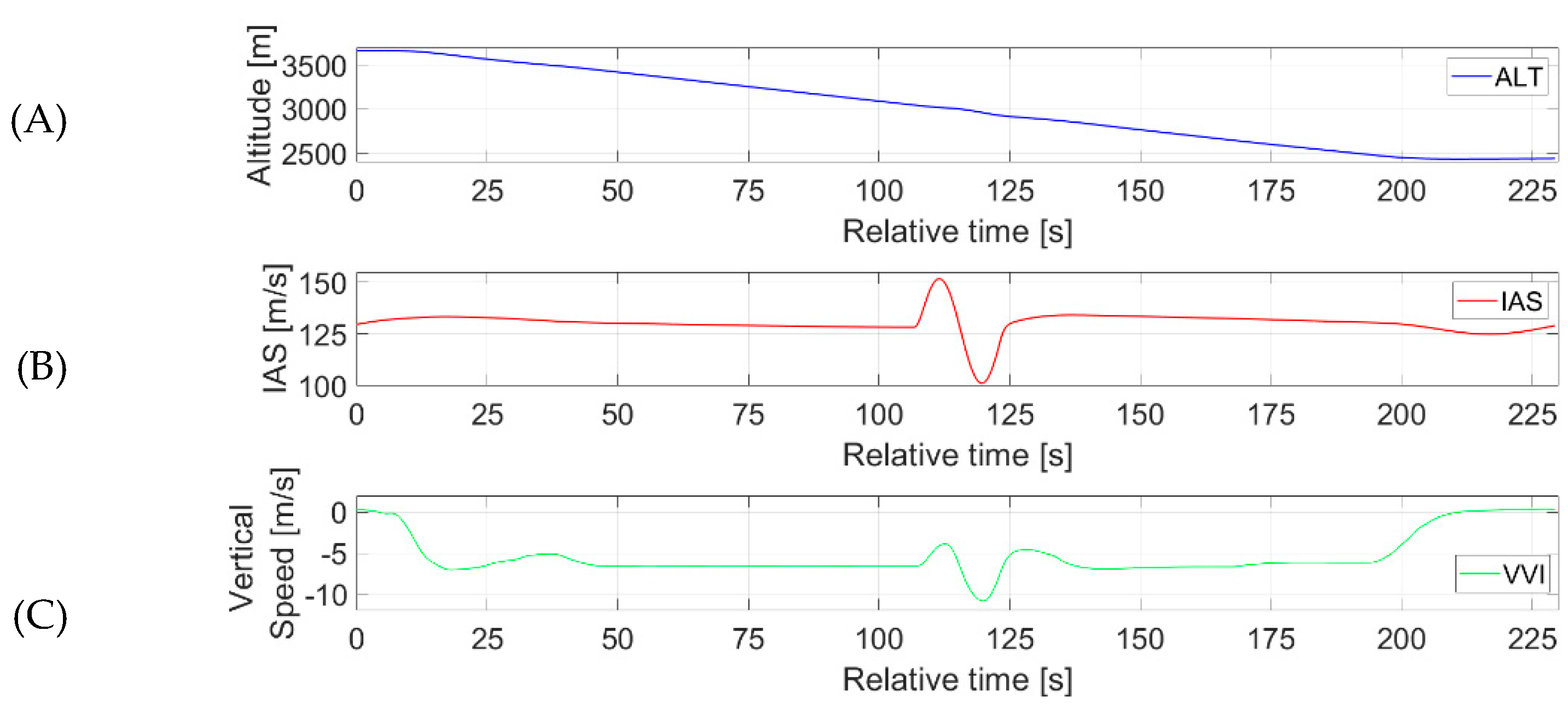
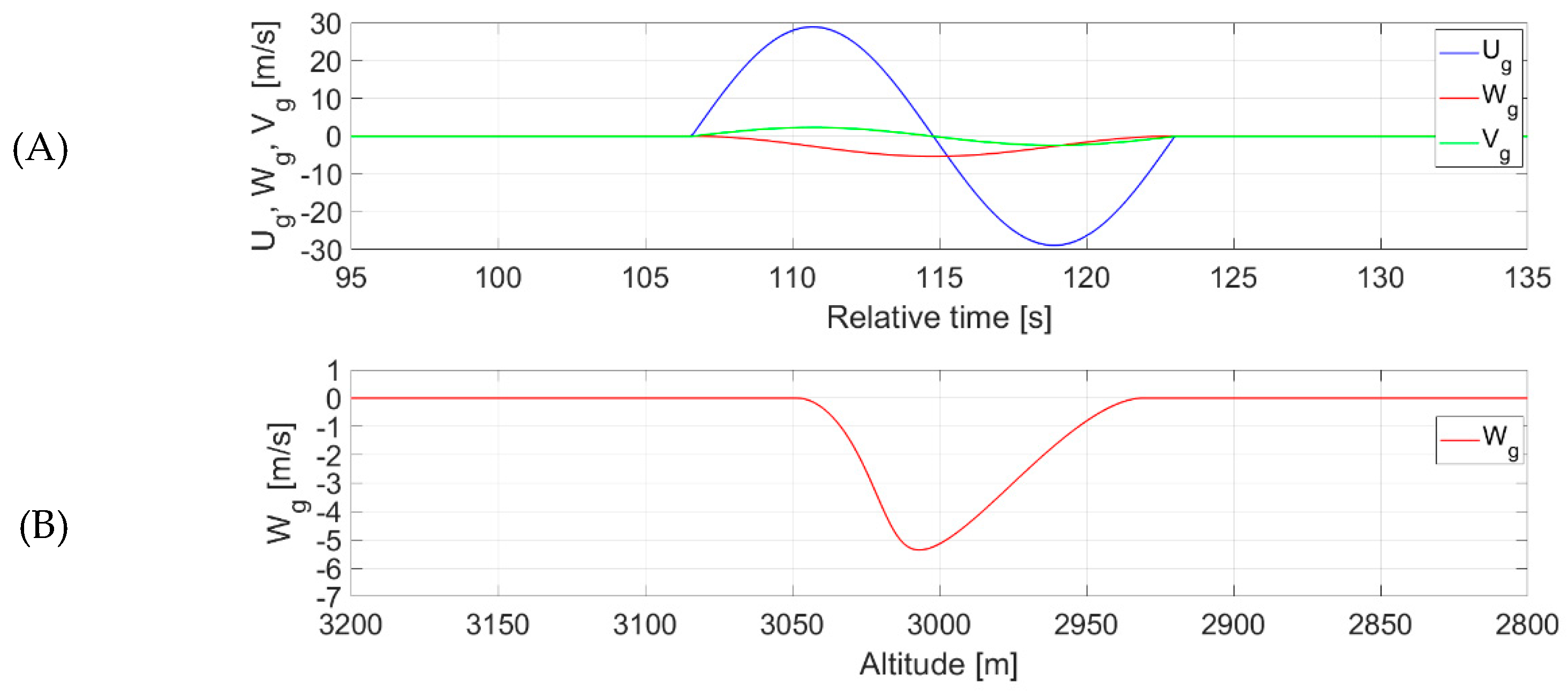
3.3. Flight Plan and Its Realisation for Estimating Head-on Gusts
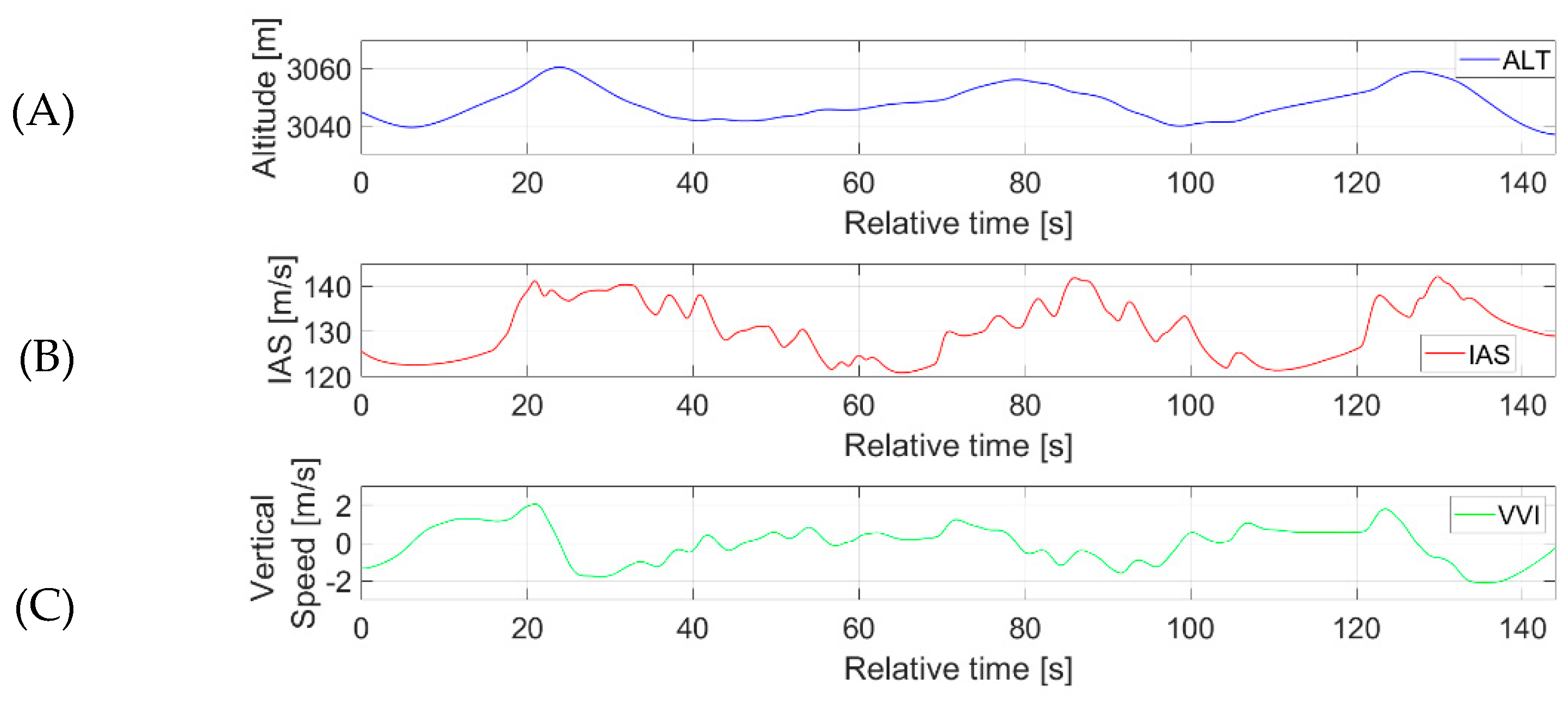
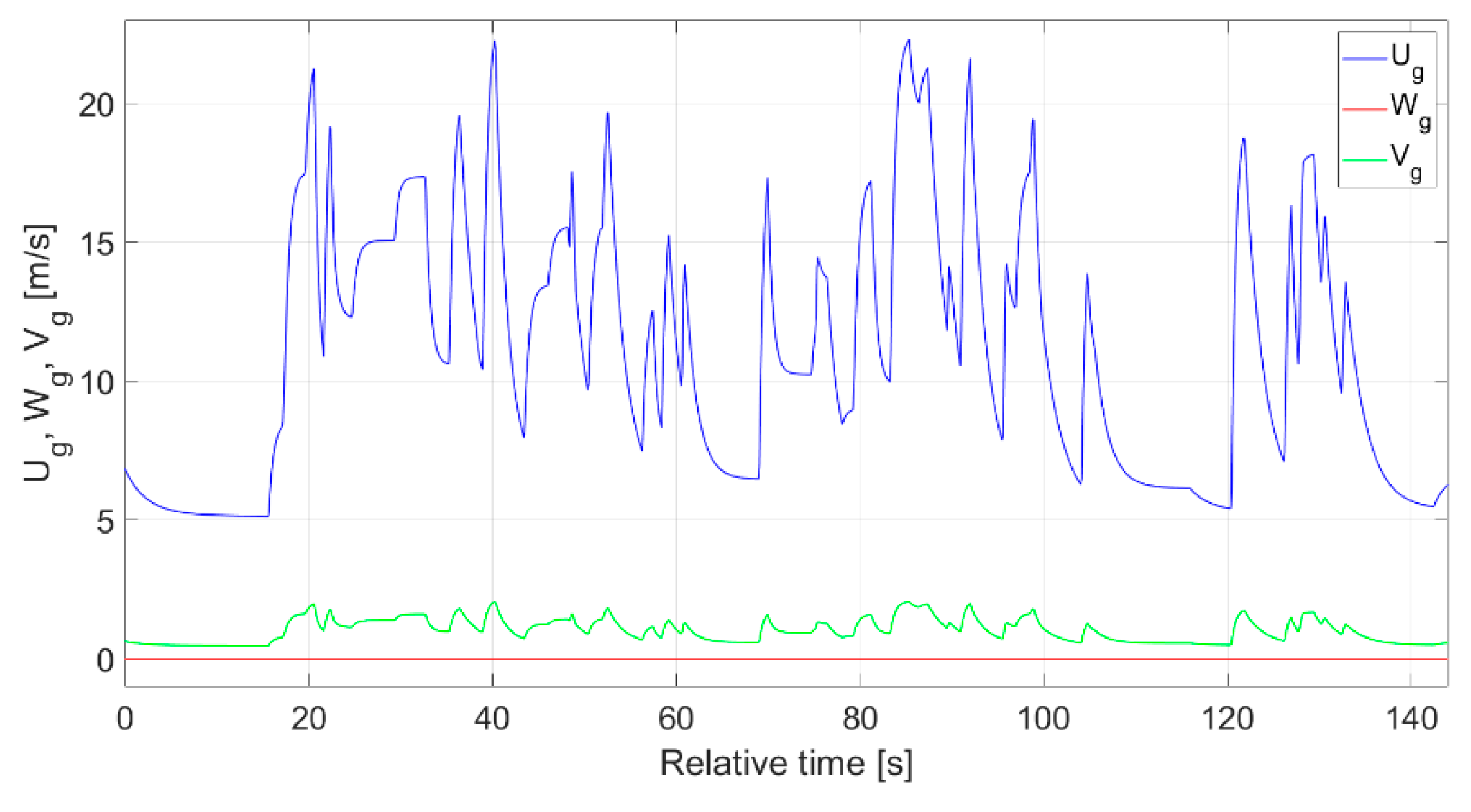
3.4. Flight Plan and Its Realisation for Estimating Side Gusts
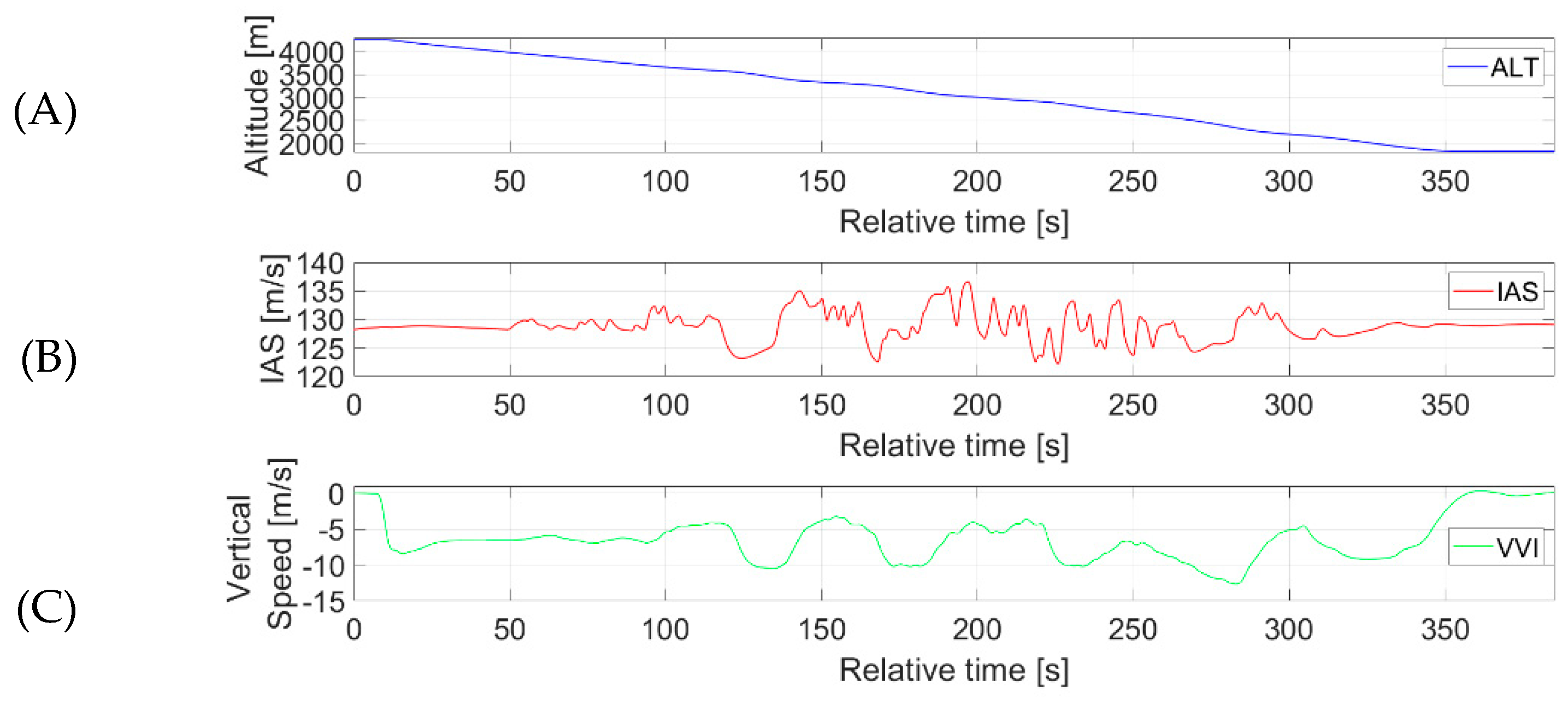
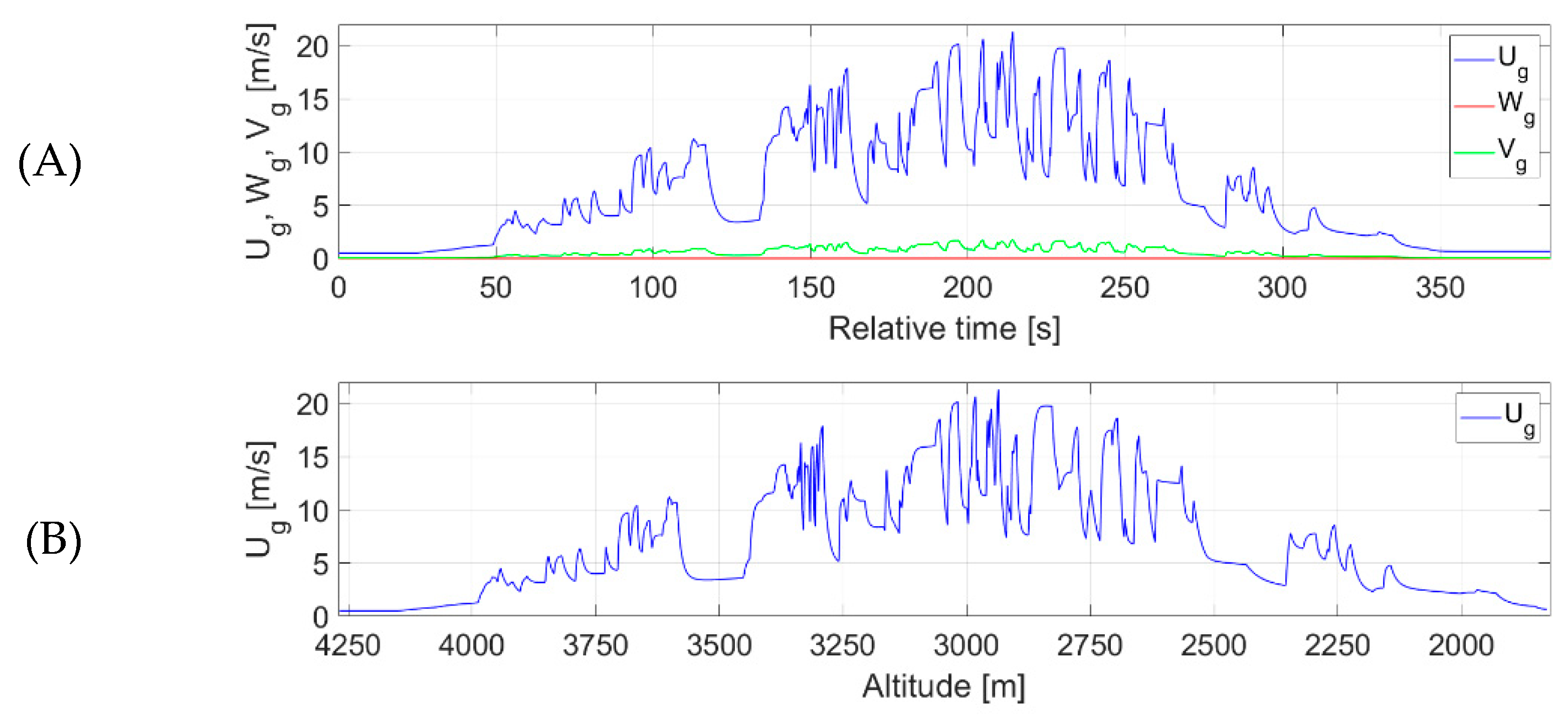
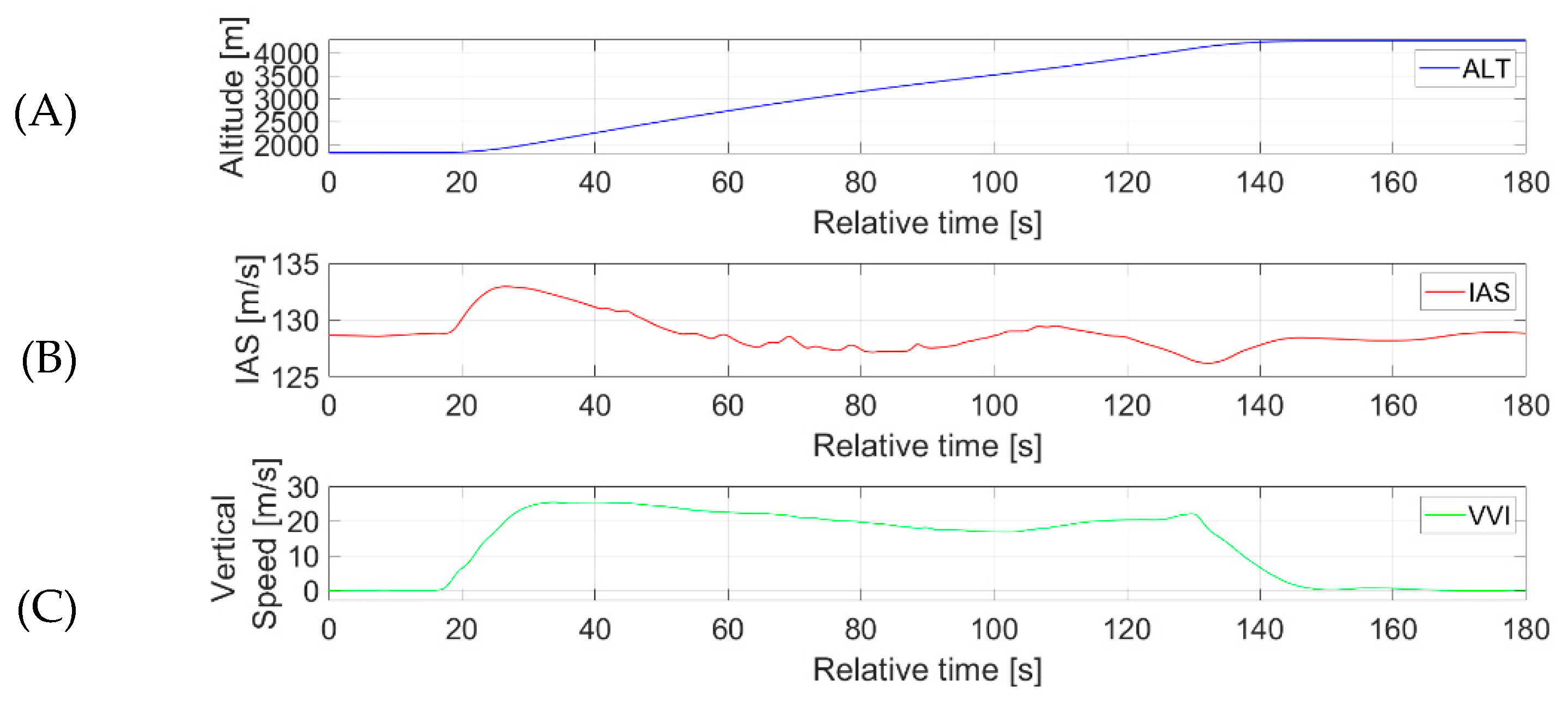
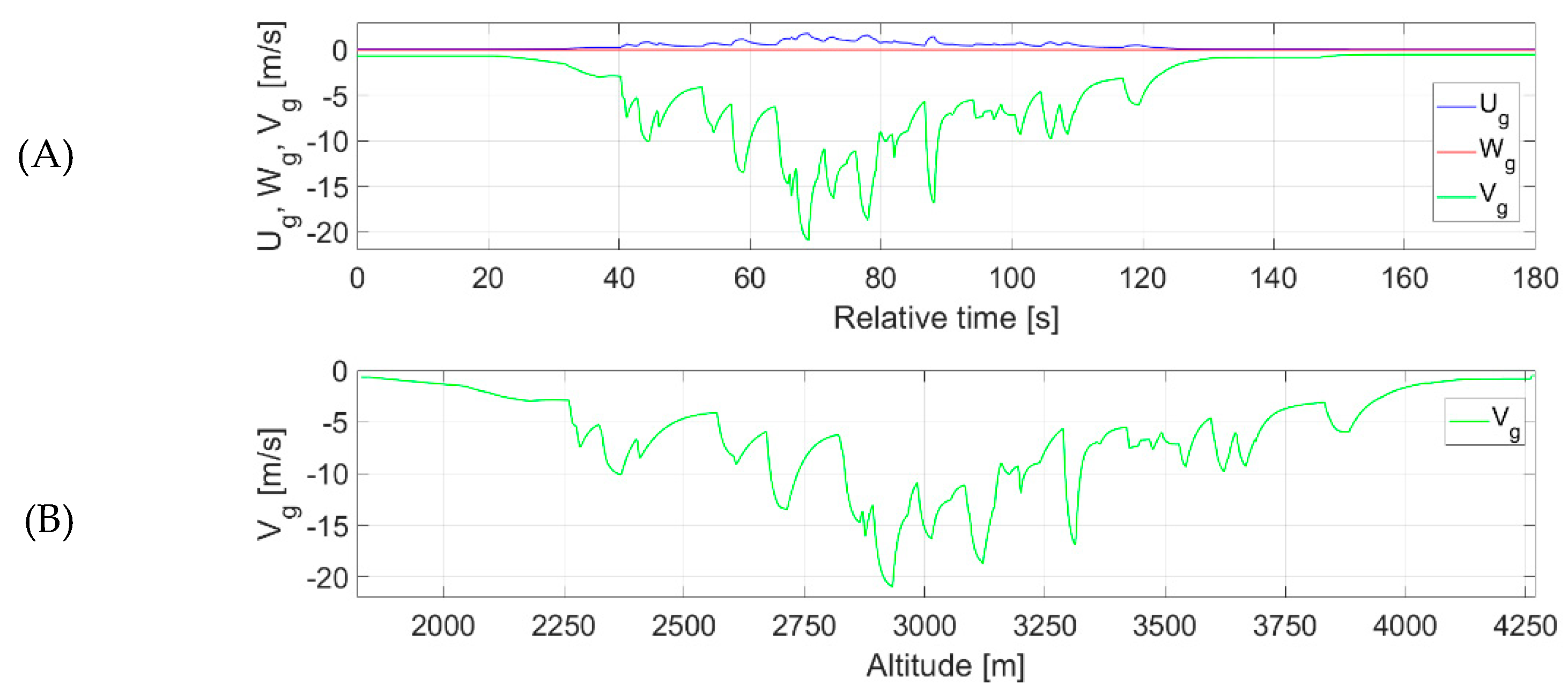
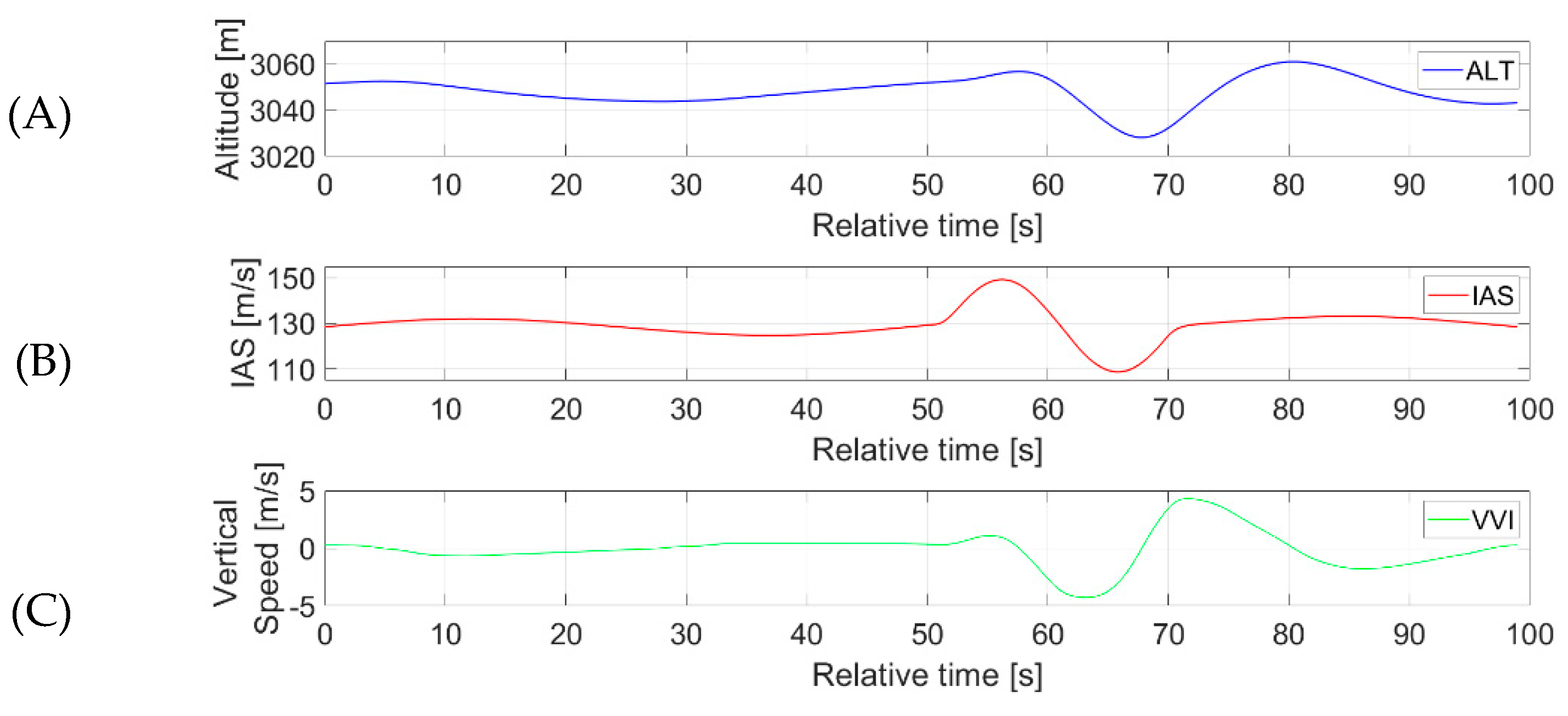
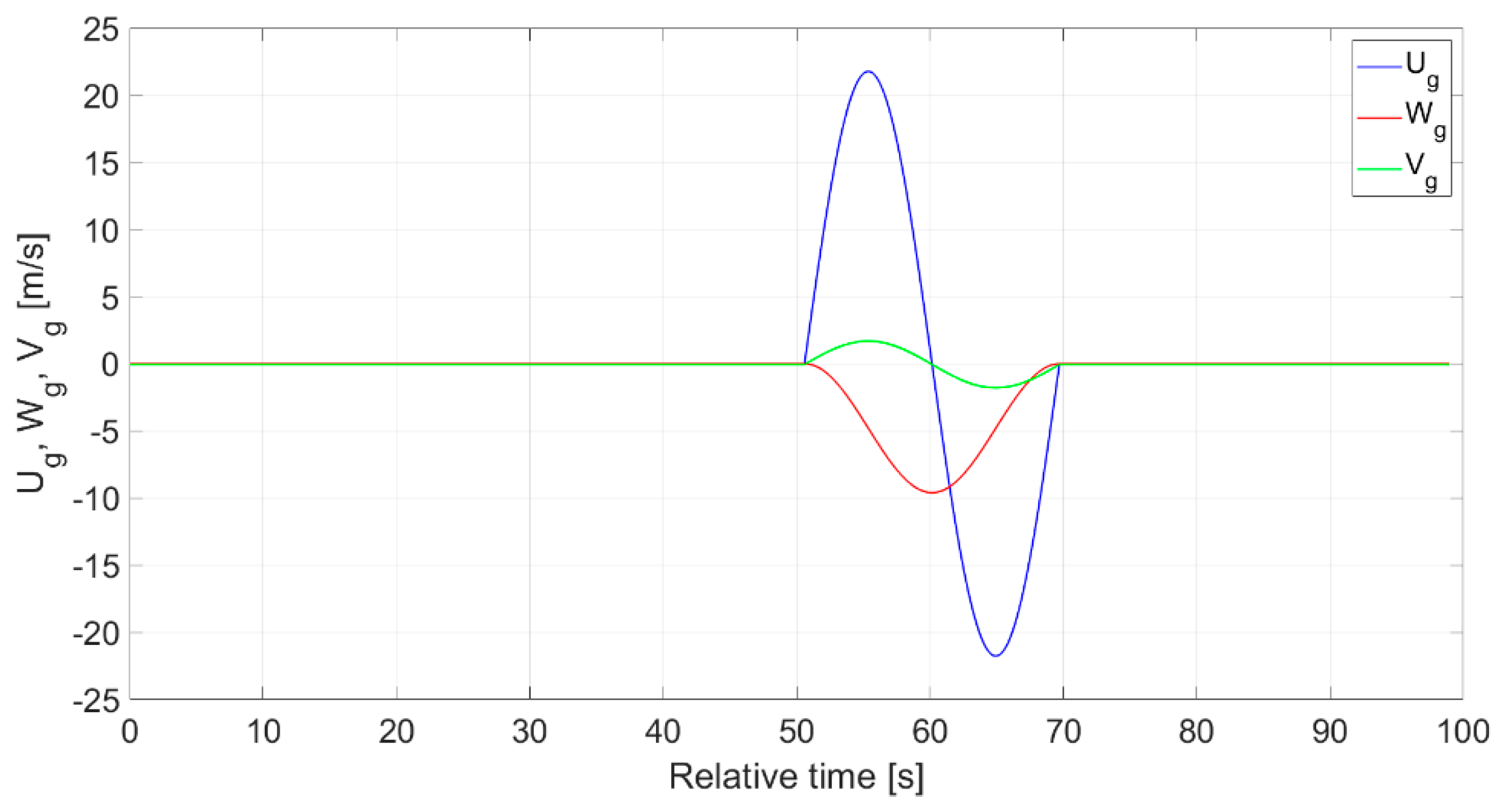
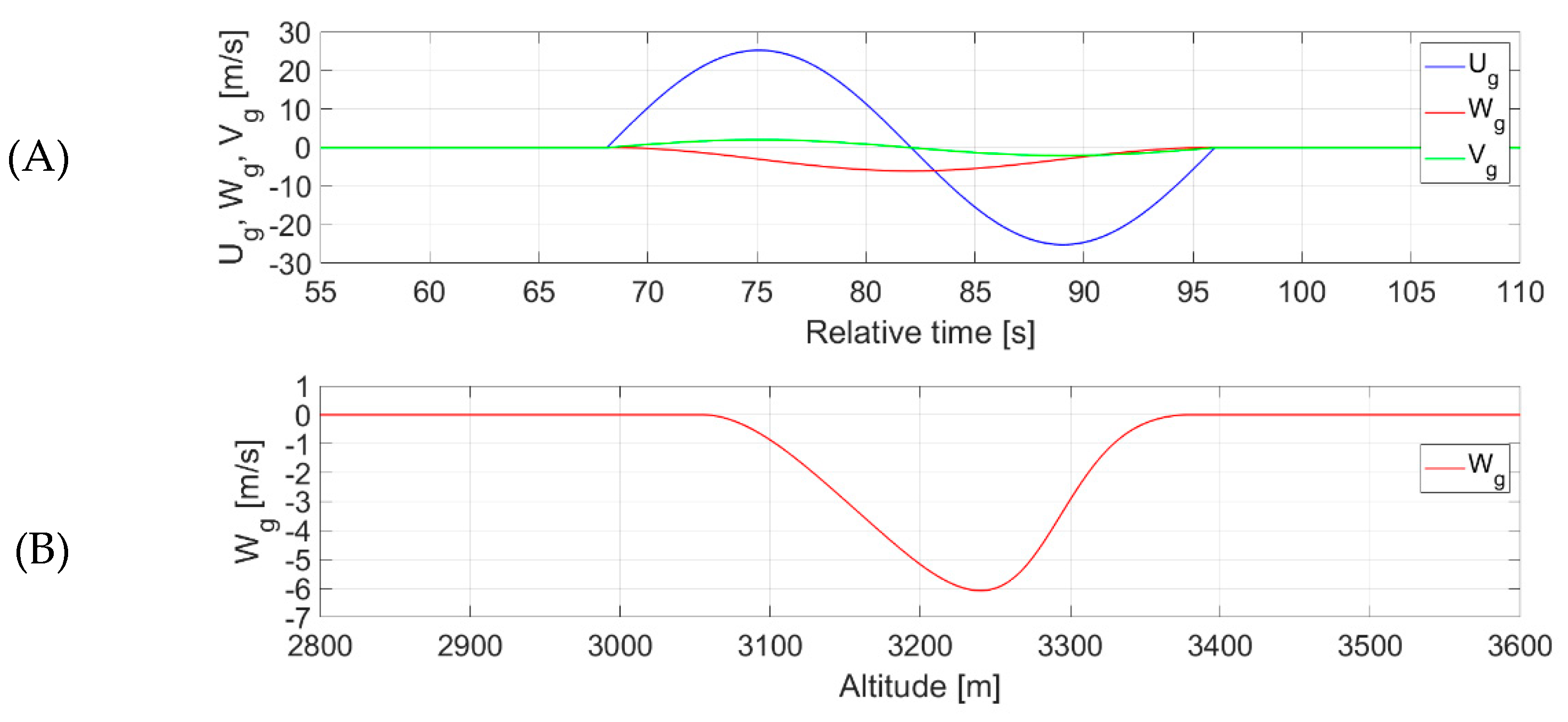
3.5. Flight Plan and Its Realization for Estimating Vertical Gusts
- Constant thrust was maintained during level flight prior to the occurrence of a microburst,
- Variable thrust as the autothrottle control system responds to a microburst,
- Simultaneous occurrence of side and frontal wind components in the available microburst model.
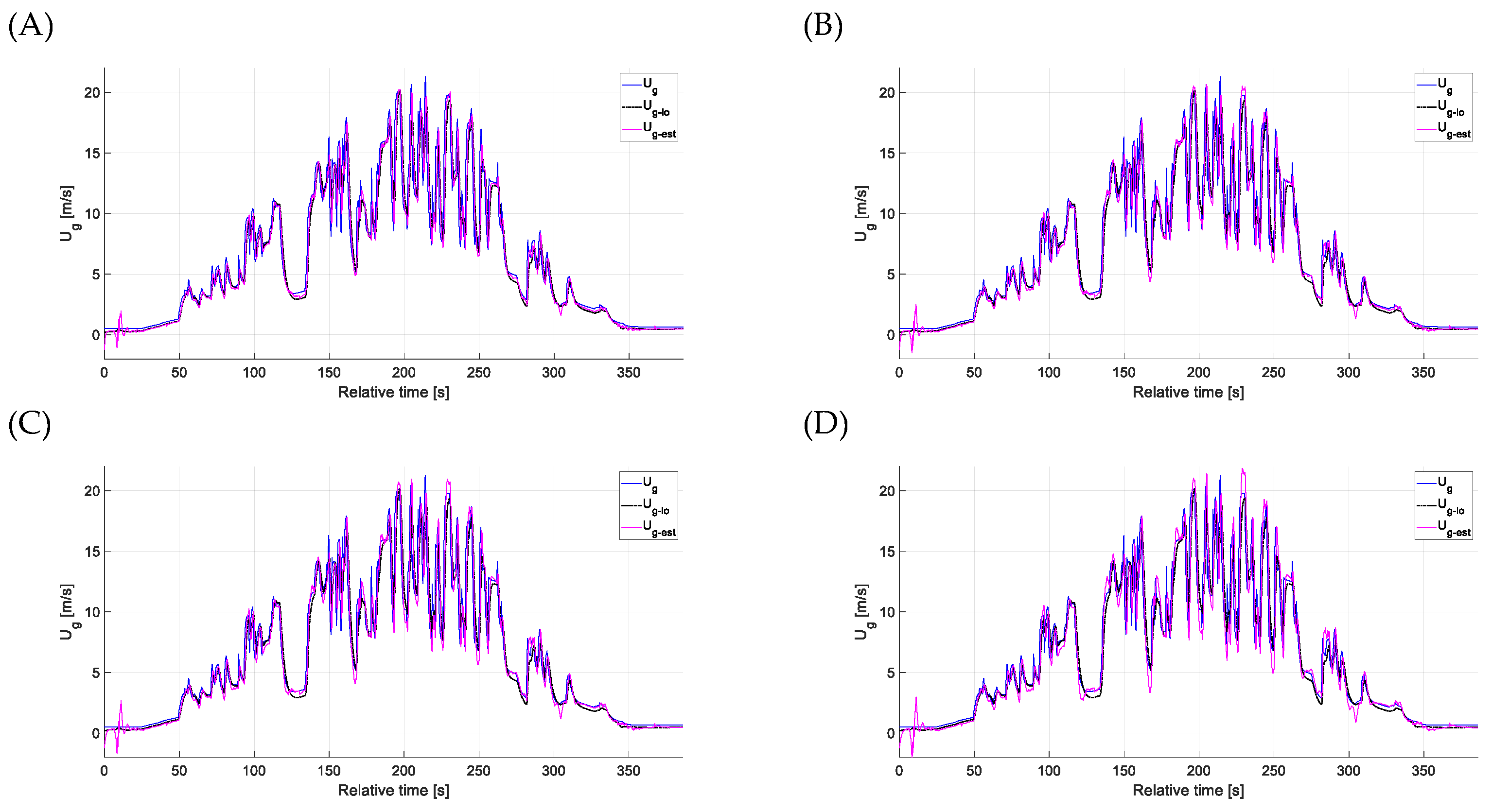
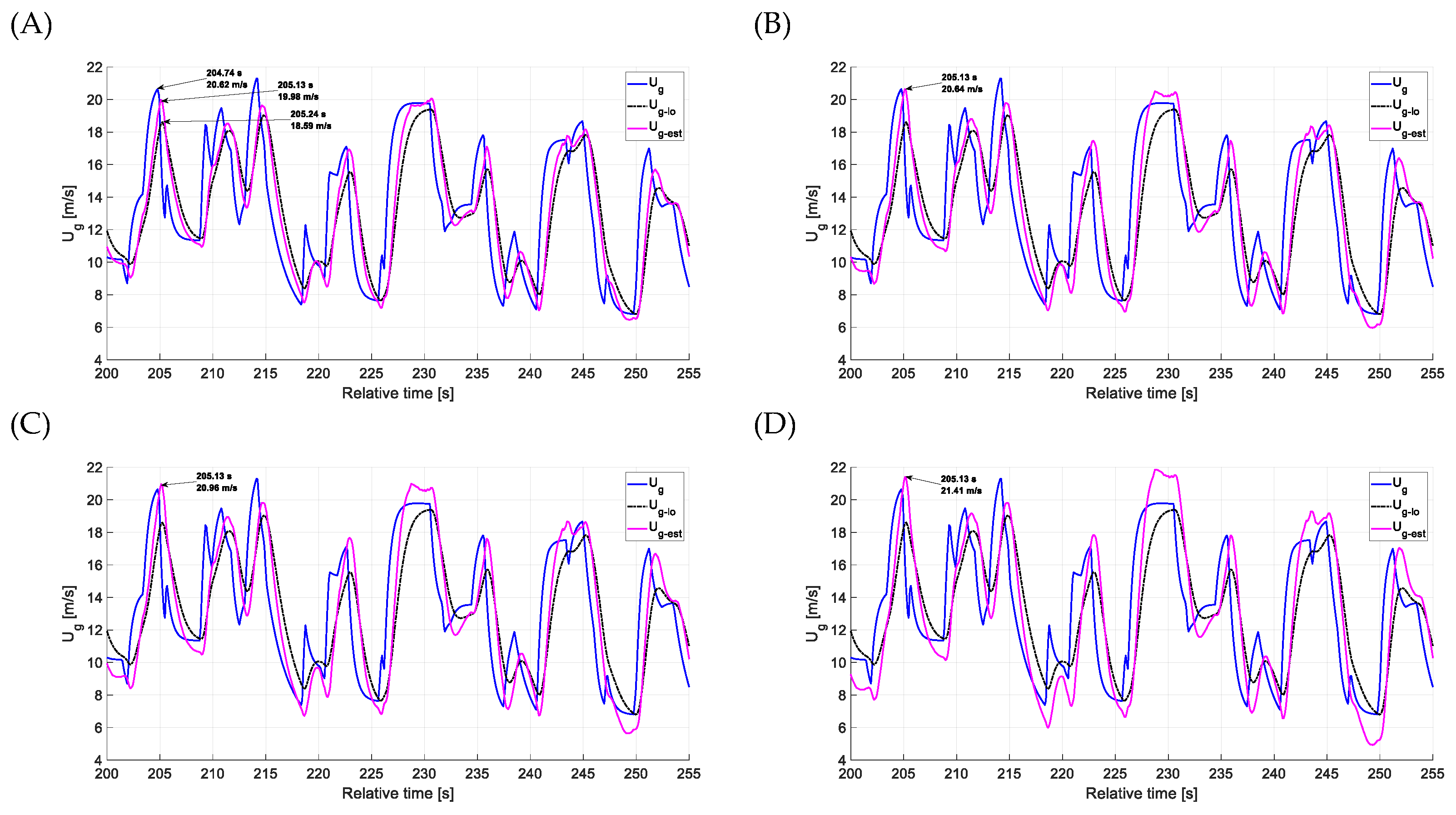
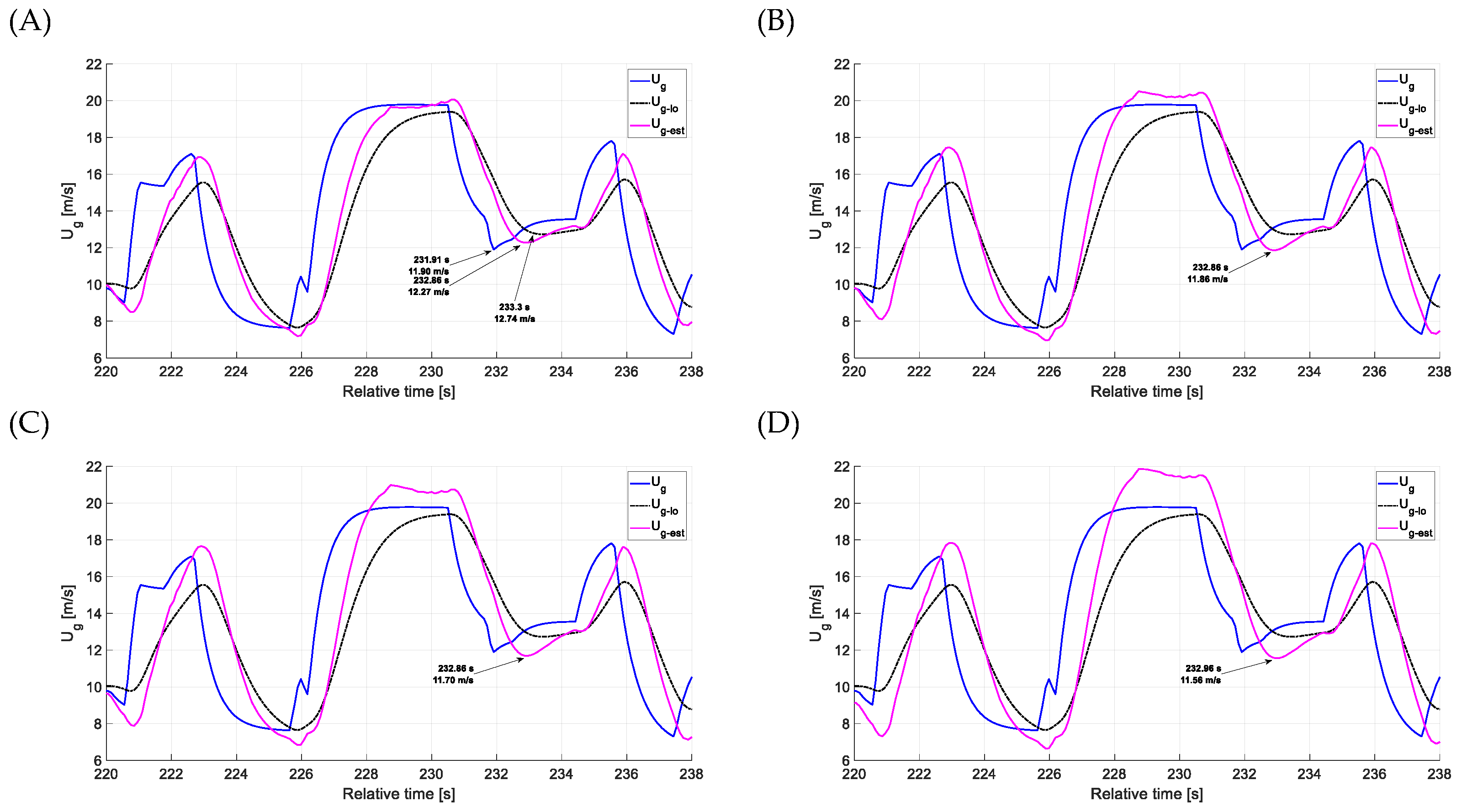
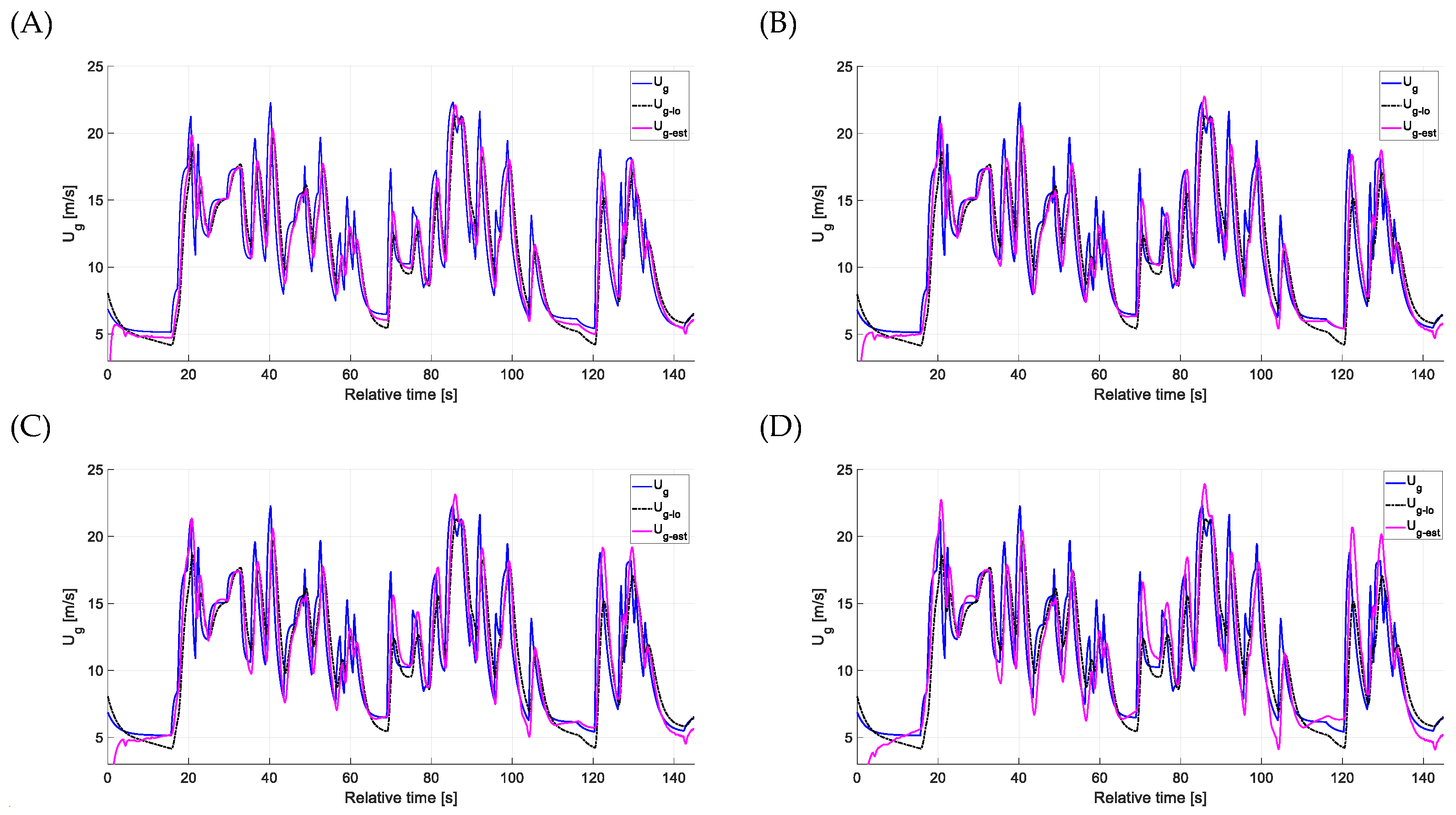
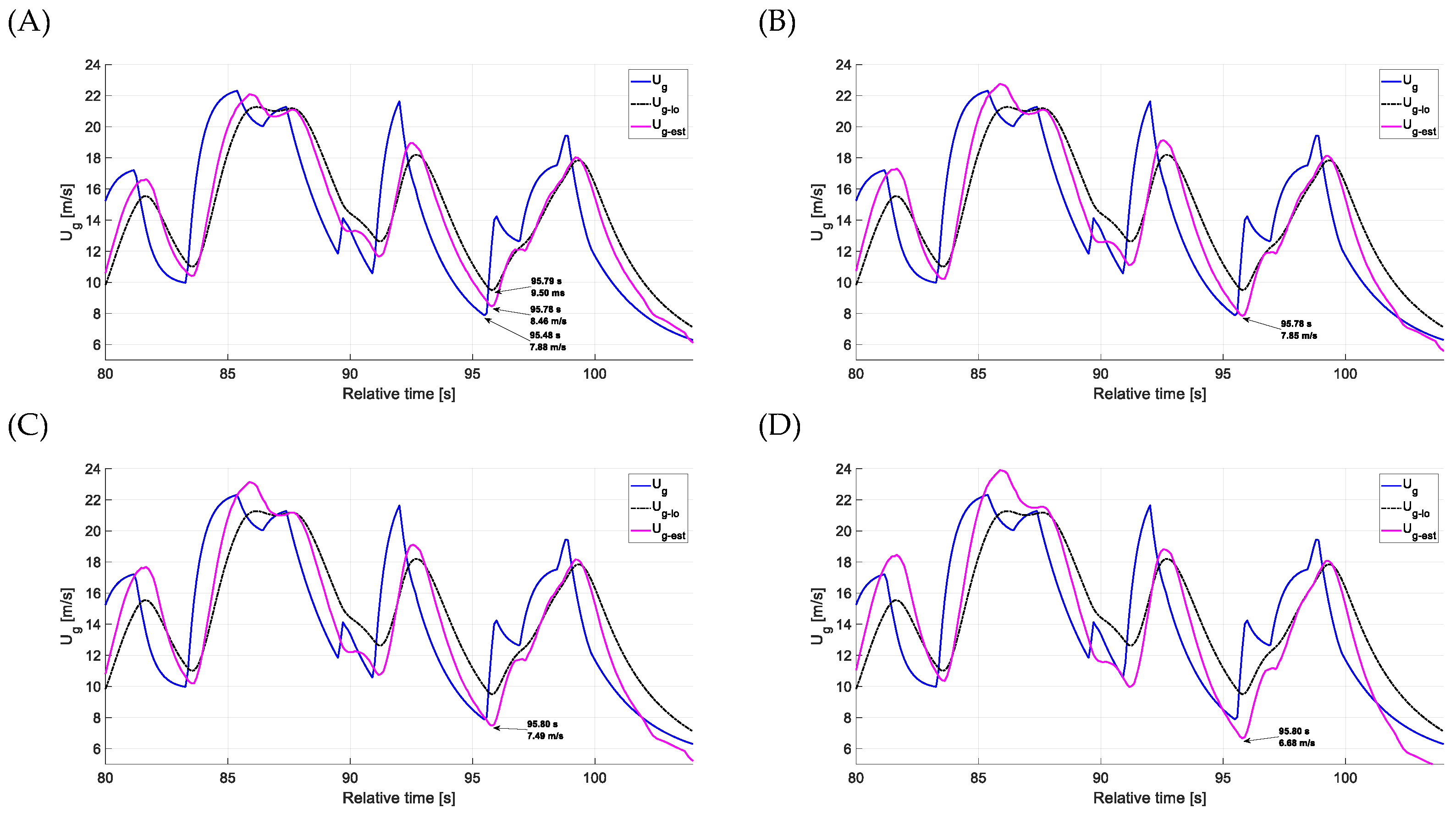
4. Results and Discussion
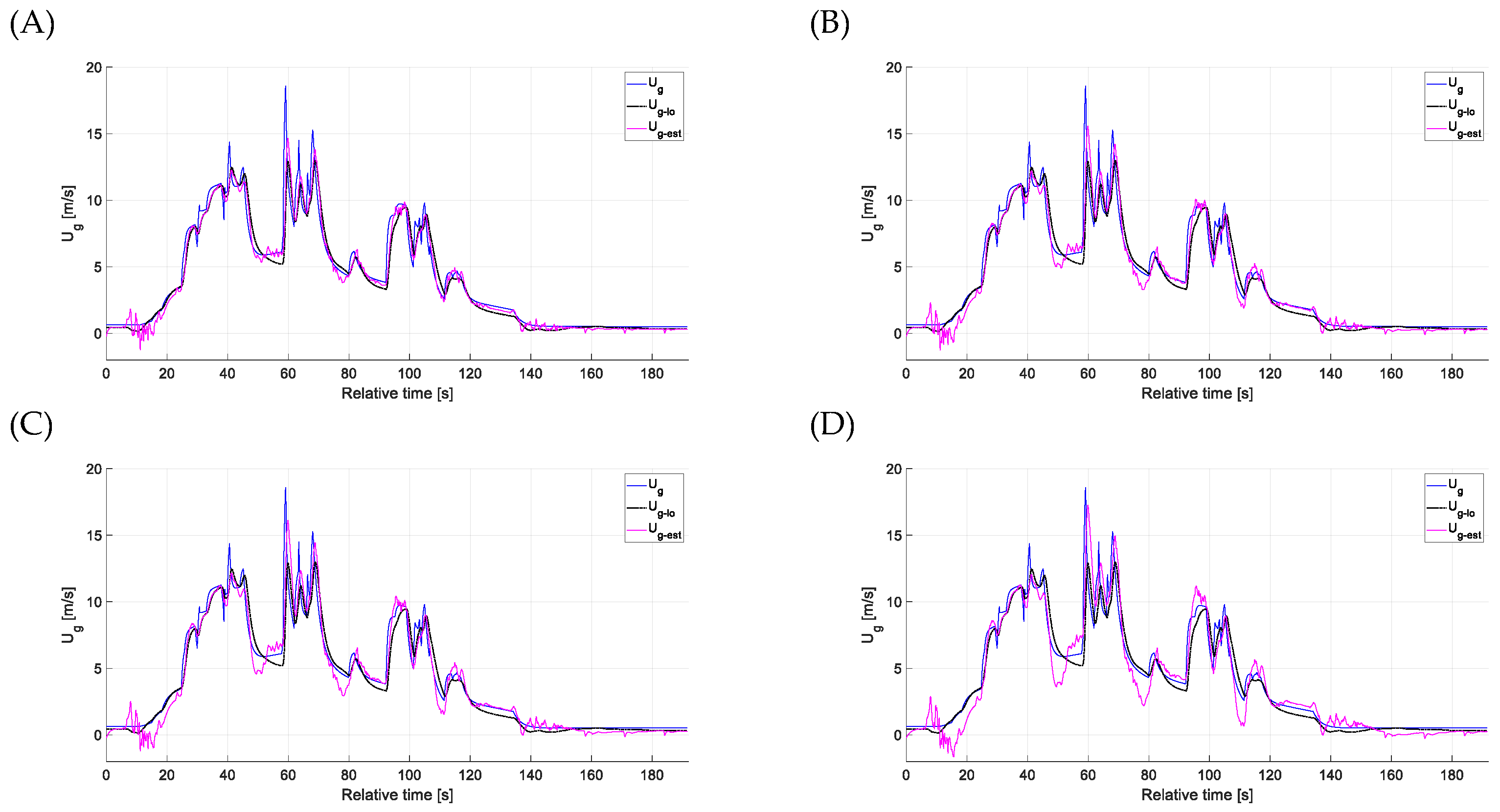
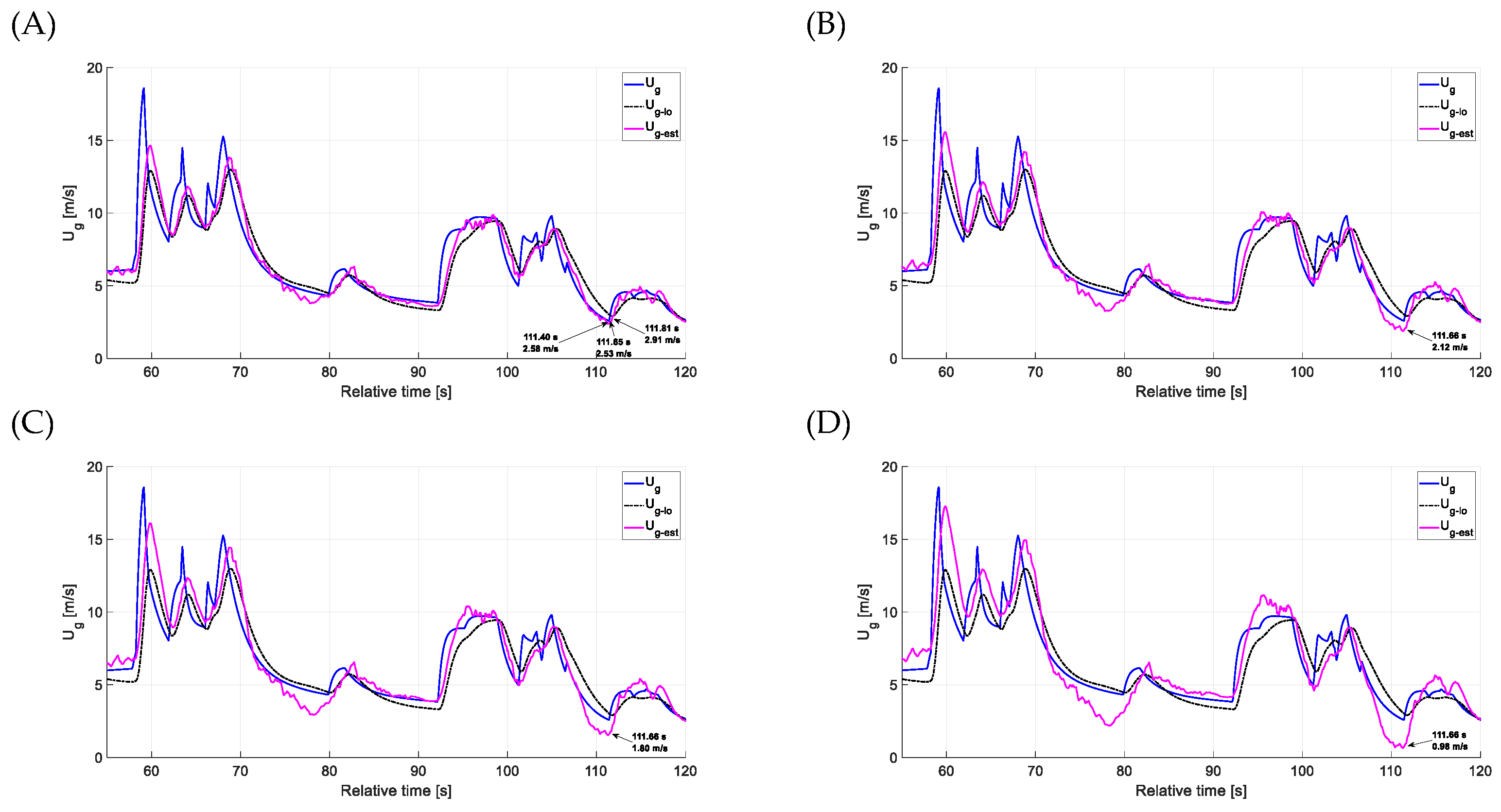
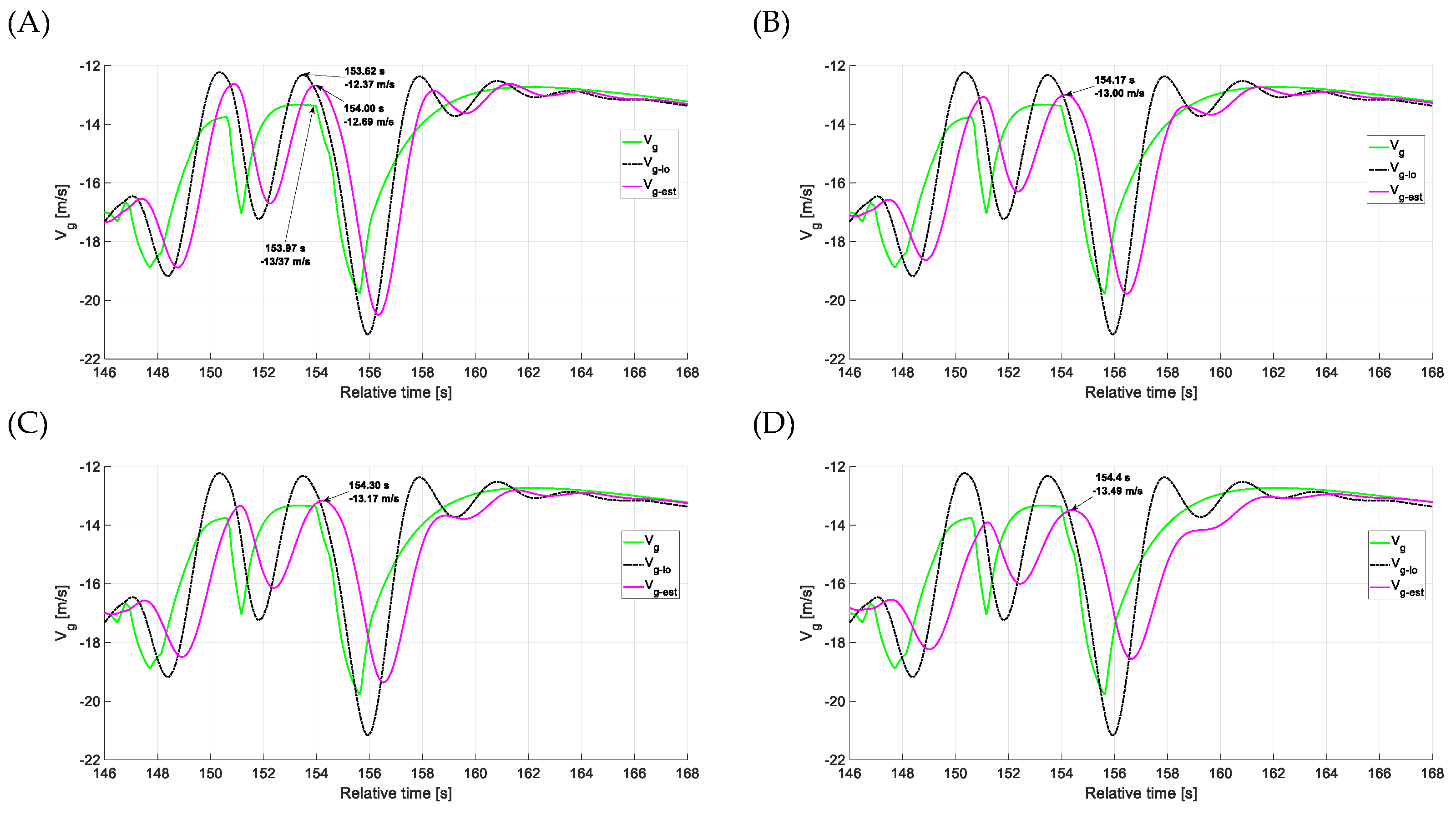
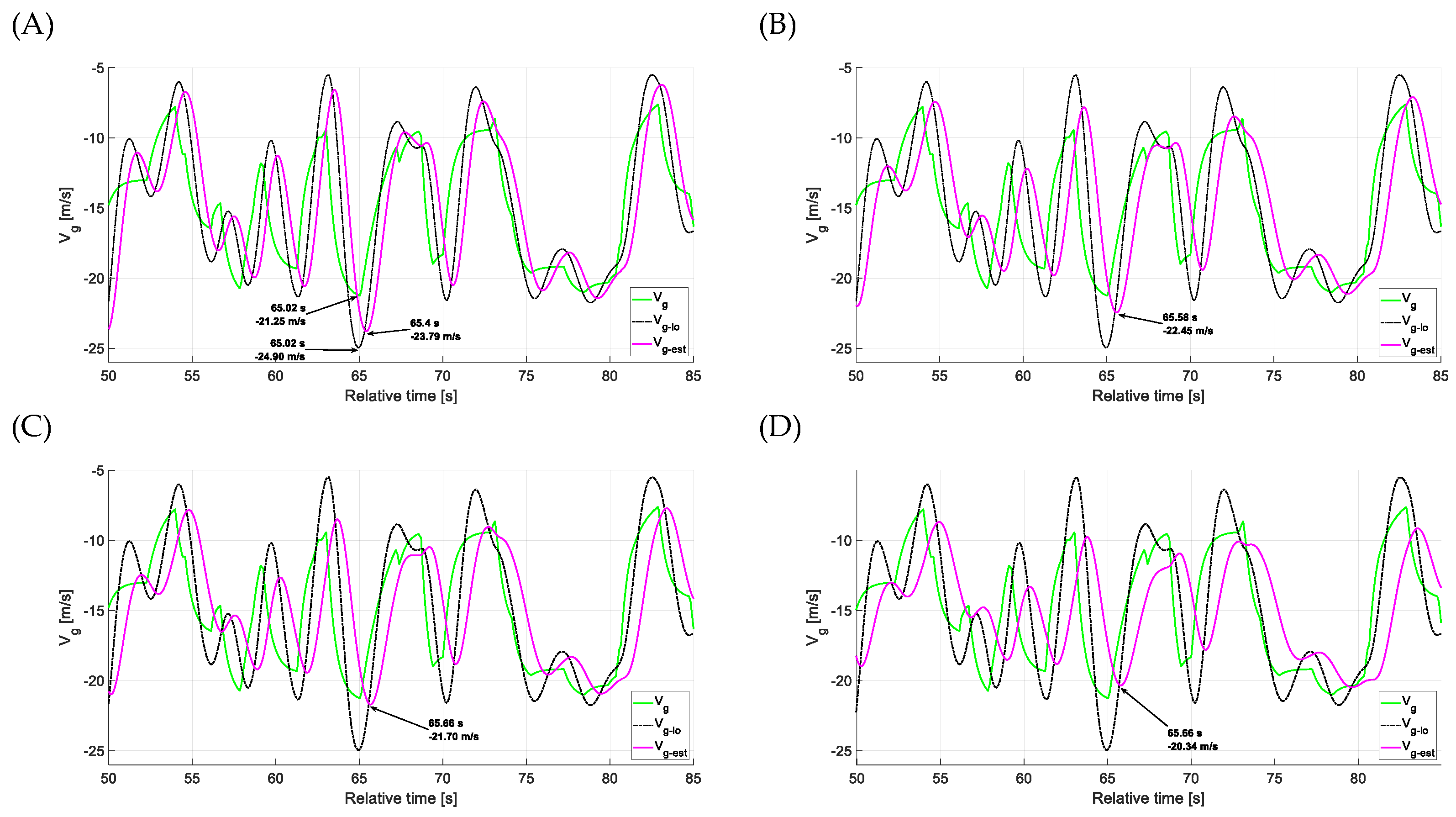
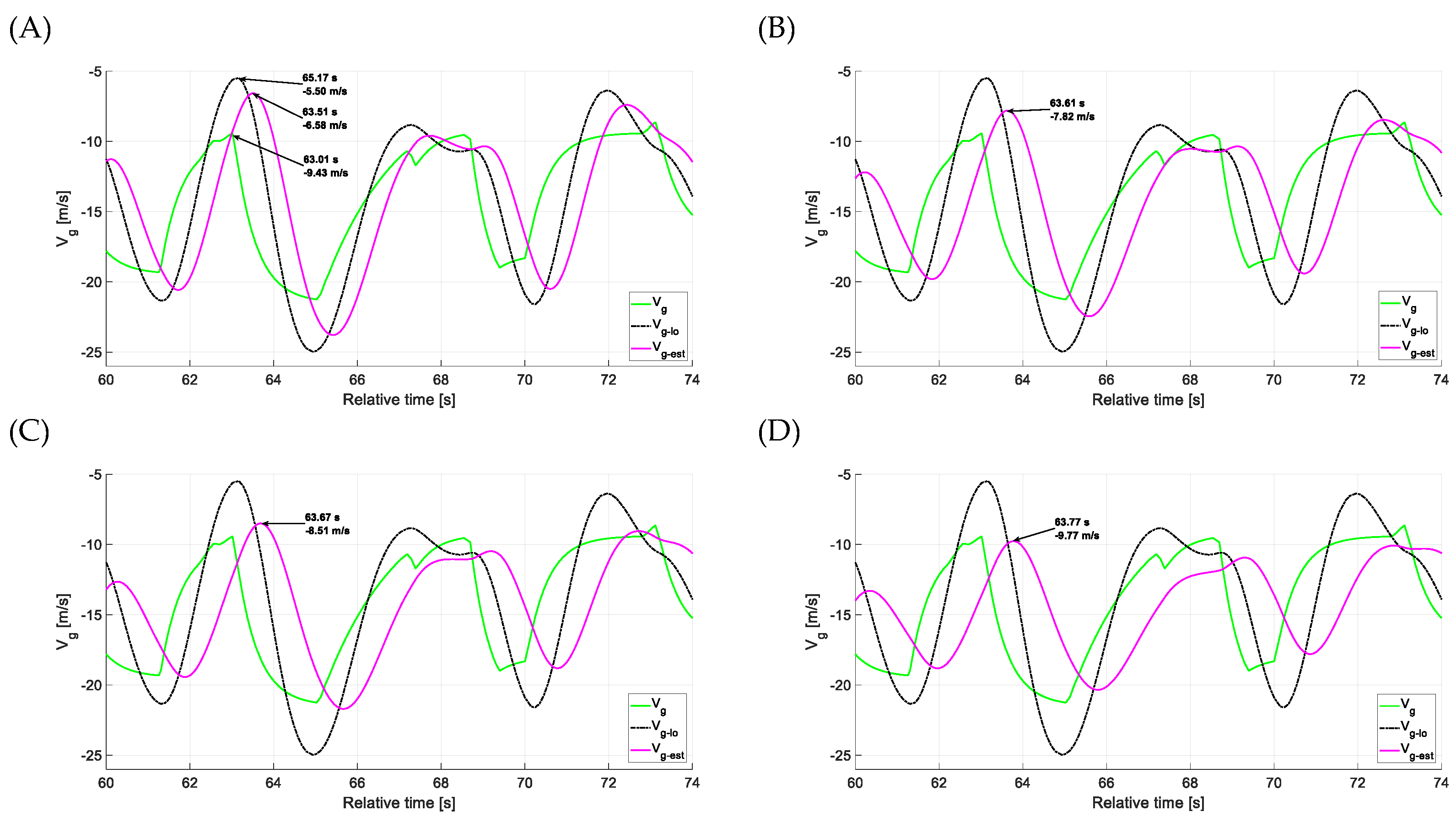
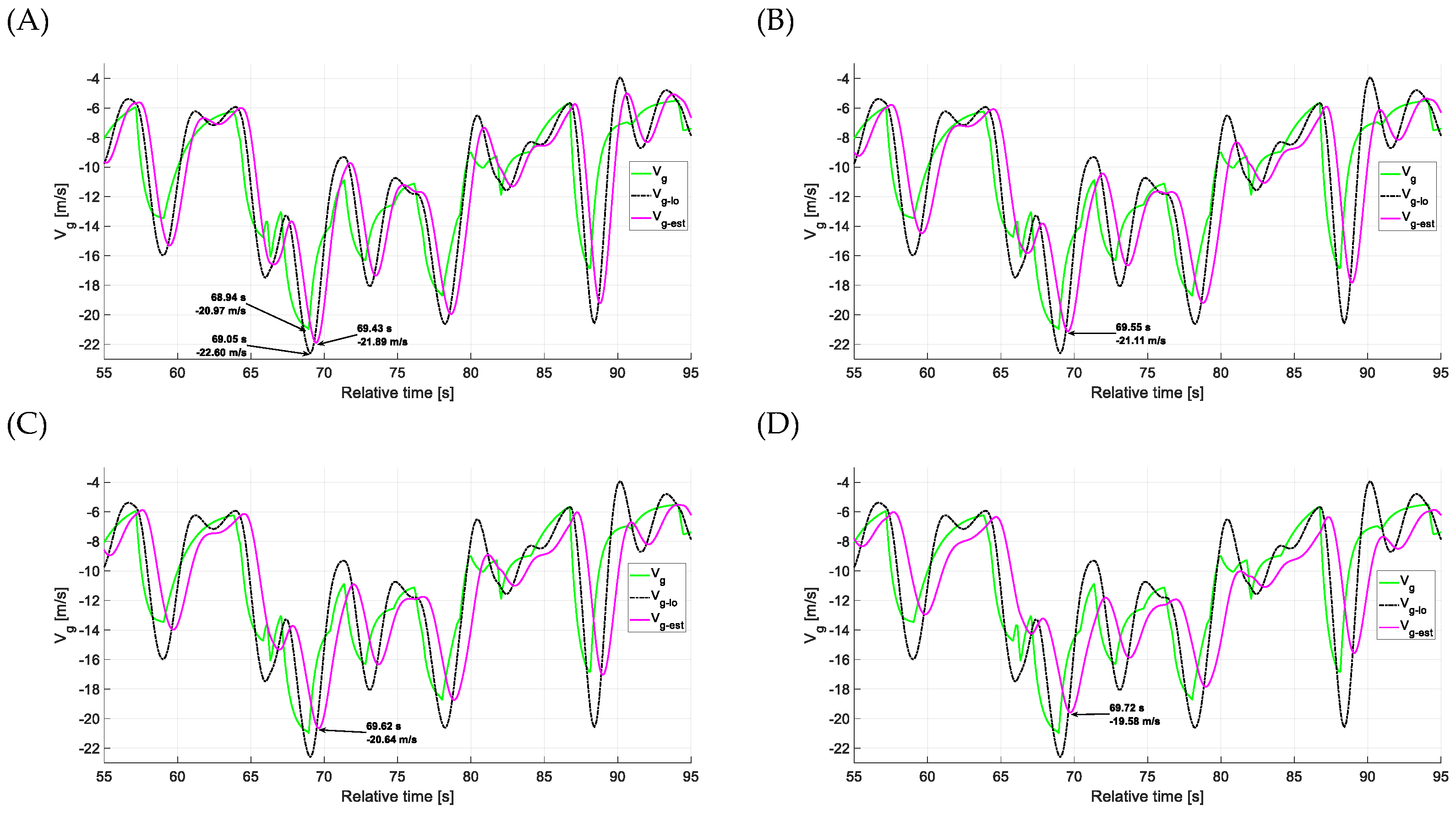
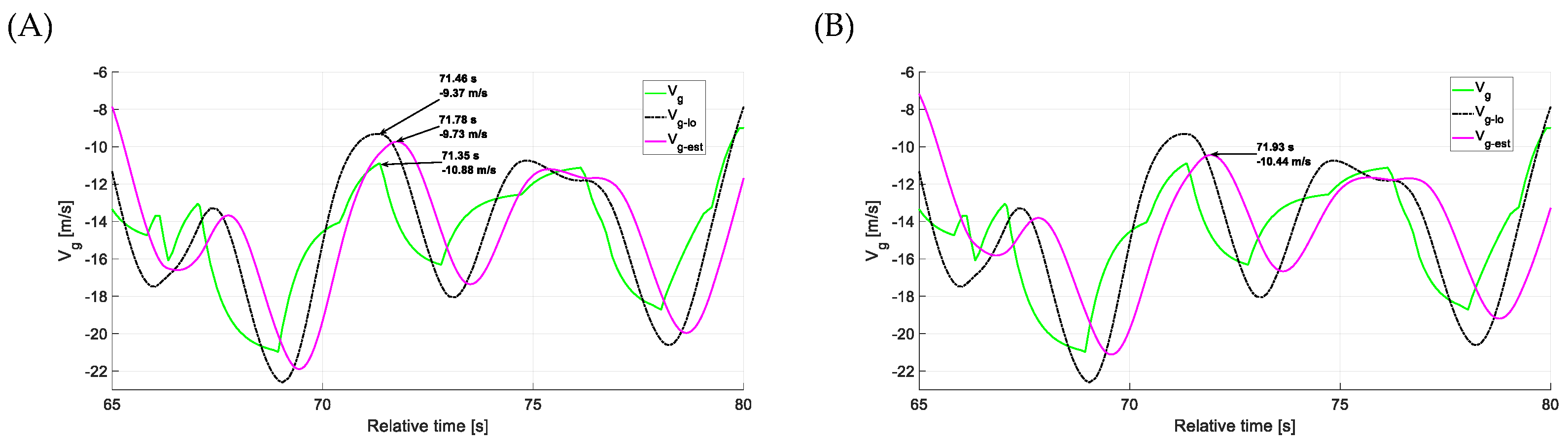
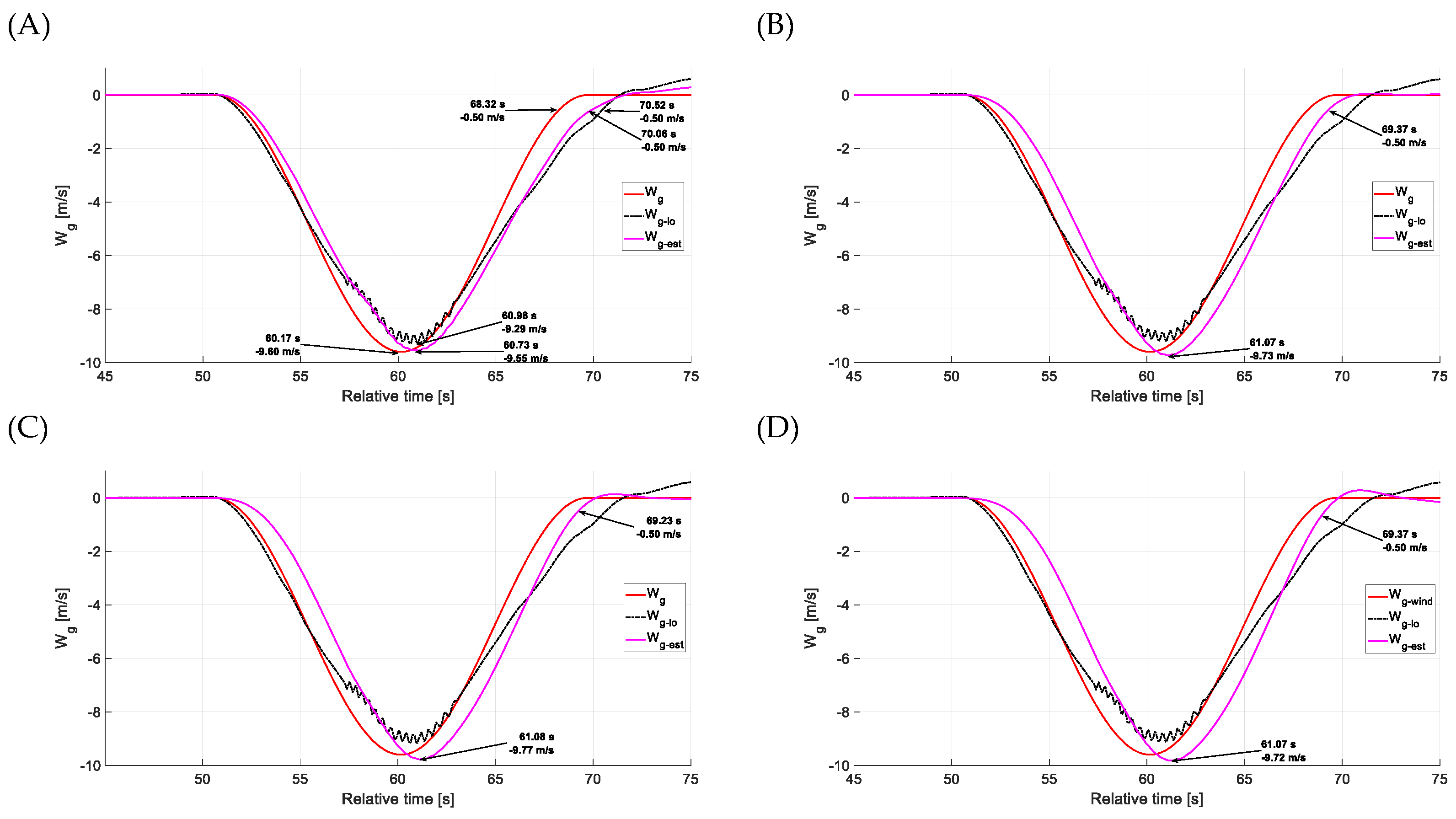
4.1. Estimation Accuracy—Head-on Gusts
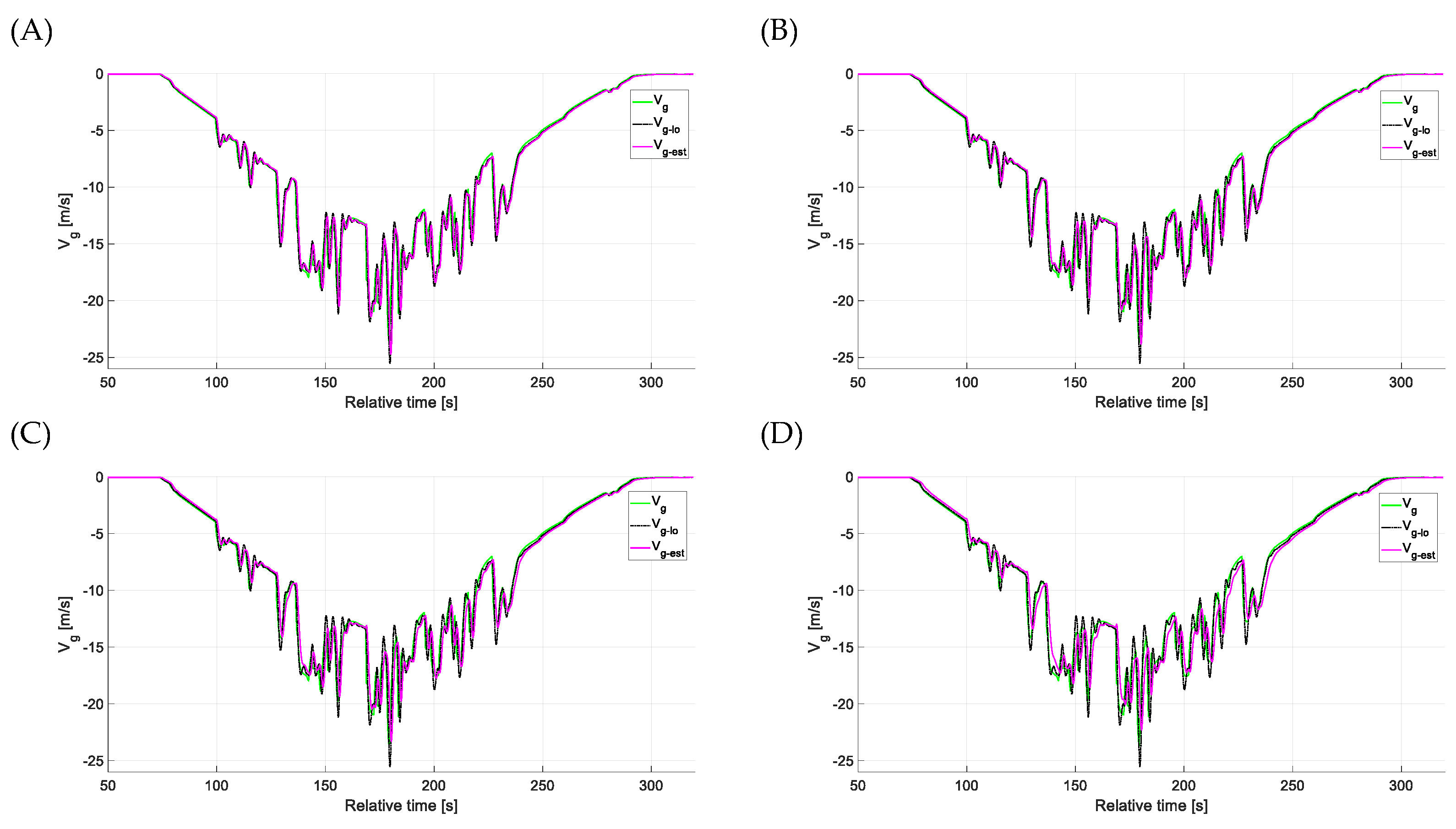
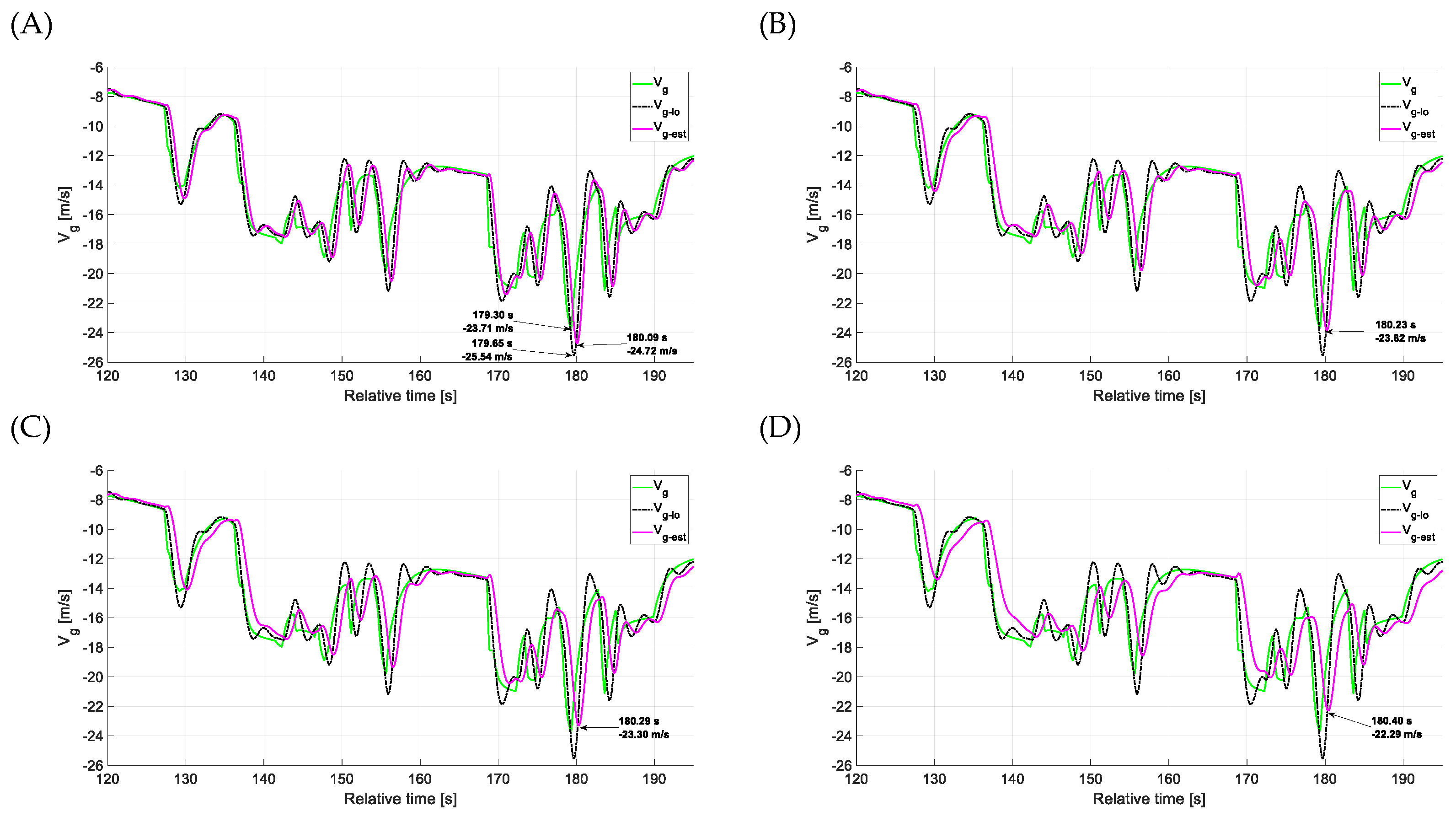
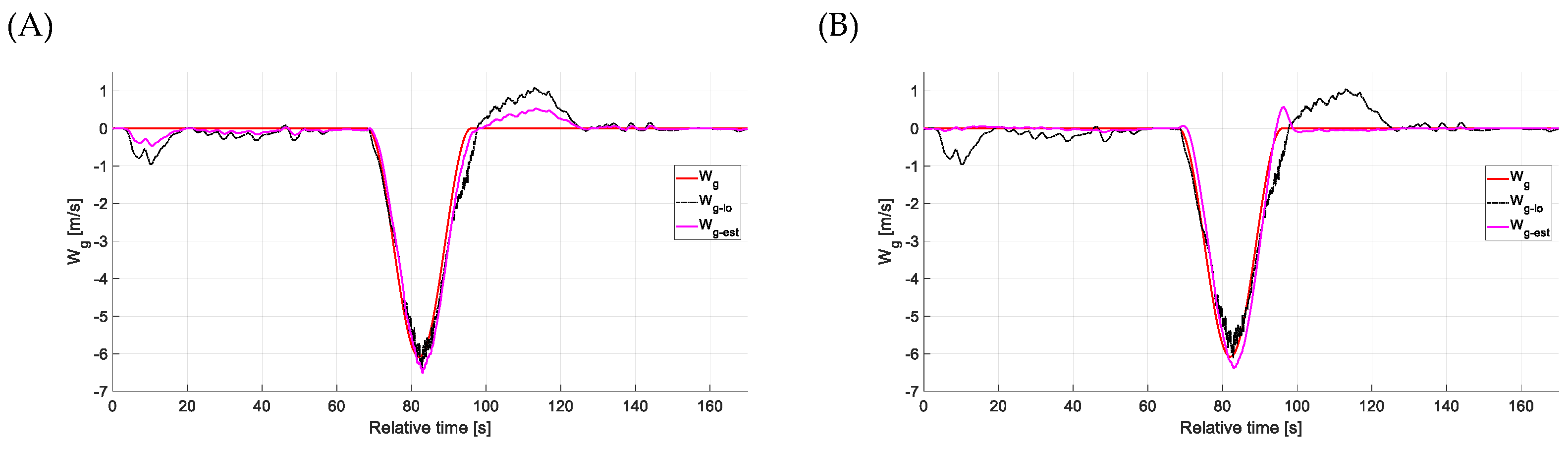
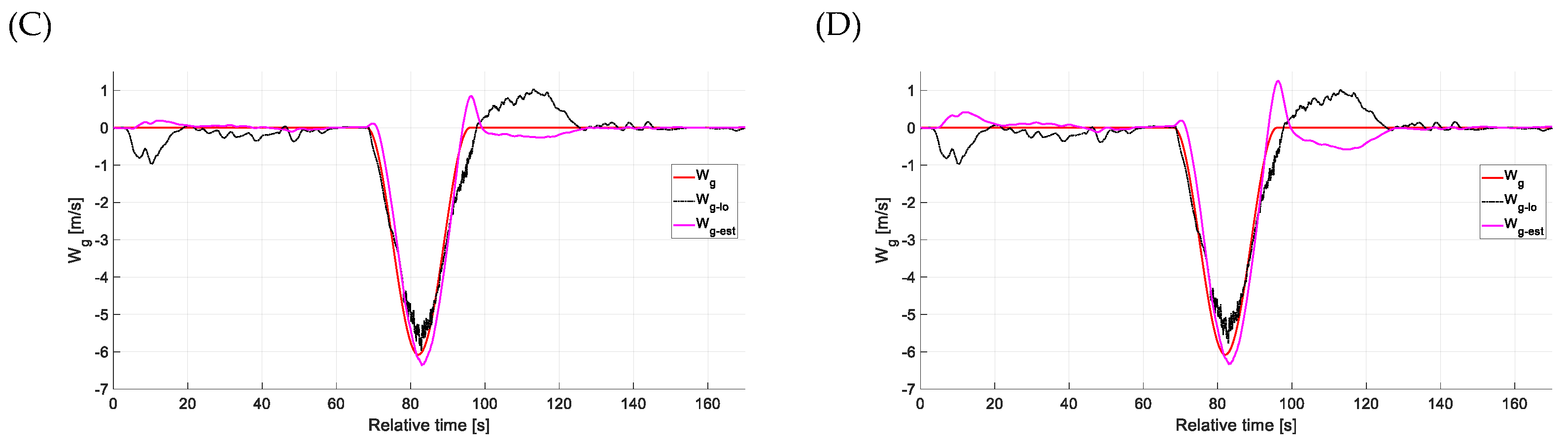
4.2. Estimation Accuracy—Side Gusts
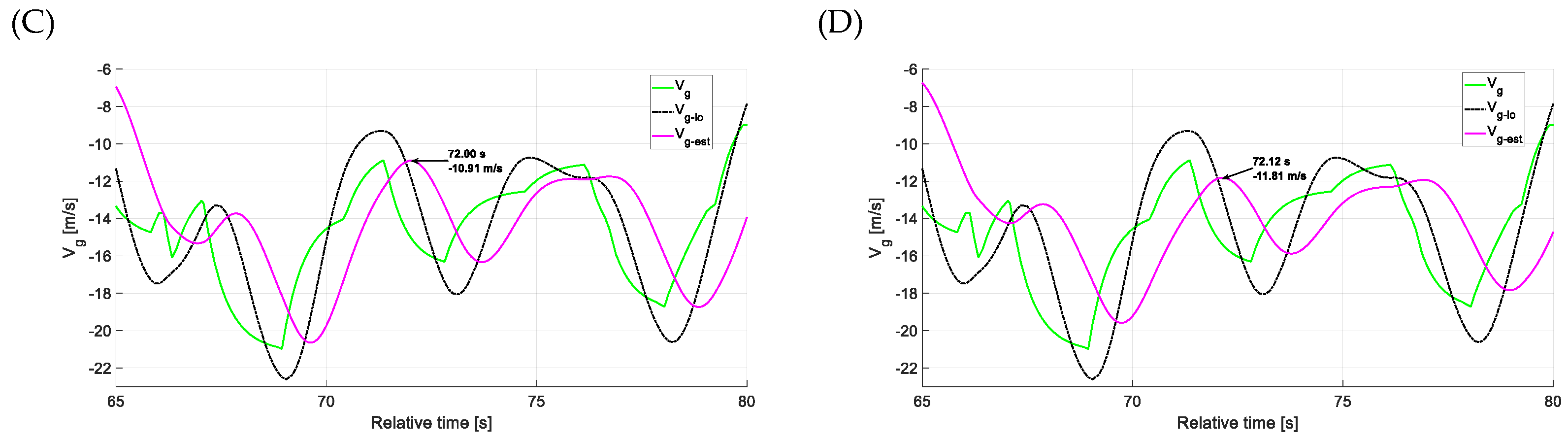
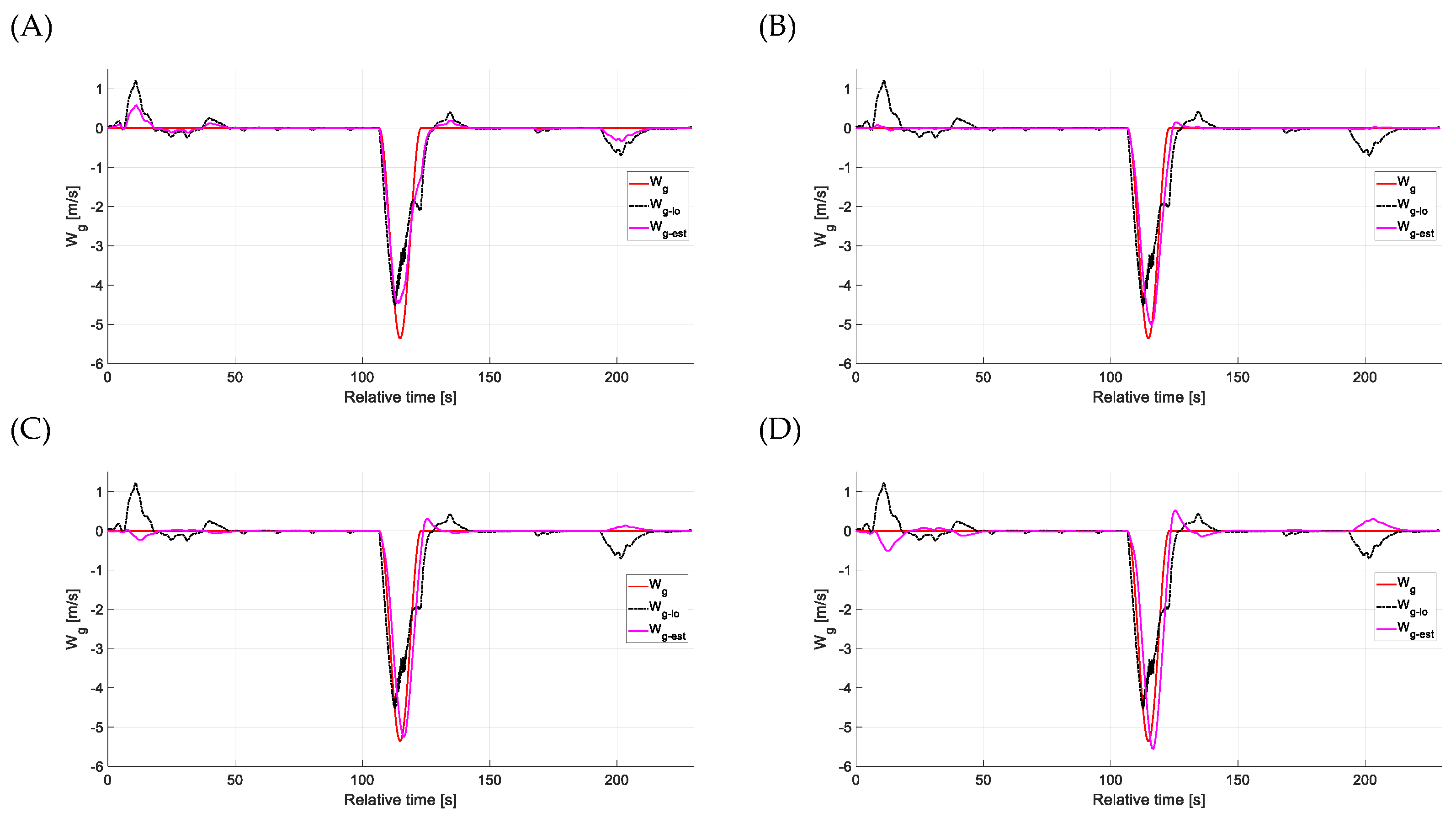
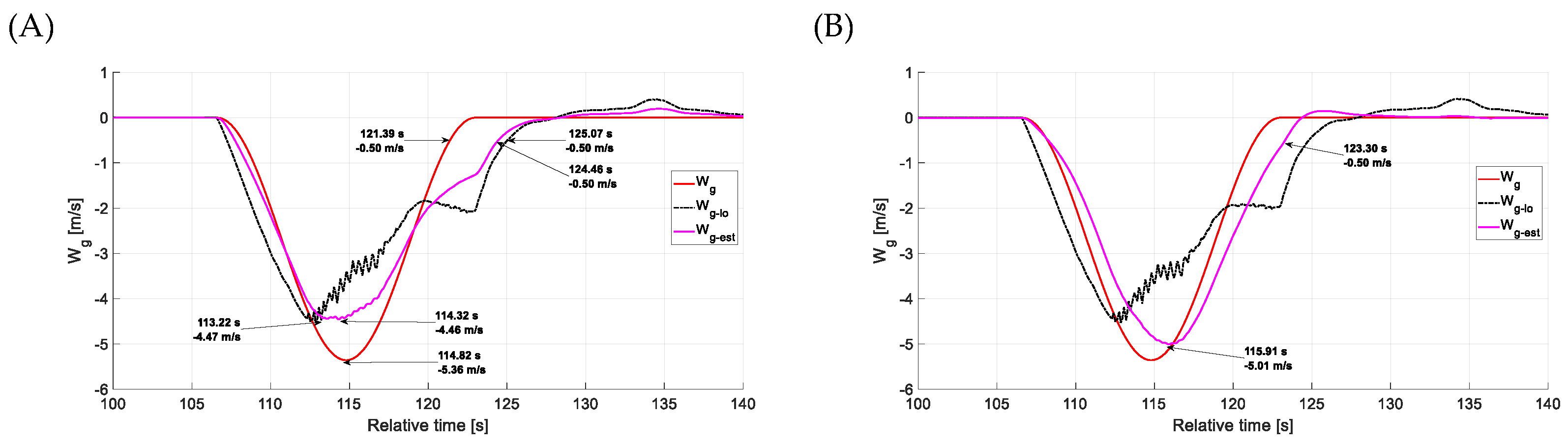
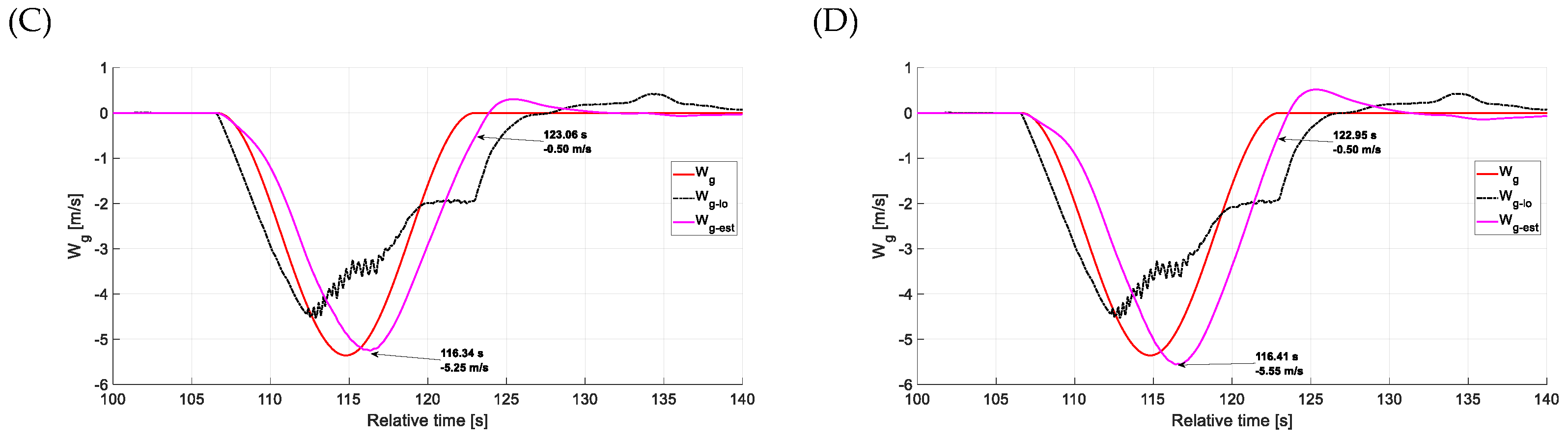
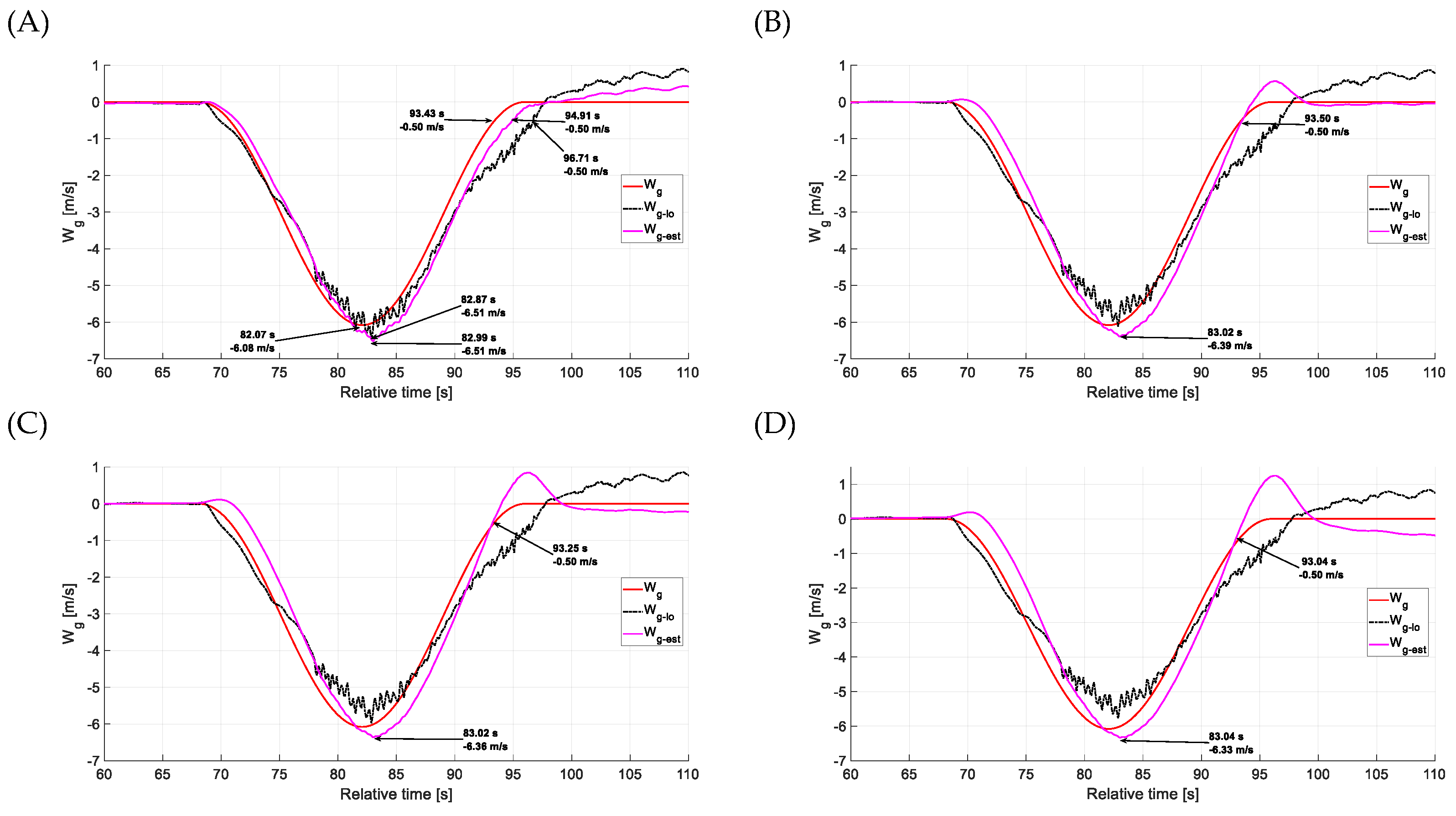
4.3. Estimation Accuracy—Vertical Gusts
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ICAO. Manual on Low-Level Wind Shear; Doc 9817 AN/449; International Civil Aviation Organization: Montréal, QC, Canada, 2005; ISBN 92-9194-609-5. [Google Scholar]
- FAA. Windshear Weather. In Wind Shear Training Aid; Federal Aviation Authority: Washington, DC, USA, 1990; Volume 2, pp. 4.2-1–4.2-133. [Google Scholar]
- Krusiec, G. On-Board Wind Shear Warning System; Rzeszów University of Technology: Rzeszów, Poland, 2010. [Google Scholar]
- O’Connor, A. Demonstration of a Novel 3-D Wind Sensor for Improved Wind Shear Detection for Aviation Operations. Master’s Thesis, Technological University Dublin, Dublin, Ireland, 2018. [Google Scholar] [CrossRef]
- O’Connor, A. Using a Wind Urchin for Airport Wind Measurements, Retrieved from Irish Meteorological Society. Master’s Thesis, Technological University Dublin, Dublin, Ireland, 2018. [Google Scholar]
- Brandl, A.; Battipede, M. Maneuver-Based Cross-Validation Approach for Angle-of-Attack Estimation. In Proceedings of the 14th WCCM-ECCOMAS Congress, Virtual, 11–15 January 2020; Volume 1700. [Google Scholar]
- The Aviation Herald. Incidents and News in Aviation. Available online: www.avherald.com (accessed on 8 May 2025).
- Kelley, N.D.; Jonkman, B.J.; Scott, G.N. Comparing Pulsed Doppler LIDAR with SODAR and Direct Measurements for Wind Assessment. In Proceedings of the American Wind Energy Association WindPower 2007 Conference and Exhibition, Los Angeles, CA, USA, 3–7 June 2007; National Renewable Energy Laboratory: Golden, CO, USA, 2007. [Google Scholar]
- Fezans, N.; Joos, H.-D.; Deiler, C. Gust load alleviation for a long-range aircraft with and without anticipation. CEAS Aeronaut. J. 2019, 10, 1033–1057. [Google Scholar] [CrossRef]
- Prudden, S.; Fisher, A.; Marino, M.; Mohamed, A.; Watkins, S.; Wild, G. Measuring wind with small unmanned aircraft systems. J. Wind. Eng. Ind. Aerodyn. 2018, 176, 197–210. [Google Scholar] [CrossRef]
- Ellrod, G.P.; Knapp, D.I. An objective clear-air turbulence forecasting technique: Verification and operational use. Weather. Forecast 1992, 7, 150–165. [Google Scholar] [CrossRef]
- Di Vito, V.; Zollo, A.L.; Cerasuolo, G.; Montesarchio, M.; Bucchignani, E. Clear Air Turbulence and Aviation Operations: A Literature Review. Sustainability 2025, 17, 4065. [Google Scholar] [CrossRef]
- Prosser, M.C.; Williams, P.D.; Marlton, G.J.; Harrison, R.G. Giles Harrison. Evidence for Large Increases in Clear-Air Turbulence Over the Past Four Decades. Geophys. Res. Lett. 2023, 50, e2023GL103814. [Google Scholar] [CrossRef]
- Forester, J. What You Need to Know about Clear Air Turbulence. Forbes, Innovation Science. Available online: https://www.forbes.com/sites/jimfoerster/2024/05/24/what-you-need-to-know-about-clear-air-turbulence/ (accessed on 28 May 2024).
- Arranz, A.; Kawoosa, V.M.; Kiyada, S.; Huang, H.; Zafra, M.; Scarr, S. The Mechanics of Turbulence. Thomson Reuters Group Limited. Available online: https://www.reuters.com/graphics/SINGAPOREAIRLINES-THAILAND/movaqnmeava/ (accessed on 22 May 2024).
- Wong, C. Singapore Airlines turbulence: Why climate change is making flights rougher. Nature 2024. [Google Scholar] [CrossRef]
- IATA. Findings and Conclusions. In Proceedings of the Go-around Safety Forum, Brussels, Belgium, 18 June 2013; International Air Transport Association: Singapore, 2013. [Google Scholar]
- Tomczyk, A. Zastosowanie Analitycznej Redundancji Pomiarów w Układzie Sterowania i Nawigacji Statku Powietrznego (Application of Analytical Redundancy of Measurements in Aircraft Control and Navigation System). In Proceedings of the Scientific Aspects Concerning Operation of Manned and Unmanned Aerial Vehicles, Dęblin, Poland, 15–17 May 2015. [Google Scholar]
- Hamke, E.E.; Enns, D.F.; Loe, G.R.; Wacker, R.A.; Schubert, O. Wind Estimation for an Unmanned Aerial Vehicle. U.S. Patent US8219267B2, 10 July 2012. [Google Scholar]
- Hall, A.P.; Marton, T.F.; Muren, P. Passive Local Wind Estimator. U.S. Patent US20140129057A1, 8 May 2014. [Google Scholar]
- Hall, A.P.; Marton, T.F.; Muren, P. Passive Local Wind Estimator. U.S. Patent US9031719B2, 12 May 2015. [Google Scholar]
- Kumon, M.; Mizumoto, I.; Iwai, Z.; Nagata, M. Wind estimation by unmanned air vehicle with delta wing. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 1896–1901. [Google Scholar]
- Meier, K.; Hann, R.; Skaloud, J.; Garreau, A. Wind Estimation with Multirotor UAVs. Atmosphere 2022, 13, 551. [Google Scholar] [CrossRef]
- Frant, M.; Kachel, S.; Maślanka, W. Gust Modeling with State-of-the-Art Computational Fluid Dynamics (CFD) Software and Its Influence on the Aerodynamic Characteristics of an Unmanned Aerial Vehicle. Energies 2023, 16, 6847. [Google Scholar] [CrossRef]
- Reuder, J.; Jonassen, M.O.; Ólafsson, H. The Small Unmanned Meteorological Observer SUMO: Recent developments and applications of a micro-UAS for atmospheric boundary layer research. Acta Geophys. 2012, 60, 1454–1473. [Google Scholar] [CrossRef]
- Brezoescu, A.; Castillo, P.; Lozano, R. Wind estimation for accurate airplane path following applications. J. Intell. Robot. Syst. 2014, 73, 823–831. [Google Scholar] [CrossRef]
- Wingrove, R.C.; Bach, R.E., Jr. Severe turbulence and maneuvering from airline flight records. J. Aircr. 1994, 31, 753–760. [Google Scholar] [CrossRef]
- Szwed, P.; Rzucidło, P.; Rogalski, T. Estimation of Atmospheric Gusts Using Integrated On-Board Systems of a Jet Transport Airplane—Flight Simulations. Appl. Sci. 2022, 12, 6349. [Google Scholar] [CrossRef]
- Bociek, S.; Gruszecki, J. Automatic Aircraft Control Systems; Oficyna wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 1999. (In Polish) [Google Scholar]
- Cook, M.V. Flight Dynamic Principal; Elsevier: Burlington, MA, USA, 2007; pp. 1–401. [Google Scholar]
- Grzybowski, P.; Klimczuk, M.; Rzucidlo, P. Distributed Measurement System Based on CAN Data Bus. Aircr. Eng. Aerosp. Technol. 2018, 90, 1249–1258. [Google Scholar] [CrossRef]
- Welcer, M.; Szczepański, C.; Krawczyk, M. The Impact of Sensor Errors on Flight Stability. Aerospace 2022, 9, 169. [Google Scholar] [CrossRef]
- Dołęga, B.; Kopecki, G.; Tomczyk, A. Analytical redundancy in control systems for unmanned aircraft and optionally piloted vehicles. Trans. Aerosp. Res. 2017, 2017, 31–44. [Google Scholar] [CrossRef]
- Kopecki, G.; Tomczyk, A.; Rzucidło, P. Algorithms of measurement system for a micro UAV. Solid State Phenom. 2013, 198, 165–170. [Google Scholar] [CrossRef]
- Dąbrowski, W.; Popowski, S. Estimation of wind parameters on flying objects. Pomiary Autom. Robot. 2013, 17, 552–557. [Google Scholar]
- Rautenberg, A.; Graf, M.S.; Wildmann, N.; Platis, A.; Bange, J. Reviewing Wind Measurement Approaches for Fixed-Wing Unmanned Aircraft. Atmosphere 2018, 9, 422. [Google Scholar] [CrossRef]
- Narkhede, P.; Poddar, S.; Walambe, R.; Ghinea, G.; Kotecha, K. Cascaded Complementary Filter Architecture for Sensor Fusion in Attitude Estimation. Sensors 2021, 21, 1937. [Google Scholar] [CrossRef]
- Lerro, A.; Brandl, A.; Gili, P. Model-free scheme for angle-of-attack and angle-of-sideslip estimation. J. Guid. Control. Dyn. 2021, 44, 595–600. [Google Scholar] [CrossRef]
- Baldwin, W.A. Method for Determining Airplane Flight-Path Angle with the Use of Airspeed and the Global Positioning System (GPS). U.S. Patent No 10,823,752, 3 November 2020. [Google Scholar]
- Mulder, J.A.; Chu, Q.P.; Sridhar, J.K.; Breeman, J.H.; Laban, M. Non-linear aircraft flight path reconstruction review and new advances. Prog. Aerosp. Sci. 1999, 35, 673–726. [Google Scholar] [CrossRef]
- X-Plane Communication Toolbox (XPC). Available online: https://software.nasa.gov/software/ARC-17185-1 (accessed on 24 February 2024).
- Welcer, M.; Sahbon, N.; Zajdel, A. Comparison of Flight Parameters in SIL Simulation Using Commercial Autopilots and X-Plane Simulator for Multi-Rotor Models. Aerospace 2024, 11, 205. [Google Scholar] [CrossRef]
- Yu, L.; He, G.; Zhao, S.; Wang, X.; Shen, L. Design and Implementation of a Hardware-in-the-Loop Simulation System for a Tilt Trirotor UAV. J. Adv. Transp. 2020, 2020, 4305742. [Google Scholar] [CrossRef]
- Bittar, A.; Figuereido, H.V.; Guimaraes, P.A.; Mendes, A.C. Guidance software-in-the-loop simulation using x-plane and simulink for UAVs. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; IEEE: Piscataway, NJ, USA; pp. 993–1002. [Google Scholar]
- Brady, C. The Boeing 737 Technical Guide; Lightning Source: Milton Keynes, UK, 2018. [Google Scholar]
- Goff, R.C. The Low-Level Wind Shear Alert System Report; Final Report for U.S. Department of Transportation; National Aviation Facilities Experimental Center: Washington, DC, USA, 1980. [Google Scholar]
- Obserwator. Dangerous Atmospheric Phenomena in Aviation: Wind and Turbulence. Available online: https://obserwator.imgw.pl/2020/07/30/dangerous-atmospheric-phenomena-in-aviation-wind-and-turbulence/ (accessed on 8 May 2025).
- Klug, L.; Ullah, J.; Lutz, T.; Streit, T.; Heinrich, R.; Radespiel, R. Gust alleviation by spanwise load control applied on a forward and backward swept wing. CEAS Aeronaut. J. 2023, 14, 435–454. [Google Scholar] [CrossRef]
- Ullah, J.; Kamoun, S.; Müller, J.; Lutz, T. Active gust load alleviation by means of steady and dynamic trailing and leading edge flap deflections at transonic speeds. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1334. [Google Scholar]


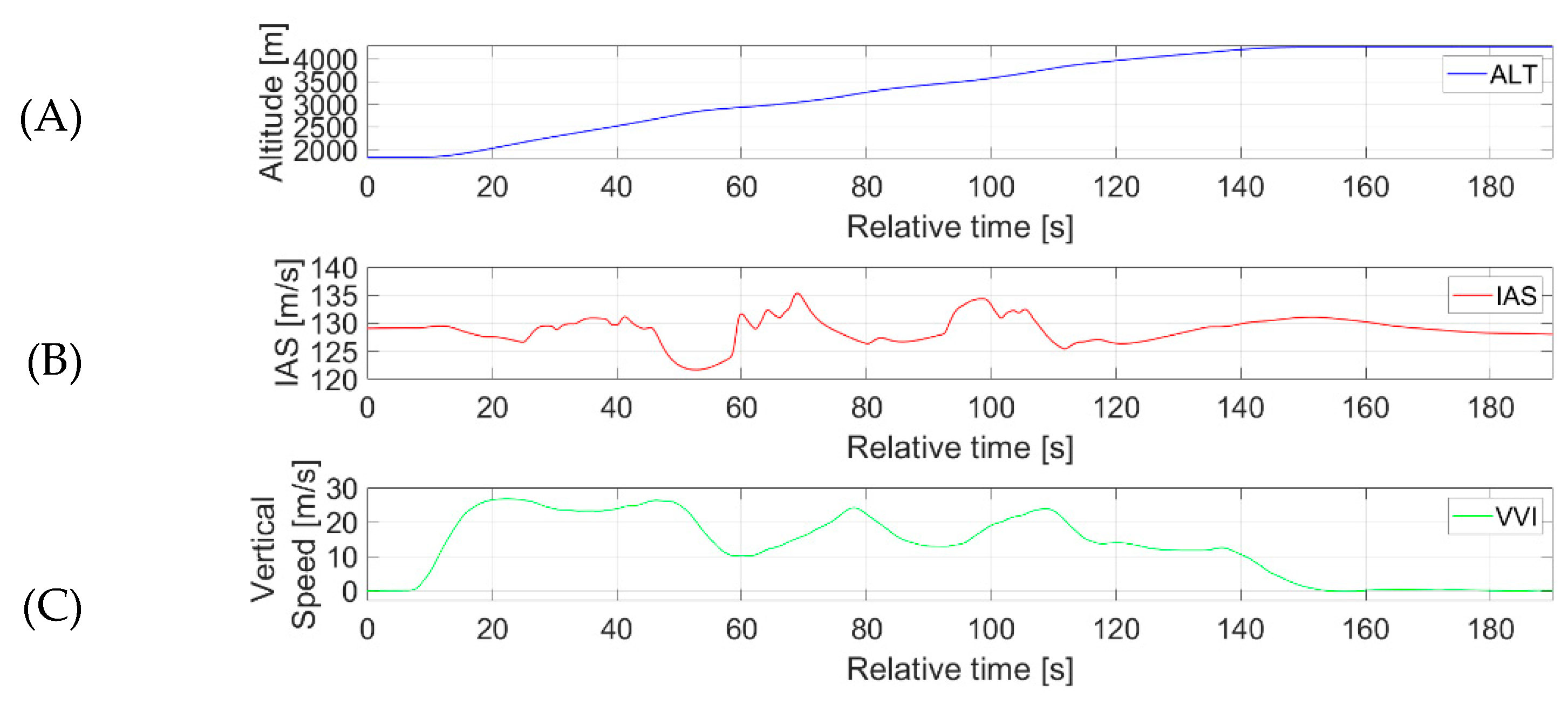

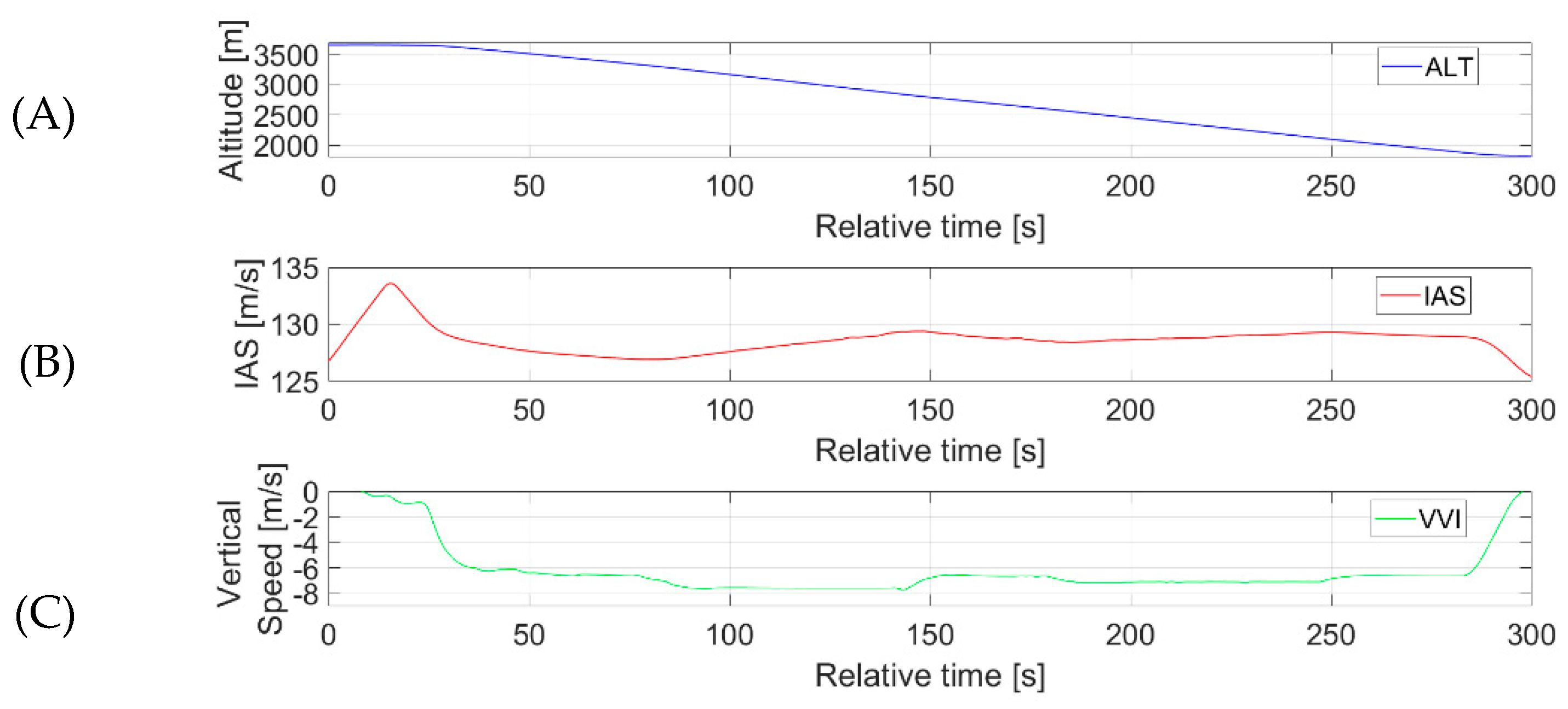
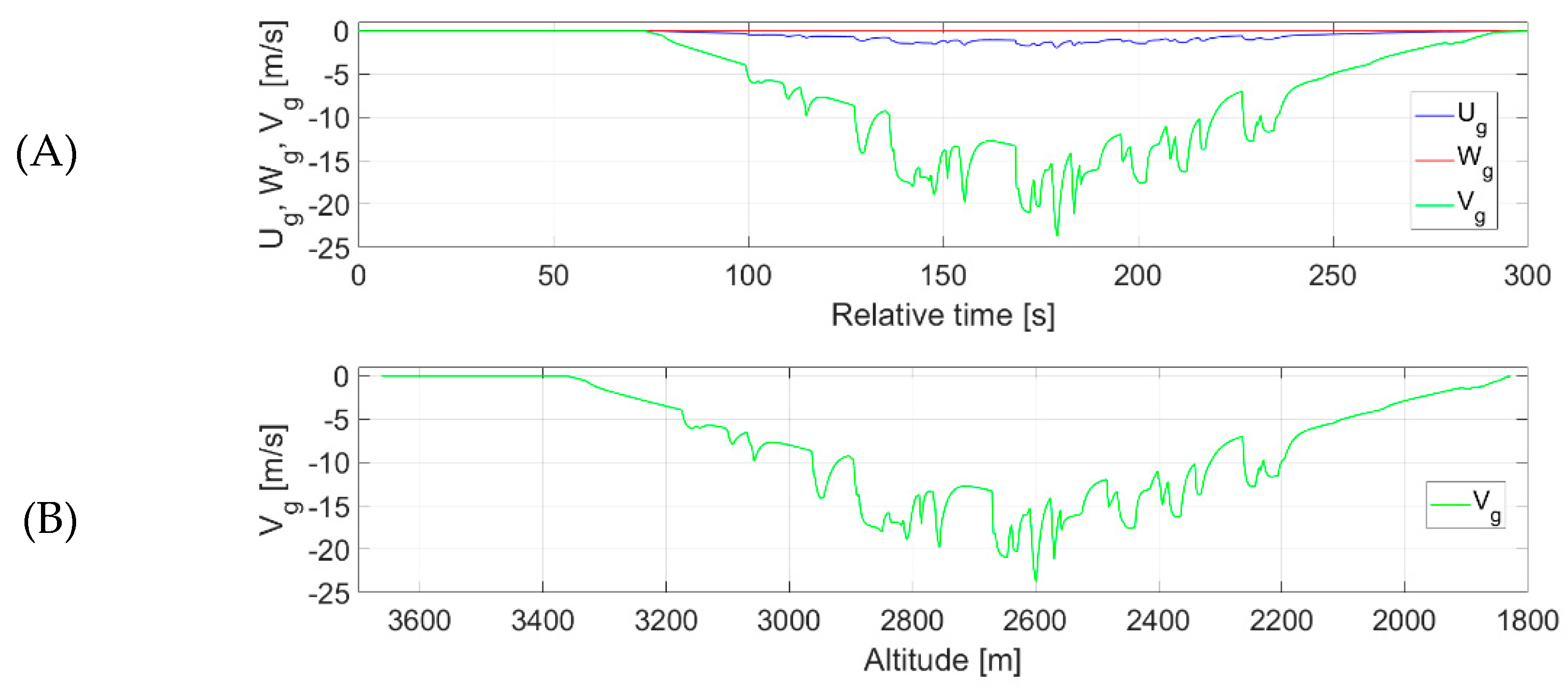

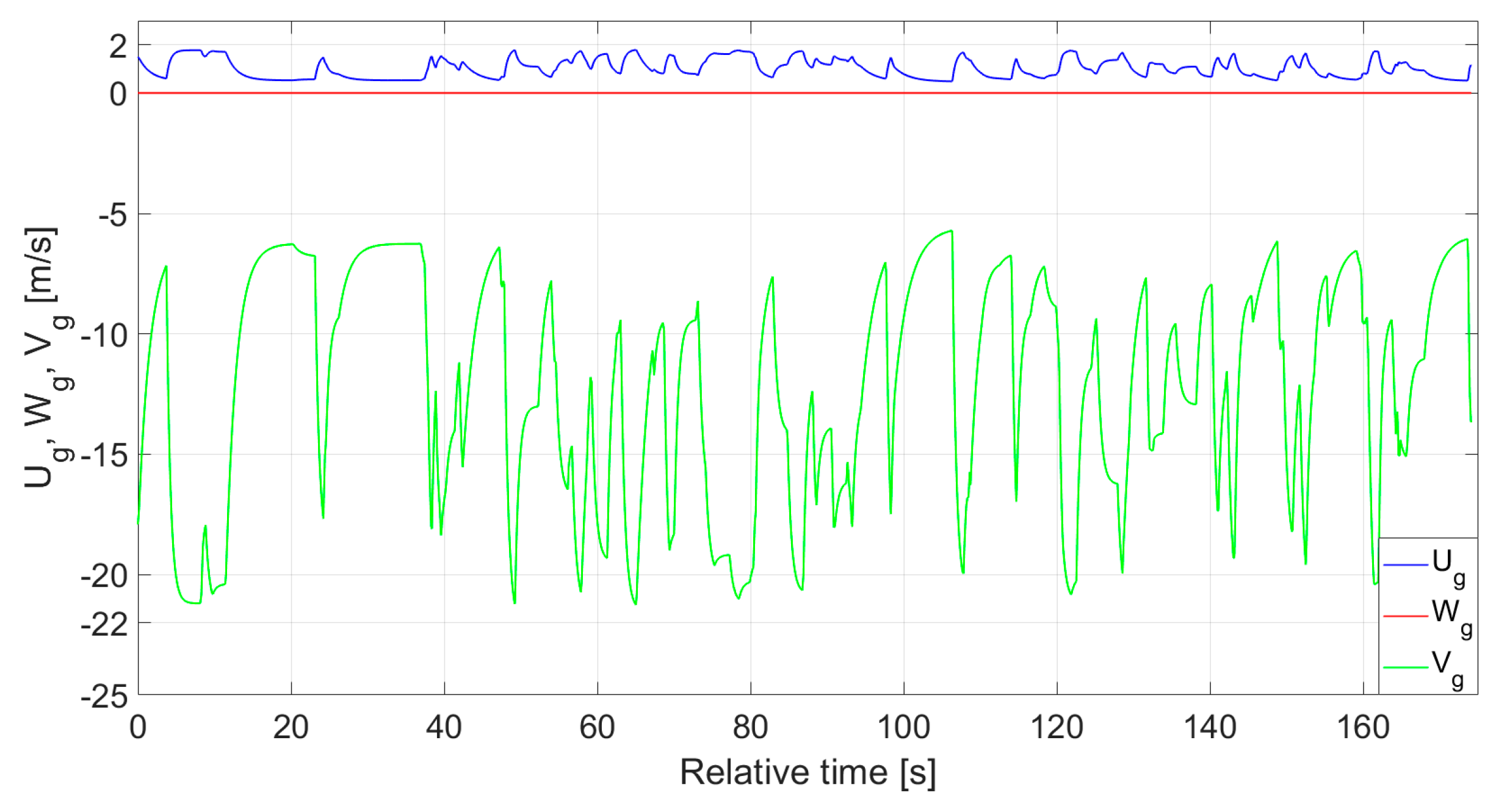






| Parameter | Source | Symbol—Unit | Sampling Frequency |
|---|---|---|---|
| Time | Simulation time | t [s] | 12.5 Hz |
| Altitude | Cockpit indicator | ALT [m] | 12.5 Hz |
| Indicated Air Speed | Cockpit indicator | IAS [m/s | 12.5 Hz |
| True Air Speed | Cockpit indicator | TAS [m/s] | 12.5 Hz |
| Ground Speed | Flight model position | GS_x [m/s] | 12.5 Hz |
| Vertical Speed | Cockpit indicator | VVI [m/s] | 12.5 Hz |
| Wind speed x (OGL) | Simulation weather | Wind_x [m/s] | 12.5 Hz |
| Wind speed y (OGL) | Simulation weather | Wind_y [m/s] | 12.5 Hz |
| Wind speed z (OGL) | Simulation weather | Wind_z [m/s] | 12.5 Hz |
| Pitch rate | Flight model position | Q [deg/s] | 12.5 Hz |
| Pitch angular acceleration | Flight model position | Q_dot [deg/s2] | 12.5 Hz |
| Horizontal Stabilizer elevator deflection | Flight model controls | HS_elev [deg] | 12.5 Hz |
| Side acceleration | Flight model position | G_side [m/s2] | 12.5 Hz |
| Magnetic Heading | Flight model position | HDG [deg] | 12.5 Hz |
| Magnetic Track | Flight model position | TRK [deg] | 12.5 Hz |
| Theta angle | Flight model position | Theta [deg] | 12.5 Hz |
| Angle of attack | Flight model position | Alpha [deg] | 12.5 Hz |
| Flight path angle | Flight model position | Flightpath [deg] | 12.5 Hz |
| F. Phase | Rising Gust Speed | Weakening Gust Speed | Average Values | |||
|---|---|---|---|---|---|---|
| Tcu | Difference | Delay | Difference | Delay | Difference | Delay |
| D/Tcu = 0.5 s | −0.64 m/s | 0.39 s | 0.37 m/s | 0.95 s | −0.135 m/s | 0.67 s |
| D/Tcu = 0.8 s | 0.02 m/s | 0.39 s | −0.04 m/s | 0.95 s | −0.01 m/s | 0.67 s |
| D/Tcu = 1.0 s | 0.34 m/s | 0.39 s | −0.20 m/s | 0.95 s | 0.07 m/s | 0.67 s |
| D/Tcu = 1.5 s | 0.79 m/s | 0.39 s | −0.34 m/s | 1.05 s | 0.225 m/s | 0.72 s |
| L/Tcu = 0.5 s | −0.20 m/s | 0.50 s | 0.58 m/s | 0.30 s | 0.19 m/s | 0.40 s |
| L/Tcu = 0.8 s | 0.46 m/s | 0.50 s | −0.03 m/s | 0.30 s | 0.215 m/s | 0.40 s |
| L/Tcu = 1.0 s | 0.84 m/s | 0.50 s | −0.39 m/s | 0.32 s | 0.225 m/s | 0.41 s |
| L/Tcu = 1.5 s | 1.61 m/s | 0.50 s | −1.20 m/s | 0.32 s | 0.205 m/s | 0.42 s |
| C/Tcu = 0.5 s | −3.94 m/s | 0.71 s | −0.05 m/s | 0.25 s | −1.995 m/s | 0.48 s |
| C/Tcu = 0.8 s | −3.02 m/s | 0.71 s | −0.46 m/s | 0.26 s | −1.74 m/s | 0.485 s |
| C/Tcu = 1.0 s | −2.47 m/s | 0.71 s | −0.78 m/s | 0.26 s | −1.625 m/s | 0.485 s |
| C/Tcu = 1.5 s | −1.33 m/s | 0.71 s | −1.60 m/s | 0.26 s | −1.465 m/s | 0.485 s |
| F. Phase | Rising Gust Speed | Weakening Gust Speed | Average Values | |||
|---|---|---|---|---|---|---|
| Tcu | Difference | Delay | Difference | Delay | Difference | Delay |
| D/Tcu = 0.5 s | 1.01 m/s | 0.79 s | −0.68 m/s | 0.03 s | 0.165 m/s | 0.41 s |
| D/Tcu = 0.8 s | 0.11 m/s | 0.93 s | −0.37 m/s | 0.20 s | −0.13 m/s | 0.565 s |
| D/Tcu = 1.0 s | −0.41 m/s | 0.99 s | −0.20 m/s | 0.33 s | −0.305 m/s | 0.66 s |
| D/Tcu = 1.5 s | −1.42 m/s | 1.10 s | 0.12 m/s | 0.43 s | −0.65 m/s | 0.765 s |
| L/Tcu = 0.5 s | 2.54 m/s | 0.38 s | −2.85 m/s | 0.50 s | −0.155 m/s | 0.44 s |
| L/Tcu = 0.8 s | 1.20 m/s | 0.56 s | −1.61 m/s | 0.60 s | −0.205 m/s | 0.58 s |
| L/Tcu = 1.0 s | 0.45 m/s | 0.64 s | −0.92 m/s | 0.66 s | 0.235 m/s | 0.65 s |
| L/Tcu = 1.5 s | −0.91 m/s | 0.64 s | 0.34 m/s | 0.76 s | −0.285 m/s | 0.70 s |
| C/Tcu = 0.5 s | −1.15 m/s | 0.43 s | 0.92 m/s | 0.49 s | −0.115 m/s | 0.46 s |
| C/Tcu = 0.8 s | −0.44 m/s | 0.58 s | 0.14 m/s | 0.61 s | −0.15 m/s | 0.595 s |
| C/Tcu = 1.0 s | 0.03 m/s | 0.65 s | −0.33 m/s | 0.68 s | −0.15 m/s | 0.665 s |
| C/Tcu = 1.5 s | 0.93 m/s | 0.77 s | −1.39 m/s | 0.78 s | −0.23 m/s | 0.775 s |
| F. Phase | Rising Gust Speed | Weakening Gust Speed | Average Values | |||
|---|---|---|---|---|---|---|
| Tcu | Difference | Delay | Difference | Delay | Difference | Delay |
| D/Tcu = 0.5 s | −0.90 m/s | −0.50 s | 0 | 3.07 s | −0.45 m/s | 1.285 s |
| D/Tcu = 1.0 s | −0.35 m/s | 1.09 s | 0 | 1.91 s | −0.175 m/s | 1.5 s |
| D/Tcu = 1.2 s | −0.11 m/s | 1.52 s | 0 | 1.67 s | −0.055 m/s | 1.595 s |
| D/Tcu = 1.5 s | 0.19 m/s | 1.59 s | 0 | 1.56 s | 0.095 m/s | 1.575 s |
| L/Tcu = 0.5 s | −0.05 m/s | 0.56 s | 0 | 1.74 s | −0.025 m/s | 1.15 s |
| L/Tcu = 1.0 s | 0.13 m/s | 0.90 s | 0 | 1.05 s | 0.065 m/s | 0.975 s |
| L/Tcu = 1.2 s | 0.17 m/s | 0.91 s | 0 | 0.91 s | 0.085 m/s | 0.91 s |
| L/Tcu = 1.5 s | 0.12 m/s | 0.90 s | 0 | 1.05 s | 0.06 m/s | 0.975 s |
| C/Tcu = 0.5 s | 0.43 m/s | 0.92 s | 0 | 1,48 s | 0.215 m/s | 1.2 s |
| C/Tcu = 1.0 s | 0.31 m/s | 0.95 s | 0 | 0.07 s | 0.155 m/s | 0.51 s |
| C/Tcu = 1.2 s | 0.28 m/s | 0.95 s | 0 | −0.18 s | 0.14 m/s | 0.385 s |
| C/Tcu = 1.5 s | 0.25 m/s | 0.97 s | 0 | −0.39 s | 0.125 m/s | 0.29 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szwed, P.; Rzucidło, P.; Grzybowski, P.; Warzocha, K. Determination of Atmospheric Gusts Using Integrated On-Board Systems of a Jet Transport Airplane—3D Problem. Appl. Sci. 2025, 15, 5687. https://doi.org/10.3390/app15105687
Szwed P, Rzucidło P, Grzybowski P, Warzocha K. Determination of Atmospheric Gusts Using Integrated On-Board Systems of a Jet Transport Airplane—3D Problem. Applied Sciences. 2025; 15(10):5687. https://doi.org/10.3390/app15105687
Chicago/Turabian StyleSzwed, Piotr, Paweł Rzucidło, Piotr Grzybowski, and Krzysztof Warzocha. 2025. "Determination of Atmospheric Gusts Using Integrated On-Board Systems of a Jet Transport Airplane—3D Problem" Applied Sciences 15, no. 10: 5687. https://doi.org/10.3390/app15105687
APA StyleSzwed, P., Rzucidło, P., Grzybowski, P., & Warzocha, K. (2025). Determination of Atmospheric Gusts Using Integrated On-Board Systems of a Jet Transport Airplane—3D Problem. Applied Sciences, 15(10), 5687. https://doi.org/10.3390/app15105687






