Abstract
To address the limitations in conventional granular morphology characterization where excessive emphasis has been placed on elongation index (EI) while neglecting flatness index (FI) and their coupled interactions, this study establishes an EI/FI co-regulated dual-parameter morphological characterization framework. Through integrated triaxial compression experiments and discrete element simulations, we systematically investigate multi-scale mechanical responses spanning macroscopic stress–strain behavior to microscopic force-chain evolution. The results show that (1) the regulation of pore structure by morphological parameters presents non-linear characteristics, and (2) the evolution of peak shear strength is predominantly governed by morphological anisotropy. (3) The parabolic relationship between the maximum dilatancy angle and the morphological parameters is shown. (4) The micro mechanical analysis reveals that EI/FI parameters have limited influence on the statistical distribution characteristics of the contact force chain, but have a significant regulatory effect on the anisotropic evolution of the force-chain network.
1. Introduction
Granular materials are widely used in critical engineering applications such as dams [1,2] and roads [3,4]. Their mechanical behavior significantly differs from continuous solid media, being governed by particle morphological characteristics, aggregate state, and internal mesoscopic contacts [5], which directly determine the design, construction methods, and long-term operational safety of engineering structures. Notably, among various influencing factors, particle shape—as a key morphological parameter—has been extensively validated by research and engineering practices to significantly regulate the macroscopic mechanical responses of granular assemblies [6,7]. This highlights the importance of studying particle morphology as a breakthrough for enhancing geotechnical material performance, urgently requiring systematic research to unravel its underlying mechanisms.
The morphological characteristics of the described particles can be quantitatively characterized by multi-scale parameters, including macroscopic morphology (such as aspect ratio and edge angle), mesoscopic roundness (profile curvature characteristics) and microscopic surface texture (roughness and pore structure) [8]. In order to reveal the regulatory mechanism of particle morphology on the mechanical behavior of stacked gravel, a systematic experimental study has been carried out. In terms of dynamic load response, Hu et al. [9] conducted a discrete element analysis, demonstrating that the ultimate bearing capacity of the slope increases with higher rock content and particle angularity but decreases with increasing aspect ratio. In terms of static loading, Zhang [10] carried out triaxial tests of soil–rock mixtures with the same stone content but different particle sizes and morphology, and the results showed that the morphology and size of blocks had a great influence on the biting force and crushing rate between particles. Mahinroost et al. [11] determined that the crushing sensitivity of angular particles was significantly higher than that of sub-angular particles in the direct shear test considering the coupling effect of water and force. Pen et al. [12] broke through traditional geometric description methods and proposed an ellipticity index based on perimeter evolution, which provided an innovative mathematical analytical framework for the quantitative characterization of complex shapes by establishing the correlation degree of the circumference of the actual particle contour and the equivalent ideal ellipse.
Laboratory tests can reflect the influence of particle morphology on the mechanical properties of granular materials from the macro perspective, but it is difficult to reveal the influence of particle morphology on the granular gravel from the microscale. Discrete element method (DEM), as a powerful tool to reveal the macro–micro mechanical response mechanism of granular materials, has shown unique advantages in the field of mesoscale research [13]. Hua et al. [14] established clump models with varying sphericity levels using the particle flow code PFC2D, based on actual rockfill particle morphology. They then revealed how morphological irregularities enhance peak strength, and finally established quantitative relationships between morphological parameters and crack propagation patterns. Zhou et al. [15] used rigid blocks to simulate granular sand particles. Through the study of simple particle models with different roundness, it is found that roundness is inversely proportional to peak deviating stress, internal friction angle, and cohesion force. Yu et al. [16] found through the discrete finite-element coupling model that the average roundness of particles increased by 0.1 units, and the breakage rate increased by 35% in the biaxial test. Zhang et al. [17] further verified by using three-dimensional DEM research that the compressive strength of non-spherical particles increased by more than 40% compared with spherical particles due to the force-chain network formed by geometric interlocking. In the above studies, clump models or cluster models of particle clusters are mostly used to simulate particle shape [18,19]. Compared with spheres [19,20,21,22] and polyhedrons [23,24,25], the simulation of particle shape can solve the problem of higher computational complexity and longer time, restore the real morphology of particles, and generate particle interlock during loading, thus limiting particle rolling.
In conclusion, many achievements have been attained in discrete element simulation studies on the influence of particle shape on its mechanical properties. However, most of the above numerical models consider the influence of particle shape on the meta-micromechanical properties of gravel solely from the elongation index (EI) of gravel particles. Limited studies have systematically investigated the synergistic effects between elongation index (EI) and flatness index (FI), particularly their coupled influence on macroscopic mechanical responses. The definitions of EI and FI are shown in Figure 1.
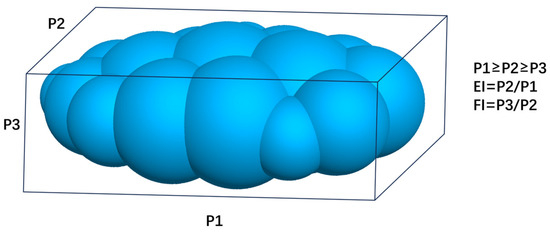
Figure 1.
A schematic diagram of the particle shape coefficient EI and FI.
Zhang et al. [26] conducted CT scanning and modeling of real particles, using the discrete element method to perform triaxial compression tests on particle assemblies with EI, FI, and their synergistic effects. They analyzed the changes in the stress–force–fabric relationship of the specimens during the shear process. This paper, based on an ideal ellipsoid model, disregards the influence of the real particle shape’s roughness and fills the gap in the research on the effect of EI and FI synergism on the dilatancy of the assembly. Additionally, based on the probability density function, a more in-depth study was conducted on the mobilization index between particles at the critical state, as well as the distribution of normal and tangential contact forces between particles.
2. Discrete Element Modeling
2.1. Single-Particle Model
With the further application of the discrete element method in the study of granular media, the regulation mechanism of particle morphology characteristics on macro–micro mechanical behavior of aggregates has become a research focus [27]. This paper breaks through the limitation of traditional single-parameter characterization, and introduces two morphological control variables, namely the EI and the FI, to build a three-dimensional multimodal morphological discrete element model. The definitions of EI and FI are based on the morphological theory of Blott et al. [28]:
where is the longest edge of the particle, is the secondary edge of the particle, and is the shortest edge of the particle.
Based on this, this study constructed 13 gravel particle models, as shown in Table 1. These models were divided into three groups (see Table 1) to investigate the effects of EI/FI synergistic variations, EI single-factor variations, and FI single-factor variations on the mechanical properties of granular assemblies. The interparticle contact parameters are listed in Table 2. The generated clumps, represented as equal-volume spheres, had diameters randomly distributed between 15 and 25 mm. The granular assemblies exhibited an initial porosity of 0.38, with a total of approximately 6000 clumps. During consolidation, the interparticle friction coefficient was set to 0.1 to generate densely compacted specimens, while during compression, the friction coefficient was adjusted to 0.5. See the particle model in Table 1.

Table 1.
Particle model.

Table 2.
Microscale parameters used in the DEM simulations.
2.2. Generation of the Particle Aggregate
To evaluate the effect of particle morphology on the mechanical response of granular materials, a numerical triaxial compression test was simulated via the particle flow code PFC 3D. A multi-shaped particle clump model, designed using Rhino 7 software, was integrated into the analysis framework, with key parameters listed in Table 1. The clump porosity command was used to generate the required porosity, and the initial porosity was set to 0.9225 (the porosity of the particle aggregate was compressed to 0.38). In consists of the following four steps:
(1) Generate numerical simulation specimen. A cylindrical specimen (height: 1.2 m, diameter: 0.6 m) was generated by randomly distributing non-contacting clumps within the volume.
(2) Pre-compaction. The particle friction coefficient was set to 0.1 and the gravitational acceleration was set to 0 to obtain a denser initial specimen under various isotropic states. If the circumferential pressure is set to 20 kPa, the cylinder height is about 0.6 m.
(3) Consolidation. Modified to test target confining pressure (200 kPa; 400 kPa; 600 kPa; 800 kPa).
(4) The particle friction coefficient was adjusted to 0.5, and a gravitational acceleration of 9.81 m/s2 was applied. Loading was terminated when the axial strain reached 60%, and all mechanical data (e.g., stress, strain, force chains, coordination numbers) were recorded during compression for subsequent macro–micro analysis.
Figure 2 shows the generation process of the specimen with the particle shape EI0.6FI0.6 and 200 kPa, including the initial generation state and the consolidation completion state.

Figure 2.
The process of generating the specimen using the isotropic compression method (EI0.6FI0.6, 200 kPa): (a) initial state; (b) final assembly. .
The effect of particle morphology on the initial void ratio of particle aggregate after consolidation has been discussed by many scholars. The previous studies mainly focused on the effect of particle EI, while the effect on FI is less discussed. Figure 3 shows the initial pore ratios of aggregates composed of different EI, FI and EI/FI particles under different lateral pressures. As can be seen from Figure 3a, the initial pore of the specimen decreases first and then increases with the increase in EI value under the same initial conditions and consolidation process. This is consistent with previous studies [29]. In Figure 3b,c, the effect of FI and EI/FI values on the initial void ratio of the particle aggregate is significantly different from that of EI. When considering FI, the initial void ratio of the particle aggregate is all small values.
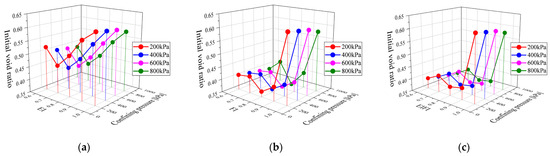
Figure 3.
The initial void ratio of specimens with different particles shape: (a) EI; (b) FI; and (c) EI/FI.
3. Results
3.1. Macro Behavior Analysis
3.1.1. Deviatoric Stress
Figure 4 shows the deviatoric stress–axial strain curves of thirteen particle aggregates with different gravel shapes at 200 kPa. All specimens were shear to an axial strain of 60%, approximating the critical state by maximum deformation, with deviatoric stress and volumetric strain, namely, near constant. It can be seen from Figure 4 that with the axial strain, the deviatoric stress increases rapidly and then decreases slowly. The shape parameters EI and FI affect the peak state and the critical state of the deviatoric stress under the same lateral pressure. The particles are not an ideal sphere; that is, when EI and FI are not 1, the curve is a unimodal distribution. The smaller the value of EI and FI, the more obvious the strain-softening phenomenon is. At 200 kPa lateral pressure, the shear strength of the particle aggregate peak state and the critical state was negatively correlated with both EI and FI. This indicates that the strength of the specimen is higher when the aggregate is flatter or more elongated. This phenomenon can be explained in the following ways: The more deviated the shape is from the ideal sphere, the more likely the particles are to undergo particle interlocking [30], and the more difficult it is for the shape to shift and rotate in the shear process, and then contribute more friction to increase the shear strength of the specimen. When the particle is an ideal sphere, the deviatoric stress–axial strain curve of the particle aggregate has no obvious peak.
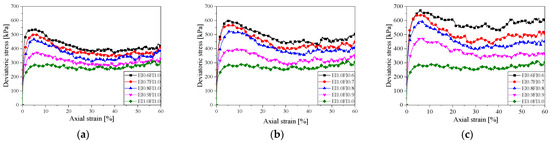
Figure 4.
Deviatoric stress–axial strain curves of specimens with different particle shapes (200 kPa): (a) EI; (b) FI; and (c) EI/FI.
3.1.2. Internal Friction Angle
The friction angle can represent the shear strength of the particle aggregate. The calculation formula is:
where is the axial stress, [kPa]; and is the lateral stress, [kPa].
Figure 5 and Figure 6 show the relationship curves between EI, FI, EI/FI and peak friction angles under different lateral pressure. It can be seen from the figure that the different particle shapes have a significant influence on the peak and critical-state friction angles, and there are differences. When the EI, FI and EI/FI values are small, the peak friction angle first decreases slowly, and when the value is greater than 0.8, the peak friction angle decreases sharply, which is consistent with the trend observed in the literature [26,27,28,29,30,31]. However, the critical-state friction angle decreases uniformly as the shape parameter increases.
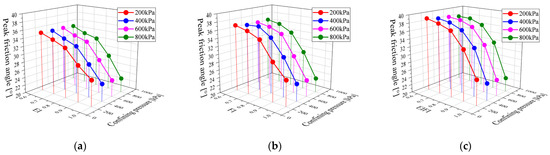
Figure 5.
Peak friction angle of specimens with different particle shapes: (a) EI; (b) FI; and (c) EI/FI.
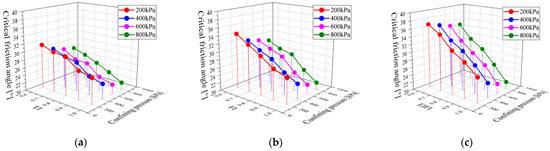
Figure 6.
Critical friction angle of specimens with different particle shapes: (a) EI; (b) FI; and (c) EI/FI.
3.1.3. Volumetric Strain and Dilatancy
Figure 7 shows the volumetric strain curves of thirteen different gravel particle aggregates at 200 kPa. It can be observed that under shear loading, the particle assembly initially undergoes contraction, subsequently transitions to dilation, and ultimately stability. The volume shrinkage in the initial phase was not significantly affected by the particle shape. The smaller the EI and FI, the larger the axial strain corresponding to the critical state, and the greater the final volume expansion. This indicates that the shear and swelling of the specimen is more flat or more elongated. Among them, the changes in EI are consistent with the findings of Nie [32,33] and Fang [31].
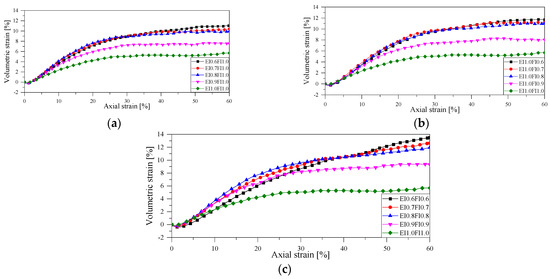
Figure 7.
Volumetric strain–axial strain curves of specimens with different particle shapes (200 kPa): (a) EI; (b) FI; and (c) EI/FI.
The maximum dilatancy angle is calculated as:
where is the increase in volumetric strain; is the increase in axial strain.
Figure 8 shows the relationship between the maximum shear dilatancy angle with lateral pressure and EI and FI. Figure 8 shows that the shear of the specimen is more affected by the shape of the particles than the lateral stress. As EI, FI, and EI/FI increase, the maximum dilatancy angle of the particle aggregate first increases and then decreases. The EI part has the same shear expansion law as Gong et al.’s [29] specimens. Figure 9 shows the change in particle arrangement during the shear process—see Figure 9a,b. The left side shows the arrangement of the specimens with different particle shapes before the start of shear after consolidation, and the right side shows the arrangement of the specimens at 60% axial strain. The particle shape in Figure 9a is EI = FI = 1, and the particle shape in Figure 9b is . A comparison of Figure 9a,b reveals that triaxial compression affects the particle arrangement, with a more noticeable impact on the non-ideal spherical particles. It is evident that when EI and FI are not equal to 1, shear causes the particles to shift from a random arrangement to a preferential horizontal orientation. Specifically, when , shear-induced displacement causes the initially random particle orientation to shift toward horizontal alignment, triggering volumetric dilatancy due to particle rearrangement. In contrast, when , the idealized spherical particle assembly tends to compact by filling interparticle voids under loading, leading to volumetric contraction. As illustrated in Figure 8 and Figure 9, higher values of EI and FI promote void-filling mechanisms, whereas lower values amplify shear-induced dilatancy dominated by particle reorientation and slippage.
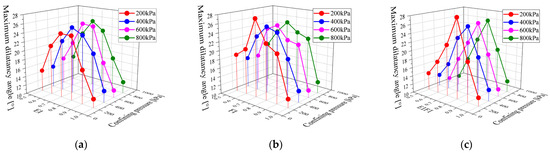
Figure 8.
Maximum dilatancy angle of specimens with different particle shapes: (a) EI; (b) FI; and (c) EI/FI.

Figure 9.
Particle arrangement changes during the shearing process: (a) EI = FI = 1; (b) .
3.2. Micro Behavior Analysis
3.2.1. Contact Network Characteristics
- Coordination number
The coordination number is the average number of collisions between each particle and the surrounding particle, which can well reflect the density and internal stability of the particle aggregate. Thornton [19] concluded that the particles with less than two collisions have basically no contribution to the stable stress state, so the mechanical average coordination number is used. The calculation formula is:
where is the total number of collisions inside the particle aggregate; is the total number of particles inside the specimen; is the number of particles with 0 collisions; is the number of particles with 1 collision.
Figure 10 shows the coordination number–axial strain curve of thirteen different gravel-shaped particles at 200 kPa. As illustrated in Figure 10, the average coordination number exhibits a significant declining trend throughout the loading process. It decreases rapidly with increasing axial strain and eventually stabilizes at a constant value. With decreasing EI and FI, the coordination number of granule aggregate increased and enhanced the degree of granule interlocking, with a more stable contact force strand and a higher shear strength of granule aggregate, which is consistent with the results in Figure 4.
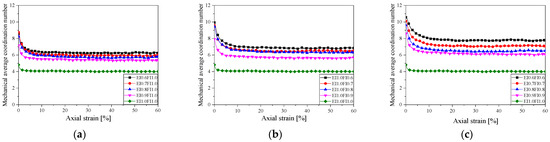
Figure 10.
Coordination number–axial strain curves of specimens with different particle shapes (200 kPa): (a) EI; (b) FI and (c) EIFI.
- Probability density
The contact force between the particles was calculated as follows:
where , are the normal and tangential components of the contact forces, [N]; and are the unit vectors of and .
The distribution characteristics of the contact network inside the particle assembly can be characterized by the probability density of the contact force between particles. Azema et al. [34] found that the probability density function of the normalized normal contact force presents an exponential function change in the strong contact part and a power-law change in the weak contact part. The calculation formula is:
where is or , [N]; is the average of or , [N]; A and B are the correlation coefficients.
- Normal and tangential contact forces
Figure 11 and Figure 12 show the relationship curves of the normalized normal contact force probability density function at 200 kPa. The internal illustration shows the correlation coefficients A and B with EI and FI, the correlation coefficient A shows a downward trend with the increase in EI and FI, and the correlation coefficient B shows an upward trend with the increase in EI and FI. Combining Figure 11 and Figure 12 shows that the probability density decreases as the normalized normal contact force increases. The normalized probability density distribution associated with different EIFI is more discrete at > 3, indicating that the normal contact force is less uniformly distributed at large strong contact forces. When 1 < < 3, the difference in probability density is not obvious, indicating a normal contact force where the strong contact force is less affected by EI and FI. When < 1, the particle aggregate’s weak contact probability density slightly decreased with the increase in EI and FI, the particles for the ideal sphere ( = 1), and the weak contact force probability density is significantly reduced, suggesting that the more particles in the ideal-sphere particle aggregate that are used to support the external load, the weaker the reduction in the weak contact force ratio of ideal-sphere specimen force-chain stability, which is also reflected in the fact that the ideal sphere finds it more difficult to carry out particle interlocking, indicating that the overall stability of the specimen is weak.
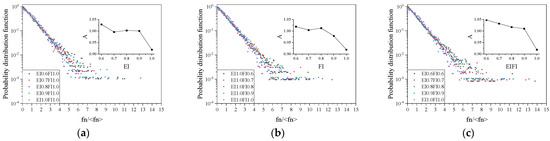
Figure 11.
Probability density function of normal contact force for specimens with different particle shapes (200 kPa, 60% axial strain, in log–linear scale): (a) EI; (b) FI; and (c) EI/FI.
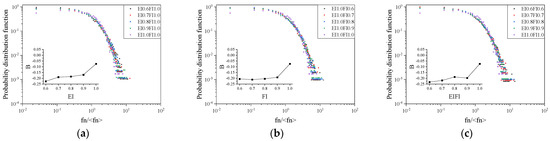
Figure 12.
Probability density function of normal contact force for specimens with different particle shapes (200 kPa, 60% axial strain, in log–log scale): (a) EI; (b) FI; and (c) EI/FI.
Figure 13 and Figure 14 show the relationship curves of the normalized tangential contact force probability density function at different scales and different EI/FI at 200 kPa. The internal insects show the correlation coefficients A and B with the relationship curve between EI and FI, and the overall law is similar to the normal contact force.
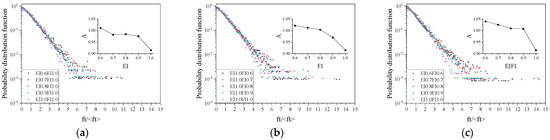
Figure 13.
Probability density function of tangential contact force for specimens with different particle shapes (200 kPa, 60% axial strain, in log–linear scale): (a) EI; (b) FI; and (c) EI/FI.
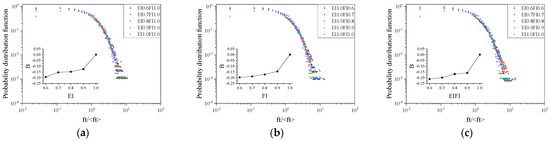
Figure 14.
Probability density function of tangential contact force for specimens with different particle shapes (200 kPa, 60% axial strain, in log–log scale): (a) EI; (b) FI; and (c) EI/FI.
- 2.
- Mobilized contacts
For granular materials, the shear strength of the particle assembly is affected by the degree of friction sliding of the internal particles, which can be characterized by the friction mobilization index [35]. The calculation formula is as follows:
where is the friction coefficient; is the tangential contact force, [N]; is the normal contact force, [N].
Figure 15 shows the friction-play exponential probability distribution function between different EI and FI at the pressure of 200 kPa. As shown in Figure 15, the probability density of the particles is high at < 0.7, and the distribution of is relatively more uniform, where is the average of the specimen friction play index. It can be seen that with the decrease in EI and FI, the of the particle aggregate gradually increases, which reflects that the more the particle shape of the constituent specimen deviates from the sphere, the higher the friction mobilization in the particle aggregate, and the more likely the particle interlocking, which is consistent with the macroscopic law mentioned above.
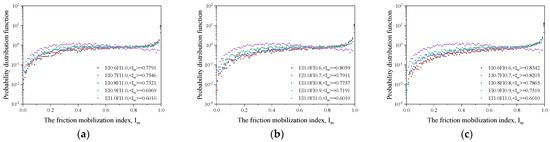
Figure 15.
Probability distribution function of friction mobilization index for specimens with different particle shapes (200 kPa, 60% axial strain): (a) EI; (b) FI; and (c) EI/FI.
When > 0.9999, the contact between particles is defined as sliding contact. Figure 16 shows the sliding contact–axial strain curve of the specimens with different EI and FI at a lateral pressure of 200 kPa. The figure shows that sliding contacts increase rapidly with rising axial strain, peak at approximately 1% axial strain, and then gradually stabilize as shearing progresses. Furthermore, the proportion of sliding contacts increases as EI and FI decrease. The results of EI part of this study were consistent with those of Gong et al. [31] and Nie et al. [26].
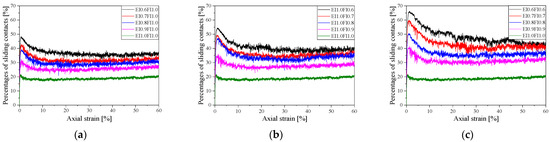
Figure 16.
Sliding contact–axial strain curves for specimens with different particle shapes (200 kPa): (a) EI; (b) FI; and (c) EI/FI.
- Strong contacts
If the normal contact force is greater than the average contact force , it is defined as a strong contact. Figure 17 shows the strong contact-strain curves under different EI and FI at a lateral pressure of 200 kPa. It can be observed that the trends of all specimens are similar, with the proportion of strong contact forces decreasing rapidly at the beginning of shear, then slightly recovering to fluctuate within a relatively stable range. The proportion of weak contact forces is minimal, less than 50%, and weak contact forces dominate the entire contact network. Except for the ideal spherical particle aggregates, the proportion of strong contact forces in other specimens remains around 36% at the critical state and is relatively stable throughout the loading process.
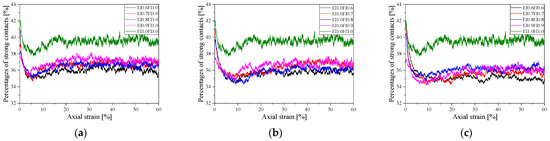
Figure 17.
Strong contact–axial strain curves for specimens with different particle shapes (200 kPa): (a) EI; (b) FI; and (c) EI/FI.
3.2.2. Fabric Anisotropy
In this paper, we reflect the degree of anisotropy between particle contact by the configuration tensor proposed by Satake et al. [36] in 1982. Specifically, the configuration tensor calculation of the unit vector of the interparticle contact normal formula is:
where is the total number of contacts between the particles in the specimen; and are the corresponding components of the contact normal vector ().
In the conventional triaxial compression test, the horizontal plane is isotropic, and the calculation formula of deviatoric fabric can be rewritten as:
where , and are the constituent components of , , respectively.
Figure 18 shows the deviatoric fabric–axial strain curves of thirteen different gravel shapes at 200 kPa. When the axial strain is less than 5%, the anisotropy of the specimen rises rapidly, and when the axial strain is greater than 5%, the slope of the curve decreases as the EI and FI increase, and the anisotropy of the specimen increases in the critical state. This means that the particles’ contact directions are more parallel to the Z axis during shear. Both EI and FI influence the anisotropy of the particle aggregate, with FI exerting a more pronounced effect.
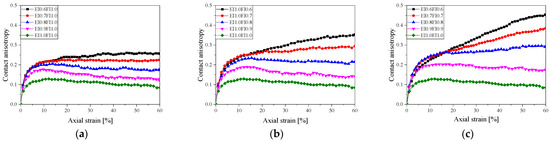
Figure 18.
Deviatoric fabric–axial strain curves for specimens with different particle shapes (200 kPa): (a) EI; (b) FI; and (c) EI/FI.
4. Conclusions
Taking gravel particles as the research object and particle morphology characteristics as the entry point, this paper uses discrete element software PFC 3D to analyze the macro-mechanical response and microscopic action mechanism of particle morphology characteristics on gravel particle deposits, and draws the following conclusions:
(1) The more the particle shape deviates from the spherical shape, the greater the peak deviatoric stress, the more detailed the strain-softening phenomenon, the greater the deviatoric stress and residual strength, and the more detailed the dilatancy. Increasing the complexity of particle morphology is conducive to enhancing the bearing capacity of gravel aggregate.
(2) With the decrease in the particle shape parameters EI and FI, the coordination number and sliding contact ratio increase, and the particle interlock effect is also enhanced. The proportion of the strong contact of spherical particles is larger than that of non-spherical particles, and the microcosmic level explains the reason for the small macroscopic strength of spherical particles.
(3) The analysis of the influence of particle shape on the friction mobilization index and the probability density of the contact force between particles in the critical state shows that the smaller EI and FI are, the larger the average value of the friction mobilization index is, the higher the degree of friction mobilization in the particle collection is, and the particle interlock is more likely to occur, which is also consistent with the macroscopic law.
Gravel particles, as a critical engineering material, exhibit significant multi-scale effects, making their study crucial in advancing the understanding of rock and soil mechanics. The particle morphology research results in this paper contribute to the development of constitutive models for particulate materials and can also provide a reference for the design of high-performance fillers in geotechnical structures.
Author Contributions
Conceptualization, Y.L.; methodology, Y.L.; software, Y.L.; validation, Y.L. and Z.C.; formal analysis, Y.L. and Z.C.; resources, H.M.; data curation, Z.C.; writing—original draft preparation, Z.C.; writing—review and editing, Y.L. and H.M.; visualization, Y.L. and Z.C.; supervision, Y.L. and H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (51808204, 52078195, U22A20232), and these supports are gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EI | Elongation Index |
| FI | Flat Index |
| DEM | Discrete Element Method |
| PFC3D | Particle Flow Code |
References
- Chakraborty, A.; Sawant, V.A. Response of embankment on liquefiable soil to sequential ground motions considering mitigation measures. Soil Dyn. Earthq. Eng. 2024, 176, 108278. [Google Scholar] [CrossRef]
- Qiu, W.; LI, Y.L.; Wen, L.F.; Wang, L.; Xu, Z.G. Experimental study on the longitudinal evolution of the overtopping breaching of concrete-face sand-gravel dams. Bull. Eng. Geol. Environ. 2023, 82, 102. [Google Scholar] [CrossRef]
- Zhou, T.; Wei, Y.J.; Jie, Y.X.; Zhang, Y.Y. Prediction intervals for concrete face sandy gravel dam settlement using Kalman filter-based kernel extreme learning machine. Measurement 2024, 236, 115094. [Google Scholar] [CrossRef]
- Wang, C.H.; Liu, S.T.; Liu, L.Q.; Chen, F.; Zhou, X.L. Deformation properties improvement of cement stabilized gravel using rubber: Laboratory and field study. Constr. Build. Mater. 2023, 393, 131975. [Google Scholar] [CrossRef]
- Gao, W.; Iqbal, J.; Hu, R.L. Investigation of geomechanical characterization and size effect of soil-rock mixture: A case study. Bull. Eng. Geol. Environ. 2021, 80, 6263–6274. [Google Scholar] [CrossRef]
- Lu, Y.; Tan, Y.; Li, X.; Liu, C.N. Methodology for Simulation of Irregularly Shaped Gravel Grains and Its Application to DEM Modeling. J. Comput. Civil Eng. 2017, 31, 04017023. [Google Scholar] [CrossRef]
- Wang, S.Y.; Chen, G.X.; Zhang, L.K.; Yuan, J. Triaxial Discrete Element Simulation of Soil–Rock Mixture with Different Rock Particle Shapes under Rigid and Flexible Loading Modes. Int. J. Geomech. 2021, 21, 1532–3641. [Google Scholar] [CrossRef]
- Lv, J.X.; Sun, X.Y.; Wang, H.L.; Wei, L.; Lan, R.Y.; He, T.Q.; Su, W.S. 3D characteristic indicator analysis and comprehensive evaluation of manufactured sand particles used in high-performance concrete. J. Asian Archit. Build 2024, 97, 110671. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Lu, Y. Study on soil-rock slope instability at mesoscopic scale using discrete element method. Comput. Geotech. 2023, 157, 105268. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Xu, W.J.; Yu, Y.Z. Triaxial tests of soil–rock mixtures with different rock block distributions. Soils Found. 2016, 56, 44–56. [Google Scholar] [CrossRef]
- Mahinroosta, R.; Oshtaghi, V. The effect of particle shape on the deformation and stress reduction of a gravel soil due to wetting. Sci. Rep. 2021, 11, 16583. [Google Scholar] [CrossRef] [PubMed]
- Pen, L.M.L.; Powrie, W.; Zervos, A.; Ahmed, S.; Aingaran, S. Dependence of shape on particle size for a crushed rock railway ballast. Granular Matter. 2013, 15, 849–861. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Han, Z.H.; Zhang, L.Q.; Zhou, J. Numerical Investigation of Mineral Grain Shape Effects on Strength and Fracture Behaviors of Rock Material. Appl. Sci. 2019, 9, 2855. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Z.X.; Zhang, J.Z.; Li, X.; Yang, H. DEM investigation on sandy soil behaviors under the influence of particle shape. Powder Technol. 2024, 441, 119835. [Google Scholar] [CrossRef]
- Wang, Y.; Nie, J.Y.; Zhao, S.W.; Wang, H. A coupled FEM-DEM study on mechanical behaviors of granular soils considering particle breakage. Comput. Geotech. 2023, 160, 105529. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, C.; Zou, J.Q.; Wang, B.S.; Song, F.N.; Yang, W.H. DEM exploration of the effect of particle shape on particle breakage in granular assemblies. Comput. Geotech. 2020, 122, 103542. [Google Scholar] [CrossRef]
- Hofmann, H.; Babadagli, T.; Zang, A.; Yoon, J.S.; Zimmermann, G. A grain based modeling study of mineralogical factors affecting strength, elastic behavior and micro fracture development during compression tests in granites. Eng. Fract. Mech. 2015, 147, 261–275. [Google Scholar] [CrossRef]
- Wang, Z.H.; Yang, S.L.; Li, L.H.; Tang, Y.S.; Xu, G.L. A 3D Voronoi clump based model for simulating failure behavior of brittle rock. Eng. Fract. Mech. 2021, 248, 107720. [Google Scholar] [CrossRef]
- Thornton, C. Numerical simulations of deviatoric shear deformation of granular media. Géotechnique 2000, 50, 43–53. [Google Scholar] [CrossRef]
- Hosn, R.A.; Sibille, L.; Benahmed, N.; Chareyre, B. Discrete numerical modeling of loose soil with spherical particles and interparticle rolling friction. Granular Matter. 2017, 19, 4. [Google Scholar] [CrossRef]
- Benmebarek, M.A.; Movahedi, R.M. Effect of Rolling Resistance Model Parameters on 3D DEM Modeling of Coarse Sand Direct Shear Test. Materials 2023, 16, 2077. [Google Scholar] [CrossRef] [PubMed]
- Aman, M.; Narasimha, M.; Raja, B. GPU based discrete element modeling for convex polyhedral shape particles: Development and validation. Powder Technol. 2025, 449, 120407. [Google Scholar]
- Sun, J.Z.; Zou, L.; Govender, N.; Martinez-Estévez, I.; Crespo, A.J.C.; Sun, Z.; Dominguez, J.M. A resolved SPH-DEM coupling method for analysing the interaction of polyhedral granular materials with fluid. Comput. Geotech. 2017, 90, 96–112. [Google Scholar] [CrossRef]
- Cui, S.W.; Tan, Y.; Lu, Y. Algorithm for generation of 3D polyhedrons for simulation of rock particles by DEM and its application to tunneling in boulder-soil matrix. Tunn. Undergr. Space Technol. 2020, 106, 103588. [Google Scholar] [CrossRef]
- Zhang, S.H.; Zhao, L.H.; Wang, X.; Huang, D.L. Quantifying the effects of elongation and flatness on the shear behavior of realistic 3D rock aggregates based on DEM modeling. Adv. Powder Technol. 2021, 32, 1318–1332. [Google Scholar] [CrossRef]
- Zuo, L.; Lourenco, S.D.N.; Baudet, B.A. Experimental insight into the particle morphology changes associated with landslide movement. Landslides 2019, 16, 787–798. [Google Scholar] [CrossRef]
- Blott, J.S.; Pye, K. Particle shape: A review and new methods of characterization and classification. Sedimentology 2008, 55, 31–63. [Google Scholar] [CrossRef]
- Gong, J.; Liu, J. Effect of aspect ratio on triaxial compression of multi-sphere ellipsoid assemblies simulated using a discrete element method. Particuology 2016, 32, 49–62. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Hu, W. Competition mechanism between dilation and interlocking in granular soils: DEM simulation and constitutive modeling. Acta Geotech. 2022, 18, 149–169. [Google Scholar] [CrossRef]
- Fang, C.F.; Gong, J.; Jia, M.T.; Nie, Z.; Li, B.; Mohammed, A. Investigating the effects of elongation and flatness on the shear be-haviour of breakable granular materials via the DEM. Granular Matter. 2022, 24, 78. [Google Scholar] [CrossRef]
- Nie, Z.H.; Fang, C.F.; Gong, J.; Yin, Z.Y. Exploring the effect of particle shape caused by erosion on the shear behaviour of granular materials via the DEM. Int. J. Solids Struct. 2020, 202, 1–11. [Google Scholar] [CrossRef]
- Nie, Z.H.; Fang, C.F.; Gong, J.; Wang, J.F. DEM study on the effect of roundness on the shear behaviour of granular materials. Comput. Geotech. 2020, 121, 103457. [Google Scholar] [CrossRef]
- Azéma, E.; Farhang, R. Force chains and contact network topology in sheared packings of elongated particles. Phys. Rev. E. 2012, 85, 031303. [Google Scholar] [CrossRef]
- Nie, J.Y.; Cao, Z.J.; Li, D.Q.; Cui, Y.F. 3D DEM insights into the effect of particle overall regularity on macro and micro mechanical behaviours of dense sands. Comput. Geotech. 2021, 132, 103965. [Google Scholar] [CrossRef]
- Satake, M. Fabric tensor in granular materials. In Proceedings of the IUTAM Conference on Deformation and Failure of Granular Materials, Delft, The Netherlands, 31 August–3 September 1982; pp. 63–68. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).