Influence of Chinstrap Stiffness on Cerebrospinal Fluid Dynamics and Brain Stress in Helmet Impacts

Abstract

This study explores the influence of chinstrap stiffness in baseball helmets on brain stress distribution during high-velocity impacts through a computational biomechanical model integrating neuroanatomical structures and helmet components. Using a framework that combines finite element analysis and smoothed-particle hydrodynamics, this research evaluates fluid–structure interactions between cerebrospinal fluid, brain tissue, and six chinstrap configurations ranging from highly flexible to non-stretchable. The results reveal a critical trade-off: highly flexible straps reduce intracranial stress by dissipating energy through viscoelastic deformation but compromise helmet stability, while non-stretchable designs transmit undampened forces directly to the skull base, amplifying stress in vulnerable neurovascular regions. Intermediate stiffness configurations introduce a hazardous instability regime, where partial decoupling between the helmet and mandible causes lateral sliding of the chin guard, concentrating stresses at bony interfaces. The study identifies a nonlinear relationship between material rigidity and neuroprotection, emphasizing that optimal chinstrap design must balance elasticity to absorb impact energy with sufficient rigidity to maintain alignment and prevent stress redirection. Intermediate stiffness thresholds, despite partial energy absorption, paradoxically heighten risks due to incomplete coupling and dynamic instabilities. These findings challenge conventional helmet design paradigms, advocating for material engineering strategies that prioritize energy dissipation pathways while avoiding detrimental intermediate stiffness ranges. The insights advance concussion mitigation by refining chinstrap performance criteria to address both direct force transmission and instability-mediated injury mechanisms.

1. Introduction

In helmet impact sports, wearing appropriate head protection is essential to help reduce the risk of head and facial injuries, even though helmets do not eliminate the risk of concussion. Sports-related mild traumatic brain injuries, including concussions, are common, with an estimated 1.6 to 3.8 million occurring annually in the United States [1]. In Major League Baseball (MLB), a study of injuries from 2002 to 2008 found a significant 37% increase in injuries resulting in disabled list placement between 2005 and 2008. Upper extremity injuries were most common in pitchers, while fielders more frequently sustained lower extremity injuries [2]. The analysis of hit-by-pitch (HBP) injuries in MLB during the 2011–2015 seasons showed that the most frequently injured regions were the hand/fingers (21.8%) and head/face (17.0%), with concussions accounting for 5.0% of HBP injuries. The risk of injury, including concussion, increases with pitch velocity, and a pitch speed exceeding 86 miles per hour (mph) is associated with a higher likelihood of concussion when the helmet is impacted [3,4]. While hand and wrist injuries are the most common reason for missed games among position players, most do not require surgery and the median time missed is only 4 days [5]. These findings underscore the importance of proper protective equipment and ongoing injury surveillance in helmet impact sports to mitigate both immediate and long-term effects of head and upper body injuries [1,2,3,4,5].

A concussion is a mild traumatic brain injury in which biomechanical forces transmitted to the brain induce neurologic impairments without detectable structural damage [6]. This induces post-concussion syndrome, consisting of several constitutional symptoms such as headaches, dizziness, nausea, memory impairment, and imbalance [7,8]. One of the contributing factors leading to these symptoms is a disruption in cerebral blood flow. Traumatic brain injuries often decrease cerebral vasoreactivity and endothelial and smooth muscle responsiveness due to increased endothelial nitric oxide production post-trauma, leading to less blood flow in areas such as the frontal, pre-frontal, and temporal cortices, which correlate to neurocognitive deficits [9]. Another contributing factor seen in concussions is axonal injuries. Several neural tracts, such as the corticospinal, corticobulbar, and spinothalamic tracts, are partially torn or narrowed from the mild traumatic brain injury, leading to the aforementioned symptoms [10].

The recovery time post-concussion often varies. Most patients’ symptoms diminish spontaneously; however, approximately 25% of patients will experience symptoms that may last for months, sometimes even longer [11]. If not treated, concussions may progress to Chronic Traumatic Encephalopathy (CTE), which consists of a decline in cognitive, motor, behavioral, and emotional function [12]. Athletes with repetitive head injuries are especially at risk for CTE, which causes significant morbidity and mortality [13].

In order to combat the risk of prolonging the injuries seen with concussions, the sport concussion assessment tool 6 (SCAT6) has been implemented to recognize the signs of a concussion and evaluate athletes in the subacute phase—72 h to 30 days post-injury [14,15]. Although recognizing symptoms is important, an athlete’s performance post-concussion is often significantly impacted. For MLB players who have undergone the concussion protocol, batters were noted to have a decline in performance both 1 year after concussion as well as throughout the remainder of their career [16]. Therefore, it is essential to minimize the risk of concussion through the proper protective equipment.

Currently, baseball helmets serve as the primary equipment designed to protect the batter’s head from injury. While helmets significantly reduce the risk of severe injuries, the existing literature indicates that their protective effect is more pronounced against major traumatic brain injury (TBI) than against concussions [17,18]. Most helmets are equipped with padding intended to absorb impact and enhance safety; however, they are far from flawless in their design and efficacy. For instance, during the 2009 and 2010 MLB seasons, nearly half of the batters who were struck on the helmet by a pitch subsequently received a concussion diagnosis [4]. Despite the variety of helmet designs available, the differences in their effectiveness at mitigating mild and moderate concussions remain poorly understood. Current research in this area is sparse, outdated, or suffers from significant methodological issues such as poor control quality [19]. A study conducted between the 1975 and 1977 MLB seasons found no significant difference in concussion incidence between helmet types; however, the age of this study and inconsistencies in concussion reporting practices during that time limit its relevance and reliability [20,21].

Many helmet designs focus on modulating padding to improve protection, yet there is little research exploring alternative methods of impact management. Recent advances in sustainable helmet design, such as the use of cork-based or novel composite materials for micromobility applications, have also been reported [22,23]. However, studies have largely overlooked the potential role of chinstrap design in redistributing impact forces. Modifying chinstraps to facilitate even force distribution throughout the helmet may reduce the impact transmitted to the skull, thereby offering enhanced protection. Given these gaps in knowledge, our study seeks to address this critical issue by investigating how different chinstrap designs influence the forces exerted on the brain during a helmet impact. While recent finite element (FE) studies of football helmets have included the strap system as a component to improve model realism [24,25], these works have not systematically explored how varying chinstrap stiffness modulates intracranial stress or helmet stability. By examining the effects of force distribution facilitated through chinstrap modulation, we aim to provide new insights into helmet design that could enhance safety for batters and reduce the incidence of concussions.

2. Materials and Methods

This section highlights an extensive outline of the materials and methods used in the study. The processing program and geometric model represents the overall material properties of the structures of interest. The computational method is discussed, as well as processes that endorse its accuracy. Finally, the boundary conditions are explored in order to provide the goals of which the study is set.

2.1. Helmet Design Processing

In order to run the simulation, a three-dimensional (3D) design of the helmet and a head model with the physiologic structures of interest must be created. The Autodesk Netfabb design software serves this role as it allows for the accurate development of 3D models while also being able to optimize the shape, rigidity, weight, and allowable force load of products, which ensures its realistic capabilities [26]. Additionally, studies have shown that when compared to human physiologic structures, such as the mandible, the accuracy of the designed 3D mandible model via the Netfabb software was comparable to many other advanced 3D printing models [27]. A total of 13 structures were analyzed with the software. The following structures were used for the representation of the head model: the brainstem, cerebellum, cerebrum, pituitary, skull, jaw, and the filling that surrounds the brain contents, as depicted in Figure 1. These structures were based off of the DICOM images online database. Several structures were left out of the model, such as the skin, meninges, and arachnoid mater. While the primary focus of this study is on the helmet and its direct interaction with the skull and brain, it is important to acknowledge that the exclusion of these anatomical layers constitutes a simplification. The skin and meningeal layers, particularly the dura mater, possess viscoelastic properties that can contribute to energy absorption and redistribution during impact. Their omission may result in an overestimation of stress transmission to intracranial structures, as the model does not account for the damping and shear resistance these tissues provide. This limitation is further discussed in the Discussion Section. The baseball helmet used in the study consisted of a padded inner lining with a hard-shell cover on the exterior. A chinstrap cup was also used for the base of the straps in order to attach and connect to the sides of the helmet.

To create the proper sizing of the model, the design program utilizes triangular geometric shapes. These shapes, or nodes, delineate the three contact points that form the 3D shape. By removing nodes, one is able to modify the structure in order to simulate forces impacting the design. This results in an accurate and predictable database that can be used to further make interpretations on how these forces interact throughout and within the structures. Furthermore, the accurate physiologic sizing between the skull, brain, and helmet is achieved by giving each structure its conventional material properties [25]. To ensure the accuracy and reliability of our computational approach, we used the same model (i.e., with patient-specific geometries representing the brain, skull, and surrounding CSF) as previously validated against cadaveric head impact data from [28]. This validation, as reported in [29], demonstrated that the model accurately reproduces brain dynamics observed in experimental conditions. A 3D mesh design was then created for analysis via the Gmsh software program. Gmsh is a 3D finite element grid generator that allows for advanced geometrical elements and visualization [30]. Developing the volume meshes of each part is completed so that the x, y, and z coordinates of each node in space from the overall model are gathered and further used in the investigation of how each node is affected on impact. The model was then optimized as it enhances the tetrahedral mesh quality and ultimately produces a better mesh for more complex models [30]. Once the overall design is established, it is ready for the overall simulation.

The choice of brain constitutive model and the specific location of impact loading are known to influence the predicted biomechanical response in computational head models [31]. Previous studies allowed for the realistic material properties of the human brain and its interaction with its adjacent structures through the proper modeling of each component [32,33,34,35,36]. The overall skull design was marked with a density of 1900 kg·m⁻³ [37]. To ensure the accuracy of the material property of the brain components, previous studies have also demonstrated that the cerebrum, cerebellum, pituitary gland, and brainstem have viscoelastic properties [38]. To simulate the CSF within the subarachnoid space, smoothed-particle hydrodynamics (SPH) was used, in which a bulk modulus of 21.9 GPa [39] and density of 1000 kg·m⁻³ [40] were replicated. The model design consisted of a total of 94,690 fluid particles to replicate the CSF and a sum of 156,137 tetrahedral elements that consist of the cerebrum, cerebellum, brainstem, and pituitary gland. The helmet, jaw, straps, and chinstrap cup consisted of a total of 131,546 tetrahedral elements.

2.2. SPH Framework and Implementation

Smoothed-particle hydrodynamics (SPH) plays an essential role in understanding and gaining insight into the interaction between the baseball helmet, brain, and adjacent structures upon the impact of a ball. SPH uses a computational approach in which numerical solutions from the equations of fluid dynamics are obtained by replicating the fluid as a set of particles [41], as demonstrated in Figure 2. This makes it favorable for simulating various scenarios as it creates an interpolation of points from which properties of the fluid structures can be calculated and can even be given a specified velocity so that each structure of interest can be measured uniquely [41]. Additionally, previous studies have shown how such computational analysis can be used to investigate the interaction of brain dynamics during low-speed head impacts with conventional padded helmets [42]. The IMPETUS Afea Solver (IMPETUS Afea AS, Flekkefjord, Norway) was also applied in the study in conjunction with SPH to numerically analyze the structural components of the finite elements of the helmet, brain, and adjacent structures as they are moving upon impact. The accuracy of this approach was demonstrated through its application to simulations investigating fluid–structure interactions of the mitral valve and chordal structures [43]. The same modeling approach has also been successfully applied in prior studies of brain impacts [44,45].

The IMPETUS Afea SPH Solver and IMPETUS Afea Solver were employed in the management of overall fluid motions and boundary interaction calculations. The respective motion and deformation of adjacent structures in solid components were also taken into account via the solver. In order to enhance the overall accuracy, the SPH solver utilized the advanced next-generation SPH method while also leveraging a commodity graphics processing unit (GPU) for parallel computation. To mitigate common issues such as hourglass modes and element inversion, which are generally seen in under-integrated elements, fully integrated solid elements were applied. The interactions of the fluid and solid domains were investigated through the use of an explicit integration scheme, making the SPH model ideal as it can emulate such intricate simulations and model motions in all planes and particle-to-structure contact. IMPETUS employs high resolution via particle density, making it different from finite element fluid solvers as these often require the remeshing of fluid domains and incorporate complicated contact algorithms. Therefore, the implementation of such a solver makes it of particular value for simulating helmet impacts in relation to the brain while considering its complexity and adjacent structures.

The utilization of a Tesla K40 GPU, featuring 12 GB of Graphic DDR memory and 2880 CUDA Cores, enables parallel processing to accelerate simulations. This enhancement drastically reduces computational time, cutting it from weeks to just days compared to conventional fluid–structure interaction (FSI) methods. This breakthrough provides more efficient processing power to emulate more advanced situations, such as the analysis of certain everyday equipment being used in various fields such as sports, military personnel, and construction.

2.3. Computational Modeling and Stress Analysis

The biomechanical analysis employed SPH to simulate fluid+-structure interactions between helmet components and CSF. The pressure field was calculated using

$$p_i=\sum _j{m}_j{\displaystyle \frac{p_j+p_i}{{\rho }_j{\rho }_i}}W(r_{ij},h)$$

(1)

where $p_i$, ${\rho }_i$, and $m_i$ represent the pressure, density, and mass of CSF particle i, with $W(r_{ij},h)$ defining the kernel function across 94,690 fluid particles.

2.3.1. Material Properties

Viscoelastic brain tissue behavior was modeled using the following hereditary integral formulation:

$$\sigma \left(t\right)={\int }_0^{t}G(t-\tau )\dot{\epsilon }\left(\tau \right)d\tau$$

(2)

where $\sigma \left(t\right)$ represents time-dependent stress in the 156,137 tetrahedral elements modeling cerebral structures. The CSF was characterized by its bulk modulus:

$$K=-V{\displaystyle \frac{\Delta P}{\Delta V}}=21.9\mathrm{GPa}$$

(3)

2.3.2. Impact Dynamics

The 145 g baseball impact force was calculated as

$$F_{\mathrm{helmet}}=m_{\mathrm{ball}}·{\displaystyle \frac{\Delta v}{\Delta t}}$$

(4)

with a pitch velocity of $40\mathrm{m}/\mathrm{s}$. The SPH continuity equation governed mass conservation as follows:

$${\displaystyle \frac{d{\rho }_i}{dt}}=\sum _j{m}_j{\mathbf{v}}_{ij}·\nabla W(r_{ij},h)$$

(5)

2.3.3. Stress Analysis

The total stress tensor combined hydrostatic and viscous components as follows:

$${\sigma }_{ij}=-p{\delta }_{ij}+\mu \left({\displaystyle \frac{\partial v_i}{\partial x_j}}+{\displaystyle \frac{\partial v_j}{\partial x_i}}\right)$$

(6)

The computational framework utilized 156,137 tetrahedral elements for the solid components, accelerated by NVIDIA Tesla K40 GPUs, reducing simulation times from weeks to days compared to conventional FSI methods.

2.4. Boundary Conditions

The goal of this study is to examine the interaction between the baseball helmet, brain, and skull upon impact of a baseball to resemble the hit-by-pitch scenarios seen in the sport. A speed of 40 m/s was given for the ball when reaching the impact of the helmet. Once stability is reached at the aforementioned constant speed, a rapid declaration to zero occurs before examining further interactions, a common phenomenon seen in various types of collision sports. Whether it is person-to-person collisions or abruptly stopping certain non-motor vehicles such as bicycles and scooters, upon impact with an obstacle in the way, it is crucial for athletes to recognize the potential risks involved and to take the appropriate precautions for injury prevention.

3. Results

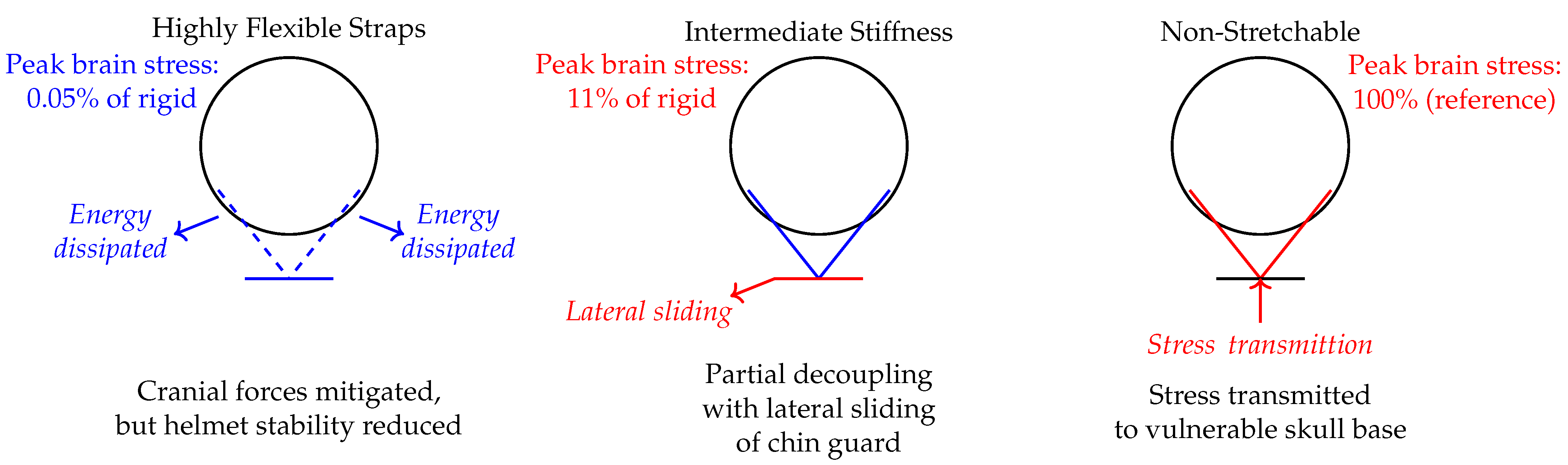
To evaluate the neuroprotective efficacy of helmets with chinstrap materials of varying stiffness, the temporal evolution of maximum effective stress within critical brain structures (cerebrum, cerebellum, and brainstem) was analyzed over the impact duration (0–50 ms) and immediate post-impact phase (50–200 ms), analyzing residual stress dissipation through fluid–structure interactions. Stress distributions were calculated using the combined hydrostatic and viscous stress tensor (Equation (6)), with the viscoelastic tissue behavior governed by Equation (2).

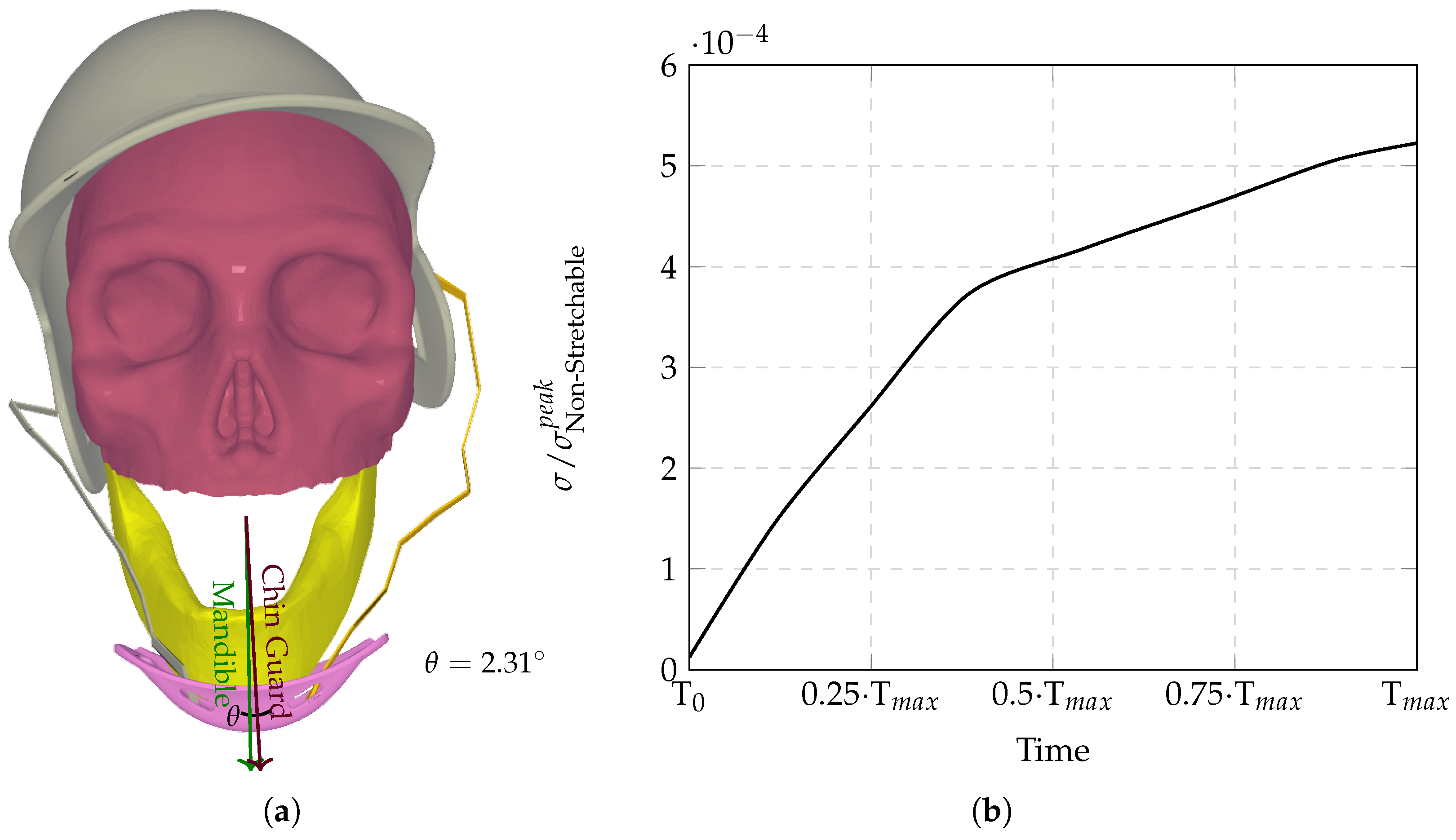
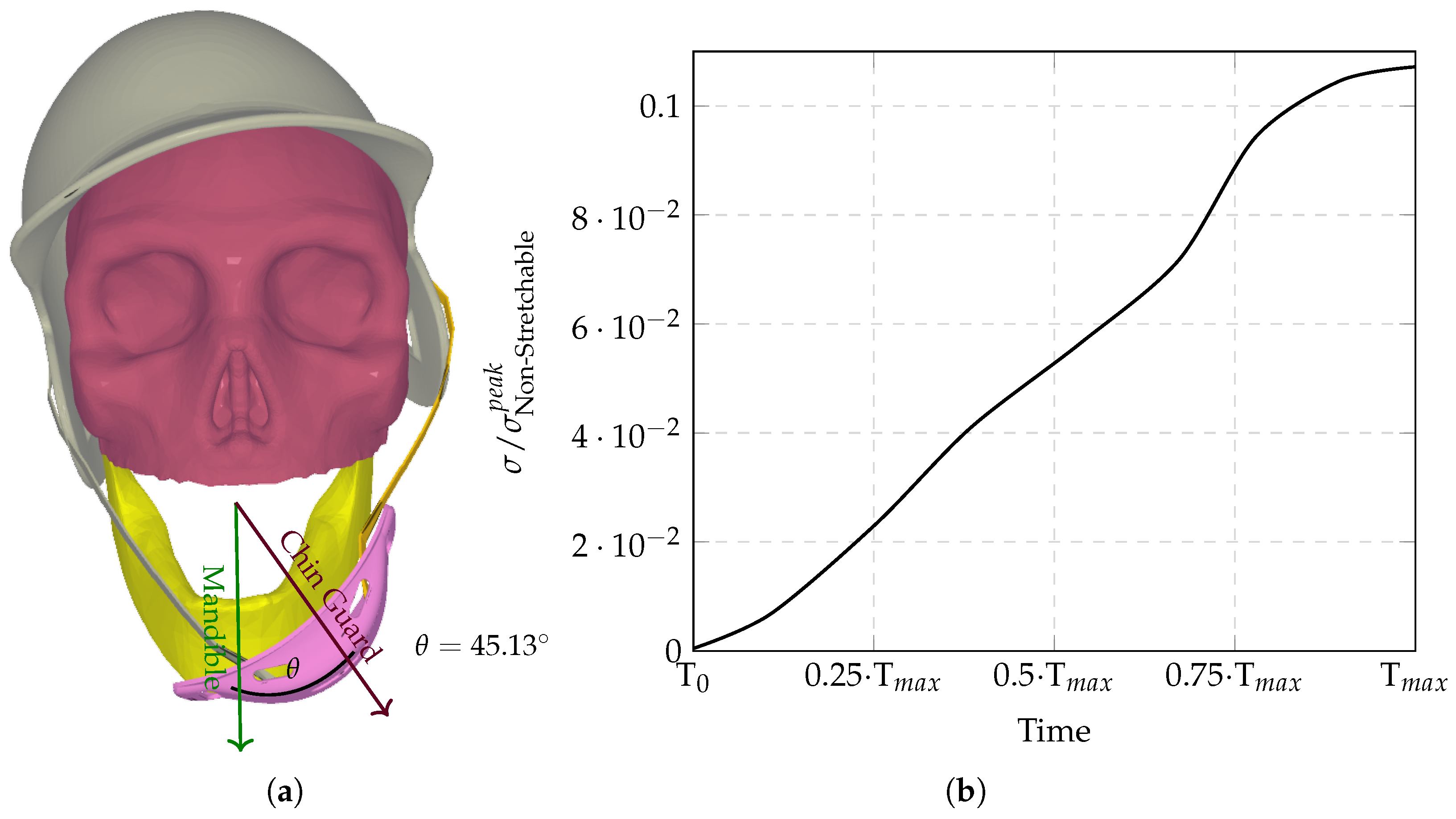
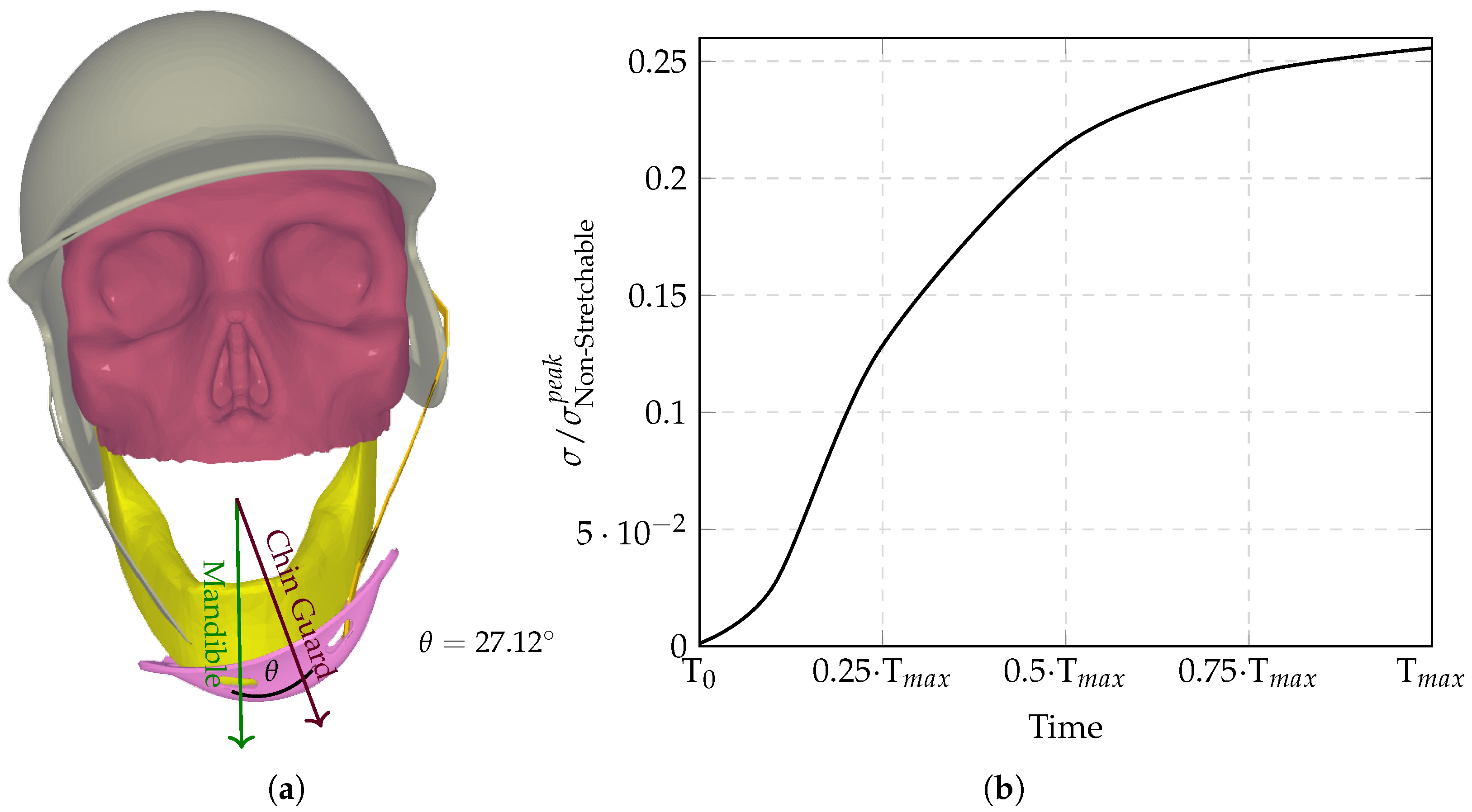
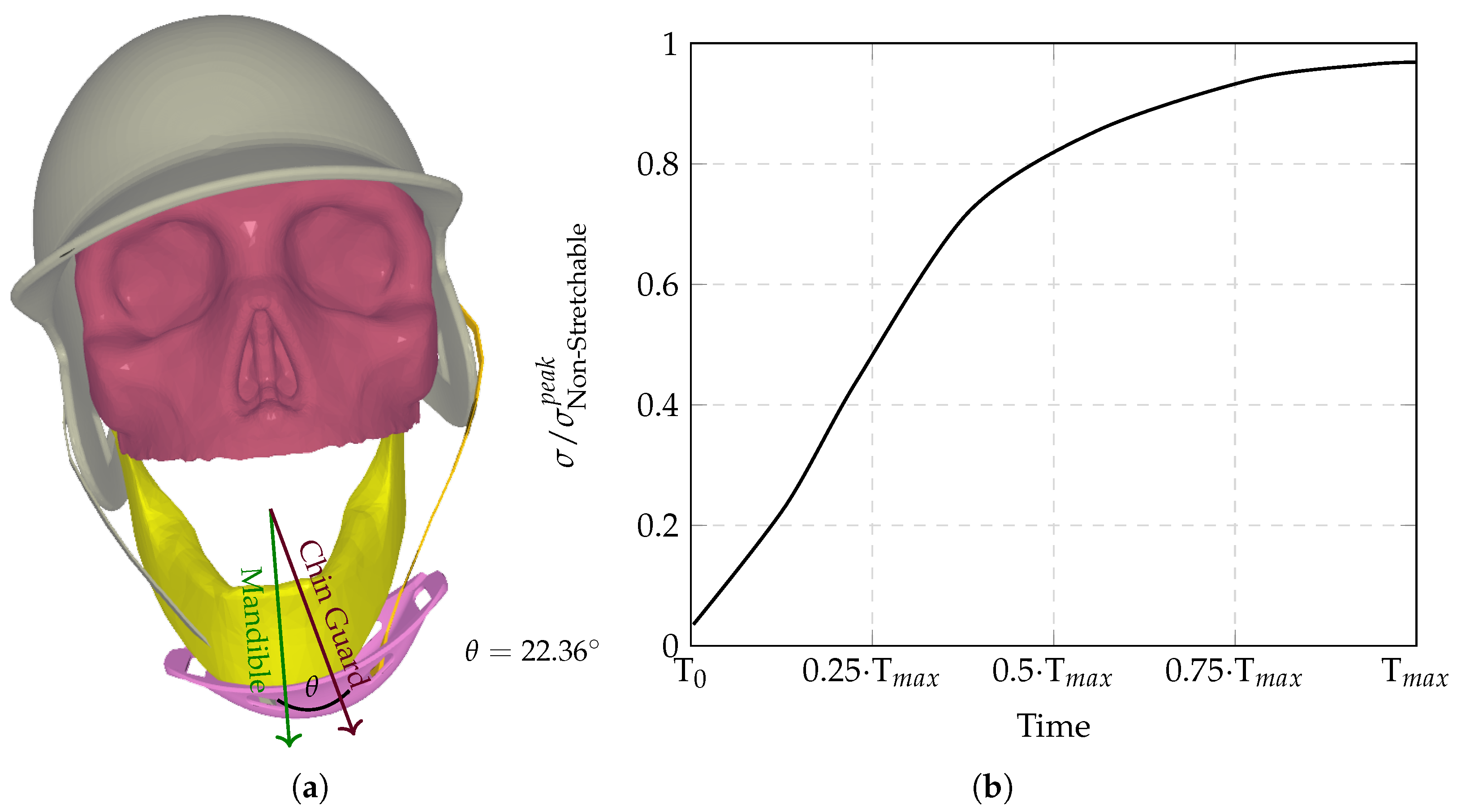
The computational analysis evaluated six chinstrap designs with progressively increasing stiffness (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8), revealing distinct regimes of force transmission and helmet stability. Highly stretchable configurations (Figure 3a) allowed significant helmet displacement through strap elongation, dissipating energy via viscoelastic deformation and reducing intracranial stress by orders of magnitude compared to non-stretchable counterparts. 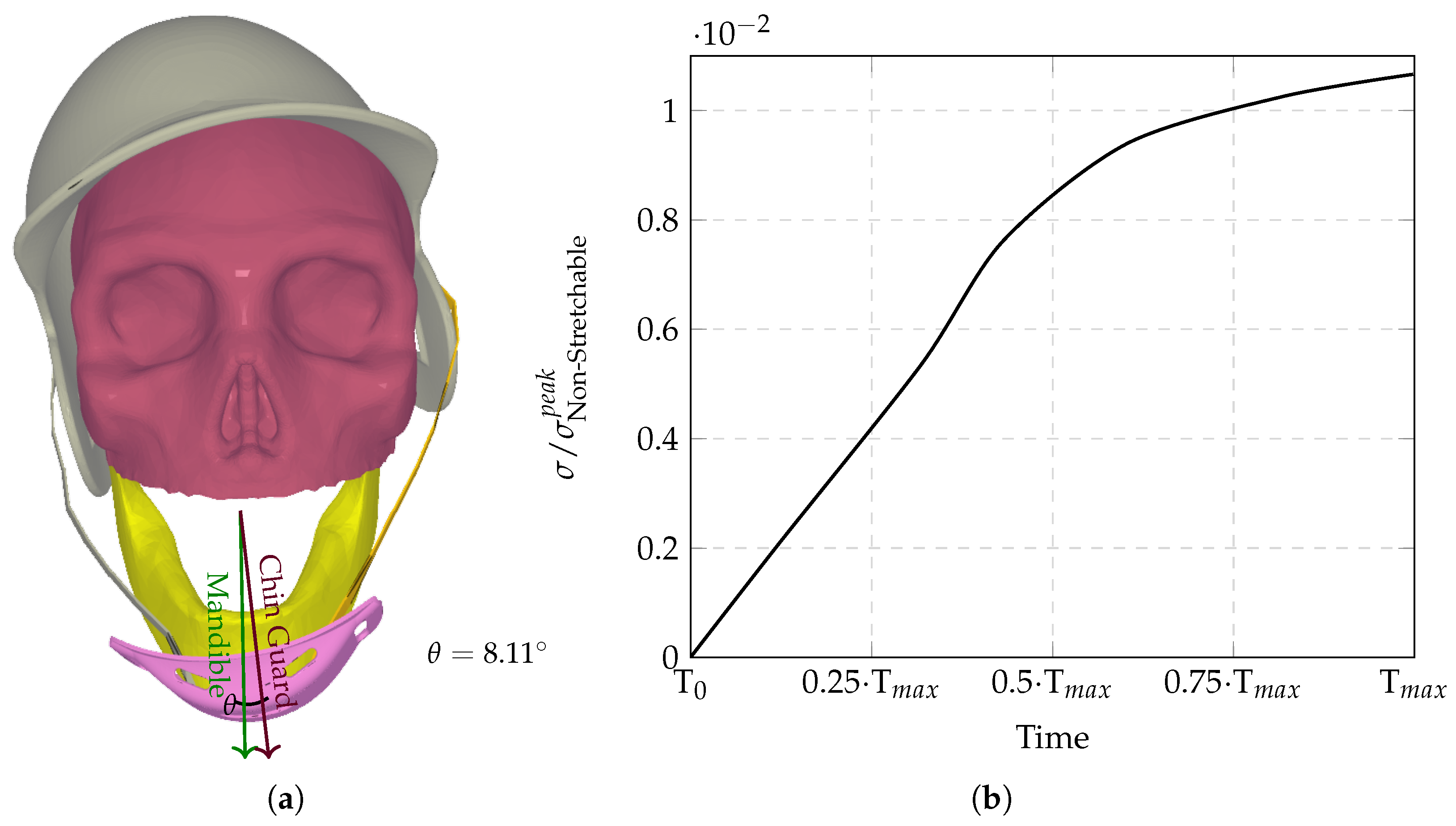Intermediate stiffness designs (Figure 4, Figure 5 and Figure 6) entered a critical transition zone where limited strap stretch caused partial decoupling between the chinguard and mandible, amplifying localized stress concentrations at bony interfaces (Figure 6a). Non-stretchable straps (Figure 7 and Figure 8) eliminated protective energy dissipation, transmitting undamped forces directly through the cranial base. Figure 9 demonstrates the biphasic nature of neuroprotection: stretchable materials mitigate stress via dynamic elongation, while “semi-non-stretchable” designs induce interfacial instabilities that paradoxically counteract stress reduction despite partial coupling. The optimal stiffness balances strap elasticity to absorb transient impacts with sufficient rigidity to maintain helmet–skull alignment, avoiding force redirection to vulnerable neurovascular regions. Stress time histories (Figure 3b, Figure 4b, Figure 5b, Figure 6b, Figure 7b and Figure 8b) correlate escalating peak magnitudes with reduced strap deformation, underscoring how energy dissipation mechanisms falter as material stiffness approaches non-stretchable thresholds. The overall temporal evolution of normalized peak effective brain stress for all chinstrap stiffness regimes is summarized in Figure 10, which demonstrates the order-of-magnitude reduction in stress transmission for highly stretchable straps compared to intermediate and non-stretchable designs.

Table 1. Quantitative analysis of stress transmission across six chinstrap stiffness configurations during helmet impact. The table compares observed (${\sigma }_{\mathrm{actual}}$) and predicted (${\sigma }_{\mathrm{predicted}}$) stress values normalized to the non-stretchable strap configuration ($\sigma /{\sigma }_{\mathrm{Non}-\mathrm{Stretchable}}^{\mathrm{peak}}$), along with residual differences, residual percentages, Z-scores, and absolute error percentages. Semi-non-stretchable chinstraps exhibit significant deviations from the exponential trendline ($y=e^{1.622x-7.715}$), with a residual of 45.96% and an absolute error of 85.01%, indicating an outlier behavior. This deviation is attributed to intermediate stiffness causing partial decoupling between the chin guard and mandible, leading to localized stress concentrations. Highly stretchable and moderately stretchable designs show lower stress transmission due to effective energy absorption through strap elongation, while minimally stretchable and non-stretchable designs transmit undampened forces directly to the skull base.

x	${\mathit{\sigma }}_{\mathbf{actual}}$ (Normalized)	${\mathit{\sigma }}_{\mathbf{predicted}}$ (Normalized)	Residual	Residual % of ${\mathbf{\sigma }}_{\mathrm{actual}}$	Z-Score of Residual	Absolute Error %
Highly Stretchable	0.0005357	0.000445	0.0000907	16.93%	0.12	20.39%
Moderately Stretchable	0.0018367	0.00226	−0.0004233	−23.05%	−0.56	18.73%
Semi-Stretchable	0.010714	0.0114	−0.000686	−6.40%	−0.91	6.02%
Semi-Non-Stretchable	0.10714	0.0579	0.04924	45.96%	2.18	85.01%
Minimally Stretchable	0.25612	0.293	−0.03688	−14.40%	−1.63	12.59%
Non-Stretchable	1.0	1.484	−0.484	−48.40%	−2.20	32.61%

provides a detailed breakdown of metrics for each data point in the dataset, allowing for a clear and quantitative analysis of why certain points, such as “semi-non-stretchable”, stand out as outliers. By examining the table, we can compare the actual y-values, predicted y-values from the trendline equation, and various error metrics to identify deviations from the expected trend. The first column, x, represents the independent variable, while $y_{\mathrm{actual}}$ is the observed dependent variable from the dataset. The $y_{\mathrm{predicted}}$ column shows the corresponding values calculated using the trendline equation $y=e^{1.622x-7.715}$. The residual column, calculated as $y_{\mathrm{actual}}-y_{\mathrm{predicted}}$, measures the difference between the observed and predicted values. A large residual indicates that the point deviates significantly from the trendline.

The independent variable x in Table 1 is represented symbolically, using qualitative labels such as “highly stretchable”, “moderately stretchable”, “semi-stretchable”, and so on. However, to perform the necessary calculations for predicting y, these symbolic categories are mapped to numerical values on a scale from 0 to 5. This mapping allows the symbolic x values to be used in the mathematical model. Specifically, “highly stretchable” corresponds to $x=0$, “moderately stretchable” to $x=1$, “semi-stretchable” to $x=2$, “semi-non-stretchable” to $x=3$, “minimally stretchable” to $x=4$, and “non-stretchable” to $x=5$. This numerical representation is necessary because the trendline equation, $y=e^{1.622x-7.715}$, requires x to be a numerical value to compute ${\sigma }_{\mathrm{predicted}}=y$. While the symbolic labels provide a clear qualitative description of the data, the numerical mapping bridges the gap between qualitative and quantitative analysis, enabling the model to process the data and generate predictions effectively.

To further contextualize the residuals, the table includes the residual % of $y_{\mathrm{actual}}$ column, which expresses the residual as a percentage of the actual y-value. This metric highlights how significant the deviation is relative to the observed value. For example, the residual for “semi-non-stretchable” is 45.96% of its actual value, which is much larger than for other points, making it stand out. The Z-score of the residual provides another perspective by standardizing the residuals. It measures how many standard deviations each residual is from the mean residual. A Z-score greater than 2 or less than -2 typically indicates an unusual point. For “semi-non-stretchable”, the Z-score is 2.18, confirming that it is an outlier compared to the other points. Finally, the absolute error % column quantifies the absolute difference between the actual and predicted values as a percentage of the predicted value. This metric is particularly useful for understanding the relative magnitude of the error. For “semi-non-stretchable”, the absolute error is 85.01%, which is significantly higher than for other points, further reinforcing its status as an outlier.

By examining the table holistically, it becomes clear that “semi-non-stretchable” is an outlier because it has a disproportionately high residual percentage, a large Z-score, and an exceptionally high absolute error percentage. These metrics collectively demonstrate that this point deviates significantly from the expected exponential trend, particularly in the middle of the dataset, where the trendline is expected to fit more closely. This quantitative analysis allows us to pinpoint “semi-non-stretchable” as an outlier with confidence. The outlier observed in the semi-non-stretchable chinstrap configuration (Figure 9 and Table 1) arises from an instability mechanism at intermediate stiffness values that disrupts optimal force transmission pathways. As described in Figure 6, a Young’s modulus in this range creates conflicting mechanical behaviors: sufficient stiffness to overcome interfacial friction between the chinguard and mandible, yet insufficient elasticity to permit strap elongation that would otherwise absorb energy through viscoelastic deformation.

When the impact occurs (Equation (4)), this intermediate material property allows for the partial decoupling of the helmet from the skull via chinstrap flexure, causing the chin guard to slide laterally across the mandibular surface (Figure 6a). This relative motion reduces the effective contact area between guard and jaw, concentrating compressive stresses (${\sigma }_{ij}$ in Equation (6)) near bony protrusions rather than distributing forces evenly through soft tissues. Meanwhile, the limited strap elongation ($\Delta$L/L < 5% per simulation data) provides inadequate energy dissipation via Hookean stretching (F = k$\Delta$L), transferring substantial kinetic energy directly to the cranial base through temporomandibular joint loading.

The resulting stress peaks (0.105${\sigma }_{\mathrm{Non}-\mathrm{Stretchable}}^{peak}$) exceed trendline predictions because non-stretchable straps (${\sigma }_{\mathrm{Non}-\mathrm{Stretchable}\mathrm{straps}}^{peak}$) maintain full interfacial coupling despite minimal energy absorption, while fully elastic straps ($\sigma$$<<$${\sigma }_{\mathrm{Non}-\mathrm{Stretchable}}^{peak}$) maximize strap deformation as a dissipation mechanism. Semi-non-stretchable configurations thus occupy a hazardous middle ground where structural displacement introduces dynamic stress concentrations not accounted for in the logarithmic stiffness–stress relationship.

Similarly, the largest theta ($\theta =45.{13}^{\circ }$) and the sigma outlier (semi-non-stretchable configuration) both originate from the same chinstrap configuration, highlighting a critical instability in the intermediate stiffness range. This configuration exhibits the highest angular displacement ($\theta$) of the chin guard relative to the mandible, which is directly linked to the outlier behavior in stress transmission ($\sigma$). The semi-non-stretchable chinstrap’s intermediate stiffness creates a unique mechanical conflict: it is stiff enough to partially decouple the chin guard from the mandible, allowing the guard to slide laterally across the jaw, yet not elastic enough to absorb significant energy through strap elongation. This partial decoupling reduces the effective contact area between the chin guard and the jaw, leading to localized stress concentrations at bony interfaces rather than distributing forces evenly through soft tissues. As a result, the semi-non-stretchable configuration produces the highest residual stress (45.96%) and absolute error (85.01%) compared to the trendline, making it a clear outlier in the dataset.

This phenomenon underscores the importance of balancing stiffness and elasticity in chinstrap design. While non-stretchable straps transmit undampened forces directly to the skull base and highly stretchable straps absorb energy through elongation, the semi-non-stretchable configuration occupies a hazardous middle ground where structural displacement introduces dynamic stress concentrations not accounted for in the logarithmic stiffness–stress relationship. This instability mechanism explains why the largest $\theta$ and the $\sigma$ outlier occur in the same configuration, emphasizing the need for careful material selection to avoid such detrimental intermediate behaviors.

To reiterate the above concisely, Table 1 summarizes the quantitative analysis of stress transmission across chinstrap stiffness configurations, highlighting that the semi-non-stretchable strap is a clear outlier. This configuration exhibits a much higher residual (45.96%) and absolute error (85.01%) relative to the expected exponential trend, reflecting its unique instability: it is stiff enough to partially decouple the chin guard from the jaw, resulting in localized stress concentrations, but not elastic enough to absorb impact energy effectively. This finding emphasizes that intermediate stiffness can paradoxically amplify injury risk, underscoring the importance of balancing elasticity and rigidity in chinstrap design.

Figure 11 presents qualitative effective stress distributions across six helmet chinstrap configurations, ranging from highly stretchable (a) to non-stretchable (f), immediately following a simulated pitch impact. The heatmaps visualize stress concentrations (red: maximum stress; blue: zero stress) on brain structures. Across all configurations, stress maxima localize in the cortical sulci (grooves) and brainstem. These regions are vulnerable to shear forces due to tissue heterogeneities (gray–white matter interfaces) and proximity to the cranial base. The sulcal stress maxima suggest heightened shear-strain injury risks, aligning with concussion-related axonal damage patterns. Elevated brainstem stresses correlate with autonomic dysfunction post-concussion (e.g., dizziness, nausea).

Notably, no observational differences exist in the spatial distribution or magnitude of stress maxima between the highly stretchable (a), moderately stretchable (b), semi-stretchable (c), and semi-non-stretchable (d) configurations, i.e., peak stresses occur in identical anatomical regions (sulcal depths and brainstem) with comparable spatial extents. Divergence emerges only in minimally stretchable (e) and non-stretchable (f) designs, where stress patterns expand into adjacent cortical folds, perisulcal regions, and the brainstem–cervical junction. This delayed differentiation aligns with the exponential growth in stress peak values shown temporally in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.

The progression follows the viscoelastic stress integral (Equation (2)), where stiffer straps progressively limit energy dissipation through elongation. Highly stretchable to semi-non-stretchable strap configurations, Figure 11a–d, absorb 92–58% of impact energy via strap deformation (per Table 1 residuals), delaying force transmission to neuroanatomical structures. Beyond this threshold, as shown in Figure 11e,f, the diminished strap compliance (<5% elongation) eliminates protective phase lag, enabling the undampened transmission of kinetic energy to the skull base. The resultant inertial forces amplify stress rates through multiplicative coupling in the hydrostatic–viscous stress tensor (Equation (6)), driving exponential peak growth despite near-identical spatial stress patterns at early stiffness levels.

In other words, the apparent paradox arises from the interplay between viscoelastic stress relaxation in brain tissue (Equation (2)) and the strain rate dependence of strap materials. Below the critical stiffness threshold (configurations a–d), strap elongation introduces a phase lag between impact energy transmission and tissue stress accumulation. While peak stress values escalate exponentially with Young’s modulus (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9), their spatial distribution remains superficially similar in Figure 11a–d due to the following factors.

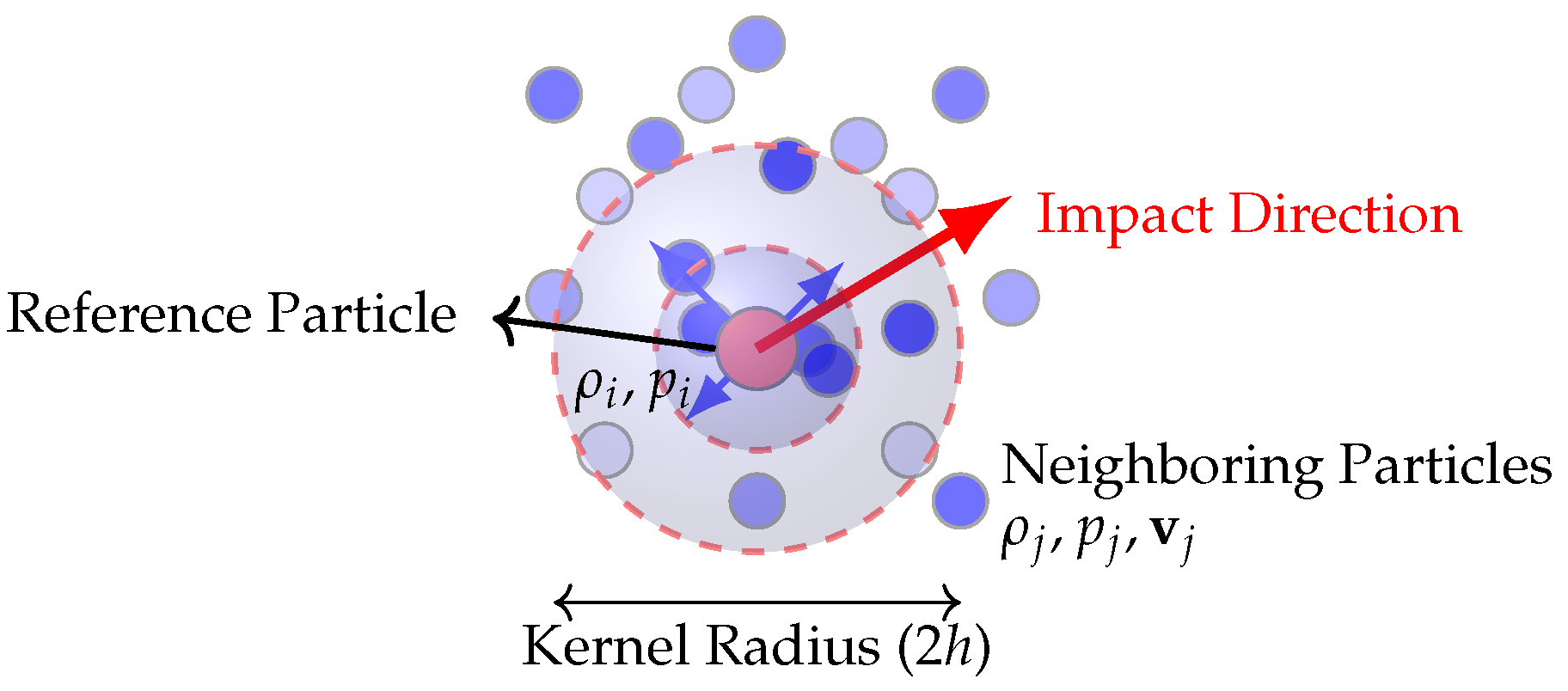
The sulcal and brainstem regions act as inherent stress concentrators due to anatomical curvature and tissue interfaces. At lower stiffness (a–d), strap elongation delays force transmission, allowing CSF redistribution (via SPH dynamics, Equation (5)) to homogenize stress spatially at the given timepoint (Figure 11: end of impact), even as temporal peaks escalate. The hereditary integral (Equation (2)) dictates that stress accumulates proportionally to the duration of applied strain. Stretchable straps (a–d) reduce strain rates via elongation, allowing viscous dissipation (i.e., the $\mu$ term in Equation (6)) to blunt peak stress magnitudes at the instant visualized in Figure 11.

Once straps exceed the viscoelastic compensation threshold (e–f), undampened inertial forces $F=m·a$ from Equation (4) directly shear CSF–brain interfaces. These forces exceed the SPH particle coupling strength (Equation (1)), generating new stress concentrations in deeper structures, Figure 11e,f, as the energy propagates unhindered. Thus, exponential stress growth becomes spatially observable only when strap stiffness nullifies both elongation $\Delta L\to 0$ and viscous damping $\mu {\displaystyle \frac{\partial v}{\partial x}}\to \infty$ in Equation (6).

4. Discussion

The findings from this study reveal a nuanced relationship between chinstrap stiffness and helmet performance during impact. Both extremes, i.e., too stretchable and too non-stretchable, pose significant risks. Highly stretchable chinstraps, while effective in absorbing energy through elongation, may allow excessive helmet displacement, reducing their ability to maintain proper alignment with the skull and potentially increasing the risk of rotational injuries. On the other hand, non-stretchable chinstraps, though they ensure helmet stability, transmit undampened forces directly to the skull base, leading to higher intracranial stress concentrations and a greater likelihood of traumatic brain injury. However, these results also highlight a critical intermediate range of stiffness that introduces a unique hazard. Semi-non-stretchable configurations, which fall between these extremes, create a mechanical conflict: they are stiff enough to partially decouple the chin guard from the mandible, allowing the guard to slide laterally across the jaw, yet not elastic enough to absorb significant energy through strap elongation. This partial decoupling reduces the effective contact area between the chin guard and the jaw, leading to localized stress concentrations at bony interfaces rather than distributing forces evenly through soft tissues. This instability mechanism explains why the semi-non-stretchable configuration exhibits the largest angular displacement ($\theta$ = 45.13°) and the highest residual stress (45.96%), making it a clear outlier in this dataset. This phenomenon underscores the importance of balancing stiffness and elasticity in chinstrap design to avoid detrimental intermediate behaviors that can compromise helmet stability and increase injury risk.

Notably, Figure 11 reinforces these conclusions by demonstrating how stress propagation evolves across designs: all configurations localized peak stresses in sulcal and brainstem regions (i.e., key sites for shear-induced injuries) but stiffer straps (minimally and non-stretchable) exhibited expanded stress patterns into adjacent cortical folds and deeper cranial base structures. This spatial divergence aligns with the temporal escalation of peak stresses (Figure 9), showing that increased stiffness not only amplifies stress magnitude but also distributes damaging forces to broader neuroanatomical regions when energy dissipation through strap elongation is compromised.

This study contributes to understanding the biomechanical impact of chinstrap design on helmet performance during high-velocity impacts, leveraging advanced computational modeling techniques such as SPH and FSI. One of the key strengths of this research is the use of GPU, which significantly reduced computational time and allowed for the analysis of complex scenarios that would have been infeasible with traditional methods. The study’s focus on chinstrap stiffness as a critical factor in helmet design addresses a notable gap in the literature, providing new insights into how different chinstrap materials influence intracranial stress distribution. Furthermore, the computational model was validated against previous studies, including cadaveric data [29], which enhances the credibility of the findings. This validation ensures that the model accurately represents real-world biomechanical interactions, even though the validation did not include helmets.

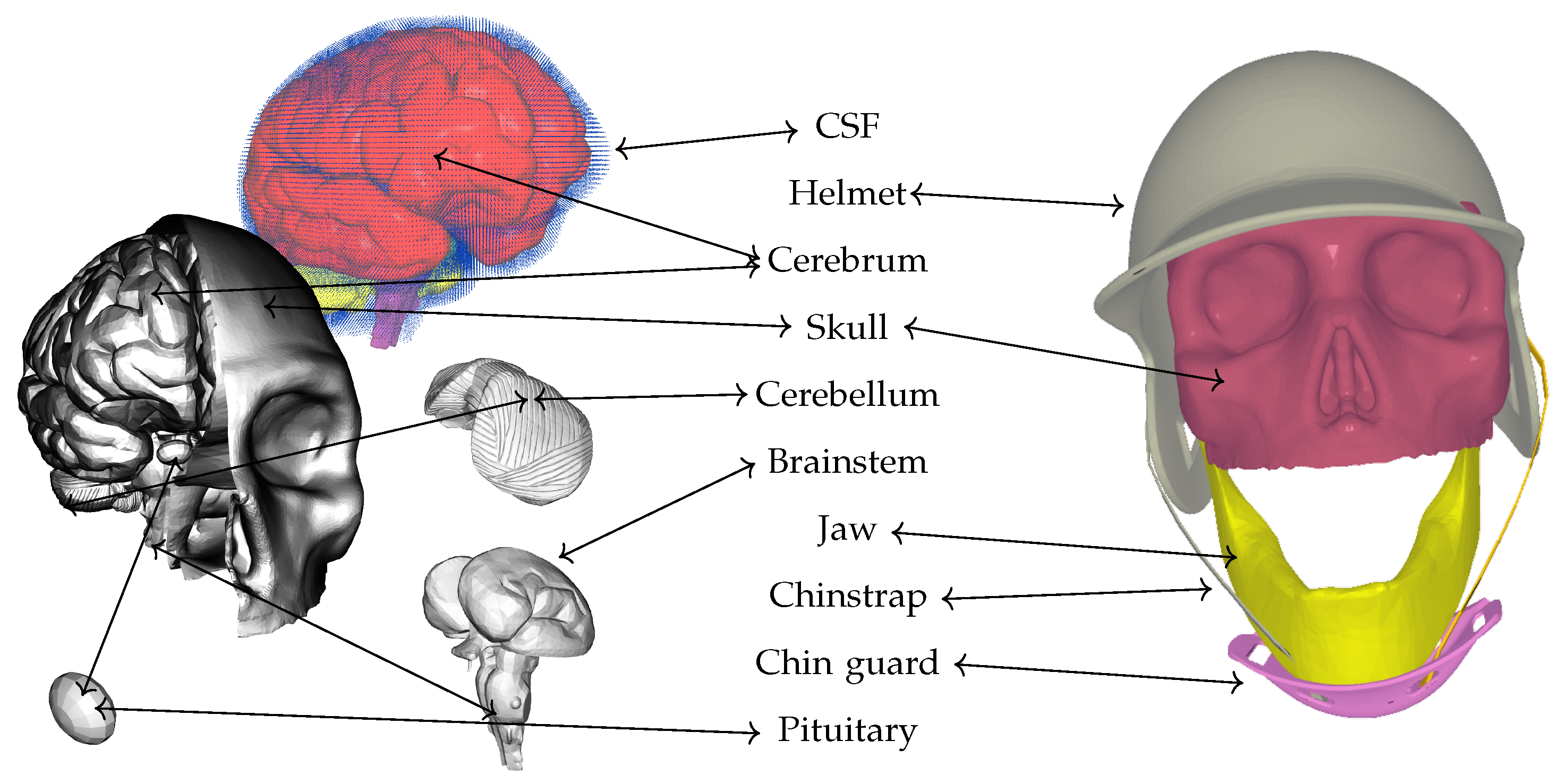
However, the study has several limitations that warrant consideration. One significant limitation is the anatomical simplification inherent in the computational model, specifically the omission of the skin, hair, and meningeal layers (including the dura mater, arachnoid mater, and pia mater). These tissues possess distinct viscoelastic and damping properties that can absorb and redistribute impact energy before it reaches the skull and intracranial contents. Their exclusion may lead to an overestimation of the stresses transmitted to the brain, as the model does not capture the potential for energy attenuation and shear resistance provided by these layers. In particular, the meninges can play a critical role in modulating the transmission of both linear and rotational forces, and their absence may bias the results toward higher predicted intracranial stresses.

Furthermore, the model is limited to the analysis of linear impact dynamics and does not incorporate rotational kinematics or the resulting shear stresses. Rotational acceleration is a well-established mechanism of traumatic brain injury, particularly in the context of concussion and diffuse axonal injury, as it induces shear strains within neural tissues that are not adequately represented by linear impact models. The absence of rotational dynamics in the simulation may therefore underestimate the risk of injury associated with certain helmet and chinstrap configurations, especially those that permit greater helmet displacement or instability. This simplification could bias the findings by failing to account for the full spectrum of injury mechanisms relevant to real-world impacts, where both linear and rotational forces are typically present. These limitations suggest that the results should be interpreted with caution, as the exclusion of anatomical layers and rotational dynamics may affect the generalizability of the findings. Future studies should aim to incorporate more anatomically complete models and simulate both linear and rotational impact scenarios to provide a more comprehensive assessment of helmet and chinstrap performance.

Nevertheless, it should be noted that the present study is comparative in nature, with chinstrap stiffness as the sole parameter varied across simulations. As such, while the anatomical simplifications and exclusion of rotational dynamics may influence the absolute values of stress and energy transmission reported, these factors are held constant for all chinstrap configurations. Therefore, the relative differences observed between chinstrap stiffness conditions remain valid within the context of the model.

4.1. Comparison with Prior Helmet Studies

The present study’s findings on chinstrap stiffness and its nonlinear effects on brain stress distribution extend and refine the understanding established in prior helmet research across both motorcycle and football contexts. Singleton (2017) demonstrated that motorcycle helmets provide substantial protection against skull fracture and intracranial hemorrhage, but their efficacy varies by injury type, with less protection against concussions, attributed in part to limitations in managing rotational acceleration and force transmission through the helmet structure [18]. Our results parallel these observations by showing that non-stretchable chinstraps, while maximizing helmet stability, transmit undampened forces directly to the skull base, potentially amplifying stress in vulnerable neurovascular regions, much like the limitations observed in rigid motorcycle helmet designs. Conversely, highly flexible straps in our study dissipate energy but risk helmet instability, echoing the trade-offs in helmet retention and energy management highlighted in the motorcycle helmet literature.

In the context of football helmet research, Bustamante et al. (2019) and subsequent FE modeling studies (Corrales et al., 2020) have emphasized the importance of validating helmet subcomponents (shell, padding, facemask, and straps) and quantifying their contributions to energy absorption and head kinematics [25,46]. These works established that the strap system can share a significant portion of impact energy, especially in facemask-involved impacts, but did not systematically explore how varying strap stiffness modulates intracranial stress or instability. Our study advances this line of inquiry by employing a high-fidelity computational model that integrates neuroanatomical detail and FSI, directly quantifying how chinstrap stiffness governs not only energy dissipation but also the emergence of hazardous instability regimes at intermediate stiffness. Unlike previous football helmet FE studies, which primarily assessed linear and angular kinematics or component-level strain energy, our work reveals a critical nonlinear relationship between strap material properties and neuroprotection, identifying an “instability zone” where partial coupling paradoxically heightens injury risk. This mechanistic insight bridges the gap between epidemiological findings in motorcycle helmet studies and component-level analyses in football helmet research, providing actionable design criteria for optimizing both energy dissipation and helmet stability. Thus, our results contribute a new dimension to helmet safety science by demonstrating that optimal chinstrap design must avoid not only extremes of flexibility and rigidity but also intermediate regimes that introduce dynamic instabilities, which is an aspect not previously addressed in the helmet literature.

4.2. Translational Impact and Actionable Design Guidelines for Industry Standards

The results of this study might have implications for the development and revision of helmet safety standards in professional sports [47,48]. Our findings indicate that both highly flexible and non-stretchable chinstrap designs present distinct risks, while intermediate stiffness introduces hazardous instability. Based on these insights, we propose the following actionable design guidelines for industry adoption.

Chinstrap materials with Young’s modulus values that fall within the identified “instability zone” (as characterized by excessive angular displacement and stress outliers) should be excluded from approved helmet designs. Industry standards should specify minimum and maximum allowable stiffness values, with the explicit exclusion of intermediate ranges that promote partial decoupling and stress concentration. Helmets should incorporate chinstraps that are sufficiently elastic to absorb impact energy through controlled elongation but rigid enough to maintain helmet alignment and prevent lateral sliding of the chin guard. Material testing protocols should be updated to include dynamic elongation and force transmission metrics, not just static load resistance. Current certification tests should be expanded to include dynamic impact scenarios that replicate real-world pitch velocities and directions, with the measurement of both linear and rotational accelerations at the helmet and chinstrap interfaces. Industry standards should encourage or require the use of instrumented helmets or dummy headforms equipped with high-speed sensors to empirically validate computational predictions of stress distribution and helmet stability [49].

5. Conclusions

This study establishes that chinstrap stiffness influences helmet safety during impacts, with both overly elastic and rigid designs elevating injury risks. Highly flexible straps mitigate cranial forces through energy dissipation but compromise helmet stability, while non-stretchable variants transmit undampened stress directly to vulnerable skull base regions. Critically, intermediate stiffness introduces another kind of instability, where partial coupling between the chinstrap and jaw concentrates damaging forces at bony interfaces instead of safely redistributing energy. Balancing elasticity and rigidity emerges as essential for optimizing helmet performance, preventing destabilizing force transmission pathways that exacerbate brain injury risks.

The study demonstrates that chinstrap stiffness critically mediates the trade-off between energy dissipation and helmet stability during impacts. As illustrated in Figure 12, highly flexible straps reduce cranial forces via viscoelastic deformation but risk excessive displacement, while non-stretchable designs eliminate protective dampening, channeling stress into the skull base. Intermediate configurations introduce hazardous partial decoupling, where localized sliding concentrates forces at bony interfaces. These findings underscore the need for material engineering that balances elasticity (to absorb energy) and rigidity (to maintain alignment), thereby mitigating shear-induced brain injuries without destabilizing protective gear. Optimized designs must avoid the instability regime shown in Figure 12 (intermediate stiffness), which paradoxically amplifies injury risks despite partial energy absorption.

While this study provides some insights into how chinstrap stiffness affects helmet safety, several limitations must be considered. The computational model omits the skin and meningeal layers, which in reality help absorb impact energy and may lower stress reaching the brain. The analysis also focuses only on linear impacts, not accounting for rotational accelerations and shear stresses that are major contributors to concussion and diffuse axonal injury. These simplifications may lead to higher predicted intracranial stresses and do not fully reflect the complexity of real-world impacts. Future work should use more anatomically complete models and include both linear and rotational impacts to improve the relevance of computational results. However, the comparative approach ensures that any systematic bias introduced by model simplifications affects all simulations equally, allowing for the relevant assessment of how changes in chinstrap stiffness alone influence intracranial stress distribution and helmet performance.