Creep–Fatigue Behavior and Life Prediction of Medium-Si-Mo Ductile Iron
Abstract
1. Introduction
2. Experimental Materials and Methods
3. Results and Analysis
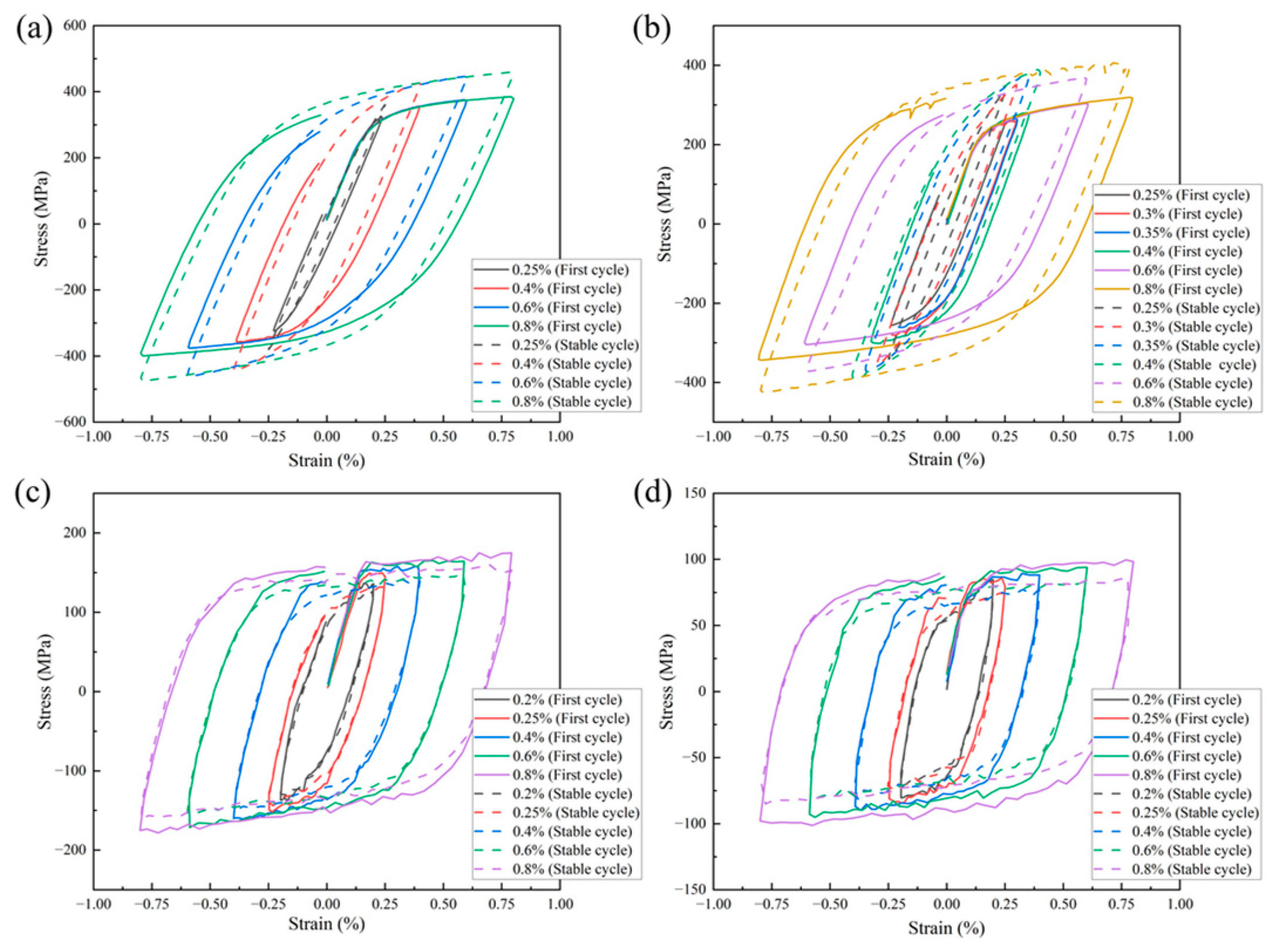
3.1. Low-Cycle Fatigue Properties
3.1.1. Stress–Strain Characteristics Under Cyclic Loading
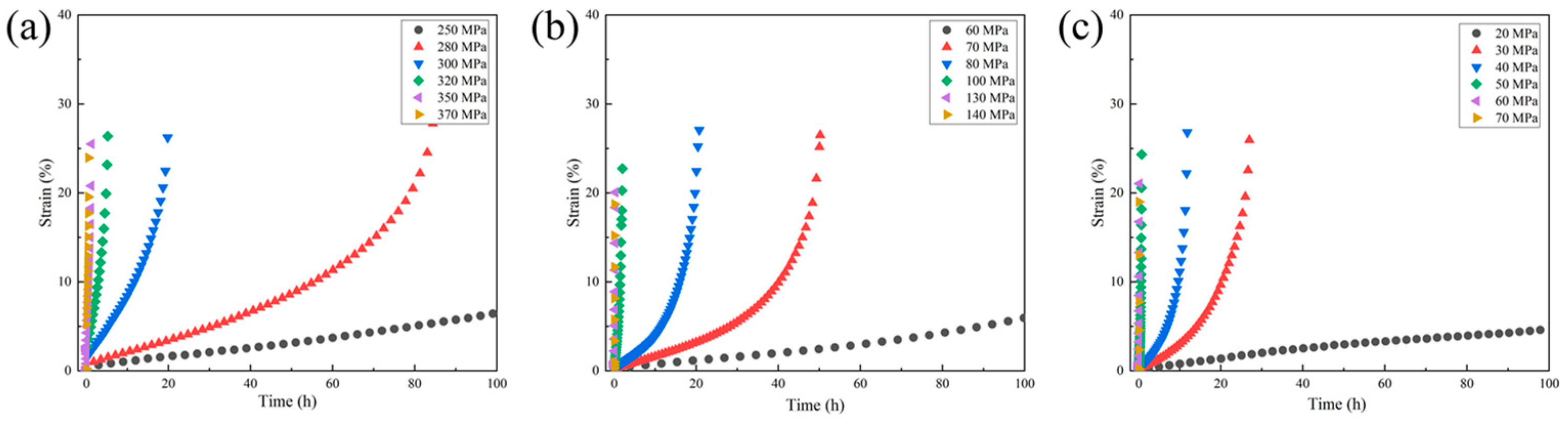
3.1.2. Characterization of Low−Cycle Life
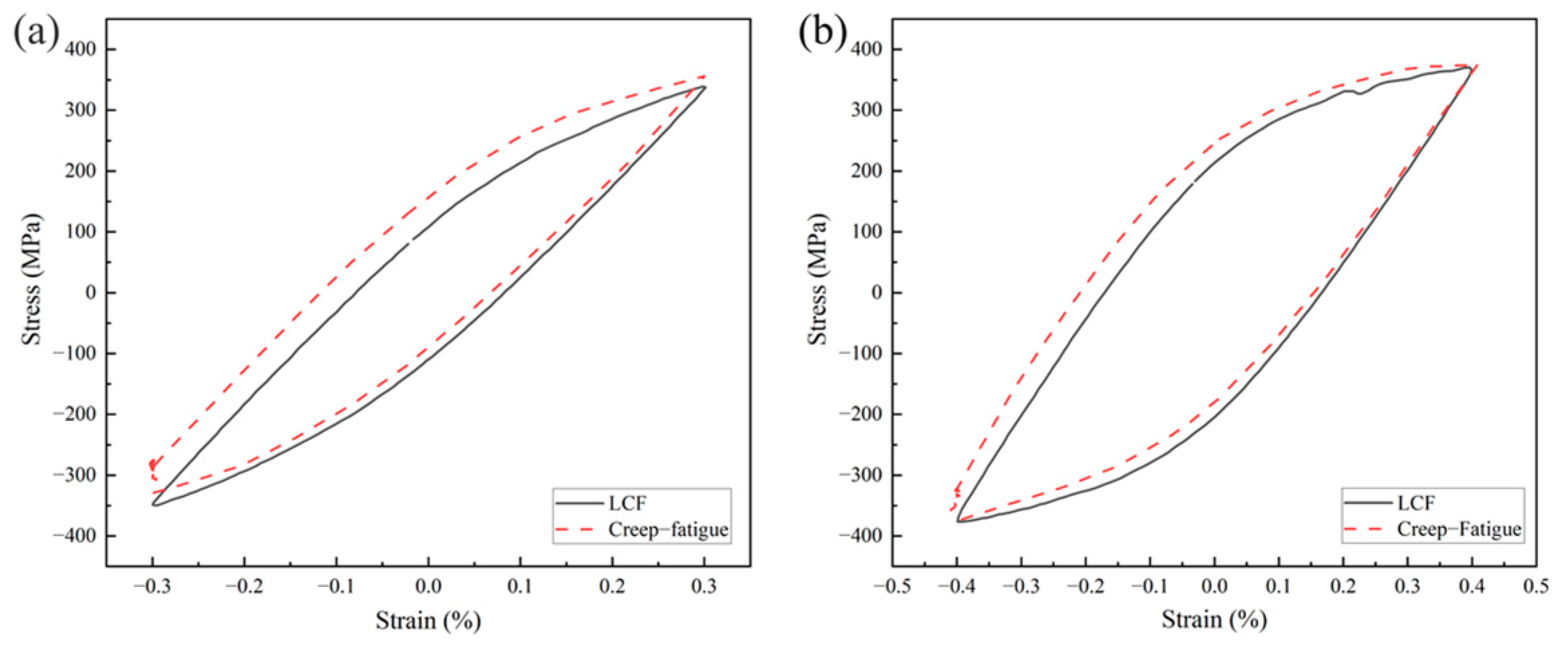
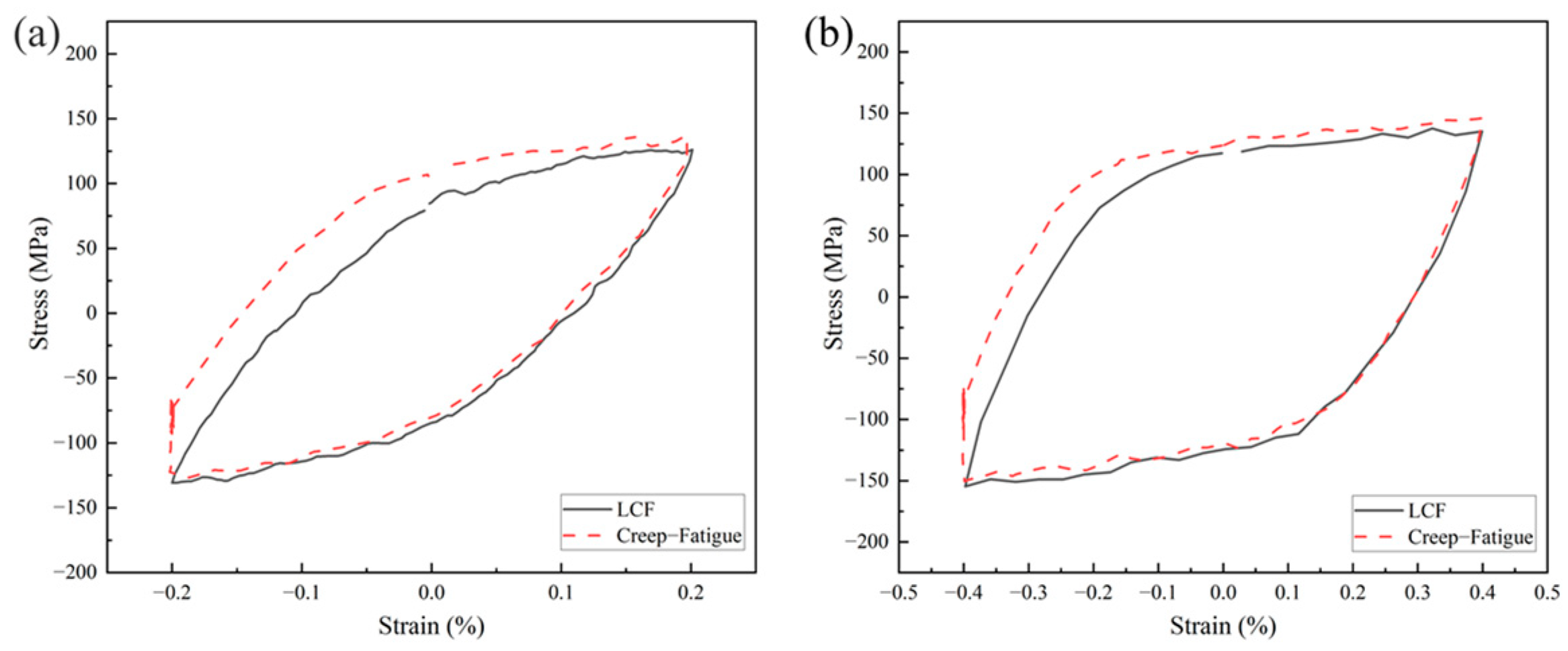
3.2. Creep–Fatigue Interaction Behavior
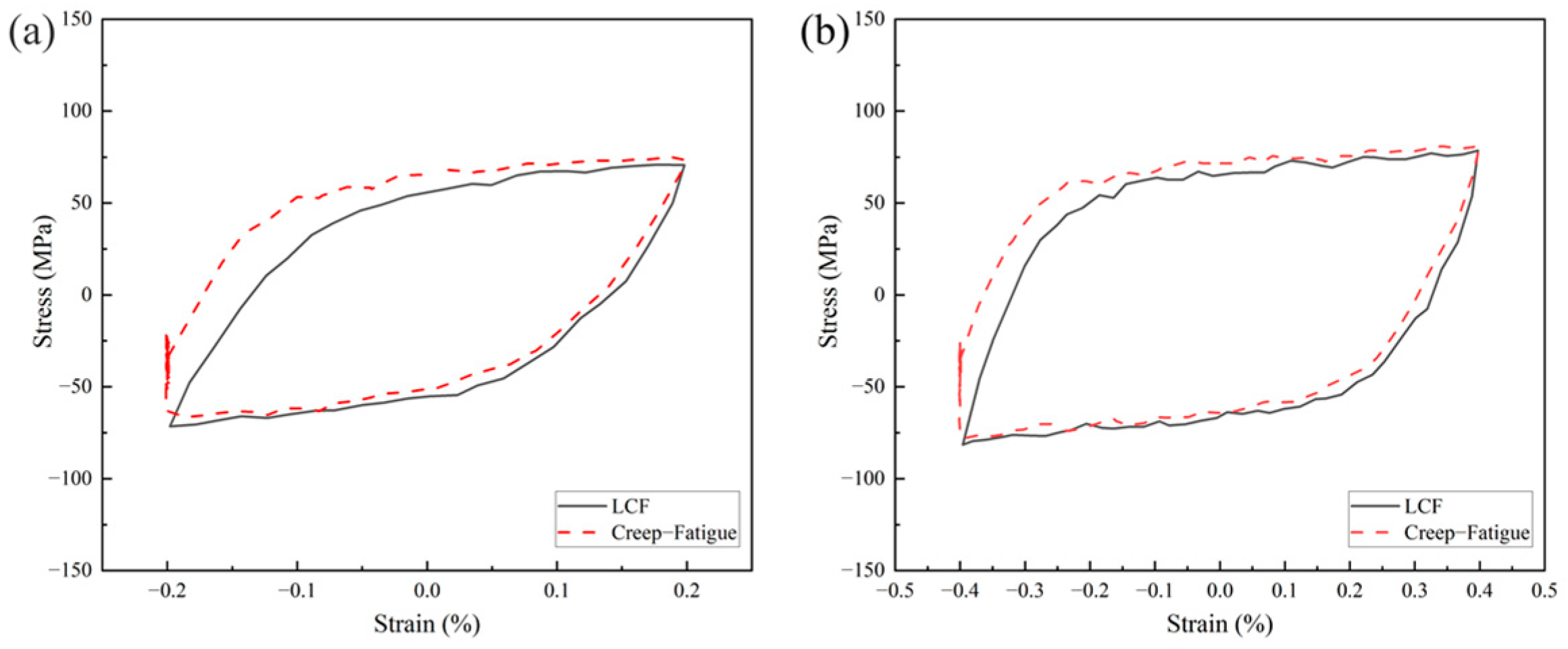
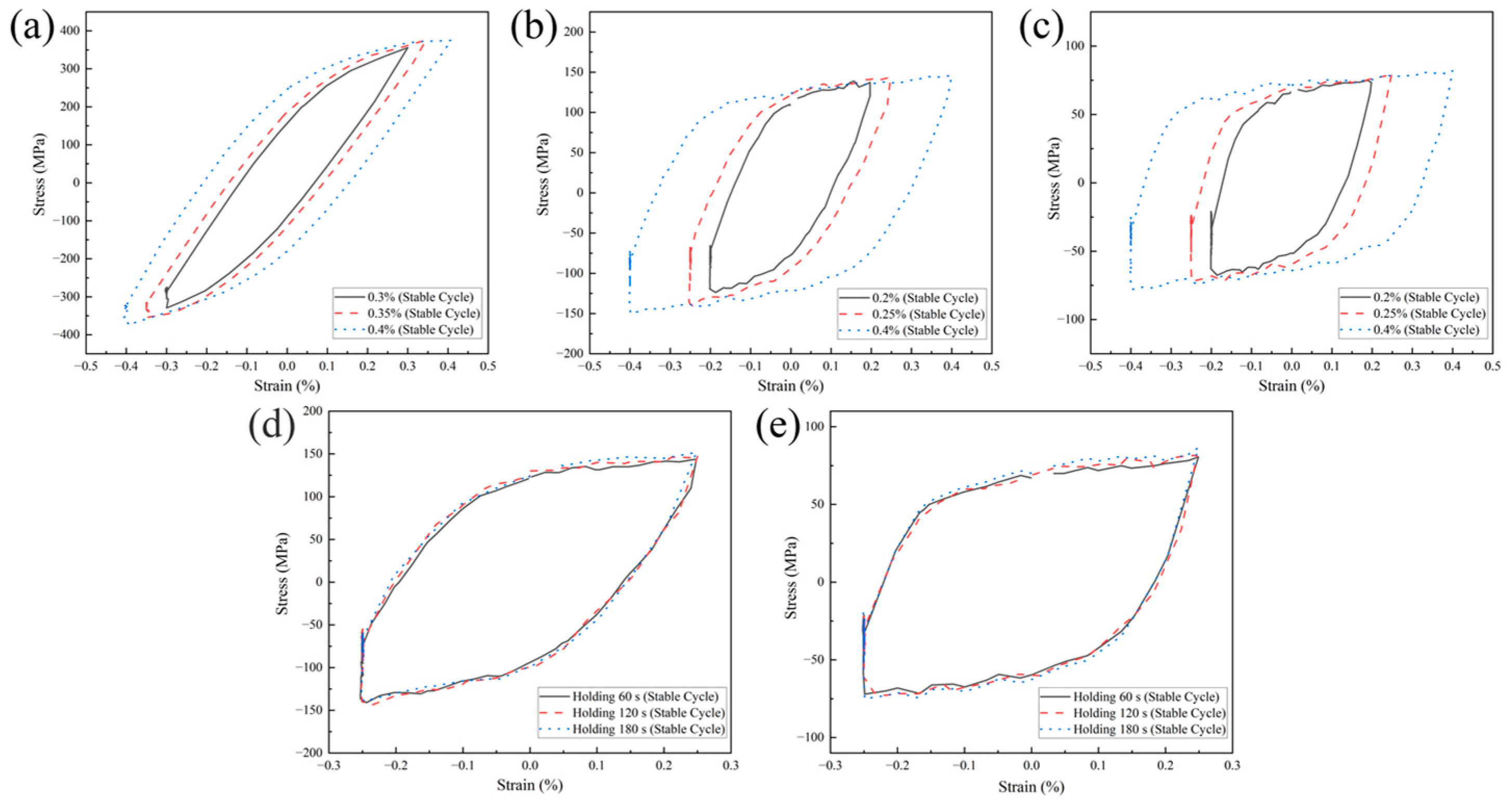
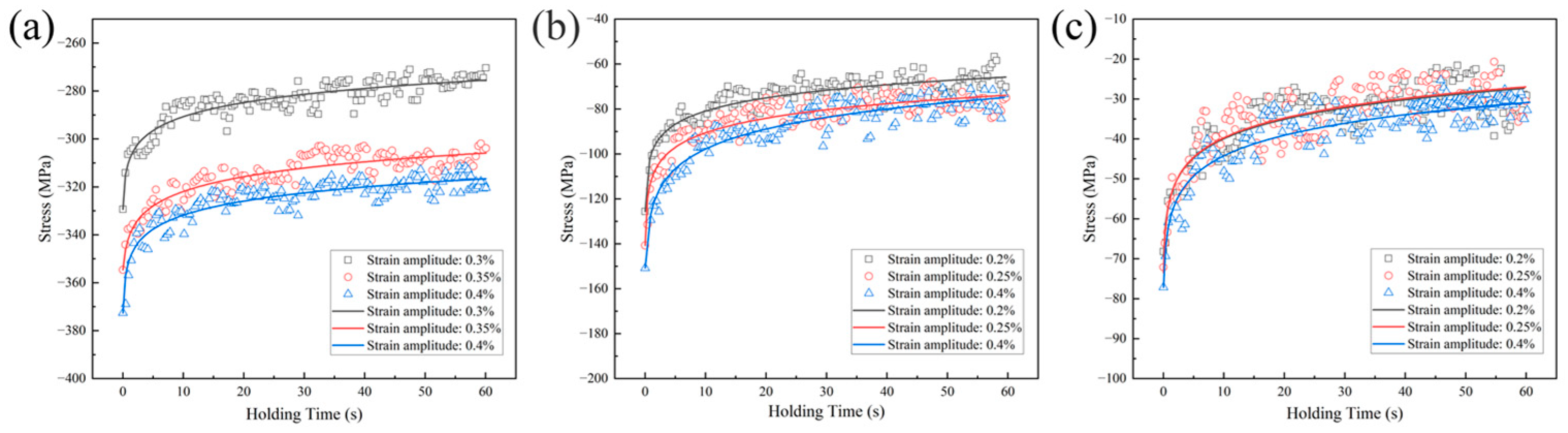
3.2.1. Stabilized Cyclic Response Characteristics Under Creep–Fatigue Interaction
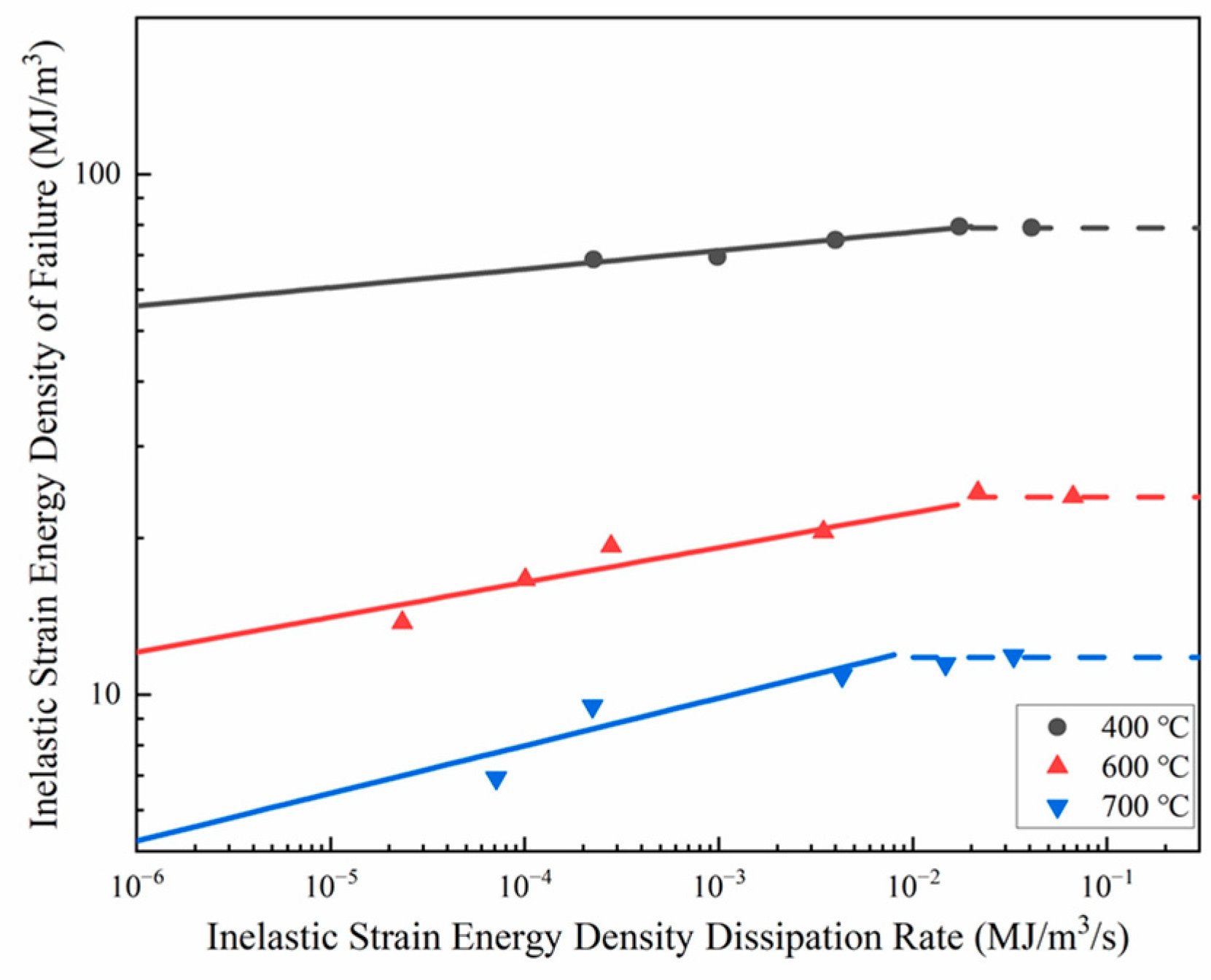
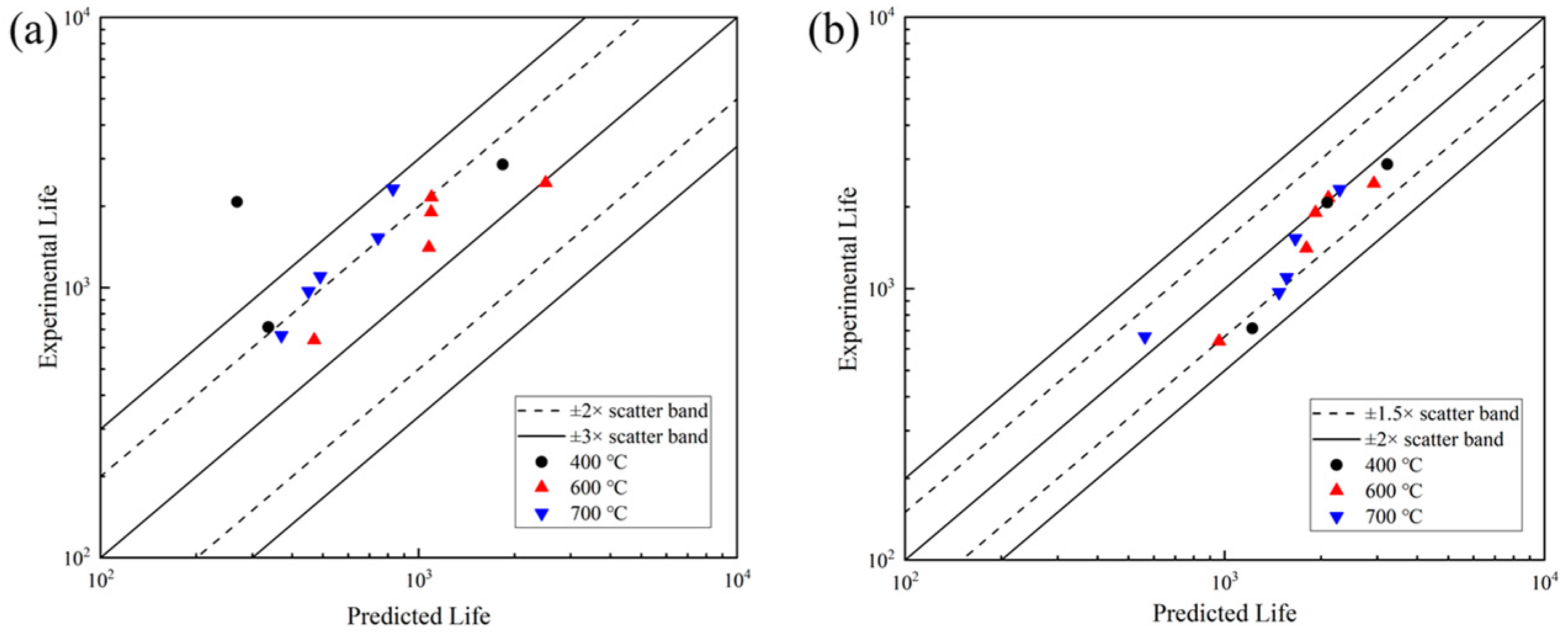
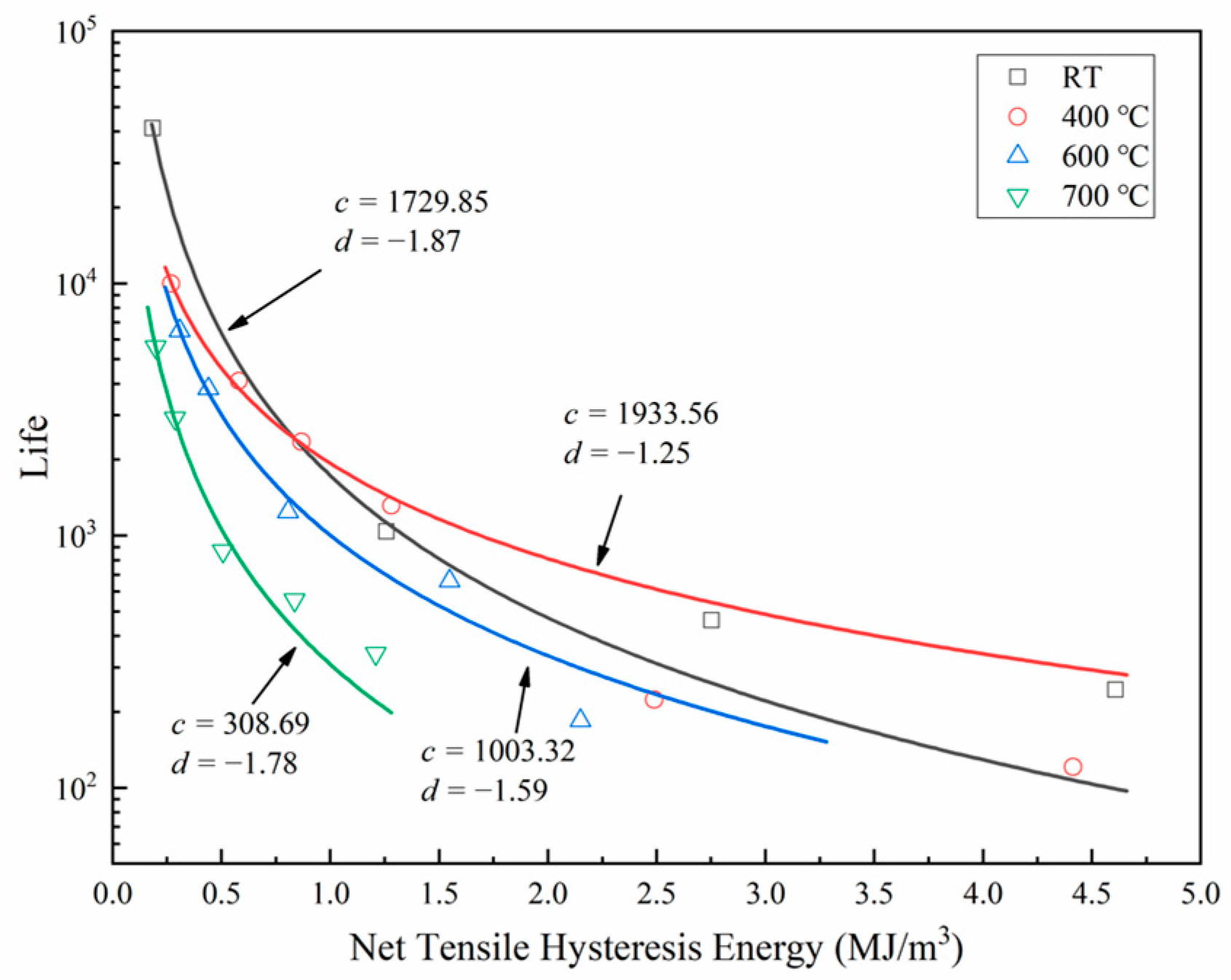
3.2.2. Investigation of Creep–Fatigue Life Prediction Models
4. Conclusions
- In low-cycle fatigue tests, medium-silicon molybdenum ductile iron exhibits cyclic hardening at room temperature and intermediate temperatures (400 °C), while significant cyclic softening occurs at elevated temperatures. Additionally, the hysteresis loops demonstrate nearly symmetric tension–compression behavior, and this material’s plastic deformation capability is enhanced with increasing temperatures.
- Under intermediate- and high-temperature conditions with dwell periods, the creep–fatigue cycles maintain the softening/hardening characteristics observed in LCF conditions. The stable cyclic yield radius and elastic modulus during loading–unloading phases remain essentially unchanged, indicating minimal alterations in the hysteresis loop shape. However, creep effects cause a slight upward shift in the yield center during a cyclic response.
- In creep–fatigue interaction cycles, strain amplitude variations do not significantly alter the overall shape of fatigue hysteresis loops but result in a more pronounced upward shift in the yield center at lower strain amplitudes compared to higher ones. At elevated temperatures, since stress relaxation primarily occurs during the initial dwell period, the stress values at the ends of the dwell times showed minimal differences across the three tested dwell periods.
- Accurate characterization of damage caused by stress relaxation during dwell periods is crucial for creep damage calculation. While the TF model showed discrepancies with the experimental results, the combined T-SEDE model and Ostergren method provided excellent creep–fatigue life predictions, with only 2 out of 13 data points falling outside the 1.5× scatter band.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, X.; Quan, G.; MacNeil, R.; Zhang, Z.; Sloss, C. Failure mechanisms and damage model of ductile cast iron under low-cycle fatigue conditions. Metall. Mater. Trans. A 2014, 45, 5085–5097. [Google Scholar] [CrossRef]
- Xiang, S.; Jonsson, S.; Hedström, P.; Zhu, B.; Odqvist, J. Influence of ferritic nitrocarburizing on the high-temperature corrosion-fatigue properties of the Si-Mo-Al cast iron SiMo1000. Int. J. Fatigue 2021, 143, 105984. [Google Scholar] [CrossRef]
- Szmytka, F.; Michaud, P.; Rémy, L.; Köster, A. Thermo-mechanical fatigue resistance characterization and materials ranking from heat-flux-controlled tests. Application to cast-irons for automotive exhaust part. Int. J. Fatigue 2013, 55, 136–146. [Google Scholar] [CrossRef]
- Ram, N.; Gautam, V. Prediction of effect of alloying elements on properties of ferritic grade Si-Mo ductile cast iron using regression analysis. Mater. Today: Proc. 2022, 62, 3855–3859. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, Z. A mechanism-based approach from low cycle fatigue to thermomechanical fatigue life prediction. J. Eng. Gas Turbines Power 2016, 138, 072503. [Google Scholar] [CrossRef]
- Di Cocco, V.; Iacoviello, F.; Cavallini, M. Damaging micromechanisms characterization of a ferritic ductile cast iron. Eng. Fract. Mech. 2010, 77, 2016–2023. [Google Scholar] [CrossRef]
- Norman, V.; Skoglund, P.; Leidermark, D.; Moverare, J. Damage mechanisms in silicon-molybdenum cast irons subjected to thermo-mechanical fatigue. Int. J. Fatigue 2017, 99, 258–265. [Google Scholar] [CrossRef]
- Seifert, T.; Riedel, H. Mechanism-based thermomechanical fatigue life prediction of cast iron. Part I: Models. Int. J. Fatigue 2010, 32, 1358–1367. [Google Scholar] [CrossRef]
- Black, B.; Burger, G.; Logan, R.; Perrin, R.; Gundlach, R. Microstructure and dimensional stability in Si-Mo ductile irons for elevated temperature applications. SAE Trans. 2002, 111, 976–991. Available online: https://www.jstor.org/stable/44718728 (accessed on 11 March 2025).
- Bartošák, M.; Novotný, C.; Španiel, M.; Doubrava, K. Life assessment of SiMo 4.06 cast iron under LCF and TMF loading conditions. Mater. High Temp. 2019, 36, 285–295. [Google Scholar] [CrossRef]
- Lekakh, S.N.; Buchely, M.; O’Malley, R.; Godlewski, L.; Li, M. Thermo-cycling fatigue of SiMo ductile iron using a modified thermo-mechanical test. Int. J. Fatigue 2021, 148, 106218. [Google Scholar] [CrossRef]
- Wu, Q.; Tan, B.; Pang, J.; Shi, F.; Jiang, A.; Zou, C.; Zhang, Y.; Li, S.; Zhang, Y.; Li, X.; et al. Low-Cycle Fatigue Damage Mechanism and Life Prediction of High-Strength Compacted Graphite Cast Iron at Different Temperatures. Materials 2024, 17, 4266. [Google Scholar] [CrossRef]
- Collini, L.; Pirondi, A. Microstructural, multilevel simulation of notch effect in ferritic ductile cast iron under low cycle fatigue. Int. J. Fatigue 2022, 162, 106993. [Google Scholar] [CrossRef]
- Kim, Y.J.; Jang, H.; Oh, Y.J. High-temperature low-cycle fatigue property of heat-resistant ductile-cast irons. Metall. Mater. Trans. A 2009, 40, 2087–2097. [Google Scholar] [CrossRef]
- Charkaluk, E.; Constantinescu, A. An energetic approach in thermomechanical fatigue for silicon molybdenum cast iron. Mater. High Temp. 2000, 17, 373–380. [Google Scholar] [CrossRef]
- Pierce, D.; Haynes, A.; Hughes, J.; Graves, R.; Maziasz, P.; Muralidharan, G.; Shyam, A.; Wang, B.; England, R.; Daniel, C. High temperature materials for heavy duty diesel engines: Historical and future trends. Prog. Mater. Sci. 2019, 103, 109–179. [Google Scholar] [CrossRef]
- Ibrahim, M.M.; Nofal, A.; Mourad, M.M. Microstructure and Hot Oxidation Resistance of SiMo Ductile Cast Irons Containing Si-Mo-Al. Metall. Mater. Trans. B 2017, 48, 1149–1157. [Google Scholar] [CrossRef]
- Öberg, C.; Zhu, B.; Jonsson, S. Creep, strain and oxidation damage in the ferritic ductile cast iron SiMo51 at 700 °C. Mater. High Temp. 2020, 37, 178–195. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, Z.; Lian, Z.; Yu, H. Thermal Fatigue Behavior and Cracking Characteristics of High Si-Mo Nodular Cast Iron for Exhaust Manifolds. J. Iron Steel Res. Int. 2013, 20, 52–57. [Google Scholar] [CrossRef]
- Ostash, O.P.; Panasyuk, V.V.; Andreiko, I.M.; Chepil’, R.V.; Kulyk, V.V.; Vira, V.V. Methods for the construction of the diagrams of fatigue crack-growth rate of materials. Mater. Sci. 2007, 43, 479–491. [Google Scholar] [CrossRef]
- GB/T 15248-2008; The Test Mehod for Axial Loading Constant-Amplitude Low-Cycle Fatigue of Metallic Materials. Standards Press of China: Beijing, China, 2008.
- Li, Z.; Han, J.; Li, W.; Pan, L. Low cycle fatigue behavior of Cr–Mo–V low alloy steel used for railway brake discs. Mater. Des. (1980–2015) 2014, 56, 146–157. [Google Scholar] [CrossRef]
- Okorokov, V.; Gorash, Y.; Mackenzie, D.; van Rijswick, R. New formulation of nonlinear kinematic hardening model, Part II: Cyclic hardening/softening and ratcheting. Int. J. Plast. 2019, 122, 244–267. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, W.; Li, S.; Wang, X. High temperature low cycle fatigue and creep-fatigue behavior of a casting Al-9Si-CuMg alloy used for cylinder heads. Mater. Sci. Eng. A 2017, 700, 397–405. [Google Scholar] [CrossRef]
- Mikkola, E.; Marquis, G.; Lehto, P.; Remes, H.; Hänninen, H. Material characterization of high-frequency mechanical impact (HFMI)-treated high-strength steel. Mater. Des. 2016, 89, 205–214. [Google Scholar] [CrossRef]
- Sornette, D.; Magnin, T.; Brechet, Y. The physical origin of the Coffin-Manson law in low-cycle fatigue. Europhys. Lett. 1992, 20, 433. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, X.; Zhang, X.; Tu, S.; Gong, J.; Zhang, C. A generalized strain energy density exhaustion model allowing for compressive hold effect. Int. J. Fatigue 2017, 104, 61–71. [Google Scholar] [CrossRef]
- Zhang, X.; Gong, J.; Xuan, F. A deep learning based life prediction method for components under creep, fatigue and creep-fatigue conditions. Int. J. Fatigue 2021, 148, 106236. [Google Scholar] [CrossRef]
- Douzian, G.; Muránsky, O.; Kruzic, J.J.; Wright, R.N.; Payten, W. Assessment of modelling methodologies for prediction of high-temperature creep-fatigue behaviour of Alloy 617. Int. J. Press. Vessel. Pip. 2020, 187, 104150. [Google Scholar] [CrossRef]
- Takahashi, Y.; Dogan, B.; Gandy, D. Systematic evaluation of creep-fatigue life prediction methods for various alloys. J. Press. Vessel Technol. 2013, 135, 061204. [Google Scholar] [CrossRef]
- Takahashi, Y. Effect of cyclic loading on subsequent creep behaviour and its implications in creep–fatigue life assessment. Mater. High Temp. 2015, 32, 492–501. [Google Scholar] [CrossRef]
- Robinson, E.L. Effect of temperature variation on the long-time rupture strength of steels. Trans. Am. Soc. Mech. Eng. 1952, 74, 777–780. [Google Scholar] [CrossRef]
- Kim, K.C.; Ma, Y.W.; Kong, B.O.; Kim, M.S.; Kang, S.T. Effect of strain rate on low cycle fatigue with hold time in 9Cr rotor steel. Mater. Res. Innov. 2013, 17, 332–336. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X.; Tu, S.; Zhu, S.; Zhang, C. A modified strain energy density exhaustion model for creep–fatigue life prediction. Int. J. Fatigue 2016, 90, 12–22. [Google Scholar] [CrossRef]
- Feltham, P. Stress relaxation in copper and alpha-brasses at low temperatures. J. Inst. Met. 1960, 89, 210–214. [Google Scholar]
- Payten, W.M.; Dean, D.W.; Snowden, K.U. A strain energy density method for the prediction of creep–fatigue damage in high temperature components. Mater. Sci. Eng. A 2010, 527, 1920–1925. [Google Scholar] [CrossRef]
- Gu, H.; Wang, R.; Kun, Z.; Wang, J.; Sun, L.; Li, K.; Liu, Y.; Zhang, X.; Tu, S. System-level creep-fatigue reliability evaluation by engineering damage mechanics incorporating cumulative damage-damage threshold interference. Int. J. Fatigue 2023, 176, 107768. [Google Scholar] [CrossRef]
- Mao, J.; Li, X.; Wang, D.; Zhong, F.; Luo, L.; Bao, S.; Ding, Z. Experimental study on creep-fatigue behaviors of chinese P92 steel with consideration of several important factors. Int. J. Fatigue 2021, 142, 105900. [Google Scholar] [CrossRef]
- Tchankov, D.S.; Vesselinov, K.V. Fatigue life prediction under random loading using total hysteresis energy. Int. J. Press. Vessel. Pip. 1998, 75, 955–960. [Google Scholar] [CrossRef]
- Ostergren, W.J. A damage function and associated failure equations for predicting hold time and frequency effects in elevated temperature, low cycle fatigue. J. Test. Eval. 1976, 4, 327–339. [Google Scholar] [CrossRef]
- Hong, S.G.; Yoon, S.; Lee, S.B. The effect of temperature on low-cycle fatigue behavior of prior cold worked 316L stainless steel. Int. J. Fatigue 2003, 25, 1293–1300. [Google Scholar] [CrossRef]

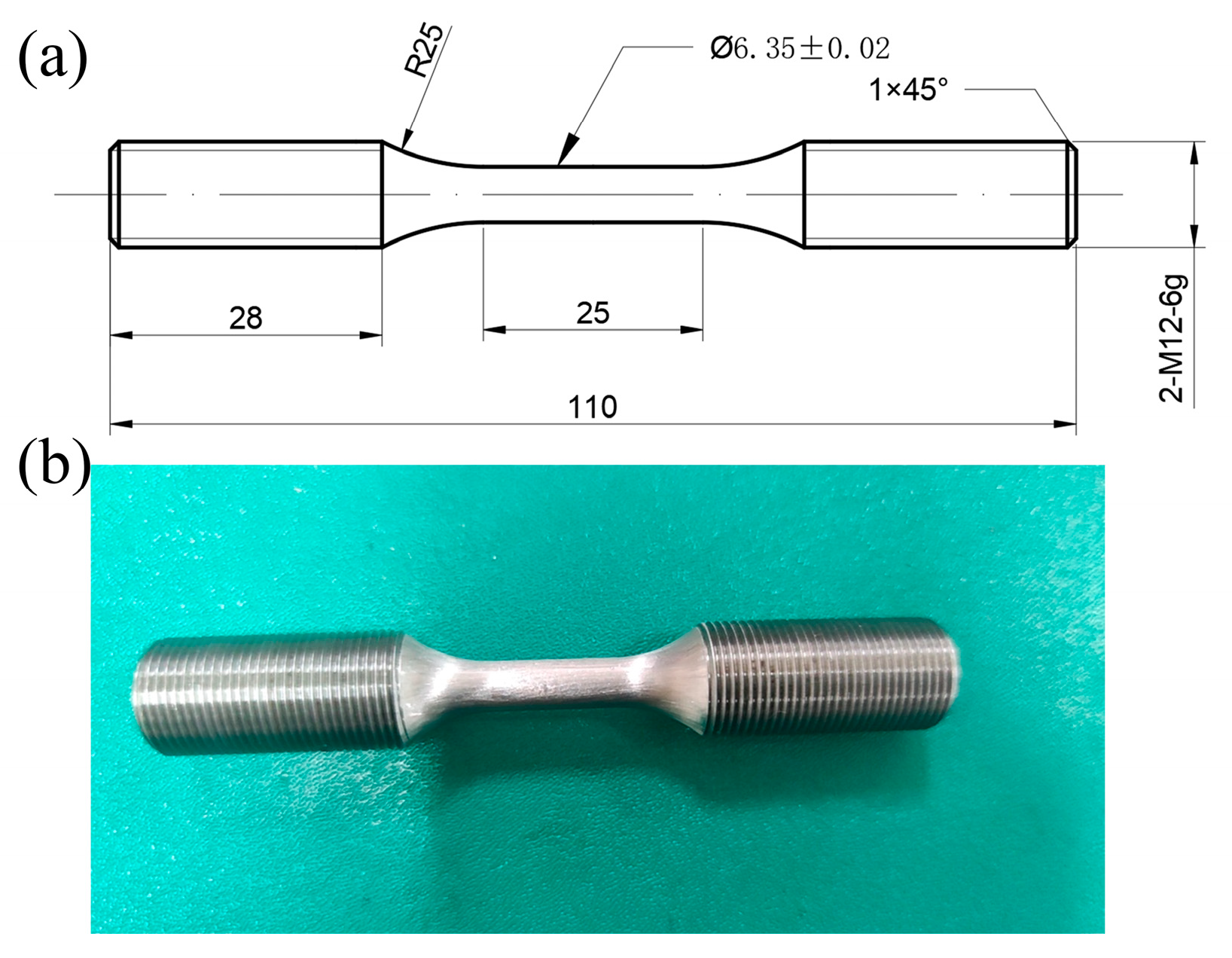




| Element | C | Si | Mn | Mo | P | S | Mg | Re |
|---|---|---|---|---|---|---|---|---|
| Quantity | 3.18 | 4.43 | 0.35 | 0.63 | 0.06 | 0.012 | 0.038 | 0.031 |
| Temperature (°C) | RT | 400 | 600 | 700 |
|---|---|---|---|---|
| (MPa) | 702.966 | 570.588 | 292.889 | 154.947 |
| 0.081 | 0.066 | 0.121 | 0.122 |
| Temperature (°C) | (MPa) | b | c | |
|---|---|---|---|---|
| RT | 664.95 | −0.054 | 0.658 | −0.786 |
| 400 | 540.36 | −0.049 | 0.095 | −0.528 |
| 600 | 299.00 | −0.100 | 0.170 | −0.541 |
| 700 | 99.45 | −0.037 | 0.805 | −0.726 |
| Temperature (°C) | 400 °C | 600 °C | 700 °C |
|---|---|---|---|
| 0.026 | 0.026 | 0.023 | |
| b | 5.57 | 3.57 | 11.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Feng, H.; Ren, P. Creep–Fatigue Behavior and Life Prediction of Medium-Si-Mo Ductile Iron. Appl. Sci. 2025, 15, 5406. https://doi.org/10.3390/app15105406
Liu M, Feng H, Ren P. Creep–Fatigue Behavior and Life Prediction of Medium-Si-Mo Ductile Iron. Applied Sciences. 2025; 15(10):5406. https://doi.org/10.3390/app15105406
Chicago/Turabian StyleLiu, Mucheng, Huihua Feng, and Peirong Ren. 2025. "Creep–Fatigue Behavior and Life Prediction of Medium-Si-Mo Ductile Iron" Applied Sciences 15, no. 10: 5406. https://doi.org/10.3390/app15105406
APA StyleLiu, M., Feng, H., & Ren, P. (2025). Creep–Fatigue Behavior and Life Prediction of Medium-Si-Mo Ductile Iron. Applied Sciences, 15(10), 5406. https://doi.org/10.3390/app15105406








