Investigating the Machining Behavior of the Additively Manufactured Polymer-Based Composite Using Adaptive Neuro-Fuzzy Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Work, Settings, and Workpiece Material
2.2. Experimental Design and Measurements
3. ANFIS-Based Modeling
4. Results and Discussion
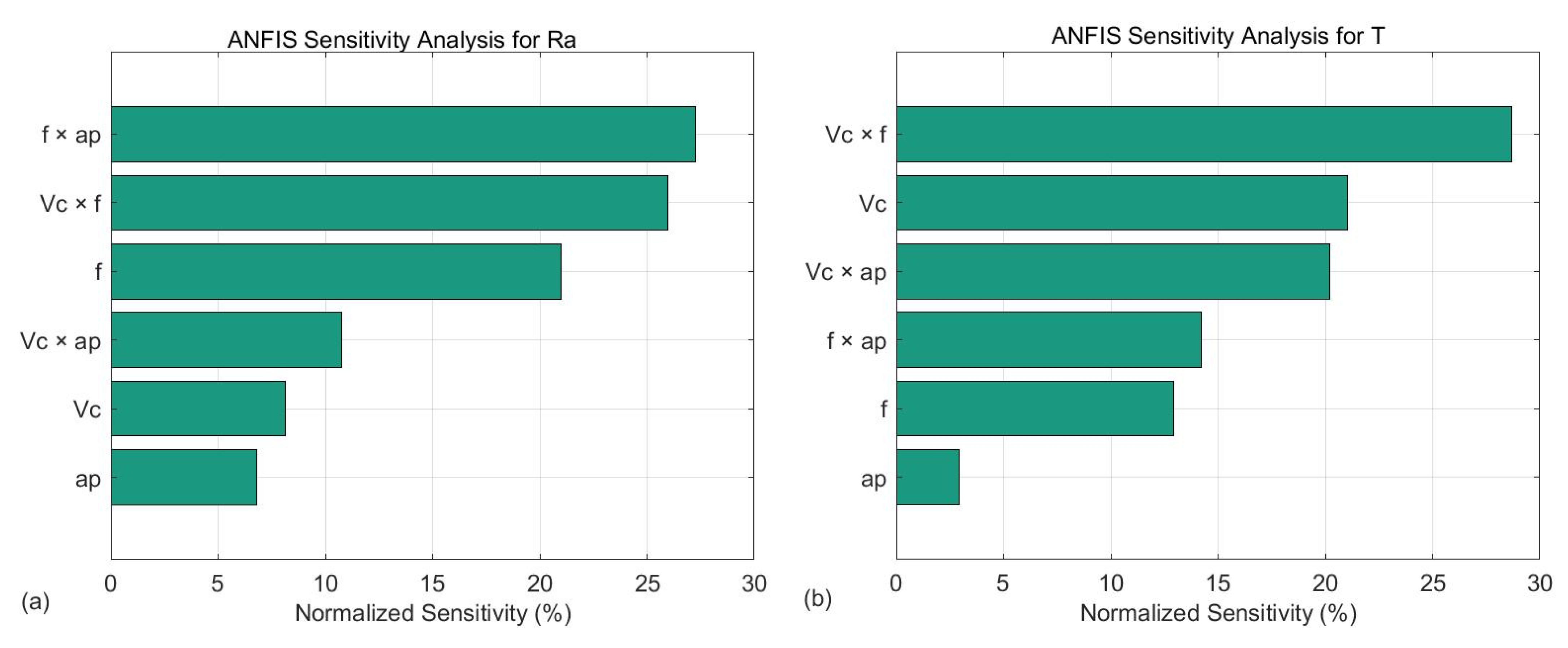
4.1. Investigation of the Inputs’ Influence on the Responses
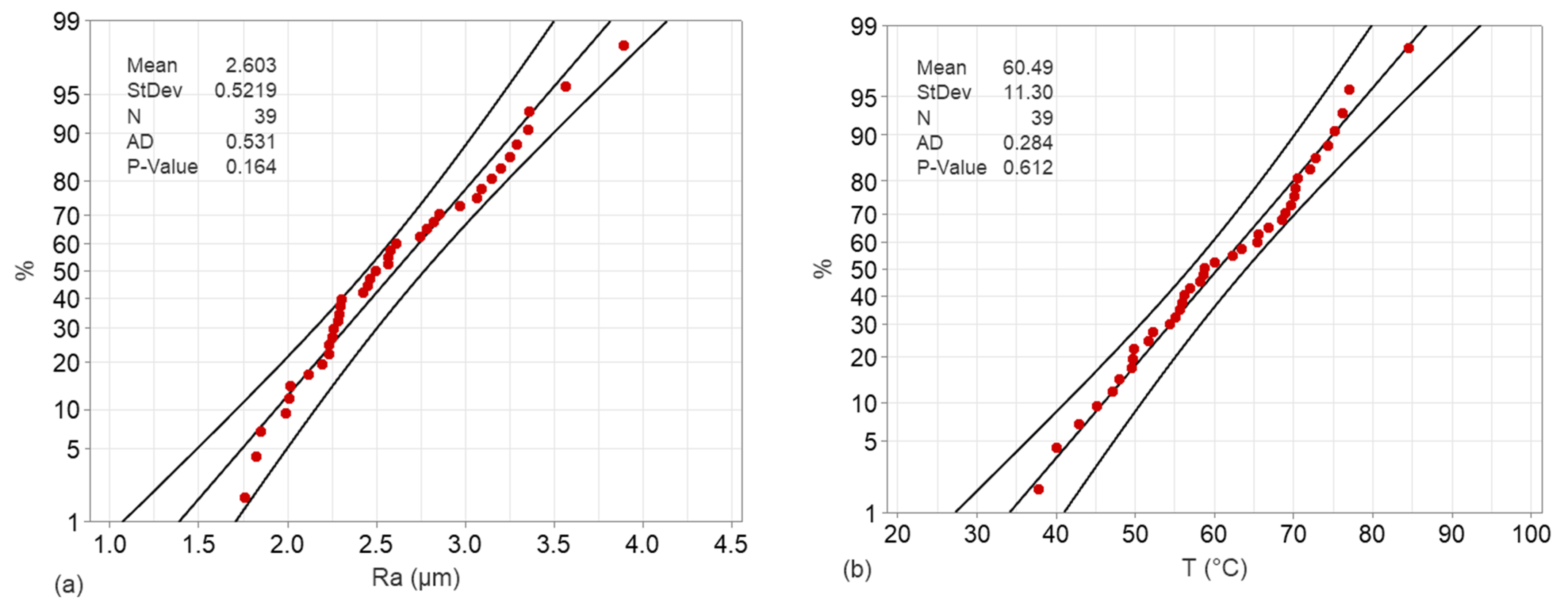
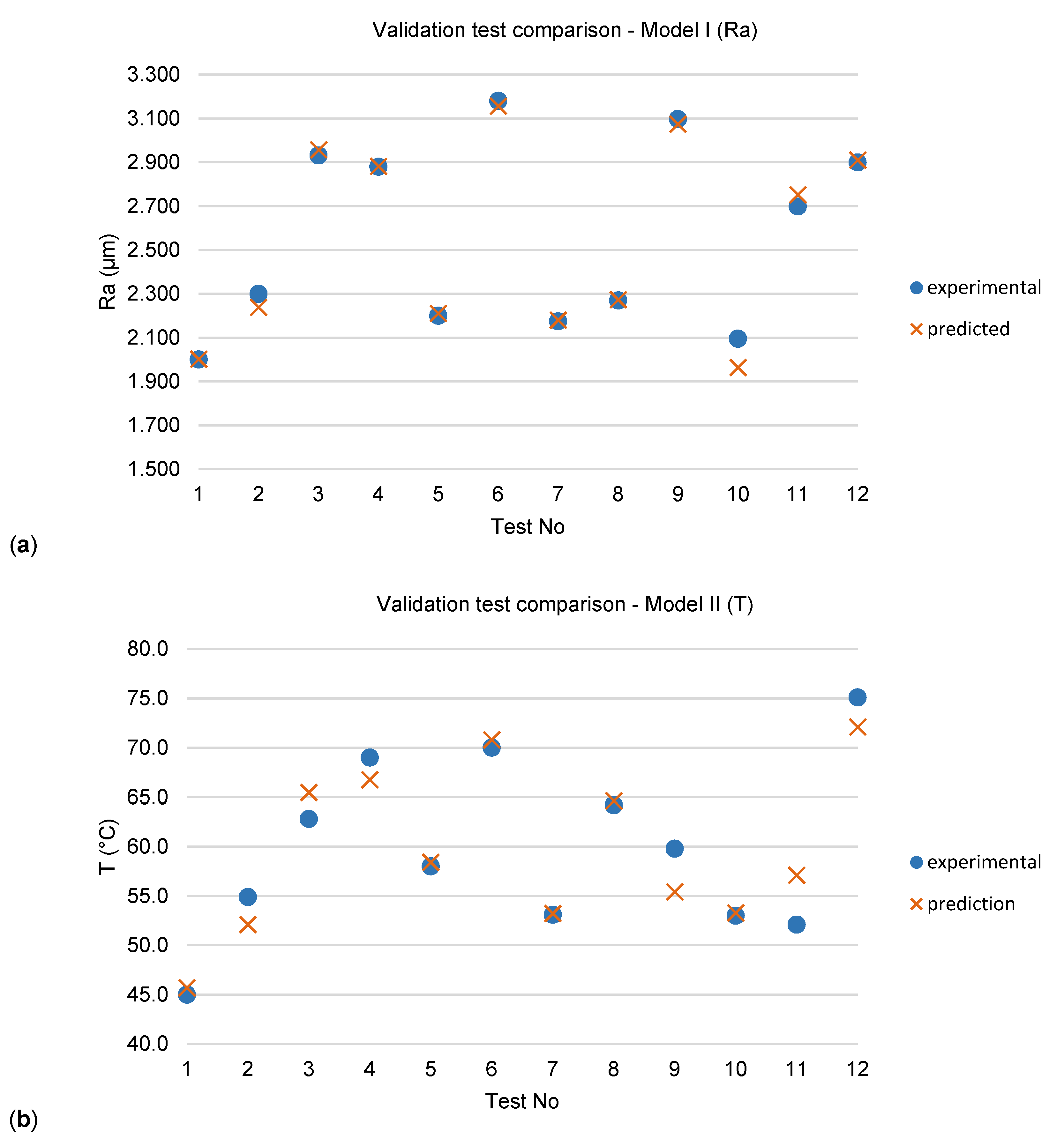
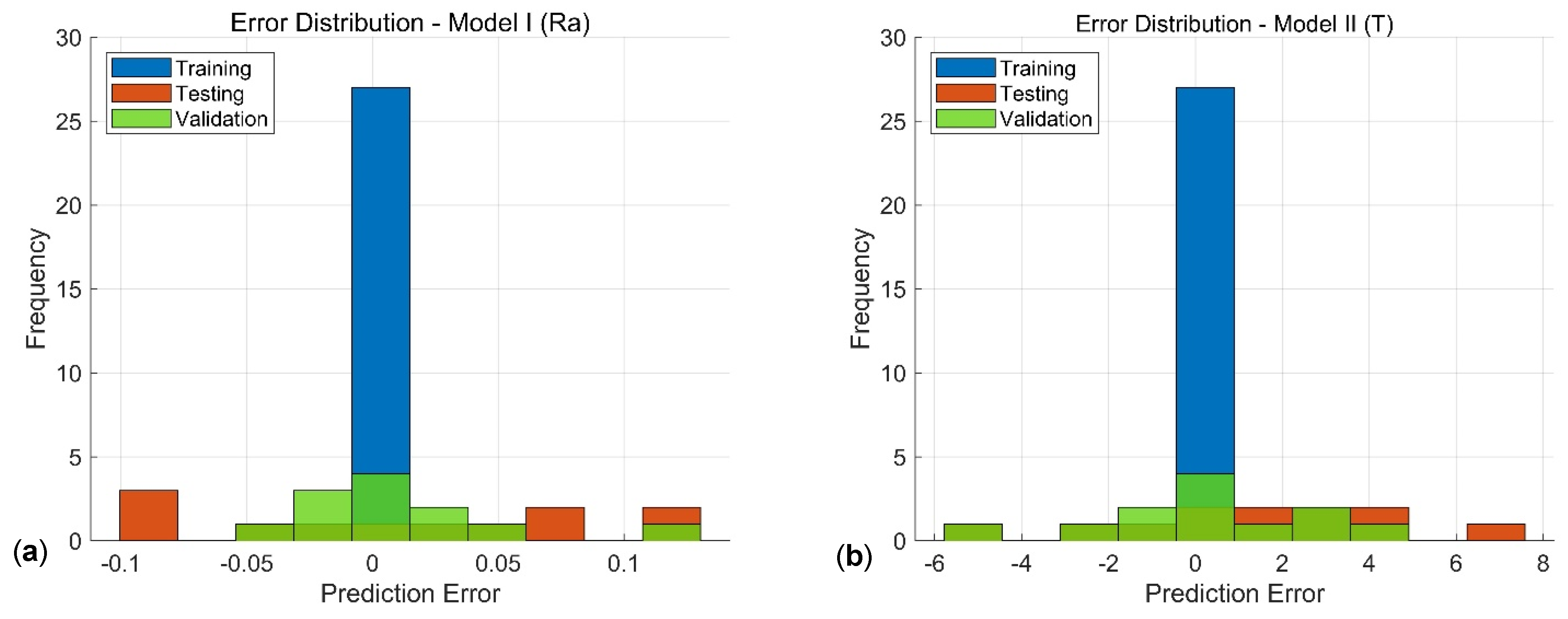
4.2. Performance Evaluation and Validation of the ANFIS Models
4.3. Response Optimization with NSGA-II
5. Conclusions
- The trials for determining the most suitable structure for the models revealed R2 values equal to 0.9920 and 0.9598 for the roughness and temperature models, respectively.
- Sensitivity analysis revealed that feed rate and its interaction with depth-of-cut had the most pronounced influence on Ra, followed by the interaction of cutting speed × feed.
- On the other hand, cutting speed and its interaction with feed were the most influential parameters affecting tool-tip temperature.
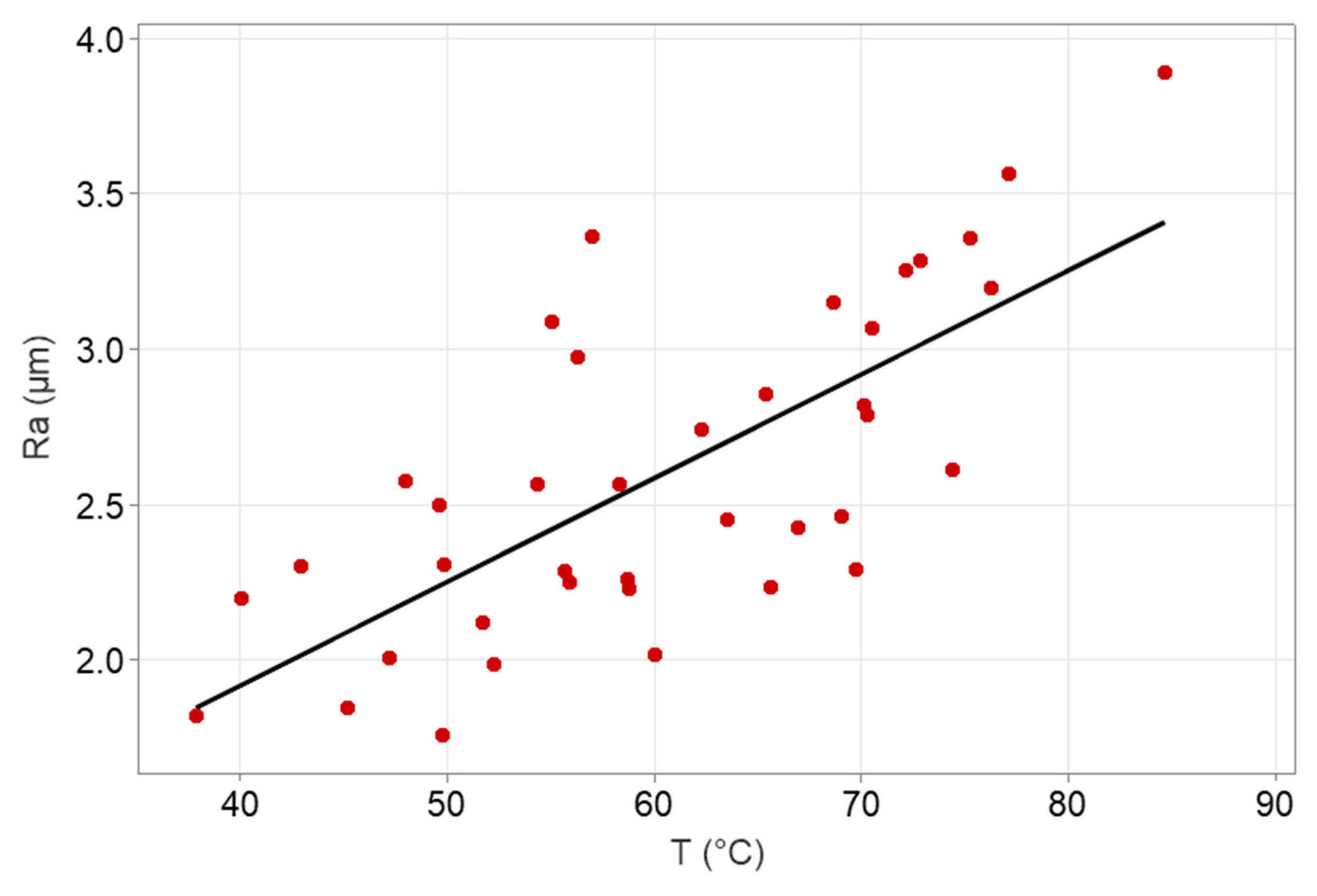
- The interaction between Ra and T was further supported through a scatter plot, which highlighted a visible correlation, suggesting that conditions leading to lower Ra generally also resulted in reduced temperatures, though with some trade-offs.
- Finally, multi-objective optimization using the NSGA-II algorithm provided a set of optimal machining conditions balancing both surface quality and thermal performance. The Pareto front indicated that cutting speeds between 100 and 200 m/min, combined with low feed rates (<0.6 mm/rev) and small depth-of-cut (~0.5 mm), lead to favorable machining outcomes. These results can guide the selection of cutting parameters for efficient and high-quality finishing turning operations of 3D-printed CFRP parts.
6. Future Work and Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| CFRP | Carbon-Fiber-Reinforced Polymer |
| GA | Genetic Algorithm |
| MF | Membership Function |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm 2 |
| PETG | Polyethylene Terephthalate Glycol |
References
- Nowakowski, Ł.; Bartoszuk, M.; Skrzyniarz, M.; Błasiak, S.; Vasileva, D. Influence of the Milling Conditions of Aluminium Alloy 2017A on the Surface Roughness. Materials 2022, 15, 3626. [Google Scholar] [CrossRef] [PubMed]
- Bektaş, B.S.; Samtaş, G. Optimisation of Cutting Parameters in Face Milling of Cryogenic Treated 6061 Aluminium Alloy and Effects on Surface Roughness, Wear, and Cutting Temperatures. Surf. Topogr. Metrol. Prop. 2022, 10, 025013. [Google Scholar] [CrossRef]
- Uzun, M.; Usca, Ü.A.; Kuntoğlu, M.; Gupta, M.K. Influence of Tool Path Strategies on Machining Time, Tool Wear, and Surface Roughness During Milling of AISI X210Cr12 Steel. Int. J. Adv. Manuf. Technol. 2022, 119, 2709–2720. [Google Scholar] [CrossRef]
- Zhang, T.; Yuan, L. Understanding Surface Roughness on Vertical Surfaces of 316 L Stainless Steel in Laser Powder Bed Fusion Additive Manufacturing. Powder Technol. 2022, 411, 117957. [Google Scholar] [CrossRef]
- Alam, S.T.; Tomal, A.N.M.A.; Nayeem, M.K. High-Speed Machining of Ti–6Al–4V: RSM-GA Based Optimization of Surface Roughness and MRR. Results Eng. 2023, 17, 100873. [Google Scholar] [CrossRef]
- Imani, L.; Henzaki, A.R.; Hamzeloo, R.; Davoodi, B. Modeling and Optimizing of Cutting Force and Surface Roughness in Milling Process of Inconel 738 Using Hybrid ANN and GA. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 920–932. [Google Scholar] [CrossRef]
- Danish, M.; Gupta, M.K.; Ghazali, S.M.; Rathore, M.F.; Krolczyk, G.M.; Alsaady, A. Tool Wear and Surface Roughness Characteristics in Sustainable Machining of Additively Manufactured Titanium Alloys. J. Mater. Res. Technol. 2024, 30, 2955–2967. [Google Scholar] [CrossRef]
- Rajput, S.S.; Upadhyay, C.; Gangopadhyay, S.; Fernandes, F. Effects of Roughing, Finishing, and Aggressive Machining Conditions on the Milling Performance of AISI 1045 Steel Using TiAlN Coated Inserts. Proc. Inst. Mech. Eng. Part B 2023, 239, 376–387. [Google Scholar] [CrossRef]
- Sredanovic, B.; Cica, D.; Borojevic, S.; Tesic, S.; Kramar, D. Optimization of Superalloy Inconel 718 Micro-Milling Process by Combined Taguchi and Multi-Criteria Decision Making Method. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 423. [Google Scholar] [CrossRef]
- Lotfi, M.; Amini, S.; Akbari, J. Surface Integrity and Microstructure Changes in 3D Elliptical Ultrasonic Assisted Turning of Ti–6Al–4V: FEM and Experimental Examination. Tribol. Int. 2020, 151, 106492. [Google Scholar] [CrossRef]
- Saez-de-Buruaga, M.; Soler, D.; Aristimuño, P.X.; Esnaola, J.A.; Arrazola, P.J. Determining Tool/Chip Temperatures from Thermography Measurements in Metal Cutting. Appl. Therm. Eng. 2018, 145, 305–314. [Google Scholar] [CrossRef]
- Sambruno, A.; Gómez-Parra, Á.; Márquez, P.; Tellaeche-Herrera, I.; Batista, M. Evaluation of Peripheral Milling and Abrasive Water Jet Cutting in CFRP Manufacturing: Analysis of Defects and Surface Quality. Fibers 2024, 12, 78. [Google Scholar] [CrossRef]
- Tzotzis, A.; Nedelcu, D.; Mazurchevici, S.N.; Kyratsis, P. Surface Quality Evaluation of 3D-Printed Carbon-Fiber-Reinforced PETG Polymer During Turning: Experimental Analysis, ANN Modeling and Optimization. Polymers 2024, 16, 2927. [Google Scholar] [CrossRef] [PubMed]
- Molina-Moya, M.Á.; García-Martínez, E.; Miguel, V.; Coello, J.; Martínez-Martínez, A. Experimental Analysis and Application of a Multivariable Regression Technique to Define the Optimal Drilling Conditions for Carbon Fiber Reinforced Polymer (CFRP) Composites. Polymers 2023, 15, 3710. [Google Scholar] [CrossRef]
- Song, Y.; Cao, H.; Wang, Q.; Zhang, J.; Yan, C. Surface Roughness Prediction Model in High-Speed Dry Milling CFRP Considering Carbon Fiber Distribution. Compos. Part B Eng. 2022, 245, 110230. [Google Scholar] [CrossRef]
- Doluk, E.; Rudawska, A.; Kuczmaszewski, J.; Miturska-Barańska, I. Surface Roughness After Milling of the Al/CFRP Stacks with a Diamond Tool. Materials 2021, 14, 6835. [Google Scholar] [CrossRef]
- Arhamnamazi, S.; Aymerich, F.; Buonadonna, P.; El Mehtedi, M.; Taheri, H. Application of Central Composite Design in the Drilling Process of Carbon Fiber-Reinforced Polymer Composite. Appl. Sci. 2024, 14, 7610. [Google Scholar] [CrossRef]
- Popan, I.A.; Bocăneț, V.I.; Softic, S.; Popan, A.I.; Panc, N.; Balc, N. Artificial Intelligence Model Used for Optimizing Abrasive Water Jet Machining Parameters to Minimize Delamination in Carbon Fiber-Reinforced Polymer. Appl. Sci. 2024, 14, 8512. [Google Scholar] [CrossRef]
- Lalegani Dezaki, M.; Mohd Ariffin, M.K.A. Post-Processing of FDM 3D-Printed Polylactic Acid Parts by CNC Trimming. In Fused Deposition Modeling Based 3D Printing; Dave, H.K., Davim, J.P., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 195–212. ISBN 978-3-030-68024-4. [Google Scholar]
- Rabalo, M.A.; Rubio, E.M.; Agustina, B.; Camacho, A.M. Hybrid Additive and Subtractive Manufacturing: Evolution of the Concept and Last Trends in Research and Industry. Procedia CIRP 2023, 118, 741–746. [Google Scholar] [CrossRef]
- Tamburrino, F.; Barone, S.; Paoli, A.; Razionale, A.V. Post-Processing Treatments to Enhance Additively Manufactured Polymeric Parts: A Review. Virtual Phys. Prototyp. 2021, 16, 218–251. [Google Scholar] [CrossRef]
- Gómez-García, D.; Díaz-Álvarez, A.; Youssef, G.; Miguélez, H.; Díaz-Álvarez, J. Machinability of 3D Printed Peek Reinforced with Short Carbon Fiber. Compos. Part C Open Access 2023, 12, 100387. [Google Scholar] [CrossRef]
- El Mehtedi, M.; Buonadonna, P.; Loi, G.; El Mohtadi, R.; Carta, M.; Aymerich, F. Surface Quality Related to Face Milling Parameters in 3D Printed Carbon Fiber-Reinforced PETG. J. Compos. Sci. 2024, 8, 128. [Google Scholar] [CrossRef]
- Ma, C.K.; Aguilar, L.; Karim, M.; Abdun Nafi, M.; Ma, J.; Jahan, M.P. Experimental Investigation of Nanosecond Laser Machining of 3D Printed Carbon Fiber Reinforced Polymer (CFRP) Composite. Manuf. Lett. 2023, 35, 399–409. [Google Scholar] [CrossRef]
- Cococcetta, N.; Jahan, M.P.; Schoop, J.; Ma, J.; Pearl, D.; Hassan, M. Post-Processing of 3D Printed Thermoplastic CFRP Composites Using Cryogenic Machining. J. Manuf. Process. 2021, 68, 332–346. [Google Scholar] [CrossRef]
- Hassan, M.; Ma, J.; Jahan, M.P. Numerical Modeling and Simulation of Machining of 3D Printed CFRP Composite. Manuf. Lett. 2022, 33, 415–427. [Google Scholar] [CrossRef]
- Tzotzis, A.; Maropoulos, P.; Kyratsis, P. A Dynamic Surface Roughness Prediction System Based on Machine Learning for the 3D-Printed Carbon-Fiber-Reinforced-Polymer (CFRP) Turning. J. Intell. Manuf. 2025, 7075. [Google Scholar] [CrossRef]
- Song, Y.; Cao, H.; Zheng, W.; Qu, D.; Liu, L.; Yan, C. Cutting Force Modeling of Machining Carbon Fiber Reinforced Polymer (CFRP) Composites: A Review. Compos. Struct. 2022, 299, 116096. [Google Scholar] [CrossRef]
- Ko, J.H.; Yin, C. A Review of Artificial Intelligence Application for Machining Surface Quality Prediction: From Key Factors to Model Development. J. Intell. Manuf. 2025. [Google Scholar] [CrossRef]
- Agu, C.M.; Ani, K.A.; Ani, O.N.; Nnaji, P.C.; Kadurumba, C.H.; Esonye, C. Application of Efficient Soft Computing Approaches for Modeling Methyl Ester Yield from Azadirachta Indica (Neem) Seed Oil: A Comparative Study of RSM, ANN and ANFIS. Green Technol. Sustain. 2024, 2, 100057. [Google Scholar] [CrossRef]
- Akhil, C.S.; Ananthavishnu, M.H.; Akhil, C.K.; Afeez, P.M.; Rahul, R. Measurement of Cutting Temperature During Machining. IOSR J. Mech. Civ. Eng. 2016, 13, 108–122. [Google Scholar] [CrossRef]
- Kohli, A.; Dixit, U.S. A Neural-Network-Based Methodology for the Prediction of Surface Roughness in a Turning Process. Int. J. Adv. Manuf. Technol. 2005, 25, 118–129. [Google Scholar] [CrossRef]
- Tzotzis, A.; Efkolidis, N.; Cheng, K.; Kyratsis, P. Multiple Regression Analysis and Non-Dominated Sorting Genetic Algorithm II Optimization of Machining Carbon-Fiber-Reinforced Polyethylene Terephthalate Glycol Parts Fabricated via Additive Manufacturing Under Dry and Lubricated Conditions. Lubricants 2025, 13, 63. [Google Scholar] [CrossRef]
- Vallejo, J.; García-Plaza, E.; Núñez, P.J.; Chacón, J.M.; Caminero, M.A.; Romero, A. Machinability Analysis of Carbon Fibre Reinforced PET-Glycol Composites Processed by Additive Manufacturing. Compos. Part A Appl. Sci. Manuf. 2023, 172, 107561. [Google Scholar] [CrossRef]
- Das, S.R.; Dhupal, D.; Kumar, A. Experimental Investigation into Machinability of Hardened AISI 4140 Steel Using TiN Coated Ceramic Tool. Meas. J. Int. Meas. Confed. 2015, 62, 108–126. [Google Scholar] [CrossRef]
- Abhishek, K.; Datta, S.; Mahapatra, S.S. Optimization of MRR, Surface Roughness, and Maximum Tool-Tip Temperature During Machining of CFRP Composites. Mater. Today Proc. 2017, 4, 2761–2770. [Google Scholar] [CrossRef]
- Marani, M.; Songmene, V.; Zeinali, M.; Kouam, J.; Zedan, Y. Neuro-Fuzzy Predictive Model for Surface Roughness and Cutting Force of Machined Al–20 Mg2Si–2Cu Metal Matrix Composite Using Additives. Neural Comput. Appl. 2020, 32, 8115–8126. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Mofakkirul Islam, M. Prediction of Tool Wear and Surface Finish Using ANFIS Modelling During Turning of Carbon Fiber Reinforced Plastic (CFRP) Composites. Manuf. Lett. 2024, 41, 658–669. [Google Scholar] [CrossRef]
- Siva Kumar, M.; Rajamani, D.; El-Sherbeeny, A.M.; Balasubramanian, E.; Karthik, K.; Hussein, H.M.A.; Astarita, A. Intelligent Modeling and Multi-Response Optimization of AWJC on Fiber Intermetallic Laminates Through a Hybrid ANFIS-Salp Swarm Algorithm. Materials 2022, 15, 7216. [Google Scholar] [CrossRef]
- Benkhelladi, A.; Laouissi, A.; Laouici, H.; Bouchoucha, A.; Karmi, Y.; Chetbani, Y. Assessment of Hybrid Composite Drilling and Prediction of Cutting Parameters by ANFIS and Deep Neural Network Approach. Int. J. Adv. Manuf. Technol. 2024, 135, 589–606. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man. Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man. Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Sada, S.O.; Ikpeseni, S.C. Evaluation of ANN and ANFIS Modeling Ability in the Prediction of AISI 1050 Steel Machining Performance. Heliyon 2021, 7, e06136. [Google Scholar] [CrossRef]
- El Mehtedi, M.; Buonadonna, P.; El Mohtadi, R.; Aymerich, F.; Carta, M. Surface Quality Related to Machining Parameters in 3D-Printed PETG Components. Procedia Comput. Sci. 2024, 232, 1212–1221. [Google Scholar] [CrossRef]
- Maier, R.; Bucaciuc, S.G.; Mandoc, A.C. Reducing Surface Roughness of 3D Printed Short-Carbon Fiber Reinforced Composites. Materials 2022, 15, 7398. [Google Scholar] [CrossRef] [PubMed]
- Parandoush, P.; Deines, T.; Lin, D.; Zhang, H.; Ye, C. Mechanical Finishing of 3D Printed Continuous Carbon Fiber Reinforced Polymer Composites via CNC Machining. In Proceedings of the Volume 1: Additive Manufacturing; Manufacturing Equipment and Systems; Bio and Sustainable Manufacturing; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar]
- Ginoux, G.; Paux, J.; Allaoui, S. New Preparation Method of Microstructurally and Mechanically Standardized PETG Specimens by Material Extrusion Additive Manufacturing and Machining. Addit. Manuf. 2023, 66, 103471. [Google Scholar] [CrossRef]
- El Mehtedi, M.; Buonadonna, P.; El Mohtadi, R.; Loi, G.; Aymerich, F.; Carta, M. Optimizing Milling Parameters for Enhanced Machinability of 3D-Printed Materials: An Analysis of PLA, PETG, and Carbon-Fiber-Reinforced PETG. J. Manuf. Mater. Process. 2024, 8, 131. [Google Scholar] [CrossRef]
- Venkatesh, R.; Kathiravan, S.; Prabhakaran, R.; Ramar, M.; Jerold John Britto, J.; Rajakarunakaran, S. Experimental Investigation on Machinability of Additive Manufactured PLA and PETG Polymers Under Dry Turning Process BT—Recent Advances in Materials Technologies; Rajkumar, K., Jayamani, E., Ramkumar, P., Eds.; Springer Nature: Singapore, 2023; pp. 553–561. [Google Scholar]
- Tezel, T. The Effect of Machining Parameters on the Surface Quality of 3D Printed and Cast Polyamide. Mach. Sci. Technol. 2021, 25, 703–720. [Google Scholar] [CrossRef]
- Rawal, S.; Sidpara, A.M.; Paul, J. A Review on Micro Machining of Polymer Composites. J. Manuf. Process. 2022, 77, 87–113. [Google Scholar] [CrossRef]
- Dilberoglu, U.M.; Yaman, U.; Dolen, M. A Comprehensive Guide to Milling Techniques for Smoothing the Surfaces of 3D-Printed Thermoplastic Parts. Rapid Prototyp. J. 2024, 30, 1648–1662. [Google Scholar] [CrossRef]
- Wang, Q.; Jia, X. Optimization of Cutting Parameters for Improving Exit Delamination, Surface Roughness, and Production Rate in Drilling of CFRP Composites. Int. J. Adv. Manuf. Technol. 2021, 117, 3487–3502. [Google Scholar] [CrossRef]
- Zeelanbasha, N.; Senthil, V.; Mahesh, G. A Hybrid Approach of NSGA-II and TOPSIS for Minimising Vibration and Surface Roughness in Machining Process. Int. J. Oper. Res. 2020, 38, 221–254. [Google Scholar] [CrossRef]
- Sen, B.; Kumar, R.; Kanabar, B.; Kedia, A.; Kumar, A.V.; Bhowmik, A. Comparative Analysis of NSGA-II and TLBO for Optimizing Machining Parameters of Inconel 690: A Sustainable Manufacturing Paradigm. J. Mater. Eng. Perform. 2024. [Google Scholar] [CrossRef]
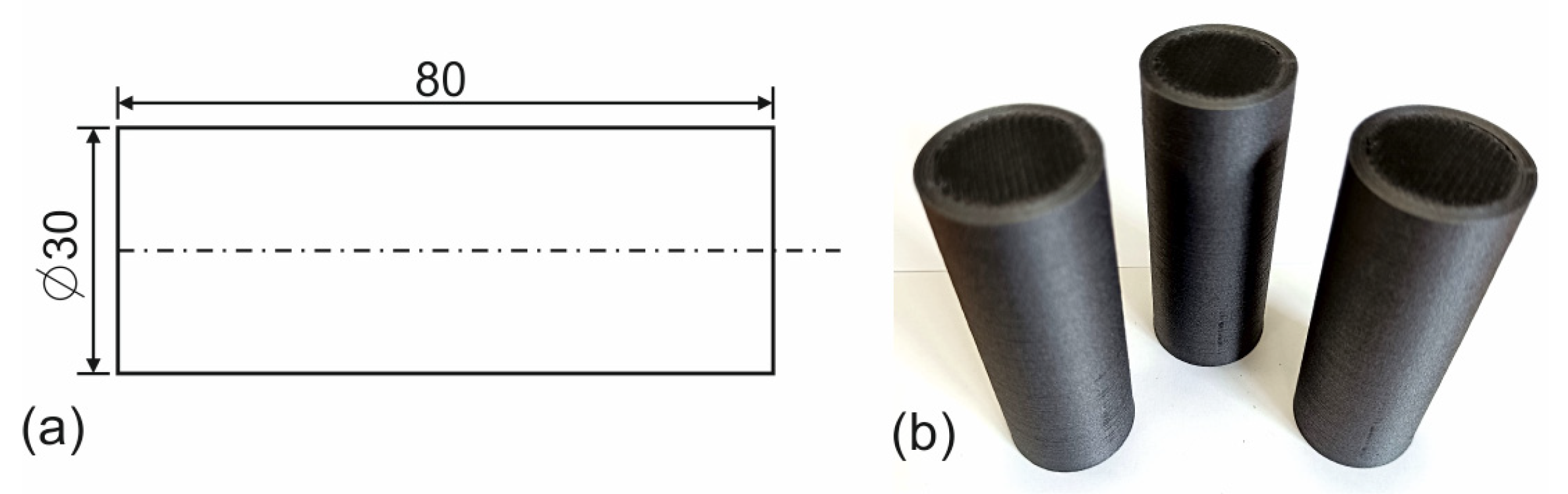


| Setting | Value |
|---|---|
| Printing Nozzle temperature | 255 °C |
| Plate temperature | 70 °C |
| Filament | 1.75 mm |
| Printing Nozzle diameter | 0.6 mm |
| Layer | 0.2 mm |
| Printing speed | 40 mm/s |
| Flow | 100% |
| Shell thickness | 3 mm |
| Experiment No. | Vc (m/min) | f (mm/rev) | ap (mm) | Ra (μm) | T (°C) | |
|---|---|---|---|---|---|---|
| Training Data | 1 | 115 | 0.05 | 0.50 | 1.823 | 37.9 |
| 2 | 115 | 0.05 | 1.25 | 2.198 | 40.1 | |
| 3 | 115 | 0.05 | 2.00 | 2.301 | 43.0 | |
| 4 | 115 | 0.08 | 0.50 | 2.009 | 47.2 | |
| 5 | 115 | 0.08 | 1.25 | 2.580 | 48.0 | |
| 6 | 115 | 0.08 | 2.00 | 2.308 | 49.9 | |
| 7 | 115 | 0.11 | 0.50 | 2.566 | 54.4 | |
| 8 | 115 | 0.11 | 1.25 | 3.090 | 55.1 | |
| 9 | 115 | 0.11 | 2.00 | 3.362 | 57.0 | |
| 10 | 200 | 0.05 | 0.50 | 1.762 | 49.8 | |
| 11 | 200 | 0.05 | 1.25 | 1.989 | 52.3 | |
| 12 | 200 | 0.05 | 2.00 | 2.253 | 55.9 | |
| 13 | 200 | 0.08 | 0.50 | 2.020 | 60.0 | |
| 14 | 200 | 0.08 | 1.25 | 2.744 | 62.3 | |
| 15 | 200 | 0.08 | 2.00 | 2.466 | 69.0 | |
| 16 | 200 | 0.11 | 0.50 | 2.788 | 70.3 | |
| 17 | 200 | 0.11 | 1.25 | 3.067 | 70.5 | |
| 18 | 200 | 0.11 | 2.00 | 3.255 | 72.1 | |
| 19 | 285 | 0.05 | 0.50 | 2.121 | 51.7 | |
| 20 | 285 | 0.05 | 1.25 | 2.262 | 58.7 | |
| 21 | 285 | 0.05 | 2.00 | 2.453 | 63.5 | |
| 22 | 285 | 0.08 | 0.50 | 2.429 | 66.9 | |
| 23 | 285 | 0.08 | 1.25 | 3.288 | 72.8 | |
| 24 | 285 | 0.08 | 2.00 | 2.616 | 74.4 | |
| 25 | 285 | 0.11 | 0.50 | 3.199 | 76.2 | |
| 26 | 285 | 0.11 | 1.25 | 3.566 | 77.1 | |
| 27 | 285 | 0.11 | 2.00 | 3.890 | 84.6 | |
| Testing Data | 28 | 150 | 0.06 | 0.75 | 1.850 | 45.2 |
| 29 | 175 | 0.09 | 1.50 | 2.893 | 56.3 | |
| 30 | 225 | 0.07 | 1.75 | 2.295 | 69.7 | |
| 31 | 250 | 0.06 | 1.00 | 2.237 | 65.6 | |
| 32 | 130 | 0.07 | 1.50 | 2.329 | 49.6 | |
| 33 | 185 | 0.10 | 0.90 | 2.856 | 65.4 | |
| 34 | 260 | 0.07 | 1.30 | 2.932 | 68.6 | |
| 35 | 145 | 0.09 | 0.60 | 2.253 | 58.8 | |
| 36 | 210 | 0.06 | 1.60 | 2.286 | 55.7 | |
| 37 | 270 | 0.09 | 0.80 | 2.821 | 70.1 | |
| 38 | 190 | 0.07 | 1.10 | 2.478 | 58.3 | |
| 39 | 240 | 0.10 | 1.40 | 3.357 | 75.2 |
| Structure | RMSE | R2 | |||
|---|---|---|---|---|---|
| MF Number | MF Type | Model I | Model II | Model I | Model II |
| 2-2-2 | Triangular | 0.1932 | 2.6039 | 0.8438 | 0.9394 |
| Trapezoidal | 0.2107 | 4.4552 | 0.8141 | 0.8226 | |
| Gaussian | 0.1906 | 3.0474 | 0.8478 | 0.9170 | |
| Generalized bell-shaped | 0.1953 | 3.4949 | 0.8404 | 0.8909 | |
| 3-3-3 | Triangular | 0.0430 | 2.1223 | 0.9920 | 0.9598 |
| Trapezoidal | 0.0962 | 2.9568 | 0.9583 | 0.9219 | |
| Gaussian | 0.0998 | 2.5242 | 0.9612 | 0.9431 | |
| Generalized bell-shaped | 0.1006 | 2.5679 | 0.9576 | 0.9411 | |
| 4-4-4 | Triangular | Too high | Too high | Too low | Too low |
| Trapezoidal | Too high | Too high | Too low | Too low | |
| Gaussian | Too high | Too high | Too low | Too low | |
| Generalized bell-shaped | 0.2111 | Too high | 0.8134 | Too low | |
| Test No. | Vc (m/min) | f (mm/rev) | ap (mm) |
|---|---|---|---|
| 1 | 145 | 0.06 | 0.90 |
| 2 | 165 | 0.07 | 1.00 |
| 3 | 180 | 0.095 | 1.75 |
| 4 | 220 | 0.09 | 1.10 |
| 5 | 245 | 0.065 | 0.80 |
| 6 | 260 | 0.085 | 1.30 |
| 7 | 175 | 0.06 | 1.60 |
| 8 | 200 | 0.07 | 1.90 |
| 9 | 125 | 0.10 | 1.40 |
| 10 | 235 | 0.055 | 0.70 |
| 11 | 155 | 0.09 | 1.15 |
| 12 | 270 | 0.08 | 1.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzotzis, A.; Nedelcu, D.; Mazurchevici, S.-N.; Kyratsis, P. Investigating the Machining Behavior of the Additively Manufactured Polymer-Based Composite Using Adaptive Neuro-Fuzzy Learning. Appl. Sci. 2025, 15, 5373. https://doi.org/10.3390/app15105373
Tzotzis A, Nedelcu D, Mazurchevici S-N, Kyratsis P. Investigating the Machining Behavior of the Additively Manufactured Polymer-Based Composite Using Adaptive Neuro-Fuzzy Learning. Applied Sciences. 2025; 15(10):5373. https://doi.org/10.3390/app15105373
Chicago/Turabian StyleTzotzis, Anastasios, Dumitru Nedelcu, Simona-Nicoleta Mazurchevici, and Panagiotis Kyratsis. 2025. "Investigating the Machining Behavior of the Additively Manufactured Polymer-Based Composite Using Adaptive Neuro-Fuzzy Learning" Applied Sciences 15, no. 10: 5373. https://doi.org/10.3390/app15105373
APA StyleTzotzis, A., Nedelcu, D., Mazurchevici, S.-N., & Kyratsis, P. (2025). Investigating the Machining Behavior of the Additively Manufactured Polymer-Based Composite Using Adaptive Neuro-Fuzzy Learning. Applied Sciences, 15(10), 5373. https://doi.org/10.3390/app15105373









