A Viscoelastic-Plastic Creep Model for Initial Damaged Coal Sample Affected by Loading Rate
Abstract
1. Introduction
2. Experimental Method and Procedure
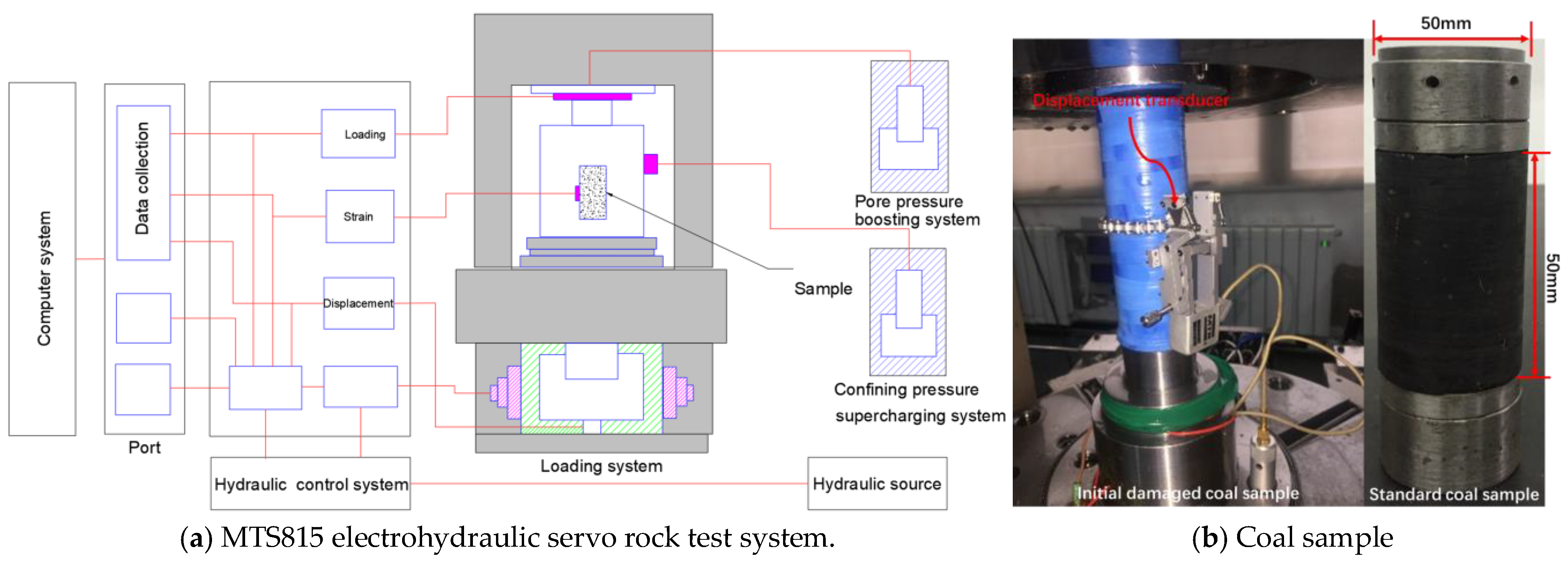
2.1. Experimental Equipment and Standard Samples Preparation
2.2. Initially Damaged Coal Sample Preparation Method
2.3. Triaxial Compressive Strength (TCS) of Initially Damaged Coal Specimen
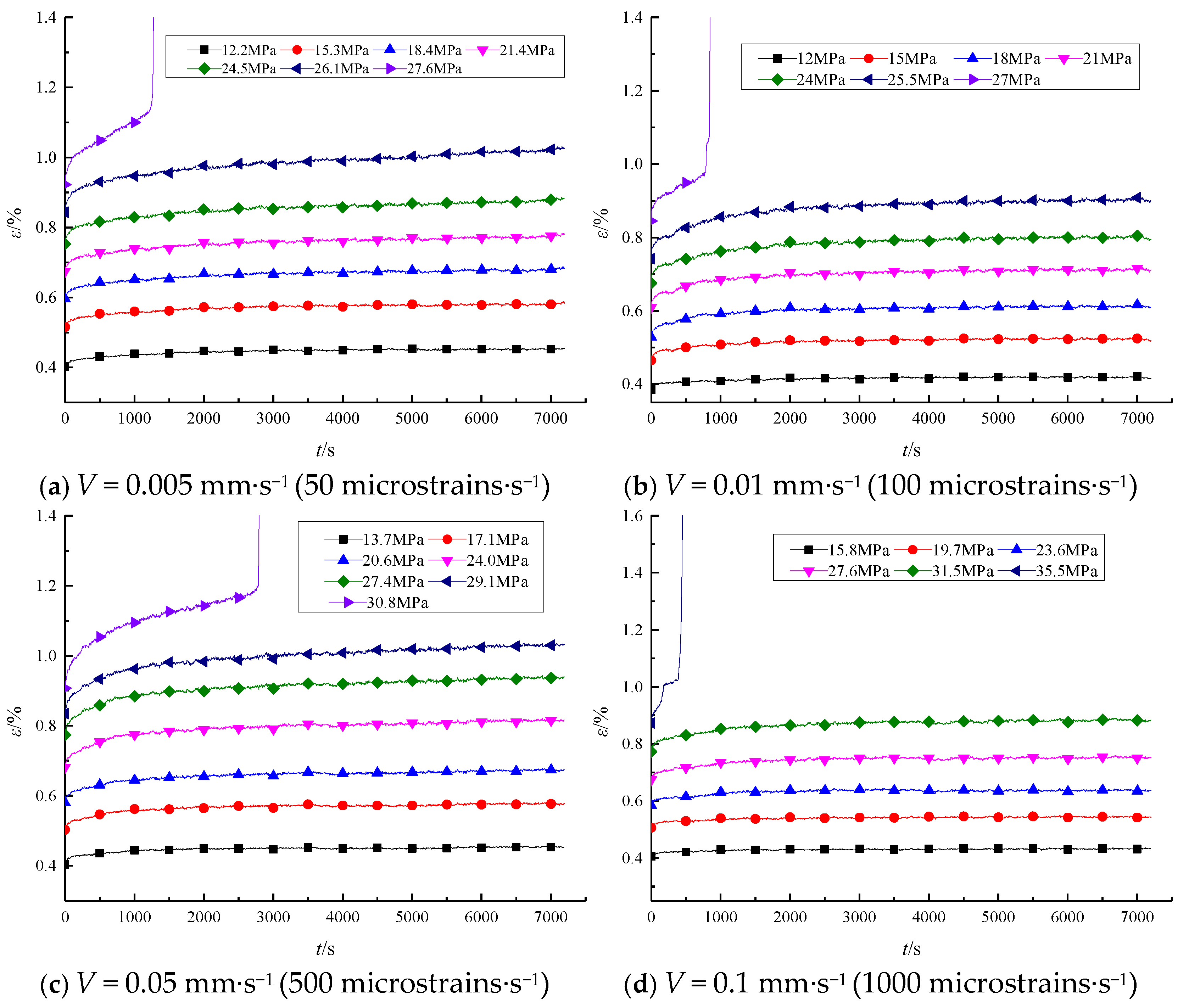
2.4. Triaxial Graded Creep Tests
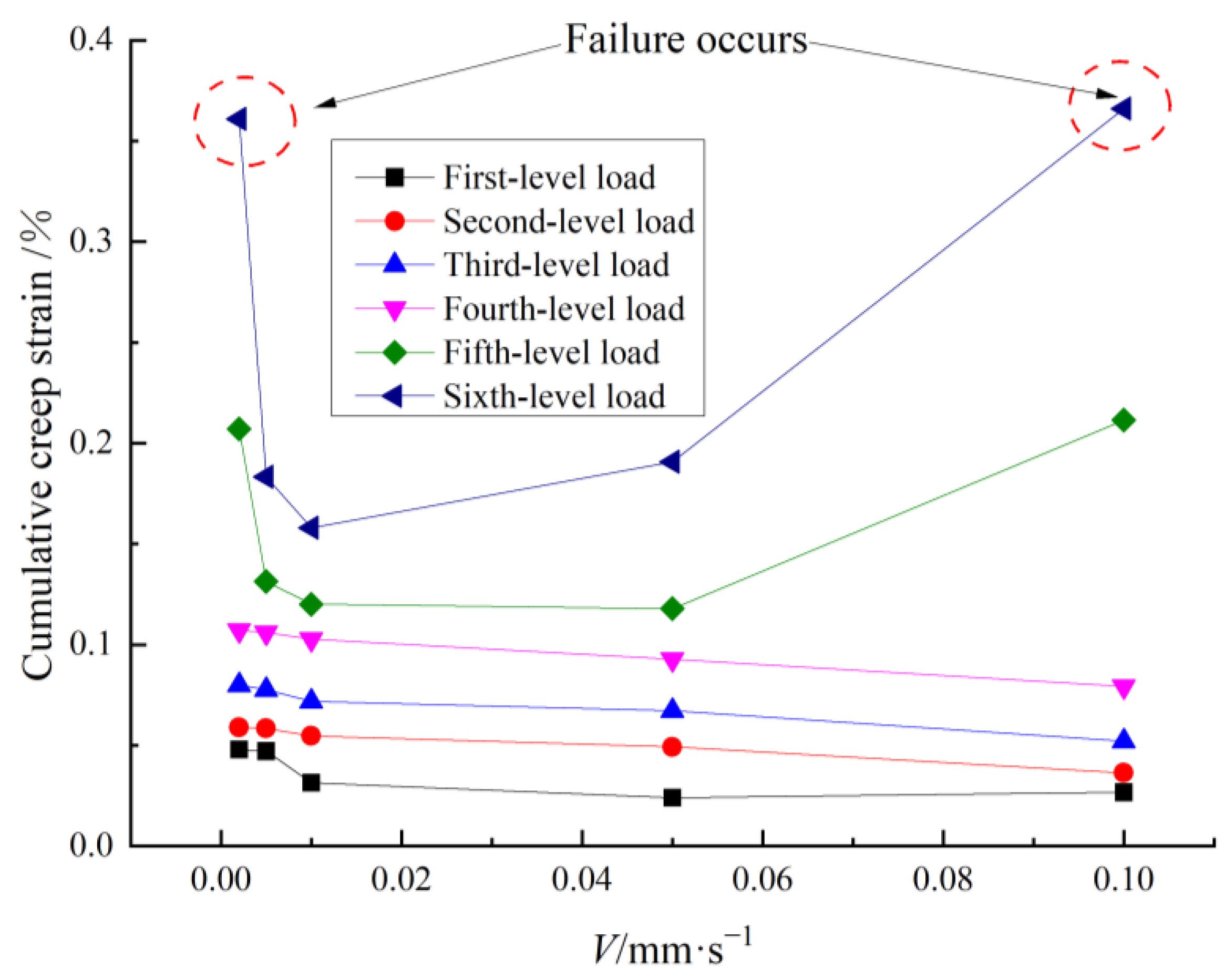
3. Creep Properties of Coal Sample with Initial Damage
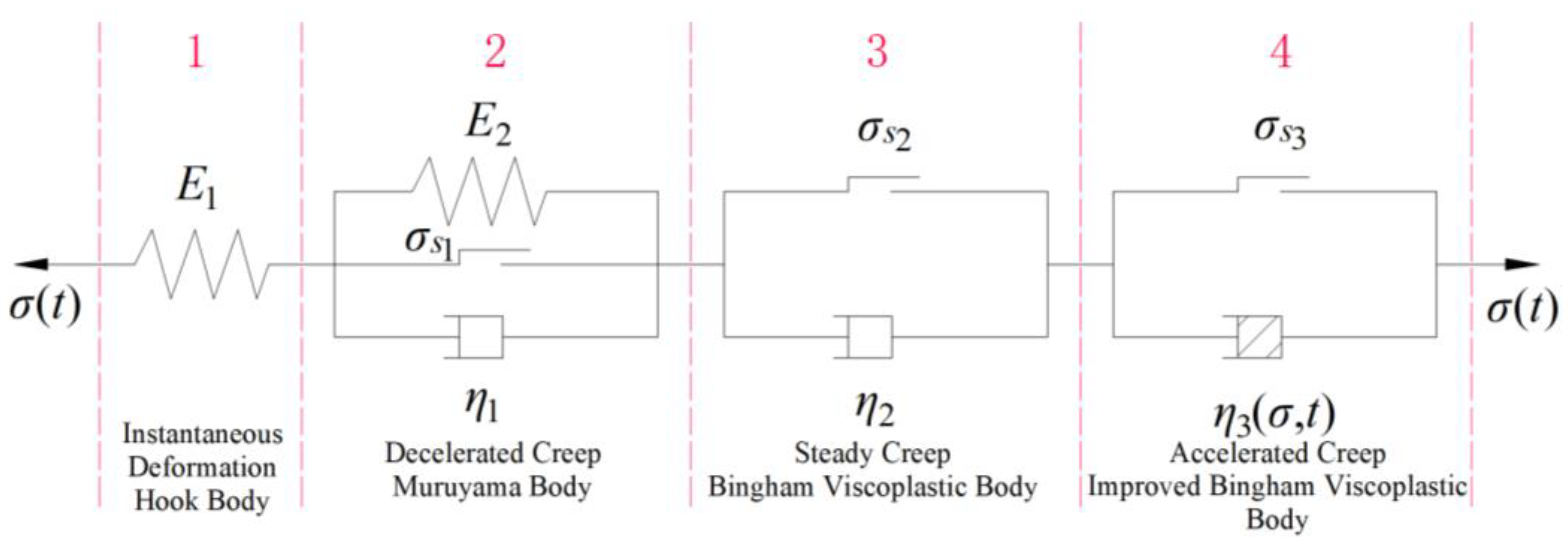
4. Integer-Order Nonlinear Creep Model
4.1. Integer-Order Nonlinear Viscoelastic-Plastic Creep Model
4.2. Three-Dimensional Extension of the Integer-Order Nonlinear Viscoelastic-Plastic Creep Model
5. Parameter Recognition and Verification of the Creep Damage Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, H.; Lu, J.; Li, C.; Li, M.; Gao, M. Experimental Study on the Mechanical and Failure Behaviors of Deep Rock Subjected to True Triaxial Stress: A Review. Int. J. Min. Sci. Technol. 2022, 32, 915–950. [Google Scholar] [CrossRef]
- He, M.; Wang, Q. Rock Dynamics in Deep Mining. Int. J. Min. Sci. Technol. 2023, 33, 1065–1082. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, D.; Wang, J.; Wang, X.; Cong, Y.; Wang, Z. A Nonlinear Creep Model of Rocks Based on Memory-Dependent Derivative. Constr. Build. Mater. 2023, 391, 131618. [Google Scholar] [CrossRef]
- Wang, J.; Yang, S.; Qi, Y.; Cong, Y. Creep Characteristics and Damage Model of Coal–Rock Combinations with Different Height Ratios. Sci. Rep. 2023, 13, 23072. [Google Scholar] [CrossRef]
- Hou, R.; Xu, L.; Zhang, D.; Shi, Y.; Shi, L. Experimental Investigations on Creep Behavior of Coal under Combined Compression and Shear Loading. Geofluids 2021, 2021, 9965228. [Google Scholar] [CrossRef]
- Yang, Y.; Lai, X.; Luo, T.; Yuan, K.; Li, G. Study on Creep Constitutive Model of Stratified Siltstone and Its Application to Instability Analysis in Mining. Environ. Earth Sci. 2022, 81, 270. [Google Scholar] [CrossRef]
- Wang, D.; Wang, E.; Feng, X.; Wei, M.; Li, D.; Liu, Q.; Li, B.; Zhang, X. Triaxial Creep Damage–Catastrophe Instability Characteristics and a Nonlinear Constitutive Model of Gas-Bearing Coal. Bull. Eng. Geol. Environ. 2022, 81, 437. [Google Scholar] [CrossRef]
- Zhao, Z.; Dai, W.; Yang, J.; Zhou, M.; Liu, Z. Creep Mechanical Tests and Shear Rheological Model of the Anchorage Rock Mass under Water–rock Coupling. PLoS ONE 2023, 18, e0284569. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Tan, Y.; Ma, Q.; Wu, B.; Wang, H. Creep Constitutive Model and Numerical Realization of Coal-Rock Combination Deteriorated by Immersion. Minerals 2022, 12, 292. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Xie, W.; Chen, H. Creep Behaviors of Extremely Soft and Fractured Coal Rock with Different Moisture Contents and Rare Secondary Creep Performance. Nat. Resour. Res. 2023, 32, 357–371. [Google Scholar] [CrossRef]
- Tarifard, A.; Görög, P.; Török, Á. Long-Term Assessment of Creep and Water Effects on Tunnel Lining Loads in Weak Rocks Using Displacement-Based Direct Back Analysis: An Example from Northwest of Iran. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 31. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J.; Zhang, J.; Yao, W.; Cai, Y.; Zhou, X. Anisotropic Time-Dependent Deformation and Damage Constitutive Model of Rock under True Triaxial Compression. Mech. Time-Depend. Mater. 2024, 28, 2177–2203. [Google Scholar] [CrossRef]
- Yin, D.; Wang, F.; Zhang, J.; Li, F.; Zhu, C.; Feng, F. Experimental Study on the Short-Term Uniaxial Creep Characteristics of Sandstone-Coal Composite Samples. Minerals 2021, 11, 1398. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X. Study on Nonlinear Damage Creep Model for Rocks under Cyclic Loading and Unloading. Adv. Mater. Sci. Eng. 2021, 2021, 5512972. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, J.; Spearing, A.J.S.; Chai, J.; Dong, C. Experimental Study of the Creep Properties of Coal Considering Initial Damage. Int. J. Rock Mech. Min. Sci. 2021, 139, 104629. [Google Scholar] [CrossRef]
- King, M.S. Creep in Model Pillars of Saskatchewan Potash. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1973, 10, 363–371. [Google Scholar] [CrossRef]
- Fujii, Y.; Kiyama, T.; Ishijima, Y.; Kodama, J. Circumferential Strain Behavior during Creep Tests of Brittle Rocks. Int. J. Rock Mech. Min. Sci. 1999, 36, 323–337. [Google Scholar] [CrossRef]
- Ladanyi, B.; Gill, D.E. Design of Tunnel Linings in a Creeping Rock. Int. J. Min. Geol. Eng. 1988, 6, 113–126. [Google Scholar] [CrossRef]
- Itô, H.; Sasajima, S. A Ten Year Creep Experiment on Small Rock Specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 113–121. [Google Scholar] [CrossRef]
- Itô, H. The Phenomenon and Examples of Rock Creep. In Rock Testing and Site Characterization; Elsevier: Amsterdam, The Netherlands, 1993; pp. 693–708. [Google Scholar]
- Russell, G. Photographic Sensitizers in Gelatin. Nature 1956, 178, 280. [Google Scholar] [CrossRef]
- Danesh, N.N.; Chen, Z.; Connell, L.D.; Kizil, M.S.; Pan, Z.; Aminossadati, S.M. Characterisation of Creep in Coal and Its Impact on Permeability: An Experimental Study. Int. J. Coal Geol. 2017, 173, 200–211. [Google Scholar] [CrossRef]
- Kachanov, M. A Simple Technique of Stress Analysis in Elastic Solids with Many Cracks. Int. J. Fract. 1985, 28, R11–R19. [Google Scholar] [CrossRef]
- Chan, K.S.; Bodner, S.R.; Fossum, A.F.; Munson, D.E. A Damage Mechanics Treatment of Creep Failure in Rock Salt. Int. J. Damage Mech. 1997, 6, 121–152. [Google Scholar] [CrossRef]
- Ayari, M.L.; Sun, B.K.; Hsu, T.R. A Continuum Damage Mechanics Model for Cyclic Creep Fracture. Eng. Fract. Mech. 1994, 47, 215–222. [Google Scholar] [CrossRef]
- Tomanovic, Z. Rheological Model of Soft Rock Creep Based on the Tests on Marl. Mech. Time-Depend. Mater. 2006, 10, 135–154. [Google Scholar] [CrossRef]
- Maranini, E.; Yamaguchi, T. A Non-Associated Viscoplastic Model for the Behaviour of Granite in Triaxial Compression. Mech. Mater. 2001, 33, 283–293. [Google Scholar] [CrossRef]
- Mazzotti, C.; Savoia, M. Nonlinear Creep Damage Model for Concrete under Uniaxial Compression. J. Eng. Mech. 2003, 129, 1065–1075. [Google Scholar] [CrossRef]
- Sercombe, J.; Hellmich, C.; Ulm, F.-J.; Mang, H. Modeling of Early-Age Creep of Shotcrete. I: Model and Model Parameters. J. Eng. Mech. 2000, 126, 284–291. [Google Scholar] [CrossRef]
- Guo, J.; Zong, D.; Ma, L. Creep Damage Characteristics and Constitutive Model of Pre-Damage Coal. Eng. Fail. Anal. 2024, 158, 108002. [Google Scholar] [CrossRef]
- Jiang, Y.; Liang, B.; Wang, D.; Luan, H.; Zhang, G.; Dong, L.; Chen, L. Experimental Study on Failure Mechanical Properties and Acoustic Emission Characteristics of Soft Rock–Coal Combination under Dynamic Disturbance. Eng. Fail. Anal. 2024, 158, 108016. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Tang, J.-Z.; Elsworth, D. Creep Rupture and Permeability Evolution in High Temperature Heat-Treated Sandstone Containing Pre-Existing Twin Flaws. Energies 2021, 14, 6362. [Google Scholar] [CrossRef]
- Ding, Z.; Feng, X.; Wang, E.; Sa, L.; Wang, D.; Zhang, Q.; Hu, Q.; Zhao, X. Fracture Response and Damage Evolution Features of Coal Considering the Effect of Creep Damage under Dynamic Loading. Eng. Fail. Anal. 2023, 148, 107204. [Google Scholar] [CrossRef]
- Bao, M.; Chen, Z.; Nian, G.; Zhang, L.; Zhu, T. Study on Creep Properties of Weak Layer Rock of Slope under Damage Coupling. Bull. Eng. Geol. Environ. 2024, 83, 154. [Google Scholar] [CrossRef]
- Song, H.; Zuo, J.; Liu, H.; Zuo, S. The Strength Characteristics and Progressive Failure Mechanism of Soft Rock-Coal Combination Samples with Consideration given to Interface Effects. Int. J. Rock Mech. Min. Sci. 2021, 138, 104593. [Google Scholar] [CrossRef]
- Wang, D.; Wang, E.; Liu, X.; Feng, X.; Wei, M.; Li, D.; Li, B.; Liu, Q.; Zhang, X.; Yang, H.; et al. Non-Linear Response of Acoustic Emission and Electric Potential During Creep Failure of Coal under Stepwise Increasing Loads: Insights from Multifractal Theory. Nat. Resour. Res. 2024, 33, 2113–2133. [Google Scholar] [CrossRef]
- Fan, D.; Zhang, C.; Ji, Y.; Zhao, X.; Zhao, Z.; He, M. Permeability Evolution of Rough Fractures in Gonghe Granite Subjected to Cyclic Normal Stress at Elevated Temperatures: Experimental Measurements and Analytical Modeling. Rock Mech. Rock Eng. 2024, 57, 11301–11318. [Google Scholar] [CrossRef]
- Li, F.; Ma, T.; Yang, Y. Numerical Study on the Rate-Dependent Behavior of Geogrid Reinforced Sand Retaining Walls. Geomech. Eng. 2021, 25, 195–205. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.; Li, C. Laboratory Testing and Modeling of Creep Deformation for Sandstone Including Initial Temperature Damage. Rock Mech. Rock Eng. 2023, 56, 2479–2495. [Google Scholar] [CrossRef]
- Xie, Q.; Chen, Y.; Lyu, H.; Gu, J.; Chen, Y.; Cui, H.; Wu, P. Dynamic Mechanical Properties and Energy Dissipation Analysis of Frozen Sandstone with Initial Damage. Front. Earth Sci. 2023, 11, 1128634. [Google Scholar] [CrossRef]
- Li, S.; Wang, T.; Zhang, F.; Yao, X. Experimental Study of the Dynamic Characteristics of Sandstone with Preexisting Creep Damage. Mech. Time-Depend. Mater. 2022, 26, 955–973. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Tang, J.-Z.; Wang, S.-S.; Yang, D.-S.; Zheng, W.-T. An Experimental and Modeling Investigation on Creep Mechanical Behavior of Granite Under Triaxial Cyclic Loading and Unloading. Rock Mech. Rock Eng. 2022, 55, 5577–5597. [Google Scholar] [CrossRef]
- Su, T.; Zhou, H.; Zhao, J.; Liu, Z.; Dias, D. A Fractional Derivative-Based Numerical Approach to Rate-Dependent Stress–Strain Relationship for Viscoelastic Materials. Acta Mech. 2021, 232, 2347–2359. [Google Scholar] [CrossRef]
- Fairhurst, C.; Hudson, J. Draft ISRM Suggested Method for the Complete Stress-Strain Curve for Intact Rock in Uniaxial Compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1999, 36, 281–289. [Google Scholar] [CrossRef]
- Deng, H.; Li, J.-L.; Deng, C.-J.; Wang, L.; Lu, T. Analysis of Sampling in Rock Mechanics Test and Compressive Strength Prediction Methods. Rock Soil Mech. 2011, 32, 3399–3403. [Google Scholar]
- Song, Z.P.; Wang, J.X.; Jiang, A.; Liu, X.; Zhang, X. Ultrasonic Tests on Schist with Saturated Fractures under Uniaxial Compression. Chin. J. Rock Mech. Eng. 2014, 33, 2377–2383. [Google Scholar]
- Huang, P.; Zhang, J.; Damascene, N.J.; Wang, Z.; Li, M. Effect of Loading Rate on Mechanical Behavior of Coal Samples with Initial Damage Accumulation. Mech. Time-Depend. Mater. 2022, 26, 309–322. [Google Scholar] [CrossRef]
- Ali, Z.; Karakus, M.; Nguyen, G.D.; Amrouch, K. Effect of Loading Rate and Time Delay on the Tangent Modulus Method (TMM) in Coal and Coal Measured Rocks. Int. J. Coal Sci. Technol. 2022, 9, 81. [Google Scholar] [CrossRef]
- Wei, E.; Hu, B.; Li, J.; Cui, K.; Zhang, Z.; Cui, A.; Ma, L. Nonlinear Viscoelastic-Plastic Creep Model of Rock Based on Fractional Calculus. Adv. Civ. Eng. 2022, 2022, 3063972. [Google Scholar] [CrossRef]
- Wang, J.; Yang, S.; Qi, Y.; Cong, Y. Study on Bingham Fractional Damage Model of Backfill Material under Different Moisture Content Conditions. PLoS ONE 2024, 19, e0295254. [Google Scholar] [CrossRef]
- Huang, X.; Cao, H.; Jia, B. Optimization of Levenberg Marquardt Algorithm Applied to Nonlinear Systems. Processes 2023, 11, 1794. [Google Scholar] [CrossRef]




| Loading Rates/mm·s⁻¹ (Microstrains·s−1) | Triaxial Compressive Strength (TCS)/MPa |
|---|---|
| 0.005 (50) | 30.50 |
| 0.010 (100) | 30.00 |
| 0.050 (500) | 34.25 |
| 0.100 (1000) | 39.43 |
| Loading Rates/mm·s−1 (Microstrains·s−1) | Loading Stress (Proportion of TCS)/MPa |
|---|---|
| 0.005 (50) | 12.2 (40%) |
| 15.3 (50%) | |
| 18.4 (60%) | |
| 21.4 (70%) | |
| 24.5 (80%) | |
| 26.1 (85%) | |
| 27.6 (90%) | |
| 0.010 (1000) | 12.0 (40%) |
| 15.0 (50%) | |
| 18.0 (60%) | |
| 21.0 (70%) | |
| 24.0 (80%) | |
| 25.5 (85%) | |
| 27.0 (90%) | |
| 0.050 (500) | 13.7 (40%) |
| 17.1 (50%) | |
| 20.6 (60%) | |
| 24.0 (70%) | |
| 27.4 (80%) | |
| 29.1 (85%) | |
| 30.8 (90%) | |
| 0.100 (1000) | 15.8 (40%) |
| 19.7 (50%) | |
| 23.6 (60%) | |
| 27.6 (70%) | |
| 31.5 (80%) | |
| 35.5 (90%) |
| V/mm·s−1 | σ1–σ3 | K/GPa | G0/GPa | G1/GPa | η1/GPa·h | η2/GPa·h | ηc/GPa·h | α |
|---|---|---|---|---|---|---|---|---|
| 0.005 | 12.2 | 5.226 | 1.0014 | 7.8705 | 3.2220 | - | - | - |
| 15.3 | 5.2464 | 1.0140 | 11.5109 | 8.2670 | - | - | - | |
| 18.4 | 0.9280 | 1.8270 | 10.5516 | 4.9341 | - | - | - | |
| 21.4 | 0.4296 | 1.6345 | 9.4184 | 5.1057 | 1.9520 | - | - | |
| 24.5 | 0.4370 | 1.8047 | 10.0072 | 2.1598 | 7.1888 | - | - | |
| 26.1 | 0.5314 | 3.5944 | 7.3451 | 5.5411 | 6.5304 | 3.2011 | 76.8 | |
| 27.6 | 0.3781 | 1.6321 | 8.4501 | 5.8510 | 0.5313 | 3.2145 | 45.4 | |
| 0.01 | 12.0 | 6.8729 | 1.0953 | 13.1982 | 2.3849 | - | - | - |
| 15.0 | 0.9642 | 2.0594 | 10.4216 | 3.5060 | - | - | - | |
| 18.0 | 0.5760 | 5.9033 | 10.2757 | 4.4911 | - | - | - | |
| 21.0 | 0.6740 | 3.1974 | 10.8972 | 8.3033 | - | - | - | |
| 24.0 | 12.830 | 1.1541 | 8.4180 | 3.8084 | 0.3305 | - | - | |
| 25.5 | 7.9332 | 1.0650 | 7.7545 | 3.7684 | 3.5917 | 2.0055 | 56.3 | |
| 27.0 | 8.6911 | 1.0220 | 8.8841 | 3.2509 | 3.9112 | 2.7123 | 71.0 | |
| 0.05 | 13.7 | 0.7721 | 3.4427 | 9.8614 | 1.4964 | - | - | - |
| 17.1 | 0.6101 | 5.7079 | 7.9588 | 2.9583 | - | - | - | |
| 20.6 | 1.3977 | 1.7510 | 8.8411 | 2.7169 | - | - | - | |
| 24.0 | 0.5584 | 6.4483 | 7.1948 | 3.4242 | 1.6842 | - | - | |
| 27.4 | 4.8800 | 1.2038 | 7.8248 | 4.2479 | 2.1687 | - | - | |
| 29.1 | 0.4242 | 3.2182 | 12.3183 | 5.4993 | 7.4177 | 3.0738 | 46.0 | |
| 30.8 | 0.4579 | 3.3866 | 4.8155 | 1.3154 | 1.9944 | 3.2081 | 8.2 | |
| 0.1 | 15.8 | 0.6634 | 11.2076 | 21.1316 | 3.4952 | - | - | - |
| 19.7 | 7.4510 | 1.3789 | 17.5394 | 6.2641 | - | - | - | |
| 23.6 | 0.6675 | 6.8392 | 21.8978 | 7.2299 | - | - | - | |
| 27.6 | 1.2806 | 2.2003 | 14.7146 | 12.3827 | 0.4193 | - | - | |
| 31.5 | 3.0127 | 1.3061 | 12.4878 | 4.2972 | 4.8699 | - | - | |
| 35.5 | 4.1327 | 1.4932 | 12.944 | 1.5625 | 1.2069 | 8.4631 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, P.; Wei, Y.; Li, M.; Topal, E.; Teng, X.; Wang, W. A Viscoelastic-Plastic Creep Model for Initial Damaged Coal Sample Affected by Loading Rate. Appl. Sci. 2025, 15, 5265. https://doi.org/10.3390/app15105265
Huang P, Wei Y, Li M, Topal E, Teng X, Wang W. A Viscoelastic-Plastic Creep Model for Initial Damaged Coal Sample Affected by Loading Rate. Applied Sciences. 2025; 15(10):5265. https://doi.org/10.3390/app15105265
Chicago/Turabian StyleHuang, Peng, Yimei Wei, Meng Li, Erkan Topal, Xinyong Teng, and Wei Wang. 2025. "A Viscoelastic-Plastic Creep Model for Initial Damaged Coal Sample Affected by Loading Rate" Applied Sciences 15, no. 10: 5265. https://doi.org/10.3390/app15105265
APA StyleHuang, P., Wei, Y., Li, M., Topal, E., Teng, X., & Wang, W. (2025). A Viscoelastic-Plastic Creep Model for Initial Damaged Coal Sample Affected by Loading Rate. Applied Sciences, 15(10), 5265. https://doi.org/10.3390/app15105265