Dual Partial Reversible Data Hiding Using Enhanced Hamming Code

Abstract

Traditional reversible data hiding (RDH) methods prioritize the exact recovery of the original cover image; however, this rigidity often hinders both capacity and design flexibility. This study introduces a partial reversible data hiding (PRDH) framework that departs from conventional standards by allowing reversibility relative to a generated cover image rather than the original. The proposed system leverages a dual-image structure and an enhanced HC(7,4) Hamming code to synthesize virtual pixels, enabling efficient and low-distortion syndrome-based encoding. Notably, it achieves embedding rates up to 1.5 bpp with PSNR values exceeding 48 dB. While the proposed method avoids auxiliary data, its reliability hinges on paired image availability, which is a consideration for real-world deployment. Demonstrated resilience to RS-based steganalysis suggests viability in sensitive domains such as embedding structured metadata in diagnostic medical imagery. Nonetheless, further evaluation across more diverse image types and attack scenarios is necessary in order to confirm its generalizability.

1. Introduction

Although the internet facilitates global communication, it cannot always be regarded as a fully secure channel, especially when handling sensitive information. Therefore, appropriate security protocols must be employed to ensure that confidential information is exchanged safely. A common approach to defending internet communications is to encrypt messages during transmission. However, because encrypted messages are often easy to recognize, they may themselves become targets of attack. An alternative method known as data hiding (DH) [1,2,3,4] involves embedding information within digital media. Because this process can appear the same as ordinary data transmission, it tends to draw less attention from potential attackers. Leveraging this characteristic can further strengthen the security of data exchanges.

DH can be broadly classified into reversible (RDH) and non-reversible (N-RDH) methods. RDH techniques have the characteristic that the original cover image can be fully restored after extracting the hidden data from the stego image. Several representative RDH algorithms have been proposed to date, including difference expansion (DE)-based methods [5,6,7], histogram shifting (HS) techniques [8,9,10], and prediction error expansion (PEE) [11].

First introduced by Tian in [5], the DE approach has demonstrated excellent performance in terms of embedding capacity. The histogram shifting (HS) method [8], first introduced in 2006, is regarded as an improvement over previous techniques due to the relatively lower distortion it causes to the cover medium. However, RDH schemes require a location map to embed data and recover the original cover image. While this method achieves good visual quality and reasonable embedding capacity, it has the drawback of requiring the transmission of two peak points and a zero-point pair to the receiver. PEE [11] involves obtaining prediction errors from the neighborhood of each pixel and embedding information bits into the expanded errors. If the difference between the original and predicted pixels is large, the embedding process can cause significant distortion to the cover image. DH methods based on ordered prediction can reduce distortion at low embedding rates.

On the other hand, secret sharing [12] has the feature that while n participants create n shadows using the same cover image to share data, the data can only be reconstructed when there are shadows of $k(k\le n)$ participants. If the number of participants is less than k, then data reconstruction will fail. In terms of data confidentiality, secret sharing is very powerful and can be used in various applications.

Dual image-based RDH [13,14,15,16,17,18,19,20,21,22,23,24,25,26] adopts some features of secret sharing, utilizing $n(=k=2)$ cover images. Thus, two shadow images are required to recover the original image. Chang et al. (2007) [13] introduced a dual-image RDH method using the exploitation modification direction (EMD). In their approach, two quinary secret data points are used to form a pair of stego pixels, with cover pixel pairs referenced according to the main and secondary diagonals of the EMD matrix. Later, Chang et al. (2013) [14] proposed an improved method for enhancing the visual quality of the stego images.

Lee and Huang (2013) [15] enhanced the visual quality of stego images by limiting modifications during the data hiding process to at most plus or minus one. Qin et al. [16] proposed an asymmetric dual-image RDH method in which the first stego image is generated using the EMD technique and the second is created based on three rule analyses applied to the first image. As a result, the first stego image experiences greater distortion compared to the second.

Lu et al. (2015) [17] discovered that the LSB-matching technique, originally used in N-RDH, could be adapted for dual-image schemes. However, because direct application was not feasible, they devised seven new rules for pixel recovery and applied them to the dual-image restoration process. They then demonstrated the effectiveness of their proposed method through experiments. In a separate work, Lu et al. (2015) [18] introduced a dual-image-based data hiding strategy utilizing a center folding technique. In this approach, secret data values are first compressed using the folding strategy, allowing more data to be embedded. The folded secret data are then hidden across two stego image pixels. Building on this, Yao et al. (2017) [19] focused on improving the visual quality of stego images by identifying and enhancing areas where Lu’s [18] method could be further optimized.

Jana et al. (2018) [21] proposed a method that extracts seven-pixel blocks from the original image and duplicates them into two arrays. The least significant bits (LSBs) of each array are adjusted using odd parity, increasing error resilience during transmission. Secret message bits are embedded into specific positions within these arrays while deliberately excluding certain predesignated positions reserved for integrity checks. During the embedding phase, bit modifications may introduce errors, which are subsequently detected and corrected by the receiver using Hamming (7,4) error correction codes. While this method demonstrates innovative integration of error-correcting codes, its low embedding capacity (0.21 bpp) limits its suitability for applications requiring high payloads.

Chen and Hong (2021) [23] introduced a dual-image RDH scheme utilizing the exploiting modification direction (EMD) method, achieving reversibility without additional overhead. While their method represents an improvement in eliminating auxiliary data, it falls short of surpassing earlier EMD-based methods such as that of Chang et al. (2013) [14]. In addition, it involves complex orientation combinations, which increase implementation complexity and make optimization difficult.

Lee and Chan (2024) [26] proposed a novel dual-image RDH method based on vector coordinates with triangular order coding (TOC), achieving superior embedding capacity and image quality without requiring additional side information. Their method focuses on position-based embedding, allowing for flexible adjustment of capacity via the k parameter. Wan et al.(2025) [27] proposed a multi-party RDH framework for medical information that utilizes texture-guided hierarchical quantization coding (TGHQC) to enhance embedding capacity and security. Additionally, both image owners and data providers perform data embedding through a dual embedding mechanism, allowing for role-specific data access. This method maintains data reversibility and security, thereby improving the efficiency of medical information management. Zhan et al. (2024) [28] proposed a reversible fragile watermarking scheme based on the insect matrix reversible embedding algorithm to enable full recovery of untampered cover images. Upon tampering, adaptive dual recovery schemes are employed to restore corrupted data while maintaining high image quality. Moreover, image-rendering techniques are introduced to enhance the accuracy of tampering detection, particularly in cases of tampering coincidence.

This study proposes an enhanced dual-image RDH method based on the HC(7,4) Hamming code to overcome limitations in prior methods. By applying this Hamming code to pixel groups across two cover images, our method significantly increases embedding capacity, reaching 1.5 bpp, which is over seven times greater than in Jana et al. (2018) [21]. In addition, our method ensures high visual quality with PSNR values between 48 and 49 dB, outperforming methods such as that of Chang et al. (2013) [14]. Compared to complex EMD-based design of Chen and Hong (2021) [23], our scheme offers a simpler and more efficient solution. Unlike halftone-based methods [25], it supports general grayscale images while guaranteeing full reconstructability, making it suitable for secure high-capacity RDH applications.

The key contributions of this paper are summarized as follows: (1) The proposed scheme achieves a high embedding capacity of up to 1.5 bpp by applying enhanced Hamming codes to virtual pixels constructed from two cover images, offering a significant improvement over prior dual-image RDH methods. (2) Despite the high embedding rate, our method maintains excellent stego image quality with PSNR values of 48–49 dB, demonstrating a balanced tradeoff between capacity and imperceptibility. (3) The proposed method’s robustness against statistical steganalysis is validated through RS analysis, confirming its resistance to detection and ensuring security in data hiding applications. (4) The reversibility of both cover images is guaranteed without additional side information, making the proposed scheme applicable to sensitive fields such as medical imaging and secure communications. (5) The proposed method is computationally efficient, relying on simple bitwise operations and lookup tables, enabling practical implementation in real-time systems.

The rest of this paper is organized as follows: Section 2 reviews the Hamming code used as a single error-correcting code along with the RDH method; Section 3 presents the proposed partial RDH method based on dual images; Section 4 presents the experimental results; and Section 5 presents the conclusions.

2. Preliminaries

2.1. Hamming Code

Error detection and correction are fundamental techniques for ensuring the reliability of data transmission. These processes are based on the principle of redundancy, wherein additional bits are appended to a message y according to predefined mathematical rules to enable error detection and correction at the receiver. Among various error control coding schemes, Hamming Code (HC) [29] has been widely adopted due to its simplicity and effectiveness in correcting single-bit errors. As a single-error-correcting linear block code with a minimum Hamming distance of three, HC remains a prevalent choice for many practical applications in digital communication.

In the notation $HC(n,k)$, n denotes the total length of a codeword, k represents the number of information bits, and $(n-k)$ corresponds to the number of parity bits. Given a k-bit information vector x, the corresponding n-bit codeword y is generated through the relation $y=xG$, where G is the $k\times n$ generator matrix. Errors may occur during transmission, resulting in a received vector $\tilde{y}$. The error vector is defined as $e=y-\tilde{y}$. If $e=0$, this implies that no error has occurred and that $\tilde{y}=y$.

To detect and correct errors, a parity-check matrix H of size $(n-k)\times n$ is employed, satisfying the relation $GH=0$. Applying the parity check matrix to the received word yields the syndrome $S=\tilde{y}H$. The syndrome S corresponds to a specific row of H, with its index indicating the position of the erroneous bit.

This relationship can be further elaborated as follows:

$$\tilde{y}·H^T=(e\oplus y)·H^T=e·H^T+y·H^T=e·H^T$$

(1)

where $y·H^T=0$ by construction; consequently, the syndrome directly reflects the error pattern, enabling accurate and efficient error correction. Consider the example of HC(7,4) with the following parity check matrix H (Equation (2)):

$$H=\left[\begin{array}{ccccccc}1& 0& 1& 1& 1& 0& 0\\ 1& 1& 1& 0& 0& 1& 0\\ 0& 1& 1& 1& 0& 0& 1\end{array}\right].$$

(2)

Example: Suppose that the received string is $\tilde{y}=\left(1110111\right)$. The syndrome is computed as $\tilde{y}H=\left[101\right]$. This syndrome corresponds to the 4th row of H, indicating an error in the 4th bit position. Therefore, the corrected string is $\left(1111111\right)$. If $\tilde{y}H=\left(000\right)$, this implies that no errors occurred.

2.2. Sun et al.’s RDH

Sun et al. [25] proposed an embedding procedure based on dual images utilizing the Hamming Code (7,4). Given a cover image I, two identical copies ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$ are generated. For the first cover image ${\mathbf{I}}_1$, a block $B_{1j}$ of size $1\times 7$ is selected and transformed into a codeword $y_j$. Binary hidden bits ${\delta }_j$ are embedded into $y_j$ by flipping its syndrome, computed using Equation (1) with ${\delta }_j$.

To apply changes to $y_j$, the new syndrome is calculated as ${\tilde{s}}_j=s_j\oplus {\delta }_j$. The new syndrome ${\tilde{s}}_j$ is then converted into a decimal value $D\left({\tilde{s}}_j\right)$, with $y_j$ modified as follows (Equation (3)):

$$y_{j,i}=\left\{\begin{array}{c}{y}_{j,i}, \mathrm{if} i\ne D\left({\tilde{s}}_j\right)\\ 1-y_{j,i}, \mathrm{if} i=D\left({\tilde{s}}_j\right)\end{array}\right.$$

(3)

where $i=1,2,\dots ,7$. For example, if $D\left({\tilde{s}}_j\right)=3$, then the least significant bit (LSB) of the third pixel in the block $y_j$ is flipped. The resulting new block $B_{1j}^{\prime }$ updates the corresponding block $B_{1j}$ in the image ${\mathbf{I}}_1$.

To construct the second stego image ${\mathbf{I}}_2$, the embedding process involves modifying $B_{2j}$ based on the hidden bits ${\delta }_j$. First, the block $B_{2j}$ is converted into $t_j$, representing the LSBs of the first three pixels of $B_{2j}$. The hidden bit ${\delta }_j$ is embedded into $t_j$ by applying $t_j=t_j\oplus {\delta }_j$. The modified blocks $B_{2j}^{\prime }$ are then used to reconstruct the stego image ${\mathbf{I}}_2^{\prime }$.

Based on this background knowledge, the following section provides a detailed explanation of the proposed dual PRDH method.

2.3. Definition of Partial Reversible Data Hiding

In conventional reversible data hiding (RDH) schemes, the cover image is identical to the original image, making complete recovery of the original content possible after data extraction. In contrast, the proposed method deliberately modifies the original image to generate two cover images by applying HC(7,4) Hamming code transformations to selected pixel groups. This controlled transformation enables efficient data embedding while preserving image quality and reversibility with respect to the generated cover images.

As a result, the recovery process yields the cover images rather than the original image itself. A cover image differs slightly from the original due to the deterministic bit-level modifications applied during the encoding phase. This characteristic underlies the terminology of partially reversible data hiding (PRDH); while the embedding and extraction processes are fully reversible with respect to the cover images, the transformation from the original to the cover images is not reversible without additional information, which by design is not retained.

In this dual-image PRDH framework, both cover images are constructed with pixel-wise modifications that preserve high fidelity to the original (PSNR exceeding 48 dB in our experiments), and both can be precisely recovered from the corresponding stego images. In this way, the proposed scheme achieves strong perceptual quality and operational reversibility while intentionally sacrificing full recovery of the unmodified original image in favor of increased embedding capacity and structural simplicity.

3. Proposed Scheme

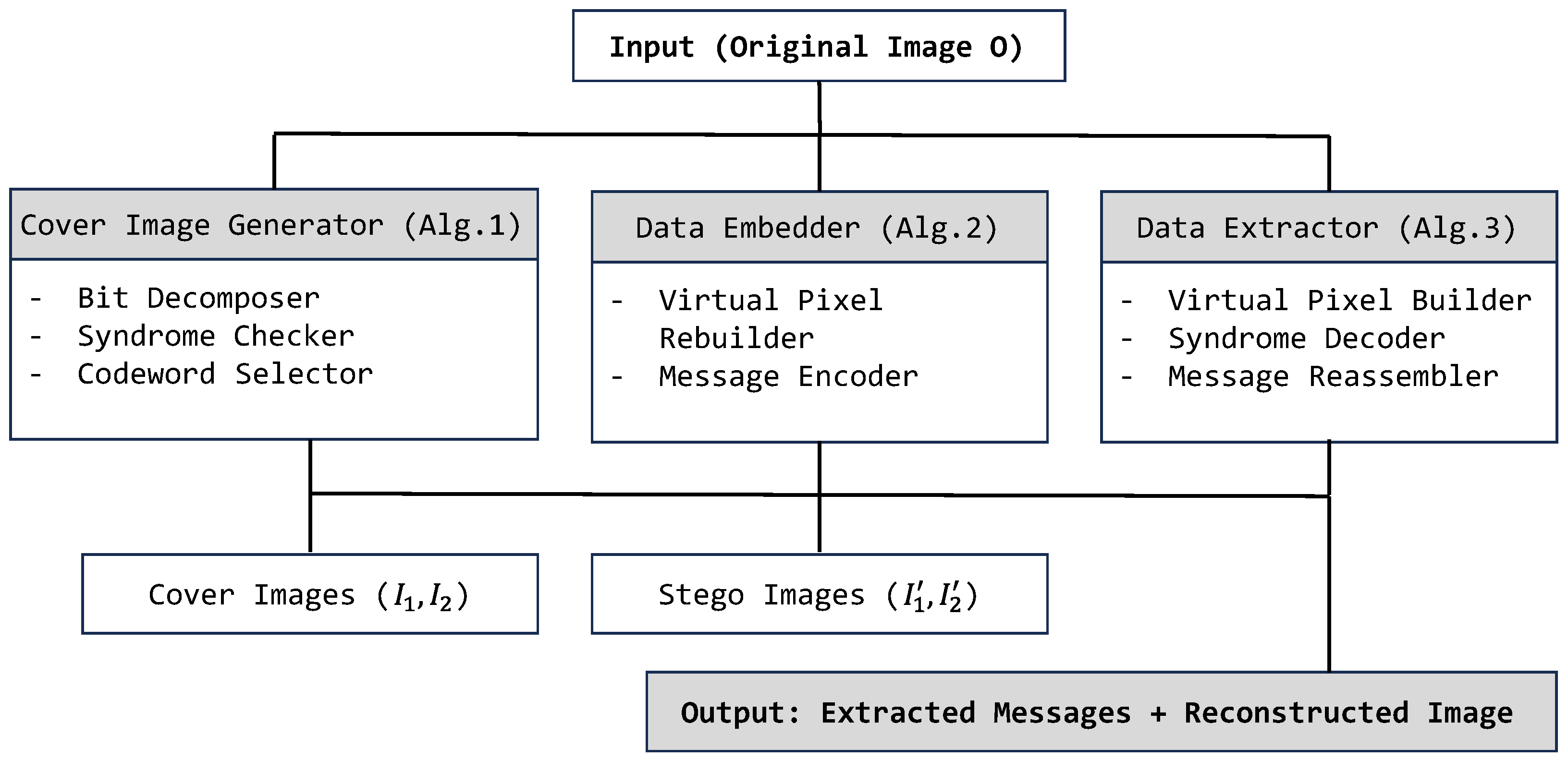
In this section, we propose an improved HC(7,4)-based dual-image reversible data hiding (RDH) technique. The overall conceptual workflow is illustrated in Figure 1, which briefly outlines the transition from the original image through the structurally correlated cover image generation to the subsequent embedding process. Figure 1 provides a high-level overview; in turn, Figure 2 shows the internal architecture, clearly detailing the module interactions, data flow, and role of each component.

Unlike conventional dual-image RDH techniques that simply replicate the original image into two identical cover images ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$, our method performs a controlled bit-level transformation using an enhanced HC(7,4) Hamming code. This transformation introduces fine-grained structural modifications in the bit-plane, enabling error correction while preserving visual fidelity. Initially, ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$ are generated by duplicating the original image. Then, for each pair of corresponding pixels from ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$, a virtual 7-bit vector y is constructed by selecting specific bits from both pixels.

If the virtual vector y fails to satisfy the Hamming code condition $y{H}^T=0$, a precomputed lookup table (LUT) is used to identify the closest codeword in the zero-syndrome coset. The selected codeword is then split and reassigned to the two pixels in such a way that structural similarity with the original is maintained. This process is applied iteratively across all pixels, resulting in two modified cover images that remain visually close to the original while ensuring compatibility with reversible data embedding in the following stage.

Figure 2 presents a more comprehensive block-level system architecture comprising three functional modules: the cover image generator, the data embedder, and the data extractor. These modules respectively correspond to Algorithms 1–3, and are designed for modular independence and engineering clarity.

Algorithm 1 Generation of Cover Images

Require: Original image O (grayscale, 8-bit)

Ensure: Cover images ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$ satisfying HC(7,4) constraints

1: ${\mathbf{I}}_1\leftarrow O$; ${\mathbf{I}}_2\leftarrow O$ 2: for$j=1$ to $size\left(O\right)$ do 3:      Read pixel $x_j$ from O                    ▹ Original pixel 4:      Extract $x_j^1$ and $x_j^2$ from $x_j$               ▹ Bit vectors from pixel 5:      Construct virtual pixel y             ▹ Selected bits from $x_j^1$ and $x_j^2$ 6:      $\tilde{\alpha }\leftarrow b2d(a_4 a_3 a_2 a_1)$                          ▹ Decimal from $x_j^1$ 7:      $\tilde{\beta }\leftarrow b2d(b_3 b_2 b_1)$                                ▹ Decimal from $x_j^2$ 8:      if $y{H}^T\ne 0$then                     ▹ Coset condition check 9:           Initialize ${\epsilon }_{min}\leftarrow \infty$, $h_{opt}\leftarrow \varnothing$ 10:        for each codeword h in LUT do             ▹ Candidate codeword 11:               $\alpha \leftarrow b2d(h_7 h_6 h_5 h_4)$                 ▹ Decimal upper bits 12:               $\beta \leftarrow b2d(h_3 h_2 h_1)$                   ▹ Decimal lower bits 13:                $\epsilon \leftarrow {(\alpha -\tilde{\alpha })}^2+{(\beta -\tilde{\beta })}^2$                ▹ Similarity measure 14:                if $\epsilon <{\epsilon }_{min}$ then 15:                      ${\epsilon }_{min}\leftarrow \epsilon$ 16:                      $h_{opt}\leftarrow h$                   ▹ Update best codeword 17:                end if 18:         end for 19:         Update $x_j^1$ and $x_j^2$ with $h_{opt}$ 20:      end if 21:      Save $x_j^1$ to ${\mathbf{I}}_1\left(j\right)$, $x_j^2$ to ${\mathbf{I}}_2\left(j\right)$ 22: end for

Algorithm 2 Embedding Procedure

Require: Two cover images ${\mathbf{I}}_1$, ${\mathbf{I}}_2$; secret bits $M=(m_1,m_2,\dots ,m_n)$

Ensure: Two stego images $\Delta {\mathbf{I}}_1$, $\Delta {\mathbf{I}}_2$

1: $\Delta {\mathbf{I}}_1\leftarrow {\mathbf{I}}_1$; $\Delta {\mathbf{I}}_2\leftarrow {\mathbf{I}}_2$ 2: $k\leftarrow 1$                             ▹ Secrect bit index 3: for $j=1$ to $size\left({\mathbf{I}}_1\right)$ do 4:      Access pixel $x_j$ from ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$ 5:      Construct virtual pixel y according to Equation (4) 6:      $\tilde{\alpha }\leftarrow b2d(a_4 a_3 a_2 a_1)$ 7:      $\tilde{\beta }\leftarrow b2d(b_3 b_2 b_1)$ 8:      Extract secret bits $m_k^{k+2}$ (3 bits) 9:      if coset(y) ≠ target coset leader derived from $m_k^{k+2}$ then 10:          Initialize ${\epsilon }_{min}\leftarrow \infty$, $h_{opt}\leftarrow \varnothing$ 11:          for each codeword h in LUT do 12:                $\alpha \leftarrow b2d(h_7 h_6 h_5 h_4)$ 13:                $\beta \leftarrow b2d(h_3 h_2 h_1)$ 14:                $\epsilon \leftarrow {(\alpha -\tilde{\alpha })}^2+{(\beta -\tilde{\beta })}^2$ 15:                if $\epsilon <{\epsilon }_{min}$ then 16:                      ${\epsilon }_{min}\leftarrow \epsilon$ 17:                      $h_{opt}\leftarrow h$ 18:                end if 19:           end for 20:           Update $x_j^1$ and $x_j^2$ according to Equation (6) 21:      end if 22:      Save updated $x_j^1$ to $\Delta {\mathbf{I}}_1\left(j\right)$; $x_j^2$ to $\Delta {\mathbf{I}}_2\left(j\right)$ 23:      $k\leftarrow k+3$                      ▹ Move to next 3 secret bits 24: end for

Algorithm 3 Extraction and Recovery Procedure

Require: Two stego images $\Delta {\mathbf{I}}_1$, $\Delta {\mathbf{I}}_2$

Ensure: Recovered cover images ${\mathbf{I}}_1$, ${\mathbf{I}}_2$, and extracted secret bits m

1: Initialize: $k\leftarrow 1$ 2: for$j=1$ to $size(\Delta {\mathbf{I}}_1)$ do 3:      Access pixel data from $\Delta {\mathbf{I}}_1$ and $\Delta {\mathbf{I}}_2$ 4:      Reconstruct virtual pixel y using selected bits 5:      Calculate syndrome $S\leftarrow y{H}^T$             ▹ Extract hidden bits 6:      Store S into $m(k:k+2)$; $k\leftarrow k+3$ 7:      $\tilde{\alpha }\leftarrow b2d(a_4 a_3 a_2 a_1)$; $\tilde{\beta }\leftarrow b2d(b_3 b_2 b_1)$ 8:      Initialize ${\epsilon }_{min}\leftarrow \infty$, $h_{opt}\leftarrow \varnothing$ 9:      for each codeword h in LUT do 10:                $\alpha \leftarrow b2d(h_7 h_6 h_5 h_4)$; $\beta \leftarrow b2d(h_3 h_2 h_1)$ 11:                $\epsilon \leftarrow {(\alpha -\tilde{\alpha })}^2+{(\beta -\tilde{\beta })}^2$ 12:                if $\epsilon <{\epsilon }_{min}$ then 13:                      ${\epsilon }_{min}\leftarrow \epsilon$; $h_{opt}\leftarrow h$ 14:                end if 15:      end for 16:      Update $x_j^1$ and $x_j^2$ based on $h_{opt}$           ▹ Recover cover pixels 17:      Save $x_j^1$ into ${\mathbf{I}}_1\left(j\right)$; $x_j^2$ into ${\mathbf{I}}_2\left(j\right)$ 18: end for

The process begins with the Cover Image Generator, which takes the original image O and produces two structurally optimized cover images ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$ using HC(7,4)-based syndrome modulation. These images are generated to support reliable and low-distortion embedding.

Next, the Data Embedder receives the cover images and a payload bitstream, then embeds the payload through a syndrome-modulated mapping strategy using a preconstructed lookup table. This process results in two stego images ${\mathbf{I}}_1^{\prime }$ and ${\mathbf{I}}_2^{\prime }$ containing the hidden information while preserving high image fidelity.

Finally, the Data Extractor takes the stego images as input, reconstructs the original message by performing parity-check-based extraction, and reverses the embedding steps to accurately restore the original image. This module ensures lossless recovery of both the hidden data and the original content.

3.1. Generation of Cover Images

In this subsection, we present the process for generating two cover images using the improved HC(7,4) scheme. The detailed procedure is summarized in Algorithm 1.

Initially, two copies of the original image are created, denoted by ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$. For each pixel $x_j$ in the original image O, the same value is assigned to the corresponding pixels in ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$, denoted as $x_j^1$ and $x_j^2$, respectively. Each of these pixel values is represented in 8-bit binary format as

$$\begin{array}{cc}\hfill x_j^1& =(a_8 a_7 a_6 a_5 a_4 a_3 a_2 a_1),\hfill \\ \hfill x_j^2& =(b_8 b_7 b_6 b_5 b_4 b_3 b_2 b_1),\hfill \end{array}$$

where $a_i$ and $b_i$ represent individual bits of $x_j^1$ and $x_j^2$.

A virtual 7-bit pixel y is then constructed by concatenating selected bits from $x_j^1$ and $x_j^2$:

$$y=(a_4 a_3 a_2 a_1||b_3 b_2 b_1)$$

(4)

where $\left|\right|$ denotes bit-wise concatenation. Here, $a_4$ corresponds to the most significant bit (MSB) of y and $b_1$ to the least significant bit (LSB) of y.

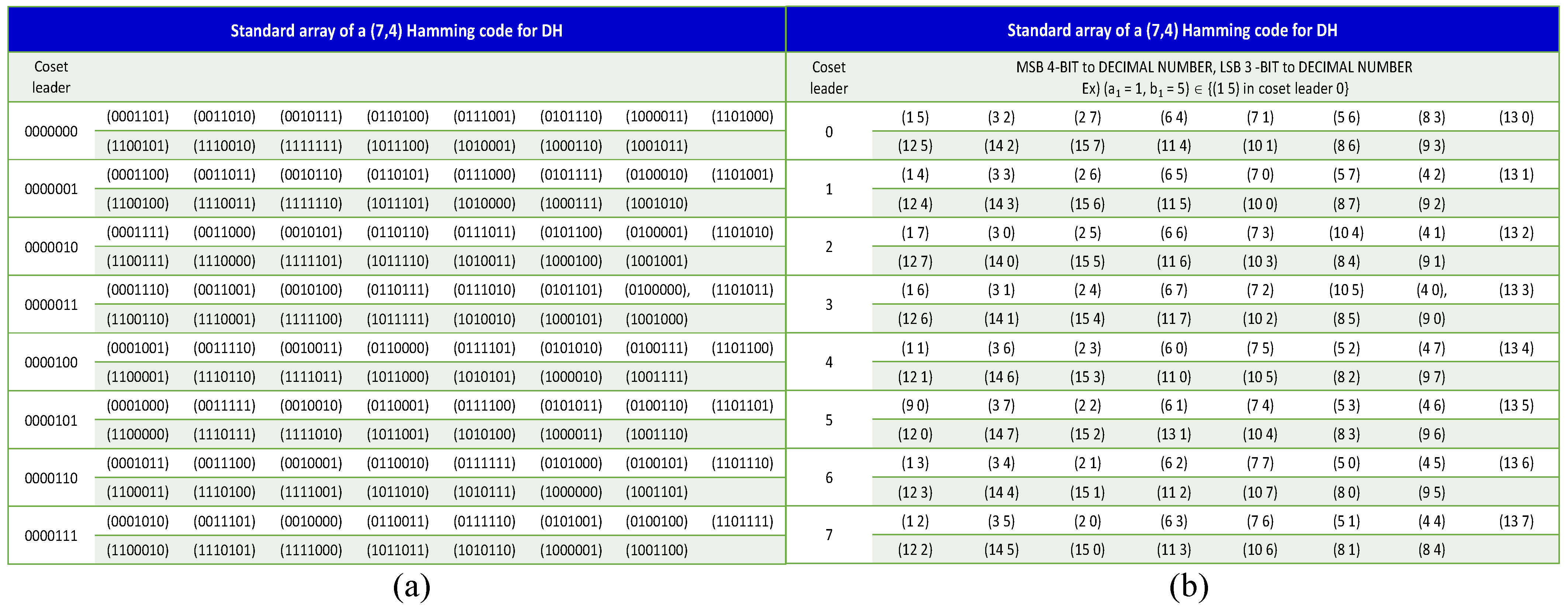
To ensure that y satisfies the Hamming code constraint $y{H}^T=0$, a syndrome check is performed. If the condition is not satisfied, the closest valid codeword is selected from a preconstructed lookup table (LUT) derived from the standard array of HC(7,4) codewords, as shown in Figure 3. This enables efficient correction by identifying the nearest codeword within the corresponding coset. The following algorithm corresponds to the Cover Image Generator module described in Figure 2, and performs syndrome-based modifications to construct cover images $I_1$ and $I_2$.

To formalize this process, the selection of the most suitable codeword h is defined as a distortion minimization problem over the zero-syndrome coset ${\mathcal{C}}_0$:

$$\underset{h\in {\mathcal{C}}_0}{min}\epsilon \left(h\right)={(\alpha -\tilde{\alpha })}^2+{(\beta -\tilde{\beta })}^2$$

(5)

where h is a candidate codeword from the LUT and $\tilde{\alpha },\tilde{\beta }$ are derived from the original bits of $x_j^1$ and $x_j^2$, respectively. This formulation explicitly expresses the objective of minimizing perceptual distortion while satisfying HC(7,4) compliance.

Here, $\epsilon$ quantifies the difference between the original and candidate virtual pixel representations. The codeword $h=(h_7,h_6,h_5,h_4,h_3,h_2,h_1)$ that minimizes $\epsilon$ is selected as the best match. Among these bits, the first four $(h_7,h_6,h_5,h_4)$ are written into the least significant bits of $x_j^1$ in ${\mathbf{I}}_1$ and the last three $(h_3,h_2,h_1)$ are written into the least significant bits of $x_j^2$ in ${\mathbf{I}}_2$.

This process is repeated for every pixel in the original image. As a result, two structurally correlated cover images ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$ are generated, both of which are optimized for low-distortion reversible data embedding.

3.2. Data Embedding

In this subsection, we describe the detailed procedure for embedding secret data into two cover images by applying the improved HC(7,4) scheme. The overall process is summarized in Algorithm 2.

In HC(7,4) codes, coset leaders correspond to eight distinct patterns, which can be naturally represented by 3-bit binary numbers ranging from 000 to 111. Thus, in the proposed embedding scheme, each group of three secret bits is directly mapped to a target coset leader. This mapping forms the basis for aligning the virtual pixel structure with the intended secret message. For each pixel location, the corresponding values from ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$ are accessed to reconstruct the virtual pixel y by selecting and concatenating specific bits, as defined in Equation (4).

To embed secret data, a group of three consecutive secret bits $m_k^{k+2}$ is selected. The three bits are interpreted as the target coset leader corresponding to the intended secret message. Thus, the coset leader pattern is defined as a 3-bit sequence indicating the desired coset class for the constructed virtual pixel.

Although the same error minimization formula presented in Equation (5) is employed, its purpose in this phase differs from that in cover image generation (Section 3.1). While the previous minimization aimed solely at ensuring codeword validity, here it is driven by the secret bits to align the virtual pixel with the target coset leader while minimizing visual distortion.

If the current virtual pixel y does not belong to the desired coset (i.e., the syndrome of y does not match the target coset leader pattern), then the closest matching codeword h is selected from the lookup table (LUT) by minimizing the error $\epsilon$ as defined in Equation (5).

After selecting the optimal codeword h, the cover pixel bits are updated according to

$$\left\{\begin{array}{c}{x}_j^1=(a_8 a_7 a_6 a_5\left|\right|h_7 h_6 h_5 h_4),\\ x_j^2=(b_8 b_7 b_6 b_5 b_4\left|\right|h_3 h_2 h_1).\end{array}\right.$$

(6)

Finally, the modified pixels are stored into the stego images $\Delta {\mathbf{I}}_1$ and $\Delta {\mathbf{I}}_2$. The full embedding process is outlined in Algorithm 2.

3.3. Data Extraction And Recovery Procedure

In this subsection, we describe the procedure for extracting the hidden information and recovering the original cover images from the two stego images $\Delta {\mathbf{I}}_1$ and $\Delta {\mathbf{I}}_2$ generated during the embedding process (Section 3.3). Based on the virtual pixel construction method described in Section 3.1 and the syndrome computation process defined in Section 3.3, the extraction and recovery are performed sequentially for each pixel pair in the stego images.

For data extraction, the virtual pixel y is reconstructed at each pixel position and the syndrome S is recalculated using the previously defined parity-check matrix H. Each extracted syndrome directly corresponds to a group of three secret bits, which are sequentially collected to form the hidden message vector m.

Following extraction, the recovery of the original cover images proceeds by leveraging the property that all virtual pixels belonged to the zero-syndrome coset prior to embedding. In this way, the codeword associated with the zero syndrome that minimizes the discrepancy from the current stego pixel is identified for each virtual pixel. The optimal codeword is determined by minimizing the Euclidean error between the extracted bits and the candidate codewords, following the error metric introduced in Section 3.1.

After the nearest codeword is found, the cover pixel values are reconstructed accordingly, restoring the two original cover images ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$.

The overall extraction and recovery process is summarized in Algorithm 3.

3.4. Numerical Examples

3.4.1. Generating Two Cover Images

Suppose that a pixel in the original image is provided by

$$\begin{array}{c}\hfill x_j={\left[1 0 0 1 1 1 0\right]}^T.\end{array}$$

Following the generation procedure described in Section 3.1, two cover pixels are derived as follows:

(1)

Initialization: Copy the original pixel to create two initial cover pixels

$$\begin{array}{cc}\hfill x_j^1& =\left[1 0 0 1 1 1 0\right],\hfill \\ \hfill x_j^2& =\left[1 0 0 1 1 1 0\right].\hfill \end{array}$$

(2)

Virtual Pixel Construction: A virtual pixel y is constructed by selecting four LSB bits from $x_j^1$ and three LSB bits from $x_j^2$, as defined in Equation (4):

$$\begin{array}{c}\hfill y=\left[1 1 1 0 1 1 1\right].\end{array}$$

This process compresses the essential information of two pixels into a compact 7-bit structure, facilitating efficient error management.

(3)

Decimal Conversion: The selected bits are separated into two groups and converted into decimal:

$$\begin{array}{cc}\hfill \tilde{\alpha }& =b2d\left(\left[1 1 1 0\right]\right)=14,\hfill \\ \hfill \tilde{\beta }& =b2d\left(\left[1 1 1\right]\right)=7.\hfill \end{array}$$

(4)

Codeword Selection: To ensure that the virtual pixel belongs to a valid codeword set, the closest matching codeword is identified by minimizing the error defined in Equation (5):

$$\begin{array}{cc}\hfill \epsilon & =min\left({({\alpha }_i-\tilde{\alpha })}^2+{({\beta }_i-\tilde{\beta })}^2\right)\hfill \\ \hfill & =min\left({(15-14)}^2+{(7-7)}^2\right)=1.\hfill \end{array}$$

Thus, the optimal codeword h is determined as:

$$\begin{array}{c}\hfill h=\left[1 1 1 1 1 1 1\right].\end{array}$$

(5)

Cover Pixel Reconstruction: Using the selected codeword h, the two cover pixels are reconstructed according to Equation (6):

$$\begin{array}{cc}\hfill x_j^1& =\left[1 0 0 1 1 1 1\right],\hfill \\ \hfill x_j^2& =\left[1 0 0 1 1 1 1\right].\hfill \end{array}$$

(6)

Assignment: The updated pixels $x_j^1$ and $x_j^2$ are assigned to their respective positions within the cover images ${\mathbf{I}}_1$ and ${\mathbf{I}}_2$.

(7)

Iteration: The above process is repeated for each pixel of the original image to complete the construction of the two cover images.

3.4.2. Data Embedding Phase

Assume that the secret bits to be embedded are

$$\begin{array}{c}\hfill m=\left[1 0 1\right].\end{array}$$

The two cover pixels prepared for embedding are

$$\begin{array}{c}\hfill x_j^1=\left[1 0 0 1 1 1 1\right],x_j^2=\left[1 0 0 1 1 1 1\right].\end{array}$$

The embedding process proceeds as follows:

(1)

Virtual Pixel Reconstruction: A virtual pixel is formed:

$$\begin{array}{c}\hfill y=\left[1 1 1 1 1 1 1\right].\end{array}$$

(2)

Target Coset Leader Mapping: The secret bits $m=\left[1 0 1\right]$ correspond to a coset leader index of 5.

(3)

Optimal Codeword Identification: Among the codewords associated with coset leader 5, the optimal codeword minimizing the error is selected:

$$\begin{array}{cc}\hfill \epsilon & =min\left({(14-15)}^2+{(7-7)}^2\right)=1,\hfill \\ \hfill h& =[1 1 1 0 1 1 1].\hfill \end{array}$$

(4)

Stego Pixel Reconstruction: The cover pixels are updated as follows:

$$\begin{array}{cc}\hfill x_j^1& =[1 0 0 1 1 1 0],\hfill \\ \hfill x_j^2& =[1 0 0 1 1 1 1].\hfill \end{array}$$

These updated pixels are stored in the stego images $\Delta {\mathbf{I}}_1$ and $\Delta {\mathbf{I}}_2$ respectively.

3.4.3. Data Extraction and Recover Phase

Given two stego pixels

$$\begin{array}{c}\hfill x_j^1=\left[1 0 0 1 1 1 0\right],x_j^2=\left[1 0 0 1 1 1 1\right],\end{array}$$

extraction and recovery are performed as follows:

(1)

Virtual Pixel Reconstruction: Reconstruct the virtual pixel

$$\begin{array}{c}\hfill y=\left[1 1 1 0 1 1 1\right].\end{array}$$

(2)

Syndrome Computation: Compute the syndrome to extract the embedded bits:

$$\begin{array}{c}\hfill S=y{H}^T=\left[1 0 1\right]=5,\end{array}$$

recovering the secret bits $m=\left[1 0 1\right]$.

(3)

Cover Pixel Recovery: To restore the original cover images, the closest codeword associated with zero syndrome is selected:

$$\begin{array}{cc}\hfill \epsilon & =min\left({(15-14)}^2+{(7-7)}^2\right)=1,\hfill \\ \hfill h& =\left[1 1 1 1 1 1 1\right].\hfill \end{array}$$

The recovered cover pixels are

$$\begin{array}{cc}\hfill x_j^1& =\left[1 0 0 1 1 1 1\right],\hfill \\ \hfill x_j^2& =\left[1 0 0 1 1 1 1\right].\hfill \end{array}$$

Thus, both the hidden secret data and the cover images are perfectly restored.

4. Experimental Results and Discussions

In this section, we present the experimental evaluation of the proposed partial reversible data hiding (PRHB) method based on the enhanced HC(7,4) Hamming code. The primary objective of the experiments is to demonstrate the feasibility and advantages of the proposed technique through comprehensive simulations. All experiments were conducted on a system equipped with a Core i5-8250U processor (1.60 GHz) and 8 GB of RAM, utilizing Matlab R2019b as the simulation platform. This study aims to improve both embedding capacity and image quality through a dual-image RDH scheme. The proposed approach addresses prior limitations by incorporating structured virtual pixel construction and optimized codeword selection.

Unlike conventional RDH, our design avoids side-information overhead and achieves near-constant embedding performance across all tested images. The improvements introduced in the data embedding process can be summarized as follows:

• Optimized Virtual Pixel Construction: Virtual pixels are generated from two cover images to enhance error correction performance.
• Complete Data Recovery Without Auxiliary Information: The embedded data can be perfectly extracted without the need for any additional side information.
• Adaptive Tradeoff Between Embedding Capacity and Visual Distortion: The method employs an adaptive adjustment strategy to maintain a balance between data embedding rate and image quality.
• High Stego Image Quality: The visual quality of the stego images is preserved, as quantitatively measured by the peak signal-to-noise ratio (PSNR) [2].

To objectively evaluate the performance of the proposed method, extensive experiments were carried out using nine standard 512 × 512 grayscale images from the USC-SIPI dataset [30] (Figure 4). The evaluation metrics included embedding capacity (EC), embedding rate (ER, measured in bits per pixel, bpp, Equation (7)), and PSNR.

By comparing these metrics with those achieved by conventional dual-image-based RDH methods, the superiority of the proposed scheme in terms of both capacity and visual quality is clearly demonstrated. The embedding rate (ER) is defined by Equation (7):

$$ER={\displaystyle \frac{C}{2\times N\times N}}\left(bpp\right).$$

(7)

The PSNR [2] is widely employed as an objective metric to evaluate the quality of marked images. It quantifies the difference between the reference image and the distorted (or marked) image in a logarithmic scale. The PSNR is defined by Equation (8):

$$PSNR=10{log}_{10}\left({\displaystyle \frac{{255}^2}{MSE}}\right)$$

(8)

where ${255}^2$ represents the square of the maximum possible pixel value in an 8-bit image. The mean squared error (MSE), provided by Equation (9), measures the average squared intensity difference between corresponding pixels of the original and marked images:

$$MSE={\displaystyle \frac{1}{N\times N}}\sum _{i=1}^{N\times N}{(x_i-x_i^{\prime })}^2.$$

(9)

In this expression, $x_i$ and $x_i^{\prime }$ denote the pixel values of the original and marked images at position i, respectively. The error term $e={(x_i-x_i^{\prime })}^2$ reflects the squared deviation at each pixel. A lower MSE value indicates smaller distortion, leading to a higher PSNR value, which implies better perceived image quality. Typically, for 8-bit images, PSNR values for acceptable lossy compression range from 30 dB to 50 dB. A higher PSNR generally correlates with improved visual fidelity.

Table 1. Comparison of PSNR for all enhanced HC(7,4) PRDH when embedding bits is 10,000 bits.

Images	PSNR(CI–OI)	PSNR(CI–OI)	PSNR(SI–CI)	PSNR(SI–CI)	PSNR(SI–OI)	PSNR(SI–OI)
	#1	#2	#1	#2	#1	#2
Elaine	47.0974	48.6768	67.1575	68.0772	47.0974	48.6768
Peppers	47.1624	48.7094	67.1219	67.7983	47.1326	48.6648
Airplane	47.2557	48.7013	67.1827	68.1199	47.2268	48.6643
Boat	47.3741	48.7739	67.2000	68.0625	47.345	48.7325
Goldhill	47.1820	48.7160	67.3303	68.1748	47.1572	48.6749
Couple	46.9334	48.5882	67.2376	68.0349	46.9039	48.5485
Baboon	47.2004	48.7209	67.2417	67.8930	47.1744	48.6777
Zelda	47.2009	48.7249	67.1814	67.9371	47.1751	48.685o
Barbara	47.3593	48.6522	67.3372	68.1084	47.3307	48.6082
Average	47.1962	48.696	67.2211	68.0229	47.1715	48.6592

presents a comparative analysis of PSNR values for cover images (#1 and #2) and stego images (#1 and #2) when embedding 10,000 bits using the enhanced HC(7,4) PRDH method. The evaluation focuses on three key PSNR measurements:

• PSNR(CI−OI): The PSNR between the original image (OI) and the cover image (CI), indicating the degree of modification introduced by the cover image generation process.
• PSNR(SI−CI): The PSNR between the cover image and the stego image (SI), measuring the level of distortion caused by data embedding.
• PSNR(SI−OI): The PSNR between the stego image and the original image, providing an overall assessment of image quality after data embedding.

Across all test images, PSNR(CI−OI) exhibits stable values around 47 dB for cover image #1 and 48 dB for cover image #2, indicating that the initial cover image generation introduces minimal distortion. Notably, PSNR(SI−CI) reaches approximately 67 dB for stego image #1 and 68 dB for stego image #2, demonstrating that the data embedding process maintains high image quality with minimal impact on the cover image. The final PSNR(SI−OI) values, which range between 47 dB and 48.7 dB, further confirm that the proposed method effectively preserves the original image quality. Given these results, PSNR(SI−CI) was selected as the primary metric for evaluating stego image quality in this study, as it directly reflects the influence of the embedding process while isolating any distortions introduced during cover image generation. These findings validate the efficiency of our enhanced HC(7,4) PRDH method in achieving high embedding capacity while maintaining superior image fidelity.

Table 2. Comparison of maximum embedding ratio with different methods.

Images	Lee et al. [15]	Liu et al. [20]	Lin et al. [24]	Chen et al. [22]	Chen et al. [23]	Jana et al. [21]	Proposed
Elaine	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Pepper	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Airplane	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Boat	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Goldhill	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Couple	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Baboon	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Zelda	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Barbara	1.09	1.00	1.07	1.14	1.56	0.21	1.50
Average	1.09	1.00	1.07	1.14	1.56	0.21	1.50

presents a comparative analysis of the maximum embedding ratio (ER) across various reversible data hiding methods, including those proposed by Lee et al. (2013) [15], Liu et al. (2018) [20], Lin et al. (2019) [24], Chen et al. (2020) [22], Chen et al. (2021) [23], and Jana et al. (2018) [21], alongside our proposed method.

Among the evaluated techniques, the highest embedding ratio is achieved by the method of Chen et al. (2021) [23], which reaches a maximum ER of 1.56, demonstrating its superior capacity for data embedding. Our proposed method achieves an ER of 1.50, which is the second-highest among the compared methods and only 0.06 lower than Chen et al. (2021) [23]. Despite this slight reduction in embedding capacity, our approach maintains a balance between embedding efficiency and computational complexity, offering a simpler and more efficient process for data hiding, extraction, and restoration.

Other methods, such as those presented by Lee et al. (2013) [15], Liu et al. (2018) [20], and Lin et al. (2019) [24], which exhibit embedding ratios ranging from 1.00 to 1.14. In comparison, our proposed method offers a significant improvement in data hiding capacity. Notably, the method presented by Jana et al. (2018) [21] has the lowest embedding ratio of 0.21, indicating a strong tradeoff between image quality preservation and data embedding capacity. Overall, our proposed method provides a near-optimal embedding ratio while maintaining computational efficiency, making it a strong candidate for practical reversible data hiding applications where both high capacity and low complexity are required.

Note: The embedding ratio (ER) is constant at 1.50 across all tested images. This is a deterministic result of the proposed scheme, with a standard deviation of 0.00. This consistency reflects the deterministic nature of the proposed embedding mechanism and demonstrates its robustness across diverse image contents.

Table 3. Comparison of maximum bpp and PSNR of existing methods and our proposed method.

Method	Measure	Elaine	Peppers	Barbara	Goldhill
Chang et al. (2007) [13]	bpp	1.00	1.00	1.00	1.00
	PSNR#1	45.12	45.14	45.13	45.13
	PSNR#2	45.13	45.15	45.11	45.14
Chang et al. (2013) [14]	bpp	1.53	1.53	1.53	1.53
	PSNR#1	39.89	39.94	39.89	39.9
	PSNR#2	39.89	39.94	39.89	39.9
Lee & Huang (2013) [15]	bpp	1.07	1.07	1.07	1.07
	PSNR#1	49.76	49.75	49.75	49.77
	PSNR#2	50.42	50.34	50.44	50.54
Qin et al. (2015) [16]	bpp	1.00	1.00	1.00	1.00
	PSNR#1	52.11	51.25	52.12	52.12
	PSNR#2	41.58	41.52	41.58	41.58
Lu et al. (2015) [17]	bpp	1.00	1.00	1.00	1.00
	PSNR#1	51.13	51.15	49.22	49.23
	PSNR#2	51.15	51.14	49.2	49.18
Jana et al. (2018) [21]	bpp	0.21	0.21	0.21	0.21
	PSNR#1	52.71	52.67	52.7	52.73
	PSNR#2	52.81	52.72	52.76	52.78
Proposed scheme	bpp	1.50	1.50	1.50	1.50
	PSNR#1	48.19	48.2	48.22	48.2
	PSNR#2	49.01	49.02	48.96	49.06

presents a comparative analysis of the embedding capacity (bpp) and peak signal-to-noise ratio (PSNR) across existing reversible data hiding methods, including those proposed by Chang et al. (2007) [13], Chang et al. (2013) [14], Lee & Huang (2013) [15], Qin et al. (2015) [16], Lu et al. (2015) [17], and Jana et al. (2018) [21], alongside our proposed approach.

Among the evaluated methods, the highest embedding rate is achieved by Chang et al. (2013) [14] with 1.53 bpp, followed closely by our proposed method, which attains 1.50 bpp. In contrast, the method by Jana et al. (2018) [21] exhibits the lowest embedding rate, limited to 0.21 bpp. Notably, Qin et al. (2015) [16] and Jana et al. (2018) [21] achieve the highest PSNR values, exceeding 52 dB, albeit at the cost of significantly lower embedding rates. This trend suggests an inherent tradeoff between embedding capacity and image quality, where methods optimizing for PSNR often exhibit lower data-hiding capability.

Our proposed scheme effectively balances embedding capacity and image quality, achieving a competitive 48–49 dB PSNR while maintaining a high embedding rate. Compared to other methods with similar embedding rates, such as that of Chang et al. (2013) [14], our approach demonstrates superior PSNR performance, indicating reduced distortion in the stego images. This suggests that the proposed method offers an optimal tradeoff between embedding rate and visual fidelity, making it a strong candidate for practical reversible data hiding applications.

The proposed method shows a fixed embedding rate of 1.50 bpp across all images, resulting in a standard deviation of 0.00. In addition, the PSNR values exhibit only minor variations (standard deviation ≤ 0.06 dB), confirming our method’s consistent visual quality across different images.

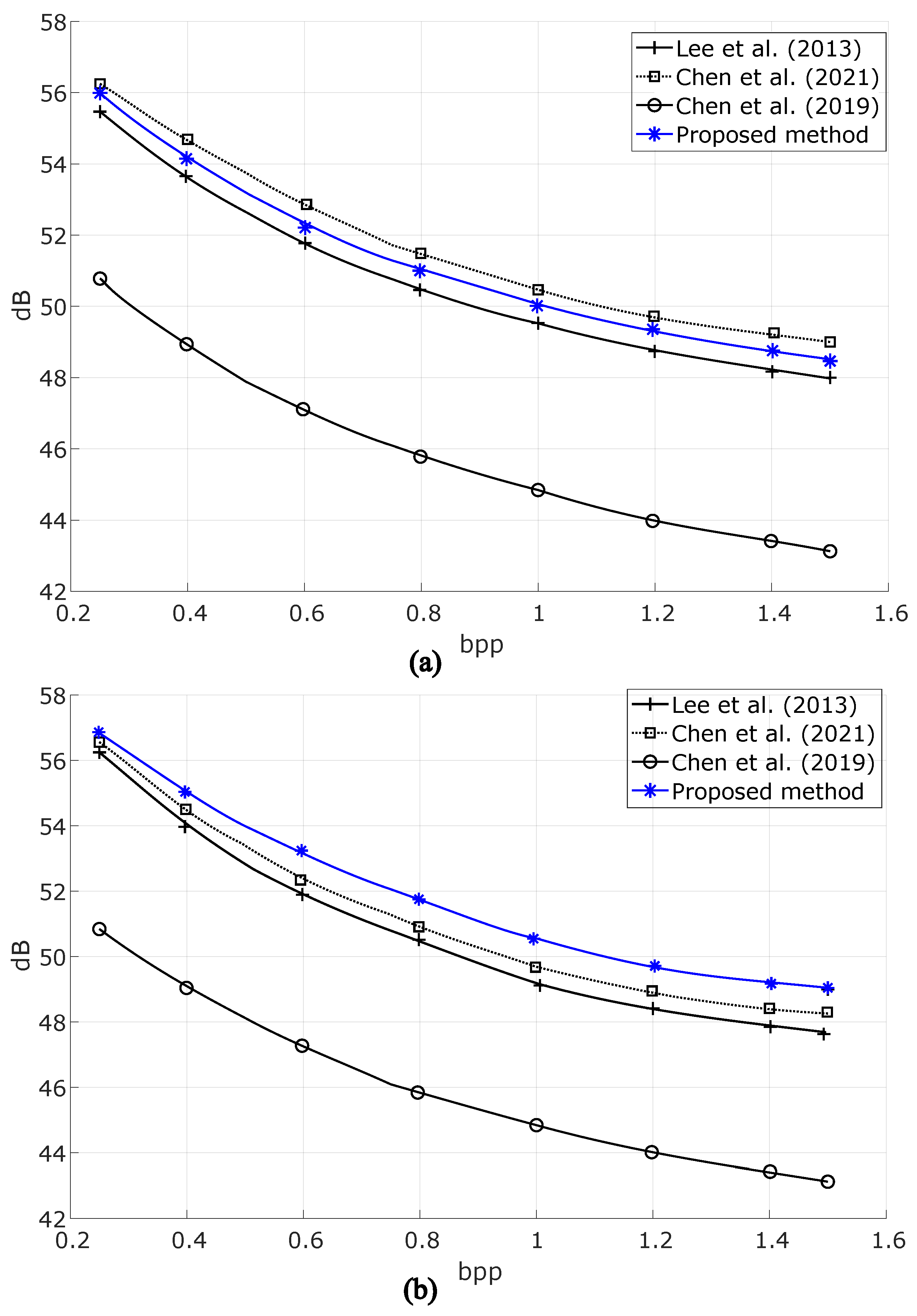
Figure 5a presents a comparative analysis of the average PSNR of stego image #1 across different reversible data hiding methods. The embedding rate (ER) of the proposed method is measured at 1.5 bpp. Among the evaluated techniques, the method proposed by Chen et al. (2021) [23] is also capable of embedding up to 1.5 bpp, although achieving a PSNR approximately 1–2 dB higher than the proposed method. Overall, except for the method of Chen et al. (2019) [22], all evaluated techniques maintain a marked image quality above 48 dB even at embedding rates exceeding 1.5 bpp, demonstrating a balance between high embedding capacity and imperceptibility.

In Figure 5b, the relationship between PSNR and bpp for stego image #2 is illustrated. At an embedding rate of 0.2 bpp, the proposed method achieves a PSNR of 56.83 dB, marking the highest recorded value among all evaluated approaches. Furthermore, the proposed method consistently maintains the highest PSNR across the entire embedding range up to 1.5 bpp, ensuring superior image quality preservation. On the other hand, the method of Chen et al. (2021) [23] achieves the second-highest PSNR performance among the evaluated techniques, further demonstrating its effectiveness in maintaining image quality.

Overall, our proposed method effectively balances high embedding capacity and PSNR, making it a competitive solution for reversible data hiding. The ability to sustain high PSNR values across a broad embedding range highlights its robustness in preserving image quality while embedding a substantial amount of data.

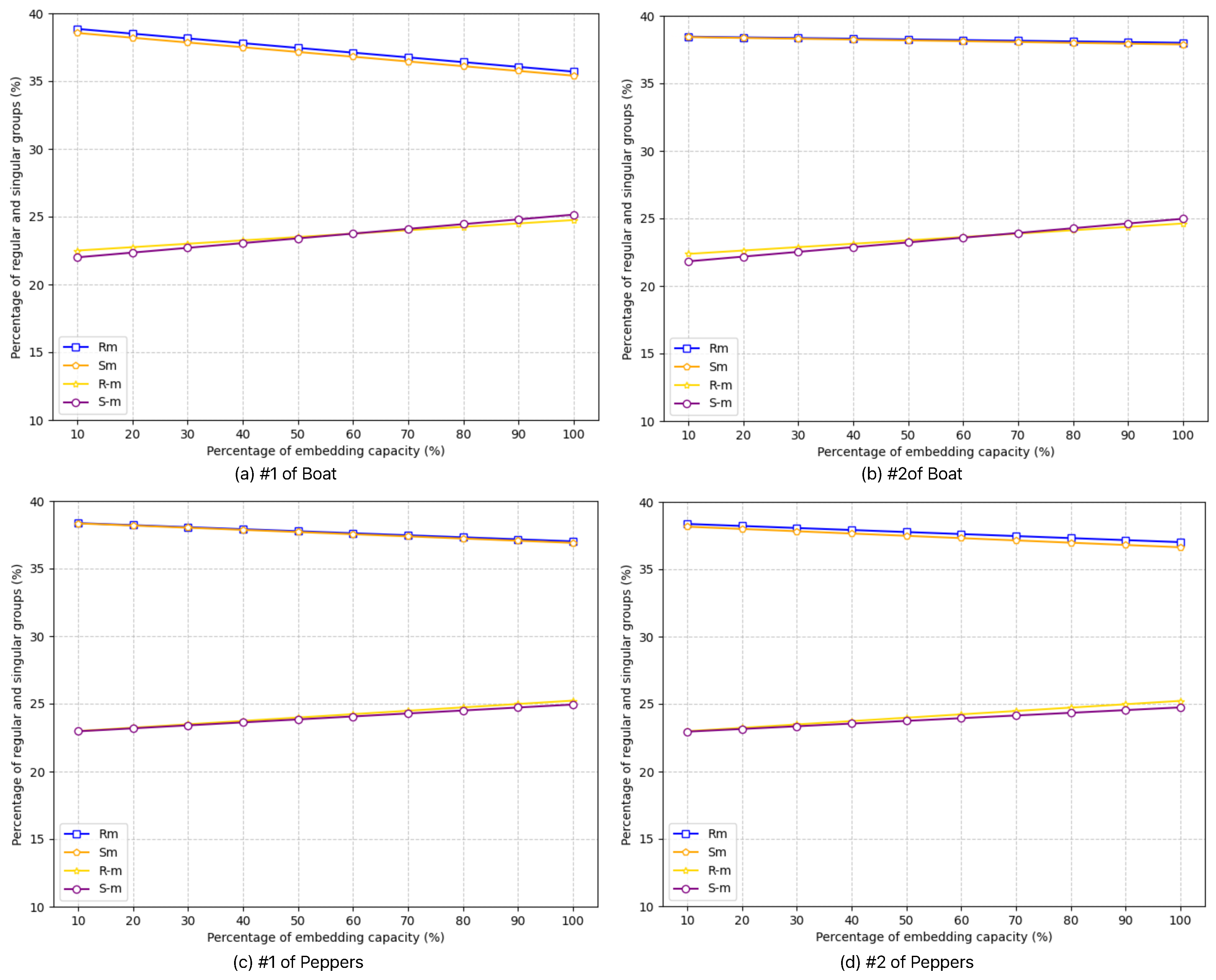
The RS analysis results in Figure 6 illustrate the resistance of the proposed method against regular–singular (RS) analysis attacks. RS analysis is a commonly used statistical attack technique that helps detect the presence of hidden information in an image by analyzing local pixel patterns. In this method, each shadow image is divided into three distinct categories:

• Regular Group (RM or R-M)—Represents smooth pixel regions that follow predictable patterns.
• Singular Group (SM or S-M)—Represents highly textured or noisy pixel regions.
• Unchanged Group (U)—Represents pixels that remain stable and are not affected by the embedding process.

The RM and SM (or R-M and S-M) values indicate the proportion of regular and singular pixels, respectively, under different masks (M or -M). In our experiments, four consecutive pixels were grouped together, with the applied mask M is defined as [0,1,1,0].

The statistical relationship between the regular and singular groups must satisfy the following conditions:

$$RM+SM\le 1,R-M+S-M\le 1,$$

(10)

$$RM\approx R-M,SM\approx S-M.$$

(11)

From Figure 6, it can be observed that both shadow images (number 1 and number 2) conform to the constraints defined in Equations (10) and (11), ensuring that the statistical integrity of the stego images is preserved. This indicates that the proposed method effectively maintains a balanced distribution of regular and singular groups, making it resilient against RS analysis attacks.

Furthermore, the similarity between RM and R-M as well as SM and S-M, across different shadow images suggests that the embedding operation does not introduce significant statistical anomalies that could be exploited by steganalysis techniques. This highlights the robustness of the proposed scheme in preserving the natural statistical properties of the host image while embedding data.

In conclusion, the RS analysis results confirm that the proposed method maintains imperceptibility and structural consistency, reducing the likelihood of detection by statistical steganalysis techniques. The ability to resist RS analysis ensures that the hidden information remains undetectable, making the method a strong candidate for secure reversible data hiding applications.

Furthermore, a deeper analysis of the comparative results reveals the underlying reasons for the differences in performance among existing methods. For instance, the scheme proposed by Chang et al. (2013) [14] achieves a relatively high embedding capacity of 1.53 bpp; however, this comes at the cost of significantly reduced image quality, with PSNR values falling below 40 dB. This degradation can be attributed to their approach of embedding two bits per pixel pair, which introduces substantial pixel distortion and consequently lowers visual fidelity.

In contrast, the EMD-based method by Chen and Hong (2021) [23] demonstrates more balanced performance, offering reversibility without overhead and maintaining stable PSNR values for the first stego image. Nonetheless, their results indicate that the second stego image tends to exhibit slightly inferior image quality. This disparity is likely due to the nature of EMD-based embedding, where error adjustments are not evenly distributed and one image inevitably bears a greater share of modification, leading to perceptible quality differences.

The proposed method effectively addresses these issues by employing enhanced HC(7,4) codes in combination with virtual pixel grouping and error pattern optimization, resulting in a more uniform distribution of distortion across both stego images. Consequently, the experimental results demonstrate that the proposed method achieves a balance between embedding capacity and perceptual quality, maintaining PSNR values between 48 and 49 dB and outperforming several existing techniques.

The proposed method is also computationally efficient. Unlike matrix embedding or EMD-based techniques, which often require complex orientation checks and iterative optimization, the proposed scheme relies on simple bitwise operations, Hamming code lookups, and XOR computations. This design not only reduces computational overhead but also enables straightforward hardware or software implementation. Thus, the proposed method is well suited for real-time applications and resource-constrained environments. For example, it can be applied in medical imaging systems or secure communication platforms that require high performance and low computational overhead.

In addition to these performance advantages, the computational efficiency of the proposed method is noteworthy. Unlike matrix embedding or EMD-based techniques, which often require complex orientation checks and iterative optimization, the proposed scheme relies on simple bitwise operations, Hamming code lookups, and XOR computations. This design not only reduces computational overhead but also enables straightforward hardware or software implementation. Thus, the proposed method is well suited for real-time applications or resource-constrained environments where both high performance and low computational complexity are critical, such as medical imaging systems and secure communication platforms.

To further support this claim, we analyzed the algorithm’s complexity and conducted runtime evaluations. The core procedures in both the embedding and extraction phases involve selecting an optimal codeword from a fixed-size lookup table containing sixteen valid HC(7,4) codewords. For each pixel, this search requires only basic integer operations and a minimal comparison loop. As such, the algorithm runs in constant time per pixel, resulting in an overall time complexity of $\mathcal{O}\left(N\right)$ for an image with N pixels.

To empirically validate this efficiency, we measured the execution time of the full embedding and extraction process on a $512\times 512$ grayscale image using Matlab R2019b on a system equipped with an Intel Core i5-8250U processor (1.60 GHz) and 8 GB RAM. The total runtime including all encoding, decoding, and pixel reconstruction steps was approximately 0.97 s. These results demonstrate that the proposed method is computationally lightweight and suitable for low-latency applications. However, we acknowledge that strict real-time constraints in high-resolution or embedded systems may require additional platform-specific optimization, which is a topic for future research.

Although the proposed method provides excellent performance in terms of embedding capacity and image quality, it inherits the common limitation of LSB-based RDH schemes in that it is not robust against lossy image compression such as JPEG. Because the embedded data reside in the least significant bits, such transformations tend to remove or distort the hidden content. This tradeoff reflects a key difference between RDH and robust watermarking, and points toward a promising future research direction in transform-domain RDH.

5. Conclusions

In this paper, we proposed a dual partial reversible data hiding (PRDH) method based on an enhanced Hamming Code (HC(7,4)) to improve embedding capacity while maintaining high image quality. By constructing virtual pixels from two cover images and applying optimized error correction, our method achieves full reversibility with respect to the cover images and significantly increases embedding capacity. Experimental results demonstrate that the proposed approach achieves an embedding rate of up to 1.5 bpp with PSNR values consistently exceeding 48 dB, outperforming existing dual-image RDH techniques. While the proposed scheme guarantees accurate recovery of the generated cover images after data extraction, it does not support reconstruction of the original image itself. This limitation results from the intentional omission of auxiliary data during the cover image generation phase. Transformation from the original image to the cover image is deterministic but not reversible; as such, the proposed method offers partial reversibility. This tradeoff enables a more efficient embedding process but limits the applicability of the scheme in domains that require exact preservation of the original image, such as legal evidence processing or lossless medical archiving. In addition, we evaluated the computational complexity and runtime of the proposed method. The algorithm runs in linear time with respect to image size and achieves embedding and extraction within approximately one second for a $512\times 512$ image on a standard laptop, demonstrating its lightweight design and practical applicability to latency-sensitive environments. Future work will explore the extension of the proposed framework to color images and video sequences as well as the integration of adaptive error correction and cryptographic mechanisms to further enhance robustness. The application of this approach to compressed image formats and its performance under advanced steganalysis attacks also remain promising directions. As with typical LSB-based RDH techniques, the proposed method is inherently fragile under lossy transformations such as JPEG compression. Because the embedded data reside in the least significant bits, such operations can distort or remove the hidden information. Therefore, the proposed scheme is best suited for uncompressed or lightly compressed domains where exact data reversibility is required. Future research will explore transform-domain extensions and robustness-enhancing strategies to improve resilience against compression and modern steganalysis attacks, including those based on neural networks. Although the proposed method is theoretical in scope, its efficient encoding structure and high visual fidelity suggest potential utility in practical domains such as medical image management and secure communications. Future research will explore its integration into application-specific frameworks, addressing requirements such as compatibility with standardized formats (e.g., DICOM) and clinical distortion tolerances.

While the proposed method shows promise for secure communication and metadata-preserving archiving, its applicability to clinical or forensic systems requiring perfect image reconstruction remains limited, and integration into existing pipelines is suggested as future work.