Identifying the Initial Corrosion Fatigue Failure Based on Dropping Electrochemical Potential
Abstract
1. Introduction
1.1. Corrosion Fatigue of Standard Duplex Stainless-Steel X2CrNiMoN22-5-3
1.2. Aim and Interest of This Study
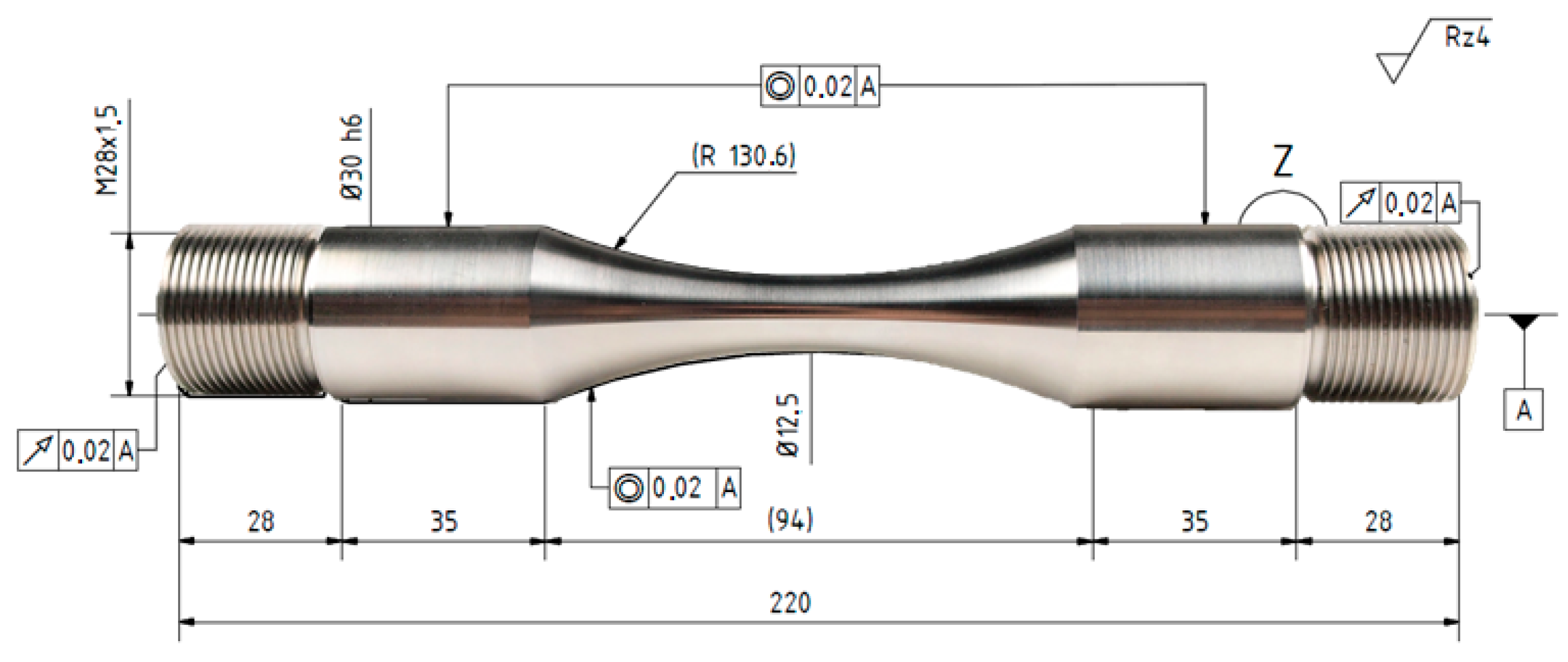
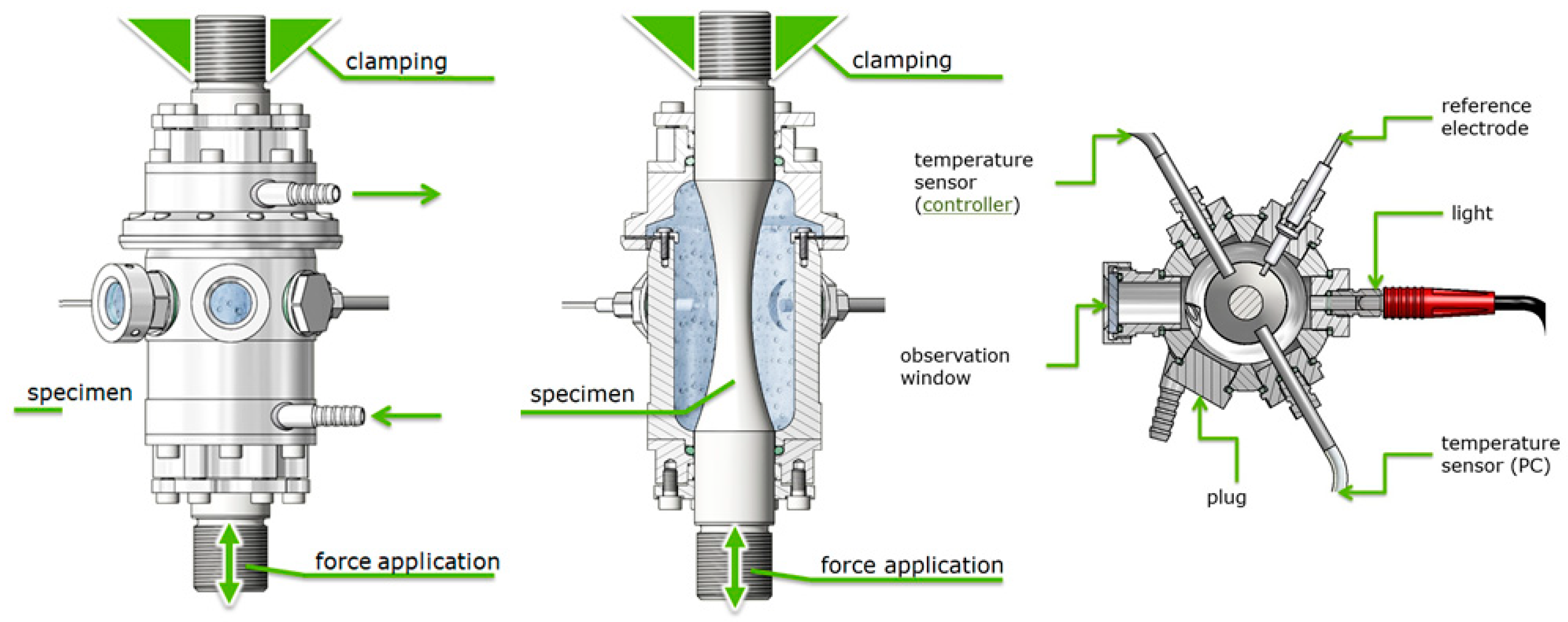
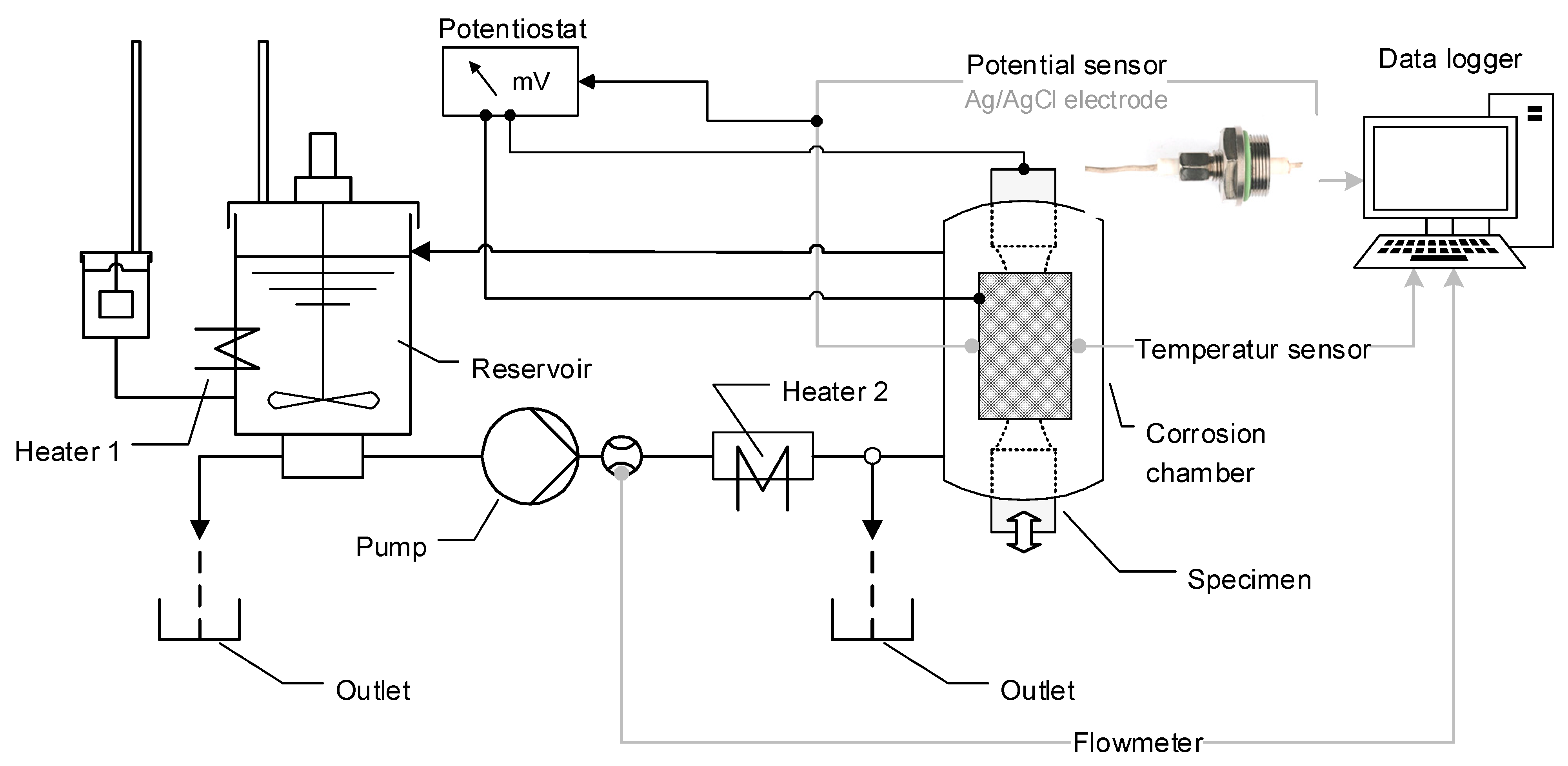
2. Materials and Methods
3. Results and Discussion
3.1. Evaluation of the Electrode
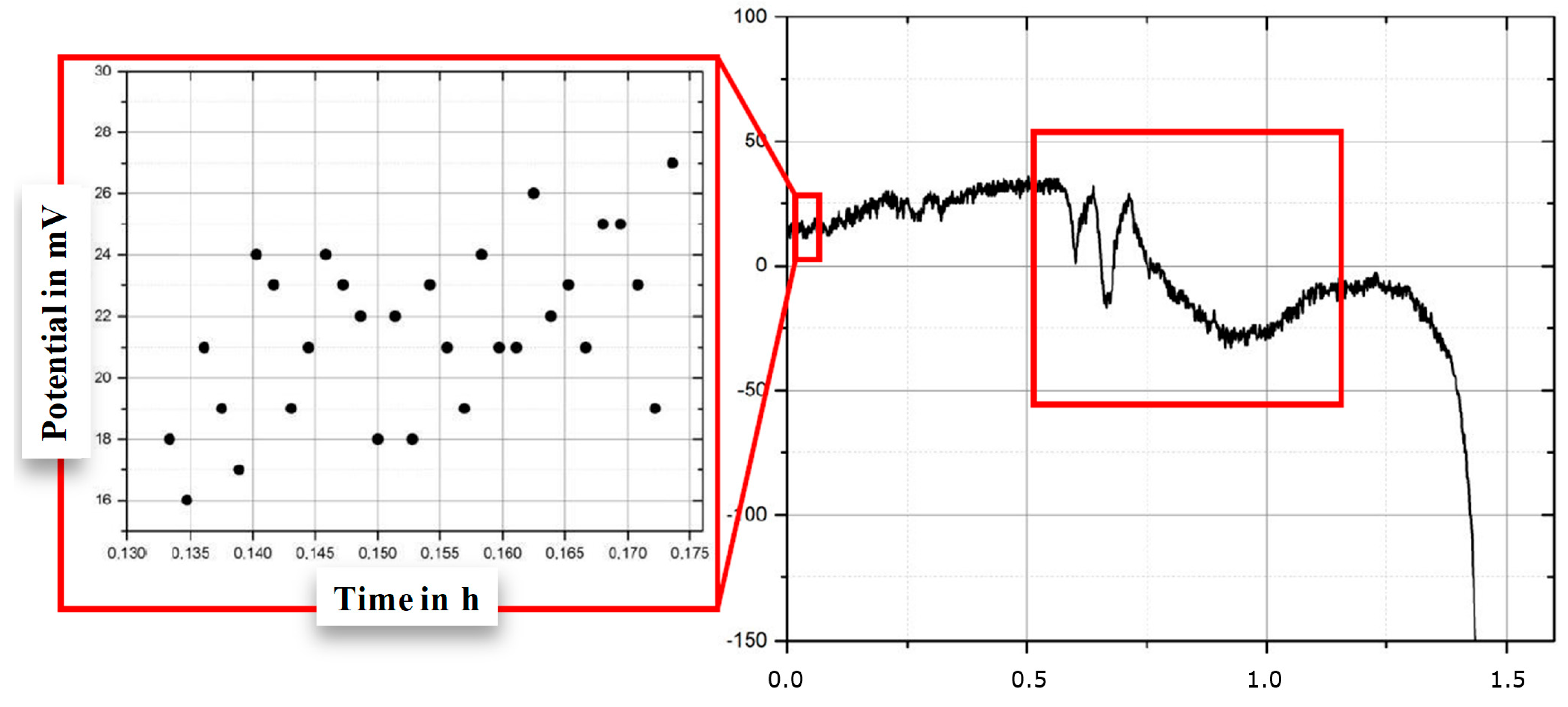
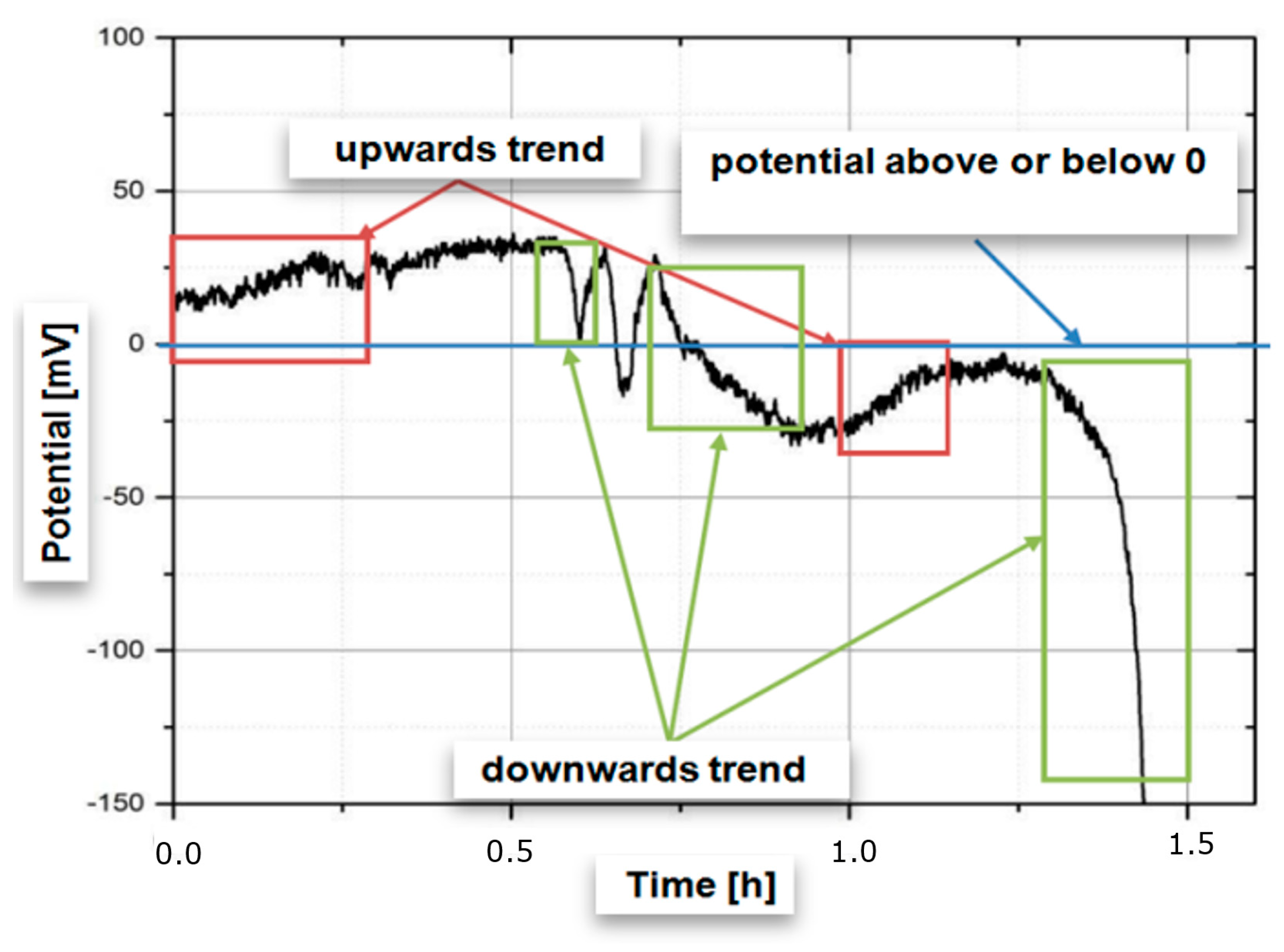
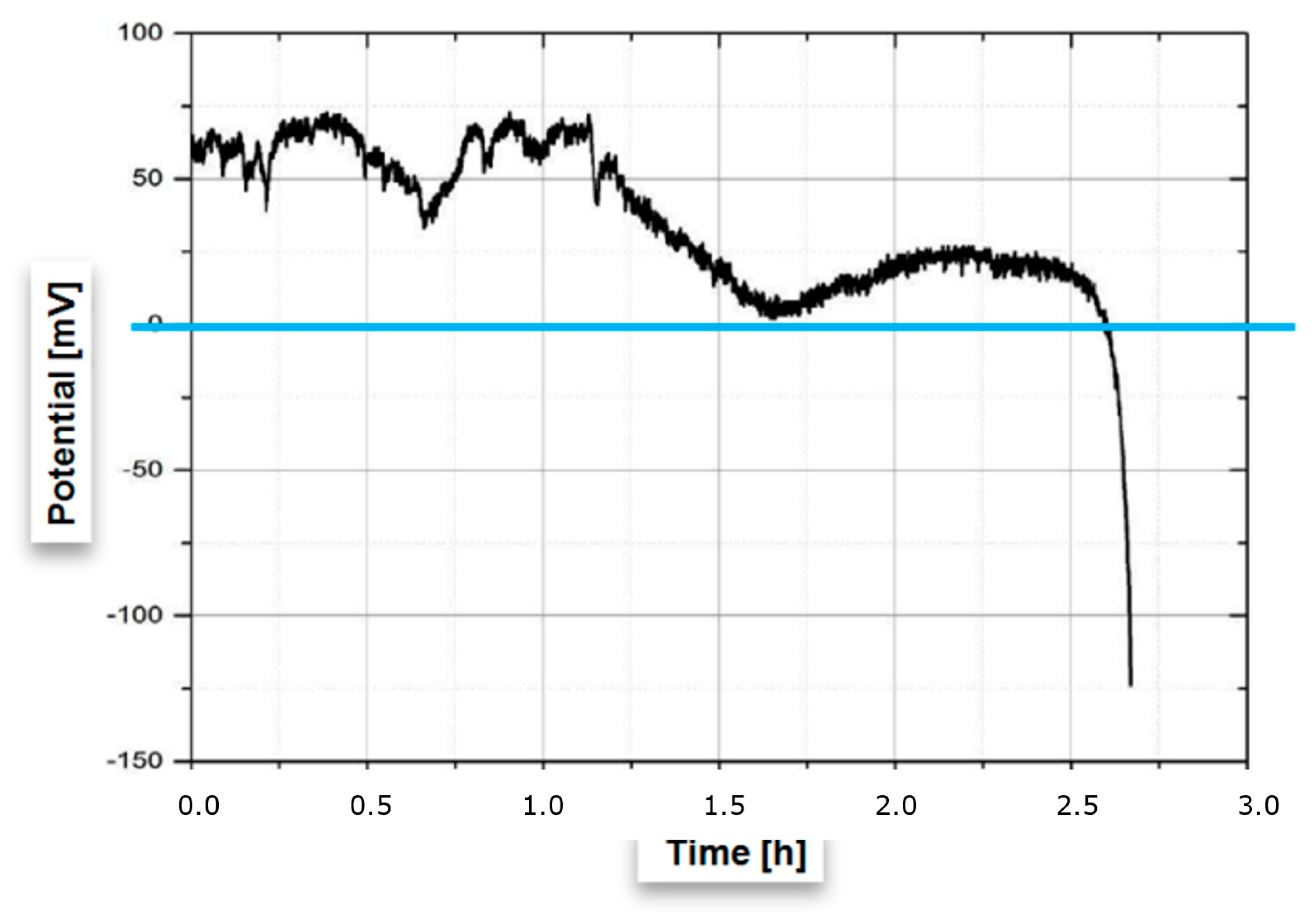
3.2. Relating the Electrical Potential to Fatigue Failure
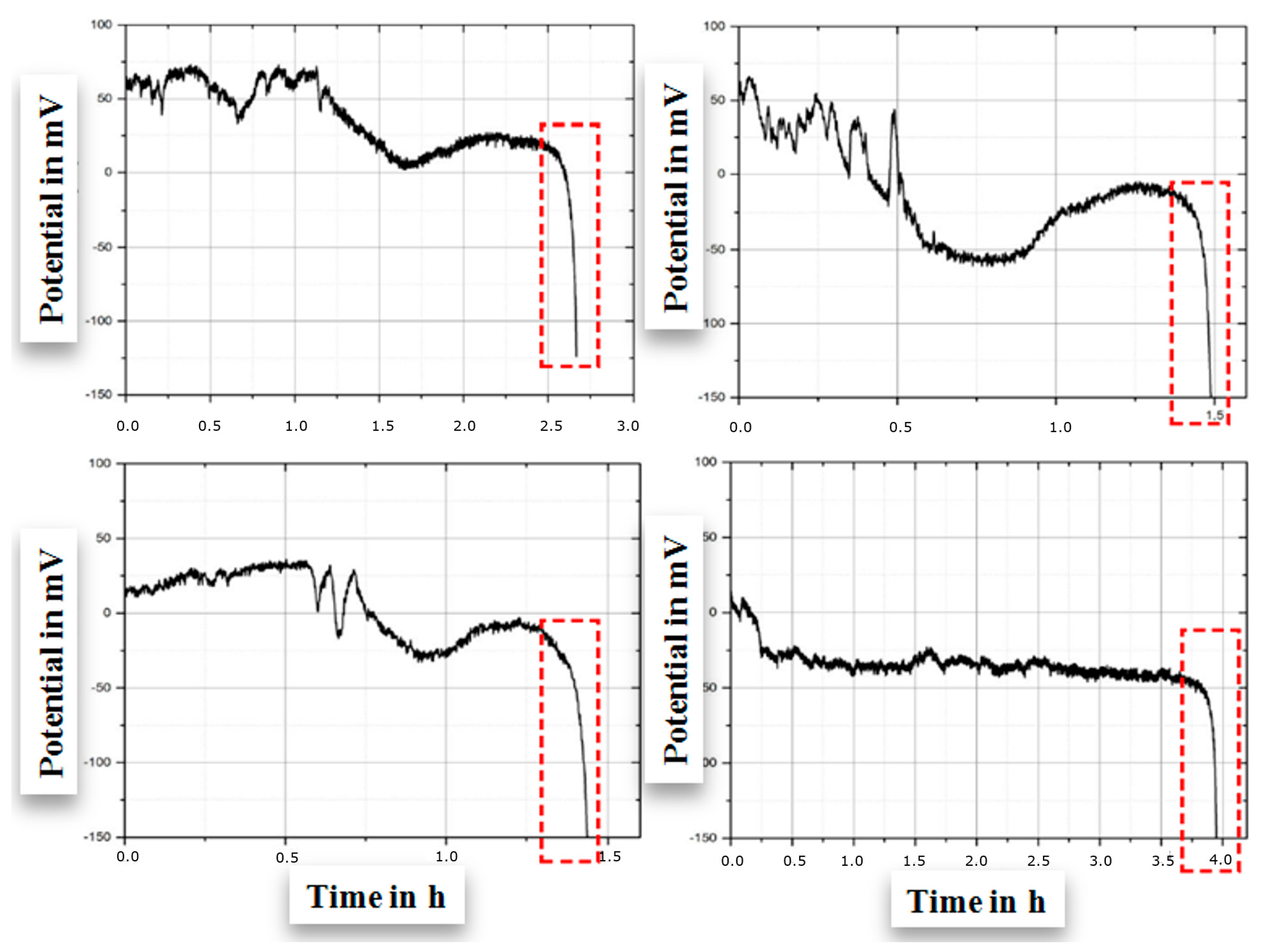
3.3. Estimating Early Failure from Electrical Potential
- .
- The arithmetic mean of numbering is = 5.5 for the mean of time courses 1 to 10;
- is the distance between x-values and the arithmetic mean of numbering of the particular time course with respect to the Cartesian grid to the second power. Because the numbering remains the same in each time course, it contributes as a constant to simplify Equation (7) to calculate the gradient. Inserting numbers 1 to 10, the gradient is 82.5.
- Each data point is compared to zero;
- For positive values, the time course is marked;
- After completion of 10 positive values, the time course is eliminated and not evaluated;
- Only fully negative data series are evaluated.
- Arithmetic means are calculated for all time courses completed with negative num-bers (non-marked);
- Balances of arithmetic mean values are calculated giving a trend for balance ≥ 0 (zero is interpreted as positive value);
- Intermission for ≥10 positive balances leads to a delay in data points.
- Conditions 1 and 2 need to be fulfilled;
- Gradient (m) and coefficient of determination (R2) immediately after fulfillment of condition 2;
- m ≤ −1;
- R2 ≥ 0.8;
- Two sub-conditions need to be fulfilled;
- Determination of experiment for three consecutive time courses applying to both sub-conditions.
- If m ≤ −1, mark the time course;
- If m ≥ −1, reset.
- If R2 ≥ 0.8, mark the time course;
- If R2 ≤ 0.8 reset.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomas, J.P.; Wei, R.P. Corrosion fatigue crack growth of steels in aqueous solutions I: Experimental results and modeling the effects of frequency and temperature. Mater. Sci. Eng. 1992, 159, 205–221. [Google Scholar] [CrossRef]
- Mu, L.J.; Zhao, W.Z. Investigation on Carbon Dioxide Corrosion Behaviors of 13Cr Stainless Steel in Simulated Strum Water. Corros. Sci. 2010, 2, 82–89. [Google Scholar] [CrossRef]
- Unigovski, Y.B.; Lothongkum, G.; Gutman, E.M.; Alush, D.; Cohen, R. Low-cycle fatigue behavior of 316L-type stain-less steel in chloride solutions. Corr. Sci. 2009, 51, 3014–3120. [Google Scholar] [CrossRef]
- Holtam, C.M.; Baxter, D.P.; Ashcroft, I.A.; Thomson, R.C. Effect of crack depth on fatigue crack growth rates for a C–Mn pipeline steel in a sour environment. Int. J. Fatigue 2010, 32, 288–296. [Google Scholar] [CrossRef]
- Thorbjörnsson, I. Corrosion fatigue testing of eight different steels in an Icelandic geothermal environment. Mater. Des. 1995, 16, 97–102. [Google Scholar] [CrossRef]
- Pfennig, A.; Wolf, M.; Heynert, K.; Böllinghaus, T. First In-Situ Electrochemical Measurement During Fatigue Testing of In-jection Pipe Steels to Determine the Reliability of a Saline Aquifer Water CCS-Site in the Northern German Basin Original. Energy Procedia 2014, 63, 5773–5786. [Google Scholar] [CrossRef]
- Zhang, W.; Fang, K.; Hua, Y.; Wang, S.; Wang, X. Effect of machining-induced surface residual stress on initiation of stress corrosion cracking in 316 austenitic stainless steel. Corros. Sci. 2016, 108, 173–184. [Google Scholar] [CrossRef]
- Evgeny, B.; Hughes, T.; Eskin, D. Effect of surface roughness on corrosion behaviour of low carbon steel in inhibited 4 M hydrochloric acid under laminar and turbulent flow conditions. Corros. Sci. 2016, 103, 196–205. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Q.; Yang, X.X.; Wang, Y.; Liu, J.; Li, Z. Impact of surface roughness and humidity on X70 steel corrosion in su-percritical CO2 mixture with SO2, H2O, and O2. J. Supercrit. Fluids 2016, 107, 286–297. [Google Scholar] [CrossRef]
- Lee, S.M.; Lee, W.G.; Kim, Y.H.; Jang, H. Surface roughness and the corrosion resistance of 21Cr ferritic stainless steel. Corros. Sci. 2012, 63, 404–409. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Mhaede, M.; Basha, M.; Wollmann, M.; Wagner, L. The effect of shot peening parameters and hydroxyapatite coating on surface properties and corrosion behavior of medical grade AISI 316L stainless steel. Surf. Coat. Technol. 2015, 280, 347–358. [Google Scholar] [CrossRef]
- Kleemann, U.; Zenner, H. Structural component surface and fatigue strength—Investigations on the effect of the surface layer on the fatigue strength of structural steel components. Mater. Werkst. 2006, 37, 349–373. [Google Scholar] [CrossRef]
- Sanjurjo, P.; Rodríguez, C.; Pariente, I.; Belzunce, F.; Canteli, A. The influence of shot peening on the fatigue behaviour of duplex stainless steels. Procedia Eng. 2010, 2, 1539–1546. [Google Scholar] [CrossRef]
- Abdulstaar, M.; Mhaede, M.; Wollmann, M.; Wagner, L. Investigating the effects of bulk and surface severe plastic deformation on the fatigue, corrosion behaviour and corrosion fatigue of AA5083. Surf. Coat. Technol. 2014, 254, 244–251. [Google Scholar] [CrossRef]
- Wu, X.; Guan, H.; Han, E.H.; Ke, W.; Katada, Y. Influence of surface finish on fatigue cracking behavior of reactor pressure vessel steel in high temperature water. Mater. Corros. 2006, 57, 868–871. [Google Scholar] [CrossRef]
- Alvarez-Armas, I. Duplex Stainless Steels: Brief History and Some Recent Alloys. Recent Pat. Mech. Eng. 2008, 1, 51–57. [Google Scholar] [CrossRef]
- Schultze, S.; Göllner, J.; Eick, K.; Veit, P.; Heyse, H. Selektive Korrosion von Duplexstahl. Teil 1: Aussagekraft herkömmlicher und neuartiger Methoden zur Untersuchung des Korrosionsverhaltens von Duplexstahl X2CrNiMoN22-5-3 unter besonderer Berücksichtigung der Mikrostruktur. Mater. Corros. 2010, 52, 26–36. [Google Scholar] [CrossRef]
- Prosek, T.; Le Gac, A.; Thierry, D.; Le Manchet, S.; Lojewski, C.; Fanica, A.; Johansson, E.; Canderyd, C.; Dupoiron, F.; Snauwaert, T.; et al. Low-Temperature Stress Corrosion Cracking of Austenitic and Duplex Stainless Steels Under Chloride Deposits. Corrosion 2014, 70, 1052–1063. [Google Scholar] [CrossRef]
- Pfennig, A.; Wolf, M.; Kranzmann, A. Corrosion and Corrosion Fatigue of Steels in Downhole CCS Environment—A Summary. Processes 2021, 9, 594. [Google Scholar] [CrossRef]
- Wolf, M. Phänomenologie der Schwingungsrisskorrosion von austenitisch-ferritischen Duplexstählen in hoch salzhaltigen wässrigen Lösungen. Ph.D. Thesis, University OVG Magdeburg, Magdeburg, Germany, 2018. [Google Scholar]
- Wolf, M.; Pfennig, A. Deriving early corrosion fatigue failure of steels from frequency drop and electrochemical potential. In Proceedings of the 8th International Conference on Materials Sciences and Nanomaterials (ICMSN 2024), Edingburgh, UK, 9–12 July 2024. [Google Scholar]
- DIN EN ISO 11782-1:2008-08; Corrosion of Metals and Alloys—Corrosion Fatigue Testing—Part 1: Cycles to Failure Testing (ISO 11782-1:1998); German version EN ISO 11782-1:2008. ISO: Geneva, Switzerland, 2008.
- Förster, A.; Norden, B.; Zinck-Jørgensen, K.; Frykman, P.; Kulenkampff, J.; Spangenberg, E.; Erzinger, J.; Zimmer, M.; Kopp, J.; Borm, G.; et al. Baseline characterization of the CO2SINK geological storage site at Ketzin, Germany. Environ. Geosci. 2006, 13, 145–161. [Google Scholar] [CrossRef]
- Forster, A.; Schoner, R.; Förster, H.-J.; Norden, B.; Blaschke, A.-W.; Luckert, J.; Beutler, G.; Gaupp, R.; Rhede, D. Reservoir characterization of a CO2 storage aquifer: The Upper Triassic Stuttgart Formation in the Northeast German Basin. Mar. Pet. Geol. 2010, 27, 2156–2172. [Google Scholar] [CrossRef]
- Bäßler, R.; Sobetzki, J.; Klapper, H.S. Corrosion resistance of high-alloyed materials in artificial geothermal fluids. In NACE International Corrosion Conference Series, Proceedings of the Corrosion 2013, Orlando, FL, USA, 17–21 March 2013; Paper No. 2327; NACE Corrosion Conference & Expo: Orlando, FL, USA, 2013. [Google Scholar]
- Cammann, K.; Galster, H. Das Arbeiten Mit Ionenselektiven Elektroden; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Baucke, F.G.K. Standardpotentiale der Silber/Silber-Chlorid-Elektrode in 3,5 m und in ges. KCl Unter Verwendung Entsprechender (“Cl−-Ionensensitiver”) Membranelektroden (0–95 °C). Chemie Ing. Tech. CIT 1975, 47, 565–566. [Google Scholar] [CrossRef]
- Kuckartz, U.; Rädiker, S.; Ebert, T.; Schehl, J. Statistik: Eine verständliche Einführung, 1st ed.; Springer Fachmedien: Wiesbaden, Germany, 2010; pp. 233–238. ISBN 978-3-531-16662-9. [Google Scholar]
- Hüftle, M. Modelle und Methoden der Zeitreihenanalyse; Universität Hannover: Hannover, Germany, 2006. [Google Scholar]
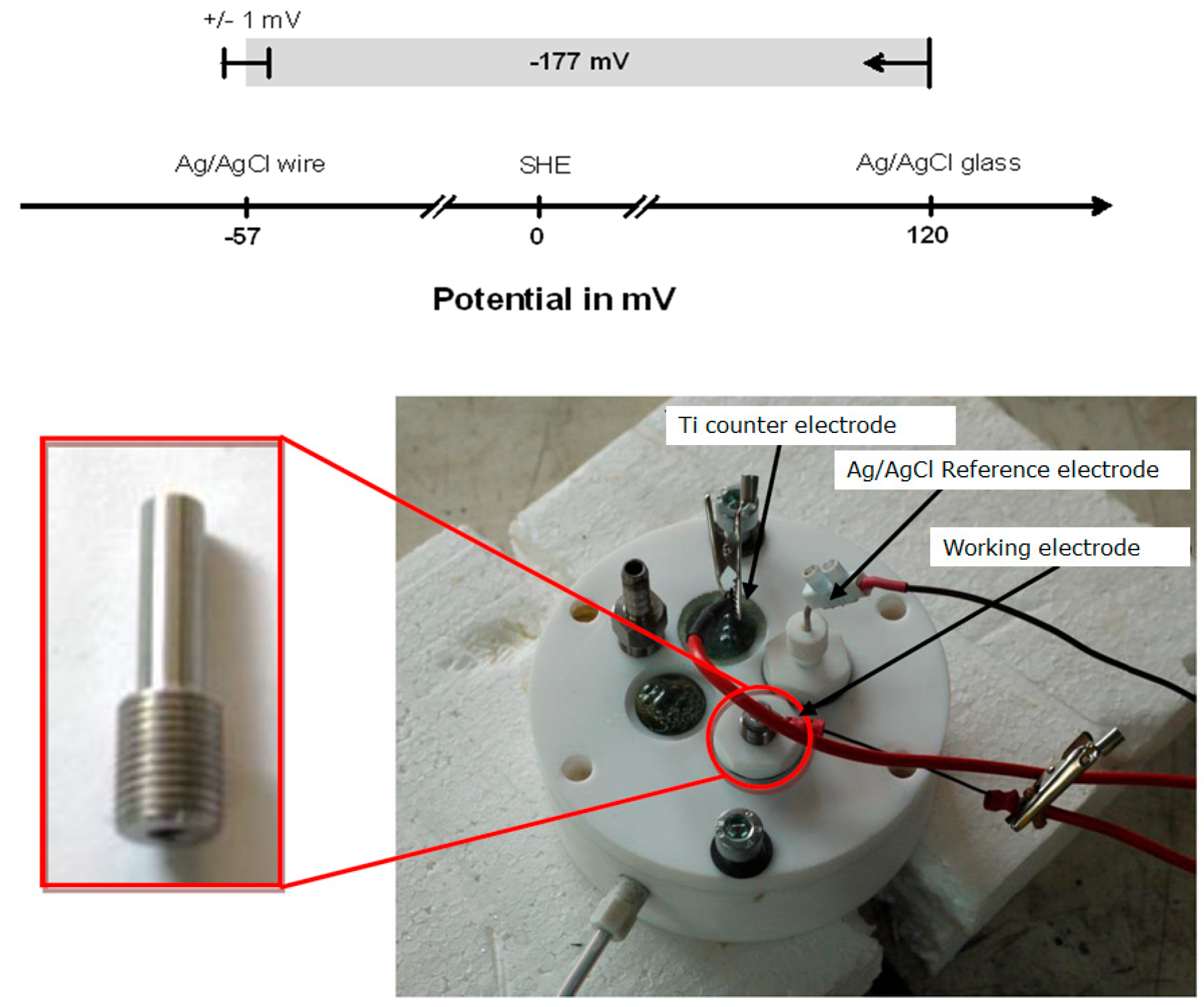

| Phases | C | Si | Mn | Cr | Mo | Ni | N |
|---|---|---|---|---|---|---|---|
| α & γ ** | 0.023 | 0.48 | 1.83 | 22.53 | 2.92 | 5.64 | 0.15 |
| α * | 0.02 | 0.55 | 1.59 | 24.31 | 3.62 | 3.81 | 0.07 |
| γ * | 0.03 | 0.47 | 1.99 | 20.69 | 2.17 | 6.54 | 0.28 |
| According to the Northern German Basin or According to Stuttgart Formation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NaCl | KCl | CaCl2 × 2H2O | MgCl2 × 6H2O | NH4Cl | ZnCl2 | SrCl2 × 6H2O | PbCl2 | Na2SO4 | Ph Value | |
| g/L | 98.22 | 5.93 | 207.24 | 4.18 | 0.59 | 0.33 | 4.72 | 0.30 | 0.07 | 5.4–6 |
| NaCl | KCl | CaCl2 × 2H2O | MgCl2 × 6H2O | Na2SO4 × 10H2O | KOH | NaHCO3 | ||||
| g/L | 224.6 | 0.39 | 6.45 | 10.62 | 12.07 | 0.321 | 0.048 | |||
| Ca+ | K2+ | Mg2+ | Na2+ | Cl− | SO42− | HCO3− | pH value | |||
| g/L | 1.76 | 0.43 | 1.27 | 90.1 | 14.33 | 3.6 | 0.04 | 8.2–9 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pfennig, A.; Simkin, R. Identifying the Initial Corrosion Fatigue Failure Based on Dropping Electrochemical Potential. Appl. Sci. 2025, 15, 403. https://doi.org/10.3390/app15010403
Pfennig A, Simkin R. Identifying the Initial Corrosion Fatigue Failure Based on Dropping Electrochemical Potential. Applied Sciences. 2025; 15(1):403. https://doi.org/10.3390/app15010403
Chicago/Turabian StylePfennig, Anja, and Roman Simkin. 2025. "Identifying the Initial Corrosion Fatigue Failure Based on Dropping Electrochemical Potential" Applied Sciences 15, no. 1: 403. https://doi.org/10.3390/app15010403
APA StylePfennig, A., & Simkin, R. (2025). Identifying the Initial Corrosion Fatigue Failure Based on Dropping Electrochemical Potential. Applied Sciences, 15(1), 403. https://doi.org/10.3390/app15010403






