Abstract
Locating community facilities is a long-term, daunting task for governments, requiring ongoing budget or policy updates for gradual improvement. This study proposes a bi-objective multi-scenario dynamic model (BOMSDM) for community-facility siting, which aims to maximize service efficiency and social equity while considering variable facility numbers and inter-community competition. This study also provides a framework to demonstrate how the newly proposed model operates. This framework includes the BOMSDM itself, the data collection and processing method, and the constrained NSGA-II as the computational algorithm. Under this framework, the BOMSDM, along with three comparative frameworks derived from traditional models—including a random allocation non-incremental model, a random allocation incremental model, and an average allocation non-incremental model—was applied to a real-world scenario in Shaoxing. The results demonstrate the effectiveness and superiority of BOMSDM: it significantly outperforms the realistic solution in terms of service efficiency, fairness, and community allocation rate. Compared to alternative frameworks, BOMSDM sacrifices some objective values in scenarios without facility redundancy to ensure higher community coverage while exhibiting rapid improvement in objective values when redundancy is present, highlighting the framework’s flexibility. This framework provides government decision-makers with an effective tool for community-facility site selection.
1. Introduction
Facility location is a well-known classic problem referring to locating at least one new facility among several candidate locations to optimize at least one objective function like cost, profit, revenue, travel distance, etc. [1]. At the same time, the facility location is a critical element in strategic planning for a wide range of private and public firms, as it provides the foundation for the development of industry, services, politics, commerce, and the economy [2]. Currently, the emergence of homeworking and an aging population has led to an increasing reliance on communities, calling for more comprehensive public services at the community level, which has raised concerns about community facilities.
Community facilities encompass diverse services, albeit with variations in scope between different countries or regions. Generally, community facilities refer to facilities such as education, healthcare, sanitation, and cultural amenities that are provided at the community level, typically funded by the government or publicly supported [3,4]. The decentralization of public service facilities at the community level helps enhance the multi-level public facilities system, which serves to alleviate pressure on public resources during times of public crisis, which is a consensus that has been solidified in the post-pandemic era [5]. Additionally, through the construction of community facilities, the social assets within communities, particularly in deteriorated communities, can be preserved and enhanced [6,7].
While the construction of community facilities offers numerous benefits, the locating of community facilities presents significant challenges for policymakers. Unlike city or regional-level facilities, community facilities are smaller in scale but greater in number, requiring substantial financial and time investments from local governments or firms. In China, the government has adopted an efficient way to address these challenges: local governments fund their development using the jurisdiction of the community committee (the primary-level administrative organization in China) as the physical boundary of the community, with one facility allocated per community. The type and number of facilities serve as key performance indicators for evaluating the community committee. This strategy has enabled the rapid advancement of community-facility construction in China in recent years.
However, this strategy faces some practical challenges. First, the number of facilities allocated is uncertain, generally depending on the government’s budget, which is limited and variable, often disbursed in phases. Even with sufficient budget to cover all communities, certain ones will be selected for pilots to assess the effectiveness of community facilities when a new community-facility project is carried out. Second, performance evaluations of community facilities have sparked inter-community competition, with the intensity of competition typically tied to the number of facilities allocated. When budgets are tight, every community vies to have facilities allocated within their jurisdiction. Conversely, when there is a surplus, this competition may diminish. Based on the aforementioned scenarios, we pose a central question: how can we optimize the location of community facilities to maximize the efficiency and equity of service while accommodating dynamic changes in the number of facilities and inter-community competition?
The siting of community facilities is often a long-term, enduring decision that evolves through sustained governmental budget allocations or policy updates. To enhance flexibility in decision-making, dynamic strategies for facility location are frequently employed [8,9,10]. Dynamic facility location strategies typically account for variables such as the number of facilities, their capacity, and resident demand over the planning horizon and involve periodic revisions to facility location decisions to adapt to changing infrastructure investments and service needs [11]. Among all dynamic facility location problems, the temporal dimension constitutes a main aspect of the dynamics [12]. In particular, multi-period models are considered the most effective approach in addressing dynamic challenges such as the incremental increase in facility numbers and phased policy changes [13,14,15].
This study aims to provide a modeling and operating framework for facility location, which includes constructing a new community-facility location model, specifying the methods for data acquisition and processing, and defining the algorithm for the model. The core task is to propose a dynamic model that improves service provision efficiency and equity by considering facility number variations and inter-community competition. To address the complex issue of community-facility location, our research explores the facility location decision-making process from both temporal and spatial dimensions, integrating dynamic strategies. Temporally, we simulate the gradual development of the community-facility network through a multi-period incremental strategy. Spatially, we introduce community boundaries as a spatial constraint to simulate inter-community competition for facilities. Furthermore, we establish corresponding “facility-community allocation” strategies that adapt based on the cumulative number of facilities within the planning area. In addition, taking the cumulative facility number, incremental strategy, and facility-community allocation strategies as constraints, as well as the efficiency and equity of facility location as its two fundamental objectives, we construct a bi-objective multi-scenario dynamic model (BOMSDM) for community-facility location problems. Finally, an empirical case is presented to evaluate the effectiveness and superiority of the newly developed model.
The remainder of this paper is organized as follows: Section 2 reviews the literature on community-facility location and dynamic facility location problems and highlights the contributions of this study. Section 3 details the construction and solution methods of the BOMSDM and introduces three comparative models. Section 4 provides an overview of the study area, along with the data sources and preprocessing methods for each dataset used. Section 5 presents the simulation results of the BOMSDM and compares them with real-world solutions and the outcomes of the three comparative models. Additionally, the sensitivity testing of the model’s optimization capability was conducted under different levels of facility redundancy. In Section 6, we discuss the performance, applicability, and limitations of BOMSDM. Finally, Section 7 concludes the study.
2. Literature Review
2.1. Facility Location Problems
Facility location problems (FLPs) involve selecting a subset of locations from a set of candidates and determining which demand points will be served by each facility [16]. FLPs have long been a classic subject in various disciplines, such as geography, operations research, and management science. The study of facility location problems dates back to the early 20th century, with Alfred Weber’s work on the warehouse location problem, which aimed to minimize the total travel distance between warehouses and customers [17]. In the 1960s to 1980s, several key models were introduced by researchers such as Hakimi [18,19], Toregas, Swain, ReVelle, and Bergman [20], and Church and Velle [21], including the P-Median model, P-Center model, Set Covering Location Problem (SCLP), and Maximal Covering Location Problem (MCLP). Many of the classical models in facility location research have been developed based on these foundational models. For example, by combining several models and incorporating multi-objective optimization, researchers developed the multi-objective facility location problem [1,22]. These models often seek compromise solutions using Pareto optimality or other multi-objective techniques, such as weighted methods and goal programming. In the 1990s, researchers began to include uncertain parameters in these models, addressing issues such as demand fluctuations and cost uncertainties through methods like robust optimization and the fuzzy set theory [23,24]. Similarly, building upon these classic static models, researchers have introduced time-varying constraints to account for demand fluctuations, population changes, or shifts in transportation networks, thereby developing dynamic location models [12,25].
Overall, after several decades of research, facility location problems have produced a wealth of findings. For more detailed information on FLPs, readers may refer to the reviews by Owen and Daskin [2], Farahani, Fallah, Ruiz, Hosseini and Asgari [26], Revelle, Eiselt and Daskin [27], Melo, Nickel and Saldanha-Da-Gama [28], Turkoglu and Genevois [29], and Rossit and Nesmachnow [30], which provide comprehensive overviews of the topic. However, conducting a comprehensive review of all these facilities is beyond the scope of this paper. We have instead focused on reviewing community-facility location problems (CFLPs) and dynamic facility location problems, which are closely related to our work.
2.2. Community-Facility Location Problems
This section provides a detailed analysis of the optimization objectives, constraints, research methodologies, and adaptability of studies on CFLPs. As shown in Table 1, most studies on CFLPs have focused on healthcare and medical facilities [31,32,33,34,35,36,37,38,39], which may be attributed to the increasing awareness of public health and the close attention paid to primary medical facilities after the pandemic. Additionally, there is a small body of research in the literature that has involved community emergency facilities [40,41] and community waste collection facilities [42,43].

Table 1.
Review of community-facility location problems (CFLPs) studies.
We also found that efficiency and equity were the most fundamental and common objectives in previous research. Among them, efficiency objectives were well-developed, covering various stages of facility location and operation, including the economic benefits of facility siting [34,36,42], service supply efficiency [37,38,40], facility coverage [33,34,43,44], and facility accessibility [32,34,35,36,38,40,41,42,44]. In contrast, equity objectives were relatively limited in the reviewed studies. For instance, Tao, Cheng, Dai, and Rosenberg developed a spatial optimization model for residential care facilities to maximize accessibility equity [39], while Khodaparasti, Maleki, Bruni, and Beraldi aimed to ensure that second-level facilities were well-dispersed by minimizing the distance between primary and secondary facilities [38]. This indicates that the focus on equity has primarily been on spatial equity, which ensures equal spatial proximity between residents in different areas. The fairness of facility service distribution among different groups, which refers to social equity, has been neglected [45].
In terms of constraints, previous CFLP research commonly used facility capacity, the number of facilities, threshold distance, and demand point-facility assignment, which usually refers to a demand point being assigned to only one facility. However, in our review of CFLP studies, we found only one instance where the spatial relationship between proposed facilities and communities was considered. Zhuo, Li, and Zhang addressed this by minimizing the maximum planned transportation distance from each community to promote a balanced distribution of community hospitals [35]. Nevertheless, this study did not consider the physical boundaries of communities or differences in community size, thus failing to ensure facilities were allocated to specific communities.
We also noticed that, among the studies mentioned above, only two considered the issue of the multi-scenario application of models. Ma, Zou, Shin, Kang, Gao, Siu, and Zhang developed nine scenarios based on different types of community facilities and allocation strategies and then used GIS to identify the ideal distribution of community facilities [46]. Khodaparasti et al. [38] established three scenarios and corresponding strategies based on existing facilities; the proposed solutions balanced the equity, local accessibility, and efficiency of community-based health programs.
Based on the above review, it is evident that research models for CFLPs remain limited and have yet to account for many practical requirements and constraints. For example, issues such as inter-community competition for facilities and the social equity of facility allocation are often overlooked. Moreover, the use of singular scenarios further restricts the applicability of these models.
2.3. Dynamic Facility Location Problems
Facility location problems under uncertainty are a key area of focus within the broader study of facility location problems, encompassing uncertainties in the number of facilities [47], facility capacity [48,49], and demand [50,51]. Facility location decisions must be dynamically adjusted to address such uncertainties based on varying real-world needs. Generally, dynamic facility location problems involve two main considerations: first, the inheritance and updating of facilities across different scenarios, and second, the corresponding location decisions tailored to each scenario.
In previous studies, early in 1973, Wesolowsky was among the first to expand the static facility location problem by allowing positional adjustments for facilities at different stages [52]. Currently, Ratick and Velle are developing a multi-criteria model, testing dynamic location strategies under varying facility quantity scenarios [53]. Manzini and Gebennini innovatively designed and applied mixed-integer programming optimization models to address dynamic, multi-stage, multi-commodity location allocation challenges [25]. Research by Sonmez and Lim [47], Ashfari, Sharifi, ElMekkawy and Peng [54], Maliki, Souier, Dahane, and Abdelaziz [55] similarly proposed multi-stage facility update models that tackle uncertainty in decision variables through the dynamic relocation and augmentation of facilities. Moreover, scholars have developed multi-period incremental service facility location models for non-essential service facilities such as libraries, senior care facilities, and recycling stations, considering the high costs of facility relocation. In 2009, Albareda-Sambola first introduced the multi-period incremental service facility location problem, aiming to establish new facilities within a limited timeframe to dynamically meet the demands of a specified customer group [56]. Arulselvan and Skutella provided an incremental framework establishing a sequence of open facilities and a sequence of service customers constrained by fixed correspondences in 2015 [57]. Building on Albareda-Sambola’s work, in 2020, Shi, Chen, Zhou, and Zhang incorporated user preferences into a multi-period bi-objective integer programming model [58]. The richness of findings in this area is well-documented, as evidenced by studies such as those by Snyder [23], Kchaou Boujelben and Boulaksil [59], Pérez-Gosende, Mula, and Díaz-Madroñero [60].
Considerations have been made to the heritage and updating of facilities across different periods. Building upon this foundation, a limited number of scholars have introduced constraints on facility inheritance and updating methods. Oliveira, Camargo, Júnior, and Martins presented a computational study on two variants of the dynamic multi-period two-level incapacitated facility location problem, focusing on dynamic decision-making regarding allocation relationships between primary factories and secondary facilities in 2021 [61]. Later, Fadda, Manerba, and Tadei introduced three interrelated models, conducting analyses under two scenarios of facility redundancy to offer optimal decision support tailored to various redundancy contexts [62].
To the best of our knowledge, previous studies on dynamic facility location problems have placed limited emphasis on dynamic decision-making for facility siting and have not considered the spatial allocation relationships between facilities and their managing entities. As mentioned in Chapter One, competition for community facilities exists among communities, with the intensity of this competition fluctuating following facility number constraints. Thus, it is essential to develop allocation strategies for facilities that are tailored to varying facility number scenarios.
2.4. Contributions
The main contributions of this model can be summarized as follows:
- (1)
- This study is the first to introduce the issue of inter-community-facility competition in the community-facility location problem, and it simulates this issue through the implementation of a spatial allocation strategy constraint termed facility-community allocation.
- (2)
- By incorporating a social equity objective into the framework and defining the methods and processes to compute this objective, this study aims to maximize the equity of community facilities’ distribution among different demographic groups.
- (3)
- This study establishes a dual dynamic model in both time and space dimensions (see Section 3.1) to address the incremental demand for community facilities in successive periods of facility allocation, as well as the need to adopt different facility-community allocation strategies as the number of facilities increases.
3. Model Development
3.1. Problem Description
BOMSDM is a multi-period incremental model that imposes no limitations on the number of periods. Based on the cumulative total of facilities at a given period, the proposed model establishes three distinct scenarios: (i) Scenario I: a facility-insufficient scenario, where the total number of available facilities accumulated over all previous periods falls short of meeting the needs of all communities; (ii) Scenario II: facility-sufficient scenario, where the cumulative facility count precisely matches the number of communities; (iii) Scenario III: facility-redundant scenario, where the cumulative number of facilities exceeds the community demand.
The BOMSDM includes two facility-community allocation strategies: (i) the average allocation strategy, in which facility siting is constrained by community boundaries, ensures that each community has an equal number of facilities (when the number of facilities is a multiple of the number of communities) or a difference of no more than one (when the number of facilities is not a multiple of the number of communities); and (ii) the random allocation strategy, which permits facility siting without boundary constraints, selecting randomly from all candidate locations.
Corresponding facility-community allocation strategies are set for the three scenarios as illustrated in Figure 1: (i) in Scenario I, the average allocation strategy is employed to ensure that community facilities are allocated to as many communities as possible; (ii) in Scenario II, the average allocation strategy ensures a one-to-one correspondence between community facilities and communities; and (iii) in Scenario II, facilities exceeding the number of communities are allocated using a random strategy, where each community initially receives one facility, with the remaining community facilities allocated randomly.
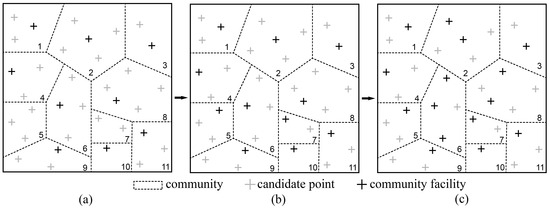
Figure 1.
Illustrations of dynamic strategies in BOMSDM. (a) An illustration of a solution in Scenario I with 11 communities, 34 candidate points, and 9 community facilities. (b) An illustration of a solution in Scenario II with 11 communities, 34 candidate points, and 11 community facilities. (c) An illustration of a solution in Scenario III with 11 communities, 34 candidate points, and 15 community facilities.
In addition, we set two fundamental objectives for BOMSDM: (i) the fair distribution of community facilities among different demographic groups to minimize service distribution inequality. We assessed service distribution equity using the service distribution Gini coefficient (SDGC). (ii) The second objective aimed to maximize the service supply of community facilities to ensure efficient utilization, and the objective was reflected by the service supply rate (SSR). Constraints were imposed on facility-community allocation to ensure community facilities were allocated to different communities and on the number of community facilities to reflect a varying facility number constraint.
In real-world scenarios, it is hard to simultaneously achieve these two objectives. This study introduces Pareto non-dominated solutions to enable decision-makers to choose the final solution based on their preferences, providing an ideal optimization decision-making process of seeking the optimal solution first and making the decision later [63,64].
To simplify the computational analysis, we made the following assumptions: (i) Both present and future development needs are adequately considered when setting community facilities, so capacity limitation can be ignored. (ii) Residents access community facilities on foot, unaffected by road conditions or vehicular congestion.
The sets, parameters, and decision variables in the BOMSDM are defined as follows:
Sets
: Set of demand points, indexed by ;
: Set of candidate points of community facilities, indexed by ;
: Set of communities, indexed by ;
: Set of periods indexed by .
Parameters
: The demand amount at the demand point ;
: The amount of service supplied from the facility point to demand point ;
: The amount of service received at the demand point in ;
: The distance attenuation factor;
: The walking distance from the demand point to the facility point ;
: The service threshold distance, which indicates the acceptable travel distance from the demand point to facility point ;
: The accumulative percentage of the number of demand points in the first groups, when the demand points at each level are sorted by service coverage from low to high in ;
: The accumulative percentage of the number of demand points at the first groups, when the demand points at each level are sorted by service coverage from low to high in ;
: The number of groups of demand points (integer);
: The total number of community facilities located in , including the facilities that have been located before and which will be located in (integer);
: The number of communities (integer).
3.2. Mathematical Model
3.2.1. Objective 1: Maximize Service Distribution Equity
In this study, service distribution equity is reflected by the service distribution Gini coefficient (SDGC), which serves as a quantitative indicator for assessing the service distribution equity among different socioeconomic groups (socioeconomic groups are defined in Section 4.2.1). The Gini coefficient is a relative index initially defined by Gini [65] to measure the degree of unequal distribution. At present, the Gini coefficient has been widely used to measure the equity of the distribution of public resources, such as medical services [66], education [22], water resources [67], etc. The Gini coefficient ranges between 0 and 1, with values closer to 0 indicating better equity. And a Gini coefficient below 0.2 signifies optimal equity. By introducing the Gini coefficient calculation formula [13], the objective of maximizing SDGC in period can be expressed as follows:
3.2.2. Objective 2: Maximize Service Efficiency
In this study, we employed the service supply rate (SSR) to evaluate service efficiency. The SSR represents the ratio of the total service supply provided by all community facilities located to the total service demand within all demand points. Generally, one facility point does not provide uniform service to all demand points within its service threshold distance range. The amount of service supplied from the facility point to the demand point is determined by the demand amount , and the service distance . In this study, is defined as follows:
We adopted the Gaussian function to calculate the distance attenuation factor , as it can reflect the distance attenuation effect more accurately and has been widely used in the literature to capture the impact of distance on demand [68,69]. The Gaussian function is expressed as follows:
It should be considered that, in practice, community facilities should be accessible to all residents nearby. This means that within the service threshold distance, the demand point receives a service that may come from multiple facility points. Thus, in period , the amount of service received for a single demand point is as follows:
Then, the objective of maximizing service efficiency in period can be expressed as follows:
Constraints:
In this model, constraint (6) decides the number of community facilities to be located in ; constraints (7)–(9) restrict the facility-community allocation strategies of the community facilities in three scenarios; constraints (10) and (11) guarantee the incremental strategy, respectively; constraint (10) ensures that each candidate point can be selected once at most throughout the entire community facilities allocation period; and constraint (11) states that once a demand point is served by a community facility, this service relationship is sustained in subsequent scenarios. Constraint (12) limits the service supply accepted by each demand point to no more than its demand capacity; constraint (13) defines the binary variables.
3.3. Models for Comparative Analysis
To assess the impact of facility-community allocation constraints and multi-period incremental constraints, the BOMSDM is compared with three other models. In Model I, the random allocation incremental model employs a random allocation strategy and removes the incremental strategy from BOMSDM, similar to the approaches used in studies by Current et al. [53] and Sonmez and Lim [47]. In Model II, the random allocation incremental model, a random allocation strategy is also utilized but incorporates an incremental strategy akin to those employed by Arulselvan et al. [57] and Shi et al. [58]. In Model III, the average allocation non-incremental model maintains an average allocation strategy among communities at all stages without using an incremental strategy. Specifically, formula (9) is modified as follows for Model III:
The introduction of these three models serves to validate the effectiveness of the dynamic allocation strategy, while Models I and III allow for a comparative assessment of the utility of incremental strategy. A detailed comparison of the four models is presented in Table 2.

Table 2.
A comparison between the BOMSDM and Models I, II, and III.
3.4. Optimization Method
The BOMSDM proposed in the previous section can be classified as an NP-hard problem. This section introduced the non-dominated sorting genetic algorithm-II (NSGA-II), which is a method widely recognized for its applicability to complex multi-objective optimization problems [70]. For its efficient search and computing ability, NSGA-II has been regarded as a state-of-the-art algorithm for solving multi-objective problems [71].
To enhance the computational performance of our model, we incorporated constraints into the chromosome generation process of NSGA-II, in which a chromosome referred to one solution of BOMSDM. In Appendix A, we explain the design of the chromosome generation for BOMSDM. For the rest of the calculation process of NSGA-II, we adopt the strategies proposed by Deb et al. [70]; the process includes initializing the population (randomly generated initial solutions, which can then be optimized through subsequent genetic operations), non-dominated sorting, crowding distance calculation, selection, crossover and mutation, merge parent and offspring populations, non-dominated sorting and crowding distance calculation (again), and the final population output. After each generation, non-dominated sorting and crowding distance calculations are applied to select the next population. The process continues until the stopping criteria are met, and the final population consists of a set of non-dominated solutions. The general process of NSGA-II can be referred to in references [72,73] and others. The pseudocode for the improved NSGA-II algorithm used in this paper is provided in Appendix A.
4. Empirical Study
4.1. Study Area
To validate BOMSDM’s effectiveness, 83 communities in the central area of Shaoxing City (including four urban villages) were selected as a study case (area 53,826,540 m2), as illustrated in Figure 2. Like most cities, this region represents typical residential spatial differentiation [74]. These residential zones are fragmented into communities of varying sizes, with the largest community spanning 3,807,589 m2 and the smallest at 47,807 m2. These characteristics render the area suitable for testing the model proposed. The residential spatial differentiation contributes to enlarging the results and scope of two objectives, while differences in community sizes can examine the impact of facility-community allocation constraints on overall efficiency and fairness.
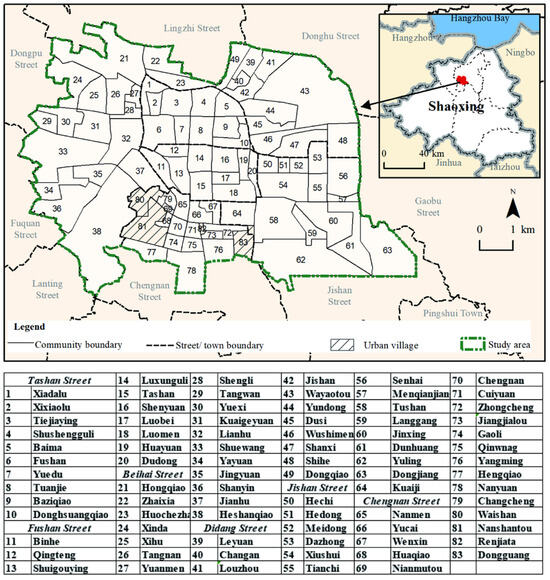
Figure 2.
Distribution of communities within the study area.
In 2019, Shaoxing became one of the pilot cities for “Zero Waste Cities”. Funded by the district-level government, the allocation of recycling stations was carried out as an essential community facility. By 2020, a total of 79 stations were constructed, each allocated to one community (four urban villages were not required to build recycling stations, but the residential buildings within them needed to be covered by services). However, some of the stations incurred losses due to poor site selection, leading to closures or relocation [75], leaving only 72 stations remaining by the end of 2023. The realistic solution of recycling stations can serve as a reference for testing the effectiveness of the BOMSDM.
4.2. Data Sourcing and Processing
4.2.1. Demand Points
For this study, the demand point set comprised all residential buildings within 83 communities. We obtained data for a total of 18,359 buildings with an outline including the number of floors, as well as boundary data for 414 residential areas from Amap (lbs.amap.com), one of China’s most advanced navigation maps in February 2024, and 12,081 residential buildings was extracted. Then, we supplemented the unavailable data of historic residence buildings with cross-checking by field investigation and satellite maps. Finally, a demand point set of 13,776 residential buildings was created. According to the model’s assumption, we adopted the housing floor area as the service demand indicator for each building.
In China, housing is pivotal as the primary asset for residents, reflecting disparities in urban resource allocation and socioeconomic status [76]. Hence, the socioeconomic groups of residents can be defined by the types of houses. We addressed the types of residential buildings by considering housing prices and the attributes of residential areas [77]. Four data items from 378 residential areas were collected from China’s largest real estate trading platform, Anjuke (shaoxing.anjuke.com), in February 2024: the average housing price of real-time transactions, building age, plot ratio, and property fees. Then, we classified all residential buildings into four groups through hierarchical cluster analysis in SPSS. We manually identified and categorized the remaining 36 residential areas with no real estate data. Specifically, Group 1 included villas, townhouses, and new high-end high-rise residences, characterized by high housing prices, a low or relatively low building age, and high property fees. Group 2 primarily comprised high-rise residential buildings of relatively high quality, which are distinguished by relatively high housing prices, high plot ratios, and relatively high property fees. Group 3 encompassed both old multi-story houses of relatively high quality and high-rise housing of lower quality, featuring median housing prices, relatively high building age, and low property fees. Group 4 mainly comprised old multi-story houses of low quality, characterized by low or relatively low housing prices, a relatively high building age, relatively low plot ratios, and low property fees. Meanwhile, those historical residential buildings with serious data missing were categorized into Group 5 separately. The distribution of five groups of residential buildings is shown in Figure 3.
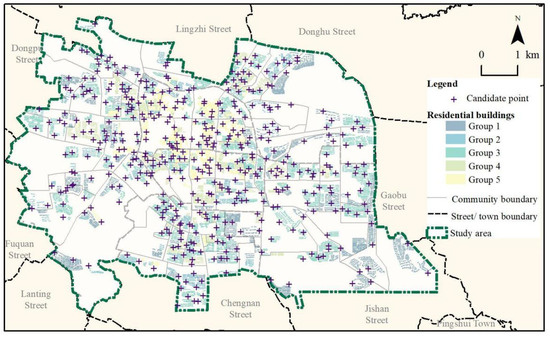
Figure 3.
Distribution of residential buildings and candidate points.
4.2.2. Candidate Points
For candidate points selection, we obtained the location data of existing recycling stations from the Shaoxing Public Data Open Platform (https://data.sx.gov.cn/kf/open/table, accessed on 12 August 2024) and referred to select preferences expressed by them. First, according to the size of residential areas, we assigned 1–3 candidate points to each of them at their entrances. Second, we eliminated overlapping points and merged nearby points within a straight-line distance of less than 50 m. Finally, a total of 447 candidate points were selected (Figure 3).
4.2.3. Travel Distances and Service Threshold Distance
Furthermore, we limited the service threshold distance of community facilities to 500 m, which is the service threshold distance of the community facilities set in the Chinese National Standard “Planning and Design Standards for Urban Residential Areas”.
5. Results
This section shows the calculation results of the empirical study. The calculations were conducted through the NSGA-II on MATLAB R2021a. The parameters were set as follows: the initial population size, which corresponds to the number of solutions in the initial solution set, was 40; the variation probability was 0.01; and the crossover probability was set at 0.8. The number of iterations for each model’s computation was not fixed; we conducted experiments with varying iteration counts to identify the iteration number that exhibited good convergence and minimized computational time. The specific number of iterations for each calculation is shown in Table 3.

Table 3.
A comparison between the result of the BOMSDM and Models I, II, and III.
5.1. Comparison Between BOMSDM and the Realistic Solution
The results of the realistic solution and optimized solutions of BOMSDM with the same number of facilities are illustrated in Figure 4. It shows that the realistic solution allocates facilities to 60 communities, with an SDGC of 0.226 and an SSR of 0.283, indicating relatively good equity (though not reaching the optimal level below 0.2) but poor efficiency.
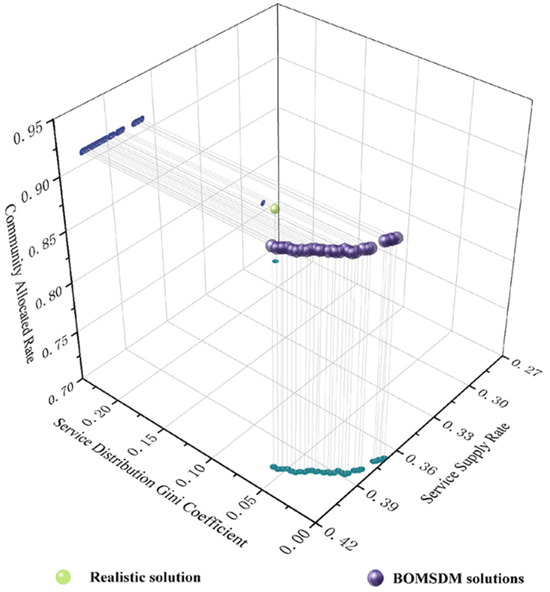
Figure 4.
The comparison between the BOMSDM and the realistic solution.
Setting the total number of facilities to 72 aligns with the realistic number of recycling stations, where the BOMSDM produces a total of 29 Pareto optimal solutions (Table S1). Figure 4 shows that in all solutions, facilities are evenly distributed among 72 different communities, and the SDGCs and SSRs are significantly improved compared to the realistic solution. All solutions achieve SDGCs below 0.2, with a mean value of 0.027, representing an 88.1% enhancement over the realistic solution. The average SSR is 0.390, which is a 37.8% improvement over the realistic solution. The highest SSR recorded is 0.405, representing a 43.1% increase compared to the realistic solution.
5.2. Results of Different Models
To compare the performance differences among the BOMSDM, Models I, II, and III were tested across three scenarios set in Section 3.1: (i) In Scenario I, with 72 facilities, the strategy of Model III aligned with that of BOMSDM, while Model I shared its strategies with Model II. (ii) In Scenario II, we set the total number of facilities to 79, which is equal to the number of communities requiring facilities, and subsequently computed all four models. In this scenario, BOMSDM and Model III inherited the median solutions from their Pareto sets obtained in Scenario I, specifically [SDGC = 0.009, SSR = 0.412] and [SDGC = 0.025, SSR = 0.392], respectively. (iii) In Scenario III, we increased the total number of facilities by 40, making the total number of facilities in this scenario 1.5 times the number of communities that needed to be allocated. Similarly, we computed all four models in this scenario, with BOMSDM and Model III inheriting the median solutions from the Pareto sets in Scenario II, namely [SDGC = 0.049, SSR = 0.418] and [SDGC = 0.007, SSR = 0.440].
Based on the emergence of multiple Pareto optimal solution sets in each computation (Table S2), we calculated the average and median values of SDGC and SSR for each set, along with the maximum SSR and minimum SDGC obtained. Additionally, we computed the community allocation rate (CAR) for each solution, representing the proportion of communities that were allocated facilities relative to the total number of communities to illustrate the degree of balance in the distribution of facilities among communities (Table 3).
The results indicate that, compared to Model I, the BOMSDM exhibits higher average SDGC values in Scenarios I and II, surpassing Model I by 0.019 and 0.027, respectively, while still maintaining an optimal level of fairness. Additionally, the average SSR for the BOMSDM is lower than that of Model I by 0.022 and 0.01. Thus, it is evident that the BOMSDM incurs a loss in efficiency and fairness compared to Model I, which is unconstrained by facility-community allocation and incremental strategy limits. When the number of allocated facilities is further increased to a redundant level, in Scenario III, the average SDGC of the BOMSDM is 0.009, which is still higher than 0.006 in Model I. However, in terms of SSR, the average value of the BOMSDM surpasses that of Model I by 0.029. This trend is similarly reflected in the median and optimal values available in each scenario. This indicates that in Scenario III, the fairness of the solutions obtained by the BOMSDM remains lower than that of Model I, whereas, in terms of efficiency, the BOMSDM now matches or exceeds Model I. However, BOMSDM achieves a significant increase in CAR, with enhancements of 30.2%, 27.8%, and 17.8% across the three scenarios.
The situation for Model II mirrors that of Model I: in Scenario II, the BOMSDM sacrifices 0.039 in average SDGC and 0.02 in average SSR for a 36.5% increase in CAR. In Scenario III, all performance metrics of the BOMSDM surpass those of Model II. When compared to Model III, BOMSDM’s advantages are particularly pronounced in Scenario III, where the use of a random allocation strategy leads to enhanced fairness and efficiency. Notably, the BOMSDM’s average SSR exceeds that of Model III by 17.5%.
Figure 5 presents the site selection decisions for selected examples from the four models, focusing on the median solutions from all Pareto sets. The figure illustrates the distribution of facilities in each scenario, along with the newly constructed facilities at each stage. The results indicate that the BOMSDM and Model II are more cost-effective compared to the other two modes. Through an incremental strategy, they reduce the number of new facilities in the last two scenarios: in Scenario II, the BOMSDM and Model II require the construction of only seven new facilities, whereas Model I and Model III require nearly nine times that number on average. Similarly, in Scenario III, the BOMSDM and Model II only need to build 40 new facilities, while Model I requires an average of 118 new facilities, and Model III requires an average of 109.
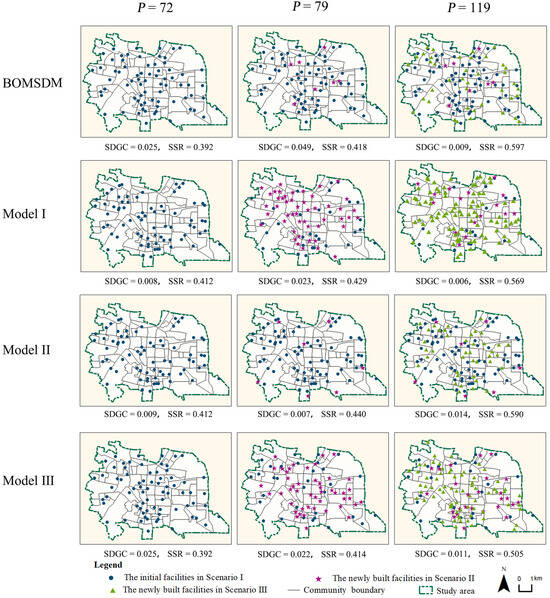
Figure 5.
The illustration of one selected solution generated by the 4 models.
Furthermore, the BOMSDM demonstrates a more balanced and efficient allocation of facilities among communities. As illustrated, both Model I and Model II, which employ static random strategies, exhibit a clustering of facilities in certain communities; for instance, in Scenario I of Model I, the community of Wayaotou in the northeast corner contains five facilities, while 30 communities lack any facilities. In contrast, Scenario III of the BOMSDM ensures that all communities have at least one facility, with larger communities receiving a proportionately greater number of facilities, reflecting real-world conditions more accurately. In Model III, which employs a static average distribution strategy, community size is overlooked in Scenario III.
5.3. Sensitivity Analyses
In Section 5.2, we observe an intriguing phenomenon: In Scenario I, the average SDGC of the BOMSDM is approximately 2.4 times higher than that of Model I and Model II (which produce consistent results in Scenario I), while the average SSR is 4.9% lower. In Scenario II, the average SDGC of the BOMSDM is approximately 1.4 times and 4.9 times higher than that of Model I and Model II, respectively, while the average SSR is 2.3% and 4.6% lower. These findings suggest that the BOMSDM exhibits the less effective optimization of objective values in both Scenario I and Scenario II, implying that community allocation strategies indeed exert a certain negative impact on the efficiency and equity of facility distribution. However, in Scenario III, BOMSDM’s performance approaches or even surpasses that of Model I and Model II. Specifically, for SDGC, the mean value of BOMSDM drops to 0.009, which is 50% higher than Model I but lower than the mean value of Model II; for SSR, BOMSDM’s mean value is 5.2% higher than Model I, and 0.2% higher than Model II. This indicates that as the number of facilities increases, the negative impact of community allocation strategies gradually diminishes. This section analyzes the sensitivity of the parameter of facility redundancy to the solutions. In this study, we defined the baseline facility quantity as one facility allocated per community, with redundancy defined as the excess number of facilities beyond the baseline, i.e.,
We initiated at 0 and incrementally increased it by five in ten cumulative measurements, with the mean value results reported in Figure 6 (See Table S3 for details). The results indicate that when R is between 0 and 10, the BOMSDM quickly optimizes both objectives. However, as R reaches 15 to 20, the SSR obtained by BOMSDM exceeds that of other models. This suggests that, in this instance, although BOMSDM partially sacrifices the two objective values due to the inter-community allocation constraints in the early stages, this shortfall can be compensated when redundancy reaches 15 to 20, which corresponds to approximately 20% of the total number of communities.
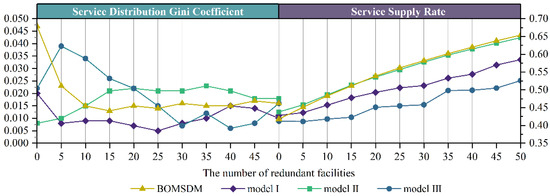
Figure 6.
The impact of facility redundancy.
6. Discussion
6.1. The Effectiveness of the BOMSDM
By comparing the BOMSDM with the realistic solution and traditional models proposed in the previous literature and conducting a sensitivity analysis of facility redundancy on the BOMSDM’s results, based on the research findings, we derive the following three key conclusions:
First, the empirical study demonstrates that the BOMSDM is effective because, compared to the realistic solution, the proposed BOMSDM significantly enhances the efficiency of community facilities’ service provision and promotes social equity in service distribution while maintaining SDGC within the optimal fairness range. This study reveals that in Shaoxing City, the existing distribution of recycling stations shows low service efficiency, likely due to independent facility placement by community committees, causing overlapping service areas between neighboring communities, or poor accessibility resulting from decision-making errors, which highlights the necessity of a global optimization model for facility location. The BOMSDM addresses these issues by considering both individual facility constraints and overall service efficiency, offering decision-makers an effective tool for global optimization.
Second, in the empirical study on the site selection of recycling stations in Shaoxing, we found that BOMSDM is superior because, compared to traditional models with random facility-community allocation strategies, the BOMSDM may slightly sacrifice global service efficiency and fairness but substantially improve the balance in the allocation of community facilities among communities. Previous location optimization models, such as those by Current et al. [53], Sonmez and Lim [47], Arulselvan et al. [57], and Shi et al. [58], provide effective global frameworks for optimizing facility efficiency and equity. These models focus on placing facilities in high-demand areas, such as population centers, to maximize accessibility, coverage, and supply. However, in practice, this can lead to a different form of inequity and waste, as concentrating facilities in dense urban areas may lead to redundancy, while remote or peripheral communities are excluded. Unlike traditional models, the BOMSDM innovatively prioritizes equity in facility allocation, ensuring service delivery to marginalized communities.
Third, through the sensitivity testing of facility redundancy in the empirical study, we found that BOMSDM achieves optimal optimization capability when there is a certain level of facility redundancy. In this research, when the facility redundancy reached approximately 20%, the target values obtained by the BOMSDM closely aligned with those from Model II, which employs a random strategy. This finding indicates that, in this instance, the BOMSDM can effectively offset the target value losses incurred from earlier facility-community allocation constraints through the strategic addition of a limited number of redundant facilities. This underscores the superiority of the BOMSDM’s scenario-based dynamic strategy. Additionally, it offers valuable insights for decision-makers, highlighting the necessity of incorporating a certain degree of redundancy beyond the existing 1:1 facility-community allocation strategy to enhance operational efficiency.
6.2. The Applicability of the BOMSDM
The BOMSDM proposes a balanced and fair distribution strategy to address a competition issue related to facility-community-allocation, which may arise in FLPs across different levels of administrative divisions. For instance, public welfare facilities such as high-quality schools, comprehensive hospitals, and large-scale parks may become competitive targets at the street or district level. Even at the city level, competition can arise for scarce public facilities such as commercial centers, theme parks, and transportation hubs. In this context, the model proposed in this study will provide an adjustable tool for FLPs where facility competition exists between administrative units.
Although our study focuses on an exploratory test of a single case, there is reason to believe that the BOMSDM exhibits broader applicability. First, the efficiency and equity objectives proposed by the model are fundamental optimization goals for FLPs [78,79], using conventional methods such as coverage and the Gini coefficient. Additionally, the model imposes no restrictions on key factors like community size, housing volume, or the number and increments of facilities, which suggests that the model is likely applicable to facilities at other levels, such as neighborhood-level or district-level facilities. Finally, the data used in this study are easily accessible through public sources, such as maps and real estate websites for road and housing data and government planning documents for administrative boundaries. The number of new facilities is based on government budgets. A key consideration is that facility candidate points are chosen subjectively. In this study, we used the main entrances of communities as candidates, though in practice, factors like population distribution, facility type, and site suitability could lead to multiple candidate points within a community.
6.3. The Limitations of the BOMSDM
In this study, the BOMSDM obtained a set of Pareto optimal solutions with dual objectives. However, we did not design a method for selecting an implementation solution from the whole set because, in reality, the weighting of the two objectives heavily depends on the decision-makers’ highly uncertain preferences.
In addition, this study focused on social equity and efficiency in service provision, with particular attention paid to the uncertainty of the facility number and inter-community competition. However, these objectives and constraints do not fully capture the complexity of real-world CFLPs. Future research could optimize the model in several ways: First, new objectives could be introduced to enhance its comprehensiveness, such as incorporating facility investment costs, accessibility, and environmental impacts as optimization goals [80,81,82]. Second, uncertain parameters could be added to improve the model’s adaptability, such as varying facility capacity, uncertain demand or demand patterns, and fluctuating facility service areas [43,83,84]. Third, the model could be further validated in extreme scenarios, such as the community allocation of medical or disaster relief resources in emergencies or the impact of increased online services on existing facility systems. Overall, although the BOMSDM underwent preliminary testing in this study, it is still not a mature model. Future work will require further validation in more diverse scenarios to confirm its robustness and applicability.
Another limitation of the BOMSDM is the utilization of the NSGA-II algorithm with constraints. Although it performs well in handling bi-objective models, after adding constraints, the integrated algorithm requires a considerable number of iterations to achieve convergent results when facing large-scale instances. Furthermore, our analysis reveals that models employing a non-incremental strategy yield inferior target values compared to those utilizing incremental strategies. This discrepancy may be attributed to the greater computational burden and the tendency of genetic algorithms to become ensnared in local optimization traps. Therefore, we look forward to future research that can develop or introduce more efficient algorithms.
7. Conclusions
This study proposes a framework for the community-facility location problem, which includes a bi-objective multi-scenario dynamic model as its core, along with a comprehensive set of methods for data acquisition and processing and model computation. The newly proposed model optimizes two objectives: service supply efficiency, reflected by the service supply rate (SSR), and social equity in the service distribution, represented by the service distribution Gini coefficient (SDGC). Additionally, considering the facility number uncertainty and the potential competition among communities for these facilities, the BOMSDM introduces a multi-period incremental strategy and establishes dynamic facility-community allocation strategies that vary according to three scenarios: facility insufficient, facility sufficient, and facility redundant. This framework enables the construction of a dual dynamic model that incorporates both temporal and spatial dimensions. The model is solved using the constrained NSGA-II algorithm, yielding Pareto optimal solutions for SSR and SDGC.
To validate the effectiveness and superiority of the BOMSDM, we compared it with three other models: a random allocation non-incremental model, a random allocation incremental model, and an average allocation non-incremental model. We took the allocation of recycling stations across 83 communities in Shaoxing City as a real-world case. The experimental results demonstrate that, compared to real-world solutions, the proposed model significantly improves the efficiency of service provision and social equity in service distribution while also promoting a more balanced distribution of community facilities across communities. Compared to other models, the incremental and dynamic facility-community allocation strategy of the BOMSDM helps reduce the number of new facilities constructed or relocated, enhancing the economic feasibility of facility development while more efficiently achieving the efficiency and equity goals set by the model. Furthermore, empirical validation reveals that when facilities are insufficient, the BOMSDM may prioritize the community allocation rate, compromising overall efficiency and equity to reduce inter-community competition. However, as facility redundancy increases, the gap between the BOMSDM and random allocation models gradually diminishes. This study addresses the complex issues of facility location and resource allocation, providing theoretical foundations and optimization solutions for decision-makers.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app15010402/s1, Table S1: The detailed Pareto solutions produced by BOMSDM in Scenario I with P = 72; Table S2: The detailed results produced by 4 models in three scenarios; Table S3: The detailed results produced by 4 models with different R values.
Author Contributions
Conceptualization, S.Z. and H.H.; methodology, S.Z.; software, S.Z.; validation, A.D.; formal analysis, A.D.; writing—original draft preparation, S.Z.; writing—review and editing, H.H.; visualization, S.Z.; supervision, H.H.; funding acquisition, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Center for Balance Architecture of Zhejiang University (Project No: K Heng 20203512-02B, Index and planning methods of resilient cities) and by the Zhejiang Federation of Social Sciences (Project No: 2024-18, Research on the Spatial Mechanism and Institutional Optimization of Rural Civilization Construction in Zhejiang in the New Era).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
| Algorithm A1: NSGA-II with Constraints |
|
The chromosome structure in BOMSDM comprises a set of candidate points with a specific quantity . Although the selection of candidate points within a chromosome is random, we established certain conditions to achieve our siting strategy. Specifically, (i) we built a set to store the community codes corresponding to the locations of the selected candidate points. When searching for a new candidate point, if the community code of a potential point was already present in the set, it was excluded; otherwise, it was added to the set of selected candidate points. (ii) We designated a set of mandatory candidate points to retain the selected points from the previous period. (iii) When , the configuration of candidate points followed the strategy outlined in (i); we maintained a dataset to store the unselected candidate points and randomly select candidates from it.
References
- Farahani, R.Z.; SteadieSeifi, M.; Asgari, N. Multiple Criteria Facility Location Problems: A Survey. Appl. Math. Model. 2010, 34, 1689–1709. [Google Scholar] [CrossRef]
- Owen, S.H.; Daskin, M.S. Strategic Facility Location: A Review. Eur. J. Oper. Res. 1998, 111, 423–447. [Google Scholar] [CrossRef]
- New York City Mayor’s Office of Environment Coordination. City Environment Quality Review Technical Manual. Available online: https://www.nyc.gov/site/oec/environmental-quality-review/2014-technical-manual.page (accessed on 25 March 2024).
- The Government of Hong Kong Special Administrative Region Hong Kong Planning Standards and Guides. Available online: https://www.pland.gov.hk/pland_en/tech_doc/hkpsg/index.html (accessed on 25 March 2024).
- McShane, I.; Coffey, B. Rethinking Community Hubs: Community Facilities as Critical Infrastructure. Curr. Opin. Environ. Sustain. 2022, 54, 101149. [Google Scholar] [CrossRef]
- Engels, B. The Historical Rise and Fall of Community Facility Provision Standards in the Metropolitan Planning of Melbourne. Plan. Perspect. 2019, 34, 693–724. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, X.; Wu, G. The Network Governance of Urban Renewal: A Comparative Analysis of Two Cities in China. Land Use Policy 2021, 106, 105448. [Google Scholar] [CrossRef]
- Chand, S. Decision/Forecast Horizon Results for A Single Facility Dynamic Location/Relocation Problem. Oper. Res. Lett. 1988, 7, 247–251. [Google Scholar] [CrossRef]
- Thanh, P.N.; Bostel, N.; Péton, O. A Dynamic Model for Facility Location in the Design of Complex Supply Chains. Int. J. Prod. Econ. 2008, 113, 678–693. [Google Scholar] [CrossRef]
- Chandra Majhi, R.; Ranjitkar, P.; Sheng, M. Optimal Allocation of Dynamic Wireless Charging Facility for Electric Vehicles. Transp. Res. Part D Transp. Environ. 2022, 111, 103461. [Google Scholar] [CrossRef]
- Silva, A.; Aloise, D.; Coelho, L.C.; Rocha, C. Heuristics for the Dynamic Facility Location Problem with Modular Capacities. Eur. J. Oper. Res. 2021, 290, 435–452. [Google Scholar] [CrossRef]
- Arabani, A.B. Facility Location Dynamics: An Overview of Classifications and Applications. Ind. Eng. 2012, 62, 408–420. [Google Scholar] [CrossRef]
- Cheng, T.; Liu, C.; Yang, H.; Wang, N.; Liu, Y. From Service Capacity to Spatial Equity: Exploring a Multi-Stage Decision-Making Approach for Optimizing Elderly-Care Facility Distribution in the City Centre of Tianjin, China. Sustain. Cities Soc. 2022, 85, 104076. [Google Scholar] [CrossRef]
- Mirdar Harijani, A.; Mansour, S.; Karimi, B.; Lee, C.-G. Multi-Period Sustainable and Integrated Recycling Network for Municipal Solid Waste—A Case Study in Tehran. J. Clean. Prod. 2017, 151, 96–108. [Google Scholar] [CrossRef]
- Bakker, H.; Nickel, S. The Value of the Multi-Period Solution Revisited: When to Model Time in Capacitated Location Problems. Comput. Oper. Res. 2024, 161, 106428. [Google Scholar] [CrossRef]
- Erdoğan, G.; Stylianou, N.; Vasilakis, C. An open source decision support system for facility location analysis. Decis. Support Syst. 2019, 125, 113116. [Google Scholar] [CrossRef]
- Weber, A. Über Den Standort Der Industrien; JCB Mohr: Tübingen, Germany, 1922. [Google Scholar]
- Hakimi, S.L. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Hakimi, S.L. Optimum Distribution of Switching Centers in a Communication Network and Some Related Graph Theoretic Problems. Oper. Res. 1965, 13, 462–475. [Google Scholar] [CrossRef]
- Toregas, C.; Swain, R.; ReVelle, C.; Bergman, L. The Location of Emergency Service Facilities. Oper. Res. 1971, 19, 1363–1373. [Google Scholar] [CrossRef]
- Church, R.; Velle, C.R. The Maximal Covering Location Problem. Pap. Reg. Sci. 1974, 32, 101–118. [Google Scholar] [CrossRef]
- Sharma, G.; Patil, G.R. Spatial and Social Inequities for Educational Services Accessibility—A Case Study for Schools in Greater Mumbai. Cities 2022, 122, 103543. [Google Scholar] [CrossRef]
- Snyder, L.V. Facility Location under Uncertainty: A Review. IIE Trans. 2006, 38, 547–564. [Google Scholar] [CrossRef]
- Gülpınar, N.; Pachamanova, D.; Çanakoğlu, E. Robust Strategies for Facility Location under Uncertainty. Eur. J. Oper. Res. 2013, 225, 21–35. [Google Scholar] [CrossRef]
- Manzini, R.; Gebennini, E. Optimization Models for the Dynamic Facility Location and Allocation Problem. Int. J. Prod. Res. 2008, 46, 2061–2086. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Fallah, S.; Ruiz, R.; Hosseini, S.; Asgari, N. OR Models in Urban Service Facility Location: A Critical Review of Applications and Future Developments. Eur. J. Oper. Res. 2019, 276, 1–27. [Google Scholar] [CrossRef]
- Revelle, C.S.; Eiselt, H.A.; Daskin, M.S. A Bibliography for Some Fundamental Problem Categories in Discrete Location Science. Eur. J. Oper. Res. 2008, 184, 817–848. [Google Scholar] [CrossRef]
- Melo, M.T.; Nickel, S.; Saldanha-Da-Gama, F. Facility Location and Supply Chain Management— Review. Eur. J. Oper. Res. 2009, 196, 401–412. [Google Scholar] [CrossRef]
- Turkoglu, D.C.; Genevois, M.E. A Comparative Survey of Service Facility Location Problems. Ann. Oper. Res. 2020, 292, 399–468. [Google Scholar] [CrossRef]
- Rossit, D.G.; Nesmachnow, S. Waste Bins Location Problem: A Review of Recent Advances in the Storage Stage of the Municipal Solid Waste Reverse Logistic Chain. J. Clean. Prod. 2022, 342, 130793. [Google Scholar] [CrossRef]
- Hagimoto, A.; Ishigaki, A.; Takashima, R. Facility Location Selection Considering Distance and Transportation Mode. In Proceedings of the 2022 12th International Congress on Advanced Applied Informatics (IIAI-AAI), Kanazawa, Japan, 2–7 July 2022; pp. 609–614. [Google Scholar]
- Mishra, S.; Sahu, P.K.; Sarkar, A.K.; Mehran, B.; Sharma, S. Geo-Spatial Site Suitability Analysis for Development of Health Care Units in Rural India: Effects on Habitation Accessibility, Facility Utilization and Zonal Equity in Facility Distribution. J. Transp. Geogr. 2019, 78, 135–149. [Google Scholar] [CrossRef]
- Redi, A.A.N.P.; Flame, R.R.F.; Redioka, A.A.N.A.; Winarno, W.; Kurniawan, A.C. Maximum Covering Location Problem to Select Facility Location for Operation Timbang in the City of Iloilo, Philippines. J. Sist. Dan Manaj. Ind. 2022, 6, 135–142. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, K.; Chen, Y.; Ma, L. Multi-Objective Two-Level Medical Facility Location Problem and Tabu Search Algorithm. Inf. Sci. 2022, 608, 734–756. [Google Scholar] [CrossRef]
- Zhuo, M.; Li, J.; Zhang, R. Redesigning Deployments of Community Hospitals with A Location-Allocation Model. IFAC-Pap. 2022, 55, 1272–1277. [Google Scholar] [CrossRef]
- Li, X.; Pan, Y.; Jiang, S.; Huang, Q.; Chen, Z.; Zhang, M.; Zhang, Z. Locate Vaccination Stations Considering Travel Distance, Operational Cost, and Work Schedule. Omega 2021, 101, 102236. [Google Scholar] [CrossRef]
- Song, L.; Liu, C.; Li, B. Optimal Selection of Location for Community Hospitals a Case of Huilongguan Region in Beijing. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2803–2806. [Google Scholar]
- Khodaparasti, S.; Maleki, H.R.; Jahedi, S.; Bruni, M.E.; Beraldi, P. Enhancing Community Based Health Programs in Iran: A Multi-Objective Location-Allocation Model. Health Care Manag. Sci. 2017, 20, 485–499. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Y.; Dai, T.; Rosenberg, M.W. Spatial Optimization of Residential Care Facility Locations in Beijing, China: Maximum Equity in Accessibility. Int. J. Health Geogr. 2014, 13, 33. [Google Scholar] [CrossRef]
- Jin, J.G.; Shen, Y.; Hu, H.; Fan, Y.; Yu, M. Optimizing Underground Shelter Location and Mass Pedestrian Evacuation in Urban Community Areas: A Case Study of Shanghai. Transp. Res. Part A Policy Pract. 2021, 149, 124–138. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Keum, H.-J.; Han, K.-Y.; Hong, W.-H. A Hierarchical Flood Shelter Location Model for Walking Evacuation Planning. Environ. Hazards 2021, 20, 432–455. [Google Scholar] [CrossRef]
- Rossit, D.G.; Toutouh, J.; Nesmachnow, S. Exact and Heuristic Approaches for Multi-Objective Garbage Accumulation Points Location in Real Scenarios. Waste Manag. 2020, 105, 467–481. [Google Scholar] [CrossRef]
- Zhuo, Q.; Yan, W. Optimizing the Number and Location of Household Waste Collection Sites by Multi-Maximal Covering Location Model: An Empirical Study in Minamata City, Kumamoto Prefecture, Japan. J. Clean. Prod. 2022, 379, 134644. [Google Scholar] [CrossRef]
- Ma, Y.; Zou, G.; Shin, J.; Kang, Y.; Gao, S.; Siu, K.W.M.; Zhang, S. Locating Community-Based Comprehensive Service Facilities for Older Adults Using the GIS-NEMA Method in Harbin, China. J. Urban Plan. Dev. 2021, 147, 05021010. [Google Scholar] [CrossRef]
- Faghihinejad, F.; Zoghifard, M.; Amiri, A.M.; Monajem, S. Evaluating Social and Spatial Equity in Public Transport: A Case Study. Transp. Lett. 2023, 15, 1420–1429. [Google Scholar] [CrossRef]
- Ma, M. Challenges in Current Construction and Demolition Waste Recycling: A China Study. Waste Manag. 2020, 118, 610–625. [Google Scholar] [CrossRef] [PubMed]
- Sonmez, A.D.; Lim, G.J. A Decomposition Approach for Facility Location and Relocation Problem with Uncertain Number of Future Facilities. Eur. J. Oper. Res. 2012, 218, 327–338. [Google Scholar] [CrossRef]
- Cheng, C. Distributionally Robust Facility Location with Uncertain Facility Capacity and Customer Demand. Omega 2024, 122, 102959. [Google Scholar] [CrossRef]
- Nasrabadi, A.M. Considering Short-Term and Long-Term Uncertainties in Location and Capacity Planning of Public Healthcare Facilities. Eur. J. Oper. Res. 2020, 281, 152–173. [Google Scholar] [CrossRef]
- Cavdur, F.; Kose-Kucuk, M.; Sebatli, A. Allocation of Temporary Disaster Response Facilities under Demand Uncertainty: An Earthquake Case Study. Int. J. Disaster Risk Reduct. 2016, 19, 159–166. [Google Scholar] [CrossRef]
- Li, D.; Xiong, Q.; Huang, G.; Du, B.; Feng, H. How to Share Benefits of Old Community Renewal Project in China? An Improved Shapley Value Approach. Habitat Int. 2022, 126, 102611. [Google Scholar] [CrossRef]
- Wesolowsky, G.O. Dynamic Facility Location. Manag. Sci. 1973, 19, 1241–1248. [Google Scholar] [CrossRef]
- Current, J.; Ratick, S.; ReVelle, C. Dynamic Facility Location When the Total Number of Facilities Is Uncertain: A Decision Analysis Approach. Eur. J. Oper. Res. 1998, 110, 597–609. [Google Scholar] [CrossRef]
- Ashfari, H. Facility Location Decisions within Integrated Forward/Reverse Logistics under Uncertainty. Procedia CIRP 2014, 17, 606–610. [Google Scholar] [CrossRef]
- Maliki, F. A Multi-Objective Optimization Model for a Multi-Period Mobile Facility Location Problem with Environmental and Disruption Considerations. In Annals of Operations Research; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–26. [Google Scholar]
- Albareda-Sambola, M.; Fernández, E.; Hinojosa, Y.; Puerto, J. The Multi-Period Incremental Service Facility Location Problem. Comput. Oper. Res. 2009, 36, 1356–1375. [Google Scholar] [CrossRef]
- Arulselvan, A.; Maurer, O.; Skutella, M. An Incremental Algorithm for the Uncapacitated Facility Location Problem. Networks 2015, 65, 306–311. [Google Scholar] [CrossRef]
- Shi, J.; Chen, W.; Zhou, Z.; Zhang, G. A Bi-Objective Multi-Period Facility Location Problem for Household e-Waste Collection. Int. J. Prod. Res. 2020, 58, 526–545. [Google Scholar] [CrossRef]
- Kchaou Boujelben, M.; Boulaksil, Y. Modeling International Facility Location under Uncertainty: A Review, Analysis, and Insights. IISE Trans. 2018, 50, 535–551. [Google Scholar] [CrossRef]
- Pérez-Gosende, P.; Mula, J.; Díaz-Madroñero, M. Overview of Dynamic Facility Layout Planning as a Sustainability Strategy. Sustainability 2020, 12, 8277. [Google Scholar] [CrossRef]
- De Oliveira, P.B.; De Camargo, R.S.; De Miranda Júnior, G.; Martins, A.X. A computational study of a decomposition approach for the dynamic two-level uncapacitated facility location problem with single and multiple allocation. Comput. Ind. Eng. 2021, 151, 106964. [Google Scholar] [CrossRef]
- Fadda, E.; Manerba, D.; Tadei, R. How to Locate Services Optimizing Redundancy: A Comparative Analysis of K -Covering Facility Location Models. Socio-Econ. Plan. Sci. 2024, 94, 101938. [Google Scholar] [CrossRef]
- Monfared, M.S.; Monabbati, S.E.; Kafshgar, A.R. Pareto-Optimal Equilibrium Points in Non-Cooperative Multi-Objective Optimization Problems. Expert Syst. Appl. 2021, 178, 114995. [Google Scholar] [CrossRef]
- Wang, Z.; Rangaiah, G.P. Application and Analysis of Methods for Selecting an Optimal Solution from the Pareto-Optimal Front Obtained by Multiobjective Optimization. Ind. Eng. Chem. Res. 2017, 56, 560–574. [Google Scholar] [CrossRef]
- Gini, C. Measurement of Inequality of Incomes. Econ. J. 1921, 31, 124. [Google Scholar] [CrossRef]
- Rong, P.; Zheng, Z.; Kwan, M.-P.; Qin, Y. Evaluation of the Spatial Equity of Medical Facilities Based on Improved Potential Model and Map Service API: A Case Study in Zhengzhou, China. Appl. Geogr. 2020, 119, 102192. [Google Scholar] [CrossRef]
- Correa-Parra, J.; Vergara-Perucich, J.F.; Aguirre-Nuñez, C. Water Privatization and Inequality: Gini Coefficient for Water Resources in Chile. Water 2020, 12, 3369. [Google Scholar] [CrossRef]
- Dai, D. Racial/Ethnic and Socioeconomic Disparities in Urban Green Space Accessibility: Where to Intervene? Landsc. Urban Plan. 2011, 102, 234–244. [Google Scholar] [CrossRef]
- Hu, S.; Song, W.; Li, C.; Lu, J. A Multi-Mode Gaussian-Based Two-Step Floating Catchment Area Method for Measuring Accessibility of Urban Parks. Cities 2020, 105, 102815. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Turan, H.H.; Kahagalage, S.D.; Jalalvand, F.; El Sawah, S. A Multi-Objective Simulation–Optimization for a Joint Problem of Strategic Facility Location, Workforce Planning, and Capacity Allocation: A Case Study in the Royal Australian Navy. Expert Syst. Appl. 2021, 186, 115751. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A Comprehensive Survey on NSGA-II for Multi-Objective Optimization and Applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Murugan, P.; Kannan, S.; Baskar, S. NSGA-II Algorithm for Multi-Objective Generation Expansion Planning Problem. Electr. Power Syst. Res. 2009, 79, 622–628. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, L.; Shi, D.; Hui, E.C. Urban Residential Space Differentiation and the Influence of Accessibility in Hangzhou, China. Habitat Int. 2022, 124, 102556. [Google Scholar] [CrossRef]
- Zhejiang Daily. The First Anniversary of Shaoxing’s Recycling of Renewable Resources: A Little “Sweet” a Little “Difficult”. Available online: https://baijiahao.baidu.com/s?id=1652425522227288025&wfr=spider&for=pc (accessed on 4 April 2024).
- Chung, H. Neighbourhood Redevelopment and the Making of a Housing Middle Class: Can Gentrification Explain China’s Spatial and Social Changes? GeoJournal 2021, 86, 1375–1388. [Google Scholar] [CrossRef]
- Song, W.; Huang, Q.; Gu, Y.; He, G. Unraveling the Multi-Scalar Residential Segregation and Socio-Spatial Differentiation in China: A Comparative Study Based on Nanjing and Hangzhou. J. Geogr. Sci. 2021, 31, 1757–1774. [Google Scholar] [CrossRef]
- Mandell, M.B. Modelling Effectiveness-Equity Trade-Offs in Public Service Delivery Systems. Manag. Sci. 1991, 37, 467–482. [Google Scholar] [CrossRef]
- McAllister, D.M. Equity and Efficiency in Public Facility Location. Geogr. Anal. 1976, 8, 47–63. [Google Scholar] [CrossRef]
- Tao, Z.; Zhao, M. Planning for Equal Transit-Based Accessibility of Healthcare Facilities: A Case Study of Shenzhen, China. Socio-Econ. Plan. Sci. 2023, 88, 101666. [Google Scholar] [CrossRef]
- Mohsenizadeh, M.; Tural, M.K.; Kentel, E. Municipal Solid Waste Management with Cost Minimization and Emission Control Objectives: A Case Study of Ankara. Sustain. Cities Soc. 2020, 52, 101807. [Google Scholar] [CrossRef]
- Slavík, J.; Dolejš, M.; Rybová, K. Mixed-Method Approach Incorporating Geographic Information System (GIS) Tools for Optimizing Collection Costs and Convenience of the Biowaste Separate Collection. Waste Manag. 2021, 134, 177–186. [Google Scholar] [CrossRef]
- Correia, I.; Melo, T. Integrated Facility Location and Capacity Planning under Uncertainty. Comput. Appl. Math. 2021, 40, 175. [Google Scholar] [CrossRef]
- Shavarani, S.M. Multi-Level Facility Location-Allocation Problem for Post-Disaster Humanitarian Relief Distribution: A Case Study. J. Humanit. Logist. Supply Chain Manag. 2019, 9, 70–81. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).