Proposes Geometric Accuracy and Surface Roughness Estimation of Anatomical Models of the Pelvic Area Manufactured Using a Material Extrusion Additive Technique
Abstract
1. Introduction
2. Materials and Methods
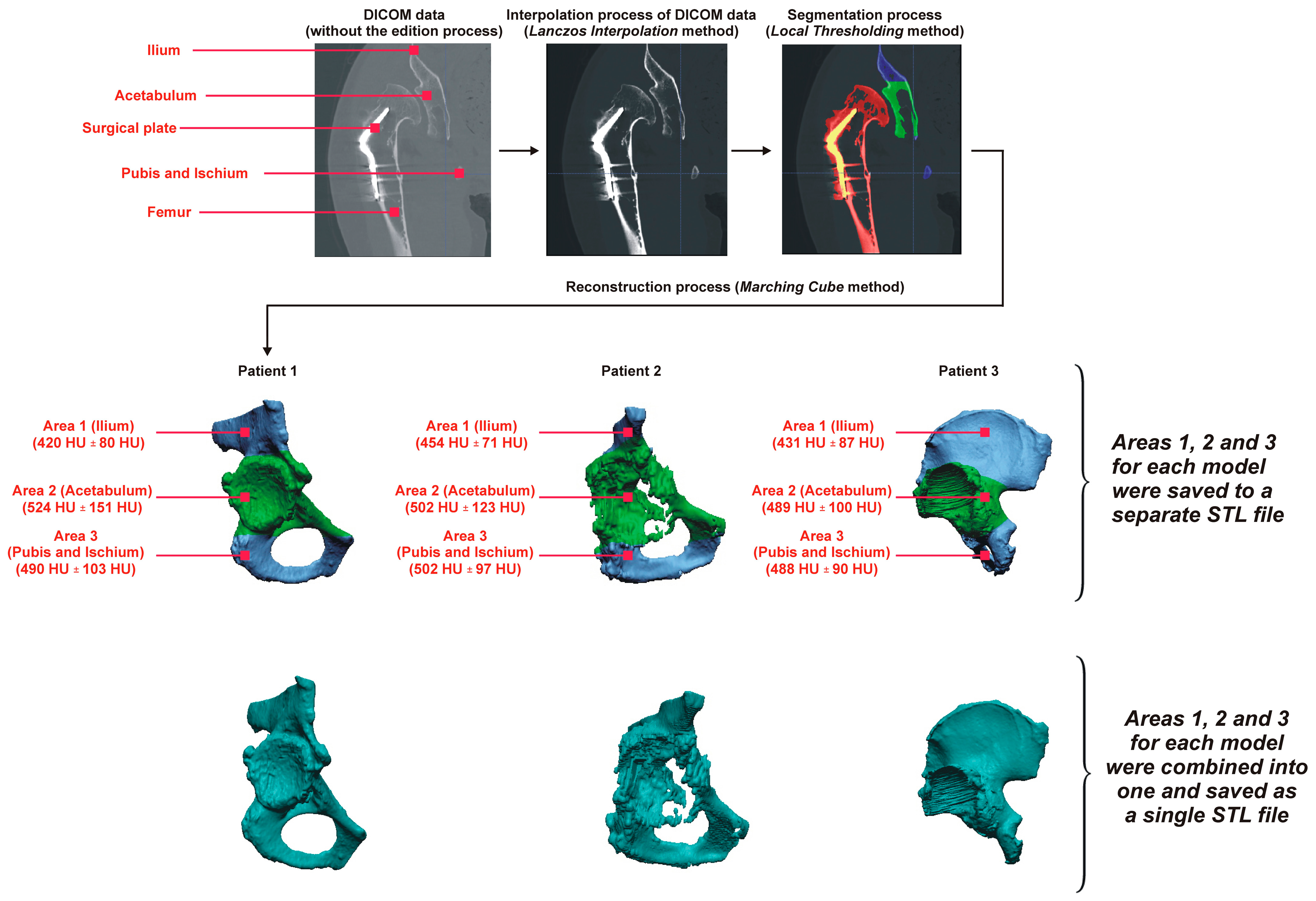
2.1. Procedure to Obtain a Digital Pelvic Model
- Cell selection (iso-voxel);
- Classification of the position of each vertex (internal/external);
- Creation of an index i;
- Finding the edges intersected by the contour surface according to the case table for the index i of the cell;
- Determination of intersection points, linear interpolation;
- Attaching the determined points (triangles) to the contour surface;
- Transfer to the next cell.
2.2. Procedure to Manufacture a Pelvic Model
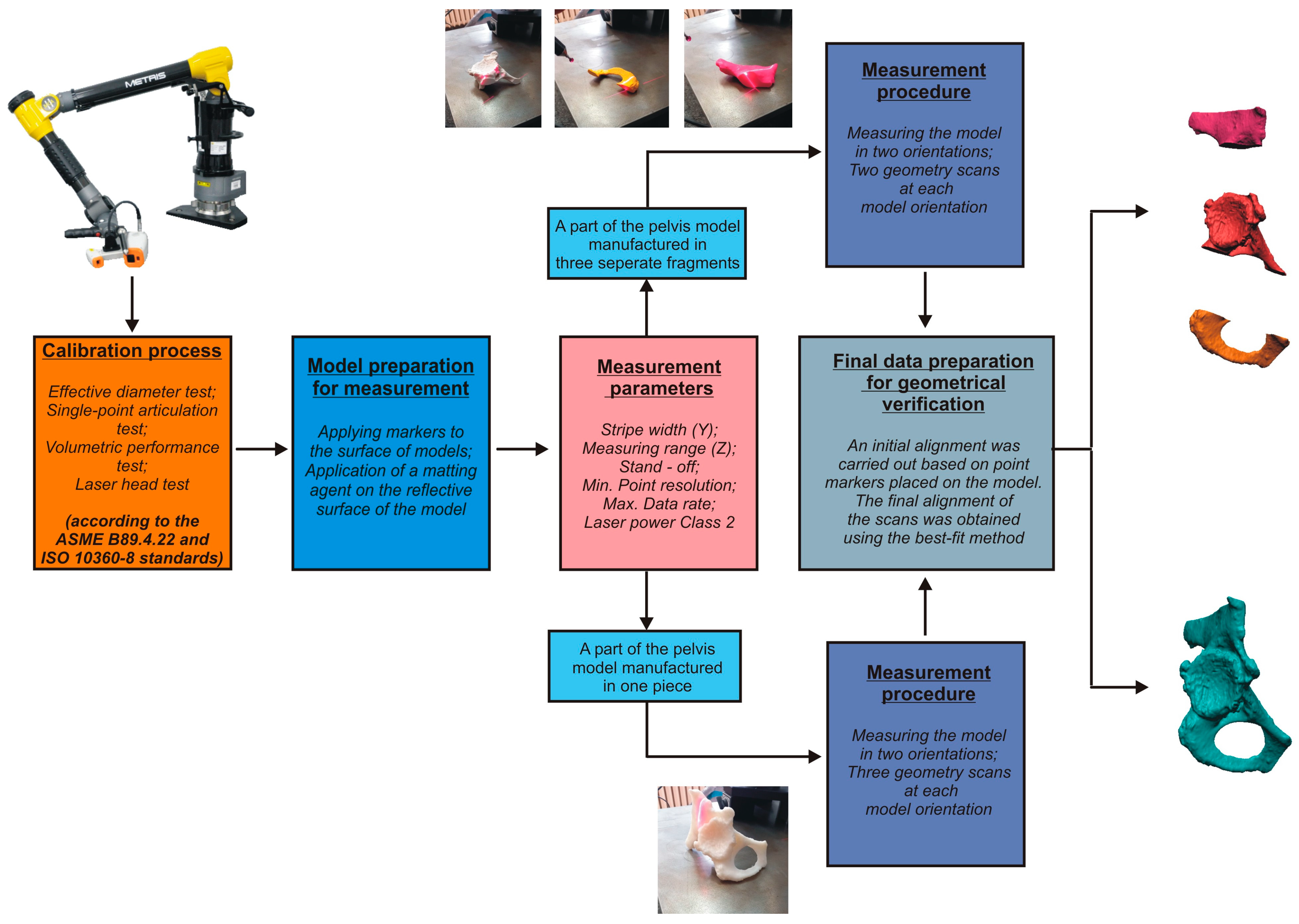
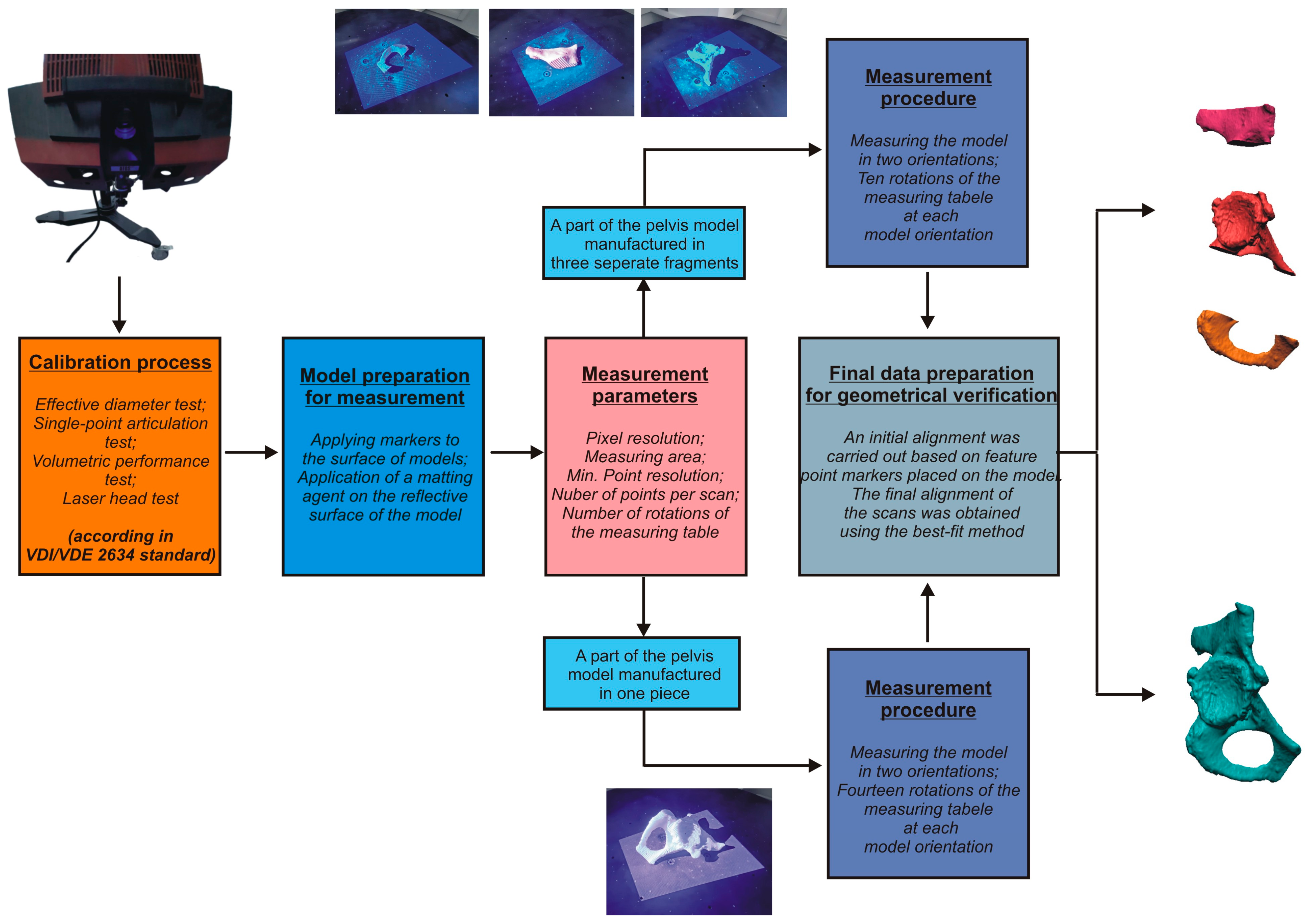
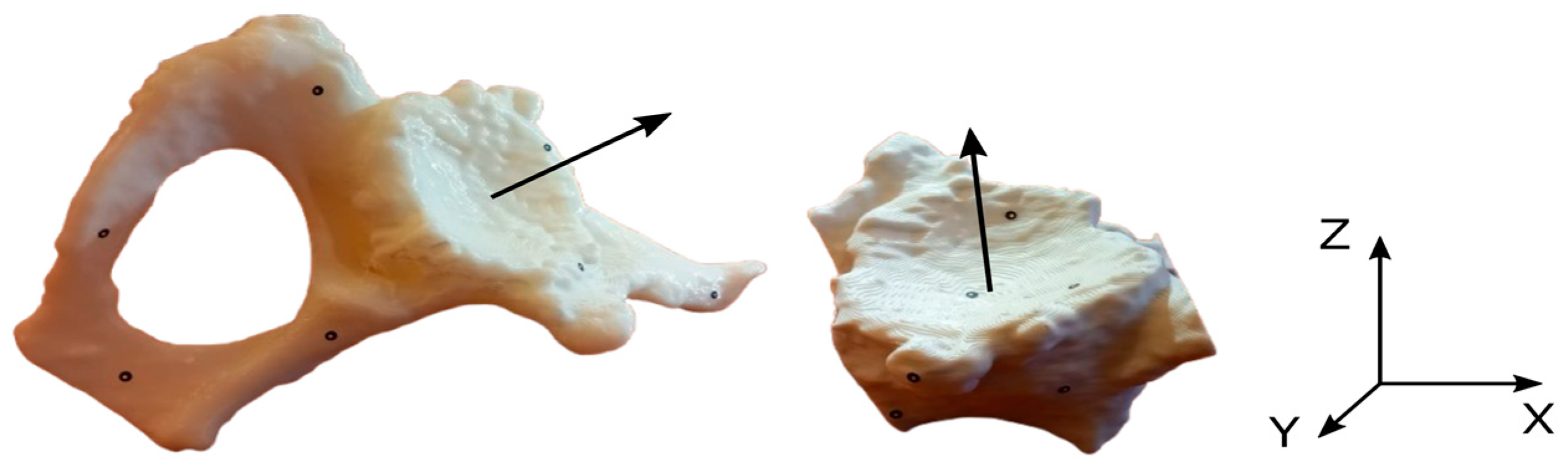
2.3. Development of Procedures for Verifying Geometrical Accuracy
- Conducting the systems calibration process;
- Development of a geometry measurement procedure that enables accurate and complete digitization of the geometry of anatomical structures;
- Development of a procedure to evaluate the geometrical accuracy.
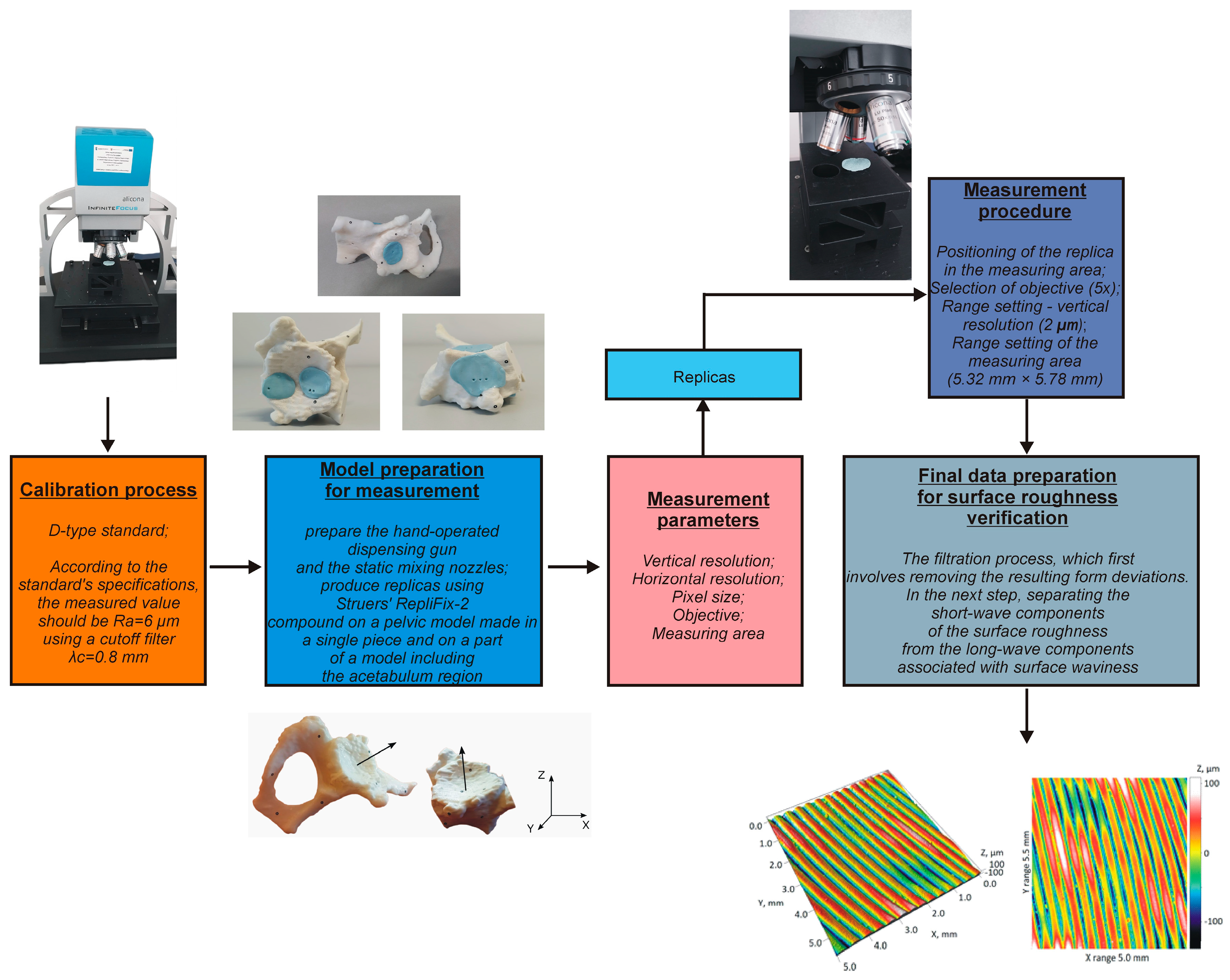
2.4. Development of Procedures for Verifying Surface Roughness Parameters
- Conducting the systems calibration process;
- Development of a surface roughness measurement procedure;
- Development of a procedure to evaluate the surface roughness parameters.
- Sa—the arithmetical mean height of the surface (6):
- Sq—root mean square height of the surface (7):
- Spk + Sk + Svk—the sum of reduced peak height (Spk), core height (Sk), and reduced dale depth (Svk). Spk, Sk, and Svk are parameters related to the material ratio curve (Figure 8)
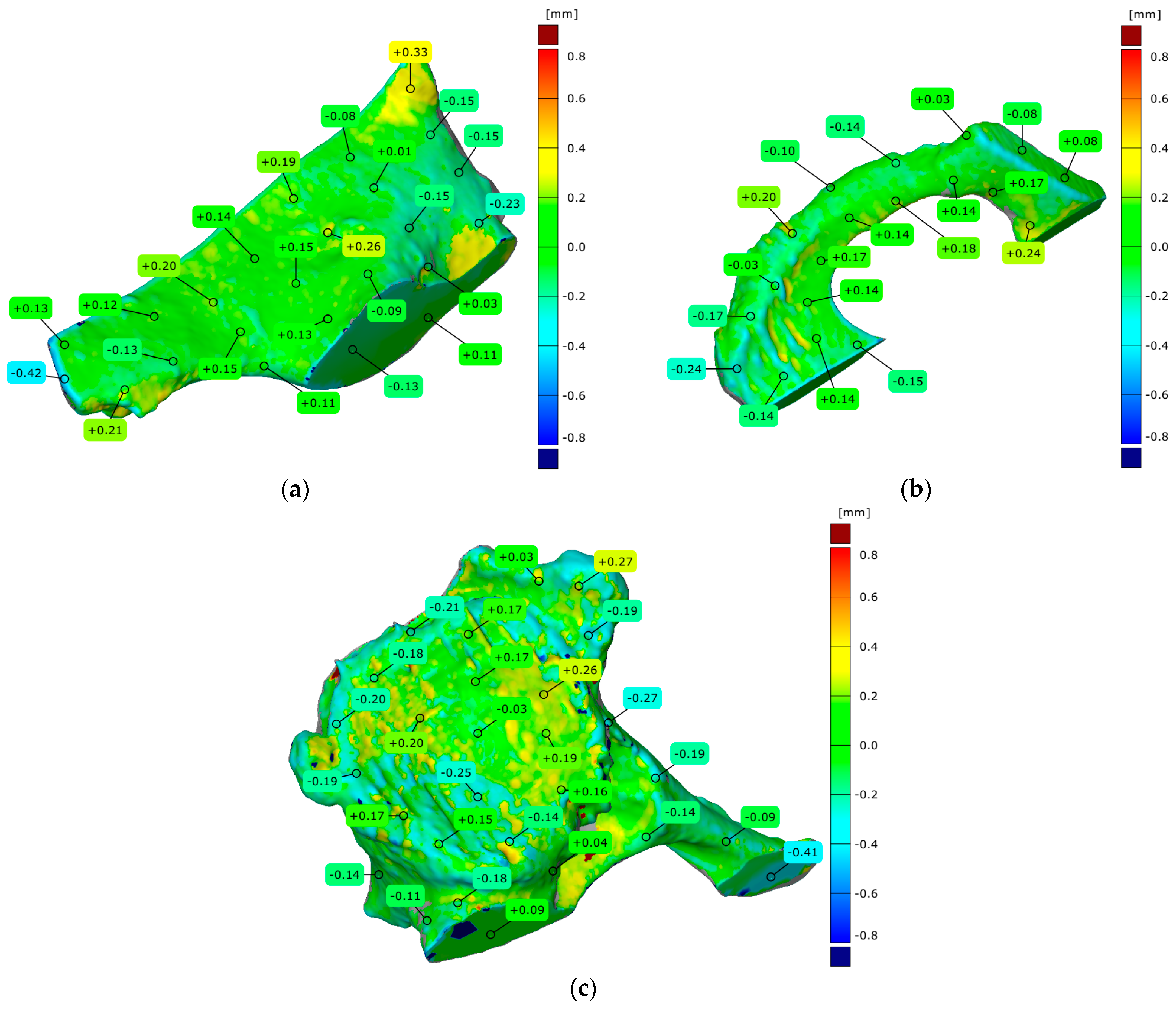
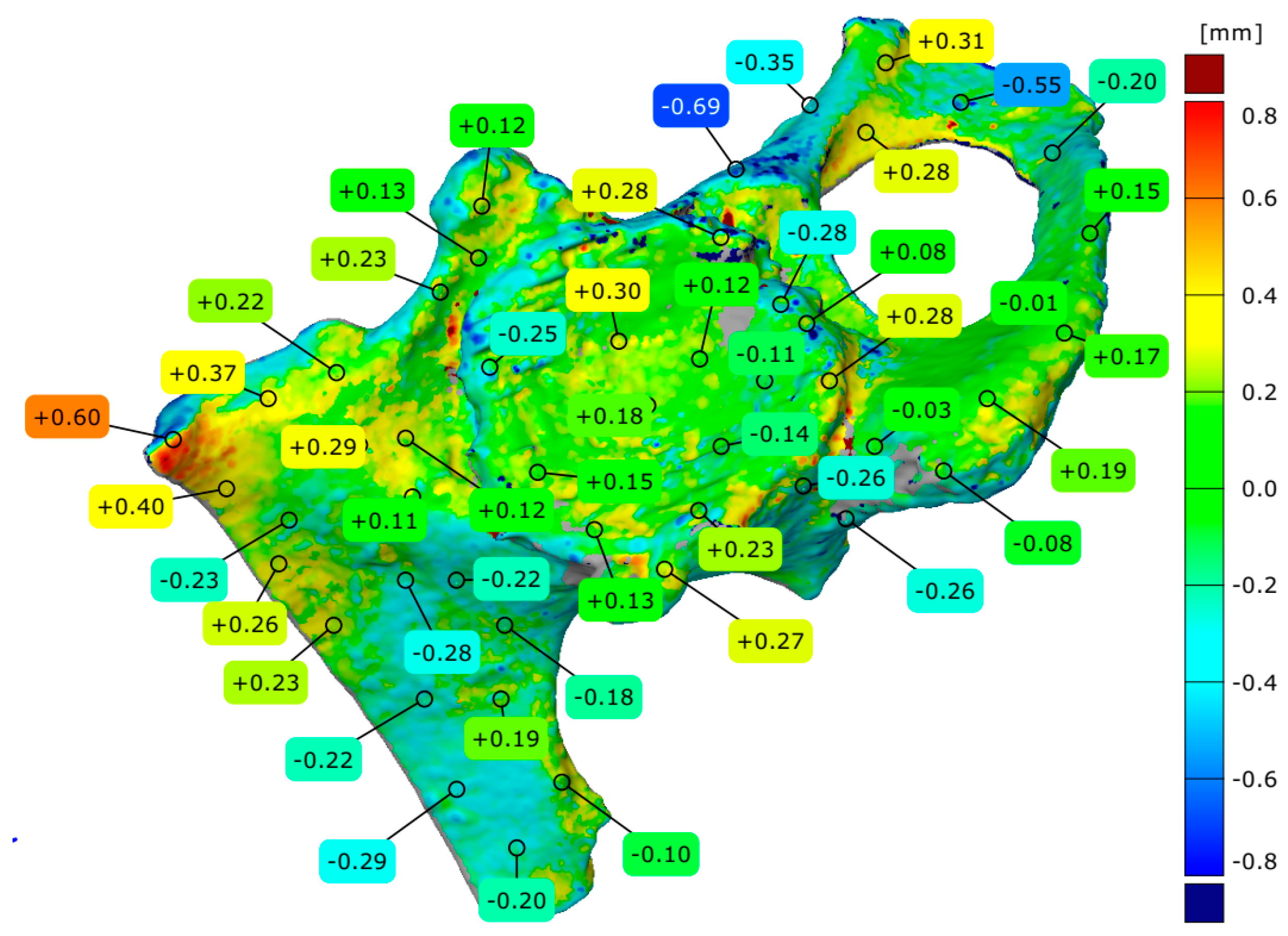
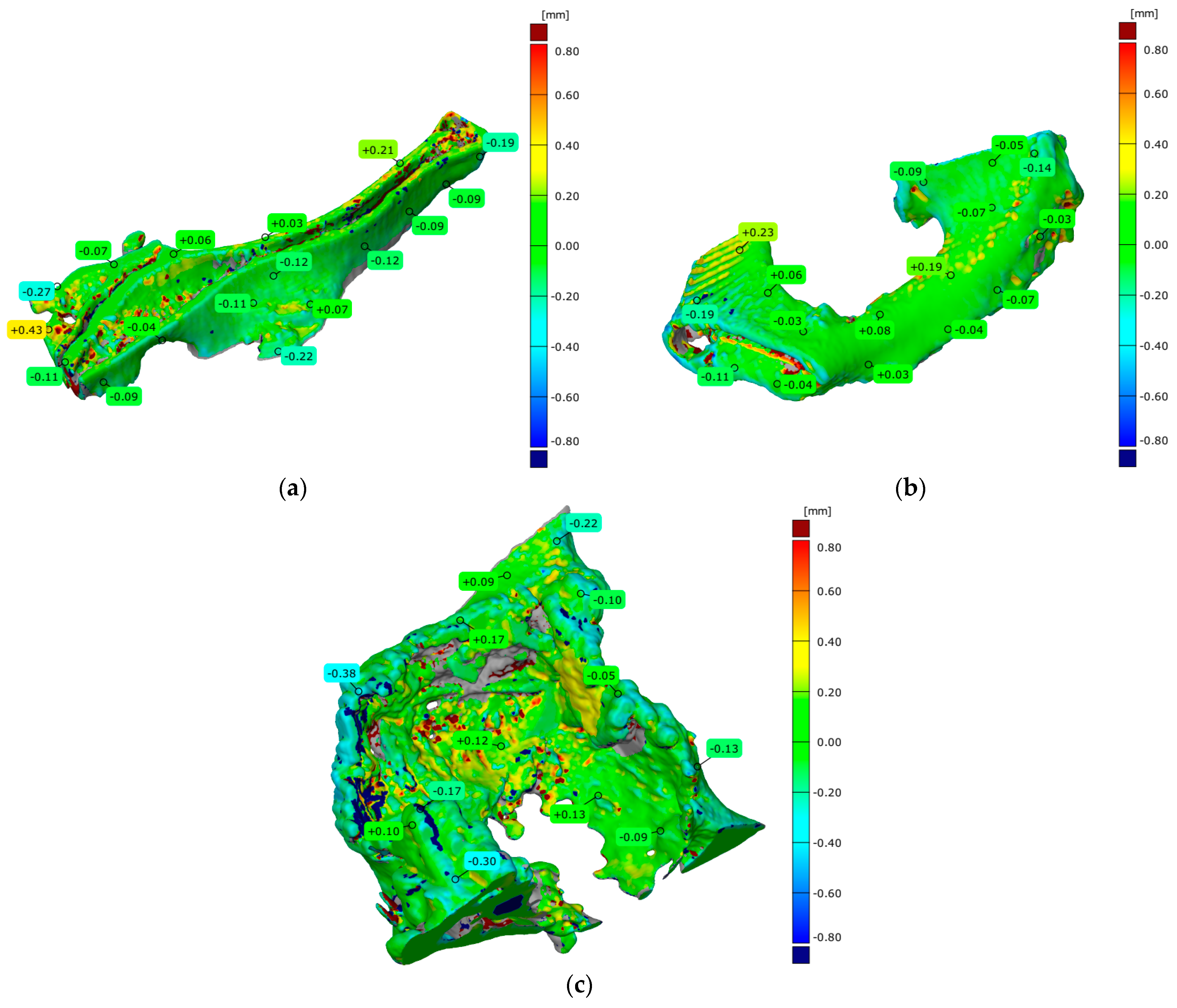
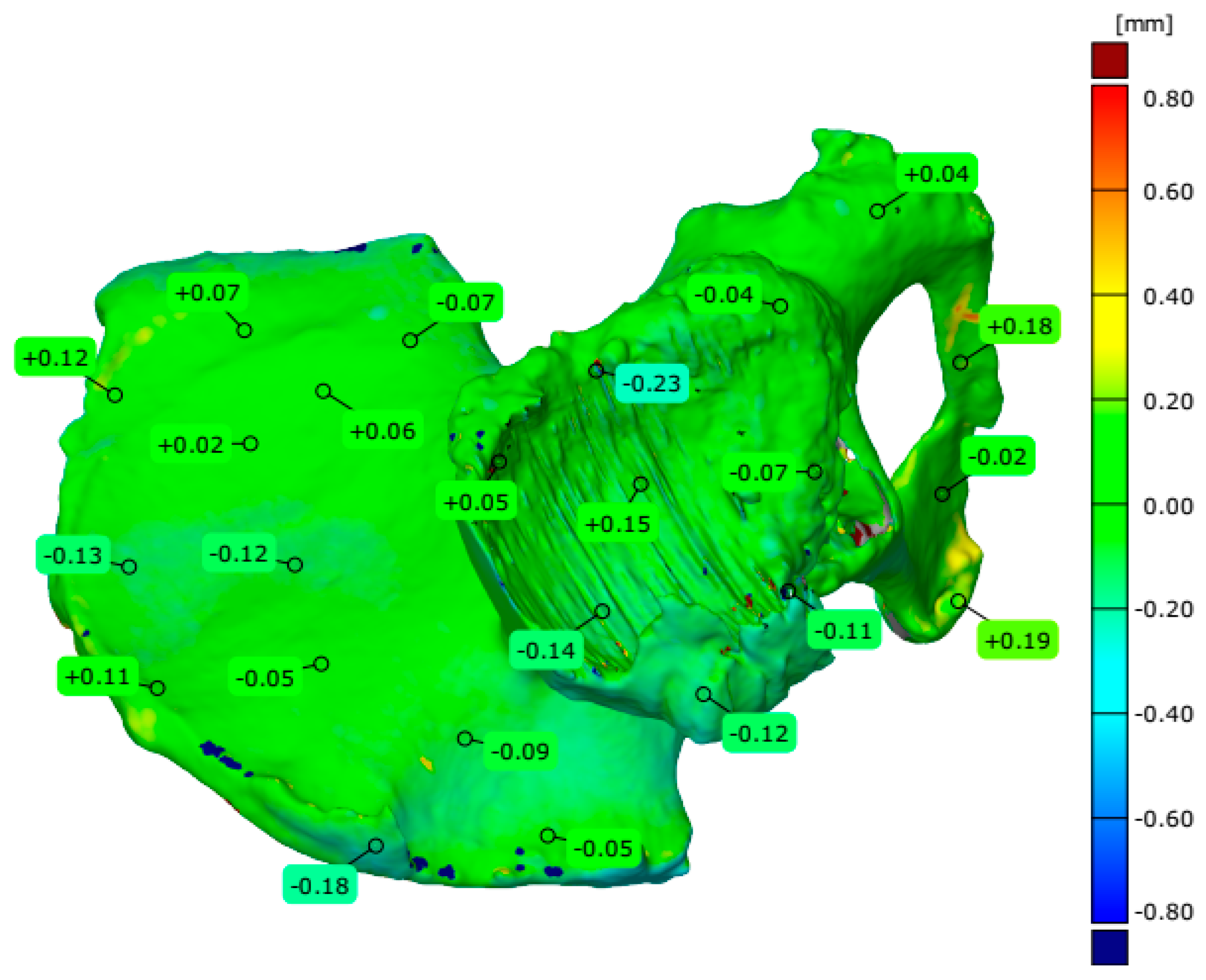
3. Results
4. Discussion
4.1. Analysis of the Reconstruction Process and Additive Manufacturing of Models
4.2. Analysis of Adopted Measurement Procedures Implemented on the Atos II Triple Scan, the Measuring Arm with a Laser Head System and Alicona InfiniteFocusG4 Optical Microscope
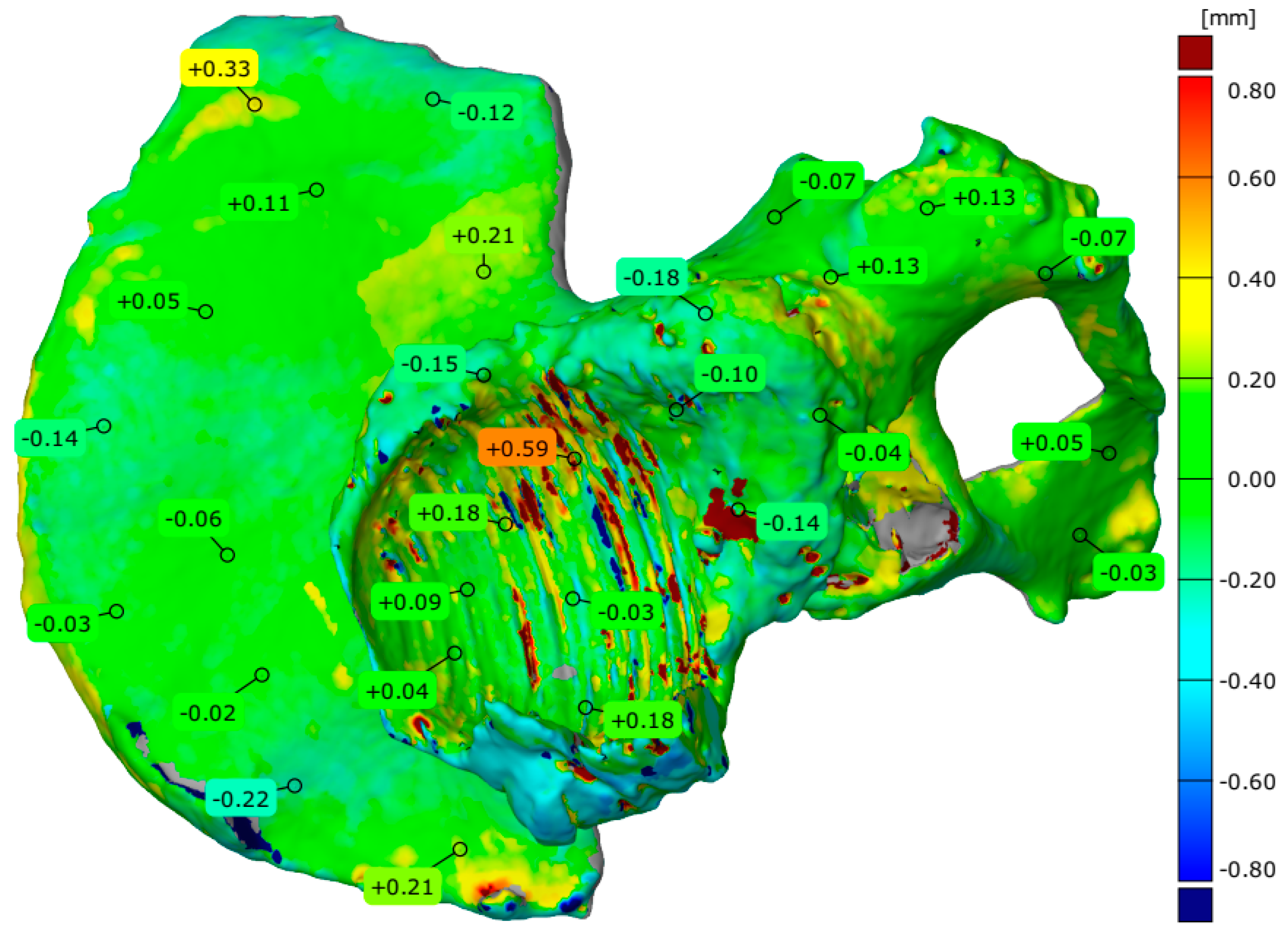
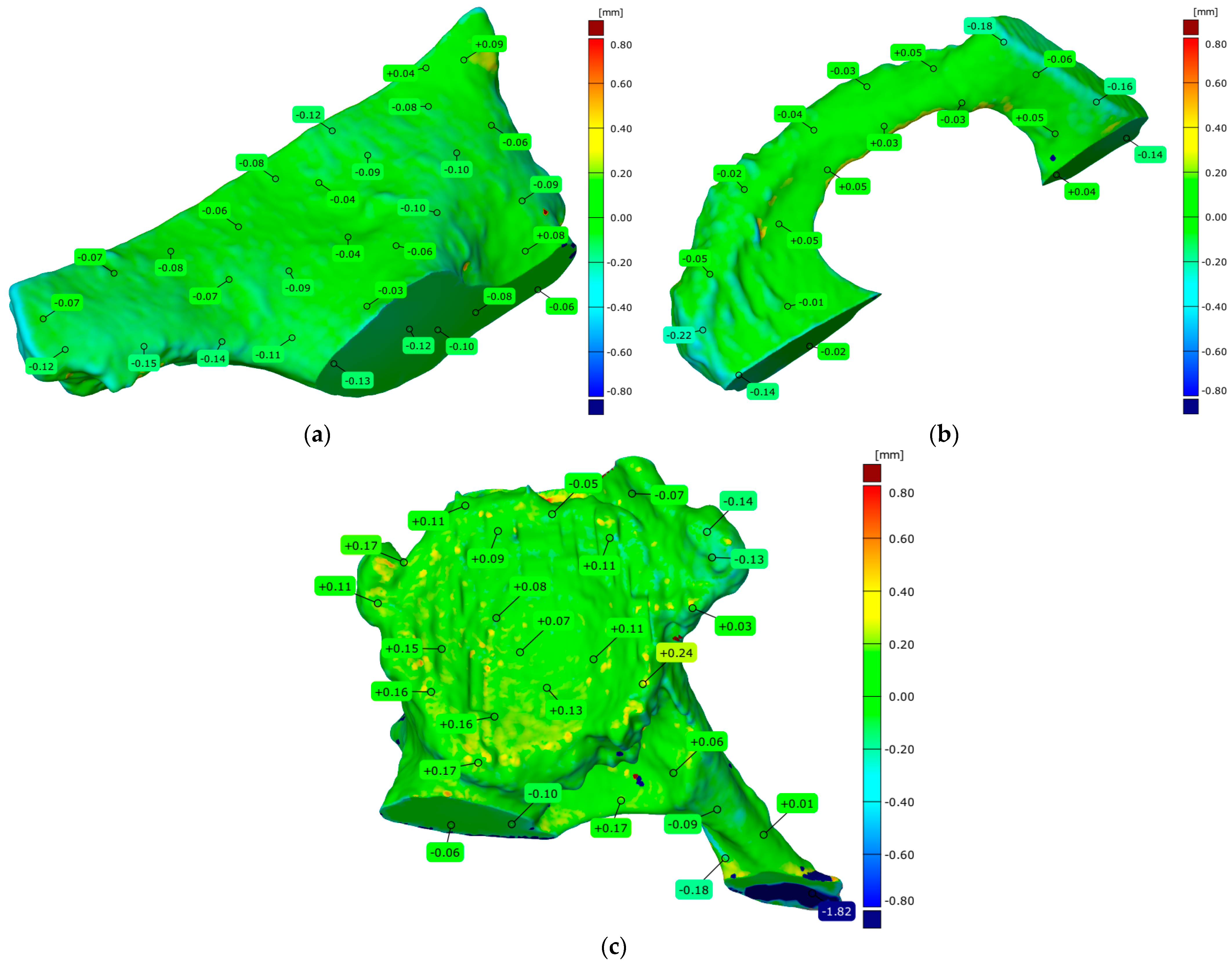
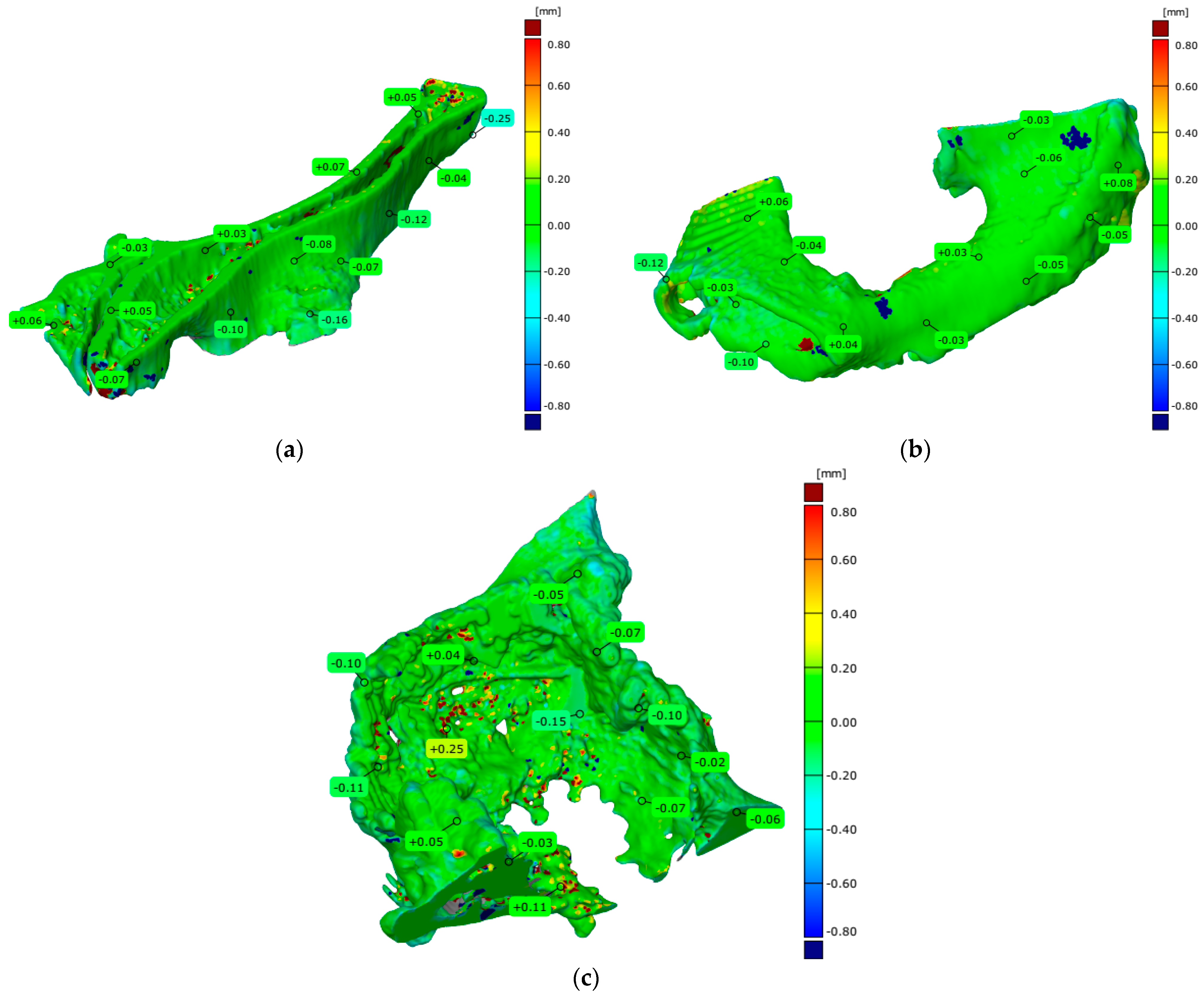
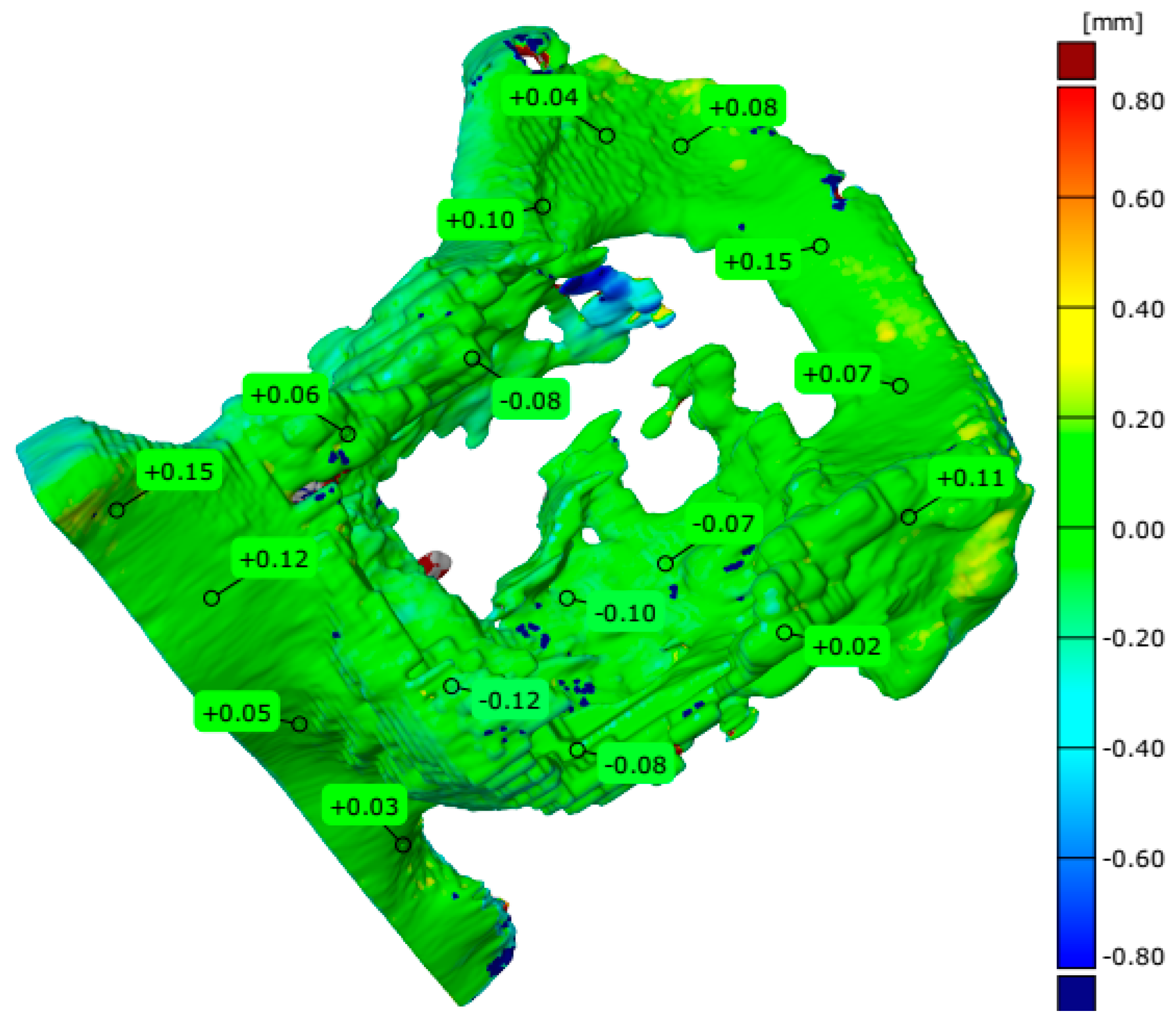
4.3. Evaluation of Geometrical Accuracy and Surface Roughness
4.4. Evaluation of the Surgical Procedure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ng, K.G.; Jeffers, J.R.; Beaulé, P.E. Hip joint capsular anatomy, mechanics, and surgical management. JBJS 2019, 101, 2141–2151. [Google Scholar] [CrossRef]
- Zaghloul, A.; Mohamed, E.M. Hip joint: Embryology, anatomy and biomechanics. Biomed. J. Sci. Tech. Res. 2018, 12, 9304–9318. [Google Scholar] [CrossRef]
- Zilkens, C.; Tiderius, C.J.; Krauspe, R.; Bittersohl, B. Current knowledge and importance of dGEMRIC techniques in diagnosis of hip joint diseases. Skelet. Radiol. 2015, 44, 1073–1083. [Google Scholar] [CrossRef] [PubMed]
- Yamate, S.; Hamai, S.; Lyman, S.; Konishi, T.; Kawahara, S.; Yamaguchi, R.; Motomura, G. Clinical evaluation of hip joint diseases: Total hip arthroplasty to support patients’ quality of life. J. Jt. Surg. Res. 2023, 1, 18–25. [Google Scholar] [CrossRef]
- Song, J.; Zhang, G.; Liang, J.; Bai, C.; Dang, X.; Wang, K.; Liu, R. Effects of delayed hip replacement on postoperative hip function and quality of life in elderly patients with femoral neck fracture. BMC Musculoskelet. Disord. 2020, 21, 487. [Google Scholar] [CrossRef] [PubMed]
- Harsanyi, S.; Zamborsky, R.; Krajciova, L.; Kokavec, M.; Danisovic, L. Developmental dysplasia of the hip: A review of etiopathogenesis, risk factors, and genetic aspects. Medicina 2020, 56, 153. [Google Scholar] [CrossRef] [PubMed]
- Sziver, E.; Nagy, E.; Preszner-Domján, A.; Pósa, G.; Horvath, G.; Balog, A.; Tóth, K. Postural control in degenerative diseases of the hip joint. Clin. Biomech. 2016, 35, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.W.; Lau, L.C.; Cheung, J.P.; Choi, S.W. Cancer-Causing Effects of Orthopaedic Metal Implants in Total Hip Arthroplasty. Cancers 2024, 16, 1339. [Google Scholar] [CrossRef]
- Saikko, V.; Shen, M. Wear comparison between a dual mobility total hip prosthesis and a typical modular design using a hip joint simulator. Wear 2010, 268, 617–621. [Google Scholar] [CrossRef]
- Guo, L.; Naghavi, S.A.; Wang, Z.; Varma, S.N.; Han, Z.; Yao, Z.; Liu, C. On the design evolution of hip implants: A review. Mater. Des. 2022, 216, 110552. [Google Scholar] [CrossRef]
- Hilton, T.L.; Campbell, N.; Hosking, K. Additive manufacturing in orthopaedics: Clinical implications. SA Orthop. J. 2017, 16, 63–67. [Google Scholar] [CrossRef][Green Version]
- Cortis, G.; Mileti, I.; Nalli, F.; Palermo, E.; Cortese, L. Additive manufacturing structural redesign of hip prostheses for stress-shielding reduction and improved functionality and safety. Mech. Mater. 2022, 165, 104173. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A. Current status and challenges of Additive manufacturing in orthopaedics: An overview. J. Clin. Orthop. Trauma 2019, 10, 380–386. [Google Scholar] [CrossRef] [PubMed]
- Paramasivam, V.; Singh, G.; Santhanakrishnan, S. 3D printing of human anatomical models for preoperative surgical planning. Procedia Manuf. 2020, 48, 684–690. [Google Scholar] [CrossRef]
- Ravi, P.; Chepelev, L.L.; Stichweh, G.V.; Jones, B.S.; Rybicki, F.J. Medical 3D printing dimensional accuracy for multi-pathological anatomical models 3D printed using material extrusion. J. Digit. Imaging 2022, 35, 613–622. [Google Scholar] [CrossRef]
- Turek, P.; Budzik, G. Estimating the accuracy of mandible anatomical models manufactured using material extrusion methods. Polymers 2021, 13, 2271. [Google Scholar] [CrossRef] [PubMed]
- Salmi, M.; Paloheimo, K.S.; Tuomi, J.; Wolff, J.; Mäkitie, A. Accuracy of medical models made by additive manufacturing (rapid manufacturing). J. Cranio-Maxillofac. Surg. 2013, 41, 603–609. [Google Scholar] [CrossRef] [PubMed]
- Turek, P. Evaluation of surface roughness parameters of anatomical structures models of the mandible made with additive techniques from selected polymeric materials: Rapid communication. Polimery 2022, 67, 162–167. [Google Scholar] [CrossRef]
- ISO/ASTM TR 52916:2022; Additive Manufacturing for Medical—Data—Optimized Medical Image Data. ISO: Geneva, Switzerland, 2022.
- ISO/IEC 3532-1:2023; Information Technology—Medical Image-Based Modeling for 3D Printing—Part 1: General requirements. ISO: Geneva, Switzerland, 2023.
- ISO/IEC 3532-2: 2024; Information Technology—Medical Image-Based Modeling for 3D Printing—Part 2: Segmentation. ISO: Geneva, Switzerland, 2024.
- Ng, K.G.; Lamontagne, M.; Labrosse, M.R.; Beaulé, P.E. Comparison of anatomical parameters of cam femoroacetabular impingement to evaluate hip joint models segmented from CT data. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 293–302. [Google Scholar] [CrossRef]
- Liu, H.; Qian, H.; Zhao, J. Automatic extraction of 3D anatomical feature curves of hip bone models reconstructed from CT images. Bio-Med. Mater. Eng. 2015, 26, S1297–S1314. [Google Scholar] [CrossRef]
- Salazar, D.A.; Cramer, J.; Markin, N.W.; Hunt, N.H.; Linke, G.; Siebler, J.; Zuniga, J. Comparison of 3D printed anatomical model qualities in acetabular fracture representation. Ann. Transl. Med. 2022, 10, 391. [Google Scholar] [CrossRef]
- Turek, P.; Filip, D.; Przeszłowski, Ł.; Łazorko, A.; Budzik, G.; Snela, S.; Paszkiewicz, A. Manufacturing polymer model of anatomical structures with increased accuracy using cax and am systems for planning orthopedic procedures. Polymers 2022, 14, 2236. [Google Scholar] [CrossRef] [PubMed]
- Kantaros, A.; Petrescu, F.I.T.; Abdoli, H.; Diegel, O.; Chan, S.; Iliescu, M.; Ungureanu, L.M. Additive Manufacturing for Surgical Planning and Education: A Review. Appl. Sci. 2024, 14, 2550. [Google Scholar] [CrossRef]
- Solórzano-Requejo, W.; Ojeda, C.; Díaz Lantada, A. Innovative design methodology for patient-specific short femoral stems. Materials 2022, 15, 442. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, C.J.A.; Guimarães, R.M.D.R.; Pontim, C.E.; Gasoto, S.C.; Setti, J.A.P.; Soni, J.F.; Schneider, B., Jr. An overview of 3D anatomical model printing in orthopedic trauma surgery. J. Multidiscip. Healthc. 2023, 16, 875–887. [Google Scholar] [CrossRef] [PubMed]
- Chohan, J.S.; Singh, R. Pre and post processing techniques to improve surface characteristics of FDM parts: A state of art review and future applications. Rapid Prototyp. J. 2017, 23, 495–513. [Google Scholar] [CrossRef]
- Haque, M.E.; Banerjee, D.; Mishra, S.B.; Nanda, B.K. A numerical approach to measure the surface roughness of FDM build part. Mater. Today Proc. 2019, 18, 5523–5529. [Google Scholar] [CrossRef]
- Reddy, V.; Flys, O.; Chaparala, A.; Berrimi, C.E.; Amogh, V.; Rosen, B.G. Study on surface texture of fused deposition modeling. Procedia Manuf. 2018, 25, 389–396. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M.; Gibson, I.; Rosen, D.; Khorasani, M. Material extrusion. In Additive Manufacturing; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 171–201. [Google Scholar] [CrossRef]
- Wang, T.M.; Xi, J.T.; Jin, Y. A model research for prototype warp deformation in the FDM process. Int. J. Adv. Manuf. Technol. 2007, 33, 1087–1096. [Google Scholar] [CrossRef]
- Gordon, E.R.; Shokrani, A.; Flynn, J.M.; Goguelin, S.; Barclay, J.; Dhokia, V. A surface modification decision tree to influence design in additive manufacturing. In Sustainable Design and Manufacturing; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 423–434. [Google Scholar] [CrossRef]
- Srinivasan, R.; Ruban, W.; Deepanraj, A.; Bhuvanesh, R.; Bhuvanesh, T. Efect on infll density on mechanical properties of PETG part fabricated by fused deposition modelling. Mater. Today Proc. 2020, 27, 1838–1842. [Google Scholar] [CrossRef]
- Maier, R.; Bucaciuc, S.-G.; Mandoc, A.C. Reducing Surface Roughness of 3D Printed Short-Carbon Fiber Reinforced Composites. Materials 2022, 15, 7398. [Google Scholar] [CrossRef] [PubMed]
- Melentiev, R.; Harakály, G.; Stögerer, J.; Mitteramskogler, G.; Wagih, A.; Lubineau, G.; Grande, C.A. High-resolution metal 3D printing via digital light processing. Addit. Manuf. 2024, 85, 104156. [Google Scholar] [CrossRef]
- Shin, S.; Ko, B.; So, H. Structural effects of 3D printing resolution on the gauge factor of microcrack-based strain gauges for health care monitoring. Microsyst. Nanoeng. 2022, 8, 12. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Yao, K.; He, G.; Zhou, Z.; Sun, D. Surface roughness improvement of 3D printed microchannel. J. Micromechanics Microeng. 2020, 30, 065003. [Google Scholar] [CrossRef]
- ISO/ASTM 52902:2023; Additive Manufacturing—Test Artefacts—Geometric Capability Assessment of Additive Manufacturing Systems. ISO: Geneva, Switzerland, 2023.
- Barcena, A.J.R.; Ravi, P.; Kundu, S.; Tappa, K. Emerging Biomedical and Clinical Applications of 3D-Printed Poly (Lactic Acid)-Based Devices and Delivery Systems. Bioengineering 2024, 11, 705. [Google Scholar] [CrossRef] [PubMed]
- Šljivić, M.; Pavlović, A.; Ilić, J.; Stanojević, M.; Todorović, S. Comparing the accuracy of professional and consumer grade 3D printers in complex models production. FME Trans. 2017, 45, 348–353. [Google Scholar] [CrossRef]
- B89.4.22; Methods for Performance Evaluation of Articulated Arm Coordinate Measuring Machines (CMM). American Society of Mechanical Engineers (ASME): New York, NY, USA, 2004.
- ISO 10360-8:2013; Geometrical Product Specifications (GPS)—Acceptance and Reverification Tests for Coordinate Measuring Systems (CMS)—Part 8. CMMs with Optical Distance Sensors. ISO: Geneva, Switzerland, 2013.
- Rokicki, P.; Budzik, G.; Kubiak, K.; Dziubek, T.; Zaborniak, M.; Kozik, B.; Bernaczek, J.; Przeszlowski, L.; Nowotnik, A. The assessment of geometric accuracy of aircraft engine blades with the use of an optical coordinate scanner. Aircr. Eng. Aerosp. Technol. 2016, 88, 374–381. [Google Scholar] [CrossRef]
- Dziubek, T.; Oleksy, M. Application of ATOS II optical system in the techniques of rapid prototyping of epoxy resin-based gear models. Polimery 2017, 62, 44–52. [Google Scholar] [CrossRef]
- Brajlih, T.; Tasic, T.; Valentan, B.; Hadžistevi’c, M.; Pogacar, V.; Drstvenšek, I.; Balic, J.; Acko, B. Possibilities of Using ThreeDimensional Optical Scanning in Complex Geometrical Inspection. Stroj. Vestn. J. Mech. Eng. 2011, 57, 826–833. [Google Scholar] [CrossRef]
- VDI/VDE 2634 Blatt 3. Available online: https://www.vdi.eu/guidelines/vdivde_2634_blatt_3-optische_3_d_messsysteme_bildgebende_systeme_mit_flaechenhafter_antastung/ (accessed on 28 September 2024).
- ISO 21920-1:2021; Geometrical Product Specifications (GPS)—Surface Texture: Profile, Part 1: Indication of Surface Texture. ISO: Geneva, Switzerland, 2021.
- Newton, L.; Senin, N.; Gomez, C.; Danzl, R.; Helmli, F.; Blunt, L.; Leach, R. Areal topography measurement of metal additive surfaces using focus variation microscopy. Addit. Manuf. 2019, 25, 365–389. [Google Scholar] [CrossRef]
- Bazan, A.; Turek, P.; Przeszłowski, Ł. Comparison of the contact and focus variation measurement methods in the process of surface topography evaluation of additively manufactured models with different geometry complexity. Surf. Topogr. Metrol. Prop. 2022, 10, 035021. [Google Scholar] [CrossRef]
- Bazan, A.; Turek, P.; Przeszłowski, Ł. Assessment of InfiniteFocus system measurement errors in testing the accuracy of crown and tooth body model. J. Mech. Sci. Technol. 2021, 35, 1167–1176. [Google Scholar] [CrossRef]
- Liu, K.; Li, Z.; Ma, Y.; Lian, H. 3D-printed pelvis model is an efficient method of osteotomy simulation for the treatment of developmental dysplasia of the hip. Exp. Ther. Med. 2020, 19, 1155–1160. [Google Scholar] [CrossRef]
- Fang, C.; Cai, H.; Kuong, E.; Chui, E.; Siu, Y.C.; Ji, T.; Drstvenšek, I. Surgical applications of three-dimensional printing in the pelvis and acetabulum: From models and tools to implants. Der Unfallchirurg 2019, 122, 278. [Google Scholar] [CrossRef]
- Hughes, A.J.; DeBuitleir, C.; Soden, P.; O’Donnchadha, B.; Tansey, A.; Abdulkarim, A.; Hurson, C.J. 3D printing aids acetabular reconstruction in complex revision hip arthroplasty. Adv. Orthop. 2017, 1, 8925050. [Google Scholar] [CrossRef] [PubMed]
- Di Laura, A.; Henckel, J.; Wescott, R.; Hothi, H.; Hart, A.J. The effect of metal artefact on the design of custom 3D printed acetabular implants. 3D Print. Med. 2020, 6, 23. [Google Scholar] [CrossRef] [PubMed]
- King, J.; Whittam, S.; Smith, D.; Al-Qaisieh, B. The impact of a metal artefact reduction algorithm on treatment planning for patients undergoing radiotherapy of the pelvis. Phys. Imaging Radiat. Oncol. 2022, 24, 138–143. [Google Scholar] [CrossRef]
- Santarelli, C.; Argenti, F.; Uccheddu, F.; Alparone, L.; Carfagni, M. Volumetric interpolation of tomographic sequences for accurate 3D reconstruction of anatomical parts. Comput. Methods Programs Biomed. 2020, 194, 105525. [Google Scholar] [CrossRef] [PubMed]
- Akmal, J.S.; Salmi, M.; Hemming, B.; Teir, L.; Suomalainen, A.; Kortesniemi, M.; Lassila, A. Cumulative inaccuracies in implementation of additive manufacturing through medical imaging, 3D thresholding, and 3D modeling: A case study for an end-use implant. Appl. Sci. 2020, 10, 2968. [Google Scholar] [CrossRef]
- Budzik, G.; Turek, P.; Traciak, J. The influence of change in slice thickness on the accuracy of reconstruction of cranium geometry. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 231, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Bonaldi, L.; Pretto, A.; Pirri, C.; Uccheddu, F.; Fontanella, C.G.; Stecco, C. Deep learning-based medical images segmentation of musculoskeletal anatomical structures: A survey of bottlenecks and strategies. Bioengineering 2023, 10, 137. [Google Scholar] [CrossRef]
- Liang, H.; Ji, T.; Zhang, Y.; Wang, Y.; Guo, W. Reconstruction with 3D-printed pelvic endoprostheses after resection of a pelvic tumour. Bone Jt. J. 2017, 99, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Bastawrous, S.; Wake, N.; Levin, D.; Ripley, B. Principles of three-dimensional printing and clinical applications within the abdomen and pelvis. Abdom. Radiol. 2018, 43, 2809–2822. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Luo, D.; Xie, K.; Wang, L.; Hao, Y. Design and Application of 3D Printing Based Personalised Pelvic Prostheses. J. Shanghai Jiaotong Univ. (Sci.) 2021, 26, 361–367. [Google Scholar] [CrossRef]
- Mendřický, R. Impact of applied anti-reflective material on accuracy of optical 3D digitisation. Mater. Sci. Forum 2018, 919, 335–344. [Google Scholar] [CrossRef]
- Msallem, B.; Sharma, N.; Cao, S.; Halbeisen, F.S.; Zeilhofer, H.-F.; Thieringer, F.M. Evaluation of the Dimensional Accuracy of 3D-Printed Anatomical Mandibular Models Using FFF, SLA, SLS, MJ, and BJ Printing Technology. J. Clin. Med. 2020, 9, 817. [Google Scholar] [CrossRef]
- El-Katatny, I.; Masood, S.H.; Morsi, Y.S. Error analysis of FDM fabricated medical replicas. Rapid Prototyp. J. 2010, 16, 36–43. [Google Scholar] [CrossRef]
- Yang, L.; Li, S.; Li, Y.; Yang, M.; Yuan, Q. Experimental investigations for optimizing the extrusion parameters on FDM PLA printed parts. J. Mater. Eng. Perform. 2019, 28, 169–182. [Google Scholar] [CrossRef]
- Hooshmand, M.J.; Mansour, S.; Dehghanian, A. Optimization of build orientation in FFF using response surface methodology and posterior-based method. Rapid Prototyp. J. 2021, 27, 967–994. [Google Scholar] [CrossRef]
- Mendricky, R.; Fris, D. Analysis of the accuracy and the surface roughness of fdm/fff technology and optimisation of process parameters. Teh. Vjesn. 2020, 27, 1166–1173. [Google Scholar] [CrossRef]
- Jiang, S.; Hu, K.; Zhan, Y.; Zhao, C.; Li, X. Theoretical and experimental investigation on the 3D surface roughness of material extrusion additive manufacturing products. Polymers 2022, 14, 293. [Google Scholar] [CrossRef] [PubMed]
- García, E.; Núñez, P.J.; Chacón, J.M.; Caminero, M.A.; Kamarthi, S. Comparative study of geometric properties of unreinforced PLA and PLA-Graphene composite materials applied to additive manufacturing using FFF technology. Polym. Test. 2020, 91, 106860. [Google Scholar] [CrossRef]
- García Plaza, E.; López, P.J.N.; Torija, M.Á.C.; Muñoz, J.M.C. Analysis of PLA geometric properties processed by FFF additive manufacturing: Effects of process parameters and plate-extruder precision motion. Polymers 2019, 11, 1581. [Google Scholar] [CrossRef] [PubMed]











| Parameters | Value |
|---|---|
| Stripe width (Y) | 100 mm |
| Measuring range (Z) | 100 mm |
| Stand-off | 100 mm |
| Min. point resolution | 0.050 mm |
| Max. data rate | 150 Hz |
| Laser power Class 2 | 660 nm |
| Parameters | Value |
| Pixel resolutions cameras | 5,000,000 |
| Measuring area | 150 mm × 100 mm × 100 mm |
| Min. point resolution | 0.058 mm |
| Number of points per scan | 5,000,000 |
| Number of rotations of the measuring table (model manufactured in one piece/in three separate parts) | 14/10 |
| Parameters | Value |
|---|---|
| Vertical resolution | 2 µm |
| Horizontal resolution | 7.8 µm |
| Pixel size | 1.75 µm × 1.75 µm |
| Objective | Objective 5× |
| Measuring area | 5.32 mm × 5.78 mm |
| Measuring Arm with a Laser Head | |
|---|---|
| Acceptance Test According to ASME B89.4.22 | Measured Value/Maximum Permission Error (2σ) |
| Effective diameter test | ±0.005 mm/±0.008 mm |
| Single-point articulation test | ±0.020 mm/±0.024 mm |
| Volumetric performance test | ±0.030 mm/±0.035 mm |
| Laser head test (flat plate) | ±0.018 mm |
| Atos II Triple Scan | |
| Acceptance test according to VDI/VDE 2634 | Measured value/Maximum permission error (2σ) |
| Probing error | ±0.004 mm/±0.006 mm |
| Sphere–spacing error | ±0.008 mm/±0.020 mm |
| Maximum error (2σ) | |
| Flatness measurement error | ±0.022 mm |
| Parameters | The Pelvis Models Manufactured in Three Separate Parts | A Part of the Pelvis Models Manufactured in One Piece | Measuring System | ||
|---|---|---|---|---|---|
| Area One | Area Two | Area Three | |||
| Number of valid points | 405,012 | 373,325 | 406,635 | 970,494 | Measuring arm with a laser head |
| Maximum deviation [mm] | 0.860 | 1.065 | 2.087 | 4.926 | |
| Minimum deviation [mm] | −0.550 | −0.446 | −0.704 | −1.157 | |
| Range [mm] | 1.410 | 1.511 | 2.791 | 6.083 | |
| Mean deviation [mm] | −0.041 | 0.007 | −0.013 | −0.090 | |
| Standard deviation [mm] | 0.156 | 0.119 | 0.139 | 0.295 | |
| Root Mean Square [mm] | 0.161 | 0.119 | 0.139 | 0.308 | |
| Number of valid points | 373,737 | 227,964 | 280,525 | 717,041 | Atos II Triple Scan |
| Maximum deviation [mm] | 1.220 | 0.680 | 1.338 | 3.024 | |
| Minimum deviation [mm] | −0.571 | −0.496 | −0.821 | −0.949 | |
| Range [mm] | 1.792 | 1.176 | 2.159 | 3.973 | |
| Mean deviation [mm] | −0.091 | −0.034 | −0.010 | −0.010 | |
| Standard deviation [mm] | 0.161 | 0.133 | 0.169 | 0.251 | |
| Root Mean Square [mm] | 0.185 | 0.137 | 0.169 | 0.251 | |
| Parameters | Surface Roughness on the Part of the Pelvis Model Manufactured in One Piece, Normal Vector of the Acetabulum Area at a Significant Angle to the Z Axis | |||
|---|---|---|---|---|
| Along Applied Layers | From the Side of the Surface Contact with the Support Material | In the Acetabulum Area | ||
| Sa | Mean | 48.17 µm | 201.96 µm | 52.08 µm |
| Std. Dev. | 13.70 µm | 24.44 µm | 5.76 µm | |
| Sq | Mean | 58.59 µm | 243.86 µm | 65.77 µm |
| Std. Dev. | 16.39 µm | 28.48 µm | 7.60 µm | |
| Spk + Sk + Svk | Mean | 245.45 µm | 1028.09 µm | 307.21 µm |
| Std. Dev. | 71.11 µm | 103.03 µm | 36.71 µm | |
| Surface roughness on an acetabulum model, normal vector of the acetabulum area almost parallel to the Z axis | ||||
| Sa | Mean | 29.29 µm | 160.64 µm | 85.21 µm |
| Std. Dev. | 2.08 µm | 22.09 µm | 8.34 µm | |
| Sq | Mean | 36.04 µm | 192.32 µm | 102.45 µm |
| Std. Dev. | 2.76 µm | 25.68 µm | 11.15 µm | |
| Spk + Sk + Svk | Mean | 149.94 µm | 768.75 µm | 427.96 µm |
| Std. Dev. | 17.96 µm | 74.18 µm | 62.84 µm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turek, P.; Snela, S.; Budzik, G.; Bazan, A.; Jabłoński, J.; Przeszłowski, Ł.; Wojnarowski, R.; Dziubek, T.; Petru, J. Proposes Geometric Accuracy and Surface Roughness Estimation of Anatomical Models of the Pelvic Area Manufactured Using a Material Extrusion Additive Technique. Appl. Sci. 2025, 15, 134. https://doi.org/10.3390/app15010134
Turek P, Snela S, Budzik G, Bazan A, Jabłoński J, Przeszłowski Ł, Wojnarowski R, Dziubek T, Petru J. Proposes Geometric Accuracy and Surface Roughness Estimation of Anatomical Models of the Pelvic Area Manufactured Using a Material Extrusion Additive Technique. Applied Sciences. 2025; 15(1):134. https://doi.org/10.3390/app15010134
Chicago/Turabian StyleTurek, Paweł, Sławomir Snela, Grzegorz Budzik, Anna Bazan, Jarosław Jabłoński, Łukasz Przeszłowski, Robert Wojnarowski, Tomasz Dziubek, and Jana Petru. 2025. "Proposes Geometric Accuracy and Surface Roughness Estimation of Anatomical Models of the Pelvic Area Manufactured Using a Material Extrusion Additive Technique" Applied Sciences 15, no. 1: 134. https://doi.org/10.3390/app15010134
APA StyleTurek, P., Snela, S., Budzik, G., Bazan, A., Jabłoński, J., Przeszłowski, Ł., Wojnarowski, R., Dziubek, T., & Petru, J. (2025). Proposes Geometric Accuracy and Surface Roughness Estimation of Anatomical Models of the Pelvic Area Manufactured Using a Material Extrusion Additive Technique. Applied Sciences, 15(1), 134. https://doi.org/10.3390/app15010134









