Impulsive Control Discrete Fractional Neural Networks in Product Form Design: Practical Mittag-Leffler Stability Criteria

Abstract

The planning, regulation and effectiveness of the product design process depend on various characteristics. Recently, bio-inspired collective intelligence approaches have been applied in this process in order to create more appealing product forms and optimize the design process. In fact, the use of neural network models in product form design analysis is a complex process, in which the type of network has to be determined, as well as the structure of the network layers and the neurons in them; the connection coefficients, inputs and outputs have to be explored; and the data have to be collected. In this paper, an impulsive discrete fractional neural network modeling approach is introduced for product design analysis. The proposed model extends and complements several existing integer-order neural network models to the generalized impulsive discrete fractional-order setting, which is a more flexible mechanism to study product form design. Since control and stability methods are fundamental in the construction and practical significance of a neural network model, appropriate impulsive controllers are designed, and practical Mittag-Leffler stability criteria are proposed. The Lyapunov function strategy is applied in providing the stability criteria and their efficiency is demonstrated via examples and a discussion. The established examples also illustrate the role of impulsive controllers in stabilizing the behavior of the neuronal states. The proposed modeling approach and the stability results are applicable to numerous industrial design tasks in which multi-agent systems are implemented.

1. Introduction

The engineering design process is a collective task that includes finding innovative ways to create products that are functional and meet clients’ wants and needs, as well as planning, testing and improving the design. In order to predict, analyze and control the complex behavior of engineering systems and accelerate the design process, modeling and engineering simulations have been intensively used in the last few decades. The potential of artificial neural networks (ANNs) as a modeling technique in modern product development has been conclusively proven [1,2,3,4].

In particular, ANNs are applicable also in product form design problems. This bio-inspired intelligence approach has been applied recently in planning, decision-making, forecasting, optimization, automation and other activities related to product form design analysis. For example, the paper [5] addressed a neural network-based approach for product design. The authors in [6] considered fuzzy neural networks as an integral part of a hybrid technique used in an automatic product form search. The proposed neural network approach has been also applied in optimization tasks in accordance with the designer’s required product form. The paper [7] used neural network models to analyze the best design combination of product form elements. The authors in [8] proposed an ANN model to relate design parameters and produce a product form aesthetics design depending on customer perceptions in a more systematic and intelligent manner. The paper [9] considered a hybrid product form design method based on a specific class of ANNs from the perspective of multi-objective optimization. The paper [10] considers a number of ANN models, examining how a given product form affects the product image as perceived by customers. In [11], an ANN-based method is proposed to quantify the design preferences regarding product forms.

In fact, product form design is an integrative part of the industrial design process since “industrial design balanced the tensions between form and function, machine and human experience” [12]. The shift from decorative arts to modernism was captured in the late 1800s by architect Louis Henry Sullivan, who stated that “form follows function” [13]. The above key principle of modernism influenced a new design language that emphasized geometry, precision, simplicity and economy in product form design. The influential Bauhaus school, which grew out of modernism, developed design principles that can be applied to any product [14]. Later, form formation and form classification in industrial design and architecture were systematically explored in [15,16]. Recently, industrial designers have sought to incorporate advances in technology and artificial intelligence into product form design to create aerodynamic curves, groove lines and wing tails that exemplify speed and technological progress [12]. The ANN approach used does not only help to improve existing functionalities, but also changes the ways that products can be designed.

Despite the advantages of employing ANN models in product form design problems, the number of existing results in the area is still not satisfactory. This is due mainly to the fact that applying neural network models in product form design analysis is a very complicated process that includes the construction of the neural network model; the exploration of the inputs, outputs and connection coefficients; training, etc. Furthermore, the current state of this research area mainly shows the usage of integer-order ANN models. However, fractional calculus offers a more flexible mechanism that has not been completely applied to the ANN models in the product form design area.

Fractional-order models are relevant and significant in numerous scientific areas of study. The generalization, flexibility and nonlocality offered by fractional-order methods make them important and useful in solving various types of fractional-order problems in science, engineering and technology [17,18,19]. Recent advancements in fractional-order ANN modeling have led to significant progress in understanding complex real-world phenomena, studied in many areas of science and engineering [20,21,22]. In particular, the applicability of fractional discrete neural networks models is motivated from the point of view of computer simulation and the actual applications of neural networks. This explains the growing research activity in the design, research and application of discrete fractional neural networks [23,24,25,26,27,28,29,30]. Despite the many reported results, the topic of using discrete fractional ANNs as a modeling approach in product form design is still unexplored. Unique existing results in the area are reported in [31], where a delta discrete fractional operator is considered. The paper [31] also studies various shape classifications and their shape formation, which supports the use of fractional-order ANNs in product form analysis, since fractal components appear very frequently in industrial design product shapes [32,33]. In addition, fractional-order modeling methods allow the advantages of fractional calculus to be used in describing the behavior of real materials and allow some restrictions imposed by integer-order models to be overcome [34]. The main purpose of the research conducted in this paper is to contribute to the development of this area.

In addition, the design and functioning of the neural network models used in product form design require the application of appropriate control techniques in the modeling process. Such control mechanisms also ensure that the final designed product form achieves the desired performance. Numerous researchers in the industrial design area have studied the importance of different design control strategies [35,36,37]. In particular, nonlinear controllers [23], linear controllers [28,31], feedback controllers [29] and adaptive controllers [30] are widely applied in the reported discrete fractional-order ANN models.

The impulsive control technique is one of the simplest to implement and involves less expensive control mechanisms [38]. As such, intensive research has been performed on this control strategy. It has been intensively applied to integer-order and fractional-order continuous models [39,40,41,42,43,44,45]. However, unfortunately, very little research has been done on the dynamic behavior of fractional-order discrete-time neural network models under impulsive controllers [46,47]. Impulsive controllers, moreover, have not been applied to ANN models used in the field of product form design. Consequently, the investigation of the dynamics of impulsive control fractional discrete ANN models, as well as their applications, is an attractive and important subject. The impulsive control strategy seems very appropriate in product form design, since the process can be subject to external and internal noise, such as unwanted variations in some product form design characteristics or system failure due to a minor inconvenience or a major accident [35]. Moreover, extensive research has concluded that impulsive controllers can be used to stabilize some unstable ANN models, i.e., as a tool for robust design. Moreover, they allow the use of both industrial design knowledge and ANN approaches, which is an additional focus in this paper.

It is relevant to note that in most of the existing ANN models applied in product form design analysis, only training techniques are considered, and the stability behavior is ignored. However, it is well known that the stability of states of ANN models plays a key role in characterizing the qualitative behavior of such models, and that the study of the qualitative properties of the solutions of various types of equations related to science and engineering is crucial to overcome the poor model results when using new initial conditions. It is also well known that the use of new initial conditions in a trained NN model may lead to instability and “instability is the Achilles’ heel of modern AI and a paradox, with training algorithms finding unstable NNs despite the existence of stable ones” [48]. Hence, stability is one of the most important issues if an ANN model is to be used in practical applications [49]. This has motivated numerous studies on the development of stable neural control strategies for different types of ANN models [38,40,41,42,44,50,51,52], including fractional-order neural networks of a continuous and discrete nature [23,24,27,28,30,43,46,47]. For discrete fractional-order neural network models, considerable investigations have been devoted to investigating the Mittag-Lefller stability properties [28,30], which generalize the exponential stability ones.

It is well known that, in many applications, mathematically ideal, stable behavior is impossible. In such cases, the concept of practical stability, defined in [53], is much more appropriate. In terms of practical stability, the behavior of a neuronal state is still acceptable but not necessarily mathematically stable when other states that are initially close to it oscillate close to it. Recently, theoretical studies of practical stability have become very mature and it is increasingly applied in engineering [54,55,56,57,58]. The practical stability notion has been also studied for linear fractional discrete-time systems [59,60,61]. Practical stability results for fractional nonlinear discrete NN models are reported only in the paper [31], without considering impulsive effects. Accordingly, there are no practical stability results on impulsive fractional discrete impulsive ANN models so far, which leads to the lack of a theoretical basis or performance analysis of such systems.

Prompted by the above analysis, the purpose of this work is to design a discrete fractional-order neural network model that extends some existing models used in product form design. Appropriate impulsive controllers and practical stability concepts are also considered.

The summary of the proposed contribution is as follows.

(i)

A new fractional nonlinear neural network modeling approach is applied to extend and generalize some existing ANN models applied in product form design analysis [5,6,7,8,9,10,11]. The proposed bio-inspired neural network approach is based on the use of discrete fractional calculus [62,63]. Such ANN models have higher degrees of accuracy and freedom than existing integer-order models and can help engineering designers and researchers to better understand the behavior of ANN models, overcoming major difficulties in experimental modeling.

(ii)

Compared with the discrete fractional-order ANN model introduced in [31], appropriate impulsive controllers are considered to control the qualitative behavior of the proposed model. The extended impulsive version will allow the implementation of impulsive control methods in the design process of the product form in cases of external and internal disturbing noise. Although impulsive control theory has gained great popularity in several scientific areas, such as biology, population dynamics, computer sciences and some others, it has not been applied to neural network models in product form design, and the goal of this research is to fill this gap.

(iii)

Since mathematically ideal, stable behavior is impossible for many applied problems, including engineering design problems, the notion of practical stability, namely global practical Mittag-Leffler practical stability, is adopted for the introduced impulsive control fractional neural network model. Thus, the proposed research not only contributes to the development of new fractional-order neural network models in product form design, but also proposes the use of the formulated framework to gain a fundamental scientific understanding of the dynamical properties of such models.

(iv)

Since Lyapunov stability techniques play a critical role in the design and stability analysis of adaptive systems [49,64], the fractional Lyapunov method is applied to investigate the practical stability behavior of the proposed model and establish efficient stability criteria. The proposed results are new and complement the existing results proposed in [31] for the impulsive case considering a nabla fractional discrete operator. Moreover, the derived stability results can be applied to synchronization issues for discrete fractional neural networks via impulsive controllers, which have not been studied before.

The rest of the paper is organized as follows. Section 2 is devoted to the introduction of the impulsive control discrete fractional model, which generalizes some existing models proposed in product form design. The necessary background related to discrete fractional calculus is also provided. The notion of the global practical Mittag-Leffler stability is defined for the constructed neural network model. Some definitions and lemmas concerning the fractional Lyapunov method are finally given. The main practical stability results for the new impulsive fractional discrete model are established in Section 3. Examples and a discussion of the results proposed are presented in Section 4. Some conclusions are stated in Section 5.

2. The Proposed Model and Strategies

2.1. Notations

The following notions will be used through the paper. ${\mathbb{R}}^n$ stands for the set of all n-dimensional real vectors. The norm of a vector $z\in {\mathbb{R}}^n$, $z={(z_1,z_2,\dots ,z_n)}^T$ is denoted by $\left|\right|z\left|\right|=\sqrt{{\sum }_{h=1}^n{z}_h^2}$. For any $a\in \mathbb{R}$, ${\mathbb{N}}_a=\{a,a+1,a+2,\dots \}$ and ${\mathbb{N}}_0=\{0,1,2,\dots \}$, $\mathbb{N}={\mathbb{N}}_0\setminus \left\{0\right\}$. For $\phi :{\mathbb{N}}_1\to \mathbb{R}$, the difference operator is denoted by $\nabla \phi \left(\eta \right)=\phi \left(\eta \right)-\phi (\eta -1).$

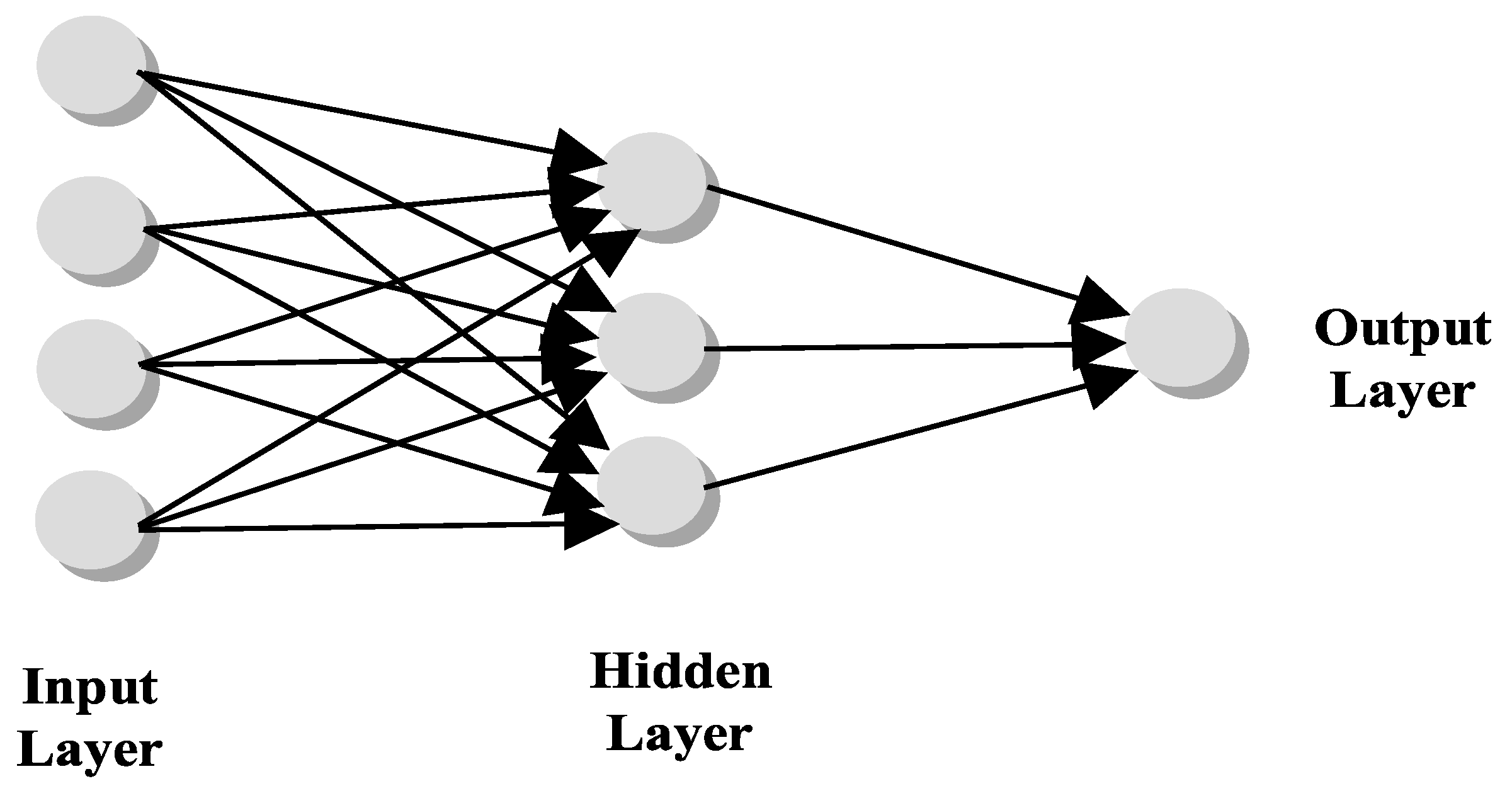
2.2. Integer-Order Neural Network Models in Product Form Design

One objective of this study is the extension of some existing neural network models in product form design.

As a bio-inspired approach, ANNs attempt to mimic some of the learning abilities of the human brain. They are composed of elements that process information depending on the received signals and their weights and are located in several layers. A typical neural network model consisting of three layers (input, hidden and output) is demonstrated in Figure 1 [3].

Starting from the input layer, the network elements propagate the signals from layer to layer until the outputs are generated by the output layer. Various activation functions, including linear, sigmoid and tangent (Figure 2), are applied to generate the outputs of the neurons in the hidden layer and the outputs of the neurons in the output layer.

In reviewing the available results related to the use of neural networks in industrial form design, in most of the constructed neural network models, the input variables are the initial design concepts, while the output variables represent the optimal design solution. For example, the ANN used in [7] for product design with respect to the product form and product image can be represented by the equation

$$y_k=f\left(\sum _{j=1}^m{w}_{jk}{x}_j-{\theta }_k\right),1\le k\le p,$$

where $y_k$ are the outputs, $x_j$ are the input variables, $f(·)$ is the activation function, $w_{jk}$, $j=1,2,\dots ,m$, $k=1,2,\dots ,p$ are the connection weights, and ${\theta }_k$ are threshold values.

The neural network model used to predict personal design preferences in form finding in [11] can be represented by the equation

$$\widehat{y}=Sigmoid(w\ast x+b),$$

where $\widehat{y}$ is the value in the current neuron, x is the value in the previous neuron(s), $Sigmoid$ is the sigmoid activation function, and w and b are the parameters, which represent the learning activity of the network.

The generalization of some discrete ANN models used in engineering design has been proposed in [51] by the discrete-time neural network

$$z_h(t+1)=-a_h{z}_h\left(t\right)+\sum _{j=1}^n{w}_{hj}{f}_j\left(z_j\left(t\right)\right)+{\Theta }_h,1\le h\le n,$$

(1)

where n is the number of elements in the neural network model (1), $z_j\left(k\right)$ is the state of the input j at the discrete time t, $t=1,2,\dots$, ${(z_1\left(t\right),z_2\left(t\right),\dots ,z_n\left(t\right))}^T$$w_{hj}$ are the connection weights, $f_j\left(z_j\left(t\right)\right)$ are the activation functions corresponding to different neurons j$(j=1,2,\dots ,n)$, and ${\Theta }_h$ is the external bias of the neuron h. The generalized model (1) takes into account the ability to consider different activation functions for different neurons. Moreover, constants $a_h>0$ are added to consider the possibility of the neuron h$(h=1,2,\dots ,n)$ resetting its potential to the resting state when isolated from other nodes and inputs.

The initial conditions related to model (1) are in the form

$$z_h\left(0\right)=z_h^0,z_h^0\in \mathbb{R},h=1,2,\dots ,n.$$

(2)

The existing literature supports the fact that ANN models of type (1) are extremely important in product form design analysis to explore the relationships between some initial design variables (inputs) $z_h^0$ and output variables (outputs) $z_h\left(t\right)$ at any stage t of the design process, and, finally, to predict the optimal design solution. The visualization presented in Figure 3 demonstrates the role of the activation function, connection weights and external biases at discrete time t.

Each design variable $z_h$ at $t+1$ receives signals from all previous variables $z_h\left(t\right)$, which represent the design parameters (concepts) at t. The input variables $z_h\left(t\right)$ are activated by means of different (in general) activation functions. Each connection between the activated cells has a different weight. The output $z_h(t+1)$ is the design variable in the next stage of the design process, which depends on the sum of all activated previous variables, the external biases and the net inputs.

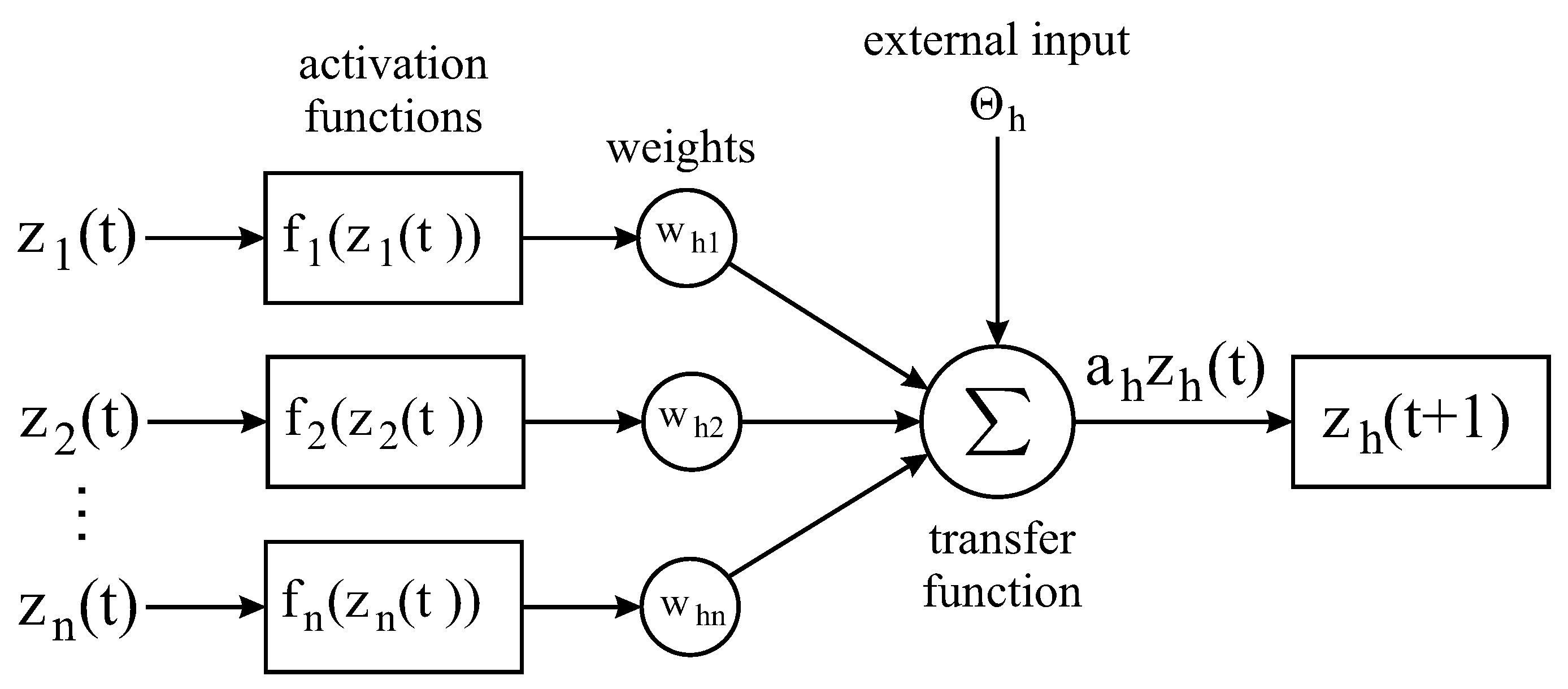
2.3. The Proposed Fractional Discrete Calculus Neural Network Modeling Approach

Considering the important role of ANN models in the product form design process, the development of more flexible models is attracting increasing attention. The goal of this paper is to propose a discrete fractional-order modeling approach in order to generalize the existing integer-order models. To this end, the necessary background from discrete fractional calculus [62,63] will be presented here.

Definition 1

([29,62]). For $\alpha \in \mathbb{R}$ and $\eta \in \mathbb{R}-\{\dots ,-2,-1,0\}$, the rising factorial of η is given by

$${\eta }^{\overline{\alpha }}=\frac{\Gamma (\eta +\alpha )}{\Gamma \left(\eta \right)}$$

with $0^{\overline{\alpha }}=0,$ where Γ is the Gamma function.

Definition 2

([28,29]). For $0<\alpha <1$, the Caputo nabla fractional difference for the function $\phi :{\mathbb{N}}_1\to \mathbb{R}$ of order α is given as

$${}^C\nabla _0^{\alpha }\phi \left(\eta \right)=\frac{1}{\Gamma (1-\alpha )}\sum _{s=1}^{\eta }{(\eta -s+1)}^{\overline{-\alpha }}\nabla \phi \left(s\right),\eta \in {\mathbb{N}}_1.$$

Using the above fractional discrete operator, model (1) can be extended to the following discrete fractional-order neural network model

$${}^C\nabla _0^{\alpha }{\mathcal{Z}}_h\left(\eta \right)=-a_h{\mathcal{Z}}_h\left(\eta \right)+\sum _{j=1}^n{w}_{hj}{f}_j\left({\mathcal{Z}}_j\left(\eta \right)\right)+{\Theta }_h,\eta \in {\mathbb{N}}_0,$$

(3)

where the fractional order $0<\alpha <1$, ${\mathcal{Z}}_h\left(\eta \right)$, represents the state at $\eta$; the parameters $a_h$, $w_{hj}$, $f_j$, ${\Theta }_h$ are as in (1); and we consider the initial conditions as ${\mathcal{Z}}_h\left(0\right)={\mathcal{Z}}_h^0\in \mathbb{R}$, $h=1,2,\dots ,n$.

Remark 1.

In this paper, the fractional calculus approach is used to generalize some ANN models proposed in industrial product form design. The proposed discrete fractional-order model (3) extends the existing integer-order models [5,6,7,8,9,10,11] to the fractional-order case. Compared to other existing works, the use of the fractional-order operator in (3) overcomes the limitations of using integer-order differences. Additionally, the proposed fractional-order model (3) can best describe fractal and more undetermined forms [14,31], rather than integer-order ANN models. As a special case, if $\alpha =1$ holds, then model (3) is reduced to an integer-order model of type (1).

Remark 2.

Different from the fractional-order model applied in [31], the nabla fractional operator is used in (3). Hence, the proposed model and established results contribute to the development of the field and provide more opportunities for applied researchers to adopt the fractional-order modeling approach that best suits the respective applied problem.

In the practical stability analysis of the introduced model, the following properties of the fractional Caputo nabla difference will be used [25,26,28,29,62,63].

Lemma 1

( [25,28]). If $\phi :{\mathbb{N}}_0\to \mathbb{R}$ and $0<\alpha <1$, then

$${}^C\nabla _0^{\alpha }{\phi }^2\left(\eta \right)\le 2\phi \left(\eta \right){}^C\nabla _0^{\alpha }\phi \left(\eta \right),\eta \in {\mathbb{N}}_0.$$

Lemma 2

([25,29]). If $\phi :{\mathbb{N}}_0\to \mathbb{R}$ and $0<\alpha <1$, then

$${}^C\nabla _0^{\alpha }\left|\phi \left(\eta \right)\right|\le sign\left(\phi \left(\eta \right)\right){}^C\nabla _0^{\alpha }\phi \left(\eta \right),\eta \in {\mathbb{N}}_0.$$

Moreover, the nabla discrete Mittag-Leffler function, defined by [28]

$${\mathbb{E}}_{\overline{{\gamma }_1,{\gamma }_2}}(\lambda ,\zeta )=\sum _{l=0}^{\infty }{\lambda }^l\frac{{\zeta }^{\overline{l{\gamma }_1+{\gamma }_2-1}}}{\Gamma ({\gamma }_{1}l+{\gamma }_2)}$$

for $\lambda \in \mathbb{R}$, $\left|\lambda \right|<1$, ${\gamma }_1,{\gamma }_2,\zeta \in \mathbb{C}$ with $Re\left({\gamma }_1\right)>0$, will be used in the subsequent analysis.

For the case ${\gamma }_2=1$,

$${\mathbb{E}}_{\overline{{\gamma }_1}}(\lambda ,\zeta )={\mathbb{E}}_{\overline{{\gamma }_1,1}}(\lambda ,\zeta )=\sum _{l=0}^{\infty }{\lambda }^l\frac{{\zeta }^{\overline{l{\gamma }_1}}}{\Gamma ({\gamma }_{1}l+1)}.$$

For a more complete background regarding discrete fractional calculus, the reader is referred to [62,63,65]. For more results regarding discrete fractional-order neural networks, see [23,24,25,26,27,28,29,30].

2.4. Impulsive Controllers

At present, there are various control approaches adopted to discrete fractional-order neural network models to ensure the stability, synchronization, quazi-synchronization and stabilization of the states [23,24,25,26,27,28,29,30].

Since, in response to external or internal noise, ANN models are often subject to short-term perturbations, the present paper will consider impulsive controllers. Such controllers can be also used to artificially control the behavior of the process modeled.

Let ${\eta }_l$,

$$0<{\eta }_1<{\eta }_2<\dots ,\underset{l\to \infty }{lim}{\eta }_l=\infty$$

(4)

be the control times.

Consider the impulsive control discrete fractional neural network model defined by

$$\left\{\begin{array}{c}{}^C\nabla _0^{\alpha }{\mathcal{U}}_h\left(\eta \right)=-a_h{\mathcal{U}}_h\left(\eta \right)+{\sum }_{j=1}^n{w}_{hj}{f}_j\left({\mathcal{U}}_j\left(\eta \right)\right)+{\Theta }_h,\eta \in {\mathbb{N}}_0,\eta \ne {\eta }_l,\hfill \\ \\ {\mathcal{U}}_h\left({\eta }_l\right)=V_{hl}\left({\mathcal{U}}_h({\eta }_l-1)\right),l\in {\mathbb{N}}_1,\hfill \\ \\ \mathcal{U}\left(0\right)={\mathcal{U}}^0,\hfill \end{array}\right.$$

(5)

where $0<\alpha <1$, $V_{hl}$, determine the control law at the instants ${\eta }_l$, $l\in {\mathbb{N}}_1$, $h=1,2,\dots ,n$ and ${\mathcal{U}}^0={({\mathcal{U}}_1^0,\dots ,{\mathcal{U}}_n^0)}^T$ represent the initial data.

The impulsive controllers $V_{hl}$, $h=1,2,\dots ,n$ are applied only at moments ${\eta }_l$, $l\in {\mathbb{N}}_1$ and these control gains can appropriately control the states of the impulse-free discrete fractional-order neural network model (3).

In fact, short-term (impulsive) perturbations exist in industrial product form design problems and they can greatly affect the stability of the model. The relationship between the input variables and output variables in a neural network product form design model can be impulsively changed in response to internal transient stimuli such as exterior supporting forces that result in a structural change in the form diagram [11], personal preferences, changing rules, updates to the weights, innovative impulses [66,67] or external noise in the threshold values. For example, the use of pulse control design is crucial in the form design of many products used in industrial and power electronics, such as power converters and other switching-mode devices [68]. Moreover, impulses can be used as a control mechanism at the fixed moments ${\eta }_l$, $l\in {\mathbb{N}}_1$ with the control actions determined by the functions $V_{hl}$, which represent the functional relationships between the states at the ${\eta }_l-1$ and ${\eta }_l$ instances, in order to develop the product form variables at the next stage and identify the most stable settings for the output values. The fact that the fixed instances of impulsive controllers are predetermined is beneficial in reducing the resource requirements for control updates and for the application of the transmitted information.

Remark 3.

A hybrid discrete fractional and impulsive strategy is used in defining model (5). Several authors have studied the dynamic properties and the potential applications of discrete fractional neural network models [23,24,25,26,27,28,29,30]. The paper [31] proposed such a neural network modeling approach for product form design. Different from [23,24,25,26,27,28,29,30,31], impulsive controllers are considered in model (5). The combined modeling technique will increase the power of the ANN model and will extend the area of its applicability in engineering design.

Remark 4.

There are a few papers about impulsive discrete fractional-order systems [46,47]. However, none of the reported results consider practical stability concepts.

2.5. Mittag-Leffler Practical Stability Concept

Next, the Mittag-Leffler stability concept studied in [28,30] will be extended to the practical Mittag-Leffler stability case. The practical stability notions considered in [53,54,55,56,57,58] will be adopted in system (5) via the next definition.

Definition 3.

The impulsive fractional discrete neural network model (5) is said to be globally practically Mittag-Leffler stable if, for any ${\mathcal{U}}^0\in {\mathbb{R}}^n$, there exist constants $\mathcal{L},\beta >$ and $A\ge 0$ such that

$$\left|\right|\mathcal{U}\left(\eta \right)\left|\right|<{\left[\mathcal{M}\left({\mathcal{U}}^0\right){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )\right]}^{\beta }+A,\eta \in {\mathbb{N}}_0,$$

where $0<\alpha <1$, $\mathcal{M}\left(0\right)=0$, $\mathcal{M}\left(u\right)\ge 0$, $\mathcal{M}\left(u\right)$ is locally Lipschitz for $u\in {\mathbb{R}}^n$.

Remark 5.

Definition 3 extends the Mittag-Leffler stability definition for the discrete fractional-order neural networks given in [28,30] to the practical stability case. When $A=0$, Definition 3 is reduced to the global Mittag-Leffler stability of the zero solution of (5). The practical stability notion is a successful alternative when mathematical stability is impossible, insignificant or pointless in a set time. For practical stability, the corresponding state may not be mathematically stable, but its behavior may be acceptable from an applied point of view. Thus, practical stability concepts are more often studied for models used in applied sciences [54,55,56,57,58,59,60].

Remark 6.

After appropriate substitutions, Definition 3 can be reformulated for the global practical Mittag-Leffler stability properties of non-zero states.

Remark 7.

Stability properties are directly related to synchronization issues. If the impulse-free system (3) is considered as a drive system and the impulsive control system (5) as a response system, then the synchronization error will be $\mathcal{Y}\left(\eta \right)=\mathcal{U}\left(\eta \right)-\mathcal{Z}\left(\eta \right)$. In this case, the global practical Mittag-Leffler stability for the synchronization error system is

$$\left\{\begin{array}{c}{}^C\nabla _0^{\alpha }{\mathcal{Y}}_h\left(\eta \right)=-a_h{\mathcal{Y}}_h\left(\eta \right)+{\sum }_{j=1}^n{w}_{hj}{f}_j\left({\mathcal{Y}}_j\left(\eta \right)\right),\eta \in {\mathbb{N}}_0,\eta \ne {\eta }_l,\hfill \\ \\ {\mathcal{Y}}_h\left({\eta }_l\right)=V_{hl}\left({\mathcal{Y}}_h({\eta }_l-1)\right),l\in {\mathbb{N}}_1,\hfill \\ \\ \mathcal{Y}\left(0\right)={\mathcal{Y}}^0,\hfill \end{array}\right.$$

(6)

where $f_j\left({\mathcal{V}}_j\left(\eta \right)\right)=f_j\left({\mathcal{U}}_j\left(\eta \right)\right)-f_j\left({\mathcal{Z}}_j\left(\eta \right)\right)$ and $\mathcal{Y}\left(0\right)=\mathcal{U}\left(0\right)-\mathcal{Z}\left(0\right)$ will lead to global practical Mittag-Leffler synchronization between the drive and the response systems [28]. Thus, the impulsive controllers will be used to globally practically Mittag-Leffler synchronize the states of the impulsive system (5) with those of system (3). Note that the impulsive synchronization mechanism has been applied to continuous fractional-order neural network models [41,69,70,71], but this control strategy has not been studied for the discrete case.

Remark 8.

One of the main goals in using the neural network approach in the design of industrial products is to achieve an optimal design solution by applying appropriate learning rules. However, the stable behavior of the optimal solution (equilibrium) of the neural network model is also essential for applications. In fact, the correct operation of a neural network model (even a trained one) depends essentially on its stability behavior [48]. Is the equilibrium stable or can small perturbations in the initial data lead to its instability and poor performance? For integer-order neural network models, the globally asymptotic stable equilibrium behavior is the most important stability behavior to guarantee convergence to a global optimal solution independently of the initial data, i.e., independently of spurious suboptimal responses [42]. The particular case of global exponential stability guarantees a fast convergence rate. For fractional-order systems, the Mittag-Leffler notion of global stability is a generalization of global exponential stability for integer-order systems, and, as such, it is preferred in applications [28,30,43].

2.6. Fractional Lyapunov Function Strategy

In this section, some fundamentals regarding the Lyapunov function technique in discrete fractional calculus will be given.

Consider a class $V_0$ of all positive definite and decreasing functions $V:{\mathbb{N}}_0\times {\mathbb{R}}^n\to \mathbb{R}$ such that $V({\eta }_l,0)=0$, $l\in {\mathbb{N}}_1$.

Lemma 3

([46]). If, for a function $V\in V_0$, there exists a constant $\mathcal{L}$, such that $0<\mathcal{L}<1$ and

(i) ${}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))\le -\mathcal{L}V(\eta ,\mathcal{U}\left(\eta \right)),\eta \ne {\eta }_l,\eta \in {\mathbb{N}}_0,l\in {\mathbb{N}}_1,0<\alpha <1$;

(ii) $V({\eta }_l,\mathcal{U}\left({\eta }_l\right))\le V({\eta }_l-1,\mathcal{U}({\eta }_l-1)),l\in {\mathbb{N}}_1,$

then

$$V(\eta ,\mathcal{U}\left(\eta \right))\le V(0,{\mathcal{U}}^0){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta ),\eta \in {\mathbb{N}}_0.$$

Remark 9.

Lemma 3 is an impulsive generalization of Corollary 3 in [26] and of Lemma 6 in [28]. For impulse-free models, similar results are reported in [25,65].

The following generalization of Lemma 3 will also be useful.

Lemma 4.

If, in Lemma 3, condition (i) is replaced by

$\left(i^{\ast }\right)$${}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))\le -\mathcal{L}V(\eta ,\mathcal{U}\left(\eta \right))+\sigma ,\eta \ne {\eta }_l,\eta \in {\mathbb{N}}_0,l\in {\mathbb{N}}_1,\sigma >0$,

then

$$V(\eta ,\mathcal{U}\left(\eta \right))\le \left(V(0,{\mathcal{U}}^0)-\frac{\sigma }{\mathcal{L}}\right){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )+\frac{\sigma }{\mathcal{L}},\eta \in {\mathbb{N}}_0.$$

Proof. 

Consider the function

$$\mathcal{E}(\eta ,\mathcal{U}\left(\eta \right))=V(\eta ,\mathcal{U}\left(\eta \right))-\frac{\sigma }{\mathcal{L}},\eta \in {\mathbb{N}}_0.$$

Obviously, for the above function, condition (ii) of Lemma 3 is true, i.e.,

$$\mathcal{E}({\eta }_l,\mathcal{U}\left({\eta }_l\right))\le \mathcal{E}({\eta }_l-1,\mathcal{U}({\eta }_l-1)),l\in {\mathbb{N}}_1.$$

(7)

For $\eta \ne {\eta }_l$, $l\in {\mathbb{N}}_1$, condition $\left(i^{\ast }\right)$ implies

$${}^C\nabla _0^{\alpha }\mathcal{E}(\eta ,\mathcal{U}\left(\eta \right))\le -\mathcal{L}V(\eta ,\mathcal{U}\left(\eta \right))+\sigma =-\mathcal{L}\mathcal{E}(\eta ,\mathcal{U}\left(\eta \right)).$$

(8)

Thus, from (7) and (8), and applying Lemma 3, it follows that

$$V(\eta ,\mathcal{U}\left(\eta \right))\le \left(V(0,{\mathcal{U}}^0)-\frac{\sigma }{\mathcal{L}}\right){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )+\frac{\sigma }{\mathcal{L}},\eta \in {\mathbb{N}}_0.$$

□

Remark 10.

Lemma 4 is an impulsive generalization of Lemma 6 in [26]. Lemma 3 is a particular case of Lemma 4 for $\sigma =0$.

Remark 11.

The Lyapunov function strategy is a universal method for the study of the stability of solutions of numerous dynamical systems, including neural networks. The Lyapunov function candidate is applied to estimate the distances between the trajectories of the optimal model solution (optimal design solution in product form design) and all other state trajectories that satisfy specific initial conditions [49,64].

3. Global Practical Mittag-Leffler Stability Results

The following hypotheses will be important in the following.

${\mathcal{H}}_1$. The activation functions $f_j$ in model (5) are such that $f_j\left(0\right)=0,j=1,2,\dots ,n$, and, for any $u_1,u_2\in \mathbb{R}$, there exist positive constants ${\mathcal{F}}_j$ such that

$$|f_j\left(u_1\right)-f_j\left(u_2\right)|\le {\mathcal{F}}_j|u_1-u_2|,j=1,2,\dots ,n.$$

${\mathcal{H}}_2$. The impulsive controllers $V_{hl}$ are such that

$$V_{hl}\left({\mathcal{U}}_h({\eta }_l-1)\right)=(1-{\rho }_{hl}){\mathcal{U}}_h({\eta }_l-1),$$

where ${\rho }_{hl}$ are constants such that $0<{\rho }_{hl}\le 2$, $h=1,2,\dots ,n$, $l\in {\mathbb{N}}_1.$

Theorem 1.

Suppose that hypotheses ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ hold. If the following inequalities

$${\mathcal{L}}_1=\underset{1\le h\le n}{min}\left(2a_h\right)>\underset{1\le h\le n}{max}\sum _{j=1}^n\left({\mathcal{F}}_j|w_{hj}|+{\mathcal{F}}_h\left|w_{jh}\right|\right)={\mathcal{L}}_2>0,$$

(9)

$$\mathcal{L}={\mathcal{L}}_1-{\mathcal{L}}_2,0<\mathcal{L}<1,$$

(10)

$$\sum _{h=1}^n|{\mathcal{U}}_h\left(\eta \right)\left|\right|{\Theta }_h|<\sigma ,\sigma >0,\eta \in {\mathbb{N}}_0$$

(11)

hold, then the impulsive control discrete fractional-order neural network model (5) is globally practically Mittag-Leffler stable.

Proof. 

Consider a Lyapunov function of the type

$$V(\eta ,\mathcal{U}\left(\eta \right))=\frac{1}{2}\sum _{h=1}^n{\mathcal{U}}_h^2\left(\eta \right),\eta \in {\mathbb{N}}_0.$$

(12)

First, the $\alpha$-order Caputo nabla fractional difference of $V(\eta ,\mathcal{U}(\eta \left)\right)$ will be calculated along the trajectories of system (5) for $\eta \ne {\eta }_l$, $l\in {\mathbb{N}}_1$.

From Lemma 1, it follows that

$$\begin{array}{cc}\hfill {}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))& \le \sum _{h=1}^n{\mathcal{U}}_h{\left(\eta \right)}^C{\nabla }_0^{\alpha }{\mathcal{U}}_h\left(\eta \right)\hfill \\ \\ \hfill & =\sum _{h=1}^n{\mathcal{U}}_h\left(\eta \right)\left[-a_h{\mathcal{U}}_h\left(\eta \right)+\sum _{j=1}^n{w}_{hj}{f}_j\left({\mathcal{U}}_j\left(\eta \right)\right)+{\Theta }_h\right].\hfill \end{array}$$

(13)

According to hypothesis ${\mathcal{H}}_1$, there exist positive constants ${\mathcal{F}}_j$ such that

$$\begin{array}{cc}\hfill {}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))& \le \sum _{h=1}^n\left[-a_h{\mathcal{U}}_h^2\left(\eta \right)+\sum _{j=1}^n|w_{hj}|{\mathcal{F}}_j|{\mathcal{U}}_h\left(\eta \right)\left|\right|{\mathcal{U}}_j\left(\eta \right)|+|{\mathcal{U}}_h\left(\eta \right)\left|\right|{\Theta }_h|\right]\hfill \\ \\ \hfill & \le \sum _{h=1}^n\left[-a_h{\mathcal{U}}_h^2\left(\eta \right)+\frac{1}{2}\sum _{j=1}^n\left|w_{hj}\right|{\mathcal{F}}_j\left({\mathcal{U}}_h^2\left(\eta \right)+{\mathcal{U}}_j^2\left(\eta \right)\right)\right.\hfill \\ \\ \hfill & +|{\mathcal{U}}_h\left(\eta \right)\left|\right|{\Theta }_h\left|\right].\hfill \end{array}$$

(14)

Then, from (11) and (9), it follows that

$$\begin{array}{cc}\hfill {}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))& \le -\underset{1\le h\le n}{min}\left(2a_h\right)V(\eta ,\mathcal{U}\left(\eta \right))\hfill \\ \\ \hfill & +\underset{1\le h\le n}{max}\sum _{j=1}^n\left({\mathcal{F}}_j|w_{hj}|+{\mathcal{F}}_h\left|w_{jh}\right|\right)V(\eta ,\mathcal{U}\left(\eta \right))+\sigma \hfill \\ \\ \hfill & =-({\mathcal{L}}_1-{\mathcal{L}}_2)V(\eta ,\mathcal{U}\left(\eta \right))+\sigma \hfill \\ \\ \hfill & =-\mathcal{L}V(\eta ,\mathcal{U}\left(\eta \right))+\sigma ,\eta \ne {\eta }_l,\hfill \end{array}$$

(15)

where $0<\mathcal{L}<1$.

Next, for $\eta ={\eta }_l$, $l\in {\mathbb{N}}_1$, hypothesis ${\mathcal{H}}_2$ implies that

$$\begin{array}{cc}\hfill V({\eta }_l,\mathcal{U}\left({\eta }_l\right))=\frac{1}{2}\sum _{h=1}^n{\mathcal{U}}_h^2\left({\eta }_l\right)& =\frac{1}{2}\sum _{h=1}^n{(1-{\rho }_{hl})}^2{\mathcal{U}}_h^2({\eta }_l-1)\hfill \\ \\ \hfill & \le \frac{1}{2}\sum _{h=1}^n{\mathcal{U}}_h^2({\eta }_l-1)=V({\eta }_l-1,\mathcal{U}({\eta }_l-1)).\hfill \end{array}$$

(16)

From (15) and (16), according to Lemma 4, it follows that

$$V(\eta ,\mathcal{U}\left(\eta \right))\le \left(V(0,{\mathcal{U}}^0)-\frac{\sigma }{\mathcal{L}}\right){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )+\frac{\sigma }{\mathcal{L}},\eta \in {\mathbb{N}}_0.$$

(17)

Hence,

$$\sum _{h=1}^n{\mathcal{U}}_h^2\left(\eta \right)\le \left(\sum _{h=1}^n{\mathcal{U}}_h^2\left(0\right)-\frac{2\sigma }{\mathcal{L}}\right){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )+\frac{2\sigma }{\mathcal{L}},\eta \in {\mathbb{N}}_0,$$

which implies that

$$\left|\right|\mathcal{U}\left(\eta \right)\left|\right|<\left|\right|{\mathcal{U}}^0\left|\right|{\left[{\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )\right]}^{1/2}+{\left(\frac{2\sigma }{\mathcal{L}}\right)}^{1/2},\eta \in {\mathbb{N}}_0.$$

Therefore, Definition 3 is satisfied for $\mathcal{M}\left({\mathcal{U}}^0\right)=\left|\right|{\mathcal{U}}^0{\left|\right|}^2$, $\beta =1/2$ and $A={\left(\frac{2\sigma }{\mathcal{L}}\right)}^{1/2}$, and, thus, the impulsive control discrete fractional-order neural network model (5) is globally practically Mittag-Leffler stable. □

Remark 12.

Theorem 1 offers global practical Mittag-Leffler stability results for the generalized impulsive fractional-order neural network model (5). The fact that the stability criteria are in the form of inequalities between the model parameters make them easy to implement. The practical significance of the proposed stability analysis is as follows: if the activation functions and the impulsive controllers satisfy hypotheses ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$, and the model parameters satisfy conditions (9)–(11), then the impulsive control discrete fractional-order neural network model (5) is globally practically Mittag-Leffler stable.

Remark 13.

Note that condition (11) in Theorem 1 imposes strict restrictions. Although these limitations are justified from a practical point of view, weaker criteria for the global practical Mittag-Leffler stability of model (5) will be offered in the next result.

Theorem 2.

Suppose that hypotheses ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ hold. If the following inequalities

$$0<\widehat{\mathcal{L}}=\underset{1\le h\le n}{min}\left[a_h-{\mathcal{F}}_h\sum _{j=1}^n\left|w_{jh}\right|\right]<1,$$

(18)

$$\sum _{h=1}^n\left|{\Theta }_h\right|<\widehat{\sigma },\widehat{\sigma }>0$$

(19)

hold, then the impulsive control discrete fractional-order neural network model (5) is globally practically Mittag-Leffler stable.

Proof. 

The following Lyapunov function is defined:

$$V(\eta ,\mathcal{U}\left(\eta \right))=\sum _{h=1}^n\left|{\mathcal{U}}_h\left(\eta \right)\right|,\eta \in {\mathbb{N}}_0.$$

(20)

Then, we calculate the $\alpha$-order Caputo nabla fractional difference of $V(\eta ,\mathcal{U}(\eta \left)\right)$ along the trajectories of system (5) for $\eta \ne {\eta }_l$, $l\in {\mathbb{N}}_1$.

Lemma 2 implies that

$$\begin{array}{cc}\hfill {}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))& \le \sum _{h=1}^{n}sign{\left({\mathcal{U}}_h\left(\eta \right)\right)}^C{\nabla }_0^{\alpha }{\mathcal{U}}_h\left(\eta \right)\hfill \\ \\ \hfill & =\sum _{h=1}^n\left[-a_h|{\mathcal{U}}_h\left(\eta \right)|+\sum _{j=1}^n|w_{hj}\left|\right|f_j\left({\mathcal{U}}_j\left(\eta \right)\right)|+|{\Theta }_h|\right].\hfill \end{array}$$

(21)

According to hypothesis ${\mathcal{H}}_1$, there exist positive constants ${\mathcal{F}}_j$ such that

$${}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))\le -\sum _{h=1}^n\left[a_h-{\mathcal{F}}_h\sum _{j=1}^n\left|w_{jh}\right|\right]|{\mathcal{U}}_j\left(\eta \right)|+\sum _{h=1}^n\left|{\Theta }_h\right|.$$

(22)

From (18) and (19), it follows that

$${}^C\nabla _0^{\alpha }V(\eta ,\mathcal{U}\left(\eta \right))\le -\widehat{\mathcal{L}}V(\eta ,\mathcal{U}\left(\eta \right))+\widehat{\sigma },\eta \ne {\eta }_l,l\in {\mathbb{N}}_1.$$

(23)

Next, for $\eta ={\eta }_l$, $l\in {\mathbb{N}}_1$, hypothesis ${\mathcal{H}}_2$ implies that

$$\begin{array}{cc}\hfill V({\eta }_l,\mathcal{U}\left({\eta }_l\right))=\sum _{h=1}^n\left|{\mathcal{U}}_h\left({\eta }_l\right)\right|& =\sum _{h=1}^n|(1-{\rho }_{hl})\left|\right|{\mathcal{U}}_h({\eta }_l-1)|\hfill \\ \\ \hfill & \le \sum _{h=1}^n\left|{\mathcal{U}}_h({\eta }_l-1)\right|=V({\eta }_l-1,\mathcal{U}({\eta }_l-1)).\hfill \end{array}$$

(24)

Then, using (23), (24) and Lemma 4, it is obtained that

$$V(\eta ,\mathcal{U}\left(\eta \right))\le \left(V(0,{\mathcal{U}}^0)-\frac{\widehat{\sigma }}{{}^{^}L}\right){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )+\frac{\widehat{\sigma }}{\widehat{\mathcal{L}}},\eta \in {\mathbb{N}}_0.$$

(25)

Hence,

$$\sum _{h=1}^n\left|{\mathcal{U}}_h\left(\eta \right)\right|\le \left(\sum _{h=1}^n\left|{\mathcal{U}}_h\left(0\right)\right|-\frac{\widehat{\sigma }}{{}^{^}L}\right){\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )+\frac{\widehat{\sigma }}{\widehat{\mathcal{L}}},\eta \in {\mathbb{N}}_0.$$

(26)

Using (26) and the Minkowski-type inequality, it follows that

$$\left|\right|\mathcal{U}\left(\eta \right)\left|\right|\le \sum _{h=1}^n|{\mathcal{U}}_h\left(\eta \right)|\le \sum _{h=1}^n\left|{\mathcal{U}}_h\left(0\right)\right|{\mathbb{E}}_{\overline{\alpha }}(-\mathcal{L},\eta )+\frac{\widehat{\sigma }}{\widehat{\mathcal{L}}},\eta \in {\mathbb{N}}_0,$$

which, by Definition 3 for $\mathcal{M}\left({\mathcal{U}}^0\right)={\sum }_{h=1}^n\left|{\mathcal{U}}_h\left(0\right)\right|$, $\beta =1$ and $A=\frac{\widehat{\sigma }}{{}^{^}L}$, implies that the impulsive control discrete fractional-order neural network model (5) is globally practically Mittag-Leffler stable. □

Remark 14.

The global Mittag-Leffler stability for discrete fractional-order neural networks has been investigated in [28,30] with the use of the Lyapunov direct method. However, so far, there have been no results regarding the global practical stability of Mittag-Leffler for such neural networks. Considering this, in Theorems 1 and 2, the practical stability case is presented and effective criteria are established. The obtained results can also be used in the study of the global practical Mittag-Leffler synchronization of the states. Hence, applying the stability analysis offered in this section to the error system (6), global practical Mittag-Leffler synchronization results for the drive and response systems (3) and (5), respectively, can be obtained directly under impulsive controllers that satisfy hypothesis ${\mathcal{H}}_2$.

Remark 15.

The results obtained in Theorems 1 and 2 are related to a neural network model that generalizes and extends some existing models applied in product form design analysis [5,6,7,8,9,10,11]. Thus, the proposed results complement some existing ones. Moreover, different from [5,6,7,8,9,10,11], instead of proposing learning rules, this paper is devoted to the practical stability behavior of the states.

Remark 16.

The application of the direct Lyapunov method allows the stability properties of model (5) to be investigated without using the exact solution format. This is one of the remarkable advantages of this strategy. The suitable Lyapunov function serves as a measure of the distances between the states. Thus, the Lyapunov strategy is intensively applied in numerous engineering applied problems [23,24,25,26,27,28,29,30,31,38,42,43,46,49,51,53,56,57,64].

Remark 17.

Different from the stability results proposed for discrete fractional-order neural networks [24,27,28,30], including those applied in product form design [31], impulsive controllers are proposed in this paper. The use of such a mechanism is motivated by applications [68]. It also makes it possible to apply its advantages in controlling the practical stability properties and avoiding unwanted behavior in the states.

Remark 18.

The practical stability concept has been studied for linear discrete fractional-order systems in [59,60,61]. However, the authors of [59,60,61] did not consider the Mittag-Leffler practical stability properties. Moreover, the impulsive effects were ignored. Thus, the proposed results complement some existing ones and provide more flexible tools for applications.

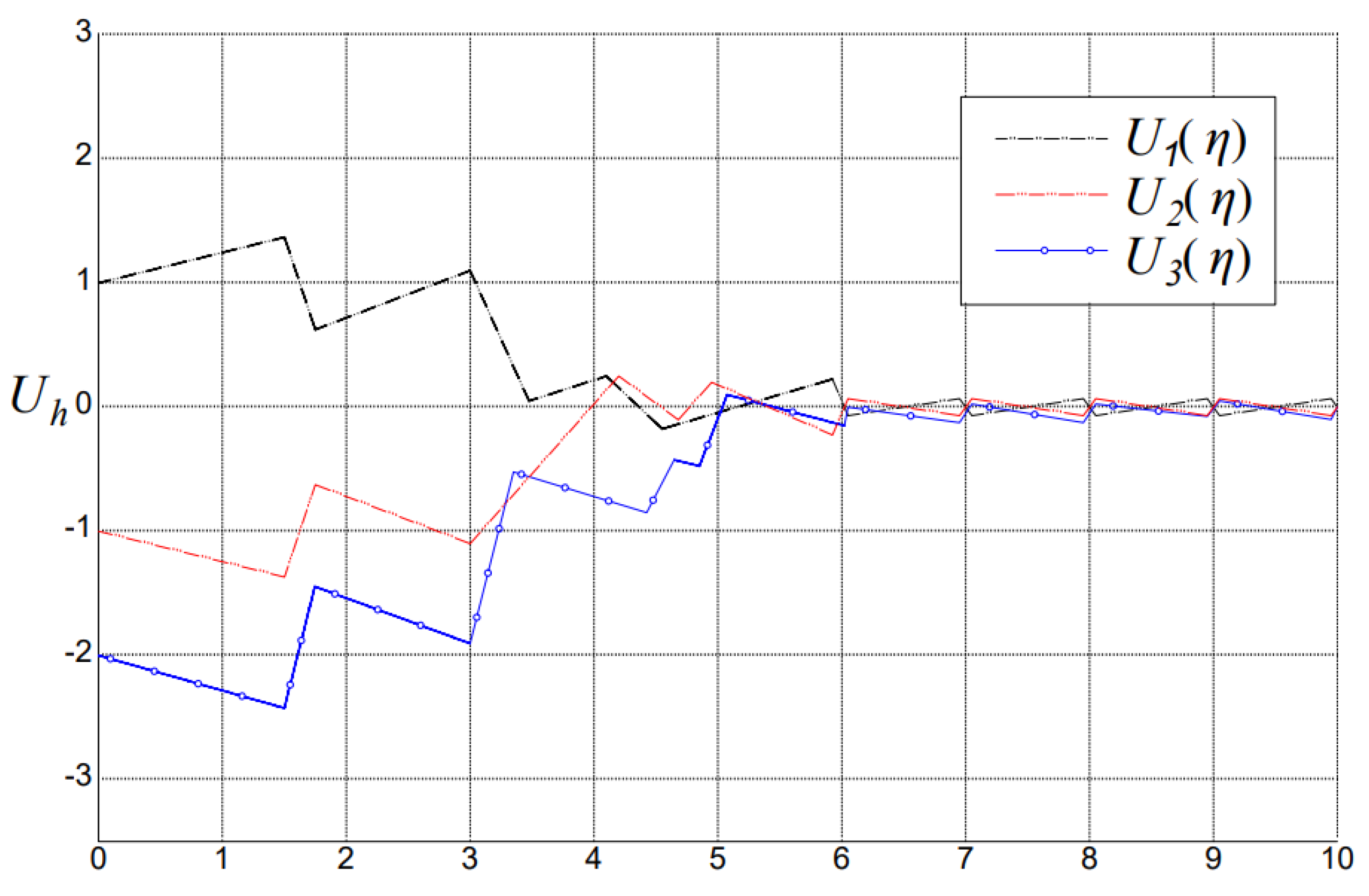
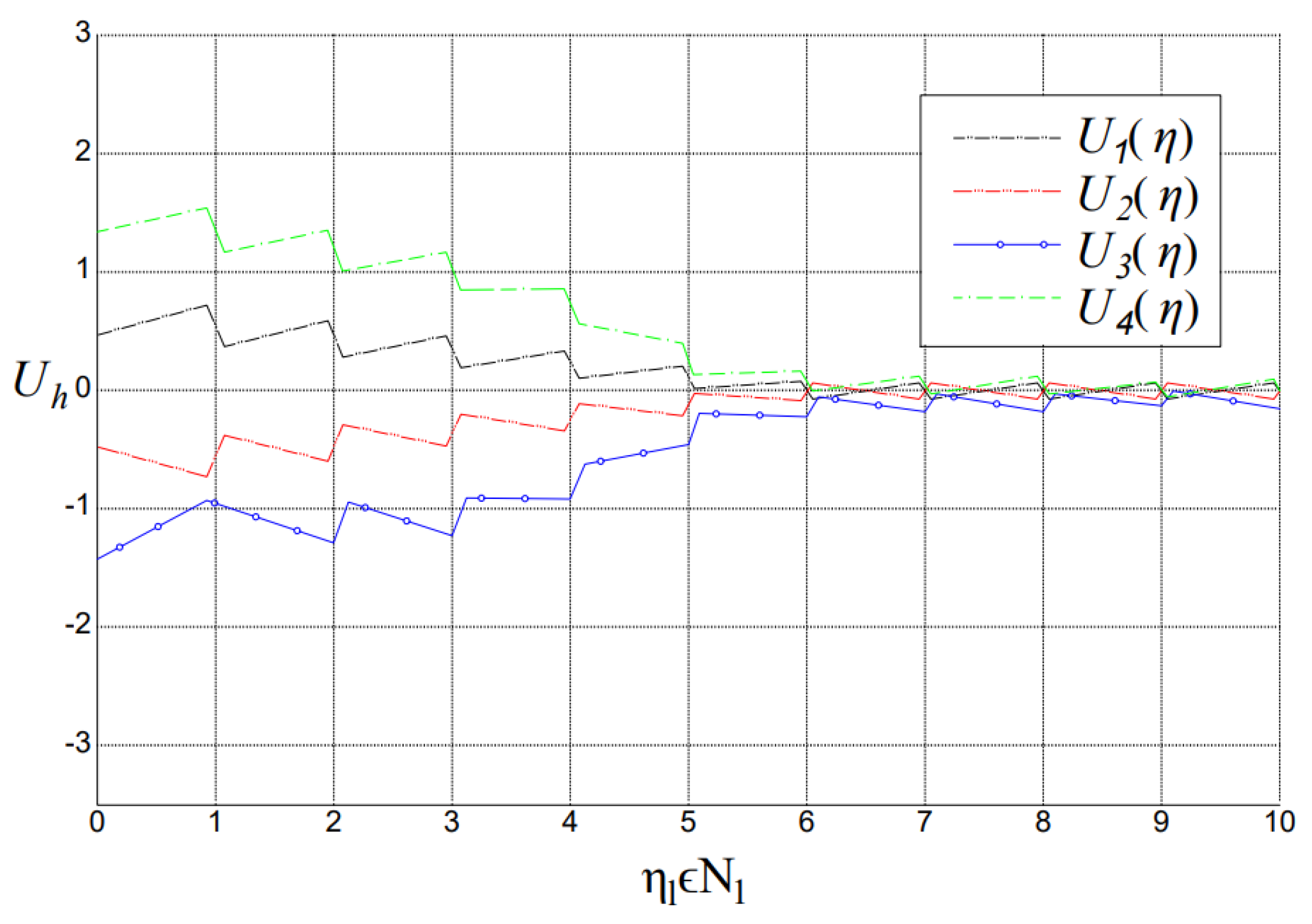
4. Discussion and Examples

It is not surprising that biotechnology-inspired collective intelligence methods are intensively applied in the field of engineering design to study various multi-agent systems. In particular, such methods are also applied in product form design problems [5,6,7,8,9,10,11]. Using different neural network models, researchers have attempted to better understand the connections between an initial design idea and the desired output to achieve the goals of modern design.

The implementation of the fractional calculus approach in neural network modeling leads to the design of more flexible models. However, this method has not been well studied for neural network models used in the area of product form design [31].

Given the advantages of discrete fractional-order neural network models, in this study, a generalization of some existing models applied in the product form design is proposed by using the nabla fractional operator. Moreover, different from the model proposed in [31], impulsive controllers are proposed. Examining such a control technique enables the use of its well-known advantages [40,42,44,45]. There are many cases where the impulse control technique can provide an efficient means to deal with systems that cannot undergo continuous control inputs.

The advanced properties of the hybrid fractional-order impulsive model system (5) make it an appropriate extension of some integer-order neural network models used in product form design analysis. For example, model (5) can be described as follows.

• A fractional-order generalization of the neural network model designed in [5], in which the state variables ${\mathcal{U}}_h\left(\eta \right)$, $(h=1,2,\dots ,n)$ represent the form parameters at the discrete time $\eta$. Using the generalized model (5), it is possible to study the dependence of the product image on the configuration parameters and element shapes using the fractional-order differences between their current and previous values.
• A fractional-order generalization of the form design model introduced in [6], in which the state variables ${\mathcal{U}}_h\left(\eta \right)$, $(h=1,2,\dots ,n)$ are defined as word pairs or a set of target image values and their respective weights, and there is a set of 21 output-node data.
• A fractional-order generalization of the neural network model considered in [7], aimed at achieving a desirable product image depending on the best combination of form elements used to study the mobile phone’s form, in which the state variables ${\mathcal{U}}_h\left(\eta \right)$, $(h=1,2,\dots ,n)$ are defined as 27 form elements (input neurons) extracted by morphological analysis, namely the top shape (${\mathcal{U}}_1$), body shape (${\mathcal{U}}_2$), bottom shape (${\mathcal{U}}_3$), body length and width ratio (${\mathcal{U}}_4$), function button style (${\mathcal{U}}_5$), number button arrangement (${\mathcal{U}}_6$), screen size (${\mathcal{U}}_7$), screen mask and function buttons (${\mathcal{U}}_8$) and outline division style (${\mathcal{U}}_9$), and the outputs are the evaluation values for the desirable product image.
• A fractional-order generalization of the neural network model considered in [11], which generates forms that have a greater possibility of satisfying the architect’s personal design taste and consists of 21 input variables ${\mathcal{U}}_0$ that represent numbers that are sufficient to identify a form from others, as well as two hidden layers of 50 neuronal variables ${\mathcal{U}}_h\left(\eta \right)$ each and one output variable, which denotes the score of the form.

In all above-discussed generalizations, $w_{hj}$ are the weights between the neurons (states) in the input and output layers, $f_j$ is the activation function (in most practical cases, sigmoid) and ${}^C\nabla _0^{\alpha }{\mathcal{U}}_h\left(\eta \right)$ is the Caputo nabla fractional difference, which generalizes the integer-order difference between the current and previous states of the state variable ${\mathcal{U}}_h\left(\eta \right)$. Hence, using a fractional-order generalized model of type (5), it is possible to study the dependence of the output variables (product image) on the input variables (the configuration parameters and element shapes) using the fractional-order differences between their current and previous values. Moreover, in all extended models, impulsive controllers are proposed at some instances, at which impulsive control is performed to avoid the unwanted behavior of the states. The fixed moments ${\eta }_l$, $l\in {\mathbb{N}}_1$ are the intervention times, and the functions $V_{hl}$ determine the control actions.

In addition, instead of considering learning mechanisms, as in [5,6,7,8,9,10,11], this paper investigates the specific stability behavior of the neuronal states and formulates rigorous results that can be applied to the concrete model. In fact, learning algorithms allow optimal solutions to be reached in different design tasks. For example, in [6], the goal of the created learning rule is the best-fitting shape. However, the issue of the stability of a trained neural network model is also very important [48,49], but the investigations in this area are not sufficient. In this paper, the concept of the global practical Mittag-Leffler stability is introduced to the impulsive discrete fractional-order neural network model, which has not been considered for such systems. The introduced concept extends the Mittag-Leffler stability notion investigated in [28,30]. The practical stability extensions [53] of classical stability concepts are more appropriate for applied problems [54,55,56,57,58] when the corresponding system is not mathematically Mittag-Leffler stable, but its behavior is acceptable.

The comparison demonstrated in

Table 1. Comparison with existing stability, synchronization and control results on discrete fractional-order neural networks.

Discrete Fractional-Order Neural Networks	[28]	[30]	[31]	This Research
Mittag-Leffler stability and synchronization	√	√	√	√
Practical stability	×	×	√	√
Practical Mittag-Leffler stability and synchronization	×	×	×	√
Impulsive controllers	×	×	×	√
Applied in product form design	×	×	√	√

displays the novelty offered in this paper. Table 1 also illustrates that the study of the fractional-order neural network modeling framework in engineering design is far from complete and needs further development.

In Theorems 1 and 2, global practical Mittag-Leffler stability results are established using the fractional Lyapunov method. The obtained novel stability and impulsive control criteria provide new perspectives and tools that could be extremely useful, as they provide a framework enabling control to better design fractional-order neural network models that are resilient in the face of impulsive shocks. From the applied point of view, if the restrictions of the model’s parameters satisfy conditions ${\mathcal{H}}_1$, (9) and (18), and the impulsive controllers are such that condition ${\mathcal{H}}_2$ is true, then the constructed fractional-order neural network model is globally practically Mittag-Leffler stable. The conditions of Theorem 2 are less restrictive. Having different stability criteria is very useful in applications, which will be demonstrated through examples in the next section.

Example 1.

Consider the impulsive discrete fractional-order neural network model (5) for $n=3$, $\alpha =0.96$, $a_h=3.5$, $h=1,2,3$, $f_j\left(u_j\right)=\frac{1}{2}\left(\right|u_j+1|-|u_j-1\left|\right)$, $u_j\in \mathbb{R}$, $j=1,2,3$, with the connection weights given as

$$\begin{array}{c}\hfill W=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right]=\left[\begin{array}{ccc}1.2& -1.4& 1.4\\ -0.8& 0.6& 0.6\\ 0.3& 0.3& -0.2\end{array}\right].\end{array}$$

and the impulsive controllers defined as

$$V_{hl}\left({\mathcal{U}}_h({\eta }_l-1)\right)=\left(1-\frac{1}{5h}\right){\mathcal{U}}_h({\eta }_l-1),$$

(27)

at the the impulsive instances ${\eta }_l$ that satisfy (4).

If

$$|{\mathcal{U}}_h\left(\eta \right)|\le {\gamma }_h,{\gamma }_h>0,\eta \in {\mathbb{N}}_0,h=1,2,3$$

and

$$\sum _{h=1}^n{\gamma }_h\left|\right|{\Theta }_h|<\sigma ,\sigma >0,\eta \in {\mathbb{N}}_0,$$

then, for the choice of the model’s parameters, hypotheses ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ hold for ${\mathcal{F}}_j=1$, $j=1,2,3$ and ${\rho }_{hl}=\frac{1}{5h}$, $h=1,2,3,$$l\in {\mathbb{N}}_1$. Moreover, conditions (9) and (10) of Theorem 1 hold, since

$$7={\mathcal{L}}_1=\underset{1\le h\le n}{min}\left(2a_h\right)>\underset{1\le h\le n}{max}\sum _{j=1}^n\left({\mathcal{F}}_j|w_{hj}|+{\mathcal{F}}_h\left|w_{jh}\right|\right)={\mathcal{L}}_2=6.3>0,$$

and

$$0<\mathcal{L}={\mathcal{L}}_1-{\mathcal{L}}_2=0.7<1.$$

According to Theorem 1, the impulsive control discrete fractional-order neural network model (5) is globally practically Mittag-Leffler stable. The global practical Mittag-Leffler stable behavior of the states is demonstrated in Figure 4.

However, condition (18) of Theorem 2 is not satisfied since

$$\widehat{\mathcal{L}}=\underset{1\le h\le n}{min}\left[a_h-{\mathcal{F}}_h\sum _{j=1}^n\left|w_{jh}\right|\right]=1.2>1.$$

Hence, for the model constructed in Example 1, the criteria established in Theorem 2 cannot be applied.

Example 2.

Consider the impulsive discrete fractional-order neural network model (5) for $n=3$, $\alpha =0.97$, $a_h=2.7$, ${\Theta }_h=0.2$, $h=1,2,3$, $f_j\left(u_j\right)=\frac{1}{2}\left(\right|u_j+1|-|u_j-1\left|\right)$, $u_j\in \mathbb{R}$, $j=1,2,3$, with the connection weights given as

$$\begin{array}{c}\hfill W=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right]=\left[\begin{array}{ccc}0.7& 0.6& -0.7\\ -0.5& 0.4& 0.9\\ 0.8& 1& -0.4\end{array}\right].\end{array}$$

and the impulsive controllers defined as

$$V_{hl}\left({\mathcal{U}}_h({\eta }_l-1)\right)=\left(1-\frac{1}{2h}\right){\mathcal{U}}_h({\eta }_l-1),$$

(28)

at the impulsive instances ${\eta }_l$ that satisfy (4).

For the choice of the model’s parameters, hypotheses ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ hold for ${\mathcal{F}}_j=1$, $j=1,2,3$ and ${\rho }_{hl}=\frac{1}{2h}$, $h=1,2,3,$$l\in {\mathbb{N}}_1$. Moreover, condition (18) of Theorem 2 is satisfied for

$$0<\widehat{\mathcal{L}}=0.7=\underset{1\le h\le n}{min}\left[a_h-{\mathcal{F}}_h\sum _{j=1}^n\left|w_{jh}\right|\right]<1,$$

and condition (19) holds for

$$\sum _{h=1}^3\left|{\Theta }_h\right|=0.6<\widehat{\sigma }<\infty .$$

According to Theorem 2, the impulsive control discrete fractional-order neural network model (5) is globally practically Mittag-Leffler stable. The global practical Mittag-Leffler stable behavior of the states is demonstrated in Figure 5.

In addition, it is clear that condition (10) of Theorem 1 is not satisfied, since

$$5.4={\mathcal{L}}_1=\underset{1\le h\le n}{min}\left(2a_h\right)>\underset{1\le h\le n}{max}\sum _{j=1}^n\left({\mathcal{F}}_j|w_{hj}|+{\mathcal{F}}_h\left|w_{jh}\right|\right)={\mathcal{L}}_2=4.2>0,$$

but

$$\mathcal{L}={\mathcal{L}}_1-{\mathcal{L}}_2=1.2>1.$$

Therefore, for the model constructed in Example 2, the criteria established in Theorem 1 cannot be applied.

Example 3.

In this example, consider first the impulse-free model (3) for $n=4$, $\alpha =0.96$, $a_h=3.8$, $h=1,2,3,4$, $f_j\left(u_j\right)=\frac{1}{2}\left(\right|u_j+1|-|u_j-1\left|\right)$, $u_j\in \mathbb{R}$, $j=1,2,3,4$, with the connection weights given as

$$\begin{array}{c}\hfill W=\left[\begin{array}{cccc}{w}_{11}& w_{12}& w_{13}& w_{14}\\ w_{21}& w_{22}& w_{23}& w_{24}\\ w_{31}& w_{32}& w_{33}& w_{34}\\ w_{41}& w_{42}& w_{43}& w_{44}\end{array}\right]=\left[\begin{array}{cccc}0.9& 0.7& -0.8& 1.2\\ 0.8& 0.9& 1.1& -0.6\\ -1.1& 0.7& -0.6& 0.7\\ -0.8& 0.3& 0.9& 0.9\end{array}\right].\end{array}$$

For the above model, hypothesis ${\mathcal{H}}_1$ holds for ${\mathcal{F}}_j=1$, $j=1,2,3,4$. Moreover, conditions (9) and (10) of Theorem 1 hold, since

$$7.6={\mathcal{L}}_1=\underset{1\le h\le n}{min}\left(2a_h\right)>\underset{1\le h\le n}{max}\sum _{j=1}^n\left({\mathcal{F}}_j|w_{hj}|+{\mathcal{F}}_h\left|w_{jh}\right|\right)={\mathcal{L}}_2=7.2>0,$$

and

$$0<\mathcal{L}={\mathcal{L}}_1-{\mathcal{L}}_2=0.4<1.$$

In addition, condition (18) of Theorem 2 is satisfied for

$$0<\widehat{\mathcal{L}}=\underset{1\le h\le n}{min}\left[a_h-{\mathcal{F}}_h\sum _{j=1}^n\left|w_{jh}\right|\right]=0.3<1.$$

However, for specific ${\Theta }_h$, $h=1,2,3,4$, the model may not be stable or practically stable, even in cases when both conditions (11) and (19) are satisfied. A simulation is shown in Figure 6 for ${\Theta }_h=0.8$, $h=1,2,3,4$ such that conditions (11) and (19) are satisfied.

Hence, external bias contributes to the stability behavior of a state.

However, if we consider impulsive controllers in the corresponding response system (5) defined as

$$V_{hl}\left({\mathcal{U}}_h({\eta }_l-1)\right)=\left(1-\frac{1}{3h}\right){\mathcal{U}}_h({\eta }_l-1),$$

(29)

at the the impulsive instances ${\eta }_l$ that satisfy (4), then all conditions of Theorems 1 and 2 hold for ${\rho }_{hl}=\frac{1}{3h}$, $h=1,2,3,4$, $l\in {\mathbb{N}}_1$.

Therefore, the impulsive control model (5) is globally practically Mittag-Leffler stable with the trajectories shown in Figure 7.

Remark 19.

The constructed examples demonstrate the efficacy of the established criteria. They also show that, depending on the parameters of the designed model, it is necessary to apply different criteria, which motivates the search for diverse criteria. In addition, Example 3 demonstrates that suitable impulsive controllers can be used to stabilize the unstable behavior of an impulse-free model.

5. Conclusions

In this paper, a discrete fractional-order neural network model is introduced, which extends some neural network models applied in product form design. The effects of short-term perturbations on the neural states are also considered by adding appropriate impulsive controllers. The combined extended practical Mittag-Leffler stability concept is defined for the introduced model, and sufficient conditions are derived by using the Lyapunov function method. The benefits of the practical stability notion make the obtained results more relevant to real-world applications. The proposed results also complement some Mittag-Leffler stability results for discrete fractional-order neural networks for the practical stability case, considering impulsive controllers. A discussion and illustrative examples are given to demonstrate the novelty and the effectiveness of the contributed results. Applying the proposed discrete fractional calculus modeling approach to some neural network models used in engineering design is an important task for future research. Moreover, given the advantages of the practical stability notion, it will be important to extend the research on this concept to other real-world problems in science and engineering.