Rotational Convolution Design in Convolutional Neural Networks for Direct 3D Electromagnetic Tomography
Abstract
1. Introduction
1.1. Advancements in 3D Electromagnetic Tomography
- It is impossible to obtain a complete 3D description of the whole object. The present technology is limited to integrating a series of two-dimensional images within the human mind to approximate a three-dimensional structure. Therefore, there is a desire to obtain intuitive and accurate three-dimensional images that display the spatial structure of the object under inspection, providing richer information than two-dimensional images.
- Although the 2D system can reconstruct two-dimensional gray-scale images, the detection targets are definitively distributed in three dimensions. Unlike CT, EMT is a soft field, which means that the image reconstruction process is ill posed. In other words, the reconstructed two-dimensional sectional distribution is influenced not only by the object’s actual distribution on that section but also by the coupling effect of the three-dimensional distribution surrounding the section. In light of this consideration, studying the three-dimensional distribution of the target is a more straightforward process than reconstructing two-dimensional images.
1.2. Deep Learning Innovations in Electrical Tomography
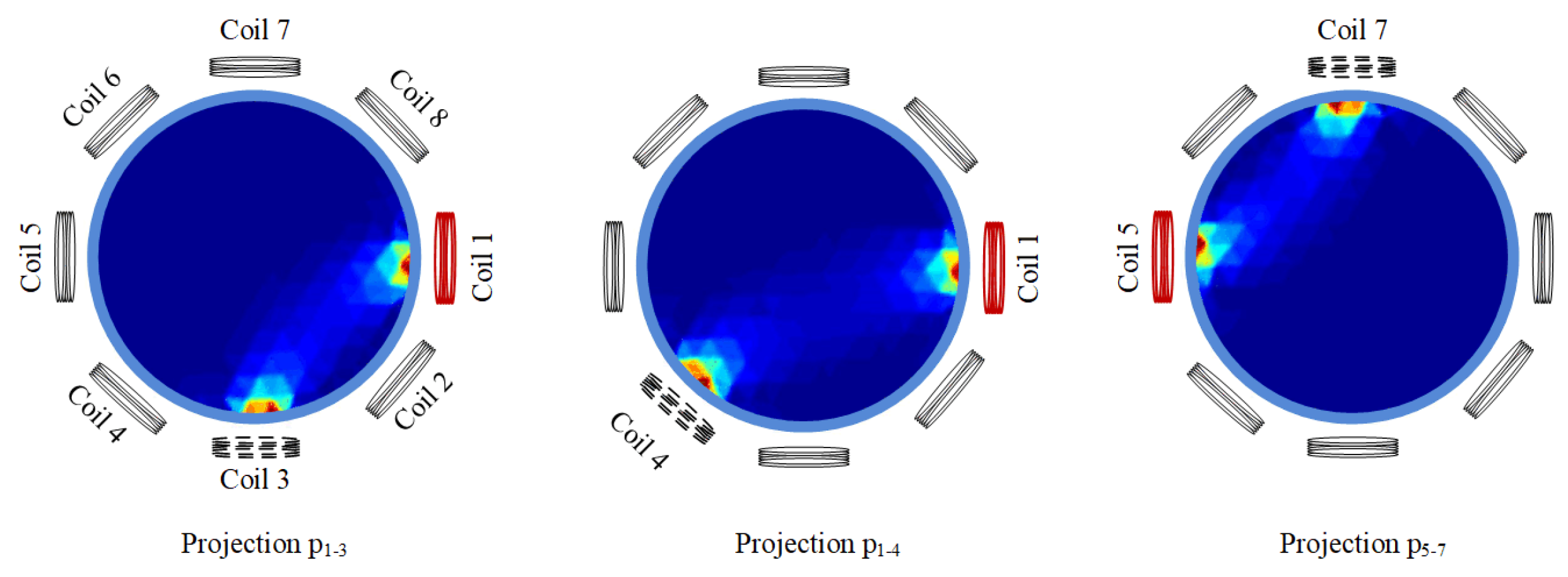
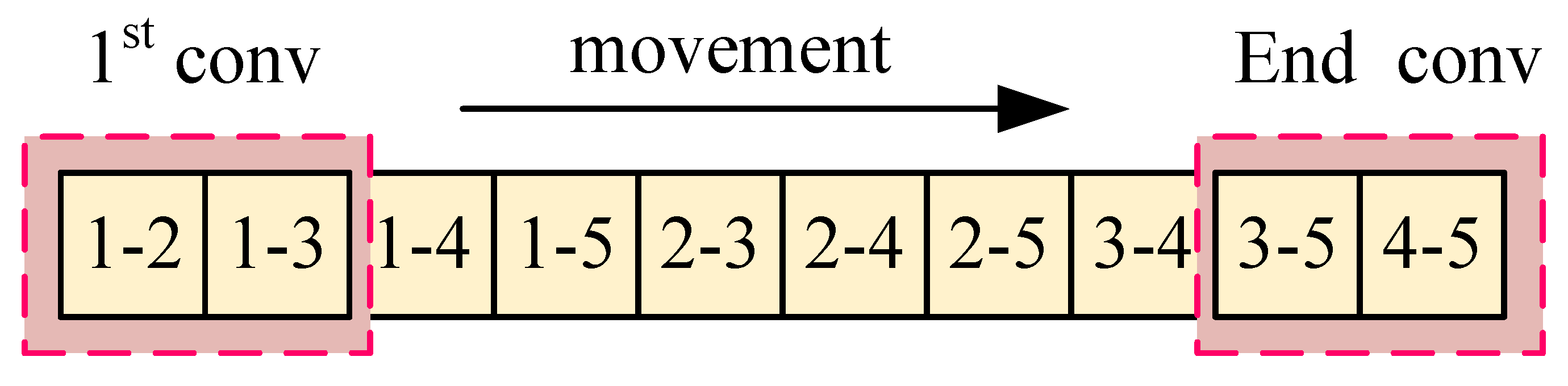
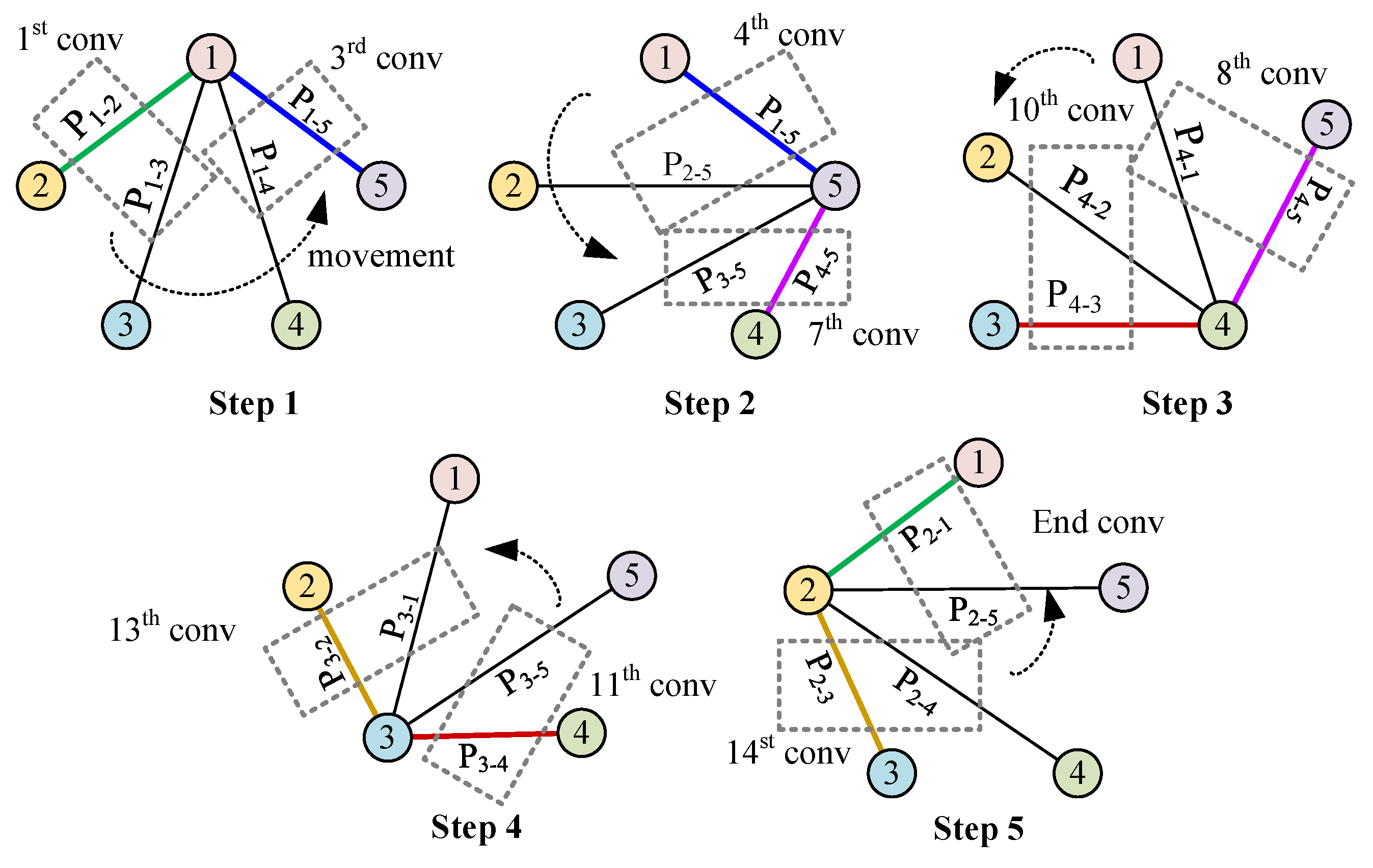
1.3. Convolution Patterns in EMT: A Projection-Based Approach
2. Theory and Model
2.1. EMT Theory
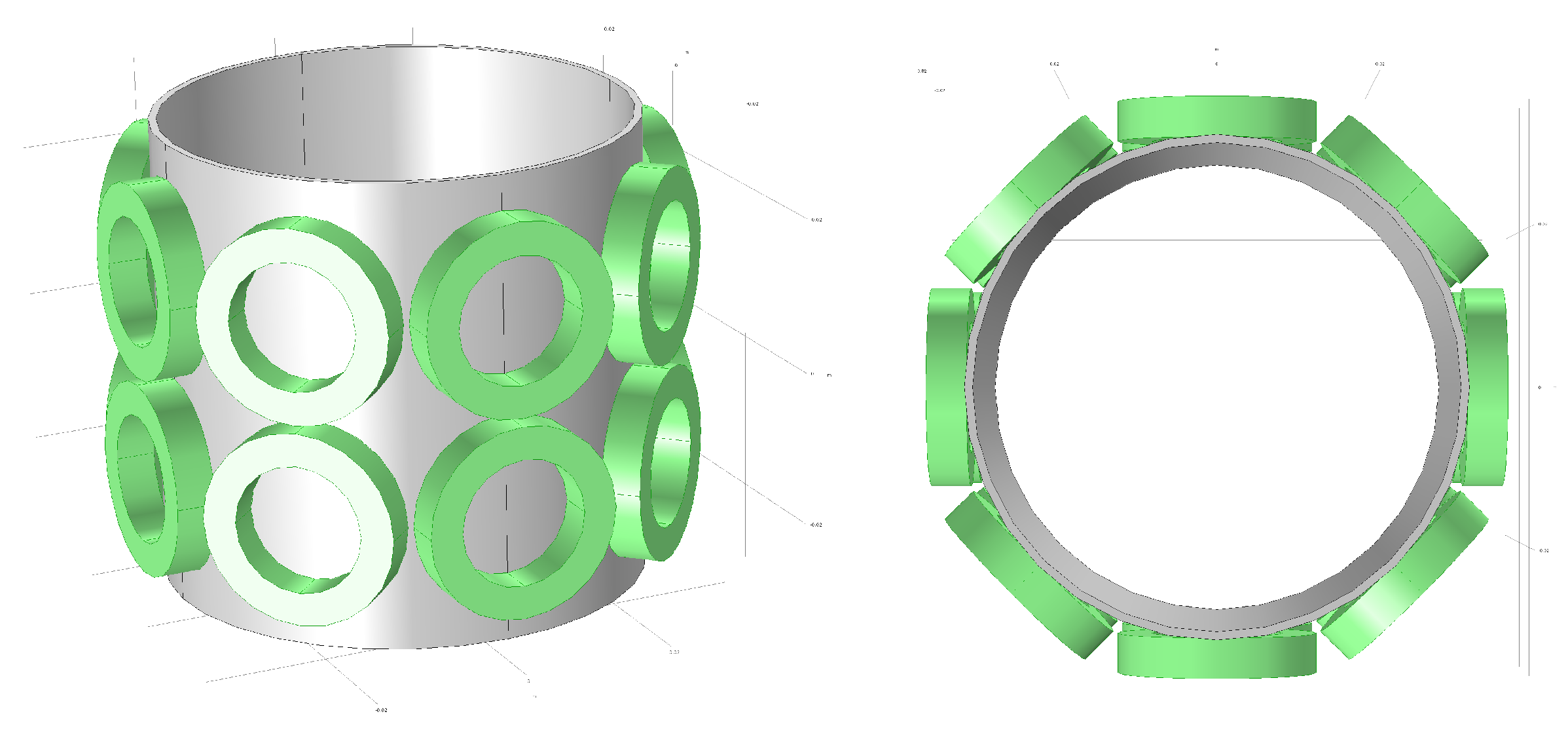
2.2. The 16-Coil 3D EMT Model
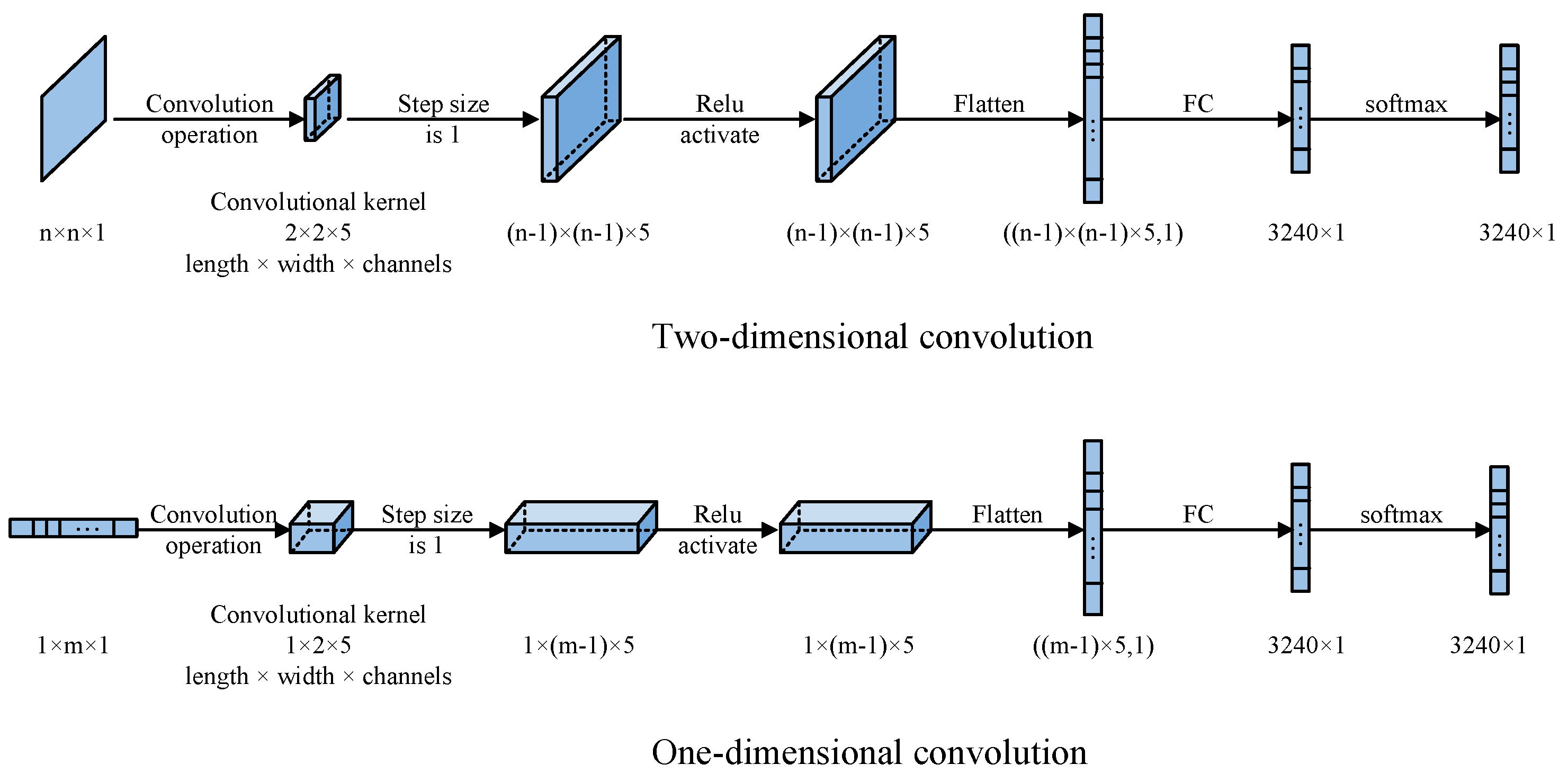
2.3. Convolutional Neural Networks
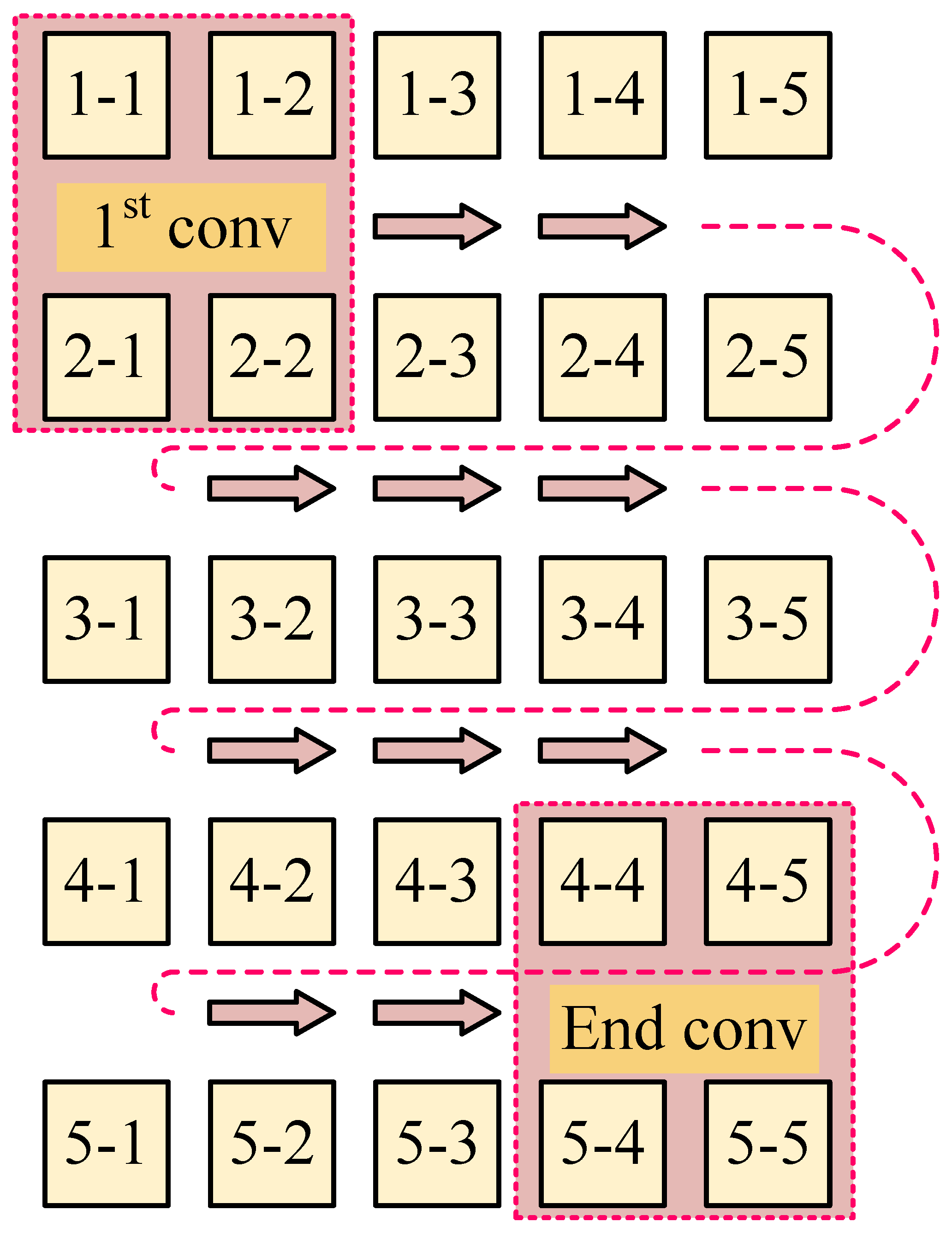
3. The Design of the New Rotational Convolution Pattern
3.1. Comparison of Convolution Patterns
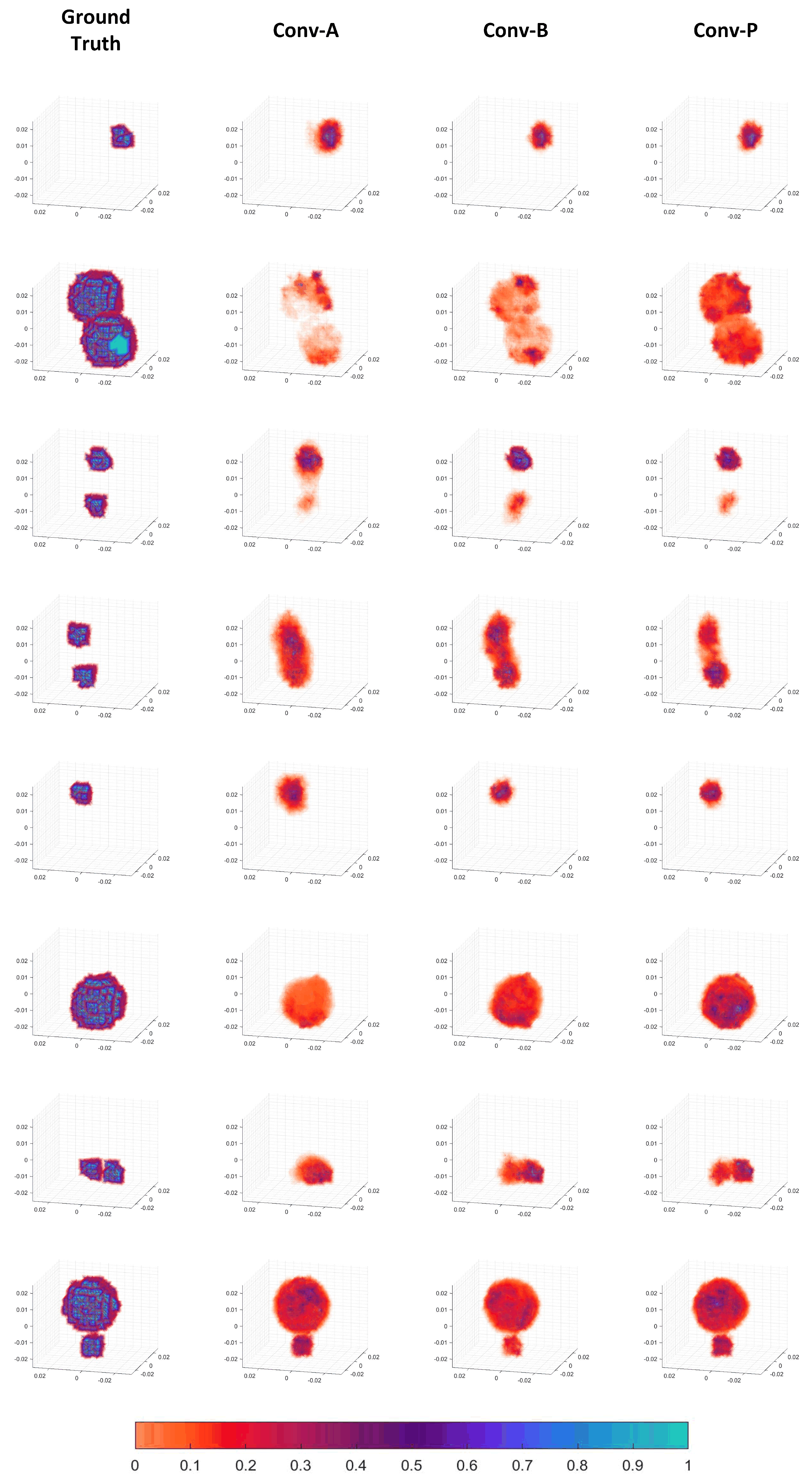
3.2. Reconstructed Images
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, W.; Peyton, A.J. A planar emt system for the detection of faults on thin metallic plates. Meas. Sci. Technol. 2006, 17, 2130. [Google Scholar] [CrossRef]
- Ma, L.; Soleimani, M. Hidden defect identification in carbon fibre reinforced polymer plates using magnetic induction tomography. Meas. Sci. Technol. 2014, 25, 055404. [Google Scholar] [CrossRef]
- Terzija, N.; Yin, W.; Gerbeth, G.; Stefani, F.; Timmel, K.; Wondrak, T.; Peyton, A.J. Use of electromagnetic induction tomography for monitoring liquid metal/gas flow regimes on a model of an industrial steel caster. Meas. Sci. Technol. 2010, 22, 015501. [Google Scholar] [CrossRef]
- Zakaria, Z.; Rahim, R.A.; Mansor, M.S.B.; Yaacob, S.; Ayub, N.M.N.; Muji, S.Z.M.; Rahiman, M.H.F.; Aman, S.M.K.S. Advancements in transmitters and sensors for biological tissue imaging in magnetic induction tomography. Sensors 2012, 12, 7126–7156. [Google Scholar] [CrossRef] [PubMed]
- Peyton, A.J.; Yu, Z.Z.; Lyon, G.; Al-Zeibak, S.; Ferreira, J.; Velez, J.; Linhares, F.; Borges, A.R.; Xiong, H.L.; Saunders, N.H.; et al. An overview of electromagnetic inductance tomography: Description of three different systems. Meas. Sci. Technol. 1996, 7, 261. [Google Scholar] [CrossRef]
- Korjenevsky, A.; Cherepenin, V.; Sapetsky, S. Magnetic induction tomography: Experimental realization. Physiol. Meas. 2000, 21, 89. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Liu, Z.; Xu, L.J.; Xu, L.A. Multi-excitation-mode electromagnetic tomography (emt) system. In Proceedings of the 2nd World Congress on Industrial Process Tomography, Hannover, Germany, 29–31 August 2001; pp. 247–255. [Google Scholar]
- Yin, W.; Chen, G.; Jiang, J.; Cui, Z. The design of a fpga-based digital magnetic induction tomography (mit) system for metallic object imaging. In Proceedings of the 2010 IEEE Instrumentation & Measurement Technology Conference Proceedings, Austin, TX, USA, 3–6 May 2010; pp. 363–366. [Google Scholar]
- Soleimani, M.; Lionheart, W.R.B. Absolute conductivity reconstruction in magnetic induction tomography using a nonlinear method. IEEE Trans. Med Imaging 2006, 25, 1521–1530. [Google Scholar] [CrossRef] [PubMed]
- Palka, R.; Gratkowski, S.; Stawicki, K.; Baniukiewicz, P. The forward and inverse problems in magnetic induction tomography of low conductivity structures. Eng. Comput. 2009, 26, 843–856. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, L.; Soleimani, M. Dual modality ect–mit multi-phase flow imaging. Flow Meas. Instrum. 2015, 46, 240–254. [Google Scholar] [CrossRef]
- Ma, L.; McCann, D.; Hunt, A. Combining magnetic induction tomography and electromagnetic velocity tomography for water continuous multiphase flows. IEEE Sens. J. 2017, 17, 8271–8281. [Google Scholar] [CrossRef]
- Wei, H.; Soleimani, M. Three-dimensional magnetic induction tomography imaging using a matrix free krylov subspace inversion algorithm. Prog. Electromagn. Res. 2012, 122, 29–45. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, R.; Wang, C.; Liu, R. Real-time in vivo magnetic induction tomography in rabbits: A feasibility study. Meas. Sci. Technol. 2020, 32, 035402. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Li, Y.; Zhao, P.; Wang, J. Research on direct 3d electromagnetic tomography technique. IEEE Sens. J. 2020, 20, 4758–4767. [Google Scholar] [CrossRef]
- Soleimani, M.; Lionheart, W.R.B. Image reconstruction in three-dimensional magnetostatic permeability tomography. IEEE Trans. Magn. 2005, 41, 1274–1279. [Google Scholar] [CrossRef]
- Wang, Q.; Li, K.; Zhang, R.; Wang, J.; Sun, Y.; Li, X.; Duan, X.; Wang, H. Sparse defects detection and 3d imaging base on electromagnetic tomography and total variation algorithm. Rev. Sci. Instruments 2019, 90, 124703. [Google Scholar] [CrossRef] [PubMed]
- Klein, M.; Erni, D.; Rueter, D. Three-dimensional magnetic induction tomography: Improved performance for the center regions inside a low conductive and voluminous body. Sensors 2020, 20, 1306. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Liu, X.; Zhang, W.; Liu, R.; Xu, C. Numerical simulations of magnetic induction tomography system based on a 3d head model. Int. J. Appl. Electromagn. Mech. 2022, 70, 377–386. [Google Scholar] [CrossRef]
- Feldkamp, J.R. Single-coil magnetic induction tomographic three-dimensional imaging. J. Med. Imaging 2015, 2, 013502. [Google Scholar] [CrossRef][Green Version]
- Xiao, J.; Liu, Z.; Zhao, P.; Li, Y.; Huo, J. Deep learning image reconstruction simulation for electromagnetic tomography. IEEE Sens. J. 2018, 18, 3290–3298. [Google Scholar] [CrossRef]
- Chen, R.; Huang, J.; Song, Y.; Li, B.; Wang, J.; Wang, H. Deep learning algorithms for brain disease detection with magnetic induction tomography. Med. Phys. 2021, 48, 745–759. [Google Scholar] [CrossRef]
- Xiang, J.; Dong, Y.; Yang, Y. Fista-net: Learning a fast iterative shrinkage thresholding network for inverse problems in imaging. IEEE Trans. Med. Imaging 2021, 40, 1329–1339. [Google Scholar] [CrossRef] [PubMed]
- Vu, M.T.; Jardani, A. Convolutional neural networks with segnet architecture applied to three-dimensional tomography of subsurface electrical resistivity: Cnn-3d-ert. Geophys. J. Int. 2021, 225, 1319–1331. [Google Scholar] [CrossRef]
- Fabijańska, A.; Banasiak, R. Graph convolutional networks for enhanced resolution 3d electrical capacitance tomography image reconstruction. Appl. Soft Comput. 2021, 110, 107608. [Google Scholar] [CrossRef]
- Ye, M.; Zhou, T.; Li, X.; Yang, L.; Liu, K.; Yao, J. U2-net for 3d electrical impedance tomography with combined electrodes. IEEE Sens. J. 2022, 23, 4327–4335. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Tan, C.; Lv, S.; Dong, F.; Takei, M. Image reconstruction based on convolutional neural network for electrical resistance tomography. IEEE Sens. J. 2018, 19, 196–204. [Google Scholar] [CrossRef]
- Zheng, J.; Ma, H.; Peng, L. A cnn-based image reconstruction for electrical capacitance tomography. In Proceedings of the 2019 IEEE International Conference on Imaging Systems and Techniques (IST), Abu Dhabi, United Arab Emirates, 8–10 December 2019; pp. 1–6. [Google Scholar]
- Chen, R.; Zhao, S.; Wu, W.; Sun, Z.; Wang, J.; Wang, H.; Han, G. A convolutional neural network algorithm for breast tumor detection with magnetic detection electrical impedance tomography. Rev. Sci. Instruments 2021, 92, 064701. [Google Scholar] [CrossRef]
- Li, F.; Tan, C.; Dong, F. Electrical resistance tomography image reconstruction with densely connected convolutional neural network. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, B.; Liu, K.; Zhu, C.; Pan, H.; Jia, J.; Wu, H.; Yao, J. Shape reconstruction with multiphase conductivity for electrical impedance tomography using improved convolutional neural network method. IEEE Sens. J. 2021, 21, 9277–9287. [Google Scholar] [CrossRef]
- Kłosowski, G.; Hoła, A.; Rymarczyk, T.; Mazurek, M.; Niderla, K.; Rzemieniak, M. Using machine learning in electrical tomography for building energy efficiency through moisture detection. Energies 2023, 16, 1818. [Google Scholar] [CrossRef]
- Li, X.; Lu, R.; Wang, Q.; Wang, J.; Duan, X.; Sun, Y.; Li, X.; Zhou, Y. One-dimensional convolutional neural network (1d-cnn) image reconstruction for electrical impedance tomography. Rev. Sci. Instruments 2020, 91, 124704. [Google Scholar] [CrossRef] [PubMed]
- Hubel, D.H.; Wiesel, T.N. Receptive fields of single neurones in the cat’s striate cortex. J. Physiol. 1959, 148, 574. [Google Scholar] [CrossRef] [PubMed]
- Radon, J. On the determination of functions from their integral values along certain manifolds. IEEE Trans. Med. Imaging 1986, 5, 170–176. [Google Scholar] [CrossRef] [PubMed]
| Train Set | CC | IE | PSNR (dB) | SSIM |
| Conv-A | 0.7840 | 0.7685 | 18.0234 | 0.8397 |
| Conv-B | 0.8006 | 0.6927 | 18.4263 | 0.8624 |
| Conv-P | 0.8438 | 0.5721 | 18.7501 | 0.8702 |
| Test Set | CC | IE | PSNR (dB) | SSIM |
| Conv-A | 0.7689 | 0.7974 | 18.0841 | 0.8422 |
| Conv-B | 0.7735 | 0.7363 | 18.2479 | 0.8631 |
| Conv-P | 0.8052 | 0.6398 | 18.3705 | 0.8695 |
| p (Conv-A, Conv-B) | p (Conv-A, Conv-P) | p (Conv-B, Conv-P) |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Liu, Z. Rotational Convolution Design in Convolutional Neural Networks for Direct 3D Electromagnetic Tomography. Appl. Sci. 2024, 14, 3182. https://doi.org/10.3390/app14083182
Zhao P, Liu Z. Rotational Convolution Design in Convolutional Neural Networks for Direct 3D Electromagnetic Tomography. Applied Sciences. 2024; 14(8):3182. https://doi.org/10.3390/app14083182
Chicago/Turabian StyleZhao, Pengfei, and Ze Liu. 2024. "Rotational Convolution Design in Convolutional Neural Networks for Direct 3D Electromagnetic Tomography" Applied Sciences 14, no. 8: 3182. https://doi.org/10.3390/app14083182
APA StyleZhao, P., & Liu, Z. (2024). Rotational Convolution Design in Convolutional Neural Networks for Direct 3D Electromagnetic Tomography. Applied Sciences, 14(8), 3182. https://doi.org/10.3390/app14083182






