Noise Differentiation and Atom Number Measurement in Optical Lattice Clocks by Analyzing Clock Stabilities with Various Parameters
Abstract
1. Introduction
2. Methods
2.1. Theory
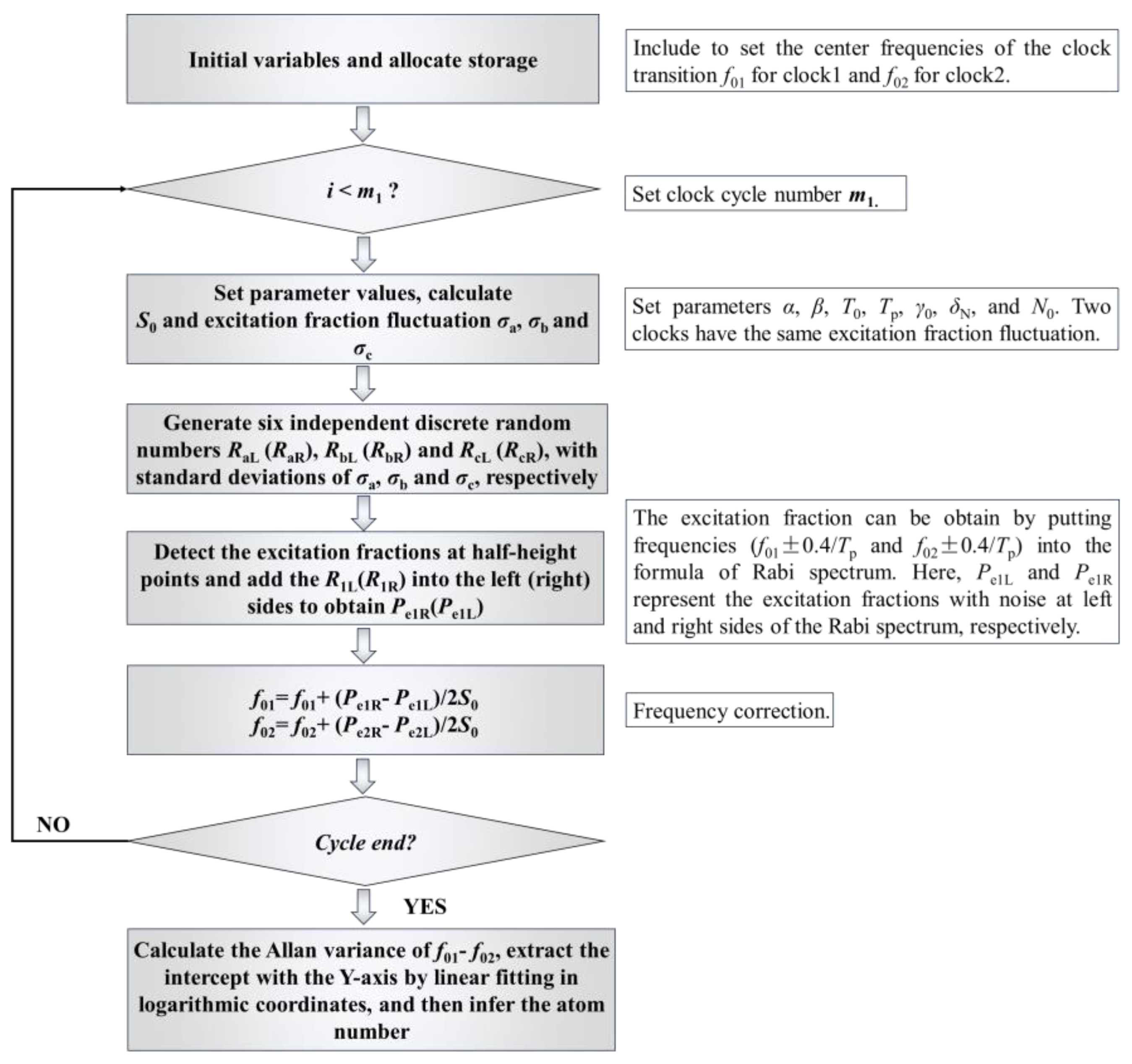
2.2. Numerical Simulation Method
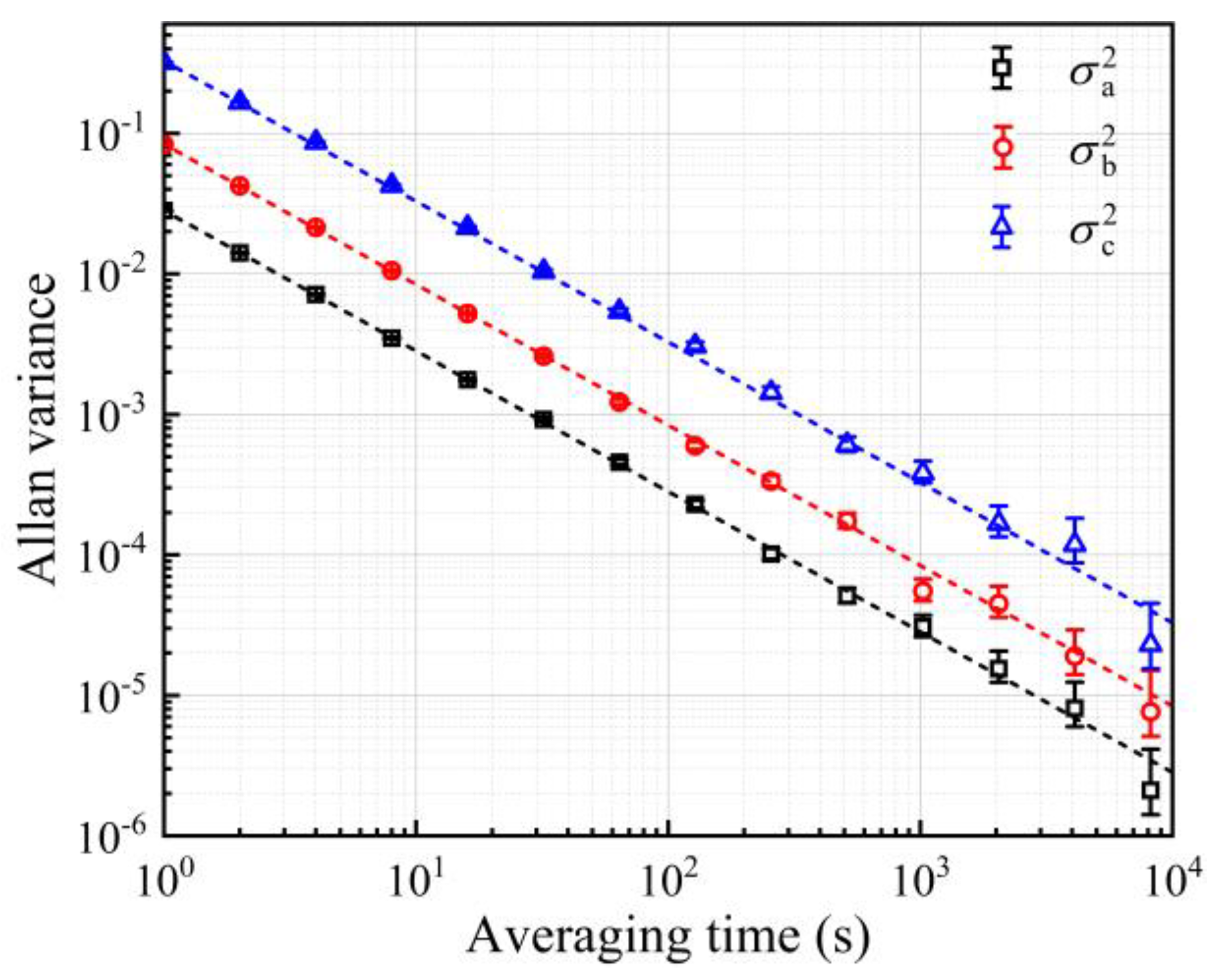
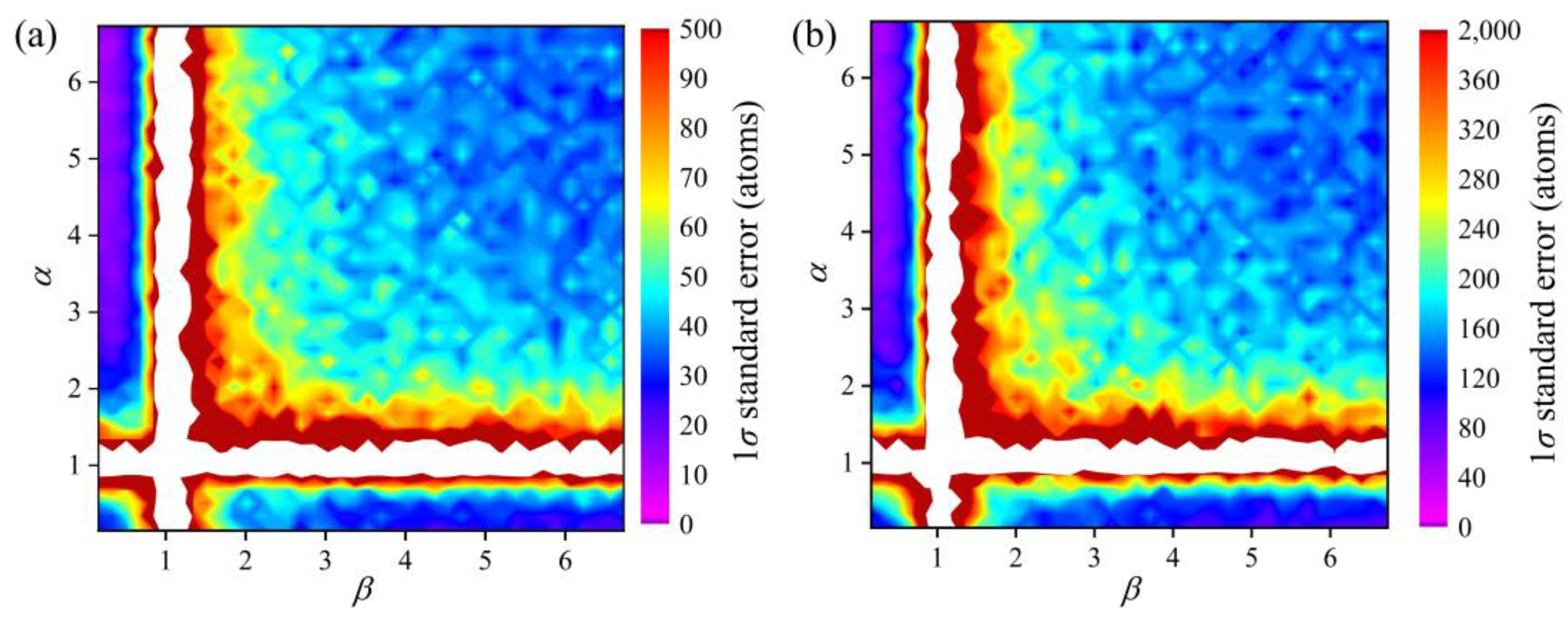
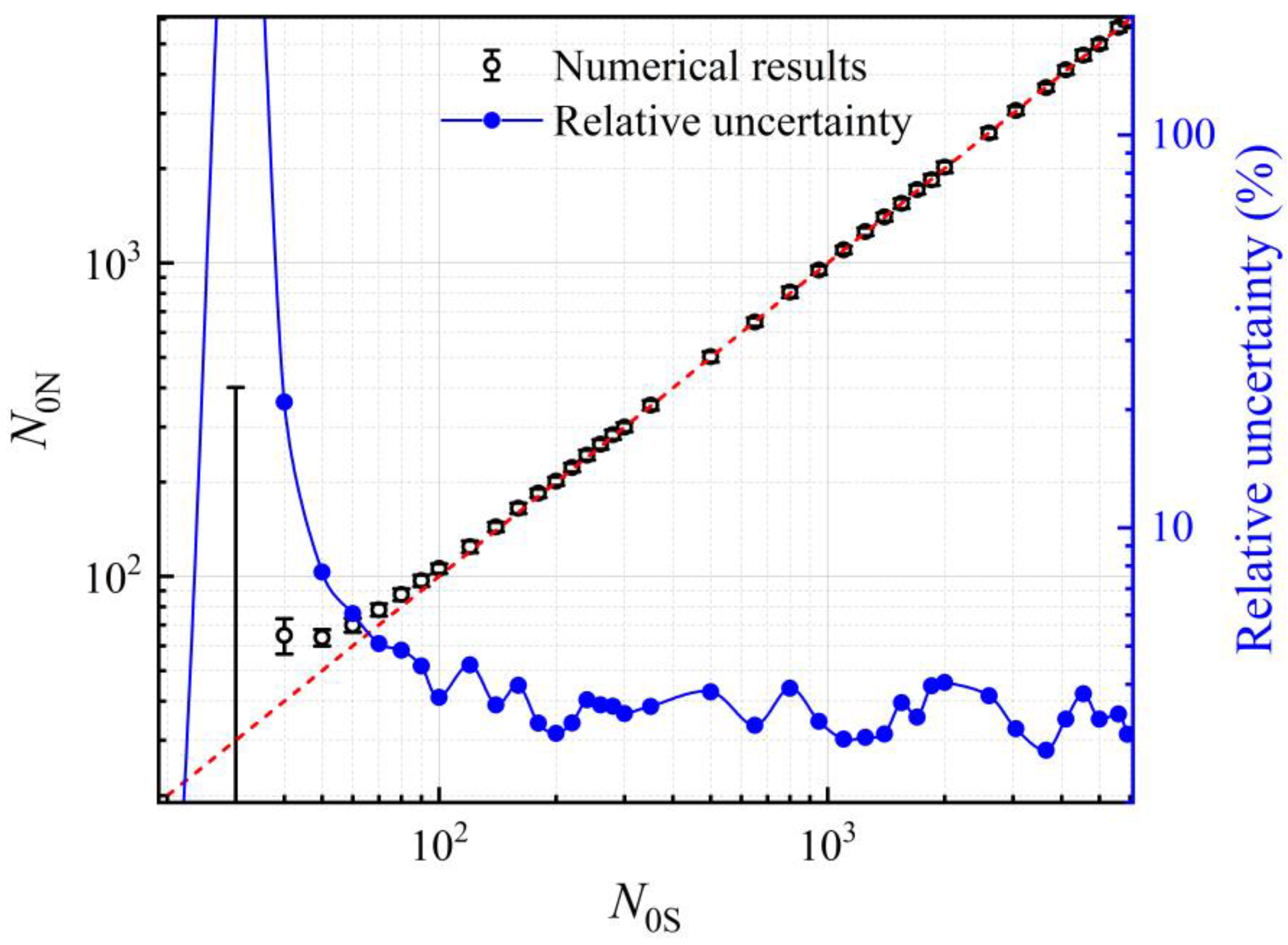
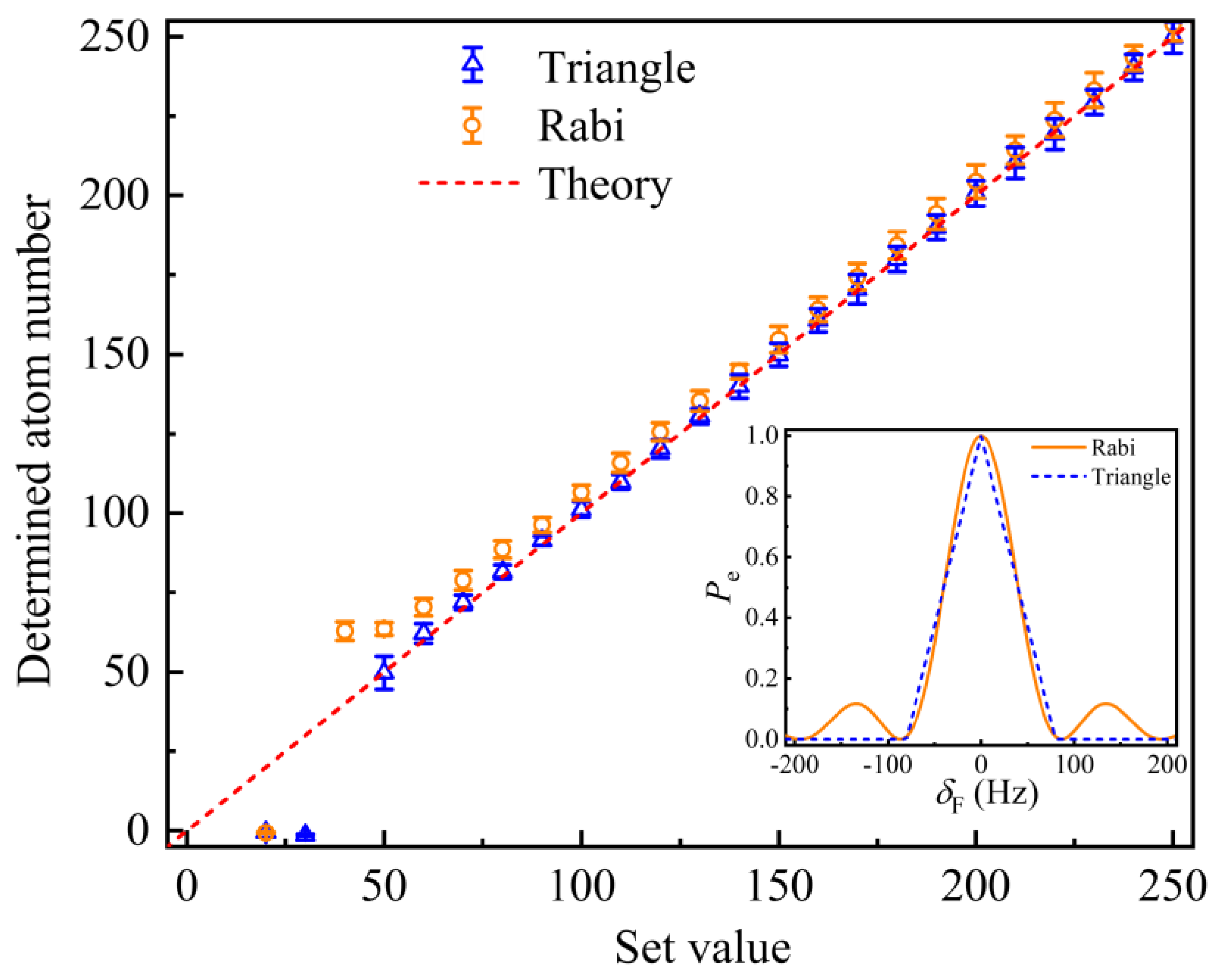
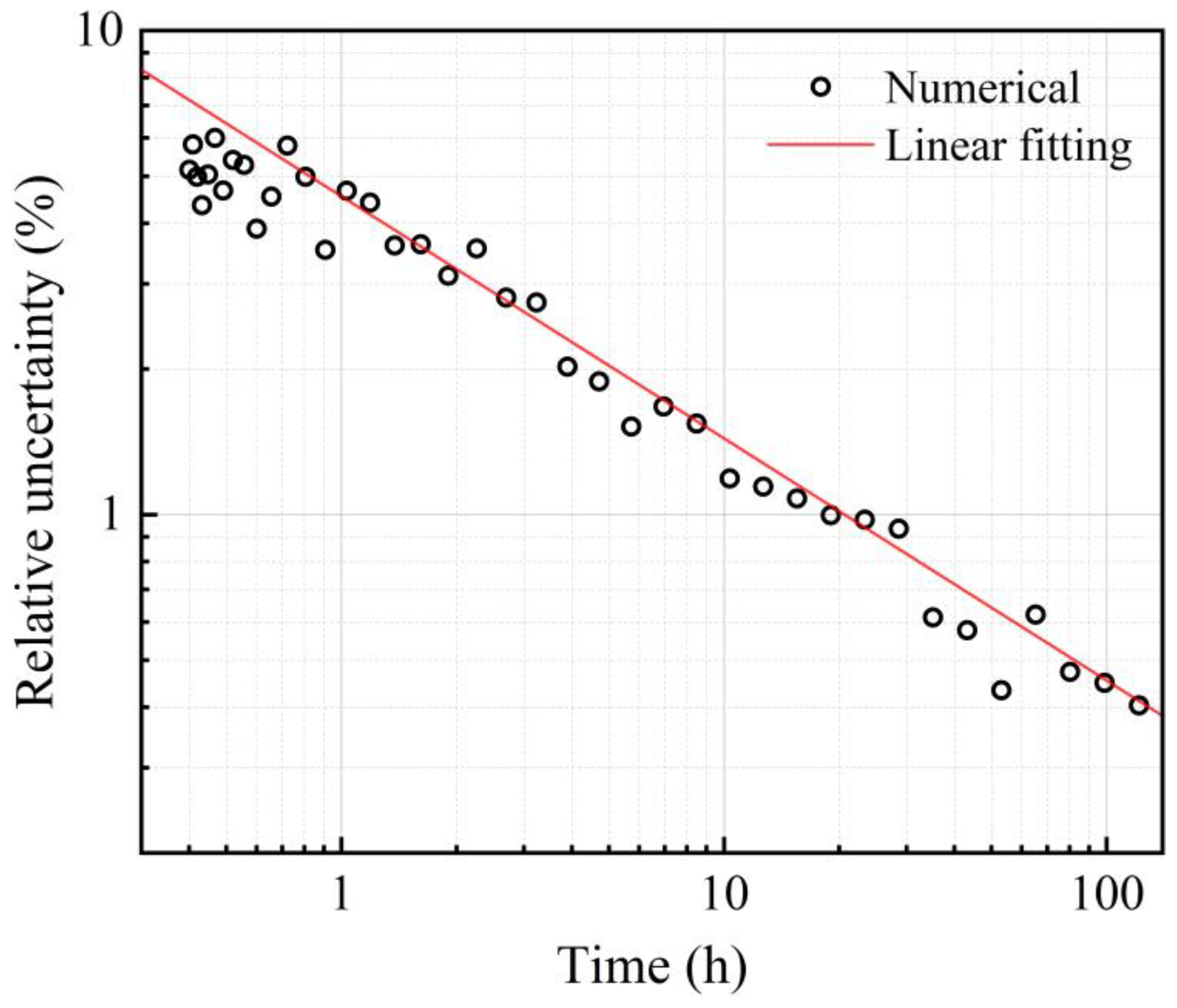
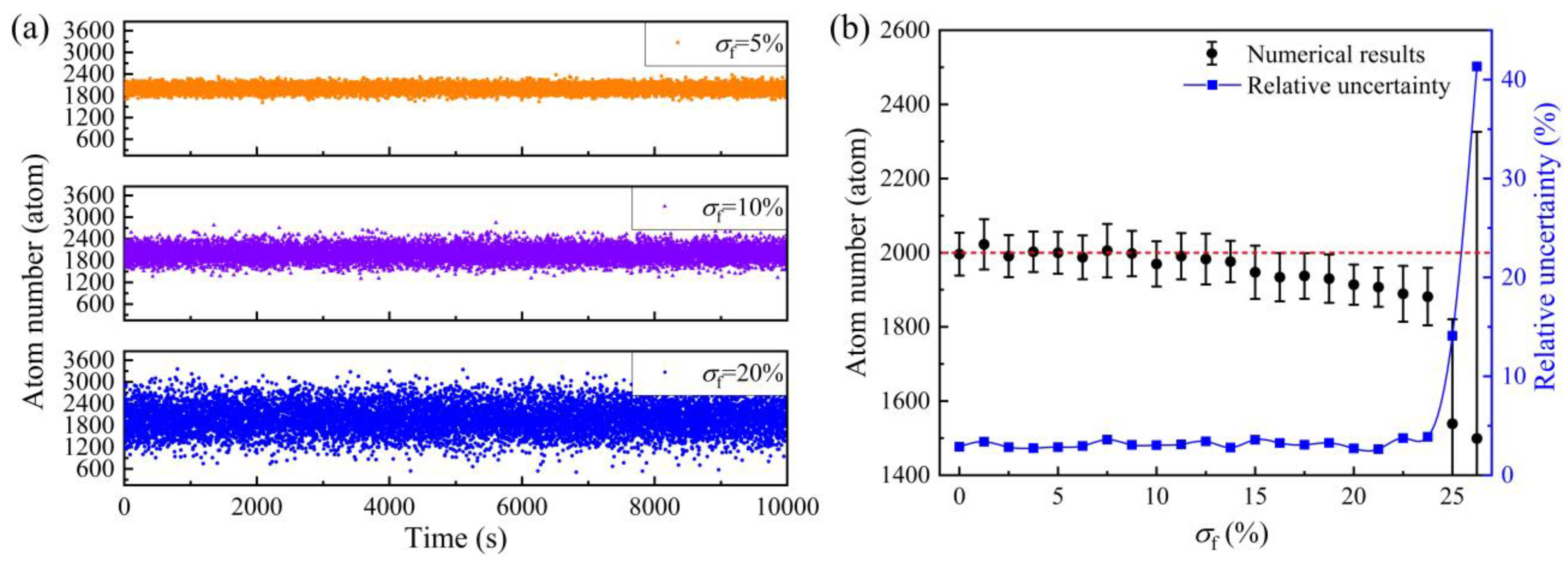
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bothwell, T.; Kedar, D.; Oelker, E.; Robinson, J.M.; Bromley, S.L.; Tew, W.L.; Ye, J.; Kennedy, C.J. JILA SrI optical lattice clock with uncertainty of 2.0 × 10−18. Metrologia 2019, 56, 065004. [Google Scholar] [CrossRef]
- McGrew, W.F.; Zhang, X.R.; Fasano, J.S.; Schäffer, A.; Beloy, K.; Nicolodi, D.; Brown, R.C.; Hinkley, N.; Milani, G.; Schioppo, M.; et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 2018, 564, 87. [Google Scholar] [CrossRef] [PubMed]
- Brewer, S.M.; Chen, J.S.; Hankin, A.M.; Clements, E.R.; Chou, C.W.; Wineland, D.J.; Hume, D.B.; Leibrandt, D.R. 27Al+ quantum-logic clock with a systematic uncertainty below 10−18. Phys. Rev. Lett. 2019, 123, 033201. [Google Scholar] [CrossRef]
- Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995. [Google Scholar] [CrossRef] [PubMed]
- Nunn, J.; Dorner, U.; Michelberger, P.K.; Lee, C.; Langford, N.K.; Walmsley, I.A.; Jaksch, D. Quantum memory in an optical lattice. Phys. Rev. A 2010, 82, 022327. [Google Scholar] [CrossRef]
- Daley, A.J.; Boyd, M.M.; Ye, J.; Zoller, P. Quantum computing with Alkaline-earth-metal atoms. Phys. Rev. Lett. 2008, 101, 170504. [Google Scholar] [CrossRef] [PubMed]
- Yin, M.J.; Lu, X.T.; Li, T.; Xia, J.J.; Wang, T.; Zhang, X.F.; Chang, H. Floquet engineering Hz-level Rabi spectra in shallow optical lattice clock. Phys. Rev. Lett. 2022, 128, 073603. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.T.; Wang, T.; Li, T.; Zhou, C.H.; Yin, M.J.; Wang, Y.B.; Zhang, X.F.; Chang, H. Doubly modulated optical lattice clock: Interference and topology. Phys. Rev. Lett. 2021, 127, 033601. [Google Scholar] [CrossRef]
- Schwarz, R.; Dörscher, S.; Al-Masoudi, A.; Benkler, E.; Legero, T.; Sterr, U.; Weyers, S.; Rahm, J.; Lipphardt, B.; Lisdat, C. Long term measurement of the 87Sr clock frequency at the limit of primary Cs clocks. Phys. Rev. Res. 2020, 2, 033242. [Google Scholar] [CrossRef]
- Takamoto, M.; Ushijima, I.; Ohmae, N.; Yahagi, T.; Kokado, K.; Shinkai, H.; Katori, H. Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photon. 2020, 14, 411. [Google Scholar] [CrossRef]
- Miyake, H.; Pisenti, N.C.; Elgee, P.K.; Sitaram, A.; Campbell, G.K. Isotope-shift spectroscopy of the 1S0→3P1 and 1S0→3P0 transitions in strontium. Phys. Rev. Res. 2019, 1, 033113. [Google Scholar] [CrossRef]
- Kennedy, C.J.; Oelker, E.J.; Robinson, M.; Bothwell, T.; Kedar, D.; Milner, W.R.; Marti, G.E.; Derevianko, A.; Ye, J. Precision metrology meets cosmology: Improved constraints on ultralight dark matter from atom-cavity frequency comparisons. Phys. Rev. Lett. 2020, 125, 201302. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Zhang, X.F.; Wang, T. Density shift of optical lattice clocks via the multiband sampling exact diagonalization method. Phys. Rev. A 2023, 108, 033304. [Google Scholar] [CrossRef]
- Rey, A.M.; Gorshkov, V.C.A.; Kraus, V.M.; Martin, J.; Bishof, M.; Swallows, M.D.; Zhang, X.; Benko, C.; Ye, J.; Lemke, N.D.; et al. Probing many-body interactions in an optical lattice clock. Ann. Phys. 2014, 340, 311. [Google Scholar] [CrossRef][Green Version]
- Gregor, O.K.; Melina, P.; Gustav, W.; Mark, B.; Olivier, M.; Wolf, K. Atom number calibration in absorption imaging at very small atom numbers. Cent. Eur. J. Phys. 2012, 10, 1054. [Google Scholar]
- Reinaudi, G.; Lahaye, T.; Wang, Z.; Guery-Odelin, D. Strong saturation absorption imaging of dense clouds of ultracold atoms. Opt. Lett. 2007, 32, 3143. [Google Scholar] [CrossRef]
- Hueck, K.; Luick, N.; Sobirey, L.; Siegl, J.; Lompe, T.; Moritz, H.; Clark, L.W.; Chin, C. Calibrating high intensity absorption imaging of ultracold atoms. Opt. Express 2017, 25, 8670. [Google Scholar] [CrossRef]
- Bothwell, T.; Kennedy, C.J.; Aeppli, A.; Robinson, J.M.; Oelker, E.; Staron, A.; Ye, J. Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature 2022, 602, 420. [Google Scholar] [CrossRef]
- Aeppli, A.; Chu, A.J.; Bothwell, T.; Kennedy, C.J.; Kedar, D.; He, P.; Rey, A.M.; Ye, J. Hamiltonian engineering of spin-orbit-coupled fermions in a Wannier-Stark optical lattice clock. Sci. Adv. 2022, 8, eadc9242. [Google Scholar] [CrossRef]
- Santarelli, G.; Laurent, P.; Lemonde, P.; Clairon, A.; Mann, A.G.; Chang, S.; Luiten, A.N.; Salomon, C. Quantum projection noise in an atomic fountain: A high stability cesium frequency standard. Phys. Rev. Lett. 1999, 82, 4619. [Google Scholar] [CrossRef]
- Al-Masoudi, A.; Dörscher, S.; Häfner, S.; Sterr, U.; Lisdat, C. Noise and instability of an optical lattice clock. Phys. Rev. A 2015, 92, 063814. [Google Scholar] [CrossRef]
- Lu, X.T.; Xia, J.J.; Lu, B.Q.; Wang, Y.B.; Wang, T.; Chang, H. Determining the atom number from detection noise in a one-dimensional optical lattice clock. Appl. Phys. Lett. 2022, 120, 151104. [Google Scholar] [CrossRef]
- Takamoto, M.; Takano, T.; Katori, H. Frequency comparison of optical lattice clocks beyond the Dick limit. Nat. Photon. 2011, 5, 288. [Google Scholar] [CrossRef]
- Lu, X.T.; Zhou, C.H.; Li, T.; Wang, Y.B.; Chang, H. Synchronous frequency comparison beyond the Dick limit based on dual-excitation spectrum in an optical lattice clock. Appl. Phys. Lett. 2020, 117, 231101. [Google Scholar] [CrossRef]
- Campbell, S.L.; Hutson, R.B.; Marti, G.E.; Goban, A.; Darkwah Oppong, N.; McNally, R.L.; Sonderhouse, L.; Robinson, J.M.; Zhang, W.; Bloom, B.J.; et al. A Fermi-degenerate three-dimensional optical lattice clock. Science 2017, 358, 90. [Google Scholar] [CrossRef]
- Lemonde, P.; Laurent, P.; Santarelli, G.; Abgrall, M.; Sortais, Y.; Bize, S.; Nicolas, C.; Zhang, S.; Clairon, A.; Dimarcq, N.; et al. Frequency Measurement and Control: Advanced Techniques and Future Trends; Springer: Berlin/Heidelberg, Germany, 2001; Volume 79, pp. 131–153. [Google Scholar]
- Dick, G.J. Local oscillator induced instabilities in trapped ion frequency standards. In Proceedings of the 19th Annual Precise Time and Time Interval Meeting, Redendo Beach, CA, USA, 1–3 December 1987; pp. 133–147. [Google Scholar]
- Nicholson, T.L.; Martin, M.J.; Williams, J.R.; Bloom, B.J.; Bishof, M.M.; Swallows, D.; Campbell, S.L.; Ye, J. Comparison of two independent Sr optical clocks with 1 × 10−17 stability at 103 s. Phys. Rev. Lett. 2012, 109, 230801. [Google Scholar] [CrossRef]
- Wang, Y.B.; Yin, M.J.; Ren, J.; Xu, Q.F.; Lu, B.Q.; Han, J.X.; Guo, Y.; Chang, H. Strontium optical lattice clock at the National Time Service Center. Chin. Phys. B 2018, 27, 023701. [Google Scholar] [CrossRef]
- Orenes, D.B.; Sewell, R.J.; Lodewyck, J.; Mitchell, M.W. Improving short-term stability in optical lattice clocks by quantum nondemolition measurement. Phys. Rev. Lett. 2020, 128, 153201. [Google Scholar] [CrossRef]
- Pedrozo-Peñafie, E.; Colombo, S.; Shu, C.; Adiyatullin, A.F.; Li, Z.Y.; Mendez, E.; Braverman, B.; Kawasaki, A.; Akamatsu, D.; Xiao, Y.H.; et al. Entanglement on an optical atomic-clock transition. Nature 2020, 588, 414. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Guo, F.; Lu, X.; Chang, H. Noise Differentiation and Atom Number Measurement in Optical Lattice Clocks by Analyzing Clock Stabilities with Various Parameters. Appl. Sci. 2024, 14, 1758. https://doi.org/10.3390/app14051758
Zhao G, Guo F, Lu X, Chang H. Noise Differentiation and Atom Number Measurement in Optical Lattice Clocks by Analyzing Clock Stabilities with Various Parameters. Applied Sciences. 2024; 14(5):1758. https://doi.org/10.3390/app14051758
Chicago/Turabian StyleZhao, Guodong, Feng Guo, Xiaotong Lu, and Hong Chang. 2024. "Noise Differentiation and Atom Number Measurement in Optical Lattice Clocks by Analyzing Clock Stabilities with Various Parameters" Applied Sciences 14, no. 5: 1758. https://doi.org/10.3390/app14051758
APA StyleZhao, G., Guo, F., Lu, X., & Chang, H. (2024). Noise Differentiation and Atom Number Measurement in Optical Lattice Clocks by Analyzing Clock Stabilities with Various Parameters. Applied Sciences, 14(5), 1758. https://doi.org/10.3390/app14051758





