Full-Wavefield Migration Using an Imaging Condition of Global Normalization Multi-Order Wavefields: Application to a Synthetic Dataset
Abstract
1. Introduction
2. Methods
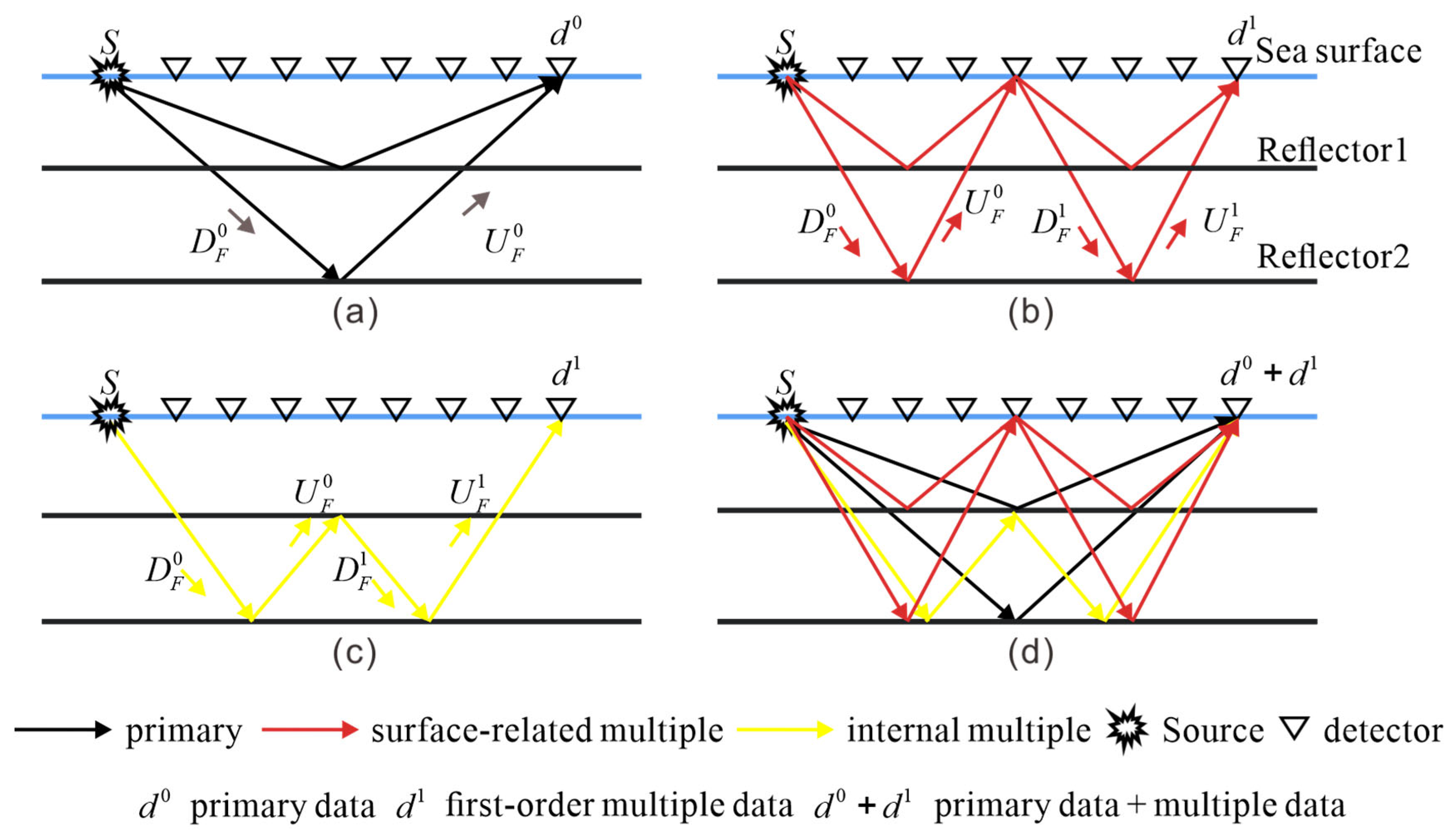
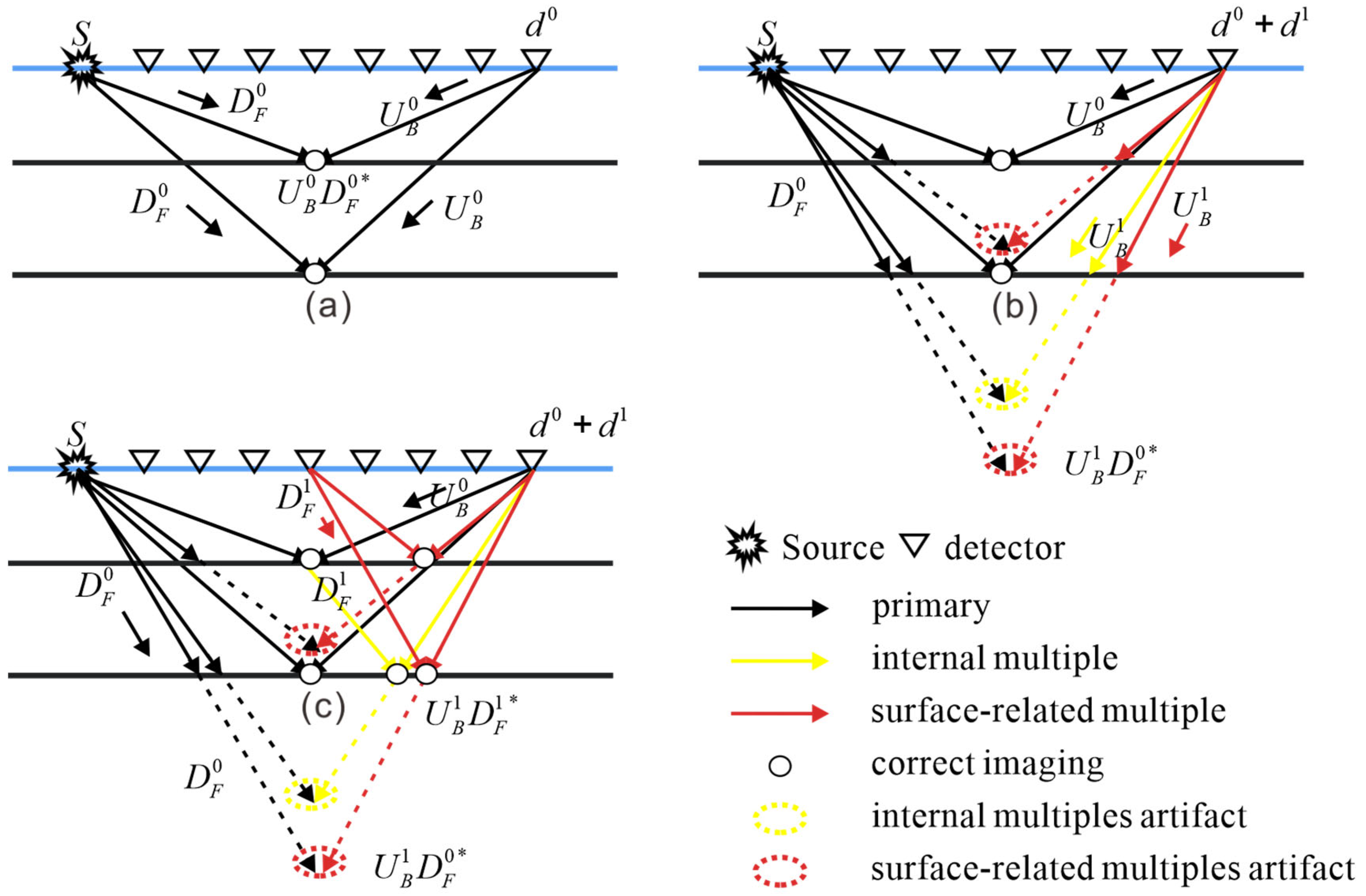
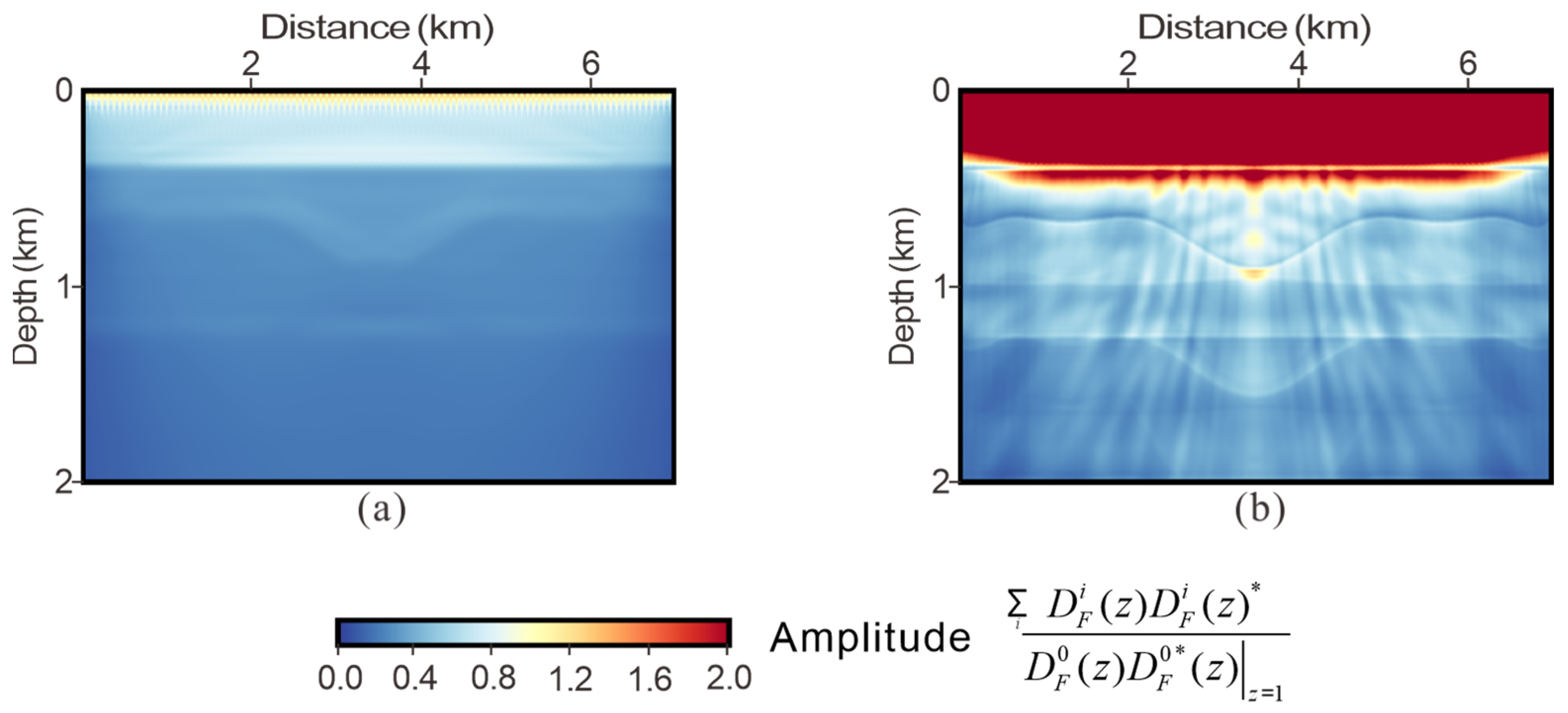
2.1. Different-Order Multiple Crosstalk Artifacts and Illumination Analysis
2.2. Multi-Order Wavefield Global Normalization Imaging Condition
2.3. Full-Wavefield Least-Squares Migration Imaging
3. Results
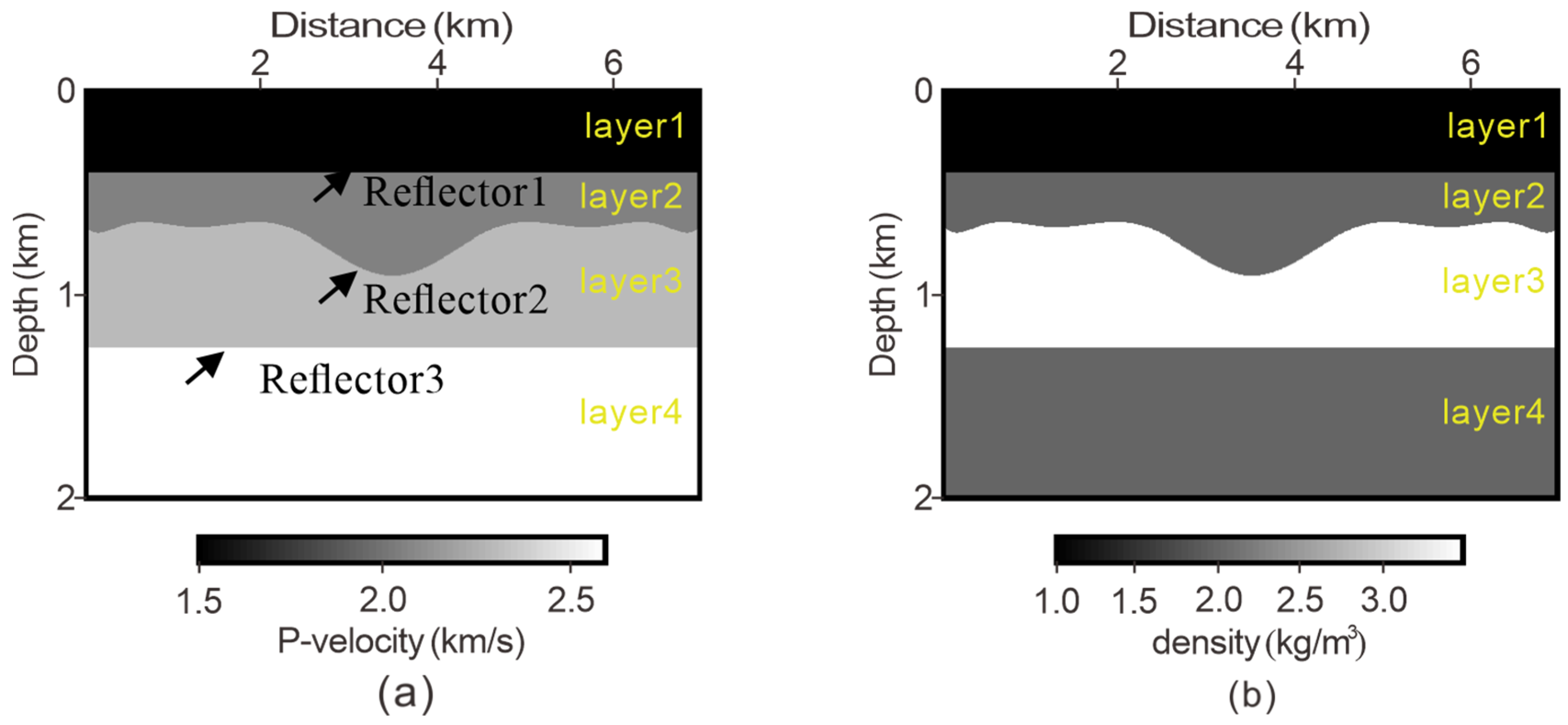
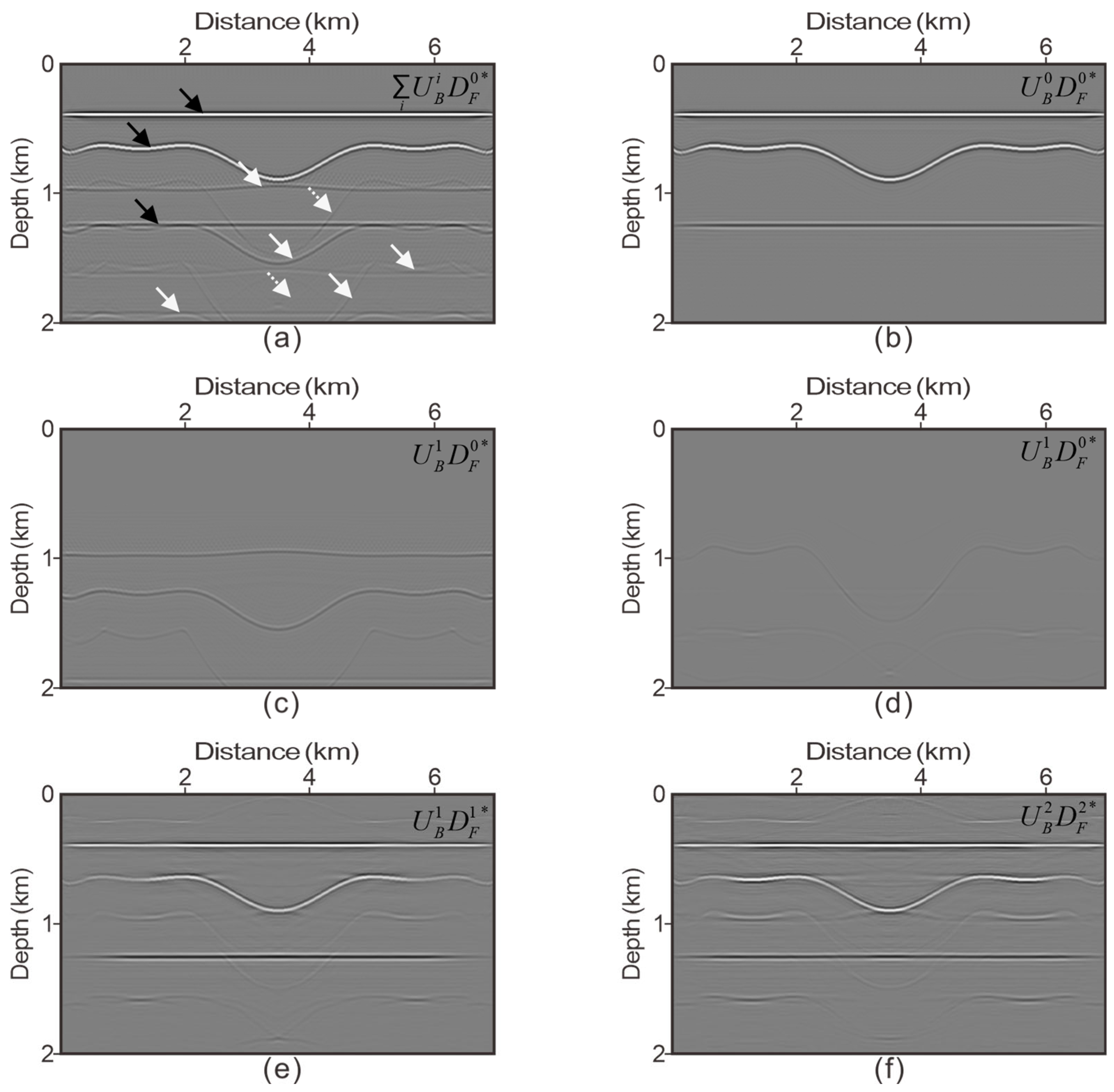
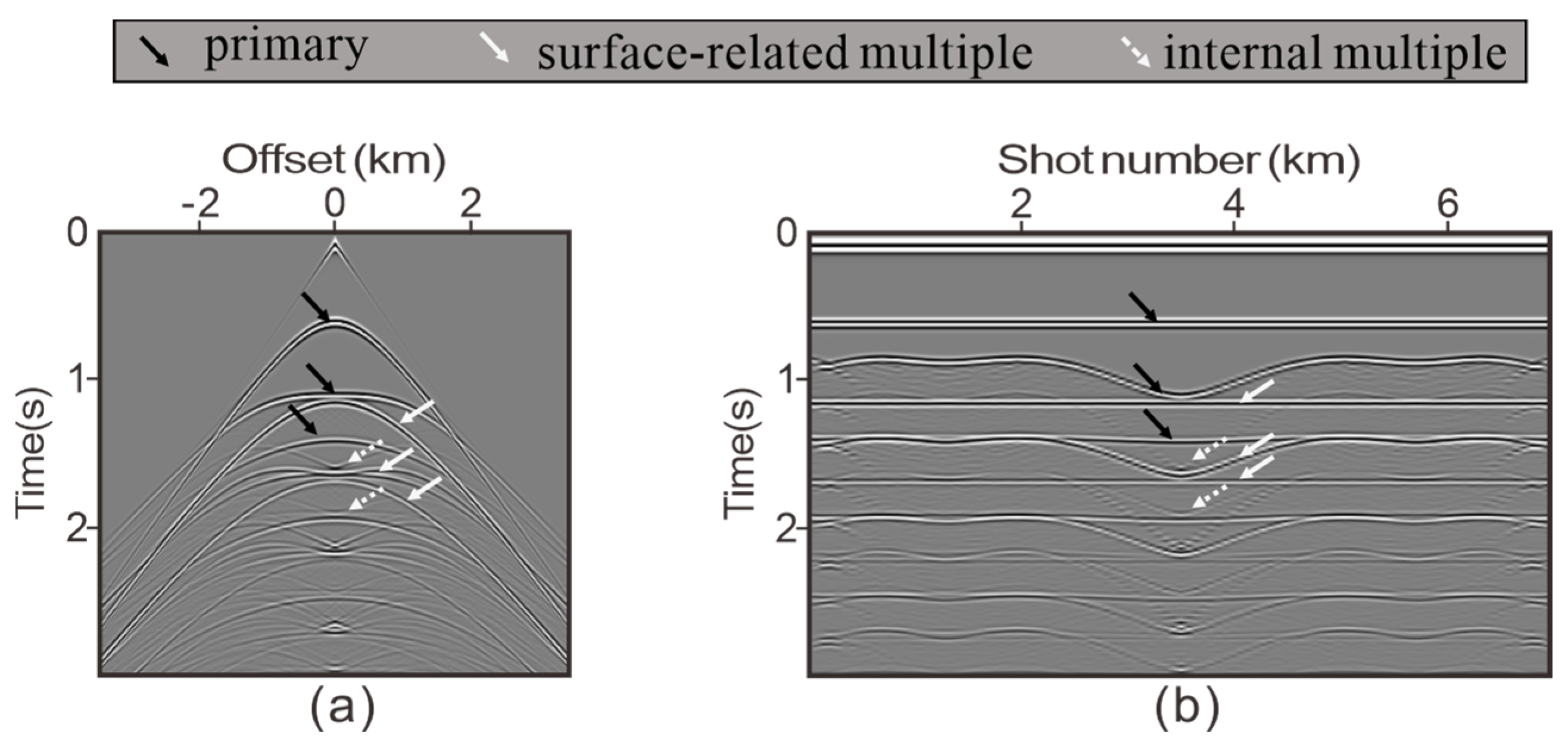
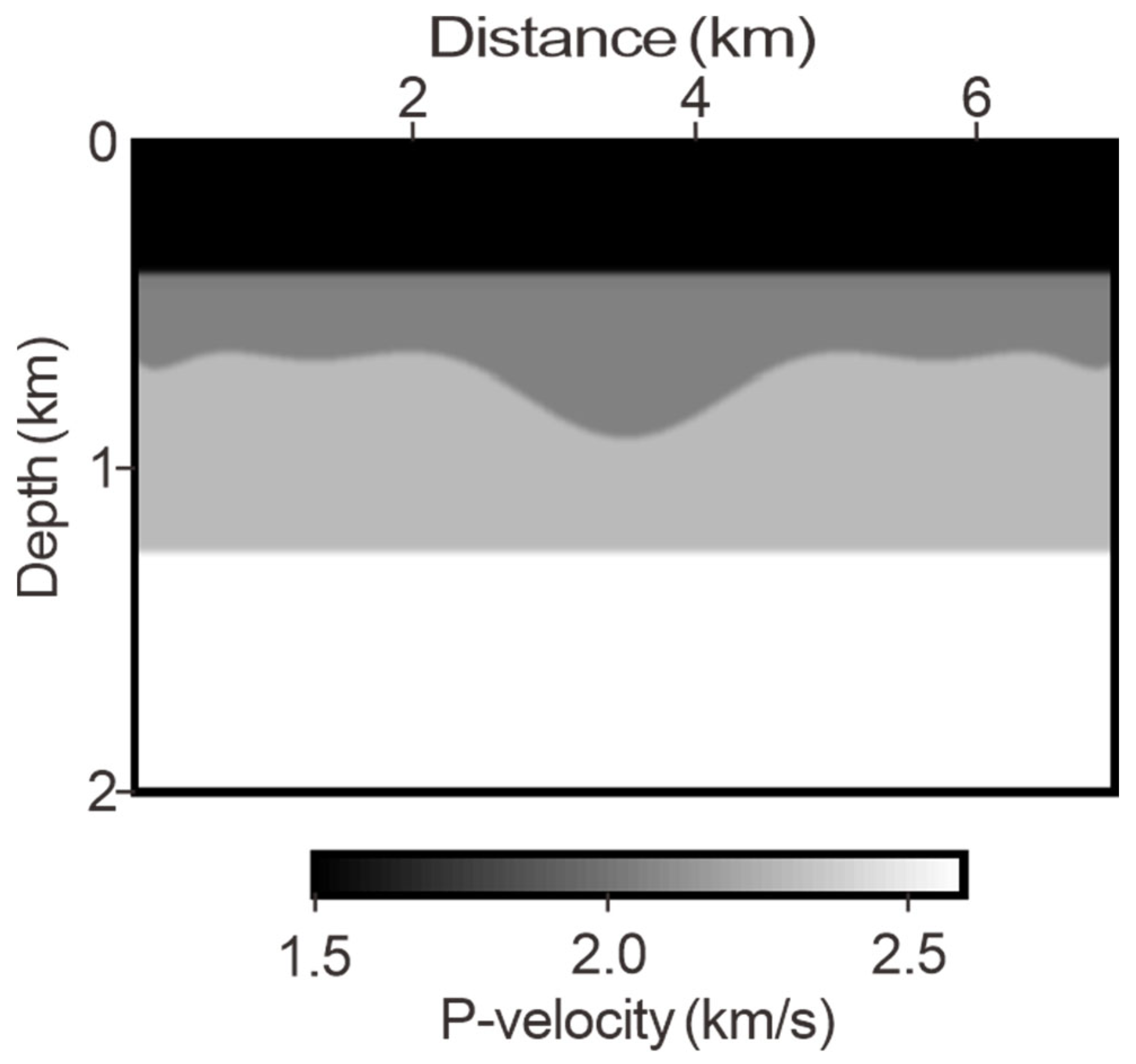
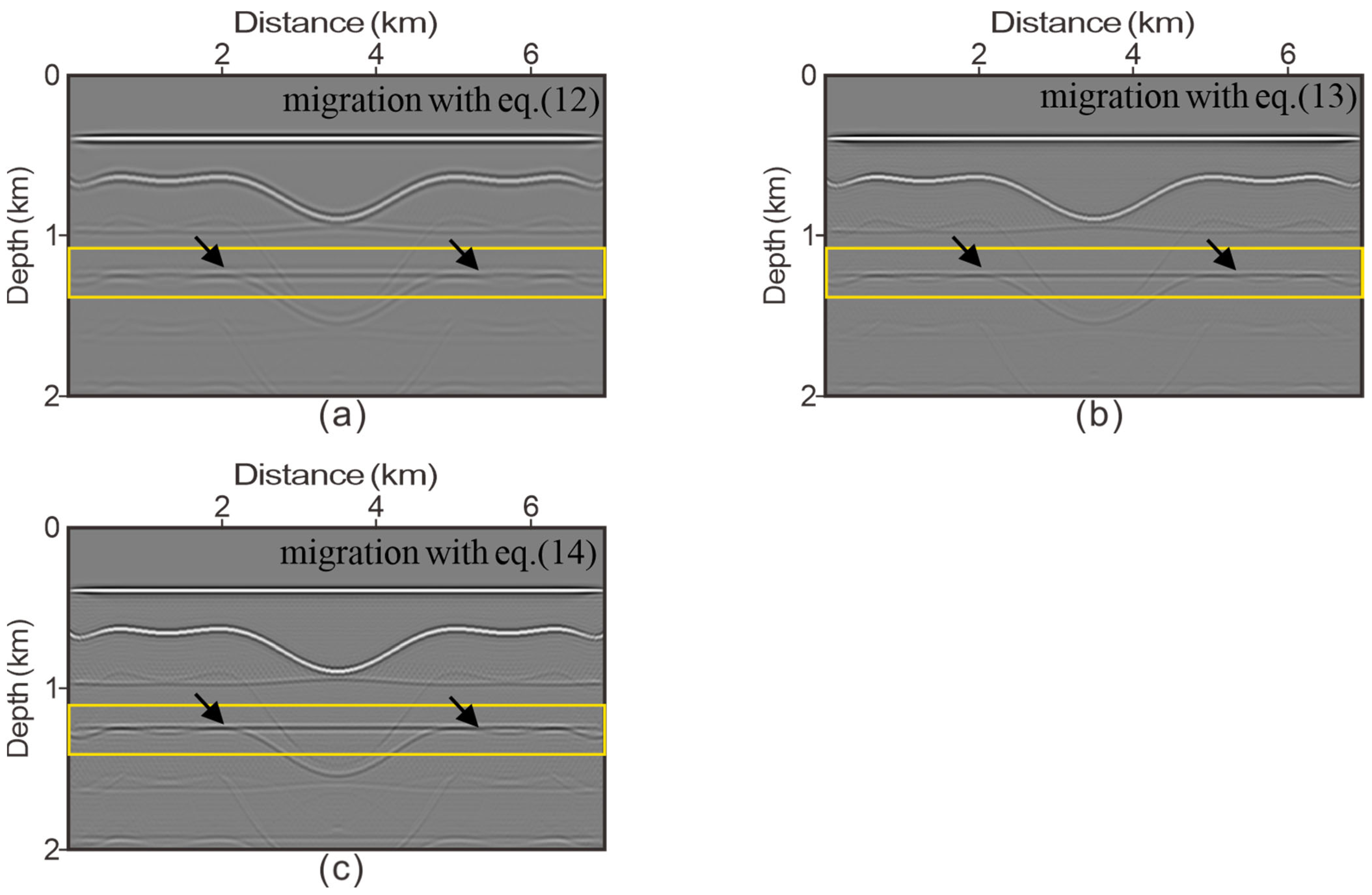
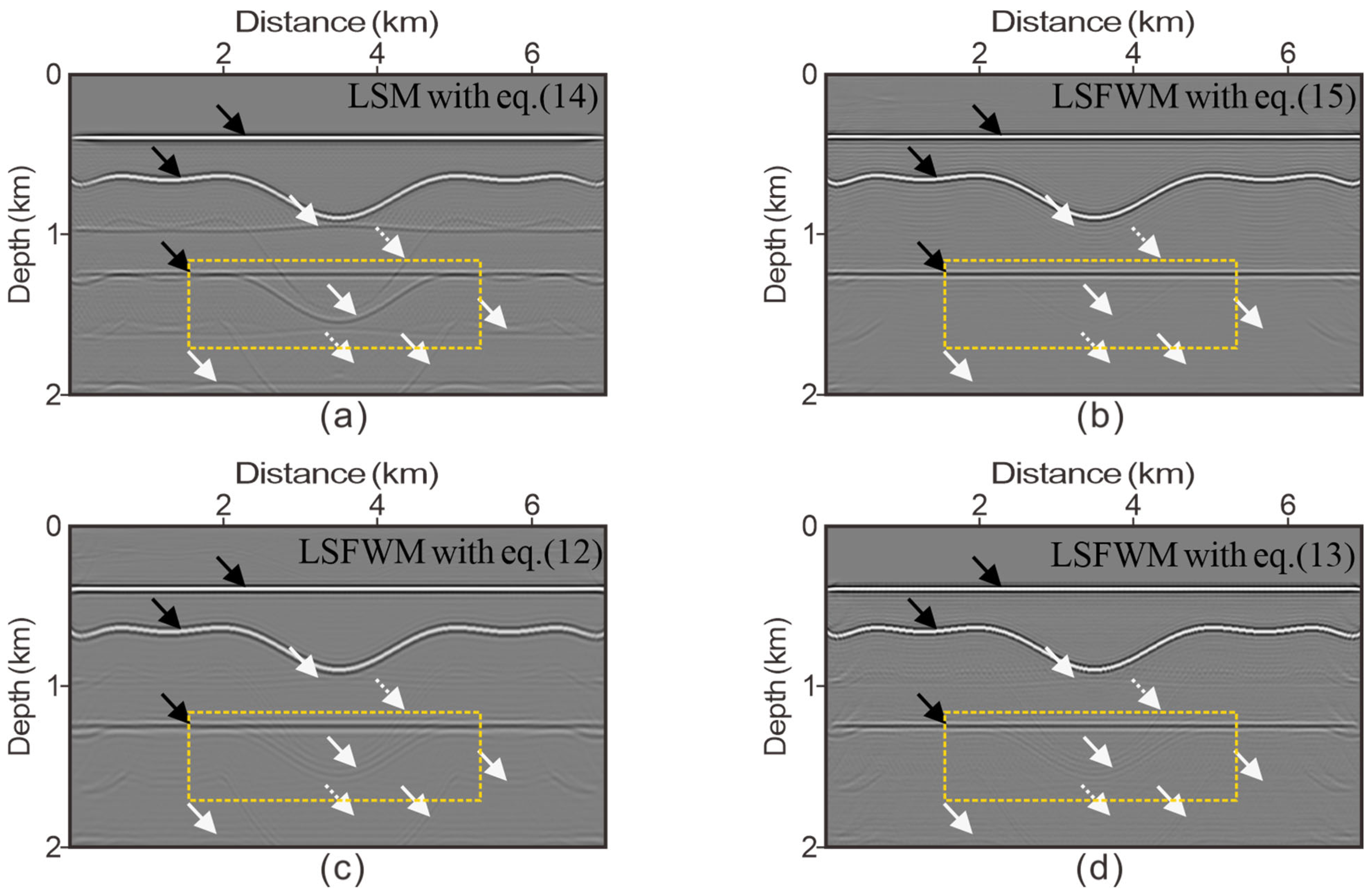
3.1. Four-Layer Model: Finite Difference Data
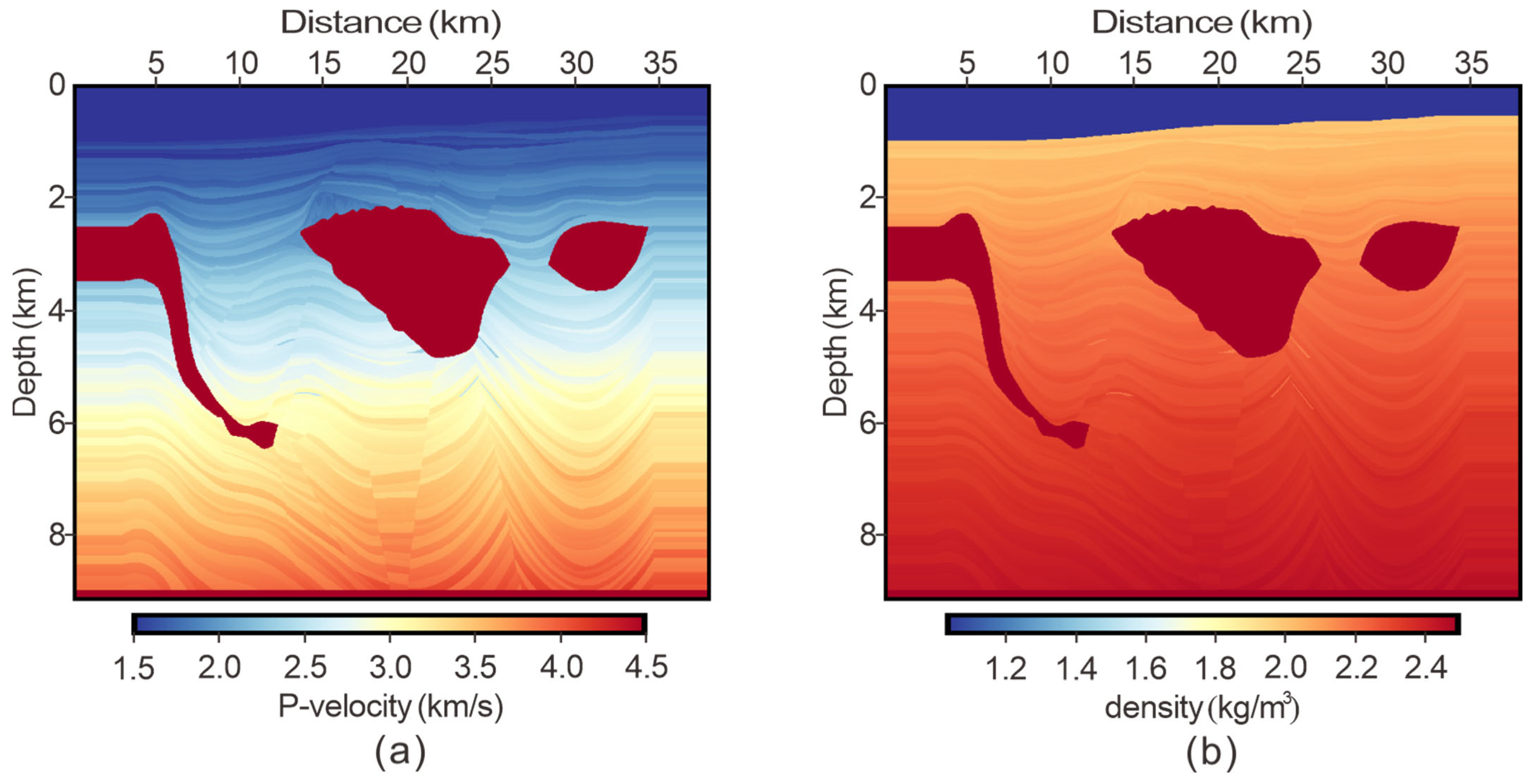
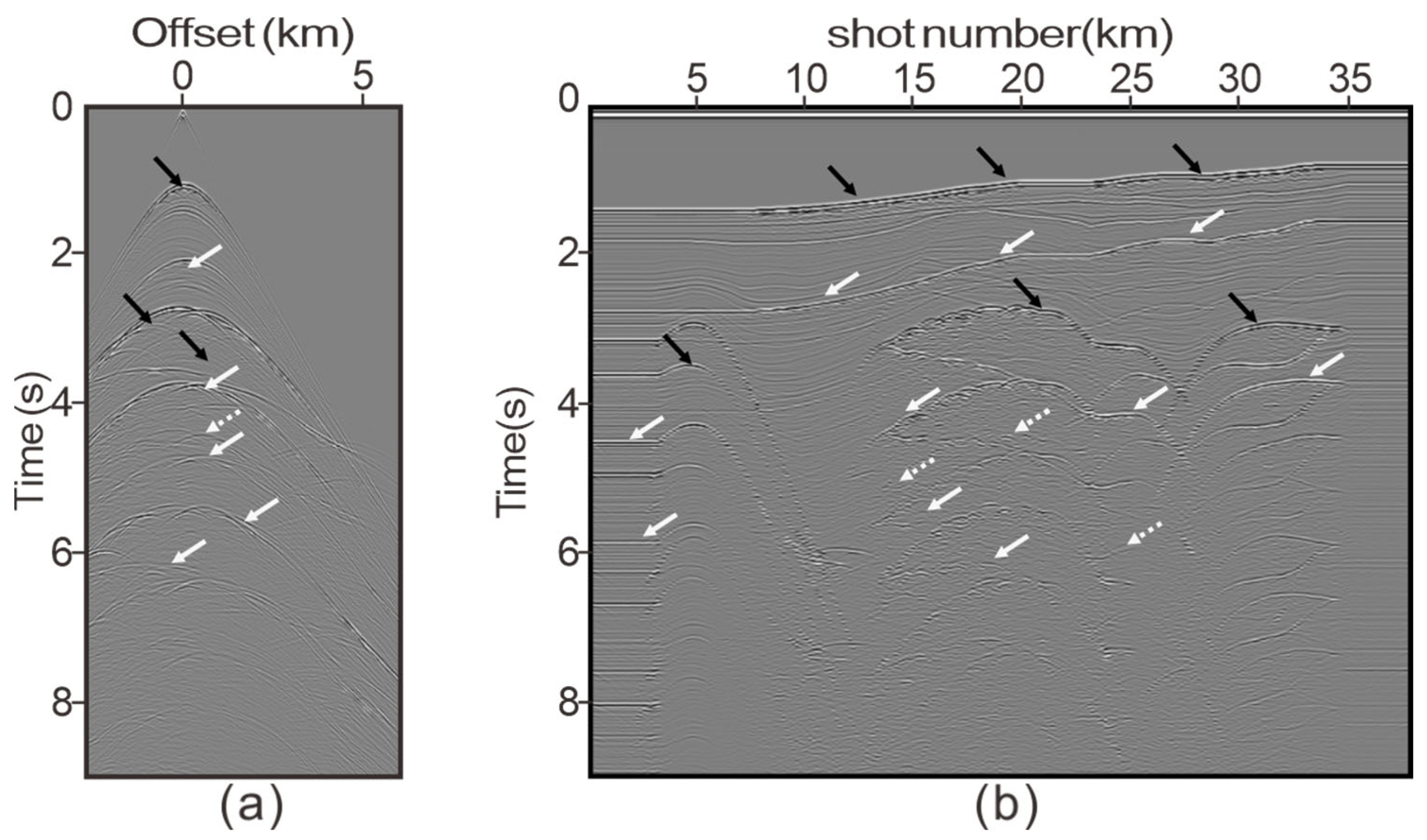
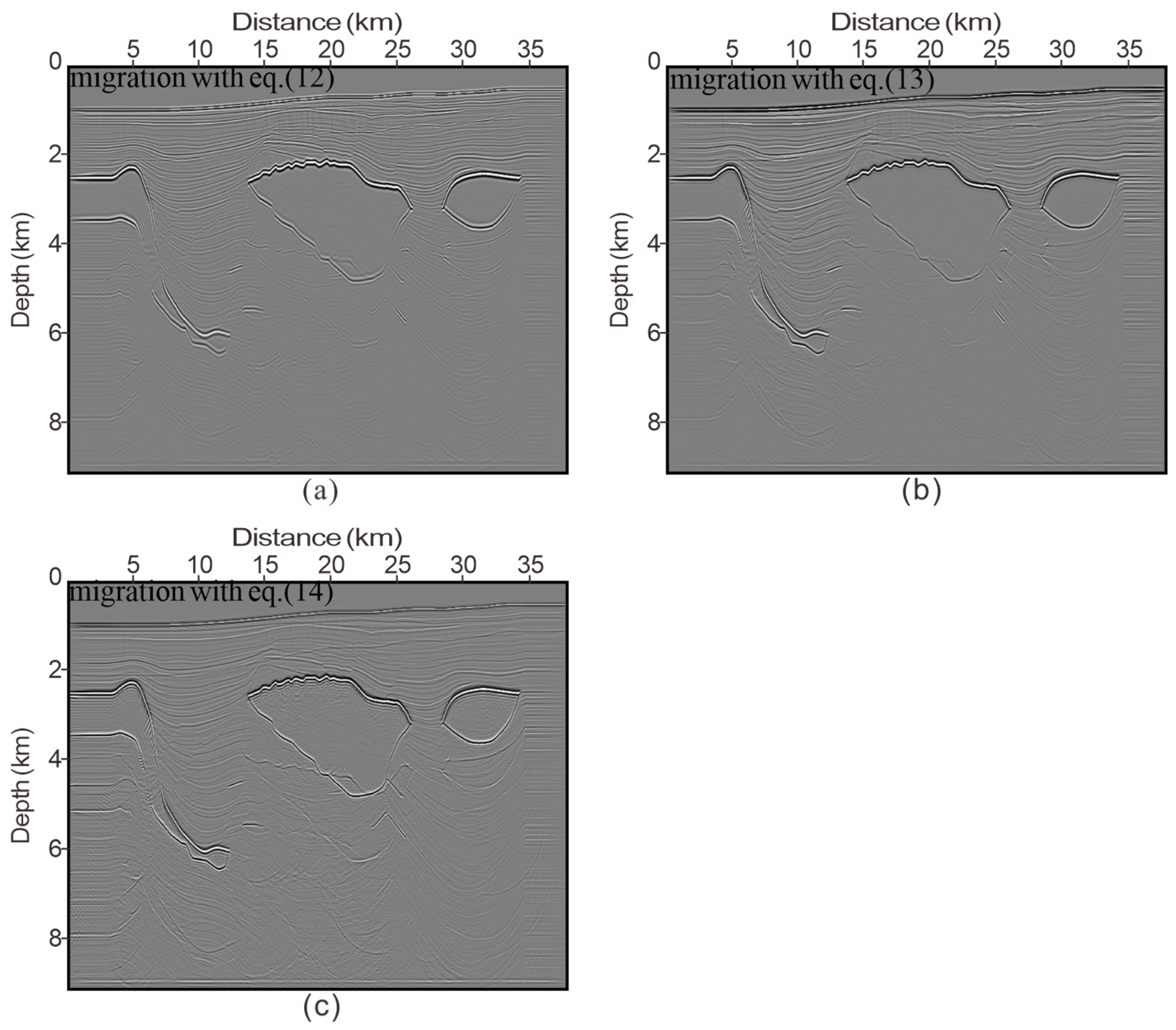
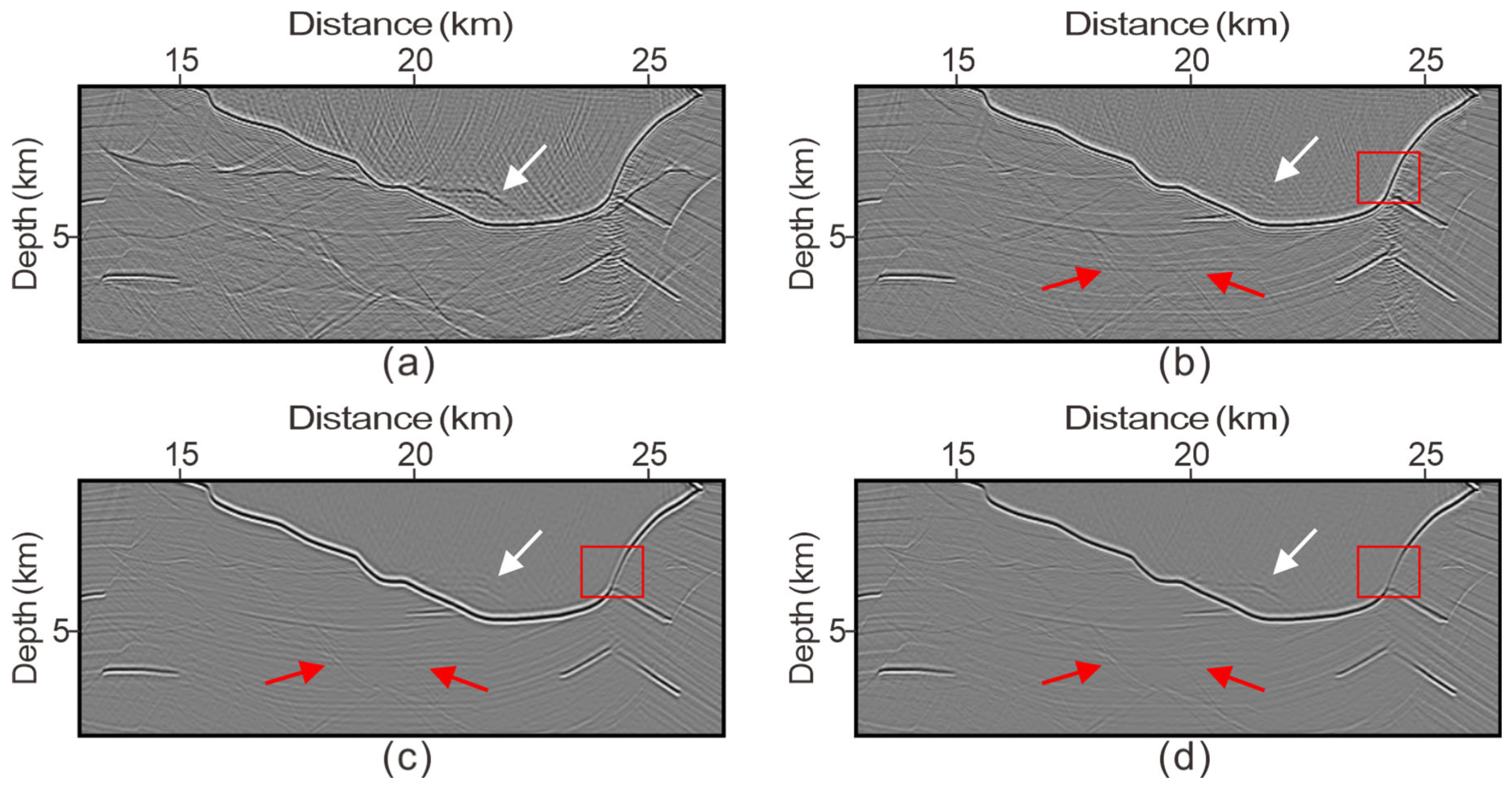
3.2. Pluto 1.5 Model: Finite Difference Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Berkhout, A.J.; Vershuur, D.J. Multiple technology: Part 2, Migration of multiple reflections. In SEG Technical Program Expanded Abstracts 1994; SEG Library: Houston, TX, USA, 1994; pp. 1497–1500. [Google Scholar]
- Guitton, A. Shot-profile migration of multiple reflections. In SEG Technical Program Expanded Abstracts 2002; SEG Library: Houston, TX, USA, 2002; pp. 1296–1299. [Google Scholar]
- Schuster, G.T.; Yu, J.; Sheng, J.; Rickett, J. Interferometric/daylight seismic imaging. Geophys. J. Int. 2004, 157, 838–852. [Google Scholar] [CrossRef]
- Brown, M.F.; Guitton, A. Least-squares joint imaging of multiples and primaries. Geophysics 2005, 70, S79–S89. [Google Scholar] [CrossRef]
- Muijs, R.; Holliger, K.; Robertsson, J.O.A. Prestack depth migration of primary and surface-related multiple reflections. In SEG Technical Program Expanded Abstracts 2005; SEG Library: Houston, TX, USA, 2005; pp. 2107–2110. [Google Scholar]
- Berkhout, A.J.; Verschuur, D.J. Imaging of multiple reflections. Geophysics 2006, 71, SI209–SI220. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, X.; Jin, D.; He, R.; Sun, H.; Zheng, Y. Reverse time migration of multiples for subsalt imaging. Geophysics 2011, 76, WB209–WB216. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, H.; Xie, X.-B.; Zheng, Y.; Li, P. Reverse time migration of internal multiples for subsalt imaging. Geophysics 2015, 80, S175–S185. [Google Scholar] [CrossRef]
- Ordoñez, A.; Söllner, W.; Klüver, T.; Gelius, L.J. Migration of primaries and multiples using an imaging condition for amplitude-normalized separated wavefields. Geophysics 2014, 79, S217–S230. [Google Scholar] [CrossRef]
- Zhang, D.; Schuster, G.T. Least-squares reverse time migration of multiples. Geophysics 2014, 79, S11–S21. [Google Scholar] [CrossRef]
- Zuberi, M.A.H.; Alkhalifah, T. Generalized internal multiple imaging. Geophysics 2014, 79, S207–S216. [Google Scholar] [CrossRef]
- Lu, S.; Whitmore, D.N.; Valenciano, A.A.; Chemingui, N. Separated-wavefield imaging using primary and multiple energy. Lead. Edge 2015, 34, 770–778. [Google Scholar] [CrossRef]
- Wong, M.; Biondi, B.L.; Ronen, S. Imaging with primaries and free-surface multiples by joint least-squares reverse time migration. Geophysics 2015, 80, S223–S235. [Google Scholar] [CrossRef]
- Nath, A.; Verschuur, D.J. Imaging with surface-related multiples to overcome large acquisition gaps. J. Geophys. Eng. 2020, 17, 742–758. [Google Scholar] [CrossRef]
- ul Haq, E.; Ji, Y.; Shahzad, K.; Mashwani, S.A.; Ullah, H.; Zaheer, M. Architectural complexities and morphological variations of the sediment waves of Plio-Pleistocene channel levee backslope of the Indus fan. Rud.-Geol.-Naft. Zb. 2022, 37, 39–54. [Google Scholar] [CrossRef]
- Yang, M.; Fang, Z.; Witte, P.; Herrmann, F.J. Time-domain sparsity promoting least-squares reverse time migration with source estimation. Geophys. Prospect. 2020, 68, 2697–2711. [Google Scholar] [CrossRef]
- Pranata, B.; Ramdhan, M.; Hanif, M.; Sulaiman, M.I.; Maulana, M.P.; Wandono; Widiyantoro, S.; Suhardja, S.K.; Hidayat, E.; Supendi, P.; et al. Seismic imaging beneath Sumatra Island and its surroundings, Indonesia, from local-regional P-wave earthquake tomography. Rud.-Geol.-Naft. Zb. 2023, 38, 119–132. [Google Scholar] [CrossRef]
- Hu, Y.; Gong, X.; Wang, B.; Wang, Z.; Han, L. Phase-Amplitude Least-Squares Reverse Time Migration With a Simultaneous-Source Based on Sparsity Promotion in the Time-Frequency Domain. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Qu, Y.M.; Ren, J.R.; Huang, C.P.; Li, Z.C.; Wang, Y.X.; Liu, C. 3-D Least-Squares Reverse Time Migration in Curvilinear-tau Domain. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Yuan, M.; Huang, J.; Liao, W.; Jiang, F. Least-squares Gaussian beam migration. J. Geophys. Eng. 2017, 14, 184–196. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Y.; Zheng, Y.; Chang, X. Limited-memory BFGS based least-squares pre-stack Kirchhoff depth migration. Geophys. J. Int. 2015, 202, 738–747. [Google Scholar] [CrossRef]
- Valenciano, A.A.; Biondi, B. 2-D deconvolution imaging condition for shot-profile migration. In SEG Technical Program Expanded Abstracts 2003; SEG Library: Houston, TX, USA, 2003; pp. 1059–1062. [Google Scholar]
- Guitton, A.; Valenciano, A.; Bevc, D.; Claerbout, J. Smoothing imaging condition for shot-profile migration. Geophysics 2007, 72, S149–S154. [Google Scholar] [CrossRef]
- Poole, T.L.; Curtis, A.; Robertsson, J.O.; van Manen, D.-J. Deconvolution imaging conditions and cross-talk suppression. Geophysics 2010, 75, W1–W12. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Li, Z.; Wang, P.; Zhang, M. One-way wave-equation migration of multiples based on stereographic imaging condition. Geophysics 2017, 82, S479–S488. [Google Scholar] [CrossRef]
- Lu, S.; Qiu, L.; Li, X. Addressing the crosstalk issue in imaging using seismic multiple wavefields. Geophysics 2021, 86, S235–S245. [Google Scholar] [CrossRef]
- Tu, N.; Herrmann, F.J. Fast imaging with surface-related multiples by sparse inversion. Geophys. J. Int. 2015, 201, 304–317. [Google Scholar] [CrossRef]
- Qu, Y.; Li, J.; Guan, Z.; Li, Z. Viscoacoustic reverse time migration of joint primaries and different-order multiples. Geophysics 2020, 85, S71–S87. [Google Scholar] [CrossRef]
- Alkhalifah, T.; Gou, Q. Subsurface wavefields based on the Generalized Internal Multiple Imaging. Geophys. J. Int. 2019, 219, 1212–1224. [Google Scholar] [CrossRef]
- Wang, G.; Guo, Q.; Alkhalifah, T.; Wang, S. Frequency-domain reflection waveform inversion with generalized internal multiple imaging. Geophysics 2021, 86, R701–R710. [Google Scholar] [CrossRef]
- Berkhout, A.J. Review Paper: An outlook on the future of seismic imaging, Part II: Full-Wavefield Migration. Geophys. Prospect. 2014, 62, 931–949. [Google Scholar] [CrossRef]
- Davydenko, M.; Verschuur, D.J. Full-wavefield migration: Using surface and internal multiples in imaging. Geophys. Prospect. 2017, 65, 7–21. [Google Scholar] [CrossRef]
- Davydenko, M.; Verschuur, D.J. Including and using internal multiples in closed-loop imaging—Field data examples. Geophysics 2018, 83, R297–R305. [Google Scholar] [CrossRef]
- Li, A.; Verschuur, D.J.; Abolhassani, S. Full wavefield migration based on eigen-decomposition propagation operators. In Proceedings of the 84th EAGE Annual Conference & Exhibition, Vienna, Austria, 5–8 June 2023; Volume 2023, pp. 1–5. [Google Scholar]
- Zhang, D.; Verschuur, D.J. Closed-loop surface-related multiple estimation with full-wavefield migration-reconstructed near offsets for shallow water. Geophysics 2021, 86, WC21–WC30. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Osen, A.; Shao, Y.; Hu, H.; Zheng, Y. Least-squares reverse time migration using controlled-order multiple reflections. Geophysics 2016, 81, S347–S357. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Zheng, Y. Reverse time migration of phase-encoded all-order multiples. Geophysics 2022, 87, S45–S52. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y. Phase-encoding-based least-squares reverse time migration of controlled-order multiples. Geophysics 2023, 88, S101–S113. [Google Scholar] [CrossRef]
- Li, J.; Qu, Y.; Li, M.; Li, Z. Viscoacoustic least-squares reverse-time migration of different-order free-surface multiples. Geophys. Prospect. 2023, 71, 29–47. [Google Scholar] [CrossRef]
- Wapenaar, K.; Broggini, F.; Slob, E.; Snieder, R. Three-Dimensional Single-Sided Marchenko Inverse Scattering, Data-Driven Focusing, Green’s Function Retrieval, and their Mutual Relations. Phys. Rev. Lett. 2013, 110, 084301. [Google Scholar] [CrossRef]
- Zhang, L.; Thorbecke, J.; Wapenaar, K.; Slob, E. Data-driven internal multiple elimination and its consequences for imaging: A comparison of strategies. Geophysics 2019, 84, S365–S372. [Google Scholar] [CrossRef]
- Staring, M.; Dukalski, M.; Belonosov, M.; Baardman, R.H.; Yoo, J.; Hegge, R.F.; van Borselen, R.; Wapenaar, K. Robust estimation of primaries by sparse inversion and Marchenko equation-based workflow for multiple suppression in the case of a shallow water layer and a complex overburden: A 2D case study in the Arabian Gulf. Geophysics 2021, 86, Q15–Q25. [Google Scholar] [CrossRef]
- Berkhout, A.J. Review Paper: An outlook on the future of seismic imaging, Part I: Forward and reverse modelling. Geophys. Prospect. 2014, 62, 911–930. [Google Scholar] [CrossRef]
- Claerbout, J.F. Toward a Unified Theory of Reflector Mapping. Geophysics 1971, 36, 467–481. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, J.; Liu, X.; Zhang, S. Oil and gas exploration in deep water area of Gulf of Mexico. Mar. Geol. Front. 2014, 30, 27–32. [Google Scholar]
- Turner, R.E.; Rabalais, N.N. The Gulf of Mexico. In World Seas: An Environmental Evaluation; Elsevier: Amsterdam, The Netherlands, 2019; pp. 445–464. [Google Scholar]
- Stoughton, D.; Stefani, J.; Michell, S. 2D Elastic Model for Wavefield Investigations of Subsalt Objectives, Deep Water Gulf of Mexico. In Proceedings of the 63rd EAGE Conference & Exhibition, Amsterdam, The Netherlands, 11–15 June 2001. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Wang, D.; Li, L. Full-Wavefield Migration Using an Imaging Condition of Global Normalization Multi-Order Wavefields: Application to a Synthetic Dataset. Appl. Sci. 2024, 14, 1389. https://doi.org/10.3390/app14041389
Zhu H, Wang D, Li L. Full-Wavefield Migration Using an Imaging Condition of Global Normalization Multi-Order Wavefields: Application to a Synthetic Dataset. Applied Sciences. 2024; 14(4):1389. https://doi.org/10.3390/app14041389
Chicago/Turabian StyleZhu, Hongyu, Deli Wang, and Lingxiang Li. 2024. "Full-Wavefield Migration Using an Imaging Condition of Global Normalization Multi-Order Wavefields: Application to a Synthetic Dataset" Applied Sciences 14, no. 4: 1389. https://doi.org/10.3390/app14041389
APA StyleZhu, H., Wang, D., & Li, L. (2024). Full-Wavefield Migration Using an Imaging Condition of Global Normalization Multi-Order Wavefields: Application to a Synthetic Dataset. Applied Sciences, 14(4), 1389. https://doi.org/10.3390/app14041389




