Abstract
Joints are the weak plane structures in coal. The existence of joints leads to coal failure, with different fracture modes and energy evolution laws. In this paper, the energy evolution and bursting liability index of coal failure with different joint inclination angles (JIAs) are analyzed. The results show that with an increase in joint inclination angle (JIA), the total energy and elastic energy of coal first decrease and then increase and the dissipation energy decreases gradually. The existence of joints changes the bursting liability of coal. With an increase in the JIA, the uniaxial compressive strength (Rc) of coal first decreases and then increases, the dynamic failure time (DT) gradually decreases, and the impact energy velocity index (WST) and the impact energy index (KE) gradually increase. With an increase in the JIA, coal went from tensile failure to shear failure and tension shear mixed failure. After coal failure, the fractal dimension was between 1.7 and 2.4, decreasing first and then increasing; the larger the JIA and the degree of fragmentation, the more energy consumed at the moment of failure and the stronger the bursting liability of coal. The results have a guiding significance for the monitoring and prevention of rock bursts in coal mines.
1. Introduction
Coal is a rock mass with abnormal joint development. The geological conditions of deep coal seams have become increasingly intricate, often exhibiting defects such as unstable coal seam angles and abundant coal joints [1,2], which make the strength and deformation characteristics of coal anisotropic [3,4,5]. The joint is a weak plane structure of coal, which is often mixed with inorganic minerals and other ingredients [6,7,8]. In terms of coal instability, the energy release, transformation law, and bursting liability are greatly affected by joints [9,10], which brings great challenges to the safe production of coal mines.
The failure of coal is accompanied by the release and transformation of energy [11]. Through uniaxial compression [12], triaxial compression [13], cyclic loading [14], and tensile failure [15] experiments, many scholars have revealed the energy release and transformation mechanism of coal rock under different failure modes and stress paths. Wang et al. [16] analyzed the influence of anisotropic joints on the energy evolution, acoustic emission (AE), and fracture mode of marble and found that the degree of crack bending determines the energy release. Jia et al. [17] studied the evolution of energy in coal samples at different sampling depths and found that both total energy and dissipated energy increased with increasing sampling depth. Zhang et al. [18] used numerical simulation methods to study the energy evolution and crack development laws of coal–rock combinations and found that the larger the height ratio of coal to rock, the faster the energy dissipation. Recently, some scholars have further analyzed the effects of strain rate, the inclination angle of coal–rock combinations, and original cracks on the energy evolution of coal rock failure [19,20,21]. However, previous studies on energy evolution laws have mostly focused on intact coal rocks or rocks with joints. As a heterogeneous body with abnormal joint development, the energy release and transformation law of coal is seriously affected by the weak plane structure of joints in the process of failure.
Bursting liability is a comprehensive reflection of various mechanical properties of a coal mass, i.e., its accumulated energy under a load that exceeds its bearing limit and which is suddenly released [22,23]. Jiang and Zhao et al. [24] studied the relationship between coal microstructure and bursting liability by means of microexperiments. Pan et al. [25] introduced the impact energy velocity index (WST) as an index of the bursting liability of coal and demonstrated its scientific rationality. Jiang et al. [26] calculated the impact kinetic energy of coal rock crushed blocks and modified the evaluation index of bursting liability by using the established criterion of impact kinetic energy. Rock burst is closely related to the stress and energy state of the coal rock mass. Shan [27] carried out uniaxial and triaxial loading experiments on coal rocks and analyzed the relationship between confining pressure and the strength and deformation failure characteristics of coal rock. Rock bursts are the result of the sudden instability of a coal rock system and the rapid release of energy [28,29,30]. When a rock burst occurs, the roof of the coal rock will sink violently, the energy flowing into the coal body will increase rapidly, and the energy of the coal rock system will gather, dissipate, and lose balance [31,32]. Due to the influence of joints, the mechanics of coal failure and the energy evolution are quite different. It is of certain guiding significance to study the relationship between coal burst tendency and the JIA from the perspective of energy.
This paper systematically conducts uniaxial compression failure experiments on coal with JIAs of 0°, 15°, 30°, 45°, 60°, 75°, and 90°, analyzing the energy evolution law of coal failure with different JIAs. The relationship between the JIA and coal bursting liability is studied, and the joint instability failure mechanism, crack propagation morphology, and fracture fractal characteristics are discussed. This study aims to reveal the evolution law of fracture impact instability of jointed coal and provide guidance for the monitoring of rock bursts in coal mines.
2. Experimental Methods
2.1. Preparation of Samples with Different JIAs
The samples were taken from the same block of coal. Using a SC-300 core drilling rig, by adjusting the inclination angle between the borehole and the joint plane, samples with seven angles (0°, 15°, 30°, 45°, 60°, 75°, and 90°) between the joint surface and the vertical plane were drilled. A total of 21 samples were drilled, with 3 samples for each JIA. They were cut and polished into φ50 mm × 100 mm standard cylinder samples.
A schematic diagram of each group is shown in Figure 1a, and a physical drawing is shown in Figure 1b. There were three samples for each JIA, and all coal samples after processing are shown in Figure 1c. The parameters of the samples were measured and numbered, as shown in Table 1.
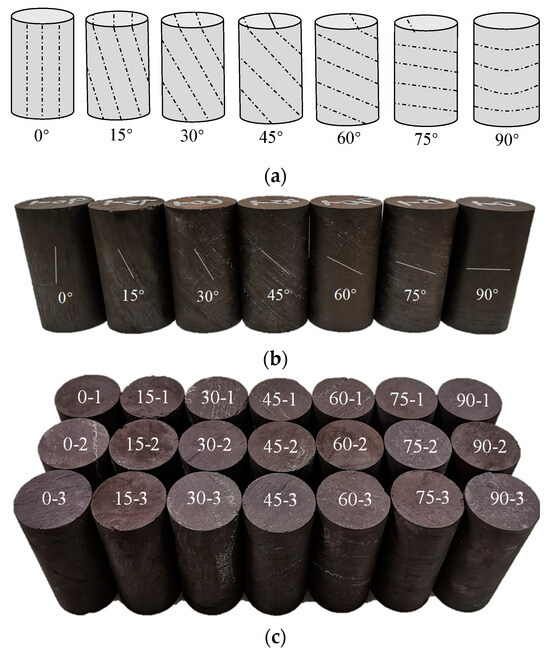
Figure 1.
Samples used in the experiments. (a) Schematic diagram, (b) Physical photograph, (c) Physical photographs of all samples.

Table 1.
Parameters of samples.
2.2. Experimental Equipment and Test Scheme
The experimental equipment included a pressure testing machine and a data acquisition instrument. The pressure testing machine was a YAW-600, which offers three control modes: displacement, test force, and deformation. The data acquisition instrument can display the test status and simultaneously draw curves for force–time, force–displacement, stress–strain, displacement–time, deformation–time, and others.
The testing procedure was as follows: Firstly, we connected the loading control system and the data acquisition system. We then selected the displacement control mode of the press and set the loading rate to 5 µm/s. At the beginning of the experiment, the load changes during the sample failure process were observed and recorded. After sample failure, we stopped loading, saved the press data, collected the debris from coal failure, took photos, and recorded the crack morphology.
3. Results
3.1. Energy Evolution Law of Coal Failure with Different JIAs
3.1.1. Energy Evolution Theory of Coal
According to the law of conservation of energy:
where is the elastic strain energy, is the dissipated energy, and is the total strain energy.
Figure 2 shows the energy distribution relationship of coal during loading. The yellow shaded area represents the elastic strain energy, and the white area represents the dissipated energy. The total energy of coal failure can be expressed as [11]:
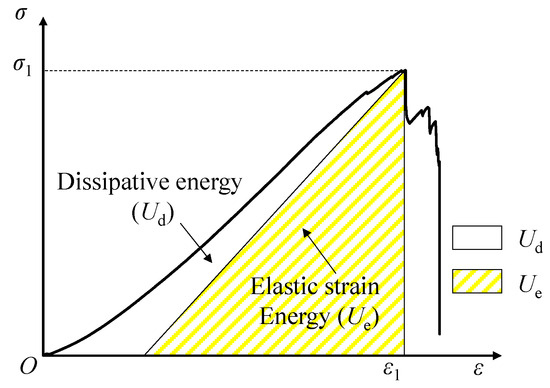
Figure 2.
Energy relationship of coal failure.
The elastic strain energy is as follows:
where is axial stress, is strain values, and are the stress and strain values at different times, respectively, and is elastic modulus.
The dissipated energy at any time during the uniaxial compression failure of coal may be described as [33]:
where and are, respectively, instantaneous stress and strain, and is the dissipated energy at any time.
3.1.2. Energy Evolution Law of Coal Failure
The energy variations associated with coal failure under different JIAs were computed using Equations (1)–(4), as illustrated in Figure 3. There are great differences between different types of energy in the coal failure process. Taking the 0°JIA coal sample as an example for analysis: in the first stage, the primary microcracks in the coal gradually close under the load, and the internal energy gradually accumulates. The load strength is small, and all three forms of energy show an increasing trend. With loading, elastic deformation of the coal occurs, and the mechanical energy was mainly transformed into elastic strain energy [11,34,35]. When the load increases further, the coal undergoes plastic deformation and internal microcracks begin to develop. Under the action of the load, the stress is rapidly released and redistributed, resulting in significant macroscopic failure of coal due to the accelerated growth of cracks. In the process of coal failure, the internal elastic strain energy is released and most of the energy is converted into dissipation energy.
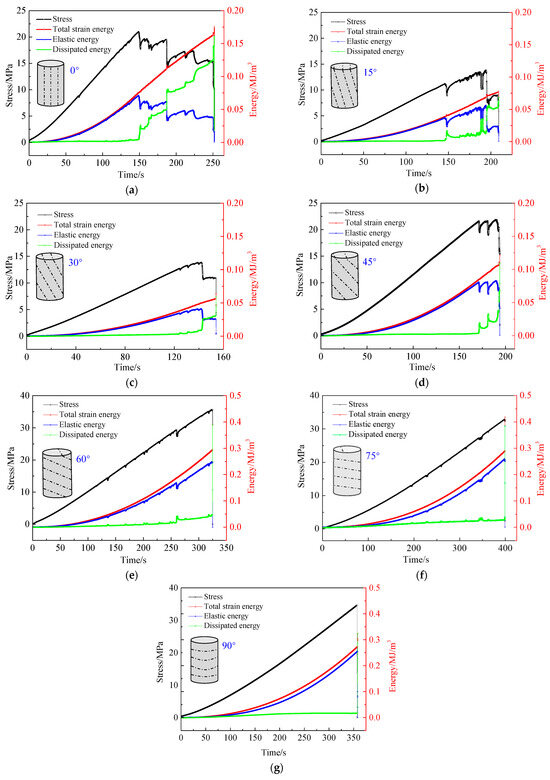
Figure 3.
Energy change characteristics of coal failure with different JIAs. (a) 0°, (b) 15°, (c) 30°, (d) 45°, (e) 60°, (f) 75°, (g) 90°.
To compare the influence of JIA on the evolution of coal failure energy, the energy of all samples was counted at the main failure time, as shown in Table 2; its change law is depicted in Figure 4. Figure 4a shows that with an increase in JIA, the total energy first decreased and then gradually increased. The average total energy was the smallest at a JIA of 30°, i.e., approximately 0.07 MJ/m3. When the JIA was 75°, the average total energy was the largest, i.e., approximately 0.36 MJ/m3. The trend of total energy first decreased and then gradually increased. The dissipation energy gradually decreased. When the JIA was 90°, the minimum dissipation energy was 0.03 MJ/m3. Figure 4b shows that the proportion of elastic strain energy to total energy increased from 22.03% to 89.65%, while the proportion of dissipated energy to total energy decreased from 77.97% to 10.35% from 0° to 90°. With a large JIA, most of the energy was accumulated in the form of elastic strain energy, which was released instantly in the case of instability, resulting in serious impact failure.

Table 2.
Energy of coal failure with different JIAs.
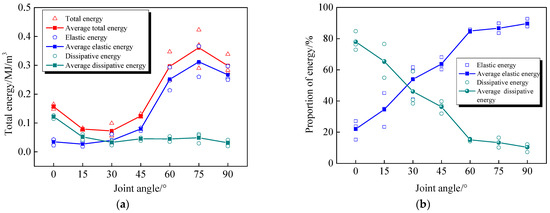
Figure 4.
Change law of energy of coal failure with different JIAs. (a) Total strain, elastic strain, and dissipation energy, (b) Elastic strain energy and dissipation energy.
3.2. The Evolution Law of the Bursting Liability of Coal with Different JIAs
3.2.1. Index of Coal Bursting Liability
The impact propensity of coal is divided into four indices: dynamic failure time (DT), uniaxial compressive strength (Rc), impact energy index (KE), and elastic strain energy index (WET) [36,37,38]. Some scholars have also put forward the impact energy velocity index (WST) [25]; the criteria are shown in Table 3.

Table 3.
Bursting liability indices of coal.
The accumulated strain energy before and after the peak value of coal is as follows:
where and are the strain energy before and after the peak, respectively, and is the strain value corresponding to the residual strength.
The KE is:
The WST of coal is the ratio of KE and DT, which represents the ratio of coal sample aggregation and released energy in a unit of time; the greater the WST, the stronger the impact capacity of the coal sample, as shown in Formula (8):
The bursting liability index has a direct relationship with the energy evolution process of coal.
3.2.2. Relationship between JIA and Coal Bursting Liability Index
The experimental results of the bursting liability index of coal with different JIAs are presented in Table 4, and the change trend is illustrated in Figure 5. It can be observed that only when the JIA was 15° the Rc of coal less than 14 MPa, indicating weak bursting liability. With an increase in JIA, the Rc of coal decreased first and then increased (Figure 5a). The DT decreased with an increase in JIA (Figure 5b). The JIA has a significant impact on the DT of coal. When the JIA was small, multiple stress drops occurred during coal failure. When the JIA ranged from 0° to 45°, the DT of coal exceeded 500 ms, indicating no bursting liability. However, when the JIA was at angles of 60°, 75°, and 90°, the DT was less than 50 ms, indicating a strong bursting liability. The KE showed a gradually increasing trend (Figure 5c). The coal with a 0° joint dip had no bursting liability, while the coal with 15° joint dip exhibited weak bursting liability. The WST gradually increased with an increase in JIA (Figure 5d). When the JIA was 0°, 15°, and 30°, the WST was less than 3, indicating no bursting liability. When the JIA was 45°, the WST was less than 100, indicating a weak bursting liability. When the JIA was 75°, the WST had a large dispersion, which led to a WST of 75°; the average impact energy velocity index was greater than 90°, but the inclined coal with 75° and 90° joint inclination was strongly inclined to impact.

Table 4.
Impact propensity index of different coal under uniaxial failure.
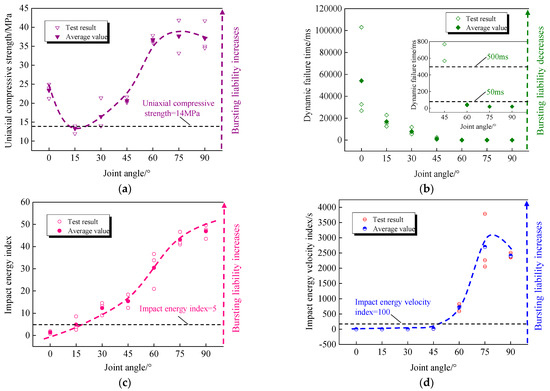
Figure 5.
Variation Law of coal bursting liability with different JIAs. (a) Uniaxial compressive strength, (b) Dynamic failure time, (c) Impact energy index, (d) Impact energy velocity index.
The results of different bursting liability indices varied slightly. With an increase in JIA, the overall impact propensity of coal presented a gradually increasing trend. Based on the findings in Section 3.2, it may be concluded that the existence of joints changes the bursting liability of coal. With an increase in JIA, the elastic strain energy accumulates before the main failure of coal, and the dissipated energy released by the coal failure increases gradually. Consequently, the coal gradually evolves from no bursting liability to strong bursting liability.
4. Discussion
4.1. Fracture Mechanism of Coal Joint
Joints are weak geological interfaces formed during the process of geological evolution; they represents defects in coal masses. To analyze the failure criterion of joint instability, previous studies have proposed the use of fracture mechanics [39,40], considering the joint as a weak structural plane within coal. Local high stress cracking at the top of the joint leads to coal failure. A stress diagram of joints with different dip angles in coal is shown in Figure 6.
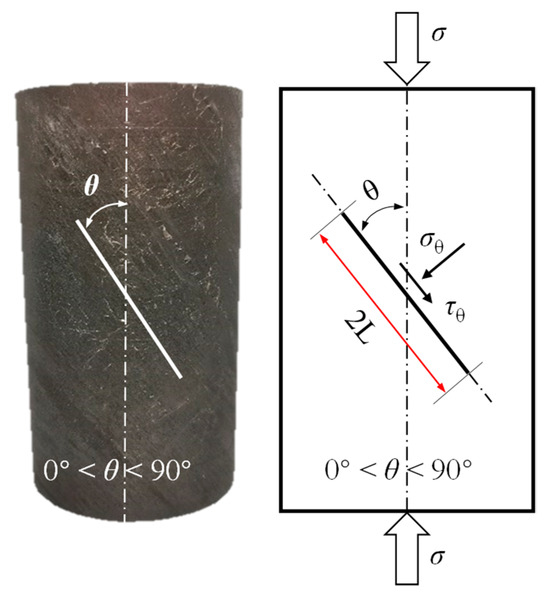
Figure 6.
Schematic diagram of coal joint force.
When the length of the joint in coal is 2 L and the angle between the joint surface and load direction is θ, the normal stress and shear stress on joint surface are as follows:
If the friction angle of the joint surface is φ, the friction coefficient of the friction surface is:
The shear stress acting on the joint surface slides along the joint surface, and the normal stress produces friction resistance to prevent the upper coal from sliding. The driving force on the slip surface can be expressed as:
The shear stress causes the coal to slide along the joint surface. The instability failure of coal is related to geometric characteristics such as JIA and joint length. With an increase in JIA from 0° to 90°, the shear stress on the joint surface first increases and then decreases, while the normal stress and friction resistance gradually increase. Therefore, for coal with the same properties, without considering factors such as joint length and friction coefficient, with an increase in JIA, the initial critical failure strength of the joint first decreases and then increases. Macroscopically, the uniaxial compressive strength of coal decreases first and then increases.
4.2. Effect of Crack Growth Morphology on Energy Evolution and Bursting Liability
The failure morphology of coal with different JIAs is depicted in Figure 7. The joint has an influence on the failure morphology and crack propagation mode of coal. According to the type of crack propagation [41], the failure cracks of coal can be classified into tension cracks (T), shear cracks (S) and tension–shear mixed failure (F).

Figure 7.
Crack propagation forms in coal with different JIAs. In the figure, T represents tension crack, S represents shear crack, and F represents tension–shear mixed failure.
When the JIA is 0°, the tensile failure mainly occurs along the joint plane. After failure, it primarily manifests as tensile cracks. Before the coal main failure, the energy is gradually released (shown in Figure 3a) and the coal shows no bursting liability. When the JIA is 15°, 30°, or 45°, both the normal stress acting on the joint surface and the shear stress along the joint surface increase gradually. According to the failure mode of coal, the number of tension cracks gradually decreases, while the number of shear failure cracks increases. When the JIA reaches 60°, 75°, or 90°, both the normal stress and friction force on the joint surface gradually reach their maximum values, while the shear stress gradually decreases. Failure occurs in the form of tension–shear mixed failure (F), resulting in vertical cracks along the direction of the joint and small splash fractures. Therefore, the coal has the greatest probability of bursting.
4.3. Influence of Debris Fractal Characteristics on Energy Evolution and Bursting Liability
The degree of debris after fragmentation can directly reflect the failure characteristics, stress state, and energy change law of coal [42,43]. The expression of the fractal dimension is as follows [44,45]:
where D is the fractal dimension of the debris, α is the slope of in the double logarithmic coordinate, L is the characteristic size of the equivalent particle size in the statistical interval, and M is the total mass of the debris.
The debris collected and screened after coal failure with different JIAs was sorted into nine sizes. Taking a 60° JIA coal sample as an example, the side length of each grid was 10 mm; the screening results are shown in Figure 8. The sieved debris was measured and weighed to calculate the fractal dimension using Formulas (13) and (14), resulting in a fractal dimension fitting curve of coal failure debris with different JIAs (Figure 9). The correlation coefficient R2 of coal with different JIAs was greater than 0.88, indicating a high correlation between lg(M(L)/M) and lgL, demonstrating that the size distribution of debris after coal failure exhibited obvious fractal characteristics.

Figure 8.
Distribution of clastic particles in coal destruction.
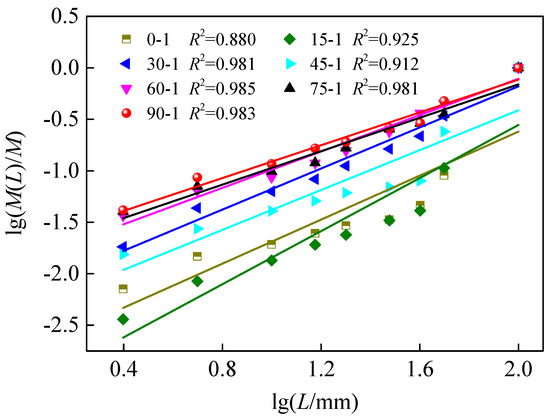
Figure 9.
lg(M(L)/M)—lg L fitting curve of coal with different JIAs.
Figure 10 shows that the fractal dimension of coal with different JIAs after failure was between 1.7 and 2.4. When the JIA was 15°, the minimum average fractal dimension was 1.79, and when the JIA was 90°, the maximum average fractal dimension was 2.29. Studies have shown that the fractal dimension of intact rock ranges from 1.7 and 2.0 [46], while the fractal dimensions of coal containing pores fall between 2.2 and 2.4 [47]. Therefore, it can be observed that the existence of joints leads to the expansion of the fractal dimension interval of coal failure, that is, the fracture degree of coal with different JIAs varies greatly, and the distribution after fracture is not uniform. The fractal dimension is closely related to the JIA. The process of coal failure effects many fractures, resulting in more thorough fragmentation. The proportion of small particle debris increases, resulting in an increase in fractal dimension.
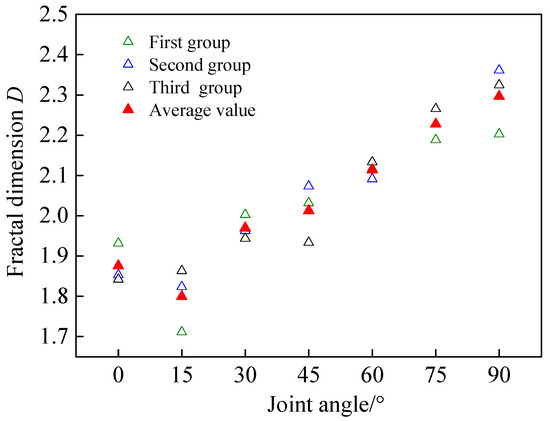
Figure 10.
Relationship between coal JIA and fractal dimension.
The larger the JIA, the more elastic strain energy is accumulated before failure; as shown in Figure 4a, as the dip angle of the joint increased from 0° to 90°, the average elastic energy increased from 22.03% to 89.65%. At the moment of failure, coal can release energy, which is transformed into surface energy Ua, kinetic energy Uk, thermal energy Un, and radiation energy Us. This is illustrated in Equation (15):
where Ua is surface energy, Uk is kinetic energy, Un is thermal energy, and Us is radiation energy.
Thermal energy Un and radiation energy Us are relatively small, and the kinetic energy Uk released under dynamic loading is generally less than 7% of the total energy [48]. Under the condition of static uniaxial compression, the released kinetic energy Uk is smaller, so the dissipated energy is approximately equal to the surface energy Ua of the new fracture surface [49]:
where Ac is the area of new crack surface caused by coal failure and Sa is the energy required per unit crack area.
Formulas (15) and (16) further demonstrate a positive correlation between the scale of coal failure debris and the dissipated energy consumed at the instant of coal instability; the more energy consumed during failure, the higher the degree of impact risk.
Field practice demonstrates that the impact risk is directly related to the amount of drilling cuttings [50]. The amount and size of drilling cuttings can effectively reflect the mechanical properties and stress distribution [51]. When the number of cuttings per meter is low, the internal stress of coal seam is low, resulting in no impact risk. When the number of cuttings per meter is high, there will be significant dynamic phenomena, such as impact sound and sticking phenomena. At this time, the internal stress level of a coal seam is high, and the impact risk is also high. Combined with the number of drilling cuttings produced by coal failure in the field drilling process, the research results of this paper are further verified; that is, with an increase in JIA, the bursting liability increases gradually and the existence of joints seriously affects the energy evolution process and bursting liability of coal.
5. Conclusions
(1) Joints influence the energy change law of coal failure. When the dip angle of the joint changes from 0°to 90°, the elastic strain energy increases from 22.03% to 89.65%, while the dissipated energy decreases from 77.97% to 10.35%.
(2) The existence of joints changes the bursting liability of coal. With an increase in JIA, the Rc of coal first decreases and then increases, the DT decreases gradually, the KE and WST gradually increase, and the bursting liability of coal increases gradually.
(3) Under the combined action of normal stress, shear stress, and friction, local cracking at the top of the joint leads to coal instability. The fractal dimension of coal with different JIA after failure ranges between 1.7 and 2.4. With an increase in JIA, the fractal dimension first decreases and then increases. The larger the fractal dimension and the higher the degree of fragmentation, the more energy is consumed at the moment of destruction, resulting in a higher degree of coal impact risk.
(4) Joints significantly affect the energy evolution law and bursting liability of coal. The degree of bursting liability of coal can be determined based on joint angles; this has guiding significance for the monitoring and prevention of coal mine rock bursts. In future research, further uniaxial loading and unloading experiments with coal with different JIAs will be carried out to establish the relationship between coal JIA and WET and to improve the indicator of bursting liability of coal with different JIAs.
Author Contributions
Conceptualization, S.Y.; methodology, S.Y.; validation, Z.L. and D.S.; formal analysis, Z.L. and H.M.; investigation, Y.N. and X.W.; resources, Y.N. and X.W.; data curation, S.Y. and H.M.; writing—original draft preparation, S.Y. and H.M.; writing—review and editing, Z.L. and D.S.; project administration, X.W.; funding acquisition, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Jiangsu Funding program for Excellent postdoctoral Talent (Grant number: 2022ZB505), the National Natural Science Foundation of China (Grant number: 52304268), the China Postdoctoral Science Foundation (Grant number: 2023M733771), the Fundamental Research Funds for the Central Universities (Grant number: 2023QN1030).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the finding of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, C.; Liu, Y.; Song, D.Z.; Xu, J.H.; Wang, Q.W.; Zhang, S.Y. Evaluation of bedding effect on the bursting liability of coal and coal-rock combination under different bedding dip angles. Adv. Geo-Energy Res. 2024, 11, 29–40. [Google Scholar] [CrossRef]
- Hou, C.; Zhang, Y.H.; Yan, Y. Effects of coal seam dip angle on the outburst in coal roadway excavation. Int. J. Min. Sci. Technol. 2019, 29, 757–764. [Google Scholar] [CrossRef]
- Mu, H.W.; Song, D.Z.; He, X.Q.; Li, Z.L.; Qiu, L.M.; Guo, H.F. Damage and fracture law of coal samples with different joint angles and their characterisation by acoustic emission. Struct. Control Health Monit. 2020, 27, e2639. [Google Scholar] [CrossRef]
- Bona, P.; Ki-Bok, M.; Nicholas, T.; Per, H.; Per, H. Three-dimensional bonded-particle discrete element modeling of mechanical behavior of transversely isotropic rock. Int. J. Rock. Mech. Min. Sci. 2018, 110, 120–132. [Google Scholar] [CrossRef]
- Lambert, C.; Coll, C. Discrete modeling of rock joints with a smooth-joint contact model. J. Rock Mech. Geotech. Eng. 2014, 6, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.B.; Wang, E.Y.; Jiang, C.B.; Zhang, D.M.; Li, M.H.; Yu, B.C.; Zhao, D. True triaxial experimental study of anisotropic mechanical behavior and permeability evolution of initially fractured coal. Nat. Resour. Res. 2023, 32, 567–585. [Google Scholar] [CrossRef]
- Li, J.; Zhao, J.; Wang, H.C.; Liu, K.; Zhang, Q.B. Fracturing behaviours and AE signatures of anisotropic coal in dynamic Brazilian tests. Eng. Fract. Mech. 2021, 252, 107817. [Google Scholar] [CrossRef]
- Ge, X.R. The mechanical behaviors and analog analytical method of joints and weak intercalations in rock mass. Rock. Soil Mech. 1979, 1, 54–75. [Google Scholar] [CrossRef]
- Cao, R.H.; Lin, H.; Cao, P. Strength and failure characteristics of brittle jointed rock-like specimens under uniaxial compression:Digital speckle technology and a particle mechanics approach. Int. J. Min. Sci. Technol. 2018, 28, 669–677. [Google Scholar] [CrossRef]
- Lu, Z.G.; Ju, W.J.; Wang, H.; Zhang, J.W.; Yi, K.; Feng, Y.L. Experimental study on anisotropic characteristics of impact tendency and failure model of hard coal. Chin. J. Rock Mech. Eng. 2019, 38, 757–768. [Google Scholar] [CrossRef]
- Xie, H.P.; Li, L.Y.; Peng, R.D.; Ju, Y. Energy analysis and criteria for structural failure of rocks. J. Rock Mech. Geotech. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef]
- Song, D.Z.; Wang, E.Y.; Li, Z.H.; Liu, J.; Xu, W.Q. Energy dissipation of coal and rock during damage and failure process based on EMR. Int. J. Min. Sci. Technol. 2015, 25, 787–795. [Google Scholar] [CrossRef]
- Peng, R.; Ju, Y.; Wang, J.G.; Xie, H.; Gao, F.; Mao, L. Energy dissipation and release during coal failure under conventional triaxial compression. Rock Mech. Rock Eng. 2014, 48, 509–526. [Google Scholar] [CrossRef]
- Meng, Q.B.; Zhang, M.W.; Han, L.J.; Pu, H.; Nie, T.Y. Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Yang, K.; Wei, Z.; Dou, L.; Chi, X.L.; Liu, W.J.; Zhang, J.Q. Research on dynamic tensile energy evolution and failure characteristics of water-bearing coal samples. J. China Coal Soc. 2021, 46, 398–411. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, W.H.; Liu, D.Q.; Hou, Z.Q.; Li, C.H. On anisotropic fracture evolution and energy mechanism during marble failure under uniaxial deformation. Rock Mech. Rock Eng. 2019, 52, 3567–3583. [Google Scholar] [CrossRef]
- Jia, Z.Q.; Li, C.B.; Zhang, R.; Wang, M.; Gao, M.Z.; Zhang, Z.T.; Zhang, Z.P.; Li, R.; Xie, J. Energy evolution of coal at different depths under unloading conditions. Rock Mech. Rock Eng. 2019, 52, 4637–4649. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, C.P.; Liu, B.; Liu, Y.; Zhang, N.; Wang, H. Numerical investigation on crack development and energy evolution of stressed coal-rock combination. Int. J. Rock Mech. Min. Sci. 2020, 133, 104417. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.C.; Zhang, S.; Ren, J.X.; Zhang, L.; Zhang, R.J.; Cui, Y.Q. Study on the energy evolution mechanism of coal and rock with impact tendency under different strain rates. Sci. Rep. 2023, 13, 13773. [Google Scholar] [CrossRef]
- Yu, Y.J.; Liu, J.J.; Yang, Y.T.; Wang, P.B.; Wang, Z.M.; Song, Z.Y.; Liu, J.M.; Zhao, S.Q. Failure energy evolution of coal–rock combination with different inclinations. Sci. Rep. 2022, 12, 19455. [Google Scholar] [CrossRef]
- Liu, Y.b.; Zhao, D.; Yin, S.; Zhang, L. Comparison of energy evolution characteristics of intact and fractured coal under true triaxial progressive stress loading. Sustainability 2023, 15, 14796. [Google Scholar] [CrossRef]
- Liu, X.F.; Wang, X.R.; Wang, E.Y.; Kong, X.G.; Zhang, C.; Liu, S.J. Effects of gas pressure on bursting liability of coal under uniaxial conditions. J. Nat. Gas Sci. Eng. 2017, 39, 90–100. [Google Scholar] [CrossRef]
- Ortlepp, W.D.; Stacey, T.R. Rockburst mechanisms in tunnels and shafts. Tunn. Undergr. Space Technol. 1994, 9, 59–65. [Google Scholar] [CrossRef]
- Jiang, Y.D.; Zhao, Y.X.; He, M.C.; Peng, S.P. Investigation on mechanism of coal mine bumps based on mesoscopic experiments. Chin. J. Rock Mech. Eng. 2007, 26, 901–907. [Google Scholar] [CrossRef]
- Pan, Y.S.; Geng, L.; Li, Z.H. Research on evaluation indices for impact tendency and danger of coal seam. J. China. Coal Soc. 2010, 35, 1975–1978. [Google Scholar] [CrossRef]
- Jiang, D.H.; Jia, C.Y.; Wang, Y.F.; Wang, Z.Y.; Huang, W.P.; Luan, H.J.; Wang, P. Study on bursting liability of coal-like material with pores and anchors based on impact kinetic energy characteristics. Sustainability 2023, 15, 3820. [Google Scholar] [CrossRef]
- Shan, P.F.; Li, W.; Lai, X.P.; Zhang, S.; Chen, X.Z.; Wu, X.C. Research on the response mechanism of coal rock mass under stress and pressure. Materials 2023, 16, 3235. [Google Scholar] [CrossRef] [PubMed]
- Khan, N.M.; Ahmad, M.; Cao, K.; Ali, I.; Liu, W.; Rehman, H.; Hussain, S.; Rehman, F.U.; Ahmed, T. Developing a new bursting liability index based on energy evolution for coal under different loading rates. Sustainability 2022, 14, 1572. [Google Scholar] [CrossRef]
- Lu, C.P.; Liu, G.J.; Liu, Y.; Zhang, H. Mechanisms of rockburst triggered by slip and fracture of coal-parting-coal structure discontinuities. Rock Mech. Rock Eng. 2019, 52, 3279–3292. [Google Scholar] [CrossRef]
- Ding, Z.; Feng, X.J.; Wang, E.Y.; Sa, L.B.; Wang, D.M.; Zhang, Q.M.; Hu, Q.J.; Zhao, X. Fracture response and damage evolution features of coal considering the effect of creep damage under dynamic loading. Eng. Fail. Anal. 2023, 148, 107204. [Google Scholar] [CrossRef]
- Mottahedi, A.; Ataei, M. Fuzzy fault tree analysis for coal burst occurrence probability in underground coal mining. Tunn. Undergr. Space Technol. 2019, 83, 165–174. [Google Scholar] [CrossRef]
- Vardar, O.; Wei, C.C.; Zhang, C.G.; Canbulat, I. An energy-based quantitative coal burst proneness rating system for development roadways. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 19. [Google Scholar] [CrossRef]
- Feng, J.J.; Wang, E.Y.; Chen, X.; Ding, H.C. Energy dissipation rate: An indicator of coal deformation and failure under static and dynamic compressive loads. Int. J. Min. Sci. Technol. 2018, 28, 397–406. [Google Scholar] [CrossRef]
- Yin, S.; Song, D.Z.; He, X.Q.; Lou, Q.; Qiu, L.M.; Li, Z.L.; Chen, P.; Li, J.; Liu, Y. Structural health monitoring of building rock based on stress drop and acoustic-electric energy release. Struct. Control Health Monit. 2022, 29, e2875. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Lu, R.; Zhang, G.Q. Analysis on energy transformation for rock in the whole process of deformation and fracture. Min. Res. Dev. 2006, 26, 8–11. [Google Scholar] [CrossRef]
- GB/T25217.1—2010; Methods for Test, Monitoring and Prevention of Rockburst—Part 1: Classification and Laboratory Test Method on Bursting Liability of Roof Strata. Standards Press of China: Beijing, China, 2010. (In Chinese)
- GB/T 25217.2—2010; Methods for Test, Monitoring and Prevention of Rock Burst—Part2: Classification and Laboratory Test Method on Bursting Liability of Coal. Standards Press of China: Beijing, China, 2010. (In Chinese)
- Jiang, F.X.; Liu, Y.; Zhai, M.H.; Guo, X.S.; Wen, J.L.; Liu, X.G. Evaluation of rock burst hazard based on the classificationof stress and surrounding rock. Chin. J. Rock Mech. Eng. 2017, 36, 1041–1052. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, W.P.; Li, L.Y.; Xie, H.P. Fractal and statistical analysis of strength of jointed rocks. Chin. J. Rock Mech. Eng. 2004, 23, 3608–3612. [Google Scholar] [CrossRef]
- Liu, H.Y. Damage Constitutive Model of Jointed Rock Mass and Its Engineering Application; Metallurgical Industry Press: Beijing, China, 2016. [Google Scholar]
- Shi, G.C.; Yang, X.J.; Yu, H.C.; Zhu, C. Acoustic emission characteristics of creep fracture evolution in double-fracture fine sandstone under uniaxial compression. Eng. Fract. Mech. 2019, 210, 13–28. [Google Scholar] [CrossRef]
- Li, C.J.; Xu, Y.; Zhang, Y.T.; Li, H.L. Study on energy evolution and fractal characteristics of cracked coal-rock-like combined body under impact loading. Chin. J. Rock Mech. Eng. 2019, 38, 2231–2241. [Google Scholar] [CrossRef]
- Xiao, X.C.; Fan, Y.F.; Wu, D.; Ding, X.; Wang, L.; Zhao, B.Y. Energy dissipation feature and rock burst risk assessment in coal-rock combinations. Rock Soil Mech. 2019, 40, 4203–4212. [Google Scholar] [CrossRef]
- Xie, H.P. Fractal-Introduction to Rock Mechanics; Science Press: Beijing, China, 2005; pp. 228–234. [Google Scholar]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. Solid Earth 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- Gao, F.; Xie, H.P.; Zhao, P. Fractal properties of size frequency distribution of rock fragments and the influence of meso-structure. Chin. J. Rock Mech. Eng. 1994, 13, 240–246. [Google Scholar] [CrossRef]
- Wang, A.W.; Gao, Q.S.; Pan, Y.S.; Song, Y.M.; Li, L. Bursting liability and energy dissipation laws of prefabricatedborehole coal samples. J. China Coal Soc. 2021, 46, 959–972. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Kou, S.Q.; Jiang, L.G.; Lindqvist, P.A. Effects of loading rate on rock fracture: Fracture characteristics and energy partitioning. Int. J. Rock Mech. Min. Sci. 2000, 37, 745–762. [Google Scholar] [CrossRef]
- Zhao, J.S. Fracture Mechanics and Fracture Physics; Huazhong University of Science and Technology Press: Wuhan, China, 2003; pp. 234–236. [Google Scholar]
- Chen, F.; Pan, Y.S.; Li, Z.H.; Wang, A.W.; Tang, Z.; Xu, L.M. Detection and study of rock burst hazard based on drilling cuttings method. Chin. J. Geol. Hazard Control 2013, 24, 124–127. [Google Scholar] [CrossRef]
- Lv, Z.Q. Drilling cuttings method tests pressure releasing technique that effects of deep-hole blasting. J. China Coal Soc. 2014, 33, 32–34. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).