Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2
Abstract
1. Introduction
2. Methods
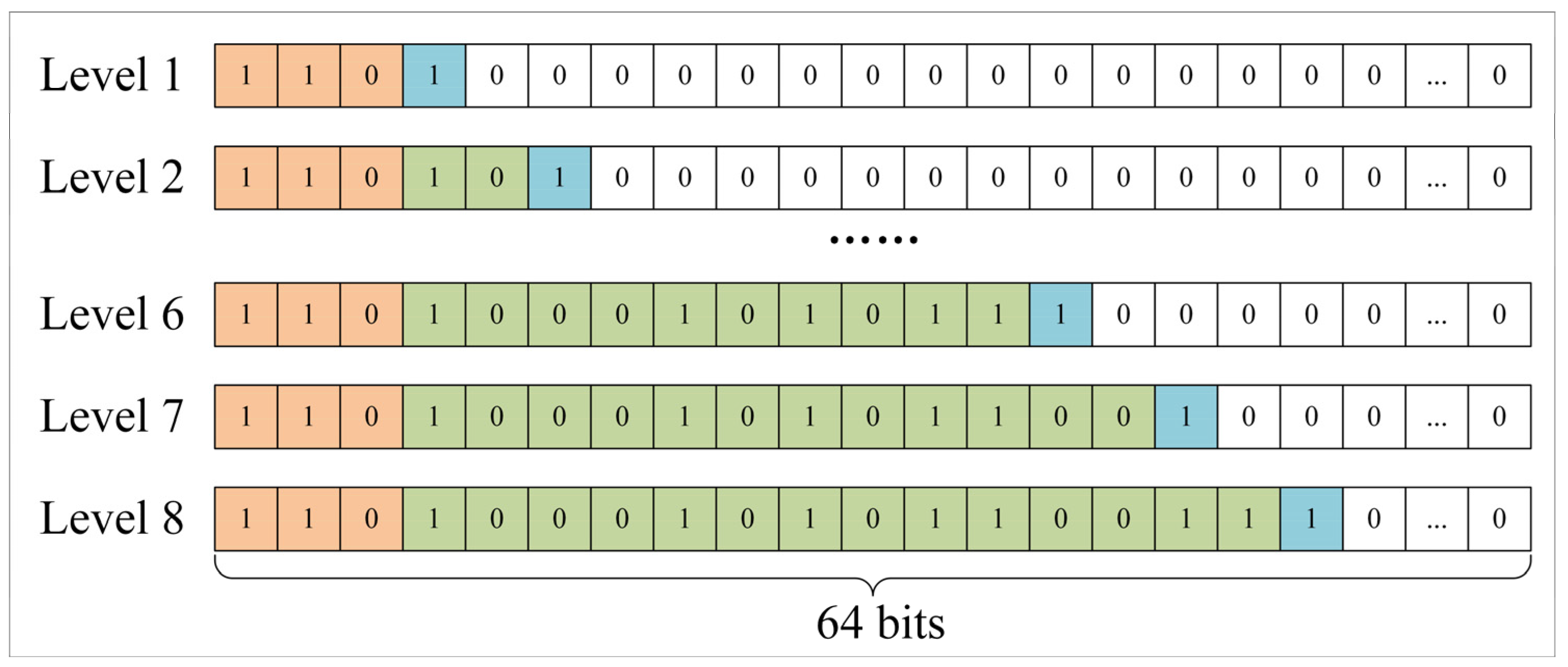
2.1. Geographical Grid Coding of Ship Positions Based on Google S2
| Algorithm 1: Google S2 encoding algorithm |
| Input: Lon, Lat, Pre Output: CellID // Step 1: Convert longitude and latitude to radians Lat, Lon→S (lat, lon) // Step 2: Establish a three-dimensional coordinate system with the center of the earth as the origin, and convert the longitude and latitude into points on the spherical rectangular coordinate system S (lat, on)→f (x, y, z) // Step 3: Spherical variable plane f (x, y, z)→g (face, u, v) // Step 4: Spherical rectangular projection correction g (face, u, v)→h (face, s, t) // Step 5: Conversion between points and coordinate axis points h (face, s, t)→H (face, i, j) // Step 6: Axis points are converted to values on the corresponding hierarchical Hilbert curves, which are combined with faceted representations to form CellID H (face, i, j)→CellID return CellID |
2.2. Determine the Set of Ships within Effective Rescue Distance in the Current Sea Area
2.2.1. Determination of Effective Rescue Distance Based on Rescue Time
2.2.2. Determination of Grid Coding Level Based on Effective Rescue Distance
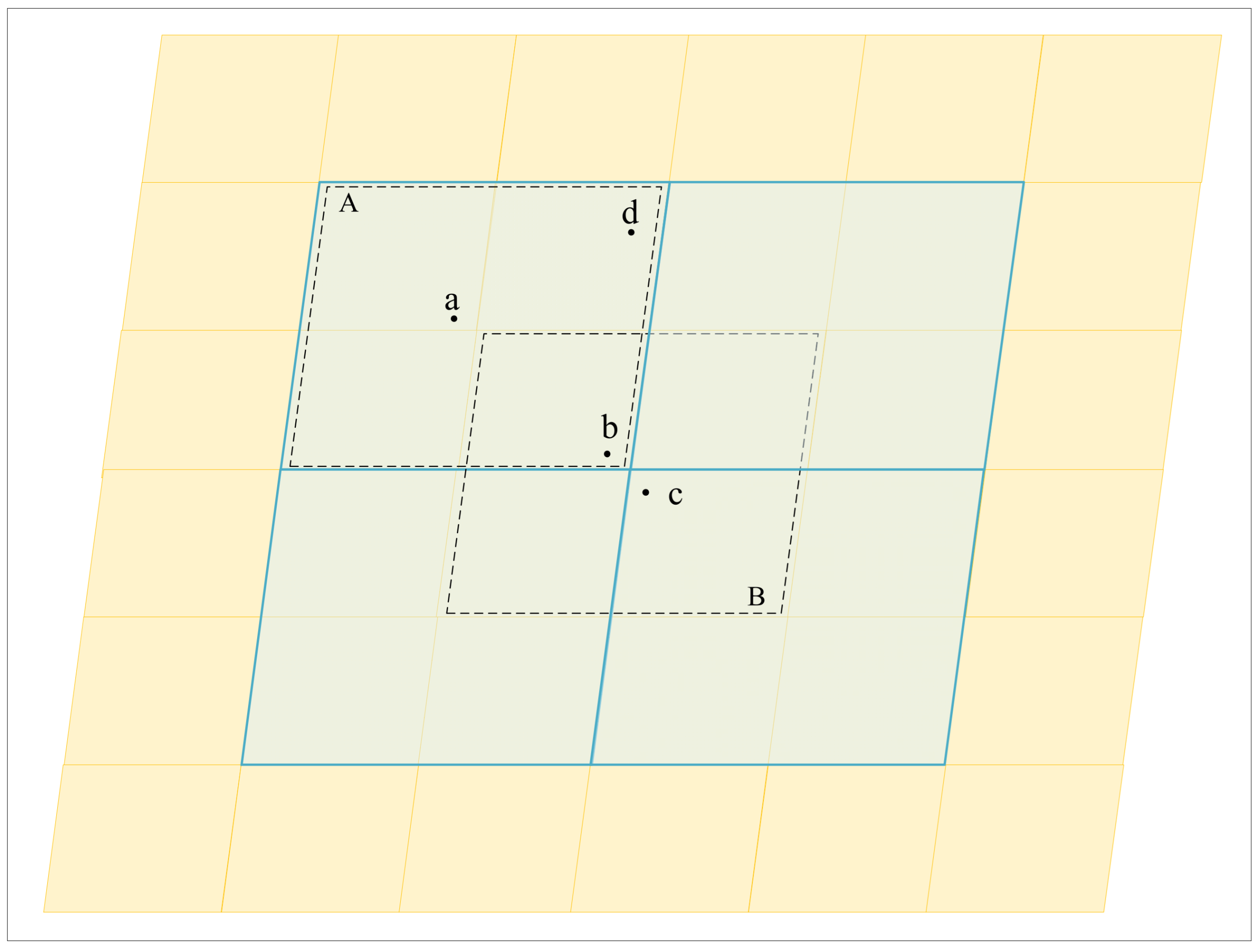
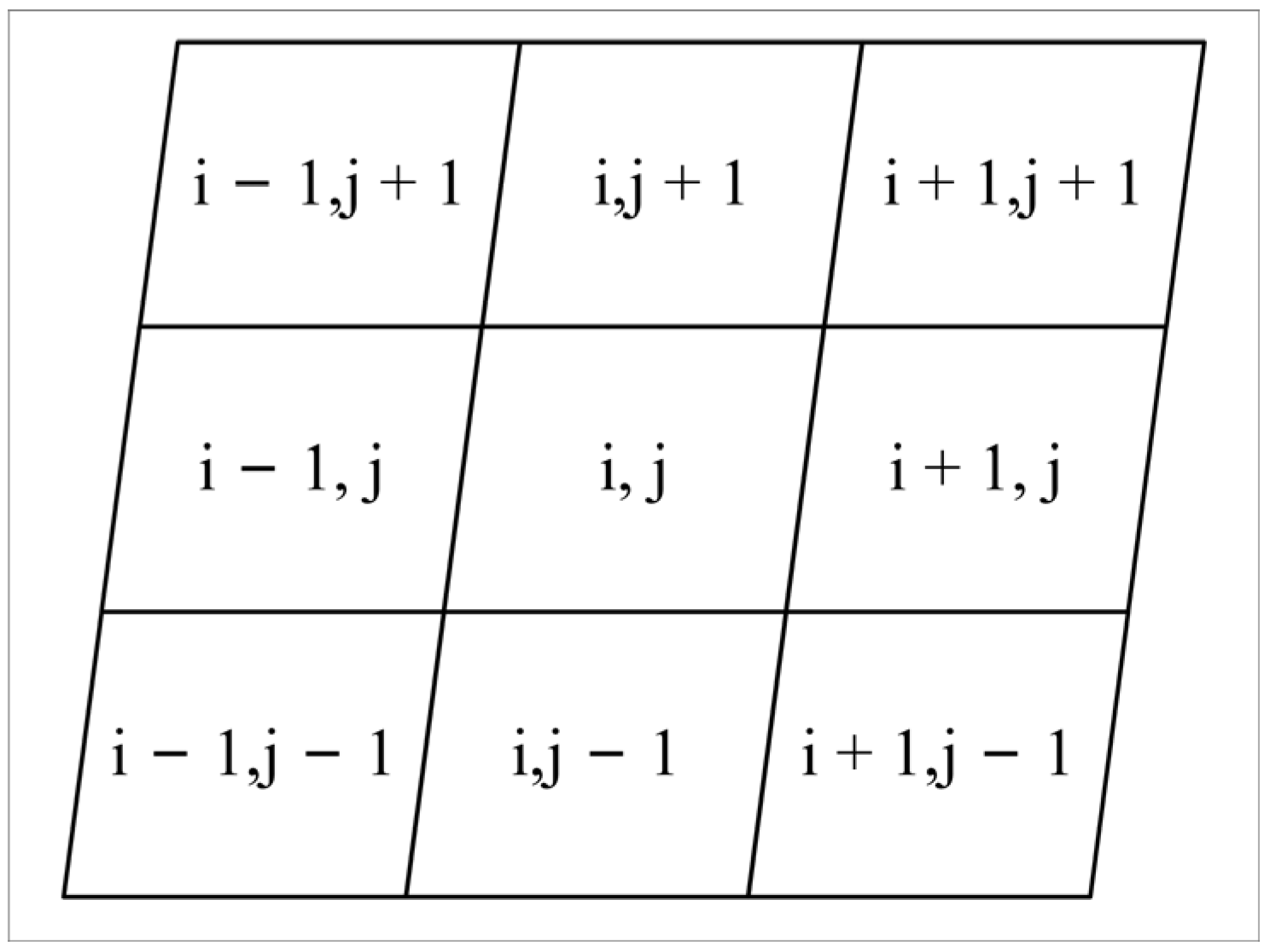
2.2.3. Search the Set of Ships Available for Rescue in the Neighborhood of the Ship in Distress According to the Effective Rescue Time
| Algorithm 2: Searching for vessels available for rescue within the determined effective rescue time and effective rescue distance in a certain sea area |
| Input: Lon, Lat, Time Output: SOA // Step 1: Determine the effective rescue distance according to the effective rescue time ShipType, Time→Distance // Step 2: Determining Google S2 encoding level based on effective rescue distance Distance→Precision // Step 3: Using Google S2 algorithm to convert the longitude and latitude information of the ship to be rescued into grid coding (lon, lat, precision)→gridcode // Step 4: Using grid coding to obtain the set of ships available for rescue gridcode→ SOA return SOA |
2.3. Sort the Set of Ships Available for Rescue According to the Distance from the Ship in Distress
| Algorithm 3: Alternative grid sorting based on neighborhood and different coding lengths |
| Input: Lon, Lat, Time, SOA Output: SOA_MD // Step 1: Determination of grid coding level based on effective rescue time and grid coding of ships in distress. (lon, lat, time)→gridcode // Step 2: Query the set of ships available for rescue within the same level and neighborhood of the ships in distress in the set of ships available for rescue. SOA, gridcode→SOA_MD // Step 3: Query the set of ships available for rescue on the ship in distress and the set of ships available for rescue in the neighborhood until the maximum level is reached. SOA, gridcode’→SOA_MD // Step 4: Output the set of ships available for rescue according to the distance from the ship in distress. return SOA_MD |
3. Experiments and Discussions
3.1. Experimental Area and Data
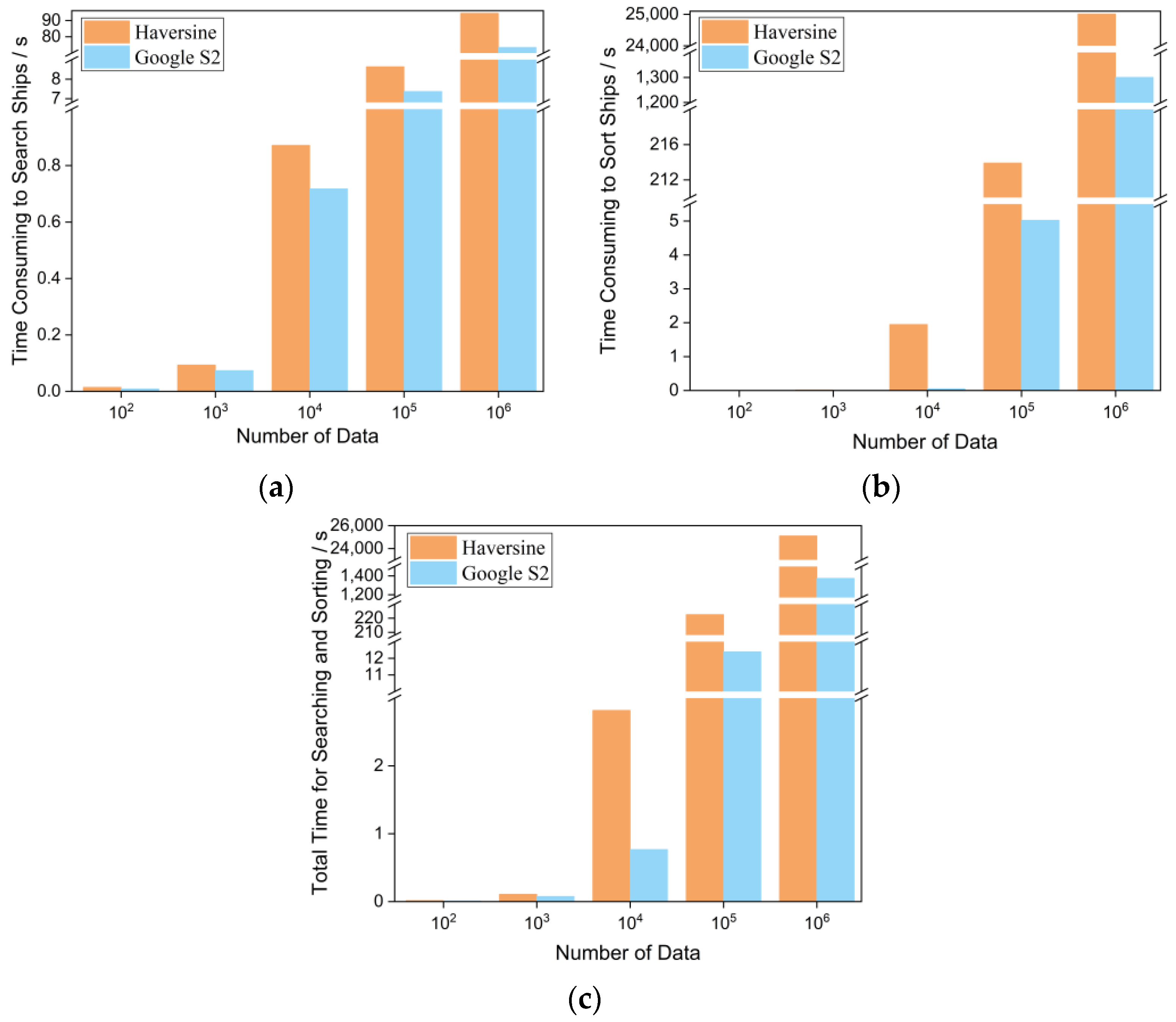
3.2. Time Retrieval Efficiency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, M.; Jiang, Q.; Liu, Y. Thoughts on informatization construction of coastal fishing ports in China. J. Fish. Res. 2021, 6, 316–321. [Google Scholar] [CrossRef]
- Daniel, P. A vision for marine fisheries in a global blue economy. Mar. Policy 2018, 87, 371–374. [Google Scholar] [CrossRef]
- FAO. The State of World Fisheries and Aquaculture 2020; Sustainability in action; FAO: Rome, Italy, 2020. [Google Scholar]
- Su, S.; Tang, Y.; Chang, B.; Zhu, W.; Chen, Y. Evolution of marine fisheries management in China from 1949 to 2019: How did China get here and where does China go next? Fish Fish. 2020, 21, 435–452. [Google Scholar] [CrossRef]
- Shen, G.; Heino, M. An overview of marine fisheries management in China. Mar. Policy 2014, 44, 265–272. [Google Scholar] [CrossRef]
- Ma, K.; Ren, L.; Zeng, J.; Wan, J. Ship rescue path planning considering adverse sea conditions. Mar. Sci. 2021, 45, 39–46. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Cong, L.; Li, J.; Zhang, J. Research on intelligent collision avoidance decision-making of unmanned ship in unknown environments. Evol. Syst. 2019, 10, 649–658. [Google Scholar] [CrossRef]
- Han, X. Current status of research on fishing vessels at home and abroad. Ship Eng. 2019, 41, 6–14. [Google Scholar]
- Huang, Y. Safety of fishing vessels operating at sea in China and its countermeasures. Shipp. Manag. 2021, 43, 10–12. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Meng, Q.; Xie, H. Ship accident consequences and contributing factors analyses using ship accident investigation reports. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 233, 35–47. [Google Scholar] [CrossRef]
- Wang, L.; Yun, Y.; Li, Q. Research on Collisions of Fishing Boats Based on Finite Element Method. In Proceedings of the 17th COTA International Conference of Transportation Professionals, Beijing, China, 5–8 July 2018; pp. 4650–4659. [Google Scholar]
- Annual Overview of Marine Casualties and Incidents 2023. Available online: https://www.emsa.europa.eu/component/flexicontent/download/7639/5052/23.html (accessed on 24 November 2023).
- Li, Z.; Liu, H.; Ai, W. Zhoushan Maritime Search and Rescue Status and Countermeasures. Shipp. Manag. 2018, 40, 28–29. [Google Scholar] [CrossRef]
- Yoo, S. Network analysis by fishing type for fishing vessel rescue. Phys. A Stat. Mech. Appl. 2019, 514, 892–901. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, L.; Min, K.; Zuo, X.; Yan, Z.; Ruan, X.; Chu, S.; Li, M. A framework for assessing the capability of maritime search and rescue in the south China sea. Int. J. Disaster Risk Reduct. 2020, 47, 101568. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, L.; Chu, S.; Song, Y. An autonomous coverage path planning algorithm for maritime search and rescue of persons-in-water based on deep reinforcement learning. Ocean Eng. 2024, 291, 116403. [Google Scholar] [CrossRef]
- Mahadi, C.M.H.C.; Mokhtar, K.; Chuah, L.F.; Chan, S.R.; Suhrab, M.I.R.; Mubashir, M.; Asif, S.; Show, P.L. An organisational search and rescue performance assessment for a cleaner environment. Clean. Eng. Technol. 2023, 14, 100641. [Google Scholar] [CrossRef]
- Peng, R.; Kong, D.; Pang, W.; Hong, W. Optimization method of ship dispatching for emergency rescue of personnel falling overboard on offshore platform. China Saf. Sci. J. 2022, 32, 208–215. [Google Scholar] [CrossRef]
- Solberg, K.E.; Jensen, J.E.; Barane, E.; Hagen, S.; Kjøl, A.; Johansen, G.; Gudmestad, O.T. Time to Rescue for Different Paths to Survival Following a Marine Incident. J. Mar. Sci. Eng. 2020, 8, 997. [Google Scholar] [CrossRef]
- Pan, K.; Pan, H.; He, Y. Strengthening maritime search and rescue capacity building to meet maritime emergency response needs. Shipp. Manag. 2014, 36, 26–29. [Google Scholar] [CrossRef]
- Lin, W.; Wang, N.; Gao, Z.; Wu, D. Associated searching and rescuing optimization of salvage vessels and helicopters in remote sea area. J. Traffic Transp. Eng. 2021, 21, 187–199. [Google Scholar] [CrossRef]
- International Maritime Organization/International Civil Aviation Organization. International Handbook on Aviation and Maritime Search and Rescue; People’s Communications Press: Beijing, China, 2003; pp. 1–286. [Google Scholar]
- National Maritime Search and Rescue Emergency Response Plan. Available online: https://www.gov.cn/yjgl/2006-01/23/content_168935.html (accessed on 24 June 2023).
- Zhou, W.; Sui, X.; Guo, X.; Jiang, Y.; Chen, T. Searching method for marine ship rescue based on grid neighborhood query. J. Geo-Inf. Sci. 2021, 23, 1422–1432. [Google Scholar] [CrossRef]
- Fan, W.; He, B.; Li, C.; Han, J.; Xu, Y.; Cui, C. Research on Spherical Distance Computation and Accuracy Comparison. Astron. Res. Technol. Publ. Natl. Astron. Obs. China 2019, 16, 69–76. [Google Scholar] [CrossRef]
- Prasetya, D.; Nguyen, P.; Faizullin, R.; Iswanto, I.; Armay, E. Resolving the shortest path problem using the haversine algorithm. J. Crit. Rev. 2020, 7, 62–64. [Google Scholar]
- Winarno, E.; Hadikurniawati, W.; Rosso, R. Location based service for presence system using haversine method. In Proceedings of the 2017 International Conference on Innovative and Creative Information Technology (ICITech), Salatiga, Indonesia, 2–4 November 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Li, X.; Feng, H.; Mei, Y.; Zhao, Y. Geographical Space Distance Calculation Algorithm Based on Three Time Polynomial Fitting Trigonometric Function. Comput. Meas. Control 2016, 24, 199–201. [Google Scholar] [CrossRef]
- S2Geometry. Available online: http://s2geometry.io/devguide/s2cell_level.html (accessed on 2 March 2023).
- Feng, Q. Research on Large-Scale Real-Time Lookup and Parallel Optimisation Based on Google S2 Algorithm; Hunan University: Changsha, China, 2020. [Google Scholar] [CrossRef]
- Liu, Y. Research on Location Privacy Protection Method Based on Google S2; Hunan University: Changsha, China, 2021. [Google Scholar] [CrossRef]
- Wu, F.; Feng, Q.; Tang, X. Real-Time Search Method for Large-Scale Regional Targets Based on Parallel Google S2 Algorithm. In Proceedings of the 2019 IEEE 21st International Conference on High Performance Computing and Communications, Zhangjiajie, China, 10–12 August 2019; pp. 1406–1413. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Zhan, W.; Yang, B.; Li, L.; Chen, F.; Meng, L. A Storage Method for Remote Sensing Images Based on Google S2. IEEE Access 2020, 8, 74943–74956. [Google Scholar] [CrossRef]
- East China Sea Fishery Research Institute; Chinese Academy of Fishery Sciences. Position-Based Marine Fishery Information Serving Method. Chinese Patent ZL2012 10332536.4, 24 September 2014. [Google Scholar]
- Zhang, P.; Wang, S. Demonstration of 4000 kW New Marine Rescue Ship Type Scheme. Shipp. Manag. 2021, 4, 26–29. [Google Scholar] [CrossRef]
- S2 Cell Statistics. Available online: https://s2geometry.io/resources/s2cell_statistics (accessed on 2 March 2023).
- Xiao, K. Study on Fast Retrieval of Remote Sensing Raster Data and Typhoon Path Vector Data Based on GeoHash and Google S2 Encoding; Shanghai Ocean University: Shanghai, China, 2022. [Google Scholar] [CrossRef]
- Python Documents. Available online: https://www.docs4dev.com/docs/zh/python/2.7.15/all/library-timeit.html (accessed on 2 March 2023).
- Wang, C.; Liu, W.D.; Song, J.X. Computer Organization and Design; Zhejiang University Publishing: Hangzhou, China, 2004. [Google Scholar]
- Amir, H.; Ahmed, M.; François, D. Data fusion in automotive applications Efficient big data stream computing approach. Pers. Ubiquitous Comput. 2017, 21, 443–455. [Google Scholar]
- National Yearbook of Fisheries Statistics 2020. Available online: https://www.cafs.ac.cn/info/1397/37342.html (accessed on 8 September 2023).
- Brahim, M.; Drira, W.; Filali, F.; Hamdi, N. Spatial data extension for Cassandra NoSQL database. J. Big Data 2016, 3, 11. [Google Scholar] [CrossRef]


| Column Name | Data Type | Null/Not Null | Comments |
|---|---|---|---|
| ID | int | Not Null | Unique identification code |
| ShipID | int | Not Null | Ship identification code |
| ShipName | varchar (50) | Not Null | Ship’s Name |
| Time | datetime | Not Null | Timestamp of position |
| Longitude | float | Not Null | Longitude of position |
| Latitude | float | Not Null | Latitude of position |
| Speed | float | Not Null | Vessel’s speed |
| Direction | float | Not Null | Vessel’s direction |
| GridCode | varchar (50) | Not Null | Google S2 Code to the ship’s position |
| ShipType | varchar (50) | Not Null | Ship Type |
| ShipTypeID | int | Not Null | Vessel Type ID |
| Speed (Nautical Miles/h) | Rescue Time/h | |||||
|---|---|---|---|---|---|---|
| 0.5 | 1 | 1.5 | 2 | 3 | 12 | |
| 8 (Fishing boat and Transport ship) | 7.4080 | 14.8160 | 22.2240 | 29.6320 | 44.4480 | 177.7920 |
| 9 (Fishing boat and Transport ship) | 8.3340 | 16.6680 | 25.0020 | 33.3360 | 50.0040 | 200.0160 |
| 10 (Fishing boat and Transport ship) | 9.2600 | 18.5200 | 27.7800 | 37.0400 | 55.5600 | 222.2400 |
| 15 (Professional rescue ship) | 13.8900 | 27.7800 | 41.6700 | 55.5600 | 83.3400 | 333.3600 |
| 20 (Professional rescue ship) | 18.5200 | 37.0400 | 55.5600 | 74.0800 | 111.1260 | 444.4800 |
| 25 (Professional rescue ship) | 23.1500 | 46.3000 | 69.4500 | 92.6000 | 138.9000 | 555.6000 |
| Level | Random Cell Min Edge Length | Random Cell Max Edge Length |
|---|---|---|
| 00 | 7842 km | 7842 km |
| 01 | 3921 km | 5004 km |
| 02 | 1825 km | 2489 km |
| 03 | 840 km | 1167 km |
| 04 | 432 km | 609 km |
| 05 | 210 km | 298 km |
| 06 | 108 km | 151 km |
| 07 | 54 km | 76 km |
| 08 | 27 km | 38 km |
| 09 | 14 km | 19 km |
| 10 | 7 km | 9 km |
| 11 | 3 km | 5 km |
| Speed (Nautical Miles/h) | Rescue Time/h | |||||
|---|---|---|---|---|---|---|
| 0.5 | 1 | 1.5 | 2 | 3 | 12 | |
| 8 (Fishing boat and Transport ship) | 10 | 09 | 09 | 08 | 08 | 06 |
| 9 (Fishing boat and Transport ship) | 10 | 09 | 09 | 08 | 08 | 06 |
| 10 (Fishing boat and Transport ship) | 10 | 09 | 08 | 08 | 07 | 05 |
| 15 (Professional rescue ship) | 10 | 08 | 08 | 07 | 07 | 05 |
| 20 (Professional rescue ship) | 09 | 08 | 07 | 07 | 06 | 04 |
| 25 (Professional rescue ship) | 09 | 08 | 07 | 07 | 06 | 04 |
| Items | Parameters |
|---|---|
| Operating System | Windows 10 Enterprise |
| CPU | Intel(R) Core (TM) i7-10510U CPU @ 1.80 GHz 2.30 GHz |
| RAM | 8.00 GB |
| MySQL | 8.0.27 |
| Python | 3.6 |
| Haversine | 2.8.0 |
| Pandas | 1.0.0 |
| s2sphere | 0.2.5 |
| Algorithm | Data Volume/Article | |||||
|---|---|---|---|---|---|---|
| 1 × 102 | 1 × 103 | 1 × 104 | 1 × 105 | 1 × 106 | ||
| Haversine | Calculation time | 0.0101 | 0.0573 | 0.5111 | 5.0309 | 55.2705 |
| Screening time | 0.0040 | 0.0359 | 0.3609 | 3.6078 | 39.1666 | |
| Sorting time | 0.0002 | 0.0144 | 1.9463 | 213.9144 | 25,008.8553 | |
| Total time | 0.0143 | 0.1076 | 2.8183 | 222.5531 | 25,103.2924 | |
| Google S2 | Processing time | 0.0044 | 0.0363 | 0.3618 | 3.6651 | 36.7658 |
| Screening time | 0.0041 | 0.0371 | 0.3560 | 3.7008 | 36.6822 | |
| Sorting time | 0.0005 | 0.0021 | 0.0503 | 5.0226 | 1300.2213 | |
| Total time | 0.0090 | 0.0755 | 0.7681 | 12.3885 | 1373.6693 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Zhou, W.; Han, H. Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2. Appl. Sci. 2024, 14, 1115. https://doi.org/10.3390/app14031115
Jiang B, Zhou W, Han H. Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2. Applied Sciences. 2024; 14(3):1115. https://doi.org/10.3390/app14031115
Chicago/Turabian StyleJiang, Bohui, Weifeng Zhou, and Haibin Han. 2024. "Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2" Applied Sciences 14, no. 3: 1115. https://doi.org/10.3390/app14031115
APA StyleJiang, B., Zhou, W., & Han, H. (2024). Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2. Applied Sciences, 14(3), 1115. https://doi.org/10.3390/app14031115





