Experimental Investigation on the Critical Dynamic Stress of Frozen Silty Clay Under Different Temperature and Moisture Conditions
Abstract
1. Introduction
2. Test Material and Methods
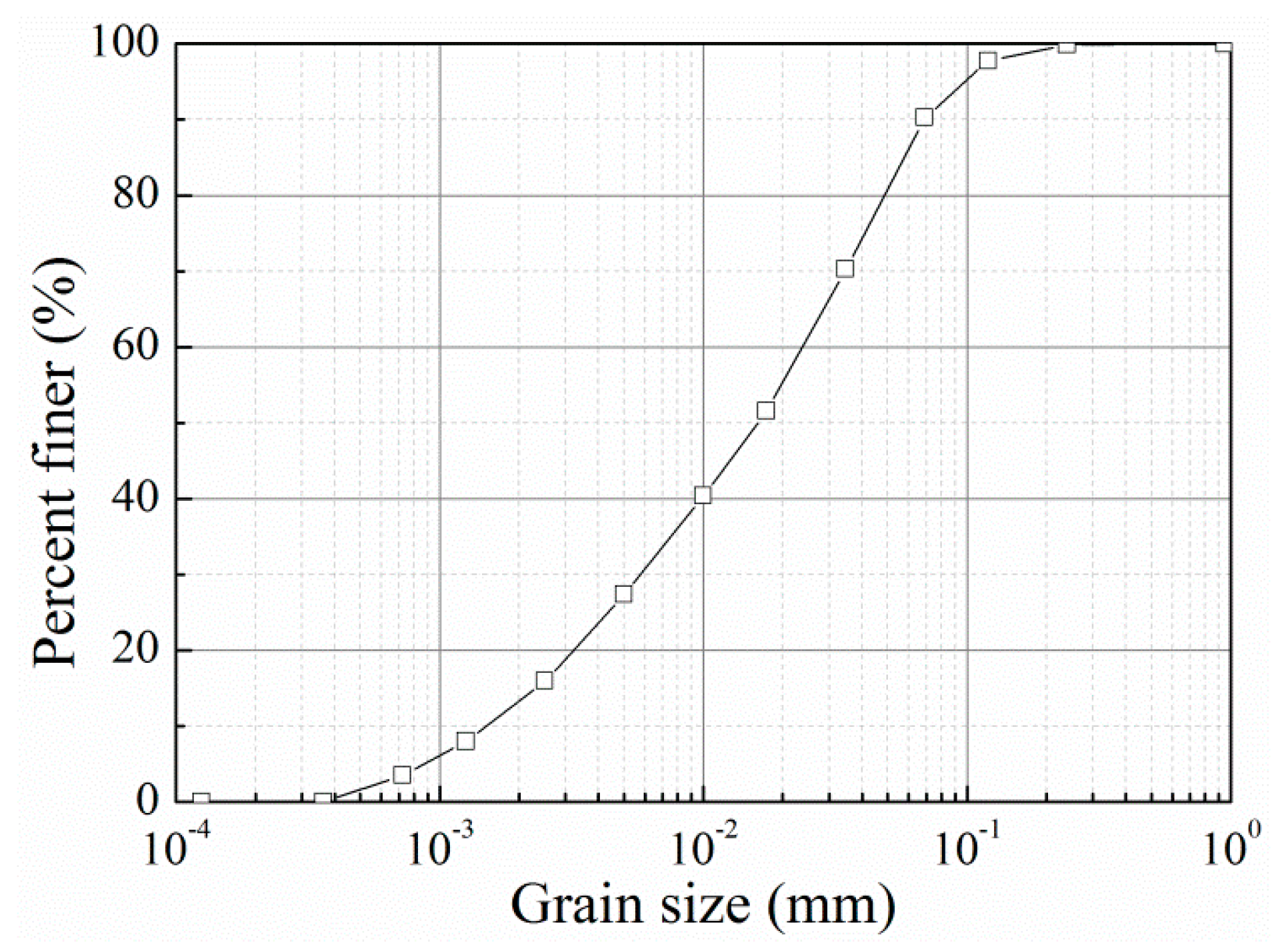
2.1. Soil and Specimen Preparation
2.2. Experimental Procedure and Operational Conditions
3. Results and Discussions
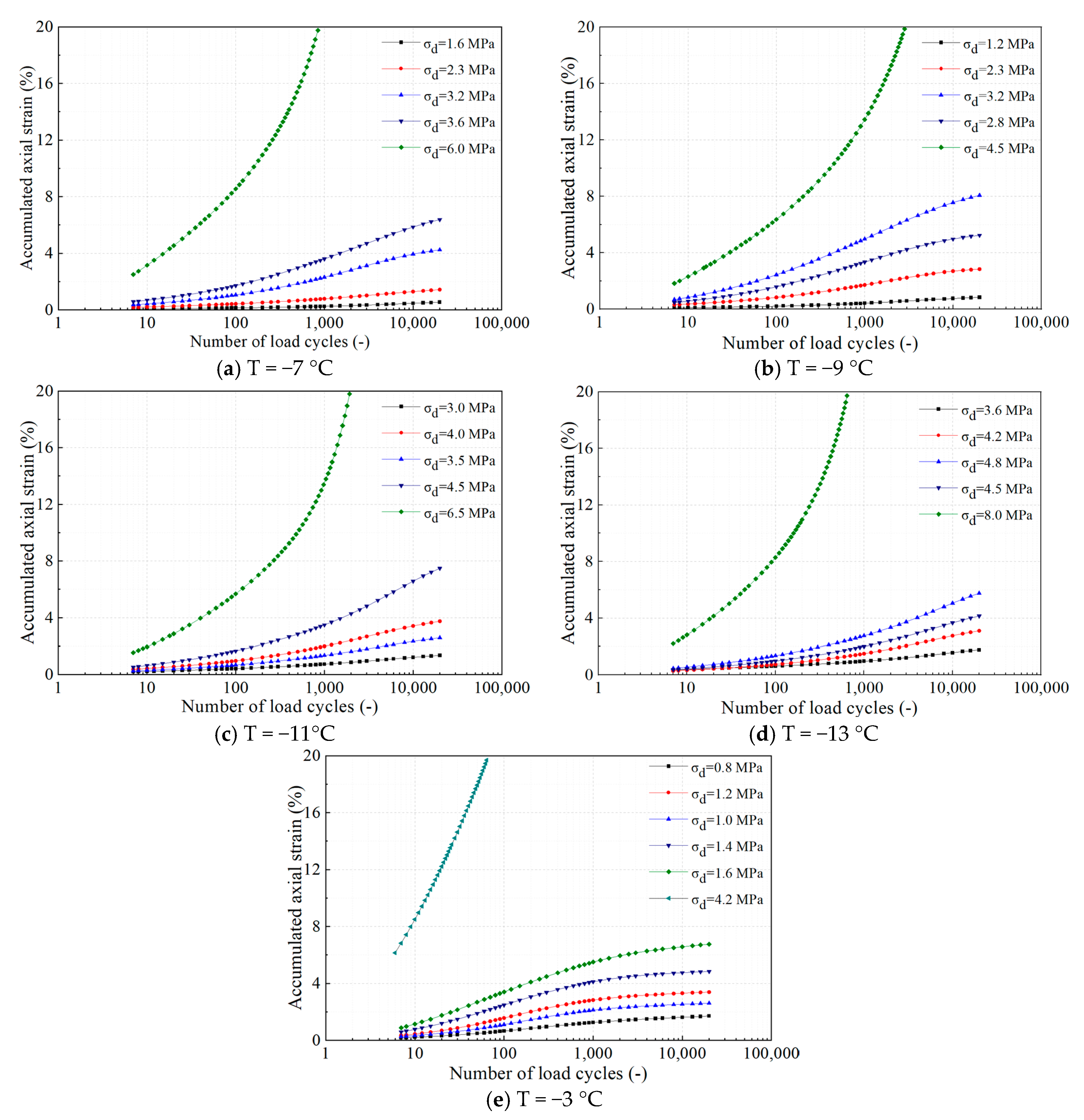
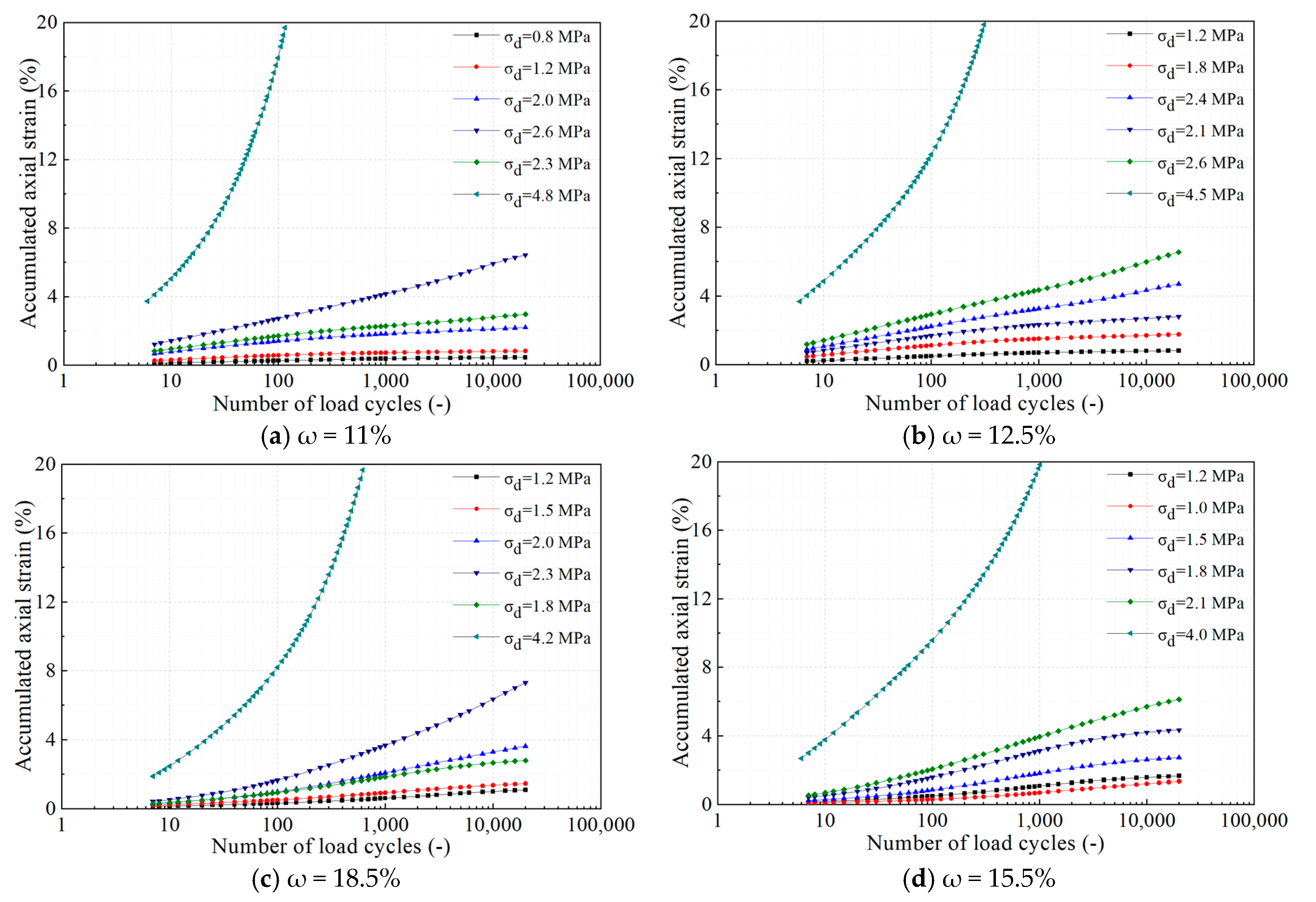
3.1. Permanent Deformation
3.1.1. Temperature Impact
3.1.2. Impact of Moisture Content
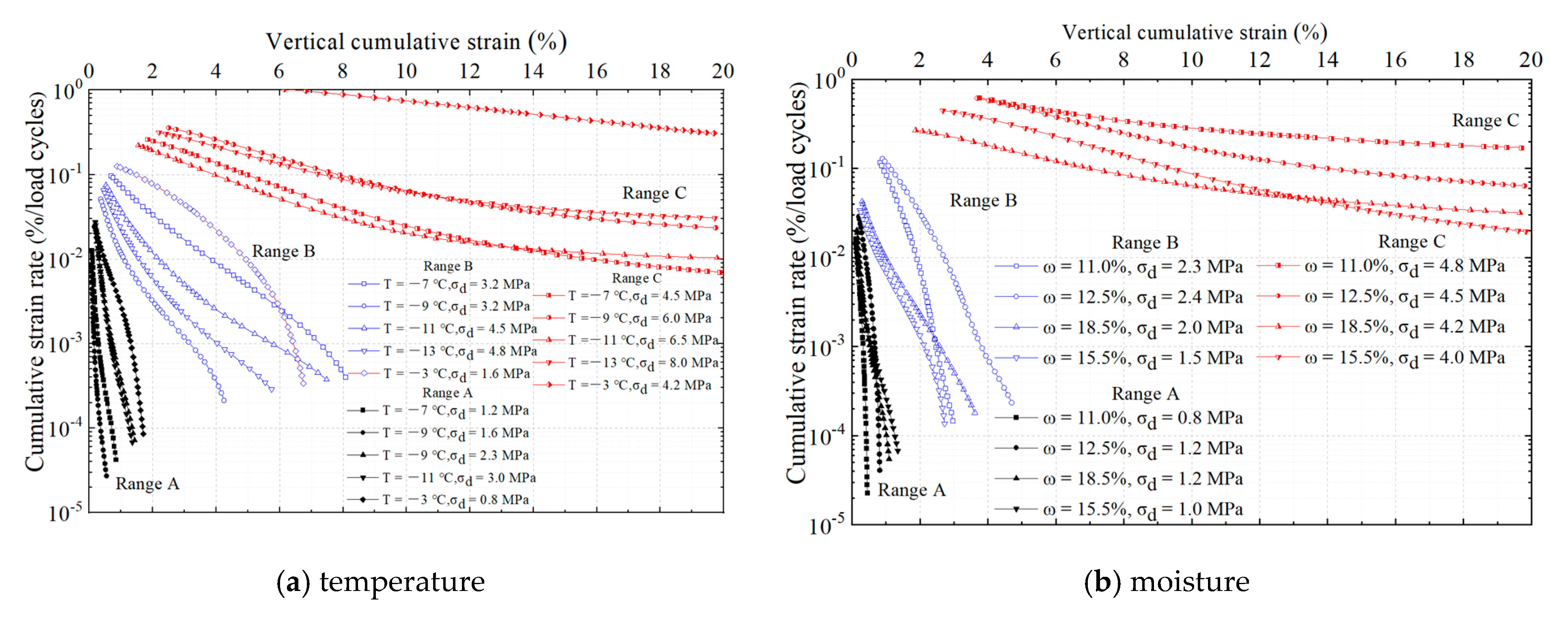
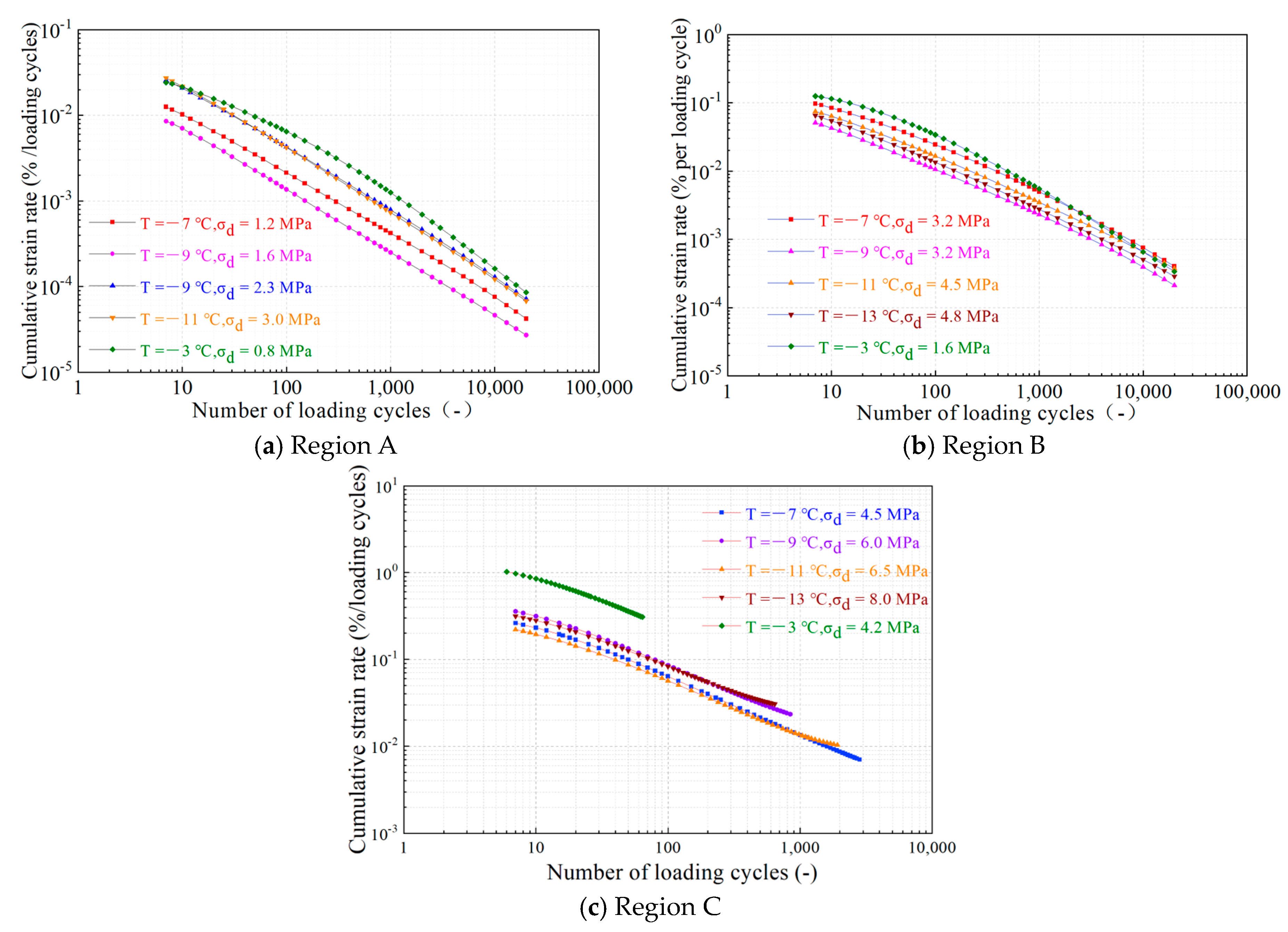
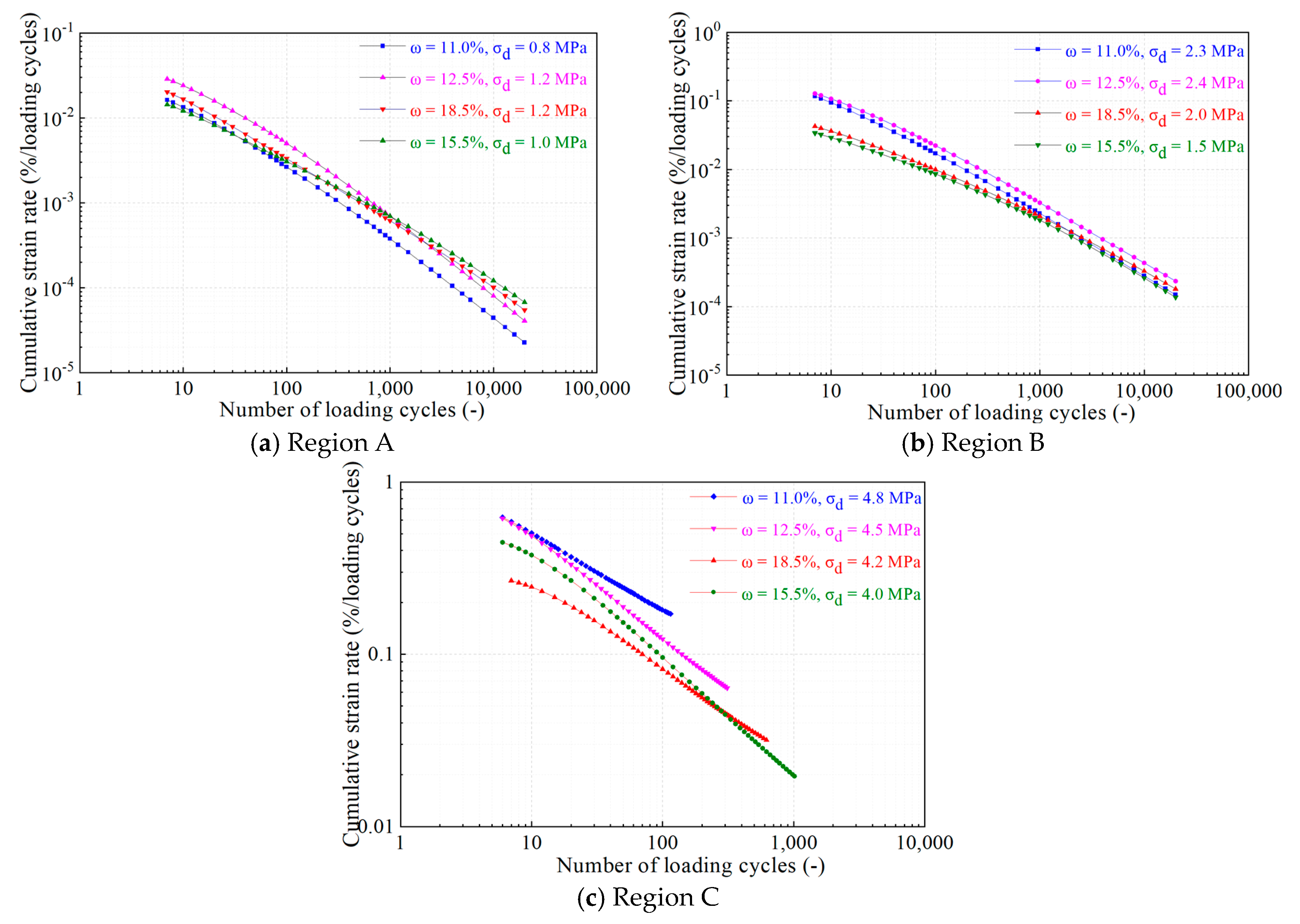
3.1.3. Different Temperature and Moisture Content Corresponding Regions
3.2. Calculation of Plastic Shakedown and Creep Limit
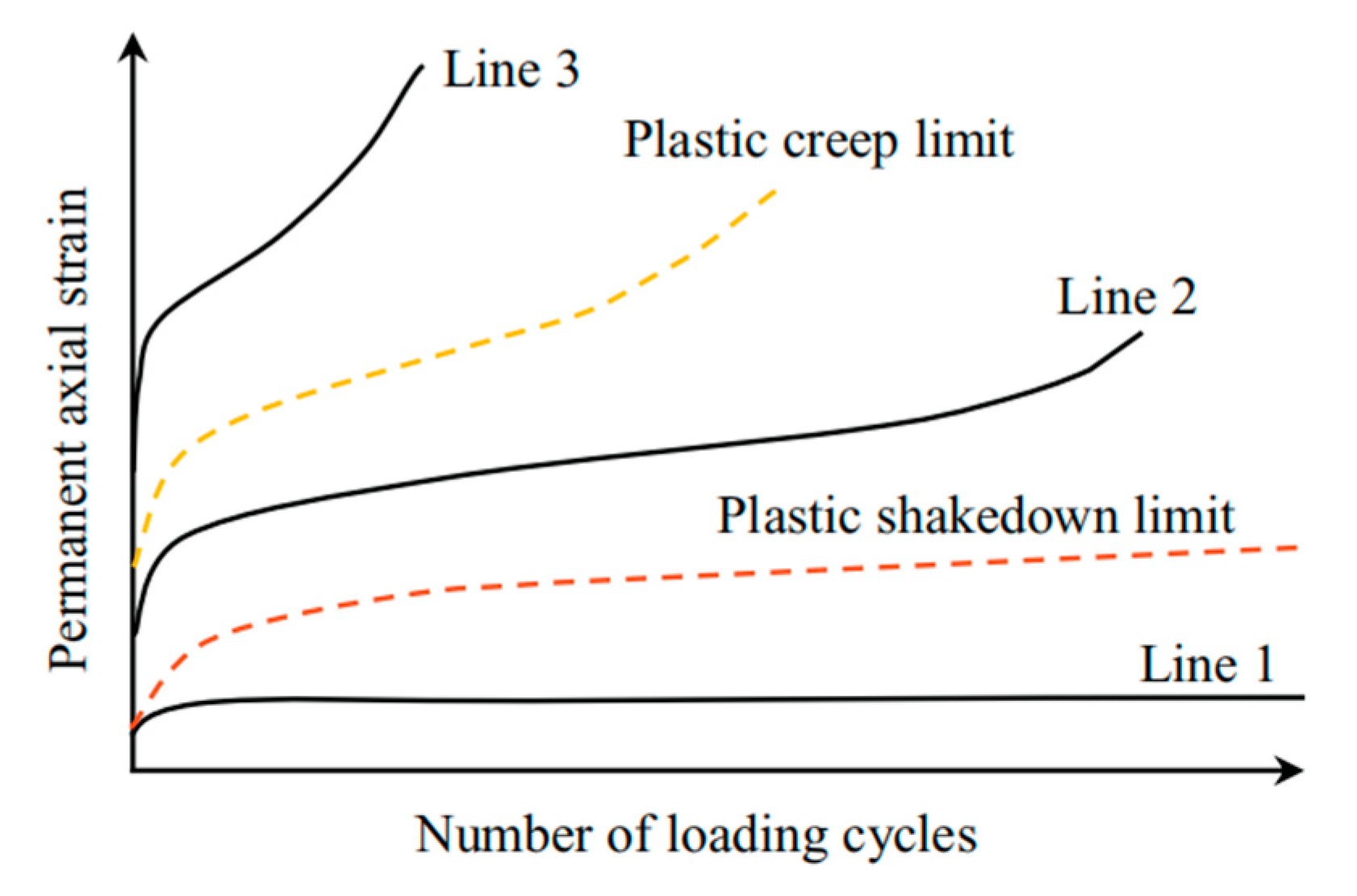
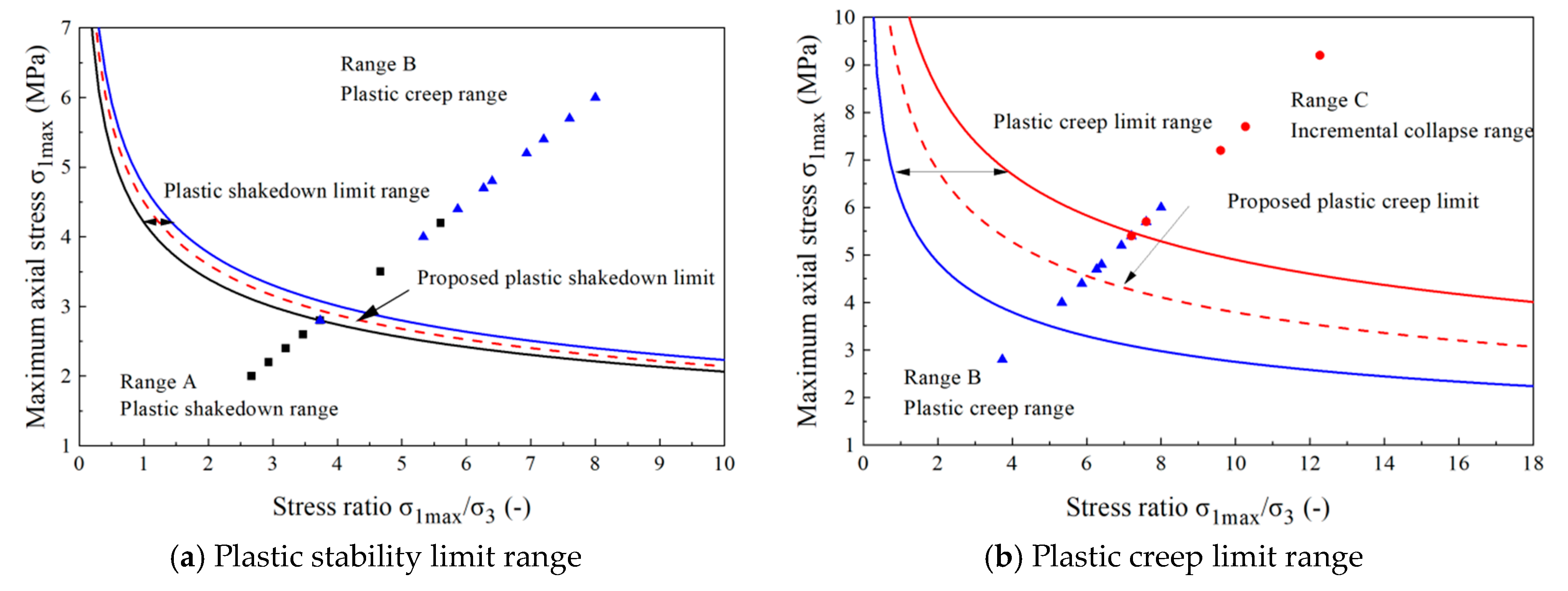
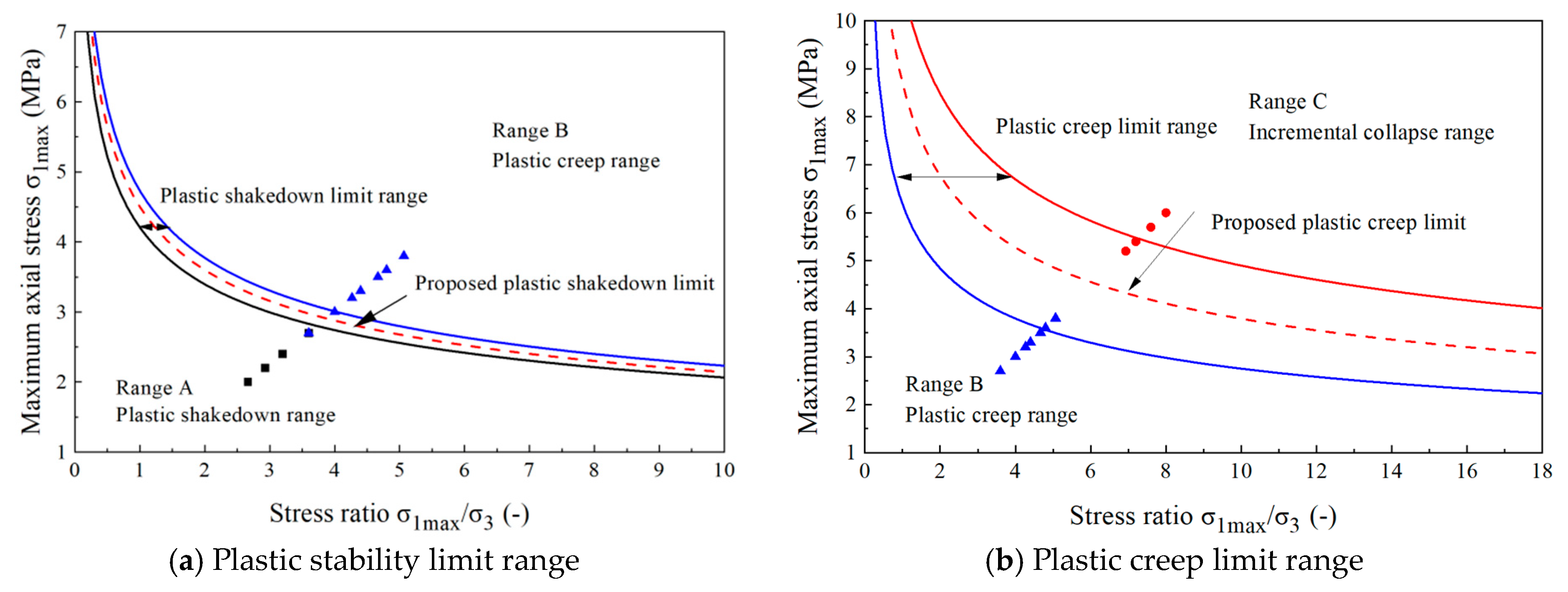
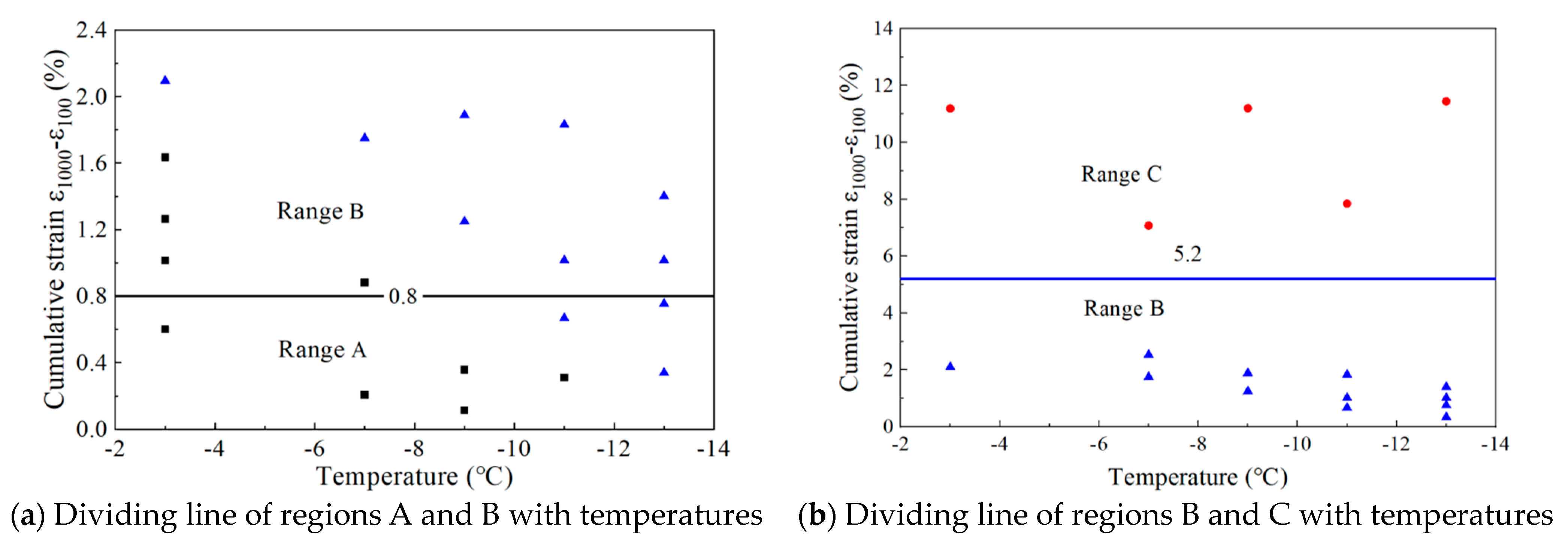
3.2.1. Threshold Intervals for the Permanent Deformation Attributes of Frozen Soil
3.2.2. Criteria for Plastic Shakedown and Creep Limits
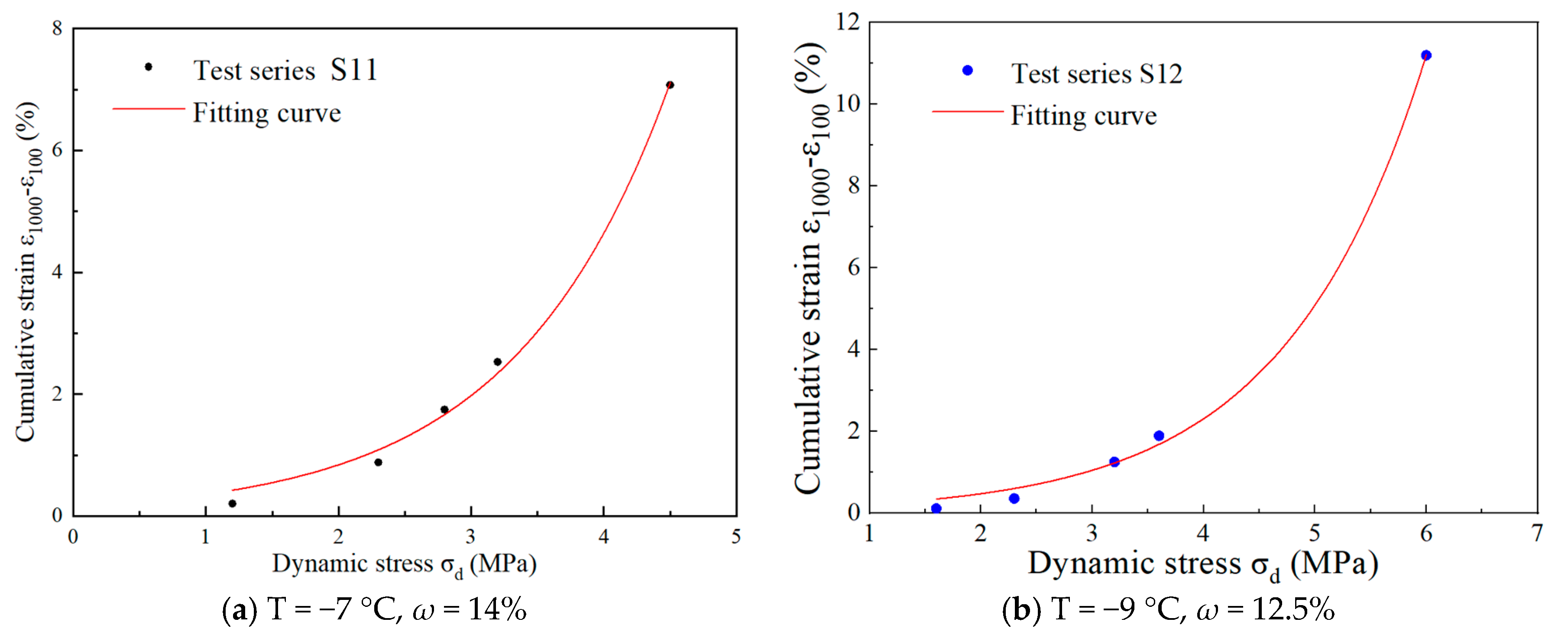
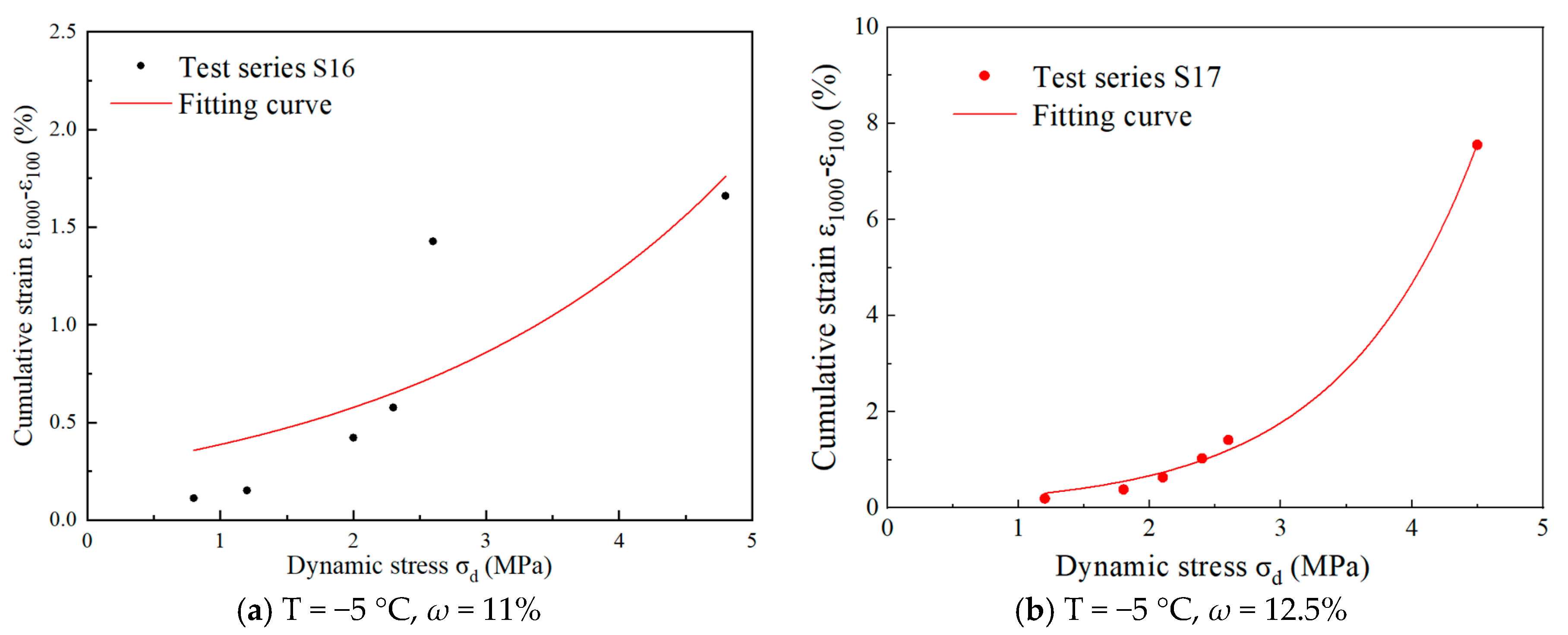
3.3. Critical Dynamic Stress
3.3.1. Calculation of CDS
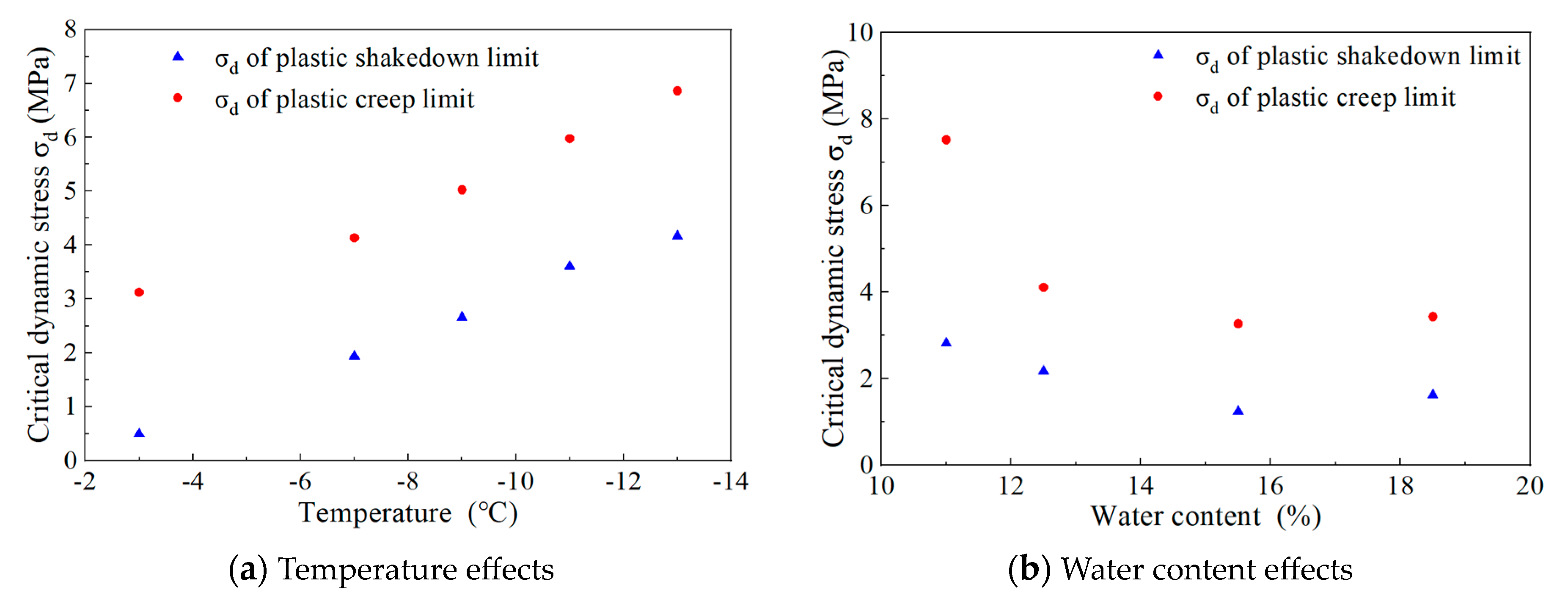
3.3.2. Impact of Temperature and Moisture Content
3.4. Discussions
4. Conclusions
- (1)
- The cumulative axial strain of frozen soil under cyclic loading is notably influenced by alterations in temperature and moisture content. Notably, under varying temperatures and water contents, the cumulative strain rate in Region A undergoes a swift decline with an increasing number of loading cycles, ultimately stabilizing at zero. Similarly, Region B experiences a rapid decrease in cumulative strain rate with more cycles. In Region C, while a general decrease is observed, certain curves exhibit a rebound trend, highlighting the complex interplay of temperature, moisture, and cyclic loading on the strain behavior of frozen soil.
- (2)
- Drawing upon the vertical CPS associated with the 100th and 1000th loading cycles, a definitive plastic stability and creep limit criterion is introduced for frozen silty clay. This criterion clearly establishes the plastic stability limit as the boundary between areas A and B, marked by a 0.8% difference, and the plastic creep limit as the threshold separating areas B and C, characterized by a 5.2% discrepancy. Employing the plastic limit criterion formula, we conclusively determine the CDS σd at both limits under varying stress levels, enabling a thorough analysis of how different temperatures and moisture contents impact this critical stress.
- (3)
- As temperature decreases, the CDS σd,s under the plasticity-stabilized creep limit exhibits a gradual upward trend in general. Assuming all other factors remain constant, lower temperatures lead to an enhancement in the strength and deformation resistance of frozen powdery clay, subsequently elevating the CDS.
- (4)
- As water content rises, the CDS σd,s under the plasticity-stabilized creep limit experiences an overall slow decline, with a slight recovery observed at a water content of 18.5%. At lower water contents, the decrease in CDS is gradual. Conversely, at higher water contents, the significant increase in the proportion of ice particles and the enhancement of their cementation result in markedly improved deformation resistance, thereby leading to an increase in the CDS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mei, Q.H.; Chen, J.; Liu, Y.Q.; Zhang, S.H.; Zhao, J.Y.; Dong, T.C.; Wang, J.C.; Zhao, Y.J. Degradation of warm permafrost and talik formation on the Qinghai–Tibet Plateau in 2006–2021. Adv. Clim. Chang. Res. 2024, 15, 275–284. [Google Scholar] [CrossRef]
- Zhao, H.; Hou, Y.; Jiang, G.; Wu, Q. Risk assessment of the crushed rock structure embankments of the Qinghai-Tibet Railway under a warming climate. Cold Reg. Sci. Technol. 2022, 196, 103509. [Google Scholar] [CrossRef]
- Zhu, Z.; Tang, C.; Ma, Y.; Luo, F.; Luo, B.; Zou, Z.; Guo, Z.; Jang, X. Train-induced vibration and subsidence prediction of the permafrost subgrade along the Qinghai-Tibet Railway. Soil Dyn. Earthq. Eng. 2022, 162, 107433. [Google Scholar] [CrossRef]
- Pan, W. Research on Thermal Stability of Railway Roadbed in the Permafrost Area of the Qinghai-Tibet Plateau. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2002. [Google Scholar]
- Ma, W.; Feng, G.; Wu, Q.; Wu, J. Analyses of temperature fields under the embankment with crushed-rock structures along the Qinghai-Tibet railway. Cold Reg. Sci. Technol. 2008, 53, 259–270. [Google Scholar] [CrossRef]
- Sha, A.; Ma, B.; Wang, H.; Hu, L.; Mao, X.; Zhi, X.; Chen, H.; Liu, Y.; Ma, F.; Liu, Z.; et al. Highway constructions on the Qinghai-Tibet Plateau: Challenge, research and practice. J. Road Eng. 2022, 2, 1–60. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Ling, X.Z.; Chen, S.J.; Zhang, F.; Wang, L.; Wang, Z.; Zou, Z. Experimental investigation on the train induced subsidence prediction model of Beiluhe permafrost subgrade along the Qinghai-Tibet Railway in China. Cold Reg. Sci. Technol. 2010, 62, 67–75. [Google Scholar] [CrossRef]
- Li, Q.L.; Ling, X.Z.; Sheng, D.C. Elasto-plastic behaviour of frozen soil subjected to long-term low-level repeated loading, part I: Experimental investigation. Cold Reg. Sci. Technol. 2016, 125, 138–151. [Google Scholar] [CrossRef]
- Lin, B.; Zhang, F.; Feng, D.; Tang, K.; Feng, X. Dynamic shear modulus and damping ratio of thawed saturated clay under long-term cyclic loading. Cold Reg. Sci. Technol. 2018, 145, 93–105. [Google Scholar] [CrossRef]
- Huang, K.; Ma, Q.; Ma, D.; Yao, Z. Strength and deformation properties of frozen sand under a true triaxial stress condition. Soils Found. 2021, 62, 101089. [Google Scholar] [CrossRef]
- Ngoma, M.C.; Kolawole, O. Porosity and bedding controls on bio-induced carbonate precipitation and mechanical properties of shale and dolomitic rocks: EICP vs MICP. Biogeotechnics 2024, 2, 100102. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, Y.; Cui, H.; He, X.; Liu, H. Dancing with crystals: Bacterial functions and interactions in biomineralization. Biogeotechnics 2024, 2, 100084. [Google Scholar] [CrossRef]
- Huang, K.; Ma, Q.; Cai, G.; Ma, D.; Yao, Z.; Zhang, H. Influence of intermediate principal stress ratio on strength and deformation characteristics of frozen sandy soil under different moisture contents. Cold Reg. Sci. Technol. 2023, 213, 103909. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Li, Q.; Zhang, F.; Li, Y. Accumulated permanent strain and critical dynamic stress of frozen silty clay under cyclic loading. Cold Reg. Sci. Technol. 2018, 153, 130–143. [Google Scholar] [CrossRef]
- Xu, X.; Li, Q.; Lai, Y.; Pang, W.; Zhang, R. Effect of moisture content on mechanical and damage behavior of frozen loess under triaxial condition along with different confining pressures. Cold Reg. Sci. Technol. 2019, 157, 110–118. [Google Scholar] [CrossRef]
- Zhao, F.; Chang, L.; Zhang, W. Experimental investigation of dynamic shear modulus and damping ratio of Qinghai-Tibet frozen silt under multi-stage cyclic loading. Cold Reg. Sci. Technol. 2019, 170, 102938. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, D.; Zhao, T.; Ma, J.; Zhao, D. An experimental research on damping ratio and dynamic shear modulus ratio of frozen silty clay of the Qinghai-Tibet engineering corridor. Transp. Geotech. 2019, 21, 100269. [Google Scholar] [CrossRef]
- Wu, G.; Li, G.; Bing, H.; Chen, D.; Tang, L.; Jia, H. Effects of confining pressure and temperature on strength and deformation behavior of frozen saline silty clay. Sci. Cold Arid Reg. 2023, 15, 1–10. [Google Scholar] [CrossRef]
- Zhu, Z.; Jia, J.; Zhang, F. A damage and elastic-viscoplastic constitutive model of frozen soil under uniaxial impact loading and its numerical implementation. Cold Reg. Sci. Technol. 2020, 175, 103081. [Google Scholar] [CrossRef]
- Zhu, Z.; Fu, T.; Ning, J.; Li, B. Mechanical behavior and constitutive model of frozen soil subjected to cyclic impact loading. Int. J. Impact Eng. 2023, 177, 104531. [Google Scholar] [CrossRef]
- Wang, D.; Liu, E.; Zhang, D.; Yue, P.; Wang, P.; Kang, J.; Yu, Q. An elasto-plastic constitutive model for frozen soil subjected to cyclic loading. Cold Reg. Sci. Technol. 2021, 189, 103341. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, Z.; Ma, Y.; Yao, Z.; Tan, Q.; Liu, Z.; Xu, J.; Zheng, S. Numerical simulation for vibration-induced settlement and permanent deformation accumulation in permafrost subgrades of the Qinghai-Tibet Railway. Comput. Geotech. 2024, 167, 106047. [Google Scholar] [CrossRef]
- Shastri, A.; Sánchez, M.; Gai, X.; Lee, M.; Dewers, T. Mechanical behavior of frozen soils: Experimental investigation and numerical modeling. Comput. Geotech. 2021, 138, 104361. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, G.; Shen, M.; Wang, Q. Dynamic responses of frozen subgrade soil exposed to freeze-thaw cycles. Soil Dyn. Earthq. Eng. 2022, 152, 107010. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Xu, L.; Peng, B. Long-term freeze–thaw cycle behavior of high-speed railway embankment in frozen soil regions and its effects on train-track dynamic interaction system. Transp. Geotech. 2024, 46, 101237. [Google Scholar] [CrossRef]
- Li, T.; Kong, L.; Guo, A. The deformation and microstructure characteristics of expansive soil under freeze–thaw cycles with loads. Cold Reg. Sci. Technol. 2021, 192, 103393. [Google Scholar] [CrossRef]
- Cui, G.; Liu, Z.; Ma, S.; Zhou, C. Dynamic characteristics of carbonate saline soil under freeze–thaw cycles in the seasonal frozen soil region. Alex. Eng. J. 2023, 81, 384–394. [Google Scholar] [CrossRef]
- Chen, Q.; Ghimire, B.; Su, L.; Liu, Y. Micro-scale investigations on the mechanical properties of expansive soil subjected to freeze-thaw cycles. Cold Reg. Sci. Technol. 2024, 219, 104128. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, W.; Zhang, S.; Mu, Y.; Li, G. Effect of freeze-thaw cycles in mechanical behaviors of frozen loess. Cold Reg. Sci. Technol. 2018, 146, 9–18. [Google Scholar] [CrossRef]
- Li, B.; Zhu, Z.; Zhang, F.; Chunyu, Z.; Li, T. Impact mechanical properties of frozen soil after experiencing freeze–thaw cycles: Experimental and numerical study. Cold Reg. Sci. Technol. 2023, 213, 103914. [Google Scholar] [CrossRef]
- Zhai, B.; Leng, W.; Xu, F.; Zhang, S.; Ye, X.; Leng, H. Critical dynamic stress and shakedown limit criterion of coarse-grained subgrade soil. Transp. Geotech. 2020, 23, 100354. [Google Scholar] [CrossRef]
- Zhao, Y.; Lai, Y.; Pei, W.; Fan, Y. An anisotropic bounding surface elastoplastic constitutive model for frozen sulfate saline silty clay under cyclic loading. Int. J. Plast. 2020, 129, 102668. [Google Scholar] [CrossRef]
- Zhou, Z.; Shen, M.; Wang, Q. Critical dynamic stress for the frozen subgrade soil. Road Mater. Pavement Des. 2023, 24, 935–959. [Google Scholar] [CrossRef]
- Peellage, W.H.; Fatahi, B.; Rasekh, H. Assessment of cyclic deformation and critical stress amplitude of jointed rocks via cyclic triaxial testing. J. Rock Mech. Geotech. Eng. 2023, 15, 1370–1390. [Google Scholar] [CrossRef]
- Li, Y.; Nie, R.; Yue, Z.; Leng, W.; Guo, Y. Dynamic behaviors of fine-grained subgrade soil under single-stage and multi-stage intermittent cyclic loading: Permanent deformation and its prediction model. Soil Dyn. Earthq. Eng. 2021, 142, 106548. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Yang, P.; Ling, X.; Zhao, Y.; Su, L. Experimental investigation on dynamic characteristics of fiber-binder modified subgrade filler after freezing-thawing under cyclic loading. Transp. Geotech. 2023, 39, 100936. [Google Scholar] [CrossRef]
- Cui, G.; Zhu, C.; Xi, C.; Ma, S.; Liu, Z.; Zhang, D. Experimental study of the dynamic characteristics of Songhua River silt with fine grains under freeze-thaw cycles using asymmetric hysteresis. Cold Reg. Sci. Technol. 2022, 196, 103511. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, W.; Li, G.; Shen, M. A novel evaluation method for accumulative plastic deformation of granular materials subjected to cyclic loading: Taking frozen subgrade soil as an example. Cold Reg. Sci. Technol. 2020, 179, 103152. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Chinese Standard for Soil Test Method. The Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing China, 2019.
- TB10102-2010; Railway Engineering Geotechnical Test Specification. People’s Republic of China Ministry of Railways/Railway Press: Beijing China, 2011.
- Wichtmann, T.; Niemunis, A.; Triantafyllidis, T. Strain accumulation in sand due to cyclic loading: Drained triaxial tests. Soil Dyn. Earthq. Eng. 2005, 25, 967–979. [Google Scholar] [CrossRef]
- Karg, C.; Haegeman, W. Elasto-plastic long-term behavior of granular soils: Experimental investigation. Soil Dyn. Earthq. Eng. 2009, 29, 155–172. [Google Scholar] [CrossRef]
- Cerni, G.; Cardone, F.; Virgili, A.; Camilli, S. Characterisation of permanent deformation behaviour of unbound granular materials under repeated triaxial loading. Constr. Build. Mater. 2012, 28, 79–87. [Google Scholar] [CrossRef]
- Wang, L.; Weng, Z.; Wang, T.; Liu, Q.; Li, G.; Zhao, Y. Critical dynamic stress and accumulative deformation evolution of embankment silty clay subjected to cyclic freeze-thaw. Shock Vib. 2021, 2021, 9068254. [Google Scholar] [CrossRef]
- Liu, H.; Wang, C.; Wu, D.; Liu, X.; Zhang, Z. Deformation and critical dynamic stress for compacted volcanic ash subjected to monotonic and dynamic loads. Constr. Build. Mater. 2022, 358, 129454. [Google Scholar] [CrossRef]

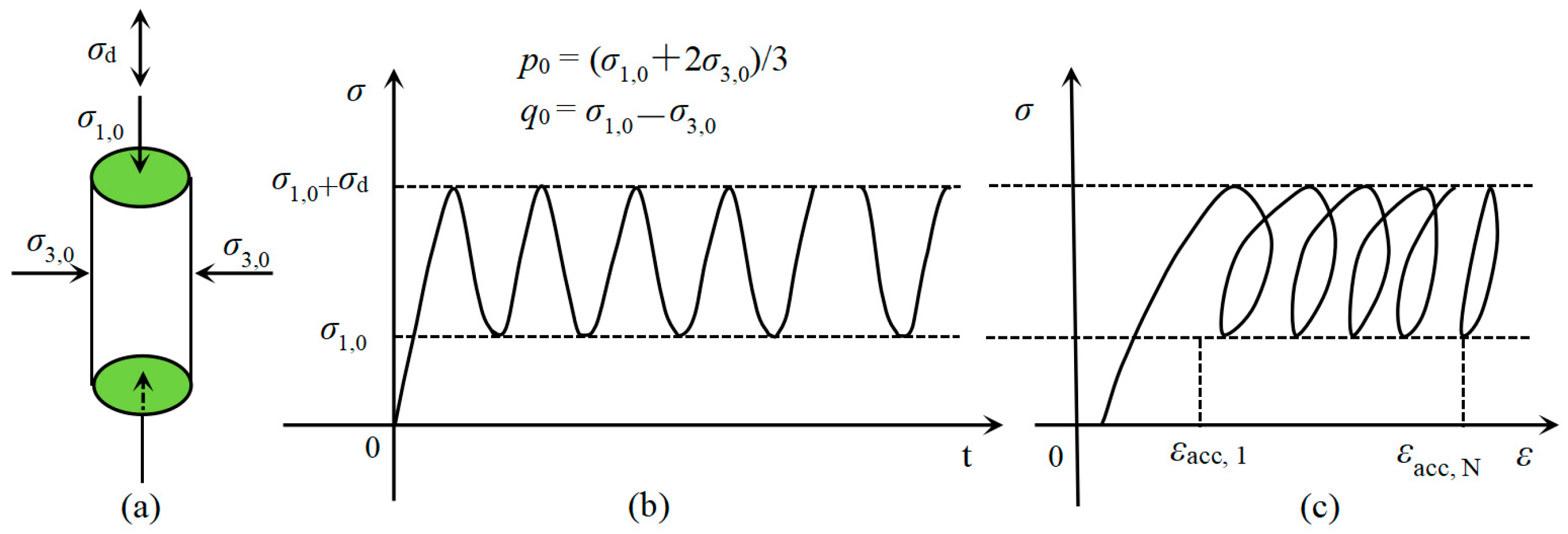
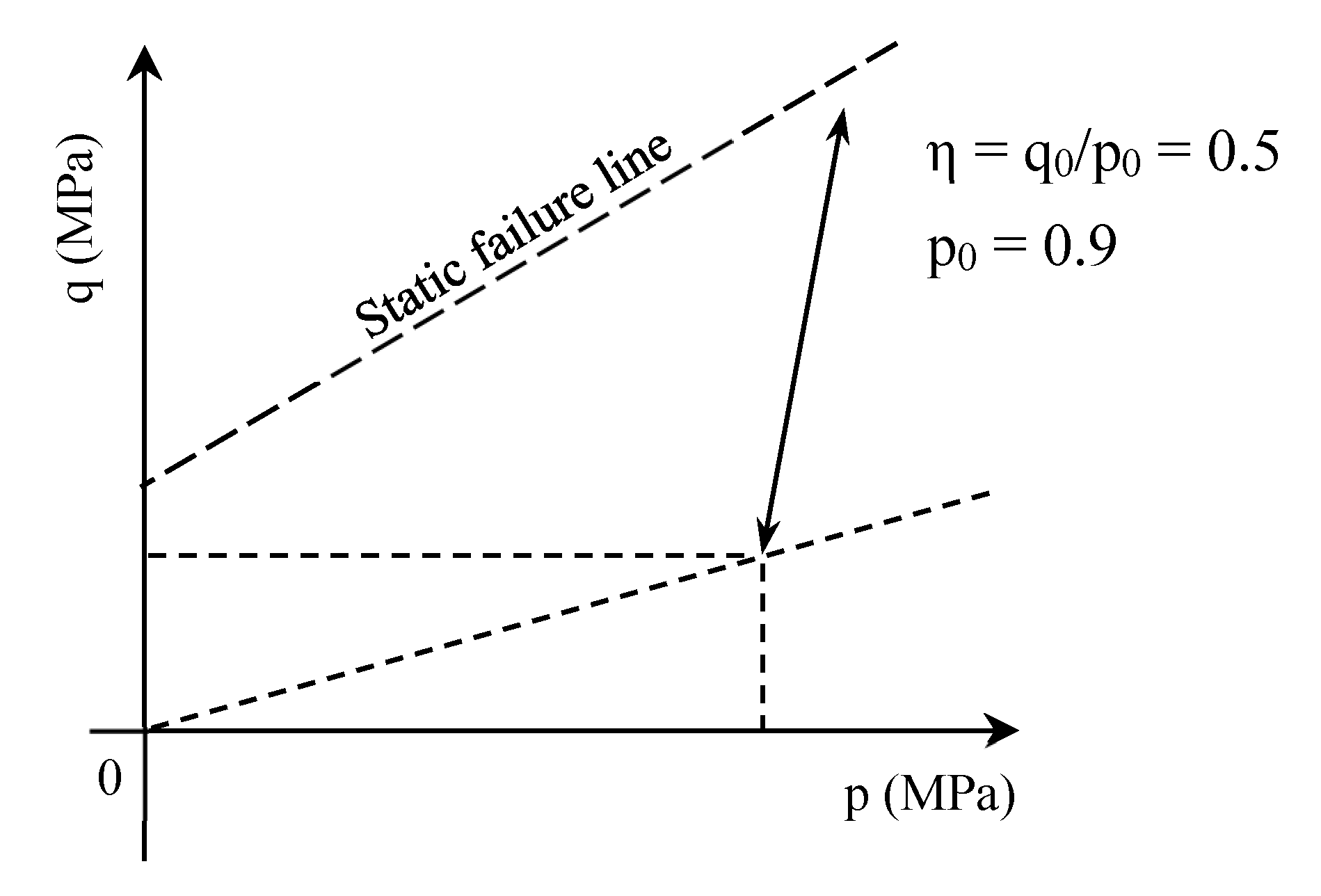

| Test Series | σ3,0 (MPa) | σ1,0 (MPa) | η0 = q0/p0 | p0 (MPa) | T (°C) | Ω (%) | σd (MPa) |
|---|---|---|---|---|---|---|---|
| S1: D51-D55 | 0.75 | 1.2 | 0.5 | 0.9 | −7 | 14 | 1.2, 2.3, 3.2, 2.8, 4.5 |
| S2: D56-D60 | 0.75 | 1.2 | 0.5 | 0.9 | −9 | 14 | 1.6, 2.3, 3.2, 3.6, 6.0 |
| S3: D61-D65 | 0.75 | 1.2 | 0.5 | 0.9 | −11 | 14 | 3.0, 4.0, 3.5, 4.5, 6.5 |
| S4: D66-D70 | 0.75 | 1.2 | 0.5 | 0.9 | −13 | 14 | 3.6, 4.2, 4.8, 4.5, 8.0 |
| S5: D71-D76 | 0.75 | 1.2 | 0.5 | 0.9 | −3 | 14 | 0.8, 1.2, 1.0, 1.4, 1.6, 4.2 |
| S6: D77-D82 | 0.75 | 1.2 | 0.5 | 0.9 | −5 | 11 | 0.8, 1.2, 2.0, 2.6, 2.3, 4.8 |
| S7: D83-D88 | 0.75 | 1.2 | 0.5 | 0.9 | −5 | 12.5 | 1.2, 1.8, 2.4, 2.1, 2.6, 4.5 |
| S8: D89-D94 | 0.75 | 1.2 | 0.5 | 0.9 | −5 | 18.5 | 1.2, 1.5, 2.0, 2.3, 1.8, 4.2 |
| S9: D95-D100 | 0.75 | 1.2 | 0.5 | 0.9 | −5 | 15.5 | 1.2, 1.0, 1.5, 1.8, 2.1, 4.0 |
| Test Sequence | Formulas εsub = a*eb*x | a | b | R2 |
|---|---|---|---|---|
| S1:D51–D55 | εsub = 0.15e0.85x | 0.15 | 0.85 | 0.994 |
| S2:D56–D60 | εsub = 0.10e0.79x | 0.10 | 0.79 | 0.998 |
| S3:D61–D65 | εsub = 0.05e0.79x | 0.05 | 0.79 | 0.997 |
| S4:D66–D70 | εsub = 0.04e0.69x | 0.04 | 0.69 | 0.999 |
| S5:D71–D76 | εsub = 0.56e0.71x | 0.56 | 0.71 | 0.995 |
| S6:D77–D82 | εsub = 0.26e0.40x | 0.26 | 0.40 | 0.626 |
| S7:D83–D88 | εsub = 0.10e0.97x | 0.10 | 0.97 | 0.997 |
| S8: D89–D94 | εsub = 0.28e0.88x | 0.15 | 1.03 | 0.996 |
| S9:D95–D100 | εsub = 0.25e0.92x | 0.25 | 0.92 | 0.997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ding, J.; Zhao, Y. Experimental Investigation on the Critical Dynamic Stress of Frozen Silty Clay Under Different Temperature and Moisture Conditions. Appl. Sci. 2024, 14, 11419. https://doi.org/10.3390/app142311419
Wang J, Ding J, Zhao Y. Experimental Investigation on the Critical Dynamic Stress of Frozen Silty Clay Under Different Temperature and Moisture Conditions. Applied Sciences. 2024; 14(23):11419. https://doi.org/10.3390/app142311419
Chicago/Turabian StyleWang, Jiahui, Jiahao Ding, and Yingying Zhao. 2024. "Experimental Investigation on the Critical Dynamic Stress of Frozen Silty Clay Under Different Temperature and Moisture Conditions" Applied Sciences 14, no. 23: 11419. https://doi.org/10.3390/app142311419
APA StyleWang, J., Ding, J., & Zhao, Y. (2024). Experimental Investigation on the Critical Dynamic Stress of Frozen Silty Clay Under Different Temperature and Moisture Conditions. Applied Sciences, 14(23), 11419. https://doi.org/10.3390/app142311419