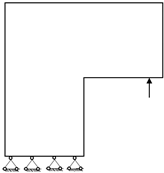
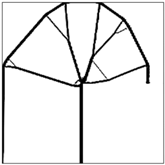
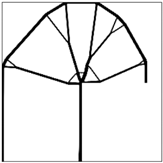
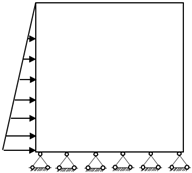
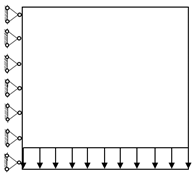
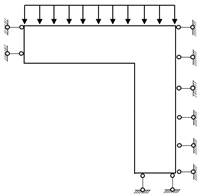
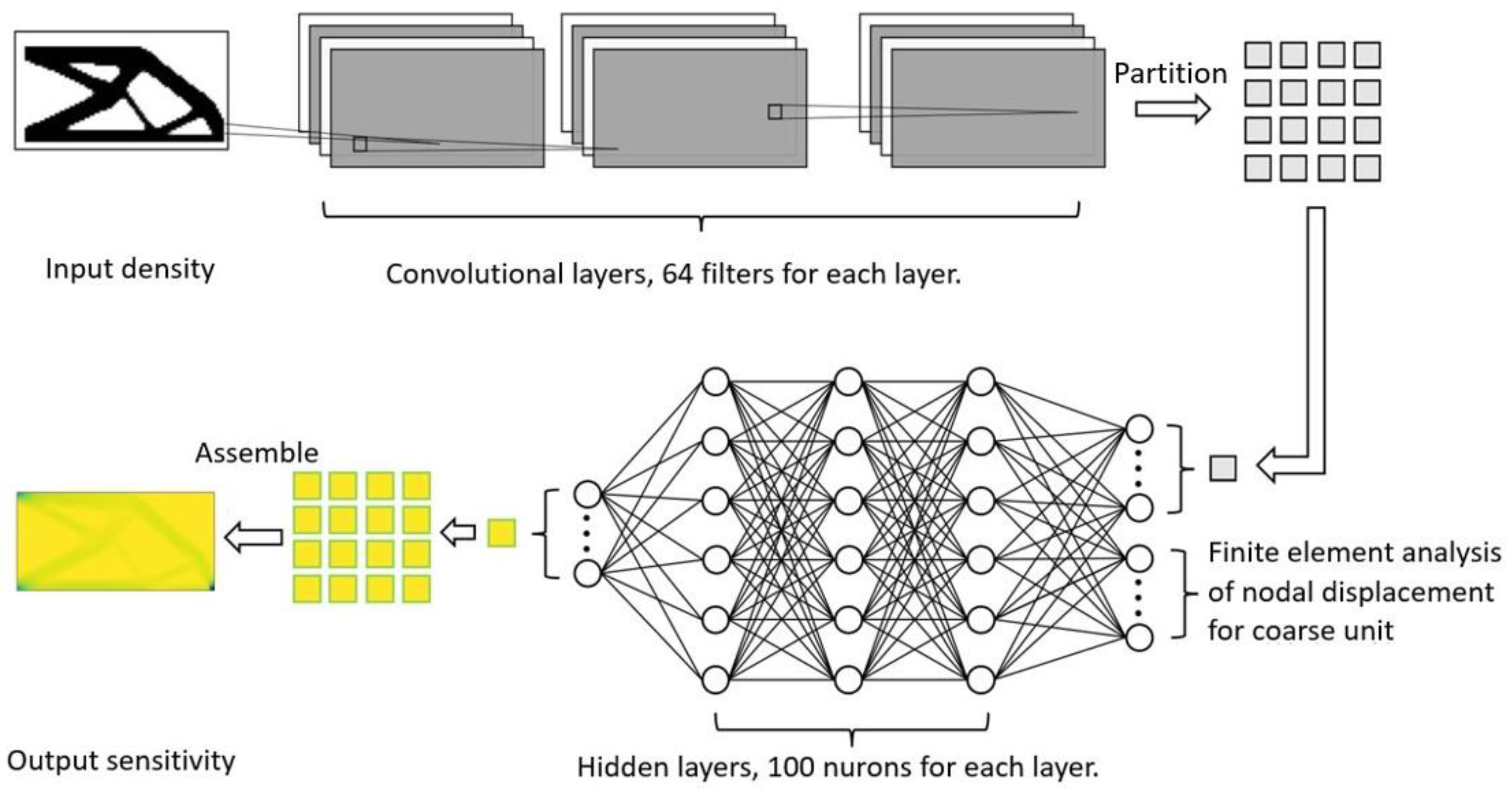
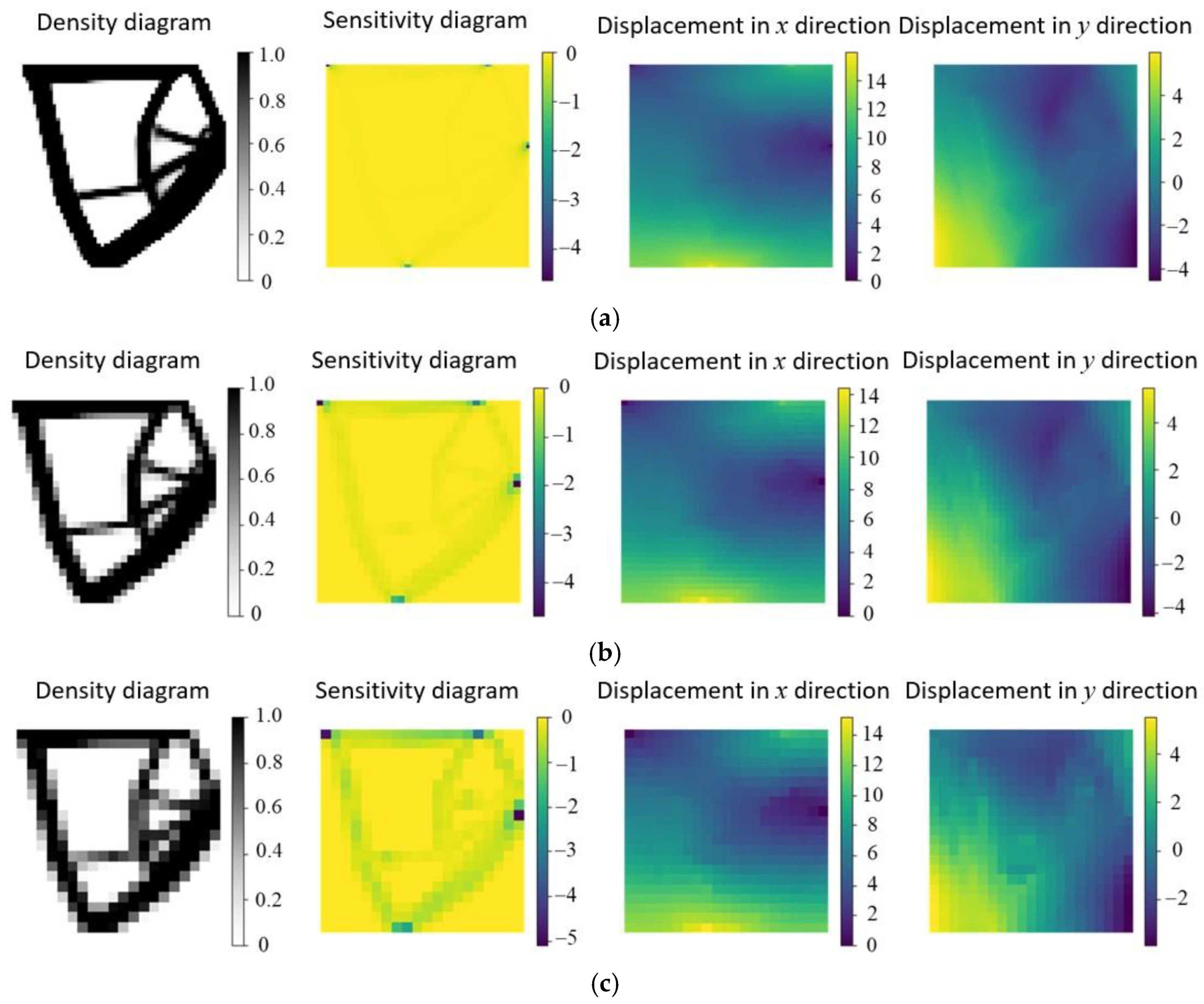
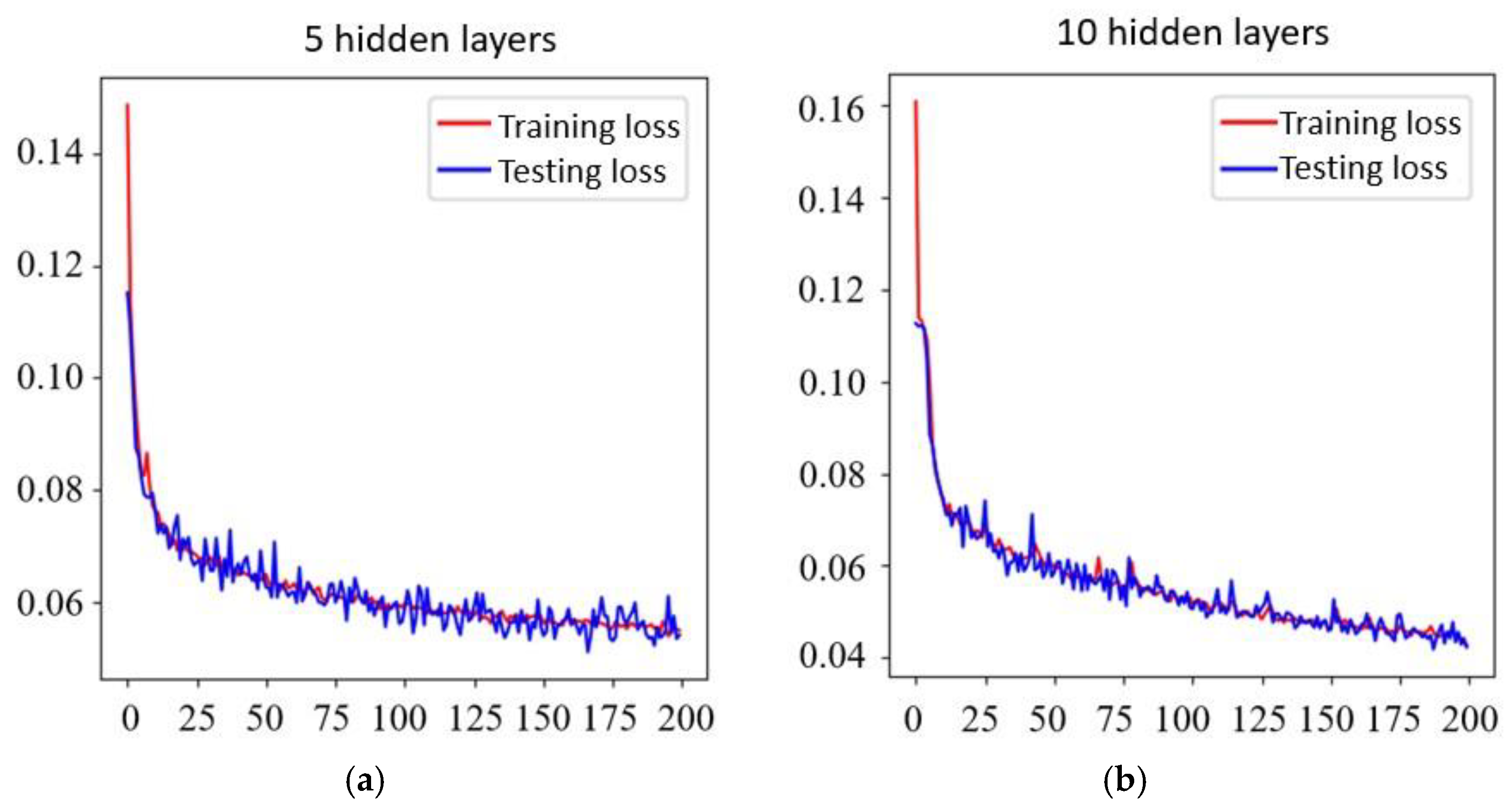
1. Introduction
The importance of topology optimization includes improving network performance, cost reduction, and improving efficiency and performance. In network topology optimization, optimizing the physical connections of network nodes can reduce latency, improve bandwidth utilization, and enhance network reliability and fault tolerance. For example, using the minimum spanning tree method can reduce network latency and congestion, and improve the network’s fault resilience. In 3D printing, topology optimization can reduce the amount of material used, thereby lowering production costs. In game modeling, a reasonable topology structure can make the model more natural and smoother in animation and deformation, reduce the number of faces in the model, and improve the running efficiency of the game. For example, by keeping quadrilaterals as the main feature, planning edge flow, and reducing unnecessary faces, the animation effect and rendering efficiency of the model can be improved.
Topology optimization uses mathematical methods to find the optimal structural design that meets mechanical requirements while reducing material usage, achieving the goal of reducing the weight. For example, in 3D printing, topology optimization can reduce material usage, lower costs, and improve product performance. In network topology optimization, reasonable node deployment and link allocation can enhance the performance and reliability of the network. For example, using greedy algorithms and genetic algorithms can optimize the location selection of network nodes and link bandwidth allocation, improving network performance and efficiency. Topology optimization can adapt to constantly changing network environments and requirements. For example, in network topology optimization, genetic algorithms can cope with complex environmental changes by simulating mechanisms such as natural selection, crossover, and mutation. Genovese et al. presented an efficient method for optimizing damping system parameters using design sensitivity analysis to relate design changes to available variables [
1].
Topics of topology optimization have received increasing attention from researchers lately. For example, Vantyghem et al. [
1,
2,
3,
4] used structural topology optimization to design a post-tensioned prestressed concrete pedestrian bridge. They used 3D concrete printing technology to construct corresponding assembly components. However, the major challenge currently hindering the widespread application of topology optimization in industrial design is the high computational cost of large-scale structural topology optimization [
5]. How to reduce the computational resource cost of structural topology optimization has been an important issue for engineers.
One type of topology optimization method discretized the optimized design area into a series of design density units. This type of method, known as the density-based topology optimization method, mainly includes solid isotropic material with a penalization (SIMP) method [
6,
7,
8]. The other most widely used method is the ESO method initially developed by Xie and Steven [
9]. Subsequently, Yang et al. [
10] made improvements to the method via the addition of efficient units to the structure, while inefficient units were removed. Another optimization method constructed high-order functions in implicit or explicit form for the boundary. This kind of method includes the level-set method [
11,
12,
13], the phase field method [
14], the moving deformable components/voids method [
15,
16,
17,
18], and the bubble method [
19,
20].
In recent years, the field of machine learning, especially deep learning, has shown excellent capabilities in terms of feature recognition and the approximation of complex relationships [
21,
22,
23,
24,
25]. From the perspective of function fitting, machine learning could be seen as a series of models. When an input–output mapping relationship was difficult to define explicitly, these frameworks provided multiple means of implementing function approximation [
26]. The deep learning field, located at the center of the flourishing development of Artificial Intelligence (AI), was based on artificial neural networks. AI performance was shown to be superior to human beings in many fields such as image recognition [
27,
28]. Thus, how to use the diverse deep neural network techniques to improve structural topology optimization has been one of the most important issues in the scientific field. The application of machine-learning-based techniques into structural topology optimization mainly focused on reducing the computational costs of finite element analyses. One of the most well-known methods was used to train artificial neural networks to predict the final structural shape. The computational costs of topology optimization iterations were considerably decreased. Several neural networks, such as convolutional neural networks (CNNs), generative adversarial networks (GANs), and moving morphable component-based (MMC) frameworks, have been well developed [
29,
30]. In addition, neural networks have been extensively used in metaheuristics, which should be appreciated [
31,
32,
33,
34]. Multi-objective optimization has also been extensively studied [
35,
36,
37].
To increase the efficiency of the machine learning models, it is necessary to limit the size of the training dataset and number of elements. Many researchers avoided the full connection layer with a fixed number of input parameters. For example, Zheng et al. [
38] designed a large grid domain to ensure the flexibility of input data. The size of data input into a surrogate-based model could range from 4000 to 26,000 [
39]. The other issue with the surrogate-based approach regards how to prevent disconnection in the optimized structure. Yu et al. [
40] generated volume fractions between 0.2 and 0.8 for two-dimensional structures with specific boundary conditions under randomly distributed loading. Nakamura and Suzuki [
41] increased the number of training data while disconnection still existed. Woldseth et al. [
21] found that discontinuity in the structure might result from a high mean average error (MAE) in the training model. Mechanical response information has been added to the loss function to prevent disconnection [
42,
43].
In the solid mechanics area, physics-informed neural networks (PINNs) [
44] and deep operator networks (DeepONets) [
45] are two well-developed techniques that have impressed many researchers in recent years. PINN added physical information constraints of partial differential equations to the loss function of the network training process. DeepONet, on the other hand, used neural networks for nonlinear mapping in different vector spaces. To reduce the computational cost of finite element analyses, researchers [
46,
47,
48,
49,
50] have been enlightened by some conventional topology optimization acceleration methods, such as Deep Belief Network (DBN) [
51,
52]. For instance, Kallioras et al. [
53,
54] used Deep Belief Network (DBN) to predict the unit density change throughout the entire iteration process.
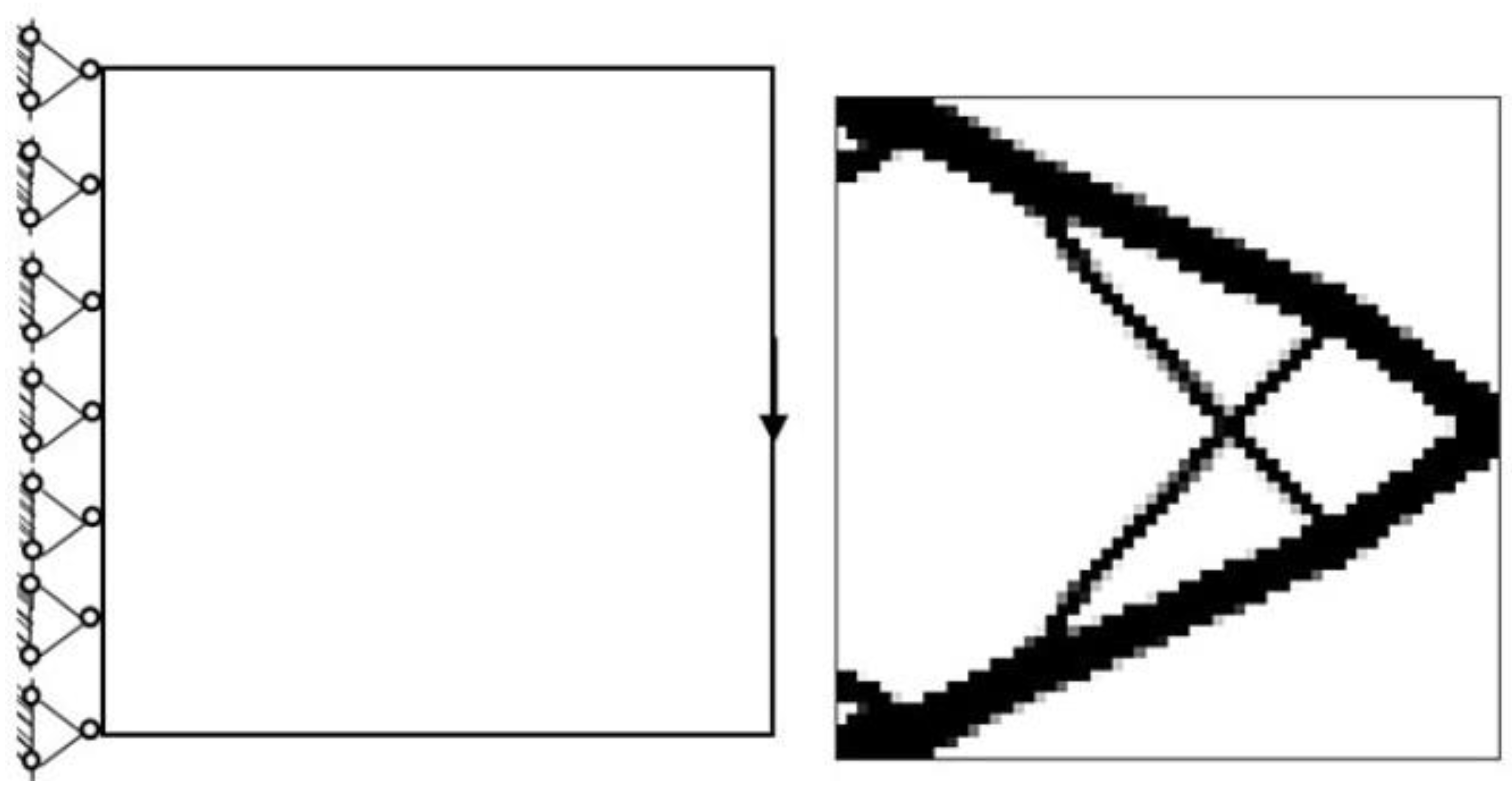
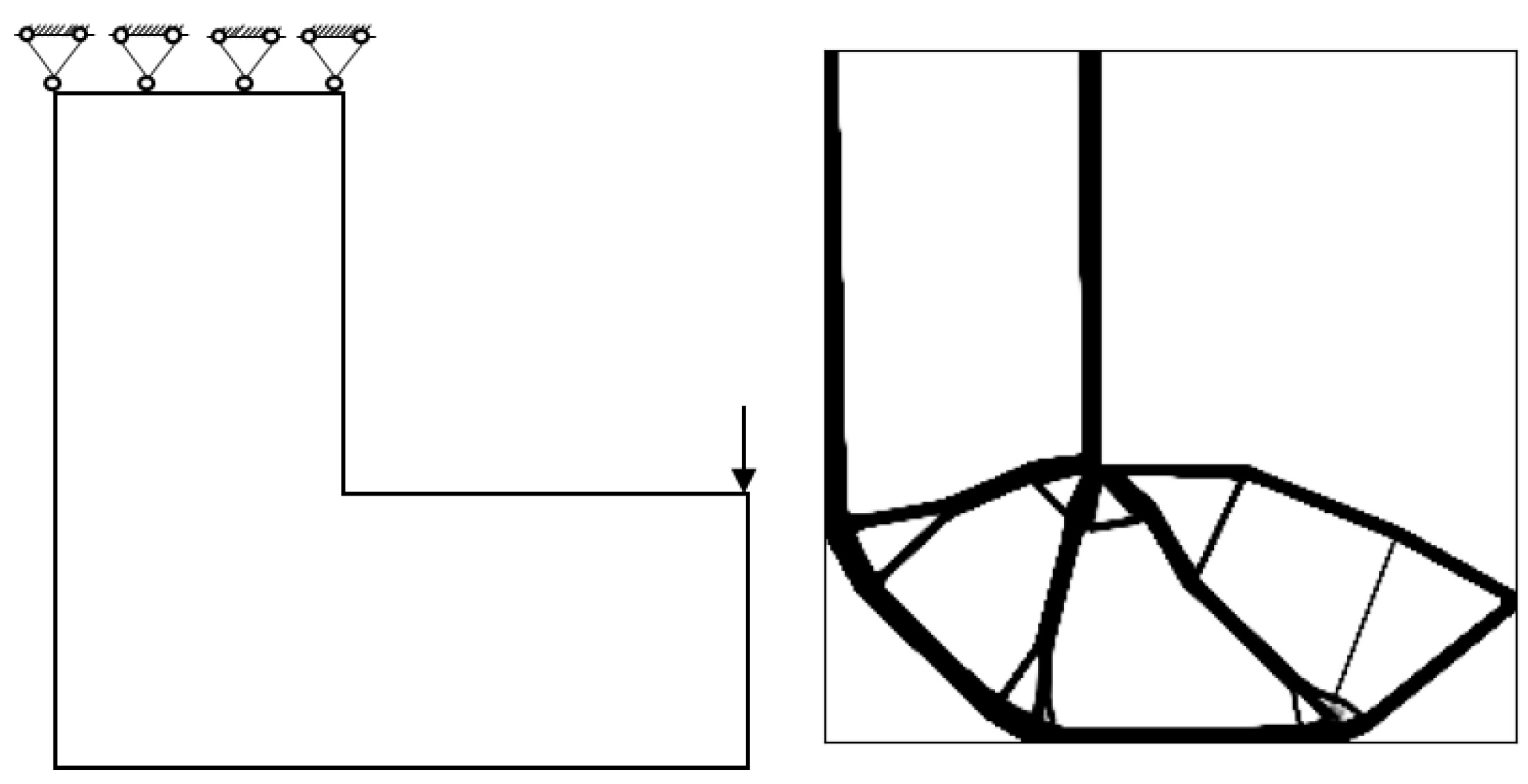
However, in most studies, using deep neural networks was not sufficiently accurate for topology optimization, mainly because it was required to perform finite element analyses of the full-scale structure at each iteration. Thus, it is necessary to improve the efficiency of finite element computation as well as the convergence of iterations during optimization. This study developed a novel partitioned deep learning algorithm to enhance structural topology optimization. The method decomposed a full-scale structure into several partitions at a coarse scale. The partition-based architecture was adopted to train the neural networks at both coarse and fine scales to reduce the computational costs of finite element analyses during topology optimization. Novel neural networks were used to optimize various types of structures of different meshes, partition numbers, and parameters. In addition, patterns of sensitivity maps were analyzed with various visualization tools to assess structural performance with high accuracy. Computational efficiency was considerably increased when the neural network technique was adopted.
The main contents of this paper are given as follows.
Section 2 presents the theoretical background of the deep learning topology optimization method.
Section 3 introduces the construction and training of the partitioned neural network model.
Section 4 evaluates the accuracy and efficiency of neural network models in some numerical examples.
Section 5 visualizes the sensitivity of neural networks with different partition numbers for several representative structures.
Section 6 summarizes the contributions and limitations of this study, and points out several directions for further research in the future.
5. Results and Discussion
Comparing two multi-objective meta-heuristic algorithms involves several steps to ensure a comprehensive and fair evaluation. Here are some of the best practices and metrics to consider. First of all, clearly specify the objectives that the algorithms aim to optimize. This could include maximizing/minimizing multiple conflicting objectives. Secondly, select a diverse set of benchmark problems that are widely used in the literature for multi-objective optimization. These problems should vary in complexity, dimensionality, and characteristics. Then, choose appropriate performance metrics to evaluate the algorithms. Common metrics include convergence metrics, measurement of the volume of the objective space covered by the Pareto front, evaluation of the distance from a set of solutions to the true Pareto front, and assessment of how well the solutions cover the Pareto front. Next, ensure both algorithms are properly tuned for their parameters to guarantee a fair comparison. Run each algorithm multiple times to account for stochasticity in results. Use statistical tests to analyze the significance of the results. In addition, use statistical methods to analyze the performance of the algorithms. Common approaches include Wilcoxon rank-sum test, analysis of variance, and effect size measures. Also, graphical representations help in understanding the performance visually, such as Pareto front visualization, boxplots, and convergence plots. Furthermore, evaluate the robustness of the algorithms by testing them on different problem instances or varying conditions. Finally, measure and compare the computational time and resources required by each algorithm to reach the results. This includes execution time and memory usage. If applicable, consider any specific characteristics of the problem domain that may impact the performance or suitability of the algorithms. In general, a thorough comparison involves a combination of quantitative metrics, statistical analysis, visual representation, and consideration of robustness and computational efficiency. This holistic approach ensures that the strengths and weaknesses of each algorithm are well understood, leading to informed conclusions about their relative performances.
5.1. Convergency
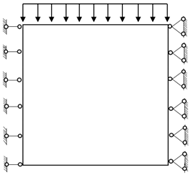
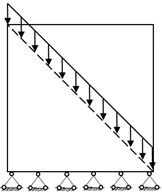
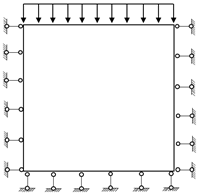
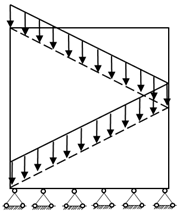
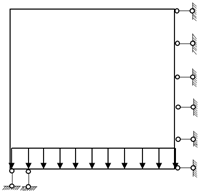
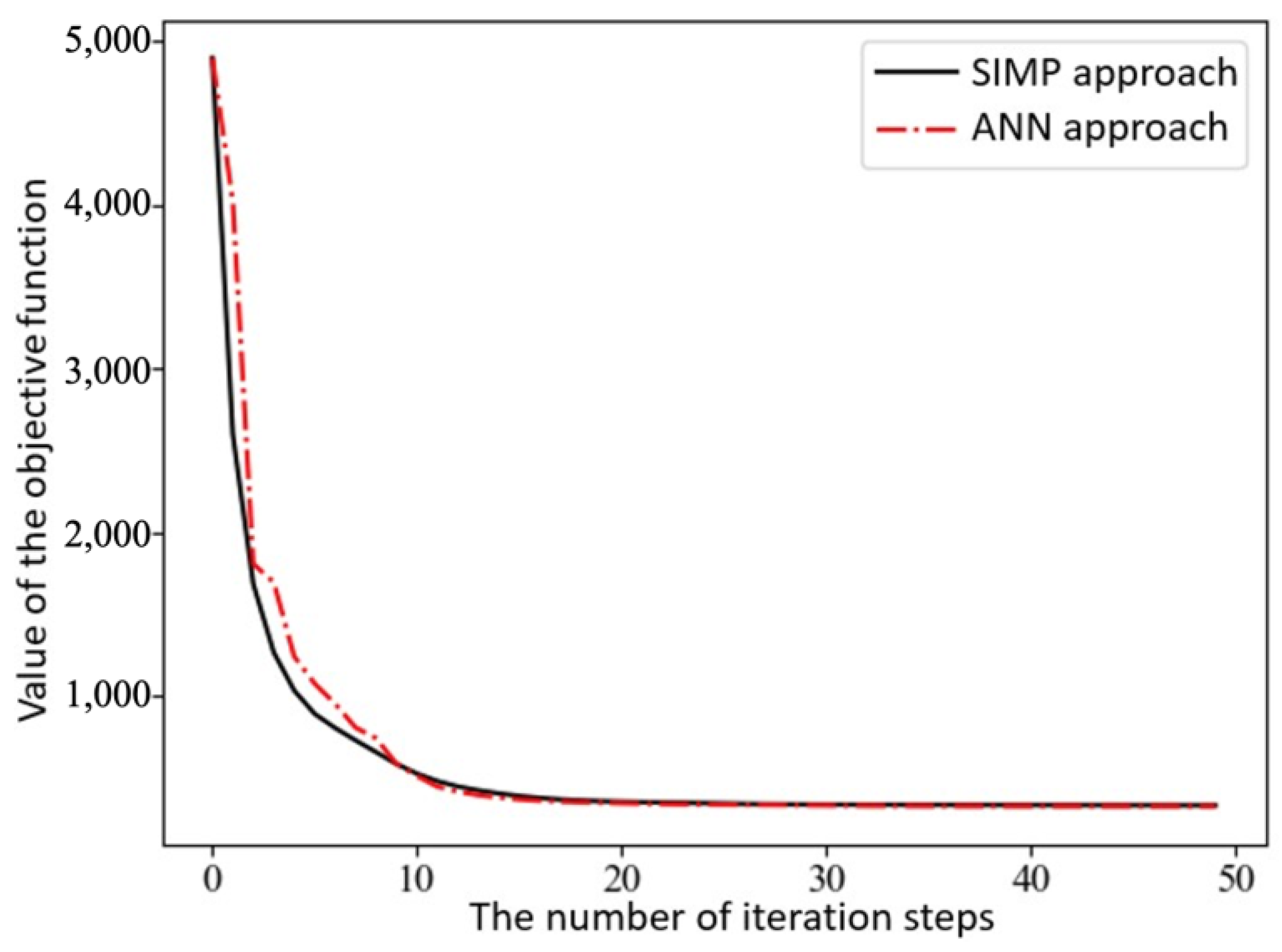
The SIMP method is used for the numerical examples given in the previous section. The decline of the optimization objective functions is shown in
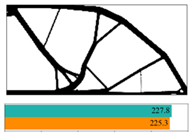
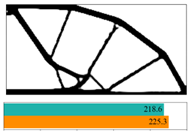
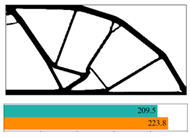
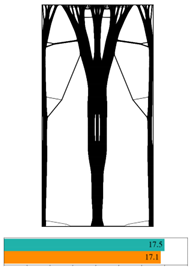
Figure 11. It is indicated that most of them reach convergence from 10 to 20 steps, although the rate of convergence of random structures is different.
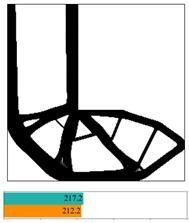
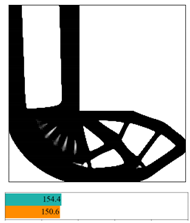
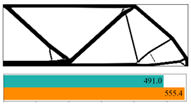
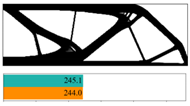
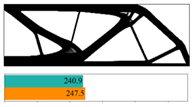
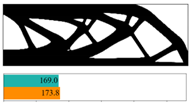
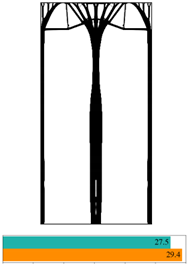
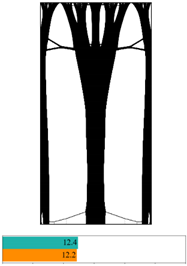
The final convergent values of the objective function using the partitioned deep learning algorithm-aided optimization method newly developed in this paper are similar.
Figure 12 made a comparison between iterative objective functions of SIMP and ANN.
5.2. Effect of Partition Number on Optimization
Table 1,
Table 2 and
Table 3 list the neural network prediction results for three different grid numbers and two block dimensions, where sensitivity filters with a radius of 4 are applied to all cases with a partition number
Np = 3.
It is demonstrated that the proposed method can be generalized to different cases. That is, the method is applicable for different target volume fractions and filtering radii. More numerical examples and experiments are given in
Appendix A.
5.3. Effect of Topology Optimization Parameter on Optimization
Table 4,
Table 5 and
Table 6 compare the previous numerical examples with various target volume fractions and filtering radii. It is indicated that sensitivity is independent of the target volume fraction, density filtering radius and other parameters of topology optimization. More numerical examples and experiments are given in
Appendix A.
5.4. Proportion of FEA Time Consumption
Next, the proportion of FEA time consumption in the entire process of SIMP and ANN methods is investigated. The main source of consumption in finite element calculation is the sparse matrix equation solver. The computational cost in other steps is represented by the density updating of the optimization solver. The test results are shown in
Figure 13.
It is demonstrated that the finite element computation takes more than 90% of the total operation time of the SIMP method. This result is in good agreement with one obtained by Mukherjee et al. [
5]. Also, the proportion represented by running time in finite element computations via neural network methods with different partitions and different design variables is explored, as shown in
Figure 14.
It is observed that the computational cost and ratio of finite element method are lower than those of traditional SIMP method. The larger the dimension of partitioning is, the smaller the computational cost and proportion of finite element analysis are. It is indicated that the proposed technique effectively alleviates excessive works of finite element computation during topology optimization. In addition, as the number of structural grids increases, the time proportion of neural network inference in the entire process gradually decreases. It is inferred that under the condition of millions of elements, as are seen in actual application scenarios, the additional computational consumption of neural network prediction can be ignored. That is, using neural network methods to enhance large-scale structural topology optimization is feasible.
6. Conclusions
This study proposes a partitioned deep learning algorithm to aid structural topology optimization. The main conclusions obtained from this study are summarized as follows. First, in the training phase of neural networks, it is found that using random structural training datasets significantly improves the prediction accuracy of neural networks for different structures. The larger the size of the training dataset is, the higher the prediction accuracy is. In addition, selecting several steps of data training in the early stage of iteration convergence results in a high prediction accuracy for the model. Also, it is demonstrated that the smaller the size of partition is, the better the training result is. Secondly, the topology configuration obtained from the novel approach is similar to that derived using the SIMP method. The difference in structural performance between the two approaches is less than 10%. Also, compared with the SIMP method, the neural network method of structural optimization significantly increases computational efficiency. As the number of partitions in the neural network further increases, the difference in cost proportion when fully using finite element computation further increases.
However, this study only investigated a small number of partitions. That is, it is possible that the generalization performance could be improved using neural networks only for simple problems. In addition, in this study, only two-dimensional plane stress problems were considered. Further explorations into the use of the proposed method in three-dimensional complex structures with large numbers of partitions will be necessary in the future.