Water Demand (or Specific Surface) of Aggregate as a Dominating Factor for SCC Composition Design
Abstract
1. Introduction
2. Methods
2.1. Water Demand vs. Specific Surface
2.2. The Experimental Methods of Water Demand/Specific Surface Assessment
2.3. Models of Water Demand/Specific Surface Area Based on Aggregate Grading Curve
- k—consistency coefficient of the concrete mix (proportional to the thickness of the water film on the aggregate grains; value constant for all fractions in consideration);
- dj—maximum grain size contained in a given aggregate fraction (mm);
- dj−1—minimum size of grain contained in a given aggregate fraction (mm).
- φa—volume concentration (absolute volume) of aggregate in the total volume of concrete mix (typically in dm3/m3);
- φa i—volume concentration of aggregate grains of fraction i;
- dm i—average diameter of grains of fraction i;
- ki—volumetric shape factor for fraction i (for a sphere k = π/6);
- fi—surface shape factor for fraction i (for a sphere f = π).
- RSS is the relative specific surface area;
- yj is the mass fraction of fraction j in the grain size distribution of aggregate;
- dmj—average grain diameter of the fraction with the upper dimension dj (mm);
- c—a coefficient depending on the consistency level and/or the shape of the grains.
2.4. The Method for Determining the Relative Thickness of Aggregate Coating with Cement Paste
- tm—average distance of aggregate grains in the concrete mix;
- dm—average grain size of aggregate in the aggregate composition;
- tm is determined from the formula given by Oh et al. [9].
- Vexc—volume of the excess paste in the mix (i.e., the volume of paste overfilling the intergranular spaces in the mix) (mm3);
- SSO—specific surface area of the aggregate (mm2/mm3) calculated from Formula (7);
- φsolids—volume concentration of the solid phase (i.e., aggregate (a) + cement (c) + additions (ad)).
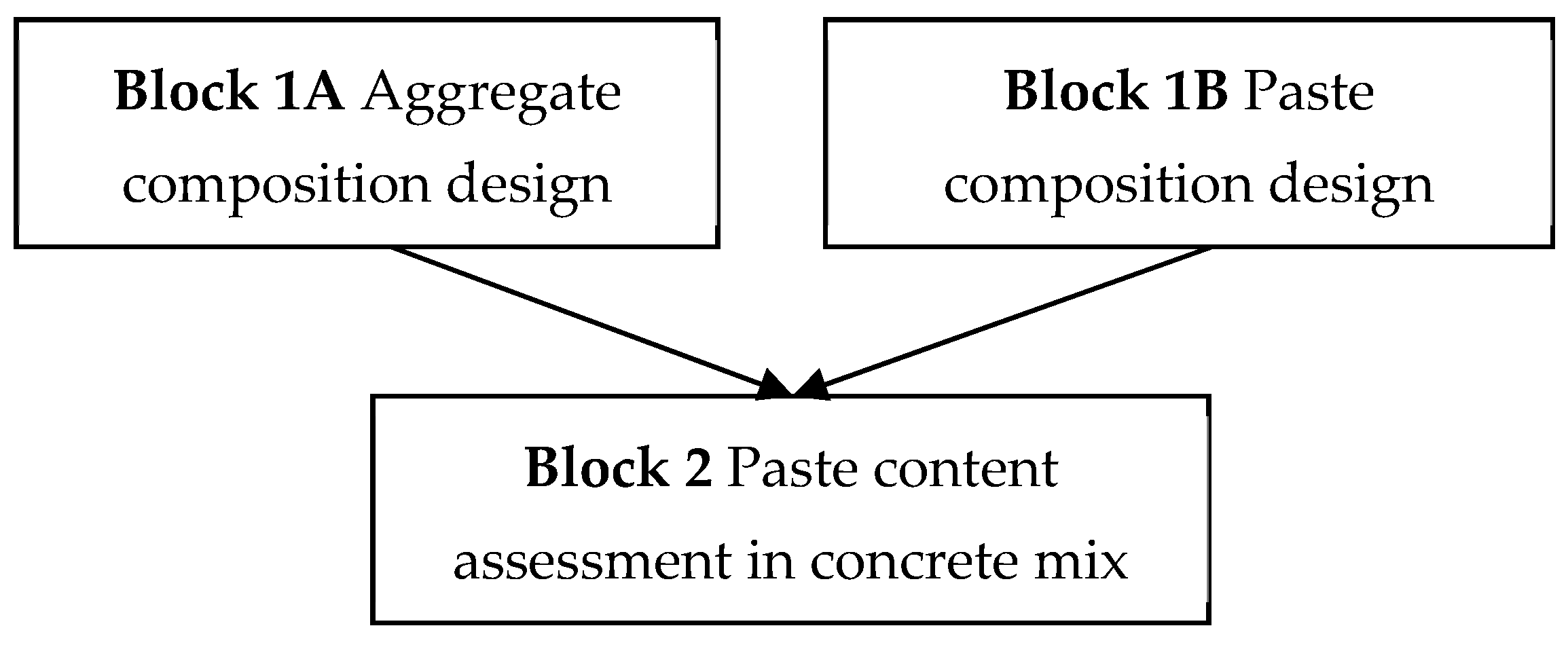
2.5. The Auhor’s Method of SCC Composition Design
2.5.1. The Method Principle
2.5.2. Aggregate Block (1A)
2.5.3. Cement Paste Block (1B)
2.5.4. Paste Content Assessment in Fresh Concrete Block (2)
2.6. The Assumptions of the Research Program
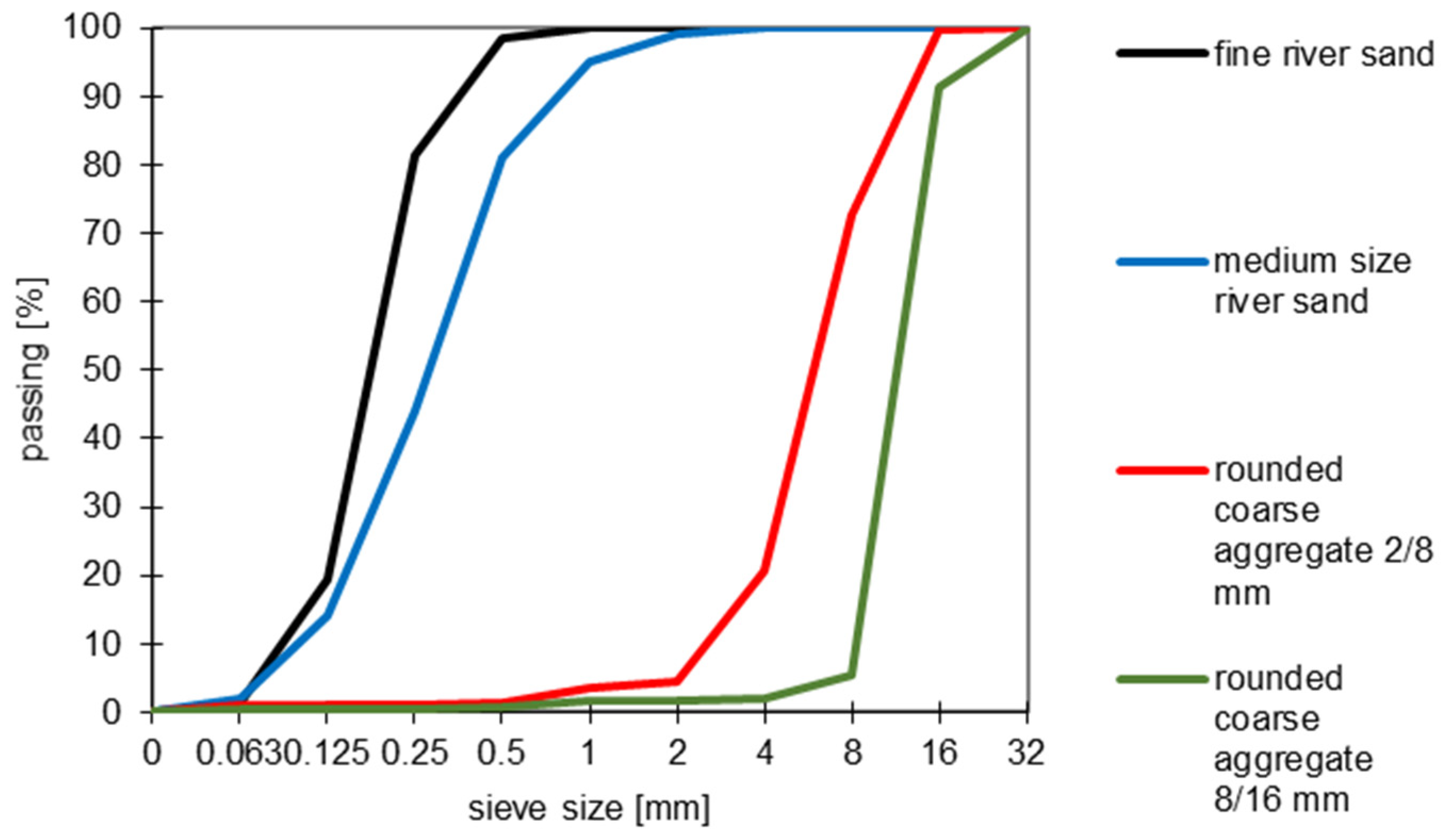
3. Materials
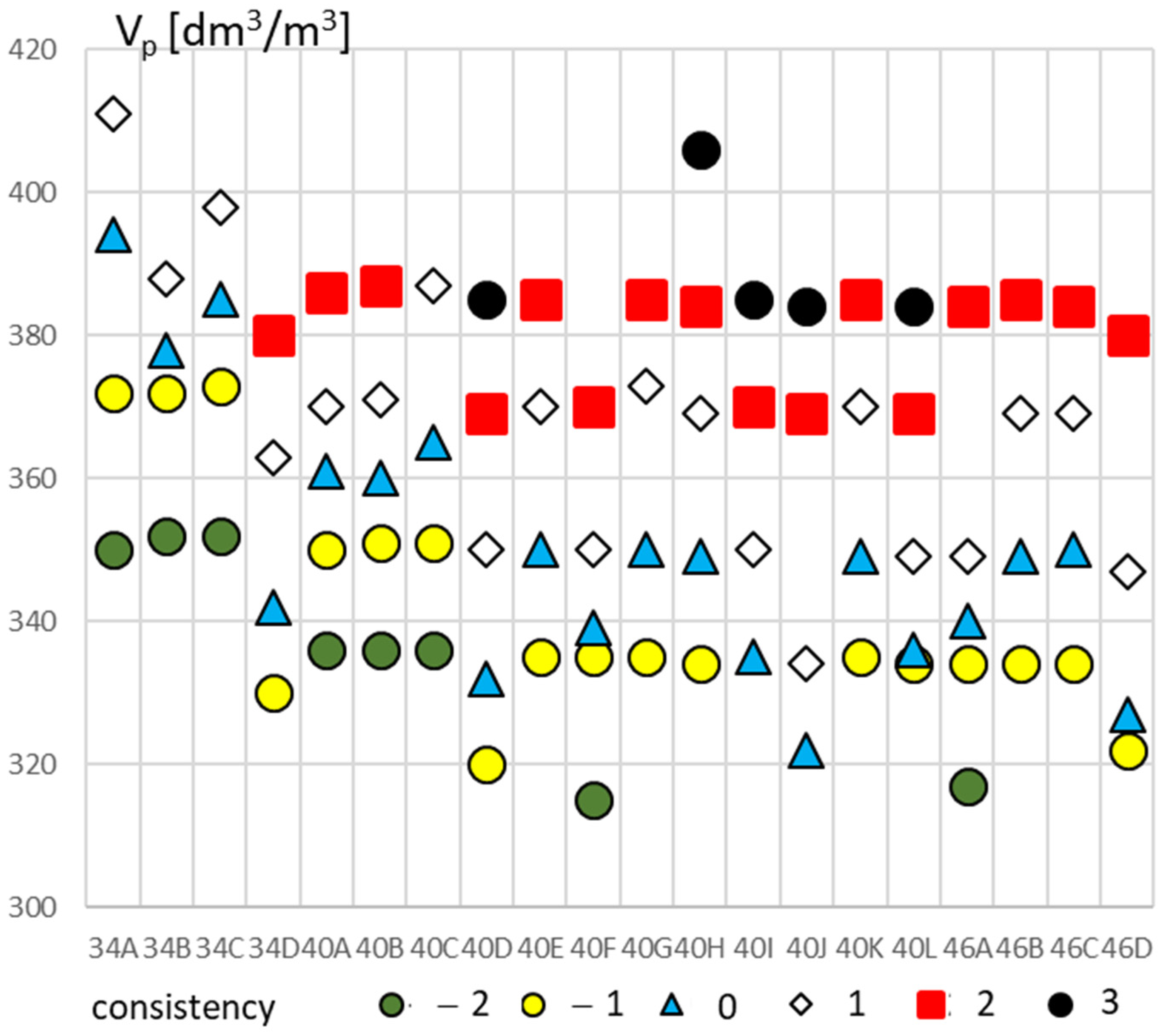
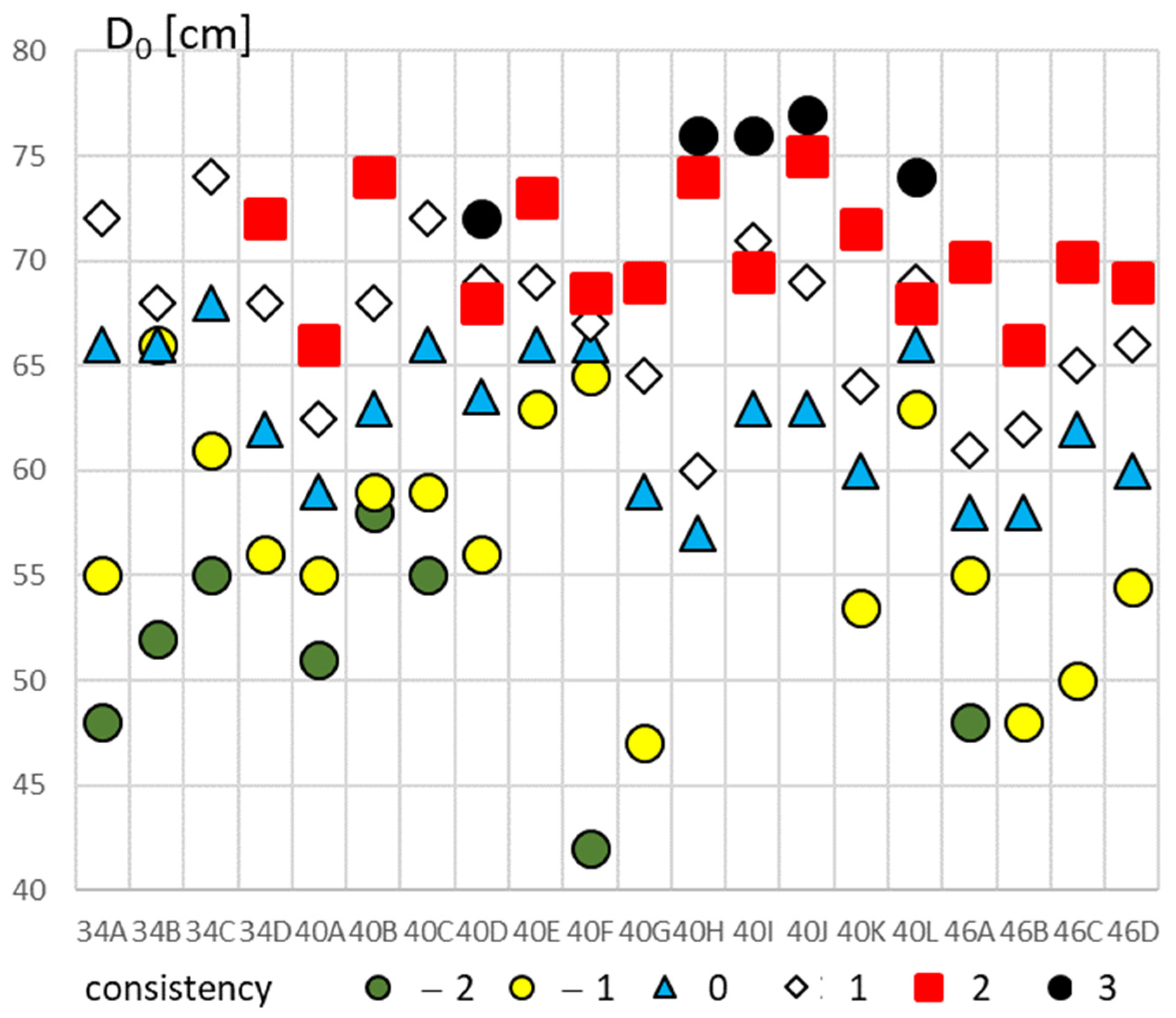
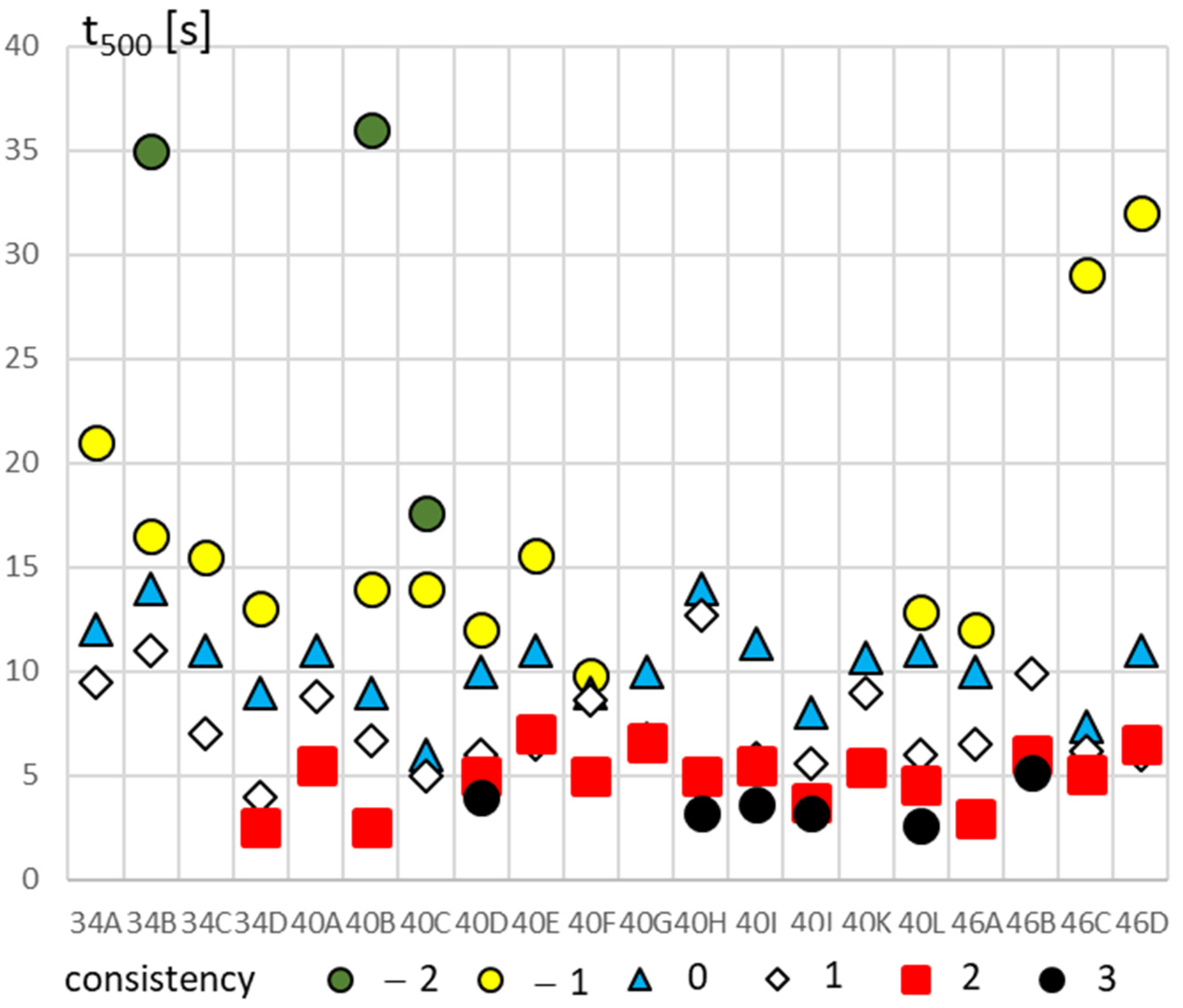
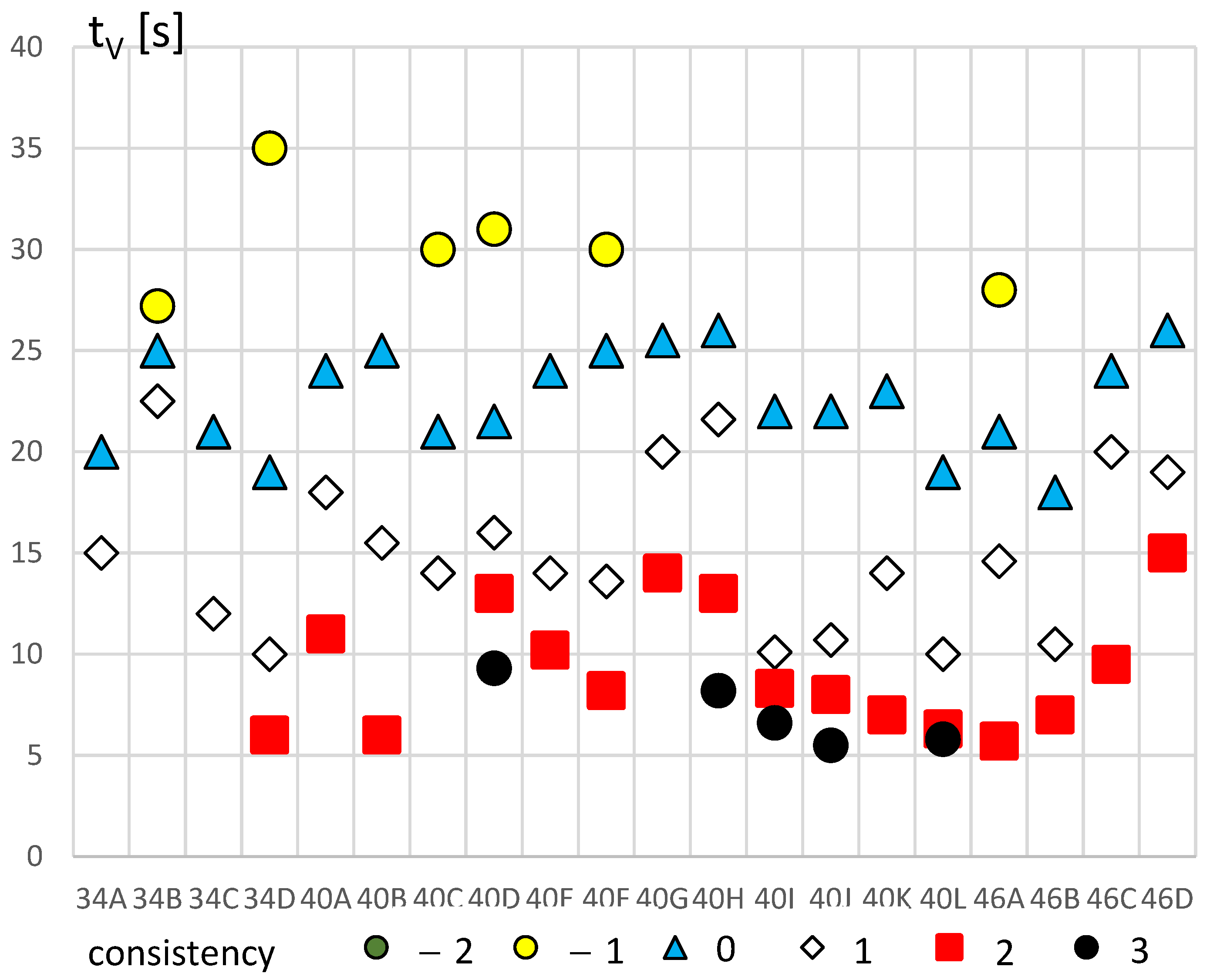
4. Research Program and Main Results
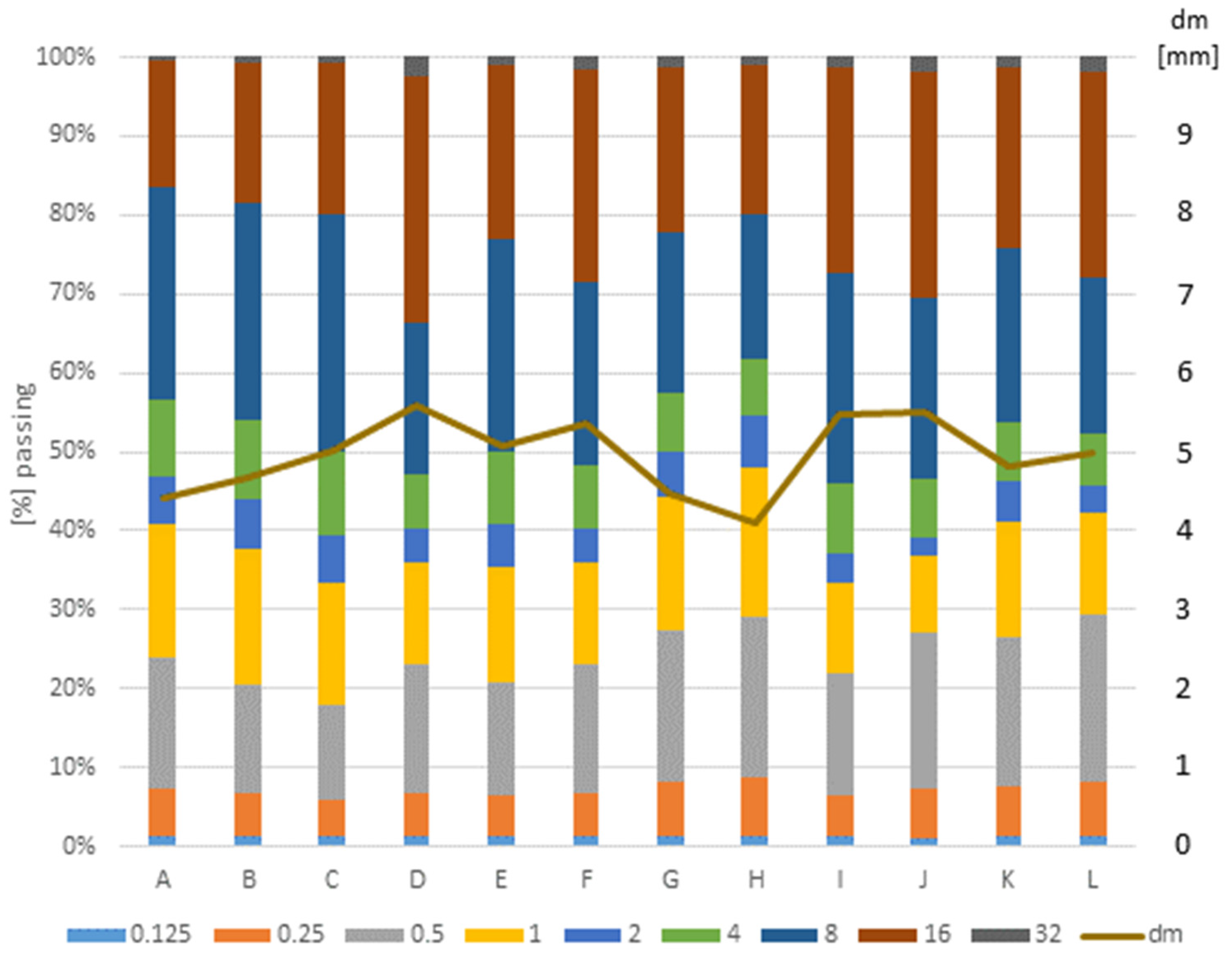
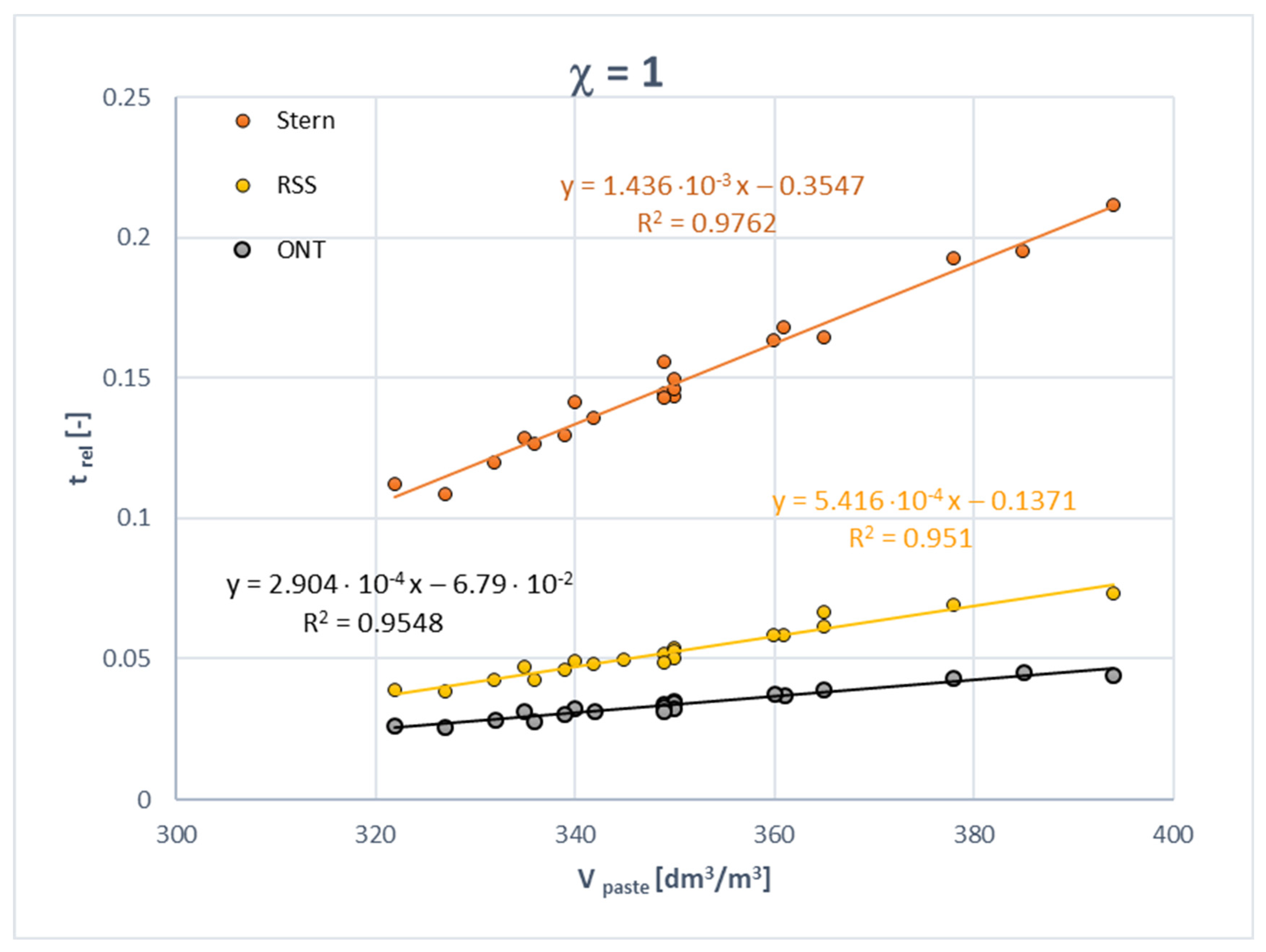
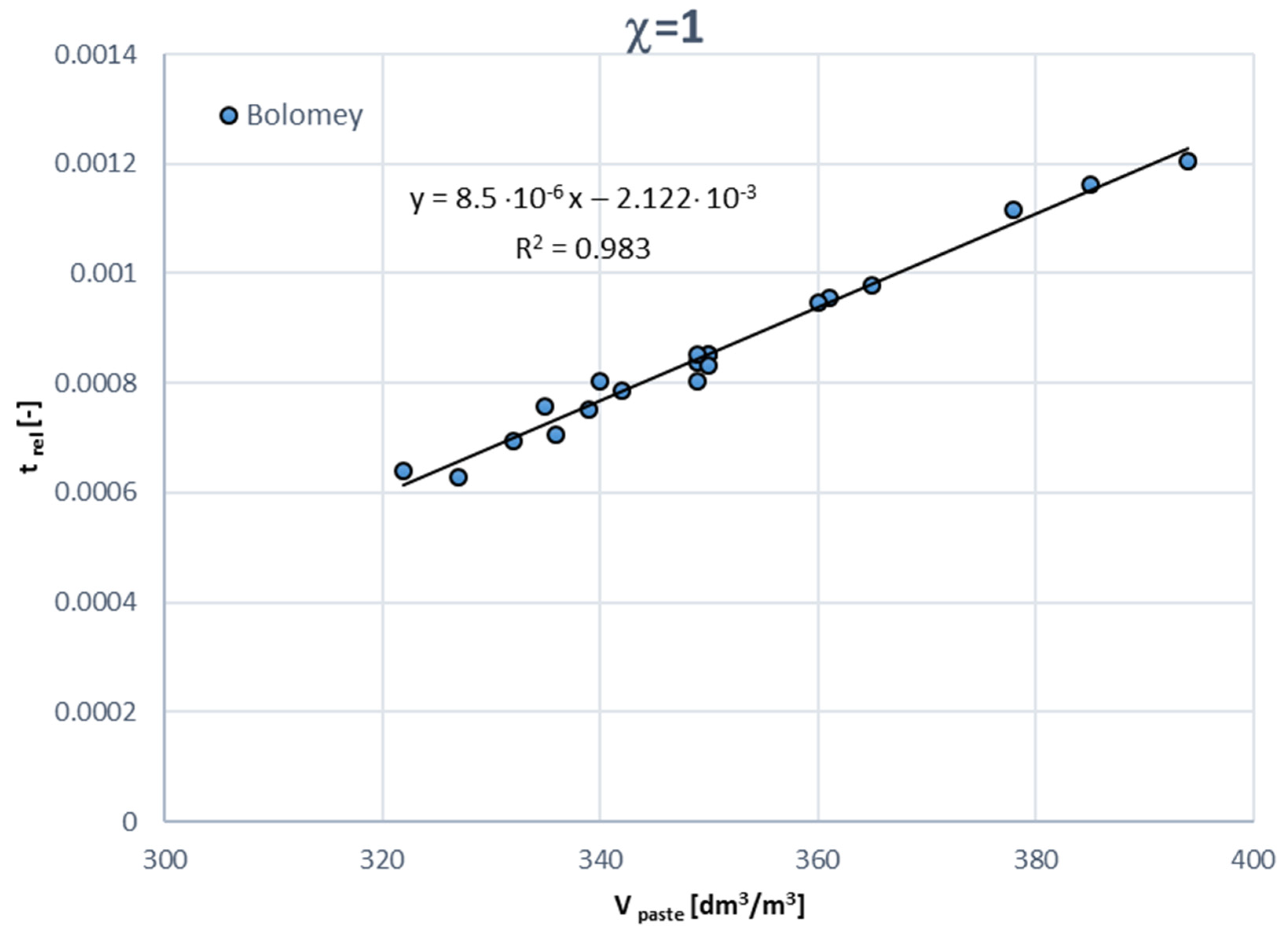
4.1. Aggregate Block (1A)
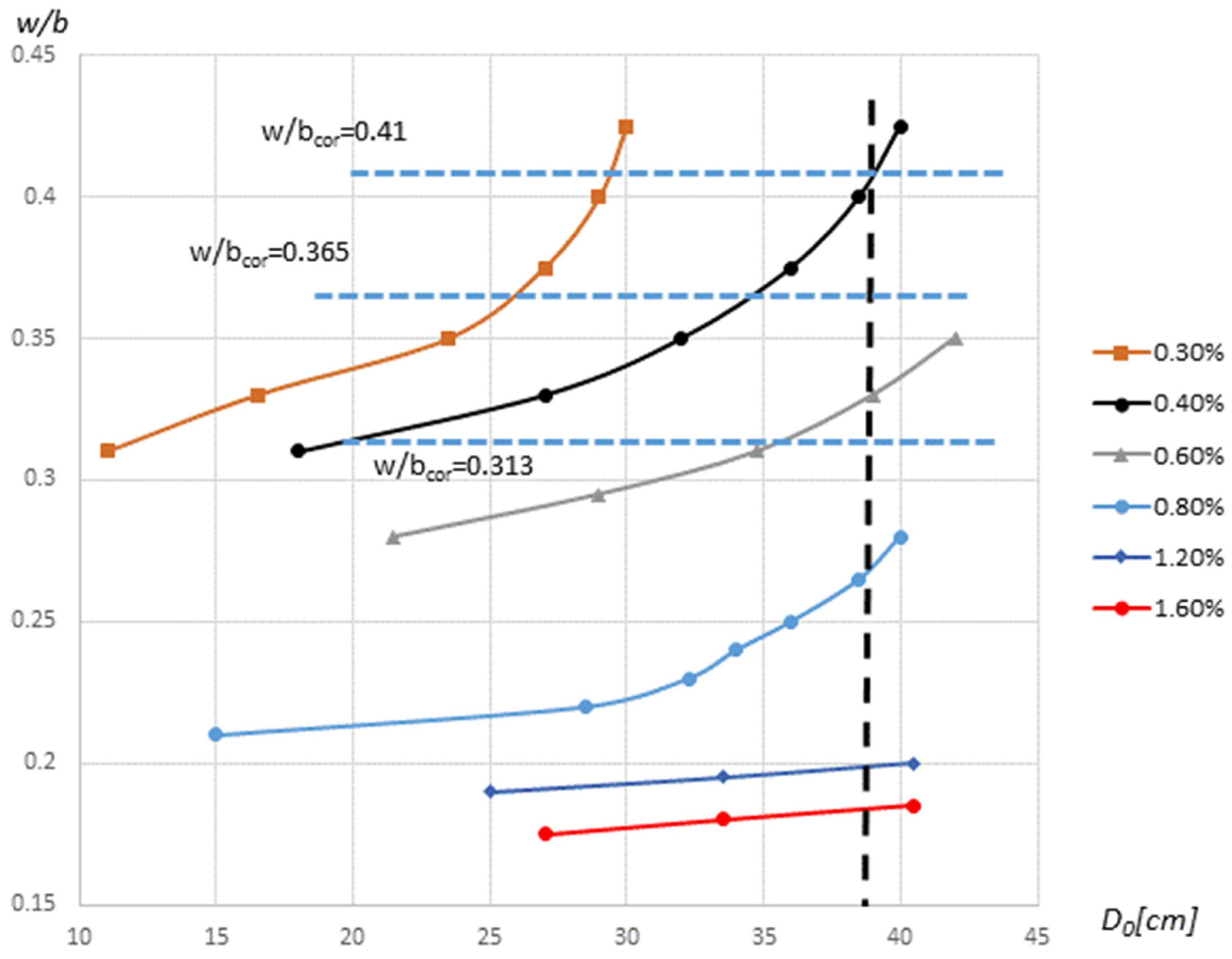
4.2. Cement Paste Block (1B)
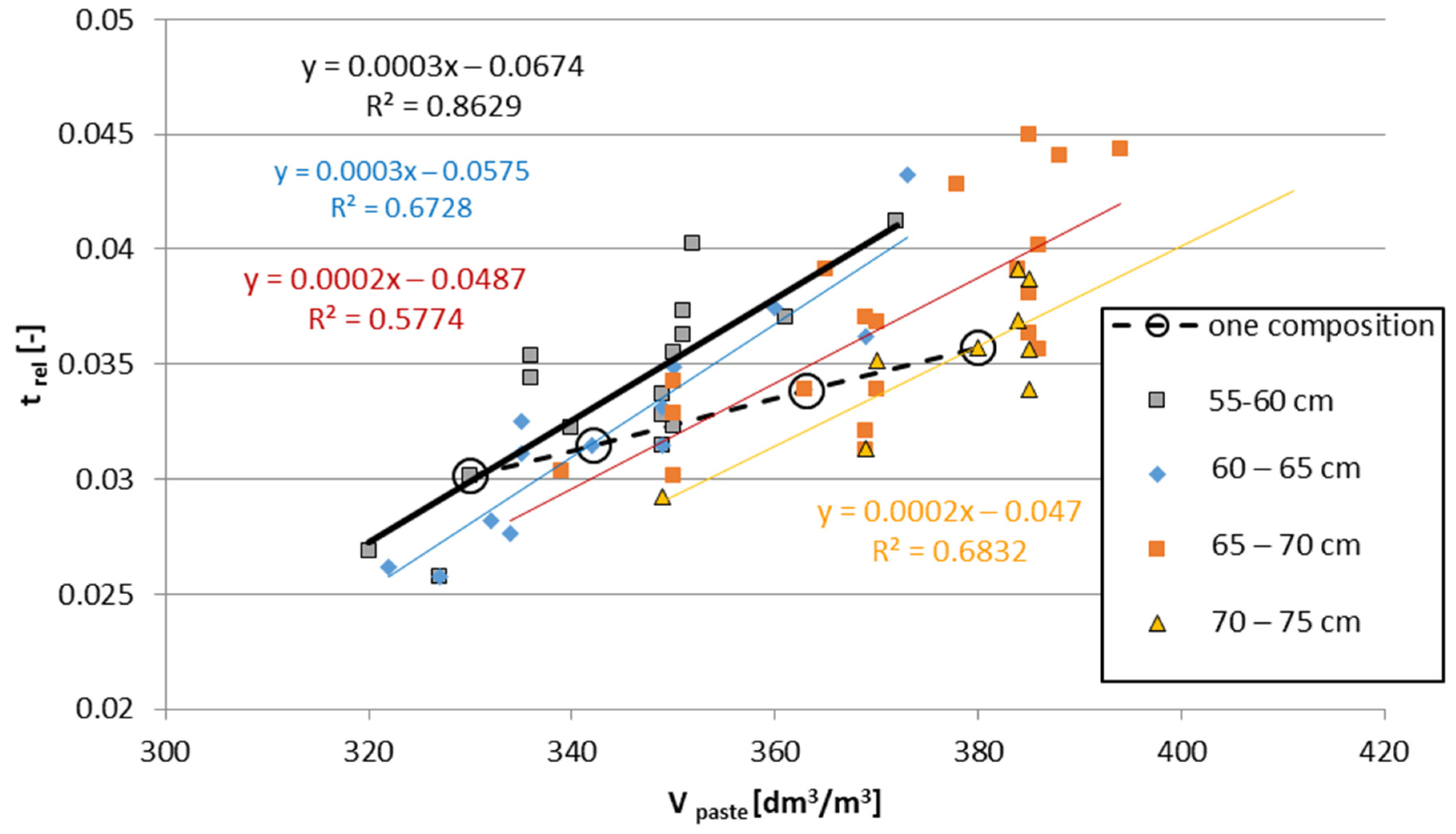
4.3. Fresh Concrete Block (2)
5. Discussion
- Design 4 mixes of extreme compositions in terms of trel using the method proposed in Section 2.5.2 and Section 2.5.3. This means that 2 extreme values of both w/b ratios (for extreme ∑p obtaining) and water demand/specific surface of aggregate (for extreme ∑a obtaining) are to be selected. As a quick indicator of the second value, a sand (i.e., aggregate up to 2 mm)-to-total aggregate ratio (s/a) may be used.
- Test the designed mixes according to Section 2.5.4. The target is to obtain the assumed consistency level.
- Calculate trel values for the designed concrete compositions and plot linear regression curve in the Vp − trel space to obtain the minimum paste demand line.
- Design composition conforming to a pre-assumed specification (e.g., strength class, etc.) of trel within the range covered by the line and read predicted Vp for this case.
- Prepare the trial batch using predicted Vp and adjust (rise) sp if necessary.
6. Conclusions
- The water demand/specific surface area of aggregate is a key factor determining the content of cement paste necessary to achieve self-compaction ability of concrete.
- The traditional methods of water demand/specific surface of aggregate assessment (Stern, Bolomey/Loudon based, RSS) are also valid in the SCC case and they may be used without any alteration. The best fit was obtained for traditional non-linear water demand models (by Stern and by Bolomey).
- The presented method allows to predict paste volume of SCC basing on specific surface/water demand of aggregate and the simple procedure to obtain cement paste of the proper fluidity. The capability to allow prediction of superplasticizer dosage needs further work.
- The method allows to assess minimum paste demand for any specified range for slump flow, t500, and V-funnel tests.
- The disadvantage of the described approach is the need to use an arbitrarily determined integrated coefficient containing the total effect of grain shape, unit conversion, model constants, etc. Therefore:
- The applicability of the model should be limited to a fixed set of component aggregates used to compose the aggregate skeleton.
- The comparability of results between compositions containing aggregate of the same type (e.g., rounded) but of different origin should be considered limited.
- The comparability of results between types of aggregates (rounded/crushed) should be considered questionable.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Component Units/ Composition Notation | Vpaste dm3/m3 | c kg/m3 | w kg/m3 | ad kg/m3 | sp kg/m3 | Sand Fine kg/m3 | Sand Coar-Se kg/m3 | Agg 2/8 kg/m3 | Agg 8/16 kg/m3 | D0 cm | t500 s | tV s |
| 34A-2 | 350 | 400 | 177 | 120 | 3.5 | 114 | 684 | 866 | 46 | 48 | ||
| 34B-2 | 352 | 402 | 178 | 121 | 3.5 | 24 | 722 | 880 | 79 | 52 | 35 | |
| 34C-2 | 352 | 402 | 178 | 121 | 3.5 | 0 | 658 | 967 | 81 | 55 | 42 | |
| 40A-2 | 336 | 352 | 183 | 106 | 2.3 | 116 | 699 | 885 | 47 | 51 | ||
| 40B-2 | 336 | 352 | 183 | 106 | 2.3 | 25 | 739 | 902 | 81 | 58 | 36 | |
| 40C-2 | 336 | 352 | 183 | 106 | 2.3 | 0 | 675 | 991 | 83 | 55 | 17.6 | |
| 40F-2 | 315 | 330 | 172 | 99 | 2.1 | 258 | 386 | 902 | 258 | 42 | ||
| 46A-2 | 317 | 307 | 184 | 92 | 1.6 | 120 | 719 | 910 | 48 | 48 | ||
| 34A-1 | 372 | 425 | 188 | 127 | 3.7 | 110 | 661 | 837 | 44 | 55 | 21 | |
| 34B-1 | 372 | 425 | 188 | 127 | 3.7 | 23 | 699 | 853 | 77 | 66 | 16.5 | 27.2 |
| 34C-1 | 373 | 426 | 188 | 128 | 3.7 | 0 | 637 | 936 | 78 | 61 | 15.5 | 57.5 |
| 34D-1 | 330 | 377 | 167 | 113 | 3.3 | 233 | 466 | 615 | 447 | 56 | 13 | 35 |
| 40A-1 | 350 | 367 | 191 | 110 | 2.4 | 114 | 684 | 866 | 46 | 55 | 51 | |
| 40B-1 | 351 | 368 | 191 | 110 | 2.4 | 24 | 723 | 882 | 79 | 59 | 14 | |
| 40C-1 | 351 | 368 | 191 | 110 | 2.4 | 0 | 659 | 969 | 81 | 59 | 14 | 30 |
| 40D-1 | 320 | 336 | 174 | 101 | 2.2 | 236 | 473 | 624 | 454 | 56 | 12 | 31 |
| 40E-1 | 335 | 351 | 183 | 105 | 2.3 | 117 | 583 | 875 | 175 | 63 | 15.6 | |
| 40F-1 | 335 | 351 | 183 | 105 | 2.3 | 250 | 375 | 875 | 250 | 64.5 | 9.8 | 30 |
| 40G-1 | 335 | 351 | 183 | 105 | 2.3 | 236 | 451 | 751 | 311 | 47 | ||
| 40H-1 | 334 | 350 | 182 | 105 | 2.3 | 219 | 656 | 656 | 219 | 39 | ||
| 40K-1 | 335 | 351 | 183 | 105 | 2.3 | 261 | 537 | 705 | 245 | 53.5 | 41.2 | |
| 40L-1 | 334 | 350 | 182 | 105 | 2.3 | 419 | 367 | 629 | 335 | 63 | 12.9 | |
| 46A-1 | 334 | 324 | 194 | 97 | 1.7 | 117 | 701 | 888 | 47 | 55 | 12 | 28 |
| 46B-1 | 334 | 324 | 194 | 97 | 1.7 | 25 | 742 | 905 | 82 | 48 | ||
| 46C-1 | 334 | 324 | 194 | 97 | 1.7 | 0 | 677 | 994 | 83 | 50 | 29 | |
| 46D-1 | 322 | 312 | 187 | 94 | 1.6 | 236 | 472 | 622 | 453 | 54.5 | 32 | |
| 34A 0 | 394 | 450 | 199 | 135 | 3.9 | 106 | 638 | 808 | 43 | 65 | 12.5 | 19.5 |
| 34A 0R | 394 | 450 | 199 | 135 | 3.9 | 106 | 638 | 808 | 43 | 67 | 11 | 20.5 |
| 34B 0 | 378 | 432 | 191 | 129 | 3.8 | 23 | 693 | 845 | 76 | 66 | 14 | 25 |
| 34C 0 | 385 | 440 | 194 | 132 | 3.8 | 0 | 625 | 918 | 77 | 67 | 11 | 22.5 |
| 34C 0R | 386 | 441 | 195 | 132 | 3.8 | 0 | 624 | 916 | 77 | 68.5 | 10.5 | 20.5 |
| 34D 0 | 342 | 391 | 173 | 117 | 3.4 | 229 | 458 | 604 | 439 | 62 | 8 | 20 |
| 34D 0R | 342 | 391 | 173 | 117 | 3.4 | 229 | 458 | 604 | 439 | 62 | 10 | 18 |
| 40A 0 | 361 | 379 | 197 | 114 | 2.5 | 112 | 672 | 852 | 45 | 58 | 11 | 24.5 |
| 40A 0R | 361 | 379 | 197 | 114 | 2.5 | 112 | 672 | 852 | 45 | 60 | 11 | 23.5 |
| 40B 0 | 360 | 377 | 196 | 113 | 2.5 | 24 | 713 | 869 | 78 | 63 | 9 | 25 |
| 40C 0 | 365 | 383 | 199 | 115 | 2.5 | 0 | 645 | 948 | 79 | 67 | 7 | 20 |
| 40C 0R | 365 | 383 | 199 | 115 | 2.5 | 0 | 645 | 948 | 79 | 65.5 | 5.3 | 21.5 |
| 40D 0 | 332 | 348 | 181 | 104 | 2.3 | 232 | 465 | 613 | 446 | 63.5 | 10 | 21.5 |
| 40E 0 | 350 | 367 | 191 | 110 | 2.4 | 114 | 570 | 855 | 171 | 67 | 10 | 24.5 |
| 40E 0R | 350 | 367 | 191 | 110 | 2.4 | 114 | 570 | 855 | 171 | 65 | 12 | 23.5 |
| 40F 0 | 339 | 355 | 185 | 107 | 2.3 | 249 | 373 | 870 | 249 | 66 | 9 | 25 |
| 40G 0 | 350 | 367 | 191 | 110 | 2.4 | 231 | 441 | 734 | 304 | 58 | 10.5 | 24.5 |
| 40G 0R | 350 | 367 | 191 | 110 | 2.4 | 231 | 441 | 734 | 304 | 60 | 9 | 26 |
| 40H 0 | 349 | 366 | 190 | 110 | 2.4 | 214 | 641 | 641 | 214 | 57 | 14 | 27 |
| 40H 0R | 349 | 366 | 190 | 110 | 2.4 | 214 | 641 | 641 | 214 | 57 | 13 | 25 |
| 40I 0 | 335 | 351 | 183 | 105 | 2.3 | 196 | 765 | 589 | 196 | 62.5 | 12 | 22 |
| 40I 0R | 335 | 351 | 183 | 105 | 2.3 | 196 | 765 | 589 | 196 | 63 | 10.5 | 22 |
| 40J 0 | 321 | 337 | 176 | 101 | 2.2 | 469 | 202 | 760 | 358 | 62 | 7.5 | 21.5 |
| 40J 0R | 322 | 338 | 176 | 101 | 2.2 | 468 | 201 | 758 | 357 | 64 | 8.5 | 22 |
| 40K 0 | 349 | 366 | 190 | 110 | 2.4 | 255 | 525 | 691 | 240 | 59 | 11.5 | 24 |
| 40K 0R | 350 | 367 | 191 | 110 | 2.4 | 254 | 523 | 689 | 240 | 60.5 | 10 | 22 |
| 40L 0 | 336 | 352 | 183 | 106 | 2.3 | 418 | 366 | 627 | 334 | 66 | 11 | 19 |
| 46A 0 | 340 | 330 | 197 | 99 | 1.7 | 116 | 694 | 880 | 46 | 58 | 10 | 21 |
| 46B 0 | 350 | 339 | 203 | 102 | 1.8 | 24 | 723 | 882 | 80 | 59.5 | 10 | 17 |
| 46B 0R | 348 | 337 | 201 | 100 | 1.8 | 24 | 727 | 886 | 80 | 56 | 12 | 18.5 |
| 46C 0 | 350 | 339 | 203 | 102 | 1.8 | 0 | 660 | 970 | 81 | 62 | 8 | 23 |
| 46C 0R | 350 | 339 | 203 | 102 | 1.8 | 0 | 660 | 970 | 81 | 61 | 7 | 25 |
| 46D 0 | 327 | 317 | 190 | 95 | 1.6 | 234 | 468 | 618 | 449 | 60 | 11 | 26 |
| 34A + 1 | 411 | 469 | 207 | 141 | 4.1 | 103 | 620 | 785 | 41 | 72 | 9.5 | 15 |
| 34B + 1 | 388 | 443 | 196 | 133 | 3.9 | 23 | 681 | 831 | 75 | 68 | 10 | 23 |
| 34B + 1R | 387 | 442 | 196 | 133 | 3.9 | 23 | 683 | 833 | 75 | 68 | 11.5 | 22 |
| 34C + 1 | 398 | 454 | 201 | 136 | 4 | 0 | 612 | 899 | 75 | 74 | 7 | 12 |
| 34D + 1 | 363 | 415 | 183 | 124 | 3.6 | 222 | 443 | 585 | 425 | 68 | 4 | 10 |
| 40A + 1 | 370 | 388 | 202 | 116 | 2.5 | 110 | 663 | 840 | 44 | 62.5 | 8.8 | 18 |
| 40B + 1 | 370 | 388 | 202 | 116 | 2.5 | 23 | 701 | 856 | 77 | 68 | 7 | 15 |
| 40B + 1R | 372 | 390 | 203 | 117 | 2.5 | 23 | 698 | 852 | 77 | 68 | 6.5 | 16 |
| 40C + 1 | 387 | 406 | 211 | 122 | 2.6 | 0 | 623 | 915 | 76 | 72 | 5 | 14 |
| 40D + 1 | 349 | 366 | 190 | 110 | 2.4 | 227 | 453 | 599 | 435 | 68.5 | 6.3 | 16 |
| 40D + R | 350 | 367 | 191 | 110 | 2.4 | 226 | 452 | 597 | 434 | 69.5 | 5.6 | 16 |
| 40E + 1 | 370 | 388 | 202 | 116 | 2.5 | 111 | 553 | 829 | 166 | 69 | 6.5 | 14 |
| 40F + 1 | 349 | 366 | 190 | 110 | 2.4 | 245 | 368 | 858 | 245 | 66.5 | 9 | 13 |
| 40F + 1R | 351 | 368 | 192 | 111 | 2.4 | 243 | 366 | 854 | 243 | 67 | 8.2 | 14 |
| 40G + 1 | 373 | 391 | 203 | 117 | 2.5 | 223 | 425 | 708 | 293 | 64.5 | 6.8 | 20 |
| 40H + 1 | 369 | 387 | 201 | 116 | 2.5 | 207 | 622 | 622 | 207 | 60 | 12.7 | 21.6 |
| 40I + 1 | 350 | 367 | 191 | 110 | 2.4 | 192 | 748 | 575 | 192 | 71 | 5.8 | 10.1 |
| 40J + 1 | 334 | 350 | 182 | 105 | 2.3 | 460 | 197 | 745 | 350 | 69 | 5.6 | 10.7 |
| 40K + 1 | 370 | 388 | 202 | 116 | 2.5 | 247 | 508 | 668 | 232 | 64 | 9 | 14 |
| 40L + 1 | 349 | 366 | 190 | 110 | 2.4 | 410 | 359 | 615 | 328 | 69 | 6 | 10 |
| 46A + 1R | 349 | 338 | 202 | 101 | 1.8 | 114 | 685 | 868 | 46 | 59.5 | 7 | 15.5 |
| 46A + 1 | 350 | 339 | 203 | 102 | 1.8 | 114 | 683 | 866 | 46 | 62 | 6 | 13.5 |
| 46B + 1 | 369 | 358 | 214 | 107 | 1.9 | 23 | 703 | 857 | 77 | 62 | 9.9 | 10.5 |
| 46C + 1 | 369 | 358 | 214 | 107 | 1.9 | 0 | 641 | 942 | 79 | 65 | 6.2 | 20 |
| 46D + 1 | 347 | 336 | 201 | 101 | 1.7 | 227 | 454 | 599 | 436 | 66 | 6 | 19 |
| 46D + 1R | 348 | 337 | 201 | 100 | 1.8 | 226 | 453 | 597 | 435 | 67 | 6.5 | 18 |
| 34D + 2 | 380 | 434 | 192 | 130 | 3.8 | 216 | 431 | 569 | 414 | 72 | 2.5 | 6 |
| 40A + 2 | 386 | 405 | 210 | 121 | 2.6 | 108 | 646 | 818 | 43 | 66 | 5.5 | 11 |
| 40B + 2 | 387 | 406 | 211 | 122 | 2.6 | 23 | 683 | 833 | 75 | 74 | 2.5 | 6 |
| 40D + 2 | 369 | 387 | 201 | 116 | 2.5 | 219 | 439 | 579 | 421 | 68 | 5 | 13 |
| 40E + 2 | 385 | 404 | 210 | 121 | 2.6 | 108 | 540 | 809 | 162 | 73 | 7 | 10.2 |
| 40F + 2 | 370 | 388 | 202 | 116 | 2.5 | 237 | 355 | 829 | 237 | 68.5 | 5 | 8.2 |
| 40G + 2 | 385 | 404 | 210 | 121 | 2.6 | 218 | 417 | 695 | 288 | 69 | 6.6 | 14 |
| 40H + 2 | 384 | 403 | 209 | 121 | 2.6 | 202 | 607 | 607 | 202 | 74 | 5 | 13 |
| 40I + 2 | 370 | 388 | 202 | 116 | 2.5 | 186 | 725 | 558 | 186 | 69.5 | 5.5 | 8.3 |
| 40J + 2 | 369 | 387 | 201 | 116 | 2.5 | 436 | 187 | 706 | 332 | 75 | 3.7 | 8 |
| 40K + 2 | 385 | 404 | 210 | 121 | 2.6 | 241 | 496 | 652 | 227 | 71.5 | 5.4 | 7 |
| 40L + 2 | 369 | 387 | 201 | 116 | 2.5 | 397 | 348 | 596 | 318 | 68 | 4.6 | 6.3 |
| 46A + 2 | 384 | 372 | 223 | 112 | 1.9 | 108 | 648 | 821 | 43 | 70 | 3 | 5.7 |
| 46B + 2 | 385 | 373 | 223 | 112 | 1.9 | 23 | 685 | 835 | 75 | 66 | 6 | 7 |
| 46C + 2 | 384 | 372 | 223 | 112 | 1.9 | 0 | 626 | 920 | 77 | 70 | 5.1 | 9.5 |
| 46D + 2 | 380 | 368 | 220 | 110 | 1.9 | 216 | 431 | 569 | 414 | 69 | 6.5 | 15 |
| 40D + 3 | 385 | 404 | 210 | 121 | 2.6 | 214 | 428 | 565 | 411 | 72 | 4 | 9.3 |
| 40H + 3 | 406 | 426 | 221 | 128 | 2.8 | 195 | 585 | 585 | 195 | 76 | 3.2 | 8.2 |
| 40I + 3 | 385 | 404 | 210 | 121 | 2.6 | 181 | 708 | 544 | 181 | 76 | 3.6 | 6.6 |
| 40J + 3 | 384 | 403 | 209 | 121 | 2.6 | 425 | 182 | 689 | 324 | 77 | 3.2 | 5.5 |
| 40L + 3 | 384 | 403 | 209 | 121 | 2.6 | 388 | 339 | 582 | 310 | 74 | 2.6 | 5.8 |
References
- Ashisch, D.K.; Verma, S.K. An overview on mixture design of SCC. Struct. Concr. 2019, 20, 371–395. [Google Scholar] [CrossRef]
- De Schutter, G.; Gibbs, J.; Domone, P.; Bartos, P.J.M. Self-Compacting Concrete; Whittles Publishing: Scotland, UK, 2008; ISBN 978-1904445-30-2. [Google Scholar]
- Urban, M. The new conception of SCC composition design: Theoretical background, evaluation, presentation of procedure and examples of usage. Mater. Struct. 2015, 48, 1321–1341. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Z.; Lv, K.X.; Wu, L. A review on mixture design methods for SCC. Constr. Build. Mat. 2015, 84, 387–398. [Google Scholar] [CrossRef]
- Kohler, E.P.; Fowler, D.W.; Foley, E.H.; Rogers, G.J.; Watanachet, S.; Jung, M.J. SCC for Precast Structural Applications: Mixture Proportions, Workability, and Early-Age Hardened Properties. CTR Technical Report; The University of Texas at Austin: Austin, TX, USA, 2008; pp. 51–66. [Google Scholar]
- Trejo, D.; Hendrix, G. Influence of Aggregate and Proportions on Flowing Concrete Characteristics. ACI Mater. J. 2018, 115, 171–180. [Google Scholar] [CrossRef]
- Zuo, W.; Liu, J.; Tian, Q.; Xu, W.; She, W.; Feng, P.; Miao, C. Optimum design of low-binder SCC based on particle packing theories. Constr. Build. Mater. 2018, 163, 938–948. [Google Scholar] [CrossRef]
- Sebaibi, N.; Benzerzour, M.; Sebaibi, Y.; Abriak, N.-E. Composition of SCC using the CPM, the Chinese method and the European standard. Constr. Build. Mater. 2013, 43, 382–388. [Google Scholar] [CrossRef]
- Brouwers, H.J.H.; Radix, H.J. SCC: Theoretical and experimental study. Cem. Concr. Res. 2005, 35, 2116–2136. [Google Scholar] [CrossRef]
- Li, P.; Ran, J.; Nie, D.; Zhang, W. Improvement of mix design method based on paste rheological threshold theory for SCC using different mineral additions in ternary blends of powders. Constr. Build. Mater. 2021, 276, 122194. [Google Scholar] [CrossRef]
- Kheder, G.F.; Al Jadri, R.S. New method for proportioning SCC based on compressive strength requirements. ACI Mater. J. 2010, 107, 490–497. [Google Scholar]
- Kuczyński, W. (Ed.) Budownictwo Betonowe, t. 1 Technologia betonu, cz. 2. Projektowanie betonów. In Concrete Engineering, Part 1 Technology of Concrete; Arkady: Warszawa, Poland, 1972. (In Polish) [Google Scholar]
- Urban, M. Zawartość zaczynu jako główne kryterium projektowania BSZ. (Paste content as a main criterion for SCC composition design). Mater. Bud. 2017, 540, 83–86. [Google Scholar]
- Urban, M. Two limiting lines technique to obtain minimum paste demand of self-consolidating concrete. ACI Mater. J. 2019, 116, 131–138. [Google Scholar] [CrossRef]
- Oh, S.G.; Noguchi, T.; Tomosawa, F. Toward mix design for rheology of SCC. In Proceedings of the PRO 007: 1st International RILEM Symposium, Stockholm, Sweden, 13 September 1999; pp. 361–372. [Google Scholar]
- Marquardt, I.; Vala, J.; Diederichs, U. Optimization of SCC mixes. In Proceedings of the 2nd International Symposium on SCC, Tokyo, Japan, 23–25 October 2001; pp. 295–302. [Google Scholar]
- Xie, Y.; Liu, Y.; Long, G. A mix design method for SCC. In Proceedings of the PRO 054: 5th International RILEM Symposium on Self-Compacting Concrete, Ghent, Belgium, 3–5 September 2007; pp. 189–198. [Google Scholar]
- Su, N.; Hsu, K.-H.; Chai, H.-W. A simple mix design method for SCC. Cem. Concr. Res. 2001, 31, 1799–1807. [Google Scholar] [CrossRef]
- Liu, L.; Lei, M.; Gong, C.; Gan, S.; Yang, Z.; Kang, L.; Jia, C. A robust mix design method for SCC. Constr. Build. Mater. 2022, 352, 128927. [Google Scholar] [CrossRef]
- Sedran, T.; de Larrard, F. Optimization of self-compacting concrete thanks to packing model. In Proceedings of the PRO 007: 1st International RILEM Symposium, Stockholm, Sweden, 13 September 1999; pp. 321–332. [Google Scholar]
- Okamura, H.; Ozawa, K. Mix design method for SCC. Concr. Libr. JSCE 1995, 25, 107–120. [Google Scholar]
- Van, B.K.; Montgomery, D. Mixture proportioning method for SCC HPC with minimum paste volume. In Proceedings of the PRO 007: 1st International RILEM Symposium, Stockholm, Sweden, 13 September 1999; pp. 373–384. [Google Scholar]
- Alyamac, E.; Ince, R. A preliminary concrete mix design for SCC with marble powders. Constr. Build. Mater. 2009, 29, 1201–1210. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B. Mix design method for self-compacting recycled aggregate concrete targeting slump-flow and compressive strength. Constr. Build. Mater. 2023, 404, 133309. [Google Scholar] [CrossRef]
- Nataraja, M.C.; Gadkar, A.; Jogin, G. A simple mix proportioning method to produce SCC based on compressive strength requirement by modification to IS 10262:2009. Indian Concr. J. 2018, 92, 15–23. [Google Scholar]
- Jamroży, Z. Beton i jego technologie. In Concrete and Its Technologies; PWN: Warszawa/Kraków, Poland, 2006; ISBN 83-01-13253-1. (In Polish) [Google Scholar]
- Piasta, J.; Piasta, W.G. Beton zwykły. In Ordinary Concrete; Arkady: Warszawa, Poland, 1994; ISBN 83-213-3667-1. (In Polish) [Google Scholar]
- Śliwiński, J. Beton zwykły–projektowanie i podstawowe właściwości. In Ordinary Concrete–Design and Basic Properties; Polski Cement: Kraków, Poland, 1999; ISBN 83-907640-3-2. (In Polish) [Google Scholar]
- Wang, Q.; Jingjang, H.; Sun, J.; Ho, J. Determining the specific surface area of coarse aggregate based on sieving curve via image-analysis approach. Constr. Build. Mater. 2021, 305, 124728. [Google Scholar] [CrossRef]
- Cepuritis, R.; Garboczi, E.J.; Ferraris, C.F.; Jacobsen, S.; Sorensen, B.E. Measurement of particle size distribution and specific surface area for crushed concrete aggregate fines. Adv. Powder Technol. 2017, 28, 706–720. [Google Scholar]
- Maroof, M.A.; Mahboubi, A.; Noorzad, A. A new method to determine specific surface area and shape coefficient of a cohesionless granular medium. Adv. Powder Technol. 2020, 31, 3038–3049. [Google Scholar] [CrossRef]
- Wong, H.H.C.; Kwan, A.K.H. Packing density of cementitious materials: Part 1—Measurement using a wet packing method. Mater. Struct. 2008, 41, 689–701. [Google Scholar] [CrossRef]
- Kwan, A.K.H.; Li, L.G. Combined effects of water film, paste film and mortar film thicknesses on fresh properties of concrete. Constr. Build. Mater. 2014, 50, 598–608. [Google Scholar] [CrossRef]
- Bucher, R.; Diederich, P.; Mouret, M.; Escadeillas, G.; Cyr, M. SCC using flash-metakaolin: Design method. Mater. Struct. 2015, 48, 1717–1737. [Google Scholar] [CrossRef]
- Barrioulet, M.; Legrand, C. Influence of the interstitial paste on the flow ability of fresh concrete. The importance of water retained by the aggregates. Mater. Struct. 1977, 10, 365–373. [Google Scholar]
- Bolomey, J. Module de Finese d’Abrams et Calcul de L’eau de Gachage des Betons; EMPA: Zurich, Switzerland, 1930. [Google Scholar]
- Stern, O. Zielsiechere Betonbildung; Springer Verlag: Berlin, Germany, 1934. [Google Scholar]
- EN 933-1:2012; Test for Geometrical Properties of Aggregate—Part 1: Determination of Particle Size Distribution—Sieving Method. British Standards Institution: London, UK, 2012.
- Westerholm, M.; Lagerblad, B.; Silfwerbrand, J.; Forssberg, E. Influence of fine aggregate characteristics on the rheological properties of mortars. Cem. Concr. Compos. 2008, 30, 274–282. [Google Scholar] [CrossRef]
- Bengtsson, M.; Evertsson, C.M. Measuring characteristics of aggregate material from vertical shaft impact crushers. Miner. Eng. 2006, 19, 1479–1486. [Google Scholar] [CrossRef]
- De Schutter, G.; Poppe, A.-M. Quantification of the water demand of sand in mortar. Constr. Build. Mater. 2004, 18, 517–521. [Google Scholar] [CrossRef]
- EN 206:2013; Concrete—Specification, Performance, Production and Conformity. British Standards Institution: London, UK, 2013.
- EN 12350 -8: 2019; Testing Fresh Concrete—Part 8: Self-Compacting Concrete—Slump-Flow Test. British Standards Institution: London, UK, 2019.
- EN 12350 -9: 2012; Testing Fresh Concrete—Part 9: Self-Compacting Concrete—V-Funnel Test. British Standards Institution: London, UK, 2012.

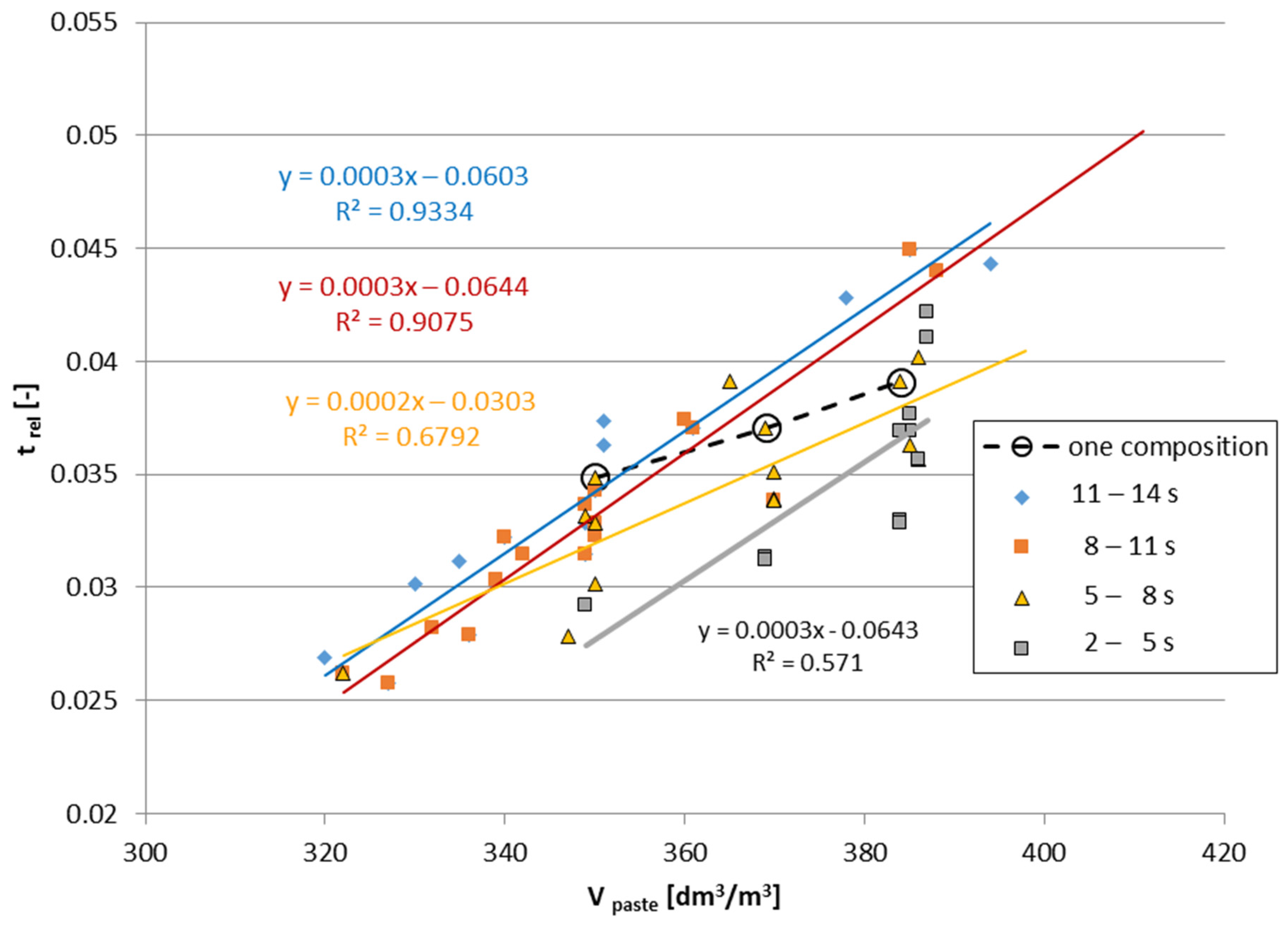
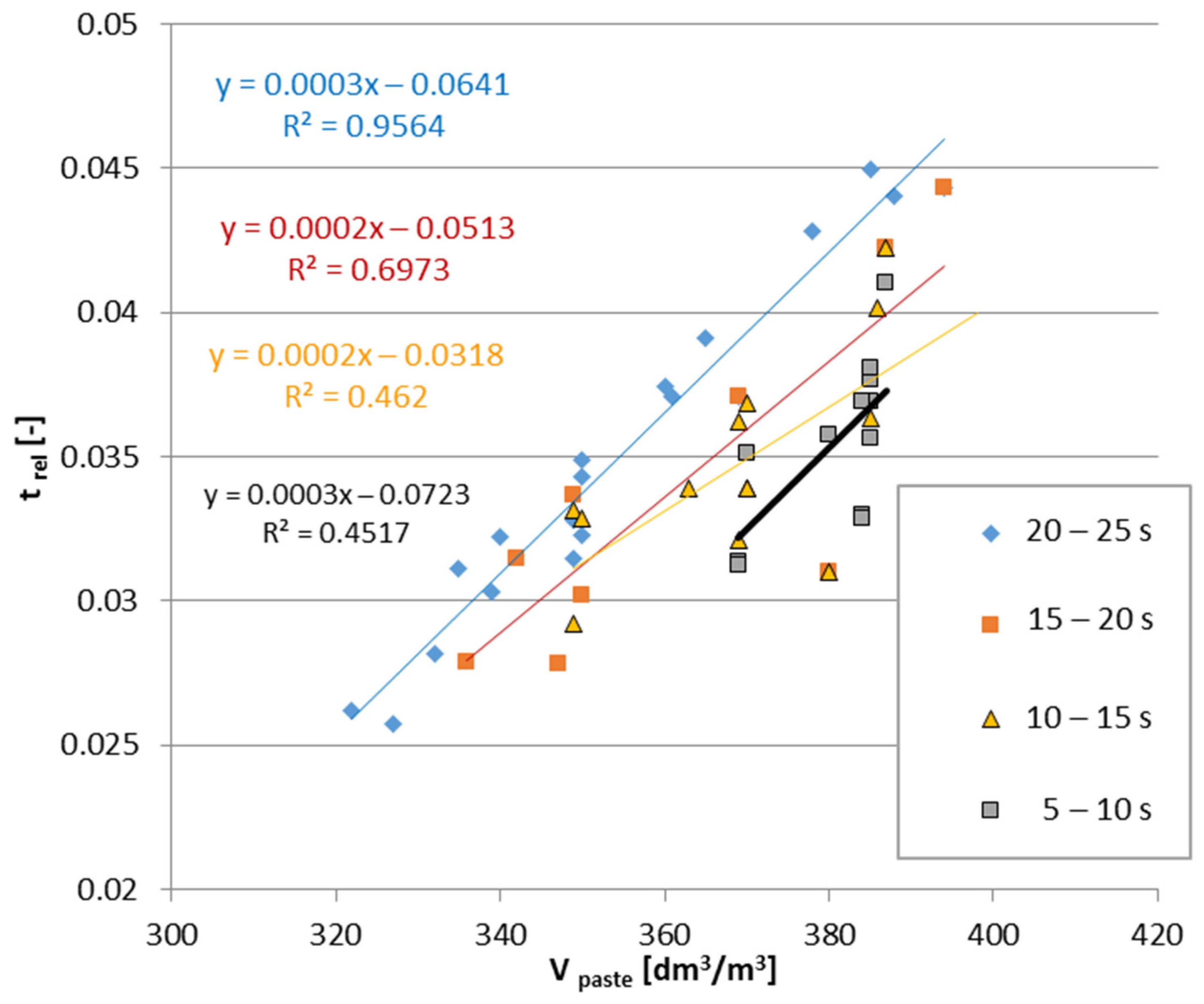
| Parameter | Value | ||||||
|---|---|---|---|---|---|---|---|
| ad/c | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| D0 stab [cm] | 34 | 36 | 37 | 38 | 38 | 38 | 37 |
| Parameter | Paste | ||
|---|---|---|---|
| w/b | 0.34 | 0.40 | 0.46 |
| w/bkor | 0.313 | 0.365 | 0.417 |
| sp [% b] | 0.67 | 0.5 | 0.4 |
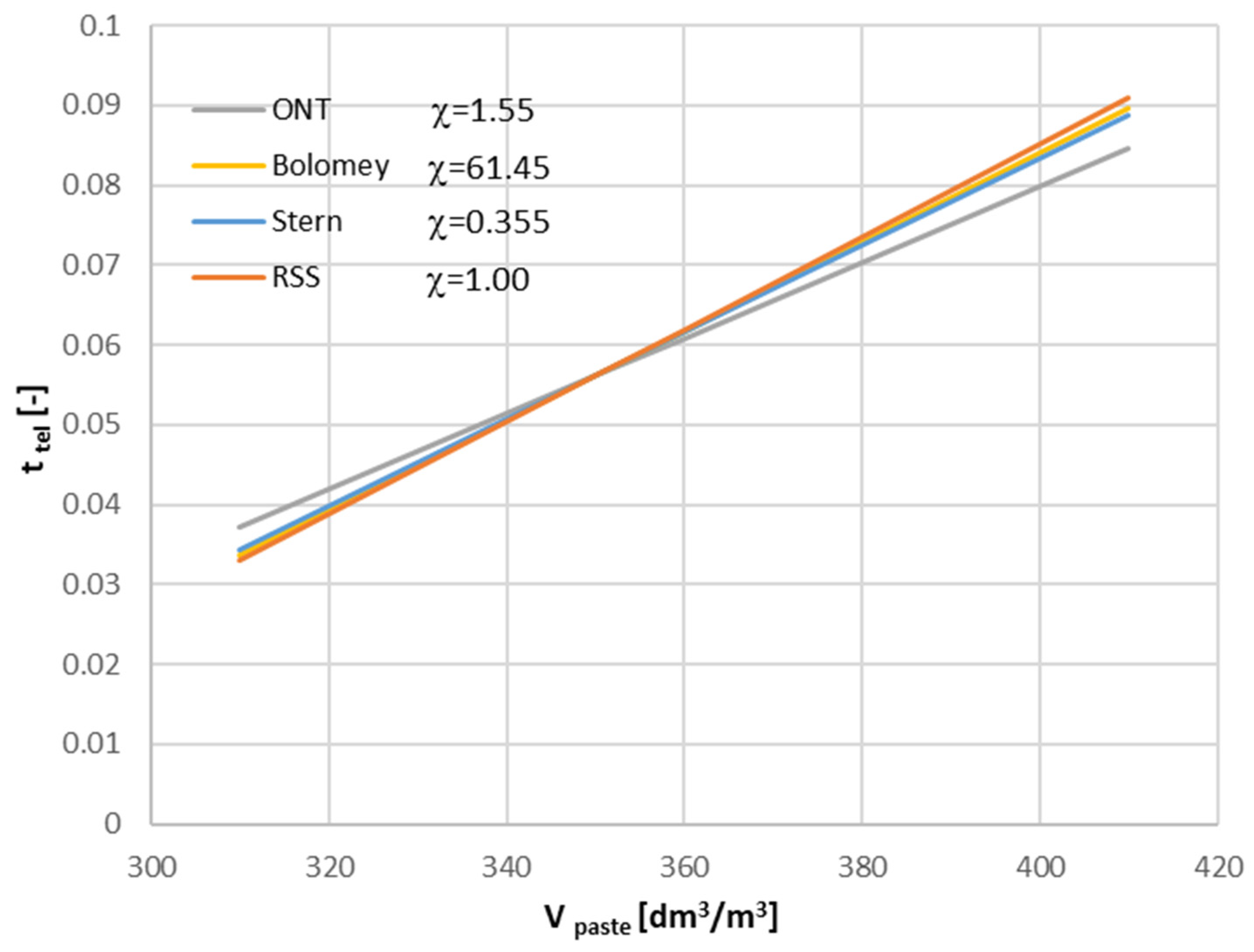
| Shape of Grains/ Aggregate Type | χO | χR | χS | χB | trel (Vp = 350) |
|---|---|---|---|---|---|
| Ideal spheres | 1.66 | 1.07 | 0.38 | 65.80 | 0.0561 |
| Rounded grains (river origin) | 1.55 | 1.00 | 0.355 | 61.45 | 0.0524 |
| Coarse aggregate partly crushed (grit) + river sand | 1.50 | 0.97 | 0.34 | 59.45 | 0.0507 |
| Crushed coarse aggregate + river sand | 1.43 | 0.92 | 0.325 | 56.70 | 0.0484 |
| Only crushed grains | 1.33 | 0.86 | 0.305 | 52.725 | 0.0449 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urban, M. Water Demand (or Specific Surface) of Aggregate as a Dominating Factor for SCC Composition Design. Appl. Sci. 2024, 14, 11108. https://doi.org/10.3390/app142311108
Urban M. Water Demand (or Specific Surface) of Aggregate as a Dominating Factor for SCC Composition Design. Applied Sciences. 2024; 14(23):11108. https://doi.org/10.3390/app142311108
Chicago/Turabian StyleUrban, Maciej. 2024. "Water Demand (or Specific Surface) of Aggregate as a Dominating Factor for SCC Composition Design" Applied Sciences 14, no. 23: 11108. https://doi.org/10.3390/app142311108
APA StyleUrban, M. (2024). Water Demand (or Specific Surface) of Aggregate as a Dominating Factor for SCC Composition Design. Applied Sciences, 14(23), 11108. https://doi.org/10.3390/app142311108